Tuning the electronic properties of monolayer and bilayer PtSe₂via strain engineering

Abstract

The recently synthesized monolayer PtSe₂ belongs to the class of two-dimensional transition metal dichalcogenide (TMDC) materials (Nano Lett., 2015, 15, 4013). Based on first-principles calculations, we show that the band gaps of monolayer and bilayer PtSe₂ can be tuned over a wide range via strain engineering. Both isotropic and uniaxial strains are investigated. For bilayer PtSe₂, the vertical out-of-plane strain is also considered. In most cases, the strain can reduce the band gap except for the bilayer PtSe₂ under the isotropic strain (ε ≤ 4%) for which the band gap can be slightly enlarged. Importantly, the monolayer can be transformed from the indirect-gap to the direct-gap semiconductor at the compressive strain of ε_y = −8%. Moreover, the bilayer can undergo the semiconductor-to-metal (S–M) transition at a critical vertical strain due to the chemical interaction (p orbital coupling) between the Se atoms of the two opposite layers. Overall, the ability to modulate the band gap of monolayer and bilayer PtSe₂ over an appreciable range of strains opens up new opportunities for their applications in nanoelectronic devices.

---

Introduction

Two dimensional (2D) graphene has attracted intensive research interest over the past ten years^1–5 due to its novel properties such as unconventional quantum Hall effect, superior electronic conductivity, and high mechanical strength. However, the zero-band gap apparently hinders the wide application of graphene in optoelectronic nanodevices. This situation has led to extensive efforts devoted to the exploration of other 2D materials with finite band gaps such as phosphorene,^6–10 BN,¹¹ transition-metal dichalcogenides (TMDCs),^12–17 and transition-metal trichalcogenides (TMTCs).^18,19 The general formula of 2D TMDCs is MX₂, where M is a transition metal in groups 4–10 while X is a chalcogen. Depending on the combination of metal and chalcogen, bulk TMDCs display diverse properties, ranging from insulators (HfS₂), semiconductors (MoS₂, WS₂), semimetals (WTe₂, TiSe₂), metals (NbS₂, VSe₂) to superconductors (NbSe₂, TaS₂).²⁰ Low-dimensional counterparts of bulk MX₂ may preserve certain bulk properties but can also bring new characteristics due to quantum confinement effects.^21–23 For example, low-dimensional TMDCs can offer new opportunities for research in many fields, such as in catalysis, energy storage, sensing and electronic devices.

To date, most experimental studies of 2D TMDCs have been mainly focused on semiconducting MX₂ with group 6 transition metals (Mo, W), e.g., MoS₂, MoSe₂, and WSe₂. Recently, many other monolayer TMDCs beyond MoX₂ and WX₂ have been shown to exhibit unique physical or chemical properties as well. Specifically, Wang et al. reported a newly synthesized PtSe₂ monolayer.²⁴ Unlike the conventional method for the fabrication of MX₂ through exfoliation or chemical vapor deposition, the synthesis of PtSe₂ can be achieved via the direct deposition of Se atoms on a Pt substrate. Through angle-resolved photoemission spectroscopy (ARPES) and band structure calculations, it is found that monolayer PtSe₂ is a semiconductor, contrary to the semimetal properties of its bulk counterpart. Moreover, the photo-degradation experiment suggests that monolayer PtSe₂ can serve as a visible light-driven photocatalyst.

Many previous theoretical studies^25–28 have shown that the electronic structures of 2D TMDCs can be notably modified by external electric fields or by in-plane strains. In this study, we show the strain-dependent electronic properties of monolayer and bilayer PtSe₂ on the basis of the first-principles computations. Both isotropic and uniaxial in-plane strains are considered. In addition, for the bilayer PtSe₂, we also considered normal compressive strain (out-of-plane vertical strain). We found that monolayer PtSe₂ can maintain its indirect semiconducting character under strain except for the uniaxial compressive strain beyond −8% along the y direction (see below for definition), which induce a transition from the indirect semiconductor to the direct one. In general, the strains can reduce the band gap of monolayer PtSe₂ regardless of the magnitude and direction of the strain. Under an isotropic in-plane strain, the tensile strain appears to be more effective for reducing the band gap of monolayer PtSe₂ than the compressive strain except for the case of 8% tensile strain. On the other hand, the trend is opposite in the case of uniaxial strain. For the bilayer PtSe₂, the isotropic in-plane compressive strain can enlarge the band gap first and then reduce the band gap, while the isotropic tensile strain reduces the band gap continuously. Hence, the strain-engineering behavior of monolayer or bilayer PtSe₂ is very different from that of MoS₂.²⁵ Furthermore, the reversible semiconductor-to-metal transition is predicted for the PtSe₂ bilayer under normal compressive strain in the critical range of 0.4 < ε ≤ 0.45. The transition stems from the p orbital coupling of the inner Se atoms of the two layers.

Computational methods

All the calculations are performed using the density functional theory within the generalized gradient approximation, as implemented in the Vienna Ab initio Simulation Package (VASP) 5.3.3 code.²⁹ The all-electron plane-wave basis set within the projector augmented wave (PAW) method is adopted with 5d⁹6s¹ and 4s²4p⁴ treated as valence electrons for Pt and Se, respectively, and the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional is selected. The cutoff energy for expansion of the wavefunction into plane waves is set to be 360 eV, and a k-point set of 25 × 25 × 1 is used for total-energy computation and a dense k-point set of 40 × 40 × 1 is used for electronic structure computation. The conjugate-gradient scheme is employed for the geometric relaxation until the force on each atom is less than 0.01 eV Å⁻¹, and the total energy change is less than 1 × 10⁻⁵ eV. Sufficient vacuum space (≥15 Å) is used along the z direction (normal to the 2D sheet) to avoid spurious interaction among the periodic images. The van der Waals interaction originating from dynamical correlations between fluctuating charge distributions cannot be effectively described by the PBE functional. Hence, we incorporate the van der Waals interactions by adding a semi-empirical dispersion potential (D) to the conventional Kohn–Sham DFT energy, through a pair-wise force field following the Grimme's DFT-D3 method.³⁰

Results and discussion

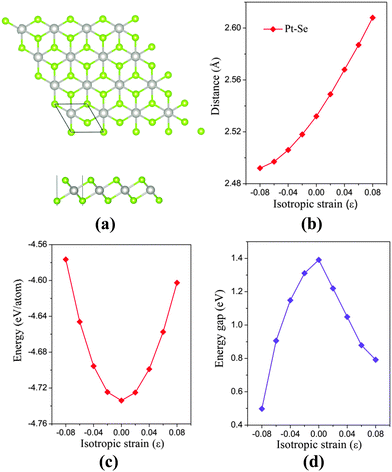
The bulk PtSe₂ belongs to the D³_3d (P3̄m1) space group of the trigonal system.³¹ As shown in Fig. 1(a), the monolayer PtSe₂ can be viewed as cleaved from the (0001) surface of the bulk PtSe₂, where one Pt atom layer is sandwiched between two Se layers. The optimized lattice parameter is 3.75 Å, very close to the experimental value of 3.70 Å.²⁴ The Pt–Se bond length and the total energy per atom of PtSe₂versus isotropic in-plane strain are examined. As shown in Fig. 1(b), the Pt–Se bond length increases almost linearly with the increasing tensile strain, but shows a gentle decrease with the increasing compressive strain. The bond length alteration surely correlates with the energy change. As shown in Fig. 1(c), the isotropic strain shows asymmetric quadratic dependence on the total energy per atom. The energy is −4.576 eV per atom at the compressive strain ε = −8%, but is −4.602 eV per atom at the tensile strain of ε = 8%. Therefore, from the energetic point of view, the tensile strain is easier to implement than the compressive strain.

Fig. 1 (a) Top and side views of monolayer PtSe₂. The green and gray balls represent Pt and Se atoms, respectively. (b) Pt–Se bond length versus isotropic in-plane strain. (c) Total energy per atom of the monolayer PtSe₂versus isotropic strain. (d) Computed band gap of monolayer PtSe₂versus isotropic strain.

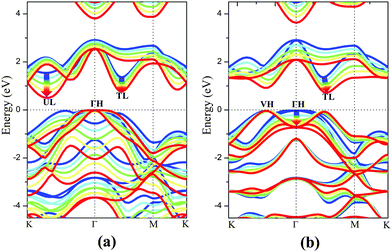
The electronic structure of monolayer PtSe₂ under the isotropic strain is shown in Fig. 2(a) and (b). The strain-free monolayer PtSe₂ is an indirect semiconductor with a band gap of 1.39 eV, consistent with the previously predicted value of 1.41 eV (PBE).³² The valence band maximum (VBM) and conduction band minimum (CBM) are located at ΓH and TL points (see Fig. 2(a) and (b)), respectively. Upon increasing the compressive strain, the VBM remains at the ΓH point, while the CBM is shifted downward (Fig. 2(a)). When the compressive strain reaches −4%, the UL point exhibits lower energy than the TL point, leading to the relocation of the CBM. In contrast, as shown in Fig. 2(b), the tensile strain can significantly lower the position of ΓH point so that the VBM is shifted from the ΓH to the VH point whose energy remains unchanged, regardless of the tensile strain. In addition, the CBM (TL point) is shifted downward with the increasing tensile strain. In general, the band gap of the monolayer PtSe₂ can be reduced by either the compressive or the tensile strain. As plotted in Fig. 1(d), the band gap of monolayer PtSe₂ decreases linearly from 1.39 to 0.88 eV with the increasing tensile strain up to ε = 6%, and then to 0.79 eV at ε = 8%. However, the band gap of monolayer PtSe₂ is correlated parabolically with the compressive strain, decreasing from 1.39 to 0.5 eV at ε = −8%. Moreover, it is known that semi-local DFT methods (such as the PBE functional) can markedly over-delocalize electrons. To address this issue, we performed an independent benchmark computation based on the DFT+U method as it can give more reasonable electronic properties than the semi-local DFT methods.^33,34 We examined several values of U and found for U = 4 eV, the relaxed lattice constant of the monolayer PtSe₂ is 3.725 Å, which is very close to the experimental value of 3.70 Å. The computed band structures of monolayer PtSe₂ under the isotropic strain ε = −8%, 0% and 8% are plotted as shown in Fig. S1 (ESI†). It can be seen that the semiconducting character remains unchanged although the computed band gap is lowered by 0.1–0.4 eV for U = 4 eV.

Fig. 2 Computed band structures of monolayer PtSe₂ under (a) isotropic compressive, and (b) isotropic tensile strain. The bands with different colors denote the band structures under different strain, i.e., blue (ε = 0%), cyan (ε = ± 2%), green (ε = ± 4%), yellow (ε = ± 6%) and red (ε = ± 8%). The Fermi level is located at 0 eV.

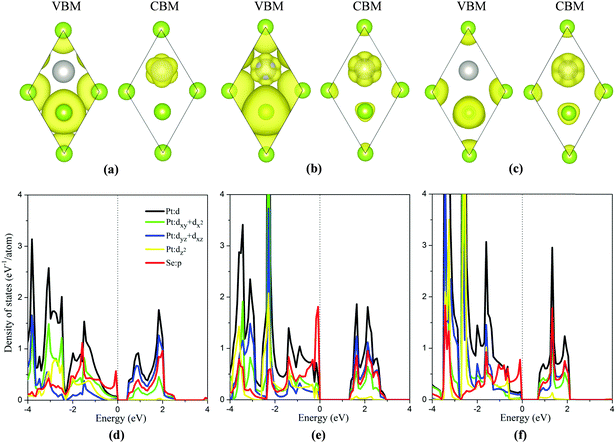
To analyze the strain dependent electronic properties, the partial density of state (PDOS) and partial charge densities corresponding to the VBM and the CBM of the monolayer PtSe₂ at the isotropic strain of −8%, 0% and 8%, respectively, are plotted as shown in Fig. 3(a)–(f). As shown in Fig. 3(b) and (e), for the strain-free monolayer, the VBM (ΓH point) is mainly contributed by Se p orbitals and the coupling between the Pt d orbitals (mainly d_xy + d_x²) and Se p orbitals. Yet the CBM (TL point) is mainly contributed by Pt d_yz + d_xz orbitals and, to less extent, by Se p orbitals and Pt d_xy + d_x² orbitals. At the isotropic strain, as shown in Fig. 3(a), (c), (d) and (f), the VBM is mainly contributed by Se p orbitals and also slightly by Se-p and Pt-d coupling, different from the strain-free case. The isotropic strain significantly lowers the coupling between the Pt d orbitals and Se p orbitals near the VBM. However, the electronic component of the CBM under strain somewhat differs from that without strain. Fig. 2(a) and (b) clearly shows that, under isotropic strain, the change of band gap of monolayer PtSe₂ is mainly induced by the location change of CBM. As shown in Fig. 3(f), at a tensile strain of 8%, the CBM (TL point) is mainly contributed by the Pt d_xy + d_x² orbitals, Se p orbitals and somewhat by Pt d_yz + d_xz orbitals, apparently different from the case of zero strain. We therefore conclude that the electronic component of CBM is changed by the tensile strain, causing the descent of CBM energy and band gap reduction for the monolayer PtSe₂. As for the monolayer PtSe₂ under compressive strain, Fig. 3(d) shows that the electronic component of CBM is little changed, and is still contributed mainly by the Pt d_yz + d_xz orbitals. But the repulsion of charge density of the d_yz + d_xz orbitals can be enhanced under compressive strain, thereby lowering the CBM (UL point) and resulting in band gap reduction for the monolayer PtSe₂.

Fig. 3 Partial charge densities corresponding to the VBM and CBM, and partial densities of states (PDOS) of the monolayer PtSe₂ under isotropic strain of −8% (a and d), 0% (b and e) and 8% (c and f), respectively. Due to the specific symmetry, the contribution from d_xy is the same as that from d_x², and the contribution from d_yz is the same as that from d_xz. The isosurface value is 0.001.

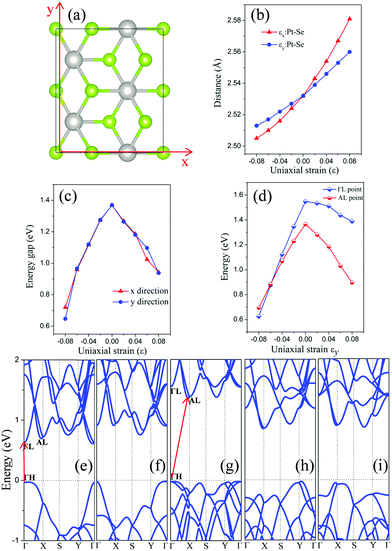
We have also considered uniaxial strain along either the x or the y direction (see Fig. 4(a)). The computed electronic structure of the monolayer PtSe₂ based on the rectangle supercell under the uniaxial strain are shown in Fig. 4(e)–(i) and in the ESI,† Fig. S2. At zero strain, the VBM is located at the ΓH point and the CBM at the AL point (Fig. 4(g)). As in the case of the isotropic strain, the uniaxial strain along either the x- or the y-direction can significantly lower the energy of CBM, but makes little change to the VBM (less than 50 meV), thereby reducing the band gap of the PtSe₂ monolayer. Moreover, the uniaxial compressive strain along either the x- or the y-direction does not change the VBM position (always at the Γ point), similar to the case of isotropic strain. Interestingly, the monolayer PtSe₂ undergoes the indirect-to-direct transition at the compressive strain of ε_y = −8% along the y direction, contrary to the isotropic strain. However, such a transition is not seen with the strain in the x direction even with a compressive strain of up to ε_x = −8%. In Fig. 4(d), the change in the energy value of AL and ΓL points (with respect to the Fermi level) is plotted as a function of the strain ε_y. It can be seen that the energy difference (E_AL − E_ΓL) decreases almost linearly with the increasing compressive strain ε_y and becomes negative as ε_y is beyond −6%, causing an indirect-to-direct transition. Hence, we conclude that the indirect-to-direct transition can be attributed in part to the difference in strain dependence of E_AL and E_ΓL. The curves of band gap of monolayer PtSe₂versus uniaxial strain are plotted as shown in Fig. 4(c). Notably, the uniaxial strain along x- and y-directions results in exactly the same modulation to the band gap in the strain range of −6% (0.96 eV gap) to 4% (1.19 eV gap) and to strain 8% (0.94 eV gap). A slight difference is seen at the uniaxial strain of −8% and 6%, where the band gap E_g (ε_x = −8%) is 0.72 eV, E_g (ε_y = −8%) is 0.65 eV, E_g (ε_x = 6%) is 1.03 eV, and E_g (ε_y = 6%) is 1.10 eV. Fig. 4(b) shows the plot of Pt–Se bond length versus uniaxial strain, where the slope of the two curves is quite different. As a result, the monolayer PtSe₂ shows direct semiconducting character at ε_y = −8% (Fig. 4(e)), but indirect semiconducting character at ε_x = −8% (Fig. 4(f)). In general, the uniaxial strain can modulate the band gap of the monolayer PtSe₂ but less strongly compared to the isotropic strain. The specific uniaxial strain (ε_y = −8%), however, can transform the monolayer PtSe₂ from an indirect semiconductor to a direct one.

Fig. 4 (a) A rectangle supercell of monolayer PtSe₂ where x- and y-directions are defined. (b and c) Pt–Se bond length and band gap of monolayer PtSe₂versus uniaxial strain, respectively. (d) The energy of the AL and ΓL points with respect to the Fermi level versus ε_y. Computed band structure of monolayer PtSe₂ with strain values of (e) ε_y = −8%, (f) ε_x = −8%, (g) ε = 0%, (h) ε_x = 8% and (i) ε_y = 8%. The Fermi level is set to be 0 eV.

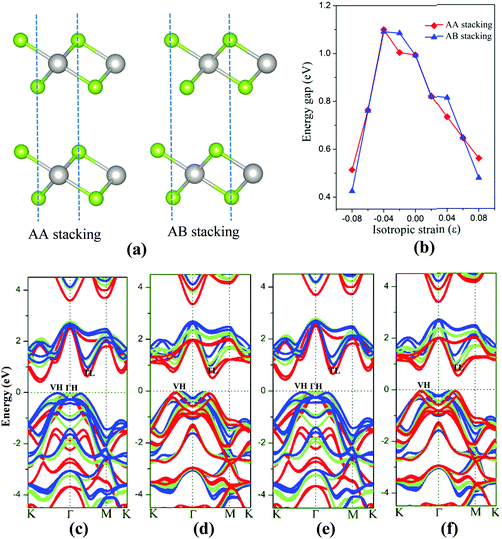
The 2D bilayer materials may possess different electronic properties from the monolayer counterpart due in part to the weak van der Waals interlayer interaction. First, the electronic structures of bilayer PtSe₂ under the isotropic strain are examined. Two different stacking patterns, namely, the AA-stacking and AB-stacking, are shown in Fig. 5(a). Our DFT computations show that both types of PtSe₂ bilayers are almost degenerate in energy and also exhibit similar band structures. As shown in Fig. 5(c) and (e), both PtSe₂ bilayers are indirect semiconductors with a band gap of 0.99 eV. The VBM and CBM are located at VH and TL points (see Fig. 5(c) and (e)), respectively. With the compressive strain, the position of VBM changes from the VH to the ΓH point but with small energy variation (<50 meV), while the CBM is kept at the TL point and moves up slightly for ε ≤ 4% and then downward to the Fermi level. As a result, the band gap of PtSe₂ bilayers firstly increases for ε ≤ 4%, from 0.99 to 1.09 eV (see Fig. 5(b)) and then decreases for ε ≥ 4%, from 1.09 to 0.43 or 0.51 eV (Fig. 5(b)). Fig. 5(d) and (f) shows the tensile strain-dependent band structures of both PtSe₂ bilayers, where one can see that the position of VBM moves slightly toward the K point with little energy change while the CBM is shifted toward the Fermi level. Therefore, the tensile strain reduces the band gap of PtSe₂ bilayers from 0.99 eV to 0.48 or 0.56 eV (Fig. 5(b)).

Fig. 5 (a) Atomic structure of two kinds of PtSe₂ bilayers. (b) Band gap of PtSe₂ bilayers versus isotropic strain. Computed band structure of AA stacking bilayers under (c) ε = −8 to 0%, (d) ε = 0–8% and AB stacking bilayers under (e) ε = −8 to 0%, (f) ε = 0–8%. The bands with different colors represent the band structures under various strain values, i.e., blue (ε = 0%), green (ε = ±4%) and red (ε = ±8%). The Fermi level is located at 0 eV.

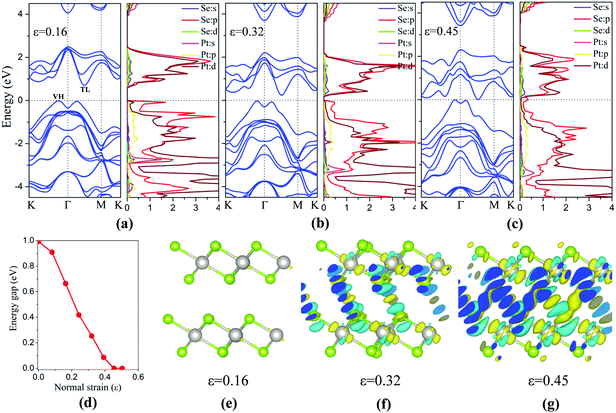
Besides the in-plane strain, the electronic structures of the bilayer can also be modulated by applying an out-of-plane vertical strain. Taking the AB-stacking PtSe₂ bilayer as an example, the vertical compressive strain (VCS) is defined as ε = (d₀ − d)/d₀ where d₀ and d are the equilibrium and constrained interlayer distance, respectively. In the constrained configuration, the positions of the Pt atoms remain unchanged while other atoms are relaxed. The band structures of the bilayer under different VCS values are shown in Fig. 6(a)–(c), where it can be seen that the double degeneracy is lifted gradually due to the increasing interlayer chemical interaction as the interlayer distance decreases. The VBM is still located at the VH point with little change in energy, while the CBM (TL point) is shifted towards the Fermi level as the VCS increases, thereby reducing the band gap (Fig. 6(d)). It is interesting that the semiconductor-to-metal (S–M) transition occurs when the VBM and CBM crosses the Fermi level at the critical VCS (0.4 < ε ≤ 0.45; see Fig. 6(c)). To assess the experimental feasibility of the S–M transition, we estimated the required pressure as done previously by others.^35,36 The applied pressure (P) is calculated from the energy cost per unit cell in reducing the interlayer distance by Δd = d₀ − d, that is, P = (E₀ − E)/((d₀ − d) × A), where A is the area of unit cell, and E and E₀ are the energies of strained and unstrained bilayers. As a result, the estimated transition pressure is between 1.2 and 3.6 GPa.

Fig. 6 (a–c) Computed band structure and partial densities of states of PtSe₂ bilayer under three different VCS values, with the corresponding differential charge densities plotted in (e–g). The Fermi level is located at 0 eV. (d) Band gap of bilayer versus normal strain.

To gain more insights into the electronic properties of the bilayer under VCS, the PDOSs are computed (Fig. 6(a)–(c)). With the increasing VCS, the contribution to the CBM from Pt d and Se p orbitals increases, while that to the VBM from Se p orbitals decreases. From Fig. 6(c), it is seen that density of states near the Fermi level is mostly contributed by Se p orbitals, giving the metal character of the bilayer. This is due to the enhanced interlayer interaction that leads to the p orbital interaction of the inner Se atoms of the two opposite layers. This conclusion can be further supported through redistribution of the charges, computed by taking the difference between the total charge of the bilayer and the two isolated PtSe₂ layers (see Fig. 6(e)–(g)). The redistribution of the charge mainly arises around the inner Se atoms of the two layers. As expected, for a low VCS (ε ≤ 0.16), almost no charge redistribution is observed. With the increasing VCS, the degree of charge redistribution also increases, indicating enhanced Se–Se interaction which can lead to the S–M transition.

Conclusion

In conclusion, we investigate band-gap engineering of semiconducting PtSe₂ monolayer and bilayer through applied isotropic, uniaxial, as well as vertical strains based on the first-principles calculations. Our electronic structure computations demonstrate that the electronic properties of PtSe₂ monolayer and bilayer are dependent on both the magnitude and direction of the strain. As a result, the band gap can be tuned over a wide range. In addition, the PtSe₂ monolayer can transform from an indirect semiconductor into a direct one when the compressive strain ε_y = −8%, which may be exploited for special applications in nanoelectronics. Furthermore, a reversible semiconductor-to-metal transition is predicted for the PtSe₂ bilayer under critical VCSs (0.4 < ε ≤ 0.45, 1.2 GPa < P ≤ 3.6 GPa). This stems from the p orbital coupling of the inner Se atoms of the two layers. The possibility of reversibly tuning the band gap by about 1.0 eV through application of different strains will render the 2D PtSe₂ a potential candidate for optoelectronic applications.

Acknowledgements

P. F. Li and L. Li contributed equally to this work. This work was supported by USTC Qian-ren B Summer Research Fund and by the University of Nebraska's Holland Computing Center.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2014, 306, 666.
2. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197.
3. K. S. Novoselov, E. McCann, S. V. Morozov, V. I. Falko, M. I. Katsnelson, U. Zeitler, D. Jiang, F. Schedin and A. K. Geim, Nat. Phys., 2006, 2, 177.
4. Y. B. Zhang, Y. W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201.
5. Q. Tang, Z. Zhou and Z. Chen, Nanoscale, 2013, 5, 4541.
6. L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372.
7. J. Dai and X. C. Zeng, J. Phys. Chem. Lett., 2014, 5, 1289.
8. Y. H. Xu, J. Dai and X. C. Zeng, J. Phys. Chem. Lett., 2015, 6, 1996.
9. M. H. Wu, H. Fu, L. Zhou, K. L. Yao and X. C. Zeng, Nano Lett., 2015, 15, 3557.
10. H. Guo, N. Lu, J. Dai, X. J. Wu and X. C. Zeng, J. Phys. Chem. C, 2014, 118, 14051.
11. D. Pacile, J. C. Meyer, C. O. Girit and A. Zettl, Appl. Phys. Lett., 2008, 92, 133107.
12. B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147.
13. Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699.
14. H. S. S. Ramakrishna Matte, A. Gomathi, A. K. Manna, D. J. Late, R. Datta, S. K. Patiand and C. N. R. Rao, Angew. Chem., Int. Ed., 2010, 49, 4059.
15. J. Feng, L. Peng, C. Wu, X. Sun, S. Hu, C. Lin, J. Dai, J. Yang and Y. Xie, Adv. Mater., 2012, 24, 1969.
16. P. J. Jeon, S. Min, J. S. Kim, S. R. A. Raza, K. Choi, H. S. Lee, Y. T. Lee, D. K. Hwang, H. J. Choi and S. Im, J. Mater. Chem. C, 2015, 3, 2751.
17. H. Fang, S. Chuang, T. C. Chang, K. Takei, T. Takahashi and A. Javey, Nano Lett., 2012, 12, 3788.
18. J. Dai and X. C. Zeng, Angew. Chem., Int. Ed., 2015, 54, 7572.
19. M. Li, J. Dai and X. C. Zeng, Nanoscale, 2015, 7, 15385.
20. M. Chhowalla, H. S. Shin, G. Eda, L. Li, K. P. Loh and H. Zhang, Nat. Chem., 2013, 5, 263.
21. T. Cao, G. Wang, W. Han, H. Ye, C. Zhu, J. Shi, Q. Niu, P. Tan, E. Wang, B. Liu and J. Feng, Nat. Commun., 2012, 3, 887.
22. H. Zeng, J. Dai, W. Yao, D. Xiao and X. Cui, Nat. Nanotechnol., 2012, 7, 490.
23. K. F. Mak, K. He, J. Shan and T. F. Heinz, Nat. Nanotechnol., 2012, 7, 494.
24. Y. Wang, L. Li, W. Yao, S. Song, J. T. Sun, J. Pan, X. Ren, C. Li, E. Okunishi, Y. Q. Wang, E. Wang, Y. Shao, Y. Y. Zhang, H. Yang, E. F. Schwier, H. Iwasawa, K. Shimada, M. Taniguchi, Z. Cheng, S. Zhou, S. Du, S. J. Pennycook, S. T. Pantelides and H. J. Gao, Nano Lett., 2015, 15, 4013.
25. P. Lu, X. Wu, W. Guo and X. C. Zeng, Phys. Chem. Chem. Phys., 2012, 14, 13035.
26. N. Lu, H. Guo, L. Li, J. Dai, L. Wang, W. Mei, X. Wu and X. C. Zeng, Nanoscale, 2014, 6, 2879.
27. A. Ramasubramaniam, D. Naveh and E. Towe, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205325.
28. P. Johari and V. B. Shenoy, ACS Nano, 2012, 6, 5449.
29. G. Kresse and J. Furthmuller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
30. S. Grimme, J. Antony, S. Ehrlich and S. Krieg, J. Chem. Phys., 2010, 132, 154104.
31. G. Y. Guo and W. Y. Liang, J. Phys. C: Solid State Phys., 1986, 19, 995.
32. H. L. Zhuang and R. G. Hennig, J. Phys. Chem. C, 2013, 117, 20440.
33. V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767.
34. P. Guss, M. E. Foster, B. M. Wong, F. P. Doty, K. Shah, M. R. Squillante, U. Shirwadkar, R. Hawrami, J. Tower and D. Yuan, J. Appl. Phys., 2014, 115, 034908.
35. L. Kou, B. Yan, F. Hu, S. Wu, T. O. Wehling, C. Felser, C. Chen and T. Frauenheim, Nano Lett., 2013, 13, 6251.
36. L. Kou, S. Wu, C. Felser, T. Frauenheim, C. Chen and B. Yan, ACS Nano, 2014, 8, 10448.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c6tc00130k

---