Electrically conductive thermoplastic elastomer nanocomposites at ultralow graphene loading levels for strain sensor applications†
Hu
Liu
a,
Yilong
Li
a,
Kun
Dai
*a,
Guoqiang
Zheng
a,
Chuntai
Liu
*a,
Changyu
Shen
a,
Xingru
Yan
b,
Jiang
Guo
b and
Zhanhu
Guo
*b
aSchool of Materials Science and Engineering, The Key Laboratory of Material Processing and Mold of Ministry of Education, Zhengzhou University, Zhengzhou, Henan 450001, P. R. China. E-mail: kundai@zzu.edu.cn; ctliu@zzu.edu.cn; Tel: +86-371-63887969
bIntegrated Composites Laboratory (ICL), Department of Chemical & Biomolecular Engineering, University of Tennessee, Knoxville, TN 37996, USA. E-mail: zguo10@utk.edu
First published on 24th November 2015
Abstract
An electrically conductive ultralow percolation threshold of 0.1 wt% graphene was observed in the thermoplastic polyurethane (TPU) nanocomposites. The homogeneously dispersed graphene effectively enhanced the mechanical properties of TPU significantly at a low graphene loading of 0.2 wt%. These nanocomposites were subjected to cyclic loading to investigate the influences of graphene loading, strain amplitude and strain rate on the strain sensing performances. The two dimensional graphene and the flexible TPU matrix were found to endow these nanocomposites with a wide range of strain sensitivity (gauge factor ranging from 0.78 for TPU with 0.6 wt% graphene at the strain rate of 0.1 min−1 to 17.7 for TPU with 0.2 wt% graphene at the strain rate of 0.3 min−1) and good sensing stability for different strain patterns. In addition, these nanocomposites demonstrated good recoverability and reproducibility after stabilization by cyclic loading. An analytical model based on tunneling theory was used to simulate the resistance response to strain under different strain rates. The change in the number of conductive pathways and tunneling distance under strain was responsible for the observed resistance-strain behaviors. This study provides guidelines for the fabrication of graphene based polymer strain sensors.
1. Introduction
Strain sensors based on the resistance change upon exposing to mechanical deformation have drawn great interest owing to their widespread applications including health monitoring,1–3 movement detection4–6 and structural health monitoring.7,8 High sensitivity, good reproducibility, a wide test scope under different mechanical conditions, and good processability are imperatively demanded for satisfactory strain sensing. Recently, conductive polymer composite (CPC) based strain sensors have attracted attention due to their quick response in the form of electrical resistance variation when subjected to tensile or compressive strain.9–24 CPC based strain sensors are usually fabricated by dispersing one or more electrically conductive fillers in the insulating polymeric matrix. The selection of a polymer matrix with favorable stretchability and excellent processability is important for strain sensing. However, some CPCs including carbon nanotubes (CNTs)/epoxy,25,26 CNTs/poly(propylene) (PP),20 and carbon black (CB)/PP27 can only be used in a small strain range due to the limited stretchability of the matrix and poor filler–polymer interaction. Though strain sensors with rubber28 serving as the polymer matrix have demonstrated nice stretchability, poor processability is a challenge. Thermoplastic polyurethane (TPU), a kind of elastomer, has been used in fabricating strain sensors with higher detection limits. For example, Fan et al. reported the stable conductive CNTs/TPU fibers with high reversibility for monitoring large strains up to 400%.29 Deng et al. prepared two CNTs/TPU CPCs by extrusion10 and solution processes,16 respectively, both of which showed good strain sensing ability for a maximum strain of 30%.Meanwhile, the morphology of conductive fillers, which affects the geometry of the conductive network significantly, was discovered to play a key role in the strain sensing of CPCs. Nanoscale materials such as nanowires, nanotubes and graphene have been used as promising fillers to fabricate CPCs for strain sensors. In particular, graphene, a single layer of carbon atoms with a two dimensional structure, has been considered as a good candidate owing to its large specific surface area, intriguing low electrical resistivity, and excellent thermal and mechanical properties.30–32 Compared with other nanofillers, graphene possesses more extraordinary features when used for strain sensors. In other words, the superior mechanical flexibility, high restorability and carrier mobility enable its application in highly sensitive strain sensors with good reproducibility. The large specific surface area makes it capable of providing larger sensing area per unit volume when it is subjected to strain. Its high quality crystal lattice with a low electrical noise makes it more stable than other fillers. Herein, graphene nanosheets used as strain sensors have been reported, but the very limited strain amplitude becomes an obstacle for practical applications. For example, Zhao et al. reported the piezoresistive sensitivity of nanographene films under strain amplitude less than 0.5%.33 Hempel et al. also demonstrated percolative networks of graphene layers with high strain sensitivity under strain amplitude less than 2%.34 Structural design has been used as a strategy to improve the stretchability of graphene-based strain sensors. Bae et al. adopted reactive ion etching and stamping techniques to fabricate transparent graphene-based strain sensors, and a non-monotonic resistance change against tensile strain up to 7.1% was observed.35 Samad et al. also reported a resistance increase of 120% upon a strain of 30% in the graphene foam composites.36 Due to its complication and high-cost, structural design still cannot meet the real demand for graphene-based strain sensors.
In addition, an ultralow percolation threshold,37 a crucial aspect in fabricating CPCs, can make composites having good mechanical properties, good processability and low cost under the premise of good electrical conductivity. Due to the good electrical conductivity of graphene, a series of graphene-based CPCs with low percolation threshold could be reached. For example, Stankovich et al. reported the graphene/polystyrene composites with a percolation threshold of 0.1 vol%.38 Polyurethane acrylate based composites with a percolation threshold of 0.07 vol% were also prepared.39 Based on the discussions, it is both scientifically interesting and necessary to fabricate graphene/TPU based strain sensors with a low percolation threshold through a simple preparation process.
In this study, conductive graphene/TPU nanocomposites with ultralow electrical percolation threshold were prepared by a combination of co-coagulation and the compression molding technique and the feasibility for a strain sensor was evaluated. The gauge factor was introduced to study the strain sensitivity of CPCs. The effects of filler loading, strain amplitude and strain rate on the strain sensing behaviors were studied by cyclic loading. An analytical model based on tunneling theory was applied to disclose the strain sensing mechanism under different strain rates.
2. Experimental
2.1 Materials and chemicals
Aqueous suspension with 0.45 wt% graphene was purchased from Chengdu Organic Chemicals Co. Ltd, China. The total oxygen content was 3.59 wt% and polyvinyl pyrrolidone was used as the dispersing agent. Polyester-based thermoplastic polyurethane (TPU) (Elastollan 1185A) with a density of 1.12 g cm−3 and a melt flow index of 17.5 g/10 min (215 °C, 10 kg) was obtained from BASF Co. Ltd. It was dried at 80 °C under vacuum for 12 h before usage. Dimethylformamide (DMF) and methanol were supplied by Zhiyuan Reagent Co., Ltd, Tianjin, China. All of the organic solvents were used as received without any further treatment.2.2 Preparation of graphene/TPU nanocomposites
The TPU nanocomposites with different loading levels of graphene were fabricated by the co-coagulation plus compression molding technique (Fig. 1). Briefly, 2.0 g of TPU was dissolved in 50 mL of DMF at 40 °C by vigorous stirring for 30 min. The required amount of aqueous graphene dispersion was mixed with 15 mL of DMF and treated under ultrasonication (SCIENTZ-II, 285W, Ningbo Scientz Biotechnology Co. Ltd, China) for 10 min to disperse the graphene homogenously. Subsequently, the TPU/DMF and graphene/DMF were mixed together and sonicated for an additional 30 min. The mixture was then added dropwise into 300 mL of methanol under strong stirring to obtain the flocculate of graphene/TPU. The obtained flocculate was filtered, dried at 80 °C under vacuum for 20 h, and hot pressed at 210 °C for 10 min under a pressure of 15 MPa. The thickness of the nanocomposite sample was 0.5 mm. The neat TPU control sample was also fabricated in the same manner for comparison. The obtained nanocomposites were denoted as TPU-xG, where x represents the mass loading of graphene, and G is the abbreviation of graphene. For example, TPU-0.2G represents the TPU-graphene nanocomposites containing 0.2 wt% graphene.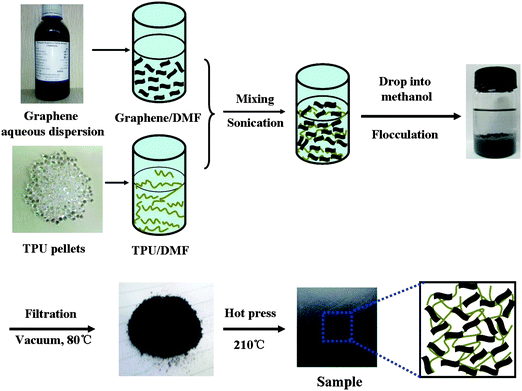 | ||
| Fig. 1 Schemes of the process for the fabrication of graphene/TPU composites by the co-coagulation plus compression molding technique. | ||
2.3 Characterization
Atom force microscopy (AFM) images of graphene after sonication in DMF were taken in the non-tapping mode on a VEECO Nanoscope IV instrument. The samples were prepared by spin-coating graphene solution on a mica plate and drying in a vacuum oven.X-ray diffraction (XRD) was recorded on a Rigaku Ultima IV X-ray Diffractometer, equipped with a Cu tube and a scintillation detector beam. The samples were scanned with a scan step of 0.02° in the range of 2° to 40°.
Fourier transform infrared spectroscopy (FT-IR) was conducted on a Nicolet Nexus 870 instrument in attenuated total reflection (ATR) mode. All the spectra were obtained in the range from 500 to 4000 cm−1.
Differential scanning calorimetry (DSC) analysis was carried out using a MDSC 2920 instrument. The samples were heated to 220 °C at a heating rate of 10 °C min−1 and held isothermally for 5 min to eliminate the effect of thermal history. Then the samples were cooled down to −70 °C and reheated to 220 °C at the same rate. All the tests were performed under the protection of N2 at a flow rate of 20 mL min−1.
Field emission scanning electron microscopy (FE-SEM) measurement was performed using a JEOL JSM-7500F instrument. The specimens were prepared by immersing into liquid nitrogen for an hour and breaking quickly. The fracture surfaces were then coated with a thin layer of platinum for better imaging.
Transmission electron microscopy (TEM) measurement was performed using a JEOL JEM-1230 instrument at an acceleration voltage of 90 kV. The specimen was mixed with epoxy resin and cured at 70 °C for 24 h in a vacuum. Ultra-thin sections (∼100 nm) were prepared using a Leica UC-7 ultramicrotome with a diamond knife at −90 °C.
The mechanical analyses were conducted on an electrical universal testing machine with a 100 N load cell (UTM2203, Shenzhen Suns Technology Stock Co. Ltd, China). The rectangular strips with dimensions of 40 × 4 × 0.5 mm3 were cut off from the films for the mechanical performance test. The specimens were tested with a strain rate of 0.1 min−1 using an initial grip-to-grip separation of 16 mm under ambient conditions. At least five strips were tested for each sample.
As for the volume resistance, the composite films were cut into strips with dimensions of 40 × 10 × 0.5 mm3 and measured using a precision digital resistor (Model TH2683, Changzhou Tonghui Electronics Co. Ltd, China) under a constant voltage of 10 V. For each sample, at least five strips were tested. The volume conductivity was calculated by using eqn (1):
| σ = L/RS | (1) |
For cyclic loading, the rectangular strip with dimensions of 40 × 10 × 0.5 mm3 was clamped with a pair of aluminum electrodes and a gage length of 20 mm was created. Silver paste was used to ensure good contact between the electrode and the strip. The precision digital resistor and the universal testing machine were coupled with a computer to record the strain sensing behaviors upon cyclic loading online (Fig. S1, ESI†).
3. Results and discussion
3.1 Morphologies of graphene dispersed in DMF
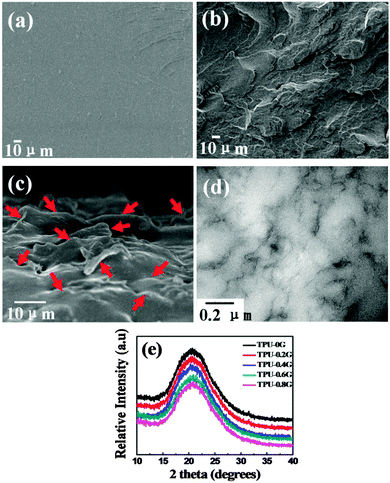
In this study, the graphene aqueous dispersion was dispersed in DMF to observe the morphology of graphene before use. As shown in Fig. S2 (ESI†), graphene is uniformly distributed in DMF without obvious graphene aggregates. In the AFM topography (Fig. 2a), the thickness of graphene is observed to be about 0.96 nm, showing a full exfoliation of graphene after the ultrasonic dispersion in DMF.38,40,41 The FE-SEM image (Fig. 2b) also identifies the presence of individual graphene sheets, indicating again that graphene has been fully exfoliated.3.2 Interfacial bonding between graphene and TPU
The hydrogen bonding, the strongest van der Waals interaction in the absence of direct chemical bonding between the filler and the matrix, usually affects the properties of the CPCs greatly.42,43 The FT-IR spectrum of neat TPU shows the basic functional groups of TPU, Fig. S3 (ESI†). The peaks at 3324 and 1074 cm−1 correspond to the N–H and C–O–C stretching vibrations, respectively. The peaks at 2955 and 2870 cm−1 are assigned to the alkene–CH stretching vibrations. Two additional peaks at 1730 and 1700 cm−1 represent the free and hydrogen-bonded C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups, respectively. Taking a closer view of the dashed square, Fig. 3(a), blue shifts of the N–H group are observed in the FT-IR spectra after being decorated with graphene, i.e. TPU-0.8G exhibits a blue shift from 3324 to 3331 cm−1 of the N–H group. It verifies that the H-bonding interaction exists between the N–H groups of TPU and the remaining oxygenated groups of graphene, showing an interaction between TPU and graphene.
O groups, respectively. Taking a closer view of the dashed square, Fig. 3(a), blue shifts of the N–H group are observed in the FT-IR spectra after being decorated with graphene, i.e. TPU-0.8G exhibits a blue shift from 3324 to 3331 cm−1 of the N–H group. It verifies that the H-bonding interaction exists between the N–H groups of TPU and the remaining oxygenated groups of graphene, showing an interaction between TPU and graphene.
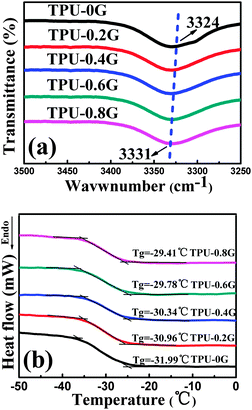 | ||
| Fig. 3 (a) Blue shifts of the N–H group in the FT-IR spectra and (b) DSC curves of neat TPU and its graphene nanocomposites with different graphene contents. | ||
From the DSC curves in Fig. 3(b), the glass transition temperature (Tg) increases from −31.99 °C for TPU to −29.41 °C for TPU-0.8G. The enhancement of Tg shows that the TPU chains were indeed constrained by the H-bonding interaction, similar effects were also demonstrated in other reported systems such as single-walled carbon-nanotube reinforced poly(vinyl alcohol) nanocomposites44 and graphene reinforced poly(vinyl alcohol) nanocomposites.45
3.3 Morphology characterization of graphene in TPU
In the fabrication process, graphene is prone to aggregate and restack due to the van der Waals force between graphene layers. This aggregation and restacking can reduce the mechanical properties and electrical conductivity significantly. The uniform dispersion of graphene is thus crucial to obtain high-quality nanocomposites. The dispersion quality of graphene in TPU was detected by FE-SEM. Fig. 4 shows the morphology of the freeze-fractured surface of neat TPU and TPU-0.2G. In contrast to the smooth surface of TPU (Fig. 4a), the incorporation of graphene resulted in a much rough surface (Fig. 4b). The flake-like morphology is the graphene sheets wrapped by the TPU matrix, which is attributed to the good adhesion between them. To better observe the dispersion state of graphene, the freeze-fractured surface of the composites was immersed in DMF to etch the TPU matrix. In Fig. 4c, lots of laminar structures are observed to be uniformly distributed in the cross-section of the nanocomposites, although some TPU nanocomposites are still adhered to the graphene sheets. TEM was used to further characterize the dispersion state of graphene in the TPU matrix (Fig. 4d), it can be seen that most graphene are obscure due to its very thin nature, whereas parts of them are clear, probably attributed to the stacked structure of graphene itself. In addition, graphene with a wrinkle structure was finely distributed through the TPU matrix without obvious aggregation. This indicates that the graphene sheets have been homogeneously dispersed in the TPU matrix.The dispersion of graphene in TPU was further characterized by XRD. Fig. 4e displays the XRD patterns of TPU and its nanocomposites with different graphene loadings. The pure TPU exhibits a broad typical diffraction peak ranging from 15° to 28° and centered at 20.5°, which can be assigned to a low degree of crystallinity of the polymer.37,46 The graphene/TPU nanocomposites with different graphene loadings only show the diffraction peak of pure TPU. It is generally believed that the XRD pattern would present a broad diffraction peak at 24° if the graphene layers are restacked during the preparation.47 However, in the present paper, the disappearance of this peak reveals that graphene has been dispersed as individual graphene sheets in the TPU matrix.48,49 This result is similar to Kang's research about graphene oxide/carboxylated acrylonitrile butadiene rubber nanocomposites.42
3.4 Mechanical properties of graphene reinforced TPU
Fig. 5(a) shows the typical stress–strain curves of TPU and its nanocomposites with different graphene loadings. The mechanical properties were observed to be significantly improved in the graphene/TPU nanocomposites as compared with those of pure TPU. As shown in Fig. 5(b), the specific strength and specific elongation of the nanocomposites with a graphene loading of only 0.2 wt% were improved by about 124% and 100%, respectively, compared to those of pure TPU. The large improvement of mechanical properties is attributed to the homogeneous dispersion of graphene in the TPU matrix, and the hydrogen bonding between graphene and the TPU matrix. In addition, as shown in Fig. 3(b), good interfacial adhesion and no extraction of graphene were observed from the cross-section of broken composites, causing an efficient stress transfer between the two components.50,51 The unexpected toughening effect of the addition of graphene is similar to the graphene/poly(ethylene succinate) nanocomposite system.47 However, the specific strength and the specific elongation of nanocomposites were decreased gradually with further increasing the graphene loading. The reason is that the deformation degree of the TPU molecular chains under loading was limited at a higher graphene content, causing the reduction in fracture strain.52 In addition, the specific modulus is increased obviously upon increasing the graphene loading. For example, the specific modulus is increased by about 263% from ∼10.1 MPa for pure TPU to ∼36.8 MPa for the nanocomposites with a graphene loading of 0.8 wt%.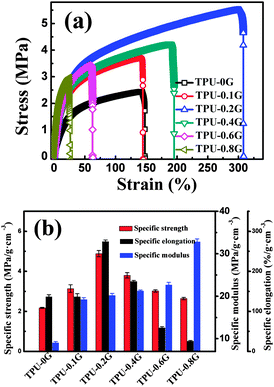 | ||
| Fig. 5 (a) Representative stress–strain curves of TPU and its composites with different graphene contents; and (b) specific mechanical properties of TPU composites as a function of graphene loading. | ||
3.5 Strain sensing behavior of the graphene reinforced TPU nanocomposites
| σ = σ0(m − mc)t | (2) |
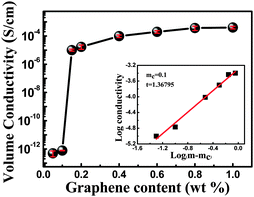 | ||
| Fig. 6 Volume conductivity as a function of graphene loading; the percolation threshold is determined by eqn (2) (mc = 0.1 wt%). The inset shows the log conductivity vs. log (m − mc). | ||
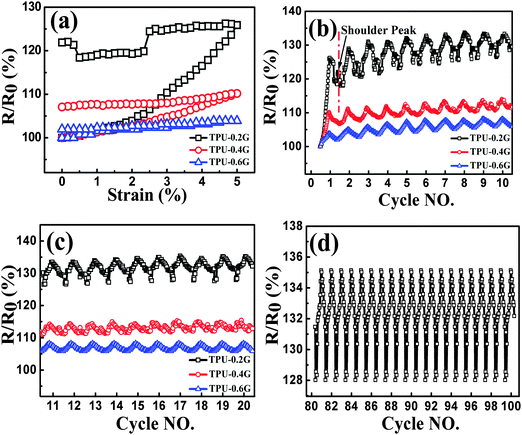
During the cyclic loading as shown in Fig. 7b and c, the nanocomposites exhibiting different trends during the unloading process, good recoverability and reproducibility after stabilization by cyclic loading were obtained. Taking a closer view of these three bands, for TPU-0.2G, the ‘shoulder peak’ as mentioned above arises from the first cycle, the peak appears after the 5th cycle for TPU-0.4G. No peak is observed for the TPU-0.6G sample. The observed different ‘shoulder peak’ phenomena can be ascribed to the distinct formation state of the conductive network. For TPU-0.6G, the graphene conductive network is not easy to be destructed with an easier reconstruction of the conductive paths in the nanocomposites with high loadings, causing different competitive processes compared with that of TPU-0.2G and TPU-0.4G. In addition, about 100 cycles were conducted for TPU-0.2G, the strain sensing behavior still showed good recoverability and reproducibility until cycles 81–100 (Fig. 7d); no fracture and electrical shot were found during the cyclic loading test, showing great potential for practical applications.
The strain gauge factor (GF, defined as (ΔR/R0)/ε, ΔR is the instantaneous change in resistance, and ε is the strain) is applied to evaluate the strain sensitivity of CPCs.13 At the strain of 5%, the GFs of TPU-0.2G, TPU-0.4G and TPU-0.6G are 5.2, 2.0 and 0.78, respectively. It is evident that the CPCs with lower loading of graphene have higher sensitivity. Interestingly, upon increasing the cycle number, (R/R0)5% (the R/R0 value at the strain of 5%) increases firstly and then tends to be constant, exhibiting good reproducibility after stabilization by cyclic loading (Fig. S4, ESI†). This trend is opposite to the CNTs/TPU system.16 The main reason is that part of graphene wrinkles or crimps in the cyclic loading process, leading to the decreased number of plane–plane contact.57 The intrinsically entangled structure of CNTs is beneficial to avoid the damage of conductive paths and leads to a better conductive network under the rearrangement of the CNT network during the cyclic loading process.
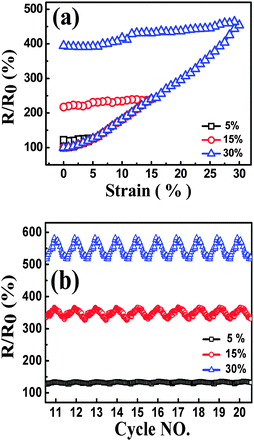 | ||
| Fig. 8 Resistance-strain behavior of TPU-0.2G, up to different strain amplitudes at the strain rate of 0.1 min−1, during the 1st cycle (a) and cyclic loading (cycles 11–20) (b). | ||
Then the strain-dependent response as a function of strain amplitude under cyclic loading is discussed, and the samples also show good recoverability and reproducibility after stabilization by cyclic loading when the samples were subjected to different strain amplitudes, Fig. 8(b). Before reaching the stable state, the responsive curve tends to be stable from the 6th cycle for the sample with the strain amplitude of 30%, the 10th cycle for the sample with the strain amplitude of 15%, and the 15th cycle for the sample with the strain amplitude of 5% (Fig. S5, ESI†). The phenomenon of a stable state appearing at different points can be explained as follows: during the loading–unloading process, the molecular chains were rearranged, inducing a rearrangement of graphene sheets in the nanocomposites under the cyclic strain; the imperfect graphene conductive network was broken and a stable one was rebuilt. After several cycles, the breakdown and reformation of the graphene networks approached an equilibrium state gradually. Under the same strain rate, for the test with larger strain amplitude, the conductive network needs longer time to achieve auto-regulation in a single cycle. Thus, R/R0 with larger strain amplitude during cyclic strain shows a reproducible phenomenon in fewer cycles.
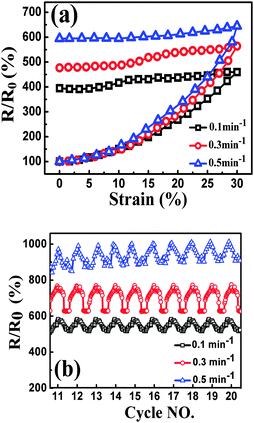 | ||
| Fig. 9 Resistance-strain behavior of TPU-0.2G, up to 30% strain at different strain rates, during the 1st cycle (a) and cyclic loading (cycles 11–20) (b). | ||
Similar to the strain sensing behavior under different graphene content and strain amplitude, good recoverability and reproducibility after stabilization by cyclic loading were achieved under different strain rates during cyclic loading, Fig. 9b. At a higher strain rate of 0.5 min−1, a conspicuous ‘shoulder peak’ is observed to exist during the unloading procedure. However, it is virtually absent for the test at a rate of 0.1 min−1 (Fig. S7, ESI†). As mentioned above, the ‘shoulder peak’ is the result of destruction and reconstruction of conductive paths. At the same strain amplitude, a lower strain rate means a longer time to accomplish the course of destruction and reconstruction of conductive paths. The sample with a low strain rate has enough time to reach an equilibrium state, thus no evident ‘shoulder peak’ is observed. Some researchers have used modeling to understand the strain sensing mechanism of the CPCs, but the mechanism under different strain rates has scarcely been investigated. Here, a model based on tunneling theory is carried out to understand the mechanism of strain sensing under different strain rates.62,63 The resistance of CPCs can be calculated using eqn (3) and (4):
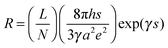 | (3) |
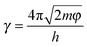 | (4) |
When stress is applied on the CPCs, the resistance will be altered because of particle separation. In other words, the inter-particle distance changes linearly and proportionally upon increasing the strain from s0 to s. The s can be expressed as follows:
| s = s0(1 + Cε) | (5) |
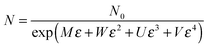 | (6) |
The substitution of eqn (5) and (6) into eqn (3) yields:
| R = B(1 + Cε)exp[A + (2M + AC)ε + 2Wε2 + 2Uε2 + 2Vε2] | (7) |
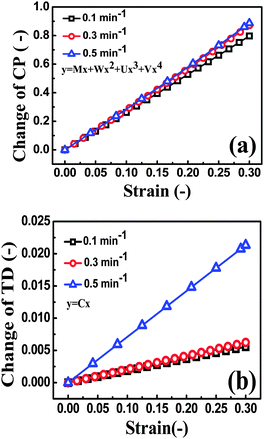
As shown in Fig. 10, a good agreement between the experimental and theoretical data was obtained. It means that eqn (7), derived from tunneling theory, can describe the experimental data quite well (Table S1, ESI†). The change in conductive pathways (CP) and tunneling distance (TD) against strain is calculated and plotted in Fig. 11a and b. At the strain rate of 0.5 min−1, the change of CP is observed to be bigger than that at 0.3 and 0.1 min−1 during the loading process. According to eqn (6), the number of CP at the strain rate of 0.5 min−1 is decreased faster than that at 0.3 and 0.1 min−1. The TD at the strain rate of 0.5 min−1 increases at a higher rate than that at 0.3 and 0.1 min−1. The above two aspects give evidence that higher sensitivity is obtained at the strain rate of 0.5 min−1.
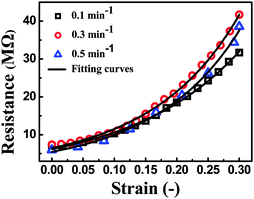 | ||
| Fig. 10 Experimental (dots) and theoretical (solid lines) data of resistance as a function of strain. | ||
3.6 Mechanism of graphene/TPU nanocomposites as strain sensors
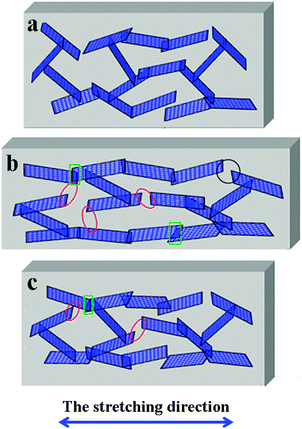
To better understand the observed phenomenon, a scheme about the change of graphene networks in a single cycle is provided to illustrate the mechanism. The original graphene conductive network is shown in Fig. 12a, the plane–plane contact of graphene conductive networks is formed in TPU. When the CPCs are stretched (Fig. 12b), due to the superior mechanical flexibility of graphene, it stretches and wriggles with the TPU macromolecular chains, resulting in the breakage of conductive pathways (red ellipse) and the increase of the tunneling distance between graphene (black circle). At the same time, some new conductive pathways (green rectangle) are reconstructed. The destruction of the conductive network is predominant in the loading process, so an increasing R/R0 is observed. During the unloading process, some damaged conductive networks return to their original states, the R/R0 of samples is decreased, while some are irreversible (Fig. 12c) due to the hysteresis effect of the composites, leading to an irreversible resistance at the end of every cycle. In the following cycles, a gradual increase in the maximum R/R0 is observed, which is caused by the formation of irreversible destruction of graphene networks under cyclic strain. After several cycles, the formation and destruction of conductive graphene networks reach a balance, thus the CPCs show a good strain sensing reproducibility after stabilization by cyclic loading.4. Conclusions
Graphene/TPU CPCs were prepared using the co-coagulation plus compression molding technique. The graphene sheets, which have a good H-bonding interaction with the TPU matrix, have been distributed in the TPU matrix homogeneously. Due to the good dispersion of graphene in the TPU matrix, an ultralow percolation threshold of 0.1 wt% was achieved. A significant enhancement of the mechanical properties of graphene/TPU nanocomposites was also obtained. The tensile strength and the elongation at break were enhanced by about 124% and 100%, respectively, by the addition of only 0.2 wt% graphene. The graphene/TPU nanocomposites subjected to cyclic loading were examined to investigate the influences of graphene content, strain amplitude and strain rate on the strain sensing behavior. The results showed that the imperfect conductive network of CPC with a lower graphene content, which is easy to be destructed under loading, caused higher sensitivity; the competition between the destruction and reconstruction of the conductive paths created an interesting ‘shoulder peak’ during the unloading process. Larger strain amplitude generated higher sensitivity and better reproducibility due to the serious damage and longer time to realize the auto-regulation of graphene conductive paths during cyclic loading. A higher strain rate induced higher sensitivity because the CPCs suffered larger stress, causing more destruction of the graphene conductive network. An analytical model derived from tunneling theory was used to fit the resistance response to strain under different strain rates. The change in the number of conductive pathways and tunneling distance under strain was responsible for the resistance-strain sensing behaviors. In other words, the CPCs exhibit good sensitivity and sensing stability for different strain patterns and possess good recoverability and reproducibility after stabilization by cyclic loading, showing good discernment in strain sensing. Due to the fascinating strain sensing behaviors, the CPCs composed of the TPU matrix and graphene have great potential for applications as strain sensors to meet various demands in detecting various external environment stimuli.Acknowledgements
The authors gratefully acknowledge the financial support of this work by National Natural Science Foundation of China-Henan Talents Fostering joint Funds (Contract Number: U1204507), Special Science Foundation for Excellent Youth Scholars of Zhengzhou University (Contract Number: 1421320041), National Natural Science Foundation of China (Contract Number: 11572290) and National Program on Key Basic Research Project (973 Program, Contract Number: 2012CB025903). Z. Guo appreciates the start-up fund from the University of Tennessee Knoxville.References
- M. Li, H. Li, W. Zhong, Q. Zhao and D. Wang, ACS Appl. Mater. Interfaces, 2014, 6, 1313–1319 CAS.
- F. Carpi and D. D. Rossi, IEEE Trans. Inf. Technol. Biomed., 2005, 9, 295–318 CrossRef PubMed.
- A. Lymberis and S. Olsson, Telemed. J. E Health, 2003, 9, 379–386 CrossRef PubMed.
- D. D. L. Chung, Carbon, 2012, 50, 3342–3353 CrossRef CAS.
- C. Yan, J. Wang, W. Kang, M. Cui, X. Wang, C. Y. Foo, K. J. Chee and P. S. Lee, Adv. Mater., 2014, 26, 2022–2027 CrossRef CAS PubMed.
- T. Yamada, Y. Hayamizu, Y. Yamamoto, Y. Yomogida, A. Izadi-Najafabadi, D. N. Futaba and K. Hata, Nat. Nanotechnol., 2011, 6, 296–301 CrossRef CAS PubMed.
- H. Zhao, Y. Zhang, P. D. Bradford, Q. Zhou, Q. Jia, F.-G. Yuan and Y. Zhu, Nanotechnology, 2010, 21, 305502 CrossRef PubMed.
- I. Kang, M. J. Schulz, J. H. Kim, V. Shanov and D. L. Shi, Smart Mater. Struct., 2006, 15, 737–748 CrossRef CAS.
- G. T. Pham, Y.-B. Park, Z. Liang, C. Zhang and B. Wang, Composites, Part B, 2008, 39, 209–216 CrossRef.
- E. Bilotti, R. Zhang, H. Deng, M. Baxendale and T. Peijs, J. Mater. Chem., 2010, 20, 9449–9455 RSC.
- D. Ponnamma, K. K. Sadasivuni, M. Strankowski, Q. Guo and S. Thomas, Soft Matter, 2013, 9, 10343–10353 RSC.
- L. Lin, S. Liu, Q. Zhang, X. Li, M. Ji, H. Deng and Q. Fu, ACS Appl. Mater. Interfaces, 2013, 5, 5815–5824 CAS.
- J. R. Bautista-Quijano, F. Aviles and J. V. Cauich-Rodriguez, J. Appl. Polym. Sci., 2013, 130, 375–382 CrossRef CAS.
- P. Costa, A. Ferreira, V. Sencadas, J. C. Viana and S. Lanceros-Méndez, Sens. Actuators, A, 2013, 201, 458–467 CrossRef CAS.
- P. Slobodian, P. Riha and P. Saha, Carbon, 2012, 50, 3446–3453 CrossRef CAS.
- R. Zhang, H. Deng, R. Valenca, J. H. Jin, Q. Fu, E. Bilotti and T. Peijs, Compos. Sci. Technol., 2013, 74, 1–5 CrossRef CAS.
- S. M. A. Darbandi, M. Nouri and J. Mokhtari, Fibers Polym., 2012, 13, 1126–1131 CrossRef.
- M. K. Shin, J. Oh, M. Lima, M. E. Kozlov, S. J. Kim and R. H. Baughman, Adv. Mater., 2010, 22, 2663–2667 CrossRef CAS PubMed.
- R. Zhang, M. Baxendale and T. Peijs, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 195433 CrossRef.
- J. Zhao, K. Dai, C. Liu, G. Zheng, B. Wang, C. Liu, J. Chen and C. Shen, Composites, Part A, 2013, 48, 129–136 CrossRef CAS.
- H. Wei, D. Ding, S. Wei and Z. Guo, J. Mater. Chem. A, 2013, 1, 10805–10813 CAS.
- J. Zhu, S. Wei, J. Ryu and Z. Guo, J. Phys. Chem. C, 2011, 115, 13215–13222 CAS.
- Z. S. Levin, C. Robert, J. F. Feller, M. Castro and J. C. Grunlan, Smart Mater. Struct., 2013, 22, 015008 CrossRef.
- Y. Si, J. Yu, X. Tang, J. Ge and B. Ding, Nat. Commun., 2014, 5, 5802 CrossRef CAS PubMed.
- Alamusi, W. F. Yuan, Surina, Y. Li, N. Hu, H. M. Ning, Y. L. Liu, L. K. Wu, S. Atobe and H. Fukunaga, Appl. Phys. Lett., 2013, 103, 221903 CrossRef.
- M. H. G. Wichmann, S. T. Buschhorn, J. Gehrmann and K. Schulte, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 245437 CrossRef.
- M. Knite, V. Teteris, A. Kiploka and J. Kaupuzs, Sens. Actuators, A, 2004, 110, 142–149 CrossRef CAS.
- S. Tadakaluru, W. Thongsuwan and P. Singjai, Sensors, 2014, 14, 868–876 CrossRef PubMed.
- Q. Fan, Z. Qin, S. Gao, Y. Wu, J. Pionteck, E. Mäde and M. F. Zhu, Carbon, 2012, 50, 4085–4092 CrossRef CAS.
- A. K. Geim, Science, 2009, 324, 1530–1534 CrossRef CAS PubMed.
- W. Yuan and G. Shi, J. Mater. Chem. A, 2013, 1, 10078–10091 CAS.
- C. Soldano, A. Mahmood and E. Dujardin, Carbon, 2010, 48, 2127–2150 CrossRef CAS.
- J. Zhao, C. He, R. Yang, Z. Shi, M. Cheng, W. Yang, G. Xie, D. Wang, D. Shi and G. Zhang, Appl. Phys. Lett., 2012, 101, 063122 CrossRef.
- M. Hempel, D. Nezich, J. Kong and M. Hofmann, Nano Lett., 2012, 12, 5714–5718 CrossRef CAS PubMed.
- S.-H. Bae, Y. Lee, B. K. Sharma, H.-J. Lee, J.-H. Kim and J.-H. Ahn, Carbon, 2013, 51, 236–242 CrossRef CAS.
- Y. A. Samad, Y. Li, A. Schiffer, S. M. Alhassan and K. Liao, Small, 2015, 11, 2380–2385 CrossRef PubMed.
- J. Sandler, M. S. P. Shaffer, T. Prasse, W. Bauhofer, K. Schulte and A. H. Windle, Polymer, 1999, 40, 5967–5971 CrossRef CAS.
- S. Stankovich, D. A. Dikin, G. H. B. Dommett, K. M. Kohlhaas, E. J. Zimney, E. A. Stach, R. D. Piner, S. T. Nguyen and R. S. Ruoff, Nature, 2006, 442, 282–286 CrossRef CAS PubMed.
- K.-H. Liao, Y. Qian and C. W. Macosko, Polymer, 2012, 53, 3756–3761 CrossRef CAS.
- S. Stankovich, R. D. Piner, X. Chen, N. Wu, S. T. Nguyen and R. S. Ruoff, J. Mater. Chem., 2006, 16, 155–158 RSC.
- Y. Si and E. T. Samulski, Nano Lett., 2008, 8, 1679–1682 CrossRef CAS PubMed.
- H. Kang, K. Zuo, Z. Wang, L. Zhang, L. Liu and B. Guo, Compos. Sci. Technol., 2014, 92, 1–8 CrossRef CAS.
- N. Yousefi, M. M. Gudarzi, Q. Zheng, X. Y. Lin, X. Shen, J. Jia, F. Sharif and J.-K. Kim, Composites, Part A, 2013, 49, 42–50 CrossRef CAS.
- L. Liu, A. H. Barber, S. Nuriel and H. D. Wagner, Adv. Funct. Mater., 2005, 15, 975–980 CrossRef CAS.
- J. Liang, Y. Huang, L. Zhang, Y. Wang, Y. Ma, T. Guo and Y. Chen, Adv. Funct. Mater., 2009, 19, 2297–2302 CrossRef CAS.
- O. Menes, M. Cano, A. Benedito, E. Giménez, P. Castell, W. K. Maser and A. M. Benito, Compos. Sci. Technol., 2012, 72, 1595–1601 CrossRef CAS.
- J. Zhao, X. Wang, W. Zhou, E. Zhi, W. Zhang and J. Ji, J. Appl. Polym. Sci., 2013, 130, 3212–3220 CrossRef CAS.
- Y. Cao, J. Feng and P. Wu, Carbon, 2010, 48, 3834–3839 CrossRef CAS.
- T. T. Tung, M. Castro, T. Y. Kim, K. S. Suh and J. F. Feller, J. Mater. Chem., 2012, 22, 21754–21766 RSC.
- T. Kuila, S. Bose, C. E. Hong, M. E. Uddin, P. Khanra, N. H. Kim and J. H. Lee, Carbon, 2011, 49, 1033–1037 CrossRef CAS.
- A. K. Appel, R. Thomann and R. Mülhaupt, Polymer, 2012, 53, 4931–4939 CrossRef CAS.
- M. Liu, C. Zhang, W. W. Tjiu, Z. Yang, W. Wang and T. Liu, Polymer, 2013, 54, 3124–3130 CrossRef CAS.
- J.-C. Huang, Adv. Polym. Technol., 2002, 21, 299–313 CrossRef CAS.
- J. F. Gao, Z. M. Li, Q. J. Meng and Q. Yang, Mater. Lett., 2008, 62, 3530–3532 CrossRef CAS.
- I. Balberg, Phys. Rev. Lett., 1987, 59, 1305–1308 CrossRef CAS PubMed.
- L. Supriya, S. Unal, T. E. Long and R. O. Claus, Chem. Mater., 2006, 18, 2506–2512 CrossRef CAS.
- J. Du, L. Zhao, Y. Zeng, L. Zhang, F. Li, P. Liu and C. Liu, Carbon, 2011, 49, 1094–1100 CrossRef CAS.
- K. Yamaguchi, J. J. C. Busfield and A. G. Thomas, J. Polym. Sci., Part B: Polym. Phys., 2003, 41, 2079–2089 CrossRef CAS.
- J. N. Aneli, G. E. Zaikov and L. M. Khananashvili, J. Appl. Polym. Sci., 1999, 74, 601–621 CrossRef CAS.
- H. J. Qi and M. C. Boyce, Mech. Mater., 2005, 37, 817–839 CrossRef.
- B. Bending, K. Christison, J. Ricci and M. D. Ediger, Macromolecules, 2014, 47, 800–806 CrossRef CAS.
- P. Sheng, E. K. Sichel and J. I. Gittleman, Phys. Rev. Lett., 1978, 40, 1197–1200 CrossRef CAS.
- X. W. Zhang, Y. Pan, Q. Zheng and X. S. Yi, J. Polym. Sci., Part B: Polym. Phys., 2000, 38, 2739–2749 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5tc02751a |
| This journal is © The Royal Society of Chemistry 2016 |