Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Two- and three-photon processes during photopolymerization in 3D laser printing†
Anna
Mauri
 a,
Pascal
Kiefer
a,
Pascal
Kiefer
 b,
Philipp
Neidinger
cd,
Tobias
Messer
b,
N. Maximilian
Bojanowski‡
a,
Liang
Yang§
ab,
Sarah
Walden
d,
Andreas-Neil
Unterreiner
b,
Philipp
Neidinger
cd,
Tobias
Messer
b,
N. Maximilian
Bojanowski‡
a,
Liang
Yang§
ab,
Sarah
Walden
d,
Andreas-Neil
Unterreiner
 c,
Christopher
Barner-Kowollik
c,
Christopher
Barner-Kowollik
 ad,
Martin
Wegener
ab,
Wolfgang
Wenzel
ad,
Martin
Wegener
ab,
Wolfgang
Wenzel
 a and
Mariana
Kozlowska
a and
Mariana
Kozlowska
 *a
*a
aInstitute of Nanotechnology (INT), Karlsruhe Institute of Technology (KIT), Kaiserstraße 12, 76131 Karlsruhe, Germany. E-mail: mariana.kozlowska@kit.edu
bInstitute of Applied Physics (APH), Karlsruhe Institute of Technology (KIT), Kaiserstraße 12, 76131 Karlsruhe, Germany
cInstitute of Physical Chemistry (IPC), Karlsruhe Institute of Technology (KIT), Kaiserstraße 12, 76131 Karlsruhe, Germany
dSchool of Chemistry and Physics, Centre for Materials Science, Queensland University of Technology (QUT), 2 George Street, Brisbane, QLD 4000, Australia
First published on 15th July 2024
Abstract
The performance of a photoinitiator is key to control efficiency and resolution in 3D laser nanoprinting. Upon light absorption, a cascade of competing photophysical processes leads to photochemical reactions toward radical formation that initiates free radical polymerization (FRP). Here, we investigate 7-diethylamino-3-thenoylcoumarin (DETC), belonging to an efficient and frequently used class of photoinitiators in 3D laser printing, and explain the molecular bases of FRP initiation upon DETC photoactivation. Depending on the presence of a co-initiator, DETC causes radical generation either upon two-photon- or three-photon excitation, but the mechanism for these processes is not well understood so far. Here, we show that the unique three-photon based radical formation by DETC, in the absence of a co-initiator, results from its excitation to highly excited triplet states. They allow a hydrogen-atom transfer reaction from the pentaerythritol triacrylate (PETA) monomer to DETC, enabling the formation of the reactive PETA alkyl radical, which initiates FRP. The formation of active DETC radicals is demonstrated to be less spontaneous. In contrast, photoinitiation in the presence of an onium salt co-initiator proceeds via intermolecular electron transfer after the photosensitization of the photoinitiator to the lowest triplet excited state. Our quantum mechanical calculations demonstrate photophysical processes upon the multiphoton activation of DETC and explain different reactions for the radical formation upon DETC photoactivation. This investigation for the first time describes possible pathways of FRP initiation in 3D laser nanoprinting and permits further rational design of efficient photoinitiators to increase the speed and sensitivity of 3D laser nanoprinting.
Introduction
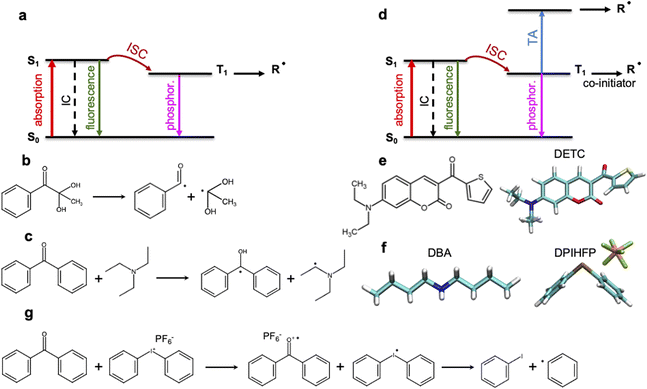
3D laser nanolithography is intensely investigated1,2 to enable manufacturing of devices with increasing speed and resolution.2,3 The strong three-dimensional spatial confinement of the exposed region in two-photon polymerization (TPP) enables resolutions that cannot be achieved using traditional one-step one-photon absorption (1PA) processes.2,4,5 Despite the tremendous progress in recent years,6 3D laser nanoprinting using TPP still faces different limitations7–10 in resolution and speed that correlates strongly with the threshold laser power. This, in part, results from the limitations of the available photoinitiators (PIs) and resins: Kiefer et al.11 have reported a strong dependence of the printing sensitivity on the TPP initiation and, therefore, on the photochemical properties of the photoinitiator. Unfortunately, the photoinduced properties of common PIs cannot be deduced straightforwardly from their chemical composition and the electronic structure in the ground state or the lowest triplet state. Moreover, despite significant progress in 3D laser nanoprinting and the design of new two-photon PIs,12–16 a deep understanding of the photophysical and photochemical processes occurring upon multiphoton absorption is still scarce.17,18 Molecular-based structure–activity relationships for the dependencies observed experimentally, as well as the virtual design of new PIs towards higher 3D laser nanoprinting sensitivity should be improved.Multiphoton photoinitiation involves complex photophysical processes between the excited states of the photoinitiator that goes beyond the conventional studies of the reactivity of photoactive molecules. It is commonly known that light irradiation often enables excitation of PI molecules from the ground state (S0) to the singlet excited state (S1), e.g. by two-photon absorption in TPP. From there, intersystem crossing to a triplet excited state (often T1) occurs (see Fig. 1a). This process can be followed by a cleavage reaction of the PI into two highly reactive radical fragments that start the polymerization.4,5 This photochemical cleavage, often assigned to Norrish type I PIs,4,5,19 is schematically depicted in Fig. 1b and is characterized by an α-scission of aldehydes and ketones (such as indole, pyrrole, (thio)phenol and aniline19–21) into two free radical intermediates. The photoinitiation process proceeds without α-scission in the case of PIs that behave as, so-called, Norrish type II PIs, such as benzophenone, thioxanthone, or ketocoumarins,19–23 where co-initiators are also added to the photoresist and two radicals are formed: one on the co-initiator and the other on the PI, respectively (see Fig. 1c). Depending on the nature of the triplet excited state of the Norrish type II PI (mostly T1) and a co-initiator molecule, there are different pathways towards radical formation: hydrogen abstraction, electron transfer or a combination of both, e.g. a hydrogen atom transfer (HAT) reaction,19,24 where carbon-centered radical intermediates25 are formed via photoexcited electron transfer followed by a proton transfer.22,26 HAT reactions were reported to occur with, e.g., amines or amine synergists,25 which play the role of a hydrogen donor. Noticeable preference for an electron-based transfer reaction was observed in the case of electron-accepting co-initiators, e.g. onium salts (Fig. 1g).19,27
The performance of PIs used in 3D laser nanoprinting depends on the radical generation mechanism and the reactivity of the radical formed, as well as the effectiveness of the S0 → S1 transition, which controls the light absorbance characteristics of photoinitiator molecules. As depicted in Fig. 1, it is modulated by the intersystem crossing (ISC) between singlet and triplet states that depends on the spin–orbit coupling (SOC); it competes with internal conversion (IC) and radiative decay either from a singlet or a triplet state. Therefore, sufficiently fast ISC and long-living triplet states (in the case of Norrish type II PIs) are also required for the radical generation process. In addition, for two-photon based 3D printing of materials, high 2PA cross sections are important.28
Among the most sensitive photoresist systems that have successfully been applied in 3D laser nanoprinting, the combination of pentaerythritol triacrylate (PETA) monomer, that is cross-linking upon FRP, with 7-diethylamino-3-thenoylcoumarin (DETC) photoinitiator,1,4,5,11,29,30 is broadly used. DETC has shown high printing efficiency even in formulations with 0.25 and 0.50 wt%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,4,11,17,29 of the initiator. Higher DETC concentrations are difficult to achieve due to limited solubility in PETA.2,11 It should be noted that other PIs, specifically Norrish type I, may show similar efficiency in 3D laser nanoprinting as DETC, but for much higher concentrations.2,4,11 Owing to its chemical structure (depicted in Fig. 1e), DETC behaves as Norrish type II PI23 and, for photoresists with co-initiators, shows N = 2 photon absorption dependence (using femtosecond lasers with around 800 nm).4 It was also reported to efficiently initiate polymerization in 3D laser nanoprinting without any co-initiator.4,29 In such a case, absorption of three photons of the same energy was required.29 Similar N = 3 photon absorption dependence of DETC was reported in other 3D printing studies, which suggested the singlet–singlet transition by 2PA and triplet–triplet transition by 1PA (i.e. triplet absorption, TA) to higher triplets4,31 (schematically depicted in Fig. 1d). N-photon absorption in both cases was estimated using the “reciprocity law” of the laser power at the polymerization threshold with exposure time.29 Presently, there is a lack of understanding of the different N-photon absorption of DETC and the radical formation mechanism with the use of this and similar PIs. This limits the further optimization of initiators for rapid 3D laser nanoprinting.
2,4,11,17,29 of the initiator. Higher DETC concentrations are difficult to achieve due to limited solubility in PETA.2,11 It should be noted that other PIs, specifically Norrish type I, may show similar efficiency in 3D laser nanoprinting as DETC, but for much higher concentrations.2,4,11 Owing to its chemical structure (depicted in Fig. 1e), DETC behaves as Norrish type II PI23 and, for photoresists with co-initiators, shows N = 2 photon absorption dependence (using femtosecond lasers with around 800 nm).4 It was also reported to efficiently initiate polymerization in 3D laser nanoprinting without any co-initiator.4,29 In such a case, absorption of three photons of the same energy was required.29 Similar N = 3 photon absorption dependence of DETC was reported in other 3D printing studies, which suggested the singlet–singlet transition by 2PA and triplet–triplet transition by 1PA (i.e. triplet absorption, TA) to higher triplets4,31 (schematically depicted in Fig. 1d). N-photon absorption in both cases was estimated using the “reciprocity law” of the laser power at the polymerization threshold with exposure time.29 Presently, there is a lack of understanding of the different N-photon absorption of DETC and the radical formation mechanism with the use of this and similar PIs. This limits the further optimization of initiators for rapid 3D laser nanoprinting.
Here, we report quantum mechanical (QM) calculations of DETC in the ground and excited states to fully elucidate the relevant photophysical processes and photochemical reactions of DETC in the presence and absence of co-initiators such as dibutylamine (DBA) and diphenyliodonium hexafluorophosphate (DPIHFP). On this basis, we reveal the radical formation mechanisms upon the multiphoton activation of this PI in 3D laser nanoprinting. In combination with experimental data (3D laser nanoprinting), we analyze the two-photon and three-photon processes in DETC photosensitization and identify pathways for an efficient radical generation. Among the hypothetical radical polymerization mechanisms considered, we explain in detail the intermolecular HAT of DETC with DBA and PETA, as well as demonstrate the impact of the photoinduced electron transfer of DETC in the presence of DPIHFP. We investigate the formation of alkyl radicals by PETA or DBA via the reaction of monomers or co-initiators with DETC in higher triplet states. Moreover, we reveal the alkyl radicals formed as the source of the most reactive radical species necessary for FRP of PETA in 3D laser nanoprinting with DETC. We believe that our contribution is important in rationalizing experimental observations that have been poorly understood for many years and in comprehending the designing principles for new PIs for faster 3D printing. Given the limitations and challenges of available QM methods, we attempted to demonstrate possible pathways of radical generation and polymerization initiation.
Computational details
Geometry optimization and rates calculation
All calculations were performed using Density Functional Theory (DFT) and Time-Dependent DFT (TD-DFT) methods. Ground state geometry optimization of DETC was performed using temperature annealing approach utilizing the CAM-B3LYP32 functional with def2-TZVP33 basis set and Grimme's D3-dispersion correction with Becke–Johnson damping, i.e. D3(BJ).34 Global minimum structures in the ground state were used for excited state calculations (singlet and triplet states), including spectra generation and optimization of excited states using TD-CAM-B3LYP-D3(BJ)/def2-TZVP. T2 and T5 excited states could not be properly optimized and therefore were not reported in the paper. Geometry optimization was performed using Gaussian16 Rev. C.01![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 35 with default ultra-fine grid for numerical integrations and energy convergence criterion of 10−8 Hartree. Calculations were performed both in the gas phase and acetonitrile (ACN) solvent using polarizable-continuum-model (PCM)36 implicit solvent model, i.e., for excited states non-equilibrium solvation method for all single point calculations and equilibrium PCM procedure for excited states geometry optimizations. All optimized geometries obtained were confirmed with vibrational analysis and, in the case of excited states, confirmed also via molecular orbitals analysis. The computational scheme used was optimized considering available experimental data and calculations of 0–0 transition energy ν00
35 with default ultra-fine grid for numerical integrations and energy convergence criterion of 10−8 Hartree. Calculations were performed both in the gas phase and acetonitrile (ACN) solvent using polarizable-continuum-model (PCM)36 implicit solvent model, i.e., for excited states non-equilibrium solvation method for all single point calculations and equilibrium PCM procedure for excited states geometry optimizations. All optimized geometries obtained were confirmed with vibrational analysis and, in the case of excited states, confirmed also via molecular orbitals analysis. The computational scheme used was optimized considering available experimental data and calculations of 0–0 transition energy ν00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37,38 (i.e., between vibrational states of the ground and the first singlet excited electronic states), as described in Section 2 in ESI.† The quality of the TD-DFT setup for vertical excitation energies of DETC was confirmed by the GW (one-body Green's function with the dynamically screened Coulomb interaction) approximation and Bethe–Salpeter equation (BSE)39,40 implemented in TURBOMOLE v7.4
37,38 (i.e., between vibrational states of the ground and the first singlet excited electronic states), as described in Section 2 in ESI.† The quality of the TD-DFT setup for vertical excitation energies of DETC was confirmed by the GW (one-body Green's function with the dynamically screened Coulomb interaction) approximation and Bethe–Salpeter equation (BSE)39,40 implemented in TURBOMOLE v7.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41 (see Tables S2 and S22†). Analysis of the charge (electron and hole) differences between the ground and excited states were performed using Multiwfn (version 3.6) analyzer.42
41 (see Tables S2 and S22†). Analysis of the charge (electron and hole) differences between the ground and excited states were performed using Multiwfn (version 3.6) analyzer.42
Spin-unrestricted DFT scheme (U)CAM-B3LYP-D3(BJ) was used for the optimization of radicals and biradicals considered in this study. All thermodynamic quantities were computed after vibrational analysis using implicit ACN (PCM model) using (U)CAM-B3LYP-D3(BJ)/def2-TZVP level of theory in Gaussian16. The reaction temperature of 298 K and pressure of 1 atm were considered. Rates for IC, ISC and Reversible Intersystem Crossing (RISC) were calculated employing the Franck–Condon approximation (FC)43 (see details in ESI†) using MOMAP 2022A (2.3.3)44–49 (Molecular Materials Property Prediction Package). TD formalism was used. The radiative rate constants, i.e., fluorescence and phosphorescence, were calculated using DETC optimized singlet and triplet state structures at ACN and in the gas phase with MOMAP. Adiabatic Hessian (AH) potential energy surfaces (PES) model within TD-DFT was used for the computation of all the radiative rates.
Absorption spectra calculation
1PA,50 2PA51,52 and three-photon absorption (3PA)52,53 spectra were computed both in the gas phase and implicit ACN and PETA (PCM model) using TD-CAM-B3LYP-D3(BJ)/def2-TZVP in Dalton 2020.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 54 and Gaussian16 Rev. C.01 (only 1PA). 2PA and 3PA spectra were calculated considering a single laser beam, linearly polarized light with parallel polarization (as experimental set-up); transition moments were defined on two- and three photons of the same frequency, respectively. Spectra were plotted using half width at half maximum (HWHM) of 0.1 eV and Lorentzian type broadening function. TA spectra were computed with TD-(U)CAM-B3LYP-D3(BJ)/def2-TZVP approach in ACN starting from the T1 optimized geometry, obtained via TD-DFT using Gaussian16. To evaluate the intensities of transitions between two vibronic states, the Franck–Condon principle was employed considering that the nuclear positions are mostly unaltered by the electron jump which takes place during the electronic transition.
54 and Gaussian16 Rev. C.01 (only 1PA). 2PA and 3PA spectra were calculated considering a single laser beam, linearly polarized light with parallel polarization (as experimental set-up); transition moments were defined on two- and three photons of the same frequency, respectively. Spectra were plotted using half width at half maximum (HWHM) of 0.1 eV and Lorentzian type broadening function. TA spectra were computed with TD-(U)CAM-B3LYP-D3(BJ)/def2-TZVP approach in ACN starting from the T1 optimized geometry, obtained via TD-DFT using Gaussian16. To evaluate the intensities of transitions between two vibronic states, the Franck–Condon principle was employed considering that the nuclear positions are mostly unaltered by the electron jump which takes place during the electronic transition.
Vibrationally resolved singlet and triplet spectra were computed at TD-DFT level of theory within the Franck–Condon55,56 (FC) approximation at 100 K with Adiabatic Hessian (AH-G16) as PES model. Spectra were plotted with HWHM of 80 cm−1 (i.e., 0.01 eV), convergence factor of 1.0 × 10−4 a.u. and Lorentzian type broadening function. The energy transitions from vibrational levels of the initial state to the vibrational levels of the final state, i.e., higher triplet excited state, were considered. The strength of a particular transition was obtained as a result of the population of that state and the overlap between initial and final vibrational wavefunctions for that transition. Spectra were computed using Dynavib57,58 in implicit ACN with TD-CAM-B3LYP-D3(BJ)/def2-TZVP level of theory, starting from the lowest triplet excited state and higher triplet excited states. Due to significant geometry differences between T1 and T3 states in ACN (see Fig. S11†), which go beyond the harmonic vibrational potentials within FC approximation, the corresponding spectrum could not be generated. Several different models, employed for the computation of the PES, i.e. time-independent and -dependent FC and non-Condon simulation including Duschinsky effect59 and FC and non-Condon simulations based on linear coupling model (LCM) model,60,61 have not improved the output.
Experiments
To investigate the polymerization laser threshold of various DETC-containing resists, the previously reported setup11 was applied. Herein, a mode-locked femtosecond laser oscillator (Mai Tai HP, Spectra-Physics), working at Rp = 80 MHz repetition rate and λ = 820 nm center wavelength, a microscope lens (Leica HCX PL APO 100x/1.4-0.7 Oil CS) for beam focussing in oil-immersion mode, and an acousto-optic modulator (AA MT80-A1.5-IR) were utilized. The resists were prepared by adding 7-diethylamino-3-thenoylcoumarin (DETC; 30 μmol), dibutylamine (DBA; 7.5 μmol, 15 μmol, 30 μmol, 60 μmol, and 120 μmol), or diphenyliodonium hexafluorophosphate (DPIHFP, 15.6 μmol, 31.2 μmol, and 62.4 μmol), respectively, to pentaerythritol triacrylate (PETA; 2 g) in a vial under constant stirring. DETC was purchased from Exciton. DPIHFP (>97.5% purity) was purchased from TCI. PETA (technical grade) and DBA (99.5% purity) were purchased from Sigma-Aldrich.To measure the laser polymerization threshold for a given exposure time texp, separated points of the photoresist were illuminated with different laser powers P. The lowest laser power, which still forms a visible polymer dot29 after development with acetone is then defined as the laser polymerization threshold power Pth.
Results and discussion
One-photon and multiphoton absorption
Quantum mechanical calculations of photochemical processes and photoreactivity of molecules are either computationally very expensive or not accurate enough, i.e. via the use of multireference based post-Hartree–Fock methods or DFT formalism, respectively. To calibrate the accuracy of the computational protocol a set of DFT and GW approximation Bethe–Salpeter equation (GW-BSE)39,40 calculations were performed and compared to available experimental data (Sections 1, 2 and 7 in ESI†) as well as several wavefunction-based methods (Section 5 in ESI†). Considering reported 1PA and emission data of DETC in PETA4 and in acetonitrile (ACN) (see Fig. S3†), we have calculated 1PA spectra using linear-response TD-DFT with long-range corrected CAM-B3LYP32 to describe the one-photon process (Fig. 2a, S2, and Table S1†). The calculated 1PA spectrum of DETC in ACN, as well as the excitation energies computed with GW-BSE approach and the values of E0–0 energies (ν00![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37,38i.e., between the ground vibrational states of the two electronic states considered) show good agreement with the experiment. The 1PA spectrum of DETC (visualized in Fig. 2a) indicates the blue-shifted absorption maximum (by ∼60 nm) in comparison with the measured spectrum of DETC in ACN (359.30 nm vs. 421 nm). However, the consideration of vibronic effects modulates the red-shift in spectra, being closer to the experiment (see Fig. S2 and S3†). The computation of absorption and emission energies has also been performed while including corrected linear response (cLR)62 and state specific (SS) corrections for the solvation model, i.e., external iteration (EI).63,64 This data is reported in Tables S6–S8.† The value of E0–0 is 439.04 nm (2.82 eV) with cLR instead of 407.44 nm (3.04 eV) with LR, indicating an impact of state-specific formulations in TD-DFT. The experimental Stokes shift of DETC in ACN is 460.50 nm (2.69 eV, see Table S3†), which could be well reproduced using an optimized computational protocol. The calculated emission characteristics of DETC are consistent with the reported literature data as well, i.e., the fluorescence rate in ACN is 4.30 × 108 s−1 (Table S20†), while the experimentally reported values in toluene and methanol (22) are ∼2–4 × 109 s−1.
37,38i.e., between the ground vibrational states of the two electronic states considered) show good agreement with the experiment. The 1PA spectrum of DETC (visualized in Fig. 2a) indicates the blue-shifted absorption maximum (by ∼60 nm) in comparison with the measured spectrum of DETC in ACN (359.30 nm vs. 421 nm). However, the consideration of vibronic effects modulates the red-shift in spectra, being closer to the experiment (see Fig. S2 and S3†). The computation of absorption and emission energies has also been performed while including corrected linear response (cLR)62 and state specific (SS) corrections for the solvation model, i.e., external iteration (EI).63,64 This data is reported in Tables S6–S8.† The value of E0–0 is 439.04 nm (2.82 eV) with cLR instead of 407.44 nm (3.04 eV) with LR, indicating an impact of state-specific formulations in TD-DFT. The experimental Stokes shift of DETC in ACN is 460.50 nm (2.69 eV, see Table S3†), which could be well reproduced using an optimized computational protocol. The calculated emission characteristics of DETC are consistent with the reported literature data as well, i.e., the fluorescence rate in ACN is 4.30 × 108 s−1 (Table S20†), while the experimentally reported values in toluene and methanol (22) are ∼2–4 × 109 s−1.
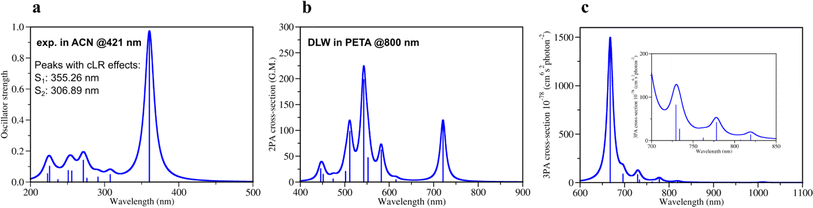 | ||
| Fig. 2 Theoretically calculated spectra of DETC using TD-CAM-B3LYP/def2-TZVP: (a) one-photon absorption spectrum and (b) two-photon absorption spectrum in acetonitrile (PCM implicit solvent model) (c) three-photon absorption spectrum in the gas phase with the insertion of the zoomed spectrum in the region 700–850 nm. All spectra were obtained starting from the optimized ground state geometry of DETC using CAM-B3LYP-D3(BJ)/def2-TZVP level of theory. Spectra were plotted using half width at half maximum (HWHM) of 0.1 eV and Lorentzian type broadening function. Vibrationally-resolved 1PA spectrum is depicted in Fig. S2.† Note: DLW denotes direct laser writing. | ||
For the estimation of the character of vertical excitations of DETC, the transition orbitals and the analysis of its charge transfer (CT) characteristics65 have been performed. They are depicted and described in detail in Section 3 in ESI,† where the comparison with the spin-component scaled coupled cluster (SCS-CC2) method is provided. From Table S12,† it is clearly seen that CT in DETC is rather strong: transitions S0 → S1, S0 → T1 and S0 → T7 exhibit less negative t parameters, suggesting higher CT, while the remaining transitions have highly negative t values, indicating a mixed character of CT and local exciton (LE) transitions, as depicted in Fig. S6.† The change of the electronic structure of DETC following light-induced transitions, the molecular orbitals (MOs) and the electron density delocalization over its π-conjugated system are depicted in Fig. S4–S7† and explained in detail in Section 3 in ESI.†
The quality of calculated 1PA spectra directly impacts the accuracy of 2PA spectra necessary to evaluate the efficiency of PI in TPP. Even if 1PA and 2PA involve strictly defined transitions between ground and excited states of a molecule, the underlying light-induced processes are different in nature and follow different selection rules, e.g., in terms of symmetry of the state and the electric dipole transitions. Therefore, not all molecules are both 1PA and 2PA active, however, the calculated 2PA spectrum of DETC (Fig. 2b) reveals its 2PA activity. The 2PA spectrum of DETC in ACN shows maximum absorption at 720.84 nm with the highest calculated cross-section at this wavelength of 119.0 GM (Fig. 2b, and Table S13†). The spectrum possesses a blue-shift in comparison to experiments16,66 which is a repercussion of the blue-shift in the 1PA spectrum (Fig. 2a), where the calculated and measured absorption maximum are located at 359.30 nm and 421.00 nm, respectively (see Table S1 and Fig. S3†). The calculated 2PA cross-section is higher than the recently reported 2PA cross-sections of DETC in dichloromethane (82 GM)16 and dimethyl sulfoxide (40 GM)66 at 780 nm and 800 nm, respectively. The calculated 2PA using the implicit representation of these solvents is reported in Fig. S8.† Considering spectral shifts in the 1PA spectra, they still demonstrate good correlations.2–5,30,31 Here, we note that the direct comparison of 2PA cross-sections between experiment and theory is challenging due to the high sensitivity of cross-section values to the variety of experimental parameters and referencing methods, as well as the selection of parameters for the calculation of theoretical spectra51 and consideration of environmental, i.e., solvent, effects. Moreover, experimentally reported 2PA cross-sections of DETC differ between 82 GM and 40 GM, depending on the solvent and measurement technique (two-photon induced fluorescence and z-scan, respectively).16,66 Several factors contribute to the discrepancy in these values. Firstly, the determination of 2PA absorption cross-sections using two-photon fluorescence has an accuracy limited to 8–10%.67 Secondly, it is known that z-scan data typically underestimates 2PA cross-section by up to a factor of 2.5–5,68 bringing the true value measured via z-scan closer to 100–200 GM. Finally, it is important to keep in mind that neither of the mentioned experimental studies of DETC considered the potential for higher-order absorption processes.
To evaluate the possibility for DETC to simultaneously absorb three photons during singlet–singlet 3PA, the respective spectrum in the gas phase was calculated (Fig. 2c, and Table S14†). A peak related to S0 → S1 transition was found to be at 1010.74 nm with a 3PA cross-section of 5.6 × 10−78 cm6 s2 photon−1. The cross-section values related to transitions between S0 and higher excited states using the laser wavelength of 819–778 nm (i.e., S0 → S3, S0 → S4 and S0 → S5) are in the range of 1–42 × 10−78 cm6 s2 photon−1. Therefore, theoretical calculations indicate that DETC might be prone to instantaneously absorb three photons, leading to very high singlet excited states. Since such highly excited states tend to relax rapidly via conical intersections (typical vibrational frequencies of modes coupled to the electronic transition have been calculated to be on the order 20 THz, i.e., 50 fs),69 which are unstable, they will decay to the lowest singlet excited state. Since the S1 state is typically reached via 2PA using femtosecond lasers, no additional photons (i.e., more than 2) would be detected in the nonlinearity fits of the threshold laser power versus exposure time in the TPP (discussed further). Due to the same reason, 3PA processes may not be observed at all using fluorescence as the detection system, since two- and three-photon induced fluorescence quantum yields can significantly vary due to channel branching in the excited state manifold (singlet and/or triplet in nature) of dye molecules. It has been shown for fluorene derivatives that shifting the excitation wavelength from the UV to the near-infrared region significantly increases the contribution of three-order processes compared to first and second order.70 3PA processes were not considered in the fits to the z-scan data of DETC.66 Therefore, accurate excitation wavelength z-scan data would be needed to simultaneously analyze contributions both from two- and three order processes.71 To the best of our knowledge, no such analysis has been performed on DETC, likely due to experimental challenges such as contributions from self-phase modulation, impulsive stimulated Raman scattering, wavelength-dependence of higher-order processes etc.
Multiphoton 3D laser nanoprinting using DETC
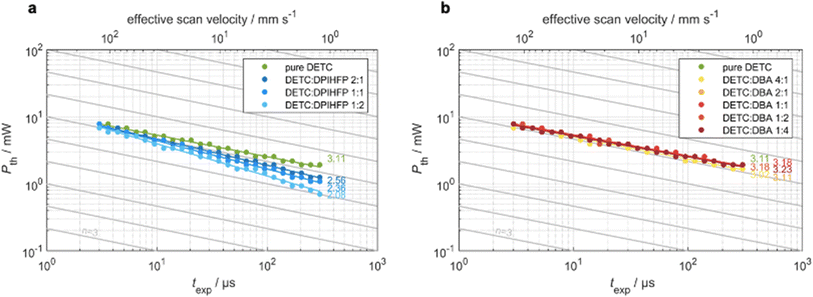
To analyze the various aspects of DETC performance in 3D laser nanoprinting, we investigate different photoresist compositions, i.e., with pure DETC as the photoinitiator and after the addition of the co-initiators: DBA or DPIHFP. Both co-initiators were considered since they were demonstrated to decrease the threshold laser power for rapid 3D laser nanoprinting.11 Here, DBA was found to be more efficient than triethylamine, which is a more typical amine-based co-initiator than DBA. Moreover, no lowering in the degree of co-sensitization due to volatility, side reactions or concentration-induced absorption changes, reported for other co-initiators based on tertiary amines, have been noticed.72 Point exposure experiments were performed using PETA as a monomer to evaluate the initiation mechanism of these photoresist compositions. In Fig. 3, we observe significant differences in the experimental threshold laser power vs. exposure time, i.e., different scaling behaviors, for all resist systems. Here, the N ∼ 2 photon dependence11 is solely observed for resists comprising DETC and DPIHFP (Fig. 3a). As previously reported, pure DETC shows N ∼ 3 scaling.29 No changes in scaling after the addition of the DBA as a co-initiator are observed (Fig. 3b).The underlying mechanisms for radical generation in all these cases may proceed via photoinduced HAT, electron transfer or TA. With onium salts, DETC is most likely to participate in electron transfer (ET) and/or energy transfer from the photoexcited sensitizer to the iodonium cation, followed by the rapid decomposition of the resulting unstable diaryliodine radical that prevents back electron transfer and renders the overall process irreversible.27,58 HAT was reported for DETC (and similar ketocoumarins) with amine-based co-initiators.4,73,74 Since ET happens on the picosecond timescale,75 it is faster than HAT, which was shown to be a diffusion modulated process.76 This agrees with the observation from 3D printing of PETA: the electron transfer process between DETC and DPIHFP results in the 2PA-initiated polymerization. The HAT reaction between DBA and DETC, involving a two-step intermolecular transfer (see Fig. 1c), should not occur from the T1 excited state of DETC, because the nonlinearity does not decrease from N = 3 to 2, as observed for onium salt. As mentioned above, 3PA of DETC has not been reported up to date, however such a process may well occur, in addition to 2PA, as was reported for other chromophores.77 This may be the reason why the nonlinearity dependence is slightly higher than N = 3. Such 3PA with 775–800 nm may excite DETC to S3–S5 states. However, due to fast decay to the S1 excited state, higher singlet states of DETC do not participate in the radical formation. Therefore, TA, resulting in highly reactive DETC triplet states, seems to be more probable to occur. This should allow the polymerization reaction, while the radical reaction channel from the T1 state of DETC is hindered due to diffusion-controlled reactions, particularly in high-viscosity resins.76
We have compared the reactivity of DETC (in the T1 state) in HAT reaction with DBA in terms of reaction energy profile and transition state that leads to the radical formation according to Fig. 1c. Obtained energies and reaction mechanisms are depicted in Fig. S19 and Table S25.† HAT reaction from co-initiator to DETC is not spontaneous from S0 state of DETC since the Gibbs free energy is 48.19 kcal mol−1 in ACN. Upon photoactivation of DETC and the formation of the T1 state, the Gibbs free energy lowers to 0.44 kcal mol−1 and the energy barrier (from the transition state calculation) is 6.72 kcal mol−1. Thus, it allows HAT with the rate of 7.33 × 107 s−1, calculated employing the Eyring equation78 at room temperature and pressure, in ACN. Therefore, HAT between DBA and DETC in the T1 state should theoretically occur, resulting in the N ∼ 2 in 3D printing, however, it is not observed in printing conditions. Recently, Xue et al.79 have reported that the reaction of benzylidene ketone PIs with the amine-based co-initiators is predominantly controlled by material diffusion rather than by an activation process. We believe this may be the reason why resists with DBA do not show two-photon scaling during 3D printing of PETA using DETC, reported in Fig. 3b. The QM calculations of HAT reaction between DETC and DBA are presented in Section 8 in ESI.†
Consequently, bimolecular radical initiation shows a dependence on the exposure time and the concentration of the co-initiator (Fig. 3a). For longer exposure times or higher concentrations of DPIHFP, the bimolecular mechanism dominates over TA, however, it lowers the sensitivity of printing.
Photophysical processes of DETC upon singlet–singlet excitation
The photosensitization of PIs can be activated in T1 triplet state (see Fig. 1), which, in principle, is achieved when SOC, thus, the ISC from singlet to triplet excited states is high enough. The direct SOC between the S1 state of DETC and the T1 state is 0.97 cm−1 and happens with an ISC rate of 8.84 × 104 s−1 (see Table 1). This observation suggests that the ISC pathways via conical intersections and other triplet states would impact the photoactivation of DETC. Indeed, after geometry optimization (see description in ESI†), analysis of electronic properties and calculation of SOC and ISC rates involving two singlet states (S1 and S2) and several triplet (T1, T3, T4, T6, while T2 and T5 did not converge) states of DETC, we can conclude that direct ISC between S1 → T1 should not be the main pathway for the formation of the T1 state. From the Jablonski diagram of DETC in ACN, depicted in Fig. 4, it can be stated that upon absorption from the ground state, S1 excited state couples strongly to the T3 excited state with the SOC of 7.55 cm−1 (see Table 1), resulting in a fast and efficient ISC rate of ∼1.72 × 108 s−1. Here, we have to note several important observations. Firstly, the T3 state, optimized in ACN, shows a twist of −97.7° of the thiophenyl group of DETC with respect to the core (dihedral angle C9–C8–C11–C17, see Fig. S1, S10, and S11†). Such a perpendicular-like position, as previously noted by Tozer et al.80 is unnatural for the DETC molecule and contrasts with the dihedral angle in the ground state geometry of −45.9°. It is not present in the case of T3 computed in the gas phase, where the twist is only by −41.45°. Such strong structural differences were not observed between the ground state and the S1 geometries optimized in ACN and gas phase (see Fig. S11†). Secondly, we encountered the poor convergence of the correlation function in the computation of ISC rates between T3 and S1, which were both optimized in implicit ACN (see explanation in Section 6 in ESI, Table S19a and Fig. S16†). This suggests an influence of the polarization included by the implicit solvent and subtle (complex) electronic nature of higher excited states of DETC that could not be resolved with the LR-TD-DFT. Higher level methods and the consideration of nonequilibrium conditions might be necessary, however it is beyond the present investigations. The ISC rate successfully converged utilizing the T3 state optimized in the gas phase (see Fig. S16†), therefore it was used for the computation of photophysical rates of DETC (Table 1).| Nonradiative rate | Rate (s−1) | NACME (au) | λ (eV) | |
|---|---|---|---|---|
| a T3 was optimized in the gas phase, while S1, S2 and T1 in ACN. The energy gap considered was computed between T3 and S1, S2 or T1 in ACN and SOC in ACN. | ||||
| IC | S1 → S0 | 1.60 × 108 | 0.009 | 0.205 |
| S2 → S0 | NA | 0.004 | 1.341 | |
| T6 → T1 | 1.25 × 1010 | 0.006 | 0.171 | |
| T4 → T1 | 4.50 × 1010 | 0.006 | 0.478 | |
| T3 → T1 | 1.76 × 1011 | 0.003 | 0.572 | |
| Radiative rate | Rate (s−1) | ΔE (eV) | Lifetime (s) |
|---|---|---|---|
| Fluorescence | 4.30 × 108 | 3.04 | 2.33 × 10−9 |
| Phosphorescence | 7.69 × 10−1 | 2.09 | 1.30 |
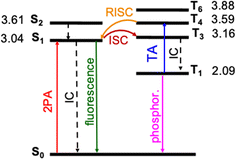 | ||
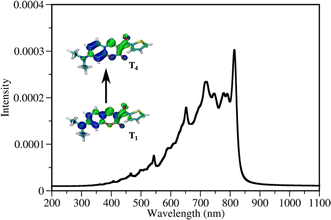
| Fig. 4 Jablonski diagram of DETC. Excited states were optimized in acetonitrile (PCM model) using TD-CAM-B3LYP-D3(BJ)/def2-TZVP level of theory. Adiabatic energy values, including zero-point-energy (ZPE) correction, are reported in eV. Rates of transitions between different states, calculated using electronic structure parameters, obtained with TD-DFT approach, are listed in Table 1. Note: besides phosphorescence, nonradiative decay from the lowest triplet state to the ground state can also occur (not shown in the figure). | ||
The energy difference between the S1 and T3 states in ACN is −0.12 eV, as depicted in Fig. 4, i.e., the adiabatic T3 state lies slightly higher than the S1 state. According to the calculation of the vertical energy differences by several wavefunction-based methods using the optimized structures from TD-DFT (see Tables S16 and S17† with the respective explanation), the T2 state in ACN is closer to the S1 state, but both T2 and T3 are still higher than S1. However, all post-HF-based energies obtained represent only the differences in the vertical energies, while TD-DFT data are for the optimized states. Unfortunately, the T2 state of DETC could not be reliably optimized in TD-DFT in both ACN and the gas phase to evaluate the competitiveness of the ISC via S1 → T2 transition. We assume that this fact may be connected to the limitations of the LR-TD-DFT for this specific state, i.e., the transition electron density of T2 (as well as T5, which could not be obtained) is differently captured in TD-DFT than in SCS-CC2 in ACN (see Fig. S7†). Electron density differences for other states of DETC are more consistent within TD-DFT and SCS-CC2, therefore, we rely on them.
The ISC between S1 → T3 shows dominant ππ* → nπ* character (60% in the gas phase), supporting El-Sayed rule81–83 for ISC processes. It also indicates vibronic spin–orbit interactions that increase the SOC.84 Since SOC is impacted by the way the solvent effects are included (see Table S18†), for all calculations we use the SOC with the included non-equilibrium effects for the solvent, resulting in data that correlates better with experiments (Table S19†). Even if such SOC value is lower than in the gas phase, the ISC rate, considering the ΔE(S1–T3) of −0.12 eV is still reasonable (1.72 × 108 s−1), competing with IC (1.60 × 108 s−1) and fluorescence (4.30 × 108 s−1). We have to point out that the parameters described and the shape of molecular orbitals during the transitions are strongly dependent on molecular vibrations, vibronic couplings and solvation effects, resulting in the mixing of nπ* and ππ* states, which is observed for S1 → T3. Therefore, more detailed analysis of transition dynamics and subtle differences should be accessed by a higher level of theory and non-adiabatic molecular dynamics to obtain more realistic values. This was not in the scope of the current investigation.
Once DETC reaches T3 state, it undergoes fast IC decay to the T1 state with the rate of 1.76 × 1011 s−1 (Table 1). The lifetime of 1.16 × 10−5 s (11.6 μs) for the non-radiative decay of T1 (i.e., ISC T1–S0) allows other processes to occur. Charge density analysis, i.e., the localization of electron-donating (hole) and electron-accepting (electron) parts of T1 excited state of DETC demonstrates the activation of carbonyl moiety (atoms C11–O12, see areas in green in Fig. S6†) with higher local electron densities that should participate in electron transfer and HAT. Therefore, DETC should be prone to attack the amine-based co-initiator permitting H-atom transfer reaction. However, as discussed above, it is hindered in the present study. This is shown by the deviation of nonlinearities far away from 2 that is expected for the typical Norrish type II PIs after PI activation to the T1 state.
Multiphoton activation of DETC to higher triplet states
DETC initiates FRP in the absence of any co-initiator molecule with the use of three photons at ∼800 nm2,4,11,29,30 (see Fig. 3). It is an interesting observation since DETC ketyl radicals alone are less active: the bond dissociation energy of O–H bond in ketyl radicals is relatively low (e.g. 16 kcal mol−1 in acetone85). This indicates a different pathway for PI photoreactivity in TA, shifting the electronic state of DETC to higher triplet states. To define which triplet excited state can be reached by the upcoming third photon during 3D printing, a one-photon based triplet–triplet excitations in ACN were calculated (listed in Tables S21, and S22†).The presence of a peak located at 815 nm (see Table S21†), i.e. value close to the fs laser wavelength used in experiment, confirms the TA absorption of photons in the T1 state. However, such a treatment neglects the influence of vibronic coupling of the electronic transition, providing a simplified view of absorption spectra. To overcome this limitation and to assign the transition to the activated triplet state, vibrationally resolved triplet spectra55 for several transitions between T1 → Tn (n = 4, 6) were computed (see Fig. S17†). Among spectra obtained, the transition T1 → T4 overlaps with the experimentally used photon energy (see Fig. 5). Therefore, the excitation of DETC in 3D printing should allow the transition of the PI most probably to the T4 state with the charge density difference depicted on the upper left panel in Fig. 5. Interestingly, the oscillator strength of TA at the printing wavelength is much higher for DETC than for other Norrish type II PIs.18,31 Fast TA may also be the reason why the HAT reaction with DBA (from T1 of DETC) is hindered, indicating a high probability of the DETC photoreactivity from higher triplet states. Note that in such states DETC may also decay to the lowest triplet state (calculated ICT4−T1 is 4.50 × 1010 s−1, see Table 1) or return to singlet states via reverse intersystem crossing (RISC). RISC rates of DETC from the T3–T4 states (e.g. rate of 5.39 × 109 s−1 for T3 → S1, 2.44 × 109 s−1 for T4 → S1), might compete with IC permitting deactivation of DETC, i.e. its depletion, which was also reported to occur using the second inhibition laser source of 800 nm (femtosecond)4 and 808 nm (continuous).24
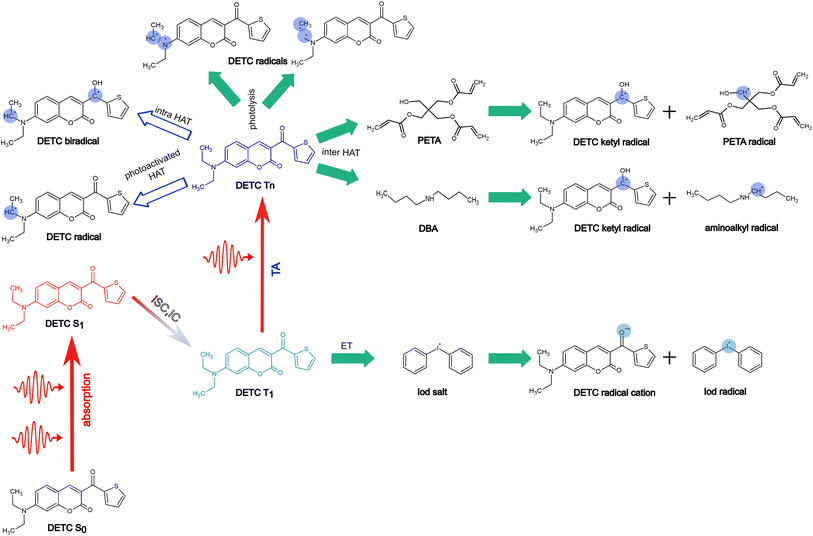
Mechanisms of radical formation
To further estimate the radical formation of DETC in high triplet states, initiating FRP, several mechanisms were considered. Similarly, to the formation of aminoalkyl radicals of DBA (see Fig. 1c) photoactivated H-abstraction reaction85 was calculated for DETC (see Section 9.1). Higher C–H activation possibility with lower bond dissociation enthalpy (BDE) is triggered by PI in high triplets (BDE lower than 8.8 kcal mol−1 in comparison to 82 kcal mol−1 in S0, see Table S26†). However, the process is not spontaneous (see the Gibbs free energy values in Table S27†) and could not even compete with spontaneous internal conversion (Table 1), disabling the radical formation via C–H bond breaking, depicted in Fig. S21a.† This is also the reason for the hindered formation of the hypothetically highly reactive DETC biradicals that were suggested to occur for similar chromophore molecules43,86–88 (see Section 9.3 in ESI†). Indeed, if such biradicals are formed, they should initiate FRP from an excited state of DETC (higher than T3) spontaneously (see Section 10 in ESI†). However, neither such intramolecular HAT was confirmed experimentally, nor the calculated Gibbs free energies vs. nonradiative decay should permit it. Unfortunately, transition state calculations using higher triplet states of DETC could not be obtained to further predict the kinetics of this reaction. Interestingly, the formation of DETC radicals via photolysis should in theory be spontaneous (Section 9.2). The cleavage of N14–C15, C15–C16 or C8–C11 bonds of DETC (see Fig. S21c†) is thermodynamically more favorable in T4 (Table S29†) with the Gibbs free energy even −26.96 kcal mol−1 in the case of N14–C15 bond cleavage. However, the entropic contribution to the Gibbs free energy, calculated using the vibrational frequencies within harmonic approximation and considering implicit ACN, is relatively high, i.e., of around 0.05 kcal mol−1 K−1. This may be impacted by explicit treatment of solvent and anharmonic effects, therefore, experimental validation of DETC photolysis is essential. Such a reaction should also be kinetically accessible to compete with spontaneous IC or RISC processes, which happen with the rate of 4.50 × 1010 s−1/1.25 × 1010 s−1 and 2.44 × 109 s−1/1.38 × 108 s−1 from T4/T6 excited state, respectively (see Table 1). Fig. S21† illustrates the key finding regarding the formation of DETC radicals according to the mentioned reaction mechanisms. This study indicates that if DETC spontaneously form reactive radicals for FRP in 3D printing, they may originate from photolysis. Moreover, the formation of the DETC ketyl radical (shown in Fig. 1c) is possible, however, it is less reactive than other possible species (Table S32† and ref. 89 and 90).Since the photoresist contains also PETA monomers, we have investigated the impact of DETC on the radical formation directly by PETA. The mechanism of PETA radical formation should be similar to the reaction between DETC and the DBA co-initiator (Section 8 in ESI†). The intermolecular HAT should involve the C–H bond cleavage of the alkyl chain of PETA upon DETC attack via the carbonyl functional group (see Fig. 6). C–H bond cleavage of PETA without DETC possesses high BDE (the lowest value is of 84.05 kcal mol−1, see Table S23 and Fig. S18†) and it requires a higher number of photons to enable the 3D printing.2,4,29 (in general, such printing loses its resolution in comparison to the photoresists that include DETC). According to the Gibbs free energies reported in Fig. 6 and Table S24,† the C–H cleavage of PETA with the inter-HAT reaction in the presence of DETC should be easier permitted if DETC is in, e.g., T1 state, resulting in the formation of the R1 or R2 type PETA radical. However, such a reaction is still not spontaneous.
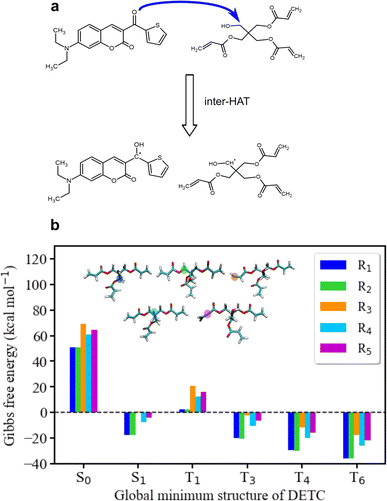 | ||
| Fig. 6 Radical reaction mechanisms between DETC and PETA. (a) HAT reaction between DETC in a high triplet state and PETA in the ground state that leads to the formation of a ketyl radical on DETC and an alkyl radical on PETA (R1 or R2) that consequently initiates the polymerization (R1 is reported in the figure). It is important to note that all carbon atoms in the alpha position with respect to the central carbon atom in the pentaerythritol fragment of PETA are equally susceptible to form radicals. (b) Gibbs free energy of the reaction involving different PETA radicals (R1–R5, see Fig. S18†) as a function of the electronic state of DETC (see Table S24†). Energies were computed employing (U)CAM-B3LYP-D3(BJ)/def2-TZVP approach in implicit ACN. | ||
The formation of radicals with the participation of the T1 state of DETC (for photoresists without co-initiator) was suggested in several reports.4,16,17,91 To our knowledge, there is no experimental evidence of such radicals formed or reaction mechanisms reported. Since the Gibbs free energy of a similar HAT reaction between DETC (in T1) and DBA is even lower than for the reaction with PETA (0.44 kcal mol−1vs. 5.47 kcal mol−1, see Table S25†) and this reaction could not be observed in the printing conditions (see Fig. 3b) (even if the reaction rate is 7.33 × 107 s−1 as calculated using the activation energy barrier presented in Fig. S19†), we tend to believe that the HAT reaction between PETA and DETC should not occur, when DETC is in T1 excited state. The Gibbs free energy for this reaction when DETC is in higher triplet states is significantly reduced, i.e., even to −29.47 kcal mol−1 or to −35.62 kcal mol−1 for DETC in T4 and T6 triplet states, respectively (Fig. 6b and Table S25†). Thus, they are more prone to compete with internal photophysical processes in DETC, suggesting reactions to happen from such states. Due to the convergence problems in optimizing transition states involving PETA and DETC in high triplet states, we cannot provide rates of such reactions, however, the radical formation pathway mentioned helps in rationalizing experimental observations. It should be noted that the calculated rates and Gibbs free energies represent values in equilibrium conditions without population distribution of excited states, various decay pathways, light intensity etc. They were aimed to reveal molecular bases of the complex processes during TPP with DETC.
From all reaction pathways examined, we conclude that DETC may be susceptible to radical generation through the inter-HAT involving the PETA monomer or photolysis, which are both spontaneous even in the absence of a co-initiator. Experimental confirmation of an exact radical species by, e.g., the in-depth analysis of the chemical composition of the 3D laser printed materials is still necessary. Since these processes are more spontaneous with the participation of DETC in higher triplet states, reached upon TA, the third-order dependency and exceptional efficiency of this PI in FRP are experimentally observed.
In Fig. 7, we summarize pathways of the multiphoton activation of DETC in 3D printing with fs lasers of the wavelength of ∼800 nm, as well as the radical generation mechanisms considered in this work. Pathways, resulting in possibly the most active radical formation, are marked with the filled green arrows, whereas pathways that are hindered due to various reasons, explained in Section 9 in ESI† (i.e. DETC radicals), are marked with empty blue arrows. Note that different PETA radicals with the activated carbon atoms in the alpha position with respect to the central carbon atom in the pentaerythritol fragment of PETA can occur. The mechanisms of FRP are explained in detail in Section 10 in ESI.† More investigation from an experimental point of view is, therefore, necessary to further validate theoretically predicted radical formation mechanisms and the reactivity of DETC in its T1 state in comparison to the higher triplet states.
Conclusions
3D laser nanoprinting techniques and photoresist systems have advanced significantly over the past decade. A consensus has emerged that the PI is a key ingredient in the complex interplay of factors that control the speed and resolution of 3D laser nanoprinting. However, the molecular basis of photoactivation during 3D printing is still not well understood. Herein, we have provided an in-depth analysis of the photoactivation and photoreactivity of DETC, one of the most efficient, presently used, multiphoton photoinitiators, to explain the mechanisms of FRP in 3D printing using DETC. We have demonstrated the second-order scaling of the DETC reactivity with DPIHFP onium salt and provided a molecular understanding of the formation of radicals in a two-component bimolecular system comprising DETC and the DBA co-initiator as well as DETC and the PETA monomer.We have shown that in a one-component system, i.e., in the absence of a co-initiator, the FRP initiation with nonlinearity of 2 is not allowed, since the electronic structure of DETC in the T1 excited state does not permit active radical formation, which typically occurs for unimolecular processes for Norrish type I PIs. The BDE of C–H, C–C or C–N bond cleavage of DETC, aimed to open the pathway for reactive radicals, is too high in T1 (∼22–51 kcal mol−1). However, bond breaking affinity of DETC changes significantly upon TA absorption of the third photon at ca. 800 nm. This wavelength fits well to the triplet–triplet transition of DETC from its T1 to higher triplet states, e.g., T4, modulating the electronic structure of DETC towards easier H-atom abstraction reactions or C–C and C–N bond cleavage. However, H-atom abstraction-based hypothetical pathways for the radical creation are not spontaneous and cannot compete with fast internal conversion to T1, hindering the formation of active DETC radicals and biradicals during 3D printing that could directly initiate FRP. The Gibbs free energy of photolysis of DETC in high excited states shows higher spontaneity (i.e., −0.52 to −26.96 kcal mol−1 from the T4 excited state), however further experimental validation is required.
We demonstrate that the radicals that could, indeed, initiate FRP (especially in the absence of a co-initiator) are alkyl-based radicals of PETA, formed upon H-atom abstraction reaction between from PETA to DETC. The rate of this reaction, from the T1 excited state of DETC, should be lower than the reaction of DETC with DBA (i.e., the rate of 7.33 × 107 s−1). Since the latter is not observed experimentally, we demonstrate that the formation of reactive radicals occurs in the presence of DETC excited to higher triplet states. In both cases, for PETA and DBA, HAT with DETC in high triplets should be spontaneous. When these reactions are capable of competing with photophysical processes, such as IC and RISC, they will initiate FRP according to mechanisms suggested in this study.
The provided in-depth investigation of DETC photosensitization permits the understanding of the pathways initiating polymerization of photoresist compositions comprising DETC during 3D printing. It addresses ongoing challenges in rapid 3D laser nanoprinting by providing possible ways for more sensitive PIs, such as enhanced capabilities of HAT abstraction either from a co-initiator or a monomer used in a such photopolymerization.
Data availability
The raw data of this publication are permanently available on our institutional repository and can be referenced via this link https://www.radar-service.eu/radar/en/dataset/KjeSQpjIkSHeqhFY?token=ZOuvquDpJMfFJJufuEfO.Author contributions
A. M.: quantum mechanical calculations, investigation, data analysis and visualization, drafting the paper, paper review and editing; P. K.: nonlinearity measurements, experiment-theory feedback loops and analysis, paper review and editing; P. N.: discussion, data interpretation, paper review and editing; T. M.: nonlinearity measurements, discussion and data interpretation, paper review and editing; N. M. B: discussion, data interpretation, paper review and editing; L. Y.: discussion, data interpretation, paper review and editing; S. W.: discussion, data interpretation, paper review and editing; A. N. U.: discussion, data interpretation, paper review and editing; C. B. K.: discussion, data interpretation, paper review and editing; M. W.: discussion and data interpretation, paper review and editing; W. W.: discussion and data interpretation, funding acquisition, resources, paper review and editing; M. K.: conceptualization, supervision, project administration, investigation, data analysis, funding acquisition, paper writing, review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research has been funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy for the Excellence Cluster “3D Matter Made to Order” (Grant No. EXC-2082/1-390761711) and by the Carl Zeiss Foundation. C. B. K. acknowledges the Australian Research Council (ARC) for funding in the context of a Laureate Fellowship. M. K. acknowledges funding by the Ministry of Science, Research and Art of Baden-Württemberg (Germany) under Brigitte-Schlieben-Lange-Programm. The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/575-1 FUGG (JUSTUS 2 cluster) under project bw20F004. We acknowledge support by the KIT-Publication Fund of the Karlsruhe Institute of Technology. We acknowledge Guangjun Tian, Yanshan University (China), for providing the Dynavib code and for the assistance in ensuring its proper utilization.Notes and references
- C. Barner-Kowollik, M. Bastmeyer, E. Blasco, G. Delaittre, P. Müller and B. Richter,
et al., 3D Laser Micro- and Nanoprinting: Challenges for Chemistry, Angew. Chem., Int. Ed., 2017, 56(50), 15828–15845 CrossRef CAS PubMed
.
- J. Fischer, J. B. Mueller, J. Kaschke, T. J. A. Wolf, A. N. Unterreiner and M. Wegener, Three-dimensional multi-photon direct laser writing with variable repetition rate, Opt. Express, 2013, 21(22), 26244–26260 CrossRef PubMed
.
- X. He, T. Li, J. Zhang and Z. Wang, STED Direct Laser Writing of 45 nm Width Nanowire, Micromachines, 2019, 10(11), 726 CrossRef PubMed
.
- J. Fischer, J. B. Mueller, A. S. Quick, J. Kaschke, C. Barner-Kowollik and M. Wegener, Exploring the Mechanisms in STED-Enhanced Direct Laser Writing, Adv. Opt. Mater., 2015, 3(2), 221–232 CrossRef CAS
.
- J. Fischer and M. Wegener, Three-dimensional optical laser lithography beyond the diffraction limit, Laser Photonics Rev., 2013, 7(1), 22–44 CrossRef CAS
.
- E. Sedghamiz, M. Liu and W. Wenzel, Challenges and limits of Mechanical Stability in 3D Direct Laser Writing, Nat. Commun., 2022, 13, 2115 CrossRef CAS PubMed
.
- Z. Bai, J. Wei, X. Liang, K. Zhang, T. Wei and R. Wang, High-speed laser writing of arbitrary patterns in polar coordinate system, Rev. Sci. Instrum., 2016, 87(12), 125118 CrossRef PubMed
.
- H. Yuk, B. Lu, S. Lin, K. Qu, J. Xu and J. Luo,
et al., 3D printing of conducting polymers, Nat. Commun., 2020, 11(1), 1604 CrossRef CAS PubMed
.
- M. Hippler, E. D. Lemma, S. Bertels, E. Blasco, C. Barner-Kowollik and M. Wegener,
et al., 3D Scaffolds to Study Basic Cell Biology, Adv. Mater., 2019, 31(26), 1808110 CrossRef PubMed
.
- S. J. Zhang, Y. Li, Y. K. Wang, L. P. Liu, H. D. Wang and Y. F. Xiao,
et al., Controlling Young's modulus of polymerized structures fabricated by direct laser writing, Appl. Phys. A, 2015, 118(2), 437–441 CrossRef CAS
.
- P. Kiefer, V. Hahn, M. Nardi, L. Yang, E. Blasco and C. Barner-Kowollik,
et al., Sensitive Photoresists for Rapid Multiphoton 3D Laser Micro- and Nanoprinting, Adv. Opt. Mater., 2020, 8(19), 2000895 CrossRef CAS
.
- T. Chi, P. Somers, D. A. Wilcox, A. J. Schuman, V. Iyer and R. Le,
et al., Tailored thioxanthone-based photoinitiators for two-photon-controllable polymerization and nanolithographic printing, J. Polym. Sci., Part B: Polym. Phys., 2019, 57(21), 1462–1475 CrossRef CAS
.
- B. Holzer, M. Lunzer, A. Rosspeintner, G. Licari, M. Tromayer and S. Naumov,
et al., Towards efficient initiators for two-photon induced polymerization: fine tuning of the donor/acceptor properties, Mol. Syst. Des. Eng., 2019, 4(2), 437–448 RSC
.
- P. Hu, W. Qiu, S. Naumov, T. Scherzer, Z. Hu and Q. Chen,
et al., Conjugated Bifunctional Carbazole-Based Oxime Esters: Efficient and Versatile Photoinitiators for 3D Printing under One- and Two-Photon Excitation, ChemPhotoChem, 2020, 4(3), 224–232 CrossRef CAS
.
- M. Tromayer, P. Gruber, A. Rosspeintner, A. Ajami, W. Husinsky and F. Plasser,
et al., Wavelength-optimized Two-Photon Polymerization Using Initiators Based on Multipolar Aminostyryl-1,3,5-triazines, Sci. Rep., 2018, 8(1), 17273 CrossRef PubMed
.
- J. Tang, X. Xu, X. Shen, C. Kuang, H. Chen and M. Shi,
et al., Ketocoumarin-Based Photoinitiators for High-Sensitivity
Two-Photon Lithography, ACS Appl. Polym. Mater., 2023, 5(4), 2956–2963 CrossRef CAS
.
- P. Somers, Z. Liang, T. Chi, J. E. Johnson, L. Pan and B. W. Boudouris,
et al., Photo-activated polymerization inhibition process in photoinitiator systems for high-throughput 3D nanoprinting, Nanophotonics, 2023, 12, 1571–1580 CrossRef CAS
.
- N. Liaros, S. A. Gutierrez Razo, M. D. Thum, H. M. Ogden, A. N. Zeppuhar and S. Wolf,
et al., Elucidating complex triplet-state dynamics in the model system isopropylthioxanthone, iScienc, 2022, 25(1), 103600 CrossRef CAS PubMed
.
- S. Dadashi-Silab, S. Doran and Y. Yagci, Photoinduced Electron Transfer Reactions for Macromolecular Syntheses, Chem. Rev., 2016, 116(17), 10212–10275 CrossRef CAS PubMed
.
- C. S. Colley, D. C. Grills, N. A. Besley, S. Jockusch, P. Matousek and A. W. Parker,
et al., Probing the Reactivity of Photoinitiators for Free Radical Polymerization: Time-Resolved Infrared Spectroscopic Study of Benzoyl Radicals, J. Am. Chem. Soc., 2002, 124(50), 14952–14958 CrossRef CAS PubMed
.
- Y. Yagci, S. Jockusch and N. J. Turro, Photoinitiated Polymerization: Advances, Challenges, and Opportunities, Macromolecules, 2010, 43(15), 6245–6260 CrossRef CAS
.
- B. Jana, S. R. Inamdar and H. M. Suresh Kumar, Effect of quencher and temperature on fluorescence intensity of laser dyes: DETC and C504T, Spectrochim. Acta, Part A, 2017, 170, 124–130 CrossRef CAS PubMed
.
- J. L. R. Williams, D. P. Specht and S. Farid, Ketocoumarins as photosensitizers and photoinitiators, Polym. Eng. Sci., 1983, 23(18), 1022–1024 CrossRef CAS
.
- S. Sarkar, K. P. S. Cheung and V. Gevorgyan, C–H functionalization reactions enabled by hydrogen atom transfer to carbon-centered radicals, Chem. Sci., 2020, 11(48), 12974–12993 RSC
.
- J. Xie, P. Xu, Y. Zhu, J. Wang, W. C. C. Lee and X. P. Zhang, New Catalytic Radical Process Involving 1,4-Hydrogen Atom Abstraction: Asymmetric Construction of Cyclobutanones, J. Am. Chem. Soc., 2021, 143(30), 11670–11678 CrossRef CAS PubMed
.
- J. P. Fouassier, D. Ruhlmann, B. Graff, F. Morlet-Savary and F. Wieder, Excited state processes in polymerization photoinitiators, Prog. Org. Coat., 1995, 25(3), 235–271 CrossRef CAS
.
- J. Kabatc, J. Ortyl and K. Kostrzewska, New kinetic and mechanistic aspects of photosensitization of iodonium salts in photopolymerization of acrylates, RSC Adv., 2017, 7(66), 41619–41629 RSC
.
- K. J. Schafer, J. M. Hales, M. Balu, K. D. Belfield, E. W. Van Stryland and D. J. Hagan, Two-photon absorption cross-sections of common photoinitiators, J. Polym. Sci., Part A: Polym. Chem., 2004, 162(2–3), 497–502 CAS
.
- L. Yang, A. Münchinger, M. Kadic, V. Hahn, F. Mayer and E. Blasco,
et al., On the Schwarzschild Effect in 3D Two-Photon Laser Lithography, Adv. Opt. Mater., 2019, 7(22), 1901040 CrossRef CAS
.
- J. Fischer and M. Wegener, Three-dimensional direct laser writing inspired by stimulated-emission-depletion microscopy [Invited], Opt. Mater. Express, 2011, 1(4), 614–624 CrossRef CAS
.
- B. Harke, W. Dallari, G. Grancini, D. Fazzi, F. Brandi and A. Petrozza,
et al., Polymerization Inhibition by Triplet State Absorption for Nanoscale Lithography, Adv. Mater., 2013, 25(6), 904–909 CrossRef CAS PubMed
.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393(1–3), 51–57 CrossRef CAS
.
- A. Schäfer, H. Horn and R. Ahlrichs, Fully optimized contracted Gaussian basis sets for atoms Li to Kr, J. Chem. Phys., 1992, 97(4), 2571–2577 CrossRef
.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the damping function in dispersion corrected density functional theory, J. Comput. Chem., 2011, 32(7), 1456–1465 CrossRef CAS PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, et al., Gaussian 16, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed
.
- G. Scalmani and M. J. Frisch, Continuous surface charge polarizable continuum models of solvation. I. General formalism, J. Chem. Phys., 2010, 132(11), 114110 CrossRef PubMed
.
- F. J. Avila Ferrer, J. Cerezo, E. Stendardo, R. Improta and F. Santoro, Insights for an Accurate Comparison of Computational Data to Experimental Absorption and Emission Spectra: Beyond the Vertical Transition Approximation, J. Chem. Theory Comput., 2013, 9(4), 2072–2082 CrossRef CAS PubMed
.
- D. Jacquemin, A. Planchat, C. Adamo and B. Mennucci, TD-DFT Assessment of Functionals for Optical 0–0 Transitions in Solvated Dyes, J. Chem. Theory Comput., 2012, 8(7), 2359–2372 CrossRef CAS PubMed
.
- K. Krause and W. Klopper, Implementation of the Bethe–Salpeter equation in the TURBOMOLE program, J. Comput. Chem., 2017, 38(6), 383–388 CrossRef CAS PubMed
.
- M. J. van Setten, F. Weigend and F. Evers, The GW -Method for Quantum Chemistry Applications: Theory and Implementation, J. Chem. Theory Comput., 2013, 9(1), 232–246 CrossRef CAS PubMed
.
-
TURBOMOLE V7.4 2019, A development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, since 2007, available from https://www.turbomole.org/
.
- T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592 CrossRef CAS PubMed
.
- G. Temel, D. S. Esen and N. Arsu, One-component benzoxazine type photoinitiator for free radical polymerization, Polym. Eng. Sci., 2012, 52(1), 133–138 CrossRef CAS
.
- Z. Shuai and Q. Peng, Organic light-emitting diodes: theoretical understanding of highly efficient materials and development of computational methodology, Natl. Sci. Rev., 2017, 4(2), 224–239 CrossRef CAS
.
- Y. Niu, W. Li, Q. Peng, H. Geng, Y. Yi and L. Wang,
et al., MOlecular MAterials Property Prediction Package (MOMAP) 1.0: a software package for predicting the luminescent properties and mobility of organic functional materials, Mol. Phys., 2018, 116(7–8), 1078–1090 CrossRef CAS
.
- Q. Peng, Y. Yi, Z. Shuai and J. Shao, Excited state radiationless decay process with Duschinsky rotation effect: Formalism and implementation, J. Chem. Phys., 2007, 126(11), 114302 CrossRef PubMed
.
- Q. Peng, Y. Niu, Q. Shi, X. Gao and Z. Shuai, Correlation Function Formalism for Triplet Excited State Decay: Combined Spin–Orbit and Nonadiabatic Couplings, J. Chem. Theory Comput., 2013, 9(2), 1132–1143 CrossRef CAS PubMed
.
- Y. Niu, Q. Peng and Z. Shuai, Promoting-mode free formalism for excited state radiationless decay process with Duschinsky rotation effect, Sci. China, Ser. B: Chem., 2008, 51(12), 1153–1158 CrossRef CAS
.
- Y. Niu, Q. Peng, C. Deng, X. Gao and Z. Shuai, Theory of Excited State Decays and Optical Spectra: Application to Polyatomic Molecules, J. Phys. Chem. A, 2010, 114(30), 7817–7831 CrossRef CAS PubMed
.
- P. Jo/rgensen, H. J. A. Jensen and J. Olsen, Linear response calculations for large scale multiconfiguration self-consistent field wave functions, J. Chem. Phys., 1988, 89(6), 3654–3661 CrossRef
.
- M. T. P. Beerepoot, D. H. Friese, N. H. List, J. Kongsted and K. Ruud, Benchmarking two-photon absorption cross sections: performance of CC2 and CAM-B3LYP, Phys. Chem. Chem. Phys., 2015, 17(29), 19306–19314 RSC
.
- C. Hättig, O. Christiansen and P. Jo/rgensen, Multiphoton transition moments and absorption cross sections in coupled
cluster response theory employing variational transition moment functionals, J. Chem. Phys., 1998, 108(20), 8331–8354 CrossRef
.
- P. Cronstrand, P. Norman, Y. Luo and H. Ågren, Few-states models for three-photon absorption, J. Chem. Phys., 2004, 121(5), 2020–2029 CrossRef CAS PubMed
.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast and L. Boman,
et al., The Dalton quantum chemistry program system: The Dalton program, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4(3), 269–284 CAS
.
- F. Santoro, A. Lami, R. Improta, J. Bloino and V. Barone, Effective method for the computation of optical spectra of large molecules at finite temperature including the Duschinsky and Herzberg–Teller effect: The Qx band of porphyrin as a case study, J. Chem. Phys., 2008, 128(22), 224311 CrossRef PubMed
.
- G. Herzberg and E. Teller, Schwingungsstruktur der Elektronenübergänge bei mehratomigen Molekülen, Z. Phys. Chem., 1933, 21B(1), 410–446 CrossRef
.
-
G. Tian, S. Duan, W. Hua, and Y. Luo, DynaVib Version 1.0, R Inst Technol Swed, 2012 Search PubMed
.
- Y. Pan, L. Li, F. Qiu, Y. Wei, W. Hua and G. Tian, On the spectral profile change in the Q band absorption spectra of metalloporphyrins (Mg, Zn, and Pd): A first-principles study, J. Chem. Phys., 2019, 150(16), 164308 CrossRef PubMed
.
- E. v. Lenthe, E. J. Baerends and J. G. Snijders, Relativistic regular two-component Hamiltonians, J. Chem. Phys., 1993, 99(6), 4597–4610 CrossRef
.
- G. Tian and Y. Luo, Isomer-Dependent Franck–Condon Blockade in Weakly Coupled Bipyridine Molecular Junctions, J. Phys. Chem. C, 2014, 118(27), 14853–14859 CrossRef CAS
.
- G. Tian and Y. Luo, Fluorescence and Phosphorescence of Single C 60 Molecules as Stimulated by a Scanning Tunneling Microscope, Angew. Chem., Int. Ed., 2013, 52(18), 4814–4817 CrossRef CAS PubMed
.
- M. Caricato, B. Mennucci, J. Tomasi, F. Ingrosso, R. Cammi and S. Corni,
et al., Formation and relaxation of excited states in solution: A new time dependent polarizable continuum model based on time dependent density functional theory, J. Chem. Phys., 2006, 124(12), 124520 CrossRef PubMed
.
- R. Improta, G. Scalmani, M. J. Frisch and V. Barone, Toward effective and reliable fluorescence energies in solution by a new state specific polarizable continuum model time dependent density functional theory approach, J. Chem. Phys., 2007, 127(7), 074504 CrossRef PubMed
.
- R. Improta, V. Barone, G. Scalmani and M. J. Frisch, A state-specific polarizable continuum model time dependent density functional theory method for excited state calculations in solution, J. Chem. Phys., 2006, 125(5), 054103 CrossRef PubMed
.
- S. Wu, L. A. Galán, M. Roux, F. Riobé, B. Le Guennic and Y. Guyot,
et al., Tuning Excited-State Properties of [2.2]Paracyclophane-Based Antennas to Ensure Efficient Sensitization of Lanthanide Ions or Singlet Oxygen Generation, Inorg. Chem., 2021, 60(21), 16194–16203 CrossRef CAS PubMed
.
- Y. Zhang, Y. Su, Y. Zhao, Z. Wang and C. Wang, Two-Photon 3D Printing in Metal–Organic Framework Single Crystals, Small, 2022, 18(18), 2200514 CrossRef CAS PubMed
.
- S. De Reguardati, J. Pahapill, A. Mikhailov, Y. Stepanenko and A. Rebane, High-accuracy reference standards for two-photon absorption in the 680–1050 nm wavelength range, Opt. Express, 2016, 24(8), 9053 CrossRef CAS PubMed
.
- N. S. Makarov, M. Drobizhev and A. Rebane, Two-photon absorption standards in the 550-1600 nm excitation wavelength range, Opt. Express, 2008, 16(6), 4029 CrossRef CAS PubMed
.
- C. A. Farfan and D. B. Turner, A systematic model study quantifying how conical intersection topography modulates photochemical reactions, Phys. Chem. Chem. Phys., 2020, 22(36), 20265–20283 RSC
.
- I. Cohanoschi, K. D. Belfield and F. E. Hernández, Three-photon absorption enhancement in symmetrical charge transfer pull–pull fluorene derivatives, Chem. Phys. Lett., 2005, 406(4–6), 462–466 CrossRef CAS
.
- M. P. Shortell, E. A. Jaatinen, J. Chang and E. R. Waclawik, Using pulse transit delay in Z-scan to discriminate between excited-state absorption and other nonlinear processes in ZnO nanocones, Opt. Express, 2014, 22(6), 6222 CrossRef PubMed
.
- J. Lalevée, X. Allonas and J. P. Fouassier, N–H and α(C–H) Bond Dissociation Enthalpies of Aliphatic Amines, J. Am. Chem. Soc., 2002, 124(32), 9613–9621 CrossRef PubMed
.
- M. Abdallah, F. Dumur, A. Hijazi, G. Rodeghiero, A. Gualandi and P. G. Cozzi,
et al., Keto-coumarin scaffold for photoinitiators for 3D printing and photocomposites, J. Polym. Sci., 2020, 58(8), 1115–1129 CrossRef CAS
.
- M. Abdallah, A. Hijazi, B. Graff, J. P. Fouassier, G. Rodeghiero and A. Gualandi,
et al., Coumarin derivatives as versatile photoinitiators for 3D printing, polymerization in water and photocomposite synthesis, Polym. Chem., 2019, 10(7), 872–884 RSC
.
- G. L. Thornton, R. Phelps and A. J. Orr-Ewing, Transient absorption spectroscopy of the electron transfer step in the photochemically activated polymerizations of N -ethylcarbazole and 9-phenylcarbazole, Phys. Chem. Chem. Phys., 2021, 23(34), 18378–18392 RSC
.
- D. S. Achilias, A Review of Modeling of Diffusion Controlled Polymerization Reactions, Macromol. Theory Simul., 2007, 16(4), 319–347 CrossRef CAS
.
- L. Ravotto, S. L. Meloni, T. V. Esipova, A. E. Masunov, J. M. Anna and S. A. Vinogradov, Three-Photon Spectroscopy of Porphyrins, J. Phys. Chem. A, 2020, 124(52), 11038–11050 CrossRef CAS PubMed
.
- H. Eyring, The Activated Complex in Chemical Reactions, J. Chem. Phys., 1935, 3(2), 107–115 CrossRef CAS
.
- T. Xue, Y. Li, X. Li, B. Huang, Q. Song and J. Nie,
et al., Benzylidene ketones as visible light radical photoinitiator: The effects of electron-donating group and co-initiator, J. Polym. Sci., Part A: Polym. Chem., 2021, 418, 113395 CAS
.
- P. Wiggins, J. A. G. Williams and D. J. Tozer, Excited state surfaces in density functional theory: A new twist on an old problem, J. Chem. Phys., 2009, 131(9), 091101 CrossRef PubMed
.
- C. M. Marian, Spin–orbit coupling and intersystem crossing in molecules: Spin–orbit coupling, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(2), 187–203 CAS
.
-
V. Balzani, P. Ceroni, and A. Juris, Photochemistry and photophysics: concepts, research, applications, Wiley-VCH, Weinheim, 2014, p. 472 Search PubMed
.
- S. K. Lower and M. A. El-Sayed, The Triplet State and Molecular Electronic Processes in Organic Molecules, Chem. Rev., 1966, 66(2), 199–241 CrossRef CAS
.
- T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Spin–Vibronic Mechanism for Intersystem Crossing, Chem. Rev., 2018, 118(15), 6975–7025 CrossRef CAS PubMed
.
- L. Capaldo, D. Ravelli and M. Fagnoni, Direct Photocatalyzed Hydrogen Atom Transfer (HAT) for Aliphatic C–H Bonds Elaboration, Chem. Rev., 2022, 122(2), 1875–1924 CrossRef CAS PubMed
.
- S. K. Dogruyol, Z. Dogruyol and N. Arsu, A thioxanthone-based visible photoinitiator: Thioxanthone-based Visible Photoinitiator, J. Polym. Sci., Part A: Polym. Chem., 2011, 49(18), 4037–4043 CrossRef CAS
.
- G. Temel, B. Enginol, M. Aydin, D. K. Balta and N. Arsu, Photopolymerization and photophysical properties of amine linked benzophenone photoinitiator for free radical polymerization, J. Polym. Sci., Part A: Polym. Chem., 2011, 219(1), 26–31 CAS
.
- G. Ding, C. Jing, X. Qin, Y. Gong, X. Zhang and S. Zhang,
et al., Conjugated dyes carrying N, N-dialkylamino and ketone groups: One-component visible light
Norrish type II photoinitiators, Dyes Pigm., 2017, 137, 456–467 CrossRef CAS
.
- J. P. Fouassier, D. Ruhlmann, Y. Takimoto, M. Harada and M. Kawabata, New three-component initiation systems in UV curing: A time-resolved laser-spectroscopy investigation, J. Polym. Sci., Part A: Polym. Chem., 1993, 31(9), 2245–2248 CrossRef CAS
.
- X. Pan, M. A. Tasdelen, J. Laun, T. Junkers, Y. Yagci and K. Matyjaszewski, Photomediated controlled radical polymerization, Prog. Polym. Sci., 2016, 62, 73–125 CrossRef CAS
.
- J. E. Johnson, Y. Chen and X. Xu, Model for polymerization and self-deactivation in two-photon nanolithography, Opt. Express, 2022, 30(15), 26824 CrossRef CAS PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc03527e |
| ‡ Present address: Organic and Carbon Nanomaterials Unit, Okinawa Institute of Science and Technology Graduate University, Japan. |
| § Present address: Suzhou Institute for Advanced Research, University of Science and Technology of China (USTC), 215127 Suzhou, China. |
| This journal is © The Royal Society of Chemistry 2024 |