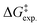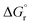Open Access Article
Open Access ArticleStraightforward computational determination of energy-transfer kinetics through the application of the Marcus theory†
Albert
Solé-Daura
 and
Feliu
Maseras
and
Feliu
Maseras
 *
*
Institute of Chemical Research of Catalonia (ICIQ-CERCA), The Barcelona Institute of Science and Technology, Avgda. Països Catalans, 16, 43007 Tarragona, Spain. E-mail: fmaseras@iciq.es
First published on 7th August 2024
Abstract
Energy transfer (EnT) photocatalysis holds the potential to revolutionize synthetic chemistry, unlocking the excited-state reactivity of non-chromophoric compounds via indirect sensitization. This strategy gives access to synthetic routes to valuable molecular scaffolds that are otherwise inaccessible through ground-state pathways. Despite the promising nature of this chemistry, it still represents a largely uncharted area for computational chemistry, hindering the development of structure–activity relationships and design rules to rationally exploit the potential of EnT photocatalysis. Here, we examined the application of the classical Marcus theory in combination with DFT calculations as a convenient strategy to estimate the kinetics of EnT processes, focusing on the indirect sensitization of alkenes recently reported by Gilmour, Kerzig and co-workers for subsequent isomerization [Zähringer et al., J. Am. Chem. Soc., 2023, 145, 21576]. Our results demonstrate a remarkable capability of this approach to estimate free-energy barriers for EnT processes with high accuracy, yielding precise qualitative assessments and quantitative predictions with typical discrepancies of less than 2 kcal mol−1 compared to experimental values and a small mean average error (MAE) of 1.2 kcal mol−1.
1 Introduction
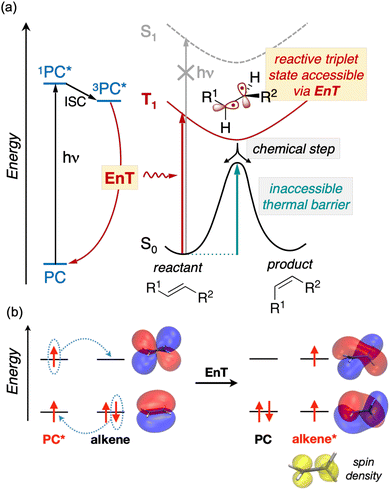
In addition to advancing societal sustainability goals by harnessing solar light as a renewable source of energy, photocatalysis taps the unique reactivity of excited states. This unlocks the synthesis of essential molecular scaffolds crucial to industries like fine chemicals, which are otherwise inaccessible through ground state reactivity.1 However, the high energy-laying nature of singlet excited states in readily-available nonactivated substrates precludes their direct excitation and hence, hinders their excited-state reactivity triggered by solar light.In this regard, Energy Transfer (EnT) photocatalysis represents a powerful strategy to enable the indirect sensitization and excited-state reactivity of nonactivated compounds,2–5 as illustrated in Fig. 1a. Typically, upon light irradiation, a photocatalyst (PC) undergoes excitation to a singlet excited state, subsequently evolving to a triplet state, 3PC*, through intersystem crossing (ISC). The latter is then proposed to sensitize the substrate via triplet–triplet EnT, regenerating the ground state of the PC and yielding the triplet excited state of the substrate, T1, from which reactivity takes place. Together with Single Electron Transfer (SET), EnT processes constitute complementary fundamental pillars of photocatalysis, enabling the reactivity of compounds in distinct redox and electronic states, respectively. So far, EnT photocatalysis has been successfully applied to key processes within organic synthesis, including the deracemization of chiral alkenes via selective E/Z isomerization, thermally-unaffordable cycloaddition reactions, or even to promote difficult organometallic steps that are challenging to occur on the ground state, as exemplified in recent reviews.2–5 For the specific case of alkene isomerization, EnT allows forming the T1 triplet state of the alkene, bypassing that of high-energy laying singlet excited states, as illustrated in Fig. 1. The T1 triplet state can be regarded as a biradical species, whereby an electron has been formally transferred to the π-type highest occupied molecular orbital (HOMO) of the alkene to the π* lowest unoccupied molecular orbital (LUMO) (Fig. 1b). In the triplet-state manifold, regardless their E or Z isomerism, alkenes are known to experience a rotation about the C–C bond to reach configurations with a torsion angle close to 90° to minimize spin-pair repulsion.5,6 Subsequently, while the T1 state decays to the S0 ground state, the torsion angle twists back to either ca. 0 or 180°, yielding E and Z isomers in presumably equal amounts. Notably, if one of the isomers is less susceptible to be sensitized than the other, racemic mixtures can be effectively deracemized to form the least reactive partner.
While EnT processes hold great potential and are gaining increasing interest, they still represent a largely unexplored area for computational chemistry, most likely due to the intricacies involved in modeling processes that diverge from conventional bond-formation and bond-breaking phenomena. This lack of mechanistic knowledge hinders the development of design rules to control or improve the efficiency of EnT photocatalysis and hence, limits its success to costly experimental trial and error approaches.
So far, many efforts have been devoted to develop computational strategies to estimate the kinetics of EnT events building upon the Marcus theory.7–9 The Marcus theory was originally developed to investigate the energy landscape, and in turn the kinetics, of SET processes, constituting a well-established approach that is still largely adopted nowadays (see Section 2, Methods, for details). According to the Dexter mechanistic picture,10,11 triplet–triplet EnT can be regarded as two concomitant electron transfer events (from the highest singly occupied molecular orbital (SOMO) of the donor to the LUMO of the acceptor and from the HOMO of the acceptor to the lowest SOMO of the donor), as shown in Fig. 1b. This conceptual view of EnT motivated the application of the Marcus theory to delve into EnT events. So far, efforts have been devoted to determine or estimate the electronic coupling between initial and final states,12–26 which is needed to calculate EnT rates through a semi-classical formulation of the Marcus theory, where the electronic coupling is explicitly included in the pre-exponential term of the rate constant equation (see Fig. S1†). Although accurate, this strategy requires the complex and computationally-demanding inclusion of quantum effects, rendering its application unpractical and far from trivial. As a matter of fact, EnT processes in the recent literature on computational photocatalysis are often overlooked or their evaluation is limited to the analysis of matching energy levels between donor and acceptor molecules,6,27–30 suggesting that the substantial complexity of the semi-classical Marcus theory discourages their exploration. A much more convenient approach, based on a purely classical variant of the Marcus theory (Fig. S1†) has been recently introduced in a couple of works.31,32 This assumes no electronic coupling between reactant and product states, allowing the estimation of EnT free-energy barriers through straightforward DFT calculations, avoiding the need of computing electronic coupling terms via more sophisticated and costly computational techniques. So far, this approach has been extensively and successfully used to estimate the kinetics of SET processes,33–38 but its application to EnT processes is markedly less explored. In fact, this simpler approach has been only applied to a very limited scope of systems and even though it allowed explaining experimental trends in a qualitative fashion,31,32 the resulting free-energy barriers were not contrasted with experimental kinetic data, making it difficult to evaluate the quantitative accuracy of this approach.
To bridge this gap, we systematically examined the potential of classical Marcus theory as a cost-effective and easy-to-use computational alternative to more sophisticated methods for estimating EnT barriers, assessing its performance against experimental data. Recently, the groups of Gilmour and Kerzig39 reported a detailed kinetic investigation on the indirect sensitization of alkenes by a variety of PCs, offering a unique and compelling opportunity to probe the computational application of the Marcus theory to model EnT. Here, we leveraged this unparalleled set of kinetic data as a robust experimental reference to compare our results with. Moreover, we explored for the first time the application of an ‘asymmetric’ variant of the Marcus theory (see Section 2, Methods).40 The latter approach accounts for possible deviations from the ideal behavior that has been conventionally assumed in previous studies, in which both reactants and products electronic states are described by parabolic functions of the same amplitude, thus pushing the computational modeling of EnT processes beyond the current state of the art. Indeed, we demonstrate that the proposed approach allows for excellent prediction of EnT free-energy barriers, with a mean average error (MAE) of 1.2 kcal mol−1 compared to experimental values derived from rate constants. Hence, our results evidence that the classical Marcus theory in combination with inexpensive DFT calculations can be used as a practical and inexpensive strategy to readily estimate the kinetics of EnT events, which we hope provides inspiration and motivates computational research on EnT photocatalysis, ultimately triggering substantial advances in this emerging field.
2 Methods
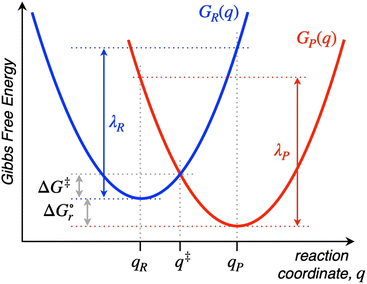
Named after Rudolph A. Marcus, the Marcus theory was originally proposed in 1956 (ref. 7) to provide a fundamental explanation to SET kinetics. Marcus was awarded the Nobel Prize in Chemistry in 1992, largely based on the foundational contributions of this theory.9 This theory regards the free-energy basins describing the electronic states of reactants (GR(q)) and products (GP(q)) as symmetric parabolic functions when projected on the reaction coordinate (q) dimension, as illustrated in Fig. 2: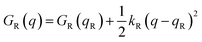 | (1) |
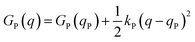 | (2) |
Thus, by adopting a non-adiabatic scheme whereby there is no coupling between reactants and products states at the transition region, the free-energy barrier of the SET event can be estimated from the free-energy difference between the reactants, GR(qR), and the crossing point of both parabolas, that is, at q = q‡, where GR(q) = GP(q) (see Fig. 2). For the sake of simplicity, it is commonly assumed that both parabolas have the same exact width, (i.e. kR = kP), which leads to the following expression for the free-energy barrier:
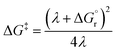 | (3) |
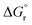 is the reaction Gibbs free energy, and λ accounts for the so called ‘reorganization energy’, which is defined as the energy difference between the reactants in their equilibrium configuration, GR(qR), and in the equilibrium configuration of the products state, GR(qP) (Fig. 2). This gives access to the λ parameter as obtained from the reactants-state potential-energy surface (λR). The same magnitude can be also measured on the products-state surface, yielding λP. Ideally, when the amplitudes of both parabolas are equal, λP = λR = λ. In non-ideal scenarios, however, λP and λR might entail slight variations. Hence, from a computational standpoint, the reorganization energy is typically determined as an arithmetic average of λP and λR. Notably, the reaction coordinate is a function not only of the nuclear coordinates of the substrates involved in the reaction, but also of those of the solvent molecules surrounding them, which need to reorganize to accompany the reactant molecules throughout their transition from the configuration of the reactants (qR) to the that of the products (qP), crossing q‡, the crossing point between the parabolas that describe reactants and products states. Thus, in order to calculate λR as GR(qP) − GR(qR), for instance, the GR(qR) term can be estimated by relaxing both nuclear coordinates to the equilibrium configuration, qR. However, the GR(qP) term requires making use of non-equilibrium configurations on the GR surface, that is, nuclear coordinates and solvation cavities optimized for qP and not for qR. The latter can be easily achieved by means of a feature for implicit solvation models implemented in the Gaussian quantum chemistry package (see Computational details section).
is the reaction Gibbs free energy, and λ accounts for the so called ‘reorganization energy’, which is defined as the energy difference between the reactants in their equilibrium configuration, GR(qR), and in the equilibrium configuration of the products state, GR(qP) (Fig. 2). This gives access to the λ parameter as obtained from the reactants-state potential-energy surface (λR). The same magnitude can be also measured on the products-state surface, yielding λP. Ideally, when the amplitudes of both parabolas are equal, λP = λR = λ. In non-ideal scenarios, however, λP and λR might entail slight variations. Hence, from a computational standpoint, the reorganization energy is typically determined as an arithmetic average of λP and λR. Notably, the reaction coordinate is a function not only of the nuclear coordinates of the substrates involved in the reaction, but also of those of the solvent molecules surrounding them, which need to reorganize to accompany the reactant molecules throughout their transition from the configuration of the reactants (qR) to the that of the products (qP), crossing q‡, the crossing point between the parabolas that describe reactants and products states. Thus, in order to calculate λR as GR(qP) − GR(qR), for instance, the GR(qR) term can be estimated by relaxing both nuclear coordinates to the equilibrium configuration, qR. However, the GR(qP) term requires making use of non-equilibrium configurations on the GR surface, that is, nuclear coordinates and solvation cavities optimized for qP and not for qR. The latter can be easily achieved by means of a feature for implicit solvation models implemented in the Gaussian quantum chemistry package (see Computational details section).
As observed for electron transfer processes, the application of eqn (3) may lead to rough barrier estimates if kR and kP significantly differ.41–43 In these cases, when kR ≠ kP (see Fig. S2† for an illustrative example), the more sophisticated analytical expression given in eqn (4) can be derived40 and employed to relate the free-energy barrier with λP, λR and 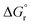 .
.
 | (4) |
In this work, the above expressions are applied in conjunction with DFT-derived reorganization energies and reaction free energies with the aim of evaluating their potential to estimate free-energy barriers for EnT events.
3 Results and discussion
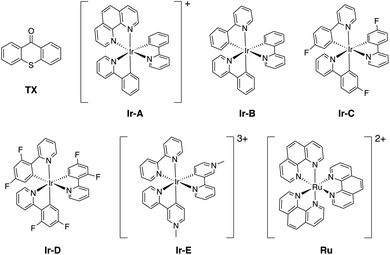
As introduced above, we employed a recent work by Gilmour, Kerzig and co-workers39 as an experimental frame of reference to investigate the application of the classical Marcus theory to EnT photocatalysis. This contribution reports the indirect sensitization of several alkenes (substrates 1–4, represented in Fig. 3) via EnT for subsequent E/Z isomerisation. To this end, thioxanthone (TX) was primarily used as a PC. TX is an aromatic ketone (see Fig. 4 for molecular structure) that upon light absorption and singlet-to-triplet ISC, forms a long-lived triplet excited state, labeled as 3TX* (lifetime of 77 μs),44 which serves to sensitize olefinic substrates following the scheme depicted in Fig. 1. A thorough kinetic study enabled determining rate constants for the EnT events from 3TX* to both the E and the Z isomers of substrates 1–4, which allowed explaining the observed selectivity in terms of E/Z ratios.39 In addition, the EnT-enabled reactivity of substrate 3 was further analyzed using a variety of Ir(III)- and Ru(II)-based PCs, for which experimental rate constants were also determined.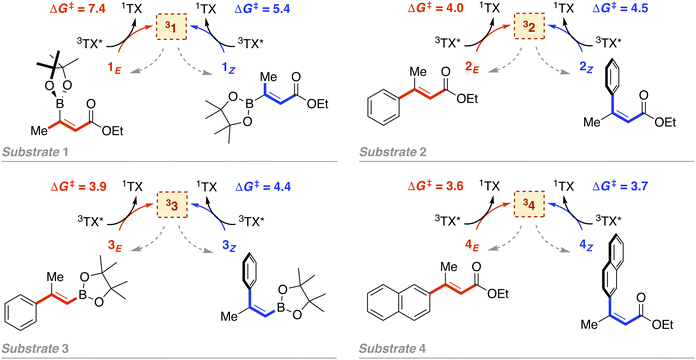 | ||
| Fig. 3 Indirect sensitization of alkenes 1–4via EnT using TX as a PC. E and Z alkenes are highlighted in red and blue, respectively. Gibbs free-energy barriers derived from experimental rate constants39 are given in kcal mol−1. | ||
In the following, we first focused on investigating the EnT processes involving TX and substrates 1–4, then transitioning to extend our exploration to the transition metal-based PCs represented in Fig. 4.
3.1 Sensitization of alkenes 1–4 with thioxanthone
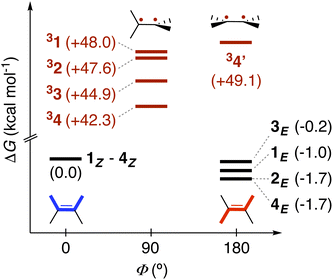
Leveraging the kinetic data reported for the EnT processes from 3TX* to substrates 1–4,39 we derived the Gibbs free-energy barriers given in Fig. 3 through the Eyring equation to obtain an experimental reference to compare our computational predictions with. Within the context of the Marcus theory, the distinct EnT barriers displayed by 1–4 may be ascribed to differences in the thermodynamic driving force (that is, the reaction free energy) and in the reorganization energy (vide supra).Firstly, we carried out DFT calculations to analyze both the singlet and triplet potential energy surfaces of 1–4, aiming to characterize the minima that correspond to the reactants and products of the EnT process. As shown in Fig. 5, E isomers were predicted to be slightly more stable than their Z counterparts, in line with previous computational results,39 although they were all found to lie within a narrow range of <2 kcal mol−1 in terms of Gibbs free energy.
As introduced above, alkenes form a biradical centered on both carbon atoms of the former double bond upon sensitization, which twists towards a torsion angle (Φ) of ca. 90° (see Fig. 1 and 5).5,39,45,46 Such a configuration was indeed obtained when performing geometry optimizations of 1–3 in the triplet state, starting from either the E or the Z configuration. However, for substrate 4, we were able to characterize two minima on the triplet surface, labeled as 34 and 34′, respectively, as shown in Fig. 5 (see Section 2 in the ESI for further details†). Hence, the free-energy barriers for EnT to 1–3 can be calculated assuming the formation of 31–33 regardless the original substrate isomerism (E or Z). However, those concerning 4Z and 4E are required to derive from the thermodynamics of 34 and 34′ formation, respectively, despite that the less stable 34′ might ultimately evolve towards 34via thermal fluctuations after the EnT event. Importantly, all characterized triplet species are found within a range of +42.3 and +50.8 kcal mol−1 relative to their respective ground states. This supports that, from a thermodynamic perspective, they all can be spontaneously sensitized by TX, for which we determined a higher triplet free energy of +57.2 kcal mol−1.
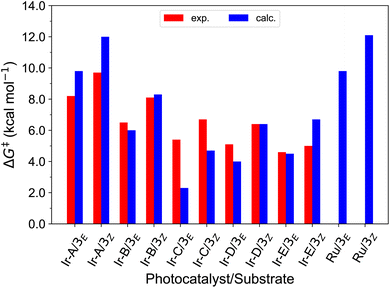
With this in hand, the reaction free-energies and reorganization energies compiled in Table 1 were obtained for the sensitization of 1–4 by the triplet excited state of TX. As inferred from the above analysis of triplet-state energies, all the analyzed EnT processes were found to be thermodynamically favorable, with 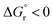 (Table 1, second column). Among them, substrates with highly-conjugated double bonds were found to yield to the most favorable reaction free energies (2, 3 and 4Z). This can be explained by the fact that such conjugation enhances the delocalization of the radicals formed upon sensitization, reducing spin pair repulsion and consequently, stabilizing the triplet state. According to the Marcus theory, a stronger thermodynamic driving force translates into lower free-energy barriers and hence, faster EnT process (see eqn (3) and (4)).
(Table 1, second column). Among them, substrates with highly-conjugated double bonds were found to yield to the most favorable reaction free energies (2, 3 and 4Z). This can be explained by the fact that such conjugation enhances the delocalization of the radicals formed upon sensitization, reducing spin pair repulsion and consequently, stabilizing the triplet state. According to the Marcus theory, a stronger thermodynamic driving force translates into lower free-energy barriers and hence, faster EnT process (see eqn (3) and (4)).
| Substrate | λ R | λ P | Symmetric approachc | Asymmetric approachd | ||||
|---|---|---|---|---|---|---|---|---|
| ΔG‡ | ΔΔG‡e | ΔG‡ | ΔΔG‡e | |||||
| a Energies in kcal mol−1. b Gibbs free energy barriers derived from experimental rate constants reported in ref. 39. c Values obtained assuming kR = kP, through eqn (3). d Values obtained assuming kR ≠ kP, through eqn (4). e Difference between DFT-derived and experimental barriers. | ||||||||
| 1 E | 7.4 | −8.2 | 76.6 | 36.9 | 10.4 | 3.0 | 8.4 | 1.0 |
| 1 Z | 5.4 | −9.2 | 75.8 | 30.2 | 9.1 | 3.7 | 6.2 | 0.8 |
| 2 E | 4.0 | −12.1 | 66.0 | 25.8 | 6.2 | 2.3 | 3.4 | −0.6 |
| 2 Z | 4.5 | −13.3 | 64.5 | 37.2 | 6.9 | 2.4 | 5.4 | 0.9 |
| 3 E | 3.9 | −11.9 | 67.8 | 27.4 | 6.6 | 2.7 | 3.8 | −0.1 |
| 3 Z | 4.4 | −12.1 | 67.7 | 37.9 | 7.8 | 3.4 | 6.2 | 1.8 |
| 4 E | 3.6 | −6.4 | 15.3 | 13.3 | 1.1 | −2.5 | 1.0 | −2.6 |
| 4 Z | 3.7 | −14.4 | 64.0 | 26.5 | 5.2 | 1.5 | 2.5 | −1.2 |
Still, our results also suggest that efficient radical delocalization in the absence of steric constraints that trigger a rotation about the C–C bond in the triplet state leads to less favorable EnT reaction energies, which may be in turn detrimental for the EnT rate, as exemplified by the 4E substrate. Conspicuously, this implies the existence of a sweet spot whereby electronic and steric effects are balanced, leading to optimal EnT kinetics. However, it is important noting that EnT barriers do not only depend on the reaction free energy, but also on the reorganization energy, which strongly benefits from minimal molecular rearrangements upon EnT, as discussed below.
A notable feature of the calculated reorganization energies is that, except for 4E, they are distinctly different when measured on either the reactants (λR) or the products (λP) surface, being ca. 31 kcal mol−1 larger, on average, when determined on the reactants (3TX* + alkene) surface (Table 1). This indicates that the curvature of the products-state surface along the reaction coordinate is less pronounced than that of the reactants. While the contribution of TX to both λ is rather similar (4.8 vs. 4.1 kcal mol−1, Table S1†), those of the alkenes to λR and λP significantly differ, being responsible for the observed disparities. This can be attributed to the fact that the rotation about the C–C bond of the alkene entails a much smaller energy penalty on the triplet state, where the double bond character is lost. Thus, the asymmetric formulation of the Marcus theory (kR ≠ kP, eqn (4)) might be more appropriate than the symmetric one (kR = kP, eqn (3)) to estimate EnT free-energy barriers for these systems. In fact, as shown in Table 1 and graphically illustrated in Fig. 6, the free-energy barriers obtained from the asymmetric approach are consistently closer to the experimental values compared to those obtained through the application of the symmetric one. Typically, the barriers estimated through the asymmetric Marcus formula (eqn (4)) exhibit remarkably small deviations from experimental values of less than 2 kcal mol−1.
 | ||
| Fig. 6 Comparison of the free-energy barriers for EnT from 3TX* to both E and Z isomers of 1–4 as obtained from experimental rate constants39 (red bars) and from DFT calculations through the application of the asymmetric Marcus theory approach (blue bars). | ||
The largest deviations from the experimental behavior are observed for substrate 4. Albeit the discrepancies compared to experimental barriers are still small (−2.6 and −1.2 kcal mol−1 for E and Z isomers, respectively), the estimated barriers are both underestimated and unlike the experimental ones, they present different magnitudes for both isomers. The high degree of consistency between experimental and calculated barriers for 1–3 and the small calculated barriers for 4E and 4Z (1.0 and 2.5 kcal mol−1, respectively) prompted us to hypothesize that the rate of EnT for these substrates is not controlled by the EnT process itself but by diffusion. This implies that the entropy-governed barrier for bringing 3TX* and the alkene together is higher than the intrinsic barrier for the EnT process. Indeed, diffusion barriers are usually of the order of 3–4 kcal mol−1,47 which would explain both the height of the experimentally-determined barriers and the similar kinetics observed for 4E and 4Z, as their underlying diffusion rate is not expected to vary significantly due to their very much resembling physicochemical nature. Thus, EnT steps that are predicted to take place through free-energy barriers of <3 kcal mol−1, it is reasonable to assume that entropic diffusion barriers control the overall sensitization rate, leading to rate constants of the order of 1010 M−1 s−1. It is worth noting that even though 4E and 4Z exhibit significantly different reaction free energies and reorganization energies (Table 1, last two rows), these differences largely cancel out when plugged into eqn (4), resulting in similar free-energy barriers.
Overall, for substrates 1–3, the theoretically-derived rate constants are in good agreement with the experimental ones, the largest deviations of one order of magnitude laying within the range of computational uncertainly (see Table S3†). Moreover, the ratios between theoretical rate constants for E and Z-isomer sensitization align with experimental ones (see Table S3†), reproducing the experimental preference for forming one isomer or the other. As shown in Table 2, the development of microkinetic models using theoretically-derived EnT barriers demonstrate that experimental selectivity trends in terms of E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z ratios at the photostationary state can be qualitatively (if not quantitatively) reproduced (see Fig. S4 for further details†). For substrate 1, a quantitatively accurate E
Z ratios at the photostationary state can be qualitatively (if not quantitatively) reproduced (see Fig. S4 for further details†). For substrate 1, a quantitatively accurate E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z can be successfully predicted (Table 2, entry 1). Although the experimental selectivity toward the Z isomer was also reproduced for substrates 2 and 3, larger discrepancies of up to 30% in products distributions were obtained. Still, a shift of only +1.5 kcal mol−1 on the lowest EnT barrier for each substrate, decreasing the ΔΔG‡ of EnT to E and Z isomers accordingly, leads to E
Z can be successfully predicted (Table 2, entry 1). Although the experimental selectivity toward the Z isomer was also reproduced for substrates 2 and 3, larger discrepancies of up to 30% in products distributions were obtained. Still, a shift of only +1.5 kcal mol−1 on the lowest EnT barrier for each substrate, decreasing the ΔΔG‡ of EnT to E and Z isomers accordingly, leads to E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z ratios that are much closer to the experimental ones (Table 2, entries 3 and 5). We acknowledge that other aspects such as the electronic coupling between substrates and PCs can certainly have an impact on the EnT rate. However, our results reinforce that the classical Marcus theory can be successfully applied to predict EnT kinetics and experimental selectivity trends, albeit precise quantitative assessment of product distributions lies within the range of chemical accuracy. For substrate 4, conversely, the sensitization rate is proposed not to be governed by the obtained, very low EnT barriers, but rather by diffusion ones. Thus, for diffusion-controlled alkene sensitization, selective deracemization can become challenging. However, according to our calculations, it could be attained by photocatalysts with lower triplet energies, which render the EnT step slower than diffusion and hence, rate-limiting, allowing to discriminate between both isomers.
Z ratios that are much closer to the experimental ones (Table 2, entries 3 and 5). We acknowledge that other aspects such as the electronic coupling between substrates and PCs can certainly have an impact on the EnT rate. However, our results reinforce that the classical Marcus theory can be successfully applied to predict EnT kinetics and experimental selectivity trends, albeit precise quantitative assessment of product distributions lies within the range of chemical accuracy. For substrate 4, conversely, the sensitization rate is proposed not to be governed by the obtained, very low EnT barriers, but rather by diffusion ones. Thus, for diffusion-controlled alkene sensitization, selective deracemization can become challenging. However, according to our calculations, it could be attained by photocatalysts with lower triplet energies, which render the EnT step slower than diffusion and hence, rate-limiting, allowing to discriminate between both isomers.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z ratios39 and theoretical ones, derived from EnT rate constants obtained through the asymmetric Marcus theory
Z ratios39 and theoretical ones, derived from EnT rate constants obtained through the asymmetric Marcus theory
| Entry | Substrate |
E![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z ratio exp. Z ratio exp. |
Calc. |
|---|---|---|---|
| a Applied shift of +1.5 in kcal mol−1 to the lowest EnT barrier. | |||
| 1 | 1 | 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
97.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2.7 2.7 |
| 2 | 2 | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 76 76 |
2.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 97.2 97.2 |
| 3 | 2 | 25.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74.8 74.8 |
|
| 4 | 3 | 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 69 69 |
1.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 98.4 98.4 |
| 5 | 3 | 17.9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 82.1 82.1 |
|
3.2 Sensitization of 3 with transition metal-based photocatalysts
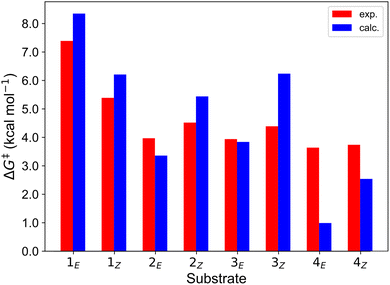
Finally, we further extended our computational analysis to the Ir(III)- and Ru(II)-based PCs represented in Fig. 4, which were experimentally tested against 3E and 3Z. All Ir(III)-containing PCs were observed to successfully sensitize both substrates, although with varying kinetics presumably due to different triplet-state energies, ranging from 55.6 (Ir-A) to 67.1 (Ir-E) kcal mol−1.39 Conversely, no reaction could be attained when using Ru as a PC, which was ascribed to the fact that its triplet energy (50.5 kcal mol−1) is not high enough to allow EnT to the alkenes.As shown in Fig. 7, the asymmetric Marcus equation also provides a rather accurate estimate of EnT free-energy barriers for Ir(III)-based PCs (see Table S2† for numerical values), the largest discrepancies being observed for (Ir-C), which account for 3.0 and 2.0 kcal mol−1. These results reinforce that the classical Marcus theory can indeed serve as a handy tool to evaluate the feasibility of EnT processes through fundamental DFT calculations and to perform computational screenings of potential PC candidates to promote specific photocatalytic transformations, thus saving experimental time and resources. Also, further analysis of the obtained data confirmed that the thermodynamic driving force for the EnT, determined by the triplet-state energy of the PC is indeed an important factor governing the kinetics of the process, as the barriers roughly inversely correlate with the calculated reaction free energies (Fig. S5†). Nevertheless, the reorganization energies of the PCs have a great impact on the heights of the barriers as well (see Fig. S5 and related text in the ESI†). Notably, the smaller reorganization energies obtained for TX and its 2,7-dimethoxy-9H-thioxanthen-9-one derivative (MeOTX) compared to Ir-based ones, explains why they sensitize substrates faster than Ir-based PCs with similar triplet energies, as reported by Gilmour, Kerzig and co-workers39 (see Section 5 of the ESI for further details†).
 | ||
| Fig. 7 Comparison of the free-energy barriers for the sensitization of 3E and 3Zvia EnT by the triplet excited states of transition metal-based PCs as obtained from experimental rate constants39 (red bars) and from DFT calculations through the application of the asymmetric Marcus theory approach (blue bars). | ||
Surprisingly, the calculated barriers obtained for the active Ir-A and the inactive Ru were found to be nearly identical (see Fig. 7 and Table S2†). As determined experimentally39 and further supported by our calculations (Table S5†), the triplet energy of Ru is lower than that of Ir-A, i.e. the singlet-triplet energy gap is narrower for Ru. Accordingly, the thermodynamic driving force for EnT events is smaller for Ru compared to Ir-A (see Table S2†). Nevertheless, the triplet energy of Ir-A was calculated to be ca. 4 kcal mol−1 lower than the experimentally-determined one; while the calculated reorganization energies (λ) were found to be smaller for Ru (Table S1†), so that when plugged into eqn (4), the differences in 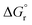 and λ values largely cancel out, leading to very similar barriers. This poses two potential hypotheses:
and λ values largely cancel out, leading to very similar barriers. This poses two potential hypotheses:
In the present context, there are two competitive processes that the catalysts may undergo after triplet-state formation: (i) the EnT to the alkene, which involves nearly equal barriers for both Ru and Ir-A; or (ii) the relaxation to the ground state, which is faster for Ru according to shorter excited state lifetime compared to Ir-A (420 vs. 787 ns).48 On these grounds, the competition between these two processes may hamper the sensitization of substrates by Ru, while still enabling Ir-A to get involved in EnT before decaying to the ground state, explaining thus the experimental outcomes.
Alternatively, given that the calculated triplet energy of Ir-A is somewhat lower than the experimental one, it is indeed likely that our calculations slightly underestimates the exergonic character of EnT events involving the Ir-A photocatalyst (Table S5†), leading to overestimated free-energy barriers (by ca. 2 kcal mol−1), as shown in 7. Although these differences may seem subtle, especially considering that the limits of computational accuracy are generally accepted to range between 1-2 kcal mol−1, they can have a significant impact on the competition between pathways. In fact, assuming a hypothetical case whereby unproductive relaxation and EnT take place through barriers of the same height, a shift of only +1 kcal mol−1 on the EnT barrier changes the distribution of pathways from 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 to 84.4
50 to 84.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15.6, according to a Böltzmann distribution.
15.6, according to a Böltzmann distribution.
Hence, one should note that besides the height of EnT barriers, other parameters such as the ability of the PC to absorb photons, the lifetime of the excited states of the PC, or the accuracy of triplet energies governing EnT free-energies may need to be carefully assessed to safely evaluate the feasibility of photocatalytic processes based on EnT. Moreover, particularly careful assessments need to be made when analyzing EnT processes that involve high enough barriers to allow competing side processes to come into play. Besides the unproductive relaxation of the photocatalyst to the ground state, these may include triplet–triplet annihilation or even degradation of the photocatalysts via loss of ligands in metal-based complexes or hydrogen-atom transfer events involving aromatic ketones such as TX.
4 Conclusions
In this work, we explored the application of the Marcus theory in combination with computational methods to estimate the free-energy barriers underlying energy transfer (EnT) processes, which are fundamental events to photocatalysis. Building upon the indirect sensitization of alkenes with photocatalysts (PCs) via triplet–triplet EnT as a representative example, our results support that the Marcus theory can be effectively applied in combination with DFT-derived reaction free energies and reorganization energies to provide an accurate estimate of EnT barriers, with typical discrepancies of less than 2 kcal mol−1 compared to experimental data.Moreover, our computational exploration also revealed that the use of the ‘asymmetric’ variant of the Marcus theory, whereby reactants- and products-state surfaces are described by symmetric parabolas of different width provides more accurate barriers for the sensitization of alkenes via EnT with an overall mean average error (MAE) of 1.2 kcal mol−1, given that the products surface along the reaction coordinate is significantly flatter due to the biradical nature of the excited alkene. Conversely, the ‘symmetric’ approach, in which both parabolas are assumed of the same width leads to larger discrepancies, with a higher, although still acceptable MAE of 2.3 kcal mol−1. It is worth noting that this approach may be prospectively combined with the Dynamic Vertical Triplet Energy approach49 to refine triplet-state energies and in turn, EnT reaction free energies, further enhancing the predictive ability of the Marcus theory.
We hope that this research inspires the scientific community to delve into the intricacies of EnT processes through the performance of straightforward DFT calculations, which serve as a cost-effective alternative to more sophisticated and computationally-demanding wave function-based methods and semi-classical Marcus expressions that require modeling quantum effects such as the electronic coupling between states. Notably, the adoption of this computational protocol is poised not only to unlock unprecedented computational screenings to streamline and optimize experimental work, but also to elucidate the structure–activity relationships that govern these processes. This, in turn, paves the way for the strategic design of novel photocatalytic systems with enhanced efficiency, thus triggering substantial advances in the emerging field of EnT photocatalysis.
5 Computational details
DFT calculations were carried out at the B3LYP-D3BJ50–54 level of theory using the Gaussian 16 (rev A.03) quantum chemistry package.55 Geometry optimizations and frequency calculations were performed using the cc-pVDZ basis set56 to describe main group elements and the LANL2DZ(f) basis set57,58 and associated pseudopotentials for Ir and Ru metal centers. Electronic energies were corrected by performing single-point calculations on the optimized structures using a more extended basis set, consisting of aug-cc-pVTZ59 and LANL2TZ(f)58,60 for main group elements and metal centers, respectively. Solvent effects of acetonitrile (ε = 35.688) were introduced both in geometry optimizations and energy calculations through the IEF-PCM implicit solvent model,61 as implemented in Gaussian 16. Benchmark studies using a series of commonly employed density functionals were conducted. These studies show that the selected methodology successfully reproduces the triplet energies of the analyzed PCs (Tables S4 and S5†) and that there is no significant difference among the tested hybrid GGA functionals (Table S4†). A dataset collection of the optimized structures for the species discussed in this work is available in the ioChem-BD repository62 and can be accessed viaDOI: https://doi.org/10.19061/iochem-bd-1-319.Free-energy barriers for EnT through the application of the Marcus theory were determined as follows. Given the generic EnT process in eqn (5),
 | (5) |
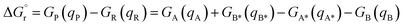 | (6) |
| λR = VA*(qA) − VA*(qA*) + VB(qB*) − VB(qB) | (7) |
| λP = VA(qA*) − VA(qA) + VB*(qB) − VB*(qB*) | (8) |
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
A. S.-D.: conceptualization, methodology, data curation, formal analysis, investigation, visualization, writing – original draft, writing – review & editing. F. M.: conceptualization, methodology, funding acquisition, project administration, resources, software, supervision, validation, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funding is acknowledged from CERCA Programme/Generalitat de Catalunya and Spanish Ministerio de Ciencia e Innovación MCIN/AEI (PID2020–112825RB-IOO and CEX2019–000925-S).References
- D. M. Schultz and T. P. Yoon, Science, 2014, 343, 1239176 CrossRef PubMed.
- S. Dutta, J. E. Erchinger, F. Strieth-Kalthoff, R. Kleinmans and F. Glorius, Chem. Soc. Rev., 2024, 53, 1068–1089 RSC.
- Q.-Q. Zhou, Y.-Q. Zou, L.-Q. Lu and W.-J. Xiao, Angew. Chem., Int. Ed., 2019, 58, 1586–1604 CrossRef CAS PubMed.
- F. Strieth-Kalthoff, M. J. James, M. Teders, L. Pitzer and F. Glorius, Chem. Soc. Rev., 2018, 47, 7190–7202 RSC.
- F. Strieth-Kalthoff and F. Glorius, Chem, 2020, 6, 1888–1903 CAS.
- T. Neveselý, J. J. Molloy, C. McLaughlin, L. Brüss, C. G. Daniliuc and R. Gilmour, Angew. Chem., Int. Ed., 2022, 61, e202113600 CrossRef PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus, J. Phys. Chem., 1963, 67, 853–857 CrossRef CAS.
- R. A. Marcus, Angew. Chem., Int. Ed., 1993, 32, 1111–1121 CrossRef.
- D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850 CrossRef CAS.
- D. L. Dexter and J. H. Schulman, J. Chem. Phys., 1954, 22, 1063–1070 CrossRef CAS.
- J. E. Subotnik, J. Vura-Weis, A. J. Sodt and M. A. Ratner, J. Phys. Chem. A, 2010, 114, 8665–8675 CrossRef CAS PubMed.
- Y. Si, W. Liang and Y. Zhao, J. Phys. Chem. C, 2012, 116, 12499–12507 CrossRef CAS.
- B. Shi, F. Gao and W. Liang, Chem. Phys., 2012, 394, 56–63 CrossRef CAS.
- X. Yang and E. R. Bittner, J. Phys. Chem. A, 2014, 118, 5196–5203 CrossRef CAS PubMed.
- Y. Si, B. Yang, H. Qin, J. Yuan, S. Wang, H. Chen and Y. Zhao, J. Phys. Chem. C, 2015, 119, 8014–8022 CrossRef CAS.
- C. J. Suess, J. D. Hirst and N. A. Besley, J. Comput. Chem., 2017, 38, 1495–1502 CrossRef CAS PubMed.
- L. Cupellini, S. Giannini and B. Mennucci, Phys. Chem. Chem. Phys., 2018, 20, 395–403 RSC.
- H. Zong, J. Wang, X. Mu, X. Xu, J. Li, X. Wang, F. Long, J. Wang and M. Sun, Phys. Chem. Chem. Phys., 2018, 20, 13558–13565 RSC.
- T. S. Lee, Y. L. Lin, H. Kim, R. D. Pensack, B. P. Rand and G. D. Scholes, J. Phys. Chem. Lett., 2018, 9, 4087–4095 CrossRef CAS PubMed.
- H. Zong, X. Mu, J. Wang, H. Zhao, Y. Shi and M. Sun, Spectrochim. Acta, Part A, 2019, 209, 228–233 CrossRef CAS PubMed.
- L. Benatto, C. A. M. Moraes, G. Candiotto, K. R. A. Sousa, J. P. A. Souza, L. S. Roman and M. Koehler, J. Mater. Chem. A, 2021, 9, 27568–27585 RSC.
- X.-X. You, J. Gao, Y.-C. Duan, Y. Geng, M. Zhang, L. Zhao and Z.-M. Su, J. Photochem. Photobiol., A, 2022, 432, 114058 CrossRef CAS.
- A. N. Carneiro Neto, R. T. J. Moura, L. D. Carlos, O. L. Malta, M. Sanadar, A. Melchior, E. Kraka, S. Ruggieri, M. Bettinelli and F. Piccinelli, Inorg. Chem., 2022, 61, 16333–16346 CrossRef CAS PubMed.
- X. Jiang, J. Gao, S. Huang, K. Zhang, L. Tang, M. Li, R. He and W. Shen, J. Phys. Chem. C, 2023, 127, 5950–5957 CrossRef CAS.
- A. De, C. Mora Perez, A. Liang, K. Wang, L. Dou, O. Prezhdo and L. Huang, J. Am. Chem. Soc., 2024, 146, 4260–4269 CrossRef CAS PubMed.
- Z. Zhang, D. Yi, M. Zhang, J. Wei, J. Lu, L. Yang, J. Wang, N. Hao, X. Pan, S. Zhang, S. Wei and Q. Fu, ACS Catal., 2020, 10, 10149–10156 CrossRef CAS.
- V. K. Soni, S. Lee, J. Kang, Y. K. Moon, H. S. Hwang, Y. You and E. J. Cho, ACS Catal., 2019, 9, 10454–10463 CrossRef CAS.
- K. Zhu, Y. Ma, Z. Wu, J. Wu and Y. Lu, ACS Catal., 2023, 13, 4894–4902 CrossRef CAS.
- Y. Zhao, V. A. Voloshkin, E. A. Martynova, B. Maity, L. Cavallo and S. P. Nolan, Chem. Commun., 2024, 60, 3174–3177 RSC.
- E. M. Sherbrook, H. Jung, D. Cho, M.-H. Baik and T. P. Yoon, Chem. Sci., 2020, 11, 856–861 RSC.
- M. Hong, M. Kim, J. Yoon, S.-H. Lee, M.-H. Baik and M. H. Lim, JACS Au, 2022, 2, 2001–2012 CrossRef CAS PubMed.
- Z.-H. Qi and J. Ma, ACS Catal., 2018, 8, 1456–1463 CrossRef CAS.
- A. de Aguirre, I. Funes-Ardoiz and F. Maseras, Angew. Chem., Int. Ed., 2019, 58, 3898–3902 CrossRef CAS.
- J. B. Diccianni, J. Katigbak, C. Hu and T. Diao, J. Am. Chem. Soc., 2019, 141, 1788–1796 CrossRef CAS.
- Z. Benedek, M. Papp, J. Olah and T. Szilvasi, ACS Catal., 2020, 10, 12555–12568 CrossRef CAS.
- A. Solé-Daura, Y. Benseghir, M.-H. Ha-Thi, M. Fontecave, P. Mialane, A. Dolbecq and C. Mellot-Draznieks, ACS Catal., 2022, 12, 9244–9255 CrossRef.
- S. C. Mallojjala, V. O. Nyagilo, S. A. Corio, A. Adili, A. Dagar, K. A. Loyer, D. Seidel and J. S. Hirschi, J. Am. Chem. Soc., 2022, 144, 17692–17699 CrossRef CAS PubMed.
- T. J. B. Zähringer, M. Wienhold, R. Gilmour and C. Kerzig, J. Am. Chem. Soc., 2023, 145, 21576–21586 CrossRef PubMed.
- X. Wang, J. Huang, Y. Liu and S. Chen, Chem. Sci., 2023, 14, 13042–13049 RSC.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701 CrossRef CAS.
- M. C. Henstridge, E. Laborda and R. G. Compton, J. Electroanal. Chem., 2012, 674, 90–96 CrossRef CAS.
- Y. Zeng, P. Bai, R. B. Smith and M. Z. Bazant, J. Electroanal. Chem., 2015, 748, 52–57 CrossRef CAS.
- N. F. Nikitas, P. L. Gkizis and C. G. Kokotos, Org. Biomol. Chem., 2021, 19, 5237–5253 RSC.
- T. Neveselý, M. Wienhold, J. J. Molloy and R. Gilmour, Chem. Rev., 2022, 122, 2650–2694 CrossRef PubMed.
- T. Kratz, P. Steinbach, S. Breitenlechner, G. Storch, C. Bannwarth and T. Bach, J. Am. Chem. Soc., 2022, 144, 10133–10138 CrossRef CAS PubMed.
- M. Besora and F. Maseras, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1372 Search PubMed.
- K. Teegardin, J. I. Day, J. Chan and J. Weaver, Org. Process Res. Dev., 2016, 20, 1156–1163 CrossRef CAS PubMed.
- M. Popescu and R. Paton, ChemRxiv, 2024, DOI:10.26434/chemrxiv-2024-zt9wc.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- T. H. Dunning Jr, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- A. Ehlers, M. Böhme, S. Dapprich, A. Gobbi, A. Höllwarth, V. Jonas, K. Köhler, R. Stegmann, A. Veldkamp and G. Frenking, Chem. Phys. Lett., 1993, 208, 111–114 CrossRef CAS.
- R. A. Kendall, T. H. Dunning Jr and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- L. E. Roy, P. J. Hay and R. L. Martin, J. Chem. Theory Comput., 2008, 4, 1029–1031 CrossRef CAS PubMed.
- E. Cances, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef CAS.
- M. Álvarez-Moreno, C. de Graaf, N. Lopez, F. Maseras, J. M. Poblet and C. Bo, J. Chem. Inf. Model., 2015, 55, 95–103 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional computational results regarding reaction free energies, reorganization energies and free-energy barriers. List of cartesian coordinates for optimized geometries. See DOI: https://doi.org/10.1039/d4sc03352c |
| This journal is © The Royal Society of Chemistry 2024 |