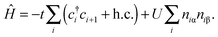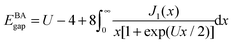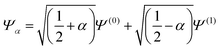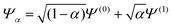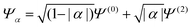Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The derivative discontinuity of the exchange–correlation functional
Paula
Mori-Sánchez
*a and
Aron J.
Cohen
*b
aDepartamento de Química and Instituto de Física de la Materia Condensada (IFIMAC), Universidad Autónoma de Madrid, 28049, Madrid, Spain. E-mail: paula.mori@uam.es
bDepartment of Chemistry, University of Cambridge, Lensfield Rd, Cambridge, CB2 1EW, UK. E-mail: ajc54@cam.ac.uk
First published on 2nd June 2014
Abstract
The derivative discontinuity is a key concept in electronic structure theory in general and density functional theory in particular. The electronic energy of a quantum system exhibits derivative discontinuities with respect to different degrees of freedom that are a consequence of the integer nature of electrons. The classical understanding refers to the derivative discontinuity of the total energy as a function of the total number of electrons (N), but it can also manifest at constant N. Examples are shown in models including several hydrogen systems with varying numbers of electrons or nuclear charge (Z), as well as the 1-dimensional Hubbard model (1DHM). Two sides of the problem are investigated: first, the failure of currently used approximate exchange–correlation functionals in DFT and, second, the importance of the derivative discontinuity in the exact electronic structure of molecules, as revealed by full configuration interaction (FCI). Currently, all approximate functionals, including hybrids, miss the derivative discontinuity, leading to basic errors that can be seen in many ways: from the complete failure to give the total energy of H2 and H2+, to the missing gap in Mott insulators such as stretched H2 and the thermodynamic limit of the 1DHM, or a qualitatively incorrect density in the HZ molecule with two electrons and incorrect electron transfer processes. Description of the exact particle behaviour of electrons is emphasised, which is key to many important physical processes in real systems, especially those involving electron transfer, and offers a challenge for the development of new exchange–correlation functionals.
I. Introduction
The total energy of a system of electrons moving in an external potential, vext(r), in density functional theory (DFT)1,2 is given by| E[ρ] = Ts[ρ] + ∫ρ(r)vext(r)dr + J[ρ] + Exc[ρ] | (1) |
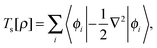 | (2) |
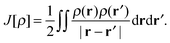 | (3) |
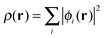 , are solutions of the Kohn–Sham equation
, are solutions of the Kohn–Sham equation| (−½∇2 + vext(r) + vJ(r) + vxc(r))ϕi(r) = εiϕi(r) | (4) |
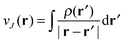 and the exchange–correlation potential is given by the functional derivative of the exchange–correlation energy,
and the exchange–correlation potential is given by the functional derivative of the exchange–correlation energy, 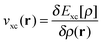 . This is exact Kohn–Sham DFT. With the exact functional, the solution of the Kohn–Sham equation (eqn (4)) to minimise the total energy (eqn (1)) yields the exact energy and density of the Schrödinger equation. However, the exact form of Exc[ρ] is unknown and it is necessary to use density functional approximations (DFA). DFAs have both an approximate energy expression, EDFAxc, and approximate Kohn–Sham potential, vDFAxc(r), giving rise to approximate density, ρDFA(r), and eigenvalues, {εDFAi}.
. This is exact Kohn–Sham DFT. With the exact functional, the solution of the Kohn–Sham equation (eqn (4)) to minimise the total energy (eqn (1)) yields the exact energy and density of the Schrödinger equation. However, the exact form of Exc[ρ] is unknown and it is necessary to use density functional approximations (DFA). DFAs have both an approximate energy expression, EDFAxc, and approximate Kohn–Sham potential, vDFAxc(r), giving rise to approximate density, ρDFA(r), and eigenvalues, {εDFAi}.
A. Density functional approximations
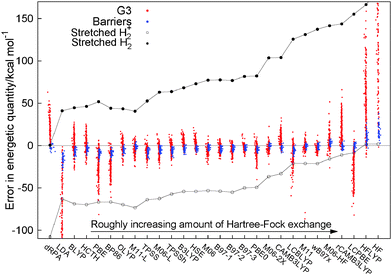
There are many different functional forms, starting with semilocal functionals that range from the local density approximation (LDA)3–5 to the generalized gradient approximation (GGA)6–10 and meta-GGA functionals.11–14 There are also many functionals that mix in Hartree–Fock exact exchange in some manner, such as hybrid functionals with a varying degree of constant admixture of exact exchange, from B3LYP (20% HF) to PBE0 (25%) to M06-2X (54%) and M06-HF (100%).15–21 In the last decade many functionals have emerged that examine the idea of range-separation, with functionals that include all the long-range part of HF exchange (LC-BLYP, LC-ωPBE) to CAMB3LYP and ωB97xd22–25 to mixing in only the short range part of Hartree–Fock.26,27 All these functionals use only the occupied orbitals and fit in a general sense to the first four rungs of Jacob's ladder of density functional approximations.28 On the fifth rung there have been some ideas that use the unoccupied orbitals and eigenvalues in functionals such as B2PLYP,29 which mix in some MP2-like terms or the random phase approximation (RPA), for example direct RPA (dRPA)30,31 which uses the Coulomb only response in the adiabatic fluctuation dissipation theorem.Fig. 1 presents a similar figure to Fig. 8 of ref. 32 to illustrate the performance of a large range of functionals for a set of thermochemical data (the heats of formation of the G3 set33) and a set of reaction barrier heights.34,35 For each of the functionals the calculated error of an energetic quantity for every individual molecules is represented by a single dot, in Fig. 1 each red dot is the error in the heat of formation of a molecule in the G3 set and each blue dot is one of the errors in a reaction barrier height. The results for dRPA for thermochemistry are only for the G2 set36 and the barriers are the DHB24 set37 and the results for these are taken from the paper and ESI of ref. 38 all other calculations are post-B3LYP.32 This allows one to see the performance of many different functionals in a global manner. In addition to the usual thermochemistry and barriers for each individual functional we also plot the errors for the two simplest molecules in the whole of chemistry infinitely stretched H2+ and infinitely stretched H2. Individually these molecules are known to be difficult for functionals to describe with stretched H2+ (ref. 39) epitomising self-interaction error40,41 and stretched H2 the problem of static correlation.42 The errors for these two molecules, as one can see in Fig. 1, are very large but importantly connected. One can see that in changing functionals it is only possible to improve one error but with a corresponding failure on the other, the two seem connected. No functional is able to describe correctly these two simple molecules. It is this connection between different systems that epitomises the challenge of making one functional that can act discontinuously for different particle numbers, which is a markedly different challenge to the usual atomization energies of the G3 set or barrier heights.
While there has been much improvement in the prediction of thermochemistry and reaction barriers over many years, using many different ideas in functionals, there is no functional that can reproduce the energy of these two simple systems. This can be viewed in two ways: one, is that the challenges of chemistry are not so related to the electronic structure of stretched H2/H2+, which has lead to the concept that DFT (and more specifically DFAs) works well as long as one does not stretch bonds. It is hoped that these errors do not cause a problem in the systems under study. However, the other view is that if current approximations are not able to correctly describe these two simple systems, then it should not be expected that for an unknown chemical they will give the correct answer. The key is not to just focus on the system, but on the behaviour of the electrons themselves. The errors in stretched H2/H2+ show a fundamental failure to correctly describe the electrons in those molecules and, as such, the description of similar electronic structure in many other systems will also fail. If these errors are not corrected, the inconsistencies of functionals will continue to dominate over the true behaviour of electrons.
B. Newer ideas in functionals
There are several groups working on new ideas in DFT, which is greatly needed to address the qualitative problems that can be seen in simple model systems. For example, Gori-Giorgi and coworkers are looking at the strictly-interacting λ → ∞ limit of the adiabatic connection for ideas based on strictly correlated electrons (SCE).43–45 The concept of SCE can deal with problem of stretched H2. Other notions beyond DFT, such as partition DFT, have been developed to attempt to tackle some of these problems.46 Burke and coworkers have also looked at exact Kohn–Sham calculations in 1D using the exact functional by doing a DMRG calculation via a density perspective.47 The particle–particle RPA (ppRPA) has been developed for electronic structure theory by van Aggelen, Yang and Yang,48 showing a relation with ladder coupled-cluster.49,50 Becke also has used real space ideas to address non-dynamical correlation and delocalization error using inverse hole models.51,52 There are schemes to combat this issue beyond DFT, from combining multiconfigurational methods with DFT53–55 to embedding methods in quantum chemistry56–59 as well as ideas in density-matrix functional theory. Hopefully, the culmination of these theories will provide new functionals to be able to apply to a large spectrum of chemistry and physics without the drawbacks of many of the currently used functionals.C. Challenge for DFAs
In this paper we highlight the difficult question of the derivative discontinuity of the exchange–correlation functional. The issue of describing the energies of stretched H2+ and stretched H2 with the same functional epitomises this challenge in a clear manner, but there are many other ways to the view the problem. This is a much larger issue than just that of stretching molecules, it is to correctly describe the energy of the electrons in all situations. An improved functional should be able to accurately describe the general behaviour of electrons, especially in interesting physical processes where competing effects act equally. This is the key problem to tackle, so that DFT calculations can describe the important chemical reactions and responses to electric and magnetic fields that are needed for the correct understanding of the behaviour of electrons in enzyme catalysis, Li-ion batteries, solar cells and many other technological applications.II. Derivative discontinuity of the energy versus number of electrons
The famous paper from Perdew, Parr, Levy and Balduz in 198260 showed that the energy for a system with fractional electron number is given by a straight line connecting integer electron numbers| E(N + δ) = (1 − δ)E(N) + δE(N + 1) | (5) |
| ρN+δ(r) = (1 − δ)ρN(r) + δρN+1(r). | (6) |
We will focus on understanding manifestations of the derivative discontinuity in the total energy of integer systems. However, much of the understanding of the DD is often related to the exact Kohn–Sham potential, which was shown by Levy and Perdew61 to undergo a jump by a constant when passing through the integer. This constant, C, is the derivative discontinuity, as ε → 0
| vN−εxc(r) = vNxc(r) |
| vN+εxc(r) = vNxc(r) + C. |
A. Hydrogen atom and flat plane condition
Consider the energy of a hydrogen atom, going from H+ to H−, but with a possibly fractional number of electrons, N = nα + nβ, 0 ≤ N ≤ 2 and also nα ≤ 1 and nβ ≤ 1. This is a very simple system to help understand fractional numbers of electrons. The behaviour of the exact energy is given by the flat plane condition, which is a very stringent test of approximate functionals.72 Especially important is the understanding of the behaviour at N = 1, where two planes intersect giving an energy derivative discontinuity, and to consider adding and subtracting fractional numbers of electrons. More complicated surfaces were also investigated in the work of Gal and Geerlings.73DFAs really struggle to describe the flat plane and they completely fail to recover the discontinuous behaviour seen in the exact behaviour of the energy at N = 1. It is this failure that is connected to (or the root of) all the subsequent failures that we see. For the nα = nβ line, approximate functionals massively fail, as they need to know that on going from E[0.4α,0.4β] → E[0.5α,0.5β] → E[0.6α,0.6β] they have passed through one electron. Compare this with the edge of the flat plane, E[0.8α,0β] → E[1.0α,0β] → E[1.0α,0.2β], where there is a change of the orbital being occupied (from α to β) on passing through the integer. It is clear from the energy expressions of eqn (1) that without a change of orbitals, the only term that can give the discontinuity is the exchange–correlation term. This is where the failure of current functionals and the challenge for future functionals lie. There is also a large discontinuity in the density with electron addition f+ = ρH− − ρH very spatially different from electron removal f− = ρH − ρH+.
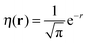 (note the discontinuity could be reduced slightly if the basis function is chosen to be give the correct density at N = 2, i.e.
(note the discontinuity could be reduced slightly if the basis function is chosen to be give the correct density at N = 2, i.e.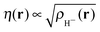 ). Additionally, the use of one basis function provides a direct connection to the Hubbard model where there is also one basis function per site. One of the features of the flat plane condition is that it considers fractional numbers of electrons, which can lead to conceptual confusion as well as technical challenges in extending methods to fractional numbers of electrons.74,75 However, the flat plane condition was developed to explain the root cause in functionals of a general problem that affects real systems and hence can be equally seen in integer systems.
). Additionally, the use of one basis function provides a direct connection to the Hubbard model where there is also one basis function per site. One of the features of the flat plane condition is that it considers fractional numbers of electrons, which can lead to conceptual confusion as well as technical challenges in extending methods to fractional numbers of electrons.74,75 However, the flat plane condition was developed to explain the root cause in functionals of a general problem that affects real systems and hence can be equally seen in integer systems.
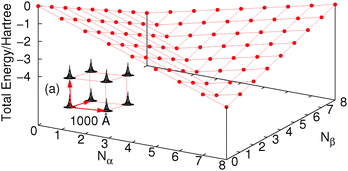
Let us consider a cube of 8 hydrogen atoms (each with one basis function). For this system FCI calculations can be easily carried out with different numbers of electrons and spins as in Fig. 2, where we have used a very large (1000 Å) distance along the edge of the cube just for simplicity. The density at each H atom is constrained by the basis set so an increase in energy happens when more than one electron per site is added; this is exactly the same as in the Hubbard model, where the on-site repulsion U causes an increase in energy past half-filling. Of course if the basis set allowed, these electrons would be unbound from the molecule (or as in a real H atom they would be much more diffuse to slightly lower in energy). These issues could be circumvented by changing the nucleus to be a He atom so that the attraction to the nucleus makes it much more favourable in energy. The real challenge for functionals it is to give the line of discontinuity crossing 8 electrons (one electron per H atom).
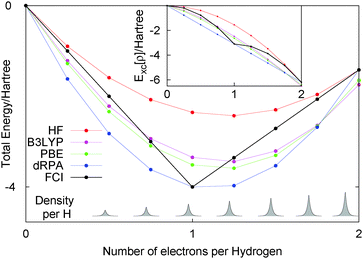
Let us just consider a single line in the flat plane with Nα = Nβ, i.e. only closed shell systems. For this line, calculations with any functional can be easily carried out as the density and orbitals are known. Fig. 3 shows the performance of HF, dRPA, PBE, B3LYP and FCI. First, the FCI energy with 16 electrons (i.e. two electrons per site) is the same as HF, as the basis set does not allow for any electron correlation. As DFT functionals such as PBE and B3LYP treat correlation in a completely different manner, they have a slightly lower energy at 16 electrons. We could have considered just exchange functionals but have left in the correlation part so that one can see the relatively small effect of dynamic correlation functionals.
Overall, all the approximate methods completely fail to reproduce any discontinuous behaviour of the total energy, and have a smooth behaviour in contrast to the correct answer of FCI. For less than one electron per site the energy decreases by −0.5Eh per electron, and for more than one electron per site the energy increases by 0.13Eh per electron. This H8 molecule clearly illustrates the same physics as fractional electron numbers in one single H atom and also the same error of functionals, the missing derivative discontinuity. This example illustrates the important point that the missing derivative discontinuity in functionals can manifest itself as an error in the energy of integer systems.
B. The 1-dimensional Hubbard model
The Hubbard model76 has a very simple Hamiltonian; for a set of sites, i, with creation operators (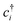 ) and annihilation operators (ci) and the number operator
) and annihilation operators (ci) and the number operator 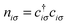 , it contains only hopping terms to nearest neighbour sites and an on site repulsion when occupied by two electrons. It is specified by two parameters t and U
, it contains only hopping terms to nearest neighbour sites and an on site repulsion when occupied by two electrons. It is specified by two parameters t and UThe physics depends only on the ratio U/t so we will fix t = 1 and vary U. It is a much studied system in strongly correlated condensed matter physics as it is a very simple model which describes interacting electrons in narrow energy bands, and which has been applied to problems as diverse as superconductivity, band magnetism, and the metal–insulator transition. The interplay between the delocalised hopping, t, and the localised repulsion, U, can lead to interesting balance in physical behaviours. Here we will examine the 1-dimensional Hubbard model (1D-HM) to highlight the connection with hydrogen atoms and derivative discontinuities, especially that seen at half filling. For the 1D-HM the exact answer is known in the thermodynamic limit using the Bethe-Ansatz, for example, the gap of the 1D-HM is given by77
The Hubbard model is symmetric around half filling (except that above half-filling an electron-interaction term is included) i.e. for a system with 2N sites and doping fraction of M/N
| E[N + M] = E[N − M] + MU. | (7) |
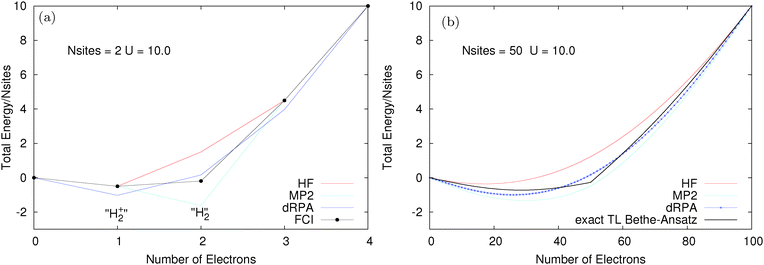
We consider finite Hubbard rings (chains with periodic boundary conditions) where exact results can be computed using FCI. The size of the chain can be increased and the large number of site limit corresponds to the thermodynamic limit. The two site Hubbard model has a very clear connection to infinitely stretched hydrogen molecule, with one electron this corresponds to H2+ and with two electrons to H2. Fig. 4 shows the total energy for two different Hubbard models, both with t = 1 and a large values of U = 10. The two site model is examined in Fig. 4a. The performance of methods is exactly as expected from calculations on stretched H2+/H2; HF and MP2 are good for one electron but fail for two electrons (HF is too high due to static correlation error and MP2 diverges to −∞ as U is increased). dRPA performs better for two electrons at the cost of a massive error for one electron.81 Here, dRPA would still give a gap at half-filling (N = 2). However, as shown for the 50 site model in Fig. 4b, the real problem arises in approaching the thermodynamic limit, where methods such as HF, dRPA or even MP2, smooth out and all semblance of a gap at half-filling disappears. However, the exact Bethe-Ansatz results give a very large gap. The complete failure of functionals to give a derivative discontinuity means that their results on the Hubbard model are completely physically incorrect as they miss one of the key behaviours of true Hubbard electrons.
C. Fractional nuclei: HZ{2e}
A picture of the discontinuous behaviour of the electrons is beautifully illustrated in the two electron example of an H2 like molecule changing the nuclear charge of one of the protons to be fractional, giving HZ{2e}.82 This encompasses a set of systems connected by a very simple change to the one-electron potential. This is a smooth and continuous change to the Hamiltonian, however, how does the electronic structure behave on these small changes, does it also change smoothly? As demonstrated in Fig. 5 the answer is, of course, that it depends. In some cases, as illustrated in short bond distances of HZ{2e}, the electron also moves smoothly on this change. However, at long distances, the electron moves discontinuously, being either on the H or the Z, it is not shared between them.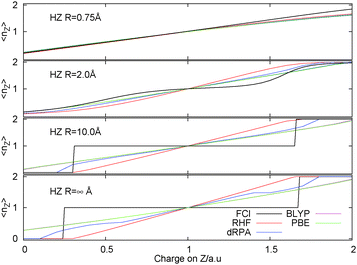 | ||
| Fig. 5 Occupation of Z atom, 〈nZ〉, as the nuclear charge on the Z atom is varied at four different bond lengths comparing FCI and several different approximate DFT functionals. | ||
The true behaviour of electrons, as given by FCI calculations, is simple to understand for HZ{2e} at stretched bond lengths. When Z = 0 there are two electrons on the H atom (i.e. H−) and as Z increases an electron moves from the H to the Z when the energy of putting one electron on the Z atom gives a lower energy. This occurs when the energy of one electron on the Z atom, 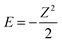 , is lower than the negative of the electron affinity of the H atom (EA(H) = 0.0277 a.u.). This happens at Z = 0.235. The atoms are too far apart to be bonded and no fractional electron transfer happens, as can be understood from the PPLB straight line interpolation of the true FCI energy of eqn (5). Something similar happens around Z = 1.67, where it becomes more energetically favourable to have two electrons on the Z atom and none on the H (at that point the electron affinity of the Z atom crosses 0.5). This is simple and clear, it is just the qualitative failure of functionals that is surprising.
, is lower than the negative of the electron affinity of the H atom (EA(H) = 0.0277 a.u.). This happens at Z = 0.235. The atoms are too far apart to be bonded and no fractional electron transfer happens, as can be understood from the PPLB straight line interpolation of the true FCI energy of eqn (5). Something similar happens around Z = 1.67, where it becomes more energetically favourable to have two electrons on the Z atom and none on the H (at that point the electron affinity of the Z atom crosses 0.5). This is simple and clear, it is just the qualitative failure of functionals that is surprising.
Consider Z = 1, i.e. the H2 molecule, all functionals get a qualitatively correct density due to the symmetry of the problem. However, they respond completely incorrectly to a small change in one of the atoms. DFAs smoothly move electrons when in fact they should not do so; no fractional charge is seen from FCI calculations. This turns the well known static-correlation error in the energy into a qualitative failure in the density. Approximate energy functionals are not able to describe the integer nature of electrons and they do not penalise correctly the splitting up of an electron in these stretched cases.
The HZ{2e} system is very interesting and has advantages over very similar physics that can be seen in asymmetric Hubbard models or Anderson models in that functionals can be simply tested and their performance directly analyzed in real space. The conclusion is that they all fail for this problem. The reasons can be traced back to the failure of functionals for the closed-shell line of the flat plane (see Fig. 3). Along that line these functionals have no clear knowledge that they have passed through one electron and this translates into the problems seen in the density for these systems. This example is very illustrative but it is a slightly hard test as it requires self-consistent determination of the density. For methods such as dRPA, which is usually evaluated with PBE (sometimes HF) orbitals, it requires a self-consistent calculation83 to highlight a problem in the density rather than energy, as carried out for Fig. 5.
III. The derivative discontinuity as a challenge for vxc(r)?
Our main view is that the derivative discontinuity must be understood as a challenge for the energy, Exc[ρ]. For example, in the HZ{2e} problem, a functional that correctly gives the energy for the transfer of an electron would also give a qualitatively correct electron density and energy. For the set of HZ{2e} systems, if the energy is wrong then the density will follow, giving rise to a qualitatively incorrect transfer. An equivalent, but in our view, confusing way to phrase this challenge is about the Kohn–Sham potential. To illustrate this point take the case Z = 1.5 for a stretched geometry as an example. Let us ask the question what is the exact Kohn–Sham potential that gives rise to integer number of electrons on each atom. This is clear in the HZ{2e} system, as we have access to the exact Kohn–Sham potential, vs(r) = vext(r) + vJ(r) + vxc(r). This comes from a very simple rearrangement of eqn (4), substituting in the fact that the density is only made of one orbital,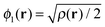 , giving rise to
, giving rise to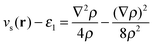 | (8) |
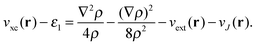 | (9) |
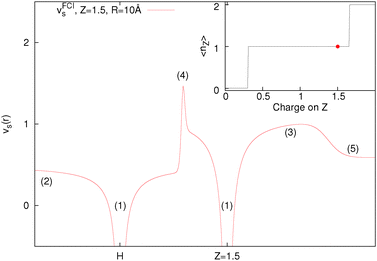
Many plots have been seen in the literature, in both ground state and time-dependent analysis of the potential, for example.84–89 The way to understand any features of the potential is that they are present as a consequence given a particular electron density, i.e. the exact Kohn–Sham potential (eqn (8)) is just a restatement of the density. This is shown in Fig. 6, where we just evaluate eqn (8) with an already minimised FCI density. If the potential shows any bumps it is because it comes from a density that gives rise to that structure, not the other way around. Furthermore, what gives rises to such a density is what is energetically favourable (for example, to have one electron each end), so it is the energy that is key.
Fig. 6 is produced by FCI calculation in a large basis set, but it is completely understandable and the same as that given by a density of the form ρ(r) = n1e−2r + n2e−3(r−10). The divergences at the nuclei (labels (1)) are because ∇2ρ goes as 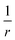 . For an exponent e−2αr, the potential at large r goes to
. For an exponent e−2αr, the potential at large r goes to 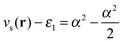 , so on the side of the H atom, e.g. label (2), it goes to a value of +½ and on the side of the Z = 1.5 atom it goes to a value of
, so on the side of the H atom, e.g. label (2), it goes to a value of +½ and on the side of the Z = 1.5 atom it goes to a value of 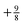 at label (3). The bump in the middle at label (4) is where ∇ρ goes to zero because of the overlapping densities, and the second term on the RHS of eqn (8) disappears, so a value of roughly the average of 12 and 1.52 is obtained. Finally, the change at label (5) is because at long range the e−2r from the H atom dominates over the e−3r behaviour from the Z atom, and from label (5) onwards the structure is a continuation of the line approaching the bump at label (4). Understanding all these features in the potential is of course relatively simple and known, and it should help to dispel any mysterious nature of them.
at label (3). The bump in the middle at label (4) is where ∇ρ goes to zero because of the overlapping densities, and the second term on the RHS of eqn (8) disappears, so a value of roughly the average of 12 and 1.52 is obtained. Finally, the change at label (5) is because at long range the e−2r from the H atom dominates over the e−3r behaviour from the Z atom, and from label (5) onwards the structure is a continuation of the line approaching the bump at label (4). Understanding all these features in the potential is of course relatively simple and known, and it should help to dispel any mysterious nature of them.
We want to stress that the bump in the middle (at label (4)) which has repeatedly been related to the derivative discontinuity, is just because ∇ρ goes to zero at some point in between the atoms where the density is very small, and this can even be thought of as a non-covalent interaction (NCI).90 It is not related to any deeper physics and in particular is nothing to do with stopping electrons moving from one side to another. It should also be noted that the one thing that is not determined by this potential is the constants in front of the density (n1 and n2), this always cancels out. As such, it could be possible to have 0.8 electrons on the H atom and 1.2 electrons on the Z atom with an identical potential (note that the Z atom density would not respond to having more than 1 electron for the potential to remain unchanged). In general, these steps and bumps do not stop the electrons moving, however, having a correct energy functional does.
IV. Unrestricted calculations
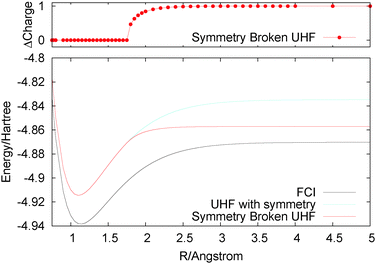
Most of the problems we have highlighted to do with the integer nature of electrons and the derivative discontinuity are in fact well captured by unrestricted type methods. For example, the energies of infinitely stretched H2+ and infinitely stretched H2 are both given by UHF. As H2 is stretched, there is at some bond distance a symmetry breaking (at the Coulson–Fischer point) beyond which the alpha and beta densities can be found each on one of the atoms. Therefore, the spin density is incorrect but the total density and energy are very good. Also for HZ{2e} UHF recovers a discontinuity, and even for the Hubbard model UHF does very well, giving qualitatively correct gaps for all values of U. Of course, there are other known problems for UHF, such as stretching of F2, for which RHF gives a reasonable minimum in terms of geometry but the minimum is actually above the dissociated atoms. RHF also dissociates incorrectly due to static correlation error and in this case the change to UHF does more than just correct the infinite limit, it actually means that UHF curve has no minimum91 (the Coulson–Fischer point is before the minimum in the RHF curve). For F2 one may argue that a method such as UB3LYP gives a reasonable representation of the stretching. Another similar example is given by the stretching of O22+.92Another system that shows up a qualitative problem of the UHF method is that of stretching of He2+. Here, the problem is in symmetry breaking, as illustrated in Fig. 7. Infinitely stretched He2+ with symmetry gives two He½+ atoms. UHF would give too high an energy due to its localization error (a concave behaviour of the energy for fractional systems). However, this too high energy is avoided by breaking the symmetry to give dissociation products of He and He+. This itself does not seem wrong, but the examination of the dissociation curve indicates that the symmetry breaking occurs at too short bond lengths, leading to an incorrect smooth transfer of electrons around 1.8 Å. Also the UHF curve falls off far too quickly compared to the FCI curve. This, of course, is very similar to the symmetry breaking in the spin densities seen in the UHF stretching of H2, which is often argued to be acceptable93 as in H2 the total density is not qualitatively wrong, whereas in the case of He2+ it is incorrect. For He2+, DFT methods such as UB3LYP dissociate with half an electron on each atom but give a completely wrong and much too low energy due to the delocalisation error. Similar symmetry breaking by UHF can be seen in many systems, for example.94
V. Fractional electron transfer coordinate
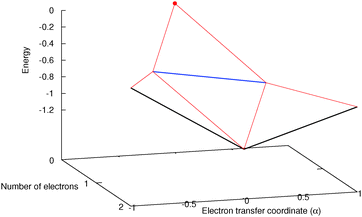
To understand in more detail the problem of the derivative discontinuity in HZ, let us consider the simplest case of HZ stretched to large distance (like 1000a0). We now examine the transfer of electrons from one end of the molecule to another, in just one particular HZ system. In a single basis function per atom calculation this is very easy, as FCI gives just a trivial number of states. Let us first look at the system with one electron, where the FCI states are either one electron on the H, ΨH with energy EH, or one electron on the Z, ΨZ with energy EZ. Let us now consider a state that is a general coherent sum of these,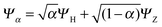 , 0 ≤ α ≤ 1. As ΨH and ΨZ are FCI wavefunctions (one is the ground state the other is the first excited state), they are orthogonal and eigenfunctions of the many-body Hamiltonian, so it is trivially obtained that E[Ψα] = αEH + (1 − α)EZ and ρα(r) = αρH(r) + (1 − α)ρZ(r). This is very akin to fractional numbers of electrons as given by PPLB (eqn (5)), such that when α is varied the energy varies linearly and the electron moves smoothly from the H to the Z. In contrast to PPLB all possible values of electron transfer, α, correspond to an integer system with one electron and are represented by a wavefunction.
, 0 ≤ α ≤ 1. As ΨH and ΨZ are FCI wavefunctions (one is the ground state the other is the first excited state), they are orthogonal and eigenfunctions of the many-body Hamiltonian, so it is trivially obtained that E[Ψα] = αEH + (1 − α)EZ and ρα(r) = αρH(r) + (1 − α)ρZ(r). This is very akin to fractional numbers of electrons as given by PPLB (eqn (5)), such that when α is varied the energy varies linearly and the electron moves smoothly from the H to the Z. In contrast to PPLB all possible values of electron transfer, α, correspond to an integer system with one electron and are represented by a wavefunction.
HZ with two electrons can be analyzed similarly. In this case, at the stretching limit, there are three singlet states with first order density matrices  ,
, 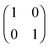 and
and 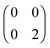 . The FCI wavefunctions that reduce down to give these density matrices are eigenfunctions of the Hamiltonian and orthogonal, so a linear combination of them will give a linear combination of both density matrices and energies. With more basis functions the idea is similar but the analysis more complex as there are many more possible states (one basis function excludes any excited states of the atoms) (Fig. 9).
. The FCI wavefunctions that reduce down to give these density matrices are eigenfunctions of the Hamiltonian and orthogonal, so a linear combination of them will give a linear combination of both density matrices and energies. With more basis functions the idea is similar but the analysis more complex as there are many more possible states (one basis function excludes any excited states of the atoms) (Fig. 9).
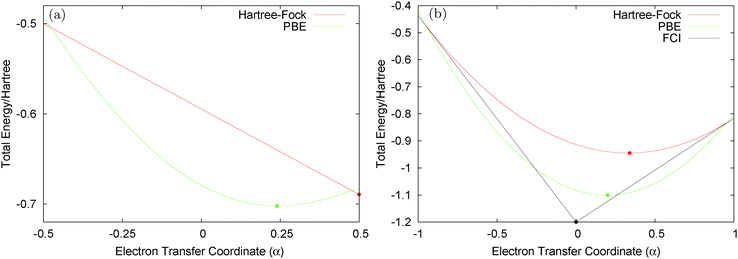
Consider the case of HZ with Z = 1.2 from FCI and compare it with a functional such as PBE, as shown in Fig. 8. First, for one electron (HZ{1e}), where Hartree–Fock and FCI are equivalent, there is a straight line interpolation between the energies of the two atoms. Of course, a minimization of the FCI leads to one electron wholly on one side or the other, in this case the Z atom, as it is much lower in energy. The behaviour of the energy with a functional such as PBE is qualitatively incorrect for one electron, as it does not have the correct linear straight line interpolation, but instead the energy varies smoothly (almost parabolically) with electron transfer. This leads to an incorrect minimum at around 0.26 electron on the H atom and 0.74 electron on the Z atom. The same result could be found with the compatible fractional calculations on each atom and piecing them back together, however, it is very good to see it in an integer electron system with a corresponding wavefunction. To summarise, in Fig. 8, PBE gives a good energy for the ground state Ψ = Ψ(0) (and also for the first excited state Ψ = Ψ(1)) but incorrectly gives a much lower energy for a wavefunction 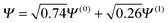 .
.
For the two electron system (HZ{2e}), FCI has a minimum with one electron on each atom (Ψ(0)) and two excited states, one with two electrons on the Z atom (Ψ(1)) and the other with two electrons on the H atom (Ψ(2)). The straight line interpolations to be considered are between the ground state and first excited state and between the ground state and the second excited state. These are the lowest energy ones, a higher energy would be given by the interpolation between the first and second excited states. For any of these wavefunctions, the HF and PBE energies can be trivially evaluated from the density matrix, given that Ts[ρ] for any two electron system is the von-Weizsäcker expression 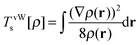 . It is observed in Fig. 8 that both HF and PBE qualitatively fail to describe the electron transfer in this system. The energy on electron transfer is incorrectly smooth for both methods and with minima at the wrong values, HF at 0.33 electron on the H and 1.67 electron on the Z atom, and PBE with 0.4 electron on the H and 1.6 electron on the Z atom. In terms of the wavefunction, PBE is able to give a good energy for the excited states Ψ = Ψ(1) and Ψ(2), but due to its static correlation error PBE is unable to give a good energy for Ψ = Ψ(0). This means that PBE gives an incorrect minimum at
. It is observed in Fig. 8 that both HF and PBE qualitatively fail to describe the electron transfer in this system. The energy on electron transfer is incorrectly smooth for both methods and with minima at the wrong values, HF at 0.33 electron on the H and 1.67 electron on the Z atom, and PBE with 0.4 electron on the H and 1.6 electron on the Z atom. In terms of the wavefunction, PBE is able to give a good energy for the excited states Ψ = Ψ(1) and Ψ(2), but due to its static correlation error PBE is unable to give a good energy for Ψ = Ψ(0). This means that PBE gives an incorrect minimum at 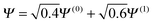 . In general, density functional approximations favour an incorrect fractional charge transfer. Understanding all the possible states of this one system is perhaps a much simpler challenge than understanding many different systems (i.e. changing the molecule by changing Z) and yet captures the same physics.
. In general, density functional approximations favour an incorrect fractional charge transfer. Understanding all the possible states of this one system is perhaps a much simpler challenge than understanding many different systems (i.e. changing the molecule by changing Z) and yet captures the same physics.
VI. Perspectives for the future
The key picture of the derivative discontinuity of the total energy is shown by FCI calculations in Fig. 2 and 3, where the density increases smoothly but the derivative of the energy is discontinuous on passing through one electron per site. Therefore, there is an intrinsic discontinuity in the exchange–correlation term that is a consequence of the particle nature of electrons. Approximate functionals in the literature completely miss this behaviour and the failure in the total energies is clear as, for example, in the qualitative breakdown to describe the energies of stretched H2 and stretched H2+. This error can be transformed into an error in the density as shown in the two electron example, HZ{2e} (Fig. 5). This leads to qualitative failures to describe charge transfer, with an artificial bias to fractionally transfer electrons. Remarkably, this is seen in systems with integer number of electrons characterised by a wavefunction, in contrast to the delocalization error typical of fractionally charged systems.It is clear that the problems caused by missing the derivative discontinuity are not just about stretching molecules, but it is the same physics that occurs in transition metal complexes, chemical reactions, or especially in electron transfer processes. Our hope is that the use of simple chemical model systems gives a more complete understanding of the nature of all types of electronic behaviour that occur in the intricate nature of electronic structure.
The bumps of the exchange–correlation potential at the bond regions, where the density is very small, have been shown to have no effect on how electrons move and, therefore, do not capture the challenge of the derivative discontinuity. This illustrates the point that when the understanding appears quite paradoxical, it is just a clue that a deeper comprehension of the problem is needed.
We have highlighted the importance of the derivative discontinuity as a challenge for the energy functional at an integer number of electrons. We hope that understanding the examples given in this work can help highlight the avenue for development of new exchange–correlation functionals that contain the physics of the derivative discontinuity and represent the integer nature of electrons. This is needed so that DFT can play its role in helping tackle many important technological applications by correctly describing the movements of electrons in systems such as batteries and solar cells, chemical reactions in proteins, and transition metal compounds.
Acknowledgements
We gratefully acknowledge funding from the Royal Society (AJC) and Ramon y Cajal (PMS). PMS also acknowledges grant FIS2012-37549 from the Spanish Ministry of Science.References
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864, DOI:10.1103/PhysRev.136.B864.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133, DOI:10.1103/PhysRev.140.A1133.
- P. A. M. Dirac, Proc. Cambridge Philos. Soc., 1930, 26, 376 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS PubMed.
- J. P. Perdew and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 45, 13244 CrossRef.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef.
- N. C. Handy and A. J. Cohen, Mol. Phys., 2001, 99, 403 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1988, 88, 1053 CrossRef CAS PubMed.
- A. D. Becke and M. R. Roussel, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 3761 CrossRef CAS.
- J. M. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1997, 107, 8554 CrossRef CAS PubMed.
- F. A. Hamprecht, A. J. Cohen, D. J. Tozer and N. C. Handy, J. Chem. Phys., 1998, 109, 6264 CrossRef CAS PubMed.
- T. W. Keal and D. J. Tozer, J. Chem. Phys., 2005, 123, 121103 CrossRef PubMed.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS PubMed.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 234109 CrossRef PubMed.
- J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615 RSC.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef PubMed.
- J. P. Perdew and K. Schmidt, in Density Functional Theory and its Application to Materials, AIP Conference Proceedings, ed. V. VanDoren, C. VanAlsenoy and P. Geerlings, 2001, vol. 577, pp. 1–20.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- D. Bohm and D. Pines, Phys. Rev., 1952, 85, 332 Search PubMed.
- F. Furche, J. Chem. Phys., 2008, 129, 114105 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. T. Yang, Chem. Rev., 2012, 112, 289 CrossRef CAS PubMed.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 2000, 112, 7374 CrossRef CAS PubMed.
- Y. Zhao, B. J. Lynch and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 2715 CrossRef CAS.
- Y. Zhao, N. Gonzalez-Garcia and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 2012 CrossRef CAS PubMed.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 1997, 106, 1063 CrossRef CAS PubMed.
- J. J. Zheng, Y. Zhao and D. G. Truhlar, J. Chem. Theory Comput., 2009, 5, 808 CrossRef CAS.
- Y. Yang, H. van Aggelen, S. N. Steinmann, D. Peng and W. Yang, J. Chem. Phys., 2013, 139, 174110 CrossRef PubMed.
- R. Merkle, A. Savin and H. Preuss, J. Chem. Phys., 1992, 97, 9216 CrossRef CAS PubMed.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048 CrossRef CAS.
- P. Mori-Sánchez, A. J. Cohen and W. T. Yang, Phys. Rev. Lett., 2008, 100, 146401 CrossRef.
- A. J. Cohen, P. Mori-Sánchez and W. T. Yang, J. Chem. Phys., 2008, 129, 121104 CrossRef PubMed.
- P. Gori-Giorgi, M. Seidl and G. Vignale, Phys. Rev. Lett., 2009, 103, 166402 CrossRef.
- P. Gori-Giorgi and M. Seidl, Phys. Chem. Chem. Phys., 2010, 12, 14405 RSC.
- A. Mirtschink, M. Seidl and P. Gori-Giorgi, Phys. Rev. Lett., 2013, 111, 126402 CrossRef.
- J. Nafziger and A. Wasserman, arXiv preprint arXiv:1305.4966, 2013.
- L. O. Wagner, E. Stoudenmire, K. Burke and S. R. White, Phys. Chem. Chem. Phys., 2012, 14, 8581 RSC.
- H. van Aggelen, Y. Yang and W. Yang, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 030501 CrossRef.
- D. Peng, S. N. Steinmann, H. van Aggelen and W. Yang, J. Chem. Phys., 2013, 139, 104112 CrossRef PubMed.
- G. E. Scuseria, T. M. Henderson and I. W. Bulik, J. Chem. Phys., 2013, 139, 104113 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 2005, 122, 064101 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 2013, 138, 074109 CrossRef PubMed.
- A. Savin, Int. J. Quantum Chem., Symp., 1988, 22, 59 CrossRef CAS.
- J. Grafenstein and D. Cremer, Chem. Phys. Lett., 2000, 316, 569 CrossRef CAS.
- A. Stoyanova, A. M. Teale, J. Toulouse, T. Helgaker and E. Fromager, J. Chem. Phys., 2013, 139, 134113 CrossRef PubMed.
- G. Knizia and G. K. L. Chan, Phys. Rev. Lett., 2012, 109, 186404 CrossRef.
- G. Knizia and G. K. L. Chan, J. Chem. Theory Comput., 2013, 9, 1428 CrossRef CAS.
- C. Huang, M. Pavone and E. A. Carter, J. Chem. Phys., 2011, 134, 154110 CrossRef PubMed.
- F. Libisch, C. Huang, P. Liao, M. Pavone and E. A. Carter, Phys. Rev. Lett., 2012, 109, 198303 CrossRef.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz, Jr., Phys. Rev. Lett., 1982, 49, 1691 CrossRef CAS.
- J. P. Perdew and M. Levy, Phys. Rev. Lett., 1983, 51, 1884 CrossRef CAS.
- E. J. Baerends, O. V. Gritsenko and R. van Meer, Phys. Chem. Chem. Phys., 2013, 15, 16408 RSC.
- T. Stein, H. Eisenberg, L. Kronik and R. Baer, Phys. Rev. Lett., 2010, 105, 266802 CrossRef.
- S. Refaely-Abramson, R. Baer and L. Kronik, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 075144 CrossRef.
- L. Kronik, T. Stein, S. Refaely-Abramson and R. Baer, J. Chem. Theory Comput., 2012, 8, 1515 CrossRef CAS.
- T. Stein, J. Autschbach, N. Govind, L. Kronik and R. Baer, J. Phys. Chem. Lett., 2012, 3, 3740 CrossRef CAS.
- I. Dabo, A. Ferretti, N. Poilvert, Y. Li, N. Marzari and M. Cococcioni, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115121 CrossRef.
- E. Kraisler and L. Kronik, Phys. Rev. Lett., 2013, 110, 126403 CrossRef.
- E. Kraisler and L. Kronik, J. Chem. Phys., 2014, 140, 18A540 CrossRef PubMed.
- M. A. Mosquera and A. Wasserman, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 052506 CrossRef.
- J.-D. Chai and P.-T. Chen, Phys. Rev. Lett., 2013, 110, 033002, DOI:10.1103/PhysRevLett.110.033002.
- P. Mori-Sánchez, A. J. Cohen and W. T. Yang, Phys. Rev. Lett., 2009, 102, 066403 CrossRef.
- T. Gal and P. Geerlings, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 81, 032512 CrossRef.
- W. Yang, P. Mori-Sánchez and A. J. Cohen, J. Chem. Phys., 2013, 139, 104114 CrossRef PubMed.
- S. N. Steinmann and W. Yang, J. Chem. Phys., 2013, 139, 074107 CrossRef PubMed.
- J. Hubbard, Proc. R. Soc. A, 1963, 276, 238 CrossRef.
- E. H. Lieb and F. Y. Wu, Phys. Rev. Lett., 1968, 20, 1445 CrossRef.
- N. A. Lima, M. F. Silva, L. N. Oliveira and K. Capelle, Phys. Rev. Lett., 2003, 90, 146402 CrossRef CAS.
- V. V. França, D. Vieira and K. Capelle, New J. Phys., 2012, 14, 073021 CrossRef.
- K. Capelle and V. L. Campo Jr., Phys. Rep., 2013, 528, 91 CrossRef CAS PubMed.
- P. Mori-Sánchez, A. J. Cohen and W. T. Yang, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 042507 CrossRef.
- A. J. Cohen and P. Mori-Sánchez, J. Chem. Phys., 2014, 140, 044110 CrossRef PubMed.
- P. Mori-Sánchez, W. T. Yang and A. J. Cohen, 2014, manuscript in preparation.
- J. P. Perdew, in Density Functional Methods in Physics, ed. R. M. Dreizler, Providencia, 1985, pp. 265–308 Search PubMed.
- O. V. Gritsenko, R. van Leeuwen and E. J. Baerends, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 52, 1870 CrossRef CAS.
- N. Helbig, I. V. Tokatly and A. Rubio, J. Chem. Phys., 2009, 131, 224105 CrossRef CAS PubMed.
- D. G. Tempel, T. J. Martinez and N. T. Maitra, J. Chem. Theory Comput., 2009, 5, 770 CrossRef CAS.
- M. Hellgren and E. K. U. Gross, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 022514 CrossRef.
- J. I. Fuks, P. Elliott, A. Rubio and N. T. Maitra, J. Phys. Chem. Lett., 2013, 4, 735 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-Garcia, A. J. Cohen and W. T. Yang, J. Am. Chem. Soc., 2010, 132, 6498 CrossRef CAS PubMed.
- V. Klimo and J. Tiňo, Collect. Czech. Chem. Commun., 1981, 46, 1365 CrossRef CAS.
- R. H. Nobes, D. Moncrieff, M. W. Wong, L. Radom, P. M. W. Gill and J. A. Pople, Chem. Phys. Lett., 1991, 182, 216 CrossRef CAS.
- J. P. Perdew, A. Savin and K. Burke, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 51, 4531 CrossRef CAS.
- T. Stein, C. A. Jiménez-Hoyos and G. E. Scuseria, J. Phys. Chem. A, 2014 DOI:10.1021/jp410713d.
| This journal is © the Owner Societies 2014 |