Engineering the crystallization behavior of an organic compound mixed with polymers using hidden liquid phase domains†
Gagan N.
Kangovi
and
Sangwoo
Lee
 *
*
Department of Chemical and Biological Engineering, Rensselaer Polytechnic Institute, Troy, New York 12180, USA. E-mail: lees27@rpi.edu
First published on 30th July 2019
Abstract
The crystallization behavior of pyrene mixed with polystyrene, poly(ethylene-alt-propylene), or poly(2-vinylpyridine) is investigated using the differential scanning calorimetry (DSC) technique to understand the effects of polymers on the crystallization behavior of organic compounds. Extensive DSC characterization reveals that all the crystallization curves of pyrene as a function of polymer composition have upper critical crystallization temperatures. We believe the upper critical behavior suggests that the crystallization of pyrene in the polymer solutions are directed and assisted by the spinodal limits of the hidden liquid–liquid phase domains located inside the two-phase domains of pyrene crystals and polymer-rich liquid phases. We also observed that, for pyrene mixed with relatively non-polar polystyrene or poly(ethylene-alt-propylene), the crystallization temperature curves of pyrene shift with the melting temperature curves of pyrene crystals. This result is consistent with the classical Flory–Huggins theory which describes the thermodynamic behavior of polymer solutions using the chemical compatibility between the solvent and polymer. In contrast, the crystallization curve of pyrene mixed with relatively polar poly(2-vinylpyridine) is observed in the higher temperature domain despite the melting temperature curve of the pyrene crystals with poly(2-vinylpyridine) being shifted to the lower temperature domain due to the favorable chemical compatibility between pyrene and poly(2-vinylpyridine) compared to those with the other relatively non-polar polymers. We attribute the contrasting melting and crystallization behavior of pyrene in the poly(2-vinylpyridine) solutions to the high dipole moment of poly(2-vinylpyridine) that induces an enlarged hidden liquid phase domain due to the attractive interactions between poly(2-vinylpyridine) segments. These findings show that polymers are effective and versatile additives for controlled crystallization of organic compounds using the hidden liquid–liquid phase domains.
Design, System, ApplicationThe crystallization process directly impacts the structures and morphologies of crystalline compounds that control the properties of the crystalline solids. However, the control of crystallization is challenging due to the stochastic nature of the nucleation step. This report describes new avenues to utilize polymers for controlled crystallization of organic compounds through engineering the hidden liquid phase domains inside the two-phase domain of an organic crystal and a polymer solution. We found that the crystallization behavior of pyrene, a model organic crystalline compound, mixed with a set of representative polymers show upper critical crystallization temperatures suggesting that the crystallization of pyrene is directed and assisted by the spinodal limits of hidden liquid phase domains. Since the phase behavior of polymer solutions can be designed by the choice of polymer species and molecular weights of polymers, the spinodal-assisted crystallization behavior of organic compounds mixed with polymers can be also designed accordingly. This connection between the crystallization and hidden liquid phase domains provides important insights into engineering the crystallization process of organic compounds such as pharmaceutically active ingredients using the thermodynamics of polymer solutions to obtain target crystal structures and properties. |
1. Introduction
The control of crystal structures and morphologies of solid compounds is important for various practical applications such as materials engineering, device fabrication, and pharmaceutical use of crystalline molecules. For example, the mechanical properties of carbon steel drastically change with the microstructures of crystal grains controlled by crystallization and heat-treatment processes.1,2 Electrical properties of organic conducting materials are significantly influenced by their crystal structures and morphologies.3–7 The solubility of pharmaceutically active ingredients, which is the limit of their biological availability, also varies with their crystalline structures.8–12Since the structures and morphologies of crystalline compounds are significantly controlled by the crystallization process,13,14 understanding the thermodynamics and kinetics of the crystallization process is important to obtain target structures and properties of crystals. However, because the nucleation step, initiation of the crystallization process, is highly stochastic and often difficult to predict,15,16 external compounds such as seeding materials and selective solvents are widely employed for controlled and reliable production of crystal products.14,17–22 A well-controlled crystallization process is also important in obtaining target crystal structures because the crystal structures, i.e., polymorphs, change with the domain size of crystal grains as observed from representative experimental systems, such as glycine, ice, and model spherical particles;23–25 the size of crystal domains determined by the crystallization process also controls the crystal structures.
The classical nucleation theory delineates that the formation of a new phase domain, which is driven by the free energy difference between the initial and new phases, must overcome the kinetic energy barrier imposed by interfacial energy between the new and metastable phases.26 Since interfacial energy is proportional to the difference between the cohesive energy densities of two phases in contact,27 forming an intermediate phase that has a cohesive energy density close to those of the new phases lowers the interfacial energy and subsequently lowers the kinetic energy barrier of nucleation. For the crystallization process in a binary liquid mixture, ten Wolde and Frenkel pointed out that hidden liquid phase domains inside the two-phase domains of crystals and saturated solutions could be important for controlled crystallization as the fluctuation-induced dense liquid-like domains near critical points can serve as domains that lower the kinetic energy barrier for nucleation.28 The importance of the hidden liquid phase domains in the nucleation process for crystallization is also recognized for semi-crystalline polymers.29–32 The spinodal curve of the hidden liquid phase domain of semi-crystalline polymers induces the phase separations of liquid phase domains in which the polymer chains are believed to adopt chain conformations close to the crystalline states and consequently lower the energy barriers for crystallization of the polymer chains. These examples show the importance of hidden liquid phase domains for the crystallization, perhaps, of all material classes.30
Although the crystallization behavior of semi-crystalline polymers assisted by the hidden liquid–liquid phase domains has been reported,29–32 as far as we are aware, the idea of using polymers as crystallization-controlling agents for crystallizing other compounds has never been considered except in our earlier report.33 We believe that the thermodynamics of polymer solutions suggests that polymers are ideal compounds for controlled crystallization of organic molecules using the spinodal limits of hidden liquid–liquid phase domains; the locations of the critical points of liquid phase domains are compositionally asymmetric due to the large size of polymer chains,34 and, therefore, the required amount of polymers for spinodal-assisted crystallization can be minimized. Also, the nearly unlimited choice of polymer species and continuously variable molecular weights of polymers enable to nearly freely tune the location of the critical points of the liquid domains for target crystallization conditions. However, despite these advantages of polymers as crystallization-assisting compounds, so far, polymers mostly have been examined to quantify the solubility of organic crystal compounds in a polymer matrix or to control the dissolution kinetics of organic crystals with polymer excipients.35–38
In this article, we report the crystallization temperatures of pyrene mixed with a set of representative model polymers, polystyrene (PS), poly(ethylene-alt-propylene) (PEP), and poly(2-vinylpyridine) (P2VP), shown in Fig. 1, using the differential scanning calorimetry (DSC) technique to provide insights into the controlled crystallization of organic compounds using polymers. We found that all the crystallization curves of pyrene mixed with the model polymers display upper critical crystallization temperatures which suggest the existence of hidden liquid–liquid phase domains of pyrene-rich and polymer-rich solutions inside the two-phase domains of pyrene crystals and polymer solutions. For pyrene mixed with the relatively non-polar polymers, PS and PEP, the crystallization curves of pyrene shift along with the melting curves of pyrene crystals. This result is consistent with the classical Flory–Huggins theory that describes the phase behavior of polymer solutions and the solubility of crystals in polymers using the interaction parameter, the relative chemical compatibility between the solvent and polymer;39,40 the locations of the melting curves of pyrene crystals and the spinodal curves of the hidden liquid phase domains are both dependent on the interaction parameter. In contrast, the crystallization curve of pyrene mixed with the relatively polar polymer P2VP is found to be located in the higher temperature domain despite the melting temperature curve of pyrene crystals with P2VP existing in the low-temperature domain due to the favorable chemical compatibility between pyrene and P2VP, which we reported earlier.38 We attribute the high-temperature crystallization curve of pyrene with P2VP to the relatively strong dipole moments of P2VP segments which promote the association of the P2VP chain segments and consequently shift up the hidden liquid phase domain to the high-temperature domain. These results show that polymers are effective and versatile molecules for engineering the crystallization of organic compounds.
2. Experimental section
2.1. Materials
Styrene (Acros, 99%) was purified twice over di-n-butylmagnesium and vacuum distilled. 2-Vinylpyridine (Acros) was dried with activated basic alumina. Isoprene (Acros, 98%) was purified over n-butyllithium twice and vacuum distilled. The purified monomers were immediately used for polymerization using a high vacuum anionic polymerization technique.41sec-Butyllithium (Aldrich, 1.4 M solution in cyclohexane) and pyrene (Alfa Aesar) were used as received. Pyrene had a nominal purity of 98%, but we could not detect noticeable impurities by gas chromatography and mass spectroscopy analysis. Tetrahydrofuran (Sigma-Aldrich, HPLC grade) was purified with activated alumina pellets (BASF F-200). Cyclohexane (Sigma-Aldrich, ACS grade) was purified with activated alumina (BASF F-200) and copper catalyst pellets (BASF Q-5). Nickel(II) 2-ethylhexanoate (Aldrich, 0.1 M solution in 2-ethylhexanoic acid) and triethylaluminum (Aldrich, 1 M solution in hexane) were used as received for catalyst preparation for hydrogenation.2.2. Polymer synthesis and characterization
Polystyrene and polyisoprene were synthesized in cyclohexane at 40 °C.42 Poly(2-vinylpyridine) was polymerized in tetrahydrofuran at −78 °C.43 Poly(ethylene-alt-propylene) was synthesized by hydrogenation of polyisoprene in cyclohexane at 77 °C and 600 psi for 24 h using a Ni–Al catalyst.44 Complete hydrogenation of polyisoprene was confirmed with 1H NMR spectroscopy. The synthesized polymers were precipitated in methanol (polystyrene and polyisoprene) or hexane (poly(2-vinylpyridine)) and dried under dynamic vacuum at elevated temperatures. The molecular weight distributions of the synthesized polymers were determined using size exclusion chromatography systems (SEC, Agilent) equipped with a refractive index detector. Three consecutive PLgel Mixed-C columns were used as the stationary phase, and tetrahydrofuran (30 °C) or N,N-dimethylformamide (45 °C) as the mobile phase (1 ml min−1). Monomer configurations and number-averaged molecular weights of the synthesized polymers were determined by 1H NMR spectroscopy (Bruker 800 MHz spectrometer). NMR characterization did not find any sign of residual solvents or other impurities from the dried polymers.2.3. Differential scanning calorimetry (DSC) characterization
Homogeneous binary mixtures of the model polymers and pyrene were prepared by dissolving weighed polymers and pyrene in dichloromethane in vials, drying the solutions in aluminum pans at room temperature, homogenizing the dried mixtures on a hot plate at 165 °C for 15 minutes, and rapidly quenching the mixtures in liquid nitrogen. The compositions of the prepared binary mixtures were confirmed with 1H NMR spectroscopy. Thermal properties of the mixtures were characterized using a Q2000 (TA Instruments) differential scanning calorimeter (DSC), and the polymer and pyrene samples (5–10 mg) were contained in hermetic pans.DSC thermograms were obtained to measure the crystallization temperatures of pyrene by the following heat-treatment procedure. The sample was heated to 200 °C, higher than the melting temperature of pyrene (Tm,PY = 154 °C), and annealed for 20 min to homogenize the pyrene and polymer mixtures, and cooled to −50 °C at the rates of 5 °C min−1, 10 °C min−1, 20 °C min−1 and 30 °C min−1.
3. Results and discussion
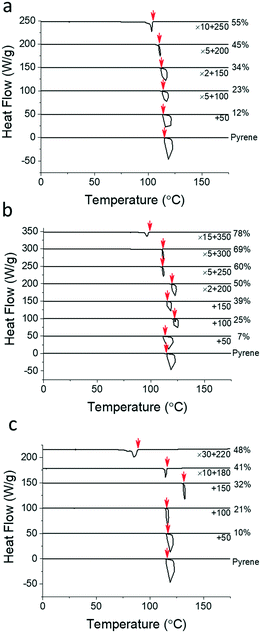
Table 1 summarizes the molecular characterization results of the PS, PEP, and P2VP polymers employed for this study. These polymers have comparable number-averaged molecular weights, Mn = 20 to 26 kg mol−1, and degrees of polymerization, N = 159 to 187, based on the molar volume of crystalline pyrene.38Fig. 2 shows the representative cooling thermograms of the pyrene and polymer mixtures obtained at 10 °C min−1 to determine the pyrene crystallization temperatures, Tc (see Fig. S1–S4 in the ESI† for the thermograms at the other cooling rates). The initiation temperatures of pyrene crystallization marked with red arrows are taken as the crystallization temperatures of pyrene in homogeneous mixtures.33 The Tc values of pyrene crystallization are measured from at least three different samples and averaged.| Polymer | M n (kg mol−1) | Đ | ρ (g cm−3) | N |
|---|---|---|---|---|
| a Number-averaged molecular weight. b Polydispersity by SEC. c Density at 25 °C.45–47 d Degree of polymerization based on the molar volume of pyrene (159 cm3 mol−1) in the crystalline state.48 e Determined by SEC using polystyrene standards. f Determined based on the Mn of precursor polyisoprene (24.8 kg mol−1) assuming 100% hydrogenation of polyisoprene which is confirmed with 1H NMR spectroscopy. The Mn of precursor polyisoprene was determined by SEC using a polystyrene standard and the Mark–Houwink parameters of polyisoprene in tetrahydrofuran at 30 °C, a = 0.731 and k = 15.7 × 10−5 dl g−1.49 The polyisoprene chains have 94% 1,4- and 6% 3,4-configurations. g Determined by the end-group analysis using 1H NMR spectroscopy. | ||||
| Polystyrene | 23.4e | 1.13 | 1.04 | 159 |
| Poly(ethylene-alt-propylene) | 25.5f | 1.09 | 0.86 | 187 |
| Poly(2-vinylpyridine) | 20.3g | 1.02 | 1.12 | 166 |
Fig. 3 presents the phase diagrams of the binary mixtures of pyrene and PS, PEP, and P2VP elucidated from the extensive DSC characterization. The characterization data of the mixtures are summarized in Table S1 in the ESI.† The melting temperatures of pyrene crystals characterized from the heating DSC thermograms in our earlier study asymptotically decrease with the volume fraction of the polymer component ϕp.38 The depressed melting temperature of pyrene crystals in a polymer solution, Tm, has the following relationship:
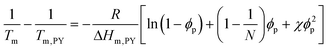 | (1) |
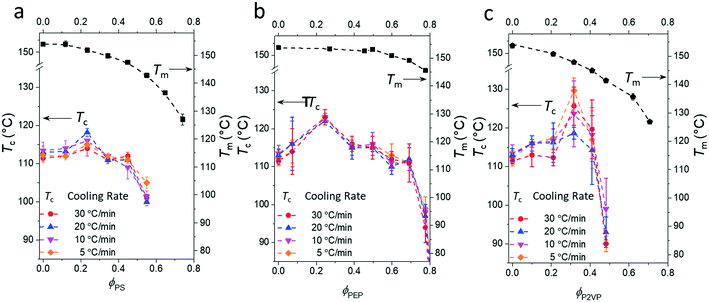 | ||
| Fig. 3 Phase diagrams of the binary mixtures of pyrene and (a) polystyrene (PS), (b) poly(ethylene-alt-propylene) (PEP), or (c) poly(2-vinylpyridine) (P2VP) showing the crystallization temperatures, Tc, and the melting temperatures, Tm, of pyrene crystals. The melting temperatures are taken from ref. 38. | ||
In contrast, all the crystallization curves of pyrene extracted from the cooling DSC thermograms in Fig. 3 and S1–S4 in the ESI† have reproducible upper critical crystallization temperatures that cannot be explained with the classical nucleation theory. The Gibbs energy of the formation of a spherical nucleus by the classical nucleation theory (the spherical geometry of the nucleus is assumed for simplicity) is
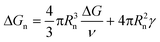 | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S where kB is the Boltzmann constant, T is the temperature, and S = ϕPY/ϕePY is the supersaturation ratio, where ϕPY is the volume fraction of pyrene of a metastable homogeneous mixture and ϕePY is the equilibrium volume fraction of pyrene of the polymer-rich phase in the phase-separated state. Partial differentiation of eqn (2) gives the critical nucleus radius:
S where kB is the Boltzmann constant, T is the temperature, and S = ϕPY/ϕePY is the supersaturation ratio, where ϕPY is the volume fraction of pyrene of a metastable homogeneous mixture and ϕePY is the equilibrium volume fraction of pyrene of the polymer-rich phase in the phase-separated state. Partial differentiation of eqn (2) gives the critical nucleus radius: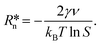 | (3) |
In our earlier work, we estimated the size of the critical nucleus for pyrene crystallization in the PS solution using eqn (3) and found that the critical nucleus size increases with the volume fraction of PS (see Fig. 10 in ref. 33). However, this result based on the classical nucleation theory of supersaturated solutions cannot explain the upper critical behavior of the crystallization temperature curves in Fig. 3. We also conducted annealing experiments of homogeneous pyrene and PS solutions in the temperature window between the melting and crystallization curves of pyrene to confirm that the upper critical temperatures are not caused by delayed initiation events. We found that these annealing experiments did not initiate pyrene crystallization at least over periods of several hours, and this result suggests that the origin of the upper critical features neither originate from the slow nucleation process nor from the growth process. Because the formation of nuclei is a dynamic and time-dependent process,26 the critical nucleus size from eqn (2) cannot be the single factor that regulates the initiation rates of crystallization. However, the upper critical crystallization temperatures, which are consistently observed from all the pyrene and polymer mixtures investigated in this study, suggest that a certain thermodynamic factor is involved in the critical behavior of the crystallization curves.
We believe that the crystallization of pyrene observed from the cooling ramps of DSC experiments are initiated by preceding liquid–liquid phase separations of the supercooled solutions into pyrene-rich and polymer-rich phases directed by the hidden liquid phase domains with upper critical solution temperatures as schematically represented in Fig. 4. When the supercooled homogeneous pyrene and polymer solutions reach the spinodal limit of the hidden liquid phase domain, liquid phase separation immediately occurs by diffusion.51 The formation of spinodally induced liquid phase domains also decreases the kinetic energy barrier of the nucleation events for crystallization because the interfacial energy, which is the kinetic energy barrier of nucleation and is proportional to the difference between the cohesive energy densities of two phases in contact, also decreases.27 The dense liquid phase induced by the spinodal decomposition reduces the interfacial energy and the kinetic energy barrier for the formation of crystal nuclei. Furthermore, the crystallizing compounds in the dense phase are believed to have densely-packed molecular conformations which are close to the states of crystals and consequently have lower kinetic energy barriers of nucleation for crystallization.29
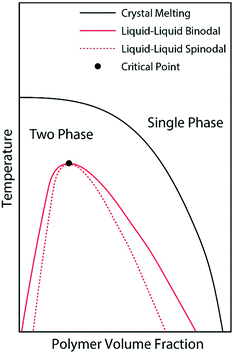 | ||
| Fig. 4 Schematic phase diagram representation of the pyrene and polymer solutions after the phase diagrams in ref. 28, 52 and 53. The liquid phase domain is located in the two-phase domain of pyrene crystal and polymer solutions. | ||
However, although the upper critical temperatures of crystallization curves strongly suggest the existence of hidden liquid–liquid phase domains, the locations of the critical points do not quantitatively align with the prediction of the classical Flory–Huggins theory.34 The volume fractions of polymers of the critical points extracted from the crystallization curves by the DSC measurements are ϕPS,c ≈ 0.23, ϕPEP,c ≈ 0.25, and ϕP2VP,c ≈ 0.32, and these critical compositions are at least three times larger than the critical point composition based on the Flory–Huggins theory, 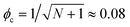 . We attempted to construct binodal curves by assuming the crystallization curves as spinodal limits of the hidden liquid–liquid phase domains but failed to obtain physically reasonable binodal behaviors. It is not clear why these critical points significantly deviate from the theoretical quantity. A suggestive observation of the phase behavior regarding the inconsistent critical temperatures we would note is that the crystallization of pure pyrene also occurs in a very narrow temperature range, TPY,c = 113 °C ± 2 °C, regardless of the cooling rates employed in this study (5–30 °C min−1). We conducted annealing experiments of the supercooled pure pyrene in the molten state in the temperature window between the melting and crystallization temperatures of pure pyrene and observed that the supercooled pure pyrene in this temperature window did not crystallize at least over several hours of annealing periods as the pyrene and polymer solutions did not crystallize in the annealing tests. The long-lasting metastability and narrow crystallization temperature of pure pyrene appear to indicate that the crystallization of molten pyrene is also preceded by liquid–liquid phase separation directed by a hidden liquid phase domain in the temperature–density phase space which is similar to the spinodal-assisted crystallization of semi-crystalline polymers.29,30Fig. 5 shows a schematic representation of the phase space of the pyrene and P2VP solution with the assumed hidden liquid phase domains in the temperature–density (ρ) and the temperature–composition (ϕP2VP) phase planes. We speculate that the critical point of the hidden liquid phase domain of pure pyrene in the temperature–density plane influences the liquid phase domain in the temperature–composition domain of the pyrene and polymer solutions because the critical points must have a continuous transition between these phase space domains.
. We attempted to construct binodal curves by assuming the crystallization curves as spinodal limits of the hidden liquid–liquid phase domains but failed to obtain physically reasonable binodal behaviors. It is not clear why these critical points significantly deviate from the theoretical quantity. A suggestive observation of the phase behavior regarding the inconsistent critical temperatures we would note is that the crystallization of pure pyrene also occurs in a very narrow temperature range, TPY,c = 113 °C ± 2 °C, regardless of the cooling rates employed in this study (5–30 °C min−1). We conducted annealing experiments of the supercooled pure pyrene in the molten state in the temperature window between the melting and crystallization temperatures of pure pyrene and observed that the supercooled pure pyrene in this temperature window did not crystallize at least over several hours of annealing periods as the pyrene and polymer solutions did not crystallize in the annealing tests. The long-lasting metastability and narrow crystallization temperature of pure pyrene appear to indicate that the crystallization of molten pyrene is also preceded by liquid–liquid phase separation directed by a hidden liquid phase domain in the temperature–density phase space which is similar to the spinodal-assisted crystallization of semi-crystalline polymers.29,30Fig. 5 shows a schematic representation of the phase space of the pyrene and P2VP solution with the assumed hidden liquid phase domains in the temperature–density (ρ) and the temperature–composition (ϕP2VP) phase planes. We speculate that the critical point of the hidden liquid phase domain of pure pyrene in the temperature–density plane influences the liquid phase domain in the temperature–composition domain of the pyrene and polymer solutions because the critical points must have a continuous transition between these phase space domains.
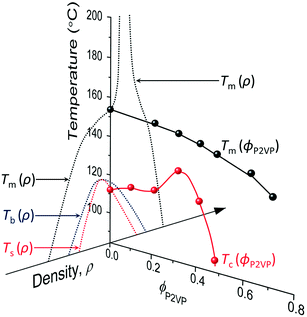 | ||
| Fig. 5 Phase space representation of the crystallization and melting temperatures of pyrene mixed with poly(2-vinylpyridine). The phase diagram of pure pyrene in the temperature–density plane is taken from the phase diagrams in ref. 29 and 53. The arrowhead of the density axis indicates the direction of larger density. The crystallization temperature of pyrene is assumed to start from the spinodal limit in the high-density liquid side. | ||
Although the critical points of crystallization curves do not quantitatively align with those of the theory, we assumed the crystallization curves as spinodal limits to conduct a semi-quantitative analysis of the effective interaction parameters of pyrene and the polymers. From the crystallization curves, the effective interaction parameters between pyrene and the polymers are extracted using the Flory–Huggins theory. The Flory–Huggins theory models the Gibbs energy of mixing per mole of lattice sites for polymer solutions:
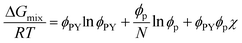 | (4) |
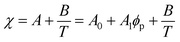 | (5) |
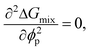 | (6) |
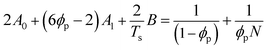 | (7) |
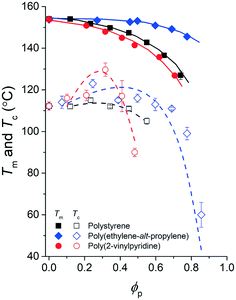 | ||
| Fig. 6 Phase diagram of the pyrene and polymer mixtures with extracted spinodal curves. The experimental melting temperatures of pyrene crystals, Tm, are noted with solid symbols, and the crystallization temperatures of pyrene, Tc, are noted with open symbols. The spinodal curves (dashed lines) extracted based on the Tc values using eqn (7) are presented over the Tc values. | ||
Table 2 summarizes the A0, A1, and B parameters of the effective interaction parameters from eqn (5) extracted from the crystallization temperatures using eqn (7) and the melting temperatures of pyrene crystals from eqn (1) in our earlier report.38 The χ values extracted based on the crystallization and melting temperatures using the Flory–Huggins theory do not quantitatively agree as shown in Fig. S5 in the ESI.† The inconsistent effective interaction parameters extracted by different experimental techniques have been reported for various polymer systems, and the origin of the inconsistency is still not well understood.55,56 In our case, even the assumed spinodal limit temperatures based on the crystallization points are not likely quantitatively correct as signaled by the critical points deviating from the theoretical volume fractions of polymers in the mixtures.
| Polymer | From liquid–liquid spinodala | From liquid–crystal binodalb | ||||
|---|---|---|---|---|---|---|
| A 0 | A 1 | B (K) | A 0 | A 1 | B (K) | |
| a Parameters are extracted using eqn (7). b Parameters are extracted using eqn (1).38 c The magnitude of the extracted parameter is ∼10−3 which is practically zero. | ||||||
| Polystyrene | −5.9 | −0.3 | 2565 | 1.3 | 0.7 | −527 |
| Poly(ethylene-alt-propylene) | −10.0 | 0.5 | 4240 | −6.0 | 0.8 | 2665 |
| Poly(2-vinylpyridine) | 0.0c | −0.3 | 305 | 4.0 | 1.6 | −1872 |
Although the effective interaction parameters do not quantitatively agree, the relative locations of the crystallization melting curves in Fig. 6 show interesting behaviors. For pyrene mixed with the relatively non-polar PS and PEP polymers, the locations of the crystallization and melting temperature curves shift together, i.e., the location of the melting curve is coupled with the location of the crystallization curve. This behavior is qualitatively consistent with the classical Flory–Huggins theory that describes the phase behavior of polymer solutions with chemical compatibility between the polymer and solvent, i.e., favorable chemical interaction between pyrene and the polymer simultaneously lowers the melting and crystallization temperatures. However, the critical crystallization temperature of pyrene mixed with P2VP is higher than the critical crystallization temperatures of pyrene mixed with the other relatively non-polar polymers despite the melting temperatures of the pyrene crystals mixed with P2VP being lower than those of pyrene crystals with the other polymers. This contrasting crystallization and melting temperature behavior of pyrene mixed with P2VP cannot be explained with the classical Flory–Huggins theory because it is unlikely that the favorable chemical compatibility between pyrene and P2VP indicated by the low melting temperature of pyrene crystals suddenly changes to be unfavorable with temperature, shifts up the liquid phase domain to high temperature, and, consequently, results in the high-temperature critical crystallization temperature (Fig. 6).
We believe that the relatively high critical crystallization temperature of pyrene with P2VP is due to the strong dipole–dipole interactions between the segments of P2VP, i.e., attractive self-interaction of P2VP chains. Budkov and co-workers propose the second virial coefficient of polymer chains that have permanent freely rotating dipoles on the polymer backbone in a good solvent:57
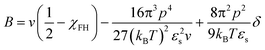 | (8) |
It is worth noting that, for colloidal solutions, phase domains of the liquid states of colloids arise due to the attractive interaction between colloidal particles, and the liquid phase domains of colloidal solutions become larger, i.e., shift up toward the high-temperature domain, as the range of interparticle attraction increases.28,59,60 The importance of the attractive interparticle interaction between colloidal particles for the formation of liquid phase domains aligns with the dipole–dipole attractive interaction between the segments of P2VP. The attractive interaction enlarges the hidden liquid phase domain, shifts up the critical point to higher temperature, and promotes the high-temperature crystallization of pyrene. The crystallization behavior of pyrene mixed with the model polymers in this article shows that polymers are effective and highly versatile macromolecular solvents for engineering the crystallization behavior of organic compounds.
Finally, we note that our earlier X-ray scattering characterization38 demonstrated that the size of pyrene crystals decreases with the polymer composition as the two-dimensional X-ray scattering patterns show more powder-like signatures for the higher polymer composition mixtures (see Fig. S3† in ref. 38). This result confirms that the crystallization curves directed by the hidden liquid phase domains control the degree of supercooling required for the initiation of crystallization, change the nucleation rates, and, consequently, vary the size of crystal domains.26
4. Summary and conclusion
In this article, we located the crystallization and melting temperatures of pyrene mixed with model polymers in the temperature and composition phase space using the DSC technique. We found strong evidence showing that the crystallization temperatures of pyrene are directed by the spinodal limits of hidden liquid phase domains located inside the two-phase domain of pyrene crystal and polymer solutions. For pyrene mixed with the relatively non-polar PS and PEP polymers, the crystallization temperatures shift with the melting temperatures of pyrene crystals which is consistent with the Flory–Huggins theory. In contrast, the crystallization of pyrene mixed with P2VP occurred in the higher temperature domain despite the melting temperatures of pyrene crystals with P2VP being relatively lower due to the favorable chemical compatibility between pyrene and P2VP. The inconsistency between the results of the crystallization of pyrene mixed with P2VP and the classical Flory–Huggins theory is attributed to the strong self-interactions between the chain segments of P2VP that enlarge the hidden liquid phase domain and shift up the crystallization curve to the high-temperature domain.These results show that with a judicious choice of polymeric solvents and processing conditions one can engineer the crystallization process of organic compounds to obtain target crystal structures and grain morphologies using hidden liquid–liquid phase domains.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
An acknowledgement is made to the donors of the American Chemical Society Petroleum Research Fund for the partial support of this research. We thank Jian Qin for the helpful discussion.References
- W. D. J. Callister and D. G. Rethwisch, Fundamentals of Materials Science and Engineering, John Wiley & Sons, Hoboken, NJ, 3rd edn, 2008, pp. 243–269 Search PubMed.
- K.-E. Thelning, Steel and its heat treatment, Butterworth-Heinemann, Oxford, 2nd edn, 1984 Search PubMed.
- J. S. Brooks, Chem. Soc. Rev., 2010, 39, 2667–2694 CAS.
- B. A. Collins, Z. Li, J. R. Tumbleston, E. Gann, C. R. McNeill and H. Ade, Adv. Energy Mater., 2013, 3, 65–74 CrossRef CAS.
- Y. Liu, J. Zhao, Z. Li, C. Mu, W. Ma, H. Hu, K. Jiang, H. Lin, H. Ade and H. Yan, Nat. Commun., 2014, 5, 5293 CrossRef CAS PubMed.
- Y. Xu, X. Huang, J. Yuan and W. Ma, ACS Appl. Mater. Interfaces, 2018, 10, 24037–24045 CrossRef CAS PubMed.
- G. Wang, F. S. Melkonyan, A. Facchetti and T. J. Marks, Angew. Chem., Int. Ed., 2019, 58, 4129–4142 CrossRef CAS PubMed.
- J. Bauer, S. Spanton, R. Henry, J. Quick, W. Dziki, W. Porter and J. Morris, Pharm. Res., 2001, 18, 859–866 CrossRef CAS.
- R. C. Snyder, S. Veesler and M. F. Doherty, Cryst. Growth Des., 2008, 8, 1100–1101 CrossRef CAS.
- D. E. Wurster and P. W. Taylor, Jr., J. Pharm. Sci., 1965, 54, 670–676 CrossRef CAS PubMed.
- N. Blagden, M. de Matas, P. T. Gavan and P. York, Adv. Drug Delivery Rev., 2007, 59, 617–630 CrossRef CAS PubMed.
- M. Pudipeddi and A. T. M. Serajuddin, J. Pharm. Sci., 2005, 94, 929–939 CrossRef CAS PubMed.
- D.-K. Bučar, R. W. Lancaster and J. Bernstein, Angew. Chem., Int. Ed., 2015, 54, 6972–6993 CrossRef PubMed.
- S. L. Morissette, S. Soukasene, D. Levinson, M. J. Cima and Ö. Almarsson, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 2180–2184 CrossRef CAS PubMed.
- G. M. Maggioni and M. Mazzotti, Cryst. Growth Des., 2017, 17, 3625–3635 CrossRef CAS.
- S. Auer and D. Frenkel, Nature, 2001, 409, 1020–1023 CrossRef CAS PubMed.
- M.-J. Lee, N.-H. Chun, I.-C. Wang, J. J. Liu, M.-Y. Jeong and G. J. Choi, Cryst. Growth Des., 2013, 13, 2067–2074 CrossRef CAS.
- B. Ray, S. Elhasri, A. Thierry, P. Marie and J.-M. Guenet, Macromolecules, 2002, 35, 9730–9736 CrossRef CAS.
- J. F. Jackson and L. Mandelkern, Macromolecules, 1968, 1, 546–554 CrossRef CAS.
- B. Van Eerdenbrugh, J. A. Baird and L. S. Taylor, J. Pharm. Sci., 2010, 99, 3826–3838 CrossRef CAS PubMed.
- M. Klimakow, K. Rademann and F. Emmerling, Cryst. Growth Des., 2010, 10, 2693–2698 CrossRef CAS.
- Crystallization: Basic Concepts and Industrial Applications, ed. W. Beckmann, Wiley-VCH, Weinheim, Germany, 2013 Search PubMed.
- T. L. Malkin, B. J. Murray, A. V. Brukhno, J. Anwar and C. G. Salzmann, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 1041–1045 CrossRef CAS PubMed.
- Q. Jiang and M. D. Ward, Chem. Soc. Rev., 2014, 43, 2066–2079 RSC.
- L. Chen, H. S. Lee and S. Lee, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 7218–7223 CrossRef CAS PubMed.
- K. F. Kelton, in Solid State Physics, ed. E. Henry and T. David, Academic Press, San Diego, CA, 1991, vol. 45, pp. 75–177 Search PubMed.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic press, Waltham, MA, 3rd edn, 2011 Search PubMed.
- P. R. ten Wolde and D. Frenkel, Science, 1997, 277, 1975–1978 CrossRef CAS PubMed.
- P. D. Olmsted, W. C. K. Poon, T. C. B. McLeish, N. J. Terrill and A. J. Ryan, Phys. Rev. Lett., 1998, 81, 373–376 CrossRef CAS.
- E. L. Heeley, C. K. Poh, W. Li, A. Maidens, W. Bras, I. P. Dolbnya, A. J. Gleeson, N. J. Terrill, J. P. A. Fairclough, P. D. Olmsted, R. I. Ristic, M. J. Hounslow and A. J. Ryan, Faraday Discuss., 2003, 122, 343–361 RSC.
- R. H. Gee, N. Lacevic and L. E. Fried, Nat. Mater., 2005, 5, 39 CrossRef PubMed.
- Z. Wang, J. Ju, J. Yang, Z. Ma, D. Liu, K. Cui, H. Yang, J. Chang, N. Huang and L. Li, Sci. Rep., 2016, 6, 32968 CrossRef PubMed.
- G. N. Kangovi, S. Park and S. Lee, Macromolecules, 2018, 51, 7274–7283 CrossRef CAS.
- P. C. Hiemenz and T. P. Lodge, Polymer Chemistry, CRC Press, Boca Raton, FL, 2nd edn, 2007 Search PubMed.
- T. Mandal, W. Huang, J. M. Mecca, A. Getchell, W. W. Porter and R. G. Larson, Soft Matter, 2017, 13, 1904–1913 RSC.
- Y. Sun, J. Tao, G. G. Z. Zhang and L. Yu, J. Pharm. Sci., 2010, 99, 4023–4031 CrossRef CAS PubMed.
- J. Huang, R. J. Wigent and J. B. Schwartz, J. Pharm. Sci., 2008, 97, 251–262 CrossRef CAS PubMed.
- G. N. Kangovi and S. Lee, Macromolecules, 2017, 50, 8678–8687 CrossRef CAS.
- P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, NY, 1953 Search PubMed.
- T. Nishi and T. T. Wang, Macromolecules, 1975, 8, 909–915 CrossRef CAS.
- S. Ndoni, C. M. Papadakis, F. S. Bates and K. Almdal, Rev. Sci. Instrum., 1995, 66, 1090–1095 CrossRef CAS.
- R. P. Quirk, Anionic Polymerization Principles and Practical Applications, Marcel Dekker, New York, 1996 Search PubMed.
- M. F. Schulz, A. K. Khandpur, F. S. Bates, K. Almdal, K. Mortensen, D. A. Hajduk and S. M. Gruner, Macromolecules, 1996, 29, 2857–2867 CrossRef CAS.
- S. F. Hahn, J. Polym. Sci., Part A: Polym. Chem., 1992, 30, 397–408 CrossRef CAS.
- J. Brandrup and E. H. Immergut, Polymer Handbook, Wiley-Interscience, Hoboken, NJ, 4th edn, 1999 Search PubMed.
- A. Shizuo, Y. Masafumi and O. Yoshihiro, Bull. Chem. Soc. Jpn., 1975, 48, 1417–1422 CrossRef.
- S.-H. Choi, F. S. Bates and T. P. Lodge, J. Phys. Chem. B, 2009, 113, 13840–13848 CrossRef CAS PubMed.
- W.-K. Wong and E. F. Westrum Jr, J. Chem. Thermodyn., 1971, 3, 105–124 CrossRef CAS.
- C. Jackson, Y.-J. Chen and J. W. Mays, J. Appl. Polym. Sci., 1996, 61, 865–874 CrossRef CAS.
- B. Ruiz, M. Jazbinsek and P. Günter, Cryst. Growth Des., 2008, 8, 4173–4184 CrossRef CAS.
- J. W. Cahn, Trans. Metall. Soc. AIME, 1968, 242, 166–180 CAS.
- H. Tanaka and T. Nishi, Phys. Rev. A: At., Mol., Opt. Phys., 1989, 39, 783–794 CrossRef CAS PubMed.
- V. J. Anderson and H. N. W. Lekkerkerker, Nature, 2002, 416, 811 CrossRef CAS PubMed.
- K. F. Freed and A. I. Pesci, J. Chem. Phys., 1987, 87, 7342–7344 CrossRef CAS.
- I. C. Sanchez, Polymer, 1989, 30, 471–475 CrossRef CAS.
- M. Tambasco, J. E. G. Lipson and J. S. Higgins, Macromolecules, 2006, 39, 4860–4868 CrossRef CAS.
- Y. A. Budkov, N. N. Kalikin and A. L. Kolesnikov, Eur. Phys. J. E: Soft Matter Biol. Phys., 2017, 40, 47 CrossRef PubMed.
- D. W. van Krevelen, Properties of Polymers: Their Correlation With Chemical Structure; Their Numerical Estimation and Prediction from Additive Group Contributions, Elsevier Science, Amsterdam, Netherlands, 4th edn, 2014, p. 331 Search PubMed.
- R. Evans, D. Frenkel and M. Dijkstra, Phys. Today, 2019, 72, 38–39 CrossRef CAS.
- A. P. Gast, C. K. Hall and W. B. Russel, J. Colloid Interface Sci., 1983, 96, 251–267 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9me00063a |
| This journal is © The Royal Society of Chemistry 2020 |