Tuning the electrostatic energy landscape within the pores of covalent organic frameworks: post-synthetic modification reactions and structural imperfections

Abstract

It is well established that collective electrostatic effects resulting from the periodic arrangement of polar entities determine the energy-level alignment at conventional, 2D extended interfaces by introducing a discontinuity in the electrostatic energy. This suggests that exploiting the assemblies of (di)polar entities should be a useful way for tuning the electronic properties of materials. While realizing such structures has turned out to be a formidable challenge in most cases, assemblies of polar substituents can be elegantly realized in the pore walls of covalent organic frameworks. In the current manuscript state-of-the art dispersion-corrected density functional theory simulations supported by electrostatic considerations are employed to show (i) how polar groups decorating the pores present in stacked 2D COFs can be used to control the electrostatic energy within the pores, (ii) how variations in the stacking motifs impact the obtained results, (iii) what role localized chemical defects play in the described effects, and (iv) to what extent post-synthetic modification reactions described in the literature for the studied COFs bear the potential of an a posteriori tuning of the electrostatic energy. Notably, in the latter case additional complications arise from the bulky, yet flexible nature of the substituents produced in the said reactions. Additionally, it is suggested how heterostructures of differently substituted groups of COF layers could be used to spatially modulate the energy landscape within pores, providing a vision for realizing materials in which any type of charge-transfer reaction can be confined to specific regions and in which the localization of differently charged ionic species can be controlled.

---

1 Introduction

Covalent organic frameworks, COFs,^1,2 have attracted significant interest due to possible applications in a variety of fields^3,4 including photocatalysis,⁵ electro-catalysis,⁶ energy storage,^7–15 optoelectronics (including sensing),^16–18 and photovoltaics.^19–22 Usually, these applications exploit the porous nature of COFs and the possibility to infiltrate guest molecules. Thus, the interaction between species inside the pores and the frameworks is of utmost importance. In particular, controlling the energetic alignment between electronic states in the guests and in the COF matrix is crucial. It, for example, determines charge separation in guest–host heterojunctions,^{18–20,23,24} redox-processes occurring in COFs, e.g., when they are used as battery electrodes,^14,25 and also applications in the area of (photo)catalysis.^26,27 For example, when using COFs as working electrodes in batteries,¹² one has to consider that the energetic positions of the COF frontier states directly impact electrochemical reduction and oxidation potentials,^25,28 and, in turn, metal-ion binding and the redox stability of batteries. Moreover, in the context of photovoltaics, the positions of frontier orbitals and redox potentials have been shown to strongly influence the open-circuit voltage of solar cells.²⁹ These examples illustrate that, if one is able to control the electronic level alignment, one is also able to massively impact the efficiency of all of the aforementioned processes. A common strategy for tuning the level alignment is incorporating electron-poor or electron rich entities into COFs making use of inductive and/or resonance effects. These functional groups are included in the COF backbones either directly or as substituents to chemically tune the COFs' ionization energies and electron affinities.¹⁵

Recently, a complementary approach for controlling the interface energetics of COF channels has been suggested based on concepts established for conventional, macroscopic interfaces, which are present, for example, at the electrodes of (organic) electronic devices.³⁰ The approach relies on so-called collective (or cooperative) electrostatic effects.^31–35 These are present at virtually all interfaces and, for example, can be used to modify electrode work-functions^31–36 to a degree that contact resistances are modified by several orders of magnitude and that the polarity of the injected charge carriers can be switched.^36,37 Such collective electrostatic effects arise from the superposition of the electric fields and electrostatic potentials of periodic arrangements of polar entities (often approximated as dipoles). It is well established that, when these dipoles are arranged in a 2D periodic fashion, they trigger a step in the local electrostatic energy, as is illustrated in Fig. 1(a). This figure shows the superposition of the electrostatic energies created by point dipoles arranged in an (infinitely extended) square lattice in the (x,y) plane (c.f., ref. 35). This plane of dipoles is located at the z-position marked by a semi-transparent green arrow and the location of the individual point dipoles can be inferred from the locations of the discontinuities of ΔE. The observed step in electrostatic energy, ΔE_step, is proportional to the dipole density.^31–35 It directly translates into a change in the alignment of the electronic states localized in the materials on the two sides of the dipole layer. At interfaces, these materials could be, for example, a metal electrode and an organic semiconductor.³¹ While for conventional interfaces one would be typically dealing with a “classical” 2D dipole arrangement, in the case of COFs the dipoles decorating the pore walls at the interface between the COF-scaffolds and guest molecules are arranged in more complex topologies. For example, when dealing with COF sheets, one often encounters approximately circular pores, whose perimeter can contain polar groups. For an eclipsed stacking of such COF sheets, an essentially cylindrical arrangement of dipoles is generated, as shown in Fig. 1(b). Importantly, collective electrostatics also works for such dipole assemblies. This becomes evident in Fig. 1(b), where the electrostatic energy of an electron is shown for such a cylindrical pore in a plane perpendicular to the pore axis (here, the z-axis). Also, in this case, there is a significant shift in electrostatic energy between the spatial region within the dipole assembly and the region outside the pore. In the following sections, this shift will be referred to as ΔE_pore. In an actual material, such a dipole arrangement will again result in a shift between the electronic states inside and outside the cylinder of dipoles (i.e., between states localized on molecules within the pore and in the COF matrix). Notably, within the employed electrostatic model the magnitude of the shift is again determined only by the dipole density. For a given dipole density the absolute values of the shifts are the same for the 2D extended and the cylindrical pore cases. This is independent of the number of dipoles in each COF-sheet, provided that the diameter of the pore is linearly scaled with that number, as illustrated in panels (c) and (d). What is, however, important is the number of stacked layers, as can be inferred from panels (e) and (f), which show cross-sections comprising the central axes of the pores (i.e., within the (x,z) planes) for a three layer and a quasi-infinitely extended stack: in the latter case, one again obtains a “global” energy shift between the regions inside and outside the pore. Conversely, for a finite stack this shift diminishes away from the dipoles. Moreover, for less than ∼10 layers also, the magnitude of the shift inside the pore is noticeably reduced³⁰ (by 42% for the 3 layers in panel (e)). Another relevant consequence of collective electrostatics is that according to ref. 31 at roughly a tenth of the inter-dipole distance the electric field has largely decayed, such that the shift in electrostatic energy becomes rather flat. This is consistent with the plots in Fig. 1 and has two main consequences: (i) for a perfectly ordered arrangement of point dipoles, the electrostatic energy is largely constant within the region enclosed by the dipoles, and variations occur only in the vicinity of the pore walls. (ii) There is no fundamental change in the shift of the electrostatic energy when comparing a single cylindrical dipole arrangement and an assembly of such polar structures.

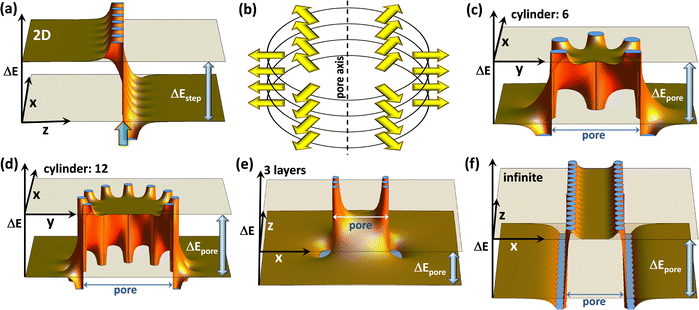Fig. 1 The electrostatic model. The shift in electrostatic energy of electrons, ΔE, for a planar arrangement of point dipoles (with dipole moments perpendicular to the plane) (a), and for cylindrical dipole arrangements ((c)–(f)). In (a) the dipoles are arranged in the (x,y)-plane at the z-position marked by the green arrow, and the step in electrostatic energy between regions to the left and to the right of the dipole layer, ΔE_step, is indicated. Panel (b) illustrates the cylindrical arrangement of dipoles, surrounding, e.g., a pore in a COF, for a situation with six dipoles per COF plane. Panels (c) and (d) show cross-sections for a plane perpendicular to the pore axis that coincides with one of the planes containing dipoles for six and twelve dipoles per plane. The shifts in electrostatic energy between regions inside and outside the cylindrical dipole arrangement, ΔE_pore, are identical for both situations provided that the dipole densities are the same (i.e., provided that the pore diameter scales linearly with the number of dipoles). Panels (e) and (f) show cross-sections parallel to the pore axis for three layers of dipoles and for a quasi-infinite stack of layers containing dipoles. All plots have been generated using Mathematica 11.3 (ref. 38) by summing up electrostatic potentials of point-dipoles arranged as described in detail in the ESI.† The absolute magnitudes of ΔE scale linearly with the dipole moments and with one over the distance between dipoles squared, while the shapes of the plots depend on the aspect ratios. A possible structure (inspired by the COFs discussed below) that yields plots like those shown here consists of dipoles spaced by 9 Å along the circles (resulting in a circle diameter of 54/π Å) with the planes containing the dipoles spaced by 4 Å.

The predictions of the simple electrostatic model generated by the superposition of the potentials of point dipoles are fully confirmed by dispersion-corrected density-functional theory calculations on DUT-177 (ref. 14) and its derivatives.³⁰ DUT-177 represents a layered COF formed by thianthrene-based elements with six –CN substituents pointing towards the pore centres. In fact, when studying slabs consisting of eleven DUT-177 layers, the difference in the electrostatic energies within the pores amounted to as much as 1.39 eV, when comparing –CN and –NH₂ substituted systems. Moreover, it was observed that when including C₆₀ molecules in the pores of DUT-177, the shifts in electrostatic energies directly resulted in modifications of the level alignment between states in the guest molecules and the host matrix. A detailed analysis in ref. 30 revealed that these “electrostatic” shifts occur in addition to the aforementioned “chemical” shifts due to the inductive and mesomeric effects of electron rich and poor substituents.

Considering that “electrostatic” shifts can be traced back to superposition of electrostatic potentials of charge distributions, one should expect effects like those discussed in ref. 30 for DUT-177 in other materials also. Indeed, there exist many examples of COFs comprising pore walls decorated with regularly arranged polar groups:⁴ besides nitrile groups (e.g., in COF-316,³⁹ JUC-505,⁴⁰ or DUT-177 (ref. 14)), ketones (e.g., in DAAQ-TFP⁷ and in JUC-506 (ref. 40)) or halogens (e.g., in COF-F⁴¹) have also been used. Moreover, the aforementioned polar groups can be altered in post-synthetic modification reactions,^7,14,39 generating amidoximes,³⁹ amines,⁴⁰ or polysulfides.¹⁴ A similar situation prevails when switching the polarity of the substituents via a redox reaction, e.g., when converting ketones to alcohols.⁷

Such post-synthetic modifications are of particular interest in the context of the present paper, where a central topic will be how exactly they change the potential within the pores. There are several aspects that will potentially complicate the situation: the complexity of the introduced groups that can result in dipole directions not perpendicular to the pore walls and that renders approximating the charge distributions within substituents by dipoles too simplistic, the flexibility of some groups that can result in different configurations with markedly different properties, and the bulkiness of some groups that reduces the pore diameter and that can also lead to significant distortions of the COF-planes. A further complication in this context will be that in the studied systems multiple polymorphs are conceivable and it will be necessary to assess to what extent structural variations in the polymorphs impact the electrostatic energies within the pores. As stacking motifs of COF layers can vary throughout actual samples,⁴² the impact of stacking disorder also needs to be addressed briefly. Moreover, (post-synthetic) chemical modifications will typically not be fully quantitative, which calls for studying the impact of heterogeneous dipole assemblies and of defective structures. Finally, the question arises whether suitably altered COF heterostructures can be exploited for generating pockets of electrostatic energy or structures with potential gradients along the pore axes. To study these effects, electrostatic considerations will be combined with quantum-mechanical simulations on variants of dioxin-linked COFs, as illustrated in Fig. 2. This will reveal additional strategies for exploiting collective electrostatics as a new design concept for controlling the electronic structure of porous materials by tuning the level-alignment between states localized in the COF matrix and in guest molecules.

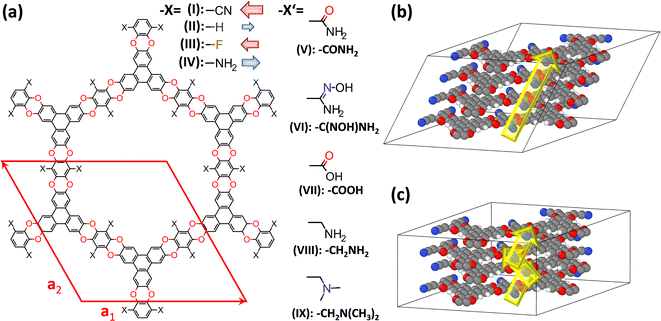Fig. 2 Structures of the investigated systems. (a) Chemical structures of the studied COFs based on polyarylethers (CPAEs). The base-structure with X = –CN has been termed COF-316 (ref. 39) and JUC-505 (ref. 40) in the literature, while it will be denoted as CPAE–CN in the present context; the red diamond represents the unit-cell of the structure. It is defined such that the a₁- and a₂-directions coincide with the COF planes, while a₃ describes the out-of-plane stacking. Considered derivatives of CPAE–CN comprise COFs in which the strongly polar –CN groups were replaced by less polar –F substituents (CPAE–F) and by substituents with opposite polarity, namely –H (CPAE–H) and –NH₂ (CPAE–NH₂) (–X substituents), as well as systems that can be realized by post-synthetic modifications (–X′ substituents). The latter comprise amides (CPAE–CONH₂)³⁹ and amidoximes (CPAE–C(NOH)NH₂)³⁹ – both interesting for uranium sequestration-,⁴³ carboxylic acids (CPAE–COOH),⁴⁰ amines (CPAE–CH₂NH₂),⁴⁰ and dimethylamines (CPAE–CH₂N(CH₃)₂). Note that for an easier identification of the systems, they are also identified using roman numbers. The red and blue arrows next to the “–X” substituents are indicative of the direction and size of the group's dipole moments. The difference between CPAE–NH₂ and CPAE–CH₂NH₂ is the methyl-spacer in the latter system, which results in a strongly increased flexibility of the substituents. Panels (b) and (c) show two possible stacking motifs that were considered in the current paper. In the structure in (b), consecutive layers are slipped in the same direction such that the unit cell contains atoms of only one layer and the displayed structure corresponds to four unit-cells stacked on top of each other in the a₃ direction. In panel (c) consecutive layers are slipped in opposite directions. Consequently, every unit cell contains atoms from two different layers such that in the picture only two unit-cells stacked in the a₃ direction are shown. Colour code – dark: C; orange: N; red: O; white: H; plots produced using Marvinsketch (https://www.chemaxon.com/) and OVITO.⁴⁴

2 Studied materials

In the current manuscript, the focus will be on 2D, polyarylether based covalent organic frameworks, in which triangular 2,3,6,7,10,11-hexahydroxytriphenylene and linear tetrafluorophthalonitrile building blocks are connected by dioxin linkers (see Fig. 2, material I). The base material containing –CN substituents decorating the pore wall was first presented essentially simultaneously in ref. 39 and 40 and was termed COF-316 and JUC-505. A distinct feature of COF-316/JUC-505 is its extreme chemical stability under both acidic and basic conditions, which allows a variety of post-synthetic modification reactions.^39,40 These reactions change the substituents facing the pore walls under sometimes rather extreme conditions, allowing the covalent introduction of new functionalities into the COFs.³⁹ For example, Zhang et al. introduced amides³⁹ and amidoximes³⁹ maintaining the porosity and crystallinity of the materials, and Guan et al.⁴⁰ introduced carboxylic acids and amines (the latter including a methylene-spacer; see “–X′” substituents in Fig. 2(a)) without changing the diffraction patterns of the materials. Beyond these experimentally realized substituents, a fully methylated variant of the amine was also considered, for reasons that will become apparent later. The change in the chemical decoration of the pore walls resulting from these modifications is expected to also massively change the electrostatic energy within the pores. The same applies to the other considered materials, which primarily serve as model materials in which the strongly polar –CN groups are replaced by less polar –F substituents and by substituents with opposite polarity, namely –H and –NH₂ (see “–X” substituents in Fig. 2(a)). To illustrate the general validity of the observed effects, a COF with distinctly larger pores has also been modelled. Its properties are discussed in section S6 of the ESI.†

As in the current manuscript in total nine chemically distinct variants of COF-316/JUC-505 will be studied, a more general acronym is introduced such that the various COFs will be termed CPAE-“substituent”. Here, CPAE refers to the COF consisting of polyarylethers and for the substituent the nomenclature introduced in Fig. 2(a) will be used. In addition, different COFs are numbered to ease their identification in the various plots. Augmented versions of the COF names will be introduced, when referring to variants of the stacking conformations (see below).

A challenge with CPAE-type COFs arises from the fact that most of them (in particular the systems with non-branched substituents) are essentially flat. Thus, the 2D COF planes can glide relative to each other. This contrasts the situation for the previously studied DUT-177, whose wrinkled structure induces steric driving forces that result in a close to eclipsed stacking.^14,30 For COF-316/JUC-505 the stacking motive is not fully understood. On the one hand, a staggered stacking has been excluded based on porosity³⁹ and diffraction data.⁴⁰ Such a stacking also appears unrealistic, as it would result in a massive reduction of inter-layer van der Waals attractions.⁴⁵ On the other hand, it is known that (in the absence of steric driving forces) π-systems do not stack in an eclipsed pattern,^46–49 as Pauli repulsion is maximized for such a stacking motive and far outweighs the impact of van der Waals attraction and attractive charge-penetration effects.^47,50,51 Deviations from an eclipsed stacking of polar COFs can be further increased by electrostatic repulsion of polar entities with equivalent partial charges,⁵² although this effect is rather minor.⁴⁵ Importantly, as the magnitude of Pauli repulsion depends on the orbital overlap of wavefunctions in adjacent layers (including their relative phases), it can be marginalized by inter-layer slips often smaller than ∼2 Å.^52,53 For example, for COF-1 the global minimum structure has been found for layers slipped by 1.75 Å in the direction of the pore walls.⁴⁵

A fully comprehensive study of possible stacking motifs of the various COFs studied here is beyond the scope of the present paper. Still, full geometry optimizations of lattice parameters and atomic positions of 26 systems in total (including mixed-linker structures) were performed starting from typically two distinct initial structures. They were constructed by slipping consecutive layers either in the direction of the substitution axes (in the a₁-direction, as indicated in Fig. 2) or in directions close to parallel to the pore walls. For most systems, only structures with consecutive layers slipped in the same directions (c.f., Fig. 2(b)) were considered. For CPAE–CN also, the impact of alternating stacking motifs was tested (c.f., Fig. 2(c)), despite the significantly increased computational effort due to the two COF layers contained in the resulting alternating cell. The main parameters of all optimized structures are summarized in Tables S2 and S3† and their structures are shown in Fig. S1 in the ESI.† In short, for the majority of the systems both geometry optimizations ended in identical structures with layers slipped parallel to the a₁ axis, while in some systems (especially in some of the amines) optimizations converged into an alternative minimum structure with an angle of roughly 20° between the a₁ axis and the slip direction. Essentially isoenergetic minima for both structural motifs were observed for CPAE–CN and CPAE–NH₂. In view of the majority of the structures being slipped in the a₁ direction, that conformation was chosen as the reference structure for CPAE–CN. There is also a structure with marginally lower energy (by 4 meV per substituent), which is slipped in a direction inclined by 22° relative to the a₁ direction. In the following sections, it will be referred to as CPAE–CN*. A “*” will also be used for denoting alternative local minimum structures of other systems. The observation of two local minima with somewhat different slip directions is in line with the rather weak dependence of the total energy on the slip direction observed in a more systematic conformational screening of COF-1 in ref. 45. The calculated equilibrium slip distances were rather small, ranging between 1.5 Å and 4.6 Å similar to the situation in COF-1.^45,52,53 The differences in the magnitudes of the slips arise from variations in the bulkiness of the substituents and from differences in their ability to form inter-layer H-bonds. They, however, hardly affect the inter-layer distances, which are consistently between 3.2 Å and 3.4 Å.

Inter-layer distances in that range are also found for the alternatingly slipped structures of CPAE–CN with two layers in the unit cell, which are denoted as CPAE/2-CN and CPAE/2-CN* and which have again been obtained for two different starting geometries. A detailed description of their structural and energetic properties can be found in section S2 of the ESI.† Notably, these structures turned out to be somewhat higher in energy than CPAE–CN (by 14 meV and 10 meV per substituent). Thus, and in view of the sharply increased computational costs of optimizing structures with two layers in the unit cell, alternatingly stacked COF structures were not considered for the other systems. The unfavourable energetics of the alternatingly stacked COFs is insofar somewhat surprising, as the structure of CPAE/2-CN with the a₃ unit-cell vector orthogonal to a₁ and a₂ would be most consistent⁵⁴ with the single, sharp diffraction peak seen at 2Θ angles of around 5° in the PXRD patterns in ref. 39 and 40. The exact origin of this apparent discrepancy is not fully understood yet, but it should be mentioned that the authors of ref. 39 describe experimental evidence of the presence of unreacted oligomers in the pores for a related system (COF-318). This, or, for example, remaining solvent molecules could influence the stacking motif. Moreover, in actual materials one is typically dealing with kinetically trapped structures dominated by statistical fluctuations of the stacking motifs. The latter are expected to result in structures with strongly reduced slips averaged over multiple layers. Along these lines, Zhang et al.⁵⁴ attributed the often observed mismatch between experimental and simulated XRD patterns to “inherent disorder in the stacking of layered COFs”. Consistently, Pütz et al.⁴² predicted a very high faulting probability in the stacking of COF layers and suggested “that structures inferred solely from pattern indexing or Rietveld fitting to low-quality data should be strictly interpreted in the crystallographic sense as average structures.”

Another degree of structural complexity arises from the fact that all substituents denoted by –X′ in Fig. 1(a) possess a certain degree of flexibility. Here, starting and/or intermediate conformations during the geometry optimizations were chosen such that hydrogen bonding was facilitated and that comparable orientations of functional groups within the pores were attained.

3 Methods

3.1 Quantum-mechanical simulations

The model simulations are based on analytical equations for the electrostatic energy, which can be derived in a straightforward manner; they are summarized in the ESI.† For the quantum-mechanical simulations a strategy was employed that can currently be considered as the default approach for modelling extended polar structures:⁵⁵ periodic boundary conditions were used for capturing collective electrostatic effects, and when modelling extended interfaces or when studying finite-thickness systems, the repeated slab-approach was applied (described in detail in Section 3.2). These approaches then need to be combined with a variant of dispersion-corrected density functional theory. In the present case, the Perdew–Burke–Ernzerhof (PBE) functional^56,57 was combined with a revised variant of the many-body dispersion correction.⁵⁸ As the key quantities for the present study are shifts in the electrostatic energy, the exact choice of the functional is not considered to be of primary relevance and when studying polar adsorbate layers, we typically obtained a good agreement for electrostatic shifts when comparing PBE-based simulations and well-defined experiments.^59,60

On more technical grounds, all simulations were performed using the FHI-aims code.^61–63 For the definitions of the atom-centred basis sets, the FHI-aims default “tight” settings were employed (see Table S1 in the ESI†). Only when optimizing the structures of triple-layer systems with guest molecules, “intermediate” basis sets had to be used due to the sheer size of the systems. A well converged 2 × 2 × 12 k-point grid was used for the bulk calculations, which was scaled in the k_z direction for multi-layer systems. For the slabs described in Section 3.2, a 2 × 2 × 1 grid was used (convergence tests can be found in the ESI† of ref. 30). Geometries were optimized using the Broyden–Fletcher–Shanno–Goldfarb algorithm enhanced by the trust radius method,⁶¹ with a tolerance threshold of 10⁻² eV·Å⁻¹ for all calculations except for the triple-layer systems containing guest molecules, for which a twice as high value had to be set to achieve convergence. Two complementary strategies (yielding consistent results) were used for determining the electrostatic energies of the electrons. For isovalue plots and for plotting 1D and 2D cross-sections, the Hartree potentials generated in the DFT simulations were written out on a grid (in a so-called cube-file). For determining the electrostatic energy at specific locations, electrostatic core-level shifts for suitably placed probe atoms were exploited (for details see the ESI,† where additional details concerning the DFT simulations can also be found).⁶⁴

3.2 Structural details of the studied model systems

A systematic comparison of the electrostatic energies in the pores of periodic 3D bulk structures of the COFs is prevented by the lack of an unambiguous energy reference.³⁰ Thus, slabs of finite-thickness comprising 11 COF layers (12 COF layers for the alternatingly slipped systems) were studied. For constructing the slabs, individual layers adopting the bulk structures of each system with optimized atomic positions and unit-cell parameters were stacked on top of each other at the bulk equilibrium distances. For heterostructures consisting of differently substituted layers, the bulk-simulations of all sub-systems were performed fixing the unit-cell parameters at the values obtained for CPAE–CN. Building the slabs from the bulk structures is sensible, as surface relaxations are expected to be very minor in van der Waals bonded systems. To avoid spurious interactions of neighbouring slabs resulting from the employed periodic boundary conditions, they were separated from each other by 70 Å vacuum regions. As mentioned above, such calculations are the default approach for studying the properties of interfaces and finite thickness slabs and allow the definition of a vacuum level, determined here as the electrostatic energy 30 Å above the top of the slab. The vacuum level serves as the required unambiguous reference point for the energy scale and, thus, provides a direct comparability of different COFs.³⁰ As shown in ref. 30 the chosen number of layers, size of the vacuum gap and position for determining the vacuum level provide well-converged results. Typically, in 3D slab calculations one would also electrostatically decouple periodic replicas of the slabs by introducing a self-consistently determined dipole layer into the vacuum gap.^65,66 Unfortunately, this is prevented here by a₃ not being perpendicular to the (a₁,a₂) plane. Thus, special care must be taken to avoid any asymmetry in the electrostatic energy below and above the slabs, as this – by virtue of the periodic boundary conditions – would generate a spurious field within the unit cell. Consequently, substituents on opposite sides of the linkers were aligned such that their dipole components in the pore direction (largely) cancel. As a result, for mixed substitution patterns involving non-planar substituents (–NH₂ and all –X′ substituents) only even numbers of substituents of a specific type could be considered. Obeying this design principle, noticeable spurious fields could be avoided in all systems apart from heterostructures with an asymmetric succession of layers (see Section 4.4). However, also, in these cases the spurious fields are so small that they do not have any relevant impact on the presented data.

4 Results and discussion

4.1 Tuning the electrostatic energy within pores and its dependence on the COF conformation

As a first step, the differences in the electrostatic energies of an electron (the Hartree energies) between the pore centres and the vacuum region, ΔE_pore, were calculated for the –X substituents shown in Fig. 2(a). This was done at varying degrees of substitution, yielding the ΔE_pore values shown in Fig. 3(a), where the rightmost datapoints refer to the fully substituted systems. When moving left in the plot, the –CN, –F, and –NH₂ substituents are increasingly replaced by –H groups until for the leftmost datapoints one arrives at a fully hydrogenated system. Due to the electrostatic nature of the shift,³⁰ ΔE_pore is strongly positive in a –CN decorated pore comprising dipoles pointing towards the pore centre. Conversely, it is negative for –NH₂ substituents due to the intermediately strong outward-pointing dipoles. The difference between the electron accepting and donating substituents diminishes, when gradually replacing the –CN and –NH₂ groups within the layers by –H. For fully H-decorated pores (leftmost data point in Fig. 3(a)) a reduced negative shift prevails, which is a consequence of the equivalent dipole orientations for the C–H bonds and the –NH₂ substituents (c.f., schematics in the inset of Fig. 2(a)). For the fully F-substituted system, ΔE_pore is only around +0.2 eV, as here the dipoles due to the –F substituents are largely compensated for by the remaining C–H dipoles on the triphenylenes.³⁰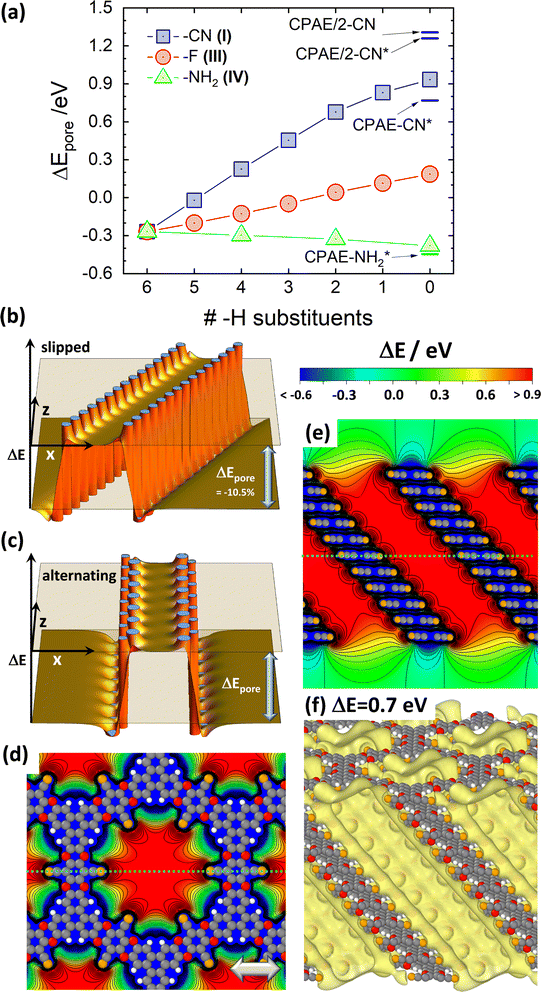

Fig. 3 Electrostatic energies in the pores for the ideal systems. (a) DFT-calculated difference between the electrostatic energy of an electron inside the centre of the pore of an 11-layer (respectively, 12-layer) CPAE–X slab and the electrostatic anergy in vacuum above the slab (i.e., the vacuum level), ΔE_pore, as a function of the degree of substitution. The vacuum level is determined 30 Å above the topmost COF layer. A value of zero “H-substituents” (rightmost datapoints) corresponds to a COF consisting of fully substituted layers (here: CPAE–CN, CPAE–F, and CPAE–NH₂). Six “H-substituents” (leftmost datapoint) corresponds to a COF in which the entire pore wall is decorated with –H groups. The substitution patterns in consecutive layers are identical. To test the impact of varying the substitution pattern, for three –H and 3 –CN substituents also the situation of an alternating substitution in consecutive layers has been tested. This yielded values of ΔE_pore differing by only 0.01 eV. The data points shown as squares, circles and triangles correspond to the reference conformations of the different COFs, while CPAE–CN* and CPAE–NH₂* are alternative (local) minimum conformations primarily differing from the reference structures in the direction of the slip of consecutive layers (see description of studied materials and section S2 in the ESI†). The two datapoints denoted as CPAE/2 refer to structures with (mostly) alternating slips of consecutive layers and were calculated for 12 layer slabs. For all other systems the inter-layer slips were identical between consecutive layers, and 11-layer slabs were considered. The results of the electrostatic model for a non-eclipsed stacking of layers in a cylindrical dipole assembly are shown in panels (b) and (c). The plots insofar differ from that shown in Fig. 1(f), as consecutive layers are shifted by half of the inter-layer distance (i.e., by 2 Å) either always in the same direction (panel (b)) or in alternating directions (panel (c)). For the situation in (b) ΔE_pore is reduced by 10.5% compared to the value in Fig. 1(f), while for the situation in (c) it is identical. Panel (d) displays the DFT-calculated electrostatic energies of an electron relative to the vacuum level, ΔE, for the 11-layer slab of CPAE–CN for a cross-section parallel to the (001) planes through the centre of the 6th layer of the slabs (as indicated by the dotted bright-blue lines in panel (e)). Panel (e) shows a cross-section parallel to the (010) plane containing the pore axis (as indicated by the dotted bright-blue line in panel (d)). Isolines are drawn every 0.1 eV and cover ΔE values between −3.0 eV and the maximum values of ΔE. Structures of individual COF layers, respectively, of atoms essentially coinciding with the planes parallel to (010) through the COF centres are superimposed on the plots of the electrostatic energy as guides to the eye. The light grey double headed arrow in panel (d) indicates the slip direction of consecutive layers. The colour scale on top of panel (e) also applies to panel (d). Panel (f) shows an isovalue plot of ΔE at a value of 0.7 eV. This means that within the region enclosed by the yellow isosurface the electrostatic energy is at least 0.7 eV higher than that in vacuum above the slab. Equivalent plots for CPAE/2 are shown in Fig. S7 in the ESI† (colour code – grey: C orange: N, red: O; white: H; plots produced using OVITO⁴⁴ and VESTA⁶⁷).

Fig. 3(a) also reveals that the magnitude of ΔE_pore significantly depends on the stacking motif of the COF layers. This is particularly evident for the –CN substituted system at full substitution, for which in addition to different shift directions, alternating stacking motifs have also been considered (see above). For the reference system CPAE–CN, ΔE_pore amounts to 0.93 eV; it drops to only 0.77 eV in the case of the quasi isoenergetic but differently slipped CPAE–CN* conformation and increases for the local minimum conformations built from alternatingly slipped COF layers (CPAE/2-CN and CPAE/2-CN*). For these it amounts to 1.26 eV and 1.31 eV, respectively. To understand the origin of this pronounced dependence of the value of ΔE_pore on the COF conformation, one has to consider two interrelated aspects: (i) the possible dependence of the magnitudes of the dipoles on the local environment, which changes due to a slip, and (ii) the impact of the detailed geometric arrangement of the dipoles on the shifts in electrostatic energy. In passing it is noted that changes in the dipole densities due to changes in the stacking distances do not play a role, as the latter vary by at most 0.04 Å amongst the CPAE–CN type systems (see Table S2†).

When comparing CPAE–CN and CPAE/2-CN, one is dealing with fundamentally different dipole arrangements, whose impact can be tested by the point-dipole model already employed for generating Fig. 1. Comparing Fig. 1(f) and 3(b) indeed reveals that a slip of consecutive polar layers results in a reduction in ΔE_pore. In fact, a more detailed analysis considering various slip distances shows that ΔE_pore drops with cos(Θ), with Θ being the angle between the a₃ vector of the unit cell and the normal to the (a₁,a₂) plane (c.f., Fig. 2). This relation can be explained by the pore walls in the slipped systems being no longer perpendicular to the directions of the dipoles. The perpendicular component of the dipoles then drops with cos(Θ). For CPAE–CN, Θ amounts to 41.1°, which would mean a geometry-induced reduction of ΔE_pore by 25% compared to an eclipsed arrangement of the COF-layers. Unfortunately, a direct comparison to this eclipsed conformation is prevented by a significant tilt of the linkers that is found when optimizing that structure. This is a consequence of the significant Pauli repulsion one faces for fully cofacial π-systems (vide supra). The tilted linkers also tilt the –CN dipoles, which reduces ΔE_pore to a value of 0.99 eV, which is rather similar to that in CPAE–CN. However, comparing Fig. 1(f) and 3(c) (including the actual electrostatically derived values of ΔE_pore) shows that within the electrostatic model not suffering from any twisting of polar groups the values of ΔE_pore are essentially identical for the alternatingly slipped and for the eclipsed stacks. Consequently, the observation that ΔE_pore in CPAE–CN is lower by 29% than that in CPAE/2-CN can be largely explained as a geometrical effect. This suggests that changes in the dipole moments and/or deviations from the point-dipole model in the actual COF play only a minor role here.

The even further reduced value of ΔE_pore in the differently slipped CPAE–CN* structure can also be mostly attributed to geometric arguments: compared to CPAE/2-CN, the value of ΔE_pore has dropped by 41%, while for the observed value of Θ = 48.1° the point-dipole model predicts a drop by 33%. Here, the deviations are larger than those for CPAE–CN. This suggests a more pronounced contribution from reduced dipole moments for the slipped CPAE–CN* structure. The magnitudes of these dipoles, on the one hand, depend on the presence of a polarizable (and, thus, screening) environment in the vicinity of the dipoles and, on the other hand, on depolarization and polarity amplifying processes caused by neighbouring dipoles. Depolarization effects have been repeatedly described for dipole arranged 2D layers,^68–70 and they have been held responsible for a reduction in the value of ΔE_step (c.f., Fig. 1(a)) at flat surfaces.^{31,34,35,71,72} Conversely, a head to tail arrangement of dipoles is expected to result in a mutual amplification of the dipole moment. In the case of CPAE–CN the slip of consecutive layers is in the direction of one of the substituent axes (see Fig. S2†). Thus, in this conformation two dipoles per layer per pore indeed approach a favourable head to tail arrangement, which results in an overall reduced impact of depolarization effects. This is not the case for CPAE–CN*, which explains the somewhat more pronounced, slip-induced drop in ΔE_pore in that system.

So far, the discussion has focused on the change in electrostatic energy in the centre of the pore. This raises the question to what extent the potential varies as a function of the position within the pore. According to Fig. 1(c), (d), and (f), the electrostatic model predicts a flat potential. This is, indeed, also confirmed by the quantum-mechanical simulations, which show that the electrostatic energy is rather constant within the pores, both for a cross-section through the pore perpendicular to (Fig. 3(d)) as well as along the pore axis (Fig. 3(e)). Only, when one approaches the pore walls there is a very steep drop in electrostatic energy, which will become relevant below, when considering molecules adsorbed within the pores. Another, less abrupt drop in the electrostatic energy occurs when approaching the top and bottom surfaces of the slabs.

Finally, the isovalue plot for ΔE_pore in Fig. 3(f) illustrates the formations of a “potential pocket” caused by the periodic arrangement of the dipoles. Within the shown isosurface the electrostatic energy is increased by at least +0.7 eV compared to the situation in the vacuum above the slab.

4.2 Impact of structural imperfections and chemical defects on ΔE_pore

As mentioned above and detailed in the ESI,† in several systems the differences in the total energies for different local minimum structures are comparably small and multiple symmetry-equivalent minima can exist. Moreover, in COFs consisting of essentially flat layers also the energy barriers between these local minima are low.⁴⁵ Thus, local variations in the stacking motives in planar COFs are inevitable, as discussed in detail in ref. 42 and 54. Such stacking faults could exist in a quasi-static fashion but could also undergo dynamic fluctuations. In view of the strong dependence of the electrostatic energy within the pores on the arrangement of neighbouring layers discussed in the previous section, one might expect this to cause a more or less pronounced static as well as a dynamic energetic disorder inside the pore. In passing it is noted that a viable strategy for avoiding or at least reducing the said conformational defects is the design of COFs consisting of polar, but non-planar sheets, as demonstrated, for example, for DUT-177.⁷³

A detailed investigation of the impact of a stacking disorder on the electrostatic energy within the pores by ab initio methods like the ones used in the current work has not been found to be feasible to date. Nevertheless, first, fundamental insights can be gained from the electrostatic model described above. Thus, to test the impact of a disorder on the slipping of consecutive layers, both the directions as well as the magnitudes of the slips in corresponding simulations were set randomly. Fig. 4(a) shows the result when limiting the maximum slip to half the inter-layer distance (i.e., δ = 2 Å, which is ∼12% of the diameter of the dipole cylinder). This value is doubled for Fig. 4(b). To show that the results in Fig. 4(a) and (b) are representative, the corresponding plots for differently seeded random slips are shown in Fig. S8 in the ESI.† Notably, for a maximum displacement of 2 Å the decrease of ΔE_pore in all considered cases is at most 0.6% and for δ = 4 Å it still remains below 2%. In fact, for smaller displacements there are hardly any variations of the electrostatic energy in the channel and for the more pronounced disorder the variations are also rather minor. This rather small impact of disorder on the energy within the pores might appear somewhat unexpected at first glance, but it can be explained by the fact that the randomly displaced structures more strongly resemble the alternatingly slipped structure in Fig. 3(c) than the unidirectionally slip structure in Fig. 3(b). Consequently, the unidirectionally displaced structure studied throughout this manuscript can be considered to represent a lower limit to the changes in electrostatic energy that can be expected in realistic systems.

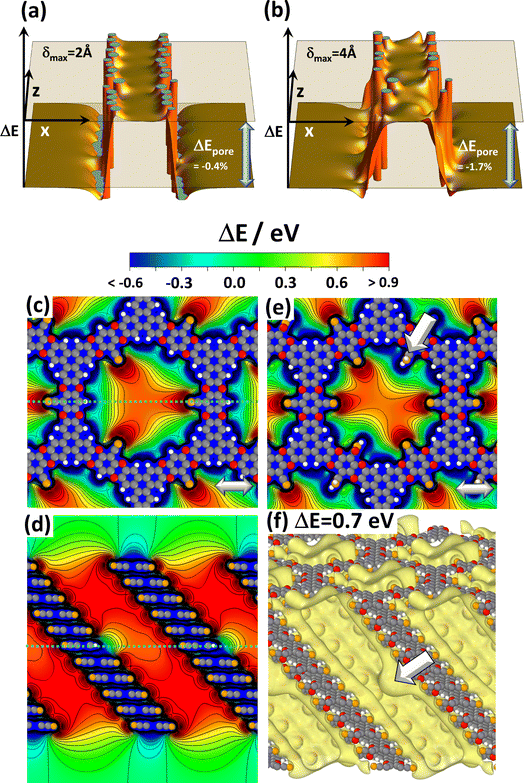Fig. 4 Impact of disorder. Panels (a) and (b) display the shift in electrostatic energy obtained with the electrostatic model comprising 6 dipoles per layer (c.f., Fig. 1(b)) for slips between consecutive layers that occur in random directions and by random magnitudes up to 2 Å in (a) and up to 4 Å in (b). The maximum slips correspond to half of the inter-layer spacing and the full inter-layer spacing assumed in the model. The diameter of the circle on which the dipoles are arranged amounts to 27/π Å. The relative decrease in ΔE_pore compared to the perfectly periodic, eclipsed stack in Fig. 1(f) amounts to −0.4% and −1.7%, respectively. Panels (c) to (f) show DFT-calculated electrostatic energies in the pores for systems comprising local chemical defects. The plots display electrostatic energies relative to the vacuum level, ΔE, for 11-layer slabs of the reference system CPAE–CN containing substitutional defects in the central layer: three –H groups instead of –CN substituents in (c) and (d) and two –CONH₂ groups in (e). The structures of individual COF layers, respectively, of atoms essentially coinciding with the planes parallel to (010) through the COF centres are superimposed on the plots of the electrostatic energy as guides to the eye. The light grey double headed arrows in panels (c) and (e) indicate the slip direction of consecutive layers. Panel (f) shows an isovalue plot of ΔE at a value of +0.7 eV for the slab in which the central layer contains two –CONH₂ defects. The two large, white arrows in panels (e) and (f) indicate the position of one of these defects (colour code – grey: C orange: N, red: O; white: H; plots produced using OVITO⁴⁴ and VESTA⁶⁷).

Conformational imperfections are not the only type of defects one would expect in COFs. The current work will not consider systems lacking entire COF building blocks as extreme cases of chemical defects. They locally disrupt the periodicity of the COF, which would be incompatible with the used periodic boundary conditions. Instead, the role of local imperfections of the substitution pattern will be addressed. This concerns missing strongly polar substituents (which are replaced by hydrogens) or –CN groups locally replaced by other functional groups through post-synthetic modifications.^32,40 To test their impact in an otherwise perfect environment, defects were introduced into the central layers of 11-layer slabs of CPAE–CN and the corresponding spatial distributions of the electrostatic energy of electrons relative to the vacuum level, ΔE, were calculated. Fig. 4(c)–(f) show the situation for three –H defects (panels (c) and (d)), and for two –CONH₂ defects (panels (e) and (f)). The latter were chosen, as the –CONH₂ post-synthetic modification described in ref. 39 has the most drastic impact on the potential within the pores (vide infra).

When comparing the vertical potential cross-section for the perfect case in Fig. 3(e) with the situation for three –H defects in panel (d), one sees that the missing –CN group impacts the electrostatic energy only locally in its immediate vicinity. This is consistent with the fact that the modification of the electrostatic energy due to an electric dipole drops quadratically with the distance from the dipole. In the horizontal cross-section in Fig. 3(c), the three H-atoms also manifest themselves via local energy variations. These largely resemble the superposition of three times the energy variation due to a single H-defect (which is shown in Fig. S9 in the ESI†). A similar situation occurs for –CONH₂ type defects featured in panel (e), with the main difference being that the quantitative impact of the defect is somewhat larger owing to the larger component of the –CONH₂ dipole in the direction opposite that of the –CN dipole. The locality of the impact of chemical imperfections is also illustrated in panel (f), where the electrostatically induced potential pocket (illustrated again as an isovalue plot at +0.7 eV) is deformed only in the immediate neighbourhood of the defect. A similar situation is observed in the isovalue plots for the other defective structures in Fig. S10 in the ESI.† The main conclusion from these data is that local chemical imperfections impact shifts in the electrostatic energy only locally and, thus, at least for low enough concentrations, have a much less drastic impact than unidirectional slips of adjacent COF layers.

4.3 Post-synthetic modifications

In the previous section, –CONH₂ groups have already been introduced as examples for post-synthetic modifications of the pore chemistry, which, if present only locally, affect the electrostatic energy only locally. In this section it will be discussed to what extent post-synthetic modifications could be used to globally change the electrostatic energy within the pores by a full conversion of all functional groups. Complications that need to be addressed arise (i) from the complexity and rather large size, as well as (ii) from the flexibility of the functional groups after the post-modification process (see –X′ substituents in Fig. 2(a) and for an overview of all structures, Fig. S1 in the ESI†). All groups contain more than two elements with different electronegativities such that the simple approximation of their internal charge distribution by a dipole moment is not fully justified anymore. Even if one stayed within the dipole approximation, for the lack of symmetry the dipole moments of the substituents would typically not point towards the pore centre and they also would not be aligned with the plane of the COF layers. Combined with the structural flexibility of the groups (in particular with their possibility to rotate around their bonds to the COF backbones), this gives rise to yet another source of electrostatic disorder. As will be discussed below, this can have a dramatic impact on the electrostatic energy within the pores. Even in the absence of disorder, the additional conformational degrees of freedom can give rise to a plethora of new conformations, where it is impossible to consider all of them. Thus, in the following discussion the focus will be on specific structures generated using chemical intuition and considering technical restrictions, as described in more detail in the Studied materials and Methods sections. The optimized unit cells of all studied structures are shown in Fig. S1 of the ESI† and, for the sake of reproducibility, the actual data files were deposited in a database. For selected cases for which conformations with significantly different electrostatic energies were identified, these alternative structures will also be described in the following section.

As a first step, the impact of the post-synthetic modification on the electrostatic energy in the centre of the pore in 11-layer slabs is discussed for fully reacted materials. The energetic shifts in the pore centres are shown as red bars in Fig. 5(a). The blue arrows denote the change in ΔE_pore relative to the reference CPAE–CN COF. The data in panel (a) reveal that ΔE_pore differs massively between different substituents. As the most extreme example, replacing the –CN substituents by –CONH₂ groups reduces the electrostatic energy in the centre of the pore by ∼1.8 eV. Other systems with significantly negative energies inside the pores are CPAE–CH₂NH₂* and CPAE–CH₂N(CH₃)₂, i.e., some of the amines. This is not unexpected, considering the data for the more simple –NH₂ substituent in Fig. 3(a). For CPAE–CONH₂ and CPAE–CH₂N(CH₃)₂ the dependences of the electrostatic energy on the degree of conversion are shown in Fig. 5(b). Starting from the fully –CN substituted COF (rightmost datapoints), the electrostatic energies gradually drop to the values for the fully reacted forms represented by the leftmost datapoints.

Fig. 5 Impact of post-synthetic modifications. (a) Difference between the electrostatic energy of an electron inside the centre of the pore of an 11-layer slab and the vacuum level, ΔE_pore, for CPAE–CN and for a variety of COFs in which the –CN substituents have been replaced by other polar groups, for example, through post-synthetic modifications (also see Fig. 2(a)). For all systems a full conversion is assumed. For CPAE–CN also the value for the alternative conformation CPAE–CN* is shown in the plot. The vertical blue arrows denote the modification of ΔE_pore through the change in substituents relative to CPAE–CN serving as the reference system. Panel (b) illustrates for two selected substituents the situation for incomplete conversion with a certain number of –CN groups per layer remaining in the system. The data points for zero “–CN substituents” correspond to the respective data for –CONH₂ and –CH₂N(CH₃)₂ in panel (a), while the data point for six “–CN substituents” represents the unmodified parent system. For the fully converted –CONH₂ system also the situation for an alternative, higher-energy conformation is illustrated for CPAE–CONH₂*. In this context it should be noted that upon increasing the density of –CONH₂ substituents, in the geometry optimizations not only the magnitudes of the slips, but also the slip-directions change as documented in Table S3 in the ESI.†

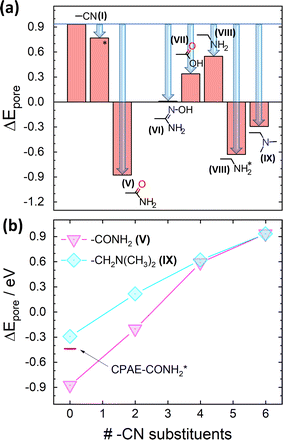
However, considering only electrostatic energies at the centres of the pores for the present systems runs the risk of generating a somewhat misleading picture due to the more complex charge distributions within the substituents introduced by the post-synthetic modification reactions. This is visible already for CPAE–CONH₂ in Fig. 6(a): the highly negative electrostatic energy reported for CPAE–CONH₂ in Fig. 5 occurs only in the centre of the pore, while in its perimeter ΔE becomes even positive with (positive) spikes in ΔE close to the atoms in the substituents bearing a partial negative charge. This is different from the situation, for example, for CPAE–CN (c.f., Fig. 3(d)), where an essentially constant electrostatic energy is found for most of the pore cross-section. In passing it is noted that the reason why the spatial distributions of the electrostatic energies in all panels of Fig. 6 do not display a six-fold symmetry is that the orientations of the rather bulky post-modification substituents depend on the substitution sites. The reason for that is that the substituents extend beyond the plane of the COF backbones they are attached to. Thus the slip of consecutive COF layers introduces site-dependent sterical constraints and triggers site-dependent ideal conformations for forming inter-substituent H-bonds. This in some cases causes noticeable distortions of the COF backbones (e.g., for –X′ = –CONH₂ especially when optimizing also the unit cell; see Fig. S5 in the ESI†).

Fig. 6 Impact of post-synthetic modifications on the electrostatic energy in the pores. DFT-calculated electrostatic energies relative to the vacuum level, ΔE, for 11-layer slabs of the lowest-energy conformations (a) and (c) and two higher-energy local minimum structures (b) and (d) for fully –CONH₂ ((a) and (b)) and –CH₂NH₂ ((c) and (d)) substituted CPAE COFs. Cross-sections are shown for planes parallel to the (001) planes of the slabs through the middle of the central layer. Atoms within ±2 Å of the chosen planes are superimposed on the plots of the electrostatic energy as guides to the eye. The reason why no individual COF-layers are plotted is that these are rather distorted (see plots in section S4 in the ESI†). Together with the extended substituents, this would result in structures with little relation to the displayed energy cross-sections. The light grey double headed arrows in panels (a)–(d) indicate the slip direction of consecutive layers. Colour code – grey: C; orange: N; red: O; white: H; plots produced using OVITO⁴⁴ and VESTA.⁶⁷

The intra-pore variation in ΔE is even more pronounced in the second (local) minimum structure found for the –CONH₂ substituent (CPAE–CONH₂*). This conformation is significantly higher in total energy than CPAE–CONH₂ (by 117 meV per substituent, see Table S3†), but it still serves the purpose of illustrating the impact of variations in substituent conformation, which are expected to occur at least locally due to thermal exs. For CPAE–CONH₂* one observes a markedly smaller reduction of the electrostatic energy in the pore centre as illustrated by the corresponding datapoint in Fig. 5(b). This is consistent with the observation that in the vertical cross-section in Fig. 6(b) the pronounced minimum in electrostatic energy in the pore centre has largely disappeared. Additionally, regions of positive electrostatic energy in specific regions of the pore have clearly increased in extent and are characterized by more positive values of ΔE.

An even more extreme situation is found for the –CH₂NH₂ substituent. There, the polar part of the substituent can rotate relatively freely inside the pore. Thus, one observes structures fundamentally different from that of CPAE–NH₂ discussed earlier. In this system, the –NH₂ groups were directly attached to the COF backbones and were, thus, pointing towards the pore centre. In the –CH₂NH₂ case, the C–N bonds no longer point towards the pore axis due to the bonding geometry imposed by the CH₂ spacer. This diminishes the impact of the dipole component along the C–N axis on ΔE. What rather counts in CPAE–CH₂NH₂ and CPAE–CH₂NH₂* are the dipoles along the N–H bonds. To illustrate this, the geometry optimizations for these COFs were started from conformations with these bonds either pointing towards the pore centres or away from them. This yielded two distinct local minima: in the lowest energy conformation termed CPAE–CH₂NH₂ both N–H bonds point away from the pore centre (see –NH₂ groups in Fig. 6(c) and S3†). In a local minimum structure termed CPAE–CH₂NH₂*, which is higher in energy by 23 meV per substituent (see Table S3†), one of the N–H bonds points essentially towards the pore centre, while the other one is aligned along the pore wall (Fig. 6(d) and S3†). These different orientations of the N–H bonds even cause different signs of ΔE_pore for the two conformations, as shown in Fig. 5(a). In fact, the absolute value of ΔE_pore between the two conformations changes by as much as 1.2 eV. The fundamentally different distributions of the electrostatic energy in the pores for the two conformations are also clearly visible in the cross-sections in Fig. 6(c) and (d). For actual COFs at finite temperatures, one would expect an even more complex energy landscape due to thermal fluctuations of the substituent orientations. Thus, for systems like CPAE–CH₂NH₂ static and dynamic disorder might even largely eliminate the impact of polar substituents on the electrostatic energy landscape.

In an attempt to enforce a structure in which the aforementioned disorder would not occur, a related substituent with a much bulkier dimethylamine terminal unit was tested (see CPAE–CH₂N(CH₃)₂ in Fig. 2(a)). This indeed stabilized the desired conformation resulting in a reduction in the centre-of-pore electrostatic energy by 1.20 eV compared to that of the parent CPAE–CN system. The resulting ΔE_pore value of 0.29 eV is, in fact, very close to the value for CPAE–NH₂ (−0.38 eV, see Table S4†). A vertical cross section of the electrostatic energy within the pore for CPAE–CH₂N(CH₃)₂ is provided in Fig. S11(c).† It shows a rather constant potential within the pores, albeit at the price of a significantly reduced pore diameter together with a heavily distorted structure (see Fig. S6†).

The remaining two substituents realized by post-synthetic modifications are –C(NOH)NH₂ and –COOH. The value of ΔE_pore for CPAE–C(NOH)NH₂ of +0.01 eV suggests that this might be an interesting candidate for realizing a pore for which the electrostatic energy equals that in vacuum, i.e., for generating a situation in which collective electrostatic effects do not play a role. A vertical cross-section of the electrostatic energy within the pores (see Fig. S11(a)†), however, reveals some local positive peaks in the electrostatic energy close to the substituents. Moreover, variations in the electrostatic energy due to structural fluctuations at finite temperatures would presumably result in at least local deviations from the nearly vanishing value of ΔE_pore. In contrast, for CPAE–COOH (like for –CONH₂) a well-defined H-bonding network amongst the substituents can be identified (see Fig. S4†). This is expected to stabilize the obtained conformation (even though the dynamic stability of the resulting structure has not been assessed yet). Interestingly, for CPAE–COOH a rather constant and clearly positive electrostatic energy within the pore is obtained (see Fig. S11(b)†). Both aspects are reminiscent of the situation in CPAE–CN (vide supra), which also means that a post-synthetic conversion of –CN to –COOH substituents would not create significant contrasts in the electrostatic energies of the pores in mixed systems.

4.4 Locally tuning the electrostatic energy landscape in COF pores

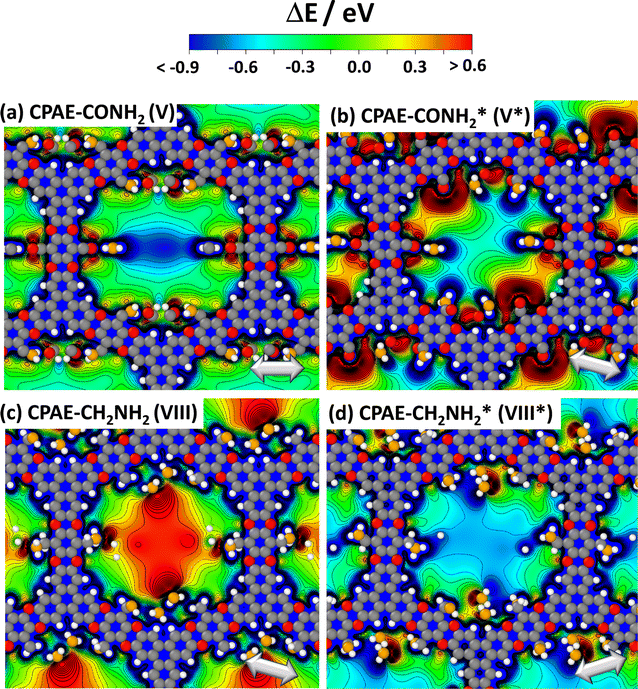
The above findings suggest that, for illustrating the local tuning of the electrostatic energy landscape within pores, heterostructures comprising regions of CPAE–CN and regions of CPAE–CONH₂ COFs are ideal. Modelling such heterostructures can also demonstrate the options one has, if one manages to perform post-synthetic modification reactions only locally in certain regions of a COF. For introducing the concept of electrostatic pore-tuning, we will, however, first consider even more simple heterostructures starting from the CPAE–CN reference system and locally (i.e., within a few layers) replacing the –CN groups by –H atoms. In the following examples, the number of layers in which a specific substituent prevails, or over which substitution-gradients are generated will be rather low, in fact, probably lower than achievable in experiments. This is merely a limitation of the computational approach, as already when considering 11-layer slabs, one is typically dealing with more than a thousand atoms in the unit cell. Nevertheless, these “small” systems will also be useful for conveying the general concepts.

For example, Fig. 7(a) and (b) illustrate two motifs for “potential pockets”, which are locally confined regions with a particularly high electrostatic energy (yellow) that are surrounded by regions with low energy (cyan). For generating a single pocket within an 11-layer slab (panel (a)), three layers of CPAE–H are followed by 5 layers of CPAE–CN and then by another three layers of CPAE–H. When plotting the energy along a line in the centre of the pore of that system (see Fig. 7(d)), one observes two regions with slightly decreased electrostatic energy close to the two surfaces of the slabs surrounding a region of significantly increased electrostatic energy in the centre. This causes gradients in the electrostatic energy (dashed red line; defined as electrostatic force acting on an electron, F). As ΔE is defined as electrostatic energy per electron, these gradients would suck positively charged species towards the central region, while keeping negatively charged species out. Besides separating charged species and driving them in specific directions, the presented potential pocket should allow a local variation of the alignment between the electronic states in guest molecules and in the COF scaffold. Consequently, all chemical processes involving charge transfer between the COF and the guest could either be promoted or inhibited. As will become evident from the following discussion and the data in ref. 30, the level alignment is also impacted by the chemical substitution of the COF, which changes its ionisation energy and electron affinity. The overall change in level alignment, however, is much larger due to the collective action of the dipoles. An additional effect that will appear in heterostructures is that the electronic levels of identical guest molecules will be shifted relative to each other if they prevail in differently substituted regions. Notably, this shift is not affected by any chemical substitution effect, but exclusively originates from the differently oriented dipoles, if the guest molecules reside in different regions of the heterostructure.

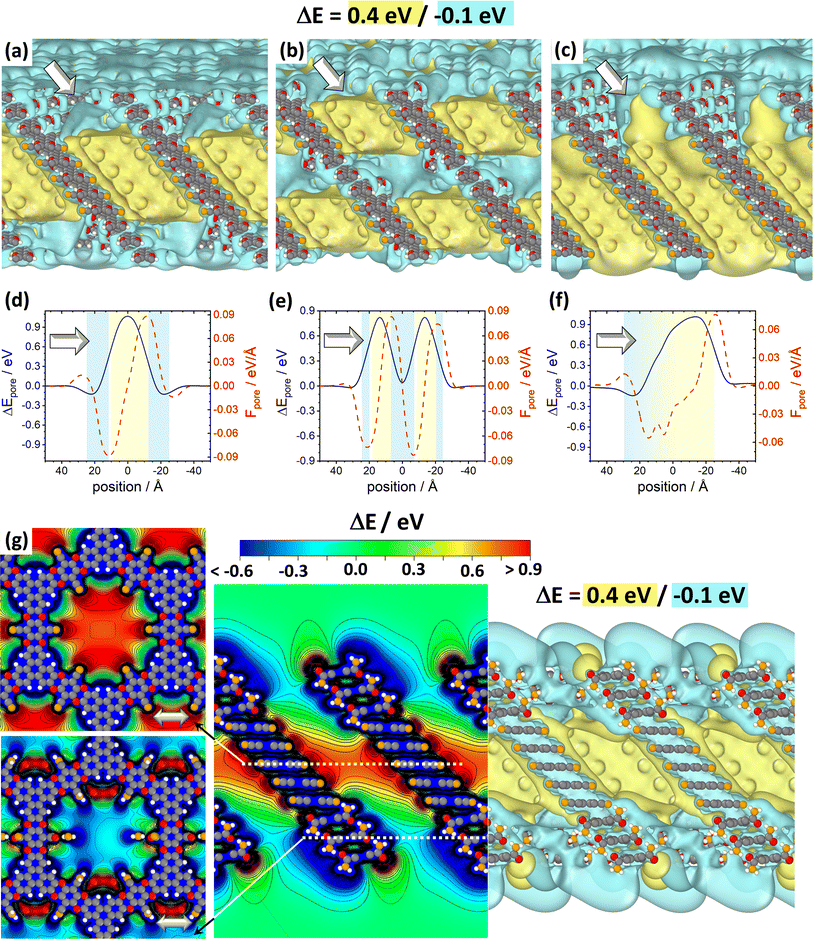Fig. 7 DFT-calculated electrostatic energies of heterolayer slabs of COFs. Panels (a)–(f) illustrate electrostatic energies relative to the vacuum level, ΔE, for CPAE–CN/CPAE–H heterostructures: the first system (panels (a) and (d)) comprises three layers of CPAE–H plus five layers of CPAE–CN plus three layers of CPAE–H; the second system (panels (b) and (e)) consists of one layer of CPAE–H plus three layers of CPAE–CN plus three layers of CPAE–H plus three layers of CPAE–CN plus one layer of CPAE–H; and the third system (panels (c) and (f)) contains a slab comprising five layers of CPAE–CN followed by 5 layers with an increasing –H to –CN ratio (1 : 5, 2 : 4, 3 : 3, 4 : 2, and 5 : 1) plus a top CPAE–H layer (i.e., a gradient structure). Panels (a)–(c) are isovalue plots at +0.4 eV and −0.1 eV illustrating the formation of differently shaped potential pockets. Panels (d)–(f) illustrate the evolution of ΔE along lines running through the centres of the pores together with the respective gradients. The white arrows in (a)–(f) indicate equivalent directions. The gradients are calculated such that negative (positive) values indicate forces pushing electrons towards more positive (more negative) positions. Light blue and light yellow shaded regions in panels (d)–(f) indicate regions aligned with CPAE–H and CPAE–CN layers, respectively. Panel (g) illustrates the situation for a slab consisting of three layers of CPAE–CONH₂, five layers of CPAE–CN, and three layers of CPAE–CONH₂. In addition to the vertical cross-section and the isovalue plot of ΔE in the central and right plots, in the leftmost plots cross-sections parallel to the (001) and (010) planes are shown. There, the situations in the centre of the bottom three CPAE–CONH₂ layers and in the centre of the five CPAE–CN layers are shown (c.f., dotted white lines in the central graph). Structures are superimposed on the plots of ΔE as guides to the eye (colour code – grey: C; orange: N; red: O; white: H; plots produced using OVITO⁴⁴ and VESTA⁶⁷).

As illustrated in panel (e), realizing multiple potential pockets (here, as a succession of 1-3-3-3-1 CPAE–H and CPAE–CN layers), generates more frequent oscillations of the energy and of the energy gradient. Conversely, when constructing a substitution gradient (which in practice could be the consequence of more efficient post-synthetic modifications near the film surface), one extends the region in which significant potential gradients prevail. This is illustrated in panels (c) and especially (f), where the situation for five CPAE–CN layers is shown, which are covered by six layers in which successively more –CN groups are replaced by –H. The related situation for six layers in which the –CN groups are successively replaced by –CONH₂ substituents is shown in Fig. S15 in the ESI.† In passing we note that panels (d)–(f) appear to indicate that electrostatic energies are never constant along the pore axis. This observation is merely a consequence of only comparably few layers with equivalent polarities stacked on top of each other in the displayed model systems. For an 11-layer slab exclusively consisting of only CPAE–CN, a region of essentially constant electrostatic energy and vanishing gradient is observed, as explicitly shown in Fig. S13.† This is also consistent with the 2D vertical cross-section of the electrostatic energy of that slab shown in Fig. 3(e).

When introducing –CONH₂ groups in the three terminal layers on both sides of the slab (Fig. 7(g)), a situation similar to that observed for –H substituents in panel (a) emerges, with a confined high electrostatic energy region in the central part of the slab. In the –CONH₂ case, the regions of negative ΔE_pore in the areas of the CPAE–CONH₂ layers are, however, much more pronounced than for CPAE–H. This is a consequence of the –CONH₂ groups being more polar than the –H groups (see above). The strong variations in electrostatic energy in the CPAE–CN/CPAE–CONH₂ slabs are, on the one hand, illustrated by the markedly different electrostatic energies observed in the two horizontal potential cross-sections shown in the leftmost panels of Fig. 7(g). On the other hand, they can also be inferred from the isovalue plot and the vertical cross-section of the electrostatic energy in the rest of panel (g). These data clearly illustrate the massive potential gradients within the pore resulting from the different substitution patterns. These gradients are also visible in the 1D potential plot along the pore centre for this system in Fig. S12(c) in the ESI.† In passing it is noted that the somewhat different details of the horizontal energy cross-sections in the CPAE–CONH₂ region in Fig. 7(g) and in 6(a) result from the different unit cells that were used in the two cases: in the former case, for technical reasons (see the Methods section), the CPAE–CN unit cell had to be applied, while for homogeneous CPAE–CONH₂ the unit cell could be fully optimized.

The situation for a periodic arrangement of groups of CPAE–CN and CPAE–CONH₂ layers is shown in Fig. 8. One can clearly identify regions of positive and negative electrostatic energy that alternate along the pore axes. Consequently, in a system like this, the efficiency of any process depending on the alignment of electronic levels in the guests and in the scaffold would be periodically modulated. Likewise, if ions were present in the channel, one would expect a periodic sequence of regions of cation and anion accumulation, and the electronic states of identical guest molecules present in the different regions would be periodically shifted.

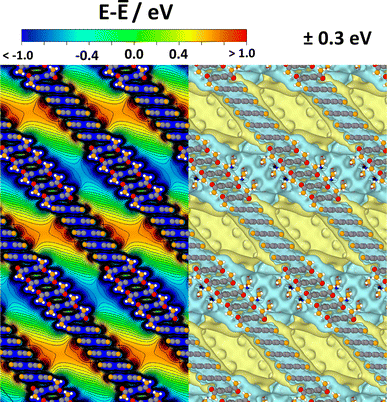Fig. 8 Electrostatic energy in a periodic COF structure comprising five layers of CPAE–CN and five layers of CPAE–CONH₂ in the unit cell. As there is no vacuum level in the periodic system, the energy is given relative to the average electrostatic energy along a line through the centre of one of the pores. In the left half of the plot, the energy is shown in the (010) plane of the structure passing through the centre of the pore, while the right half contains isovalue plots of the electrostatic energy for ±0.3 eV cut at the (010) plane through the pore centre. Colour code – grey: C; orange: N; red: O; white: H; plots produced using OVITO⁴⁴ and VESTA.⁶⁷

Finally, it should be noted that a lateral variation of substitution patterns via spatially confined post-synthetic modification reactions is also conceivable. This would offer the possibility to laterally define the regions in which specific redox or catalytic processes occurred.

4.5 Guest molecules in electrostatically tuned pores

It has already been shown in ref. 30 that shifts in the electrostatic energy translate into equivalent changes in the level alignment for guest molecules not interacting with the pore walls. This has been illustrated for C₆₀ molecules “manually” placed in the centres of the pores for COF DUT-177 at sufficiently large distances from the pore walls to exclude any direct interactions. This raises the question to what extent the situation will be modified, if guest molecules actually adsorb on the walls. The discussion of specific chemical reactions is not in the scope of the current manuscript as these strongly depend on the nature of the guest and also on the chemical reactivity of the COF substituents. Thus, the focus here will be on situations in which no specific chemical reactions are to be expected and in which one is essentially dealing with a physisorption situation. More specifically, the situation of a fully methylated ethene molecule (QME, with the methyl groups acting as spacers) in CPAE–CN and CPAE–CONH₂ bulk materials was studied. Additionally, the structures of C₆₀ contained in CPAE–CN and CPAE–NH₂ were optimized. CPAE–NH₂ was chosen in the C₆₀ case, as the channel of CPAE–CONH₂ turned out to be too narrow to host the C₆₀ molecules. In both cases molecules were placed close to the pore walls in unit cells comprising three COF layers, and then all atomic positions and the unit cells were optimized. The structures for the two QME-containing COFs are shown in Fig. 9(a) and (b). In both systems, QME physisorbs at the pore wall, essentially between two neighbouring substituents, in a region in which the shift in electrostatic energy is distinctly smaller than that in the pore centre, especially in COF–CONH₂ (see Fig. 3(d) and 6(a)). Nevertheless, if one aligns the densities of states of the two systems at the valence-band maxima (VBMs) of the COFs, the peaks associated with the highest occupied state in QME are shifted by 1.66 eV (see Fig. 9(c)). This is only slightly smaller than the difference in ΔE_pore values for CPAE–CN and CPAE–CONH₂, which amounts to 1.81 (see Table S4 in the ESI†). The similarity of the two values despite the adsorption in a region of a reduced ΔE is, however, a consequence of neglecting changes in the ionisation energies of the COF matrices due to the substitution. These changes can approximated by considering the shifts of the valence-band maxima relative to the vacuum levels for the 11-layer slabs discussed in Sections 4.1 and 4.2. Considering this, one can obtain the densities of states relative to the vacuum level as shown Fig. 9(d). Now the energetic offset between the highest occupied states in QME in CPAE–CN and CPAE–CONH₂ has dropped to 0.91 eV, which is consistent with the adsorption positions of QME in regions of reduced ΔE.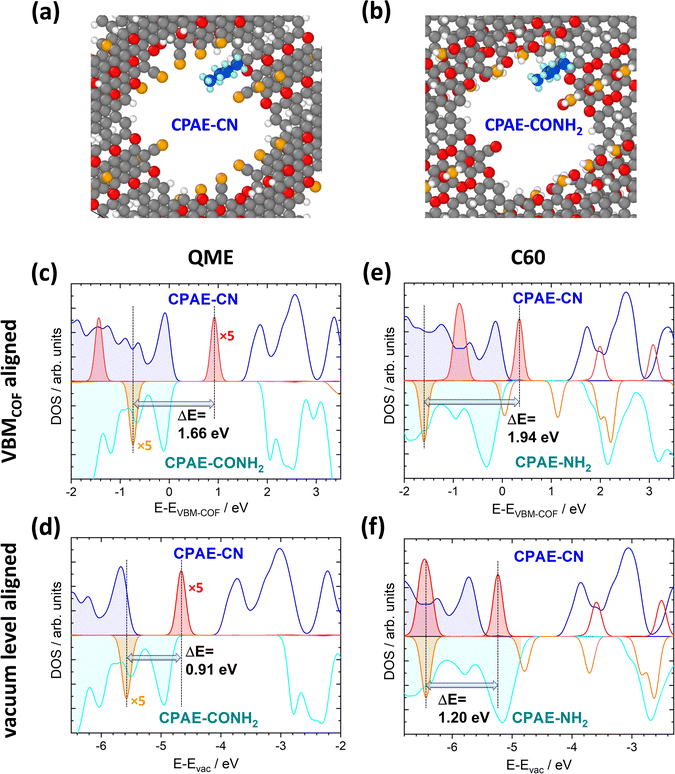

Fig. 9 Impact of collective electrostatics on the energetics of adsorbed molecules. Panels (a) and (b) show the DFT-optimized structures of one QME molecule per three COF layers in CPAE–CN (a) and CPAE–CONH₂ (b). The densities of states for the two systems projected onto the COFs (blue and cyan) and projected onto the QME molecules (red and orange, for the sake of visibility, multiplied by a factor of five) are shown in panels (c) and (d). The situation in CPAE–CN/QME is represented by positive DOS values and that in CPAE–CONH₂/QME by nominally negative DOS values. In (c) the energy scale is aligned relative to the valence-band maxima of the COFs in both bulk systems, while in panel (d) it is aligned relative to the vacuum level (with the shifts between valence band maxima and vacuum level estimated from the electronic structures of the respective 11-layer slabs not comprising guest molecules). Panels (e) and (f) contain equivalent plots for C₆₀ in CPAE–CN and CPAE–NH₂. The shaded DOSs denote occupied states, while the empty ones refer to unoccupied ones (colour code – grey: C; orange: N; red: O; white: H, in the COF; blue: C and light blue: H, in the QME molecule; structures plotted using OVITO⁴⁴).

In the case of C₆₀, the molecule again physisorbs at the pore walls between the substituents (see Fig. S17 in the ESI†). As C₆₀ is, however, much larger than QME, it primarily resides in regions with the largest ΔE values in the pore. Moreover, in CPAE–CN and CPAE–NH₂ the variations of the electrostatic energy over the pore diameter are much less pronounced than those observed for CPAE–CONH₂. Therefore, when aligning the DOSs relative to the vacuum level in Fig. 9(f), the shift of the electronic states of C₆₀ (1.20 eV) is close to the difference in the ΔE_pore values of CPAE–CN and CPAE–NH₂ (1.31 eV). In fact, the slightly reduced value for the shift of the C₆₀ DOSs is at least partly caused by a minor charge-transfer between the COF and the C₆₀ molecule resulting in Fermi-level pinning (which might well be an artefact due to the underestimation of the band gap with the used PBE functional). In passing it is noted that when aligning the DOSs at the valence-band maxima, the shift of the DOSs amounts to 1.94 eV, which even exceeds the difference in ΔE_pore. However, as discussed above, this is merely a consequence of the changes in ionisation energy of the COFs due to the substitution (also see a more detailed discussion in ref. 30).

The superposition of the chemically induced shifts due to substitution and the electrostatically induced shifts due to collective electrostatics also reveals a dilemma when trying to identify the electrostatic shifts experimentally. In all experiments relying on charge-transfer reactions between the COFs and the guests, both shifts will inevitably occur simultaneously and will typically be of a similar order of magnitude.³⁰ Thus, interpreting such experiments solely based on substitution effects is plainly wrong, at least for substitution-patterns like the ones discussed here. Still, how to differentiate between the different contributions is not obvious. One possibility to isolate “electrostatic” shifts would be measuring the electronic states of molecules infiltrated into the pores relative to the vacuum level. The standard way of doing this would be via photoelectron spectroscopy, e.g., by decorating selected parts of the system with chemically distinct marker atoms.⁷⁴ Still, even then, it will be challenging to avoid signals from guest molecules adsorbed outside the pores and to deal with the finite escape depth of photoelectrons.

5 Conclusions

Periodically assembling polar groups at pore walls in stacked two-dimensional covalent organic frameworks massively changes the electrostatic energy within the pores. This directly translates into a change of the alignment of electronic states in guest molecules and in the COF matrix.³⁰ This is expected to massively impact all processes involving guest–host charge-transfer reactions. In the present contribution, the dipole-induced shift is conceptually rationalized on the basis of an electrostatic model and explicitly demonstrated for a variety of derivatives of the particularly chemically stable COF-316 (ref. 39)/JUC-505 (ref. 40) system. As the shift is electrostatic in nature and arises from the superposition of the fields generated by the periodically arranged dipoles, it strongly depends on the density of the polar substituents in the pore walls and also on the details of the arrangement of the dipoles. The latter is, for example, strongly influenced by the stacking of the 2D COF layers and depends on the direction and magnitude of the slips between consecutive layers as well as on the overall stacking motif: for example, the shift in electrostatic energy is reduced, if successive layers are always slipped in the same direction; conversely, for alternating slips and also for structures in which slip directions between layers and (within limits) also the magnitudes of the slips vary randomly, the shifts in electrostatic energy within the pores are essentially equivalent to those of an eclipsed stacking. While certain changes in the stacking motif can globally impact the electrostatic shifts, local chemical defects (e.g., locally missing polar substituents) impact the electrostatic energy only locally. In fact, the inhomogeneities in electrostatic energy shifts become vanishingly small a few Å away from the defects.

Owing to the extreme chemical stability of COF-316 (ref. 39)/JUC-505,⁴⁰ this COF can be subjected to post-synthetic modification reactions, which change the chemical nature of the substituents. This paves the way for a chemical modification of the intra-pore electrostatic energy. However, the introduced substituents are, on the one hand, rather bulky with dipole moments not pointing towards or away from the pore centre or with charge distributions that cannot easily be modelled solely by using a dipole moment. This can result in significant local variations of the electrostatic energies within the channels. Moreover, the substituents introduced in post-modification reactions are often able to rotate, which changes the orientation of the associated charge distribution and in extreme cases, can even change the sign of the changes in electrostatic energy within the pores.

In addition to a thorough characterisation of the “electrostatic situation” for specific substitution patterns, it is also shown how the potential landscape within the pores can be manipulated through COF heterostructures consisting of groups of COF-layers with identical substituents confined by layers with other substituents or by regions comprising gradients of mixed substitution patterns. In this way, pockets of well-defined electrostatic energies can be realized. These should allow for spatial variations in the efficiency of redox reactions, of catalytic processes, or of excited state charge transfer. Sequences of pockets of high and low electrostatic energy can help to spatially separate cationic and anionic species and can introduce relative shifts in the positions of the electronic states in otherwise identical guest molecules. Moreover, heterostructures comprising composition gradients create extended regions of energy gradients, which might be exploited for realizing structures that funnel ions in specific directions.

Explicitly calculating the impact of shifts in electrostatic energy on the alignment of electronic states localized in guest molecules and in the host matrix reveals that for non-interacting molecules localized in the centre of the pore, shifts in electrostatic energy directly translate into modifications in the level alignment. These shifts occur in addition to substitution-induced changes in the ionisation energies and electron affinities of the COFs. When the guest molecules adsorb on the pore walls, the magnitude of the electrostatically introduced level shift depends on the spatial extent of the guest species and on the homogeneity of the substitution-induced energy variations within the pore: for example, for C₆₀ adsorbed close to the pore walls of CPAE–CN or CPAE–NH₂ the shifts in electrostatic energy in the pore are essentially identical to the change in level alignment; conversely, for the much smaller fully methylated ethene molecule a markedly reduced shift is observed especially for CPAE–CONH₂. This is a consequence of the π-electron system of QME getting localized in a spatial region in which electrostatically induced energetic shifts are strongly reduced due to the marked variation of the pore electrostatic energy in CPAE–CONH₂.

The presented considerations portray the intricacies of substitution-induced changes in the electrostatic energy in COF pores and lay the foundation for an electrostatic design of COF heterostructures exploiting post-synthetic modification reactions. This allows for an expansion of the tuning range of the electronic structure of COF-based guest–host systems far beyond what is accessible by inductive and mesomeric effects of substituents.³⁰ Besides, one has to keep in mind that materials with polar substituents have already been discussed in a variety of papers (see the Introduction section), and also in contexts in which the electronic level alignment is crucial for the application of the COF (e.g., for redox reactions). In all such cases, collective electrostatics plays a crucial role, but, to the best of my knowledge, has not been considered in the interpretation of the results. This suggests that a revaluation of various experimental observations might be required.

Data availability

All relevant data can be downloaded from the TU Graz data repository (https://doi.org/10.3217/y6e40-fk714 for the empty CPAE COFs⁷⁵ and https://doi.org/10.3217/63rkm-hec45 for a COF comprising a longer linker and for CPAE COFs containing C₆₀ and QME⁷⁶).

Author contributions

The idea for the current project was conceptualized by E. Zojer; he also performed all calculations, analyzed the results, compiled all plots contained in the main manuscript and in the ESI, and wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The author thanks Christian Slugovc for stimulating discussions on structures that could be realized in post-synthetic modification reactions and Robbin Steentjes for analysing which XRD patterns would result from specific structures. Support of the research activities associated with this manuscript through the TU Graz Lead Project Porous Materials @ Work for Sustainability (LP-03) is acknowledged. The computational results were obtained using the Vienna Scientific Cluster.

Notes and references

1. C. S. Diercks and O. M. Yaghi, Science, 2017, 355, eaal1585.
2. D. Jiang, Chem, 2020, 6, 2461–2483.
3. K. Geng, T. He, R. Liu, S. Dalapati, K. T. Tan, Z. Li, S. Tao, Y. Gong, Q. Jiang and D. Jiang, Chem. Rev., 2020, 120, 8814–8933.
4. R. Liu, K. T. Tan, Y. Gong, Y. Chen, Z. Li, S. Xie, T. He, Z. Lu, H. Yang and D. Jiang, Chem. Soc. Rev., 2021, 50, 120–242.
5. G.-B. Wang, S. Li, C.-X. Yan, F.-C. Zhu, Q.-Q. Lin, K.-H. Xie, Y. Geng and Y.-B. Dong, J. Mater. Chem. A, 2020, 8, 6957–6983.
6. X. Zhao, P. Pachfule and A. Thomas, Chem. Soc. Rev., 2021, 50, 6871–6913.
7. C. R. DeBlase, K. E. Silberstein, T.-T. Truong, H. D. Abruña and W. R. Dichtel, J. Am. Chem. Soc., 2013, 135, 16821–16824.
8. H. Yang, S. Zhang, L. Han, Z. Zhang, Z. Xue, J. Gao, Y. Li, C. Huang, Y. Yi, H. Liu and Y. Li, ACS Appl. Mater. Interfaces, 2016, 8, 5366–5375.
9. S. Haldar, R. Kushwaha, R. Maity and R. Vaidhyanathan, ACS Mater. Lett., 2019, 1, 490–497.
10. Y. Hu, N. Dunlap, S. Wan, S. Lu, S. Huang, I. Sellinger, M. Ortiz, Y. Jin, S. Lee and W. Zhang, J. Am. Chem. Soc., 2019, 141, 7518–7525.
11. J. Chu, Y. Wang, F. Zhong, X. Feng, W. Chen, X. Ai, H. Yang and Y. Cao, EcoMat, 2021, 3, e12133.
12. Y. Lu, Y. Cai, Q. Zhang and J. Chen, J. Phys. Chem. Lett., 2021, 12, 8061–8071.
13. D. Zhu, G. Xu, M. Barnes, Y. Li, C.-P. Tseng, Z. Zhang, J.-J. Zhang, Y. Zhu, S. Khalil, M. M. Rahman, R. Verduzco and P. M. Ajayan, Adv. Funct. Mater., 2021, 31, 2100505.
14. S. Haldar, M. Wang, P. Bhauriyal, A. Hazra, A. H. Khan, V. Bon, M. A. Isaacs, A. De, L. Shupletsov, T. Boenke, J. Grothe, T. Heine, E. Brunner, X. Feng, R. Dong, A. Schneemann and S. Kaskel, J. Am. Chem. Soc., 2022, 144, 9101–9112.
15. S. Haldar, A. Schneemann and S. Kaskel, J. Am. Chem. Soc., 2023, 145(25), 3494–13513.
16. D. Bessinger, L. Ascherl, F. Auras and T. Bein, J. Am. Chem. Soc., 2017, 139, 12035–12042.
17. L. Ascherl, E. W. Evans, M. Hennemann, D. Di Nuzzo, A. G. Hufnagel, M. Beetz, R. H. Friend, T. Clark, T. Bein and F. Auras, Nat. Commun., 2018, 9, 3802.
18. N. Keller and T. Bein, Chem. Soc. Rev., 2021, 50, 1813–1845.
19. M. Dogru, M. Handloser, F. Auras, T. Kunz, D. Medina, A. Hartschuh, P. Knochel and T. Bein, Angew. Chem., Int. Ed., 2013, 52, 2920–2924.
20. J. Guo, Y. Xu, S. Jin, L. Chen, T. Kaji, Y. Honsho, M. A. Addicoat, J. Kim, A. Saeki, H. Ihee, S. Seki, S. Irle, M. Hiramoto, J. Gao and D. Jiang, Nat. Commun., 2013, 4, 2736.
21. M. Calik, F. Auras, L. M. Salonen, K. Bader, I. Grill, M. Handloser, D. D. Medina, M. Dogru, F. Löbermann, D. Trauner, A. Hartschuh and T. Bein, J. Am. Chem. Soc., 2014, 136, 17802–17807.
22. S. Jin, M. Supur, M. Addicoat, K. Furukawa, L. Chen, T. Nakamura, S. Fukuzumi, S. Irle and D. Jiang, J. Am. Chem. Soc., 2015, 137, 7817–7827.
23. D. D. Medina, V. Werner, F. Auras, R. Tautz, M. Dogru, J. Schuster, S. Linke, M. Döblinger, J. Feldmann, P. Knochel and T. Bein, ACS Nano, 2014, 8, 4042–4052.
24. J. M. Cox, B. Mileson, A. Sadagopan and S. A. Lopez, J. Phys. Chem. C, 2020, 124, 9126–9133.
25. S. Haldar, D. Kaleeswaran, D. Rase, K. Roy, S. Ogale and R. Vaidhyanathan, Nanoscale Horiz., 2020, 5, 1264–1273.
26. L. Stegbauer, S. Zech, G. Savasci, T. Banerjee, F. Podjaski, K. Schwinghammer, C. Ochsenfeld and B. V. Lotsch, Adv. Energy Mater., 2018, 8, 1703278.
27. S. Bi, C. Yang, W. Zhang, J. Xu, L. Liu, D. Wu, X. Wang, Y. Han, Q. Liang and F. Zhang, Nat. Commun., 2019, 10, 2467.
28. D. D. Méndez-Hernández, P. Tarakeshwar, D. Gust, T. A. Moore, A. L. Moore and V. Mujica, J. Mol. Model., 2013, 19, 2845–2848.
29. R. E. M. Willems, C. H. L. Weijtens, X. de Vries, R. Coehoorn and R. A. J. Janssen, Adv. Energy Mater., 2019, 9, 1803677.
30. E. Zojer, Nano Lett., 2023, 23, 3558–3564.
31. A. Natan, L. Kronik, H. Haick and R. T. Tung, Adv. Mater., 2007, 19, 4103–4117.
32. D. Cahen, R. Naaman and Z. Vager, Adv. Funct. Mater., 2005, 15, 1571–1578.
33. G. Heimel, F. Rissner and E. Zojer, Adv. Mater., 2010, 22, 2494–2513.
34. O. L. A. Monti, J. Phys. Chem. Lett., 2012, 3, 2342–2351.
35. E. Zojer, T. C. Taucher and O. T. Hofmann, Adv. Mater. Interfaces, 2019, 6, 1900581.
36. E. Zojer, A. Terfort and M. Zharnikov, Acc. Chem. Res., 2022, 55, 1857–1867.
37. A. Petritz, M. Krammer, E. Sauter, M. Gärtner, G. Nascimbeni, B. Schrode, A. Fian, H. Gold, A. Cojocaru, E. Karner-Petritz, R. Resel, A. Terfort, E. Zojer, M. Zharnikov, K. Zojer and B. Stadlober, Adv. Funct. Mater., 2018, 28, 1804462.
38. Wolfram Research, Inc., Mathematica, Version 11.3, Champaign, IL, 2018.
39. B. Zhang, M. Wei, H. Mao, X. Pei, S. A. Alshmimri, J. A. Reimer and O. M. Yaghi, J. Am. Chem. Soc., 2018, 140, 12715–12719.
40. X. Guan, H. Li, Y. Ma, M. Xue, Q. Fang, Y. Yan, V. Valtchev and S. Qiu, Nat. Chem., 2019, 11, 587–594.
41. D.-G. Wang, N. Li, Y. Hu, S. Wan, M. Song, G. Yu, Y. Jin, W. Wei, K. Han, G.-C. Kuang and W. Zhang, ACS Appl. Mater. Interfaces, 2018, 10, 42233–42240.
42. A. M. Pütz, M. W. Terban, S. Bette, F. Haase, R. E. Dinnebier and B. V. Lotsch, Chem. Sci., 2020, 11, 12647–12654.
43. Q. Sun, B. Aguila, L. D. Earl, C. W. Abney, L. Wojtas, P. K. Thallapally and S. Ma, Adv. Mater., 2018, 30, 1705479.
44. A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012.
45. C. Winkler, T. Kamencek and E. Zojer, Nanoscale, 2021, 13, 9339–9353.
46. M. O. Sinnokrot and C. D. Sherrill, J. Am. Chem. Soc., 2004, 126, 7690–7697.
47. C. D. Sherrill, Acc. Chem. Res., 2013, 46, 1020–1028.
48. C. Sutton, C. Risko and J.-L. Brédas, Chem. Mater., 2016, 28, 3–16.
49. C. Winkler, A. Jeindl, F. Mayer, O. T. Hofmann, R. Tonner and E. Zojer, Chem. Mater., 2019, 31, 7054–7069.
50. S. M. Ryno, C. Risko and J.-L. Brédas, Chem. Mater., 2016, 28, 3990–4000.
51. G. Gryn'ova and C. Corminboeuf, J. Phys. Chem. Lett., 2016, 7, 5198–5204.
52. B. Lukose, A. Kuc, J. Frenzel and T. Heine, Beilstein J. Nanotechnol., 2010, 1, 60–70.
53. W. Zhou, H. Wu and T. Yildirim, Chem. Phys. Lett., 2010, 499, 103–107.
54. Y. Zhang, M. Položij and T. Heine, Chem. Mater., 2022, 34, 2376–2381.
55. O. T. Hofmann, E. Zojer, L. Hörmann, A. Jeindl and R. J. Maurer, Phys. Chem. Chem. Phys., 2021, 23, 8132–8180.
56. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
57. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
58. J. Hermann and A. Tkatchenko, Phys. Rev. Lett., 2020, 124, 146401.
59. T. Abu-Husein, S. Schuster, D. A. Egger, M. Kind, T. Santowski, A. Wiesner, R. Chiechi, E. Zojer, A. Terfort and M. Zharnikov, Adv. Funct. Mater., 2015, 25, 3943–3957.
60. M. Gärtner, E. Sauter, G. Nascimbeni, A. Petritz, A. Wiesner, M. Kind, T. Abu-Husein, M. Bolte, B. Stadlober, E. Zojer, A. Terfort and M. Zharnikov, J. Phys. Chem. C, 2018, 122, 28757–28774.
61. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
62. V. Havu, V. Blum, P. Havu and M. Scheffler, J. Comput. Phys., 2009, 228, 8367–8379.
63. A. Marek, V. Blum, R. Johanni, V. Havu, B. Lang, T. Auckenthaler, A. Heinecke, H.-J. Bungartz and H. Lederer, J. Phys.: Condens. Matter, 2014, 26, 213201.
64. T. C. Taucher, I. Hehn, O. T. Hofmann, M. Zharnikov and E. Zojer, J. Phys. Chem. C, 2016, 120, 3428–3437.
65. J. Neugebauer and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 16067–16080.
66. C. Freysoldt, P. Eggert, P. Rinke, A. Schindlmayr and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 235428.
67. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
68. J. Topping, Proc. R. Soc. A, 1927, 114, 67–72.
69. J. R. Macdonald and C. A. Barlow, J. Chem. Phys., 1963, 39, 412–422.
70. B. L. Maschhoff and J. P. Cowin, J. Chem. Phys., 1994, 101, 8138–8151.
71. D. Cornil, Y. Olivier, V. Geskin and J. Cornil, Adv. Funct. Mater., 2007, 17, 1143–1148.
72. M. L. Sushko and A. L. Shluger, Adv. Funct. Mater., 2008, 18, 2228–2236.
73. S. Haldar, M. Wang, P. Bhauriyal, A. Hazra, A. H. Khan, V. Bon, M. A. Isaacs, A. De, L. Shupletsov, T. Boenke, J. Grothe, T. Heine, E. Brunner, X. Feng, R. Dong, A. Schneemann and S. Kaskel, J. Am. Chem. Soc., 2022, 144, 9101–9112.
74. A. Nefedov, R. Haldar, Z. Xu, H. Kühner, D. Hofmann, D. Goll, B. Sapotta, S. Hecht, M. Krstić, C. Rockstuhl, W. Wenzel, S. Bräse, P. Tegeder, E. Zojer and C. Wöll, Adv. Mater., 2021, 33, 2103287.
75. E. Zojer, Dataset-electrostatic-design-COF-316 [data set], Graz University of Technology, 2023,  DOI:10.3217/y6e40-fk714.
76. E. Zojer, COF-316-guest molecules + alternative COF [data set], Graz University of Technology, 2024,  DOI:10.3217/63rkm-hec45.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta06996f

---