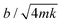Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing the physical origins of droplet friction using a critically damped cantilever†
Sankara
Arunachalam‡
 ,
Marcus
Lin‡
,
Marcus
Lin‡
 and
Dan
Daniel
and
Dan
Daniel
 *
*
Droplet Lab, Division of Physical Sciences and Engineering, King Abdullah University of Science and Technology (KAUST), Thuwal 23955–6900, Saudi Arabia. E-mail: danield@kaust.edu.sa
First published on 2nd September 2024
Abstract
Previously, we and others have used cantilever-based techniques to measure droplet friction on various surfaces, but typically at low speeds U < 1 mm s−1; at higher speeds, friction measurements become inaccurate because of ringing artefacts. Here, we are able to eliminate the ringing noise using a critically damped cantilever. We measured droplet friction on a superhydrophobic surface over a wide range of speeds U = 10−5–10−1 m s−1 and identified two regimes corresponding to two different physical origins of droplet friction. At low speeds U < 1 cm s−1, the droplet is in contact with the top-most solid (Cassie–Baxter), and friction is dominated by contact-line pinning with Ffric force that is independent of U. In contrast, at high speeds U > 1 cm s−1, the droplet lifts off the surface, and friction is dominated by viscous dissipation in the air layer with Ffric ∝ U2/3 consistent with Landau–Levich–Derjaguin predictions. The same scaling applies for superhydrophobic and underwater superoleophobic surfaces despite their very different surface topographies and chemistries, i.e., the friction scaling law derived here is universal.
1 Introduction
One conspicuous feature of wetting phenomena is the great diversity of timescales and contact-line speeds involved.1–3 A typical millimetric water droplet sitting on a surface evaporates within an hour, which translates to the contact line retracting at a speed of ∼μm s−1;4,5 in contrast, the same droplet bounces off a superhydrophobic surface within ∼ 10 ms with a contact-line speed of ∼ m s−1.6–8 To fully capture the wetting properties of a surface is therefore a daunting experimental task, requiring us to probe droplet friction—from the slowest to the fastest—over some 6 orders of magnitude.Previously, we and others introduce cantilever-based techniques to measure droplet friction.9–18 While the various techniques vary in their detailed implementations, they all rely on the same physical principle: a droplet (typically millimetric in size) is attached to a cantilever of known spring constant, and droplet friction can be determined by quantifying the cantilever deflection. Cantilever-based techniques have proven to be a simple but powerful tool to measure droplet friction with high sensitivity and precision (∼10 nN force resolutions14–16) over a wide range of surfaces—including superhydrophobic,15,16 underwater superoleophobic,14 and lubricated surfaces12—and with many advantages over traditional contact angle measurements.2,19,20
However, cantilever-based techniques are typically confined to low droplet speeds U < 1 mm s−1. This is because at higher speeds, the cantilevers suffer from ringing artefacts resulting in inaccurate friction measurements. For example, see Fig. S2b in a recent publication by Backholm et al. (2024),18 where ringing is clearly visible. In this work, we eliminate ringing by using a critically damped cantilever, greatly improving the measurement accuracy and signal-to-noise ratios at high speeds U > 10 cm s−1; friction forces can also now be measured with the fastest theoretical time resolution of 1/ωo, where ωo is the natural frequency of the cantilever.
With our setup, we are able to measure droplet friction Ffric on superhydrophobic surfaces over an unprecedented range of speeds from 10 μm s−1 to 30 cm s−1, spanning over 4 orders of magnitude. At low speeds U < 1 cm s−1, Ffric is dominated by contact-line pinning and is independent of U, consistent with previous reports.13,21 Here, we identify a new friction regime, where Ffric ∝ U2/3 for high U > 1 cm s−1 which can be attributed to viscous dissipation in the air layer, consistent with Landau–Levich–Derjaguin (LLD) formulations.22,23 We further show that the derived scaling law is universal across different superhydrophobic and underwater superoleophobic surfaces.
Our approach to fabricating critically damped cantilevers—by enclosing the cantilever inside a column of viscous liquid (e.g., water–glycerin mixture)—is simple to implement and can be used to probe the physical origins of droplet friction on various surfaces, uncovering the mechanisms behind different wetting phenomena.
2 Materials and methods
2.1 Surface preparations
Superhydrophobic Glaco samples were made by spray coating clean glass slides with a layer of hydrophobic nanoparticles (Glaco Mirror Coat Zero, Soft 99 Co). The samples were then placed vertically to dry for one hour before use, following the manufacturer's instructions. Black silicon surface was fabricated as described previously in the literature.15,24 Scanning electron micrographs of the two surfaces can be found in Fig. 6A.Underwater superoleophobic surfaces were prepared by grafting glass slides with zwitterionic poly(sulfobetaine methacrylate) brush surfaces. Details can be found in our previous publication.14 Topography of the brush layer can be found in Fig. 6B as measuring using an atomic force microscope.
2.2 Contact angle measurements
Contact angle measurements were performed for 10 μL water drops using a commercially available instrument (Kruss DSA 100) at room temperature (21 °C, 60% humidity). To measure advancing and receding contact angles (θadv and θrec), water was pumped in and out at a rate of 0.2 μL s−1. Results of the contact angle measurements are summarized in Table 1. Errors in the contact angle measurements δθ for the superhydrophobic surfaces are likely to be large. For θ = 175°, δθ can be as large as 5°, which translates to an error in Δcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ measurement of
θ measurement of 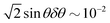 . As discussed in our previous work,2 contact-line friction is better characterized by the quantity Δcos
. As discussed in our previous work,2 contact-line friction is better characterized by the quantity Δcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = cos
θ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θrec − cos
θrec − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θadv, rather than the more conventional Δθ = θadv − θrec. Contact angle measurements cannot be done for an oil droplet on zwitterionic surface under water because it has contact angles of 180° and zero Δcos
θadv, rather than the more conventional Δθ = θadv − θrec. Contact angle measurements cannot be done for an oil droplet on zwitterionic surface under water because it has contact angles of 180° and zero Δcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ.14
θ.14
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = cos
θ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θrec − cos
θrec − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θadv
θadv
| Surface | θ adv | θ rec | Δcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ |
|---|---|---|---|
| Glaco | 172° | 168° | 1.2 × 10−2 |
| Black silicon | 174° | 170° | 1.0 × 10−2 |
2.3 Measuring friction
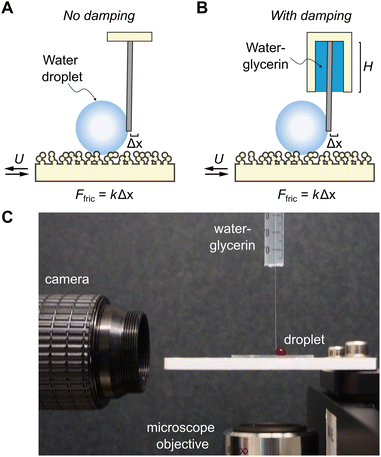
We used a cantilever-based method to measure the friction force Ffric acting on the droplet (Fig. 1A). Briefly, a water droplet (volume V = 15–30 μL) is attached by capillarity to cylindrical tubes (which act as cantilevers) of different dimensions, materials, and spring constants, as summarized in Table 2. The steel cylindrical tube is solid, while the acrylic tube is hollow with an inner diameter of 0.3 mm. Here, the droplet diameter 2R = (6V/π)1/3 = 3 mm is much larger than that of the cantilever d < 0.4 mm, such that the droplet geometry is minimally affected. At the same time, R is smaller than the capillary length of 2.7 mm, so that the droplet remains spherical.| Material | d (mm) | L (cm) | k (mN m−1) | b 0 (mg s−1) |
|---|---|---|---|---|
| Acrylic | 0.36 | 9 | 14 | 47 ± 5 |
| Acrylic | 0.36 | 6 | 55 | 105 ± 20 |
| Steel | 0.15 | 5.5 | 144 | 49 ± 5 |
The surface was moved back-and-forth at a controlled speed of U = 10−5–10−1 m s−1 using a motorized stage. Ffric can then be inferred from the cantilever deflection Δx (averaged over several cycles), since Ffric = kΔx where k = 14–144 mN m−1 is the flexular spring constant. Δx was recorded using a high speed camera (up to 1000 fps, Krontech Chronos 2.1) and determined using a cross-correlation algorithm with micron resolutions. The entire setup was placed on an optical table and enclosed to minimise vibration and draught. This way, we can reduce the inherent instrument noise to ΔFnoise = 5 nN and reliably measure forces as small as 10 nN. The inherent ΔFnoise is obtained by measuring cantilever deflection in absence of any droplet motion.
We previously named this custom-built instrument the Droplet Force Apparatus (DFA),14 whose details can be found in our previous publications.12–14 An important innovation we introduced here is the addition of a damping system. We placed the cantilever coaxially inside a cylinder (with a much larger radius of 2.5 mm) filled with water–glycerin solution (Fig. 1B). By optimizing the glycerin concentration (and hence the liquid column viscosity ηc) and liquid column height H, we can achieve a critically damped system and measure Ffric with the fastest theoretical time resolution of 1/ωo, where 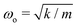 is the natural frequency of the cantilever with an attached droplet of mass m. Critical damping is achieved when
is the natural frequency of the cantilever with an attached droplet of mass m. Critical damping is achieved when 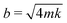 , i.e., the damping coefficient has to be tuned for specific droplet-cantilever combination for particular droplet mass m and the spring constant k. Here, the cantilever masses are much smaller than m and can be safely ignored.
, i.e., the damping coefficient has to be tuned for specific droplet-cantilever combination for particular droplet mass m and the spring constant k. Here, the cantilever masses are much smaller than m and can be safely ignored.
The DFA setup can also be integrated with microscopy (specifically reflection interference contrast microscopy) to visualize the droplet base as shown in Fig. 1C.
2.4 Measuring cantilever spring constant
The spring constant of the cantilever k can be determined using the added weight method.12,21 We placed masses (e.g., microlitre-sized water droplets) of different weights W at the cantilever tip and measured the deflection Δz optically. The slope of W vs. Δz corresponds to k. k can also be obtained from the natural frequency ωo. See details in Fig. S1, S2 and Table S1 (ESI†).2.5 Measuring damping coefficient b from free-decay oscillations
To measure the damping coefficient, we attached a solid mass with m = 25–270 mg to the cantilever. We then applied a short impulse by blowing air to the attached mass using a blower ball. As long as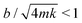 , the mass will perform an underdamped simple harmonic motion with an exponential decay envelope exp(−bt/(2m)), from which we can derive b.
, the mass will perform an underdamped simple harmonic motion with an exponential decay envelope exp(−bt/(2m)), from which we can derive b.
2.6 Visualizing droplet base
We used reflection interference contrast microscopy (RICM) to visualize the droplet base and the air film beneath it.12,14,25 Briefly, we shone monochromatic light (wavelength λ = 561 nm) from below and captured the reflection off the droplet's base using a high-speed camera (Photron Nova S20) fitted with a 5× microscope objective. The air film gives rise to thin-film interference, i.e., dark and bright fringes as the light reflected off the water–air and air–solid interfaces interfere destructively and constructively with one another. Contact-line pinning (including its absence) can be clearly observed using this technique.3 Results and discussions
3.1 Ringing artefact in underdamped cantilever
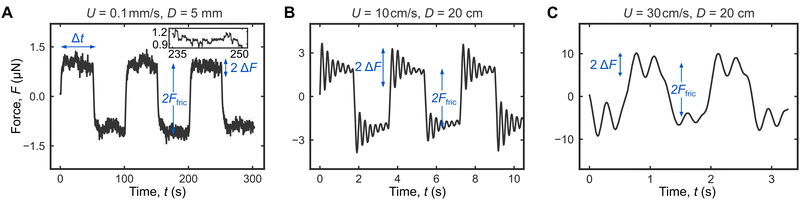
We start by measuring droplet friction without the addition of any damping system on our custom-built instrument, which we named the droplet force apparatus or DFA (Fig. 1A). Fig. 2A shows a typical force curve for a 25 μL water droplet (mass m = 25 mg) moving back and forth on a Glaco superhydrophobic surface at a controlled speed of U = 0.1 mm s−1 (3 cycles over a D = 5 mm distance). In this case, DFA is able to accurately measure the friction force Ffric = 1.0 ± 0.1 μN (Fig. 2A). At this low speed, the droplet is in contact with the topmost solid fractions, and the observed force fluctuations ΔFcontact = 0.1 μN (inset in Fig. 2A) can be attributed to contact-line pinning at the receding edge (Video S1, ESI†) and is significantly larger than the inherent instrument noise ΔFnoise = 5 nN; ΔFcontact reflects the topographical heterogeneity of superhydrophobic surfaces, i.e., it is not an experimental artefact or noise.In contrast, the observed force fluctuations ΔFGibbs at higher speeds U = 10 and 30 cm s−1 are Gibbs ringing noise, an experimental artefact that should be eliminated (Fig. 2B and C). ΔFGibbs oscillates at frequency ωo ≈ 20 rad s−1 and is associated with the failure of the underdamped cantilever to respond quickly enough to the droplet inertia ma, where m and a are the droplet's mass and acceleration. For U = 10–30 cm s−1 (Fig. 2B and C), ma ∼ mUωo ≈ 50–120 μN, much larger than Ffric = 1 μN, and we therefore observed Gibbs noise. In contrast, for U = 0.1 mm s−1 (Fig. 2A), mUωo ≈ 50 nN ≪ Ffric, and there was no Gibbs noise.
For U = 10 cm s−1, the initial ΔFGibbs = 1.3 μN and is comparable to the actual friction force Ffric = 1.9 μN. Fortunately, ΔFGibbs decays within a couple of seconds to allow for reasonably accurate Ffric measurement. The ringing noise is exarcebated at an even higher U = 30 cm s−1 with ΔFGibbs = 3.7 μN, again comparable to Ffric = 7.0 μN. However, this time ΔFGibbs does not decay quickly enough and adversely impact the accuracy of friction measurements.
The required travel distance D = UΔt quickly rises with increasing U. Ffric can be accurately measured with D = 5 mm when U = 0.1 mm s−1 (Fig. 2A). However, when U = 30 cm s−1, friction measurements remain challenging even with D = 20 cm (Fig. 2C). Without any damping system, friction measurements at high speeds are impossible for small sample sizes ∼ 1 cm. In the next section, we will discuss how these limitations can be overcome by using a critically damped cantilever.
3.2 Designing critically damped cantilever
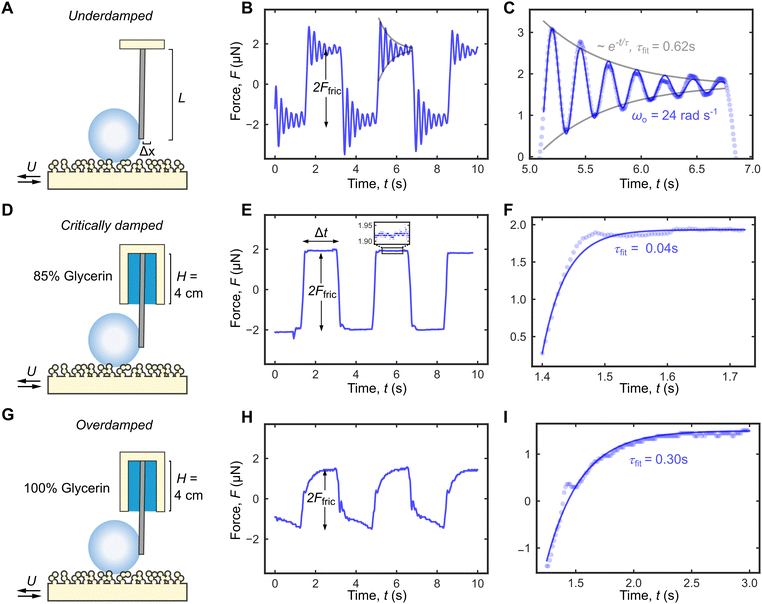
The damping coefficient b of the cantilevers can be obtained by observing the free decay oscillation of an attached solid mass m following a short impulse (Fig. 3A). For an underdamped system where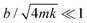 , the cantilever oscillates close to the natural frequency
, the cantilever oscillates close to the natural frequency 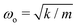 , which was observed experimentally for a wide range of k = 14–144 mN m−1 and m = 25–270 mg (Fig. 3B). We also expect the oscillations to dampen with a decay envelope of the form e−bt/(2m), which was also borned out by experiments (Fig. 3C and D).
, which was observed experimentally for a wide range of k = 14–144 mN m−1 and m = 25–270 mg (Fig. 3B). We also expect the oscillations to dampen with a decay envelope of the form e−bt/(2m), which was also borned out by experiments (Fig. 3C and D).
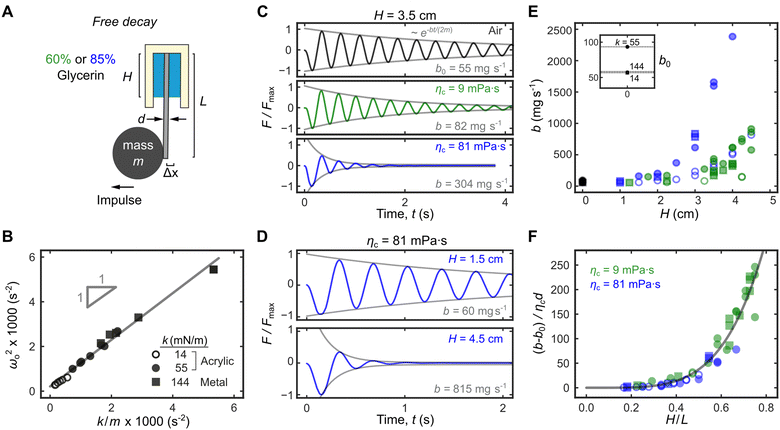 | ||
| Fig. 3 Tuning the damping system in DFA. (A) The damping coefficient b can be measured by observing the free decay oscillation of an attached mass m following an impulse. (B) The oscillation frequency ωo (in air) depends on the spring constant k and the attached mass m. For the same cantilever, b can be tuned by changing (C) the viscosity of the liquid column ηc and/or (D) the column height H. (E) b as a function of H for different cantilevers and liquid column viscosities (indicated by different markers and colours, respectively). Inset shows the damping coefficient b0 when H = 0, i.e., in air. (F) When correctly normalized, data in E collapse into a single master curve in eqn (1) (gray line). | ||
The damping coefficient b = b0 + bη has two components b0 and bη. b0 is the intrinsic damping coefficient, whose physical origin is complex but is linked to the dissipation at the fixed point of the cantilever mounted to the top wall. Experimentally, b0 can be obtained from the decay envelope in air (no liquid column). For the cantilever with k = 14 mN m−1, we obtained bo = 55 mg s−1 (Fig. 3C, Top). On the other hand, bη is the viscous component due to the liquid column, whose magnitudes can be tuned by changing the liquid column viscosity ηc (Fig. 3C) and/or the column height H (Fig. 3D). This allows us to continuously tune b from its intrinsic value of 55 mg s−1 (Fig. 3C, Top) to a maximum value of 815 mg−1 (Fig. 3D, bottom).
Fig. 3E summarizes the experimental b values for three different cantilevers (see Table 2 for detailed properties) as we vary the liquid column height H = 0–4.5 cm and viscosities ηc = 9, 81 mPa s. When bη = b − b0 is normalized by ηcd (where d is the cantilever diameter) and H normalized by the cantilever length L, the data in Fig. 3E collapse into a single master curve (Fig. 3F) that is well-described by the power law
| bη/(ηcd) = 810(H/L)4.43 | (1) |
We then used eqn 1 to optimize H and ηc to achieve critical damping, i.e., 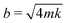 . Since there are 5 variables (bη, ηc, d, H, and L) and 3 fundamental dimensions (mass, length, and time), Buckingham π theorem guarantees that there can only be 5–3 = 2 dimensionless groups, which we have chosen here to be bη/(ηcd) and H/L. The fact that bη/(ηcd) scales with H/L suggests that the hydrodynamic damping is primarily due to Stokes flow in the liquid column, i.e., low Reynolds number flow;26 this is contrast to damping in atomic force microscope cantilevers where it is dominated by high Reynolds number flow.27 To rigorously justify the empirical fit in eqn 1 requires significant mathematical modelling outside the scope of this study.
. Since there are 5 variables (bη, ηc, d, H, and L) and 3 fundamental dimensions (mass, length, and time), Buckingham π theorem guarantees that there can only be 5–3 = 2 dimensionless groups, which we have chosen here to be bη/(ηcd) and H/L. The fact that bη/(ηcd) scales with H/L suggests that the hydrodynamic damping is primarily due to Stokes flow in the liquid column, i.e., low Reynolds number flow;26 this is contrast to damping in atomic force microscope cantilevers where it is dominated by high Reynolds number flow.27 To rigorously justify the empirical fit in eqn 1 requires significant mathematical modelling outside the scope of this study.
To illustrate the importance of using a critically damped cantilever, we performed friction measurements at a relatively high U = 10 cm s−1 using the same droplet volumes (V = 20 μL and m = 20 mg) and cantilever (k = 14 mN m−1 and 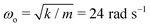 ), but with three different damping coefficients b = 50, 700, 7000 mg s−1 corresponding to underdamped, critically damped (or nearly so), and overdamped cases (Fig. 4). The underdamped case is just a cantilever with no liquid column, while the critically damped and overdamped cases are achieved by enclosing the cantilever with 85% and 100% glycerin of column height H = 4 cm.
), but with three different damping coefficients b = 50, 700, 7000 mg s−1 corresponding to underdamped, critically damped (or nearly so), and overdamped cases (Fig. 4). The underdamped case is just a cantilever with no liquid column, while the critically damped and overdamped cases are achieved by enclosing the cantilever with 85% and 100% glycerin of column height H = 4 cm. 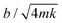 = 0.04, 0.7, and 7 for the three cases (Table 3), and the travel distance D = UΔt is fixed at 20 cm.
= 0.04, 0.7, and 7 for the three cases (Table 3), and the travel distance D = UΔt is fixed at 20 cm.
The droplet-cantilever system can be modelled as a simple harmonic oscillator, and in the underdamped case (Fig. 4A–C), we expect significant ringing artefact described by the force response function
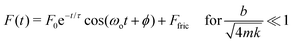 | (2) |
In contrast, for a system close to critically damped (Fig. 4D–F), there is no ringing and F(t) has the form
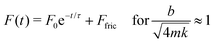 | (3) |
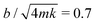 . Physically, critical damping is achieved when the droplet inertia is balanced by the viscous component: mUωo ∼ bU and hence
. Physically, critical damping is achieved when the droplet inertia is balanced by the viscous component: mUωo ∼ bU and hence 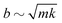 .
.
For an overdamped system (Fig. 4G–I), the force response function has a similar form to the critically damped one
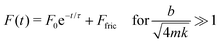 | (4) |
We obtained similar friction values for undamped and critically damped cantilevers: Ffric = 1.7 ± 0.2 μN and Ffric = 1.93 ± 0.01 μN, respectively. In contrast, Ffric = 1.50 ± 0.01 μN is significantly smaller with overly damped cantilever, likely because there is insufficient time for Ffric to reach its equilibrium value (Table 3). The advantages to using a critically damped cantilever are therefore clear. Ffric can be accurately measured with minimal ΔF, since ringing artefact can be avoided, and the cantilever responds with the fastest theoretical time possible.
3.3 Probing different origins of droplet friction on superhydrophobic surfaces
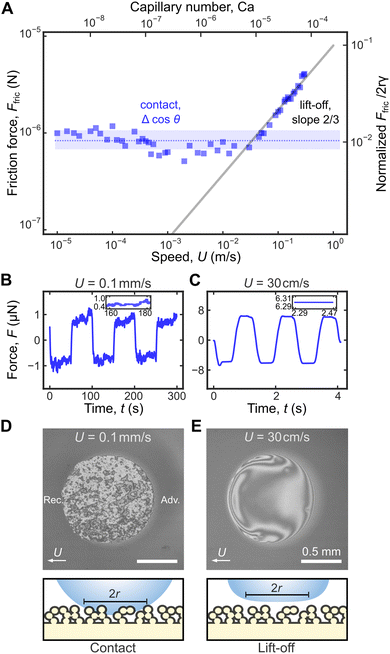
Using a critically damped cantilever, we are now able to measure Ffric over an unprecedented range of U from 10 μm s−1 to 30 cm s−1 without any Gibbs noise. We identified two regimes of droplet frictions at low and high speeds. At low U < 1 cm s−1, Ffric is independent of U, and there is significant fluctuations ΔF = 0.2 μN in the force curve (inset in Fig. 4B). In contrast, at high U > 10 cm s−1, Ffric ∝ U2/3 increases with U, and the force curve exhibits ultra-low ΔF< 10 nN (inset in Fig. 5C).To explain the physical origins of the two regimes, we shone monochromatic light (wavelength λ = 561 nm) from below to visualize the droplet base, i.e., reflection interference contrast microscopy (RICM). At low U = 0.1 mm s−1, a droplet is in contact with the topmost tips of the surface (Cassie–Baxter state). Roughness of the superhydrophobic surface results in variations in the air film thickness beneath the droplet, which manifest as bright and dark fringes due to interference effects (Fig. 5D). Between neighbouring bright and dark fringes, there is a difference in air-film thickness of ∼λ/2 or 200 nm (Fig. S4A, ESI†).
In this regime, Ffric (and the observed ΔFcontact = 0.2 μN in Fig. 5B) is attributed to contact-line pinning, resulting in discontinuous contact-line profile at the receding end (Video S1, ESI†). Furmidge's law predicts that Ffric is directly related to contact angle hysteresis, specifically that Ffric/2rγ = Δcos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = cos
θ = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θrec − cos
θrec − cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θadv, where r is droplet base radius and γ the surface tension.
θadv, where r is droplet base radius and γ the surface tension.
On the other hand, at high speeds U > 10 cm s−1, droplet motion can generate sufficient lift to balance its weight, and the the droplet completely lifts off the surface.28–30 There is no contact-line pinning, and as a result, the droplet base profiles at both the advancing front and receding end are smooth and continuous (Fig. 5E, Fig. S4B and Videos S2–S4, ESI†), with the characteristic horseshoe shape as described in previous reports.30 Contact angle measurements can no longer describe droplet friction in this limit, since there is no three-phase contact line. The lack of contact-line pinning due to droplet lift-off explains the ultra-low ΔF = ΔFnoise < 10 nN (inset in Fig. 5C) in the force curve. Note that without damping, the force curve is dominated by Gibbs noise (Fig. 2C), and we will not be able to come to this conclusion.
Instead, friction is dominated by the viscous dissipation in the air layer whose thickness h increases with U. Following the classical analysis by Landau, Levich, and Derjaguin,22,23h ∝ RCa2/3, where Ca = ηU/γ is the capillary number based on the air viscosity η = 1.85 × 10−5 Pa s and the surface tension of water γ = 72 mN m−1. Viscous dissipation occurs largely in the perimeter of the droplet base of size l ∝ RCa1/3, and we expect Ffric ∼ 2rl(ηU/h) and hence Ffric/2rγ ∼ Ca2/3 ∝ U2/3 (full line in Fig. 5A). Recently, Backholm et al. (2024) reported a similar increase of Ffric with U on superhydrophobic surfaces and proposed that Ffric ∝ U; however, Ffric ∝ U2/3 gives a better fit to their experimental data (Fig. S5, ESI†).
4 Universal droplet friction laws for super-repellent surfaces
In Fig. 5, we only looked at friction for water droplets (viscosity ηd = 10−3 Pa s) of a fixed volume V = 20 μL on a Glaco superhydrophobic surface which has a porous texture consisting of nanoparticles (Fig. 6A). In Fig. 6, we additionally measured Ffric for a wider range of volumes V = 15–30 μL not just for Glaco surface, but also for black silicon, a different superhydrophobic surface with needle-like structures. We have also included previously published friction data for silicone oil droplets (V = 20–50 μL and of much higher viscosity ηd = 10−1 Pa s) on underwater superoleophobic surface for comparison.14 Unlike superhydrophobic surface, the underwater superoleophobic surface is smooth at the nanoscale and does not rely on texturing to achieve liquid-repellency (Fig. 6B); instead, the zwitterionic brushes on the surface generate electric double-layer forces which stabilize a water layer beneath the oil droplet.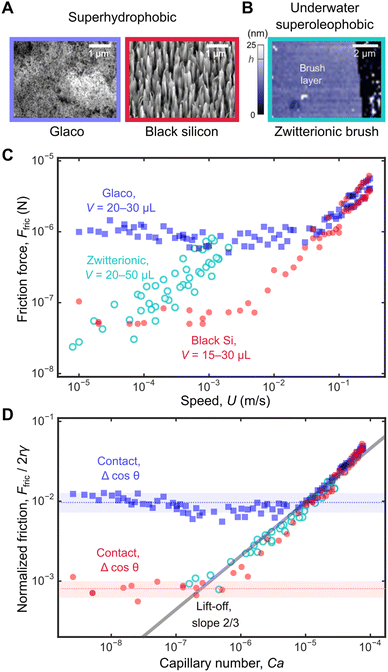 | ||
| Fig. 6 Universal friction laws on different surfaces. (A) Scanning electron micrographs of Glaco and black silicon superhydrophobic surfaces. (B) Topography of the zwitterionic brush layer (in water) obtained using atomic force microscope. On the right, the brush layer has been scratched to reveal the underlying glass surface. (C) Friction forces measured for the three surfaces over a wide range of speeds from 10 μm s−1 to 30 cm s−1. (D) The same data in C non-dimensionalized as Ffric/2rγ vs. Ca. Data for zwitterionic brush surface is taken from our previous work.14 | ||
The entire friction dataset in Fig. 6C spans a wide range of Ffric (close to 3 decades, from 20 nN to 6 μN) and droplet speeds (over 4 decades, from 10 μm s−1 to 30 cm s−1). The same data can be presented in their non-dimensionalized form Ffric/2rγ vs. Ca as shown in Fig. 6D (raw data in31). For the zwitterionic surface, we use the water–oil interfacial tension γ = 50 mN m−1 and the water viscosity η = 10−3 Pa s values to calculate Ca (c.f., water surface tension γ = 72 mN m−1 and air viscosity η = 1.8 × 10−5 Pa s for superhydrophobic surface). Parameters used to generate the non-dimensional plot is summarized in Table 4.
| Surface | Droplet (Pa s) | Outside | Droplet viscosity, ηd (Pa s) | Outside viscosity, η (Pa s) | γ (mN m−1) |
|---|---|---|---|---|---|
| Glaco | Water | Air | 10−3 | 1.8 × 10−5 | 72 |
| Black Si | Water | Air | 10−3 | 1.8 × 10−5 | 72 |
| Zwitterionic | Oil | Water | 10−1 | 1.0 × 10−3 | 50 |
As discussed previously, there are two regimes of droplet friction, one dominated by contact-line pinning and another by viscous dissipation
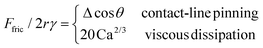 | (5) |
For Glaco surface, contact-line pinning dominates for U < 10 cm s−1 and Ca < 10−5 with constant Ffric/2rγ = (1.0 ± 0.1) × 10−2 (blue band in Fig. 6D). For black silicon, pinning is dominant for smaller U < 1 cm s−1 and Ca < 10−6, with a lower Ffric/2rγ = (8 ± 2) × 10−4 (red band in Fig. 6D), reflecting its more water-repellent nature. It is difficult to directly compare friction and contact angle measurements to confirm Furmidge's law, because of large measurement error for θ > 170° (see discussion in ‘Contact angle measurements’ subsection in ‘Materials and methods’). Previously, we showed that for an oil droplet moving on zwitterionic brush surface, the droplet is never in contact with the solid and contact-line pinning is always absent. Hence, there is no constant Ffric/2rγ regime.
Above critical speeds corresponding to Ca = 10−5 and 10−6 for Glaco and black silicon, the water droplet lifts off the surface and viscous dissipation in the air layer dominates with Ffric/2rγ = 20 Ca2/3 (full line in Fig. 6D, prefactor of 20 obtained by least squares fit to data) independent of the surface structure. There is excellent overlap between friction data for oil droplets on zwitterionic surface and for water on superhydrophobic surfaces, even though the droplet viscosities are very different (ηd is 100 times larger for oil than for water), i.e., dissipation due to internal flow of droplet is insignificant. Instead, Ffric on zwitteronic surface is always dominated by viscous dissipation in the water layer beneath the oil droplet, due to the same LLD droplet lift-off mechanism.
The scaling law in eqn (5) is therefore universal, and the Ca2/3 scaling applies equally to superhydrophobic and underwater superoleophobic surface, despite their very different surface topographies and chemistries. At even higher speeds ∼ m s−1, other dissipation mechanisms, such as aerodynamic drag can become important.32 However, since droplet speeds here U ≤ 30 cm s−1 are relatively low, the drag force Fdrag ∼ ρaR2U2/Re1/2 ∼ 20 nN is small and therefore unimportant. Re = ρaUR/η < 30 is the Reynolds number, ρa and η are the air density and viscosity, and R is the droplet radius.
5 Conclusions
To conclude, we have proposed a design for a critically damped cantilever which allows us measure droplet frictions accurately at high speeds without any ringing artefacts. We are able to then identify a new droplet friction regime on superhydrophobic surfaces where Ffric/2rγ ∼ Ca2/3 at high speeds. We further showed that this scaling is universal and remains true for both superhydrophobic and underwater superoleophobic surface, irrespective of the details of surface structure and chemistry.Author contributions
S. A. performed the bulk of the experiments. D. D. and M. L. came up with the design of the critically damped cantilever, analyzed the results, and wrote the manuscript. D. D. conceptualized the project and supervised the research.Data availability
Data for this article, including dataset for friction measurements are available at Harvard Dataverse at https://doi.org/10.7910/DVN/2J4ZTP.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by KAUST start-up fund BAS/1/1416-01-01.Notes and references
- P.-G. de Gennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef CAS.
- D. Daniel, M. Vuckovac, M. Backholm, M. Latikka, R. Karyappa, X. Q. Koh, J. V. I. Timonen, N. Tomczak and R. H. A. Ras, Commun. Phys., 2023, 6, 152 CrossRef CAS.
- P.-G. Gennes, F. Brochard-Wyart and D. Quéré, Capillarity and wetting phenomena: drops, bubbles, pearls, waves, Springer, 2004 Search PubMed.
- R. G. Picknett and R. Bexon, J. Colloid Interface Sci., 1977, 61, 336–350 CrossRef CAS.
- D. Brutin and V. Starov, Chem. Soc. Rev., 2018, 47, 558–585 RSC.
- D. Richard, C. Clanet and D. Quéré, Nature, 2002, 417, 811 CrossRef CAS PubMed.
- Y. Liu, L. Moevius, X. Xu, T. Qian, J. M. Yeomans and Z. Wang, Nat. Phys., 2014, 10, 515–519 Search PubMed.
- J. C. Bird, R. Dhiman, H.-M. Kwon and K. K. Varanasi, Nature, 2013, 503, 385–388 CrossRef CAS PubMed.
- H.-J. Butt, I. V. Roisman, M. Brinkmann, P. Papadopoulos, D. Vollmer and C. Semprebon, Curr. Opin. Colloid Interface Sci., 2014, 19, 343–354 CrossRef CAS.
- H. Suda and S. Yamada, Langmuir, 2003, 19, 529–531 CrossRef CAS.
- D. W. Pilat, P. Papadopoulos, D. Schäffel, D. Vollmer, R. Berger and H.-J. Butt, Langmuir, 2012, 28, 16812–16820 CrossRef CAS PubMed.
- D. Daniel, J. V. I. Timonen, R. Li, S. J. Velling and J. Aizenberg, Nat. Phys., 2017, 13, 1020–1025 Search PubMed.
- D. Daniel, J. V. I. Timonen, R. Li, S. J. Velling, M. J. Kreder, A. Tetreault and J. Aizenberg, Phys. Rev. Lett., 2018, 120, 244503 CrossRef CAS PubMed.
- D. Daniel, A. Y. T. Chia, L. C. H. Moh, R. Liu, X. Q. Koh, X. Zhang and N. Tomczak, Commun. Phys., 2019, 2, 105 CrossRef.
- M. Backholm, D. Molpeceres, M. Vuckovac, H. Nurmi, M. J. Hokkanen, V. Jokinen, J. V. I. Timonen and R. H. A. Ras, Commun. Mater., 2020, 1, 1–8 CrossRef.
- M. Hokkanen, M. Backholm, M. Vuckovac, Q. Zhou and R. H. A. Ras, Adv. Mater., 2021, 33, 2105130 CrossRef CAS PubMed.
- C. Hinduja, A. Laroche, S. Shumaly, Y. Wang, D. Vollmer, H.-J. Butt and R. Berger, Langmuir, 2022, 38, 14635–14643 CrossRef CAS PubMed.
- M. Backholm, T. Kärki, H. A. Nurmi, M. Vuckovac, V. Turkki, S. Lepikko, V. Jokinen, D. Quéré, J. V. I. Timonen and R. H. A. Ras, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2315214121 CrossRef CAS PubMed.
- A. Marmur, Annu. Rev. Mater. Res., 2009, 39, 473–489 CrossRef CAS.
- K. Liu, M. Vuckovac, M. Latikka, T. Huhtamäki and R. H. A. Ras, Science, 2019, 363, 1147–1148 CrossRef CAS PubMed.
- M. Backholm and O. Bäumchen, Nat. Protoc., 2019, 14, 594–615 CrossRef CAS PubMed.
- L. Landau and V. Levich, Acta Physicochim. USSR, 1942, 17, 42–54 Search PubMed.
- B. Derjaguin, Dokl. Acad. Sci. USSR, 1943, 39, 13–16 Search PubMed.
- L. Sainiemi, V. Jokinen, A. Shah, M. Shpak, S. Aura, P. Suvanto and S. Franssila, Adv. Mater., 2011, 23, 122–126 CrossRef CAS PubMed.
- L. Limozin and K. Sengupta, Chem. Phys. Chem., 2009, 10, 2752–2768 CrossRef CAS PubMed.
- G. A. Cranch, J. E. Lane, G. A. Miller and J. W. Lou, J. Appl. Phys., 2013, 113, 194904 CrossRef.
- J. E. Sader, J. Appl. Phys., 1998, 84, 64–76 CrossRef CAS.
- H. Lhuissier, Y. Tagawa, T. Tran and C. Sun, J. Fluid Mech., 2013, 733, R4 CrossRef.
- A. Gauthier, J. C. Bird, C. Clanet and D. Quéré, Phys. Rev. Fluids, 2016, 1, 084002 CrossRef.
- E. Sawaguchi, A. Matsuda, K. Hama, M. Saito and Y. Tagawa, J. Fluid Mech., 2019, 862, 261–282 CrossRef CAS.
- D. Daniel, Raw friction data, Harvard Dataverse, 2024 DOI:10.7910/DVN/2J4ZTP.
- T. Mouterde, P. S. Raux, C. Clanet and D. Quéré, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8220–8223 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00601a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |