Asymmetric toughening in the lap shear of metamaterial structural adhesives†
Chenghai
Li
a,
Qiang
Guo
a,
Robert
Chambers
b and
Shengqiang
Cai
 *ab
*ab
aDepartment of Mechanical and Aerospace Engineering, University of California, San Diego, La Jolla, CA 92093, USA. E-mail: s3cai@ucsd.edu
bMaterials Science and Engineering Program, University of California, San Diego, La Jolla, CA 92093, USA
First published on 5th August 2024
Abstract
Metamaterial structural adhesives (MSAs), whose properties primarily rely on structural design, offer promising advantages over traditional adhesives, including asymmetric, switchable, and programmable adhesion. However, the effects of thick backing structures on the adhesion properties remain largely underexplored. Herein, we investigate a series of MSAs featuring a thin adhesive layer and an asymmetric thick beam structure terminated with a film. We conduct lap shear tests on the MSAs with varying terminated film thickness (t) and beam tilting angle (θ) while maintaining an identical adhesive layer. For MSAs with a thick terminated film (t = 2 mm), the effective adhesion energy is double that of solid samples without compromising shear strength, consistent with the theoretical predictions based on the crack trapping mechanism. Conversely, for MSAs with a thin terminated film (t = 0.5 mm), the maximum shear strength and effective adhesion energy are ∼2.8 times and ∼18.6 times those of solid samples, respectively, deviating significantly from the theoretical predictions due to new crack initiations. We further explore adhesion asymmetry by tuning the beam tilting angle (θ). For MSAs with highly tilted beams (θ = 70.3°), we achieve a maximum adhesion strength asymmetry factor of τ2/τ1 ∼ 2.2 for a thick terminated film (t = 2 mm), and a maximum adhesion energy asymmetry factor of Γ1/Γ2 ∼ 5.3 for a thin terminated film (t = 0.5 mm). Our work provides useful insights for designing metamaterial structural adhesives suitable for robotic grippers, wall-climbing robots, and wearable devices, particularly those requiring asymmetric, switchable, and stimuli-responsive adhesion, and adhesives on rough surfaces or in underwater conditions.
1. Introduction
Adhesives and tapes play crucial roles in various fields in modern society. Traditional adhesives and tapes largely rely on semi-empirical modification of bulk rheological properties and interfacial chemistry of polymers to achieve strong, tunable, or stimuli-responsive adhesion.1–8 Achieving asymmetric adhesion is generally challenging through chemical modifications of bulk materials, which is strongly desired for emerging applications requiring switchable adhesion.6,7 For example, for wearable devices, tissue adhesives, robotic grippers, and wall-climbing robotics, asymmetric adhesives can enable strong attachment in one direction during service and easy detachment in the other direction after service with reversibility.9,10 Notably, metamaterial adhesives (MAs) have recently been explored, which have shown significantly enhanced adhesion, reversibility and reusability, directional and spatial programmability, universal adhesion to diverse substrates without chemical modifications, and directionally asymmetric adhesion.9–21 Representative examples of MAs include adhesive thin films with stiffness variations,11,20–23 asymmetric adhesive thin films with nonuniform thickness profiles,17,24 and kirigami-based adhesives with asymmetric cuts.9,10,14,25 Previous MAs typically resemble thin pressure sensitive adhesives utilizing two-dimensional planar patterns, comprising a thin adhesive layer and a thin, mostly non-stretchable backing layer.On the contrary, thick structural adhesives, e.g., commercial foam tapes for insulating, protecting, and sound-dampening,26–28 are typically composed of a thin adhesive layer and a relatively thick and compliant backing structure. In recent years, new structural adhesives have been developed, exhibiting some unique benefits for engineering applications in robotic grippers15,16,29 and wall-climbing robots.30,31 For example, a recent study presented a structural adhesive utilizing bistable beams within an enclosed frame as the backing, together with an adhesive tape for pick-and-release purposes.16 Another study proposed a structural adhesive for robotic grippers employing a thick backing structure composed of periodic, tilted beams and a gecko-inspired adhesive layer for enhanced grasping.15 Notably, an earlier study demonstrated that a hollow backing with symmetric vertical beams could significantly enhance the adhesion energy of gecko-inspired structural adhesives through crack trapping-induced adhesion toughening.13 Another study measured asymmetric adhesion using indentation tests and frictional properties using sliding tests of gecko-inspired structural adhesives with an asymmetric, hollow backing structure consisting of periodic tilted beams.32 However, the mechanistic understanding and quantitative influence of asymmetric backing structures on adhesion toughening and asymmetry of thick structural adhesives under shear loading remains unexplored in fracture-dominated conditions.
In this study, we develop a series of metamaterial structural adhesives (MSAs) comprising two components: a thin adhesive layer and a thick and asymmetric hollow backing consisting of tilted beams terminated with a film (Fig. 1a, top). The hollow structure was originally designed as the backing of the structural adhesive for robotic grippers, as reported in a previous study.15 Subjected to an external shear force, the hollow backing undergoes beam buckling, allowing different structural adhesives, i.e., adhesive pads of the robotic grippers, to equally share the load. In our study, we aim to combine experimental, numerical, and theoretical methods to study how the geometry of the backing structure affects the adhesion properties of MSAs under lap shear tests in fracture-dominated conditions. We conduct lap shear tests using one rigid PMMA plate and one flexible PET film (Fig. 1a).
 | ||
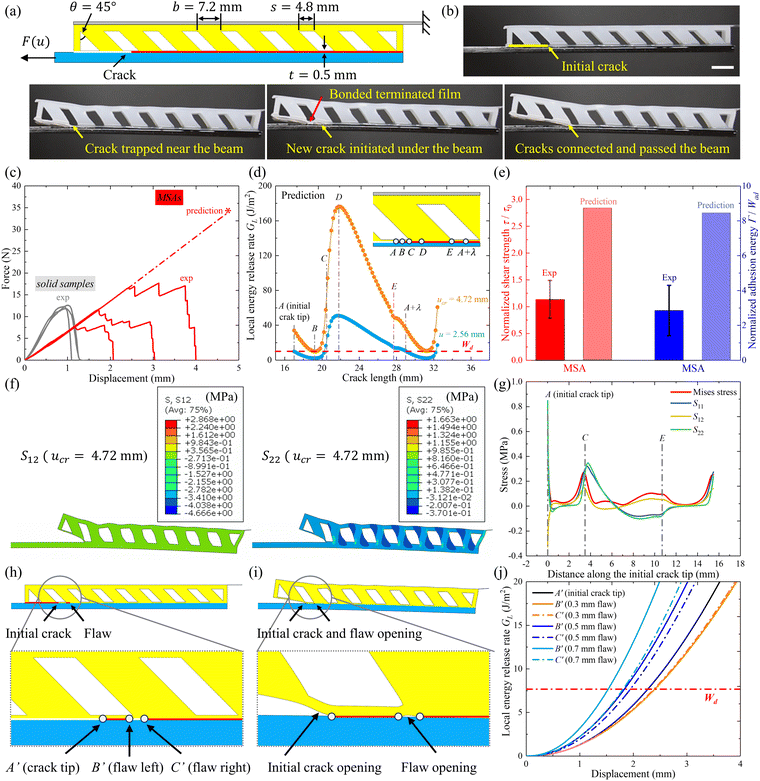
Fig. 1 Adhesion toughening arising from the crack trapping mechanism in the lap shear of metamaterial structural adhesives. (a) Schematics depicting lap shear tests for both the hollow MSA (top) and solid sample (bottom), with labeled geometric dimensions and horizontal positions. (b) Representative shear stress–displacement curves for the MSA (blue) and solid sample (black), respectively. For the solid sample, the black star symbol indicates the intrinsic shear strength τ0 and the shaded area represents the intrinsic work of adhesion Wad. For the MSA, the blue star symbol indicates shear strength τexp and the shaded area indicates the effective adhesion energy Γexp. (c) Local energy release rate GL around the crack tip versus the crack tip location X for the MSA (red lines). The black dashed line represents Wad. Yellow circles denote GL at the initial crack tip (X = X0). Red circles denote the minimum of GL at X = Xmin and X = Xmin + λ. With the increase of the applied shear displacement u, GL_min = Wad is satisfied at the critical displacement (u = ucr), leading to unstable crack propagation (blue arrow). The blue shaded area, divided by the period λ, represents the averaged energy release rate  . Note that the relationship between local energy release rate and crack length depends on the geometric parameters of the hollow backing structures, as reported in a previous theoretical study.33 . Note that the relationship between local energy release rate and crack length depends on the geometric parameters of the hollow backing structures, as reported in a previous theoretical study.33 | ||
Our results have shown that for MSAs with a relatively thick terminated film (t = 2 mm), the effective adhesion energy is approximately twice that of solid samples, without compromising their shear strength. Our theoretical and numerical analyses identify crack trapping as the toughening mechanism if the crack propagates unidirectionally following a predefined path. For hollow MSAs, with a fixed shear displacement, the energy release rate varies periodically with the crack length, causing unstable crack propagation in practical loadings and thus adhesion toughening. For MSAs with a relatively thin terminated film (t = 0.5 mm), the maximum shear strength is ∼2.8 times and ∼2.4 times that of solid samples for two opposite pulling directions, and the effective adhesion energy is ∼18.6 times and 9.8 times that of solid samples for two opposite pulling directions. However, new crack initiation at the interface may lead to a substantial deviation between experimental results and theoretical predictions based on the crack trapping mechanism. Furthermore, we explore the adhesion asymmetry by varying the beam tilting angle θ. For MSAs with a thick terminated film (t = 2 mm), a shear strength asymmetry factor of τ2/τ1 ∼ 2.2 is achieved for highly tilted beams (θ = 70.3°), while the adhesion energy asymmetry factor Γ2/Γ1 is less dependent on θ due to the crack trapping mechanism for both pulling directions. For MSAs with a thin terminated film (t = 0.5 mm), a strength asymmetry factor of τ1/τ2 ∼ 1.4 and an adhesion energy asymmetry factor of Γ1/Γ2 ∼ 5.3 are attained for highly tilted beams (θ = 70.3°). Our research may provide useful insights to develop metamaterial structural adhesives with enhanced, asymmetric, and switchable properties through simple structural designs.
2. Experimental methods
2.1 Fabrication of the MSAs
To fabricate the thick backing structures with relatively thick terminated films (t = 1, 1.5 and 2 mm) (Fig. S1a, ESI†), we first printed a rigid mold with the fused filament fabrication printer (FlashForge Guider 2) or the high-resolution polyjet printer (Connex 3 Objet 500, Stratasys). Then, we mixed parts A and B of Dragon Skin 00-30 (Smooth-on) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio. The precursor underwent mixing using the ARM-310 mixer (THINKY) at 2000 RPM for 1 min, followed by refrigeration for 5 min, and a final mixing step at 2000 rpm for 1 min. The resulting precursor was poured into the mold and left at room temperature for 4 h for curing.
1 weight ratio. The precursor underwent mixing using the ARM-310 mixer (THINKY) at 2000 RPM for 1 min, followed by refrigeration for 5 min, and a final mixing step at 2000 rpm for 1 min. The resulting precursor was poured into the mold and left at room temperature for 4 h for curing.
To fabricate the thick backing structures with relatively thin terminated films (t = 0.5 or 0.75 mm) (Fig. S1b, ESI†), we first followed the above procedures to fabricate one part of the hollow structure. We then injected the Dragon Skin precursor into a sandwiched mold with a silicone spacer (t = 0.5 or 0.75 mm) to fabricate the thin terminated film. Next, we mixed the base and curing agent of PDMS (Sylgard 184, Dow Corning) at a 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio, and then added a Pt-catalyst (Gelest SIP6831.2) at 0.5 μL g−1. The PDMS precursor was mixed for 2 min and degassed for 5 min in a vacuum pump, which was then used to bond the thin terminated film with the molded partial hollow structure. We stored the assembled sample in a 60 °C oven overnight for curing.
1 weight ratio, and then added a Pt-catalyst (Gelest SIP6831.2) at 0.5 μL g−1. The PDMS precursor was mixed for 2 min and degassed for 5 min in a vacuum pump, which was then used to bond the thin terminated film with the molded partial hollow structure. We stored the assembled sample in a 60 °C oven overnight for curing.
We listed the dimensions of hollow structures in Fig. S1c and Table S1 (ESI†). The length, height, and width of the hollow backing structure are denoted as L, H, and w, respectively. The beam tilting angle is denoted as θ. The width of a beam and the spacing between two neighboring beams are denoted as b and s, respectively. The spatial period of the hollow structure is thus λ = b + s. The number of periods/beams is denoted as N. The thickness of the terminated film is denoted as t. For each backing design, we fabricated the solid sample with the same dimensions of L × H × w to measure the intrinsic adhesion properties.
We next bonded a polyethylene terephthalate (PET) thin film (75 μm, McMaster Carr) to the top of the backing structure using the silicone adhesive (Loctite 908570). Then, we mixed the base and curing agent of PDMS at a 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio and added the Pt-catalyst (Gelest SIP6831.2) at 0.5 μL g−1. We used the PDMS precursor to bond the backing structure to a rigid polymethyl methacrylate (PMMA) plate (3 mm). We stored the assembled sample at room temperature overnight and then in a 50 °C oven for curing. The fabricated MSAs had an ultra-thin PDMS adhesive layer (t ∼ 0.08 mm) with the shear modulus (μ) of 0.3 MPa34 (Fig. 1a). Notably, both PET film and PMMA plate matched the width of the hollow backing. We prepared the solid samples using identical procedures (Fig. 1a).
1 weight ratio and added the Pt-catalyst (Gelest SIP6831.2) at 0.5 μL g−1. We used the PDMS precursor to bond the backing structure to a rigid polymethyl methacrylate (PMMA) plate (3 mm). We stored the assembled sample at room temperature overnight and then in a 50 °C oven for curing. The fabricated MSAs had an ultra-thin PDMS adhesive layer (t ∼ 0.08 mm) with the shear modulus (μ) of 0.3 MPa34 (Fig. 1a). Notably, both PET film and PMMA plate matched the width of the hollow backing. We prepared the solid samples using identical procedures (Fig. 1a).
2.2 Lap shear tests of MSAs
As shown in Fig. 1a, we introduced an initial crack with the length of C0 (Table S1, ESI†) at the interface between the PDMS adhesive layer and the PMMA plate. Then, we tested all samples using a tensile machine (5965 Dual Column Testing Systems; Instron) equipped with a 1 kN load cell. We fixed the ends of the PET film and PMMA plate to the bottom and top grippers, respectively. Then, we applied monotonic loading to all the samples at a rate of 0.05 mm s−1 until the MSAs completely debonded from the PMMA plate. Simultaneously, we recorded force–displacement curves and filmed all the tests with a digital camera (Canon 60D). In all tests, adhesive failure was consistently observed between the PDMS adhesive layer and the PMMA plate, rather than debonding between the PDMS adhesive layer and the hollow backing structure (Fig. 2b).We measured the intrinsic adhesion properties from solid samples. The intrinsic shear strength (τ0) is defined as the maximum force (Fmax) divided by the effective adhesion area (Aeff), i.e., τ0 = Fmax/Aeff, where Aeff = (L − C0) × w. The intrinsic work of adhesion (Wad) is defined as the input work to rupture the entire interface divided by Aeff, i.e.,  , where udebond is the displacement at which the force drops to zero.
, where udebond is the displacement at which the force drops to zero.
Similarly, for MSAs, we define the shear strength (τi) and the effective adhesion energy (Γi) as τi = Fi_max/Aeff and  , respectively, where i = 1 or 2 represents the two opposite pulling directions. The normalized shear strength and normalized adhesion energy of MSAs relative to solid samples are defined as τi/τ0 and Γi/Wad, respectively.
, respectively, where i = 1 or 2 represents the two opposite pulling directions. The normalized shear strength and normalized adhesion energy of MSAs relative to solid samples are defined as τi/τ0 and Γi/Wad, respectively.
2.3 Finite element simulation
We simulated the lap shear tests of MSAs in Abaqus using a static, general method. We adopted linear elastic models for both PMMA and PET, with PET characterized by a Young's modulus (E) of 2950 MPa and Poisson's ratio (ν) of 0.43, and PMMA with E of 2900 MPa and ν of 0.4. We modeled the hollow backing structure as a Neo-Hookean material with a shear modulus (μ) of 0.28 MPa. We set the bulk modulus at least 1000 times the shear modulus to account for incompressibility. As mentioned above, the PDMS adhesive layer (t ∼ 0.08 mm) is much thinner than the thinnest terminated film (t = 0.5 mm) in this study. Additionally, PDMS and the hollow backing structure have similar shear moduli. Therefore, when computing the energy release rate, it is appropriate to ignore the ultra-thin PDMS adhesive layer in the geometry of the model. We introduced a seam crack with a length of C0 at the MSA–PMMA interface. We assumed plane strain conditions using CPE4RH elements. In the FEM modeling, we applied displacement control to the end of the PMMA plate while fixing the end of the PET film (Fig. 1a). We then obtained force–displacement curves from the simulation and calculated J-integral around the crack tip. We gradually increased the crack length by a finite value dC, and repeated the above process. We varied the crack length within a range greater than the spatial period λ. Finally, with energy release rate–displacement curves at different crack lengths, we processed the data to get energy release rate–crack length curves at different applied shear displacements. Mesh refinement, especially near the crack tip, was conducted through iterative refinement until simulation results converged.3. Results
3.1 The adhesion toughening arising from the crack trapping mechanism
In engineering applications like robotic grippers15,16,29 and wall-climbing robotics,30,31 structural adhesives usually experience shear load. In this study, we focus on lap shear experiments of MSAs in fracture-dominated conditions with no normal force applied to MSAs. As shown in Fig. 1a, we attached the MSA with a flexible PET backing layer to a rigid PMMA plate. We maintained the adhesive layer (a thin PDMS film cured from its precursor) unchanged throughout this study. We introduced an initial crack of C0 at the PDMS–PMMA interface, exceeding the sample height (H) but much shorter than the sample length (L) (Table S1, ESI†). We monotonically pulled the end of PMMA plate while fixing the end of PET film until the crack propagated through the entire interface. During the pulling, we recorded force–displacement curves (Fig. 1b). As expected, the MSA displays a smaller stiffness than the solid sample.The adhesion enhancement of MSAs is achieved through the crack trapping mechanism as previously proposed,11,13,33,35,36 which is briefly reformulated as follows. We establish a horizontal X-axis, with the origin (X = 0) located at the center of the beam ahead of the crack (mark D in Fig. 1a). We assume the initial crack length is C0 with the tip located at X = X0 (mark A in Fig. 1a). When the crack propagates by a distance of λ, the crack tip reaches X = X0 + λ (mark F in Fig. 1a). To maintain stable, equilibrium crack propagation, it is required that
 | (1) |
However, for the MSA, at a fixed displacement u, due to its periodic beam structures, the local energy release rate GL varies periodically in space (Fig. 1c):
| GL(c = C0) = GL(c = C0 + λ). | (2) |
As shown in Fig. 1c, at a small displacement (u = u1), GL < Wad at the initial crack tip prevents crack propagation. At a larger displacement (u = u2), GL = Wad is satisfied at the initial crack tip, yet crack propagation is hindered because 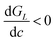 . At an even larger displacement (u = u3), the crack front propagates unstably from the initial position (yellow circle) to the position indicated by the gray circle because GL ≥ Wad. Afterwards, crack propagation stops because GL < Wad and
. At an even larger displacement (u = u3), the crack front propagates unstably from the initial position (yellow circle) to the position indicated by the gray circle because GL ≥ Wad. Afterwards, crack propagation stops because GL < Wad and  . To overcome the crack trapping, a critical displacement (u = ucr) is required to achieve GL_min = Wad at both X = Xmin and X = Xmin + λ. When the crack propagates by a period from X = Xmin to X = Xmin + λ, GL > Wad always holds true, resulting in unstable crack propagation. The total elastic energy stored in the MSAs before the critical displacement (u = ucr) is calculated as
. To overcome the crack trapping, a critical displacement (u = ucr) is required to achieve GL_min = Wad at both X = Xmin and X = Xmin + λ. When the crack propagates by a period from X = Xmin to X = Xmin + λ, GL > Wad always holds true, resulting in unstable crack propagation. The total elastic energy stored in the MSAs before the critical displacement (u = ucr) is calculated as  . Under practical monotonic loading in experiments, all the stored elastic energy is dissipated through unstable crack propagation. In addition to the energy required to separate the interface, the excess elastic energy compared to Wad is fully dissipated through inelastic processes such as damping, damage, and viscoelasticity.11,13,33,35,36
. Under practical monotonic loading in experiments, all the stored elastic energy is dissipated through unstable crack propagation. In addition to the energy required to separate the interface, the excess elastic energy compared to Wad is fully dissipated through inelastic processes such as damping, damage, and viscoelasticity.11,13,33,35,36
Therefore, for our MSAs, we defined the effective adhesion energy  by averaging the reduction of elastic energy within one period (λ) at u = ucr (the blue shaded area in Fig. 1c), which is calculated as
by averaging the reduction of elastic energy within one period (λ) at u = ucr (the blue shaded area in Fig. 1c), which is calculated as
 | (3) |
Based on the argument of the energy balance in fracture mechanics, we assume the work done by the external force is all dissipated by the formation of the new crack surface:
 | (4) |
Recall the definition of energy release rate  , where U is the elastic energy of the MSA per unit width and c is the crack length. When the crack propagates through the entire interface, with the periodic assumption in eqn (3), we have
, where U is the elastic energy of the MSA per unit width and c is the crack length. When the crack propagates through the entire interface, with the periodic assumption in eqn (3), we have
 | (5) |
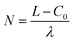 . Thus, we have
. Thus, we have | (6) |
Before the onset of crack propagation, the work done by the external force is stored as elastic energy in the MSA:
 | (7) |
 | (8) |
3.2 Experimental results and theoretical predictions
To confirm the crack trapping mechanism, we employ a hollow design featuring slender, tilted beams and a thick terminating film (the case with “b = 2.4 mm” and “t = 2 mm” in the first group of Table S1, ESI†) (Fig. 2a). As shown in Fig. S2a and Movie S1 (ESI†), the solid sample shows an initial crack opening upon the shear loading, followed by stable and fast propagation as the load increases. Eventually, adhesive failure occurs between the solid sample and PMMA plate. As shown in Fig. 2b and Movie S2 (ESI†), for the MSA, an initial crack opening is observed upon the shear loading. However, subsequent crack propagation stops on the left side of the beam. To enable further crack propagation, the loading needs to be further increased to advance the crack through the beam in an unstable manner. We observe periodic crack trapping and unstable crack propagation in experiments until the entire interface fails. Unless otherwise specified, adhesive failure was consistently observed between the PDMS adhesive layer and the PMMA plate in all tests.We plot the crack propagation distance with time and find that crack propagation of the solid sample is much faster than that of the MSA (Fig. 2c). Additionally, the MSA displays stepwise increment of crack size, indicating crack trapping and unstable crack propagation as shown in Fig. 2b and Movie S2 (ESI†).
Both solid samples and MSAs exhibit reproducible force–displacement curves, with negligible dispersion across multiple samples (solid lines in Fig. 2d). We measure the intrinsic shear strength τ0 (gray star) and work of adhesion Wad (gray shaded area) from solid samples, which exhibit weak dependence on sample dimensions (Fig. S2b and c, ESI†). Similarly, we measure the shear strength τexp (blue star) and effective adhesion energy Γexp (blue shaded area) for MSAs.
We further conduct finite element analysis to quantitatively elucidate the adhesion toughening of MSAs. We truncate the predicted force–displacement curves at the critical displacement u = ucr when GL_min = Wad is satisfied, which agree well with experimental results (dash-dot lines in Fig. 2d). Deformation profiles from finite element simulation also agree with experimental results (Fig. 2e). Next, we compute the GL-crack length relationship from the simulations. For the solid sample, GL remains nearly constant as a function of crack length provided that the initial crack is long enough (Fig. S2d, ESI†). At a critical displacement (ucr = 1.12 mm), GL = Wad and 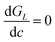 are satisfied, indicating the onset of stable crack propagation (Fig. S2d, ESI†). In contrast, for the MSA, the energy release rate GL varies periodically with the crack length (Fig. 2f), reaching GL_min = Wad at the critical displacement (ucr = 2.8 mm). As explained in Fig. 1, unstable crack propagation occurs once GL_min = Wad is satisfied, which leads to adhesion toughening.
are satisfied, indicating the onset of stable crack propagation (Fig. S2d, ESI†). In contrast, for the MSA, the energy release rate GL varies periodically with the crack length (Fig. 2f), reaching GL_min = Wad at the critical displacement (ucr = 2.8 mm). As explained in Fig. 1, unstable crack propagation occurs once GL_min = Wad is satisfied, which leads to adhesion toughening.
Experimental results reveal a shear strength of τexp = 10.7 kPa for MSAs, close to that of solid samples (τ0 = 10.2 kPa) (Fig. 2g). The predicted shear strength of MSAs is τpre = 13.6 kPa, deviating by ∼27% from numerical predictions. We attribute such discrepancy to several factors: first, Wad = 7.3 J m−2, measured from solid samples, represents an averaged work of adhesion for rupturing the entire interface rather than the work of adhesion corresponding to crack initiation; second, our simulations assume a stable equilibrium state, neglecting all inelastic processes; third, by claiming 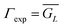 , we neglect the edge effects of the finite MSAs and viscoelastic dissipation; lastly, in the simulations, the initial crack doesn’t propagate until GL_min = Wad is satisfied (u = ucr in Fig. 1c), whereas in experiments, the crack propagates a little bit with the increase of displacement from u = u2 to u = ucr (Fig. 1c).
, we neglect the edge effects of the finite MSAs and viscoelastic dissipation; lastly, in the simulations, the initial crack doesn’t propagate until GL_min = Wad is satisfied (u = ucr in Fig. 1c), whereas in experiments, the crack propagates a little bit with the increase of displacement from u = u2 to u = ucr (Fig. 1c).
Furthermore, the experimental effective adhesion energy of MSAs is Γexp = 13.3 J m−2, nearly doubling that of solid samples (Wad = 7.3 J m−2) (Fig. 2h), showing the toughening effect. The predicted adhesion energy is 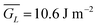 calculated with eqn (3) using the simulation results in Fig. 2f, close to our experimental results. The minor deviation from experimental results can be attributed to similar reasons discussed above.
calculated with eqn (3) using the simulation results in Fig. 2f, close to our experimental results. The minor deviation from experimental results can be attributed to similar reasons discussed above.
3.3 Effects of the beam tilting angle θ on asymmetric adhesion
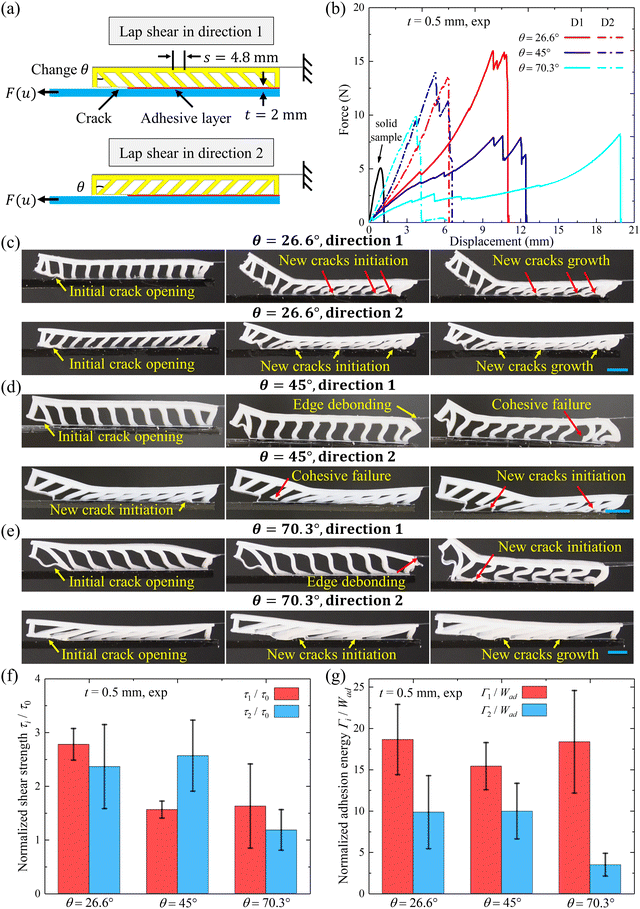
We next investigate the effects of beam tilting angle θ on adhesion asymmetry while maintaining constant beam thickness b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) cos(θ) (group 1 listed in Table S1, ESI†). We pull the samples in two opposite directions (D1 and D2, as illustrated in Fig. 3a). With the pulling direction D1, tilted beams undergo buckling followed by stretching upon shear loading and simultaneously exhibit crack trapping behaviors (Fig. S3 and Movie S3, ESI†). Conversely, with the pulling direction D2, tilted beams immediately get stretched upon shear loading (Fig. 2b and Movie S2, ESI†). Consequently, MSAs exhibit greater stiffness for the pulling direction D2 compared to D1 but are softer than solid samples (Fig. 3b). With the increase of θ, the asymmetry in force–displacement curves for D1 and D2 pulling directions becomes more pronounced. In the experiments, the crack always propagates unidirectionally following the predefined path.
cos(θ) (group 1 listed in Table S1, ESI†). We pull the samples in two opposite directions (D1 and D2, as illustrated in Fig. 3a). With the pulling direction D1, tilted beams undergo buckling followed by stretching upon shear loading and simultaneously exhibit crack trapping behaviors (Fig. S3 and Movie S3, ESI†). Conversely, with the pulling direction D2, tilted beams immediately get stretched upon shear loading (Fig. 2b and Movie S2, ESI†). Consequently, MSAs exhibit greater stiffness for the pulling direction D2 compared to D1 but are softer than solid samples (Fig. 3b). With the increase of θ, the asymmetry in force–displacement curves for D1 and D2 pulling directions becomes more pronounced. In the experiments, the crack always propagates unidirectionally following the predefined path.
For the normalized shear strength τi/τ0 (i = 1 or 2), our results show that τ1/τ0 first remains nearly constant, slightly increasing from ∼0.47 at θ = 26.6° to ∼0.51 at θ = 45°, and finally decreases significantly to ∼0.28 at θ = 70.3° (Fig. 3c). Meanwhile, τ2/τ0 first increases from ∼0.67 at θ = 26.6° to ∼1.1 at θ = 45°, and then significantly decreases to ∼0.61 at θ = 70.3° (Fig. 3d). Our numerical predictions generally agree with experimental trends but are noticeably larger (colored circles in Fig. 3c and d).
For the normalized effective adhesion energy Γi/Wad (i = 1 or 2), our results show that Γ1/Wad first significantly increases from ∼1.6 at θ = 26.6° to ∼2.4 at θ = 45°, and then significantly decreases to ∼1.4 at θ = 70.3° (Fig. 3e); Γ2/Wad first increases from ∼1.6 at θ = 26.6° to ∼2.0 at θ = 45°, and then decreases to ∼1.3 at θ = 70.3° (Fig. 3f). Our theoretical predictions generally agree with experimental results, with the exception for θ = 70.3° (colored circles in Fig. 3e and f).
Lastly, we define the adhesion asymmetry factors for strength (τ2/τ1) and effective adhesion energy (Γ2/Γ1), respectively. τ2/τ1 first significantly increases from ∼1.4 at θ = 26.6° to ∼2.2 at θ = 45°, and then stays almost constant at ∼2.2 at θ = 70.3° (Fig. 3g). Meanwhile, Γ2/Γ1 first slightly decreases from ∼0.96 at θ = 26.6° to ∼0.81 at θ = 45°, and then slightly increases to ∼0.92 at θ = 70.3° (Fig. 3h). Our numerical predictions mostly agree with our experimental findings, as indicated by the colored circles in Fig. 3g and h.
3.4 Effects of the terminated film thickness t on adhesion properties
We next conduct a parametric study examining the influence of terminated film thickness (t) on the adhesion properties. We design the second group of MSAs with identical stubby beams but varied film thickness t (see Fig. 4a and Table S1, ESI†) and test all the samples using identical experimental conditions. Our experimental results show that while the thickness t has minimal impact on the initial section of force–displacement curves, it significantly affects the latter portion (Fig. 4b). Such behavior stems from the dominance of tilted beams in carrying loads during elastic deformation, whereas the terminated film governs the energy release rate (GL) transferred to the crack tip during crack propagation, thus affecting the rupture point.13,33,35,36 Notably, when the terminated film thickness is decreased from t = 2 mm to t = 0.75 mm, the latter section of force–displacement curves shows a noticeable variation. However, further decreasing the thickness to t = 0.5 mm leads to a dramatic increase in maximum shear force, accompanied by a pronounced dispersion of experimental measurements (shown in the next section; Fig. 5c).Fig. 4c–e illustrate crack propagation dynamics of the MSAs with varied terminated film thickness. For a thick terminated film (t = 2 mm), the crack propagates unidirectionally following the predefined path, exhibiting evident crack trapping behaviors (Fig. 4c). Conversely, for a thin terminated film (t = 0.5 mm), we usually observe new crack initiations with a finite distance from the initial crack tip. Despite the presence of crack trapping behaviors, the crack propagation deviates from the predefined path (Fig. 4e). For an intermediate terminated film thickness (t = 0.75 mm), the crack consistently propagates along the predefined path, displaying clear crack trapping behaviors (Fig. 4d). While random new crack initiations may still occur, they are not discernible in our recorded videos. See Movie S4 (ESI†) for details.
Consequently, as shown in Fig. 4f, the normalized shear strength τ/τ0 slightly increases with the decrease of t, ranging from ∼0.91 ± 0.04 at t = 2 mm to ∼1.18 ± 0.37 at t = 0.5 mm. Notably, for a thin terminated film (t = 0.5 mm), τ/τ0 scatters greatly due to the randomly initiated new cracks. As shown in Fig. 4g, the normalized adhesion energy Γ/Wad generally demonstrates a nonmonotonic change with the decrease of t, ranging from ∼1.77 ± 0.16 for t = 2 mm to ∼3.1 ± 1.57 for t = 0.5 mm. Similarly, for a thin terminated film (t = 0.5 mm), Γ/Wad scatters greatly due to the randomly initiated new cracks.
For a relatively large thickness (t = 2 mm), the crack propagation follows the predefined path, and τ/τ0 and Γ/Wad are close to the theoretical predictions based on the crack trapping mechanism (yellow circles in Fig. 4f and g). In contrast, for a relatively small thickness (t = 0.5 mm), the propagation of the initial crack coexists with noticeable random new crack initiations, and τ/τ0 and Γ/Wad are significantly smaller than the theoretical predictions (yellow circles in Fig. 4f and g). For the intermediate thickness ranging from t = 1.5 mm to t = 0.75 mm, the theoretically predicted τ/τ0 and Γ/Wad (Fig. 4f and g) deviate increasingly from experimental results. This deviation coincides with the gradual transition between the two distinct crack propagation modes mentioned above (Movie S4, ESI†). Clear experimental observation of this transition is challenging, attributed to the sample's opacity and the difficulty in discerning micro-scale crack initiations.
Similarly, for the third group of MSAs with identical slender beams (Table S1, ESI†), with the decrease of terminated film thickness (t), the experimental results of adhesion properties deviate increasingly significantly from theoretical predictions (Text S1 and Fig. S4, ESI†).
3.5 New crack initiation reduces the enhancement of adhesion toughening
As discussed above, new crack initiation may be responsible for the difference between experimental results and theoretical predictions. While similar phenomena have been observed in the hollow structural adhesives with symmetric beams,13,33,35,36 they have not been systematically studied. Herein, we systematically investigate the influence of new crack initiations on adhesion toughening, using MSAs featuring stubby beams and a thin terminating film as an example (“t = 0.5 mm” cases in the second group of Table S1, ESI;†Fig. 5a). In experiments, the stochastic nature of new crack initiation results in varied crack propagation dynamics across different samples, and thus, we present another representative case in Fig. 5b and Movie S5 (ESI†), as a comparison with the results shown in Fig. 4e and Movie S4 (ESI†).In experiments, we find significant scattering in the force–displacement curves of MSAs (Fig. 5c), and consequently significantly dispersed values of τ/τ0 (Fig. 5e, left) and Γ/Wad (Fig. 5e, right), both of which are much smaller than the theoretically predicted values. Meanwhile, our simulations show that the energy release rate GL changes more rapidly with the crack length (Fig. 5d) compared to that in Fig. 2f.
To investigate the possibility of new crack initiation, we first examine the stress field at the interface between the MSA and PMMA plate (Fig. 5f). We observe pronounced stress concentration near the left and right edges of the beam (marks C and E in the inset of Fig. 5d) by plotting the stress distribution against the distance from the initial crack tip along the interface (Fig. 5g), which is likely the cause of new crack initiation.
To quantitatively assess the impacts of inevitable flaws at the interface, we introduce a flaw along the interface beneath the left side of the beam (Fig. 5h). We repeat the simulation and compute the energy release rate at the initial crack tip (A′), to the left of the flaw (B′), and to the right of the flaw (C′), respectively (Fig. 5h). Fig. 5i shows the deformation near the initial crack and the flaw (0.7 mm) with an applied displacement of u = 1.6 mm. As shown in Fig. 5j, for a relatively small flaw (0.3 mm), the energy release rate GL at the tips of the flaw is smaller than that at the initial crack tip. However, for a larger flaw size (0.5 mm or 0.7 mm), GL at the tips of the flaw exceeds that at the initial crack tip, enabling new crack propagation before the propagation of the initial crack and thus decreasing the measured adhesion energy. As the flaw size increases, the critical displacement ucr, where GL = Wad is satisfied at the flaw tips, decreases.
Though our simulations have suggested the possibility of new crack initiations, our objective in the current study does not involve the theoretical prediction of adhesion toughening in scenarios where new cracks initiate during the propagation of the initial crack, which can be extremely challenging.
3.6 Maximizing the adhesion toughening using MSAs with a thin terminated film
In this section, we experimentally explore the possibility of maximizing adhesion toughening using MSAs with slender beams and a thin terminated film (t = 0.5 mm) (group 4 listed in Table S1, ESI;†Fig. 6a). We vary the beam tilting angle θ while maintaining constant beam thickness b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(θ), and perform lap shear tests in two opposite pulling directions, respectively.
cos(θ), and perform lap shear tests in two opposite pulling directions, respectively.
Our experimental results show increased asymmetry in force–displacement curves for the two opposite pulling directions with the increase of θ (Fig. 6b). We present representative images and movies illustrating crack propagation dynamics for different designs of MSAs (Fig. 6c–e). At θ = 26.6°, new crack initiations occur along the interface during the propagation of the initial crack for both pulling directions (Fig. 6c and Movie S6, ESI†). At θ = 45°, both edge debonding from the PET film and cohesive failure within the hollow backing occur during the propagation of the initial crack for the D1 pulling direction; for the D2 pulling direction, cohesive failure and new crack initiations occur along the interface during the propagation of the initial crack (Fig. 6d and Movie S7, ESI†). At θ = 70.3°, both edge debonding from PET film and new crack initiations occur during the propagation of the initial crack for the D1 pulling direction; for the D2 pulling direction, new cracks initiate during the propagation of the initial crack (Fig. 6e and Movie S8, ESI†).
Consequently, τ1/τ0 first decreases significantly from ∼2.8 at θ = 26.6° to ∼1.6 at θ = 45°, and then remains nearly constant at ∼1.6 at θ = 70.3°; but τ2/τ0 first remains almost unchanged from ∼2.4 at θ = 26.6° to ∼2.6 at θ = 45°, and then decreases to ∼1.2 at θ = 70.3° (Fig. 6f). Similarly, Γ1/Wad first decreases from ∼18.6 at θ = 26.6° to ∼15.4 at θ = 45°, and then increases to ∼18.4 at θ = 70.3°; Γ2/Wad first remains almost constant from ∼9.8 at θ = 26.6° to ∼10.0 at θ = 45°, and then decreases to ∼3.5 at θ = 70.3° (Fig. 6g). Finally, the adhesion asymmetry factor τ2/τ1 significantly increases from ∼0.85 at θ = 26.6° to ∼1.6 at θ = 45°, and then decreases to ∼0.73 at θ = 70.3° (Fig. S5a, ESI†). Similarly, Γ2/Γ1 slightly increases from ∼0.53 at θ = 26.6° to ∼0.65 at θ = 45°, and then significantly decreases to ∼0.19 at θ = 70.3° (Fig. S5b, ESI†).
4. Discussion
In the following, we discuss several critical points that require further in-depth investigations.Our theoretical predictions of adhesion toughening, based on the crack trapping mechanism,11,13,33,35,36 agree well with experimental results when the crack propagates unidirectionally following a predefined path for a relatively thick terminated film. However, with the decrease of the terminated film thickness, the measured adhesion energy of MSAs deviates significantly from theoretical predictions, which is attributed to new crack initiations based on experimental observations and numerical simulations. However, the transition between the two distinct crack propagation modes remains unclear and may indicate the involvement of the fracto-adhesive length scale, which characterizes the thickness-dependent adhesion properties, as systematically investigated in a previous study on the lap shear of soft hydrogels.39 Note that currently, the length scales governing the fracture and adhesion of discrete metamaterials are yet to be explored,9,12,40,41 which calls for more comprehensive theoretical and experimental investigations.
Recently, stretchable and low-hysteresis composites comprising hard and soft phases have been developed to enhance both the fracture toughness and fatigue resistance.34,42,43 While the stress deconcentration mechanism has been widely used to elucidate toughening effects, the periodically varied relationship between energy release rate versus crack length based on the crack trapping mechanism provides an alternative way to predict the fracture and fatigue enhancement.
In this study, lap shear tests were conducted without normal force applied to MSAs. We want to point out that lap shear tests under displacement control (using two rigid fixtures) are rare in practical applications but prevalent in lab tests,39,44–46 which can lead to significant artifacts for thick structural adhesives (Fig. S6a and b, ESI†). For both solid samples and MSAs, the maximum shear force is much higher in displacement-control mode than in zero normal force-control mode when the displacement along the thickness direction is fixed (Fig. S6c and d, ESI†). Consequently, solid samples exhibit appreciable increases in shear strength and adhesion energy in displacement-control mode (Fig. S6e and f, ESI†). For MSAs, both shear strength and effective adhesion energy show significant increases in displacement-control testing mode (Fig. S6e and f, ESI†). The reason is as follows: with displacement-control mode, the stress normal to the applied shear force increases significantly for MSAs due to beam bending, compared to solid samples. This significantly increases the friction between MSAs and PMMA substrate, resulting in mixed-mode fracture. These findings highlight the importance of carefully selecting the lap shear conditions for testing thick structural adhesives.44
Finally, we envision that there are ample opportunities for further exploration of MSAs. For example, stimuli-responsive materials can be used to fabricate either the thick backing or the adhesive layer for stimuli-responsive MSAs targeted at responsive and switchable applications.5 Besides, designing the backing structures of MSAs to better conform to rough or curved surfaces may enable strong and reversible adhesion, addressing the well-known challenge of conventional pressure sensitive adhesives.47,48 Furthermore, exploring MSAs for achieving strong and reversible adhesion in wet and underwater conditions is also important for biomedical applications and ocean explorations.49,50
5. Conclusions
In summary, we have achieved adhesion toughening and asymmetry in the lap shear of MSAs using asymmetric and thick hollow backings. By combining theoretical, numerical, and experimental investigations, we identify the crack trapping as the toughening mechanism, which leads to unstable crack propagation under practical monotonic loading and thus dissipates more energy. For MSAs with a relatively thick terminated film, the experimental results agree well with theoretical predictions based on the crack trapping mechanism when the crack propagates unidirectionally along the predefined path. However, for MSAs with a relatively thin terminated film, the experimental results deviate significantly from theoretical predictions based on the crack trapping mechanism. We attribute this discrepancy to new crack initiations, which are observed experimentally and elaborated through numerical simulations. Additionally, we explore adhesion asymmetry by varying the beam tilting angle (θ). Notably, for MSAs with t = 0.5 mm and θ = 26.6°, we achieve a maximum effective adhesion energy being ∼18.6 times that of solid samples. For MSAs with t = 0.5 mm and θ = 70.3°, we achieve a maximum adhesion energy asymmetry factor of Γ1/Γ2 ∼ 5.3. Our study provides useful insights for designing metamaterial structural adhesives for engineering applications such as robotic grippers, wall-climbing robotics, and wearable devices that require reversible and switchable adhesion.Author contributions
C. L. and S. C. conceived the study and designed the overall experiments. Q. G. provided suggestions on the interpretation of experimental results and numerical simulations. R. C. helped with 3D-printing the molds. C. L. and S. C. wrote the manuscript with input from all authors. All authors read and approved the final article.Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its ESI.†Conflicts of interest
The authors declare they have no competing interests.Acknowledgements
The authors acknowledge support from the US Army Research Office through grant no. W911NF-20-2-0182.References
- C. Creton, MRS Bull., 2003, 28, 434–439 CrossRef CAS.
- M. M. Feldstein, E. E. Dormidontova and A. R. Khokhlov, Prog. Polym. Sci., 2015, 42, 79–153 CrossRef CAS.
- S. Nam and D. Mooney, Chem. Rev., 2021, 121, 11336–11384 CrossRef CAS PubMed.
- J. Yang, R. Bai, B. Chen and Z. Suo, Adv. Funct. Mater., 2020, 30, 1901693 CrossRef CAS.
- N. D. Blelloch, H. J. Yarbrough and K. A. Mirica, Chem. Sci., 2021, 12, 15183–15205 RSC.
- Z. Liu and F. Yan, Adv. Sci., 2022, 9, 2200264 CrossRef PubMed.
- A. B. Croll, N. Hosseini and M. D. Bartlett, Adv. Mater. Technol., 2019, 4, 1900193 CrossRef.
- X. Zhao, X. Chen, H. Yuk, S. Lin, X. Liu and G. Parada, Chem. Rev., 2021, 121, 4309–4372 CrossRef CAS PubMed.
- D. Hwang, C. Lee, X. Yang, J. M. Pérez-González, J. Finnegan, B. Lee, E. J. Markvicka, R. Long and M. D. Bartlett, Nat. Mater., 2023, 22, 1030–1038 CrossRef CAS PubMed.
- Q. Li, W. Liu, C. Yang, P. Rao, P. Lv, H. Duan and W. Hong, J. Mech. Phys. Solids, 2022, 169, 105053 CrossRef.
- S. Xia, L. Ponson, G. Ravichandran and K. Bhattacharya, Phys. Rev. Lett., 2012, 108, 196101 CrossRef CAS PubMed.
- A. E. Athanasiadis, M. A. Dias and M. K. Budzik, Extreme Mech. Lett., 2021, 48, 101411 CrossRef.
- N. J. Glassmaker, A. Jagota, C.-Y. Hui, W. L. Noderer and M. K. Chaudhury, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 10786–10791 CrossRef CAS PubMed.
- R. Zhao, S. Lin, H. Yuk and X. Zhao, Soft Matter, 2018, 14, 2515–2525 RSC.
- W. Ruotolo, D. Brouwer and M. R. Cutkosky, Sci. Rob., 2021, 6, eabi9773 CrossRef PubMed.
- X. Zhang, Y. Wang, Z. Tian, M. Samri, K. Moh, R. M. McMeeking, R. Hensel and E. Arzt, Sci. Adv., 2022, 8, eadd4768 CrossRef PubMed.
- A. Ghareeb and A. Elbanna, J. Appl. Mech., 2019, 86, 071005 CrossRef CAS.
- Q. Li, X. Wan, Z. Xu, Y. He, Q. Xue and C. Yang, Extreme Mech. Lett., 2024, 67, 102128 CrossRef.
- Y. He, X. Wan, Y. Chen and C. Yang, J. Mech. Phys. Solids, 2021, 155, 104570 CrossRef CAS.
- Y. Gao, X. Jiang, P. Wang, Y. Zhong and T. Lu, Extreme Mech. Lett., 2023, 61, 102016 CrossRef.
- H. Zhu, T. Yin, X. Hu, B. Liu, H. Yu, Z. Chen, S. Qu and W. Yang, J. Mech. Phys. Solids, 2023, 175, 105304 CrossRef.
- S. Xia, L. Ponson, G. Ravichandran and K. Bhattacharya, J. Mech. Phys. Solids, 2015, 83, 88–103 CrossRef.
- S. Xia, L. Ponson, G. Ravichandran and K. Bhattacharya, J. Mech. Phys. Solids, 2013, 61, 838–851 CrossRef.
- Y. Xie, Y. Wu, Z. Wei, J. Lin and J. Qian, Eur. J. Mech. A: Solids, 2024, 103, 105159 CrossRef.
- D.-G. Hwang, K. Trent and M. D. Bartlett, ACS Appl. Mater. Interfaces, 2018, 10, 6747–6754 CrossRef CAS PubMed.
- B. W. Townsend, D. C. Ohanehi, D. A. Dillard, S. R. Austin, F. Salmon and D. R. Gagnon, Int. J. Adhes. Adhes., 2011, 31, 639–649 CrossRef CAS.
- B. W. Townsend, D. C. Ohanehi, D. A. Dillard, S. R. Austin, F. Salmon and D. R. Gagnon, Int. J. Adhes. Adhes., 2011, 31, 650–659 CrossRef CAS.
- E. Bull, J. Cholaky and S. Kuhlman, Durability of Building and Construction Sealants and Adhesives, ASTM International, 2015, vol. 5, pp. 297–327 Search PubMed.
- S. Song, D.-M. Drotlef, C. Majidi and M. Sitti, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E4344–E4353 CAS.
- G. Gu, J. Zou, R. Zhao, X. Zhao and X. Zhu, Sci. Rob., 2018, 3, eaat2874 CrossRef PubMed.
- J. Huang, Y. Liu, Y. Yang, Z. Zhou, J. Mao, T. Wu, J. Liu, Q. Cai, C. Peng, Y. Xu, B. Zeng, W. Luo, G. Chen, C. Yuan and L. Dai, Sci. Rob., 2021, 6, eabe1858 CrossRef PubMed.
- H. Yao, G. D. Rocca, P. Guduru and H. Gao, J. R. Soc., Interface, 2008, 5, 723–733 CrossRef CAS PubMed.
- L. Shen, C.-Y. Hui and A. Jagota, J. Appl. Phys., 2008, 104, 123506 CrossRef.
- Z. Wang, C. Xiang, X. Yao, P. Le Floch, J. Mendez and Z. Suo, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 5967–5972 CrossRef CAS PubMed.
- Z. He, N. M. Moyle, C.-Y. Hui, B. Levrard and A. Jagota, Tribol. Lett., 2017, 65, 1–8 CrossRef.
- W. Noderer, L. Shen, S. Vajpayee, N. Glassmaker, A. Jagota and C.-Y. Hui, Proc. R. Soc. A, 2007, 463, 2631–2654 CrossRef.
- P. Fratzl, H. S. Gupta, F. D. Fischer and O. Kolednik, Adv. Mater., 2007, 19, 2657–2661 CrossRef CAS.
- M. Hossain, C.-J. Hsueh, B. Bourdin and K. Bhattacharya, J. Mech. Phys. Solids, 2014, 71, 15–32 CrossRef.
- Y. Wang, X. Yang, G. Nian and Z. Suo, J. Mech. Phys. Solids, 2020, 143, 103988 CrossRef.
- S. Fulco, M. K. Budzik, E. D. Bain and K. T. Turner, Extreme Mech. Lett., 2022, 57, 101912 CrossRef.
- A. J. D. Shaikeea, H. Cui, M. O’Masta, X. R. Zheng and V. S. Deshpande, Nat. Mater., 2022, 21, 297–304 CrossRef CAS PubMed.
- C. Xiang, Z. Wang, C. Yang, X. Yao, Y. Wang and Z. Suo, Mater. Today, 2020, 34, 7–16 CrossRef CAS.
- C. Li, H. Yang, Z. Suo and J. Tang, J. Mech. Phys. Solids, 2020, 134, 103751 CrossRef.
- S. A. Suresh, A. Hajj-Ahmad, E. W. Hawkes and M. R. Cutkosky, J. R.Soc., Interface, 2021, 18, 20200730 CrossRef PubMed.
- H. Yuk, C. E. Varela, C. S. Nabzdyk, X. Mao, R. F. Padera, E. T. Roche and X. Zhao, Nature, 2019, 575, 169–174 CrossRef CAS PubMed.
- Y. Wang, T. Yin and Z. Suo, J. Mech. Phys. Solids, 2021, 150, 104348 CrossRef CAS.
- C. Linghu, Y. Liu, Y. Y. Tan, J. H. M. Sing, Y. Tang, A. Zhou, X. Wang, D. Li, H. Gao and K. J. Hsia, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2221049120 CrossRef CAS PubMed.
- Z. Wang, Y. Dong, R. Annapooranan, C. Li, R. Chambers and S. Cai, Appl. Mater. Today, 2024, 38, 102189 CrossRef.
- C. Lee, H. Shi, J. Jung, B. Zheng, K. Wang, R. Tutika, R. Long, B. P. Lee, G. X. Gu and M. D. Bartlett, Cell Rep. Phys. Sci., 2023, 4, 101597 CrossRef CAS.
- S. T. Frey, A. T. Haque, R. Tutika, E. V. Krotz, C. Lee, C. B. Haverkamp, E. J. Markvicka and M. D. Bartlett, Sci. Adv., 2022, 8, eabq1905 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00410h |
| This journal is © The Royal Society of Chemistry 2024 |