 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Optical deformations of azobenzene polymers: orientation approach vs. other concepts
Marina
Saphiannikova
 *a,
Vladimir
Toshchevikov
*a,
Vladimir
Toshchevikov
 b and
Nina
Tverdokhleb†
b and
Nina
Tverdokhleb†
 a
a
aInstitute Theory of Polymers, Leibniz Institute of Polymer Research Dresden, 01069 Dresden, Germany. E-mail: grenzer@ipfdd.de
bInstitute of Macromolecular Compounds, Russian Academy of Sciences, 199004 Saint Petersburg, Russia
First published on 28th February 2024
Abstract
It has been 30 years since the discovery of surface restructuring in thin azopolymer films by two independent research groups. A wide variety of topographical structures have been created by the application of two-/four-beam interference patterns, space light modulators and even helical beams. There are a number of comprehensive reviews which describe in detail the advances in superficial photopatterning of azopolymer films and macroscopic deformations of azonetworks. The theoretical approaches are only briefly touched on in these reviews and often are accompanied by the remark that the phenomenon is far from being understood. In this review, we would like to present the polymer theoretist's point of view on this intriguing problem. We begin by describing a multitude of theoretical approaches and commenting on the pluses and drawbacks of each. Importantly, we show that in most cases the presence of an azopolymer matrix is either ignored or limited to a specific class of azopolymers (liquid-crystalline or elastomeric). We then move to early orientation approaches based on the hypothesis that reorientation of azo-chromophores by modulated polarized light is the sole cause of superficial patterning. At the end of the review a modern orientation approach, as proposed by our own group, is presented. This approach has high predictive power because it can explain a large pool of experimental data for different classes of azopolymers including glassy and liquid-crystalline materials. This is made possible by taking into account both the light-induced orientation process and the change of anisotropic interactions between the chromophores upon their isomerization. Last but not least, this is the only approach that provides an estimate of the light-induced stress large enough to cause plastic deformations of glassy azopolymers. Recent finite element modeling results show remarkable similarity to real patterns and even time-dependent data are well explained. With this, we claim that the puzzle is finally understood and the orientation approach is ready for its implementation for major azopolymer classes.
Introduction
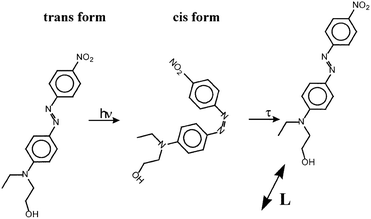
Recent advances in the fourth generation (4G) of optics reveal that modulating orientation of the anisotropic axis in liquid-crystalline (LC) materials allows the production of planar optical elements with a few micrometer thickness.1 A dramatic reduction in size and hence weight enables 4G optical solutions for space telescopes and even solar sails.2 The key process to modulate the orientation of LC molecules is based on the photoalignment of ultrathin layers composed of photosensitive anisometric molecules. Certain azobenzene (azo) dyes are among the most effective photoalignment materials. Visible light of blue-green wavelengths induces cyclic trans–cis isomerization, which results in a predominant orientation of the azobenzenes perpendicular to the light polarization, where the absorption is minimized. The azodye photoalignment layer of only a few nanometer thicknesses dictates the alignment of a micrometer-thick layer of LC molecules deposited on it. Optical patterning of the alignment layer can be performed nowadays with an extremely high resolution, see Fig. 1. Low-cost and fast fabrication of very complex orientational patterns makes it possible to produce all the variety of planar optical components with >99% efficiency across a broadband of wavelengths (from UV to IR).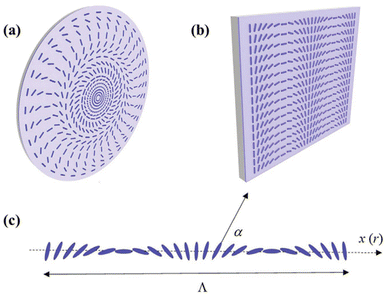 | ||
| Fig. 1 Azodye alignment patterns for 4G optical lens (a) and prism (b). The angle α describing molecular orientation varies linearly along a Cartesian coordinate x for a prism (c) and it is a parabolic function of the radial coordinate r for a lens. Reproduced from ref. 1 with permission from John Wiley & Sons, copyright 2021. | ||
The revolutionary advance of 4G optics is accompanied by no less impressive achievements in fabrication of reconfigurable topographical structures. The key process lies again in the photoalignment of azodyes, which are attached to the polymer backbones in side-chains. The photosensitive azopolymer layer has a micrometer thickness and its surface can be easily reconfigured by applying irradiation with modulated light, where either intensity or polarization varies spatially. A well-known example is the restructuring of polymer films under irradiation with a two-beam interference pattern.3,4 Here, the topographical changes mimic the distribution of light, forming sinusoidal surface relief gratings (SRGs), that appear in addition to a birefringence grating.5–7 The topography profile can be made asymmetrical by changing the angle between the two interfering beams8 or by rotating the polarization pattern produced by orthogonally polarized beams.9
Not only one-dimensional linear gratings but also two-dimensional periodic structures can be inscribed onto the film surface, see Fig. 2. The latter can be produced by two-step irradiation with the second step performed after rotating the film by 60° or 90° about its normal with respect to the writing beam.5,10 Recent examples include irradiation with a four-beam interference pattern,11 tuned to have a constant spatial intensity and simultaneous irradiation with four close wavelengths.12 These complex patterns produce two-dimensional vortex-like structures and beat-like structures. Despite a wide variety of established and new practical applications such as guiding templates for living cells,13 azo-structures with light-controlled wettability,14,15 multiplexed gratings for emerging display applications16 and many others, azopolymers still elude a clear physical mechanism that would convincingly explain the appearance of topographical structures.
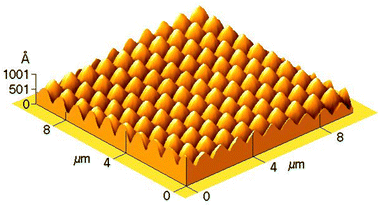 | ||
| Fig. 2 AFM topography of the cross grating produced by two-step irradiation. The second step was performed after rotating the film by 60° about its normal. Adapted from ref. 10 with permission from John Wiley & Sons, copyright 2005. | ||
It is important to point out that the spatial structure of photo-alignment and deformations in azopolymers is directly controlled by the spatial distribution of the polarization direction and intensity of light. Therefore, not only micro- and nanoscale patterns of alignment17–20 and deformations21,22 can be generated in azopolymers by irradiation with micro- and nanoscale structured light, but macroscopic deformations of azo-containing polymers have also been observed.23,24 Incorporation of azo-chromophores into liquid-crystalline polymers provides a possibility for a significant macroscopic photomechanical response in such multicomponent photosensitive materials7,25 which can be quickly controlled by variation of intensity and polarization direction of the light. As examples, a reversible bending–unbending behavior in monodomain26,27 and polydomain28,29 LC azo-containing samples under irradiation with ultraviolet and visible light can be mentioned. Imprinting complex local director distributions into LC azopolymers opens the possibility of observing fancy photo-responses: helical motions,30 three-dimensional fingerprints in cholesteric LC azonetworks,31 a light-driven artificial flytrap,32 a caterpillar-like crawling and wave-like movements.33 It is interesting to note that the motions of some of these azopolymers imitate nontrivial mechanical movements of living systems.32–34 Azobenzene-containing polymers, which can change their shape and alignment when irradiated with light, are therefore very perspective materials for the construction of light-driven sensors, actuators,35 artificial muscles36 and other photo-controllable devices.
An important property of azopolymers is that they act as transducers, wirelessly and directly converting the energy of light into mechanical stress.27,37 The spatial distribution of the stress magnitude and its principal axes can be specified with high precision using either two-/four-beam interference patterns or space light modulators. This allows a wide variety of optical deformations to be achieved, which can be further tuned by using different wavelengths of light.38 The advantage of photoinduced deformations is that they can be altered easily and quickly, for example by changing the phase of the irradiation pattern.39
In summary, the incorporation of azo-chromophores into polymers allowed researchers to produce broad classes of photosensitive materials for various applications, including inscription of SRGs onto surfaces of glassy azopolymers, macroscopic deformation of azonetworks, sophisticated photomechanical responses in LC azo-containing polymers, azo-materials for optics of fourth generation, etc. On the other hand, for the further development of azo-materials, it is necessary to have a theoretical picture that explains the experimental facts and predicts new features of these materials. Therefore, the aim of the present review is, first, to present different theoretical concepts developed for specific applications and to discuss why many of them do not work for broad classes of azo-materials. The second goal of the review is to present a modern theoretical approach based on orientation mechanism of photo-ordering and deformation and to show the universality of this orientation approach for application to all known classes of azo-materials.
Photofluidization vs. plasticization under the force
Before reviewing multiple models, especially those proposed for the explanation of SRG inscription, it is important to acknowledge the existence of azopolymers with photoinduced reversible solid-to-liquid transition. The glass transition temperature of such polymers can be decreased below the room temperature by irradiation with ultraviolet light.40–42 This makes them particularly suitable for applications as healable coatings, for example in the photo-assisted rehabilitation of pipelines.43 A special molecular design facilitates a photoinduced solid-to-liquid transition: the presence of azobenzene-type chromophores and long alkyl chains as the spacer and the tail of a side-chain.In this review, another type of glassy azopolymer will be considered, that is used for inscription of topographical structures. To ensure a long-term thermal stability of the inscribed patterns, the glassy azopolymers are applied with no decrease of Tg under irradiation with either ultraviolet or visible light.41 Only weak photosoftening has been found over the years, as described in detail in ref. 44. Moreover, an increase in temperature up to the glass transition, and hence considerable photosoftening, was found to be destructive for an inscription of SRGs.45,46 In spite of this, most models which we will discuss in the next section rely a priori on the concept of extreme light-induced plasticization47 or directional photofluidization.48,49 The need to assume that glassy azopolymers undergo a photoinduced transition into a low-viscosity fluid comes from the fact that the magnitude of predicted forces is extremely low in most models. However, significant deformations during topographical restructuring of the azopolymer in the glassy state indicate the generation of large and even giant stresses. They can be as high as 1 GPa, which was confirmed both experimentally50,51 and theoretically.44,52,53
The light-induced plasticization takes place but not due to a tremendous decrease in material parameters. It occurs similar to conventional glassy polymers when they are stretched above the yield point. The plastic flow can be induced by a high enough force. And since the visible light is able to generate considerable stresses, the azopolymers of the second type accumulate significant plastic deformation with irradiation time, which usually exceeds minutes.
Theoretical concepts
Discovery of surface relief gratings3,4 in 1995 prompted the researchers to propose different microscopic mechanisms for explanation of this puzzling phenomenon. A comprehensive review about early theoretical approaches can be found in Chapter 5 “Photoinduced mass transport” of the book “Azo Polymers” by Wang.27 Some mechanisms – thermal gradients3 and pressure gradients54,55 – are not able to explain inscription of SRGs under irradiation with the polarization interference patterns. In particular, RL and SP patterns are characterized by constant light intensity over a period of the optical grating and would not give rise to any thermal or pressure gradients. No wonder that both mechanisms were critically assessed by the research community and discarded. The mechanism of electric field gradients – original formalism proposed in 1998 by the group of Tripathy47 and its modifications56–58 – has been quite popular due to the easiness with which it explains a strong polarization dependence of the grating growth. However, already in 2004, it was shown by one of the authors59 that this mechanism leads to negligible force densities. Quite recently, yet another modification of this mechanism60 has been applied to interpret the appearance of asymmetric profiles under the interference of two beams with orthogonal polarization.9 Taking this opportunity, we provide a fresh estimate of the density of electromagnetic force in the following section to show that such a smallish force cannot deform any sample. Popular mechanisms also include anisotropic diffusion of azobenzenes,61–63 LC interactions between trans-isomers of azobenzenes64 and light-induced orientation of azobenzenes.65 In spite of a large number of theoretical interpretations that have been proposed over the years, only a couple of them consider the features of underlying molecular architecture. Neither the reorientation of azo-chromophores nor the reorganisation of the polymer matrix is taken into account in most models.A Surface relief gratings
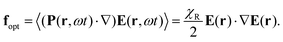 | (1) |
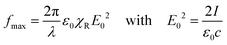 | (2) |
First, the incorporation of azo-chromophores into a polymer layer does not affect its susceptibility χR, which stays to be slightly larger than 1. Hence, eqn (1) can be applied to any polarizable medium or to any conventional polymer. However, interference patterns of laser light are only able to deform azopolymers and do not deform conventional polymers.
Second, the optical gradient force is negligible because the gradient of the light field takes place over a period of the optical grating, D = λ/(2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). With 2θ = 30°, which is a typical angle between interfering beams, D ≈ 2λ. Although Tripathy & co. did not provide any estimate, they were fully aware of a small magnitude of the optical force. Already in the very first paper,47 they refer to the experiment of Ashkin & co.:66 “such optical gradient forces, although weak, have been known to exert forces that trap and move latex microspheres in fluids.” We note that Ashkin & co. used not only a strongly focused Gaussian beam with the waist ω0 = λ/2 but also water as a carrier fluid.
θ). With 2θ = 30°, which is a typical angle between interfering beams, D ≈ 2λ. Although Tripathy & co. did not provide any estimate, they were fully aware of a small magnitude of the optical force. Already in the very first paper,47 they refer to the experiment of Ashkin & co.:66 “such optical gradient forces, although weak, have been known to exert forces that trap and move latex microspheres in fluids.” We note that Ashkin & co. used not only a strongly focused Gaussian beam with the waist ω0 = λ/2 but also water as a carrier fluid.
The only way to save the optical gradient theory was to propose an extreme light-induced plasticization of a polymer layer, which should decrease its viscosity to the value of water. This was done by presuming that the efficient trans–cis cycling is one of the critical factors that allow the motion of the polymer chains. The surface effect was named as another crucial factor. These two assumptions made the optical gradient theory solely applicable to azopolymer films. The consequences were quite dramatic. As we discuss in ref. 44, it was exactly the moment when the misleading concept of a liquidized azopolymer has been born.
Interestingly, three years later, Baldus and Zilke57 noticed that eqn (1) cannot be correct. According to the textbook of E. Schmutzer,67 the expression for electric force density should contain two terms:
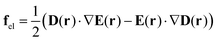 | (3) |
Yet, another modification of the optical gradient theory was proposed in 2006 by Kumar & co.,60 who included the magnetic effect and the absorption of the medium. The time-averaged electromagnetic force density is given by
| fem = −〈(∇·P)E〉 + 〈P × (∇ × E)〉 | (4) |
Finally, we would like to bring another argument against the optical gradient theory and its modifications. The experiments on light-induced reshaping of regular arrays show that individual azopolymer microposts68,69/micropillars14,70 uniaxially deform under homogeneous irradiation. The laser spot in these experiments is expanded in such a way to have constant intensity. The direction of light polarisation is also fixed. This can only mean that azopolymer samples deform even in the absence of any optical gradients.
 | ||
| Fig. 3 Photoinduced worm-like motion of the azo-molecule. After one photoisomerization cycle, it moves along its long axis by an average amount L. Reproduced from ref. 62 with permission from Elsevier, copyright 1998. | ||
The latter choice is justified by the authors “a priori by the fact that even high Tg polymers are soft with respect to movements induced by photo-induced isomerization”. The angular distribution of dyes is taken to be isotropic in ref. 62 due to weak laser intensities I ∼ 5 mW cm−2 and anisotropic in ref. 61, as predicted by angular hole burning, at intermediate I ∼ 50 mW cm−2. The angular distribution is time independent in both versions of the model: “when a molecule comes to a certain point, its orientation instantaneously relaxes to the average orientation distribution at this point”.61 The authors calculate one-directional migration of azo-molecules along the grating vector for two intensity interference patterns PP and SS. “As the dye molecules do not escape from the polymer film, and as only the upper surface of the polymer film is modulated”, an amplitude of the concentration grating δN is simply related to an amplitude δh of the SRG:
| δh/h = FδN/N | (5) |
As we can see from this short description, a crucial assumption of the model is that the mechanical switching between two isomerization states should push an azo-molecule to move along its long axis. Recent all-atomistic computer simulations do not confirm this modeling assumption. It is observed, how the azo-molecules “wobble” near their initial positions during photoisomerization cycles, being gradually reoriented under the action of linearly polarized light.72,73 No photoinduced translation diffusion has been observed. Besides, one does not find in ref. 61 and 62 any estimate of the force that could cause such large translation moves through a dense polymer matrix. It is difficult to imagine that azodyes can be catapulted over 100 nm even if they are placed into a liquid carrier. Finally, the model of anisotropic diffusion contains no information, how the spatial redistribution of azo-molecules can be translated to the polymer chains. The existence of a polymer matrix is accounted for solely through the introduction of phenomenological factor F in eqn (5): F ≈ 0.5 for the guest–host system with 50% of dye content and can achieve F ≈ 1 for side-chain azopolymers.61 In the absence of light intensity grating, the model would predict a zero amplitude of the concentration grating, and hence, no surface changes should appear under irradiation with polarization interference patterns.
The model of anisotropic diffusion has been reinvented by Bellini et al.63 in 2006 as a random-walk model of molecular motors. First, the authors consider the main characteristics of the motion. Importantly, they acknowledge that the polarization interference pattern RL inscribes a significant SRG and conclude: “matter is put in motion by the polarization gradient”. Probably, exactly this observation leads to a main assumption that azobenzene performs a one-dimensional random walk along the polarization direction. Note the difference in the assumed direction of the photoinduced diffusion compared to the original assumption made by Nunzi & co.61,62 Each isomerization event results in a motion of the azobenzene which drags the molecule to which it is grafted. Interestingly, in the case of side-chain azopolymers, the authors write that “the light-induced motion could be regarded as a consequence of the orientation of the polymers’ main chain”. Successful inscription of SRGs on azo-dendrimer films is considered as proof which overrules this assumption. As a consequence, the model fully ignores the anisotropic orientation of azobenzenes and hence a structural reorganization of the polymer matrix.
The study contains a number of valuable estimates that show (1) a negligible temperature increase of the exposed surface of the glassy azopolymer; (2) a considerable mass of the structural unit (equivalent to 60 carbon atoms in PMMA DR1) to be dragged by one azobenzene; (3) the random-walk step of 1–2 nm (“in polymers may seem quite large”). To account for the effects of a polarization interference pattern, the step is assumed to be modulated along the grating vector. It is a pity that no results are presented for this particular pattern, the effects of which are difficult to comprehend. In any case, the main assumption of the model contradicts the experimental results which proved the absence of anisotropic diffusion along the light polarization direction.74
The photoinduced molecular diffusion (PIMD) model of Juan et al.75,76 has the same central assumption as Nunzi & co.:61,62 after absorbing a photon, an azo-molecule moves along its long axis. In Monte Carlo simulations, the displacement in the direction of the molecular dipole is implemented. It is discussed that the equiprobable forward–backward displacement would not change the tendency of azobenzenes to accumulate in the lower intensity regions. The photoinduced reorientation of azobenzenes is reproduced by taking into account an angular dependence of the absorption probability. The authors claim that they have found excellent agreement with the experimental results for the Gaussian beam5 and the intensity interference patterns. A closer look reveals that the Monte Carlo simulations are done for dipole vectors distributed randomly on a 3D grid with a low occupation density. The photoinduced translation length of these dipoles is allowed to take very large values, up to 150 nm, which is defined by the grid discretization. Doing these giant jumps, the dipoles do not experience any resistance, because there is no polymer chains to which they are attached to. The MC simulations of azobenzenes are done effectively in a vacuum state. The authors conclude that the PIMD model “incorporates fundamental dipole interactions with an illumination field”,76 but do not provide any expression for these interactions which would allow estimation of the force magnitude. Besides, it is not clear how this model can explain the appearance of surface relief gratings under irradiation with the polarization interference patterns. The deformation of azopolymer microposts68,69 under homogeneous irradiation is obviously beyond comprehension for the PIMD model.
To explain light-driven spiral transport in azopolymer films, Ambrosio et al.77 in 2013 combined the concept of photoinduced anisotropic diffusion with the assumption that a free polymer surface favors the diffusion of azo-molecules. This was done to link a previously proposed phenomenological model21 with a specific microscopic mechanism. Similar to the PIMD model of Juan et al.,75,76 the angular dependent excitation probability is used to calculate the mass current density. To simplify the analysis, the orientation of azobenzenes is taken to be isotropic. The authors explain that accounting for the anisotropic orientation of azobenzenes in their microscopic model will lead to higher than quadratic order terms in the optical field. The height variations are directly related to the transverse derivatives of the mass current averaged over the film thickness. The final expression coincides with that of the phenomenological model,21 having the bulk contribution:
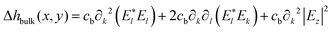 | (6) |
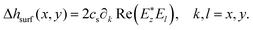 | (7) |
Ambrosio et al.77 applied their microscopic model to the intensity interference patterns PP and SS with the outcome that the amplitude of the PP grating should be exactly three times larger than the amplitude of the SS grating. The authors mention that this value does not agree with the results of most experiments. A similar discrepancy is found for irradiation with a single Gaussian beam. The authors ascribe these discrepancies mainly to neglecting light-induced orientation effects, which should stop absorption of azo-molecules and thus their movement. They speculate that this “orientational bleaching” is counteracted by mass transport. However, recent studies from Jelken et al.8,39,78 confirm that the growth of birefringence grating is saturated much earlier than the growth of surface grating, especially for PIPs such as RL and SP. This shows that the microscopic model of Ambrosio et al., similar to other models on anisotropic diffusion, lacks an essential ingredient. Namely, an explanation of how the movement of azo-molecules is coupled to the movement of polymer chains. Besides, the model experiences obvious problems in predicting the efficiency of polarization interference patterns. For example, it is predicted that the amplitude of RL grating should be the same as the amplitude of the SS grating. Similar to most models, the deformations under homogeneous irradiation, i.e. in the absence of optical gradients, cannot be explained.
A main assumption of the theory is that attractive interactions arise primarily between azo-chromophores oriented side by side, see Fig. 4. When the light polarization is along the y direction, the attractive forces are balanced everywhere due to translational symmetry along this direction. Consequently, only the x component of the electric field may contribute to the mass transport and thus the SS pattern cannot produce any grating. In the general case of elliptical polarization, the authors define effective order parameters using the linear interpolation between two limiting cases of linear and circular polarizations:
Seff = Scirce + |Slin|(1 − e)cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ, γ, | (8) |
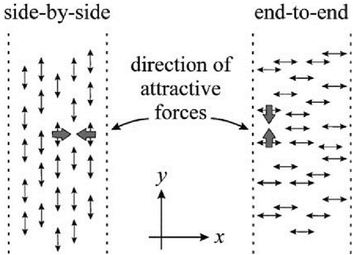 | ||
| Fig. 4 The azo-chromophores interact attractively when they are aligned by the polarized light side by side. Reproduced from ref. 64 with permission from the American Physical Society, copyright 1998. | ||
Starting from the isotropic state in the absence of irradiation, the authors show first that “there appears to be an anisotropy in the dipole moment distribution” in the molecular film that is irradiated with linearly polarized light. The interaction energy between average dipole moments at different positions is then evaluated for elastically deforming film. Under homogeneous irradiation with linearly polarized light, a free floating film is found to elongate/contract along the polarization direction when the parallel/anti-parallel alignment of neighbouring dipoles is energetically more favourable and the cis-/trans-dipole is larger than the trans-/cis-dipole. To explain deformations induced by circularly polarized light, the authors consider additionally the change in the energy of isotropic van der Waals interactions of an azo-chromophore with the surrounding molecules when it switches from the trans- to a cis-state. The van der Waals interactions together with the isotropic part of dipole–dipole interactions lead to a well creation in the irradiated molecular films with a positive expansion coefficient.
Some years later, reflecting on their own theory, Gadidei et al.84 wrote “that the absorption of linearly polarized light creates an orientational order in the film which in turn produces anisotropic deformation.” The circularly polarized light does not create an orientation order and the deformations seem to be induced only by an isotropic expansion/contraction of the molecular film. The weak point of the proposed theory was already recognized by its authors. The dipole–dipole interactions are exactly equal to zero for the molecules isotropically distributed in an infinite medium or in a spherical sample. This holds even for the dipoles perfectly aligned along the same direction. Therefore, the parameters of dipole–dipole interaction were considered in ref. 83 as phenomenological ones which should vanish with the distance from the boundaries of a finite sample. Deformation of azobenzene-containing colloidal spheres by the linearly polarized light85 speaks against the leading role of dipole–dipole interactions which vanish identically in this case. Besides, the orientational order appears after some irradiation time, whereas the surface deformations develop continuously under homogeneous irradiation.
B Macroscopic deformation of LC elastomers
To describe the influence of the dilution effect on the ordering and deformation of LC elastomers, the kinetic equation for the number density of trans-isomers nT under the light irradiation was proposed:86–88
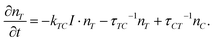 | (9) |
Here, the first term in the right-hand side describes the effect of trans–cis isomerization under irradiation with light of intensity I, kTC is the constant of photoisomerization; the second and the third terms take into account the thermal excitations from trans to cis and from cis to trans states, respectively, with characteristic times τTC and τCT. The total number n of azo-chromophores is constant and the number density nC of cis isomers obeys the condition: nT + nC = n = const.
Change in the population nT of rod-like trans isomers with time results in the shift of the critical temperature of isotropic-to-nematic phase transition T(c) of an LC elastomer,86–88 since T(c) is a function of nT. At the same time, the order parameter S and the elongation ratio λ of an LC elastomer can be found directly as functions of the ratio T/T(c) using the mean-field formulation and the theory of network elasticity:89S = S(T/T(c)) and λ = λ(T/T(c)). Thus, the solution of eqn (9) for the time-dependent number density nT(t) allowed the authors of studies86–88 to calculate the critical temperature, the order parameter and the elongation ratio as functions of time under light irradiation: T(c) = T(c)(t), S = S(t) and λ = λ(t). Theoretical predictions for the kinetics of light-induced deformation of LC elastomers are in good agreement with experimental data presented in ref. 86–88.
The kinetic eqn (9) assumes a constant value of the light intensity inside a sample. Later, the change in the intensity of light across a polymer film due to the absorbance of light was studied in a series of theoretical works by Warner & co.90–92 Variation of the light intensity across the polymer film results in the variation of the light-induced mechanical stress across the film leading to the bending deformation of the azo-containing LC polymer.
Although the theoretical formalism86–92 based on the dilution effect describes quite well the photo-ordering and deformation of LC azo-containing polymers in accordance with many experiments,93–97 it does not include the angular selectivity of trans–cis isomerization with respect to the polarization direction of the light. Eqn (9) does not take into account the angular dependence of the photoisomerization kinetics. Thus, this formalism is not applicable to describe the anisotropy of photo-ordering and deformation with respect to the polarization vector of the light as well as it cannot explain the possibility of controlling the direction of photo-deformation by variation of the polarization vector of the light, as demonstrated in many experiments.28,29,98–101 Moreover, the dilution effect is specific for LC polymers. Thus, the formalism proposed in ref. 86–92 is not applicable to photo-ordering and deformation for broad classes of azopolymers which do not demonstrate LC ordering and are initially isotropic.3,4,23,24,102 Below in the section “Kinetic equations of photoisomerization” we present a more universal picture which includes both the dilution effect and the angular selectivity of trans–cis isomerization.
| UE = qϕ, | (10) |
It is not easy to follow the authors as they use unconventional terminology. While ŷt0 seems to describe a fraction of trans-isomers, which property is defined by the vector yt is more difficult to guess. Fig. 4 from ref. 103 shows spatial oscillations of the electric field component Ex and of the component yt1 for the linearly polarized light propagating through the material. Since Ex oscillates with time, yt1 should also oscillate with time, presumably describing the induced dipole moment. As we showed in the section “Optical gradient theories”, the interaction of the oscillating electric field with the induced dipole moments leads to negligible forces. Neither azobenzene-containing elastomers, no glassy azopolymers could be deformed by such low forces.
Some modeling results based on the Bin and Oates model103 have been published in 2022 by Mehnert et al.104 This recent publication sheds more light on the basic assumptions. The main change compared to the original model103 is that “the behavior of the incident light is described by a time averaged electric field E” which interacts with the homogenized (volume averaged) dipole moments yt and yc associated with the trans- and cis-states. Although this would explain the presence of an electrostatic potential in the light-matter Lagrangian, see eqn (10), it is difficult to comprehend, why both ingredients E and yt,c are not equal to zero. The energetic costs to build spatial charges are extremely high, so even in ferroelectric nematic liquid crystals, the dipole moments are organized in such a manner to avoid their buildup.105 The dipole moment of an azobenzene moiety, both in trans and cis-states, is below a critical value of about 10D,106 when the ferroelectric crystal can be built. In other words, there is no average dipole moment in azo-compounds. The modeling in ref. 104 seems to be done for a hypothetical ferroelectric material in the presence of static electric field. This is of course far away from the material properties of real azopolymers and the physical properties of light.
Early orientation approaches
It is interesting to reflect backward that although the formation of surface relief gratings was found as an accompanying, even undesirable, phenomenon during the inscription of birefringence (holographic) gratings, nobody first came to the idea that exactly this light-induced reorientation of chromophores can be a main reason of observed photodeformations. This is especially astonishing, as the interference pattern of light dictates a unique spatially varying orientational state, an account of which would easily explain a strong polarization dependence of SRG inscription. As can be seen from the discussion of the mean-field model, Pederson et al.64 were very close to this idea. However, instead of following it directly, they proposed to correlate the orientational state of azobenzenes with the strength of attractive interactions between them. As a result, the application range of the mean-field theory became reduced to LC azopolymers and researchers working with glassy azopolymers continued a search for a better explanation.1 Side-chain orientation model of Bublitz et al
As it happens, a real birth of the orientation approach can be assigned to the year 2001, when a group of German scientists Bublitz, Fleck and Wenke proposed to consider “the alignment of the side chains with respect to the electric field vector…as the basic process forming surface reliefs”.65 Similar to Pedersen et al.,64 the general case of elliptically polarized light has been investigated. But instead of reducing the biaxial orientation state to a scalar order parameter, the numbers of side-chains along three principal axes – propagation direction and main axes of the polarization ellipse – are calculated. Normalized numbers of side-chains Ni (i = x, y, z) seem to have the same meaning as the diagonal components 〈ui2〉 of the orientation tensor, see the section “Time-dependent orientation and stress tensors”. The set of coupled kinetic equations is solved to describe the time evolution of Ni(t) at different intensities Ix and Iy, characterizing the elliptically polarized light.As “the detailed microscopic process leading to the deformation of the polymer sample is unknown”, the authors base their explanation on two assumptions: (1) the azopolymer sample is incompressible; (2) the length of the film in the grating direction x is a sole function of Nx:
| Lx = exp{−β[Nx(0) − Nx(t)]} | (11) |
![[L with combining macron]](https://www.rsc.org/images/entities/i_char_004c_0304.gif) x = LxLνy, x = LxLνy, | (12) |
Probably, this questionable transformation leads to an incorrect prediction for the phase of the SS grating in the model of Bublitz et al.:65 the peaks of the SS grating appear at the positions of the intensity maxima, see the 1st polarization state in Fig. 5. Recent results of finite element modeling107 confirm that it is not possible to inscribe the SS grating on initially isotropic azopolymer films. Actually, this also follows from the main assumptions made by Bublitz et al.65 For unconstrained films, the lengths in two other directions y and z should be given by the expressions similar to those for Lx. If the light is linearly polarized along the y-axis, the number of side-chains in x and z directions is the same, Nx(t) = Nz(t), and the unconstrained sample should uniaxially contract along x and z. Under irradiation with the SS pattern, the elongation along the y-axis is not possible due to the translational symmetry. Hence, uniaxial contraction along x and z axes will lead to a decrease in volume, which is not allowed due to the incompressibility assumption. In overall, no deformation should take place under irradiation of initially isotropic film with the SS pattern. Experimental results show that the peaks of SS gratings appear at the intensity minima.81 This hints at initial anisotropy in the azopolymer film, as we will discuss in detail later, see the section “Application of the orientation potential to SRGs”.
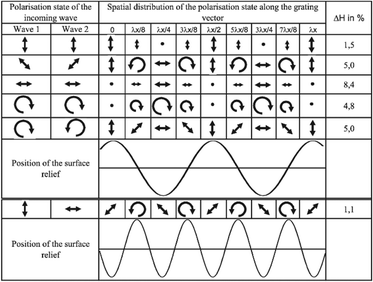 | ||
| Fig. 5 Calculated efficiency and phase of surface relief gratings produced by three intensity and three polarization interference patterns. Reproduced from ref. 65 with permission from SNCSC, copyright 2001. | ||
Otherwise, the authors correctly predict that the valleys of PP and RL gratings should appear at the positions with horizontal polarization, see the 3rd and 5th polarization states in Fig. 5. Also, the doubling of the grating period for the SP pattern (6th polarization state in Fig. 5) and the appearance of double lap structures under linearly polarized Gaussian beam are reproduced. Even, an additional peak in the center of high intensity Gaussian beam has been predicted in agreement with the experiments of Tripathy & co.56 As we can see, the model of Bublitz et al.65 has a high predictive strength. The main weakness of this model is that similar to so many other theories, the structural changes in a polymer matrix are fully ignored. Though it is recognized that the effect of side-chain reorientation strongly correlates with the deformation of the azopolymer sample, there is no yet an idea, of how to link the orientation anisotropy to the light-induced mechanical stresses.
2 Thermodynamic theory of Saphiannikova and Neher
The studies by Pedersen et al.64 and Bublitz et al.65 prompted Potsdam researchers108,109 to look for a missing link between the azobenzene reorientation and the sample deformation. It has been noticed that the orientational entropy strongly decreases upon the reorientation of azobenzenes. Assuming that “anisotropic interactions between azobenzene moieties can be neglected in the case of amorphous polymers”, as well as the change of the main chain entropy under irradiation, the free energy per one azobenzene contains only the entropy term Fazo = −TSazo, where T is the absolute temperature. The authors first consider initially isotropic unconstrained sample irradiated with linearly polarized light. Under the assumption of affine deformation and sample incompressibility, the stretching along the polarization direction reorients the chromophores parallel to this direction. This would compensate for the entropy decrease produced by the photoinduced reorientation of azobenzenes and thus minimize the free energy.Then, the authors consider the main interference patterns PP, SS and RL, which are characterized by a linear polarization at any spatial position. Similar to Pederson et al.,64 the translational symmetry along the y direction is taken into account by assuming that “elongation (contraction) along the grating vector has to be accompanied by contraction (elongation) in the direction perpendicular to the sample surface”. In agreement with experimental findings, the authors predict that polymer chains should move into the non-illuminated regions for the intensity interference patterns SS and PP. For the RL pattern, the same direction of the chain transport as for the PP pattern (from the regions with horizontal polarization) is predicted. The SS grating is noticeably smaller than PP and RL gratings, the latter having an intermediate efficiency. The authors find that it is not surprising as the electric field in the RL pattern is a linear superposition of the electric fields in the PP and SS patterns.
Additionally, thermodynamic theory allows the calculation of the orientation distribution of chromophores at any grating position, for example at peaks and valleys. The latter predictions have been compared with the Raman spectrometry results of Lagugne-Labarthet et al.110–112 Importantly, the authors seem to be the first, who provide an estimate for the light-induced stress imposed by the reorientation of chromophores. It is done by taking the derivative of the free energy per one azobenzene over strain ε:
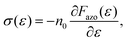 | (13) |
As follows from its name, the thermodynamic theory does not take into account time-dependent effects. Only a spatial variation in the orientation distribution is prescribed by the interference pattern. However, there is no information, how does the strength of the alignment depends on the intensity of the laser. Besides, the theory does not consider the molecular architecture of azopolymers and thus cannot explain, why some of them deform and others contract under irradiation with the linearly polarized light.
Modern orientation approach based on the orientation potential
1 Introduction of the light-induced orientation potential
A universal physically based concept, which turned out to describe reasonably photo-ordering and deformation in broad classes of azopolymers, was developed originally in a phenomenological way using the well-known experimental fact116,117 that azo-chromophores are reoriented perpendicularly to the polarization direction E of the light under irradiation. The key idea is to describe the appearing orientation anisotropy by introducing an effective orientation potential ueff, which acts on the azo-chromophores. Due to an obvious symmetry regarding the transformation E → −E, the following form of the orientation potential was proposed independently by two groups:118,119ueff(θ) = V0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (14) |
| V0 = C·I. | (15) |
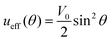 | (16) |
ueff(θ) = V0(wx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θx + wy θx + wy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θy) θy) | (17) |
2 Microscopic theory of Toshchevikov et al. application of the orientation potential to amorphous glassy azopolymers
Although the idea of replacing a complicated angular-dependent cyclic trans–cis–trans photoisomerization process with an action of some orientation potential is not trivial, this concept has been very fruitful in understanding many features of photo-ordering and deformation in broad classes of azopolymers. First of all, the introduction of the orientation potential allows the calculation of the light-induced mechanical stress appearing in amorphous glassy azopolymers under irradiation with linearly polarized light.52 The idea is based on the fact that mechanical stress is caused by the appearance of orientation anisotropy in a polymer system.125 The reorientation of azo-chromophores under the action of the orientation potential results in a rearrangement of the polymer backbones coupled to them, which leads to mechanical stress. The elementary orienting units, whose reorientation leads to the anisotropy in the material, are defined by the molecular weight of the polymer. For short macromolecules (oligomers), whose length is comparable with the Kuhn segment or shorter, the orienting units are the stiff oligomers themselves. For long azobenzene macromolecules the orienting units can be ascribed to freely-jointed Kuhn segments, which form polymer chains.According to the stress-optical law,125 the mechanical stress is proportional to the birefringence. The birefringence is proportional to the order parameter, S = 〈P2(cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)〉, where θ is the angle between the long axis of the orienting unit and the axis of anisotropy, which coincides with the polarization vector E of the light. On the other hand, at small deformations, the stress is proportional to the strain ε. Therefore, Toshchevikov et al.52 assumed that the strain is proportional to the order parameter: ε = εmaxS, where the maximum strain εmax corresponds to the fully oriented sample with S = 1. Since in such an approach, the strain is linked to the order parameter, the derivation of the free energy as a function of the strain, F = F(ε), is very similar to the formalism presented in the textbook by de Gennes and Prost126 for finding the free energy as a function of the order parameter, F = F(S), for nematic LCs. The free energy of a deformed sample under light irradiation includes three contributions: (i) total energy of chromophores under light-induced potential according to eqn (14), (ii) orientation entropy of the orienting units, and (iii) elastic energy, ∼Eε2/2, where E is the elastic Young's modulus. Since the rearrangement of the backbones of macromolecules is defined by the orientation potential (14) acting on all chromophores attached to them, the light-induced mechanical stress depends on the orientation distribution of chromophores around the backbones.
θ)〉, where θ is the angle between the long axis of the orienting unit and the axis of anisotropy, which coincides with the polarization vector E of the light. On the other hand, at small deformations, the stress is proportional to the strain ε. Therefore, Toshchevikov et al.52 assumed that the strain is proportional to the order parameter: ε = εmaxS, where the maximum strain εmax corresponds to the fully oriented sample with S = 1. Since in such an approach, the strain is linked to the order parameter, the derivation of the free energy as a function of the strain, F = F(ε), is very similar to the formalism presented in the textbook by de Gennes and Prost126 for finding the free energy as a function of the order parameter, F = F(S), for nematic LCs. The free energy of a deformed sample under light irradiation includes three contributions: (i) total energy of chromophores under light-induced potential according to eqn (14), (ii) orientation entropy of the orienting units, and (iii) elastic energy, ∼Eε2/2, where E is the elastic Young's modulus. Since the rearrangement of the backbones of macromolecules is defined by the orientation potential (14) acting on all chromophores attached to them, the light-induced mechanical stress depends on the orientation distribution of chromophores around the backbones.
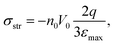 | (18) |
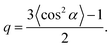 | (19) |
First of all, eqn (18) allows the estimation of the typical magnitude of the light-induced stress due to the orientation mechanism described by the proposed approach. For the laser intensity I ∼ 100 mW cm−2 and for the number density of azobenzenes n0 ≅ 1.5 × 1021 cm−3, the typical magnitude σ ∼ n0V0 ∼ 100 MPa was obtained. It is higher than the yield stress τyield ∼ 20–30 MPa estimated from tensile measurements of glassy azopolymers.115 At stresses higher than the yield stress, an azobenzene polymer should deform irreversibly and the deformation will be fixed after switching the light off. Thus, the orientation approach explains the possibility of light-induced macroscopic deformation of glassy azopolymers.
Furthermore, according to eqn (19), the sign of the light-induced stress (i.e. expansion or contraction with respect to the light polarization E) is sensitive to the orientation distribution of chromophores around the backbones of macromolecules. The shape factor q in eqn (19) can be positive or negative if the chromophores are oriented preferably along or perpendicular to the backbones of macromolecules. The dependence of the deformation direction with respect to the polarization vector E on the chemical structure was observed in experiments.26,127
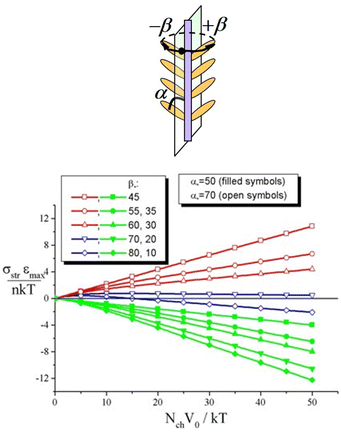 | ||
| Fig. 6 (top) Fragment of an azo-molecule with planar symmetry of azimuthal distribution of chromophores around the main chain. (bottom) Striction stress σstr as a function of the strength of the potential V0 at varying values of the angle β*. Filled and open symbols correspond to α* = 50° and α* = 70°. Adapted from ref. 52 with permission from American Chemical Society, copyright 2009. | ||
Fig. 6 (bottom) shows the dependences of the striction stress on the strength of the potential V0 for azopolymers, in which the chromophores are attached to the backbones at fixed angles α = α* and β = β*; the values α* and β* are varied in Fig. 6. One can see that at some sets of the angles the dependences σstr(V0) demonstrate non-monotonic behavior and can change the sign with increasing V0 and hence with increasing intensity of the light. Note that such non-monotonic photo-elastic behavior of azobenzene polymers has been observed in experiments. For instance, one can see in Fig. 5 and 6 of ref. 128 a non-monotonic behavior of the inscription rate with increasing light intensity: the inscription rate increases at I < 10 mW cm−2, whereas it starts to decrease at 20 mW cm−2 < I < 100 mW cm−2.
The ability of the proposed orientation approach to explain experimental results obtained by different experimental groups demonstrates the universality of this approach and opens the possibility to apply the introduced orientation potential to study photo-ordering and deformation in broad classes of azopolymers.
3 Time-dependent orientation and stress tensors
In a glassy state, a very strong coupling between the azo-chromophores and polymer backbones forces the latter to reorient with respect to the light polarization, which is accompanied by the appearance of light-induced stress.52 Assuming that m azobenzenes are rigidly attached to each of the backbone segments, the orientation potential ueff(14) can be recalculated to the orientation potential, which acts on the backbone segments under irradiation with linearly polarized light:| Ueff = qmV0(Ê·u)2. | (20) |
The orientation potential Ueff has been used by Saphiannikova & co.122 to calculate the time evolution of the 2nd order orientation tensor 〈uu〉 of rigid segments under irradiation:
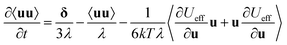 | (21) |
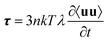 | (22) |
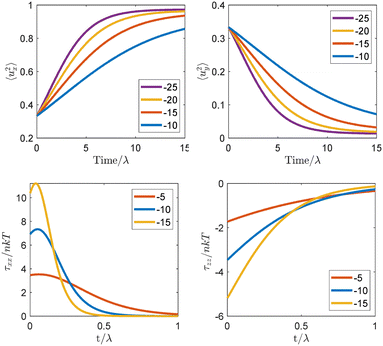 | ||
| Fig. 7 (top) Time evolution of the diagonal components 〈ux2〉 and 〈uy2〉 = 〈uz2〉 of the orientation tensor under the light linearly polarized along axis x. (bottom) Time evolution of the tensile τxx and compressive τzz components of the light-induced stress tensor for linearly and circularly polarized light, respectively. The data are shown for different strengths of the reduced potential −5 ≤ Vr ≤ −25. Reproduced from ref. 129. | ||
Assuming that the glassy azopolymers remain in the solid state upon moderate irradiation,44,53 the description of light-induced deformations is based on elastic, viscoplastic Perzyna model.130 In particular, this model relates the rate of equivalent plastic strain
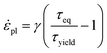 | (23) |
4 Application of the orientation potential to SRGs
As was discussed in the previous section, the relationship between the molecular structure and plastic deformations of azopolymers can be established by applying parameters such as q, n, λ, γ and τyield in the equations for the effective potential (20) and the Persyna model (23). In particular, photoinduced deformations in the side-chain azopolymers were investigated by Saphiannikova & co. during homogeneous irradiation with linearly and circularly polarized light122 and under inhomogeneous irradiation with intensity and polarization interference patterns.82,131 The orientation potential Ueff with q ≈ −0.5 was applied to explain these mechanical deformations, taking into account that azo-chromophores are attached more or less perpendicular to the backbone segments in side-chain azopolymers.85 By implementing the light-induced stress (22) in a viscoplastic material model of the finite element software ANSYS, it is shown that a square azopolymer post elongates along the electric field vector for the linearly polarized light and contracts along the propagation direction for the circularly polarized light.122 This is in agreement with the experiments of Lee & co.68 and Descrovi & co.70At the next stage of research,82 the deformations in the elongated pre-oriented colloids were modelled under intensity interference patterns. It is found that the formation of beads and wave-like structures is consistent with the experiment carried out in the group of Santer & co.82 First, colloids were elongated by homogeneous irradiation with the linearly polarized light, resulting in a strong alignment of the polymer chains along the light polarization. Then, PP and SS interference patterns with sinusoidally varying intensity were applied:
I(x) = 2I0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2(πx/D), cos2(πx/D), | (24) |
The orientation approach also reproduces the peculiar structures at the edges of a thin azopolymer film under polarization interference patterns,82 see Fig. 8. The azopolymer film is scratched and irradiated with RL and LR polarization interference patterns. The gap edges are modelled as an isotropic cuboid “glued” to the substrate surface. The stress tensor of the LR and RL interference patterns is diagonal and symmetric around the light polarization direction. To implement the rotation of light polarization, the coordinate system of each element is rotated with respect to the global coordinate system about the axis perpendicular to the glued surface. During modeling, the azopolymer protrudes into the gap at the positions where the light polarization vectors converge. Moreover, SRG appearance is mirrored when the interference pattern is changed from RL to LR, which is completely consistent with the experiment. Hence, the orientation approach correctly predicts local variations of the light-induced stress in each illumination pattern for both initially isotropic and highly oriented materials.
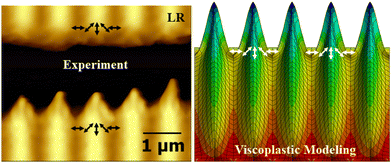 | ||
| Fig. 8 A striking resemblance of the AFM micrograph (left) and viscoplastic modeling (right) of azopolymer film irradiated with the polarization interference pattern: the light has constant intensity but its polarization rotates along the grating vector, as presented by black/white arrows. Reproduced from ref. 82 with permission from John Wiley & Sons, copyright 2022. | ||
Although the phenomenon of SRG inscription was discovered almost 30 years ago,3,4 there are still some puzzles regarding the formation of SRGs in the azopolymers depending on the type of interference patterns. Most recently, the two intriguing issues were solved, which concern the inscription of SRGs onto azopolymer thin films under irradiation with SS, PP and RL interference patterns.107 First, the initial orientation state of polymer backbones is proved to be responsible for the contradictory experimental reports about the efficiency of the SS interference pattern. According to some reports,132–135 this pattern does not inscribe a grating, whereas modest efficiency was observed in other studies.81,136,137 Different orientation states can have an influence on the phase of SS grating (Fig. 9) and its height, which is confirmed experimentally in the group of Santer & co. using special pre-treatments.107 Three types of the polymer backbone orientation were considered: isotropic, in-plane and out-of-plane, see Fig. 9 (left). In the case of in-plane orientation, the polymer main chains lie in the plane of the substrate, whereas out-of-plane orientation means that polymer backbones tend to be perpendicular to the substrate. The isotropic initial orientation, without any pre-orientation of the azopolymer, results in zero SS gratings. Two other cases can be responsible for the SS gratings inscription but with an exchange in their phase, see Fig. 9 (right).
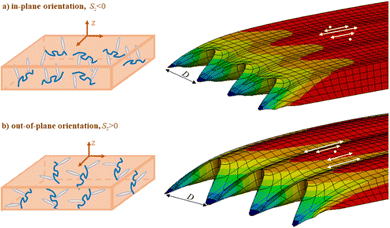 | ||
| Fig. 9 (left) Two cases of initial polymer backbone orientations: (a) in-plane orientation; (b) out-of-plane orientation. (right) Modeled SS gratings inscribed after 25 s on scratched azopolymer films for case (a) and case (b). Note different positions of the hills and protrusions in respect to the maximal intensity of light. Adapted from ref. 107. | ||
Second, a faster growth of gratings inscribed by the RL interference pattern is shown to be promoted by a weak photo-softening effect, considering that the moderate light intensity of up to 200 mW cm−2 can decrease the viscosity of glassy polymers up to one order of magnitude.44,138 For the intensity interference patterns, the parameter γ, which regulates the viscosity of the plastic flow in the Persyna model (23), was defined as
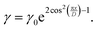 | (25) |
5 Application of the orientation potential to azonetworks
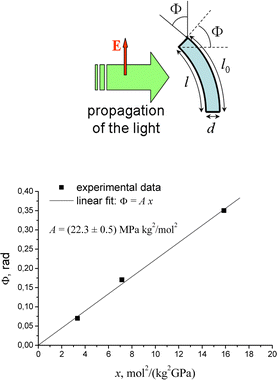
The orientation potential (14) was used in ref. 139 and 140 to study the light-induced deformation in cross-linked azo-containing polymer networks. The analysis is based on the minimization of the free energy as a function of the elongation ratio, which includes the contribution to the free energy from the entropic elasticity of network strands and from the light-induced potential acting on all chromophores in the network strands. It was shown that the direction of the light-induced deformation is very sensitive to the orientation distribution of chromophores in the side chains of network strands. Moreover, the light-induced deformation of azonetworks depends on the degree of cross-linking and on the concentration of azo-chromophores.139,140 If the crosslinks are optically neutral (i.e. they do not contain the azo-chromophores), the increase in the degree of crosslinking leads to the decrease in light-induced deformation due to the increase in Young's modulus.An interesting situation arises when the crosslinks contain azo-chromophores. As was shown experimentally for azobenzene-containing polyimide networks,23 the bending angle of light-induced deformation in this case increases with the degree of crosslinking due to the increase in the number density of optically active azo-chromophores, although Young's modulus also increases. The experimental data of ref. 23 was compared with the prediction of the orientation approach.140 According to the orientation approach, the bending angle Φ should be a linear function of a parameter x, representing a combination of structural characteristics of the material:
| Φ = A·x, where x = l0/M2Ed. | (26) |
Fig. 10 shows the experimental data presented by points replotted in the coordinates Φ = Φ(x) according to calculations in ref. 140. One can see that experimental data confirm the theoretically predicted linear dependence given by eqn (26). This result demonstrates a good predictive power of the developed orientation approach. The proportionality constant A contains the optical parameter C of the theory, which determines the strength of the orientation potential (15). The estimated value C ≅ 2.7 × 10−19 J cm2 W−1 agrees well with estimates given in other works C ∼ 10−19–10−18 J cm2 W−1.52,120,121 This shows a self-consistency of the orientation approach when applied to various azobenzene-containing polymers.
 | ||
| Fig. 10 (top) Schematic representation of the bending deformation of illuminated polymer films. (bottom) Dependence of the bending angle on the parameter x = l0/M2Ed as calculated using the data of ref. 23. Reproduced from ref. 140 with permission from AIP Publishing, copyright 2012. | ||
6 Application of the orientation potential to azo-containing LC elastomers
Next generalization of the orientation approach was the application of orientation potential (14) to study the photo-ordering and deformation in the azobenzene-containing LC polymer networks.44,141–144 The method is based on the minimization of the free energy as a function of the components of the ordering matrix. It was shown that liquid-crystalline interactions between rod-like chromophores in LC azopolymers result in the biaxial order and biaxial deformation of azobenzene containing polymers. One axis of anisotropy coincides with the polarization vector of the light E. The second axis of the biaxial ordering is related to the direction of additional alignment of azo-chromophores in the plane perpendicular to the vector E due to orientation interactions between rod-like trans-isomers of the chromophores.The biaxial state is characterized by two scalar order parameters.141–143 One of them, S = [3〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θx〉 − 1]/2, determines a usual uniaxial order of the chromophores with respect to the vector E (in present notations E is directed along the x-axis). Additional alignment in the yz-plane is described by the biaxial order parameter, μ = 〈cos2
θx〉 − 1]/2, determines a usual uniaxial order of the chromophores with respect to the vector E (in present notations E is directed along the x-axis). Additional alignment in the yz-plane is described by the biaxial order parameter, μ = 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θy〉 − 〈cos2
θy〉 − 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θz〉. Here, θξ denotes the angle between the long axis of the chromophore and the ξ-axis (ξ = x, y, z). For the uniaxial state around the vector E, one has 〈cos2
θz〉. Here, θξ denotes the angle between the long axis of the chromophore and the ξ-axis (ξ = x, y, z). For the uniaxial state around the vector E, one has 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θy〉 = 〈cos2
θy〉 = 〈cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θz〉 and μ = 0, whereas μ ≠ 0 for the biaxial state.
θz〉 and μ = 0, whereas μ ≠ 0 for the biaxial state.
In the framework of the mean-field approach, the energy of orientation LC interactions, ULC, is known to be a quadratic function of the order parameter.126 The energy ULC for the biaxial state is a function of the two scalar order parameters:141–143
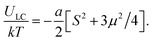 | (27) |
The equilibrium values of the order parameters S and μ for azo-chromophores under irradiation with linearly polarized light are defined by the minimum of the free energy, which includes (i) the contribution of the light-induced potential (14), (ii) energy of the orientation LC interactions (27), and (iii) contribution of orientation entropy. The interplay between these three contributions leads to a rich variety of photo-induced alignment.
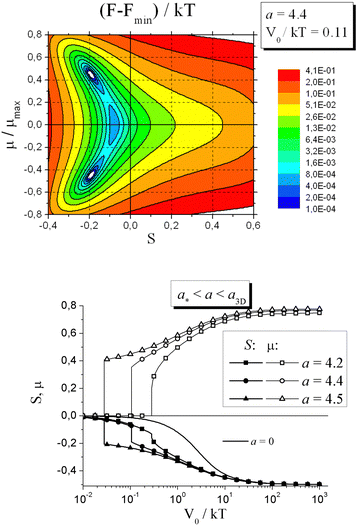 | ||
| Fig. 11 (top) Map of the free energy per one azobenzene in the logarithmic scale as a function of the order parameters S and μ at a = 4.4 and V0/kT = 0.11. (bottom) Equilibrium values of the order parameters S and μ, as functions of V0/kT at a* < a < a3D. Adapted from ref. 142 with permission from American Chemical Society, copyright 2014. | ||
At weaker strength of LC interactions, a2D < a < a*, application of light leads to the photo-induced phase transition of the 2nd order. Here, the critical value a2D = 8/3 corresponds to the isotropic-to-anisotropic phase transitions of the rod-like moieties in a 2D-space. At a2D < a < a*, the minimum of the free energy corresponding to the uniaxial state splits into two minima with nonzero values of μ at the phase transition. Again the phase transition from a uniaxial to biaxial state takes place in this case, but the order parameters change continuously, meaning that the photo-induced phase transition is of the 2nd order.
At the very weak strength of LC interactions, a < a2D, the orientation interactions are not able to form an additional order in the plane perpendicular to the polarization vector E. In this case, only uniaxial ordering is possible with S < 0 and light-induced ordering is similar to non-liquid-crystalline azonetworks, as discussed above in the Section 5.
The change in the order parameters S and μ is accompanied by the deformation of LC azonetworks. The direction of light-induced deformation (expansion or contraction with respect to the polarization vector E) depends on the orientation of azo-chromophores with respect to the main chains.44,141–144 The deformation as a function of the strength of orientation potential V0, which is proportional to the light intensity, demonstrates the same behavior as the order parameters: uniaxial deformation and phase transitions of the 1st or 2nd order from a uniaxial to biaxial deformation, depending on the strength of orientation interactions, a. Significant light-induced deformation is observed for LC azonetworks with strong orientation interaction since the change of order parameters is more pronounced in this case. The last result was confirmed in ref. 145 where the orientation potential was applied to two-component LC polymer networks containing the azo-chromophores and LC mesogens. As was shown, the presence of LC mesogenic groups reinforces the strength of LC interactions, leading to a higher degree of light-induced ordering and deformation.
We conclude this section by noting that the light-induced biaxial ordering discussed above was widely observed in experiments.117,146–149 The appearance of the light-induced biaxial ordering as well as the possibility of either expansion or contraction of azopolymers of different structures with respect to the polarization vector E were confirmed also by computer simulations.119,150,151 Development of two-component LC networks containing azo-chromophores and LC mesogens is widely used by experimentalists to enhance the photo-mechanical response as discussed in introduction. The agreement of the theoretical results obtained in the framework of the orientation potential (14) with both experimental data and computer simulations for broad classes of azobenzene-containing polymers demonstrates the great strength of the proposed orientation approach to study the photo-mechanical properties of these materials.
The only drawback of the proposed orientation approach based on orientation potential is that it does not include the effects of the bent cis-isomers. The possible solution to this problem is to introduce into the theory a parameter associated with a relative number of cis-isomers, as realized in ref. 145. More rigorous analysis of the effect of cis-isomers is based on the further generalization of the orientation approach by means of explicit consideration of kinetic equations of angular-dependent photoisomerization, as discussed in the next sections.
Generalization of the orientation approach: angular-dependent kinetics of photoisomerization
1 Kinetic equations of photoisomerization. Justification of the orientation potential
The further generalization of the orientation approach was made by Toshchevikov et al. by considering explicitly the kinetic equations of angular-dependent photoisomerization processes of azo-chromophores.53,144,152 It was demonstrated that the time evolution of the orientation distribution function of azo-chromophores n(θ, t) during the angular-dependent photoisomerization processes is the same as under the action of the orientation potential in the form of eqn (14), where the strength of the potential V0 is adjusted to the opto-mechanical parameters of azopolymers, as discussed below. This means that any physical quantities defined by the orientation distribution function n(θ, t), such as the order parameter or mechanical stress, are the same in the framework of the two formalisms based on the orientation potential (14) and on the kinetic equations of angular-dependent photoisomerization. This result justifies the heuristically introduced orientation potential (14) showing that the reorientation of azo-chromophores during the cyclic trans–cis–trans photoisomerization process can be equivalently described by the application of this orientation potential.The strength of the orientation potential, which equivalently describes reorientation of azobenzene chromorphores under trans–cis–trans photoisomerization process, is related to the opto-mechanical parameters of azopolymers. At the moment, the light is turned on, the strength of the potential V0 has the following form:53,144,152
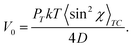 | (28) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ〉. Thus, the developed theory53,144,152 based on the kinetic equation of photoisomerization allows to relate the mechanical stress and order parameters, which are functions of V0 (see, e.g.Fig. 10 and 11), with opto-mechanical parameters of azopolymers.
χ〉. Thus, the developed theory53,144,152 based on the kinetic equation of photoisomerization allows to relate the mechanical stress and order parameters, which are functions of V0 (see, e.g.Fig. 10 and 11), with opto-mechanical parameters of azopolymers.
2 Application of the kinetic theory of photoisomerization to amorphous glassy azopolymers
It is worth to present characteristic magnitudes of the effective potential for glassy azobenzene materials, which is predicted by eqn (28) derived from the kinetic theory.53,144,152 Using geometrical characteristics of chromophores L ≈ 0.9 nm, as well as the typical values η ≈ 103 GPa s and kTC ≈ 0.4 cm2 J−1 for azo-materials near glass-transition temperature Tg,153,154 the characteristic magnitude of the effective potential at the light intensity I = 0.1 W cm−2 and at 〈sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ〉 = 1 was estimated in ref. 53, 144 and 152 as V0 ≈ 7 × 10−18 J. This value is above the strength of the carbon covalent bond UC–C ≈ 5 × 10−19 J. This theoretical prediction explains the experimental result, why the light can produce in azopolymers the mechanical force which is large enough to deform50,51,155 and even to rupture156 covalent bonds.
χ〉 = 1 was estimated in ref. 53, 144 and 152 as V0 ≈ 7 × 10−18 J. This value is above the strength of the carbon covalent bond UC–C ≈ 5 × 10−19 J. This theoretical prediction explains the experimental result, why the light can produce in azopolymers the mechanical force which is large enough to deform50,51,155 and even to rupture156 covalent bonds.
Moreover, typical values of the light-induced mechanical stress σ ∼ n0V0, according to eqn (18), can reach 4 GPa.53,144,152 It has the same order of magnitude as σ ≈ 2 GPa, as found in the experimental work,50 where it was shown that the light-induced stress in azopolymers is able to rupture the metallic layers. Thus, the kinetic theory explains the giant values of light-induced stress observed in experiments.
Another advantage of the developed kinetic theory of photoisomerization is its ability to predict the number fraction of cis-isomers of azo-chromophores. As an example, Fig. 12 shows the time dependences of the number fraction of cis-isomers at different ratios between probabilities of trans–cis, PT, and cis–trans, PC, photoisomerization processes. The factor PT/PC is defined by the wavelength of the light: PT/PC < 1 and PT/PC > 1 correspond to the regions of visible and ultraviolet light irradiation, respectively. One can see in Fig. 12 that under ultraviolet light irradiation the number fraction of the cis-isomers can reach significant values (50%), whereas under visible light irradiation, the number of cis-isomers is sufficiently low. In both cases, the angular-dependent photoisomerization results in the significant ordering and deformation of azopolymers. Theoretical predictions were compared with the results of computer simulations157 using the same parameters and scales. Fig. 12 shows excellent agreement between the results of theory and computer simulations. Thus, good agreement of the results of the proposed kinetic theory with both computer simulations and experimental data, as discussed above, demonstrates the great power of this approach to study photo-ordering and deformation in azopolymers.
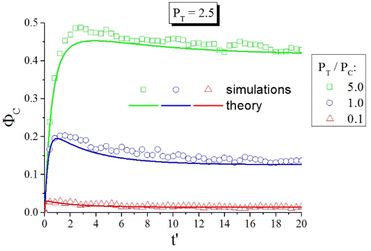 | ||
Fig. 12 The number fraction of cis-isomers ΦC as a function of time at different ratios between probabilities of trans–cis, PT, and cis–trans, PC, photoisomerization. Stochastic jumps from trans- to cis-state and back are taken to be the same: 〈sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ〉TC = 〈sin2 χ〉TC = 〈sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) χ〉CT = 0.16. The time t′ is given in units of the computer simulations157 χ〉CT = 0.16. The time t′ is given in units of the computer simulations157 . Reproduced from ref. 53 with permission from American Chemical Society, copyright 2017. . Reproduced from ref. 53 with permission from American Chemical Society, copyright 2017. | ||
3 Application of the kinetic equations of photoisomerization to azonetworks and azo-containing LC elastomers
Further development of the formalism based on the kinetic equations of photoisomerization was its application to study photo-ordering and deformation in cross-linked isotropic polymer azonetworks and for ordered azo-containing LC elastomers.53,144,152 The proposed formalism relates the time evolution of ordering and deformation of azopolymers with the intensity of light, temperature and structural characteristics of the material. In particular, increase in the intensity of light not only increases the orientation anisotropy and the magnitude of deformation but also accelerates the process of light-induced ordering and deformation. An increase in the temperature leads to a decrease in the magnitudes of light-induced ordering and deformation of azopolymers in agreement with experiments45 due to the decrease in the viscosity. An increase in the strength of orientation LC interactions between rod-like trans-isomers of chromophores, which is proportional to their number density, amplifies the magnitude of the light-induced deformation in azonetworks.As an example, Fig. 13 illustrates the time evolution of the order parameter ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) averaged over trans- and cis-isomers with varying dimensionless parameter a, which characterizes the strength of the orientation LC interactions according to eqn (27). It can be seen that the higher is a, the higher is the initial value of
averaged over trans- and cis-isomers with varying dimensionless parameter a, which characterizes the strength of the orientation LC interactions according to eqn (27). It can be seen that the higher is a, the higher is the initial value of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) at t = 0 due to the deeper LC state at stronger LC interactions. Irradiation with light with the polarization vector E parallel to the nematic director n results in a decrease in
at t = 0 due to the deeper LC state at stronger LC interactions. Irradiation with light with the polarization vector E parallel to the nematic director n results in a decrease in ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) , which even changes its sign due to the reorientation of the chromophores perpendicular to E. Increasing the strength of the LC interactions a leads to an increase in the absolute value of the order parameter
, which even changes its sign due to the reorientation of the chromophores perpendicular to E. Increasing the strength of the LC interactions a leads to an increase in the absolute value of the order parameter ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) at long times due to the higher intensity of the LC interactions.
at long times due to the higher intensity of the LC interactions.
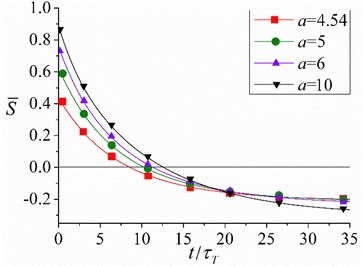 | ||
Fig. 13 Time dependences of the average order parameter ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) at different strengths of LC interactions a and at fixed all other physical parameters: PC/PT ≡ at different strengths of LC interactions a and at fixed all other physical parameters: PC/PT ≡ ![[P with combining tilde]](https://www.rsc.org/images/entities/i_char_0050_0303.gif) C = 1, D/PT ≡ C = 1, D/PT ≡ ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) = 2 × 10−2, χ = 20°. The units of time: τT = 1/PT. Adapted from ref. 144. Copyright 2017 Royal Society of Chemistry. = 2 × 10−2, χ = 20°. The units of time: τT = 1/PT. Adapted from ref. 144. Copyright 2017 Royal Society of Chemistry. | ||
Fig. 14 shows the time dependence of the elongation ratio λ of azobenzene-containing LC polymer networks at varying structural parameters a and q, the latter is defined by eqn (19). One can see that polymer networks demonstrate either expansion (λ > 1) or contraction (λ < 1) under irradiation with light, if the azo-chromophores are oriented perpendicular (q = −0.5) or parallel (q = 1) to the backbone of the network strands, respectively. Change of the sign of deformation depending on the molecular architecture of LC azonetworks was confirmed experimentally.26 Moreover, increase in the strength of LC interactions a amplifies the magnitude of light-induced deformation. This result justifies experimentally used method based on incorporation of LC mesogenic units, which amplify the intensity of orientation interactions, for the construction of azo-materials with high amplitudes of photo-deformation.25–29 Depending on the orientation distribution of azo-chromophores with respect to the main chains, azonetworks can demonstrate either expansion or contraction with respect to the polarization vector of light in agreement with experiments.26,127
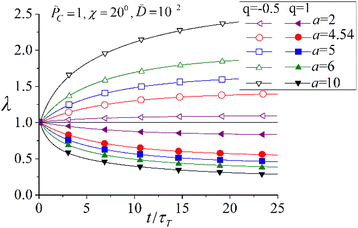 | ||
| Fig. 14 Same as Fig. 13 but for the elongation ratio λ of azobenzene-containing LC polymer networks. Reproduced from ref. 144. Copyright 2017 Royal Society of Chemistry. | ||
Thus, the proposed approach based on the angular-dependent kinetics of photoisomerization can be applied to describe photo-mechanical behaviour of azopolymers of various structures, including azonetworks and azo-containing LC polymers. In the framework of such an approach the effect of dilution of azo-containing LC polymers by bent cis-isomers is explicitly taken into account.
Conclusions
As the name suggests, the azopolymers consist of two components: polymer chains and azo-chromophores attached to them. The detailed overview of theoretical concepts proposed to describe photoinduced deformations in glassy azopolymers reveals a common but rather peculiar tendency. In some studies, the presence of polymer chains is completely ignored and all theoretical developments de facto take place in a vacuum state. In other studies, the polymer matrix is viewed as a homogeneous, low-viscosity medium. Optical gradient theories provide an extreme example here, as the sole role of azo-chromophores is to liquefy the polymer matrix and to modulate the refractive index. Starting from the models of anisotropic diffusion, the azobenzenes are considered the main and only actor. Different hypotheses are put forward about the driving mechanism but the molecular architecture of azopolymers is still ignored. This is in contrast to the theoretical concepts that have been proposed to describe the macroscopic deformations in azonetworks, which can probably be explained by the fortunate circumstance that the latter concepts were originally developed by polymer physicists.89 There, the two-constituent structure of azonetworks and the intrinsic coupling between the azo-chromophores and polymer backbones are explicitly taken into account.Another interesting observation is that the process of azobenzene reorientation is largely underestimated or simply ignored in most theoretical models, even those describing macroscopic deformation of azonetworks. However, it is precisely this process that is strongly dependent on the polarization of the light, which would not only explain the inscription of the polarization gratings, but also the deformation under homogeneous irradiation, i.e. without optical gradients. At this point, we should pay tribute to real pioneers such as Pederson et al.64 and Bublitz et al.65 who recognized the crucial importance of the reorientation processes. The only ingredient missing in early orientation approaches is the coupling of azo-chromophores to polymer scaffolds. The latter was introduced in the modern orientation approach, which is based on the concept of orientation potential developed in our group.
The introduction of the orientation potential was justified by extracting the orientation distribution of azo-chromophores from kinetic equations of the photoisomerization process. The time evolution of this distribution was found to be the same as under the action of an effective potential, that reorients chromophores perpendicular to the light polarization. Assuming that azo-chromophores are rigidly coupled to the backbone segments, the time-dependent reorientation of the polymer backbones can be calculated for different molecular architectures (e.g., main- and side-chain polymers). It has been shown that the light-induced stress arises from the alignment of polymer backbones along the polarization direction/plane in the case of linearly/circularly polarized light. This stress is on the order of 100 MPa and can cause noticeable photodeformations even in the glassy azopolymers. The appearance of a whole superficial pattern depends on the local distribution of stress and imposed boundary conditions.
The proposed orientation approach and its generalization, which exploits the angular-dependent kinetics of photoisomerization, are able to explain the photoinduced ordering and deformation observed experimentally in azopolymers of broad classes. In particular, as shown in the present review, the modern orientation approach can be used to reasonably well describe key features of the inscription of SRGs onto surfaces of glassy azopolymer films. The height of gratings is strongly influenced by the initial orientation state of the azo-chromophores and polymer backbones (isotropic, in-plane or out-of-plane), and for SS gratings even the phase can be reversed. The highest inscription efficiency typically observed for polarization patterns can be explained by a larger average photosoftening compared to that induced by intensity patterns. The peculiar structures at the edges of scratched films are completely consistent with the main directions of the light-induced stress tensor.
Directional photodeformations of glassy crosslinked and uncrosslinked azopolymers, photo-ordering and deformation of azo-containing LC polymers are also well explained. The direction of photodeformation was found to be highly sensitive to the orientation distribution of the azo-chromophores around the network strands. Therefore, molecular architecture of azopolymers can be tuned to observe expansion/contraction of a sample along the light polarization direction or concave/conclave bending. The elliptically polarized light or strong LC interactions can cause biaxial alignment and thus biaxial deformation in azonetworks.
The great predictive power of the modern orientation approach proves that the main driving force for photoinduced ordering, deformation and mass transport in azopolymers is caused by the reorientation of polymer chains with respect to the polarization direction of light. With this, we claim that the puzzle of superficial photopatterning is finally understood and the orientation approach is ready for its implementation for major azopolymer classes. The universality of the orientation approach and its predictive power to describe the photo-alignment and deformation in azopolymers of various structures open up a possibility to generalize and apply it for broader classes of azo-containing materials, such as molecular glasses,135,158,159 azobenzene-functionalized dendrimers160 and brushes,156 azobenzene-decorated plasmonic particles,161,162etc.
Author contributions
Conceptualization, M. S., V. T. and N. T.; methodology, M. S., V. T. and N. T.; validation, V. T. and N. T.; resources, M. S.; data curation, V. T. and N. T.; writing – original draft preparation, M. S., V. T. and N. T.; writing – review and editing, M. S., V. T. and N. T.; visualization, V. T. and N. T.; project administration, M. S. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. S. and N. T. acknowledge financial support from Deutsche Forschungsgemeinschaft under grant GR 3725/10-1. V. T. carried out his work at IMC RAS within the state assignment 124013000727-3.Notes and references
- N. V. Tabiryan, D. E. Roberts, Z. Liao, J.-Y. Hwang, M. Moran, O. Ouskova, A. Pshenichnyi, J. Sigley, A. Tabirian, R. Vergara, L. De Sio, B. R. Kimball, D. M. Steeves, J. Slagle, M. E. McConney and T. J. Bunning, Adv. Opt. Mater., 2021, 9, 2001692 CrossRef CAS.
- N. Tabiryan, D. Roberts, D. Steeves and B. Kimball, Photonics Spectra, 2017, 51, 46–50 Search PubMed.
- P. Rochon, E. Batalla and A. Natansohn, Appl. Phys. Lett., 1995, 66, 136–138 CrossRef CAS.
- D. Y. Kim, S. K. Tripathy, L. Li and J. Kumar, Appl. Phys. Lett., 1995, 66, 1166–1168 CrossRef CAS.
- N. K. Viswanathan, D. Y. Kim, S. Bian, J. Williams, W. Liu, L. Li, L. Samuelson, J. Kumar and S. K. Tripathy, J. Mater. Chem., 1999, 9, 1941–1955 RSC.
- A. Priimagi and A. Shevchenko, J. Polym. Sci., Part B: Polym. Phys., 2014, 52, 163–182 CrossRef CAS.
- S. L. Oscurato, M. Salvatore, P. Maddalena and A. Ambrosio, Nanophotonics, 2018, 7, 1387–1422 CrossRef CAS.
- J. Jelken, C. Henkel and S. Santer, Appl. Phys. B, 2020, 126, 149 CrossRef CAS.
- P. Pagliusi, B. Audia, C. Provenzano, M. Piñol, L. Oriol and G. Cipparrone, ACS Appl. Mater. Interfaces, 2019, 11, 34471–34477 CrossRef CAS PubMed.
- B. Stiller, T. Geue, K. Morawetz and M. Saphiannikova, J. Microscopy, 2005, 219, 109–114 CrossRef CAS PubMed.
- B. Audia, P. Pagliusi, C. Provenzano, A. Roche, L. Oriol and G. Cipparrone, ACS Appl. Polym. Mater., 2020, 2, 1597–1604 CrossRef CAS.
- B. Audia, C. M. Tone, P. Pagliusi, A. Mazzulla and G. Cipparrone, ACS Photonics, 2023, 10, 3060–3069 CrossRef CAS.
- A. Puliafito, S. Ricciardi, F. Pirani, V. Čermochová, L. Boarino, N. De Leo, L. Primo and E. Descrovi, Adv. Sci., 2019, 6, 1801826 CrossRef PubMed.
- F. Pirani, A. Angelini, S. Ricciardi, F. Frascella and E. Descrovi, Appl. Phys. Lett., 2017, 110, 101603 CrossRef.
- S. L. Oscurato, F. Borbone, P. Maddalena and A. Ambrosio, ACS Appl. Mater. Interfaces, 2017, 9, 30133–30142 CrossRef CAS PubMed.
- S. L. Oscurato, F. Reda, M. Salvatore, F. Borbone, P. Maddalena and A. Ambrosio, Adv. Mater. Interfaces, 2021, 8, 2101375 CrossRef CAS.
- V. G. Chigrinov, V. M. Kozenkov and H.-S. Kwok, Photoalignment of Liquid Crystalline Materials: Physics and Applications, Wiley Publishing, 2008 Search PubMed.
- S. Slussarenko, A. Murauski, T. Du, V. Chigrinov, L. Marrucci and E. Santamato, Opt. Express, 2011, 19, 4085–4090 CrossRef CAS PubMed.
- T. H. Ware, M. E. McConney, J. J. Wie, V. P. Tondiglia and T. J. White, Science, 2015, 347, 982–984 CrossRef CAS PubMed.
- T. Seki, J. Mater. Chem. C, 2016, 4, 7895–7910 RSC.
- A. Ambrosio, L. Marrucci, F. Borbone, A. Roviello and P. Maddalena, Nat. Commun., 2012, 3, 989 CrossRef PubMed.
- A. Bobrovsky, K. Mochalov, D. Solovyeva, V. Shibaev, M. Cigl, V. Hamplová and A. Bubnov, Soft Matter, 2020, 16, 5398–5405 RSC.
- D. H. Wang, K. M. Lee, Z. N. Yu, H. Koerner, R. A. Vaia, T. J. White and L. S. Tan, Macromolecules, 2011, 44, 3840–3846 CrossRef CAS.
- D. H. Wang, J. J. Wie, K. M. Lee, T. J. White and L. S. Tan, Macromolecules, 2014, 47, 659–667 CrossRef CAS.
- T. J. White and D. J. Broer, Nat. Mater., 2015, 14, 1087–1098 CrossRef CAS PubMed.
- A. Priimagi, A. Shimamura, M. Kondo, T. Hiraoka, S. Kubo, J. I. Mamiya, M. Kinoshita, T. Ikeda and A. Shishido, ACS Macro Lett., 2012, 1, 96–99 CrossRef CAS PubMed.
- X. Wang, Azo Polymers: Synthesis, Functions and Applications, Springer, Berlin, Heidelberg, 2017 Search PubMed.
- Y. L. Yu, M. Nakano and T. Ikeda, Nature, 2003, 425, 145 CrossRef CAS PubMed.
- H. Y. Jiang, S. Kelch and A. Lendlein, Adv. Mater., 2006, 18, 1471–1475 CrossRef CAS.
- S. Iamsaard, S. J. Asshoff, B. Matt, T. Kudernac, J. Cornelissen, S. P. Fletcher and N. Katsonis, Nat. Chem., 2014, 6, 229–235 CrossRef CAS PubMed.
- D. Q. Liu and D. J. Broer, Angew. Chem., Int. Ed., 2014, 53, 4542–4546 CrossRef CAS PubMed.
- O. M. Wani, H. Zeng and A. Priimagi, Nat. Commun., 2017, 8, 15546 CrossRef CAS PubMed.
- A. H. Gelebart, D. J. Mulder, M. Varga, A. Konya, G. Vantomme, E. W. Meijer, R. L. B. Selinger and D. J. Broer, Nature, 2017, 546, 632–636 CrossRef CAS PubMed.
- V. Y. Chang, C. Fedele, A. Priimagi, A. Shishido and C. J. Barrett, Adv. Opt. Mater., 2019, 7, 1900091 CrossRef.
- A. Ryabchun, A. Bobrovsky, J. Stumpe and V. Shibaev, Macromol. Rapid Commun., 2012, 33, 991–997 CrossRef CAS PubMed.
- F. Lancia, A. Ryabchun, A. D. Nguindjel, S. Kwangmettatam and N. Katsonis, Nat. Commun., 2019, 10, 4819 CrossRef PubMed.
- Photomechnical materials, composites and systems: wireles transduction of light into work, ed. T. J. White, John Wiley & Sons, USA, 2017 Search PubMed.
- I. K. Januariyasa, F. Borbone, M. Salvatore and S. L. Oscurato, ACS Appl. Mater. Interfaces, 2023, 15, 43183–43192 CrossRef CAS PubMed.
- J. Jelken and S. Santer, RSC Adv., 2019, 9, 20295–20305 RSC.
- H. W. Zhou, C. G. Xue, P. Weis, Y. Suzuki, S. L. Huang, K. Koynov, G. K. Auernhammer, R. Berger, H. J. Butt and S. Wu, Nat. Chem., 2017, 9, 145–151 CrossRef CAS PubMed.
- W.-C. Xu, S. Sun and S. Wu, Angew. Chem., Int. Ed., 2019, 58, 9712–9740 CrossRef CAS PubMed.
- B. Yang, F. Cai, S. Huang and H. Yu, Angew. Chem., Int. Ed., 2020, 59, 4188 CrossRef CAS.
- S. Liang, S. Li, C. Yuan, C. Liu, J. Chen and S. Wu, Polymer, 2024, 290, 126575 CrossRef CAS.
- M. Saphiannikova and V. Toshchevikov, J. Soc. Inf. Disp., 2015, 23, 146–153 CrossRef CAS.
- P. U. Veer, U. Pietsch, P. L. Rochon and M. Saphiannikova, Mol. Cryst. Liq. Cryst., 2008, 486, 1108–1120 Search PubMed.
- P. U. Veer, U. Pietsch and M. Saphiannikova, J. Appl. Phys., 2009, 106, 014909 CrossRef.
- J. Kumar, L. Li, X. L. Jiang, D. Y. Kim, T. S. Lee and S. Tripathy, Appl. Phys. Lett., 1998, 72, 2096–2098 CrossRef CAS.
- P. Karageorgiev, D. Neher, B. Schulz, B. Stiller, U. Pietsch, M. Giersig and L. Brehmer, Nat. Mater., 2005, 4, 699–703 CrossRef CAS PubMed.
- S. Lee, H. S. Kang and J. K. Park, Adv. Mater., 2012, 24, 2069–2103 CrossRef CAS PubMed.
- N. S. Yadavalli, F. Linde, A. Kopyshev and S. Santer, ACS Appl. Mater. Interfaces, 2013, 5, 7743–7747 CrossRef CAS PubMed.
- G. Di Florio, E. Brundermann, N. S. Yadavalli, S. Santer and M. Havenith, Nano Lett., 2014, 14, 5754–5760 CrossRef CAS PubMed.
- V. Toshchevikov, M. Saphiannikova and G. Heinrich, J. Phys. Chem. B, 2009, 113, 5032–5045 CrossRef CAS PubMed.
- V. Toshchevikov, J. Ilnytskyi and M. Saphiannikova, J. Phys. Chem. Lett., 2017, 8, 1094–1098 CrossRef CAS PubMed.
- C. Barrett, P. Rochon and A. Natansohn, J. Phys. Chem., 1996, 100, 8836–8842 CrossRef CAS.
- C. J. Barrett, P. L. Rochon and A. L. Natansohn, J. Chem. Phys., 1998, 109, 1505–1516 CrossRef CAS.
- S. P. Bian, J. M. Williams, D. Y. Kim, L. A. Li, S. Balasubramanian, J. Kumar and S. Tripathy, J. Appl. Phys., 1999, 86, 4498–4508 CrossRef CAS.
- O. Baldus and S. J. Zilker, Appl. Phys. B, 2001, 72, 425–427 CrossRef CAS.
- O. Baldus, A. Leopold, R. Hagen, T. Bieringer and S. J. Zilker, J. Chem. Phys., 2001, 114, 1344–1349 CrossRef CAS.
- M. Saphiannikova, T. M. Geue, O. Henneberg, K. Morawetz and U. Pietsch, J. Chem. Phys., 2004, 120, 4039–4045 CrossRef CAS PubMed.
- K. Yang, S. Z. Yang and J. Kumar, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 165204 CrossRef.
- P. Lefin, C. Fiorini and J.-M. Nunzi, Pure Appl. Optics, 1998, 7, 71–82 CrossRef CAS.
- P. Lefin, C. Fiorini and J. M. Nunzi, Opt. Mater., 1998, 9, 323–328 CrossRef CAS.
- B. Bellini, J. Ackermann, H. Klein, C. Grave, P. Dumas and V. Safarov, J. Phys.: Condens. Matter, 2006, 18, S1817–S1835 CrossRef CAS.
- T. G. Pedersen, P. M. Johansen, N. C. R. Holme, P. S. Ramanujam and S. Hvilsted, Phys. Rev. Lett., 1998, 80, 89–92 CrossRef CAS.
- D. Bublitz, B. Fleck and L. Wenke, Appl. Phys. B, 2001, 72, 931–936 CrossRef CAS.
- P. W. Smith, A. Ashkin and W. J. Tomlinson, Opt. Lett., 1981, 6, 284–286 CrossRef CAS PubMed.
- E. Schmutzer, Grundlagen der theoretischen Physik, BI Wissenschaftsverlag, 1989 Search PubMed.
- H. S. Kang, H. T. Kim, J. K. Park and S. Lee, Adv. Funct. Mater., 2014, 24, 7273–7283 CrossRef CAS.
- S. Lee, H. S. Kang, A. Ambrosio, J. K. Park and L. Marrucci, ACS Appl. Mater. Interfaces, 2015, 7, 8209–8217 CrossRef CAS PubMed.
- F. Pirani, A. Angelini, F. Frascella, R. Rizzo, S. Ricciardi and E. Descrovi, Sci. Rep., 2016, 6, 31702 CrossRef CAS PubMed.
- D. Y. Kim, L. Li, X. L. Jiang, V. Shivshankar, J. Kumar and S. K. Tripathy, Macromolecules, 1995, 28, 8835–8839 CrossRef CAS.
- M. Koch, M. Saphiannikova and O. Guskova, presented in part at the virtual DPG Spring Meeting, March, 2021.
- M. Koch, M. Saphiannikova and O. Guskova, Molecules, 2021, 26, 7674 CrossRef CAS PubMed.
- N. Mechau, M. Saphiannikova and D. Neher, Appl. Phys. Lett., 2006, 89, 251902 CrossRef.
- M. L. Juan, J. Plain, R. Bachelot, P. Royer, S. K. Gray and G. P. Wiederrecht, Appl. Phys. Lett., 2008, 93, 153304 CrossRef.
- M. L. Juan, J. Plain, R. Bachelot, P. Royer, S. K. Gray and G. P. Wiederrecht, ACS Nano, 2009, 3, 1573–1579 CrossRef CAS PubMed.
- A. Ambrosio, P. Maddalena and L. Marrucci, Phys. Rev. Lett., 2013, 110, 146102 CrossRef PubMed.
- J. Jelken, M. Brinkjans, C. Henkel and S. Santer, Proc. SPIE, 2020, 11367, 1136710 Search PubMed.
- T. G. Pedersen and P. M. Johansen, Phys. Rev. Lett., 1997, 79, 2470–2473 CrossRef CAS.
- T. G. Pedersen, P. M. Johansen, N. C. R. Holme, P. S. Ramanujam and S. Hvilsted, J. Opt. Soc. Am. B, 1998, 15, 1120–1129 CrossRef CAS.
- N. S. Yadavalli and S. Santer, J. Appl. Phys., 2013, 113, 224304 CrossRef.
- S. Loebner, B. Yadav, N. Lomadze, N. Tverdokhleb, H. Donner, M. Saphiannikova and S. Santer, Macromol. Mater. Eng., 2022, 31, 2100990 CrossRef.
- Y. B. Gaididei, P. L. Christiansen and P. S. Ramanujam, Appl. Phys. B: Lasers Opt., 2002, 74, 139–146 CrossRef CAS.
- Y. B. Gaididei, A. P. Krekhov and H. Büttner, Phys. Lett. A, 2010, 374, 2156–2162 CrossRef CAS.
- S. Loebner, N. Lomadze, A. Kopyshev, M. Koch, O. Guskova, M. Saphiannikova and S. Santer, J. Phys. Chem. B, 2018, 122, 2001–2009 CrossRef CAS PubMed.
- P. M. Hogan, A. R. Tajbakhsh and E. M. Terentjev, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 65, 041720 CrossRef CAS PubMed.
- J. Cviklinski, A. R. Tajbakhsh and E. M. Terentjev, Eur. Phys. J. E: Soft Matter Biol. Phys., 2002, 9, 427–434 CrossRef CAS PubMed.
- M. Warner and E. Terentjev, Macromol. Symp., 2003, 200, 81–92 CrossRef CAS.
- M. Warner and E. M. Terentjev, Liquid Crystal Elastomers, Clarendon, Oxford, 2003 Search PubMed.
- D. Corbett and M. Warner, Phys. Rev. Lett., 2007, 99, 174302 CrossRef CAS PubMed.
- D. Corbett, C. L. van Oosten and M. Warner, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 78, 013823 CrossRef.
- F. Serra and E. M. Terentjev, J. Chem. Phys., 2008, 128, 224510 CrossRef PubMed.
- H. Finkelmann, E. Nishikawa, G. G. Pereira and M. Warner, Phys. Rev. Lett., 2001, 87, 015501 CrossRef CAS PubMed.
- M. H. Li, P. Keller, B. Li, X. G. Wang and M. Brunet, Adv. Mater., 2003, 15, 569–572 CrossRef CAS.
- M. Camacho-Lopez, H. Finkelmann, P. Palffy-Muhoray and M. Shelley, Nat. Mater., 2004, 3, 307–310 CrossRef CAS PubMed.
- T. Ikeda, M. Nakano, Y. L. Yu, O. Tsutsumi and A. Kanazawa, Adv. Mater., 2003, 15, 201–205 CrossRef CAS.
- J. Garcia-Amorós, H. Finkelmann and D. Velasco, J. Mater. Chem., 2011, 21, 1094–1101 RSC.
- Y. L. Yu, M. Nakano and T. Ikeda, Pure Appl. Chem., 2004, 76, 1467–1477 CrossRef CAS.
- N. Tabiryan, S. Serak, X. M. Dai and T. Bunning, Opt. Express, 2005, 13, 7442–7448 CrossRef CAS PubMed.
- C. L. van Oosten, D. Corbett, D. Davies, M. Warner, C. W. M. Bastiaansen and D. J. Broer, Macromolecules, 2008, 41, 8592–8596 CrossRef CAS.
- K. M. Lee, H. Koerner, R. A. Vaia, T. J. Bunning and T. J. White, Macromolecules, 2010, 43, 8185–8190 CrossRef CAS.
- P. P. Zhang, Z. X. Lan, J. Wei and Y. L. Yu, ACS Macro Lett., 2021, 10, 469–475 CrossRef CAS PubMed.
- J. Bin and W. S. Oates, Sci. Rep., 2015, 5, 14654 CrossRef PubMed.
- M. Mehnert, W. Oates and P. Steinmann, Int. J. Numer. Meth. Eng., 2023, 124, 1602–1619 CrossRef.
- B. Basnet, M. Rajabi, H. Wang, P. Kumari, K. Thapa, S. Paul, M. O. Lavrentovich and O. D. Lavrentovich, Nat. Commun., 2022, 13, 3932 CrossRef CAS PubMed.
- H. Nishikawa, K. Shiroshita, H. Higuchi, Y. Okumura, Y. Haseba, S.-I. Yamamoto, K. Sago and H. Kikuchi, Adv. Mater., 2017, 29, 1702354 CrossRef PubMed.
- N. Tverdokhleb, S. Loebner, B. Yadav, S. Santer and M. Saphiannikova, Polymers, 2023, 15, 463 CrossRef CAS PubMed.
- M. Saphiannikova and D. Neher, J. Phys. Chem. B, 2005, 109, 19428–19436 CrossRef CAS PubMed.
- M. Grenzer, Habilitation thesis, Potsdam University, 2007.
- F. Lagugne-Labarthet, T. Buffeteau and C. Sourisseau, J. Phys. Chem. B, 1998, 102, 5754–5765 CrossRef.
- F. Lagugne-Labarthet, T. Buffeteau and C. Sourisseau, Macromol. Symp., 1999, 137, 75–82 CrossRef CAS.
- F. Lagugne-Labarthet, J. L. Bruneel, V. Rodriguez and C. Sourisseau, J. Phys. Chem. B, 2004, 108, 1267–1278 CrossRef CAS.
- N. Mechau, D. Neher, V. Börger, H. Menzel and K. Urajama, Appl. Phys. Lett., 2002, 81, 4715–4717 CrossRef CAS.
- O. Henneberg, PhD thesis, Potsdam University, 2004.
- A. Kozanecka-Szmigiel, J. Antonowicz, D. Szmigiel, M. Makowski, A. Siemion, J. Konieczkowska, B. Trzebicka and E. Schab-Balcerzak, Polymer, 2018, 140, 117–121 CrossRef CAS.
- C. Kulinna, S. Hvilsted, C. Hendann, H. W. Siesler and P. S. Ramanujam, Macromolecules, 1998, 31, 2141–2151 CrossRef CAS.
- C. C. Jung, R. Rosenhauer, M. Rutloh, C. Kempe and J. Stumpe, Macromolecules, 2005, 38, 4324–4330 CrossRef CAS.
- V. Chigrinov, S. Pikin, A. Verevochnikov, V. Kozenkov, M. Khazimullin, J. Ho, D. D. Huang and H. S. Kwok, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 061713 CrossRef PubMed.
- J. Ilnytskyi, M. Saphiannikova and D. Neher, Condens. Matter Phys., 2006, 9, 87–94 CrossRef.
- V. Toshchevikov, M. Saphiannikova and G. Heinrich, Proc. SPIE, 2009, vol. 7487, p. 74870B Search PubMed.
- M. Saphiannikova, V. Toshchevikov and J. Ilnytskyi, Nonlinear Opt., Quantum Opt., 2010, 41, 27–57 CAS.
- B. Yadav, J. Domurath, K. Kim, S. Lee and M. Saphiannikova, J. Phys. Chem. B, 2019, 123, 3337–3347 CrossRef CAS PubMed.
- A. C. Mitus, M. Saphiannikova, W. Radosz, V. Toshchevikov and G. Pawlik, Materials, 2021, 14, 1454 CrossRef CAS PubMed.
- V. Toshchevikov and M. Saphiannikova, Processes, 2023, 11, 129 CrossRef CAS.
- M. Doi and S. F. Edwards, The Theory of Polymer Dynamics, Oxford University Press, Oxford, 1988 Search PubMed.
- P. G. de Gennes and J. Prost, The Physics of Liquid Crystals, Clarendon Press, Oxford, 2nd edn, 1995 Search PubMed.
- D. Bublitz, M. Helgert, B. Fleck, L. Wenke, S. Hvilsted and P. S. Ramanujam, Appl. Phys. B: Lasers Opt., 2000, 70, 863–865 CrossRef CAS.
- T. Fukuda, H. Matsuda, T. Shiraga, T. Kimura, M. Kato, N. K. Viswanathan, J. Kumar and S. K. Tripathy, Macromolecules, 2000, 33, 4220–4225 CrossRef CAS.
- B. Yadav, PhD thesis, TU Dresden, 2023.
- P. Perzyna, Quart. Appl. Math., 1963, 20, 321–332 CrossRef.
- B. Yadav, J. Domurath and M. Saphiannikova, Polymers, 2020, 12, 735 CrossRef CAS PubMed.
- N. C. R. Holme, L. Nikolova, P. S. Ramanujam and S. Hvilsted, Appl. Phys. Lett., 1997, 70, 1518–1520 CrossRef CAS.
- N. K. Viswanathan, S. Balasubramanian, L. Li, S. K. Tripathy and J. Kumar, Jpn. J. Appl. Phys., 1999, 38, 5928–5937 CrossRef CAS.
- F. Lagugne-Labarthet, T. Buffeteau and C. Sourisseau, J. Phys. Chem. B, 1999, 103, 6690–6699 CrossRef.
- H. Rekola, A. Berdin, C. Fedele, M. Virkki and A. Priimagi, Sci. Rep., 2020, 10, 19642 CrossRef CAS PubMed.
- A. Sobolewska and S. Bartkiewicz, Appl. Phys. Lett., 2012, 101, 193301 CrossRef.
- N. S. Yadavalli, S. Loebner, T. Papke, E. Sava, N. Hurduc and S. Santer, Soft Matter, 2016, 12, 2593–2603 RSC.
- G. J. Fang, J. E. Maclennan, Y. Yi, M. A. Glaser, M. Farrow, E. Korblova, D. M. Walba, T. E. Furtak and N. A. Clark, Nat. Commun., 2013, 4, 1521 CrossRef CAS PubMed.
- V. Toshchevikov, M. Saphiannikova and G. Heinrich, J. Phys. Chem. B, 2012, 116, 913–924 CrossRef CAS PubMed.
- V. P. Toshchevikov, M. Saphiannikova and G. Heinrich, J. Chem. Phys., 2012, 137, 024903 CrossRef CAS PubMed.
- V. Toshchevikov, M. Saphiannikova and G. Heinrich, Proc. SPIE, 2012, 8545, 854507 CrossRef.
- V. Toshchevikov and M. Saphiannikova, J. Phys. Chem. B, 2014, 118, 12297–12309 CrossRef CAS PubMed.
- V. Toshchevikov, T. Petrova and M. Saphiannikova, Proc. SPIE, 2015, 9565, 956504 CrossRef.
- V. Toshchevikov, T. Petrova and M. Saphiannikova, Soft Matter, 2017, 13, 2823–2835 RSC.
- T. Petrova, V. Toshchevikov and M. Saphiannikova, Soft Matter, 2015, 11, 3412–3423 RSC.
- T. Buffeteau and M. Pezolet, Macromolecules, 1998, 31, 2631–2635 CrossRef CAS.
- Y. L. Wu, J. Mamiya, A. Kanazawa, T. Shiono, T. Ikeda and Q. J. Zhang, Macromolecules, 1999, 32, 8829–8835 CrossRef CAS.
- M. Han, S. Morino and K. Ichimura, Macromolecules, 2000, 33, 6360–6371 CrossRef CAS.
- T. Buffeteau, F. L. Labarthet, C. Sourisseau, S. Kostromine and T. Bieringer, Macromolecules, 2004, 37, 2880–2889 CrossRef CAS.
- J. M. Ilnytskyi, D. Neher, M. Saphiannikova, M. R. Wilson and L. M. Stimson, Mol. Cryst. Liq. Cryst., 2008, 496, 186–201 CrossRef CAS.
- J. M. Ilnytskyi, D. Neher and M. Saphiannikova, J. Chem. Phys., 2011, 135, 044901 CrossRef PubMed.
- V. Toshchevikov, T. Petrova and M. Saphiannikova, Polymers, 2018, 10, 531 CrossRef PubMed.
- N. Mechau, M. Saphiannikova and D. Neher, Macromolecules, 2005, 38, 3894–3902 CrossRef CAS.
- R. G. Larson, The Structure and Rheology of Complex Fluids, Oxford University Press, New York, 1999 Search PubMed.
- A. Kopyshev, N. Lomadze, D. Feldmann, J. Genzer and S. Santer, Polymer, 2015, 79, 65–72 CrossRef CAS.
- A. Kopyshev, C. J. Galvin, J. Genzer, N. Lomadze and S. Santer, Langmuir, 2013, 29, 13967–13974 CrossRef CAS PubMed.
- J. M. Ilnytskyi and M. Saphiannikova, ChemPhysChem, 2015, 16, 3180–3189 CrossRef CAS PubMed.
- R. Kirby, R. G. Sabat, J. M. Nunzi and O. Lebel, J. Mater. Chem. C, 2014, 2, 841–847 RSC.
- A. Berdin, H. T. Rekola and A. Priimagi, Adv. Opt. Mater., 2024, 12, 2301597 CrossRef CAS.
- N. S. Yadavalli, M. Saphiannikova, N. Lomadze, L. M. Goldenberg and S. Santer, Appl. Phys. A: Mater. Sci. Process., 2013, 113, 263–272 CrossRef CAS.
- C. Raimondo, F. Reinders, U. Soydaner, M. Mayor and P. Samorì, Chem. Commun., 2010, 46, 1147–1149 RSC.
- J. M. Ilnytskyi, A. Slyusarchuk and M. Saphiannikova, Macromolecules, 2016, 49, 9272–9282 CrossRef CAS.
Footnote |
| † Current address: Institute for Materials Science, TU Dresden, 01062 Dresden, Germany. |
| This journal is © The Royal Society of Chemistry 2024 |



