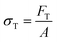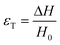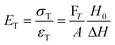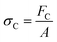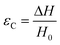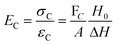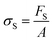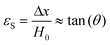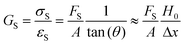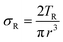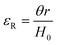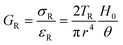Open Access Article
Open Access ArticleEducational series: characterizing crosslinked polymer networks
Chamoni W. H.
Rajawasam
a,
Obed J.
Dodo
 a,
M. A. Sachini N.
Weerasinghe
a,
Ibrahim O.
Raji
a,
Shiwanka V.
Wanasinghe
a,
Dominik
Konkolewicz
a,
M. A. Sachini N.
Weerasinghe
a,
Ibrahim O.
Raji
a,
Shiwanka V.
Wanasinghe
a,
Dominik
Konkolewicz
 *a and
Nethmi
De Alwis Watuthanthrige
*a and
Nethmi
De Alwis Watuthanthrige
 *b
*b
aDepartment of Chemistry and Biochemistry, Miami University, 651 E High St, Oxford, OH 45056, USA. E-mail: d.konkolewicz@miamiOH.edu
bLaboratory of Polymeric Materials, Department of Materials, ETH Zurich, Vladimir-Prelog-Weg 5, Zurich 8093, Switzerland. E-mail: nethmi.dealwis@mat.ethz.ch
First published on 19th December 2023
Abstract
Characterization of polymer networks presents unique challenges due to the insolubility of the materials, but this also enables characterization by new techniques that take advantage of the bulk network structure. An overview of characterization methods for polymer networks is presented, including functionality by IR, swelling and gel fraction calculations, mechanical characterization, thermal characterization, evaluation of molar masses between crosslinks and surface properties. This contribution serves as a reference for researchers aiming to evaluate network properties for the first time, or to expand the range of techniques used in network characterization.
Introduction
Crosslinked polymer networks have unique properties and characteristics which result from the binding and linking of polymer chains together to form very high molecular weight, essentially macroscopic scale molecules.1–4 In general polymer networks are used in high performance and challenging applications, where the equivalent soluble polymers would not be able to function.5,6 This often occurs above critical transitions such as glass or melt transitions, where free polymers would flow, while network polymers maintain their structure even at high temperatures, or under demanding conditions.7As highlighted in the earlier contribution, the well-established polymerization methods used to generate linear polymers, can easily be adapted to network synthesis through the addition of multifunctional monomers. However, the presence of crosslinks changes the solubility of the polymers in addition to strengthening the material. Since many common chemical characterization tools, including those applied to polymers, rely on the solubility of the molecule, crosslinking has a dramatic impact on the range of characterization tools that can be easily used for polymer networks.8–10 Although certain chemical analysis methods are no longer applicable for polymer networks, the crosslinking also enables characterization methods that are not suitable for the soluble polymer analogues of network polymers.7,8
In this series of two articles on polymer networks, the core synthesis and characterization of polymer networks are presented. These articles serve as an overview of methods used to design and develop polymer networks, as well as the methods used to evaluate the properties. These educational series articles complement other review articles in the of polymer networks.4,5,8,11–13 An earlier contribution focused on the synthesis of polymer networks.14 This current contribution, which concentrates on characterization of polymer networks, presents the most commonly used methods for evaluating the properties of polymer networks. This works covers fundamental aspects of characterization techniques of networks, including sample preparation, advantages/disadvantages, and underlying principles. The detailed exploration includes commonly employed methods such as functional groups through infrared analysis, solution/gelled (sol–gel) fraction and swelling properties, mechanical characterization, thermal analysis, internal structural analysis such as molecular weight between crosslinks and surface property analysis. The target is to provide a balanced and comprehensive understanding, ensuring accessibility for a diverse readership. A focus in this educational series article is the description of the underlying science underpinning the technique and how the information from the characterization method could impact the design of future materials. Further, the inclusion of practical information and nuanced perspectives aims to make the review valuable to both novices and discussion of advanced and integrated techniques valuable to experts in polymer chemistry.
Review of synthesis of polymer networks
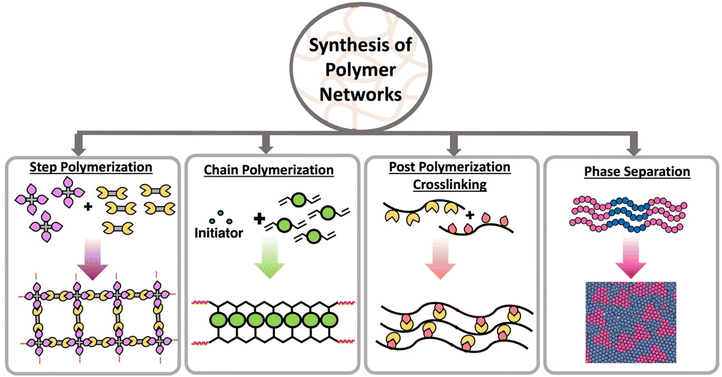
The three-dimensional mesh type structure of a polymer network is made from interconnected linear polymer chains through branching or crosslinks. This mesh structure with extensive crosslinks is developed by expanding pathways between most points in the polymer. Both chain polymerization and step polymerization are capable of synthesizing polymer networks in the presence of multifunctional monomers or multifunctional crosslinkers.15,16 Multifunctionality is the key to connecting points between polymer chains and form the network. In step polymerization, multifunctional monomers react each other forming oligomers with higher functionality which then accelerate the polymerization introducing branching points.17,18 These branching points act as crosslinks and ultimately form a polymer network. Similar to step polymerization, chain polymerization is capable of forming networks in the presence of multifunctional monomers or multifunctional crosslinkers.16,18 Further, post polymerization crosslinking of linear polymers with reactive pendant groups or reactive terminal groups create polymer networks.18,19 In addition to those strategies, some linear polymers have the ability show network properties through micro-aggregation or phase separation (Scheme 1).20Crosslinking between the monomers can occur through chemical or physical linkages. Static and dynamic (disulfide linkages, Diels–Alder, transamination, transesterification, olefin metathesis) covalent bonds can be established between two monomer units in order to form chemically crosslinked polymers. In contrast, non-covalent interactions such as ionic bonds, Hydrogen bonding, π–π interactions, metal–ligand interactions are introduced between monomer units to form physically crosslinked or “supramolecular” polymers.21 The key distinction between chemically and physically crosslinked polymers lies in their strength. Physical bonds are typically weaker and dynamic, while chemical bonds are stronger but can be either static or dynamic depending on the bond type.
Different types of polymer networks and materials
Depending on the nature of crosslinks and physical characteristics, such as water absorption and shape deformation, networks can be categorized into thermosets, thermoplastics, hydrogels and elastomers.Classical thermosets are crosslinked polymers with irreversible bonds, retaining their shape upon when heated and exhibiting highly resistant to heat melting, creep and solvents. Heating them to very high temperatures will ultimately lead thermoset polymers to degrade, but they often become softer below this temperature. The synthesis of these polymers starts with liquids and is converted to their final shapes through curing process. Once these materials are made, they cannot be reshaped by heating without degrading their structure. These stable polymers are used in applications such as adhesives, coatings and composites.22 Common examples include polyurethanes, epoxy, and Phenol-formaldehyde. Recently, there has been a rising interest in developing thermoset polymers from bio-based monomers, such as lipids and phenolic compounds to enhance sustainability.23
Thermoplastics are polymers capable of melting when heated and retaining their shape upon cooling. They may deform over time under stress, a phenomenon known as creep. Depending on the crystallinity, thermoplastics can be categorized into two main subtypes: semicrystalline and amorphous.24 Semicrystalline polymers exhibit domains with an ordered structure displaying both crystalline and amorphous states in their temperature profile (Scheme 2b). Semicrystalline polymers act as liquids above the crystalline melting temperature (Tm), and have a glass transition temperature (Tg) within the amorphous or non-crystalline regions.25 Amorphous polymers contain a random coiled structure, transitioning from glassy state with minimal chain mobility to rubbery state within a narrow temperature range (Scheme 2a).25 Above their glass transition temperature (Tg) amorphous thermoplastic materials will flow. However, crosslinked networks also have a Tg, above which the materials will be flexible and elastic, but the crosslinks resist macroscopic flow.
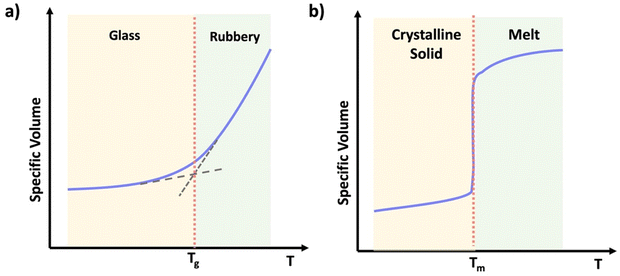 | ||
| Scheme 2 Graphical representation of specific volume vs. temperature of (a) an amorphous thermoplastic, (b) a semi-crystalline thermoplastic. | ||
Hydrogels are soft, water absorbing three dimensional materials that maintain their structure due to crosslinking and entanglements, preventing dissolution in water.26 They exhibit both solid and liquid characteristics, with unique relaxation properties. Hydrogels are composed of various bond types including ionic bonds, hydrogen bonds, covalent bonds, hydrophobic interactions.27 They can also response external stimuli such as pH, temperature, and electric field.28 These versatile materials find applications in tissue engineering, soft robotics, sensing, and artificial muscles due to their tunable properties and bio mimic nature.28–30
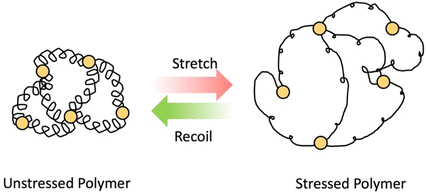
As the name implies, elastomers are elastic materials that composed of loosely joined network structure.24 They are typically above their glass transition temperature, but unable to flow due to the presence of crosslinks. These elastomers can stretch in the presence of an applied force and then go back to its original shape after force is removed (shown in Scheme 3) Usually, they show excellent elastic properties, low stiffness and low strength.31 Examples for these elastomers are polyisoprene, natural rubber, silicone elastomers, nitrile rubber, etc. These elastomers are used in variety of industrial applications such as seals, rubber septa, gaskets and tyres.31,32
Network properties
Depending on the nature of crosslinking, composition, and behavior under stress, networks may differ in their topology, heterogeneity, porosity and the viscoelastic properties. This section discusses each of these properties in brief.Network topology refers to the arrangement of polymer chains, defining the structure of a polymer network. This characteristic plays a crucial role in characterization techniques, detailing the spatial features of polymer networks.10 Various network structures, such as linear, cyclic, star, branched and grafted polymers exhibit distinct hydrodynamic volumes. For instance, linear polymers display higher hydrodynamic volumes, increased viscosity, and more entanglements compared to other topologies.33 Flory's theories emphasize the significance of polymer network topology in understanding the relationship between structure and mechanical properties.10 Noteworthy examples of unique architectures include polyrotaxanes, polycatenanes and interpenetrated networks (IPNs), with IPNs comprising multiple networks interwoven without chemical bonding.10
Polymer networks often exhibit heterogeneities arising from irregular crosslinking and structural defects at the microscopic level, such as floppy loops and dangling chain ends.13 These heterogeneities can be broadly categorized into spatial and connectivity heterogeneity. Spatial heterogeneity, characterized by an uneven distribution of crosslinks, is prevalent in polymer gels especially those with poor control over primary structure.34–36 On the other hand, connectivity heterogeneity results from polymer chain issues, such as trapped entanglements and connective defects.37 The formation of loops, whether through intermolecular crosslinking or self-crosslinking reactions, significantly influences material properties. Hence, quantifying these loops in networks is crucial for understanding the structure–property relationship. Techniques like Network Disassembly Spectroscopy and chemical degradation followed by mass spectroscopy can be used to quantify loops.38 Indirect measurements can be made by determining the molar mass between crosslinks as discussed below.39
Porosity, exemplified by the hexagonal honeycomb structure in nature, has been incorporated into various synthetic materials, including polymers.40 “Porous polymers” encompass both porous and polymer properties, with those containing with two or more pores termed “porous polymers” and those with a single pore to as “hollow polymers”.40 Porous polymers are further classified into three main categories based on pore size: microporous (diameter < 2 nm), mesoporous (2 nm < diameter < 50 nm) and macroporous (diameter > 50 nm).41 The synthesis of porous polymers involves two key factors: the chemical composition of monomers, which determines the chemical structure of the pores, and reaction conditions such as temperature and stirring rate, which influence the texture of the pores.42 These materials finds diverse applications, including separation, gas storage, catalysis, sensors, energy storage, coatings and more.40
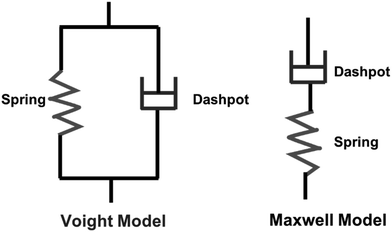
Viscoelastic behavior is a crucial aspect of polymers, encompassing both viscous liquid and elastic solid properties, allowing the materials to dissipate energy under applied stress.43 This property is commonly assessed through creep tests.44 Various factors, including crosslinking, molecular weight, chemical structure of the polymer influence this behavior.43 Two primary models, the Maxwell and Voight models are employed to describe viscoelastic behavior. The Maxwell model describes the material as a purely elastic spring and a purely viscous dashpot in series, while the Voight model connects them in parallel (Scheme 4).45
Overview of polymer network characterization
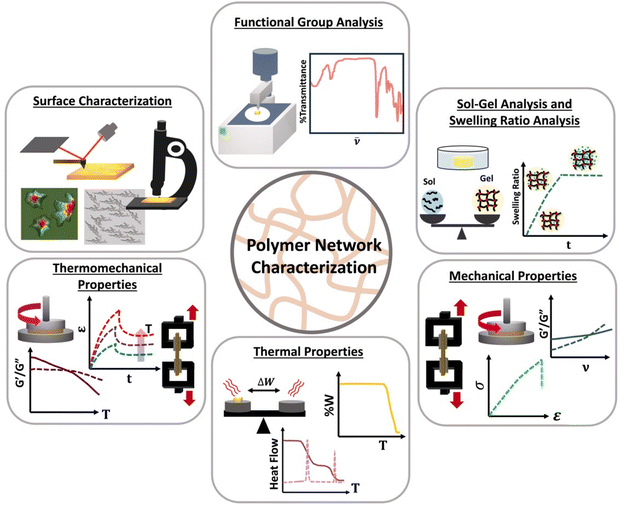
Although linear polymers can be characterized by using standard characterization methods such as size exclusive chromatography (SEC) or solution nuclear magnetic resonance spectroscopy (NMR),8 those technique are not suitable for polymer network characterization. Once gelation occurs, the state of the material changes from a flowy liquid state to a rigid network state making them insoluble and prohibiting analysis by SEC or solution NMR. Therefore, new characterization methods such as different mechanical tests are essential which are not always feasible on soluble polymers. Polymer network characterization techniques to have the ability to reveal both chemical and topological properties of the network which control the function of the material.46 Among all those characterization methods, functional group analysis (e.g., Fourier transform infrared spectroscopy-FTIR), sol–gel analysis, swelling ratios,47 molar mass between crosslinks, mechanical analysis (e.g., rheology or tensile tests), thermal analysis48,49 (e.g., differential scanning colorimetry-DSC) and surface characterization methods (e.g., scanning electron microscopy-SEM) are used to identify functional groups present, to determine the degree of crosslinking, to identify mechanical and thermal properties and to image surface morphology of a polymer network as shown in Scheme 5.Functional group analysis
Functional group analysis is one of the primary techniques used in the characterization of polymer networks, allowing for the determination of the types and quantities of specific chemical bonds or groups that are integral to the polymer network. This analysis can provide information such as the degree of crosslinking, the nature of crosslinking, the localization of phase-separation of the polymer materials and even physical characteristic features such as phase transition temperatures.50–52As noted above, conventional techniques commonly employed in soluble systems, such as SEC and solution-based NMR, cannot be used to analyze polymer networks due to their insolubility after crosslinking. While some studies have demonstrated the potential use of solution NMR and SEC in characterizing polymer networks, this needs special equipment, or chemical processing (e.g.: crosslink degradation), which complicates the characterization process.34,53 Techniques such as FTIR, Raman, solid-state NMR, and X-ray diffraction (XRD) are commonly used approaches for the functional group analysis.52,54,55
FTIR represents a non-invasive technique capable of characterizing the functional groups in materials without modifying the network structure. FTIR spectroscopy measured absorbance of infrared radiation (IR) across the IR spectrum. Absorption peaks in IR correspond to excitation of an IR active vibrational mode, which is typical for a particular functional group. If a bond within the polymer network possesses a dipole moment, this approach easily identifies the specific functional group within the polymer chains or crosslinks. By placing the samples on the attenuated total reflection (ATR) cell, FTIR measurements can be quickly performed to acquire rapid acquisition signals from the pristine polymer network. Sample preparation in ATR FTIR is simple, and can be applied to glassy, elastomeric or even viscous samples, however only the closest few nanometers of the material are sampled by the simplest method, ATR FTIR. Further, since FTIR requires the vibrational mode to have a dipole moment associated, this technique can present challenges for low polarity functional groups. Scheme 6 presents common functional groups and their distinctive absorption wavenumbers within an IR spectrum.56 FTIR primarily serves as a qualitative method for identifying functional groups, as each group has distinct extinction coefficients, ensuring specificity in identification. However, some scientific studies have demonstrated that, FTIR can quantitatively assess the extent of crosslink formation with appropriate data analysis and calibration.57,58
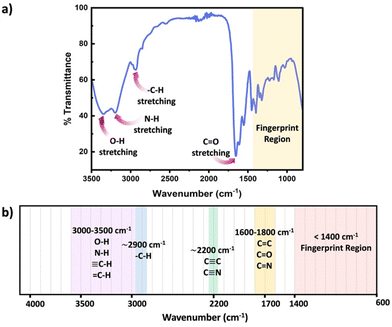 | ||
| Scheme 6 (a) Schematic diagram of a typical IR spectrum, (b) schematic representation of regions where the major bonds normally absorb. | ||
Raman spectroscopy is a complementary technique to FTIR for the determination of functional groups.59,60 While FTIR analysis gives limited information about nonpolar bonds, such as S–S bond in vulcanized rubber, Raman spectroscopy offers detailed insight into functional groups within the polymeric networks, particularly when there is a change in bond polarizability associated with the vibrational mode. Raman spectroscopy excites the molecule with laser light, and measured differences between the incident and emitted photon energies to identify vibrational energy levels and functional groups. Sample preparation is comparable to FTIR. Unique challenges with Raman arise if the network has strong fluorophores or chromophores that interact with the laser light and could present their own signals.
There are certain advantages and disadvantages associated with both IR and Raman techniques. As mentioned earlier, the FTIR technique does not depend on the sample's polarizability, unlike Raman spectroscopy, is highly dependent on the polarizability of the sample. FTIR offers lower spatial resolution in imaging applications, whereas Raman offers higher spatial resolution. Sample preparation is more straightforward for Raman compared to FTIR, with Raman needs requiring minimal or no preparation at all. This is because Raman utilizes a laser to target the sample and, information is collected through scattered lights. Instead, FTIR requires, careful attention to sample is needed for transmission IR, however, this can be avoided by using an ATR cell where the only concern is strong contact with the cell surface. FTIR spectra can experience interference from water absorption bands when using aqueous samples, while Raman is less affected by the water. However, both Raman and FTIR provide vibrational states associate with different functional groups offering rapid and, cost effective methods compared to other techniques.
An advantage of IR and related measurements is that they can be performed in real time. This can evaluate changes in network properties over time, for instance identifying monomer conversion as demonstrated by Anseth et al. in Fig. 1.61 Using IR, the concentration of double bonds could be followed over time, and the cessation of polymerization/crosslinking of diethylene glycol dimethacrylate occurs whenever the shutter is closed, confirming the photochemical process.
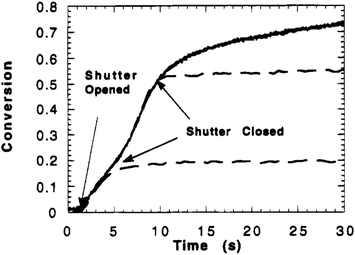 | ||
| Fig. 1 Double bond conversion versus polymerization time for diethyleneglycol dimethacrylate photopolymerized with 110 mW cm−2 of UV light and1.0 wt% Irgacure 651. Full cure (solid line) and shutter closed after 3.9 and 9.4 s (dashed line) (reproduced from ref. 61 with permission from American Chemical Society, copyright 1995). | ||
Sol–gel analysis
Polymer networks, despite being crosslinked with effectively infinite molecular weight, typically contain a fraction of the polymers that remain soluble and unconnected to the network. The presence of these chains can impact the properties of the polymer systems. This soluble polymer fraction is called the soluble or sol fraction. The insoluble, crosslinked network is referred to as the gel fraction.To separate the soluble components from the network, solvents are employed to swell the polymer network, causing the soluble polymers to dissolve and disperse into the solvent. This process involves dilution, as illustrated in Scheme 7 This can be achieved using repeated swelling in solvent or using a Soxhlet extraction process.8 The sample preparation for sol–gel analysis is straightforward, as the polymer network (typically 10 s to 100 s of mg) will be placed in a large amount of solvent either by immersion or Soxhlet. However, care must be taken to not damage the swollen gel material which can be quite brittle. The extracted gel and sol fractions can be characterized separately, although the method will only fractionate soluble and insoluble components, and very high molecular weight soluble polymers can be taking long extraction times to fully separate from the network. At the most basic level weights of the sol and gel fraction can be determined, although other techniques such as solution NMR or SEC are possible for the sol. Further consistency in functionality between the sol and gel could be determined by FTIR or Raman spectroscopy.
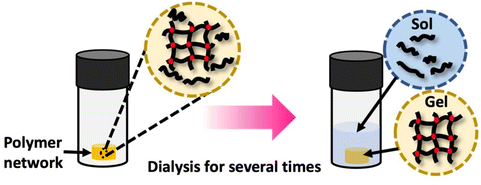 | ||
| Scheme 7 Gel extraction process: the crosslinked network is dissolved in an appropriate solvent for a specified duration. Subsequently, the weights of the dried sol fraction and gel fraction are measured. Sol–gel fraction is quantified using eqn (1). | ||
The gel fraction can be defined as follows:
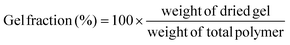 | (1) |
The corresponding sol fraction can be evaluated from the gel fraction, with
| Sol fraction + Gel fraction = 100% | (2) |
In many cases the sol fraction can impart unique properties to the overall material, such as facilitating energy dissipation.62–64 The presence of soluble polymer segments within the network allows for increased mobility and the ability to absorb and dissipate mechanical energy. However, it is important to consider that the sol fraction can also migrate or leach into the surrounding regions under specific conditions or environment. Additionally, the presence of the sol fraction can reduce the density of elastically effective network crosslinks. The soluble polymers within the sol fraction do not contribute to the load bearing network structure and essentially act as voids within the material. As a result, the density of interconnected crosslinks, which provide mechanical strength and rigidity, is decreased.65
Typically, sol–gel analysis can be used to assess the unreacted fraction of monomers in crosslinked polymer materials.66,67 However, as illustrated in Fig. 2, it can also be employed to monitor the in situ progression of the curing process in crosslinked polymers (e.g.: poly urethane(PU)).50 Initially, during gel formation, no gel is fraction is observed. Following an induction period (largely dependent on the types and ratios of isocyanate and polyol) gel formation initiates, and the gel fraction increases rapidly as the curing process advances before eventually leveling off. In the absence of sophisticated instruments for monitoring the curing process, sol–gel fraction analysis provides a straightforward and effective method to determine the progress of curing process.
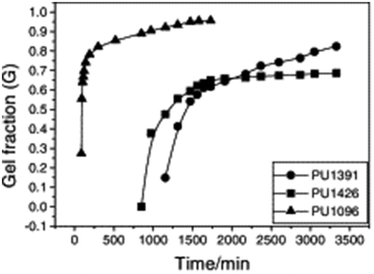 | ||
| Fig. 2 Dependence of gel fraction on the curing time of PU at room temperature (reproduced from ref. 50 with permission from Elsevier, copyright 2000). | ||
Swelling ratio analysis
One of the key features of most polymer networks is their ability to swell rather than dissolve in a solvent. The swelling behavior is a result of the network structure and the interactions between the polymer chains and the solvent molecules.69 However, the swelling ratio can be used to evaluate various properties such as density of crosslinks as will be discussed later. Scheme 8 depicted the steps involved in evaluating the swelling ratio. A solvent is introduced to a polymer network, leading to the infiltration of solvent molecules into the network structure. As a consequence, the size of the polymer network increases. Typically, excessively crosslinked polymers tend to absorb less solvent, providing insights into the internal structure of the polymer.70 Two common approaches for determining swelling ratio are gravimetry and optical analysis.71 A higher swelling ratio means the network's mass and volume will increase more upon full exposure to the solvent at equilibrium swelling. Sample preparation for swelling analysis is simple, and requires the material be measurable by weight or volume (typically 10 s of mg of network is sufficient), and it is fully immersed in the solvent to be studied. Mass or dimension is measured in the dry state, and the swollen state. The dry weight is usually measured before the swelling test. Following the chemical synthesis of the material, there may be some unreacted monomers and crosslinkers remaining within the sample matrix. Initially, these unreacted compounds should be removed from the matrix by washing the materials with a suitable solvent and drying them thoroughly until the sample weight remains constant over time. Samples that are already fully dried and free of unreacted compounds are utilized to determine the dry weight of the materials.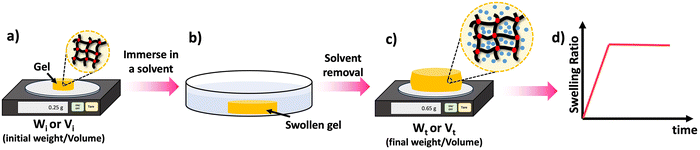 | ||
| Scheme 8 Swelling process: (a) take the dry weight/volume of the material, (b) swell the material in an appropriate solvent for a given time (t), (c) take the wet weight/volume of the swollen material, (d) calculate the swelling ratio using the eqn (3) and (4) and plot the SRs against the time to study the material's swelling kinetic profile. | ||
By comparing swelling ratios of related networks, uniformity can be determined, since more uniform networks tend to swell better. Additionally, crosslink density can be evaluated since higher crosslink densities reduce chain flexibility and restrict swelling. Care must be taken not to damage the often-brittle swollen networks during measurement. Additionally, if measuring by weight, samples with the excess solvent removed should be rapidly measured after swelling to minimize evaporation.
In the context of swelling, the choice of the solvent used in the experiment is crucial. Different polymers have solvents that are compatible with them. For instance, hydrogels can be swollen using water. Alternatively, testing swelling against a library of solvents can identify solvents that the material is likely to be compatible against and those that will at the very least affect the material properties.72
Swelling ratio (SR) can be defined either by mass or volume using eqn (3) and (4) respectively:73
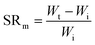 | (3) |
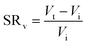 | (4) |
It is important to note that swelling ratios can be defined such that no swelling leads to either a swelling ratio of 0 or 1. This does not change the equations above substantively, other than to add/subtract the initial weight/volume in the numerator. However, it is important that the method of defining swelling ratio is clearly stated.
An elegant application of swelling ratio is an indirect measure of network homogeneity. More homogeneous network are able to reach higher swelling ratios.74 For instance Matyjaszewski et al. found that atom transfer radical polymerization (ATRP) gave more uniform polymer chains and as a result more uniform networks than conventional free radical polymerization (FRP).75 This led to higher swelling ratios as seen in Fig. 3, even after the lower critical solution temperature (LCST) induces deswelling. Interestingly the authors found a significant inhibition of deswelling due to a skin like effect on the network surface. Similar examples of higher swelling and more uniform networks have been reported in the literature.34,76
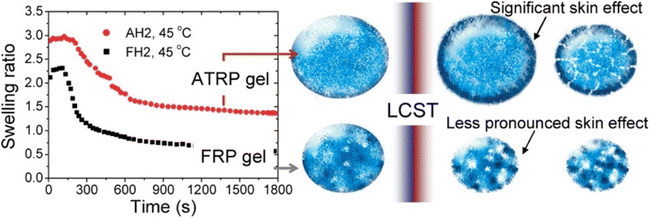 | ||
| Fig. 3 (Left) Swelling ratio over time for 2-(2-methoxyethoxy)ethyl methacrylate networks above the LCST for both ATRP and FRP networks. Right shows skin like effects on the periphery of the network (reproduced from ref. 75 with permission from American Chemical Society, copyright 2010). | ||
Mechanical analysis
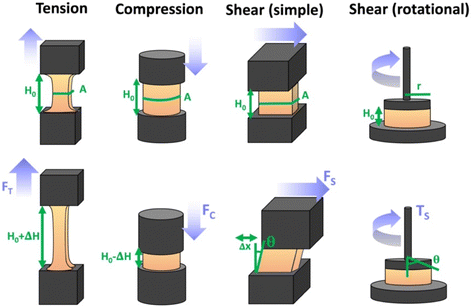
There are numerous modes of mechanical characterization, and the selection depends to a large extent on the state of the material. Most common are tension, where the material is extended, typically along one axis, compression where the materials is compressed along an axis, and shear which can either be simple, (two plates moving against each other) or rotational between parallel plates. These modes of mechanical deformation are given in Scheme 9 below, as well as the forces and characteristic displacements. In all cases mechanical analysis measures how, the polymeric material responds mechanically to applied deformation. The principal measurements are displacement and force or torque. These raw measurements of displacement and force are converted to three core concepts of: stress; strain; and modulus. Stress (σ) is the applied force, normalized by the sample's cross-sectional area. In most cases engineering stress is reported, where the cross-sectional area in the denominator is the initial cross-sectional area and unchanged throughout the analysis. Strain (ε) is the deformation, normalized by the initial sample's size, although in some cases stretch ratio (λ) is reported, where λ = ε + 1. Stress and strain are independent of the sample size and can be compared between labs or experimental series. However, in most cases the overall force and displacement are measured, negating effects of microstructures or inhomogeneity in many cases. Often to obtain detailed information of materials properties, mechanical measurements should be repeated at a range of temperatures, since properties and phase transitions can induce major changes in mechanical properties.Typical stress and strain in each mode is given in Table 1. Depending on the mode of testing sample preparation and geometry should be considered. For tensile testing rectangular or dogbone shaped materials should be used.77 If only small strain is applied, and the material is not tested to failure, either shape can be used, although high strain materials taken to failure perform better with dogbone shapes that have a higher cross-section in the grips, which limits failure from cracks that propagate from the grips. For compression tests, cylindrical samples are preferred, and to ensure there is sufficient compressive travel, the height of the cylinder (H0) should exceed its diameter. Simple shear would typically use rectangular samples, which are typically thin compared to the sample dimensions A1/2, since this type of testing is common in adhesive lap shear tests where a thin adhesive is applied to join 2 surfaces.78 Finally, rotational shear that is commonly used in parallel plate rheology uses thin circular discs. Care should be taken either to match the radius of the smaller plate, or if the sample is smaller than both plates, that it conforms to a disc of known radius. In general, for parallel plate rheology the radius will be greater than the gap between the plates (H0).
The modulus of the material is the slope of the stress–strain curve, giving a measure of the material's resistance to deformation. In general, compression and tensile testing yield the Young's modulus of a material, often labeled E or Y, while shear testing yields the shear modulus, typically denoted G. The relationship between shear and Young's modulus is given by,83
| E = 2 (1 + ν) G | (5) |
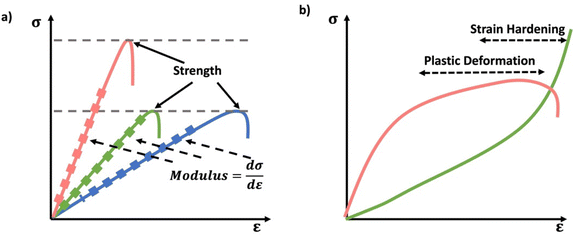
Especially at small strains the modulus of the material can be estimated as the ratio of stress to strain as if given in Table 1. The modulus is an intrinsic property of the material, and does not depend on the extent of deformation, at least not to within small deformations. Networks with a high modulus are substantially harder to deform and require larger stresses to achieve even modest deformation as demonstrated in Scheme 10. In simple mechanical tests, such as tensile, compression or lap/simple shear testing, a polymer network is strained at a constant rate until failure. This allows calculation of stress, strain and as a result peak stress, strain at break and modulus. Examples of stress–strain curves are given in Scheme 10, showing strength as peak of stress–strain curve, failure where material breaks and examples of modulus. Additionally, phenomena such as plastic deformation and strain hardening are shown. Plastic deformation is typically seen by a plateau or substantial reduction of the modulus after a given applied strain, and it is typically associated with some form of non-reversible stress–strain properties or energy dissipation.84,85 Strain hardening on the other hand leads to the reverse phenomenon, where the stress increases rapidly with applied strain, and it is associated with strain. This often occurs when networks are deformed to the point where there the bonds are close to extended due to the deformation. Strain hardening effects can be effectively captured by models such as those highlighted by Sheiko and coworkers.86
The preferred analysis mode depends on the materials physical state. Rigid polymer networks, with high amounts of crystallinity or a high glass transition temperature (substantially above room temperature) can be characterized by tensile test to failure or dynamic mechanical analysis (DMA).87 Softer elastomeric materials can be characterized by tensile analysis, compression analysis, DMA or shear rheological analysis. Very soft elastomers and hydrogels are not well-suited to tensile analysis, since they can break upon mounting the specimen and instead compression analysis is common, along with shear rheology.
Stress–strain analysis is critical for the applications of the material, since the failure strain, strength and modulus for each application are unique. A powerful example of this is from the work of Sheiko et al. who found that by careful choice of polymer architecture, they could match the mechanical properties of a diverse range of biological tissues, as indicated in Fig. 4. The key feature of these networks is their bottlebrush characteristic, where the polymer backbone has shorter but nontrivial chains emerging from it, extending the backbone.88
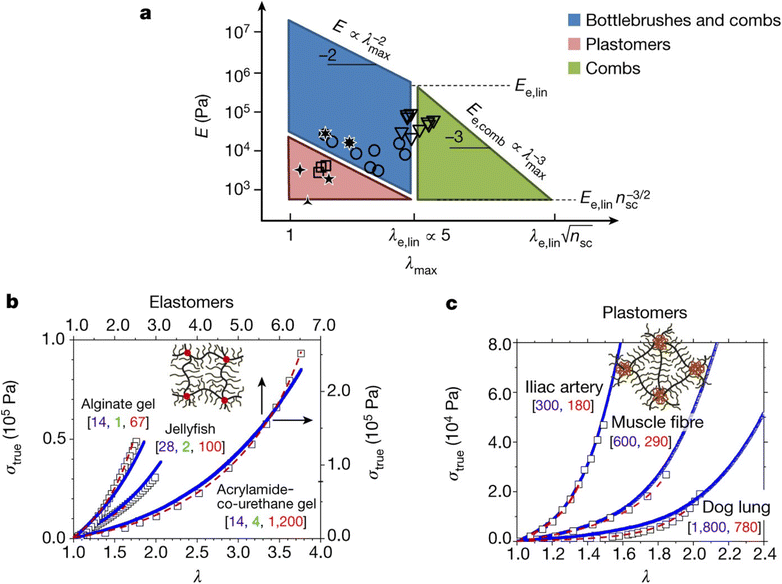 | ||
| Fig. 4 (a) PDMS bottlebrushes, combs and plastomers with the mechanical properties of biological materials. This graph shows these properties (circles, bottlebrushes with ng < 2; triangles, combs with ng > 2; squares, ABA copolymers (plastomers)), along with the properties of brain, arteries, lungs, eye lens and jellyfish. The λmax boundaries correspond to the elongations-at-break of conventional linear-chain networks (λe,lin ≈ 5) and comb-like networks that result from entanglements of the network strands. The E boundaries correspond to the entanglement plateau moduli of linear chain (Ee,lin) and comb-like chain melts. The diagonal boundaries are provided by inverse E and λmax relationships of linear and comb-like networks. The lower boundary of the blue parallelogram, Pa, corresponds to bottlebrush networks with long side chains of about 100 units. (b) Stress–strain data (squares) for alginate gel, jellyfish tissue and poly(acrylamide-co-urethane) gel, together with fitting analysis of the data (dashed red lines), and curves for PDMS bottlebrush and combs synthesized via fitting analysis with the indicated architectural [nsc, ng, nx] triplets (blue lines). (c) Stress–strain data (squares) for iliac artery, muscle and dog lung tissue, together with fitting results obtained (dashed red lines), and stress–strain curves from PMMA–PDMS–PMMA mimics (solid blue lines) with different degrees-of-polymerization of the PDMS bottlebrush backbone (nbb) and PMMA linear chains (N) as indicated by [nbb, N]. Each experimental curve in (b and c) represents the average of at least three measurements with a relative standard deviation of less than 5% (reproduced from ref. 88 with permission from Springer Nature, copyright 2017). | ||
Idealized elastic and viscous stress responses to an applied strain that is eventually removed are given in Scheme 11a. The ideal elastic material perfectly stores the energy and maintains stress while being strained, while the ideal viscous material dissipates the energy as the strain is being applied or removed with no stress during constant strain periods. Most polymer materials are to some extent viscoelastic, having both viscous and elastic characteristics. This viscoelasticity implies the polymer networks have both the ability to store (elastic) but also dissipate (viscous) energy, and the relative contribution of the viscous and elastic responses depends on the timescale of the experiment. A schematic of viscoelasticity is given below in Scheme 11b inspired by ref. 89, as a ball being dropped. The amount the ball is able to return after bouncing corresponds to the storage and the amount of height not recovered corresponds to the loss. A core feature of viscoelastic materials is the presence of a characteristic or relaxation time, typically denoted τ.90τ corresponds to the timescale at which applied stresses relax in the network through chain or segmental mobility or as is typical for dynamic networks, bond exchange. In permanently crosslinked polymer networks, this is most easily calculated through stress relaxation experiments shown in Scheme 11c. In stress relaxation experiments the sample is placed under a constant strain, and the decrease in stress is measured over time. In general, for viscoelastic crosslinked networks it is simplest to measure relaxation time, τ, through stress relaxation experiments, where the decay in stress can be fit to exponential decay.91 Systems with complex relaxation processes can be described with either a stretched exponential model,91 or a multiexponential decay with multiple relaxation times also known as a Prony series.92,93 A closely related experiment is creep, where a constant stress is applied to the material, and the strain is measured over time. Often the stress is eventually removed to measure recovery This is demonstrated in Scheme 11d. More complex models and data analysis are needed for analysis of creep data, although creep experiments can be important for evaluating stability and ability to withstand permanent deformation.
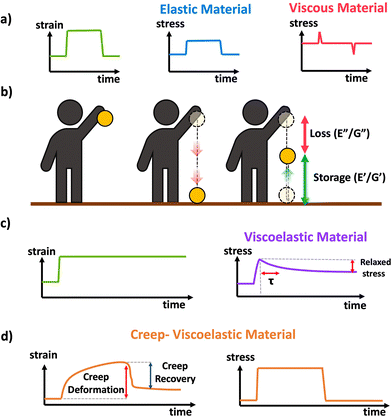 | ||
| Scheme 11 (a) Schematic of stress response to strain applied to a perfectly elastic (blue) and perfectly viscous (red) material, (b) conceptual demonstration of viscoelasticity in the context of a ball dropped (image inspired by slide 15 from ref. 89), (c) schematic response of a viscoelastic material to applied strain in a stress relaxation experiment. (d) Schematic response of a viscoelastic material to a transiently applied stress in a creep experiment. | ||
In contrast to simple constant or near constant strain rate experiments such as tensile or compression tests often taken to high strain or failure, DMA or oscillatory shear rheology applies a small deformation (typically <5% strain) to the material. DMA and small amplitude oscillatory rheology (SAOR) measure the mechanical response of the material to the applied deformation. Using small deformation in DMA and SAOR ensures that the material is in the “linear viscoelastic regime”, where stress is proportional to strain. At larger deformations, stress can be highly non-linear with regards to strain, leading to complex behaviors such as strain stiffening and plastic deformation, and eventually rupture (Scheme 10).88 Therefore, for meaningful DMA and SAOR analysis it is essential to perform a strain sweep experiment, where the modulus is measures at different applied strain values. Higher applied strain increases sensitivity and signal to noise, due to a larger measured force or torque, although it runs the risk of exiting the linear viscoelastic regime. Therefore, strain sweeps should be performed up to at least ∼10% strain to ensure that measurements are within in the “linear viscoelastic regime”, and these measurements are relatively fast and do not take substantial instrument time.
When performing DMA or SAOR experiments a sinusoidal small amplitude strain is applied to the material. In DMA or SAOR the in-phase component is consistent with elastic responses, while the out of phase responses are consistent with viscous responses. This in phase or out of phase response derives from the sinusoidal application of strain in these methods. As highlighted in Scheme 11a, elastic stress responses follow the strain, or are in phase, while viscous responses respond to changes in strain, which corresponds to being 90° out of phase with a sinusoidal strain. In practice, viscoelastic materials have both viscous and elastic properties leading to a phase difference, δ, between 0° and 90°. The phase difference, δ, between measured σ and applied strain ε is denoted δ, with tangent of δ called the dampening factor.
The viscoelastic responses are typically reported as complex moduli, with E′/G′ being the elastic or storage modulus, and E′′/G′′ being the viscous or loss modulus. E refers to the Youngs modulus, commonly measured in tensile mode for instance, and G is the shear modulus measured in shear mode, as shown in Scheme 12. The tangent of the phase difference, δ, can be related to the storage and loss moduli as follows:
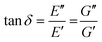 | (6) |
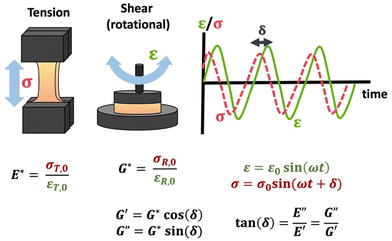 | ||
| Scheme 12 Schematic of tensile DMA and SAOR, including σ response to sinusoidally applied ε, and the complex moduli E*/G* and the storage (E′/G′) and loss (E′′/G′′) moduli. Note that σT,0, εT,0, σR,0, and εR,0 are given in Table 1. | ||
These can be studied at a constant frequency as a function of temperature (temperature sweep), to identify key thermal transitions, or at a constant temperature as a function of frequency (frequency sweep) to identify how the material may behave under different types/timescales of mechanical challenges. It is also possible to observed changes in materials properties over time by monitoring evolution of these moduli (time sweep). Additional characterization of polymer network mechanical properties can be performed using atomic force microscopy (AFM) as discussed in the section on morphological characterization.
Using DMA or SAOR can give information on the underlying polymer dynamics beyond the moduli obtained from standard stress–strain analysis.94 For instance, network dissipation and storage ability can be tuned by choice of linker. For instance, Ahmadi et al. showed that the in bipyridine based coordination bound networks the choice of the metal dramatically impacted the gel properties. Using the more strongly binding Fe gave gel like properties at essentially all studied frequencies, while the less strongly binding Co gave gels at high frequencies but allowed exchange and liquid like properties below a crossover frequency. This is seen in Fig. 5.95
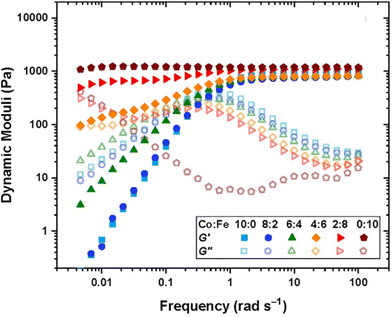 | ||
| Fig. 5 Dynamic storage (filled symbol) and loss (open symbols) moduli of transient networks formed by different combinations of metal ions, as shown in the legend at 25 °C for tetraEPh20k30Fe3 (adapted from ref. 95 with permission from American Chemical Society, copyright 2022). | ||
Molar mass between crosslinks
The molar mass of polymer between crosslinks is a fundamental aspect of networks that defines the network structure of a crosslinked polymer.96 It denotes the average molar mass of the polymer fragments between two crosslinked chains and impacts the swelling behavior and mechanical properties of the material.96 Polymers are not perfectly crosslinked as there can be a few irregularities and inconsistencies in the network.37,97,98 A typical example of the anticipated inconsistencies is the presence of dangling loops, which hang loosely on the main polymer chain.98 They are a part of the network but have no significant effect on the elasticity of the materials. The presence of dangling loops in a network increases the molar mass between elastically effective crosslinks, compared to the value based on stoichiometry. This results in softer materials than anticipated based on reaction conditions.98Although a crosslink cannot be chemically measured using the methods described below, detailed and sophisticated analysis is required, which is beyond the scope of this article. To a first approximation, the molar mass between crosslinks can be calculated using shear or Young's modulus.99 Here the experimental set up is identical to standard shear testing or DMA. However, this analysis requires the material be in the elastomeric regime, or above Tg. Additional discussion of glassy vs. elastomeric regime is given in the section on thermal analysis. The elastomeric regime having flexible materials with a modulus in the order of 1 MPa, with the material behaving as a rheological solid, i.e. E′′/G′′ < E′/G′, or equivalently tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ < 1. The key concept is that each crosslink functions as a small spring, making network deformation more difficult and resulting in a higher modulus. With more crosslinkers, or molecular scale springs, the material has a higher modulus, or is more difficult to deform. The shear modulus (G) of an ideal crosslinked elastomer can be related to molar mass of crosslink by the eqn (7);100
δ < 1. The key concept is that each crosslink functions as a small spring, making network deformation more difficult and resulting in a higher modulus. With more crosslinkers, or molecular scale springs, the material has a higher modulus, or is more difficult to deform. The shear modulus (G) of an ideal crosslinked elastomer can be related to molar mass of crosslink by the eqn (7);100
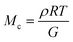 | (7) |
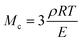 | (8) |
Swelling experiments, in addition to mechanical tests, can be used to determine the molar mass between crosslinks. Again, the swelling ratio experiments to calculate Mc can be set up the same way as for a typical swelling experiment, with essentially the same measurements. The degree of swelling in a crosslinked network depends on the interaction between the polymer and the solvent as well as the crosslinking density. The core concept here is that highly crosslinked networks have a relatively low molecular weight between crosslinks, which restricts swelling in solution. The Flory–Huggins interaction parameter (χ) and molar mass between crosslink are connected to the equilibrium degree of swelling using Flory and Rehner's theory.101
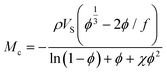 | (9) |
Although facile, it is important to note that both the modulus and swelling based relationships for molar mass between crosslinks are based on ideal conditions and provide an estimate of the effective distance between crosslinks. Deviation is expected from ideal input ratios due to factors such as chain entanglements, dangling ends incomplete crosslinking and loop formation.96,101 In particular, the formation of loops and non-infinite primary chain lengths will cause a significant discrepancy between the measured molecular weight between crosslinks evaluated by swelling or DMA and the molecular weight between crosslinks based on monomer feed. In general, the measured molecular weight between crosslinks will be higher than that predicted from reaction stoichiometry due to loops and dangling ends.
As an example, from the literature, dynamic or exchangeable crosslinks were used to correct for network defects caused by elastically ineffective loops.103 When analyzing poly(hydroxyethyl acrylate) networks crosslinked with a dynamic thiol-Michael linker heating the network allowed bond exchange to occur converting loops to crosslinks.103 This increased modulus and decreased swelling, consistent with a higher molar mass between crosslinks as seen in Fig. 6.
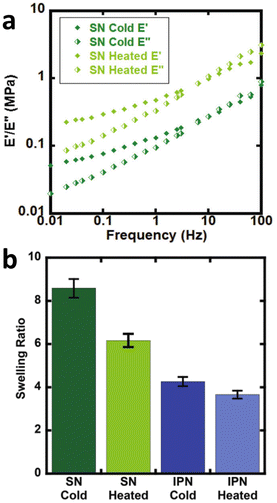 | ||
| Fig. 6 (a) Dynamic mechanical analysis showing the increase in modulus upon heating the dynamically crosslinked polymers (b) Reduction of the swelling ratio for the same materials as well as interpenetrated networks (reproduced from ref. 103 with permission from Royal Society of Chemistry, copyright 2021). | ||
Thermal analysis
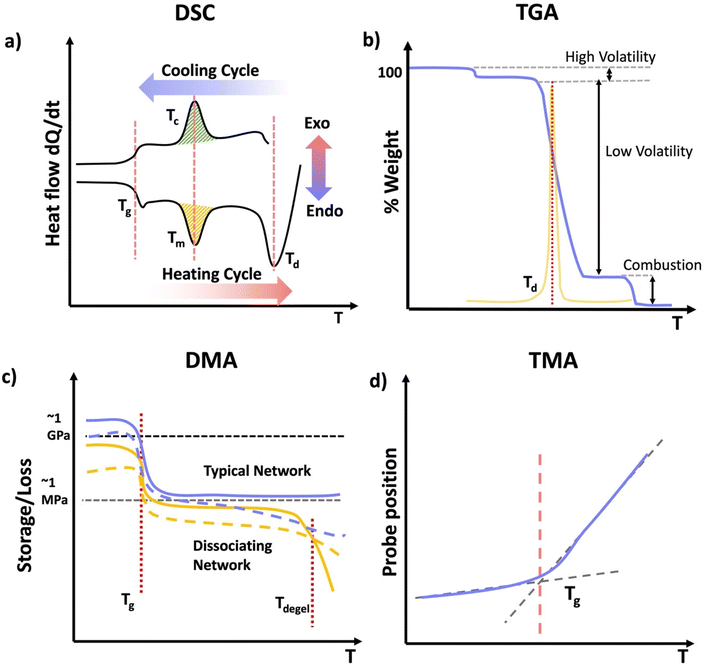
Thermal analysis of polymers consists of a set of polymer characterization techniques that provide information on changes in material properties in response to changes in temperature. A wide range of disciplines including chemical manufacturing, pharmaceuticals, food science, materials science, cosmetics, and polymer sciences use thermal analysis. Thermal analysis is used in both industry and academia to understand material properties and thermal transitions that determine a material's suitability for intended applications. Thermal analysis can provide several key temperatures including, the glass transition temperature (Tg), melt temperature (Tm), and decomposition temperature (Td). Tg correspond to the temperature where the material changes from a “vitrified” or “immobilized” liquid where chain mobility is very low, viscosity is high, and the material is glassy below Tg, to a softer, rubbery or flowing polymer above it. Tg coincides with polymer backbone mobility. Tg is ubiquitous among polymers. Tm corresponds to the temperature at which packed polymer crystal domains dissociate and form an overall amorphous polymer above Tm. Importantly, Tm only applies to polymers with semicrystalline properties, having crystalline domains in the material. Td corresponds to the temperature at which the material decomposes, or more commonly the onset of degradation. For all practical materials applications the material should be used well below Td.DSC measures the heat flow Q into or out of a material as a function of temperature or time. This is achieved using two pans, where one is blank and the other contains several milligrams of sample, which should be in good contact with the pan surface. It is important that thermal history of the sample be erased in DSC analysis by heating significantly above any glass or melt transitions. Another advantage of using an initial heating cycle is that traces of residual solvent can be removed, if the sample pan is not hermetically sealed, since this can plasticize the material and shift transition temperatures. This initial heating cycle can be embedded into the run sequence by performing multiple heat/cool cycles that span any transition of interest and rejecting the first heating cycle. For DSC analysis, a sample material is heated, cooled, or kept at a constant temperature to determine energy released or absorbed by material. Phase transitions and thermodynamic parameters such as heats of fusion or specific heat capacity can be measured by this technique. Tg can be obtained from DSC as well as in techniques such as DMA. In DSC the material will show a change in heat capacity across the Tg, typically seen as a step, with higher heat capacity above the Tg due to backbone mobility. Other parameters obtained from DSC include melting Tm for transitions from crystalline domains to amorphous states, the related crystallization temperature (Tc). These melt and crystallization phase transitions occur with defined peaks in the heat flow vs. temperature data from DSC as the crystalline domains melt (Tm) or crystalize (Tc), similar to the way that solids melt to liquids and vice versa. Since DSC measures heat flow, the data can be converted to thee enthalpy (ΔH) associated with a melt or crystallization transition, specific heat capacity (Cp) my evaluating the change in heat flow with temperature and degree of cure by calculating the total heat flow compared to the theoretical enthalpy of polymerization (Scheme 13a).104
Due to the relatively simple set up DSC can easily be used to evaluate changes in network structure and degradation over time. As an example, Chen et al. studied changes in epoxy networks over time using DSC.105 Maintaining a constant temperature of 193 °C led to degradation of the polymer network, as evidenced by a reduction in the Tg over time in most systems shown in Fig. 7, especially with materials with higher α-Terp content.
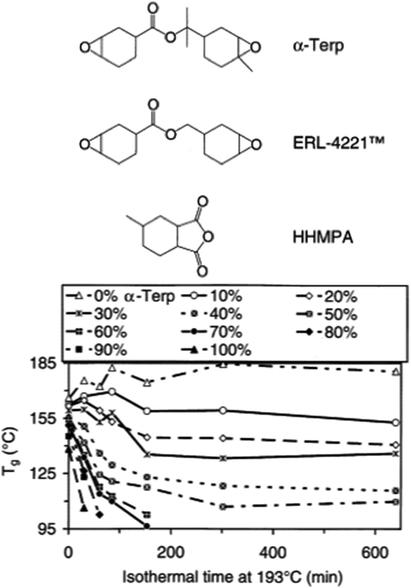 | ||
| Fig. 7 Glass transition temperatures of the samples used in swelling tests as a function of their rework times. The greater the amount of α-Terp in the material, the lower the Tg (reproduced from ref. 105 with permission from Elsevier, copyright 2004). | ||
Thermogravimetric analysis (TGA) measures the mass of a material as a function of temperature (Scheme 13b). In TGA the sample is heated at a constant heating rate, held at a constant temperature for isothermal measurements, or subjected to a non-linear temperature programming for sample controlled TGA (also called SCTA). In TGA, typically several mgs of sample are subjected to a temperature ramp. However, temperature ramp TGA is by far the most common use of TGA and identifies Td. This is typically determined by analyzing the derivative of the weight change with respect to the increase of temperature. Td represents the temperature at which the maximum degradation rate is observed during the process. This degradation temperature gives the maximum useable temperate of a material is obtained from TGA, and provides temperature limits for other analytical methods.106 Other applications of TGA include determination of oxidative stability, composition of materials, decomposition kinetics, moisture and volatile content, and estimated lifetime of a material.107 However, if the network or material has absorbed any moisture from the atmosphere, or has any residual solvent, this can show up as mass loss near the boiling point of that solvent (high volatiles in Scheme 13b). Further, due to polymer degradation (main chain scission, side group scission, elimination and depolymerization), low volatile compounds will evolve as the polymer losses its total mass. Finally, when the polymer is heated above its ignition temperature, combustion components (e.g.: carbon black) will be generated as it burns. For further characterization, TGA can be coupled with FTIR or mass spectrometry (MS) to identify the volatile compounds that evolve as a result of the thermal decomposition of polymers.107
Thermomechanical analysis (TMA) measures the deformation or changes in dimensions of a material as a function of temperature, time, and force.108 The main parameter obtained from a TMA experiment is the coefficient of thermal expansion (CTE). The specimen of the network if placed under an essentially zero force, and the material is subjected to a temperature ramp. As the material undergoes thermal expansion, the size and hence position of the probe needed to maintain the zero force increases, thereby giving the CTE. Additionally, as the material crosses the Tg, the CTE changes as new molecular motions are enabled above the Tg. Thus, the temperature where the interaction of the low and high slope CTE lines occurs is the Tg. Other parameters such as Tg and indentation softening temperature can also be obtained from TMA measurements.109
DMA is instrumental in determining moduli E′, E′′, and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ of materials as a function of temperature.110 DMA combines the mechanical analysis highlighted in the above section, with temperature ramps. Therefore, sample preparation should follow those typical of mechanical analysis, except the temperature is controlled and typically gradually increased. DMA is most commonly performed in rotational shear or tension for polymer networks. Network properties that can be identified by DMA include Tg and if applicable a temperature at which the material flows, although the latter is rare for covalently crosslinked networks, except dynamically crosslinked networks.111 As a network is heated is transitions from a glassy state with a very high modulus in the order of GPa to an rubbery material with substantially lower modulus on the order of MPa. This substantial drop in modulus occurs through the mobility of the backbone, and it typically gives a peak in tan
δ of materials as a function of temperature.110 DMA combines the mechanical analysis highlighted in the above section, with temperature ramps. Therefore, sample preparation should follow those typical of mechanical analysis, except the temperature is controlled and typically gradually increased. DMA is most commonly performed in rotational shear or tension for polymer networks. Network properties that can be identified by DMA include Tg and if applicable a temperature at which the material flows, although the latter is rare for covalently crosslinked networks, except dynamically crosslinked networks.111 As a network is heated is transitions from a glassy state with a very high modulus in the order of GPa to an rubbery material with substantially lower modulus on the order of MPa. This substantial drop in modulus occurs through the mobility of the backbone, and it typically gives a peak in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ near the center of this transition. The peak in tan
δ near the center of this transition. The peak in tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ is used to give the Tg by DMA, or equivalently SAOR. It is important to note that in many elastomeric networks near Tg, tan
δ is used to give the Tg by DMA, or equivalently SAOR. It is important to note that in many elastomeric networks near Tg, tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ > 1, however the glassy and rubbery state behave as viscoelastic solids, where tan
δ > 1, however the glassy and rubbery state behave as viscoelastic solids, where tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ < 1 both above and below Tg. A flow state occurs when tan
δ < 1 both above and below Tg. A flow state occurs when tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ > 1 above a certain temperature, or equivalently the viscous modulus E′′ exceeds the storage modulus E′ above a certain temperature. This is indicative of the network losing integrity through loss or dissociation of crosslinks in a network, leading to a viscous polymer melt like state. Regardless of the technique employed, thermal analysis of polymeric materials is an important concept to understand when navigating the physical characterization of materials. When performing DMA, it is essential to consider the materials state above and below certain transitions to avoid breaking the sample due to high strains in any glassy states or slippage from the grips/plates, which would lead to poor quality data.
δ > 1 above a certain temperature, or equivalently the viscous modulus E′′ exceeds the storage modulus E′ above a certain temperature. This is indicative of the network losing integrity through loss or dissociation of crosslinks in a network, leading to a viscous polymer melt like state. Regardless of the technique employed, thermal analysis of polymeric materials is an important concept to understand when navigating the physical characterization of materials. When performing DMA, it is essential to consider the materials state above and below certain transitions to avoid breaking the sample due to high strains in any glassy states or slippage from the grips/plates, which would lead to poor quality data.
One elegant feature of DMA And SAOR temperature sweeps is that the large change in modulus across the glass transition is also quite sensitive to changes in material properties. Therefore, temperature sweep DMA is a powerful method of identifying changes in processing polymer networks for example. Chen et al. show this though reprocessing of dynamic crosslinks of hydroxyurethanes (Fig. 8).112 Depending on the backbone, either full recovery was observed at each reprocessing, as per a polybutadiene backbone (PB) or with a small crystallization like event in poly(tetramethylene oxide) (PTMO), despite both having essentially the same final modulus.
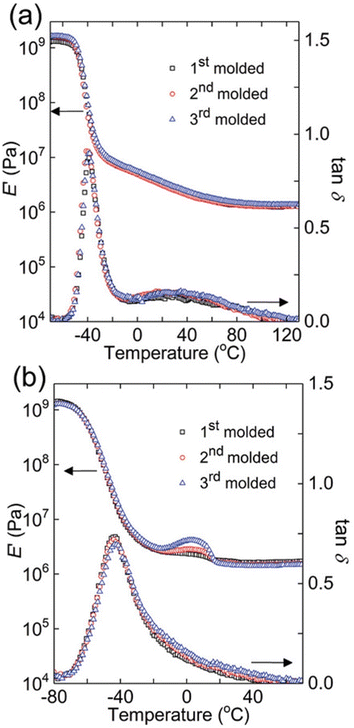 | ||
Fig. 8 Dynamic mechanical responses of (a) PB networks and (b) PTMO networks: E′ and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ as functions of temperature for 1st molded (squares), 2nd molded (circles), and 3rd molded (triangles) samples (reproduced from ref. 112 with permission from John Wiley and Sons, copyright 2019). δ as functions of temperature for 1st molded (squares), 2nd molded (circles), and 3rd molded (triangles) samples (reproduced from ref. 112 with permission from John Wiley and Sons, copyright 2019). | ||
Morphological characterization
Microscopic analysis such as SEM, transmission electron microscopy (TEM), and AFM are often utilized in studying the micro and nano-structural features of network polymers. Investigations using electron microscopes can reveal topography, morphology, composition, and crystallographic information of materials. The following discussion will focus on morphology characterization using SEM, TEM, and AFM owing to their user-friendliness, ease of sample preparation, and simplicity of image interpretation.113SEM provides high-resolution visual information on the top ∼1 μm of sample material. Utilizing an electron gun, electrons penetrate the sample surface, creating numerous low-energy secondary electrons. The intensity of these secondary electrons is influenced by the surface topography. Consequently, an image of the sample surface is formed by mapping secondary electron intensity against the position of the scanning primary electron beam. As part of sample preparation prior to SEM analysis, sample must be cleaned with solvents like isopropanol, methanol, or acetone, followed by drying with compressed gas to remove impurities such as dust, mud, soli, etc. Water-cleaned samples can be oven-dried or heated using a hot plate and surface dust can be removed by these methods or by blowing compressed gas. Hard and dry materials require chemical fixation for structural preservation. Fixatives like glutaraldehyde, sometimes combined with formaldehyde and other agents such as aldehydes, osmium tetroxide, tannic acid, and thiocarbohydrazides have been employed. Typically, samples are affixed to holders or stubs using a double-sided conductive carbon and copper tapes. Alternatively, silver paint, when completely dry, is suitable for mounting before loading into the SEM chamber. To prevent charge-up phenomenon, nonconductive samples must be coated with a conductive metal layer (e.g. Au, Pt, Os, Ir, etc. using a sputter coater).114
One of the main advantages of SEM, as shown in Fig. 9, is its ability to employ SEM images to illustrate porosity and heterogeneity in superabsorbent hydrogels regarding their co-monomer content and molecular weight.115 Prepared with hydroxyethyl cellulose (HEC) and acrylic acid (AAc), these hydrogels undergo surface changes from smooth to granular with increasing AAc content (5% to 30%), attributed to enhanced AAc homopolymerization during gel formation (Fig. 9a–d). Additionally, Fig. 9e and f depicts the influence of crosslink density on pore sizes. HEC1300/AAc gels (5% AAc) exhibit prominent heterogeneity with a dense structure and smaller pores, while HEC90 gels (5% AAc) display a relatively smoother surface. This suggests that during the gelation of high molecular weight gel, AAc mobility is hindered by higher viscosity, leading to AAc homopolymerization and the formation of a rough network structure. Similarly, SEM proves to be a valuable tool for governing hydrogel porosity and heterogeneity in other samples as well.116,117
 | ||
Fig. 9 SEM images of HEC90/AAc hydrogels (Mv = 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) containing (a) 5%, (b) 10%, (c) 20%, and (d) 30% AAc, HEC1300 (e and f) and HEC1300/AAc gels (Mv = 130 000) containing (a) 5%, (b) 10%, (c) 20%, and (d) 30% AAc, HEC1300 (e and f) and HEC1300/AAc gels (Mv = 130![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) containing 5% AAc (g and h) (magnification: ×100ae and g; ×500f and h) (reproduced from115 with permission from Elsevier, copyright 2017). 000) containing 5% AAc (g and h) (magnification: ×100ae and g; ×500f and h) (reproduced from115 with permission from Elsevier, copyright 2017). | ||
AFM allows nanoscale lateral resolution (∼10 nm) for imaging polymers, polymer composites, and polymer blends, aiding in the characterization of morphology, microstructure, and crystallinity.118 AFM consists of a pyramidal silicon tip attached to a cantilever, serving as the primary sensor, with the tip position monitored using a laser to detect progressive changes in polymer morphology. Operating in contact, non-contact and tapping modes, AFM provides versatile imaging options. In the contact or static mode, direct tip–sample contact occurs, and characterization primarily relies on information gained from the permanent repulsive interaction between the sample surface and the tip. In the non-contact or dynamic mode, the cantilever oscillates at its resonant frequency without damaging the tip or samples surface. As it approaches the surface, attractive or repulsive forces on the surface adjust the resonance frequency accordingly. Moreover, dynamic mode operations do not require a vacuum, unlike SEM and TEM imaging, allowing measurements in air or liquid media. Tapping mode, an improved version of the non-contact mode, briefly contacts the sample edges with a greater oscillation amplitude, allowing mapping of soft or fragile samples without damage.119 Phase imaging in AFM maps variations in surface properties arising from differences in adhesion, friction, and elastic forces,120 enabling the observation of the surface properties beyond sole topology. Limitations of AFM include a smaller picture size compared to SEM, HR picture quality restricted by probe tip radius, and need for complementary techniques for quantitative information on phase composition, such as X-ray and light scattering.
In the past few decades, AFM has been employed for quantifying the mechanical properties of the soft materials via force-indentation curves.68 In this method, the sample is indented using a cantilever with a specific tip and a pre-stated velocity (Scheme 14a). Once the prescribed force is attained, the cantilever reverts to its original position by moving upward and detaching from the sample. The signals obtained from the deflection and displacement of the cantilever are then considered for the subsequent processes to extract the mechanical properties of the samples. As shown in the Scheme 14b, the difference between the approach and retraction curves can be used to estimate the viscosity of the sample. The apparent stiffness of the polymer sample is measured through the force–distance curve using below equation.
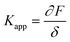 | (10) |
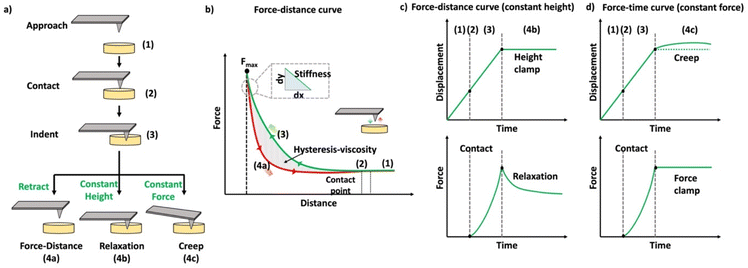 | ||
| Scheme 14 (a) Schematic representation of the methods used to quantify the mechanical properties of the materials. (b) Schematic diagram of a force–distance curve (the green curve represents the approaching curve where the probe indents the given sample until a specific force is reached, and the red curve represents the retraction curve where the cantilever retracts to the original position). (c) Schematic representation of the time-dependent indentation curve (constant height), (d) schematic representation of the time-dependent indentation curve (constant force) (reproduced with modifications from ref. 121 with permission from Springer Nature, copyright 2019). | ||
The Young's modulus can be calculated using basic model fitting to the force-indentation curves. The most commonly employed methods are Hertz, Derjaguin–Muller–Toporov (DMT), Sneddon, and Johnson–Kendall–Roberts (JKR) in these calculations.121–124 These models can be applicable for different types of indent geometries and sample properties.125 Parabolic geometries are commonly used in these type of measurements and the force calculations for this type of indent geometries are being calculates using the given Hertz model eqn (11).
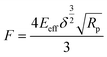 | (11) |
Indentation curves can be plotted in AFM by maintaining a constant height or force during the indentation process. In the case of constant height, the probe indents the sample to a fixed height and records the force exerted on the cantilever during a specified time, allowing observation of relaxation curves (Scheme 14c). Alternatively, when maintaining a constant load (force), the displacement of the cantilever is used to quantify the mechanical responses, especially creep behavior (Scheme 14d). AFM is employed to measure the viscoelastic properties of materials in both time and frequency domains, requiring prolonged probing or the use of oscillatory signals to assess phase lag for comprehensive examination of viscoelastic behavior.126
As illustrated in Fig. 10, AFM serves as a valuable tool for characterizing the local nano-rheological properties of softer gels, exemplified by polyacrylamide hydrogels with varying crosslinking densities, including both high and low values.127 The dynamic storage and loss stiffnesses of these samples can be accurately calculated and plotted as a function of the modulating frequency, leveraging indentation measurements. This approach obviates the necessity for larger sample sizes typically required to assess the mechanical properties. Moreover, these measurements are applicable to softer and more delicate biological materials, such as tissues and cells, facilitating the detection of their transformative behaviors.68
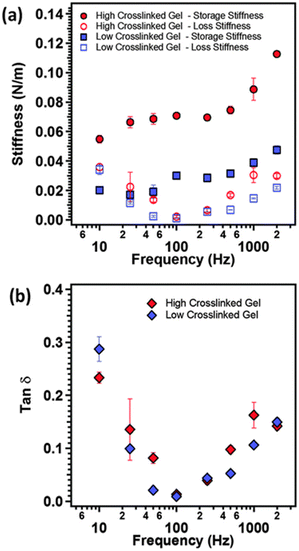 | ||
Fig. 10 (a) The storage modulus (closed symbols), loss modulus (open symbols) and (b) tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ as function of modulation frequency of the AFM cantilever for polyacrylamide gels with two different crosslinking densities (reproduced from ref. 127 with permission from Royal Society of Chemistry, copyright 2015). δ as function of modulation frequency of the AFM cantilever for polyacrylamide gels with two different crosslinking densities (reproduced from ref. 127 with permission from Royal Society of Chemistry, copyright 2015). | ||
TEM offers high-resolution (HR) 2D imaging of minute atomic structures (up to 5 × 107 magnification) by directing a high energy electron beam through an extremely thin sample,128 providing insights into interactions within nano reinforced materials and revealing information about fractures.129,130 The three main steps in TEM sample preparation are processing, embedding, and curing polymerization. The final stage, sectioning, produces thin slices for semi-transparent electron passage. However, TEM has limitations including providing only 2D projections of 3D structures, a limited sampling field of view (HR-TEM with no more than 100 nm2), the need for a vacuum environment, potential challenges in sample preparation (extremely thin slices) and achieving sufficient electron density contrast for individual polymer chains.131 Due to these constraints, TEM stands out as the most challenging techniques among available methods (including SEM and AFM). As a result, the direct applications of TEM in crosslinked polymer characterization are very rare, and the existing examples involve the use of tedious methods like as sample fixation and novel staining methods, to visualize the samples under TEM.132
Surface characterization of polymer networks
On exposure to external factors such as extreme pH, temperature changes, mechanical stress, external fields, and moisture, polymers can dramatically change the surface of polymers.133 As the interest in advanced materials intensifies, the role of surface engineering becomes increasingly pivotal. The surface of a material stands as the frontier of its interaction with the external environment and neighboring substances, shaping critical factors including adhesive properties, corrosion rates, wettability, catalytic activity, contact potential, and the intricacies of failure mechanisms. The surface of a material serves as a distinct boundary between two phases, introducing variations in both physical and chemical properties compared to the bulk material. Notably, the topmost atomic layer experiences substantial alterations due to the absence of surrounding atoms on all sides, granting the surface atom heightened bonding potential. Consequently, surface atoms exhibit increased reactivity compared to their counterparts within the material's interior. The material's overall behavior is intricately tied to the chemistry of its surface or the interfaces between layers. X-ray photoelectron spectroscopy (XPS), time-of-flight secondary ion mass spectroscopy (ToF-SIMS),134 and low-energy ion-scattering spectroscopy (LEIS) serve as instrumental techniques used to analyze, investigate, and improve the efficacy of surface engineering for diverse applications.135 Due to the tendency of many networks to swell, contact angle measurements136 are not always reliable as the solvent can be absorbed by the material in many cases.XPS which can also be referred to as electron spectroscopy for chemical analysis (ESCA) is a surface characterization technique that relies on principles of the photoelectric effect.137 This technique delivers a thorough surface characterization by revealing not only the surface elemental composition but also the chemical and electronic states of atoms within a material, contributing to depth-profiling and depth-related variations. In a standard XPS spectrum, the Y-axis, denoting the number of electrons, is plotted against the binding energy (eV) of electrons on the X-axis, adhering to fundamental spectroscopic principles. Each element manifests unique binding energy fingerprint, leading to a distinct array of XPS peaks. These peaks correspond to electronic configurations including but not limited to 1s, 2s, 2p, and 3s. An important factor to consider during sample preparation is that typical samples are 5–10 mm2 and up to 4 mm thick. Also, preparation materials that contain similar elements as the sample should be avoided. Limitations associated to XPS technique include: (i) Although XPS is non-destructive for many materials, it isn't universally applicable due to the use of an ultrahigh vacuum (UHV) chamber (<10−9 Torr), causing highly unstable samples to volatilize. (ii) Surface charging in XPS analysis of insulating specimens may cause peak shift, broadening, and asymmetry, potentially compromising data accuracy.138
XPS can be employed to determine the surface elemental composition of the polymer surfaces. Fig. 11 illustrates how Zhou et al. utilized this XPS characteristics to investigate the thermal and thermos-oxidative aging behavior of tetrafluoroethylene–propylene elastomers (FEPM) at temperatures above 300 °C.139 The XPS spectra were analyzed to distinguished differences in degradation mechanisms within FEPM vulcanizate samples. Further, this technique has found applications in various other areas including confirmation of crosslinking, and removal of dyes.140,141
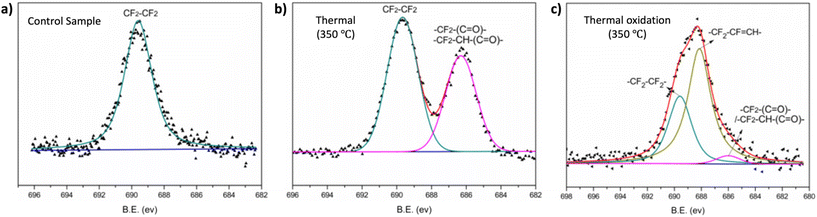 | ||
| Fig. 11 High-resolution XPS spectra of the F 1s of FEPM vulcanizate (a) before, (b) after thermal aging and (c) under thermal oxidation conditions (adapted with modifications from ref. 139 with permission from Elsevier, copyright 2020). | ||
LEIS is a surface characterization method with the capability to investigate the elemental composition of a material's outermost atomic layer through static depth profiles, covering roughly the outer 10 nm of surfaces.142 LEIS involves directing a stream of charged particles, referred to as ions, towards a surface and observing their interactions, including locations, velocities, and energy, with the surface; yielding data on the relative positions of atoms within a surface lattice and their elemental identities. Much like XPS, preparing samples for LEIS can require UHV at elevated temperatures (600–900 °C). However, the prevalent approach involves employing atomic O or H, derived from O2 or H2, to eliminate atmospheric contamination and adsorbents. This step in sample preparation is crucial for a successful surface analysis. The main limitation of LEIS is that it exhibits low sensitivity as it only detects ions within a specific energy range (usually ∼1 keV) while ignoring neutral species. This is due to the inability of the detector/electrostatic analyzer to differentiate subtle variations in atomic number or atomic weight.143
For surface characterization using ToF-SIMS, a pulsed ion beam (usually Cs or micro focused Ga) is employed to remove molecules from the outermost surface of samples. Resulting secondary ions from the atomic monolayers are then measured by monitoring their time of flight through a flight tube.137 This method for surface characterization offers surface imaging, depth profiling, and surface spectroscopy as operational modes, providing mass spectral and image data in the XY dimension and depth profile data in the Z dimension. This technique is limited to identifying foreign particles by discerning absorbed coatings or trace substances on the surface of sample materials. Similar to ToF-SIMS and XPS, Auger electron spectroscopy (AES) is another spectroscopy technique that can be used for surface analysis. Yet, XPS that is more commonly employed for surface characterization with detection sensitivity in the range of 0.1–1 at% for all the elements except H and He.
Advanced characterization methods
Solid state NMR is applicable to polymer networks, as discussed subsequently, but this requires a specialized NMR system which may not be broadly accessible. However, on number of occasions, solid state-NMR has been used to provide characteristic details of polymer networks, including molecular structure, defects of polymers, molecular dynamics, and conformation.144,145 Solid state NMR is, similar to the solution state NMR, and the primary difference lying in the sample preparation. Here, a solid is used as the sample instead of liquid samples. The resulting spectra are essentially influenced by the chemical shifts and the spin–spin splitting of the molecules.146 In the liquid state, 1H–13C dipole–dipole couplings and chemical shift anisotropy (CSA) generally do not stand out due to the rapid tumbling of the molecules within the solution. However, in the solid state, these two interactions types strongly affect spectral broadening, as the molecules do not tumble much in solid. To mitigate these effects and gain spectra with higher resolution, heteronuclear dipolar decoupling technique and magic angle spinning (MSA) methods are introduced respectively. Further signal improvement can be achieved using cross polarization (CP) technique. The combination of these techniques: dipolar decoupling, MSA and CP provides high resolution 13C NMR of polymers.145,147 Moreover, Multiple Quantum (MQ) and Magic sandwich echo (MSE) NMR methods that can employed as reliable and fast analysis tools to characterize complex structures of polymeric materials.148 MQ-NMR provides more detailed information about the molecular order, heterogeneities,149,150 dynamics of entangled polymers,151 and crosslinking density.148 Meanwhile, MES-NMR offers insights into the phase composition of polymer networks and polymer mobility.144 Additionally, the Double Quantum (DQ) NMR method has been utilized to characterize polymer properties, such as network defects,152 molecular weight between crosslinks,152 chain mobility.144 In summary, advanced NMR experiments provide important information about both structural and physical properties of complex polymers offering new insights for the analysis of novel complex polymers for various applications. However, they require specialized spectrometer setup.Scattering is any technique based on the electromagnetic wave theory where a radiation beam impinges on a sample, causing it to re-radiate the same wavelength with interference between different parts, resulting in a spatially discriminated intensity profile. While it yields 3D information on a material, direct structural details require a model for interpretation. The crystallinity of a polymer defines its optical, mechanical, chemical, and thermal properties, influencing its suitability for diverse applications. Highly crystalline polymers are rigid with elevated melting points, resisting solvent penetration. In contrast, amorphous polymers are softer, pliable, melt more slowly, and are more vulnerable to solvent penetration. XRD is an example of scattering techniques employed for identifying the bulk crystalline or amorphous phases of polymer materials.153
Owing to their elongated chain structure, polymers are highly susceptible to orientation. Herman's orientation function, analyzed using XRD, is essential for determining crystalline orientation in polymers.154,155 The formation of XRD peaks results from constructive interference between elastically scattered X-ray beams at specific angles from each set of lattice planes in a sample. To prepare samples for XRD characterization, various forms of polymers including bulk polymers with polished surfaces, thin polymeric films, and polymer solutions, can be directly measured by XRD. However, powdery samples require pre-treatment to minimize source errors. Specifically, the sample is ground into a fine powder and homogenized to reduce induced strain that might alter peak positions; particle size less than ∼10 μm (or 200-mesh) is preferred. Despite its utility, XRD has limitations. The sample must be single phased, the detection limit is for mixed materials is ∼ 2% of sample, and peak overlays could occur for reflections with high angles. Other X-ray scattering techniques include wide-angle X-ray scattering (WAXS) and small-angle X-ray scattering (SAXS), which provide information on polymer mesostructures at different length scales. The distance from sample to detector is substantially longer for SAXS (≤1 degree) compared to WAXS with 5–60 degrees, resulting from a diffraction maximum with larger angles. SAXS is able to give information on network structure at larger length scales than WAXS, typical for polymer mesostructures on the nanometer scale. SAXS is particularly relevant for complex structured polymers like IPNs, where two networks are woven through each other.156,157 Additionally, small angle neutron scattering (SANS) operates on similar length scales to SAXS, but probes scattering off of nuclei rather than electron clouds.158,159 However, SANS requires specialized equipment that is not broadly available.
The SAXS technique is frequently employed to determine local domain sizes in thermoplastic elastomers (TPEs). In Fig. 12, a scenario is distinctly presented wherein the authors observed the formation of expanded and more well-defined crystallite domains.160 This phenomenon occurs as the fraction of the hard block segment (HS) increases from 5% to 20% in TPEs based on segmented block copolymers containing poly(tetrahydrofuran) (pTHF) and terephthalate-based diamide groups (T4T). Beyond elucidating domain sizes, SAXS proves versatile in providing insights into the surface characteristics of the interpenetrating networks.
 | ||
| Fig. 12 (a) Normalized scattering intensity measured in SAXS as a function of the transfer momentum q for the four segmented block copolymers containing 5, 10, 15 and 20% HS. The solid black line stands for the reconstruction of PHS(q). (b) Kratky representation (I(q)q2 = f(q/q*)) of the same data set. The characteristic distance between the crystallites is seen through q* while the presence of q** = 2q* suggests a lamellar phase (reproduced from ref. 160 with permission from Elsevier, copyright 2016 ). | ||
For polymer characterization using dynamic light scattering (DLS) and static light scattering (SLS) techniques, DLS is effective for measuring sample with particles from approximately 1 nm to 1 μm in size, while SLS covers a range of approximately 10 nm to 1 μm. Generally homogeneous polymer networks exceed these sizes, although light scattering can identify aggregates and fillers within the network Sample particles too large for SLS should be analyzed using a microscope instead. However specialized light scattering equipment can be used when combining light scattering and rheological measurements identifying inhomogeneities in the microstructure of network polymers.161
While bulk rheology, traditionally employed to predict the viscoelastic properties of bulk materials, has limitations due to greater sample volume requirement applicability issues for various samples (Eg: soft and small samples). In contrast, microrheology, an evolving technique, investigates materials structures on a microscale, requiring only trace amount of material (thickness ranging from 1 nm to 1 μm).162,163 Active microrheology applies stress using magnetic or optical forces on materials with embedded microscopic beads to measure linear and nonlinear rheology.164 Passive microrheology, in contrast, measures viscoelastic properties without application of external force, using particle tracking to analyze hydrogel characteristics like particle diffusion, and network heterogeneity. Particle motions tracked using methods. Such as165 The MSD, denoted by Δr(s)2, represents the square of the net distance travelled by a thermally fluctuating particle within a specific time frame.
Elastic properties of the materials can be calculated through diffusion-based generalization of the Strokes–Einstein relation. However, this calculation is only valid when the materials is homogeneous, in thermal equilibrium, and when there are no-slip boundary conditions between the surrounding materials with the particle. For an elastic solid, the Laplace transform of the macroscopic modulus (G(S)) can be calculated using eqn (12).165,166
 | (12) |
The m Where KB is the Boltzmann's constant, T is the absolute temperature and r is the radius of the bead, and s is the Laplace frequency.167
Network disassembly spectrometry (NDS) is commonly employed for the structural characterization of polymers, including the quantification of loops and dangling end structures, and degradation kinetics of gels.98,168,169 This typically involves the site-selective network disassembly of few milligrams or grams of polymer materials using photolysis or chemical degradation techniques. The disassembled products of the polymer chains are primarily characterized and quantified through chromatography techniques (liquid chromatography (LC)/MS and gel permeation chromatography), fluorometric assays.34,98,170 This method enables real time data analysis of the degradation products of the networks. However, it is important to note that, in using this method, the network structure is ultimately destroyed in the pursuit of quantification.
Beyond advances in new techniques, such as NDS or microrheology, there are also important developments where instruments are being developed with multiple coupled characterization methods. Examples include combined thermal and strain measurements,171 IR-rheological analysis,172 and AFM-IR among many others. Without a doubt, this will continue to be an emerging area as techniques are coupled together and automated for facile analysis.173
Conclusions
Polymer networks characterization presents new challenges due to their insolubility, making traditional polymer characterization tools impractical. However, their rigid properties also enable new techniques to be used. Typically, a battery of methods will need to be used, to identify functionality, topology and also ultimate material properties. This article presents an overview of the commonly used techniques, allowing identification of polymer network functionality, composition, swelling, mechanical, thermal, and surface properties. Using combinations of the highlighted techniques researchers coupled with advances in synthesis, new polymer networks with properties targeted towards applications can be realized.Author contributions
D. K. and N. D. A. W. were involved in conceptualization and project administration. S. V. W., M. A. S. N. W., O. J. D., I. O. R., C. W. H. R, N. D. A. W and D. K. were involved in visualization. M. A. S. N. W., O. J. D., I. O. R., C. W. H. R, N. D. A. W and D. K. were involved in writing the original draft. All authors were involved in editing.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We thank Dr Sergei Sheiko and Dr Julia Kalow for discussion of material's mechanical properties. M. A. S. N. W. was supported by the National Science Foundation (CHE-2203727) for descriptions and overviews of synthesis and characterization methods. I. O. R. and D. K. were supported by the National Science Foundation (DMR-1749730) for descriptions of mechanical analysis and molar mass between crosslinks. This work was partially supported by United States Department of Energy, Office of Science, Basic Energy Sciences, under Award No. DE-SC0018645 (Supporting C. W. H. R.) for descriptions of sol–gel and swelling analysis. N. D. A. W. was supported by the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No. 101030516 for description of functional group analysis.References
- W. W. Graessley, Entangled Linear, Branched and Network Polymer Systems—Molecular Theories, in Synthesis and Degradation Rheology and Extrusion, Springer, 2005, pp. 67–117 Search PubMed.
- W. Burchard and S. B. Ross-Murphy, Physical Networks: Polymers and Gels, Springer Science & Business Media, 1990 Search PubMed.
- Y. Osada and A. Khokhlov, Polymer Gels and Networks, CRC Press, 2001 Search PubMed.
- C. K. Varnava and C. S. Patrickios, Polymer Networks One Hundred Years after the Macromolecular Hypothesis: A Tutorial Review, Polymer, 2021, 215, 123322 CrossRef CAS.
- C. S. Patrickios, Polymer Networks: Recent Developments, in Macromolecular symposia, Wiley Online Library, 2010, vol. 291, pp. 1–11 Search PubMed.
- S. Candau, J. Bastide and M. Delsanti, Structural, Elastic, and Dynamic Properties of Swollen Polymer Networks, in Polymer Networks, 2005, pp. 27–71 Search PubMed.
- T. Kaiser, Highly Crosslinked Polymers, Prog. Polym. Sci., 1989, 14(3), 373–450 CrossRef CAS.
- S. P. O. Danielsen, H. K. Beech, S. Wang, B. M. El-Zaatari, X. Wang, L. Sapir, T. Ouchi, Z. Wang, P. N. Johnson and Y. Hu, Molecular Characterization of Polymer Networks, Chem. Rev., 2021, 121(8), 5042–5092 CrossRef CAS PubMed.
- I. M. Barszczewska-Rybarek, A Guide through the Dental Dimethacrylate Polymer Network Structural Characterization and Interpretation of Physico-Mechanical Properties, Materials, 2019, 12(24), 4057 CrossRef CAS.
- Y. Gu, J. Zhao and J. A. Johnson, A (Macro) Molecular-Level Understanding of Polymer Network Topology, Trends Chem., 2019, 1(3), 318–334 CrossRef CAS.
- Y. Gu, J. Zhao and J. A. Johnson, Polymer Networks: From Plastics and Gels to Porous Frameworks, Angew. Chem., Int. Ed., 2020, 59(13), 5022–5049 CrossRef CAS PubMed.
- G. Yu, X. Yan, C. Han and F. Huang, Characterization of Supramolecular Gels, Chem. Soc. Rev., 2013, 42(16), 6697–6722 RSC.
- F. Di Lorenzo and S. Seiffert, Nanostructural Heterogeneity in Polymer Networks and Gels, Polym. Chem., 2015, 6(31), 5515–5528 RSC.
- M. A. S. N. Weerasinghe, O. J. Dodo, C. W. H. Rajawasam, I. O. Raji, S. V. Wanasinghe, D. Konkolewicz and N. D. A. Watuthanthrige, Educational Series: Turning Monomers into Crosslinked Polymer Networks, Polym. Chem., 2023, 14(39), 4503–4514 RSC.
- C. H. Chan, J.-T. Chen, W. S. Farrell, C. M. Fellows, D. J. Keddie, C. K. Luscombe, J. B. Matson, J. Merna, G. Moad and G. T. Russell, Reconsidering Terms for Mechanisms of Polymer Growth: The “Step-Growth” and “Chain-Growth” Dilemma, Polym. Chem., 2022, 13(16), 2262–2270 RSC.
- J. L. Mann, R. L. Rossi, A. A. A. Smith and E. A. Appel, Universal Scaling Behavior during Network Formation in Controlled Radical Polymerizations, Macromolecules, 2019, 52(24), 9456–9465 CrossRef CAS PubMed.
- V. Schamboeck, P. D. Iedema and I. Kryven, Dynamic Networks That Drive the Process of Irreversible Step-Growth Polymerization, Sci. Rep., 2019, 9(1), 2276 CrossRef PubMed.
- J. C. Hernández-Ortiz and E. Vivaldo-Lima, Crosslinking, Handbook of polymer synthesis, characterization, and processing, 2013, pp. 187–204 Search PubMed.
- G. Tillet, B. Boutevin and B. Ameduri, Chemical Reactions of Polymer Crosslinking and Post-Crosslinking at Room and Medium Temperature, Prog. Polym. Sci., 2011, 36(2), 191–217 CrossRef CAS.
- M. S. Silverstein, Interpenetrating Polymer Networks: So Happy Together?, Polymer, 2020, 207, 122929 CrossRef CAS.
- W. E. Hennink and C. F. van Nostrum, Novel Crosslinking Methods to Design Hydrogels, Adv. Drug Delivery Rev., 2012, 64, 223–236 CrossRef.
- R. L. Quirino, K. Monroe, C. H. Fleischer III, E. Biswas and M. R. Kessler, Thermosetting Polymers from Renewable Sources, Polym. Int., 2021, 70(2), 167–180 CrossRef CAS.
- S. K. Bobade, N. R. Paluvai, S. Mohanty and S. K. Nayak, Bio-Based Thermosetting Resins for Future Generation: A Review, Polym. – Plast. Technol. Eng., 2016, 55(17), 1863–1896 CrossRef CAS.
- V. R. Sastri, Engineering Thermoplastics, Plast. Med. Dev., 2010, 121–173 Search PubMed.
- I. Jones, Laser Welding of Plastics, in Handbook of Laser Welding Technologies, Elsevier, 2013, pp. 280–301e Search PubMed.
- N. A. Peppas, B. Slaughter and M. A. V. Kanzelberger, Polymer Science: A Comprehensive Reference, Hydrogels, Polym. Biol. Med., 2012, 9, 385–395 CAS.
- N. A. Peppas and A. S. Hoffman, Hydrogels, in Biomaterials science, Elsevier, 2020, pp. 153–166 Search PubMed.
- G. Gerlach and K.-F. Arndt, Hydrogel Sensors and Actuators: Engineering and Technology, Springer Science & Business Media, 2009, vol. 6 Search PubMed.
- W. Wang, R. Narain and H. Zeng, Hydrogels, in Polymer science and nanotechnology, Elsevier, 2020, pp. 203–244 Search PubMed.
- L. V. Korah, G. Anilkumar and S. Thomas, Hydrogels, DNA, and RNA Polypeptides for the Preparation of Biomaterials, in Fundamental Biomaterials: Polymers, Elsevier, 2018, pp. 85–104 Search PubMed.
- A. P. Mouritz, Introduction to Aerospace Materials, Elsevier, 2012 Search PubMed.
- V. R. Sastri, Plastics in Medical Devices: Properties, Requirements, and Applications, William Andrew, 2021 Search PubMed.
- T. Takata and D. Aoki, Topology-Transformable Polymers: Linear–Branched Polymer Structural Transformation via the Mechanical Linking of Polymer Chains, Polym. J., 2018, 50(1), 127–147 CrossRef CAS.
- J. Cuthbert, S. V. Wanasinghe, K. Matyjaszewski and D. Konkolewicz, Are RAFT and ATRP Universally Interchangeable Polymerization Methods in Network Formation?, Macromolecules, 2021, 54(18), 8331–8340 CrossRef CAS.
- Y. Gao, D. Zhou, J. Lyu, A. Sigen, Q. Xu, B. Newland, K. Matyjaszewski, H. Tai and W. Wang, Complex Polymer Architectures through Free-Radical Polymerization of Multivinyl Monomers, Nat. Rev. Chem., 2020, 1–19 Search PubMed.
- C. W. A. Bainbridge, A. Wangsadijaya, N. Broderick and J. Jin, Living Polymer Networks Prepared by Controlled Radical Polymerization Techniques, Polym. Chem., 2022, 13(11), 1484–1494 RSC.
- T. Sakai, Experimental Verification of Homogeneity in Polymer Gels, Polym. J., 2014, 46(9), 517–523 CrossRef CAS.
- J. Wang, R. Wang, Y. Gu, A. Sourakov, B. D. Olsen and J. A. Johnson, Counting Loops in Sidechain-Crosslinked Polymers from Elastic Solids to Single-Chain Nanoparticles, Chem. Sci., 2019, 10(20), 5332–5337 RSC.
- S. Wanasinghe, E. M. V. Schreiber, A. M. Thompson, J. L. Sparks and D. Konkolewicz, Dynamic Covalent Chemistry for Architecture Changing Interpenetrated and Single Networks, Polym. Chem., 2021, 12, 1975–1982 RSC.
- D. Wu, F. Xu, B. Sun, R. Fu, H. He and K. Matyjaszewski, Design and Preparation of Porous Polymers, Chem. Rev., 2012, 112(7), 3959–4015 CrossRef CAS PubMed.
- R. J. White, V. Budarin, R. Luque, J. H. Clark and D. J. Macquarrie, Tuneable Porous Carbonaceous Materials from Renewable Resources, Chem. Soc. Rev., 2009, 38(12), 3401–3418 RSC.
- V. M. Gun'ko, R. Leboda, J. Skubiszewska-Zięba, B. Gawdzik and B. Charmas, Structural Characteristics of Porous Polymers Treated by Freezing with Water or Acetone, Appl. Surf. Sci., 2005, 252(3), 612–618 CrossRef.
- K. Deshmukh, T. Kovářík, A. Muzaffar, M. B. Ahamed and S. K. K. Pasha, Mechanical Analysis of Polymers, in Polymer science and innovative applications, Elsevier, 2020, pp. 117–152 Search PubMed.
- M. Jawaid, M. Thariq and N. Saba, Durability and Life Prediction in Biocomposites, Fibre-Reinforced Composites and Hybrid Composites, Woodhead Publishing, 2018 Search PubMed.
- N. Mills, M. Jenkins and S. Kukureka, Plastics: Microstructure and Engineering Applications, Butterworth-Heinemann, 2020 Search PubMed.
- R. Wang, M. K. Sing, R. K. Avery, B. S. Souza, M. Kim and B. D. Olsen, Classical Challenges in the Physical Chemistry of Polymer Networks and the Design of New Materials, Acc. Chem. Res., 2016, 49(12), 2786–2795 CrossRef CAS PubMed.
- R. H. Colby, M. Rubinstein, J. R. Gillmor and T. H. Mourey, Scaling Properties of Branched Polyesters. 2. Static Scaling above the Gel Point, Macromolecules, 1992, 25(26), 7180–7187 CrossRef CAS.
- J. R. MacCallum, Thermogravimetric Analysis of Polymers for Assessing Thermal Degradation, Thermochim. Acta, 1985, 96(2), 275–281 CrossRef CAS.
- C. Schick, Differential Scanning Calorimetry (DSC) of Semicrystalline Polymers, Anal. Bioanal. Chem., 2009, 395, 1589–1611 CrossRef CAS.
- S. Li, R. Vatanparast and H. Lemmetyinen, Cross-Linking Kinetics and Swelling Behaviour of Aliphatic Polyurethane, Polymer, 2000, 41(15), 5571–5576 CrossRef CAS.
- D. B. Menezes, A. Reyer, A. Marletta and M. Musso, Glass Transition of Polystyrene (PS) Studied by Raman Spectroscopic Investigation of Its Phenyl Functional Groups, Mater. Res. Express, 2017, 4(1), 15303 CrossRef.
- I. M. Barszczewska–Rybarek, A New Approach to Morphology Studies on Diacrylate Polymer Networks Using X–Ray Powder Diffraction, Macromol. Chem. Phys., 2013, 214(9), 1019–1026 CrossRef.
- W. Lequieu, P. Van De Velde, F. E. Du Prez, P. Adriaensens, L. Storme and J. Gelan, Solid State NMR Study of Segmented Polymer Networks: Fine-Tuning of Phase Morphology via Their Molecular Design, Polymer, 2004, 45(23), 7943–7951 CrossRef CAS.
- J. L. Koenig, Infrared and Raman Spectroscopy of Polymers, iSmithers Rapra Publishing, 2001, vol. 12 Search PubMed.
- D. F. Sunday, E. P. Chan, S. Orski, R. C. V. Nieuwendaal and C. M. Stafford, Functional Group Quantification of Polymer Nanomembranes with Soft X-Rays, Phys. Rev. Mater., 2018, 2(3), 32601 CrossRef.
- IR Spectrum Table & Chart, https://www.sigmaaldrich.com/LK/en/technical-documents/technical-article/analytical-chemistry/photometry-and-reflectometry/ir-spectrum-table.
- B. Suthar, H. X. Xiao, D. Klempner and K. C. Frisch, A Review of Kinetic Studies on the Formation of Interpenetrating Polymer Networks, Polym. Adv. Technol., 1996, 7(4), 221–233 CrossRef CAS.
- C. Decker, Kinetic Study and New Applications of UV Radiation Curing, Macromol. Rapid Commun., 2002, 23(18), 1067–1093 CrossRef CAS.
- L. J. Dodd, C. Lima, D. Costa-Milan, A. R. Neale, B. Saunders, B. Zhang, A. Sarua, R. Goodacre, L. J. Hardwick and M. Kuball, Raman Analysis of Inverse Vulcanised Polymers, Polym. Chem., 2023, 14(12), 1369–1386 RSC.
- R. Appel, W. Xu, T. W. Zerda and Z. Hu, Direct Observation of Polymer Network Structure in Macroporous N-Isopropylacrylamide Gel by Raman Microscopy, Macromolecules, 1998, 31(15), 5071–5074 CrossRef CAS.
- K. S. Anseth, C. Decker and C. N. Bowman, Real-Time Infrared Characterization of Reaction Diffusion during Multifunctional Monomer Polymerizations, Macromolecules, 1995, 28(11), 4040–4043, DOI:10.1021/MA00115A045/ASSET/MA00115A045.FP.PNG_V03.
- P. Li, K. Xu, Y. Tan, C. Lu, Y. Li and P. Wang, A Novel Fabrication Method of Temperature-Responsive Poly(Acrylamide) Composite Hydrogel with High Mechanical Strength, Polymer, 2013, 54(21), 5830–5838 CrossRef CAS.
- J. Bai, H. Li, Z. Shi and J. Yin, An Eco-Friendly Scheme for the Cross-Linked Polybutadiene Elastomer via Thiol–Ene and Diels–Alder Click Chemistry, Macromolecules, 2015, 48(11), 3539–3546 CrossRef CAS.
- C. Bennett, P. J. Hayes, C. J. Thrasher, P. Chakma, S. V. Wanasinghe, B. Zhang, L. M. Petit, V. Varshney, D. Nepal and A. Sarvestani, Modeling Approach to Capture Hyperelasticity and Temporary Bonds in Soft Polymer Networks, Macromolecules, 2022, 55(9), 3573–3587 CrossRef CAS.
- C. Heß, B. Hartmann, M. D. Lechner, W. Nierling, C. Seidel and W. Kulicke, Influence of Soluble Polymer Residues in Crosslinked Carboxymethyl Starch on Some Physical Properties of Its Hydrogels, Starch/Staerke, 2007, 59(9), 423–429 CrossRef.
- N. M. Ranjha, J. Mudassir and S. Majeed, Synthesis and Characterization of Polycaprolactone/Acrylic Acid (PCL/AA) Hydrogel for Controlled Drug Delivery, Bull. Mater. Sci., 2011, 34, 1537–1547 CrossRef CAS.
- B. Jeong, S. W. Kim and Y. H. Bae, Thermosensitive Sol–Gel Reversible Hydrogels, Adv. Drug Delivery Rev., 2012, 64, 154–162 CrossRef.
- M. Krieg, G. Fläschner, D. Alsteens, B. M. Gaub, W. H. Roos, G. J. L. Wuite, H. E. Gaub, C. Gerber, Y. F. Dufrêne and D. J. Müller, Atomic Force Microscopy-Based Mechanobiology, Nat. Rev. Phys., 2018, 1(1), 41–57, DOI:10.1038/s42254-018-0001-7.
- J.-U. Sommer and S. Lay, Topological Structure and Nonaffine Swelling of Bimodal Polymer Networks, Macromolecules, 2002, 35(26), 9832–9843 CrossRef CAS.
- J. Sievers, K. Sperlich, T. Stahnke, C. Kreiner, T. Eickner, H. Martin, R. F. Guthoff, M. Schünemann, S. Bohn and O. Stachs, Determination of Hydrogel Swelling Factors by Two Established and a Novel Non–contact Continuous Method, J. Appl. Polym. Sci., 2021, 138(18), 50326 CrossRef CAS.
- B. Yang, B. Nagarajan and P. Mertiny, Characterization of Swelling Behavior of Carbon Nano-Filler Modified Polydimethylsiloxane Composites, J. Elastomers Plastics, 2021, 53(8), 955–974 CrossRef CAS.
- M. Chen, S. Deng, Y. Gu, J. Lin, M. J. MacLeod and J. A. Johnson, Logic-Controlled Radical Polymerization with Heat and Light: Multiple-Stimuli Switching of Polymer Chain Growth via a Recyclable, Thermally Responsive Gel Photoredox Catalyst, J. Am. Chem. Soc., 2017, 139(6), 2257–2266 CrossRef CAS.
- V. S. Raghuwanshi and G. Garnier, Characterisation of Hydrogels: Linking the Nano to the Microscale, Adv. Colloid Interface Sci., 2019, 274, 102044 CrossRef CAS.
- H. Gao and K. Matyjaszewski, Synthesis of Functional Polymers with Controlled Architecture by CRP of Monomers in the Presence of Cross-Linkers: From Stars to Gels, Prog. Polym. Sci., 2009, 34(4), 317–350, DOI:10.1016/J.PROGPOLYMSCI.2009.01.001.
- J. A. Yoon, C. Gayathri, R. R. Gil, T. Kowalewski and K. Matyjaszewski, Comparison of the Thermoresponsive Deswelling Kinetics of Poly(2-(2-Methoxyethoxy)Ethyl Methacrylate) Hydrogels Prepared by ATRP and FRP, Macromolecules, 2010, 43(10), 4791–4797 CrossRef CAS.
- R. Scherf, L. S. Müller, D. Grosch, E. G. Hübner and W. Oppermann, Investigation on the Homogeneity of PMMA Gels Synthesized via RAFT Polymerization, Polymer, 2015, 58, 36–42 CrossRef CAS.
- E. F. Gomez, S. V. Wanasinghe, A. E. Flynn, O. J. Dodo, J. L. Sparks, L. A. Baldwin, C. E. Tabor, M. F. Durstock, D. Konkolewicz and C. J. Thrasher, 3D-Printed Self-Healing Elastomers for Modular Soft Robotics, ACS Appl. Mater. Interfaces, 2021, 13(24), 28870–28877 CrossRef CAS PubMed.
- S. V. Wanasinghe, B. Johnson, R. Revadelo, G. Eifert, A. Cox, J. Beckett, T. Osborn, C. Thrasher, R. Lowe and D. Konkolewicz, 3D Printable Adhesive Elastomers with Dynamic Covalent Bond Rearrangement, Soft Matter, 2023, 19(26), 4964–4971 RSC.
- D. Roylance, Stress-Strain Curves, Massachusetts Institute of Technology study, Cambridge, 2001 Search PubMed.
- L. C. S. Nunes and D. C. Moreira, Simple Shear under Large Deformation: Experimental and Theoretical Analyses, Eur. J. Mech, A: Solids., 2013, 42, 315–322 CrossRef.
- S. M. Spivak and L. R. G. Treloar, The Behavior of Fabrics in Shear: Part III: The Relation between Bias Extension and Simple Shear, Text. Res. J., 1968, 38(9), 963–971 CrossRef.
- M. Laun, D. Auhl, R. Brummer, D. J. Dijkstra, C. Gabriel, M. A. Mangnus, M. Rüllmann, W. Zoetelief and U. A. Handge, Guidelines for Checking Performance and Verifying Accuracy of Rotational Rheometers: Viscosity Measurements in Steady and Oscillatory Shear (IUPAC Technical Report), Pure Appl. Chem., 2014, 86(12), 1945–1968 CAS.
- B. Zhang, Z. A. Digby, J. A. Flum, P. Chakma, J. M. Saul, J. L. Sparks and D. Konkolewicz, Dynamic Thiol–Michael Chemistry for Thermoresponsive Rehealable and Malleable Networks, Macromolecules, 2016, 49(18), 6871–6878 CrossRef CAS.
- J. R. McKee, J. Huokuna, L. Martikainen, M. Karesoja, A. Nykänen, E. Kontturi, H. Tenhu, J. Ruokolainen and O. Ikkala, Molecular Engineering of Fracture Energy Dissipating Sacrificial Bonds into Cellulose Nanocrystal Nanocomposites, Angew. Chem., 2014, 126(20), 5149–5153 CrossRef.
- C. G′sell and J. J. Jonas, Yield and Transient Effects during the Plastic Deformation of Solid Polymers, J. Mater. Sci., 1981, 16, 1956–1974 CrossRef.
- S. S. Sheiko and A. V. Dobrynin, Architectural Code for Rubber Elasticity: From Supersoft to Superfirm Materials, Macromolecules, 2019, 52(20), 7531–7546 CrossRef CAS.
- M. Cristea, D. Ionita and M. M. Iftime, Dynamic Mechanical Analysis Investigations of PLA-Based Renewable Materials: How Are They Useful?, Materials, 2020, 13(22), 5302 CrossRef CAS.
- M. Vatankhah-Varnosfaderani, W. F. M. Daniel, M. H. Everhart, A. A. Pandya, H. Liang, K. Matyjaszewski, A. V. Dobrynin and S. S. Sheiko, Mimicking Biological Stress–Strain Behaviour with Synthetic Elastomers, Nature, 2017, 549(7673), 497–501 CrossRef PubMed.
- T. Instruments, Dynamic Mechanical Analysis: Basic Theory & Applications Training, TA Instruments, https://www.tainstruments.com/wp-content/uploads/2020_DMA_Online_Training_Part_1.pdf.
- E. J. Bailey and K. I. Winey, Dynamics of Polymer Segments, Polymer Chains, and Nanoparticles in Polymer Nanocomposite Melts: A Review, Prog. Polym. Sci., 2020, 105, 101242 CrossRef CAS.
- A. Schiavi and A. Prato, Evidences of Non-Linear Short-Term Stress Relaxation in Polymers, Polym. Test., 2017, 59, 220–229 CrossRef CAS.
- C. Tzikang, Determining a Prony Series for a Viscoelastic Material from Time Varying Strain Data, 2000 Search PubMed.
- C. Reynolds, R. Thompson and T. McLeish, Pressure and Shear Rate Dependence of the Viscosity and Stress Relaxation of Polymer Melts, J. Rheol., 2018, 62(2), 631–642 CrossRef CAS.
- W. D. Cook, T. F. Scott, S. Quay-Thevenon and J. S. Forsythe, Dynamic mechanical thermal analysis of thermally stable and thermally reactive network polymers, J. Appl. Polym. Sci., 2004, 93(3), 1348–1359 CrossRef CAS.
- M. Ahmadi, P. Nicolella and S. Seiffert, Network Percolation in Transient Polymer Networks with Temporal Hierarchy of Energy Dissipation, Macromolecules, 2022, 55(22), 9960–9971 CrossRef CAS.
- T. R. Long, R. M. Elder, E. D. Bain, K. A. Masser, T. W. Sirk, H. Y. Jian, D. B. Knorr and J. L. Lenhart, Influence of Molecular Weight between Crosslinks on the Mechanical Properties of Polymers Formed via Ring-Opening Metathesis, Soft Matter, 2018, 14(17), 3344–3360 RSC.
- S. Panyukov, Loops in Polymer Networks, Macromolecules, 2019, 52(11), 4145–4153 CrossRef CAS.
- H. Zhou, J. Woo, A. M. Cok, M. Wang, B. D. Olsen and J. A. Johnson, Counting Primary Loops in Polymer Gels, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(47), 19119–19124 CrossRef CAS PubMed.
- Z. D. Jastrzebski, Nature and Properties of Engineering Materials, John Wiley and Sons, Inc., New York, 1976 Search PubMed.
- L. R. G. Treloar, The Elasticity and Related Properties of Rubbers, Rep. Prog. Phys., 1973, 36(7), 755 CrossRef CAS.
- P. J. Flory and J. Rehner Jr., Statistical Mechanics of Cross–linked Polymer Networks II. Swelling, J. Chem. Phys., 1943, 11(11), 521–526 CrossRef CAS.
- N. Schuld and B. A. Wolf, Polymer-Solvent Interaction Parameters, in Polymer handbook, 1999, vol. 4 Search PubMed.
- S. V. Wanasinghe, E. M. Schreiber, A. M. Thompson, J. L. Sparks and D. Konkolewicz, Dynamic Covalent Chemistry for Architecture Changing Interpenetrated and Single Networks, Polym. Chem., 2021, 12(13), 1975–1982, 10.1039/D1PY00198A.
- A. A. Thamer, H. A. Yusr and N. J. Jubier, TGA, DSC, DTG Properties of Epoxy Polymer Nanocomposites by Adding Hexagonal Boron Nitride Nanoparticles, J. Eng. Appl. Sci., 2019, 14(2), 567–574 CrossRef CAS.
- J. S. Chen, C. K. Ober, M. D. Poliks, Y. Zhang, U. Wiesner and C. Cohen, Controlled Degradation of Epoxy Networks: Analysis of Crosslink Density and Glass Transition Temperature Changes in Thermally Reworkable Thermosets, Polymer, 2004, 45(6), 1939–1950, DOI:10.1016/J.POLYMER.2004.01.011.
- R. B. Prime, H. E. Bair, S. Vyazovkin, P. K. Gallagher and A. Riga, Thermogravimetric Analysis (TGA), in Thermal analysis of polymers: Fundamentals and applications, 2009, pp. 241–317 Search PubMed.
- H. M. Ng, N. M. Saidi, F. S. Omar, K. Ramesh, S. Ramesh and S. Bashir, Thermogravimetric Analysis of Polymers, in Encyclopedia of polymer science and technology, 2002, pp. 1–29 Search PubMed.
- H. E. Bair, A. E. Akinay, J. D. Menczel, R. B. Prime and M. Jaffe, Thermomechanical Analysis (TMA) and Thermodilatometry (TD), in Thermal analysis of polymers: Fundamentals and applications, 2009, pp. 319–385 Search PubMed.
- Thermomechanical analyzer. TA instruments. https://www.tainstruments.com/pdf/brochure/BROCH-TMA-450.pdf.
- R. P. Chartoff, J. D. Menczel and S. H. Dillman, Dynamic Mechanical Analysis (DMA), in Thermal analysis of polymers: fundamentals and applications, Wiley Online Library, 2009, pp. 387–495 Search PubMed.
- N. D. A. Watuthanthrige, P. Chakma and D. Konkolewicz, Designing Dynamic Materials from Dynamic Bonds to Macromolecular Architecture, Trends Chem., 2021, 3(3), 231–247 CrossRef.
- X. Chen, L. Li, T. Wei, J. M. Torkelson, X. Chen, L. Li, T. Wei and J. M. Torkelson, Reprocessable Polymer Networks Designed with Hydroxyurethane Dynamic Cross-Links: Effect of Backbone Structure on Network Morphology, Phase Segregation, and Property Recovery, Macromol. Chem. Phys., 2019, 220(13), 1900083, DOI:10.1002/MACP.201900083.
- Q. Guo, Polymer Morphology: Principles, Characterization, and Processing, John Wiley & Sons, 2016 Search PubMed.
- A. Mohammed and A. Abdullah, Scanning Electron Microscopy (SEM): A Review, in Proceedings of the 2018 International Conference on Hydraulics and Pneumatics—HERVEX, Băile Govora, Romania, 2018, Vol. 2018, pp. 7–9.
- T. Fekete, J. Borsa, E. Takács and L. Wojnárovits, Synthesis and Characterization of Superabsorbent Hydrogels Based on Hydroxyethylcellulose and Acrylic Acid, Carbohydr. Polym., 2017, 166, 300–308 CrossRef CAS PubMed.
- M. Lin, G. Zhang, Z. Hua, Q. Zhao and F. Sun, Conformation and Plugging Properties of Crosslinked Polymer Microspheres for Profile Control, Colloids Surf., A, 2015, 477, 49–54 CrossRef CAS.
- X. Huang, D. Appelhans, P. Formanek, F. Simon and B. Voit, Synthesis of Well-Defined Photo-Cross-Linked Polymeric Nanocapsules by Surface-Initiated RAFT Polymerization, Macromolecules, 2011, 44(21), 8351–8360 CrossRef CAS.
- K. C. Khulbe, C. Y. Feng and T. Matsuura, Synthetic Polymeric Membranes: Characterization by Atomic Force Microscopy, Springer Science & Business Media, 2007 Search PubMed.
- D. Wang and T. P. Russell, Advances in Atomic Force Microscopy for Probing Polymer Structure and Properties, Macromolecules, 2018, 51(1), 3–24 CrossRef CAS.
- R. Garcıa and R. Perez, Dynamic Atomic Force Microscopy Methods, Surf. Sci. Rep., 2002, 47(6–8), 197–301 CrossRef.
- M. Krieg, G. Fläschner, D. Alsteens, B. M. Gaub, W. H. Roos, G. J. L. Wuite, H. E. Gaub, C. Gerber, Y. F. Dufrêne and D. J. Müller, Atomic Force Microscopy-Based Mechanobiology, Nat. Rev. Phys., 2018, 1(1), 41–57, DOI:10.1038/s42254-018-0001-7.
- S.-V. Kontomaris, The Hertz Model in AFM Nanoindentation Experiments: Applications in Biological Samples and Biomaterials, Micro and Nanosyst., 2018, 10(1), 11–22 CrossRef CAS.
- I. N. Sneddon, The Relation between Load and Penetration in the Axisymmetric Boussinesq Problem for a Punch of Arbitrary Profile, Int. J. Eng. Sci., 1965, 3(1), 47–57 CrossRef.
- K. L. Johnson, K. Kendall and A. A. D. Roberts, Surface Energy and the Contact of Elastic Solids, Proc. R. Soc. London, Ser. A, 1971, 324(1558), 301–313 CAS.
- M. Krieg, G. Fläschner, D. Alsteens, B. M. Gaub, W. H. Roos, G. J. L. Wuite, H. E. Gaub, C. Gerber, Y. F. Dufrêne and D. J. Müller, Atomic Force Microscopy-Based Mechanobiology, Nat. Rev. Phys., 2019, 1(1), 41–57 CrossRef.
- S. Abuhattum, D. Mokbel, P. Müller, D. Soteriou, J. Guck and S. Aland, An Explicit Model to Extract Viscoelastic Properties of Cells from AFM Force-Indentation Curves, iScience, 2022, 25(4), 104016, DOI:10.1016/J.ISCI.2022.104016.
- P. C. Nalam, N. N. Gosvami, M. A. Caporizzo, R. J. Composto and R. W. Carpick, Soft Matter Soft Matter Nano-Rheology of Hydrogels Using Direct Drive Force Modulation Atomic Force Microscopy, Soft Matter, 2015, 1–12, 10.1039/x0xx00000x.
- D. B. W. C. B. Carter, Transmission Electron Microscopy A Textbook for Materials Science, springer publication, 2009 Search PubMed.
- E. B. Stopler, O. J. Dodo, A. C. Hull, K. A. Weaver, P. Chakma, R. Edelmann, L. Ranly, M. B. Zanjani, Z. Ye and D. Konkolewicz, Carbon Nanotube Enhanced Dynamic Polymeric Materials through Macromolecular Engineering, Mater. Adv., 2020, 1(5), 1071–1076 RSC.
- H. Jinnai, Electron Microscopy for Polymer Structures, Microscopy, 2022, 71(Supplement_1), i148–i164, DOI:10.1093/JMICRO/DFAB057.
- Z. Kochovski, G. Chen, J. Yuan and Y. Lu, Cryo-Electron Microscopy for the Study of Self-Assembled Poly (Ionic Liquid) Nanoparticles and Protein Supramolecular Structures, Colloid Polym. Sci., 2020, 298, 707–717 CrossRef CAS.
- R. Kiyama, M. Yoshida, T. Nonoyama, T. Sedlačík, H. Jinnai, T. Kurokawa, T. Nakajima, J. P. Gong, R. Kiyama, T. Nonoyama, T. Sedlačík, T. Kurokawa, T. Nakajima, J. P. Gong, M. Yoshida and H. Jinnai, Nanoscale TEM Imaging of Hydrogel Network Architecture, Adv. Mater., 2023, 35(1), 2208902, DOI:10.1002/ADMA.202208902.
- L. Sabbatini and E. De Giglio, Polymer Surface Characterization, Walter de Gruyter GmbH & Co KG, 2022 Search PubMed.
- A. Prasad, N. V. Salim, M. Mozetič, L. Kailas and S. Thomas, Time–of–flight Secondary Ion Mass Spectrometric Analysis of Polymer Surfaces: A Review, J. Appl. Polym. Sci., 2022, 139(23), 52286 CrossRef CAS.
- R. J. Composto, R. M. Walters and J. Genzer, Application of Ion Scattering Techniques to Characterize Polymer Surfaces and Interfaces, Mater. Sci. Eng., R, 2002, 38(3–4), 107–180 CrossRef.
- D. Y. Kwok and A. W. Neumann, Contact Angle Measurement and Contact Angle Interpretation, Adv. Colloid Interface Sci., 1999, 81(3), 167–249, DOI:10.1016/S0001-8686(98)00087-6.
- C. M. Chan and L.-T. Weng, Surface Characterization of Polymer Blends by XPS and ToF-SIMS, Materials, 2016, 9(8), 655 CrossRef PubMed.
- M. S. Wagner, S. L. McArthur, M. Shen, T. A. Horbett and D. G. Castner, Limits of Detection for Time of Flight Secondary Ion Mass Spectrometry (ToF-SIMS) and X-Ray Photoelectron Spectroscopy(XPS): Detection of Low Amounts of Adsorbed Protein, J. Biomater. Sci., Polym. Ed., 2002, 13(4), 407–428 CrossRef CAS.
- Q. Liu, J. Li, C. Cong, H. Cui, L. Xu, Y. Zhang, X. Meng and Q. Zhou, Thermal and Thermo-Oxidative Degradation of Tetrafluoroethylene–Propylene Elastomer above 300 °C, Polym. Degrad. Stab., 2020, 177, 109180, DOI:10.1016/J.POLYMDEGRADSTAB.2020.109180.
- N. Vandencasteele and F. Reniers, Plasma-Modified Polymer Surfaces: Characterization Using XPS, J. Electron Spectrosc. Relat. Phenom., 2010, 178–179(C), 394–408, DOI:10.1016/J.ELSPEC.2009.12.003.
- L. Shi, W. Liu, X. Zhang and J. Hu, Adsorption of Methylene Blue from Aqueous Solution by Crosslinked Carboxymethyl Cellulose/Organo-Montmorillonite Composite Hydrogels, J. Polym. Res., 2023, 30(8), 1–16, DOI:10.1007/S10965-023-03674-X/FIGURES/14.
- C. V. Cushman, P. Brüner, J. Zakel, G. H. Major, B. M. Lunt, N. J. Smith, T. Grehl and M. R. Linford, Low Energy Ion Scattering (LEIS), A Practical Introduction to Its Theory, Instrumentation, and Applications, Anal. Methods, 2016, 8(17), 3419–3439 RSC.
- Y. Zheng and M. Chen, Low Energy Ion Scattering (LEIS) Spectroscopy, in Springer Handbook of Advanced Catalyst Characterization, Springer, 2023, pp. 461–484 Search PubMed.
- P. Posadas, J. L. Valentín, R. Benavente, E. Blázquez-Blázquez, A. Urtiaga, J. A. Álvarez and M. L. Cerrada, Crosslinked Networks in Electron Beam Irradiated Polyethylenes Evaluated by Proton Low-Field NMR Spectroscopy, Radiat. Phys. Chem., 2023, 204, 110694 CrossRef CAS.
- A. Martínez-Richa and R. L. Silvestri, Developments in Solid-State NMR Spectroscopy of Polymer Systems, in Spectroscopic Analyses-Developments and Applications, IntechOpen, 2017, pp. 15–30 Search PubMed.
- B. Reif, S. E. Ashbrook, L. Emsley and M. Hong, Solid-State NMR Spectroscopy, Nat. Rev. Methods Primers, 2021, 1(1), 2 CrossRef CAS PubMed.
- P. A. Mirau, A Practical Guide to Understanding the NMR of Polymers, Wiley-Interscience, 2016 Search PubMed.
- M. A. Malmierca, A. González-Jiménez, I. Mora-Barrantes, P. Posadas, A. Rodríguez, L. Ibarra, A. Nogales, K. Saalwächter and J. L. Valentín, Characterization of Network Structure and Chain Dynamics of Elastomeric Ionomers by Means of 1H Low-Field NMR, Macromolecules, 2014, 47(16), 5655–5667 CrossRef CAS.
- K. Saalwächter, Detection of Heterogeneities in Dry and Swollen Polymer Networks by Proton Low-Field NMR Spectroscopy, J. Am. Chem. Soc., 2003, 125(48), 14684–14685 CrossRef PubMed.
- F. Lange, K. Schwenke, M. Kurakazu, Y. Akagi, U. Chung, M. Lang, J.-U. Sommer, T. Sakai and K. Saalwächter, Connectivity and Structural Defects in Model Hydrogels: A Combined Proton NMR and Monte Carlo Simulation Study, Macromolecules, 2011, 44(24), 9666–9674 CrossRef CAS.
- F. Vaca Chávez and K. Saalwächter, Time-Domain NMR Observation of Entangled Polymer Dynamics: Universal Behavior of Flexible Homopolymers and Applicability of the Tube Model, Macromolecules, 2011, 44(6), 1549–1559 CrossRef.
- F. Campise, D. C. Agudelo, R. H. Acosta, M. A. Villar, E. M. Valles, G. A. Monti and D. A. Vega, Contribution of Entanglements to Polymer Network Elasticity, Macromolecules, 2017, 50(7), 2964–2972 CrossRef CAS.
- T. Hashimoto, Principles and Applications of X-Ray, Light and Neutron Scattering, Springer Nature, 2022 Search PubMed.
- N. S. Murthy, Recent Developments in Polymer Characterization Using X-Ray Diffraction, Rigaku J., 2004, 21(1), 15–24 CAS.
- N. S. Murthy, X-ray Diffraction from Polymers, in Polymer Morphology: Principles, Characterization, and Processing, 2016, pp. 14–36 Search PubMed.
- D. J. Waters, K. Engberg, R. Parke-Houben, C. N. Ta, A. J. Jackson, M. F. Toney and C. W. Frank, Structure and Mechanism of Strength Enhancement in Interpenetrating Polymer Network Hydrogels, Macromolecules, 2011, 44(14), 5776–5787 CrossRef CAS.
- S. Tan, D. Zhang and E. Zhou, SAXS Measurements of the Interface in Polyacrylate and Epoxy Interpenetrating Networks with Fractal Geometry, Polymer, 1997, 38(18), 4571–4575 CrossRef CAS.
- P. S. Singh, Small-Angle Scattering Techniques (SAXS/SANS), in Membrane Characterization, Elsevier, 2017, pp. 95–111 Search PubMed.
- M. Ballauff, SAXS and SANS Studies of Polymer Colloids, Curr. Opin. Colloid Interface Sci., 2001, 6(2), 132–139 CrossRef CAS.
- G. P. Baeza, A. Sharma, A. Louhichi, L. Imperiali, W. P. J. Appel, C. F. C. Fitié, M. P. Lettinga, E. Van Ruymbeke and D. Vlassopoulos, Multiscale Organization of Thermoplastic Elastomers with Varying Content of Hard Segments, Polymer, 2016, 107, 89–101, DOI:10.1016/J.POLYMER.2016.11.010.
- Y. A. Akpalu and Y. Lin, Multivariable Structural Characterization of Semicrystalline Polymer Blends by Small–angle Light Scattering, J. Polym. Sci., Part B: Polym. Phys., 2002, 40(23), 2714–2727 CrossRef CAS.
- A. Mukhopadhyay and S. Granick, Micro-and Nanorheology, Curr. Opin. Colloid Interface Sci., 2001, 6(5–6), 423–429 CrossRef CAS.
- R. N. Zia, Active and Passive Microrheology: Theory and Simulation, Annu. Rev. Fluid Mech., 2018, 50, 371–405 CrossRef.
- K. E. Kasza and D. A. Weitz, 4.5 Mechanical Properties of Actin Networks, 2012 Search PubMed.
- T. G. Mason and D. A. Weitz, Optical Measurements of Frequency-Dependent Linear Viscoelastic Moduli of Complex Fluids, Phys. Rev. Lett., 1995, 74(7), 1250 CrossRef CAS.
- A. Perego, D. Lazarenko, M. Cloitre and F. Khabaz, Microscopic Dynamics and Viscoelasticity of Vitrimers, Macromolecules, 2022, 55(17), 7605–7613 CrossRef CAS.
- P. Cicuta and A. M. Donald, Microrheology: A Review of the Method and Applications, Soft Matter, 2007, 3(12), 1449–1455 RSC.
- A. M. Kloxin, A. M. Kasko, C. N. Salinas and K. S. Anseth, Photodegradable Hydrogels for Dynamic Tuning of Physical and Chemical Properties, Science, 2009, 324(5923), 59–63, DOI:10.1126/science.1169494.
- H. Zhou, E.-M. Schön, M. Wang, M. J. Glassman, J. Liu, M. Zhong, D. Díaz Díaz, B. D. Olsen and J. A. Johnson, Crossover Experiments Applied to Network Formation Reactions: Improved Strategies for Counting Elastically Inactive Molecular Defects in PEG Gels and Hyperbranched Polymers, J. Am. Chem. Soc., 2014, 136(26), 9464–9470 CrossRef CAS PubMed.
- M. P. Lutolf, J. L. Lauer-Fields, H. G. Schmoekel, A. T. Metters, F. E. Weber, G. B. Fields and J. A. Hubbell, Synthetic Matrix Metalloproteinase-Sensitive Hydrogels for the Conduction of Tissue Regeneration: Engineering Cell-Invasion Characteristics, Proc. Natl. Acad. Sci. U. S. A., 2003, 100(9), 5413–5418 CrossRef CAS.
- E. M. C. Jones, A. R. Jones and C. Winters, Combined Thermographic Phosphor and Digital Image Correlation (TP+ DIC) for Simultaneous Temperature and Strain Measurements, Strain, 2022, 58(5), e12415 CrossRef CAS.
- D. Chen and W. Zhen, Performance, Interfacial Compatibility Testing and Rheonaut Technology Analysis for Simultaneous Rheology and FTIR of Poly (Lactic Acid)/Modified Saponite Nanocomposites, Polym. Test., 2021, 100, 107232 CrossRef CAS.
- A. Dazzi and C. B. Prater, AFM-IR: Technology and Applications in Nanoscale Infrared Spectroscopy and Chemical Imaging, Chem. Rev., 2017, 117(7), 5146–5173 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |