Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Synthesis and symmetry of perovskite oxynitride CaW(O,N)3†
Matthew E.
Sweers
 a,
Tzu-chen
Liu
a,
Tzu-chen
Liu
 a,
Jiahong
Shen
a,
Bingzhang
Lu
b,
John W.
Freeland
c,
Christopher
Wolverton
a,
Jiahong
Shen
a,
Bingzhang
Lu
b,
John W.
Freeland
c,
Christopher
Wolverton
 a,
Gabriela B.
Gonzalez Aviles
d and
Linsey C.
Seitz
a,
Gabriela B.
Gonzalez Aviles
d and
Linsey C.
Seitz
 *b
*b
aDepartment of Materials Science and Engineering, Northwestern University, Evanston, IL 60208, USA
bDepartment of Chemical and Biological Engineering, Northwestern University, Evanston, IL 60208, USA. E-mail: linsey.seitz@northwestern.edu
cAdvanced Photon Source, Argonne National Laboratory, Lemont, IL 60439, USA
dDepartment of Physics and Astrophysics, DePaul University, Chicago, IL 60614, USA
First published on 5th June 2024
Abstract
Perovskite oxynitrides, in addition to being promising electrocatalysts and photoabsorbers, present an interesting case study in crystal symmetry. Full or partial ordering of the O and N anions affects global symmetry and influences material performance and functionality; however, anion ordering is challenging to detect experimentally. In this work, we synthesize a novel perovskite oxynitride CaW(O,N)3 and characterize its crystal structure using both X-ray and neutron diffraction. Through co-refinement of the diffraction patterns with a range of literature and theory-derived model structures, we demonstrate that CaW(O,N)3 adopts an orthorhombic Pnma average structure and exhibits octahedral distortion with evidence for preferred anion site occupancy. However, through comparison with a large, low-symmetry unit cell, we identify the presence of disorder that is not fully accounted for by the high-symmetry model. We compare CaW(O,N)3 with SrW(O,N)3 to demonstrate the broader presence of such disorder and identify contrasting features in the electronic structures. This work signifies an updated perspective on the inherent crystal symmetry present in perovskite oxynitrides.
New conceptsWe challenge the conventional reporting of crystal symmetry in perovskite oxynitrides through our exploration of the crystal structure of CaW(O,N)3, which we synthesize for the first time. Traditional literature simplifies perovskite oxynitrides by using high-symmetry unit cells with fractional anion occupancy (e.g., sites comprised of 50% O and 50% N). While these models provide a convenient approximation, they can never accurately reflect the true nature of perovskite oxynitrides. The reality is more complex; each anion site must contain either O or N, resulting in local displacements of the anions and neighboring cations off of their high-symmetry sites due to the differing ionic radii of O2− and N3−. We demonstrate using Rietveld co-refinement that a large unit cell (≥20 atoms) with low symmetry (space group P1) and random but defined anion positions provides a more accurate fit to the X-ray and neutron diffraction patterns for CaW(O,N)3, affording unique insight into sources of disorder that are not captured within the traditional models. We find the same result for previously-reported SrW(O,N)3, indicating that this disorder is more widespread than previously realized. Thus, this work presents a new perspective on the symmetry of perovskite oxynitrides and the crystal structures we use to describe them. |
1. Introduction
For many electrochemical reaction systems, the lack of sufficiently active, durable, and affordable catalysts necessitates continued materials discovery and characterization. Heteroanionic materials, a relatively understudied class of inorganic materials that contain more than one type of anion species, have been demonstrated as attractive options for energy and electrochemistry applications owing to their highly tunable structures, compositions, and properties. For example, oxysulfides (materials containing both oxide and sulfide anions) exhibit high activity for oxygen evolution, oxygen reduction, and hydrogen evolution,1–6 including in zinc–air batteries where increased activity is attributed to sulfur-tuned Co–O covalency.7 Oxyfluorides have been demonstrated as catalysts for CO2 reduction8 and ethane oxidation9 as well as solid oxide electrolytes for fuel cells.10,11Oxynitrides, and notably perovskite oxynitrides which follow the formula AB(O,N)3, are often studied as photocatalysts12–18 and non-toxic pigments19,20 due to their tendency for visible-range band gaps. Oxynitrides are typically synthesized via ammonolysis, whereby an oxide precursor is heated under flowing ammonia to incorporate nitrogen into the material.21 The introduction of nitrogen into an oxide material can increase the covalency of the metal-anion bonds and form cations in heightened oxidation states due to nitrogen's decreased electronegativity and more negative formal charge. Beyond electronic changes, oxynitrides can take on entirely new structures from their oxide counterparts,22 unlocking new phase spaces that are inaccessible for some mixed-metal oxides. In perovskites, these phases tend to exhibit non-cubic symmetries due to distortion of the BX6 octahedra, and in some cases, ordered arrangements of anions23–26 not allowed within cubic space groups. Though slight atomic displacements of cations from high symmetry positions have been discussed,25,26 the structures reported for perovskite oxynitrides are broadly described without these displacements in mind, leading to an incomplete structural picture.
In this work, we describe the first reported synthesis of calcium tungsten oxynitride CaW(O,N)3, a perovskite oxynitride that is previously only predicted computationally, and use X-ray and neutron diffraction to investigate its crystal structure. We use Rietveld refinement complemented with density functional theory (DFT) calculations to examine its crystal structure, including octahedral distortion, anion ordering, and symmetry. Comparisons among different structural models help to identify sources of disorder, particularly from varying coordination environments. Further comparison with an analogous material, SrW(O,N)3, supports these findings and highlights variations in electronic structure.
2. Results and discussion
Following the first step of a solid state reaction of calcium carbonate and tungsten(VI) oxide via grinding and calcining at 1000 °C for 4 h (Fig. 1a, details in Methods section), X-ray diffraction (XRD) confirms phase purity of the CaWO4 scheelite intermediate (Fig. 1b) with minor additional peaks caused by Cu Kβ radiation. As expected, CaWO4 peaks occur at larger angles compared with its SrWO4 analogue due to the smaller ionic radius of Ca compared with Sr27 (Fig. S1, ESI†). The oxynitride phases CaW(O,N)3 and SrW(O,N)3 were formed via ammonolysis at 700 °C for 12 h, and 900 °C for 5 h, respectively. We note that the ammonolysis temperature of 700 °C for CaW(O,N)3 is lower than previously reported attempts to synthesize this material.22,28 The proposed overall reaction follows as provided in eqn (1) and (2) below:| WO3 + CaCO3 → CaWO4 + CO2 | (1) |
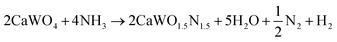 | (2) |
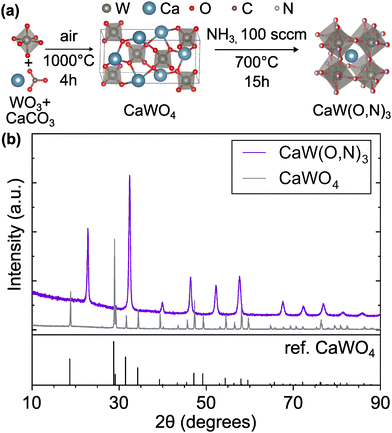 | ||
| Fig. 1 (a) Synthesis route for CaW(O,N)3 consisting of calcination of WO3 and CaCO3 precursors followed by ammonolysis of the scheelite CaWO4 intermediate. (b) XRD patterns of intermediate scheelite phases, CaWO4 and CaW(O,N)3, demonstrating their differing crystal structures. CaWO4 reference is provided.29 Crystal structure images generated using VESTA.30 | ||
Surface composition is estimated using X-ray photoelectron spectroscopy, which also confirms the lack of contaminants (Fig. S2 and Table S1, ESI†). We measured anion stoichiometry using combustion analysis, finding an overall composition of CaWO3−xNx where 1.3 ≤ x ≤ 1.6 (Table S2 (ESI†), details in Methods section). It is notable that this range captures the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 anion ratio, which could potentially allow the structure to adopt an ordered configuration of anions.
1 anion ratio, which could potentially allow the structure to adopt an ordered configuration of anions.
We performed Rietveld refinement31 on synchrotron XRD and neutron diffraction (ND) patterns of CaW(O,N)3 using several structural models (Table 1) to characterize its crystal structure. The tolerance factor for this material was calculated from Shannon radii,27 accounting for varied W oxidation states. The calculated tolerance factor ranges between 0.923 for CaWO3, which is not a stable material but represents the “oxide” extreme of the composition range, and 0.964 for CaWON2,32 where the oxidation state of W is maximized at 6+. Based on this range, one may expect this material to exhibit cubic symmetry regardless of anion stoichiometry,33–36 though the tolerance factor is more commonly used for simple stability prediction.
| Model | DFT ID | Space group | Atoms/unit cell | (O,N)3 stoichiometry | Anion disorder method | Anion site occupancy |
|---|---|---|---|---|---|---|
| C-I | — |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
5 | O1.5N1.5 | Partial occupancy | Fixed |
| C-II | — | Pnma | 20 | O1.5N1.5 | Partial occupancy | Varied |
| C-III | — | Pnma | 20 | O1.5N1.5 | Partial occupancy | Fixed |
| C-IV | — | Pnma | 20 | O1.4N1.6 | Partial occupancy | Varied |
| C-V | — | Pnma | 20 | O1.7N1.3 | Partial occupancy | Varied |
| C-VI | — | Pnma | 20 | O3 | Partial occupancy | Fixed |
| C-VII | — | Pnma | 20 | N3 | Partial occupancy | Fixed |
| C-VIII | F | P1 | 20 | O1.5N1.5 | Quasi-random | Fixed |
| C-IX | A | P1 | 60 | O1.5N1.5 | Quasi-random | Fixed |
| C-X | — | Pnma | 20 | O1.5N1.5 | Partial occupancy | Varied |
Indeed, the XRD pattern for CaW(O,N)3 displays a peak footprint matching a Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group (Fig. S3, ESI†), which is reported for SrW(O,N)3,22 though we observe minor additional peaks from the oxide CaWO4 that formed in the capillary tube during transit time between sample submission and measurement as well as mismatches between the experimental and simulated peak intensities at low Q values. Furthermore, comparison of the ND pattern with the Pm
m space group (Fig. S3, ESI†), which is reported for SrW(O,N)3,22 though we observe minor additional peaks from the oxide CaWO4 that formed in the capillary tube during transit time between sample submission and measurement as well as mismatches between the experimental and simulated peak intensities at low Q values. Furthermore, comparison of the ND pattern with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m model (C-I, Fig. S3b, ESI†) reveals numerous additional peaks that are not accounted for by CaWO4, particularly evident in the Q ≈ 2 – 10 Å−1 (d ≈ 3.1 – 0.6 Å) region. The X-ray diffraction signal is dominated by heavy elements, whereas ND is more sensitive to light atoms such as O and N. As such, the fact that extra peaks are much less apparent in XRD (see Fig. S4, ESI†) but readily observed via ND indicates the presence of octahedral distortion that forms planes of O and N atoms with new interplanar spacing while leaving Ca and W species relatively unmoved from their atomic planes.
m model (C-I, Fig. S3b, ESI†) reveals numerous additional peaks that are not accounted for by CaWO4, particularly evident in the Q ≈ 2 – 10 Å−1 (d ≈ 3.1 – 0.6 Å) region. The X-ray diffraction signal is dominated by heavy elements, whereas ND is more sensitive to light atoms such as O and N. As such, the fact that extra peaks are much less apparent in XRD (see Fig. S4, ESI†) but readily observed via ND indicates the presence of octahedral distortion that forms planes of O and N atoms with new interplanar spacing while leaving Ca and W species relatively unmoved from their atomic planes.
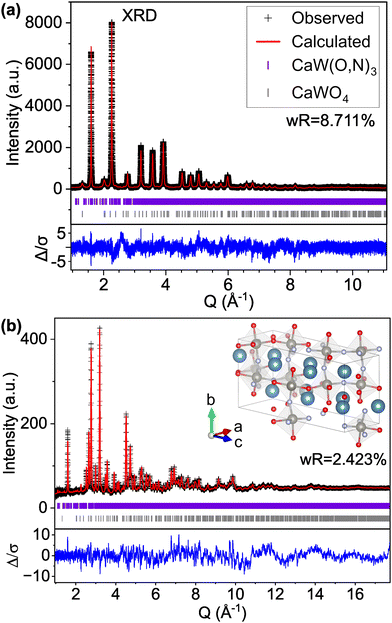
We find that the ND peak positions and intensities are much more closely matched by an orthorhombic perovskite structure with space group Pnma (model C-II, Fig. 2 and Fig. S5, ESI† and Table 2), which is widely reported37 for other perovskite oxynitrides and contains distorted octahedra. This structural change results in a significant reduction in the ND weighted residual (wR) from 12.514% for C-I (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) to 2.763% for C-II (Pnma) and does better to match very minor peaks in the XRD pattern that were unmatched by the cubic C-I model (Fig. S4, ESI†). Additionally, we find from refinement results using the Pnma structure (C-II) that N species may prefer the apical O1/N1 anion site over the O2/N2 site located in-plane with W atoms, accounting for 71% of the atoms on the O1/N1 site (Table 2 and Fig. S6, ESI†). Similar results have been found for other perovskite oxynitrides,38,39 though the preference for nitrogen to occupy the apical site is somewhat unexpected in the broader context of the literature,40,41 as it suggests that the anions prefer trans and mer configurations (see Fig. S7, ESI†). Trans configurations are generally regarded as less stable than cis ordering,23,24,26,42 and mer configurations would result in N–W–N chains that would induce localized strain due to mismatched ionic radii and result in relative instability.42 Both models contain 1
m) to 2.763% for C-II (Pnma) and does better to match very minor peaks in the XRD pattern that were unmatched by the cubic C-I model (Fig. S4, ESI†). Additionally, we find from refinement results using the Pnma structure (C-II) that N species may prefer the apical O1/N1 anion site over the O2/N2 site located in-plane with W atoms, accounting for 71% of the atoms on the O1/N1 site (Table 2 and Fig. S6, ESI†). Similar results have been found for other perovskite oxynitrides,38,39 though the preference for nitrogen to occupy the apical site is somewhat unexpected in the broader context of the literature,40,41 as it suggests that the anions prefer trans and mer configurations (see Fig. S7, ESI†). Trans configurations are generally regarded as less stable than cis ordering,23,24,26,42 and mer configurations would result in N–W–N chains that would induce localized strain due to mismatched ionic radii and result in relative instability.42 Both models contain 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 anion stoichiometry, but whereas model C-II allows O and N site occupancies to vary between sites O1/N1 and O2/N2, model C-III fixes the occupancies at 0.5 for both O and N on both anion sites. The refinement of site occupancy in C-II offers minor improvements in overall wR (from 5.041% for fixed to 4.993% for varied) and ND wR (from 2.817% for fixed to 2.763% for varied, Table S3, ESI†). Since refinement of site occupancy introduces additional degrees of freedom, we use the F-test to determine whether the observed improvement is statistically significant.43,44 Based on the number of refined parameters for both refinements and total number of observations, an F ratio of ≥2.605 would signify a ≥0.95 probability of significance. From the weighted sums of squared residuals, we calculate an F ratio of 636.3. Thus, we conclude that there is sufficient evidence for preferred anion occupancy in model C-II. This preferential occupancy of N onto one type of anion site may influence the materials’ optical and electronic properties, such as its dielectric constant.23,26,45,46
1 anion stoichiometry, but whereas model C-II allows O and N site occupancies to vary between sites O1/N1 and O2/N2, model C-III fixes the occupancies at 0.5 for both O and N on both anion sites. The refinement of site occupancy in C-II offers minor improvements in overall wR (from 5.041% for fixed to 4.993% for varied) and ND wR (from 2.817% for fixed to 2.763% for varied, Table S3, ESI†). Since refinement of site occupancy introduces additional degrees of freedom, we use the F-test to determine whether the observed improvement is statistically significant.43,44 Based on the number of refined parameters for both refinements and total number of observations, an F ratio of ≥2.605 would signify a ≥0.95 probability of significance. From the weighted sums of squared residuals, we calculate an F ratio of 636.3. Thus, we conclude that there is sufficient evidence for preferred anion occupancy in model C-II. This preferential occupancy of N onto one type of anion site may influence the materials’ optical and electronic properties, such as its dielectric constant.23,26,45,46
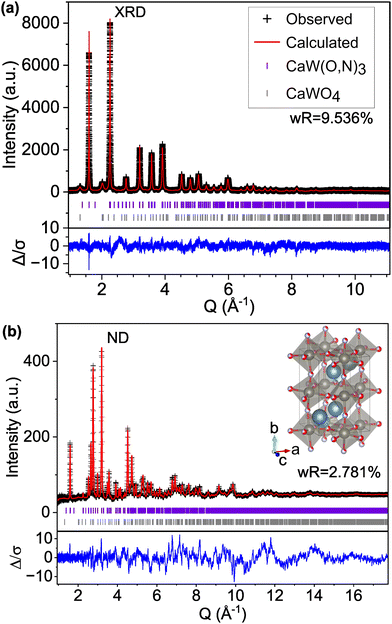 | ||
| Fig. 2 Rietveld refinement of CaW(O,N)3 (a) synchrotron XRD and (b) ND patterns to structural model C-II with the Pnma space group and anion sites fractionally occupied by O and N. | ||
| Formula | CaWO1.5N1.5 |
| Formula weight | 262.929 Da |
| Formula units per unit cell (Z) | 4 |
| S.G. # | 62 |
| S.G. | Pnma |
| Crystal system | Orthorhombic |
| a | 5.5708(1) Å |
| b | 7.8598(2) Å |
| c | 5.5326(1) Å |
| Volume | 242.245(5) Å3 |
| Site | x | y | z | Occ. | Uiso |
|---|---|---|---|---|---|
| Ca | 0.5174(4) | 0.25 | 0.5023(7) | 1 | 0.0170(2) |
| W | 0.5 | 0 | 0 | 1 | 0.01737(7) |
| O1 | 0.4895(3) | 0.25 | 0.0597(2) | 0.29(1) | 0.0120(2) |
| N1 | — | — | — | 0.71(1) | — |
| O2 | 0.2887(1) | 0.0302(1) | 0.7106(2) | 0.607(5) | 0.0068(1) |
| N2 | — | — | — | 0.393(5) | — |
We also varied the global anion stoichiometry of the Pnma model (C-II) used in Fig. 2 and Table 2 Table S3 (ESI†) to the extremities of the anion range estimated from combustion analysis (Table S2, ESI†) to test its impact on the fit. The resulting wR values for CaWO1.4N1.6 (model C-IV) and CaWO1.7N1.3 (model C-V) reported in Table 3 show no significant improvement in the fit with varied anion ratio compared with CaWO1.5N1.5 (model C-II). We further examined the impact of anion stoichiometry on predicted ND patterns by extending the model composition to CaWO3 (model C-VI) and CaWN3 (model C-VII) in Fig. S8 (ESI†). Peaks at Q ≈ 3.20, 2.77, and 2.26 Å−1 (d = 1.96, 2.27, 2.78) exhibit the greatest sensitivity to anion stoichiometry. However, while the observed pattern falls between the all-O and all-N signals, the proportions of mismatch between each model and the observed data are not consistent across peaks, suggesting that the variation in ND peak intensities cannot be accounted for by anion stoichiometry alone.
| Model | (O,N)3 stoichiometry | wR (%) | XRD wR (%) | ND wR (%) |
|---|---|---|---|---|
| C-IV | O1.4N1.6 | 5.046 | 9.544 | 2.813 |
| C-II | O1.5N1.5 | 5.029 | 9.536 | 2.781 |
| C-V | O1.7N1.3 | 5.004 | 9.524 | 2.736 |
While the Pnma structure from model C-II above provides an excellent match to the ND signal, the significant mismatch between the observed and modeled pseudocubic (001) peak intensity (≈1.6 Å−1 in the XRD pattern) indicates there is disorder that is not fully captured by the strictly defined atomic positions and symmetry. To identify additional structure candidates and further investigate anion ordering in CaW(O,N)3, we complemented our experimental approach and literature-sourced model crystal structures with structures provided by DFT calculations. We calculated the stability (defined as energy above the convex hull, Ehull, containing 0.5 mol CaO + 0.167 mol Ca3WO6 + 0.25 mol N + 0.417 mol W2N3 according to the Open Quantum Materials Database, OQMD) for structures with both ordered and disordered anion configurations and parent cells representing multiple space groups, summarized in Table 4. Notably, nearly all structures that are predicted to be relatively low in energy (Ehull < 50 meV atom−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 47,48) exhibit disordered anion configurations. We used these low energy structures for Rietveld refinement with the experimental data.
47,48) exhibit disordered anion configurations. We used these low energy structures for Rietveld refinement with the experimental data.
| DFT ID | Composition | S.G. # | Crystal system | Spage group | Anion ordering | # of atoms | E hull (eV atom−1) |
|---|---|---|---|---|---|---|---|
| A | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 60 | 0.026 |
| B | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 40 | 0.034 |
| C | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 40 | 0.034 |
| D | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 20 | 0.035 |
| E | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 20 | 0.037 |
| F | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 20 | 0.037 |
| G | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 20 | 0.038 |
| H | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 20 | 0.039 |
| I | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 20 | 0.042 |
| J | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 40 | 0.043 |
| K | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 40 | 0.047 |
| L | CaWO1.5N1.5 | 166 | Trigonal |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
Fac | 10 | 0.049 |
| M | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 160 | 0.061 |
| N | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 20 | 0.068 |
| O | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 20 | 0.071 |
| P | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 40 | 0.071 |
| Q | CaWO1.5N1.5 | 25 | Orthorhombic | Pmm2 | Cis | 10 | 0.076 |
| R | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 20 | 0.078 |
| S | CaWO1.5N1.5 | 1 | Triclinic | P1 | — | 20 | 0.08 |
| T | CaWO1.5N1.5 | 115 | Tetragonal |
P![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) m2 m2 |
Mer | 10 | 0.107 |
| U | CaWO1.5N1.5 | 65 | Orthorhombic | Cmmm | Mer | 10 | 0.111 |
| V | CaWO1.5N1.5 | 69 | Orthorhombic | Fmmm | Mer | 10 | 0.113 |
| W | CaWO1.5N1.5 | 99 | Tetragonal | P4mm | Segregated octahedra | 10 | 0.117 |
| X | CaWO1.5N1.5 | 65 | Orthorhombic | Cmmm | Mer | 10 | 0.119 |
| Y | CaWO1.5N1.5 | 47 | Orthorhombic | Pmmm | Mer | 10 | 0.121 |
| Z | CaWO1.5N1.5 | 47 | Orthorhombic | Pmmm | Trans | 10 | 0.142 |
| AA | CaWO1.5N1.5 | 65 | Orthorhombic | Cmmm | Trans | 10 | 0.144 |
| AB | CaWO1.5N1.5 | 47 | Orthorhombic | Pmmm | Trans | 10 | 0.147 |
For comparison with the Pnma structure (model C-II) which contains 20 atoms per unit cell, we first examine the low energy structures in Table 4 with at most 20 atoms per unit cell. Of this subset, model Structure F (model C-VIII) with P1 symmetry and defined anion positions provides the best fit to the experimental data (Fig. S9, ESI†), exhibiting improvement over the Pnma structure for both XRD (improving wR from 9.536% for C-II to 8.758% for C-VIII) and ND (improving ND wR from 2.781% for C-II to 2.653% for C-VIII). Notably, model C-VIII exhibits a significantly improved match to the pseudocubic (001) XRD peak intensity at Q ≈ 1.6 Å−1 compared with model C-II, though there are peaks present in the low Q region of the modeled ND pattern, particularly at 1.13 and 2.78 Å−1, that are not supported by the experimental data. By contrast, the lowest energy predicted structure (structure A, model C-IX) with the same P1 symmetry and a larger 60-atom cell provides an excellent match to both the XRD and ND patterns (Fig. 3), achieving the lowest wR values for both the XRD and ND patterns of any structure tested (structural details are provided in Tables S4 and Table S5 and Fig. S10, ESI†). Nevertheless, there are still features in the modeled ND pattern that are not present in the observed data, though these discrepancies are smaller than those apparent for smaller unit cells and approaching the order of magnitude of the background noise.
It is important to note that such improvement over the more constrained C-II model is expected given the large increase in the number of refined parameters between the models (47 parameters for C-II and 224 parameters for C-IX). Thus, we do not identify model C-IX containing P1 symmetry as the true structure of CaW(O,N); rather, we use this model to discuss sources of disorder in the material. For example, in model C-II where fractional site occupancy is used to model anion disorder, the position of the anion sites, the bond lengths, and the positions of neighboring cations all remain invariant to the identity of the anion in order to maintain symmetry. Even when we simulate additional disorder in the Pnma model through the refinement of anisotropic thermal parameters, which results in an improvement to total wR (from 4.993% for model C-II to 4.797% for model C-X), the Pnma models still only describe the long-range average crystal structure; they do not accurately represent the local distortions to Ca and W sites that physically occur in this material as a result of their varied anion coordinations.
Disordered anion configurations leave each W atom with numerous possible permutations of the WX6 octahedral environment that place W in various oxidation states and impose different perturbations to the atomic positions due to the difference in the ionic radii of O2− (1.4 Å) and N3− (1.64 Å).27 Such perturbations cannot be fully represented by a highly symmetric unit cell and would decrease the intensity of XRD peaks, which are highly sensitive to the cation symmetry due to their larger atomic numbers in this material. We propose that these perturbations have a far weaker effect on the predicted ND pattern for CaW(O,N)3 due to the fact that in the Pnma model (C-II), the anions are already displaced from high-symmetry sites due to octahedral rotation, so further displacement does not have as great an effect on the site symmetry of anions. This concept of varied local coordinations, called disproportionation, hints at the broader dichotomy prevalent within discussion of defective and non-stoichiometric materials of whether to describe materials by their local or periodic structures.49–53 Disproportionation leads to a high-symmetry average structure with lower local symmetry referred to as a “polymorphous network”.50,54–56 Polymorphism is also found in oxide and halide perovskites and is linked with band narrowing, metal-to-insulator transitions, and the formation of unique hole states.56
While a material with truly random anion placement would theoretically contain 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratios of cis
3 ratios of cis![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) trans and fac
trans and fac![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mer anion configurations (refer to Fig. S7, ESI†), respectively, the literature and our own theory-based work suggest that octahedra with cis and fac-type anion configurations would be more prevalent than those with trans and mer configurations based on energetic arguments.23,24,26,40,42,57 Indeed, in our lowest-energy predicted “anion disordered” structures, the majority of the octahedral configurations are cis-type, but not repeated in a consistent or symmetric manner. Accordingly, large unit cell size is necessary to sufficiently approximate the lack of consistently repeating anion motifs and a range of atomic displacements while maintaining a high fraction of WX6 octahedra with cis-type anion configurations.
mer anion configurations (refer to Fig. S7, ESI†), respectively, the literature and our own theory-based work suggest that octahedra with cis and fac-type anion configurations would be more prevalent than those with trans and mer configurations based on energetic arguments.23,24,26,40,42,57 Indeed, in our lowest-energy predicted “anion disordered” structures, the majority of the octahedral configurations are cis-type, but not repeated in a consistent or symmetric manner. Accordingly, large unit cell size is necessary to sufficiently approximate the lack of consistently repeating anion motifs and a range of atomic displacements while maintaining a high fraction of WX6 octahedra with cis-type anion configurations.
When we apply this understanding of atomic position perturbations resulting from varied coordination environments in heteroanionic materials to the previously reported22,28,58 perovskite oxynitride SrW(O,N)3, we find similar improvements of the fit with the experimental data. We first apply the reported structure model for this material, a cubic structure with the space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m and disordered anions (model S-I, Table 5), to the experimental data and find good agreement between peak positions in both the XRD and ND patterns, but poorly matched peak intensities as revealed by the sharp features in the Δ/σ plots (Fig. S11, ESI†). Additional structural details are reported in Table S6 (ESI†).
m and disordered anions (model S-I, Table 5), to the experimental data and find good agreement between peak positions in both the XRD and ND patterns, but poorly matched peak intensities as revealed by the sharp features in the Δ/σ plots (Fig. S11, ESI†). Additional structural details are reported in Table S6 (ESI†).
| Model | Space group | Atoms/unit cell | (O,N)3 stoichiometry | Anion disorder method | Anion site occupancy |
|---|---|---|---|---|---|
| S-I |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
5 | O1.5N1.5 | Partial occupancy | Fixed |
| S-II | P1 | 40 | O1.5N1.5 | Randomized | Fixed |
However, if we apply the concepts from model C-IX and use an anion-disordered P1 structure with a 40-atom unit cell (model S-II) that breaks the global symmetry and allows for displacement of all atomic positions, we are able to more accurately match peak intensities (Fig. 4). This results in improved fits compared with the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m structure for both the XRD pattern (16.085% wR for S-I down to 12.649% for S-II) and ND pattern (5.707% wR for S-II down to 4.431% for S-II). Hints of atomic displacement in SrW(O,N)3 were presented in a previous study of its extended X-ray absorption fine structure (EXAFS), where it was reported that the nearest neighbor scattering interaction required more than one W-anion scattering path to achieve a reasonable fit,58 as would be required for a W atom displaced from the center of its coordination octahedron. Curiously, while model S-II results in decreased residuals compared with model S-I (see Fig. 4 and Fig. S11, ESI†), there still exists clear systematic error in the peak fits, which may suggest further sources of disorder not accounted for by the P1 model.59 Similar to our findings for CaW(O,N)3, this structure still results in minor peaks in the high d (low Q) region of the calculated pattern that are on the order of magnitude of background noise. Additional structural details are provided in Tables S7 and S8 (ESI†). Based on the evidence presented in this work for both CaW(O,N)3 and SrW(O,N)3, we assert that disproportionation and polymorphism may be more widely present within perovskite oxynitrides (and potentially the broader category of oxynitrides) and should be addressed when discussing their crystal structures.
m structure for both the XRD pattern (16.085% wR for S-I down to 12.649% for S-II) and ND pattern (5.707% wR for S-II down to 4.431% for S-II). Hints of atomic displacement in SrW(O,N)3 were presented in a previous study of its extended X-ray absorption fine structure (EXAFS), where it was reported that the nearest neighbor scattering interaction required more than one W-anion scattering path to achieve a reasonable fit,58 as would be required for a W atom displaced from the center of its coordination octahedron. Curiously, while model S-II results in decreased residuals compared with model S-I (see Fig. 4 and Fig. S11, ESI†), there still exists clear systematic error in the peak fits, which may suggest further sources of disorder not accounted for by the P1 model.59 Similar to our findings for CaW(O,N)3, this structure still results in minor peaks in the high d (low Q) region of the calculated pattern that are on the order of magnitude of background noise. Additional structural details are provided in Tables S7 and S8 (ESI†). Based on the evidence presented in this work for both CaW(O,N)3 and SrW(O,N)3, we assert that disproportionation and polymorphism may be more widely present within perovskite oxynitrides (and potentially the broader category of oxynitrides) and should be addressed when discussing their crystal structures.
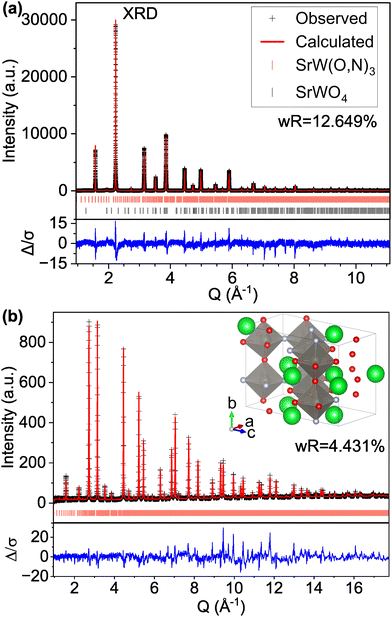 | ||
| Fig. 4 Rietveld refinement of SrW(O,N)3 (a) synchrotron XRD and (b) ND patterns using a 40-atom P1 structure suggested by our theory-based approaches (model S-II). | ||
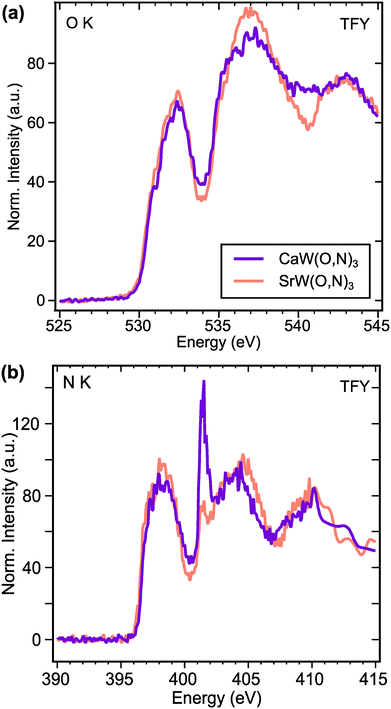
To investigate electronic structure differences between CaW(O,N)3 and its analogue SrW(O,N)3, we performed X-ray absorption spectroscopy (XAS) measurements at the O and N K-edges. For the O K-edge (Fig. 5a), the first features in the spectra occur at ∼532.2 eV and are attributed to electron transitions from O 1s states to O 2p – W 5d t2g hybridized states.60 The features in the region 533.5–538 eV are typically attributed to electron transitions from O 1s states to O 2p – W 5d eg hybridized states in tungstates,60,61 though for complex oxides, the absorption can be influenced by covalent interactions with the A-site species.61 Yashima et al. calculated via DFT the partial density of states for the CaxSr1−xWO2N composition system, from which we observe that the unoccupied Ca 3d states are expected to exist at lower energies than the Sr 4d states.22 Although the composition range calculated in that work does not extend all the way to CaWO2N, the relative energies of Ca 3d and Sr 4d states appear to align with the observed features in our XAS data. Namely, CaW(O,N)3 exhibits greater absorption intensity approximately 4 eV above the absorption edge (at ∼534 eV), whereas SrW(O,N)3 shows greater absorption intensity >5 eV above the absorption edge (at >535 eV). Since both materials are metallic, the Fermi energy should approximately align with the observed absorption edges.
For an electrically conductive material in which the O and N anions occupy the same lattice sites, we can reasonably expect O and N 2p states to hybridize with the same unoccupied electronic states above the Fermi level. This expectation is largely confirmed by the N K-edge spectra (Fig. 5b), which reflect very similar features to the O K-edge spectra. At both edges, we observe that the intensities of the anion 2p – W 5d t2g features (532.2 eV for O K and 398 eV for N K) are greater for SrW(O,N)3 than for CaW(O,N)3. This disparity suggests increased covalency between anions and 5d t2g states in SrW(O,N)3 compared with CaW(O,N)3, which contrasts with previously reported results regarding the effect of Sr vs. Ca on covalency in a perovskite.62 At higher energies in the N K-edge spectra, we observe the same trend in relative intensity as seen at the O K-edge, which we propose are attributed to the disparate energies of the Ca 3d and Sr 4d states. The sharp feature at 401.5 eV is likely a result of diffraction due to the large unit cell and is not representative of true electronic states, as it is not observed in the total electron yield (TEY) signals (Fig. S12, ESI†). Since the greatest differences in the XAS signal for CaW(O,N)3 and SrW(O,N)3 are likely a result of varied Ca and Sr d-state energies, the impact of octahedral distortion on the electronic structure is not readily observed from these spectra. However, these results provide sufficient evidence to demonstrate octahedral distortion and the existence of additional disorder in CaW(O,N)3 that may be present, yet have been previously underrecognized in a broader array of oxynitride materials.
3. Methods
3.1. Materials synthesis
Calcium carbonate (CaCO3, Sigma-Aldrich, ≥99%) and tungsten(VI) oxide (WO3, Sigma-Aldrich, 99.9%) were ground together in a stoichiometric metals ratio with a mortar and pestle, heated in an alumina crucible at 1000 °C for 4 h, and allowed to cool naturally to form CaWO4. This material was ground in a mortar and pestle for 30 min. To form SrWO4, the same procedure was followed using strontium carbonate (SrCO3, Aldrich, 99.995%) and heating to 900 °C for 12 h. Both powders appear white in color.To form CaW(O,N)3, 500 mg of the CaWO4 intermediate was loaded into a quartz boat and placed in a fused quartz tube in a tube furnace. Anhydrous ammonia was flowed through the tube at 100 sccm. The sample was heated at 3.3 °C min−1 to 700 °C and held for 15 h. The same procedure was used to form SrW(O,N)3 by placing SrWO4 in the quartz boat and heating to 900 °C for 5 h. The resulting powders are dark gray in color.
3.2. Combustion analysis
We used combustion analysis (Midwest Microlabs) to measure the nitrogen content in the material (Table S2, ESI†), which we use to estimate stoichiometry assuming a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cation ratio and negligible anion vacancy concentration. Using the H wt% values, we corrected the nitrogen weight fraction to account for adsorbed ammonia species. The range of anion stoichiometry in CaWO3−xNx we report in Table S2 (ESI†), 1.3 ≤ x ≤ 1.6, is relatively wide due to uncertainty in the hydrogen and nitrogen weight fractions.
1 cation ratio and negligible anion vacancy concentration. Using the H wt% values, we corrected the nitrogen weight fraction to account for adsorbed ammonia species. The range of anion stoichiometry in CaWO3−xNx we report in Table S2 (ESI†), 1.3 ≤ x ≤ 1.6, is relatively wide due to uncertainty in the hydrogen and nitrogen weight fractions.
3.3. Lab X-ray diffraction
For determining the structure and purity of the scheelite intermediates, we collected powder X-ray diffractograms using a Rigaku Smartlab system equipped with a Cu rotating anode using Cu Kα radiation (wavelength = 1.5418 Å). The accelerating voltage between the W filament and the anode was set at 40 kV and the tube current was 35 mA. Data were collected using a Hypix area detector. Samples were ground with a mortar and pestle before measurement.3.4. Synchrotron X-ray diffraction
High resolution synchrotron powder diffraction data were collected using the mail-in program for beamline 11-BM at the Advanced Photon Source (APS), Argonne National Laboratory using an average wavelength of 0.45904 Å. Discrete detectors covering an angular range from −6 to 16° 2θ are scanned over a 34° 2θ range, with data points collected every 0.001° 2θ and scan speed of 0.01° per s.The 11-BM instrument uses X-ray optics with two platinum-striped mirrors and a double-crystal Si(111) monochromator, where the second crystal has an adjustable sagittal bend.63 Ion chambers monitor incident flux. A vertical Huber 480 goniometer, equipped with a Heidenhain encoder, positions an analyzer system comprised of twelve perfect Si(111) analyzers and twelve Oxford-Danfysik LaCl3 scintillators, with a spacing of 2° 2θ.64 Analyzer orientation can be adjusted individually on two axes. A three-axis translation stage holds the sample mounting and allows it to be spun, typically at ∼5400 rpm (90 Hz). A Mitsubishi robotic arm is used to mount and dismount samples on the diffractometer. An Oxford Cryosystems Cryostream Plus device allows sample temperatures to be controlled over the range 80–500 K when the robot is used. Samples were measured at 298 K.
The diffractometer is controlled via EPICS.65 Data are collected while continually scanning the diffractometer 2θ arm. A mixture of NIST standard reference materials, Si (SRM 640c) and Al2O3 (SRM 676) is used to calibrate the instrument, where the Si lattice constant determines the wavelength for each detector. Corrections are applied for detector sensitivity, 2θ offset, small differences in wavelength between detectors, and the source intensity, as noted by the ion chamber before merging the data into a single set of intensities evenly spaced in 2θ.
3.5. Neutron diffraction
We collected neutron diffraction patterns using the mail-in program for the POWGEN instrument at Oak Ridge National Laboratory's Spallation Neutron Source. Approximately 3 g of each measured powder were loaded into vanadium cans for shipment and measurement. We used data from Neutron Bank 1 scanned over the time of flight (TOF) range of 3617 to 176000 μs (d-spacing of 0.354 to 6.65 Å) measured at ambient temperature.3.6. Combined refinement approach
We carried out Rietveld refinements of X-ray and neutron diffraction patterns using GSAS-II software.66 XRD and ND patterns were weighted equally during refinement. We used Inverse Chebyshev polynomials to accurately follow the curvature of the background for both diffraction patterns. For XRD, we assigned limits of 4.0° < 2θ < 48.7° to exclude regions with no peaks and/or excessively noisy background signal. Sample X displacement (perpendicular to the beam) was allowed to vary. For ND, we assigned limits of 8000 μs < TOF < 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μs to both (i) exclude highly noisy data at the extremities and (ii) include the 100
000 μs to both (i) exclude highly noisy data at the extremities and (ii) include the 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–150
000–150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 μs range where no peaks appeared in the data but several structural models displayed significant calculated peaks. Phase parameters were varied progressively in the following order: lattice parameter(s), crystallite size, microstrain, vibrational parameters (Uiso), site fraction, and atomic displacement (where possible). The scheelite oxide phases were added to CaW(O,N)3 XRD, ND, and SrW(O,N)3 XRD patterns and phase fractions were constrained to sum to 1. No oxide peaks were detected in the SrW(O,N)3 ND pattern. For structures with anion disorder modeled via fractional anion occupancy, vibrational parameters for O and N were constrained to be equivalent since they occupy the same sites. For structures with large unit cells (>20 atoms), we constrained atomic fractions and vibrational parameters for all sites within each element type to be equivalent. For the XRD pattern, a total of 1177 peaks are identified when using the Pnma model, 725 belonging to CaW(O,N)3 and 452 belonging to CaWO4. For the ND pattern, a total of 4808 peaks are identified when using the Pnma model, 2958 belonging to CaW(O,N)3 and 1850 belonging to CaWO4.
000 μs range where no peaks appeared in the data but several structural models displayed significant calculated peaks. Phase parameters were varied progressively in the following order: lattice parameter(s), crystallite size, microstrain, vibrational parameters (Uiso), site fraction, and atomic displacement (where possible). The scheelite oxide phases were added to CaW(O,N)3 XRD, ND, and SrW(O,N)3 XRD patterns and phase fractions were constrained to sum to 1. No oxide peaks were detected in the SrW(O,N)3 ND pattern. For structures with anion disorder modeled via fractional anion occupancy, vibrational parameters for O and N were constrained to be equivalent since they occupy the same sites. For structures with large unit cells (>20 atoms), we constrained atomic fractions and vibrational parameters for all sites within each element type to be equivalent. For the XRD pattern, a total of 1177 peaks are identified when using the Pnma model, 725 belonging to CaW(O,N)3 and 452 belonging to CaWO4. For the ND pattern, a total of 4808 peaks are identified when using the Pnma model, 2958 belonging to CaW(O,N)3 and 1850 belonging to CaWO4.
3.7. Density functional theory calculations
Special quasirandom structures (SQS)67 approximate random configurations employing a limited-size low-symmetry supercell. This cell is specifically chosen with cluster correlations that match as closely as possible the random values, particularly in the first few nearest neighbor shells, based on the assumption that short-range contributions to the energy typically have a stronger impact.67,68 Consequently, the objective function to minimize for generating SQS is designed in the form of:68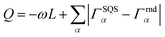 | (3) |
3.8. X-ray absorption spectroscopy
The O and N K-edge absorption spectra of CaW(O,N)3 and SrW(O,N)3 were collected at beamline 29-ID-D of the Advanced Photon Source at Argonne National Laboratory. Absorption intensity was measured using total fluorescence yield and total electron yield. Each spectrum was processed for comparison by removing linear background in the pre-edge region, normalizing the integrated area in the edge region, and removing linear post-edge background.4. Conclusions
We synthesized calcium tungsten oxynitride for the first time via ammonolysis and used combustion analysis to estimate its composition as CaWO1.4–1.7N1.3–1.6. Through comparison of Rietveld refinements of XRD and ND patterns with common perovskite structures, we identify the presence of octahedral distortion and evidence for preferred anion occupancy in this material, which may extenuate the anisotropy of materials properties already expected based on its orthorhombic Pnma average structure. Closer analysis of Rietveld refinements using DFT-predicted structures with various symmetry and anion ordering sheds light on additional disorder within the structure, which we propose stem from atomic displacements of both cations and anions resulting from varied ionic radii and configurations of nearest neighbors. Since such variations are inherent to anion-disordered materials, we postulate that these atomic displacements and polymorphism that modify electronic structure may be more prevalent than previously recognized in oxynitrides, which we also demonstrate with comparison to SrW(O,N)3.Author contributions
Matthew E Sweers was responsible for conceptualization, data curation, formal analysis, investigation, methodology, project administration, visualization, and writing of the original draft. Jiahong Shen and Tzu-chen Liu contributed investigation and methodology with DFT calculations. Bingzhang Lu performed investigation and methodology through material synthesis. John Freeland supported XAS measurements with methodology and formal analysis. Christopher Wolverton provided resources and guidance for DFT calculations. Gabriela B. Gonzalez Aviles contributed resources for ND beamtime and formal analysis of Rietveld refinements. Linsey C. Seitz was responsible for conceptualization, funding acquisition, resources, and supervision. All editors contributed to writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors recognize Brian Toby for his insight regarding qualitative and quantitative comparison of structural models. M. E. S. was supported by the Department of Defense (DoD) through the National Defense Science and Engineering Graduate (NDSEG) Fellowship Program. This work made use of the Jerome B. Cohen X-Ray Diffraction Facility supported by the MRSEC program of the NSF (DMR-2308691) at the Materials Research Center of Northwestern University and the SHyNE Resource (NSF ECCS-1542205.) We acknowledge Dr Saul Lapidus and beamline 11-BM at the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. We also acknowledge Dr Qiang Zhang at the Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. This work was supported by the National Science Foundation's MRSEC program (DMR-1720319) at the Materials Research Center of Northwestern University. This work was partially funded by NSF CAREER Award (2144365-CBET). This work made use of the Keck-II facility of Northwestern University's NUANCE Center, which has received support from the SHyNE Resource (NSF ECCS-2025633), the International Institute for Nanotechnology (IIN), and Northwestern's MRSEC program (NSF DMR-2308691). The DFT calculations were performed using computational resources from the Quest high performance computing facility at Northwestern University which is jointly supported by the Office of the Provost, the Office for Research, and Northwestern University Information Technology and also the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231 using NERSC award BES-ERCAP23792.References
- Y. Zhang, X. Wang, D. Hu, C. Xue, W. Wang, H. Yang, D. Li and T. Wu, ACS Appl. Mater. Interfaces, 2018, 10, 13413–13424 CrossRef CAS PubMed
.
- Z. Bai, S. Li, J. Fu, Q. Zhang, F. Chang, L. Yang, J. Lu and Z. Chen, Nano Energy, 2019, 58, 680–686 CrossRef CAS
.
- T. K.-C. Lê, Sorbonne Université, 2020.
- S. Nandy, T. Hisatomi, M. Nakabayashi, H. Li, X. Wang, N. Shibata, T. Takata and K. Domen, Joule, 2023, 7, 1641–1651 CrossRef CAS
.
- G. Giuffredi, A. Mezzetti, A. Perego, P. Mazzolini, M. Prato, F. Fumagalli, Y.-C. Lin, C. Liu, I. N. Ivanov, A. Belianinov, M. Colombo, G. Divitini, C. Ducati, G. Duscher, A. A. Puretzky, D. B. Geohegan and F. Di Fonzo, Small, 2020, 16, 2004047 CrossRef CAS PubMed
.
- D. Ryaboshapka and P. Afanasiev, J. Catal., 2023, 426, 30–38 CrossRef CAS
.
- J. Cai, H. Zhang, L. Zhang, Y. Xiong, T. Ouyang and Z.-Q. Liu, Adv. Mater., 2023, 35, 2303488 CrossRef CAS PubMed
.
- Y. Li, Y. Li, Y. Wan, Y. Xie, J. Zhu, H. Pan, X. Zheng and C. Xia, Adv. Energy Mater., 2019, 9, 1803156 CrossRef
.
- H. X. Dai, C. F. Ng and C. T. Au, J. Catal., 2000, 189, 52–62 CrossRef CAS
.
- F. Su, C. Xia and R. Peng, J. Eur. Ceram. Soc., 2015, 35, 3553–3558 CrossRef CAS
.
- Z. Zhang, Y. Zhu, Y. Zhong, W. Zhou and Z. Shao, Adv. Energy Mater., 2017, 7, 1700242 CrossRef
.
- D. Pergolesi, C. Lawley and T. Lippert, Sol. RRL, 2022, 6, 2200286 CrossRef CAS
.
- A. Iborra-Torres, A. N. Kulak, R. G. Palgrave and G. Hyett, ACS Appl. Mater. Interfaces, 2020, 12, 33603–33612 CrossRef CAS PubMed
.
- K. Sawada and T. Nakajima, APL Mater., 2018, 6, 101103 CrossRef
.
- G. Lin, R. Wang, T. Cao, L. Yuan and X. Xu, Inorg. Chem. Front., 2020, 7, 2629–2636 RSC
.
- C. Pan, T. Takata, K. Kumamoto, S. S. Khine Ma, K. Ueda, T. Minegishi, M. Nakabayashi, T. Matsumoto, N. Shibata, Y. Ikuhara and K. Domen, J. Mater. Chem. A, 2016, 4, 4544–4552 RSC
.
- M. Hojamberdiev, E. Zahedi, E. Nurlaela, K. Kawashima, K. Yubuta, M. Nakayama, H. Wagata, T. Minegishi, K. Domen and K. Teshima, J. Mater. Chem. A, 2016, 4, 12807–12817 RSC
.
- S. Nishimae, Y. Mishima, H. Nishiyama, Y. Sasaki, M. Nakabayashi, Y. Inoue, M. Katayama and K. Domen, Sol. RRL, 2020, 4, 1900542 CrossRef CAS
.
- R. Aguiar, D. Logvinovich, A. Weidenkaff, A. Rachel, A. Reller and S. G. Ebbinghaus, Dyes Pigm., 2008, 76, 70–75 CrossRef
.
- F. Tessier, P. Maillard, F. Chevire, K. Domen and S. Kikkawa, J. Ceram. Soc. Jpn., 2009, 117, 1–5 CrossRef CAS
.
- S. H. Elder, F. J. DiSalvo, L. Topor and A. Navrotsky, Chem. Mater., 1993, 5, 1545–1553 CrossRef CAS
.
- M. Yashima, U. Fumi, H. Nakano, K. Omoto and J. R. Hester, J. Phys. Chem. C, 2013, 117, 18529–18539 CrossRef CAS
.
- M. Yang, J. Oró-Solé, J. A. Rodgers, A. B. Jorge, A. Fuertes and J. P. Attfield, Nat. Chem., 2011, 3, 47–52 CrossRef CAS PubMed
.
- S. D. Young, J. Chen, W. Sun, B. R. Goldsmith and G. Pilania, Chem. Mater., 2023, 35, 5975–5987 CrossRef CAS
.
- K. Page, M. W. Stoltzfus, Y.-I. Kim, T. Proffen, P. M. Woodward, A. K. Cheetham and R. Seshadri, Chem. Mater., 2007, 19, 4037–4042 CrossRef CAS
.
- Y.-R. Zhang, T. Motohashi, Y. Masubuchi and S. Kikkawa, J. Ceram. Soc. Jpn., 2011, 119, 581–586 CrossRef CAS
.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef
.
- W. Li, D. Li, X. Gao, A. Gurlo, S. Zander, P. Jones, A. Navrotsky, Z. Shen, R. Riedel and E. Ionescu, Dalton Trans., 2015, 44, 8238–8246 RSC
.
- R. M. Hazen, L. W. Finger and J. W. E. Mariathasan, J. Phys. Chem. Solids, 1985, 46, 253–263 CrossRef CAS
.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS
.
- H. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS
.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS
.
- C. J. Bartel, C. Sutton, B. R. Goldsmith, R. Ouyang, C. B. Musgrave, L. M. Ghiringhelli and M. Scheffler, Sci. Adv., 2019, 5, eaav0693 CrossRef CAS PubMed
.
- W. Travis, E. N. K. Glover, H. Bronstein, D. O. Scanlon and R. G. Palgrave, Chem. Sci., 2016, 7, 4548–4556 RSC
.
- L. G. Chagas, J. L. F. Da Silva and M. P. Lima, Phys. Rev. B, 2024, 109, 014106 CrossRef CAS
.
- G. Wang, M. Lei, J. Liu, Q. He and W. Zhang, Sol. RRL, 2020, 4, 2000528 CrossRef CAS
.
- T. Wakasugi, Y. Hirose, S. Nakao, Y. Sugisawa, D. Sekiba and T. Hasegawa, ACS Omega, 2020, 5, 13396–13402 CrossRef CAS PubMed
.
- S. J. Clarke, K. A. Hardstone, C. W. Michie and M. J. Rosseinsky, Chem. Mater., 2002, 14, 2664–2669 CrossRef CAS
.
- E. Günther, R. Hagenmayer and M. Jansen, Z. Anorg. Allg. Chem., 2000, 626, 1519–1525 CrossRef
.
- X. Xu and H. Jiang, RSC Adv., 2020, 10, 24410–24418 RSC
.
- N. Charles, R. J. Saballos and J. M. Rondinelli, Chem. Mater., 2018, 30, 3528–3537 CrossRef CAS
.
- G. Pilania, A. Ghosh, S. T. Hartman, R. Mishra, C. R. Stanek and B. P. Uberuaga, npj Comput. Mater., 2020, 6, 71 CrossRef CAS
.
-
C. H. S. E. Prince, in International Tables for Crystallography, ed. E. Prince, 1st edn, 2006, vol. Volume C: Mathematical, physical and chemical tables, ch. 8. Refinement of Strucutral Parameters Search PubMed
.
-
E. Prince, Mathematical Techniques in Crystallography and Materials Science, Springer Berlin Heidelberg, Berlin, Heidelberg, 2nd edn, 1994 Search PubMed
.
- A. Fuertes, Dalton Trans., 2010, 39, 5942–5948 RSC
.
- M. Jansen and H. P. Letschert, Nature, 2000, 404, 980–982 CrossRef CAS PubMed
.
- W. Sun, S. T. Dacek, S. P. Ong, G. Hautier, A. Jain, W. D. Richards, A. C. Gamst, K. A. Persson and G. Ceder, Sci. Adv., 2016, 2, e1600225 CrossRef PubMed
.
- J. Shen, V. I. Hegde, J. He, Y. Xia and C. Wolverton, Chem. Mater., 2021, 33, 9486–9500 CrossRef CAS
.
- I. G. Aleksandr, Russ. Chem. Rev., 1988, 57, 913 CrossRef
.
- Z. Wang, X.-G. Zhao, R. Koch, S. J. L. Billinge and A. Zunger, Phys. Rev. B, 2020, 102, 235121 CrossRef CAS
.
- I. K. Jeong, T. W. Darling, J. K. Lee, T. Proffen, R. H. Heffner, J. S. Park, K. S. Hong, W. Dmowski and T. Egami, Phys. Rev. Lett., 2005, 94, 147602 CrossRef PubMed
.
- J. C. Mikkelsen and J. B. Boyce, Phys. Rev. Lett., 1982, 49, 1412–1415 CrossRef CAS
.
- A. Bianconi, N. L. Saini, A. Lanzara, M. Missori, T. Rossetti, H. Oyanagi, H. Yamaguchi, K. Oka and T. Ito, Phys. Rev. Lett., 1996, 76, 3412–3415 CrossRef CAS PubMed
.
- X.-G. Zhao, G. M. Dalpian, Z. Wang and A. Zunger, Phys. Rev. B, 2020, 101, 155137 CrossRef CAS
.
- X.-G. Zhao, Z. Wang, O. I. Malyi and A. Zunger, Mater. Today, 2021, 49, 107–122 CrossRef CAS
.
- G. M. Dalpian, Q. Liu, J. Varignon, M. Bibes and A. Zunger, Phys. Rev. B, 2018, 98, 075135 CrossRef CAS
.
- L. Clark, J. Oró-Solé, K. S. Knight, A. Fuertes and J. P. Attfield, Chem. Mater., 2013, 25, 5004–5011 CrossRef CAS
.
- B. Lu, C. B. Wahl, X. K. Lu, M. E. Sweers, H. Li, V. P. Dravid and L. C. Seitz, J. Am. Chem. Soc., 2022, 144, 13547–13555 CrossRef CAS PubMed
.
- T. R. Welberry and B. D. Butler, J. Appl. Crystallogr., 1994, 27, 205–231 CrossRef CAS
.
- J. Purans, A. Kuzmin, P. Parent and C. Laffon, Electrochim. Acta, 2001, 46, 1973–1976 CrossRef CAS
.
- J. Purans, A. Kuzmin, P. Parent and C. Laffone, Ionics, 1998, 4, 101–105 CrossRef CAS
.
- R. S. Singh and K. Maiti, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 085102 CrossRef
.
- J. Wang, B. H. Toby, P. L. Lee, L. Ribaud, S. M. Antao, C. Kurtz, M. Ramanathan, R. B. Von Dreele and M. A. Beno, Rev. Sci. Instrum., 2008, 79, 085105 CrossRef PubMed
.
- P. L. Lee, D. Shu, M. Ramanathan, C. Preissner, J. Wang, M. A. Beno, R. B. Von Dreele, L. Ribaud, C. Kurtz, S. M. Antao, X. Jiao and B. H. Toby, J. Synchrotron Radiat., 2008, 15, 427–432 CrossRef CAS PubMed
.
- L. R. Dalesio, J. O. Hill, M. Kraimer, S. Lewis, D. Murray, S. Hunt, W. Watson, M. Clausen and J. Dalesio, Nucl. Instrum. Methods Phys. Res., Sect. A, 1994, 352, 179–184 CrossRef CAS
.
- B. H. Toby and R. B. Von Dreele, J. Appl. Crystallogr., 2013, 46, 544–549 CrossRef CAS
.
- A. Zunger, S. H. Wei, L. G. Ferreira and J. E. Bernard, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS PubMed
.
- A. van de Walle, P. Tiwary, M. de Jong, D. L. Olmsted, M. Asta, A. Dick, D. Shin, Y. Wang, L. Q. Chen and Z. K. Liu, Calphad, 2013, 42, 13–18 CrossRef CAS
.
- M. Ångqvist, W. A. Muñoz, J. M. Rahm, E. Fransson, C. Durniak, P. Rozyczko, T. H. Rod and P. Erhart, Adv. Theory Simul., 2019, 2, 1900015 CrossRef
.
- A. van de Walle, Calphad, 2009, 33, 266–278 CrossRef CAS
.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 15010 CrossRef CAS
.
- J. E. Saal, S. Kirklin, M. Aykol, B. Meredig and C. Wolverton, JOM, 2013, 65, 1501–1509 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00317a |
| This journal is © The Royal Society of Chemistry 2024 |