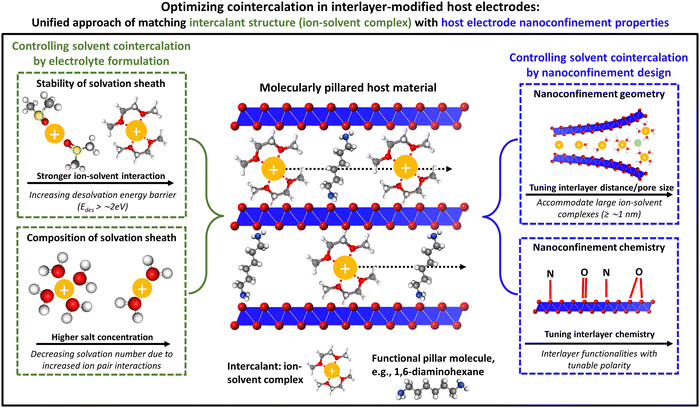
Unifying electrolyte formulation and electrode nanoconfinement design to enable new ion–solvent cointercalation chemistries

Abstract

Electrochemical ion intercalation is a multi-step process typically involving transport of solvated ions through the liquid electrolyte phase, desolvation of ions at the electrochemical liquid/solid interface, and solid-state diffusion of bare ions within the host electrode. Instead of stripping solvent molecules at the interface during the desolvation step, ions can also intercalate together with a (partially) intact solvation sheath into the host electrode, giving rise to cointercalation chemistries. The thermodynamics and kinetics of ion–solvent cointercalation processes are fundamentally different from the more common case of bare ion intercalation. They offer the possibilities of improved kinetics, modified redox potentials, and enabling intercalation chemistries that are thermodynamically inhibited for bare ions. Thus achieving, identifying, and controlling electrochemical ion–solvent cointercalation are of importance to the field of electrochemical energy storage, particularly, in order to enable post-lithium cell chemistries. Herein, we analyze current efforts of electrolyte formulation and electrode nanoconfinement design to control (achieve or inhibit) cointercalation. Analytical tools to unambiguously identify cointercalation phenomena are discussed. While most current efforts singularly focus on the electrolyte formulation, we propose a unified approach of matching electrolytes with the host's nanoconfinement environment to broaden the range and increase the effectiveness of ion–solvent cointercalation chemistries for use in multivalent ion intercalation, low-temperature batteries, supercapacitors, or dual-ion batteries.

---

Broader context

Many rechargeable batteries, like lithium-ion batteries, store energy via redox processes involving electrochemical intercalation reactions of desolvated ions within the host electrode structure, forming binary intercalation compounds (ion–host). Contrarily, when solvated ions are intercalated into host electrodes, ternary intercalation compounds (ion–solvent–host) are formed that exhibit different properties. This so-called cointercalation mechanism started to draw attention when it was shown to enable the intercalation of (solvated) sodium ions into graphite electrodes for the first time, demonstrating that it can enable novel intercalation chemistries. Furthermore, the energy barrier posed by the ion desolvation step at the electrochemical solid/liquid interface is reduced, yielding favorable kinetics of the charge storage process. Consequently, many efforts focus on controlling cointercalation phenomena, particularly for emerging cell chemistries “post-lithium”, which can be relevant for large-scale energy storage. Most research currently considers cointercalation phenomena strictly as an “electrolyte feature”, while the impact of the electrode is widely neglected or discussed in a different context. This Perspective also puts emphasis on how the electrode structure can be leveraged to control cointercalation, in particular the nanoconfinement properties of layered and 2D materials. The work consolidates and unifies the different research directions of cointercalation that study electrolyte formulation or electrode structures in separate contexts.

1. Introduction

Intercalation reactions are defined as “the insertion of ions, atoms, or molecules into the interplanar voids of a lamellar structure without destruction of the host's layered bonding network”.¹ The materials involved have a rich history. One of the first known intercalation host materials is kaolin clay (mostly consisting of kaolinite, Al₂O₃·2SiO₂·2H₂O), which has been utilized since ca. 600–700 A.D. in Chinese porcelain manufacturing.² The confinement of various guest species between the host layers via intercalation reactions offers a pathway to tailor the properties of the resulting intercalation compounds.³

Nowadays, intercalation reactions are also of particular interest to the battery field. Electrochemically driven intercalation of ions from a liquid electrolyte into a host electrode is the prevailing charge storage mechanism of state-of-the-art lithium-ion batteries (LIBs), as well as of emerging, potentially more sustainable cell chemistries such as sodium-, potassium-, magnesium-, calcium-, or zinc-ion batteries.^4,5

One of the most studied intercalation host materials is graphite, which can form intercalation compounds with various guest species. It was found that the electrochemical reduction of graphite in various alkali-ion containing organic electrolytes leads to the formation of ternary intercalation compounds consisting of ion–solvent complexes confined between the graphene layers, e.g., potassium–dimethyl sulfoxide–graphite or lithium–dimethoxyethane–graphite.^6,7 Such intercalation reactions are referred to as cointercalation reactions, when they involve the simultaneous or cooperative intercalation of several species, i.e., ions and solvents, into the host lattice. However, such ternary ion–solvent–graphite compounds are often unfavorable for application in LIBs due to their structural instability leading to graphite exfoliation during electrochemical cycling.⁸

The success of graphite as an anode material in commercial LIBs was reliant on the finding that ethylene carbonate (EC) added to the electrolyte has the ability to form a stable solid electrolyte interphase (SEI) that is electrically insulating but Li⁺ conducting.^8,9 This prevents solvent cointercalation, forcing Li⁺ desolvation at the liquid/solid interface and resulting in the formation of stable, binary intercalation compounds without solvent cointercalation.^9–11 Similarly, at liquid/solid interfaces of most researched LIB cathode materials like layered transition metal oxides, Li⁺ intercalates without its solvation sheath. As such, most research activity related to LIBs from the 1990s to the 2010s aimed to prevent or even neglected solvent cointercalation phenomena.

When research interest started to shift increasingly towards “post-lithium” cell chemistries, cointercalation chemistries gained renewed interest.^12,13 This is due to the fact that in post-lithium cells, alternative charge carriers like Na⁺, K⁺, Mg²⁺, Zn²⁺ or Ca²⁺ pose – to a varying degree – increased structural requirements to intercalation host materials. The reasons lie in their larger ionic radii and/or higher charge compared to Li⁺. Most prominently, sodium does not form thermodynamically stable binary intercalation compounds with graphite,¹⁴ but cointercalation of sodium–ether complexes into graphite shows favorable electrochemical performance and reversibility,¹⁵ enabling the use of graphite anodes even in sodium-ion battery full cells.¹⁶ Thus, leveraging cointercalation phenomena can enable cell chemistries with post-lithium charge carriers that would not be feasible with the intercalation of desolvated charge carriers. Several review-type articles give a comprehensive overview of efforts to control cointercalation phenomena via modified electrolyte formulation in layered host electrodes.^12,17,18

Besides having an impact on the thermodynamic properties of the resulting intercalation compounds, the degree of the intercalating ion's solvation also impacts the kinetics of the intercalation process. Electrochemical (co-) intercalation reactions are multi-step processes generally involving (1) transport of solvated ions through the liquid electrolyte towards the electrochemical interface, (2) full/partial desolvation of the ion (or reorganization of its solvation sheath to some extent) at the interface, (3) surface transport and/or transport through an interphase layer to an insertion site (desolvation and surface transport are usually summarized as the “charge transfer step”),¹⁹ and (4) solid-state diffusion of the intercalant through the host lattice to a vacant site (Fig. 1).^20,21

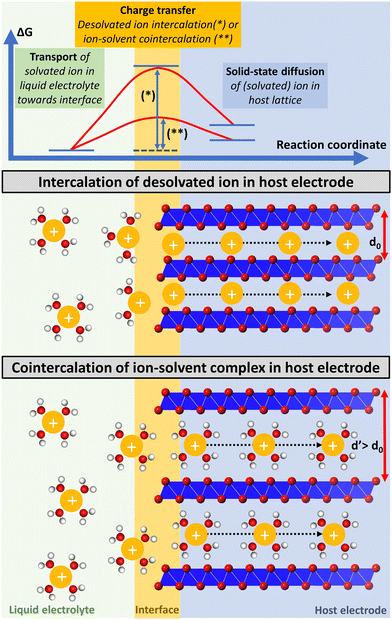Fig. 1 Schematic illustration of a multi-step electrochemical (co-) intercalation process. Solvated ion transport trough liquid electrolyte towards the electrochemical interface, where ions either keep their solvation sheath (cointercalation) or desolvate during the charge transfer step, and finally diffuse through the solid-state host towards a vacant lattice site. Exemplary energetic view of a high energy transition state of an intercalant during the charge transfer step, which is strongly reduced for cointercalation. Illustration inspired by ref. 27.

The kinetics of the charge-transfer step are strongly influenced by the desolvation process of the intercalating ion at the electrode/electrolyte interface.²² Cointercalation phenomena capitalizing on the intercalation of (partially) solvated ions with minimum reorganization of the solvation sheath into the host electrode have thus the potential to greatly reduce the charge transfer resistance.^15,23 This can be especially relevant for multivalent charge carriers and/or at low temperature operation, when full desolvation is associated with large energy barriers. Solid-state ion diffusion inside the host electrode can be accelerated by reducing hopping energy barriers of ions between adjacent lattice sites.²⁴ The Coulombic/electrostatic interaction between charge carriers and intercalation hosts can be reduced in the presence of a (partial) solvation sheath, potentially offering greater ion mobility. Thus, by directly affecting the kinetics of the charge transfer and solid-state diffusion steps, cointercalation phenomena offer the potential to enable fast-charging and more energy efficient batteries.

There are unresolved challenges associated with the implementation of cointercalation chemistry into batteries. The formation of ternary ion–solvent–host intercalation compounds is usually associated with large volume changes of the host material and/or phase transitions due to the large size of intercalants, potentially leading to host material exfoliation and degradation. Moreover, the choice of electrolytes enabling cointercalation may become limited to solvents with strong ion–solvent interactions such as ethers,^17,25 which are not always compatible in full cell chemistry. Furthermore, the fundamental mechanism of cointercalation is still under debate and needs to be resolved.²⁶

Overall, given the impact of cointercalation both on the thermodynamic stability of intercalation compounds and on the kinetics of charge transfer and solid-state diffusion processes, it is critical to develop generalizable design strategies to achieve (or suppress) ion–solvent cointercalation phenomena. Currently, such efforts are primarily targeting the electrolyte formulation, but few works are starting to develop efforts to control cointercalation by tailoring the electrode structure. Herein, we aim to bridge both research directions and propose a unifying approach of matching the structure and chemistry of ion–solvent complexes in the electrolyte with the geometrical and chemical nanoconfinement environment in layered host electrodes. We hypothesize that this will yield enhanced control over ion–solvent cointercalation and could drastically expand the playground of electrode and electrolyte chemistries, leading to an improved rate and stability of various intercalation battery concepts. Suitable characterization methods for an unambiguous identification of ion–solvent cointercalation phenomena are also presented.

2. Controlling solvent cointercalation by electrolyte formulation

Typical liquid electrolytes employed in electrochemical energy storage devices consist of ionic charge carriers (cations and anions) dissolved in a liquid solvent mixture (with the exception of ionic liquids). Electrolyte compositions are usually designed towards high ionic conductivity, their ability to form stable solid electrolyte interphases, and a wide operating voltage and temperature range.²⁸ In the bulk electrolyte, cationic charge carriers like Li⁺ or Na⁺ are typically surrounded by a shell of solvent molecules (solvation sheath). The cation solvation sheath structure is strongly influenced by cation–solvent interaction, which is primarily driven by the Coulombic attraction between cations and polar solvents.²⁹ During the charge transfer step at the electrode/electrolyte interface, the solvation sheath can be stripped off (desolvation) and “naked” cations are inserted into the solid host electrode structure.²⁹ However, utilizing specific electrolyte formulations, solvent cointercalation phenomena can be observed, that is, cations are inserted into the electrode structure together with parts or the entirety of their solvation sheath, forming ternary intercalation compounds (ion–solvent–host). This section explores how cointercalation can be achieved (or suppressed) by adjusting either the electrolyte solvent or the electrolyte salt.

2.1. Controlling ion–solvent cointercalation by adjusting electrolyte solvent

Graphite anodes became successful in LIB technology because the addition of ethylene carbonate (EC) solvent to the electrolyte prohibits solvent cointercalation due to its passivating film-forming abilities (SEI formation).¹⁰ Desolvated Na⁺ intercalation in graphite is only possible to a negligible extent, but was shown to be significantly improved by cointercalation of diglyme solvent in a pioneering work of Jache et al.¹⁵

A survey of linear ethers, linear carbonates, cyclic ethers and cyclic carbonates (Fig. 2A) reveals that reversible electrochemical sodiation of graphite is only successful in linear ether electrolytes because they exhibit cointercalation phenomena (Fig. 2B).¹⁴ Yoon et al. demonstrated the thermodynamic favorability (i.e., negative formation energies) of ternary Na⁺–diglyme–graphite compounds because they overcame the thermodynamically unfavorable local interaction of naked Na⁺ and graphene sheets.¹⁴ Their work based on density functional theory (DFT) calculations shows that high desolvation energy barriers (E_des) for Na⁺ solvated with linear ethers (E_des > 2.0 eV for the first solvent molecule) are a prerequisite for cointercalation.¹⁴ Additionally, they indicate that the lowest unoccupied molecular orbital (LUMO) level of a Na⁺–solvent complex needs to be above the electrode Fermi level to prevent chemical decomposition.¹⁴

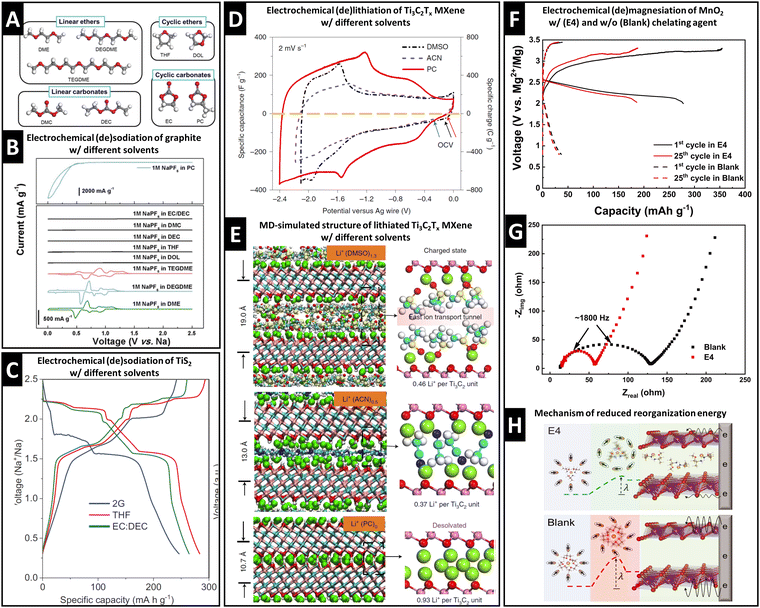Fig. 2 Concept of controlling ion–solvent cointercalation by variation of electrolyte solvent. (A) Overview of typical organic solvents including linear ethers (DME: ethylene glycol dimethyl ether, DEGDME: diethylene glycol dimethyl ether, TEGDME: tetraethylene glycol dimethyl ether), cyclic ethers (THF: tetrahydrofuran, DOL: dioxolane), linear carbonates (DMC: dimethyl carbonate, DEC: diethyl carbonate), and cyclic carbonates (EC: ethylene carbonate, PC: propylene carbonate). (B) Cyclic voltammograms of graphite in 1 M NaPF₆ electrolytes using various solvents listed in (A). Reproduced with permission from ref. 14, Copyright 2017 John Wiley & Sons. (C) Electrochemical (de)sodiation profiles of TiS₂ electrodes in 1 M NaPF₆ electrolytes in DEGDME (here: 2G), THF, and EC/DEC solvents, reproduced with permission from ref. 23, Copyright 2022 John Wiley & Sons. (D) Cyclic voltammograms of Ti₃C₂T_x MXene electrodes in 1 M LiTFSI electrolytes in dimethyl sulfoxide (DMSO), acetonitrile (ACN), and PC solvents. (E) Local molecular arrangement of lithiated Ti₃C₂T_x interlayer space including cointercalated solvent molecules from molecular dynamics simulation. Reproduced from ref. 33 with permission from Springer Nature. (F) Galvanostatic profiles of Mg_0.15MnO₂ electrodes in 0.5 M Mg(TFSI)₂ in DME electrolyte with (E4) and without (Blank) chelating agent methoxyethyl-amine, (G) electrochemical impedance spectra for both cases, (H) proposed magnesiation mechanisms for both cases with different reorganization energies for solvation sheath. Reproduced from ref. 34 with permission from AAAS.

While these conditions are also met by Li⁺–diglyme complexes, the rate and reversibility of Li⁺–diglyme cointercalation in graphite are far inferior compared to those of the corresponding Na⁺–diglyme system.³⁰ Jung et al. explained this with the different ion solvation sheath structures/configurations in both systems.³¹ Their calculations demonstrate that the nearly flat shape of Na⁺–diglyme complexes leads to significantly enhanced mobility within the graphite interlayer space. In contrast, Li⁺–diglyme complexes show a bent structure that poses steric hindrance for transport.

The comprehensive work around ternary graphite intercalation compounds demonstrates the significance of the choice of electrolyte solvent to achieve cointercalation. The feasibility and performance of solvent cointercalation correlate with (1) the solvation energy of an ion–solvent complex, (2) the thermodynamic stability of the ternary complex formed after cointercalation, as well as (3) the transport properties of ion–solvent complexes within the host electrode. Moreover, variation of the cointercalating solvent will also affect the redox potential (shift to higher redox potentials for longer glyme molecules³⁰), which is of importance for practical battery application.

Transition metal dichalcogenides (TMDs) are versatile intercalation host materials due to their wide van der Waals gap and higher electronic conductivity compared to their oxide counterparts. It was observed that electrochemical sodiation of TiS₂ is electrolyte solvent dependent. In dimethyl ether (2G), the first sodiation plateau appears at around 1.75 V vs. Na⁺/Na, noticeably lower than 2.1 V vs. Na⁺/Na in the case of tetrahydrofuran (THF) or an ethylene carbonate/diethyl carbonate mixture (EC/DEC, 1 : 1 vol%) (Fig. 2C).²³ The change in redox potential is caused by cointercalation of the 2G solvent. This is evidenced by the emergence of an expanded P3̄m1 space group similar to the parent TiS₂ host, but with an increased c-lattice parameter from 5.69 Å to 14.33 Å measured by operando synchrotron XRD and the significant electrode expansion of 39% shown by electrochemical dilatometry.²³ These findings are confirmed by theoretical calculations of the desolvation energy, where the 2G solvation sheath is shown to be the most stable among the studied solvents.²³ The lithiation of MoS₂ can also exhibit cointercalation phenomena when tetraglyme is used as an electrolyte solvent.³²

MXenes are two-dimensional transition metal carbides (and/or nitrides) that can be used as cation intercalation hosts. Wang et al. revealed that the choice of electrolyte solvent highly influences the charge storage process in Ti₃C₂T_x MXenes.³³Fig. 2D shows CVs of Ti₃C₂T_x MXenes in three electrolytes of 1 M lithium bis(trifluoromethylsulfonyl) (LiTFSI) in dimethyl sulfoxide (DMSO), acetonitrile (ACN), and propylene carbonate (PC), demonstrating the highest lithiation capacity in PC-based electrolyte.³³ A combination of in situ XRD and MD simulation correlates the Ti₃C₂d-spacings in the fully lithiated state with the interlayer species population to elucidate the origin of the solvent-dependent lithiation capacity.³³ It is shown that bare Li⁺ intercalates from PC-based electrolyte, but solvent cointercalation in DMSO- and ACN-based electrolytes (intercalants Li⁺(DMSO)_1.3 and Li⁺(ACN)_0.5) reduces available lithium intercalation sites in the Ti₃C₂ interlayer space (Fig. 2E).³³

Chelants or chelating agents can be used as electrolyte additives, exhibiting a strongly increased affinity towards cations thus replacing solvent molecules in the solvation sheath. This was demonstrated by Hou et al. with methoxyethyl-amine chelants to improve Mg²⁺ and Ca²⁺ battery chemistries.³⁴ The addition of the 1-methoxy-2-propylamine (M4) chelant to 0.5 M Mg(TFSI)₂ in DME electrolyte (TFSI = bis(trifluoromethanesulfonyl)imide, DME = 1,2-dimethoxyethane) results in a significantly increased capacity and reduced overpotential for Mg²⁺ intercalation in a layered Mg_0.15MnO₂ cathode material (Fig. 2F).³⁴ The authors demonstrate a reduced charge transfer resistance measured by electrochemical impedance spectroscopy (EIS) (Fig. 2G), suggesting a mechanism of energetically favored cointercalation of the Mg²⁺–chelant complex due to a decreased reorganization energy λ of the solvation sheath upon cointercalation (Fig. 2H).³⁴ The possibility to control cointercalation with the use of electrolyte additives instead of substituting solvents can significantly diversify available electrolyte chemistries and formulations. This is especially important considering that electrolytes must be compatible with both negative and positive electrodes in a functional battery full cell. We believe that this approach is particularly promising for multivalent battery chemistries, where high desolvation energy barriers can be encountered. Further work should also focus on investigating the mobility of ion–chelant complexes in the solid-state host electrode for improving the rate performance.

It should be noted that also the opposite effect can be achieved, that is, preferential desolvation and bare ion intercalation via electrolyte additives. For example, non-coordinating electrolyte additives (“non-solvents”) like aryl halides can reduce Coulombic attraction between Li⁺ cations and their solvation sheath by exerting dipole–dipole interactions towards the solvent.³⁵

2.2. Controlling ion–solvent cointercalation by adjusting electrolyte salt concentration

The properties of the cation solvation sheath in bulk electrolyte, such as the solvent coordination number, sheath composition, and (de)solvation energy, are also influenced by the concentration of ionic charge carriers dissolved in the electrolyte, which can have significant implications for electrochemical charge storage processes. Concentration-dependent variation of the Li⁺ solvation sheath structure can be observed with organic solvents like dimethyl sulfoxide (DMSO). Increasing the lithium bis(trifluoromethane sulfonyl)imide (LiTFSI) concentration from 1.0 M to 3.2 M causes a decrease of DMSO solvation number towards Li⁺ in the bulk electrolyte from 4.2 to 2.1, as demonstrated via the deconvolution of C–S symmetric and asymmetric stretching Raman modes that allow distinguishing free and solvating DMSO molecules.³⁶ As a result, Li⁺–DMSO cointercalation into graphite is observed for 1.0 M electrolyte, while desolvated Li⁺ intercalates from 3.2 M electrolyte (intermediate behavior is seen in the case of 2.0 M, Fig. 3A).³⁶ The study demonstrates that an increase in charge carrier concentration of the electrolyte is an effective strategy to control (in this case, suppress) solvent cointercalation.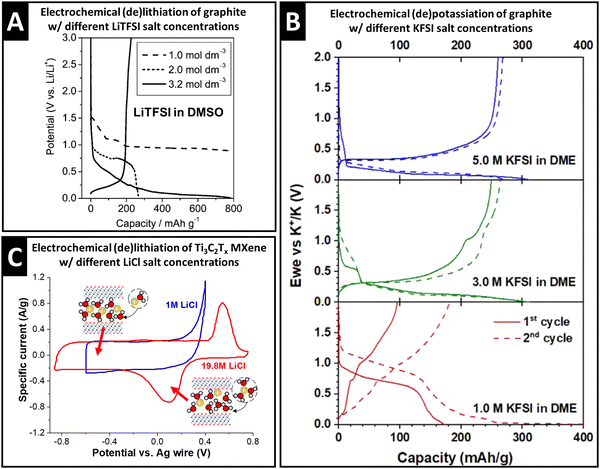

Fig. 3 Concept of controlling ion–solvent cointercalation by variation of electrolyte salt concentration. (A) Galvanostatic profiles of natural graphite electrodes in LiTFSI in DMSO electrolytes with 1.0 M, 2.0 M and 3.2 M salt concentration at 37.2 mA g⁻¹, reproduced with permission from ref. 36, Copyright 2010 American Chemical Society. (B) Galvanostatic profiles of graphite in KFSI in DME electrolytes with 5.0 M, 3.0 M, and 1.0 M salt concentrations at 25 mA g⁻¹, reproduced from ref. 37, with permission from Elsevier. (C) Cyclic voltammograms of Ti₃C₂T_x electrodes in aqueous 1.0 M and 19.8 M LiCl electrolytes at 2 mV s⁻¹, with schematics of the proposed lithiation mechanism in different potential regions, replotted and adapted with permission from ref. 41, Copyright 2021 American Chemical Society.

Similar observations are also made for the electrochemical potassiation of graphite from KFSI in 1,2-dimethoxyethane (“monoglyme”, or DME) electrolytes. While cointercalation of DME is observed in 1.0 M electrolyte, bare K⁺ intercalation into graphite occurs in 5.0 M KFSI in DME electrolyte (Fig. 3B).³⁷ Similar to the Li-DMSO system, it is also found that the small solvation number (≤2) of DME towards K⁺ in 5.0 M electrolyte thermodynamically favored desolvated K⁺ intercalation.³⁷ For K⁺ storage in a layered hydrogen titanate anode at −60 °C, cointercalation of DME solvent is necessary to reduce the interfacial charge transfer resistance. Here, the authors show that the high binding energy of DME to K⁺ can be capitalized on when the electrolyte concentration is set to 0.5 M.³⁸

Concentration-dependent effects were also demonstrated in aqueous electrolytes, most notably by the introduction of “water-in-salt” electrolytes, which can enable high voltage lithium-ion battery chemistries with water-based electrolytes.³⁹ These electrolytes are characterized by high charge carrier concentrations, where the salt exceeds the solvent in the electrolyte by volume and/or weight. It was shown that at elevated concentrations of LiTFSI dissolved in water, the electrolyte is deprived of free water solvent, cation–anion interactions are increased and anions start to replace water in the cation solvation sheath.³⁹ About two TFSI⁻-anions were observed in the Li⁺ primary solvation sheath at salt concentrations above 20 M, leading to SEI formation upon cathodic reduction due to anion decomposition and reduced electrochemical activity of water.³⁹ In highly concentrated electrolytes, an increasing influence of the type of anion on the solvation properties must also be taken into consideration.⁴⁰

Capitalizing on the changes of the solvation sheath properties in water-in-salt electrolytes and the resulting extended stable voltage window, Wang et al. investigated the lithium intercalation properties with Ti₃C₂T_x electrodes at high anodic potentials. Comparing cyclic voltammograms (CV) in both 1.0 M and 19.8 M LiCl aqueous electrolytes, the emergence of a redox couple in the highly concentrated electrolyte is observed, while an irreversible anodic process takes place in 1.0 M electrolyte (Fig. 3C).⁴¹ At the CV peak potentials, abrupt, but continuous expansion (cathodic sweep) and shrinkage (anodic sweep) of the Ti₃C₂T_x interlayer space are observed by operando XRD.⁴¹ Together with mass changes tracked via electrochemical quartz crystal microbalance with dissipation monitoring (EQCM-D), the peaks are assigned to a solid-solution cointercalation process of Li⁺ solvated with ca. 2.85 H₂O molecules (termed “desolvation-free intercalation”), which roughly corresponds to the solvation number in bulk 19.8 M LiCl electrolyte.⁴¹ It is noteworthy that cointercalation in the case of Ti₃C₂T_x MXenes is experimentally observed after increasing the salt concentration, which in theory, should weaken cation solvation (opposite effect as seen in the Li⁺–DMSO–graphite or K⁺–DME–graphite systems). The low anodic stability limit of dilute aqueous electrolyte, however, prevents investigation of potential cointercalation behavior in the 1.0 M LiCl system. The findings underline the importance of discussing and analyzing the interplay between charge carriers, solvents, and host electrodes in cointercalation systems.

In summary, formulation of the electrolyte is a powerful tool to control cointercalation phenomena. The two most prevailing strategies are either to employ one or a combination of solvents that leads to a variation of the ion desolvation energy, or to vary the salt concentration from dilute to highly concentrated, forcing a change in the composition of the solvation sheath in the liquid phase. On the one hand, choosing a solvent that yields high solvation energies of the resulting ion–solvent complexes is very suitable to achieve cointercalation. On the other hand, choosing highly concentrated electrolytes with high salt concentrations can lead to the displacement of solvent from the solvation sheath already in the liquid phase, thereby favoring desolvated intercalation. Both strategies, however, come with drawbacks. The composition of electrolyte solvents is very important to achieve a highly stable SEI composition, which is essential for stable battery cycling.⁴² Adjusting solvents in favor of achieving cointercalation may thus be detrimental to maintaining a stable SEI on the anode. On the cathode side, the low oxidation stability of strong solvents like linear ethers may not be compatible with several high-voltage cathode chemistries. Utilization of highly concentrated electrolytes can cause decreased electrolyte conductivity⁴³ as well as increased cost for electrolyte salts. Consequently, more research efforts in formulating electrolytes for cointercalation should focus particularly on the applicability of the electrolytes in practical cells.

3. Controlling solvent cointercalation by electrode nanoconfinement design

Following the charge transfer process across the electrolyte/electrode interface, the intercalants enter the bulk volume of the electrode material and diffuse to a storage site. While it was demonstrated in the previous section that this process can be significantly altered via the cointercalation of solvent molecules by targeted electrolyte formulation, this section explores how the degree of ion solvation can be controlled by structural design of the electrode material.

3.1. Controlling ion solvation by nanopore geometry

Supercapacitors store energy via the mechanism of electrical double-layer formation, where typically fully solvated ions electrosorb at the electrode/electrolyte interface.⁴⁴ A significant finding in the supercapacitor community during the mid-2000's was that tailoring the pore size in porous carbide-derived carbon electrodes to fit the size of a “naked” electrolyte ion can lead to the ion's partial or full desolvation (Fig. 4A), causing an increase in capacitance.^45,46 The quantitative correlation between the degree of (geometrical) confinement and ion desolvation in porous carbons is demonstrated by a combination of in situ small angle X-ray scattering (SAXS) and Monte Carlo simulations (Fig. 4B and C), even in porous carbons with average pore sizes larger than the solvated ion.⁴⁷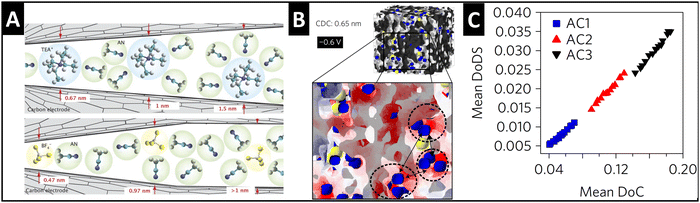

Fig. 4 Ion desolvation by tuning nanoconfinement geometry in carbon nanopores. (A) Schematic illustration of the geometric nanoconfinement environment of carbon nanopores causing (partial) desolvation of tetraethylammonium cations (TEA⁺) and tetrafluoroborate anions (BF₄⁻) from acetonitrile (ACN) solvent, reproduced with permission from ref. 46, Copyright 2008 John Wiley & Sons. (B) 3D-model of the nanoporous carbide-derived carbon electrode with well-defined nanoconfinement geometry (0.65 nm pore size) and distribution of cations (blue) and anions (yellow) at −0.6 V applied cell voltage, red color showing negative surface charge which is close to cations. (C) Positive correlation between the mean degree of (geometrical) confinement (DoC) and the mean degree of desolvation (DoDS) of activated carbons (AC1, AC2, and AC3) with different average pore sizes. Reproduced from ref. 47, with permission from Springer Nature.

Conceptually, there are striking similarities between the chemisorption of (partially) desolvated ions in (nano-)pores of porous carbons and the intercalation of (partially) solvated ions in layered or two-dimensional materials.⁴⁸ Instead of transport through a carbon nanopore network, in layered and two-dimensional electrode materials, ion transport mostly occurs via diffusion through the interlayer space. The interlayer channels confine the intercalating ions and/or solvent molecules during transport, and both the geometry and chemistry of the nanoconfined interlayer environment will have an impact on transport and redox properties. Hence, tuning interlayer confinement can be a powerful lever to influence the degree of solvation of intercalating ions and achieve or suppress ion–solvent cointercalation.

Recent work of Åvall et al. demonstrates that cointercalation of solvated sodium into graphite is accompanied by initial “flooding” of the interlayer galleries with free solvent molecules, which are subsequently replaced by more solvated sodium.²⁶ As such, it is argued that cointercalation could be seen as a mechanism to create electrolyte-accessible “micropores” within the interlayer galleries of layered intercalation hosts, offering the potential to bridge the gap between classical battery and supercapacitor materials.^26,48 The importance of nanoconfinement geometry for the accessibility of intercalants has also been observed in Ti₃C₂T_x MXene hosts, which could only accommodate ionic liquid electrolyte (in the absence of solvent) when their interlayer distance was expanded above a certain threshold via the use of pre-inserted alkylammonium pillars.⁴⁹ Overall, modification of host materials’ nanoconfinement geometry can increase the accessibility for intercalants, ranging from large cations to solvated ions to free solvent molecules. This leads to the fundamental question of whether the nanoconfined interlayer space can be considered as part of the bulk electrode or as part of the electrochemical interface, and if there can be a continuous transition from redox to double-layer behavior at such nanoconfined electrochemical interfaces.⁴⁸ Further work is required to understand the fundamental charge storage mechanism of confined electrolytes using model materials with well-defined nanoconfinement geometries.

3.2. Controlling ion solvation by surface termination chemistry

Ti₃C₂T_x MXenes exhibit variable surface terminations which can be adjusted by the synthesis conditions. Employed as electrode materials for electrochemical ion intercalation reactions, the degree of ion solvation is dependent on the electrolyte solvent, as discussed in the previous section.³³ Recent work demonstrates that the manipulation of MXene surface terminations, i.e., tuning of the nanoconfinement chemistry in the MXene interlayer space, also strongly impacts the degree of solvation of intercalating ions. Employing a molten-salt synthesis route,⁵⁰ Li et al. obtained chlorine- and nitrogen–oxygen-terminated Ti₃C₂ MXenes (Fig. 5A), respectively, which showed a strong difference in electrochemical performance.⁵¹ Tested in 3 M H₂SO₄ electrolyte, the authors observe a large increase in capacity for N,O-terminated (hydrophilic) MXene compared to Cl-terminated (hydrophobic) (Fig. 5B). This behavior is assigned to the cointercalation of water solvent, as demonstrated by the changes in interlayer spacing via in situ XRD (Fig. 5C). The hydrophilic, N–O-terminated interlayer chemistry caused a partial interlayer hydration after soaking of the electrode in electrolyte for several hours, and an increasing number of water molecules entering the interlayer space during proton intercalation.^51,52 Similar effects of nanoconfinement chemistry design were also demonstrated for lithium intercalation from organic electrolyte by Bärmann et al., who utilized acidic or basic post-synthesis treatment of Ti₃C₂T_x MXenes.⁵³ The authors found large structural changes during lithium intercalation via in situ XRD only for base-treated MXene, which was ascribed to cointercalation of carbonate solvents, which was not observed for acid-treated MXenes.⁵³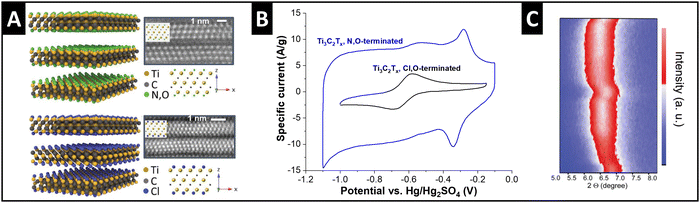

Fig. 5 Solvent cointercalation by tuning nanoconfinement chemistry in MXenes. (A) Structural models and transmission electron micrographs (high-angle annular dark-field) of N,O- and Cl-terminated Ti₃C₂T_x MXenes, (B) their cyclic voltammograms in 3 M H₂SO₄ electrolyte at 20 mV s⁻¹, and (C) in situ XRD heatmap for two full galvanostatic cycles of the N,O-terminated electrode, replotted or adapted with permission from ref. 51, Copyright 2023 John Wiley & Sons.

The findings imply that the nanoconfinement chemistry in layered host materials can impact the degree of solvation of intercalating ions. In aqueous electrolytes, the hydrophilicity of MXene surface terminations seems to contribute to solvent water cointercalation by enabling “wetting” of the interlayer space with electrolyte even prior to electrochemical cycling. It would be interesting to explore whether such an effect can be achieved for organic solvents via suitable matching of the polarity of nanoconfinement chemistry and solvent. So far, studies exploring nanoconfinement chemistry to control cointercalation are mostly limited to MXene host materials, which is likely due to their high degree of chemical tunability, particularly via their surface terminations. It is desirable to similarly gain control over cointercalation in electrode materials more readily employed in state-of-the-art batteries, such as transition metal oxides, to broaden the practical applicability of the effect.

3.3. Perspective on controlling cointercalation by electrode nanoconfinement design

The above-described findings demonstrate that targeted manipulation of the nanoconfinement environment (geometry and chemistry) of host materials has a strong influence on the degree of solvation of intercalating ions. This opens an alternative and/or complementary route besides electrolyte formulation to control cointercalation phenomena in layered electrode materials, which is thus far rarely discussed. The question we try to address in this section is therefore: How could electrode nanoconfinement enable cointercalation and how could this effect be practically implemented in a wide range of host materials relevant to many battery chemistries?

One emerging approach to manipulate the nanoconfinement environment of layered host materials that is independent of their chemical composition or morphology is the insertion of functional pillars into their interlayer space.^54,55 These can be molecules, ions, or clusters that are confined within the lattice of the host material, opening up the interlayer space. We hypothesize that such interlayer-functionalized materials can be tailored towards controlling cointercalation phenomena, particularly when organic molecular pillars are chosen which possess a high level of structural and chemical tunability.

Generally, organic molecules that modify inorganic surfaces can be seen as being comprised of two components, namely the anchoring and the functionality components, where the former establishes interaction with the host lattice (e.g., covalent, ionic, etc.) and the latter provides a certain functionality.⁵⁶ From our perspective, for molecules pillaring inorganic intercalation hosts, one can differentiate between (1) a purely geometrical pillaring approach, in which the only functionality of the pillars is to increase the interlayer distance of the host material (i.e., they act as “spacers”); or (2) a chemical pillaring approach, in which the pillars strongly interact with the electrochemically intercalating ions (or ion–solvent complexes). Arguably, there is always an interaction between pillars and intercalants; however, so far this has been insufficiently addressed.

As a perspective for purely geometrical pillaring approaches, we hypothesize that the increase of an inorganic host's interlayer distance to fit the size of the solvated ion can lead to the favorability of cointercalation without prior desolvation at the liquid/solid interface. In this case, the nanoconfinement geometry of the host material with a widened interlayer distance can be likened to a micropore in a typical supercapacitor electrode material, where electrosorption of solvated ions is commonly observed (Fig. 4).^26,48 Chemical pillaring approaches should leverage the interaction of the pillar functionality with the intercalants, specifically with the solvent. Depending on the “miscibility” of organic pillar functionality and solvent, we hypothesize that cointercalation can either be favored or unfavored, for example, by creating polar or nonpolar nanoconfinement chemistries in the host material matching with the electrolyte solvent. Recent examples of modified MXene termination chemistries determining cointercalation (hydrophilic N,O-terminations enabled solvent water cointercalation⁵¹) imply the viability of this approach (Fig. 5).

Designing the nanoconfinement environment of the host material to control cointercalation brings a range of benefits compared to the more established approach of electrolyte formulation. Because the interlayer distance can be matched with the solvated ion size, it can address the issue of excessive volumetric expansion and host material exfoliation associated with cointercalation in non-modified host materials like graphite.⁵⁷ Choosing pillars with two anchoring groups that can strongly interact with adjacent layers of the host material (e.g., by covalent bonding on either side), exfoliation could effectively be avoided and volumetric changes during reversible cointercalation could be minimized. The dependence of cointercalation phenomena on strongly solvating electrolytes like linear ethers (and their associated challenges) can further be reduced, when modified intercalation host materials enabled cointercalation from any electrolyte composition. Ideally, matching of the electrolyte solvent with the nanoconfined interlayer chemistry of the host can lead to the formation of highly mobile, nanoconfined solvent networks through which ion transport kinetics are greatly enhanced.

However, the introduction of functional pillars into the intercalation host material also brings additional challenges that need to be addressed. The interaction between functional pillars and intercalating species has to be carefully considered, avoiding parasitic/irreversible side reactions between ions and pillars, irreversible ion trapping, (electrochemically driven) pillar decomposition, or pillar dissolution in the electrolyte. A large number of pillars could further pose a steric hindrance for ion transport,⁵⁸ hence the number of pillars should be minimized, while still enabling sufficient structural integrity. In addition, pillars that only function as geometrical spacers add “dead weight” to the electrode, potentially lowering the overall specific capacity. This issue could be addressed by the addition of redox centers as functional components to the pillar molecule. Likewise, the decreased density of pillared materials may lead to lowered volumetric capacities if the storage capacity is not simultaneously increased in the widened interlayer space.

4. Characterization methods for cointercalation phenomena

Given the significance of ion–solvent cointercalation phenomena, in this section, a discussion of suitable characterization techniques to unambiguously identify and analyze cointercalation is provided. Because solvent cointercalation is an electrochemically driven process, the first step for its identification lies in the electrochemical signature of the process, which typically involves distinct changes in the potential profile compared to the corresponding desolvated ion intercalation. Secondly, structural and spectroscopic characterization of the host electrode at various states of charge (ideally in operando setting) gives important information about the structural evolution during intercalation, which differs for desolvated and solvated ion intercalation. Combining techniques that probe various length scales can be especially powerful in revealing reaction mechanisms. Furthermore, characterization of the bulk electrolyte phase and the electrode/electrolyte interphase can provide information about the nature of electrolyte solvent (e.g., whether solvent molecules are free or solvating). Finally, combination of experiments with theoretical simulations can provide the most meaningful insights and may allow efficient prediction of electrolyte or electrode combinations that enable or suppress cointercalation.

4.1. Electrochemical identification of cointercalation

The electrochemical signature during (de)intercalation (i.e., cyclic voltammogram or galvanostatic potential profile) usually exhibits distinct characteristics for solvent cointercalation. The observed electrochemical features of solvent cointercalation generally include: (1) shifts in redox potential because of the different free energy of binary versus ternary intercalation compounds, (2) emergence of pseudocapacitive features (rectangular CV or sloping galvanostatic profile) due to reduced ion–host interactions,^32,48 and/or (3) reduced maximum capacity because of space constraints and reduced electron transfer.^30,59 A comparison between Li⁺ intercalation into graphite from EC/DMC (bare Li⁺ intercalation) and diglyme (cointercalation) electrolytes clearly shows the emergence of additional peaks, shifted to higher redox potentials, and a more pseudocapacitive current contribution in the region between 0.5 and 0 V, while at the same time exhibiting reduced specific capacity (Fig. 6A).³⁰ It should be stressed that these points are merely first indicators that are not sufficient proof of ion–solvent cointercalation, but require further, more detailed investigation.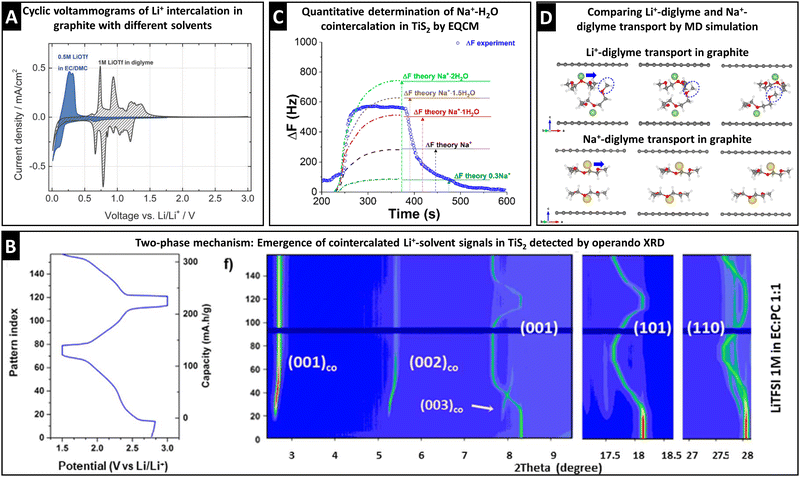

Fig. 6 Characterization of ion–solvent cointercalation. (A) Cyclic voltammograms of bare Li⁺ intercalation (blue) and Li⁺–diglyme cointercalation (grey) in graphite electrodes, reproduced from ref. 30 with permission from the Royal Society of Chemistry. (B) Operando synchrotron XRD (λ = 0.826 Å) pattern of Li⁺–solvent cointercalation in TiS₂, showing the two-phase mechanism with coexistence of Li_x⁺–TiS₂ phases from (001), (101), and (110) signals and Li_x⁺–solvent_x–TiS₂ phases from (001)_co, (002)_co, and (003)_co signals, reproduced with permission from ref. 60, Copyright 2021 IOP Publishing. (C) Resonance frequency shift from EQCM measurement during one sodiation–desodiation cycle of TiS₂ from aqueous 1 M NaCl electrolyte including theoretically calculated frequency profiles for different degrees of water cointercalation, reproduced with permission from ref. 69, Copyright 2018 American Chemical Society. (D) MD simulated transport of Li⁺/Na⁺–diglyme complexes in graphite, with initial (left), transition-state (middle) and final (right) structures, reproduced from ref. 31 with permission from Elsevier.

Electrochemical impedance spectroscopy (EIS) is powerful to probe processes in an electrochemical cell at various time scales. For solvent cointercalation, the charge transfer resistance (usually represented by a semi-circle feature in the Nyquist plot in the medium frequency range) is decreased compared to bare ion intercalation due to the lower ion desolvation energy barrier (Fig. 2G). Another important aspect that is the change in electrolyte concentration (and hence conductivity) when the bulk electrolyte is depleted of free solvent molecules while the number of ions remains constant. Electrolyte conductivity can be measured by EIS (derived from the intercept with the real impedance axis of Nyquist plot at high frequency) at various states of charge, giving (semi-) quantitative information about the insertion of free solvent molecules (i.e., non-solvating) into the host electrode.²⁶ All electrochemical measurements indicating solvent cointercalation should, however, be verified with simultaneous structural and/or physicochemical characterization.

4.2. Structural and physicochemical identification of cointercalation

Among the most useful tools to structurally identify solvent cointercalation is X-ray diffraction (XRD) at different states of charge, specifically of low-indexed reflection signals which correspond to the evolution of the most expanded lattice plane distances. It is important to differentiate between (1) the case of a two-phase (or multi-phase) reaction involving one or several phase transitions and (2) a solid-solution reaction without phase transitions. Multi-phase reactions involve the formation of a new crystal structure of the cointercalated compound in addition to the original phase. This case can be identified by the sudden appearance of new, additional reflections, most often at very low 2θ angles corresponding to significant lattice expansions due to the large size of ion–solvent complexes. In this case, the ternary intercalation compound has a structure strongly different from the deintercalated host material. It can exist next to a secondary intercalation compound if not all ions intercalate with an intact solvation sheath. Such behavior is demonstrated by Houdeville et al. in the case of lithium intercalation in TiS₂ in electrolytes with and without PC solvent, where only in the former case, a new cointercalation phase was formed and identified by the appearance of new (00l)_co signals (l = 1, 2, 3) (Fig. 6B).⁶⁰ Solid-solution reactions are characterized by continuous shifts of the reflections from the original structure without emergence of any new peak. A typical example is cointercalation reactions in Ti₃C₂T_x MXenes. Depending on the size of the ion–solvent intercalant, the shift of the Ti₃C₂T_x (0002) diffraction signal can be very large, as in the case of Li⁺–(H₂O)₃,⁴¹ or more moderate for Li⁺–(ACN)_0.5 and Li⁺–(DMSO)_1.3.³³

The expansion/shrinkage during electrochemical cycling can be macroscopically determined on a particle level by electrochemically coupled atomic force microscopy (in situ AFM) and on an electrode level by electrochemical dilatometry (ECD).^57,61 It should be noted that these methods can be sensitive to secondary influences like electrode porosity, SEI formation, or gas evolution.⁶² Also, height changes are only tracked in one dimension, which can complicate an unambiguous identification of solvent cointercalation. Hence in situ AFM and ECD should serve as complementary methods. However, they remain very useful especially when (in situ) XRD is complicated by technical limitations, such as recording diffraction signals at very low angles (e.g.,<5° 2θ with Cu Kα radiation) with in situ cells in Bragg–Brentano geometry.

Solid-state nuclear magnetic resonance (ssNMR) is a suitable tool to identify solvent cointercalation, particularly in the case of aqueous electrolytes (water cointercalation). Because the spectra of ¹H nuclei are characteristically different depending on the environment, ssNMR can distinguish the signals from surface adsorbed water, surface confined water and lattice water.⁶³ One such example of ssNMR is the clarification that the previously suspected hydronium intercalation (i.e., H⁺(H₂O)_n cointercalation) in layered α-MoO₃ does not happen, instead water is completely desolvated at the interface and merely bare protons are insert into the electrode bulk lattice.⁶³ Furthermore, ssNMR is capable of providing quantitative results, such as the quantification of intercalated water in V₂O₅·nH₂O with Zn²⁺.⁶⁴ Analysis of other solvents is also available such as the uncovered structure and dynamic behavior of the sodium–diglyme complex in the graphite electrode via the spectra of ²H,⁶⁵ combined ¹H, ¹³C and ²³Na spectra,⁶⁶ or ¹H–¹³C and ¹H–⁷Li cross-polarization experiments.⁶⁷

Electrochemical quartz crystal microbalance (EQCM) is a highly sensitive gravimetric probe for measurement of real-time electrode mass changes during electrochemical cycling. The quartz crystal microbalance measures the resonance frequency of a quartz crystal (sensor) on which the electrode material is coated. The resonance frequency shift during electrochemical operation can then be related to the electrode mass change via the Sauerbrey equation, under the condition that the electrode coating is rigidly attached to the sensor.⁶⁸ Comparing the mass change with the stored charge, the mass of the intercalant per transferred electron can be calculated, allowing to distinguish between naked and solvated ions based on their different molecular weight. Srimuk et al. demonstrated this method by identifying Na⁺ intercalates into TiS₂ together with about 1–1.5 H₂O molecules from an aqueous electrolyte (Fig. 6C).⁶⁹ Even though this method can yield quantitative information about cointercalation phenomena, it should be noted that the linear relation between resonance frequency and mass is only valid in the absence of dissipation, which requires ideally rigid coatings of active materials on the quartz sensor. This necessitates high quality and thin coatings, and electrodeposition of the active material onto the quartz sensor can be particularly effective.⁷⁰ Concerning limitations of the method, it should be noted that solvent molecules adsorbed on the surface (but not cointercalated into the bulk electrode) will also contribute to the measured signal. Furthermore, contributions from inactive electrode components (conductive additives, binders, etc.) and potential electrode dissolution during cycling need to be considered. Complementary gravimetric methods without precise, real-time information include simply weighing the electrode at various states of charge,^71,72 and thermogravimetric analysis (TGA) of electrodes at a certain state of charge.⁷³

4.3. Characterization of cointercalation by theoretical simulations

Theoretical simulations are powerful to describe the interaction between the components involved in the charge storage process, i.e., the interaction between the electrolyte components (ion–solvent interaction) and the interaction of the electrolyte within the host electrode (ion–solvent–host and/or ion–host interaction). The first step is to determine the free energy of components by density functional theory (DFT) calculations. This way, the solvation energy of various ion–solvent complexes can be determined in the bulk electrolyte phase. A comparison of the desolvation energies for selected Na⁺–solvent complexes reveals that cointercalation into graphite host electrodes takes place when the desolvation energy barrier is above ca. 2 eV.¹⁴ DFT is also suitable to calculate the free energy difference between binary and ternary intercalation compounds. It was demonstrated that the formation of binary Na⁺–graphite complexes is thermodynamically unfavorable and hence cointercalation is required to form a stable (ternary) intercalation compound.³¹

Molecular dynamics (MD) simulations provide information about time-dependent phenomena, thereby extending the (static) equilibrium information provided by DFT. In the bulk electrolyte phase, MD is useful to calculate the (dynamic) composition of the solvation sheath. This is particularly useful, for example, for highly concentrated electrolytes. MD was used to reveal the critical concentration threshold beyond which anions begin to displace solvent molecules from the cation solvation sheath.³⁹ In the context of solvent co-intercalation, MD can simulate the diffusion behavior of ion–solvent complexes in the host electrode. For example, the population of various Li⁺–solvent complexes in Ti₃C₂T_x MXene interlayers was calculated by MD for different solvents (Fig. 2E) to support the dynamic expansion of the d-spacing observed by in situ XRD.³³ A further case compares the transport of Na⁺–diglyme and Li⁺–diglyme complexes along the graphite interlayer space via ab initio molecular dynamics (AIMD), and provides a clear explanation for the higher diffusivity of the Na⁺–diglyme complex. As shown in Fig. 6D, the flat configuration of diglyme molecules coordinating Na⁺ promotes facile transport. Contrarily, diglyme molecules coordinating Li⁺ are bent thus causing steric hindrance that slows down transport.

In this section, characterization methods suitable to identify cointercalation phenomena in layered and two-dimensional host materials were summarized. As best practice, we propose that several methods should be combined to unambiguously verify the phenomenon. If researchers work with modified electrolyte formulations, it can be beneficial to also test a standard electrolyte in which no cointercalation would be expected (e.g., with a lower solvation energy or different solvation sheath in the liquid phase) to elucidate the difference in the electrochemical signature. Likewise, if modified intercalation hosts are utilized which exhibit signs of cointercalation, the corresponding, non-modified host material should be evaluated in which ion intercalation without solvating molecules is observed as a suitable comparison.

5. Future opportunities and challenges of cointercalation chemistries

Solvent cointercalation phenomena significantly impact the properties of electrochemical charge storage processes, spanning all aspects from thermodynamic to kinetic properties. In previous sections, how to control the degree of solvation of an intercalating ion was discussed, i.e., either promoting or inhibiting ion–solvent cointercalation, via either electrolyte formulation or electrode nanoconfinement design, or combinations thereof (Fig. 7). In the following, general opportunities, challenges and open questions of cointercalation phenomena will be briefly discussed with a focus on the effects on practical electrochemical applications, also highlighting the perspectives for various cell chemistries.

Fig. 7 Unified approach of matching the intercalant structure with host electrode's nanoconfinement properties. Schematic illustration of strategies for controlling the degree of ion–solvent cointercalation in 2D or layered host electrode materials: from the electrolyte side, both the stability and composition of the solvation sheath can be varied by the type of solvent and concentration of salt. From the electrode side, the nanoconfinement geometry and chemistry of the host structure can be tailored to promote or inhibit cointercalation. Optimized cointercalation chemistries will involve a concerted development and matching of both the electrolyte and electrode components.

5.1. Redox potential of cointercalation reactions

Cointercalation of an ion–solvent complex into a host lattice causes a variation of the chemical potential of the stored charge carrier, and hence, changes the redox potential of the charge storage process. In graphite intercalation compounds, cointercalation generally causes a shift to more positive redox potentials (for Li⁺, Na⁺, and K⁺ cointercalation),^30,37 whereas a more negative redox potential was found for cointercalation of Na⁺–diglyme in TiS₂.²³ Cointercalation can even lead to charge storage over a widened potential window with little contribution of distinct redox peaks (“pseudocapacitance”), for example, in Ti₃C₂T_x MXene host materials.⁵¹ So far, there has been no observable, unambiguous trend for the direction of the redox potential shift of cointercalation reactions. This lack of understanding has to be urgently addressed, because the redox potential will directly affect the cell voltage of practical devices employing cointercalation chemistries. Hence, the perspective of tailoring electrode redox potentials via controlled cointercalation offers opportunities for cell voltage optimization.

5.2. Charge storage capacity of cointercalation reactions

The specific capacity of cointercalation reactions sometimes drastically differs from bare ion intercalation, as demonstrated for the intercalation of Li⁺ and Na⁺ from different electrolytes into graphite. Here, the specific capacity for lithium–diglyme cointercalation is reduced by ca. two thirds compared to bare lithium intercalation into graphite.³⁰ For Ti₃C₂T_x MXenes tested in three different electrolyte solvents, the lithiation capacity is the highest when no solvent cointercalation is observed (PC electrolyte).³³ However, while cointercalation is far more pronounced from DMSO than from ACN electrolyte, with almost three times the number of DMSO solvent molecules cointercalating, the capacity from DMSO electrolyte is also increased by about 25% compared to ACN electrolyte.³³ This prevents drawing a clear trend between cointercalation and specific capacity from the study. In TiS₂, the specific capacity of Na⁺–diglyme cointercalation is barely reduced compared to bare Na⁺ intercalation.²³ It is likely that the reduced charge storage capacity of cointercalation in some systems is the result of geometrical effects like interlayer crowding and active site occupation by excess solvent. However, this does not address other contributors to the charge storage capacity like changes in the active sites, where there is the possibility of additional ions being stored in the strongly expanded interlayer space. Changes in the nature of the charge storage process also need to be considered like the possibility of a transition from redox to double-layer charge storage mechanisms, or a combination of their contributions.⁴⁸ Overall, the effect of cointercalation on the charge storage capacity (and mechanism) seems highly system-specific (ion, solvent, and host) and requires more fundamental understanding, especially for host materials beyond graphite. Matching of ion–solvent–host composition, especially with optimized nanoconfinement geometry and chemistry of the host material, offers the opportunity to enable cointercalation without a (significant) capacity penalty.

5.3. Transport properties of confined ion–solvent complexes

The ionic transport properties in ternary cointercalation compounds will differ from the classical solid-state diffusion of bare ions in binary intercalation compounds. First, the solvation sheath can shield the ionic charge to some extent, which will result in reduced electrostatic interaction between ions and hosts, potentially increasing diffusion rates. This likely also impacts the energetically preferred diffusion path of intercalants through the interlayer. Furthermore, as a result of cointercalation, nanoconfined solvent networks will be formed within the host lattice through which ion transport could be greatly facilitated, with the potential to blur the boundaries between solid-state and liquid ion diffusion mechanisms. This was already shown to be highly beneficial for proton transport through nanoconfined water networks in MXenes, Prussian blue analogue, or oxide host lattices, where a unique structural diffusion mechanism (i.e., Grotthuss-transport rather than common vehicular ion transport) associated with significantly faster kinetics is predicted.^74–76 Considering that similar structural diffusion is also reported for Li⁺ in superconcentrated electrolytes⁷⁷ or iodide within 1-ethyl-3-methylimidazolium/I₃ ionic crystals,⁷⁸ it seems feasible that cations may also benefit from increased diffusivity in nanoconfined (organic) electrolyte networks within host lattices. Such nanoconfined electrolyte networks likely require a combined matching of nanoconfinement properties of the host with the electrolyte composition. This could offer an avenue towards fast-charging cointercalation battery chemistries.

5.4. Electrochemical stability window

Cointercalation may widen the electrochemical stability window of electrolytes and potentially enable charge storage at highly reductive potentials without the formation of SEI layers. This prospect is especially relevant for high power batteries, where ionic transport through the SEI can limit the maximum rate. The feasibility was demonstrated for Na⁺–diglyme/triglyme complexes in graphite, where solvent reduction is prevented when the LUMO level of the ion–solvent complex is above the Fermi level of the graphite host.¹⁴ It remains an open question whether SEI layers can be formed and optimized that are penetrable for ion–solvent complexes. On the cathode side, the oxidation stability of some solvents employed in cointercalation chemistries, such as linear ethers, may not be compatible with high-voltage cathodes. This could be addressed by using host materials with a modified nanoconfinement environment, allowing cointercalation from more electrochemically stable electrolytes, or by the formulation of novel, strongly solvating electrolytes with high anodic stability.

5.5. Cointercalation chemistries for post-lithium cell chemistries

Advancing the understanding of cointercalation processes will further stimulate the development of new, post-lithium battery chemistries, for which currently the choice of electrode materials is still severely limited. In cell chemistries using multivalent charge carriers (like Zn²⁺, Mg²⁺, Ca²⁺, etc.), the ionic charges pose tremendous barriers for the insertion and transport in the cathode materials involved⁷⁹ (the cells usually rely on the respective metal anodes). High desolvation energy barriers may thermodynamically prohibit or at least kinetically limit the intercalation of fully desolvated ions in many hosts, leading to limited choice of cathode materials, large overpotentials/low energy efficiency, and poor cycling stability. A suitable strategy to alleviate these issues is the use of cointercalation chemistries, which thus far have been implemented for multivalent insertion-type cathodes by using strongly solvating electrolytes or additives.^34,79,80 Designing electrode materials with tailored nanoconfinement properties that enable the intercalation of multivalent ion–solvent complexes could significantly advance such batteries and broaden the pool of feasible electrode materials, as well as the number of electrolyte compositions which is so far very limited for multivalent chemistries.

Batteries operated at low temperatures face similar issues of high desolvation energy barriers and sluggish solid-state diffusion, which can be alleviated by cointercalation, for example, enabling K⁺ storage in a layered hydrogen titanate anode at –60 °C due to cointercalation of DME solvent.³⁸ Dual-ion batteries relying on anion intercalation into the cathode can be plagued by excessive cation cointercalation. Here, achieving favorable anion dissociation and preventing cation cointercalation in the cathode are key towards improving the electrochemical performance.⁸¹ This underlines that particular attention has to be paid to the charge storage mechanism and identifying the intercalating species, since both cation–solvent and cation–anion complexes are feasible intercalants, depending on electrolyte composition. Combined electrolyte formulation and electrode nanoconfinement design offer the opportunity to advance such new cell chemistries and enable low operating temperatures. This is due to the ability of a unified approach to both select the nature of the intercalant by electrolyte design to tailor solvation sheath composition in the liquid phase and provide the nanoconfinement geometry and chemistry required for efficient cointercalation and transport of that respective intercalant.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge funding from the German Federal Ministry of Education and Research (BMBF) in the “NanoMatFutur” program (grant No. 03XP0423) and basic funding from the Helmholtz Association.

References

1. L. B. Ebert, Intercalation Compounds of Graphite, Annu. Rev. Mater. Sci., 1976, 6, 181–211.
2. A. Weiss, A Secret of Chinese Porcelain Manufacture, Angew. Chem., Int. Ed. Engl., 1963, 2, 697–703.
3. J. Wan, S. D. Lacey, J. Dai, W. Bao, M. S. Fuhrer and L. Hu, Tuning Two-Dimensional Nanomaterials by Intercalation: Materials, Properties and Applications, Chem. Soc. Rev., 2016, 45, 6742–6765.
4. M. Armand, P. Axmann, D. Bresser, M. Copley, K. Edström, C. Ekberg, D. Guyomard, B. Lestriez, P. Novák, M. Petranikova, W. Porcher, S. Trabesinger, M. Wohlfahrt-Mehrens and H. Zhang, Lithium-Ion Batteries–Current State of the Art and Anticipated Developments, J. Power Sources, 2020, 479, 228708.
5. M. Walter, M. V. Kovalenko and K. V. Kravchyk, Challenges and Benefits of Post-Lithium-Ion Batteries, New J. Chem., 2020, 44, 1677–1683.
6. J. O. Besenhard, The Electrochemical Preparation and Properties of Ionic Alkali Metal-and NR4-Graphite Intercalation Compounds in Organic Electrolytes, Carbon, 1976, 14, 111–115.
7. N. Okuyama, T. Takahashi, S. Kanayama and H. Yasunaga, Structure and Electrical Properties of Potassium-Graphite-Dimethylsulfoxide Ternary Intercalation Compound, Physica B+C, 1981, 105, 298–301.
8. J. Asenbauer, T. Eisenmann, M. Kuenzel, A. Kazzazi, Z. Chen and D. Bresser, The Success Story of Graphite as a Lithium-Ion Anode Material-Fundamentals, Remaining Challenges, and Recent Developments Including Silicon (Oxide) Composites, Sustainable Energy Fuels, 2020, 4, 5387–5416.
9. J. O. Besenhard, M. Winter, J. Yang and W. Biberacher, Filming Mechanism of Lithium-Carbon Anodes in Organic and Inorganic Electrolytes, J. Power Sources, 1995, 54, 228–231.
10. R. Fong, U. von Sacken and J. R. Dahn, Studies of Lithium Intercalation into Carbons Using Nonaqueous Electrochemical Cells, J. Electrochem. Soc., 1990, 137, 2009.
11. T. Ohzuku, Y. Iwakoshi and K. Sawai, Formation of Lithium-Graphite Intercalation Compounds in Nonaqueous Electrolytes and Their Application as a Negative Electrode for a Lithium Ion (Shuttlecock) Cell, J. Electrochem. Soc., 1993, 140, 2490–2498.
12. M. L. Divya, Y. S. Lee and V. Aravindan, Solvent Co-Intercalation: An Emerging Mechanism in Li-, Na-, and K-Ion Capacitors, ACS Energy Lett., 2021, 4228–4244.
13. L. Li, Z. Hu, S. Zhao and S. L. Chou, Alkali and Alkaline-Earth Metal ion–solvent Co-Intercalation Reactions in Nonaqueous Rechargeable Batteries, Chem. Sci., 2021, 12, 15206–15218.
14. G. Yoon, H. Kim, I. Park and K. Kang, Conditions for Reversible Na Intercalation in Graphite: Theoretical Studies on the Interplay Among Guest Ions, Solvent, and Graphite Host, Adv. Energy Mater., 2017, 7, 1601519.
15. B. Jache and P. Adelhelm, Use of Graphite as a Highly Reversible Electrode with Superior Cycle Life for Sodium-Ion Batteries by Making Use of Co-Intercalation Phenomena, Angew. Chem., Int. Ed., 2014, 53, 10169–10173.
16. S. G. Patnaik, I. Escher, G. A. Ferrero and P. Adelhelm, Electrochemical Study of Prussian White Cathodes with Glymes – Pathway to Graphite-Based Sodium-Ion Battery Full Cells, Batteries Supercaps, 2022, 5, e202200043.
17. J. Park, Z. L. Xu and K. Kang, Solvated Ion Intercalation in Graphite: Sodium and Beyond, Front. Chem., 2020, 8, 1–14.
18. K. Subramanyan and V. Aravindan, Towards Commercialization of Graphite as an Anode for Na-Ion Batteries: Evolution, Virtues, and Snags of Solvent Cointercalation, ACS Energy Lett., 2023, 8, 436–446.
19. K. Xu, A. V. Cresce and U. Lee, Differentiating Contributions to “Ion Transfer” Barrier from Interphasial Resistance and Li+ Desolvation at Electrolyte/Graphite Interface, Langmuir, 2010, 26, 11538–11543.
20. P. G. Bruce and M. Y. Saidi, The Mechanism of Electrointercalation, J. Electroanal. Chem., 1992, 322, 93–105.
21. T. Okumura, T. Fukutsuka, K. Matsumoto, Y. Orikasa, H. Arai, Z. Ogumi and Y. Uchimoto, Lithium-Ion Transfer Reaction at the Interface between Partially Fluorinated Insertion Electrodes and Electrolyte Solutions, J. Phys. Chem. C, 2011, 115, 12990–12994.
22. V. A. Nikitina, S. Y. Vassiliev and K. J. Stevenson, Metal-Ion Coupled Electron Transfer Kinetics in Intercalation-Based Transition Metal Oxides, Adv. Energy Mater., 2020, 10, 1903933.
23. G. A. Ferrero, G. Åvall, K. A. Mazzio, Y. Son, K. Janßen, S. Risse and P. Adelhelm, Co-Intercalation Batteries (CoIBs): Role of TiS2 as Electrode for Storing Solvated Na Ions, Adv. Energy Mater., 2022, 12, 2202377.
24. V. Augustyn, Tuning the Interlayer of Transition Metal Oxides for Electrochemical Energy Storage, J. Mater. Res., 2017, 32, 2–15.
25. P. Ma, P. Mirmira, P. J. Eng, S. B. Son, I. D. Bloom, A. S. Filatov and C. V. Amanchukwu, Co-Intercalation-Free Ether Electrolytes for Graphitic Anodes in Lithium-Ion Batteries, Energy Environ. Sci., 2022, 15, 4823–4835.
26. G. Åvall, A. Ferrero, G. Janßen, K. A. Exner, M. Son, Y. Adelhelm, P. Ferrero, G. A. Janßen, K. A. Exner and M. Son, Y. In Situ Pore Formation in Graphite Through Solvent Co-Intercalation: A New Model for The Formation of Ternary Graphite Intercalation Compounds Bridging Batteries and Supercapacitors, Adv. Energy Mater., 2023, 13, 2301944.
27. K. Xu, A. von Wald Cresce and A. V. W. Cresce, Li⁺ -Solvation/Desolvation Dictates Interphasial Processes on Graphitic Anode in Li Ion Cells, J. Mater. Res., 2012, 27, 2327–2341.
28. K. Xu, Nonaqueous Liquid Electrolytes for Lithium-Based Rechargeable Batteries, Chem. Rev., 2004, 104, 4303–4417.
29. K. Xu, Electrolytes and Interphases in Li-Ion Batteries and Beyond, Chem. Rev., 2014, 114, 11503–11618.
30. B. Jache, J. O. Binder, T. Abe and P. Adelhelm, A Comparative Study on the Impact of Different Glymes and Their Derivatives as Electrolyte Solvents for Graphite Co-Intercalation Electrodes in Lithium-Ion and Sodium-Ion Batteries, Phys. Chem. Chem. Phys., 2016, 18, 14299–14316.
31. S. C. Jung, Y. Kang and Y. Han, Origin of Excellent Rate and Cycle Performance of Na + -Solvent Cointercalated Graphite vs. Poor Performance of Li + -Solvent Case, Nano Energy, 2017, 34, 456–462.
32. K. Zhang, G. Yoon, J. Zhang, M. Park, J. Yang, K. Kang and Y. M. Kang, Pseudocapacitive Behavior and Ultrafast Kinetics from Solvated Ion Cointercalation into MoS2 for Its Alkali Ion Storage, ACS Appl. Energy Mater., 2019, 2, 3726–3735.
33. X. Wang, T. S. Mathis, K. Li, Z. Lin, L. Vlcek, T. Torita, N. C. Osti, C. Hatter, P. Urbankowski, A. Sarycheva, M. Tyagi, E. Mamontov, P. Simon and Y. Gogotsi, Influences from Solvents on Charge Storage in Titanium Carbide MXenes, Nat. Energy, 2019, 4, 241–248.
34. S. Hou, X. Ji, K. Gaskell, P. Wang, L. Wang, J. Xu, R. Sun, O. Borodin and C. Wang, Solvation Sheath Reorganization Enables Divalent Metal Batteries with Fast Interfacial Charge Transfer Kinetics, Science, 2021, 374, 172–178.
35. M. Qin, Z. Zeng, Q. Wu, H. Yan, M. Liu, Y. Wu, H. Zhang, S. Lei, S. Cheng and J. Xie, Dipole–Dipole Interactions for Inhibiting Solvent Co-Intercalation into a Graphite Anode to Extend the Horizon of Electrolyte Design, Energy Environ. Sci., 2023, 16, 546–556.
36. Y. Yamada, Y. Takazawa, K. Miyazaki and T. Abe, Electrochemical Lithium Intercalation into Graphite in Dimethyl Sulfoxide-Based Electrolytes: Effect of Solvation Structure of Lithium Ion, J. Phys. Chem. C, 2010, 114, 11680–11685.
37. P. Nam, L. Pham, V. Gabaudan, A. Boulaoued, G. Åvall, F. Salles, P. Johansson, L. Monconduit and L. Stievano, Potassium-Ion Batteries Using KFSI/DME Electrolytes: Implications of Cation Solvation on the K + -Graphite (Co-)Intercalation Mechanism, Energy Storage Mater., 2022, 45, 291–300.
38. L. Que, J. Wu, Z. Lan, Y. Xie, F. Yu, Z. Wang, J. Meng and X. Zhang, Potassium-based Dual-ion Batteries Operating at -60 °C Enabled By Co-Intercalation Anode, Adv. Mater., 2023, 2307592.
39. L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, “Water-in-Salt” Electrolyte Enables High-Voltage Aqueous Lithium-Ion Chemistries, Science, 2015, 350, 938–943.
40. J. Han, A. Mariani, S. Passerini and A. Varzi, A Perspective on the Role of Anions in Highly Concentrated Aqueous Electrolytes, Energy Environ. Sci., 2023, 16, 1480–1501.
41. X. Wang, T. S. Mathis, Y. Sun, W. Y. Tsai, N. Shpigel, H. Shao, D. Zhang, K. Hantanasirisakul, F. Malchik, N. Balke, D. E. Jiang, P. Simon and Y. Gogotsi, Titanium Carbide MXene Shows an Electrochemical Anomaly in Water-in-Salt Electrolytes, ACS Nano, 2021, 15, 15274–15284.
42. H. Adenusi, G. A. Chass, S. Passerini, K. V. Tian and G. Chen, Lithium Batteries and the Solid Electrolyte Interphase (SEI)—Progress and Outlook, Adv. Energy Mater., 2023, 13, 2203307.
43. B. Ravikumar, M. Mynam and B. Rai, Effect of Salt Concentration on Properties of Lithium Ion Battery Electrolytes: A Molecular Dynamics Study, J. Phys. Chem. C, 2018, 122, 8173–8181.
44. F. Béguin, V. Presser, A. Balducci and E. Frackowiak, Carbons and Electrolytes for Advanced Supercapacitors, Adv. Mater., 2014, 26, 2219–2251.
45. J. Chmiola, G. Yushin, Y. Gogotsi, C. Portet, P. Simon and P. L. Taberna, Anomalous Increase in Carbon Capacitance at Pore Sizes Less than 1 Nanometer, Science, 2006, 313, 1760–1763.
46. J. Chmiola, C. Largeot, P. L. Taberna, P. Simon and Y. Gogotsi, Desolvation of Ions in Subnanometer Pores and Its Effect on Capacitance and Double-Layer Theory, Angew. Chem., Int. Ed., 2008, 47, 3392–3395.
47. C. Prehal, C. Koczwara, N. Jäckel, A. Schreiber, M. Burian, H. Amenitsch, M. A. Hartmann, V. Presser and O. Paris, Quantification of Ion Confinement and Desolvation in Nanoporous Carbon Supercapacitors with Modelling and in Situ X-Ray Scattering, Nat. Energy, 2017, 2, 16215.
48. S. Fleischmann, Y. Zhang, X. Wang, P. T. Cummings, J. Wu, P. Simon, Y. Gogotsi, V. Presser and V. Augustyn, Continuous Transition from Double-Layer to faradaic Charge Storage in Confined Electrolytes, Nat. Energy, 2022, 7, 222–228.
49. K. Liang, R. A. Matsumoto, W. Zhao, N. C. Osti, I. Popov, B. P. Thapaliya, S. Fleischmann, S. Misra, K. Prenger, M. Tyagi, E. Mamontov, V. Augustyn, R. R. Unocic, A. P. Sokolov, S. Dai, P. T. Cummings and M. Naguib, Engineering the Interlayer Spacing by Pre-Intercalation for High Performance Supercapacitor MXene Electrodes in Room Temperature Ionic Liquid, Adv. Funct. Mater., 2021, 31, 2104007.
50. Y. Li, H. Shao, Z. Lin, J. Lu, L. Liu, B. Duployer, P. O. Å. Persson, P. Eklund, L. Hultman, M. Li, K. Chen, X. H. Zha, S. Du, P. Rozier, Z. Chai, E. Raymundo-Piñero, P. L. Taberna, P. Simon and Q. Huang, A General Lewis Acidic Etching Route for Preparing MXenes with Enhanced Electrochemical Performance in Non-Aqueous Electrolyte, Nat. Mater., 2020, 19, 894–899.
51. L. Liu, H. Zschiesche, M. Antonietti, B. Daffos, N. V. Tarakina, M. Gibilaro, P. Chamelot, L. Massot, B. Duployer, P.-L. Taberna and P. Simon, Tuning the Surface Chemistry of MXene to Improve Energy Storage: Example of Nitrification by Salt Melt, Adv. Energy Mater., 2023, 13, 2202709.
52. H. Li, K. Xu, P. Chen, Y. Yuan, Y. Qiu, L. Wang, L. Zhu, X. Wang, G. Cai, L. Zheng, C. Dai, D. Zhou, N. Zhang, J. Zhu, J. Xie, F. Liao, H. Peng, Y. Peng, J. Ju, Z. Lin and J. Sun, Achieving Ultrahigh Electrochemical Performance by Surface Design and Nanoconfined Water Manipulation, Natl. Sci. Rev., 2022, 9, nwac079.
53. P. Bärmann, R. Nölle, V. Siozios, M. Ruttert, O. Guillon, M. Winter, J. Gonzalez-Julian and T. Placke, Solvent Co-Intercalation into Few-Layered Ti3C2Tx MXenes in Lithium Ion Batteries Induced by Acidic or Basic Post-Treatment, ACS Nano, 2021, 15, 3295–3308.
54. S. Fleischmann, M. A. Spencer and V. Augustyn, Electrochemical Reactivity under Confinement Enabled by Molecularly Pillared 2D and Layered Materials, Chem. Mater., 2020, 32, 3325–3334.
55. Y. Zhang, E. H. Ang, Y. Yang, M. Ye, W. Du and C. C. Li, Interlayer Chemistry of Layered Electrode Materials in Energy Storage Devices, Adv. Funct. Mater., 2021, 31, 2007358.
56. Y. Huang, T. A. Cohen, B. M. Sperry, H. Larson, H. A. Nguyen, M. K. Homer, F. Y. Dou, L. M. Jacoby, B. M. Cossairt, D. R. Gamelin and C. K. Luscombe, Organic Building Blocks at Inorganic Nanomaterial Interfaces, Mater. Horizons, 2022, 9, 61–87.
57. I. Escher, Y. Kravets, G. A. Ferrero, M. Goktas and P. Adelhelm, Strategies for Alleviating Electrode Expansion of Graphite Electrodes in Sodium-Ion Batteries Followed by In Situ Electrochemical Dilatometry, Energy Technol., 2021, 9, 2000880.
58. H. Banda, S. Périé, B. Daffos, P. L. Taberna, L. Dubois, O. Crosnier, P. Simon, D. Lee, G. De Paëpe and F. Duclairoir, Sparsely Pillared Graphene Materials for High-Performance Supercapacitors: Improving Ion Transport and Storage Capacity, ACS Nano, 2019, 13, 1443–1453.
59. M. Okubo, A. Sugahara, S. Kajiyama and A. Yamada, MXene as a Charge Storage Host, Acc. Chem. Res., 2018, 51, 591–599.
60. R. G. Houdeville, A. P. Black, A. Ponrouch, M. R. Palacín and F. Fauth, Operando Synchrotron X-Ray Diffraction Studies on TiS2: The Effect of Propylene Carbonate on Reduction Mechanism Operando Synchrotron X-Ray Diffraction Studies on TiS 2: The Effect of Propylene Carbonate on Reduction Mechanism, J. Electrochem. Soc., 2021, 168, 030514.
61. W.-Y. Tsai, R. Wang, S. Boyd, V. Augustyn and N. Balke, Probing Local Electrochemistry via Mechanical Cyclic Voltammetry Curves, Nano Energy, 2021, 81, 105592.
62. I. Escher, M. Hahn, G. A. Ferrero and P. Adelhelm, A Practical Guide for Using Electrochemical Dilatometry as Operando Tool in Battery and Supercapacitor Research, Energy Technol., 2022, 10, 2101120.
63. H. Guo, D. Goonetilleke, N. Sharma, W. Ren, Z. Su, A. Rawal and C. Zhao, Two-Phase Electrochemical Proton Transport and Storage in α-MoO3 for Proton Batteries, Cell Rep. Phys. Sci., 2020, 1, 100225.
64. M. Yan, P. He, Y. Chen, S. Wang, Q. Wei, K. Zhao, X. Xu, Q. An, Y. Shuang, Y. Shao, K. T. Mueller, L. Mai, J. Liu and J. Yang, Water-Lubricated Intercalation in V2O5·nH2O for High-Capacity and High-Rate Aqueous Rechargeable Zinc Batteries, Adv. Mater., 2018, 30, 1703725.
65. K. Gotoh, H. Maruyama, T. Miyatou, M. Mizuno, K. Urita and H. Ishida, Structure and Dynamic Behavior of Sodium-Diglyme Complex in the Graphite Anode of Sodium Ion Battery by 2H Nuclear Magnetic Resonance, J. Phys. Chem. C, 2016, 120, 28152–28156.
66. I. Escher, A. I. Freytag, J. M. Lopez del Amo and P. Adelhelm, Solid-State NMR Study on the Structure and Dynamics of Graphite Electrodes in Sodium-Ion Batteries with Solvent Co-Intercalation, Batteries Supercaps, 2023, 6, e202200421.
67. N. Leifer, M. F. Greenstein, A. Mor, D. Aurbach and G. Goobes, NMR-Detected Dynamics of Sodium Co-Intercalation with Diglyme Solvent Molecules in Graphite Anodes Linked to Prolonged Cycling, J. Phys. Chem. B, 2018, 122, 21172–21184.
68. N. Shpigel, M. D. Levi, S. Sigalov, L. Daikhin and D. Aurbach, In Situ Real-Time Mechanical and Morphological Characterization of Electrodes for Electrochemical Energy Storage and Conversion by Electrochemical Quartz Crystal Microbalance with Dissipation Monitoring, Acc. Chem. Res., 2018, 51, 69–79.
69. P. Srimuk, J. Lee, Ö. Budak, J. Choi, M. Chen, G. Feng, C. Prehal and V. Presser, In Situ Tracking of Partial Sodium Desolvation of Materials with Capacitive, Pseudocapacitive, and Battery-like Charge/Discharge Behavior in Aqueous Electrolytes, Langmuir, 2018, 34, 13132–13143.
70. S. Boyd, K. Ganeshan, W.-Y. Tsai, T. Wu, S. Saeed, D. Jiang, N. Balke, A. C. T. van Duin and V. Augustyn, Effects of Interlayer Confinement and Hydration on Capacitive Charge Storage in Birnessite, Nat. Mater., 2021, 20, 1689–1694.
71. H. Kim, J. Hong, G. Yoon, H. Kim, K. Y. Park, M. S. Park, W. S. Yoon and K. Kang, Sodium Intercalation Chemistry in Graphite, Energy Environ. Sci., 2015, 8, 2963–2969.
72. J. Park, S. J. Kim, K. Lim, J. Cho and K. Kang, Reconfiguring Sodium Intercalation Process of TiS2 Electrode for Sodium-Ion Batteries by a Partial Solvent Cointercalation, ACS Energy Lett., 2022, 7, 3718–3726.
73. J. Shin, D. S. Choi, H. J. Lee, Y. Jung and J. W. Choi, Hydrated Intercalation for High-Performance Aqueous Zinc Ion Batteries, Adv. Energy Mater., 2019, 9, 1900083.
74. X. Wu, J. J. Hong, W. Shin, L. Ma, T. Liu, X. Bi, Y. Yuan, Y. Qi, T. W. Surta, W. Huang, J. Neuefeind, T. Wu, P. A. Greaney, J. Lu and X. Ji, Diffusion-Free Grotthuss Topochemistry for High-Rate and Long-Life Proton Batteries, Nat. Energy, 2019, 4, 123–130.
75. Y. Sun, C. Zhan, P. R. C. Kent, M. Naguib, Y. Gogotsi and D. E. Jiang, Proton Redox and Transport in MXene-Confined Water, ACS Appl. Mater. Interfaces, 2020, 12, 763–770.
76. W. Xu, K. Zhao, X. Liao, C. Sun, K. He, Y. Yuan, W. Ren, J. Li, T. Li, C. Yang, H. Cheng, Q. Sun, I. Manke, X. Lu and J. Lu, Proton Storage in Metallic H1.75MoO3 Nanobelts through the Grotthuss Mechanism, J. Am. Chem. Soc., 2022, 144, 17407–17415.
77. K. Dokko, D. Watanabe, Y. Ugata, M. L. Thomas, S. Tsuzuki, W. Shinoda, K. Hashimoto, K. Ueno, Y. Umebayashi and M. Watanabe, Direct Evidence for Li Ion Hopping Conduction in Highly Concentrated Sulfolane-Based Liquid Electrolytes, J. Phys. Chem. B, 2018, 122, 10736–10745.
78. J. G. McDaniel and A. Yethiraj, Grotthuss Transport of Iodide in EMIM/I3 Ionic Crystal, J. Phys. Chem. B, 2018, 122, 250–257.
79. Z. Li, J. Häcker, M. Fichtner and Z. Zhao-Karger, Cathode Materials and Chemistries for Magnesium Batteries: Challenges and Opportunities, Adv. Energy Mater., 2023, 13, 2300682.
80. Q. Zong, Y. Zhuang, C. Liu, Q. Kang, Y. Wu, J. Zhang, J. Wang, D. Tao, Q. Zhang and G. Cao, Dual Effects of Metal and Organic Ions Co-Intercalation Boosting the Kinetics and Stability of Hydrated Vanadate Cathodes for Aqueous Zinc-Ion Batteries, Adv. Energy Mater., 2023, 13, 2301480.
81. Y. Yang, J. Wang, X. Du, H. Jiang, A. Du, X. Ge, N. Li, H. Wang, Y. Zhang, Z. Chen, J. Zhao and G. Cui, Cation Co-Intercalation with Anions: The Origin of Low Capacities of Graphite Cathodes in Multivalent Electrolytes, J. Am. Chem. Soc., 2023, 145, 12093–12104.

---