Investigating the potential of pyrazine dioxide based-compounds as organic electrodes for batteries†
F. Lambert abc,
A. L. Hetzel
abc,
A. L. Hetzel ab,
Y. Danten
ab,
Y. Danten d,
A. A. Franco
d,
A. A. Franco abef,
C. Gatti
abef,
C. Gatti g and
C. Frayret
g and
C. Frayret *abe
*abe
aLaboratoire de Réactivité et Chimie des Solides (LRCS), Université de Picardie Jules Verne, UMR CNRS 7314. E-mail: christine.frayret@u-picardie.fr
bHub de l’Energie; Réseau sur le Stockage Electrochimique de l’Energie (RS2E), FR CNRS 3459, 80000 Amiens Cedex, France
cThe French Environment and Energy Management Agency (ADEME), 49004 Angers Cedex 01, France
dInstitut des Sciences Moléculaires, UMR CNRS 5255, 33405 Talence, France
eALISTORE-European Research Institute, Hub de l'Energie, FR CNRS 3104, 80000 Amiens, France
fInstitut Universitaire de France, Paris 75005, France
gCNR SCITEC, CNR Istituto di Scienze e Tecnologie Chimiche “Giulio Natta”, Milano, Italy
First published on 15th June 2024
Abstract
Understanding structure–property relationship in redox-active molecular species is of central importance in various fields, including many medicinal and chemical applications. The quest for performant organic electrodes in the context of energy storage calls for pioneering studies to develop new and possibly optimal materials. Beyond modifying the molecular design of the existing compounds through functionalization, expansion of the search enabling the advent of efficient new backbones can potentially lead to breakthroughs in this research area. The number of already identified families able to constitute negative organic electrodes is much lower than that of their positive counterparts, which calls for finding ways to bridge this gap. To expand the dataset of known predicted redox potentials and in view of reaching an educated guess about the abilities of some eventual new redox active electrodes, we examined the properties of pyrazine N,N′-dioxide (PZDO) and its fully methylated functionalized derivative (TeMePzDO). The aspects and mechanisms driving the various features characteristic of these compounds were unraveled through molecular and periodic DFT calculations combined with accurate electronic structure analysis. The predicted molecular redox/crystalline intercalation potentials lead to the classification of PZDO and TeMePzDO systems within the class of negative electrodes, with features that are significantly appealing compared to those of some existing systems with backbones suited for such kind of application.
Introduction
Within the context of search for new redox active materials that are able to constitute organic electrodes for batteries, various classes of compounds have been already identified as promising candidates.1–10 Nevertheless, this research area remains active and the search space for materials of this type is still extremely vast. In complement to experimental works, computational studies may be undertaken at several levels, modelling the searched materials as molecules/clusters, polymers or crystals.11–24 Recently, the possibility to employ C-nitroso compounds (i.e. molecules having the nitroso group (R–NO), with NO attached to a carbon atom within R) in the field of organic electrode materials (OEMs) has been envisaged.25,26 Such studies involve a redox centre (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) that is distinct from the most thoroughly investigated class of compounds based on the use of carbonyl groups.
O) that is distinct from the most thoroughly investigated class of compounds based on the use of carbonyl groups.
By considering a simplified electrochemical mechanism between p-dinitrosobenzene (DNB) and di-lithium benzoquinone dioximate (Li2-BQDO), some relevant structure–property features emerged.26 We notably demonstrated that the classification of such moieties within positive OEMs relies on the energy stabilization induced by the redox center moiety upon lithiation of DNB that opposes and overcomes the energy lowering caused by the loss of ring aromaticity during this process. Such energy balance differs from the one characterizing the well-known p-benzoquinone systems, where the gain in stability is instead attributed to the large enhancement in π-conjugation. Indeed, by switching from the initial quinoid form to the reduced enolate form through a two-electron uptake, the system becomes aromatic during such an electrochemical process,21,27 thus resulting in high redox potential vs. Li+/Li, which is advantageous for positive electrode materials. The reverse situation, i.e. starting with an aromatic compound that loses its aromaticity stabilization upon the redox phenomenon, can be exploited to find possible negative electrode compounds. As an example of such a situation, injecting electrons within the pyrazine N,N′-dioxide compound shall in principle lead to the evolution from an aromatic moiety (with 4n + 2 = 6 electrons) towards a potentially anti-aromatic compound (with 4n = 8 electrons). The aromaticity loss or gain is similar in its incidence to the tuning that exploits inductive/mesomeric effects27 to achieve energy stabilization/destabilization. The only difference between both kinds of molecular modulation acting on the electrochemical activity lies in the fact that in the present case the ‘driving force’ only concerns the backbone, even though this aspect can be still additionally enhanced through appropriate substituent selection. As a matter of fact, fine-tuning through functionalization of a given framework has been explored in more detail so far than the quest for a strong loss of energy stabilization upon electron uptake or release originating solely from the backbone. Furthermore, the number of families discovered with the purpose of serving as negative electrodes is far less compared to that of positive ones, which are clearly prominent to date. This holds true both for the so-called n- and p-type redox-active classes (according to Hünig's classification)10 depending on the intake/release of electrons and counterions.
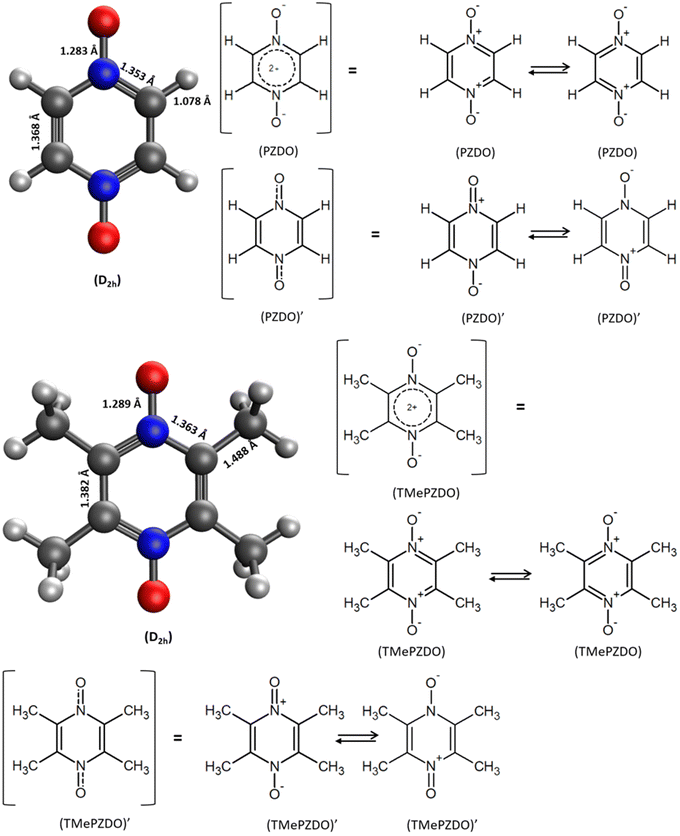
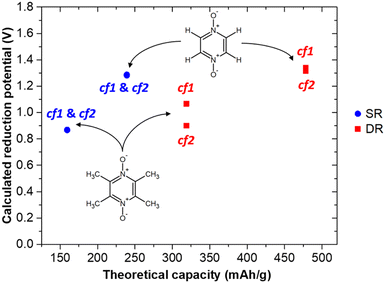
As a first step towards examination of their possible interest in this area, we report in this work a series of DFT modelling studies focused on pyrazine N,N′-dioxide (C4H4N2O2 i.e. PZDO28 (Fig. 1)) and its tetramethyl substituted counterpart, 2,3,5,6-tetramethylpyrazine-1,4-dioxide (C8H12N2O2 i.e. TeMePzDO).29 Among other applications, PZDO and some of its derivatives have been considered as potential precursors of functional materials and for possible use in the field of crystal engineering,30–35 whereas in the present investigation we aim at examining their capabilities in case of use as n-type organic electrodes of batteries. By constituting one of the smallest aromatic moieties belonging to the bis-N-oxide family, PZDO is very attractive from the viewpoint of theoretical capacity, with values equal to 239.1 mA h g−1 and 478.2 mA h g−1 for the process of Single Reduction (SR)/Double Reduction (DR), respectively. While lowering the impact of this feature with respect to PZDO, the functionalization with methyl groups, thus leading to TeMePzDO, is likely to have an impact on the redox potential. The interest for this methylated version and other potentially existing substituted forms is also ascribable to their possibly more favourable stability features with respect to some risks recently evidenced for PZDO,36 despite its decomposition temperature (above 270 °C) which is similar to that of many other organic compounds, including some of those considered as suitable electrodes. Contrary to the case of dioximate species, which were recently reported,25,26 another electrochemical versatility in incorporating the (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) redox center directly into the ring, rather than attaching it to a six-membered carbon ring (6-CMR), shall be reached. In this investigation, from both fundamental and application points of view, it is important to gain information not only on the redox activity features but also on the HOMO–LUMO gaps of this class of molecules (PZDO and TeMePzDO). Indeed, a different frontier orbital behaviour with respect to other kinds of compounds could be observed, with the eventuality of being beneficial for the conductive properties of the materials. Another relevant information to be gained is the degree of transferability of molecular electrochemical features to those occurring in crystalline materials. While the flexible nature characterizing the intermolecular packing in these redox-active organic electrode materials has been recognized as being able to generate higher rate capability compared to their inorganic counterparts,37,38 this effect along with the specific relative orientations of molecules may have an impact also on the intercalation potentials. The latter deserves to be examined and confronted with the results characterizing their molecular counterparts, considered in implicit solvation treatment. Therefore, beyond molecular DFT modelling intended to provide first access to features accompanying the redox procedure in such compounds, the lithiation of the corresponding crystalline phases of PZDO and TeMePzDO, respectively determined by Näther et al.28 and Aakeröy et al.,39 has been undertaken as well.
O) redox center directly into the ring, rather than attaching it to a six-membered carbon ring (6-CMR), shall be reached. In this investigation, from both fundamental and application points of view, it is important to gain information not only on the redox activity features but also on the HOMO–LUMO gaps of this class of molecules (PZDO and TeMePzDO). Indeed, a different frontier orbital behaviour with respect to other kinds of compounds could be observed, with the eventuality of being beneficial for the conductive properties of the materials. Another relevant information to be gained is the degree of transferability of molecular electrochemical features to those occurring in crystalline materials. While the flexible nature characterizing the intermolecular packing in these redox-active organic electrode materials has been recognized as being able to generate higher rate capability compared to their inorganic counterparts,37,38 this effect along with the specific relative orientations of molecules may have an impact also on the intercalation potentials. The latter deserves to be examined and confronted with the results characterizing their molecular counterparts, considered in implicit solvation treatment. Therefore, beyond molecular DFT modelling intended to provide first access to features accompanying the redox procedure in such compounds, the lithiation of the corresponding crystalline phases of PZDO and TeMePzDO, respectively determined by Näther et al.28 and Aakeröy et al.,39 has been undertaken as well.
Computational details
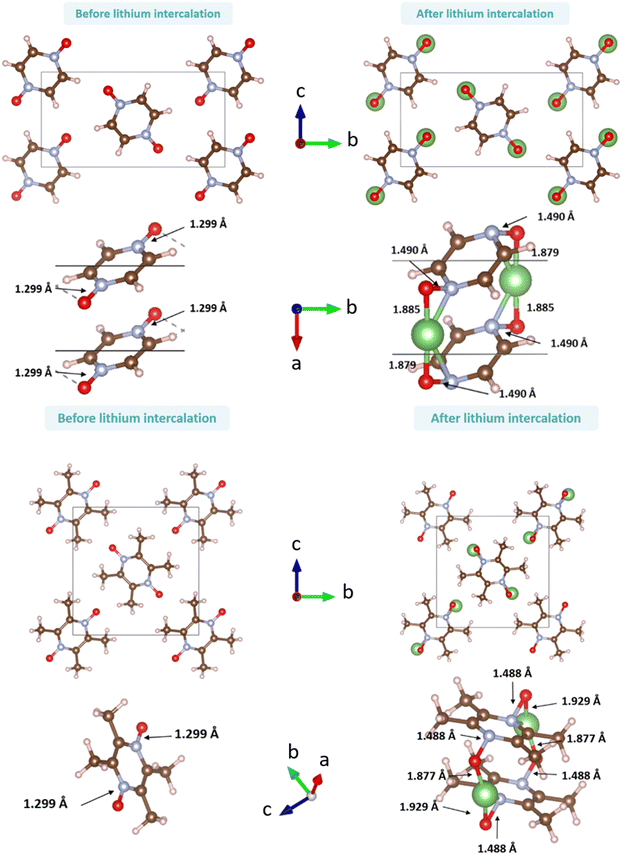
For results obtained at the level of molecular density functional theory (DFT), geometry optimizations were achieved for PZDO and TeMePzDO compounds as well as for their complexes with Li+ ions using the Gaussian40 package. These calculations employed the M06-2X functional with the polarized triple ξ-basis set 6-311+G(2d,2p) and were performed with both a very tight criterion of convergence and a superfine integration grid. All calculated structures were proven to correspond to well-defined local energy minima (no imaginary frequency) thanks to the vibrational analysis. Solvent effects were taken into account using a polarizable (continuum, i.e., via a dielectric medium) solvation model based on density (SMD)41 for which the full solute electron density is used without defining partial atomic charges. Acetonitrile was selected as the solvent (ε = 37.5) and the redox potential was estimated through the Nernst equation by following the procedure described in previous works.13,18,21,22,42,43 Similarly to our preceding investigations,21,22 we considered in this work two distinct situations which can potentially be observed in experiments for the reduction process of the investigated molecules. They correspond either to a single reduction (SR) or to a double reduction (DR). In the former case, a complex is formed involving a singly reduced molecule (thus corresponding to a monoanion), interacting with one monovalent counter-ion, Li+ (i.e. intermediate state), whereas in the DR process the doubly reduced molecule interacts with two monovalent counter-ions, Li+ (i.e. final state). The conformational counter-ion locations around any of the two kinds of organic molecules were systematically determined from the analysis of the calculated potential energy surface (PES). By selecting the most stable fully optimized structures using the above-mentioned methodology, the Electrostatic Surface Potential (ESP) maps (i.e., electron isodensity surfaces mapped with the electrostatic potential energy felt by an electron moving over this surface) were plotted. They display the potential that a unit positive charge would experience at any point of the surface due to the electron and nuclear distributions in the molecule. Red areas of these maps indicating low electrostatic potentials account for a relative abundance of electrons, whereas blue areas (characterized by high potentials) are linked to regions experiencing a relative depletion of electrons. Therefore, the minima of the ESP maps should coincide with the preferential location of alkali metal cations for the envisaged electrochemical processes. Regarding electronic structure analysis, we applied the Bader quantum theory of atoms in molecules (QTAIM) approach,44 which inter alia allows for estimating the net atomic charges (NACs),44,45 the delocalization indexes and the electron density Laplacian topology (see infra). As typical integration grids, we used 96 phi and 64 theta angular points and 200 points for the radial integration within the so-called beta sphere. The accuracy of numerical integration was monitored through the integrated Lagrangian value that was typically below 1 × 10−5 a.u. for H atoms and lower than 1 × 10−3 a.u. for heavier atoms. Electron delocalization indexes, δ(I,J), i.e. the number of electron pairs shared or delocalized between two atomic basins I and J,46 hereafter labelled as DI, and their standard deviation for the bonds within a ring were calculated using the SF-ESI package.45 The evolution of these quantities between the initial (unreduced) and the intermediate (singly reduced, SR)/final (doubly reduced, DR) forms was employed in order to estimate the associated evolution of electron delocalization within the various molecular moieties and its correlation with the energy stabilization/destabilization during the electrochemical process. Furthermore, the topology of the Laplacian of the electron density,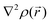 , given by the trace of the Hessian matrix of
, given by the trace of the Hessian matrix of 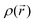 ,
, 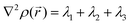 (where λi (i = 1, 3) represents the eigenvalues of this Hessian matrix), was also examined. Here, more precisely, the
(where λi (i = 1, 3) represents the eigenvalues of this Hessian matrix), was also examined. Here, more precisely, the 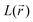 quantity, corresponding to the negative value of the Laplacian, was also considered to examine the
quantity, corresponding to the negative value of the Laplacian, was also considered to examine the 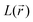 maxima in the nitrogen Valence Shell Charge Concentration (VSCC) in order to provide a further probe of the envisaged redox mechanisms. Finally, we selected the hybrid functional Heyd–Scuseria–Ernzerhof (HSE06)47 to estimate the HOMO (SOMO)–LUMO gaps of the various species using the previously optimized geometry at the M06-2X/6-311+G(2d,2p) level.
maxima in the nitrogen Valence Shell Charge Concentration (VSCC) in order to provide a further probe of the envisaged redox mechanisms. Finally, we selected the hybrid functional Heyd–Scuseria–Ernzerhof (HSE06)47 to estimate the HOMO (SOMO)–LUMO gaps of the various species using the previously optimized geometry at the M06-2X/6-311+G(2d,2p) level.
For periodical calculations, the VASP package48 was employed in order to provide a benchmark of the tested methodologies, with the objective of identifying the one that most suitably accounts for the available structural features from experiment (the delithiated phases of PZDO28 and TeMePzDO39). Full-geometry optimizations were carried out at several levels of theory by using various XC (exchange–correlation) functionals associated with various dispersion correction treatments (involving the empirical dispersion of Grimme49,50), as described hereafter. More precisely, energy minimizations were performed with several choices of XC functionals including the Perdew–Burke–Ernzerhof (PBE) variant of the GGA,51 along with the PBEsol.52 The latter52 corresponds to a revised version of the Perdew–Burke–Ernzerhof functional. It was designed for solids and was constructed to restore the correct second-order expansion for the exchange energy. PBEsol generally improves the equilibrium properties of solids and their surfaces over PBE. In order to estimate the incidence of dispersion interactions between the molecules in the crystal, the results of dispersion corrected PBE functionals (i.e. methodologies PBE-D, PBE-D*, PBE-D3 and corr-PBE-D*_0.XX defined hereafter) were compared to those obtained by using the above-mentioned non-corrected Kohn–Sham density functionals. For these benchmark studies, we used more precisely the dispersion correction proposed by Grimme (Grimme'06 scheme, i.e. DFT-D2 method as well as DFT-D3 model)49,50 introduced in the VASP package.48 By employing the initially proposed parameters (with Cij6 and R0 values taken from the DFT-D2 Grimme's model49), hereafter called PBE-D calculations, the van der Waals (vdW) forces might, however, be overestimated, resulting in an underestimation of the lattice constants. The results may thus be improved upon modification of the semiempirical vdW correction. The correction proposed by Civalleri et al.53,54 (hereafter denoted as PBE-D*), corresponding to a modification of the vdW radii that allows a softening of the dispersion interaction, was thus investigated too. It corresponds to a scaling of the Grimme's R0 values of hydrogen and heavy atoms by 1.30 and 1.05, respectively. This adjustment was determined from a manual fitting procedure, searching for the best agreement between computed and experimental cohesive energies on a set of 14 molecular crystals.53 Additionally, these scaling factors were validated through a comparative analysis of the intermolecular energy for a data set including 60 molecular crystals with a large variety of functional groups.55 In the method labelled as corr-PBED*_0.XX hereafter, another s6 value equal to a certain number, i.e., 0.XX, distinct from the 0.75 value originally proposed by Grimme – which is used for PBE-D or PBE-D* calculations – was also adopted while leaving the R0 values fixed at the PBE-D* values.56 This latter methodology was considered as efficient even in other works, see e.g. ref. 11, 57 and 58. Additionally, SCAN+rVV10 was also employed since it has been demonstrated to be a versatile van der Waals (vdW) density functional, which can potentially deliver good predictions of both energetic and structural properties for many types of bonding. After having identified the most suited methodology, i.e. the one leading to the lowest relative errors with respect to the experiment for delithiated phases (see Fig. SI1 and SI2†), the structure and relative stability of the various ‘lithiated’ models were studied for each of the two compounds by assuming a certain number of initial positioning for lithium. In this work, projector augmented wave (PAW) potentials were used to describe the electron–ion interaction.59 The wave functions were expanded in plane waves with the energy below 600 eV. Brillouin zone sampling was performed by using the Monkhorst–Pack scheme,60 with a k-point grid of 6 × 2 × 4/6 × 2 × 2 for PZDO/TeMePzDO, respectively. Minimizations were considered complete when energies were converged to better than 1 × 10−6 eV per atom and maximum residual forces were lower in magnitude than 1 × 10−3 eV Å−1. Simulations of the various lithiated and delithiated phases were performed by simultaneously relaxing both the lattice geometry and atomic positions starting from the experimental ones when available (i.e. delithiated phases) and without imposing the symmetry constraints of the space group. By assuming two biphasic-type electrochemical systems, the energy resulting from subsequent Single Point Energy (SPE) calculations was considered to estimate the redox equilibrium potential.58,61 Final SPE calculations employed a cut-off of 800 eV and the following k-point grids: 12 × 4 × 8 and 12 × 4 × 4 for PZDO and TeMePzDO, respectively, while the threshold of 1 × 10−6 eV was adopted for considering the minimizations as converged.
Results and discussion
Molecular investigation
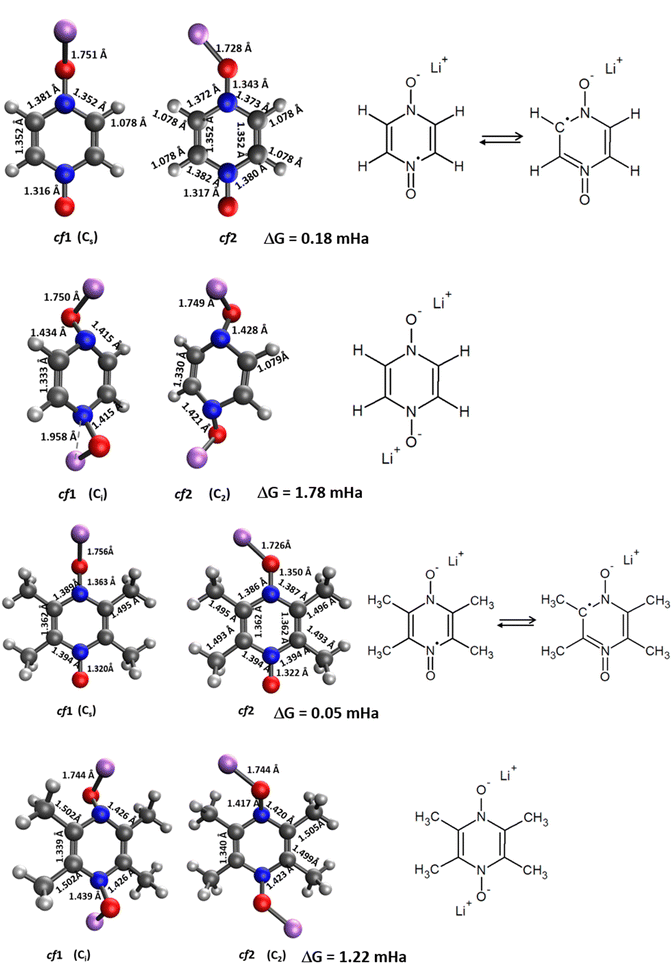
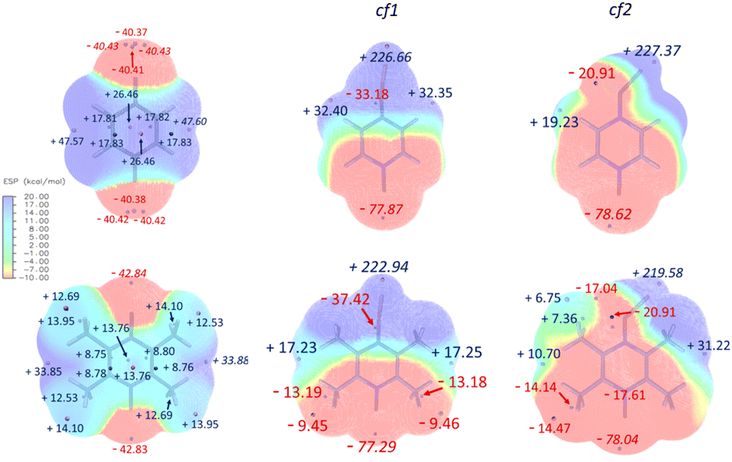
While the ESP maps (Fig. 4, left) of the initial (unreduced) PZDO and TeMePzDO systems both exhibit red areas – indicating an abundance of electrons – nearby each of the redox centres, it can be noticed that they are less extended in the case of the methylated system. Within these regions, it is possible to identify the presence of either one minimum (TeMePzDO) or several agglomerated minima (PZDO), which are all nearly aligned with the NO group. The minimum of the lowest value corresponds to −40.43 kcal mol−1 and −42.84 kcal mol−1 for PZDO and TeMePzDO, respectively. Owing to the differentiation in colours in the core framework between the two molecules, it is possible to appreciate the incidence of such functionalization, which acts as a cumulative donating effect, thus slightly decreasing the central lack in electrons for TeMePzDO compared to PZDO. Furthermore, the less expanded red area in the case of TeMePzDO is also linked to such +I inductive effect that was already proven to have an impact on the redox potential by decreasing its value, for instance, in the case of carboxylate or p-benzoquinone compounds.18,27 On the other hand, ESP maps for singly reduced species, either in conformation cf1 or cf2 (Fig. 4, middle and right, respectively), clearly evidence the fact that the presupposed site for the positioning of a further Li+ lies in the vicinity of the second redox centre (the other minima having much lower absolute values than this one).
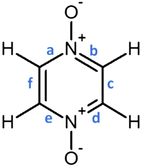
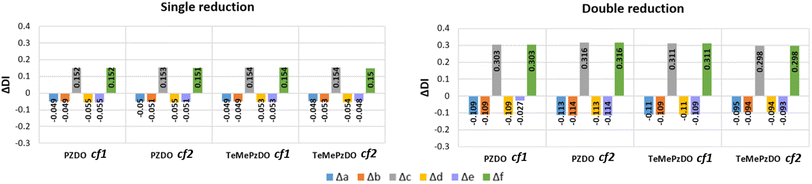
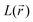 distribution within the nitrogen Valence Shell Charge Concentration (VSCC) upon electrochemical processes. Fig. 6 and 7 display the bond length or DI changes occurring upon SR and DR steps of our systems. These variations are denoted as Δxint/fin = xint/fin − xini where xini corresponds to the initial bond length/DI before the reduction process, while xint/fin represents the bond length/DI in the intermediate or in the final state involved either after SR or DR, respectively. Accordingly, a positive (negative) bond length Δx value is linked to a bond lengthening (shortening) upon one electron/two electron uptake. When the CC bond length increases (decreases), it can be noticed that the DI decreases (increases), as expected and as observed in our previous work.22 Changes indicated in Fig. 6 and 7 are reported for all unique bonds (a–f) of the molecular intermediate (SR)/final (DR) states (see Fig. 1 indicating the bond labelling). The disruption of the initial aromaticity (i.e. bond equalization of the oxidized compounds) occurring during the electrochemical process is visible through the positive/negative variation values observed, respectively, for a, b, d or e bonds and the concomitant negative/positive values, which are observed for c and f values. The length variations of PZDO upon the electrochemical process are almost identical for the conformations cf1 and cf2 in SR, and the same trend is observed for the TeMePzDO compound. In SR, it can be observed that the bond length changes are quite similar for each compound. In DR, the direction of bond length changes mimics that observed for SR, but their magnitude roughly doubles for all compounds.
distribution within the nitrogen Valence Shell Charge Concentration (VSCC) upon electrochemical processes. Fig. 6 and 7 display the bond length or DI changes occurring upon SR and DR steps of our systems. These variations are denoted as Δxint/fin = xint/fin − xini where xini corresponds to the initial bond length/DI before the reduction process, while xint/fin represents the bond length/DI in the intermediate or in the final state involved either after SR or DR, respectively. Accordingly, a positive (negative) bond length Δx value is linked to a bond lengthening (shortening) upon one electron/two electron uptake. When the CC bond length increases (decreases), it can be noticed that the DI decreases (increases), as expected and as observed in our previous work.22 Changes indicated in Fig. 6 and 7 are reported for all unique bonds (a–f) of the molecular intermediate (SR)/final (DR) states (see Fig. 1 indicating the bond labelling). The disruption of the initial aromaticity (i.e. bond equalization of the oxidized compounds) occurring during the electrochemical process is visible through the positive/negative variation values observed, respectively, for a, b, d or e bonds and the concomitant negative/positive values, which are observed for c and f values. The length variations of PZDO upon the electrochemical process are almost identical for the conformations cf1 and cf2 in SR, and the same trend is observed for the TeMePzDO compound. In SR, it can be observed that the bond length changes are quite similar for each compound. In DR, the direction of bond length changes mimics that observed for SR, but their magnitude roughly doubles for all compounds.
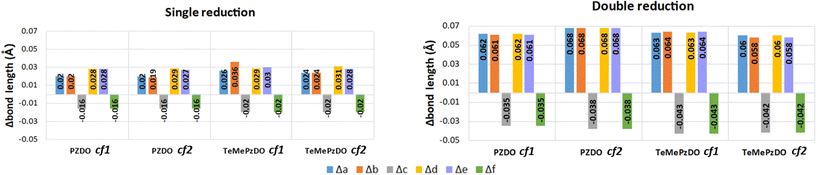 | ||
| Fig. 6 Calculated bond length variations of each bond in the ring for the single (left) and double (right) reduction process. | ||
 | ||
| Fig. 7 Calculated DI variations (ΔDI) of each bond in the ring for the single (left) and double (right) reduction process characterizing molecular species. | ||
The Δxint/fin values gathered in Fig. 6 and 7 concerning bond length and DI, respectively can be easily rationalized in terms of the resonance forms which characterize the SR and DR electronic structures of PZDO and TeMePzDO. The SR electronic structures are an intermediate between those of the initial and of the DR states; hence, the Δxint values are also lower than Δxfin in magnitude (and roughly half of the latter as just mentioned). The bond lengths in the initial state (C–C = 1.368 Å; C–N = 1.353 Å; N–O = 1.296 Å) denote the importance of the doubly charged aromatic structure. In fact, the CN bond length lies in between that of single and double CN bonds and the CC bond length is in between that of a double CC bond and the CC bond length in benzene. Also geometrically relevant are the two resonance structures implying a partial double bond character of the NO bond, whose bond length of 1.296 Å is indeed in between that of a typical single (1.36 Å) and of a double (1.22 Å) NO bond. In the DR state, the aromatic structure becomes no longer available, and the only reasonable structure corresponding to an uptake of two electrons implies an obvious decrease of the CC bond length (1.333 Å) down to the value typical for a double CC bond and an equally obvious lengthening of the CN bond (1.415 Å) up to the typical CN bond length between sp2 C and sp3 N atoms (roughly 1.40 Å). The NO bond is largely increased up to the value of 1.434 Å, in line with the fact that the O atom in DR increases its negative charge relative to the initial state. We recall here that the NO bond lengths are known to increase on passing from NO+ to NO* and NO−, because π* orbitals start to be populated after NO+. Several resonance structures may be hypothesized for the intermediate state (Fig. 8). They are distinguished by the specific atom carrying the unpaired electron. Hence, the Bader's electron spin populations (SP) allow the selection of the most relevant ones among them. Those having the unpaired electron on N atoms appear as the most favourable (structures A and D, with SP on N equal to 0.321 and 0.252 e−, respectively), followed by those where the C atoms bear the unpaired electron (structures C & C′ and F & F′, with SP amounting in total to 0.172 and 0.028 e−, respectively) and finally by those having an unpaired electron on the O atoms (B and E, with SP amounting to 0.165 and 0.001 e−, respectively). The intermediate state may thus be described as a mixture of A, D, C & C′, and B structures, listed according to their relative weight. The populations of these representative structures account for 91% of the total SP of 1. The relevance of C & C′ structures (and of F & F′ ones) along with the lack of a doubly positive charge on the ring explain why the CC bond lengths are shorter than in the initial state and, on the other hand, longer than in the DR state. Conversely, the CN bonds are longer than in the initial state since they are less deprived of electrons, but largely shorter than in the DR state where there are no relevant structures implying a double character for the CN bond. The NO bond lengths are longer than in the initial state and shorter than in the DR state given that many structures in SR imply NO* and NO− and never NO+, while the only DR structure implies just NO−. In SR, the notably longer NO distance for the NO group closer to Li+ is rationalized by the structure B being largely more favourable than structure E. Indeed, in structure B, the NO group more distant from Li+ has a radical character, NO*, differently from that closer to Li+ that has a NO− character. All that was discussed above neatly rationalizes the reason why the SR state, in terms of electronic and geometric structures, represents just an intermediate step along the initial state → DR state reaction coordinate.
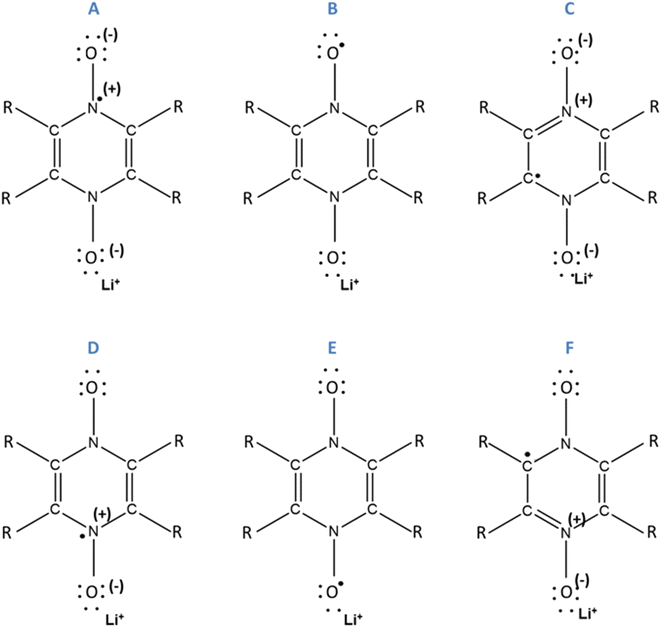 | ||
| Fig. 8 Assumed resonance structures for simple reduction. For the compound PZDO, R corresponds to H. For the compound TeMePzDO, R corresponds to a methyl group. | ||
In addition to previous comments and in view of further probing the proposed mechanism for the case of the double reduction, the 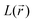 distribution within the nitrogen VSCC was examined (Table SI1†). Such distribution, as discussed below, fully agrees with the hypothesized resonance structures for PZDO and TeMePzDO. Indeed, by considering the bonded maximum (b.m.) and lone pair (LP) maximum characterizing the (3, −3) critical point (CP) of the
distribution within the nitrogen VSCC was examined (Table SI1†). Such distribution, as discussed below, fully agrees with the hypothesized resonance structures for PZDO and TeMePzDO. Indeed, by considering the bonded maximum (b.m.) and lone pair (LP) maximum characterizing the (3, −3) critical point (CP) of the 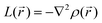 distribution, gathered in Table SI1,† it is straightforward to observe that their occurrence and location mirror the resonance structures that have been conjectured for both the initial and the double reduced forms of PZDO and TeMePzDO. Furthermore, the
distribution, gathered in Table SI1,† it is straightforward to observe that their occurrence and location mirror the resonance structures that have been conjectured for both the initial and the double reduced forms of PZDO and TeMePzDO. Furthermore, the 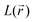 distribution within the nitrogen VSCC is very much alike in the PZDO and TeMePzDO systems, with their DR forms similarly and neatly distinguished from their initial forms. In the DR form of PZDO and TeMePzDO the N atom pyramidalizes assuming an sp3 hybridization, testified by the presence of a LP (absent in the initial forms) almost equidistant from the two C and the O atoms bonded to the N. As expected, the LP is located closer to the N nucleus than are all its bonded charge concentration CP maxima and it exhibits by far the highest
distribution within the nitrogen VSCC is very much alike in the PZDO and TeMePzDO systems, with their DR forms similarly and neatly distinguished from their initial forms. In the DR form of PZDO and TeMePzDO the N atom pyramidalizes assuming an sp3 hybridization, testified by the presence of a LP (absent in the initial forms) almost equidistant from the two C and the O atoms bonded to the N. As expected, the LP is located closer to the N nucleus than are all its bonded charge concentration CP maxima and it exhibits by far the highest 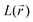 and
and 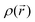 values. Conversely, bonded maxima have far higher
values. Conversely, bonded maxima have far higher 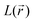 and
and 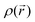 values in the initial forms because the N–C and N–O bonds lose their double bond partial character in the DR forms.
values in the initial forms because the N–C and N–O bonds lose their double bond partial character in the DR forms.
 | ||
| Fig. 9 Energy levels of the HOMO/SOMO and LUMO frontier orbitals calculated for the different molecular pyrazine dioxide, (de)-lithiated PZDO and TeMePzDO derivatives. | ||
While the SR in the case of PZDO leads to a large reduction of the band gap (with values of 1.90/1.87 eV for PZDO and 1.81/1.83 eV for its functionalized counterpart in conformations cf1/cf2, respectively), the DR is accompanied, instead, by an increase of the Eg value (i.e. ∼4.03/3.84 eV). In contrast with this observation, the TeMePzDO compound leads to a diminution of the band gap upon DR (and also upon SR but to a much lower extent). Accordingly, the methylated counterpart is characterized by a more advantageous situation for DR, with lowered bandgap compared to PZDO, reaching a value of ∼3.0 eV/3.7 eV for the conformations cf1/cf2 of TeMePzDO, respectively. The distinction of the two compounds in terms of Eg at the DR state (occurring for both conformations) is clearly linked to the much higher energy levels of the HOMO for TeMePzDO compared to PZDO, while LUMO levels are instead lower in energy for TeMePzDO; these combined effects therefore tend to shorten the gap of the methylated compound. Otherwise, the large decrease in Eg through SR in both compounds is accompanied by a shift of HOMO energy towards much higher values, while the corresponding LUMO level undergoes only a moderate energy shift upward.
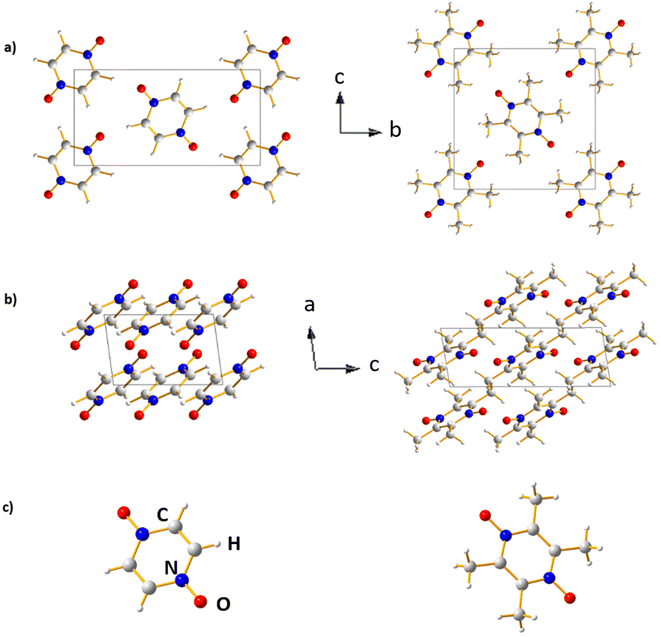
Investigation focused on crystalline materials
The crystal structures of PZDO and TeMePzDO are represented in different projections in Fig. 10. The crystal structure of PZDO28 – built up of (pyrazine N,N′-dioxide) molecules that are located on the centres of inversion – is monoclinic, of space group P21/c with the following experimental features: a = 3.7376(6) Å, b = 11.0011(18) Å, c = 5.7184(9) Å, β = 96.778(19), V = 233.48(6) Å3 and Z = 2. The molecules are stacked in the direction of the crystallographic a axis and exhibit a connection between them, which occurs through CH⋯O co-operative hydrogen bonding (HB), each O atom acting as an acceptor within such bonds. Similarly to the case of PZDO, TeMePzDO's crystalline structure39 is characterized by hydrogen bonding networks, this time involving methyl groups. It is also of monoclinic type, with Z = 2. Its space group is identical to that of PZDO (P21/c), with the following experimental lattice/angle parameters or lattice volume: a = 3.8328(9) Å, b = 10.291(3) Å, c = 10.396(3) Å, β = 98.770(9)°, and V = 405.26(17) Å3. The molecules are stacked along the crystallographic axis a. The optimized structures (Fig. 10) of the two bulk delithiated crystals (PZDO and TeMePzDO) were obtained from the full relaxation of the above-mentioned experimental ones.Fig. SI1† displays the most representative results of relative errors for the optimized crystals of PZDO relative to the corresponding experimental structural values by using different XC approximations as well as various dispersion corrections. Strong discrepancies in the reproduction of experimental values are often observed among all these various models, while largest values of relative errors seem nonetheless to be observed for a and c lattice parameters. By considering the results for the whole set of lattice parameters along with that of β angle, the corr-PBE-D*_0.52 methodology emerges as largely superior to all others. It exhibits relative errors lower than 1% irrespective of the measured quantity. If only generalised gradient correction is considered using the XC functional PBEsol, specifically designed for the treatment of solids, the a- or b-axis length is overestimated by more than 2% and a strong discrepancy with respect to the experiment is observed for the β angle. PBEsol, D, D* and PBEsol-D3 all clearly fail in describing the structural features of the system. D3 (i.e. the D3 dispersion model associated with the XC functional PBE) is among the most performant models but it does not outperform corr-PBE-D*_0.52, because of noticeably larger relative errors for the c lattice parameter. On the other hand, when associated with PBEsol, the dispersion correction reached by using D3 is clearly overestimated. With respect to the 0.XX values of the corr-PBE-D*_0.XX methodology, a clear differentiation emerges relative to the optimal 0.52 value results. Relative errors for lattice parameters are much larger for both 0.36 and 0.62 cases. The RMSD value with respect to experimental data for the intramolecular bond lengths and intermolecular distances for the corr-PBE-D*_0.52 is close to the lowest value obtained among all calculations performed and the calculated interplanar distance reproduces almost the experimental value, with a relative error lower than 1%.
Similar observations are found in the case of the TeMePzDO crystalline phase from Fig. SI2,† with again the corr-PBE-D*_0.XX methodology outperforming other calculations, although the best value of 0.XX is now shifted up to 0.62, with an excellent reproduction of both local geometry (in line especially with RMSD values) and lattice structural features.
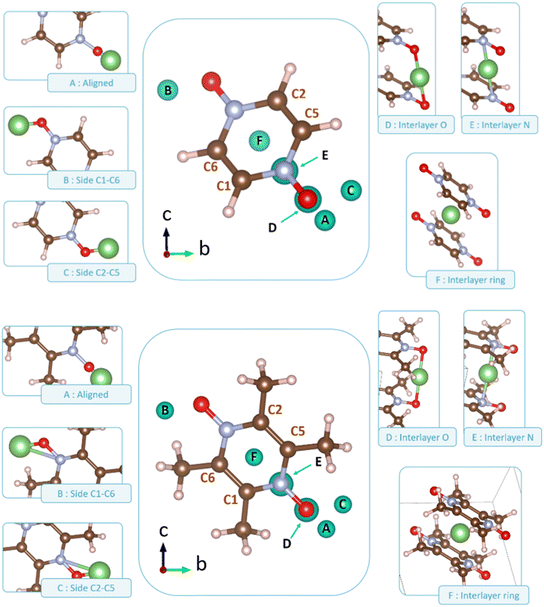
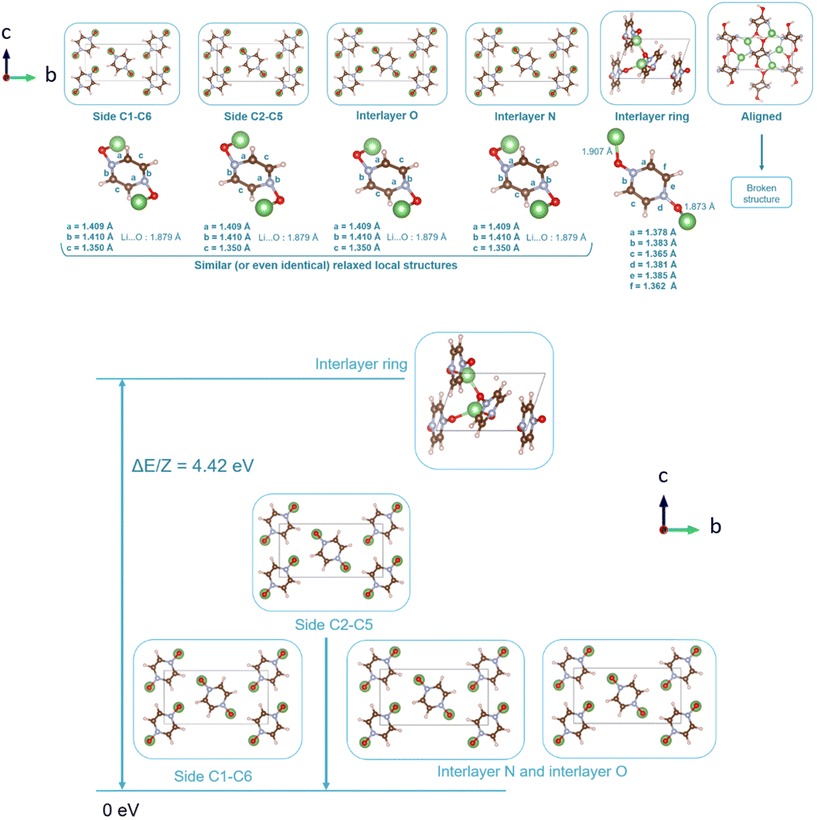
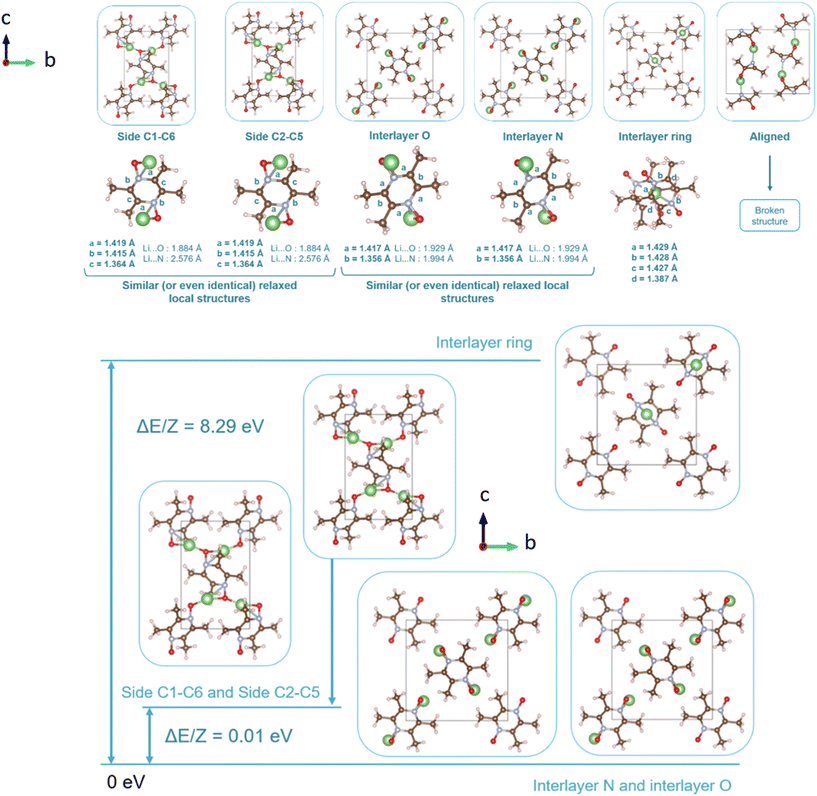
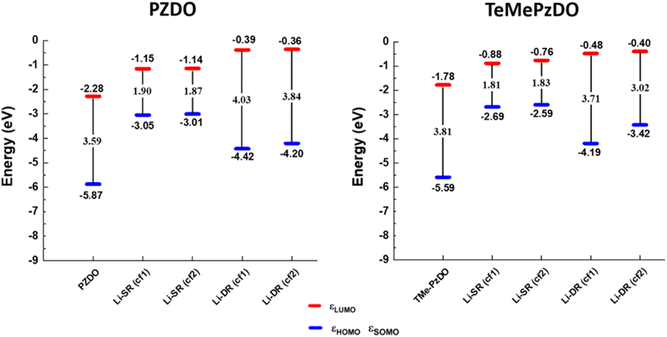
Following the benchmark investigations for both PZDO and TeMePzDO, the study of lithiation was undertaken. The methodologies having well described these two latter crystals (i.e., corr-PBE-D*_0.52 and corr-PBE-D*_0.62, respectively) are supposed to provide sufficient degree of reliability also for the lithiated phases. Despite their additional ionic bonding nature, no other treatment can be selected a priori. Therefore, by using these selected treatments, several models of initial positioning for lithium in these structures (labelled A, B, C, D, E and F and presented in Fig. 11) were relaxed. They can be classified as follows with respect to the carbonyl group positioning: (i) ‘aligned’ (A), (ii) ‘side C1–C6’ (B), and (iii) ‘side C2–C5’ (C), or as belonging to other types: (iv) ‘interlayer O’ (D), (v) ‘interlayer N’ (E), and (vi) ‘interlayer ring’ (F). The resultant most stable crystal phases obtained after geometry optimizations for PZDO and TeMePzDO are presented in Fig. 12, while further details for all models are gathered in Fig. 13 and 14.
 | ||
| Fig. 12 Representation of the crystalline phases before (left) and after (right) relaxation for PZDO (top) and TeMePzDO (bottom) (a few relevant bond lengths are reported). | ||
As can be identified from both structural and energetical aspects in Fig. 13, the relaxation of models B, C, D and E for PZDO leads to almost the same most stable lithiated crystal structure. The one originating from the geometry optimization of the interlayer N positioning, labelled as model E, is the most stable one and exhibits the following changes relative to the corresponding delithiated phase (i.e. the difference between the calculated parameters after and before intercalation divided by the parameter of the delithiated phase): Δa/a = +1.34%; Δb/b = +9.10%; Δc/c = +13.82%; Δβ/β = +11.24%; ΔV/V = +20.43%; Δd/d = −3.01%.
Regarding the same kind of results gathered for the TeMePzDO phase in Fig. 14, the model E is also the one resulting in the most stable crystal structure, although models B, C and D are very close to it. This most stable relaxed lithiated TeMePzDO crystal presents the following structural modifications (relative to the delithiated one): Δa/a = −2.26%; Δb/b = +6.35%; Δc/c = +4.13%; Δβ/β = +1.84%; ΔV/V = +7.61%; Δd/d = −2.17%. This implies that the relative volume expansion resulting from lithiation, ΔV/V, is much lower for TeMePzDO compared to PZDO. It can be noticed that the F model represents, for both systems, a specific case since the number of lithium atoms per unit formula is half that of other cases (2 vs. 4) and it thus accounts for another state of the electrochemical process. As such, model F cannot be directly compared with the other investigated models. Upon lithiation a distortion of the molecular geometry can be noticed for both PZDO and TeMePzDO. The molecules in the lithiated phases are no longer flat because the oxygen atoms now point towards the front or back of the plane, and the N–O distance takes about +0.2 Å compared to the relaxed delithiated crystal structure. By considering the Single Point Energy (SPE) calculations performed after geometry optimizations using the corr-PBE-D*_0.52 and corr-PBE-D*_0.62 methodologies, the calculated intercalation potential is, respectively, equal to 1.39 V and to 1.32 V vs. Li+/Li for PZDO and TeMePzDO crystalline phases, respectively. These trends appear to be in line with the order of magnitude previously estimated from molecular DFT calculations. The decrease of the intercalation potential from the PZDO phase to its methylated counterpart is, however, smaller than at the molecular level.
Additional studies at the molecular DFT level on molecules or molecular complexes extracted from the relaxed lithiated and delithiated crystalline phases of PZDO and TeMePzDO were performed to measure the geometry effect due to packing on the interatomic distances, delocalization indices, electrostatic interactions, Laplacian distribution, etc. These studies allow for assessing the degree of predictability of molecular DFT calculations with respect to periodical ones, the latter having a great advantage to involve actual materials characterized by specific stacking motifs leading to intermolecular interactions not available in the molecular case. The onset of intermolecular interactions then has an effect also on the intramolecular ones.
The bond lengths of the ring for the PZDO anion within the crystalline phase of the intercalated matrix (i.e. double reduction) are nearer to those of the DR conformation cf1 (Fig. SI3†). The loss of aromaticity is highlighted by the presence of two shortened double bonds (c and f, of bond length equal to 1.35 Å) and four other single ones (a, b, d and e, with a bond length of 1.41 Å). The N–O bond length significantly increases in the crystal (1.490 Å) relative to the molecular cf1 case (1.434 Å) and a similar behaviour is found for the Li–O interaction (with bond lengths equal to 1.750 Å/1.885 Å for molecular conformation (cf1)/crystalline geometries, respectively). As expected, trends of Δbond length or ΔDI are fully consistent in terms of signs with the loss of initial aromaticity of the ring. Compared to the molecular features, Δxint/fin values concerning the bond lengths of the intercalated crystal (Fig. SI4†) are roughly diminished by −0.012 to −0.022 Å. Accordingly, ΔDI also exhibits a differentiation between the two cases with a logic increase trend, which appears, however, to be less homogeneous, being much larger for a, b, d and e than for c and f (therefore enhancing a differentiation effect that may be noticed already by examining the Δbond lengths). When focusing on the TeMePzDO compound (Fig. SI3†), while the ring bond lengths of the crystalline intercalated phase are marginally nearer those characterizing the conformation cf2, the orientation of Li+ ion is very similar to the one characterizing the molecular conformation cf1. Similarly to the situation of intercalated PZDO, the presence of two double bonds is clearly evidenced, thanks to the differentiation between a, b, d and e (1.417 Å) on the one hand and c and f (1.356 Å) on the other hand. As for PZDO, the N–O/Li–O bond lengths of the intercalated TeMePzDO crystal phase are both largely increased (1.487 Å/1.929 Å) relative to the molecular doubly reduced molecular conformation cf1 (1.439 Å/1.740 Å) or cf2 (1.417 Å/1.720 Å). Δbond length for the intercalated phase of TeMePzDO is even lower for a, b, d and e bonds than in the case of PZDO and the bond length decrease for the c and f bonds is also less relevant. On the other hand, the ΔDI values describing intercalated TeMePzDO are very close to those of the molecular counterpart.
Otherwise, it is possible to estimate the point-charge electrostatic interaction energy between Li+ and O− inview of establishing a comparison between molecular and periodic calculations. This latter is almost identical for the two conformations of anions in the case of molecular doubly reduced PZDO species, whereas a distinction exists between conformations cf1 and cf2 (for the complex anion-Li+)2 in the case of DR TeMePzDO (Fig. SI5†). The value of electrostatic attraction for the conformation cf1 in the case of the molecular DR state of the TeMePzDO compound is in fact almost identical to the one characterizing the DR state of PZDO in either conformation cf1 or cf2, while a slightly higher stabilization occurs through attraction in the case of the DR conformation cf2 of the methylated compound comparatively to the three other cases (i.e. DR cf1/cf2 of PZDO and DR cf1 of TeMePzDO).
For the intercalated crystals, the comparison of the same kind of pair electrostatic interactions at the DR state leads to the observation of a reversed trend since the Li+–O− attraction is stronger in the case of PZDO,compared to the functionalized counterpart. The observed trend is consistent with the observation of a shorter Li+–O− interatomic distance for PZDO (1.885 Å) compared to that in TeMePzDO (1.929 Å). Furthermore, the Li+–O− distances for crystal phases are globally larger (thus explaining the associated lower attraction) compared to the corresponding ones for molecular complexes (lying in between 1.72 and 1.74 Å). This means that an overestimation seems to occur in this aspect when focusing on molecular species, if one wish to anticipate the trends of crystalline phases. These crude estimations based on a local point charge model are solely intended to provide a rough assessment of the bias of using molecular approaches to predict solid state behaviours. Clearly, besides the change of distance for the Li+–O− interaction, many other electrostatic intermolecular interactions, polarization effects, etc. become available and possibly relevant in the case of the solid. This surely changes the deal globally and the incidence of such effects on electrochemical features (involving both lithiated and delithiated phases) could be more thoroughly and more precisely scrutinized. Estimating crystal lattice energies11 could otherwise provide some actual clues for obtaining a rationalization of the intercalation potential trends in crystalline phases and it could be envisaged in forthcoming studies. Furthermore, it is difficult to appreciate such incidence in view of firmly generating a global trend, which could account for the distinction between molecular and crystalline features in a systematic manner. Therefore, a larger set of compounds should be examined before concluding that the molecular model overestimates the Li+–O− attraction.
Concerning the nitrogen VSCC Laplacian distribution, the analysis illustrated for the molecular case is confirmed for the molecules in the crystal. While the results for these two data sets are qualitatively the same, some interesting difference can be evidenced. In particular, the  values and the associated
values and the associated 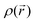 values at the
values at the 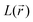 maxima are in general lowered relative to the molecular case. This is especially noticeable for the percentage and absolute value related to the nitrogen bonded maximum of the C–N bonds in the unreduced states and also for those of the N–O bonds, particularly in the DR states. While the general lowering of bonded and non bonded concentrations has been noticed previously,62 in line with the increased general sphericity of atoms induced by the crystal packing driven by intermolecular H-bond formation, the enhanced lowering of concentration for the above-mentioned bonds reflects their significant bond lengthening in the solid state relative to the molecular case.
maxima are in general lowered relative to the molecular case. This is especially noticeable for the percentage and absolute value related to the nitrogen bonded maximum of the C–N bonds in the unreduced states and also for those of the N–O bonds, particularly in the DR states. While the general lowering of bonded and non bonded concentrations has been noticed previously,62 in line with the increased general sphericity of atoms induced by the crystal packing driven by intermolecular H-bond formation, the enhanced lowering of concentration for the above-mentioned bonds reflects their significant bond lengthening in the solid state relative to the molecular case.
Conclusion
The ever-increasing demand for energy supply as well as the global climate change induces significant pressure on the worldwide research. Major shifts underway in energy storage are prone to be pursued and intensified during the next years and decades. While numerous papers reporting organic electrode materials for batteries have been published, so far, most of the studies have been focused on the positive electrode candidates. As a whole, much less investigations concern their negative counterparts, which nevertheless play a crucial role as well and deserve research activities to discover optimal systems. To this end, beyond modifying the already existing molecular architectures known as redox-active species through functionalization or other engineering aspects, the identification of new families with interesting electrochemical activity might be the prerequisite for developing performant electrodes of this type. With the objective of probing this main property along with the evaluation of the HOMO–LUMO gaps to get some clues on their electronic conductivity features, some compounds that have not been tested yet in the context of energy storage applications were thoroughly studied through computations. They belong to the heterocyclic N-oxide class of compounds, which were considered with interest from the therapeutic point of view or for their biological activities,63–65 which notably include the derivatives of quinoxaline 1,4-di-N-oxides and of phenazine N,N′-dioxides.66,67 More precisely, we selected the system PZDO, which has been envisaged not only as a potential precursor of functional materials or in the field of crystal engineering but also very recently, in its 2,5-methylated version, as an electrocatalytic system when associated with the presence of methanol in single-walled and multi-walled carbon nanotube (CNT) paper electrodes.68In the present investigation, we hypothesized that the main phenomenon related to the lithiation of PZDO shall correspond to the ring aromaticity loss upon two electron uptake, therefore enabling in principle to reach the low redox potential that is targeted for the purpose of constituting a negative electrode. Additionally, a further major aspect was provided by its complete functionalization thanks to +I (methyl) groups (TeMePzDO), supposed to magnify the redox potential lowering effect. For both compounds, molecular redox potentials as well as intercalation voltages were estimated, with the latter obtained by examining the crystalline delithiated crystals and by performing a relaxation of various lithiation models. Expected low molecular/crystalline redox/intercalation potentials were predicted for PZDO and even slightly lower for TeMePzDO. Therefore, the present study fully demonstrates the interest of selecting this kind of backbone for negative OEMs, with performances that are quite appealing compared to some existing systems. The predicted intercalation potential in the case of PZDO (∼1.4 V vs. Li+/Li) seems already lower than that of the well-known inorganic counterpart Li4Ti5O12 (LTO) characterized by 1.55 V vs. Li+/Li. It also appears as being noticeably lower than the one exhibited by the methyl-viologen, characterized by an average value of 1.9 V vs. Li+/Li; this compound being envisaged as negative electrode in anion rocking-chair and corresponding to a dication, prone to be doubly reduced thus forming neutral species, and classified as a p-type redox active material in link with the involvement of counter anions. In both comparisons, a further advantage clearly appears for PZDO related to its very high theoretical capacity. Switching to the fully methylated version of this entity slightly reduces this last feature but it allows for decreasing slightly the redox potential, which constitutes an advantage for a negative electrode. Its possible risks for such electrochemical application might also be lower than those recently observed for PZDO, therefore increasing its chances to be actually used for this purpose. Furthermore, volume expansion observed during the intercalation process seems to be much lower in the case of TeMePzDO, therefore giving the hope of easier cyclability for a material that will also be less risky for energy applications than PZDO. Otherwise, functionalization with electron-donating groups leads to an increase in the energy levels of the frontier orbitals of the molecular entity (TeMePzDO vs. PZDO). Upper/lower HOMO/LUMO levels are observed for reduced species of TeMePzDO for both singly/doubly reduced states compared to the unsubstituted complexes. Except for the single reduction case for which the observed value far below the threshold of 3 eV is clearly of relevance from the viewpoint of electronic conductivity, the band gaps (both at initial or doubly reduced states) are not likewise favourable, with values in between ∼3 and 4 eV. In the case of PZDO, the band gap concerning the double reduction is increased compared to the one characterizing the initial state, while the reverse phenomenon is observed for TeMePzDO, for which a decrease is instead observed. At the singly reduced state, the distinction between both compounds is marginal, with almost identical and low Eg values (all around 1.8 or 1.9 eV).
Apart from the direct information gained through DFT calculations providing access to both electrochemical and frontier orbital features, scrutinizing all aspects of the electronic structure was extremely instructive to confirm the various hypothesized mechanisms/substitution effects. From the fundamental viewpoint, the main ‘driving force’ for the genesis of an eventual new kind of negative electrode has been fully demonstrated by making use of bond lengths/delocalization indexes (DI) along with their changes occurring upon SR and DR. These interpretations were also assisted by Bader's electron spin population considerations in the case of the SR. The doubly charged aromatic structure was evidenced as being the most reasonable mesomeric form. Its transformation occurring upon electron uptake, accompanied by Li+ chelation effects of the reduced species, was also finely examined. Notably, the phenomenon of aromaticity loss in the DR state was highlighted through structural considerations (e.g. shortening/lengthening of C–C/C–N bond lengths) and further evidenced by examining the DI evolution, which proves the presence, at the DR state, of two non-conjugated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds. Furthermore, the concomitant occurrence at the DR state of a lone pair on each nitrogen atom has been clearly noticed thanks to the analysis of
C bonds. Furthermore, the concomitant occurrence at the DR state of a lone pair on each nitrogen atom has been clearly noticed thanks to the analysis of 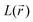 topology features. Beyond the fundamental knowledge aspects already gained in this work, the methylated versions of PZDO could give rise to some promise of novelty in the field of energy storage.
topology features. Beyond the fundamental knowledge aspects already gained in this work, the methylated versions of PZDO could give rise to some promise of novelty in the field of energy storage.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. L., C. F., and Y. D. acknowledge granted access to the HPC resources of IDRIS made by GENCI. Computations were also performed using the facilities and computing time of the supercomputer center MCIA of the University of Bordeaux and Pays de l'Adour and the supercomputer center CRIANN from the University of Rouen. This project has received funding from both the French Environment and Energy Management Agency (ADEME) and the European Regional Development Fund (ERDF) from the European Union, through a Ph.D. thesis research grant, which is gratefully acknowledged by F. L., C. F., and A. A. F. A. A. F. acknowledges the Institut Universitaire de France for the support.References
- H. Lyu, X.-G. Sun and S. Dai, Organic Cathode Materials for Lithium-Ion Batteries: Past, Present, and Future, Adv. Energy Sustainability Res., 2021, 2(1), 2000044 CrossRef CAS.
- J. Cao, J. Tian, J. Xu and Y. Wang, Organic Flow Batteries: Recent Progress and Perspectives, Energy Fuels, 2020, 34(11), 13384–13411 CrossRef CAS.
- Z. Li and Y.-C. Lu, Redox Flow Batteries: Want More Electrons? Go Organic!, Chem, 2018, 4(9), 2020–2021 CAS.
- Y. Peng, J. Xu, J. Xu, J. Ma, Y. Bai, S. Cao, S. Zhang and H. Pang, Metal-Organic Framework (MOF) Composites as Promising Materials for Energy Storage Applications, Adv. Colloid Interface Sci., 2022, 307, 102732 CrossRef CAS PubMed.
- M. Shen and H. Ma, Metal-Organic Frameworks (MOFs) and Their Derivative as Electrode Materials for Lithium-Ion Batteries, Coord. Chem. Rev., 2022, 470, 214715 CrossRef CAS.
- J. Kim, Y. Kim, J. Yoo, G. Kwon, Y. Ko and K. Kang, Organic Batteries for a Greener Rechargeable World, Nat. Rev. Mater., 2023, 8(1), 54–70 CrossRef.
- X. Liu, C.-F. Liu, S. Xu, T. Cheng, S. Wang, W.-Y. Lai and W. Huang, Porous Organic Polymers for High-Performance Supercapacitors, Chem. Soc. Rev., 2022, 51(8), 3181–3225 RSC.
- H. Zhang, Y. Gao, X.-H. Liu, Z. Yang, X.-X. He, L. Li, Y. Qiao, W.-H. Chen, R.-H. Zeng, Y. Wang and S.-L. Chou, Organic Cathode Materials for Sodium-Ion Batteries: From Fundamental Research to Potential Commercial Application, Adv. Funct. Mater., 2022, 32(4), 2107718 CrossRef CAS.
- Y. Lu and J. Chen, Prospects of Organic Electrode Materials for Practical Lithium Batteries, Nat. Rev. Chem., 2020, 4(3), 127–142 CrossRef CAS PubMed.
- P. Poizot, J. Gaubicher, S. Renault, L. Dubois, Y. Liang and Y. Yao, Opportunities and Challenges for Organic Electrodes in Electrochemical Energy Storage, Chem. Rev., 2020, 120(14), 6490–6557 CrossRef CAS PubMed.
- G. Bonnard, A.-L. Barrès, Y. Danten, D. G. Allis, O. Mentré, D. Tomerini, C. Gatti, E. I. Izgorodina, P. Poizot and C. Frayret, Experimental and Theoretical Studies of Tetramethoxy-p-Benzoquinone: Infrared Spectra, Structural and Lithium Insertion Properties, RSC Adv., 2013, 3(41), 19081–19096 RSC.
- M. T. Huynh, C. W. Anson, A. C. Cavell, S. S. Stahl and S. Hammes-Schiffer, Quinone 1e− and 2e−/2H+ Reduction Potentials: Identification and Analysis of Deviations from Systematic Scaling Relationships, J. Am. Chem. Soc., 2016, 138(49), 15903–15910 CrossRef CAS PubMed.
- D. Tomerini, C. Gatti and C. Frayret, Engineering of Unsubstituted Quinoid-like Frameworks Enabling 2 V vs. Li+/Li Redox Voltage Tunability and Related Derivatives, Phys. Chem. Chem. Phys., 2015, 17(14), 8604–8608 RSC.
- A. Khetan, High-Throughput Virtual Screening of Quinones for Aqueous Redox Flow Batteries: Status and Perspectives, Batteries, 2023, 9(1), 24 CrossRef CAS.
- S. Schwan, D. Schröder, H. A. Wegner, J. Janek and D. Mollenhauer, Substituent Pattern Effects on the Redox Potentials of Quinone-Based Active Materials for Aqueous Redox Flow Batteries, ChemSusChem, 2020, 13(20), 5480–5488 CrossRef CAS PubMed.
- N. Nagamura, R. Taniki, Y. Kitada, A. Masuda, H. Kobayashi, N. Oka and I. Honma, Electronic States of Quinones for Organic Energy Devices: The Effect of Molecular Structure on Electrochemical Characteristics, ACS Appl. Energy Mater., 2018, 1(7), 3084–3092 CrossRef CAS.
- L. Miao, L. Liu, Z. Shang, Y. Li, Y. Lu, F. Cheng and J. Chen, The Structure–Electrochemical Property Relationship of Quinone Electrodes for Lithium-Ion Batteries, Phys. Chem. Chem. Phys., 2018, 20(19), 13478–13484 RSC.
- A. E. Lakraychi, F. Dolhem, F. Djedaïni-Pilard, A. Thiam, C. Frayret and M. Becuwe, Decreasing Redox Voltage of Terephthalate-Based Electrode Material for Li-Ion Battery Using Substituent Effect, J. Power Sources, 2017, 359, 198–204 CrossRef CAS.
- R. P. Carvalho, C. F. N. Marchiori, D. Brandell and C. M. Araujo, Artificial Intelligence Driven In-Silico Discovery of Novel Organic Lithium-Ion Battery Cathodes, Energy Storage Mater., 2022, 44, 313–325 CrossRef.
- L. Niu, T. Wu, M. Chen, L. Yang, J. Yang, Z. Wang, A. A. Kornyshev, H. Jiang, S. Bi and G. Feng, Conductive Metal–Organic Frameworks for Supercapacitors, Adv. Mater., 2022, 34(52), 2200999 CrossRef CAS PubMed.
- F. Lambert, Y. Danten, C. Gatti and C. Frayret, A Tool for Deciphering the Redox Potential Ranking of Organic Compounds: A Case Study of Biomass-Extracted Quinones for Sustainable Energy, Phys. Chem. Chem. Phys., 2020, 22(36), 20212–20226 RSC.
- F. Lambert, Y. Danten, C. Gatti, B. Bocquet, A. A. Franco and C. Frayret, Carbonyl-Based Redox-Active Compounds as Organic Electrodes for Batteries: Escape from Middle–High Redox Potentials and Further Improvement?, J. Phys. Chem. A, 2023, 127(24), 5104–5119 CrossRef CAS PubMed.
- R. Shi, S. Jiao, Q. Yue, G. Gu, K. Zhang and Y. Zhao, Challenges and Advances of Organic Electrode Materials for Sustainable Secondary Batteries, Exploration, 2022, 2(4), 0220066 CrossRef PubMed.
- J. Hu, Y. Hong, M. Guo, Y. Hu, W. Tang, S. Xu, S. Jia, B. Wei, S. Liu, C. Fan and Q. Zhang, Emerging Organic Electrodes for Na-Ion and K-Ion Batteries, Energy Storage Mater., 2023, 56, 267–299 CrossRef.
- J. Wang, P. Apostol, D. Rambabu, X. Guo, X. Liu, K. Robeyns, M. Du, Y. Zhang, S. Pal, R. Markowski, F. Lucaccioni, A. E. Lakraychi, C. Morari, J.-F. Gohy, D. Gupta and A. Vlad, Revealing the Reversible Solid-State Electrochemistry of Lithium-Containing Conjugated Oximates for Organic Batteries, Sci. Adv., 2023, 9(17), eadg6079 CrossRef CAS PubMed.
- R. Russo, C. Davoisne, A. Urrutia, Y. Danten, C. Gatti, G. Toussaint, P. Stevens, C. Frayret and M. Becuwe, Impact of the Microstructure on Electrochemical Performances of Dilithium Benzoquinone Dioximate as a Positive Material for a Li-Ion Battery, ACS Appl. Polym. Mater., 2023, 5(12), 9865–9875 CrossRef CAS.
- C. Frayret, D. Tomerini, C. Gatti, Y. Danten, M. Becuwe, F. Dolhem and P. Poizot, Relating Electrochemistry of New Organic Materials for Batteries and Fundamental Understanding through DFT Calculations, Adv. Sci. Technol., 2014, 93, 146–151 Search PubMed.
- C. Näther, P. Kowallik and I. Jeß, Pyrazine N,N′-Dioxide, Acta Crystallogr., 2002, E58(11), o1253–o1254 Search PubMed.
- M. D. M. C. Ribeiro da Silva, M. A. A. Vieira, C. Givens, S. Keown and W. E. Acree, Experimental Thermochemical Study of Two Polymethylpyrazine N,N′-Dioxide Derivatives, Thermochim. Acta, 2006, 450(1), 67–70 CrossRef CAS.
- H.-L. Sun, Z.-M. Wang and S. Gao, Synthesis, Crystal Structures, and, Magnetism of Cobalt Coordination Polymers Based on Dicyanamide and Pyrazine-Dioxide Derivatives, Inorg. Chem., 2005, 44(7), 2169–2176 CrossRef CAS PubMed.
- H.-L. Sun, S. Gao, B.-Q. Ma, G. Su and S. R. Batten, Structures and Magnetism of a Series Mn(II) Coordination Polymers Containing Pyrazine-Dioxide Derivatives and Different Anions, Cryst. Growth Des., 2005, 5(1), 269–277 CrossRef CAS.
- J.-M. Shi, X. Zhang, H.-Y. Xu, C.-J. Wu and L.-D. Liu, Synthesis, Crystal Structures and Fluorescence of Cadmium(II) Coordination Polymers with Derivatives of Pyrazine-1,4-Dioxide and Thiocyanate as Mixed-Bridging Ligands, J. Coord. Chem., 2007, 60(6), 647–654 CrossRef CAS.
- R. Podgajny, D. Pinkowicz, B. Czarnecki, M. Kozieł, S. Chorąży, M. Wis, W. Nitek, M. Rams and B. Sieklucka, Role of Pyrazine-N,N′-Dioxide in [W(CN)8]N−-Based Hybrid Networks: Anion–π Interactions, Cryst. Growth Des., 2014, 14(8), 4030–4040 CrossRef CAS.
- C. B. Aakeröy, T. K. Wijethunga and J. Desper, Crystal Engineering of Energetic Materials: Co-Crystals of Ethylenedinitramine (EDNA) with Modified Performance and Improved Chemical Stability, Chem. – Eur. J., 2015, 21(31), 11029–11037 CrossRef PubMed.
- M. K. Bellas and A. J. Matzger, Achieving Balanced Energetics through Cocrystallization, Angew. Chem., Int. Ed., 2019, 58(48), 17185–17188 CrossRef CAS PubMed.
- K. A. Monogarov, I. N. Melnikov, I. A. Vatsadze, I. L. Dalinger, I. V. Ananyev and N. V. Muravyev, Pyrazine 1,4-Dioxide Is a Prolific Cocrystal Former and Energetic Material Itself, Cryst. Growth Des., 2024, 24(2), 741–746 CrossRef CAS.
- C. N. Gannett, L. Melecio-Zambrano, M. J. Theibault, B. M. Peterson, B. P. Fors and H. D. Abruña, Organic Electrode Materials for Fast-Rate, High-Power Battery Applications, Mater. Rep.: Energy, 2021, 1(1), 100008 CAS.
- Y. Liang and Y. Yao, Positioning Organic Electrode Materials in the Battery Landscape, Joule, 2018, 2(9), 1690–1706 CrossRef CAS.
- C. B. Aakeröy, T. K. Wijethunga, J. Benton and J. Desper, Stabilizing volatile liquid chemicals using co-crystallization, Chem. Commun., 2015, 51, 2425–2428 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.01, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396 CrossRef CAS PubMed.
- D. Tomerini, C. Gatti and C. Frayret, Playing with Isomerism and N Substitution in Pentalenedione Derivatives for Organic Electrode Batteries: How High Are the Stakes?, Phys. Chem. Chem. Phys., 2016, 18(4), 2442–2448 RSC.
- D. Tomerini, O. Politano, C. Gatti and C. Frayret, Electronic Structure and Energy Decomposition Analyses as a Tool to Interpret the Redox Potential Ranking of Naphtho-, Biphenyl- and Biphenylene-Quinone Isomers, Phys. Chem. Chem. Phys., 2016, 18(38), 26651–26660 RSC.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Calendron Press, Oxford, 1994 Search PubMed.
- C. Gatti, SF-ESI Code, Private Communication.
- X. Fradera, M. A. Austen and R. F. W. Bader, The Lewis Model and Beyond, J. Phys. Chem. A, 1999, 103(2), 304–314 CrossRef CAS.
- J. Heyd and G. E. Scuseria, Efficient Hybrid Density Functional Calculations in Solids: Assessment of the Heyd–Scuseria–Ernzerhof Screened Coulomb Hybrid Functional, J. Chem. Phys., 2004, 121(3), 1187–1192 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186 CrossRef CAS PubMed.
- S. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27(15), 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Erhlich and K. Helge, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100(13), 136406 CrossRef PubMed.
- B. Civalleri, C. M. Zicovich-Wilson, L. Valenzano and P. Ugliengo, B3LYP Augmented with an Empirical Dispersion Term (B3LYP-D*) as Applied to Molecular Crystals, CrystEngComm, 2008, 10(4), 405–410 RSC.
- P. Ugliengo, C. M. Zicovich-Wilson, S. Tosoni and B. Civalleri, Role of Dispersive Interactions in Layered Materials: A Periodic B3LYP and B3LYP-D* Study of Mg(OH)2, Ca(OH)2 and Kaolinite, J. Mater. Chem., 2009, 19(17), 2564–2572 RSC.
- L. Maschio, B. Civalleri, P. Ugliengo and A. Gavezzotti, Intermolecular Interaction Energies in Molecular Crystals: Comparison and Agreement of Localized Møller–Plesset 2, Dispersion-Corrected Density Functional, and Classical Empirical Two-Body Calculations, J. Phys. Chem. A, 2011, 115(41), 11179–11186 CrossRef CAS PubMed.
- M. D. King, W. D. Buchanan and T. M. Korter, Application of London-Type Dispersion Corrections to the Solid-State Density Functional Theory Simulation of the Terahertz Spectra of Crystalline Pharmaceuticals, Phys. Chem. Chem. Phys., 2011, 13(10), 4250–4259 RSC.
- G. Bonnard, A.-L. Barrès, O. Mentré, D. G. Allis, C. Gatti, P. Poizot and C. Frayret, The Low/Room-Temperature Forms of the Lithiated Salt of 3,6-Dihydroxy-2,5-Dimethoxy-p-Benzoquinone: A Combined Experimental and Dispersion-Corrected Density Functional Study, CrystEngComm, 2013, 15(15), 2809–2821 RSC.
- C. Frayret, E. I. Izgorodina, D. R. MacFarlane, A. Villesuzanne, A.-L. Barrès, O. Politano, D. Rebeix and P. Poizot, Electrochemical Properties of Crystallized Dilithium Squarate: Insight from Dispersion-Corrected Density Functional Theory, Phys. Chem. Chem. Phys., 2012, 14(32), 11398–11412 RSC.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188–5192 CrossRef.
- C. Frayret, A. Villesuzanne, N. Spaldin, E. Bousquet, J.-N. Chotard, N. Recham and J.-M. Tarascon, LiMSO4F (M = Fe, Co and Ni): Promising New Positive Electrode Materials through the DFT Microscope, Phys. Chem. Chem. Phys., 2010, 12(47), 15512–15522 RSC.
- C. Gatti, V. R. Saunders and C. Roetti, Crystal field effects on the topological properties of the electron density in molecular crystals: The case of urea, J. Chem. Phys., 1994, 101(12), 10686–10696 CrossRef CAS.
- A. M. Mfuh and O. V. Larionov, Heterocyclic N-Oxides – An Emerging Class of Therapeutic Agents, Curr. Med. Chem., 2015, 22(24), 2819–2857 CrossRef CAS PubMed.
- C. Bonifacino, G. Rodríguez, A. Pérez-Ruchel, J. L. Repetto, H. Cerecetto, C. Cajarville and M. González, Identification of N-Oxide-Containing Aromatic Heterocycles as Pharmacophores for Rumen Fermentation Modifiers, Metabolites, 2019, 9(4), 62 CrossRef CAS PubMed.
- C. Guo, H. Wang, V. M. Lynch, X. Ji, Z. A. Page and J. L. Sessler, Molecular Recognition of Pyrazine N,N′-Dioxide Using Aryl Extended Calix[4]Pyrroles, Chem. Sci., 2020, 11(22), 5650–5657 RSC.
- M. L. Lavaggi, G. Aguirre, L. Boiani, L. Orelli, B. García, H. Cerecetto and M. González, Pyrimido[1,2-a]Quinoxaline 6-Oxide and Phenazine 5,10-Dioxide Derivatives and Related Compounds as Growth Inhibitors of Trypanosoma Cruzi, Eur. J. Med. Chem., 2008, 43(8), 1737–1741 CrossRef CAS PubMed.
- D. Benitez, M. Cabrera, P. Hernández, L. Boiani, M. L. Lavaggi, R. Di Maio, G. Yaluff, E. Serna, S. Torres, M. E. Ferreira, N. Vera de Bilbao, E. Torres, S. Pérez-Silanes, B. Solano, E. Moreno, I. Aldana, A. López de Ceráin, H. Cerecetto, M. González and A. Monge, 3-Trifluoromethylquinoxaline N,N′-Dioxides as Anti-Trypanosomatid Agents. Identification of Optimal Anti-T. Cruzi Agents and Mechanism of Action Studies, J. Med. Chem., 2011, 54(10), 3624–3636 CrossRef CAS PubMed.
- S. I. Kulakovskaya, A. V. Kulikov, T. S. Zyubina, A. S. Zyubin, L. N. Sviridova, E. V. Stenina, A. G. Ryabenko, E. V. Zolotukhina and Y. A. Dobrovolskiy, Energy Adv., 2022, 1, 45–54 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt01144a |
| This journal is © The Royal Society of Chemistry 2024 |