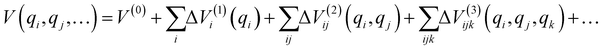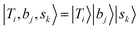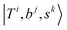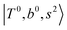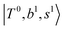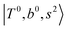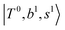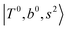Near-infrared spectroscopy of H₃O⁺⋯X_n (X = Ar, N₂, and CO, n = 1–3)

Abstract

Near-infrared (NIR) spectra of H₃O⁺⋯X_n (X = Ar, N₂, and CO, n = 1–3) in the first overtone region of OH-stretching vibrations (4800–7000 cm⁻¹) were measured. Not only OH-stretching overtones but also several combination bands are major features in this region, and assignments of these observed bands are not obvious at a glance. High-precision anharmonic vibrational simulations based on the discrete variable representation approach were performed. The simulated spectra show good agreement with the observed ones and provide firm assignments of the observed bands, except in the case of X = CO, in which higher order vibrational mode couplings seem significant. This agreement demonstrates that the present system can be a benchmark for high precision anharmonic vibrational computations of NIR spectra. Band broadening in the observed spectra becomes remarkable with an increase of the interaction with the solvent molecule (X). The origin of the band broadening is explored by rare gas tagging experiments and anharmonic vibrational simulations of hot bands.

---

Introduction

Overtone and combination bands in the near-infrared (NIR) region are attributed to the anharmonicity of molecular vibrations. NIR spectroscopy is expected to provide rich information on anharmonicity/mode coupling and vibrational dynamics of high vibrational energy levels. A number of studies on NIR spectroscopy have been accumulated so far, including analytical applications.^1–6 Theoretical modeling of vibrational overtone spectra, particularly using the local mode approach, has been conducted since the 1980s.^7–10 High-precision anharmonic vibrational calculations are requested to exactly interpret observed NIR spectra. Such calculations have been challenging in theoretical chemistry. For the fundamental (or mid-infrared, MIR) region of isolated molecules and clusters in the gas phase, however, the recent development of ab initio anharmonic vibrational computation approaches enables us to quantitatively reproduce spectral features due to anharmonic vibrational couplings.^11–23 On the other hand, for the NIR region, the number of experimental reports in the gas phase has been much less than that in the fundamental region.^24–27 This shortage is especially remarkable for gas phase clusters, in spite of the importance of cluster studies to explore the impact of intermolecular bonds such as hydrogen bonds (H-bonds).^25–27 Because gas phase spectra can be directly compared with ab initio/density functional theory (DFT) computations, benchmark data of gas phase clusters are important not only to evaluate the reliability of anharmonic vibrational approaches to the NIR region but also to elucidate the influence of intermolecular bonds on vibrational anharmonicity. Most of the bands observed in the NIR region are attributed to vibrations of X–H groups (X = O, N, and C).⁴ Therefore, the impact of H-bonds on NIR spectra is of special interest because H-bonds are formed with these functional groups.

Micro-solvated protonated water (hydronium ion), H₃O⁺⋯X_n, is the simplest model system of proton solvation. Moreover, H₃O⁺⋯X_n has also been one of the benchmark systems for the recent development of anharmonic vibrational calculation approaches.^{15–17,28,29} Though H₃O⁺⋯X_n is a simple system, its OH-stretching frequencies and mode couplings show a variety of changes by tuning H-bond strength by changing the solvent species (X) and coordination numbers (n).^17,28–31 Therefore, H₃O⁺⋯X_n has been a model case of collaboration between size-selective infrared spectroscopic experiments and anharmonic vibrational computation theories.

In the fundamental region of H₃O⁺⋯X₃ (X = Ar, CH₄, N₂, and H₂O), the association band (band around ∼2000 cm⁻¹) has been studied by McCoy et al.²⁸ This band cannot be recovered at the harmonic level and is assigned to a combination band (CB) involving the HOH-bending and frustrated rotation of H₃O⁺. Moreover, in the OH-stretching fundamental region, many infrared studies^{15,17,28–30} have demonstrated that Fermi resonance (FR, coupling between OH-stretching and overtone of OH-bending) of H₃O⁺ is sensitive to its H-bond circumstances, i.e., solvent species (proton acceptors) and the number of solvents (H-bond coordination number). Various anharmonic vibrational approaches have been applied to FR of H₃O⁺⋯X_n. CBs of OH-stretching and OH⋯N₂ intermolecular stretching have also been reported for H₃O⁺⋯(N₂)_n by Bandyopadhyay et al.³¹ The complicated interplay between FR and CB has been systematically analyzed by the discrete variable representation (DVR) approach.²⁹

Spectroscopic studies on protonated water clusters in the NIR (OH-stretching overtone) region have been very scarce. Wu et al. have pioneered an NIR study on H⁺(H₂O)_n (n = 3–5),²⁵ but their observation was limited to the overtones of the free OH-stretching band, and support from ab initio anharmonic vibrational calculations was not available at that time. An extensive study on the NIR region has been reported by McDonald et al.²⁷ They performed a systematic study on H⁺(H₂O)_n⋯Ar (n = 1–4) and bare H⁺(H₂O)_4–8. The whole first overtone region of the OH-stretching vibrations was measured. CBs of OH-stretching and bending at ∼5000 cm⁻¹ and overtones of free OH-stretching at ∼7000 cm⁻¹ were the primary features in the observed spectra. In contrast with the OH stretch fundamental region, overtones of H-bonded OH-stretching bands are very weak or almost missing except for the spectrum of H₃O⁺⋯Ar. Similar suppression of overtones of H-bonded OH-stretching bands has also been frequently reported in NIR spectroscopy of protic molecules in the gas and condensed phases.^32–37 The observed spectra were analyzed by the second-order vibrational perturbation theory (VPT2) and local mode treatment of the OH-stretching vibrations. While key aspects of the spectra were captured by these theoretical approaches, understandable deficiencies were still seen in the spectral simulations.

The previous NIR spectroscopic study on H⁺(H₂O)_n⋯Ar and H⁺(H₂O)_4–8 by McDonald et al. demonstrates that the spectral features of the OH-stretching overtones largely change with the H-bond formation.²⁷ Fine tuning of H-bond strength can be easily performed in gas phase clusters. It enables us to explore details of changes of spectral features in the NIR region with the tuning of H-bond strength, which reflects changes of mode couplings along with the variation of the H-bond environment. In the present study, we tuned the H-bond strength in H₃O⁺⋯X_n by changing the solvent (H-bond accepting) species X from Ar to N₂ and CO and also by changing the number of solvent molecules (n = 1–3). Stepwise changes in the OH stretching overtone vibrational region were observed by size-selective NIR spectroscopy of the clusters. The latest DVR simulations were also performed for quantitative reproduction and vibrational analyses of the observed spectra.

Experimental

Vibrational spectra of H₃O⁺⋯X_n (n = 1–3) clusters, where the solvating species X are Ar, N₂, and CO, were measured in the NIR region (4800–7000 cm⁻¹). These spectra were recorded by predissociation (PD) spectroscopy using a mass spectrometer which is equipped with linearly aligned tandem quadrupole mass filters connected by an octopole ion guide. Details of the experimental apparatus have been described elsewhere,³⁸ and only a brief description is given here.

The clusters were produced by electroionization in a supersonic jet expansion of the water/carrier/solvent gas mixture. The carrier gas was He or Ar. A high-pressure valve (Even–Lavie valve) was used for the supersonic jet expansion to efficiently cool the clusters and suppress their spontaneous dissociation.³⁹ The cluster of interest was mass-selected by the first stage of the mass spectrometer. The selected cluster was introduced to the octopole ion guide and was irradiated by NIR light. All the ions were introduced to the second stage of the mass spectrometer and were mass-analyzed again. By monitoring the fragment ion while scanning the light frequency, an NIR spectrum of the mass-selected cluster was obtained. In X = Ar, the nAr-loss channel was monitored. In X = N₂, the N₂-loss channel was monitored for n = 1 and 2 (only for the ∼7000 cm⁻¹ region, the 2N₂-loss channel was monitored for n = 2), and the 2N₂-loss channel was monitored for n = 3. In X = CO, all the spectra were measured by monitoring the CO-loss channel. The NIR light source was the signal output of an IR-OPO/OPA (LaserVision) pumped by an Nd:YAG laser (Spectra Physics GCR230). A short pass filter (Spectrogon SP-1900 nm, which passes light shorter than 1900 nm) was set in the optical path to fully eliminate the idler output of the OPO/OPA system in the measurement of the region higher than 5300 cm⁻¹. This is to avoid the overlap of fundamental transitions due to the coaxial idler output of the OPO/OPA system, which cannot be fully eliminated by the original filter equipped in the OPO/OPA system.

The observed NIR spectra were very noisy because of the extremely weak photodissociation fragment ion intensity. To precisely evaluate band positions in the observed spectra, we applied numerical smoothing processes to the spectra, then we applied multipeak fitting to the smoothed spectra. These smoothed spectra were used only for peak position determination, but not for the spectra shown in this article; only simple averaging of multiple scans was applied in the presented spectra.

Theoretical computations

The structures of H₃O⁺⋯X_n, (X = Ar, N₂, and CO, n = 1–3) were optimized at the MP2/aug-cc-pVDZ level. Their Cartesian coordinates and calculated vibrational modes are listed in Tables S1 and S2, respectively, in ESI.† For each H₃O⁺⋯X_n species, we include 3 OH-stretching modes (which are denoted as s), 2 OH bending modes (b), and n OH⋯X intermolecular stretching modes (T). In the MIR region, the coupling between (s) and (b) is well-known as FR and the coupling between (s) and (T) gives rise to CBs, which have been investigated in many previous works.^{15–17,28–31}

The ab initio anharmonic algorithms we used here are based on the DVR method^40,41 in which the potential energy surface (PES) and dipole moment surface (DMS) are represented by a direct product of Gauss–Hermite (GH) quadrature along these selected normal modes. In an earlier work on the MIR spectra of these solvated hydronium cations, we used five grid points for (b) and (T), and 7 grid points for (s);²⁹ nevertheless, in the NIR region, we expected that the 4-quanta excited states should be involved in vibrational analysis, thus we need more grid points on these modes to maintain the accuracy for these states.

The total number of the above grid points exceeds 5 million; to reduce the necessary computational effort, we expanded the PES using the n-mode representation (nMR) scheme proposed by Carter et al.:⁴²

where V⁽⁰⁾ is the potential energy at the equilibrium point, ΔV_i⁽¹⁾ is the change in energy within a single normal mode q_i, ΔV⁽²⁾_ij is the couplings between two modes q_i and q_j, and so on. We truncated this nMR expansion up to 4MR. We believe ΔV_i⁽¹⁾ and ΔV⁽²⁾_ij terms are most essential, thus we calculated them at the CCSD/aug-cc-pVTZ level to reach decent accuracy of the peak positions. This computational level shows good performance in our previous work of the MIR part of the H₃O⁺⋯X_n system.¹⁷ In contrast, ΔV⁽³⁾_ijk and ΔV⁽⁴⁾_ijkl terms contributed less for low excited states while they correspond to a larger number of necessary grid points, so we evaluated them at the MP2/aug-cc-pVDZ level. All of the above electronic structure calculations were conducted using Gaussian 16.⁴³ The DMS was expanded in an analogous way.

If we expand the DVR Hamiltonian directly on these 5 million grid points, the DVR Hamiltonian will be significantly larger than the earlier work, and it is very difficult to diagonalize such a large Hamiltonian directly even using sparse matrix diagonalization techniques. Therefore, we transformed this Hamiltonian into its finite-basis representation (FBR),⁴⁰ which is easier to be truncated to a diagonalizable size. The basic idea of FBR is to express the basis wavefunctions 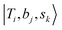as a direct product of eigenvectors of lower-dimensional DVR Hamiltonians Ĥ_T, Ĥ_b, and Ĥ_s:

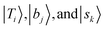where stand for the eigenstates for Ĥ_T, Ĥ_b, and Ĥ_s, respectively. In previous studies, we have utilized the FBR Hamiltonian to analyze inter-mode couplings, which only need a specific matrix element in the FBR Hamiltonian;^{16,17,29,44–47} for H₃O⁺⋯X₃, we have also shown that a truncation to 18 × 18 FBR Hamiltonian matrix still preserves most important spectral features in the MIR region.²⁹ In this work, we used a large amount of direct product wavefunctions as the basis to expand the FBR Hamiltonian, and then it was diagonalized to obtain the final eigenstate and the coupling between each basis functions using the Lanczos algorithm in SciPy.⁴⁸ We also assigned the spectra using the notation of FBR basis functions due to their close resemblance to the eigenstates. The FBR basis values which are the major contributors to the NIR region are listed in Table S3 (ESI†). Finally, we calculated the IR intensities based on the Fermi's golden rule using the eigenvectors and DMS.

Results and discussion

A. Overview of the NIR spectra of H₃O⁺⋯X_n

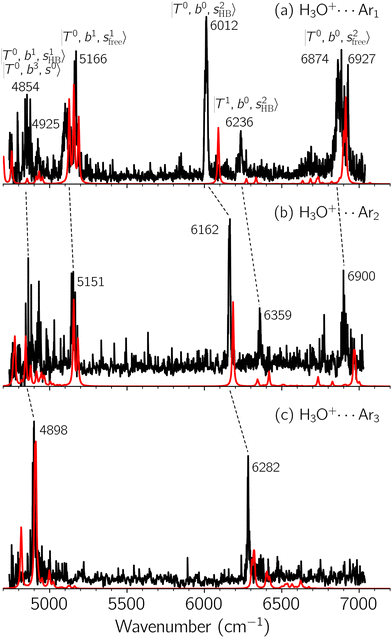
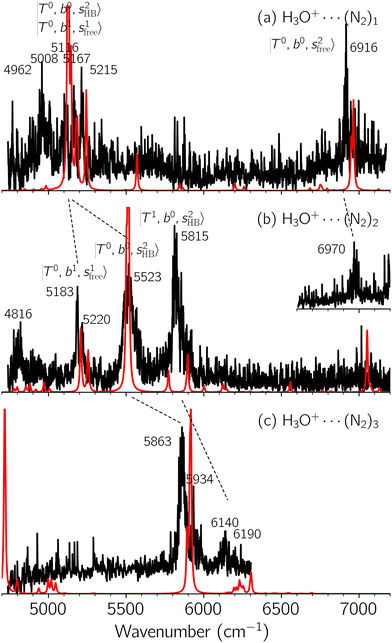
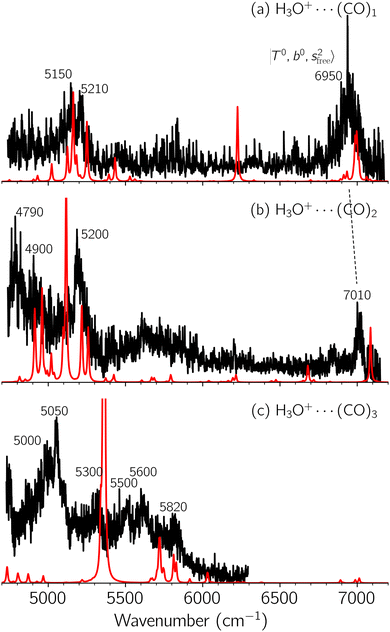
Black traces in Fig. 1–3 show the observed NIR spectra of H₃O⁺⋯X_n (n = 1–3), X = Ar, N₂, and CO, respectively, in the OH-stretching overtone region. An NIR spectrum of H₃O⁺⋯Ar in the same frequency region has been reported by McDonald et al.,²⁷ and the present spectrum well reproduces their first report. The other spectra in the present work are reported for the first time.

Fig. 1 Observed (black) and calculated (red) NIR spectra of H₃O⁺⋯Ar_n, (a) n = 1, (b) n = 2, and (c) n = 3, in the OH stretching overtone region. The observed spectra were acquired by monitoring the nAr-loss fragmentation channel, respectively. Band assignments are given by combinations of the three kinds of vibrational modes, OH⋯X intermolecular stretching (T), OH-bending (b), and OH-stretching (s). The notation denotes the upper vibrational state of the respective transition (see text for further details).

Fig. 2 Observed (black) and calculated (red) NIR spectra of H₃O⁺⋯(N₂)_n, (a) n = 1, (b) n = 2, and (c) n = 3, in the OH stretching overtone region. The N₂-loss fragmentation channel was monitored to record the observed spectra (a) and (b). Observed spectrum (c) and the inset spectrum (b) were obtained by monitoring the 2N₂-loss fragmentation channel.

Fig. 3 Observed (black) and calculated (red) NIR spectra of H₃O⁺⋯(CO)_n, (a) n = 1, (b) n = 2, and (c) n = 3, in the OH stretching overtone region. The CO-loss fragmentation channel was monitored to record all the observed spectra.

To improve the assignments and the understanding of the observed spectra, we performed an anharmonic vibrational analysis of these clusters. For comparison, the corresponding calculated spectra are also shown as red traces in the figures. Detailed assignments of the pronounced vibrational bands are listed in Table S4 in the ESI.†

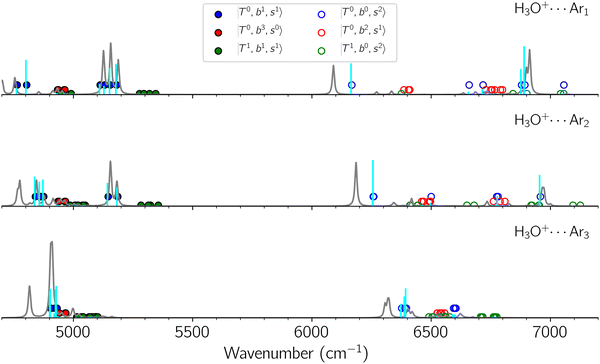
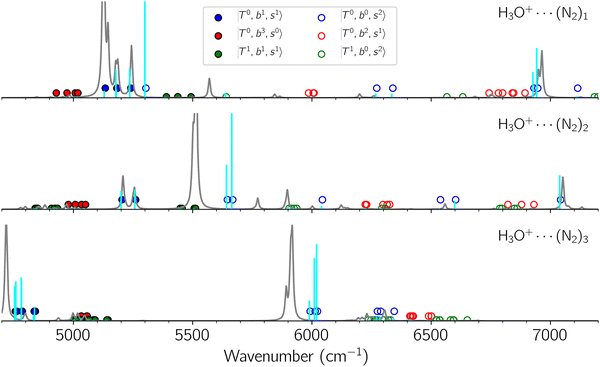
Due to the absence of fundamental transitions in the NIR spectra, it is highly non-trivial to assign the source of IR intensity, which should come from electrical anharmonicity, i.e., transition dipole beyond the linear dipole approximation; the other states may obtain IR intensity through mechanical anharmonicity, that is, intensity borrowing from the bright states through the coupling in PES. To find out the bright states in these regions, we removed the off-diagonal coupling in the FBR Hamiltonian, and the resulting spectra are shown in the cyan lines in Fig. 4–6; we then found out that “CB of 1-quantum OH-stretching and 1-quantum OH-bending”, 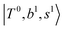, and “2-quanta overtone of OH-stretching”, 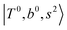, are the major bright states in these systems. Meanwhile, knowing the importance of the FR coupling and CB effect in the MIR region, we expect that the similar coupling structure will let 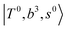and 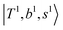borrow intensity from 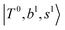, and 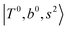may light-up 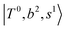and 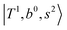if the energy difference is small enough; therefore, we also labeled the diagonal energy of these FBR basis in Fig. 4–6, which will help us understand the complicated features in the NIR spectra of these systems.

Fig. 4 Calculated spectra from FBR Hamiltonian with (grey line) and without off-diagonal coupling (cyan sticks) for H₃O⁺⋯Ar_n. The filled and empty circles represent the diagonal energies of bright states and , and the relevant states lighted up by them, respectively, which show the locations of these states without mechanical anharmonicity.

Fig. 5 Calculated spectra from the FBR Hamiltonian with (grey line) and without off-diagonal coupling (cyan sticks) for H₃O⁺⋯(N₂)_n. The filled and empty circles represent the diagonal energies of bright states and , and the relevant states lighted up by them, respectively, which show the locations of these states without mechanical anharmonicity.

Fig. 6 Calculated spectra from FBR Hamiltonian with (grey line) and without off-diagonal coupling (cyan sticks) for H₃O⁺⋯(CO)_n. The filled- and empty circles represent the diagonal energies of bright states and , and the relevant states lighted up by them, respectively, which show the locations of these states without mechanical anharmonicity.

B. Band assignments of the observed spectra

The spectra of H₃O⁺⋯Ar_n (n = 1–3) are shown in Fig. 1. Broadly speaking, 5 types of bands are seen in these spectra: (1) “CB of H-bonded OH-stretching and OH-bending”,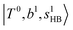 , and their FR counterpart, 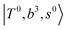, at around 4900 cm⁻¹. (2) Intense bands located in the region of 6000–6500 cm⁻¹, which are attributed to “overtones of H-bonded OH-stretching”, 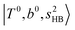. (3) Weaker bands appear at ∼+200 cm⁻¹ from 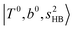in the spectra of n = 1 and 2, which are assigned to “CBs of overtones of H-bonded OH-stretching and one-quantum OH⋯X intermolecular stretching”, 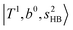. In the spectra of n = 1 and 2, there are two more bands due to the existence of free OH-stretching modes: (4) CBs of “free OH-stretching and OH-bending”, 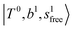, at around 5150 cm⁻¹, and (5) “overtones of free OH-stretching”, 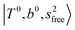, located at around 7000 cm⁻¹. For the case of n = 1, the previous study by McDonald et al.²⁷ also assigned groups (2), (4), and (5) using the VPT2 analysis on two-quanta excitation states; the peak positions in our observed spectra are in good agreement with their results.

The three OH bonds in H₃O⁺ are solvated by Ar following one by one addition of the Ar atoms; the 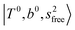bands become weaker as n increases from 1 to 2, and finally disappear at n = 3. Meanwhile, the 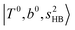bands show remarkable blue shifts with an increase of n, representing the weakening of the average strength of the H-bonds between Ar and OH. Such n-dependence of the NIR spectra is consistent with the spectra of the OH-stretching fundamental region reported in the previous work.^17,28,30 The weakening of the H-bond strength with increasing n is attributed to the anti-cooperative effect caused by the charge delocalization to the solvating Ar atoms.^30,49

In the spectra of H₃O⁺⋯(N₂)_n (n = 1–3) shown in Fig. 2, the key features have the same trends as those of H₃O⁺⋯Ar_n. In the region of 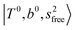, the bands are missing at n = 2 when the N₂-loss channel is monitored. This is due to the switching of the dissociation channel with the increase of vibrational excitation energy; thus, the expected band is seen in this region only when we monitor the 2N₂-loss channel. Due to the higher strength of the H-bond with N₂ than that with Ar, the 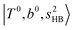bands of n = 1 are red-shifted to the region of ∼5000 cm⁻¹, where the 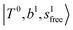bands are also expected; thus, the spectrum shows very complicated spectral features in this region. The blue shift trends (anti-cooperative effect) of the 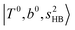bands with increasing n is also seen in H₃O⁺⋯(N₂)_n, thus the 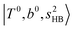bands are seen in the 5500–6000 cm⁻¹ region in n = 2 and 3. The bands at around 5200 cm⁻¹ in n = 2 are attributed to the 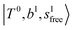bands. In contrast with Ar solvation, no clear band is seen in the ∼5000 cm⁻¹ region in n = 3.

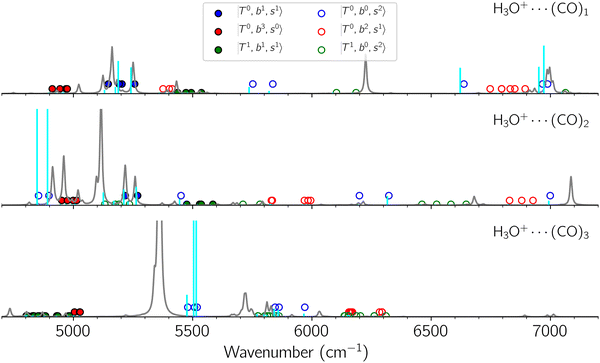
The spectral features of H₃O⁺⋯CO_n (n = 1–3) in Fig. 3 show substantial changes in comparison with those of H₃O⁺⋯Ar_n and ⋯(N₂)_n. The strength of the H-bond with CO is larger than that with Ar or N₂, which leads to even larger red-shifts of OH-stretching frequencies, thus we expect that spectral features in the region of the 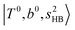bands and 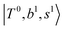bands should be more complicated than in their H₃O⁺⋯(N₂)_n counterparts. Meanwhile, the NIR spectra show significantly broadened absorption in the 5000–6000 cm⁻¹ region; even qualitative band assignments in this region are very difficult without the help of anharmonic vibrational analyses.

In the previous study on the NIR spectra of H⁺(H₂O)_n by McDonal et al.,²⁷ it has been shown that the 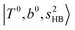bands are quite weak and/or significantly broadened while H₃O⁺⋯Ar shows a clear 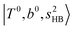band. Similar suppression of overtones of H-bonded OH-stretching bands has been reported in NIR spectroscopy in the gas and condensed phases.^32–37 In the present observations with the stepwise change of the H-bond strength, we found that the 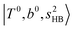band is clearly seen in H₃O⁺⋯Ar_n and H₃O⁺⋯(N₂)_n, but becomes unclear in H₃O⁺⋯(CO)_n. The threshold of the H-bond strength for the suppression of the 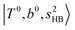band seems to exist in between H-bond formation with N₂ and CO.

C. Comparison between the observed and calculated spectra

The calculated spectra of H₃O⁺⋯Ar_n (n = 1 – 3) are shown as red traces in Fig. 1. The observed positions of (1)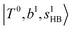 at around 4900 cm⁻¹, (2) 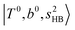at 6000–6500 cm⁻¹, (3) weaker 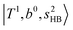band at ∼+ 200 cm⁻¹ to 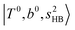, (4) 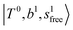at around 5150 cm⁻¹, and (5) 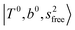located around 7000 cm⁻¹ are all in good agreement with those in the calculated spectra. However, the relative intensities of 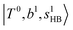and 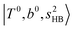are quite different in the calculated and observed spectra. A part of this discrepancy may be attributed to the difficulty of laser power normalization of the observed spectra; the signal intensity was so weak that a linear power dependence could not be confirmed in the present NIR spectra though we assumed it when processing the signal.

The spectral features of group (1) bands are quite complicated in both the observed and calculated spectra; Table S4 (ESI†) shows that these peaks are formed by strong mixing of 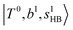and 3-quanta bending overtones 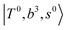, which shares the same coupling mechanism as the FR between fundamental OH-stretching 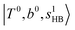and 2-quanta bending overtones 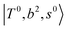in the MIR region. On the other hand, some minor peaks in these regions are contributed by further mixing of “CB of H-bonded OH-stretching, OH-bending, and one-quantum OH⋯X intermolecular stretching”, 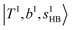; these are also in close resemblance to the MIR counterpart of the interaction between 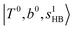and CB of fundamental H-bonded OH-stretching and one-quantum OH⋯X intermolecular stretching, 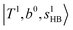.²⁹ This can be further visualized in Fig. 4, in which we can see that the diagonal energy of 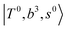(filled red circle) remains almost the same in n = 1–3; thus, the anti-cooperative effect forms the blue-shift of 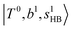(filled blue circle), which makes the FR mixing between this two type of states stronger when n increases. In contrast, in the region of group (2) and group (3) bands, the FR coupling pattern is almost absent; this is due to the energy mismatch between the 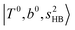and 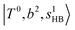states, which is also shown in Fig. 4.

The calculated spectra of H₃O⁺⋯(N₂)_n (n = 1 – 3) are shown as the red traces in Fig. 2. At n = 1, the 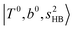bands are red-shifted to 5126 cm⁻¹, which is very close to the 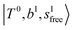bands located in this region; although the spectral feature is really complicated in this region, these two groups of bands do not couple with each other. This is also visualized in Fig. 5, where we plot the diagonal energy of 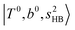as the leftmost empty-blue circle; for n = 1, the diagonal energy of this state is just a bit higher than those of 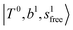, which are labeled as filled blue circles; with the inclusion of off-diagonal coupling, the 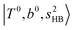state red-shifts to 5126 cm⁻¹, which is even lower than the 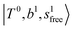states; however, even though these states are very close to each other, Table S4 (ESI†) shows that they almost do not interact with each other. In the previous section about the observed spectra, we have also mentioned the absence of bands around 5000 cm⁻¹ for H₃O⁺⋯(N₂)₃, which should be assigned as 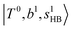; this band is predicted at 4716 cm⁻¹, which is just out of the observed spectral range.

The calculated spectra of H₃O⁺⋯(CO)_n (n = 1–3) are shown as red traces in Fig. 3. While we seem to have obtained some agreement between the observed and calculated spectra for spectral features of n = 1–2, we cannot reach a fair agreement at n = 3; meanwhile, at n = 1, the peak at 6225 cm⁻¹ in the calculated spectrum is absent in the observed spectrum. These disagreements remind us of the possibility of hot bands, which we are going to discuss in the next section.

D. Origin of the band broadening

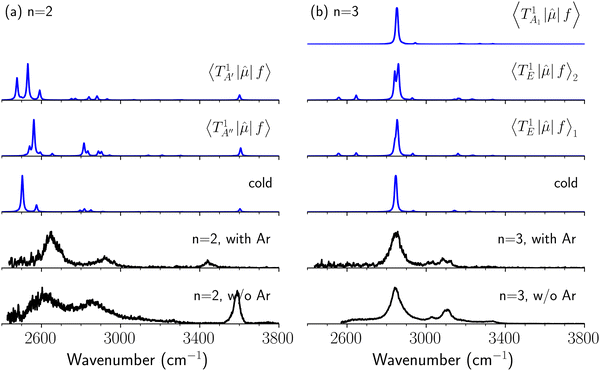
It is clearly seen that the bandwidths in the NIR spectra become wider as the magnitude of the interaction with the solvent molecule is enhanced. Band broadening is especially remarkable in the spectra of H₃O⁺⋯(CO)_n. Two origins are plausible for this band broadening. One is inhomogeneous broadening for hot bands. With an increase in the binding energy with the solvent molecule, warmer clusters survive until spectroscopic detection, and they contribute to the observed spectra. Thermal excitation of low-frequency intermolecular vibrations would shift intramolecular vibrational frequencies, especially H-bonded OH stretching, because of anharmonic coupling among vibrational modes, and frequency-shifts due to such hot bands might result in line broadening.⁵⁰ Another plausible origin is band congestion due to mode coupling, and such mode coupling finally results in homogeneous broadening due to fast intramolecular vibrational energy redistribution (IVR),^51–56 which can be accelerated with increasing H-bond strength because strong H-bonds induce strong mode couplings.⁵⁷ NIR spectroscopy has been applied to explore IVR processes in the gas phase molecules, in which vibrational energy transfer to solvents is excluded and only unimolecular processes occur.^58–62 In gas phase clusters, the impact of solvation including H-bond formation to IVR can be introduced into the system. However, the application of NIR spectroscopy to gas phase clusters has been very scarce. Electronic spectroscopy (dispersed fluorescence or stimulated emission) has been generally utilized to probe IVR processes in gas phase clusters, especially H-bonded ones. Therefore, molecules with a suitable chromophore are of interest in such studies, and clusters of aromatic molecules have been the main research subjects.^63,64

To experimentally explore the impact of hot bands on band broadening, we compared IR spectra of H₃O⁺⋯(CO)_n with those of H₃O⁺⋯(CO)_n⋯Ar. The Ar-“tagging” introduces a much weaker intermolecular bond in clusters, and warm clusters spontaneously dissociate prior to the detection; for these reasons, Ar-tagging is expected to practically cool down the tagged cluster and suppress hot bands.^65–68 However, due to the much lower production efficiency of the Ar-tagged clusters and the extremely weak absorption intensity in the NIR region, we could not observe NIR spectra of H₃O⁺⋯(CO)_n⋯Ar; therefore, we compared the spectra in the OH-stretching fundamental region to estimate the impact of hot bands.

The spectra in the fundamental region were measured under the same ion source conditions as those for the measurements of the NIR spectra shown in the above sections, and the effective temperature of H₃O⁺⋯(CO)_n (“bare” clusters) should be common for both spectra. For the OH fundamental region, we focused on the n = 2 and 3 clusters because the observed spectrum of the bare cluster of n = 1 is seriously modulated by the dissociation yield change (see Fig. S1 and its caption in the ESI† for detailed discussion). The IR spectra of bare and Ar-tagged H₃O⁺⋯(CO)_n (n = 2 and 3) in the OH-stretching fundamental region are shown in Fig. 7 with anharmonic vibrational simulated spectra of cold and hot bands. In these observed spectra, the bands located at ∼3600 cm⁻¹ are assigned to the free OH-stretching; the bands in the region of 3350–3500 cm⁻¹ are attributed to Ar-bound OH-stretching, and those below 3200 cm⁻¹ are ascribed to the CO-bound OH-stretching. The relative intensity between the CO-bound OH-stretching and free OH-stretching bands remarkably changes upon Ar-tagging in n = 2. This is because the intensities of the H-bonded OH-stretching bands would be suppressed for those bare clusters without enough thermal energy (see the discussion in the caption of Fig. S1 in the ESI†). Besides, for n = 2, we can clearly see the tails of the H-bonded OH-stretching bands to the higher frequency ends in the bare cluster spectra, but they are largely suppressed by Ar-tagging. Nevertheless, the impact of Ar-tagging is much less for n = 3; both the position and width of the observed bands are almost identical between the spectra of the bare and Ar-tagged clusters.

Fig. 7 Comparison among the observed cold (Ar-tagged) and warm (bare) spectra and calculated cold and hot band spectra of H₃O⁺⋯(CO)_n, (a) n = 2 and (b) n = 3, in the OH stretch fundamental region. In the hot band spectrum simulation, transitions from the first excited level of the OH…CO hydrogen-bond stretching modes (T_A′ and T_A′′ for n = 2, T_A1 and degenerated T_E for n = 3) are calculated.

To clarify if our NIR spectra are affected by the hot bands, we performed DVR-FBR simulations of H₃O⁺⋯(CO)_n for hot bands using the same method. In our current anharmonic vibrational analysis, the OH⋯CO intermolecular stretching (T) modes (215–277 cm⁻¹) are the lowest-possible vibrational modes in H₃O⁺⋯(CO)_n; therefore, these modes are most plausible to be thermally populated. It is also expected that the excitation of the T modes may modulate the transition energy of the H-bonded OH-stretching (s_HB) mode. Therefore, we simulated hot band spectra of H₃O⁺⋯(CO)_n, in which all transitions occur from the first excited state of the T modes, .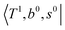

The calculated cold and hot band spectra of the fundamental region are also shown in Fig. 7 in comparison with the observed spectra of the bare and Ar-tagged clusters. For n = 2, there are two OH⋯CO intermolecular stretching modes, T_A′ (A′, 245 cm⁻¹) and T_A′′ (A′′, 253 cm⁻¹); the hot band spectrum appearing from 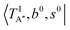shows remarkable blue shifts (∼100 cm⁻¹) of the H-bonded OH-stretching excitation, but the spectrum starting from 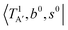behaves similar to the cold spectrum. The broadening of the observed spectrum due to the tail to the high frequency side may be qualitatively rationalized if we suppose that some contribution from the hot bands occurred from 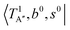. On the other hand, in the case of n = 3, there are three OH⋯CO intermolecular stretching modes, T_A1 (A₁, 216 cm⁻¹) and degenerated T_E (E, 249 cm⁻¹); in contrast with n = 2, the hot band spectra share almost the same spectral features to the cold spectra in the OH-stretching fundamental region. These hot band simulations of n = 3 are consistent with the negligible change of the observed spectrum with Ar-tagging.

Hot band simulations for the OH stretching overtone region of H₃O⁺⋯(CO)_n (n = 1–3) are compared with the observed spectra shown in Fig. 8. In the case of n = 1, the frequency shifts due to the T mode excitation are not significant; the band congestion at ∼5200 cm⁻¹ is a bit more remarkable in the hot band spectrum, and the peak at ∼6225 cm⁻¹ disappears. In the case of n = 2, as seen in the fundamental region, the excitation of the T_A′′ mode causes a remarkable (∼250 cm⁻¹) blue shift of the H-bonded OH-stretching overtone excitation band. The contribution of this hot band agrees with the observed band at ∼5600 cm⁻¹ better, of which the corresponding band is absent in the simulation of the cold spectrum. However, in the case of n = 3, the pattern of the hot band changes greatly; the hot band transition which is attributed to 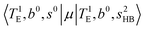shows significant intensities. This band partly explains the splitting of the nominal 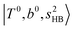bands located at ∼5000 and ∼5300 cm⁻¹ in the observed spectrum. However, hot bands alone cannot be responsible for the observed large bandwidths and multiple peaks; significant band congestion due to higher coupling terms and fast IVR are suggested to rationalize the broadening of the observed NIR spectrum of n = 3.

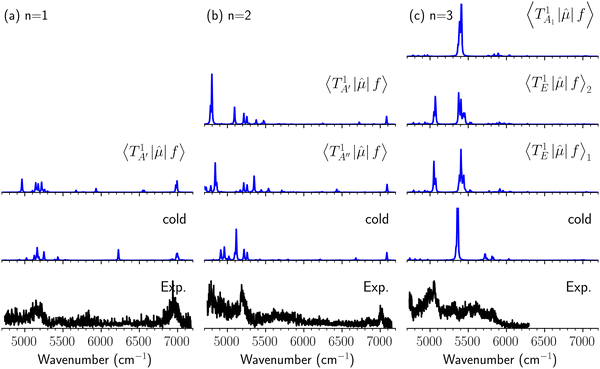Fig. 8 Comparison among the observed spectrum and simulated cold and hot band spectra of H₃O⁺⋯(CO)_n, (a) n = 1, (b) n = 2, and (c) n = 3, in the OH-stretching overtone region. The observed spectra are reproductions of those shown in Fig. 3. In the hot band spectrum simulation, transitions from the first excited level of the OH…CO hydrogen-bond stretching modes (T_A′ for n = 1, T_A′ and T_A′′ for n = 2, T_A1 and degenerated T_E for n = 3) are calculated.

Summary

The NIR spectra of the OH-stretching overtone region of H₃O⁺⋯X_n (X = Ar, N₂, and CO, n = 1–3) were observed and were compared with the ab initio anharmonic vibrational analyses. In addition to the OH-stretching overtone vibrations, the OH-stretching-bending combination bands are the main spectral features in the observed region. The suppression of the H-bonded OH overtone bands, which is frequently found in H-bonded systems, seems to occur in the spectra of X = CO while the spectra of X = Ar and N₂ are free from suppression. The anti-cooperative effect of the H-bond strength is seen in the cluster size dependence of the H-bonded OH-stretching overtones. The anharmonic vibrational simulations well reproduce the observed spectra for X = Ar and N₂, but the agreement becomes more qualitative in the spectra of X = CO. The systematic changes in the NIR spectra with an increase of the interaction between H₃O⁺ and solvent molecules demonstrate that these clusters can be a benchmark for anharmonic simulations of the NIR region of H-bonded systems. Remarkable band broadening is observed in the spectra of X = CO. Its origins were explored by the Ar-tagging experiment and hot band simulations. Not only the hot bands but also band congestion and fast IVR due to strong mode couplings are suggested to explain the band broadening.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study is partly supported by a Grant-in-Aid for Scientific Research (Project No. 21H04671) from JSPS. QRH and JLK are supported by various grants from the Ministry of Science and Technology of Taiwan (NSTC 107-2628-M001-002-MY4, NSTC 111-2113-M-001-006, NSTC 111-2113-M-001-023 and NSTC 111-2639-M-A49-001-ASP) to JLK. QRH was supported via an IAMS Junior Fellow and Academia Sinica Postdoctoral Research Fellowship. YY was supported by the Strategic Student Acceptance Program of Tohoku University. Computational resources are partly supported by the Academia Sinica and the National Center for High-Performance Computing (NCHC) of Taiwan.

References

1. H. W. Siesler, Y. Ozaki, S. Kawata and H. M. Heise, Near-Infrared Spectroscopy: Principles, Instruments, Applications, John Wiley & Sons, Ltd, 2001.
2. C. Pasquini, Near Infrared Spectroscopy: fundamentals, practical aspects and analytical applications, J. Braz. Chem. Soc., 2003, 14, 198–219.
3. K. B. Beć and C. W. Huck, Breakthrough Potential in Near-Infrared Spectroscopy: Spectra Simulation. A Review of Recent Developments, Front. Chem., 2019, 7, 48.
4. Y. Ozaki, Recent Advances in Molecular Spectroscopy of Electronic and Vibrational Transitions in Condensed Phase and Its Application to Chemistry, Bull. Chem. Soc. Jpn., 2019, 92, 629–654.
5. K. B. Beć, J. Grabska and Y. Ozaki, in Frontiers of Quantum Chemistry, ed. M. J. Wójcik, H. Nakatsuji, B. Kirtman, Y. Ozaki, Springer, Singapore, 2018, pp. 483–512.
6. Y. Ozaki, C. Huck, S. Tsuchikawa and S. B. Engelsen, Near-Infrared Spectroscopy: Theory, Spectral Analysis, Instrumentation, and Applications, Springer Nature, Singapore, 2020.
7. M. S. Child, Local Mode Overtone Spectra, Acc. Chem. Res., 1985, 18, 45–50.
8. L. Halonen, Recent Developments in the Local Mode Theory of Overtone Spectra, J. Phys. Chem., 1989, 93, 3386–3392.
9. M. Quack, Spectra and Dynamics of Coupled Vibrations in Polyatomic Molecules, Annu. Rev. Phys. Chem., 1990, 41, 839–874.
10. M. S. Child and L. Halonen, Overtone Frequencies and Intensities in the Local Mode Picture, Adv. Chem. Phys., 1984, 57, 1–58.
11. O. Vendrell, F. Gatti, D. Lauvergnat and H.-D. Meyer, Full-Dimensional (15-dimensional) Quantum-Dynamical Simulation of the Protonated Water Dimer. I. Hamiltonian Setup and Analysis of the Ground Vibrational State, J. Chem. Phys., 2007, 127, 184302.
12. O. Vendrell, F. Gatti and H.-D. Meyer, Full Dimensional (15-Dimensional) Quantum-Dynamical Simulation of the Protonated Water dimer. II. Infrared Spectrum and Vibrational Dynamics, J. Chem. Phys., 2007, 127, 184303.
13. O. Vendrell, F. Gatti and H. Meyer, Dynamics and Infrared Spectroscopy of the Protonated Water Dimer, Angew. Chem., Int. Ed., 2007, 46, 6918–6921.
14. T. L. Guasco, M. A. Johnson and A. B. McCoy, Unraveling Anharmonic Effects in the Vibrational Predissociation Spectra of H₅O₂⁺ and Its Deuterated Analogues, J. Phys. Chem. A, 2011, 115, 5847–5858.
15. J.-W. Li, M. Morita, K. Takahashi and J.-L. Kuo, Features in Vibrational Spectra Induced by Ar-Tagging for H₃O⁺ Ar_m, m = 0–3, J. Phys. Chem. A, 2015, 119, 10887–10892.
16. J. A. Tan, J.-W. Li, C. Chiu, H.-Y. Liao, H. T. Huynh and J.-L. Kuo, Tuning the Vibrational Coupling of H₃O⁺ by Changing its Solvation Environment, Phys. Chem. Chem. Phys., 2016, 18, 30721–30732.
17. Q.-R. Huang, T. Nishigori, M. Katada, A. Fujii and J.-L. Kuo, Fermi Resonance in Solvated H₃O⁺: A Counter-Intuitive Trend Confirmed via a Joint Experimental and Theoretical Investigation, Phys. Chem. Chem. Phys., 2018, 20, 13836–13844.
18. Q.-R. Huang, Y.-C. Li, K.-L. Ho and J.-L. Kuo, Vibrational Spectra of Small Methylamine Clusters Accessed by an Ab Initio Anharmonic Approach, Phys. Chem. Chem. Phys., 2018, 20, 7653–7660.
19. K. Yagi and B. Thomsen, Infrared Spectra of Protonated Water Clusters, H⁺(H₂O)₄, in Eigen and Zundel Forms Studied by Vibrational Quasi-Degenerate Perturbation Theory, J. Phys. Chem. A, 2017, 121, 2386–2398.
20. Q. Yu and J. M. Bowman, VSCF/VCI Vibrational Spectroscopy of H₇O₃⁺ and H₉O₄⁺ Using High-Level, Many-Body Potential Energy Surface and Dipole Moment Surfaces, J. Chem. Phys., 2017, 146, 121102.
21. Q. Yu and J. M. Bowman, High-Level Quantum Calculations of the IR Spectra of the Eigen, Zundel, and Ring Isomers of H⁺(H₂O)₄ Find a Single Match to Experiment, J. Am. Chem. Soc., 2017, 139, 10984–10987.
22. C. H. Duong, O. Gorlova, N. Yang, P. J. Kelleher, M. A. Johnson, A. B. McCoy, Q. Yu and J. M. Bowman, Disentangling the Complex Vibrational Spectrum of the Protonated Water Trimer, H⁺(H₂O)₃, with Two-Color IR-IR Photodissociation of the Bare Ion and Anharmonic VSCF/VCI Theory, J. Phys. Chem. Lett., 2017, 8, 3782–3789.
23. T. K. Esser, H. Knorke, K. R. Asmis, W. Schöllkopf, Q. Yu, C. Qu, J. M. Bowman and M. Kaledin, Deconstructing Prominent Bands in the Terahertz Spectra of H₇O₃⁺ and H₉O₄⁺: Intermolecular Modes in Eigen Clusters, J. Phys. Chem. Lett., 2018, 9, 798–803.
24. D. L. Howard and H. G. Kjaergaard, Influence of Intramolecular Hydrogen Bond Strength on OH-Stretching Overtones, J. Phys. Chem. A, 2006, 110, 10245–10250.
25. C.-C. Wu, C. Chaudhuri, J. C. Jiang, Y. T. Lee and H.-C. Chang, On the First Overtone Spectra of Protonated Water Clusters [H⁺(H₂O)_3–5] in the Free-OH Stretch Region, J. Chin. Chem. Soc., 2002, 49, 769–775.
26. J. P. Wagner, D. C. McDonald and M. A. Duncan, Near-Infrared Spectroscopy and Anharmonic Theory of the H₂O⁺ Ar_1,2 Cation Complexes, J. Chem. Phys., 2017, 147, 104302.
27. D. C. McDonald, J. P. Wagner, A. B. McCoy and M. A. Duncan, Near-Infrared Spectroscopy and Anharmonic Theory of Protonated Water Clusters: Higher Elevations in the Hydrogen Bonding Landscape, J. Phys. Chem. Lett., 2018, 9, 5664–5671.
28. A. B. McCoy, T. L. Guasco, C. M. Leavitt, S. G. Olesen and M. A. Johnson, Vibrational Manifestations of Strong Non-Condon Effects in the H₃O⁺ X₃ (X = Ar, N₂, CH₄, H₂O) Complexes: A Possible Explanation for the Intensity in the “Association Band” in the Vibrational Spectrum of Water, Phys. Chem. Chem. Phys., 2012, 14, 7205.
29. Q.-R. Huang, Y.-C. Li, T. Nishigori, M. Katada, A. Fujii and J.-L. Kuo, Vibrational Coupling in Solvated H₃O⁺: Interplay between Fermi Resonance and Combination Band, J. Phys. Chem. Lett., 2020, 11, 10067–10072.
30. S. G. Olesen, T. L. Gausco, G. H. Weddle, S. Hammerum and M. A. Johnson, Vibrational Predissociation Spectra of the Ar-Tagged [CH₄·H₃O⁺] Binary Complex: Spectroscopic Signature of Hydrogen Bonding to an Alkane, Mol. Phys., 2010, 108, 1191–1197.
31. B. Bandyopadhyay, T. C. Cheng and M. A. Duncan, Proton Sharing in Hydronium–Nitrogen Clusters Probed with Infrared Spectroscopy, Int. J. Mass Spectrom., 2010, 297, 124–130.
32. G. E. Hilbert, O. R. Wulf, S. B. Hendricks and U. Liddel, The Hydrogen Bond between Oxygen Atoms in Some Organic Compounds, J. Am. Chem. Soc., 1936, 58, 548–555.
33. A. Foldes and C. Sandorfy, Anharmonicity and Hydrogen Bonding. Part III. Examples of Strong Bonds. General Discussion, J. Mol. Spectrosc., 1966, 20, 262–275.
34. T. Di Paolo, C. Bourdéron and C. Sandorfy, Model Calculations on the Influence of Mechanical and Electrical Anharmonicity on Infrared Intensities: Relation to Hydrogen Bonding, Can. J. Chem., 1972, 50, 3161–3166.
35. H. G. Kjaergaard, G. R. Low, T. W. Robinson and D. L. Howard, Calculated OH-Stretching Vibrational Transitions in the Water−Nitrogen and Water−Oxygen Complexes, J. Phys. Chem. A, 2002, 106, 8955–8962.
36. T. Gonjo, Y. Futami, Y. Morisawa, M. J. Wojcik and Y. Ozaki, Hydrogen Bonding Effects on the Wavenumbers and Absorption Intensities of the OH Fundamental and the First, Second, and Third Overtones of Phenol and 2,6-Dihalogenated Phenols Studied by Visible/Near-Infrared/Infrared Spectroscopy, J. Phys. Chem. A, 2011, 115, 9845–9853.
37. Y.-L. Cheng, H.-Y. Chen and K. Takahashi, Theoretical Calculation of the OH Vibrational Overtone Spectra of 1−n Alkane Diols (n = 2–4): Origin of Disappearing Hydrogen-Bonded OH Peak, J. Phys. Chem. A, 2011, 115, 5641–5653.
38. K. Mizuse and A. Fujii, Infrared Photodissociation Spectroscopy of H⁺ (H₂O)₆·M_m (M = Ne, Ar, Kr, Xe, H₂, N₂, and CH₄): Messenger-Dependent Balance between H₃O⁺ and H₅O₂⁺ Core Isomers, Phys. Chem. Chem. Phys., 2011, 13, 7129–7135.
39. U. Even, J. Jortner, D. Noy, N. Lavie and C. Cossart-Magos, Cooling of Large Molecules below 1 K and He Clusters Formation, J. Chem. Phys., 2000, 112, 8068–8071.
40. J. C. Light and T. Carrington, Discrete-Variable Representions and Their Utilization, in Advances in Chemical Physics, ed. I. Prigogine and S. A. Rice, John Wiley & Sons, Inc, 2007, vol. 114, pp. 263–310.
41. B. Shizgal, Spectral Methods in Chemistry and Physics, Springer Netherlands, Dordrecht, 2015.
42. S. Carter, J. M. Bowman and N. C. Handy, Extensions and Tests of ‘Multimode’: A Code to Obtain Accurate Vibration/Rotation Energies of Many-Mode Molecules, Theor. Chem. Acc., 1998, 100, 191–198.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, 2016.
44. Q.-R. Huang, T. Endo, S. Mishra, B. Zhang, L.-W. Chen, A. Fujii, L. Jiang, G. N. Patwari, Y. Matsuda and J.-L. Kuo, Understanding Fermi Resonances in the Complex Vibrational Spectra of the Methyl Groups in Methylamines, Phys. Chem. Chem. Phys., 2021, 23, 3739–3747.
45. Q.-R. Huang, Y. Matsuda, R. Eguchi, A. Fujii and J.-L. Kuo, Understanding Fermi Resonances behind the Complex Vibrational Spectra of the Methyl Groups in Simple Alcohol, Thiol, and Their Ethers, J. Chin. Chem. Soc., 2021, 69, 42–50.
46. C.-K. Lin, Q.-R. Huang and J.-L. Kuo, Anharmonic Coupling behind Vibrational Spectra of Solvated Ammonium: Lighting up Overtone States by Fermi Resonance through Tuning Solvation Environments, Phys. Chem. Chem. Phys., 2020, 22, 24059–24069.
47. C.-K. Lin, R. Shishido, Q.-R. Huang, A. Fujii and J.-L. Kuo, Vibrational Spectroscopy of Protonated Amine–Water Clusters: Tuning Fermi Resonance and Lighting up Dark States, Phys. Chem. Chem. Phys., 2020, 22, 22035–22046.
48. P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt, A. Vijaykumar, A. Pietro Bardelli, A. Rothberg, A. Hilboll, A. Kloeckner, A. Scopatz, A. Lee, A. Rokem, C. N. Woods, C. Fulton, C. Masson, C. Häggström, C. Fitzgerald, D. A. Nicholson, D. R. Hagen, D. V. Pasechnik, E. Olivetti, E. Martin, E. Wieser, F. Silva, F. Lenders, F. Wilhelm, G. Young, G. A. Price, G.-L. Ingold, G. E. Allen, G. R. Lee, H. Audren, I. Probst, J. P. Dietrich, J. Silterra, J. T. Webber, J. Slavič, J. Nothman, J. Buchner, J. Kulick, J. L. Schönberger, J. V. de Miranda Cardoso, J. Reimer, J. Harrington, J. L. C. Rodríguez, J. Nunez-Iglesias, J. Kuczynski, K. Tritz, M. Thoma, M. Newville, M. Kümmerer, M. Bolingbroke, M. Tartre, M. Pak, N. J. Smith, N. Nowaczyk, N. Shebanov, O. Pavlyk, P. A. Brodtkorb, P. Lee, R. T. McGibbon, R. Feldbauer, S. Lewis, S. Tygier, S. Sievert, S. Vigna, S. Peterson, S. More, T. Pudlik, T. Oshima, T. J. Pingel, T. P. Robitaille, T. Spura, T. R. Jones, T. Cera, T. Leslie, T. Zito, T. Krauss, U. Upadhyay, Y. O. Halchenko and Y. Vázquez-Baeza, SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 2020, 17, 261–272.
49. D. Bing, T. Hamashima, A. Fujii and J.-L. Kuo, Anticooperative Effect Induced by Mixed Solvation in H⁺(CH₃OH)_m(H₂O)_n (m + n = 5 and 6): A Theoretical and Infrared Spectroscopic Study, J. Phys. Chem. A, 2010, 114, 8170–8177.
50. T. Yamashita and K. Takatsuka, Hydrogen-Bond Assisted Enormous Broadening of Infrared Spectra of Phenol-Water Cationic Cluster: An Ab Initio Mixed Quantum-Classical Study, J. Chem. Phys., 2007, 126, 074304.
51. V. E. Bondybey, Relaxation and Vibrational Energy Redistribution Processes in Polyatomic Molecules, Annu. Rev. Phys. Chem., 1984, 35, 591–612.
52. T. Elsaesser and W. Kaiser, Vibrational and Vibronic Relaxation of Large Polyatomic Molecules in Liquids, Annu. Rev. Phys. Chem., 1991, 42, 83–107.
53. K. K. Lehmann, G. Scoles and B. H. Pate, Intramolecular Dynamics from Eigenstate-Resolved Infrared Spectra, Annu. Rev. Phys. Chem., 1994, 45, 241–274.
54. D. Boyall and K. L. Reid, Modern Studies of Intramolecular Vibrational Energy Redistribution, Chem. Soc. Rev., 1997, 26, 223.
55. D. J. Donaldson, A. F. Tuck and V. Vaida, Atmospheric Photochemistry via Vibrational Overtone Absorption, Chem. Rev., 2003, 103, 4717–4730.
56. A. A. Makarov, A. L. Malinovsky and E. A. Ryabov, Intramolecular Vibrational Redistribution: from High-Resolution Spectra to Real-Time Dynamics, Phys.-Usp., 2012, 182, 1047–1080.
57. M. Kayano, T. Ebata, Y. Yamada and N. Mikami, Picosecond IR–UV Pump–Probe Spectroscopic Study of the Dynamics of the Vibrational Relaxation of Jet-Cooled Phenol. II. Intracluster Vibrational Energy Redistribution of the OH Stretching Vibration of Hydrogen-Bonded Clusters, J. Chem. Phys., 2004, 120, 7410–7417.
58. R. G. Bray and M. J. Berry, Intramolecular Rate Processes in Highly Vibrationally Excited Benzene, J. Chem. Phys., 1979, 71, 4909–4922.
59. M. G. Sowa and B. R. Henry, Overtone Line Narrowing and Intramolecular Vibrational Energy Redistribution in Substituted Toluenes, J. Chem. Phys., 1991, 95, 3040–3045.
60. B. H. Pate, K. K. Lehmann and G. Scoles, The Onset of Intramolecular Vibrational Energy Redistribution and Its Intermediate Case: The ν₁ and 2ν₁ Molecular Beam, Optothermal Spectra of Trifluoropropyne, J. Chem. Phys., 1991, 95, 3891–3916.
61. O. V. Boyarkin and T. R. Rizzo, Secondary Time Scales of Intramolecular Vibrational Energy Redistribution in CF₃H Studied by Vibrational Overtone Spectroscopy, J. Chem. Phys., 1996, 105, 6285–6292.
62. D. J. Nesbitt and R. W. Field, Vibrational Energy Flow in Highly Excited Molecules: Role of Intramolecular Vibrational Redistribution, J. Phys. Chem., 1996, 100, 12735–12756.
63. A. Callegari, U. Merker, P. Engels, H. K. Srivastava, K. K. Lehmann and G. Scoles, Intramolecular Vibrational Redistribution in Aromatic Molecules. I. Eigenstate Resolved CH Stretch First Overtone Spectra of Benzene, J. Chem. Phys., 2000, 113, 10583–10596.
64. A. Callegari, R. Pearman, S. Choi, P. Engels, H. Srivastava, M. Gruebele, K. K. Lehmann and G. Scoles, Intramolecular Vibrational Relaxation in Aromatic Molecules. 2: An Experimental and Computational Study of Pyrrole and Triazine near the IVR Threshold, Mol. Phys., 2003, 101, 551–568.
65. M. Okumura, L. I. Yeh, J. D. Myers and Y. T. Lee, Infrared spectra of the cluster ions H₇O₃⁺ H₂ and H₉O₄⁺ H₂, J. Chem. Phys., 1986, 85, 2328–2329.
66. D. J. Miller and J. M. Lisy, Hydrated Alkali-Metal Cations: Infrared Spectroscopy and ab Initio Calculations of M⁺ (H₂O)_x=2–5 Ar cluster ions for M = Li, Na, K, and Cs, J. Am. Chem. Soc., 2008, 130, 15381–15392.
67. C. T. Wolke, F. S. Menges, N. Tötsch, O. Gorlova, J. A. Fournier, G. H. Weddle, M. A. Johnson, N. Heine, T. K. Esser, H. Knorke, K. R. Asmis, A. B. McCoy, D. J. Arismendi-Arrieta, R. Prosmiti and F. Paesani, Thermodynamics of Water Dimer Dissociation in the Primary Hydration Shell of the Iodide Ion with Temperature-Dependent Vibrational Predissociation Spectroscopy, J. Phys. Chem. A, 2015, 119, 1859–1866.
68. T. Shimamori, J.-L. Kuo and A. Fujii, Stepwise Internal Energy Change of Protonated Methanol Clusters by Using the Inert Gas Tagging, J. Phys. Chem. A, 2016, 120, 9203–9208.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00458b

‡ Q.-R. Huang and K. Yano contributed equally.

---