 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Vibrational wave-packet dynamics of the silver pentamer probed by femtosecond NeNePo spectroscopy†
Max
Grellmann
 a,
Martin
DeWitt
a,
Martin
DeWitt
 b,
Daniel M.
Neumark
b,
Daniel M.
Neumark
 bc,
Knut R.
Asmis
bc,
Knut R.
Asmis
 a and
Jiaye
Jin
a and
Jiaye
Jin
 *a
*a
aWilhelm-Ostwald-Institut für Physikalische und Theoretische Chemie, Universität Leipzig, Linnéstr. 2, 04103, Leipzig, Germany. E-mail: jiaye.jin@uni-leipzig.de
bDepartment of Chemistry, University of California, Berkeley, CA 94720, USA
cChemical Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 1st February 2024
Abstract
Vibrational wave-packet dynamics on the ground electronic state of the neutral silver pentamer (Ag5) are studied by femtosecond (fs) pump–probe spectroscopy using the ‘negative ion – to neutral – to positive ion’ (NeNePo) excitation scheme. A vibrational wave packet is prepared on the 2A1 state of Ag5via photodetachment of mass-selected, cryogenically cooled Ag5− anions using a fs pump pulse. The temporal evolution of the vibrational wave packet is then probed by an ultrafast probe pulse via resonant multiphoton ionization to Ag5+. Frequency analysis of the fs NeNePo transients for pump–probe delay times from 0.2 to 8 ps reveals three primary beating frequencies at 157 cm−1, 101 cm−1 and 56 cm−1 as well as four weaker features. A comparison of these experimentally obtained beating frequencies to harmonic normal mode frequencies calculated from electronic structure calculations confirms that Ag5 in the gas phase adopts a planar trapezoidal geometry, similar to that previously observed in solid argon. The dependence of the ionization yield on the laser polarization indicates a s–d wave electron photodetachment from a ‘p-type’ occupied molecular orbital of Ag5. Franck–Condon analysis shows that both processes, photodetachment and subsequent photoionization determine the beating frequencies probed in the time-dependent cation yield. The present study extends the applicability of fs NeNePo spectroscopy to characterize the vibrational spectra in the far-IR frequency range in the absence of perturbations from a medium or a messenger atom to mass-selected neutral metal clusters with more than three atoms in the ground electronic states.
1. Introduction
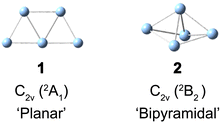
Supported small silver clusters are at the center of current research for their remarkable photoelectric properties, high reactivity and even potential antitumoral activity.1–4 They are also well known for their structural variability and susceptibility to slight perturbations in their environment. This variability manifests itself, for example in a competition between nearly isoenergetic three-dimensional and (quasi-)two-dimensional structures in a characteristic size range.5,6 The resulting structural fluxionality plays a key role in rationalizing the properties of supported metal clusters,7–10 including Ag5 on a TiO2 support.11–13 In order to better understand and predict how a cluster's fluxionality is affected by the environment, it proves helpful to study the intrinsic properties of clusters isolated in the gas phase.The silver pentamer (Ag5) has been studied in detail in cold matrices14–20 and by electronic structure calculations,21,22 but its geometric structure in the gas phase has yet to be determined experimentally. Neutral Ag5 was initially studied in a deuterocyclohexane matrix at 77 K by electron spin resonance (ESR) spectroscopy.14 The anisotropic ESR spectra in combination with semiempirical calculations suggested that Ag5 adopts a 2B2 electronic state with a distorted three-dimensional bipyramidal structure of C2v symmetry as a result of Jahn–Teller distortion (2 in Scheme 1). However, a subsequent Raman spectroscopic study of Ag5 in solid argon did not find any evidence for a three-dimensional structure, but rather assigned a planar trapezoidal structure (1 in Scheme 1).15 Ultraviolet-visible (UV-Vis) absorption spectra of mass-selected neutral Ag5 were studied in different solid matrices.16–20 None of the spectra exhibits vibrational resolution, but the presence of the same planar trapezoidal C2v structure 1 was concluded from a comparison of the UV-Vis absorption bands to the calculated electronic excitation energies from density functional theory (DFT) calculations. A vertical detachment energy (VDE) of ≈2.1 eV for Ag5− was reported by several groups using anion photoelectron spectroscopy,23–25 and assigned to a vertical transition from the planar anion ground state (1A1) to the planar neutral structure (2A1), again based on electronic structure calculations. CCSD(T) calculations also found the planar structure 1 to be the lowest in energy.21,22 The bipyramidal structure 2 was predicted to be 41 kJ mol−1 higher in energy, but to be favored on an oxide support or at high temperatures.11–13,26 The ultrafast dynamics of the Ag5−/Ag5/Ag5+ system were studied by one-color (400 nm) fs NeNePo spectroscopy, but no vibrational dynamics were resolved.27,28
Gas-phase vibrational action spectroscopy is a powerful tool to characterize the geometric structure of size-selected ionic clusters,29–33 but its application to neutral metal clusters is limited by a lack of easy accessible and intense far-infrared light sources as well as small infrared-allowed cross sections.29,34 Cryo-SEVI is an alternative method for obtaining vibrational information of neutral metal clusters by measuring the kinetic energies of slow photoelectrons.35 Fs pump–probe spectroscopy employing the NeNePo excitation scheme is another complementary approach to obtain vibrational information for mass-selected neutral metal clusters by measuring the nuclear wave-packet dynamics with femtosecond time resolution.36 Mass-selected anions trapped in a temperature-controlled, buffer-gas filled ion trap are excited with a fs laser pulse, launching nuclear vibrational dynamics in the neutral species by (single photon) electron photodetachment. The nuclear dynamics are then probed by a second, time-delayed fs laser pulse, which ionizes the neutral species. The mass-selected cation counts as a function of the delay time between the two pulses yields a transient cation signal. A frequency analysis of the oscillatory part provides vibrational information of the neutral cluster. Furthermore, the temporal features of the pump–probe spectrum around time zero and the window spectrogram as a function of the delay time uncover the transient dynamics of photodetachment and vibrational energy redistribution in the neutral cluster. Fs NeNePo spectroscopy has been mainly applied to study the wave-packet dynamics of neutral metals as well as metal-containing clusters, namely, Agn (n = 2–5 and 9),27,36–42 Ag2·O2,37 Ag2Au,43 Cu(H2O)1,2,44,45 and Cu(CD3OD).46 Recently, fs NeNePo studies on the silver dimer demonstrated that also higher-order vibrational constants of the electronic ground state X 1Σ+g can be determined isotopologue specifically.38
Here, we report our study on the vibrational wave-packet dynamics of the neutral silver pentamer probed by fs NeNePo spectroscopy. Fs NeNePo transients of Ag5 obtained by different pump wavelengths (402 nm and 510 nm) reveal oscillatory Ag5+ cation signals for the first time. The observed oscillations over several picoseconds are attributed to the vibrational wave-packet dynamics on the neutral electronic ground state, and unambiguously identify the planar structure of the silver pentamer in the gas phase for the first time. The present work highlights the potential of utilizing fs NeNePo spectroscopy to also study the structure and vibrational dynamics of neutral polyatomic metal clusters.
2. Methods
2.1 Fs NeNePo spectroscopy
The fs NeNePo transients were measured using a tandem mass spectrometer with an integrated, cryogenically cooled linear quadrupole ion trap and an Ti:sapphire femtosecond laser system, as described previously.38 Briefly, Ag5− anions produced by aggregation using a silver target (99.999%, Kurt J. Lesker) as the anode of a DC magnetron sputtering source (TORUS, Kurt J. Lesker) at liquid nitrogen temperature are mass-selected (m/z = 539) and continuously accumulated in a cryogenic linear quadrupole ion trap (filled with 0.2 mbar helium buffer gas) held at 20 K. Two fs laser pulses, referred to as the pump pulse and the probe pulse, are collinearly combined and propagate along the trap axis and focused near the center of the ion trap through a 1.5 mm thick CaF2 lens (f = +1000 mm). The excitation scheme is shown in Fig. 1. The first vertically polarized fs laser pulse (autocorrelation duration of 50 fs, ≈1 μJ per pulse) photodetaches an electron from the cold anion and launches a vibrational wave packet in the neutral Ag5. The polarization of the probe pulse is adjusted between parallel (θ = 0°) and perpendicular (θ = 90°) with respect to the polarization plane of the pump pulse by a MgF2λ/2 waveplate (EKSMA). Two different pump wavelengths, one centered at 510 nm (2.43 eV) and the other at 402 nm (3.08 eV), are applied in the present experiments. Considering the vertical detachment energy (2.11 eV) of Ag5−,23–25 single-photon detachment is possible at both wavelengths, but both remain below the excitation energy to the first accessible excited electronic state of Ag5 located at 3.3 eV above the anion ground state. The temporal evolution of the vibrational wave-packet dynamics of neutral Ag5 is then probed using a second ultrafast laser pulse (centered at 402 nm, autocorrelation duration of 50 fs, 1.0 μJ per pulse), at the magic angle (θ = 55°) to avoid rotational dynamics, ionizing Ag5 by resonant three-photon (1 + 2) ionization (ionization potential ≈ 6.4 eV).17,47 The resulting cations, including cationic fragments, are no longer confined along the trap axis, expelled from the ion trap in the axial direction, and subsequently analyzed by a second quadrupole mass filter. Fs NeNePo transients are obtained by monitoring the mass-selected cation yield for 2500 ms as a function of the delay time with a step size of 40 fs.Frequency analysis of the oscillatory part of fs NeNePo transients is performed by determining its Fourier transform (FT). First, the high-frequency oscillatory signal is extracted by removing low-frequency contributions using a symmetric least-square method.48,49 A Kaiser window function (α = 4.5) is used to balance the main-lobe width and side lobe level. Zero values are padded to the oscillations till two times the data length, in order to minimize the influence of non-integral cut of the periods. The frequency resolution of the FT amplitude spectrum is ≈4.2 cm−1, inversely proportional to the total duration (≈8 ps) of the oscillatory component. The oscillatory signal is also fitted to a sum over all cosine functions containing all significant frequency contributions, as 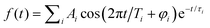 , where Ai is the oscillation amplitude, τi is the dephasing lifetime, Ti is the period of the oscillation, and φi is the initial phase of the oscillation, in order to study the initial phases and the coherence time of different frequency components.
, where Ai is the oscillation amplitude, τi is the dephasing lifetime, Ti is the period of the oscillation, and φi is the initial phase of the oscillation, in order to study the initial phases and the coherence time of different frequency components.
2.2 Computational methods
The geometry optimization and frequency calculation were performed using the GAUSSIAN 16 C.01 program.50 Geometries were optimized using density functional theory (DFT) employing the PBE functional51 with a triple-ζ basis set (def2-TZVPP)52,53 and a superfine grid (pruned 250974 for Ag atom). The harmonic vibrational frequencies were obtained from analytical second derivatives using the same method. The PBE functional has been shown to reliably reproduce basic properties,54,55 as well as the anharmonic vibrational frequencies of small metal clusters.56 The vibrational level population is calculated from Franck–Condon factors using the ezFCF software package.573. Results and discussion
3.1 Fs NeNePo transients of Ag5
Quadrupole mass spectra of silver cluster cations produced by irradiating mass-selected Ag5− anions, trapped in the ion trap, with λpump = 510 nm and λprobe = 402 nm pulses are shown in Fig. S1 (ESI†) for a delay time of +600 fs (Fig. S1a, ESI†) and −600 fs (Fig. S1b, ESI†) The polarization of the probe pulse is set to the magic angle (θ = 55°) with respect to that of the pump pulse to avoid rotational dynamics. The mass spectra demonstrate that at these pulse energies, Ag5+ is formed predominantly, independent of the delay time. Fragmentation yielding Agn+ (n < 5), mainly Ag3+, is only observed as a minor contribution. In contrast, fragmentation of Ag5 yielding Ag2 and Ag3 was found in the previous matrix isolation study performed in solid argon.15 While the Ag5+ signal increases substantially at positive delay times (Fig. S1c, ESI†), the Ag3+ yield only shows a minor increase (Fig. S1d, ESI†), indicating a different photoionization channel for the production of Ag3+ from Ag5.Time-dependent Ag5+ cation yields as a function of the delay time from −2 ps to 10 ps with a temporal interval of 40 fs were obtained for a probe pulse centered at 402 nm and pump pulses at two different wavelengths (Fig. 2). The fs NeNePo transient for λpump = 510 nm (Fig. 2a) shows consistently low cation counts at negative delay times, indicating that Ag5+ formation is inefficient and without clear time-dependence. A rise in the Ag5+ signal with weak oscillatory features is observed within 300 fs after time zero, followed by stronger oscillations. The maximum signal is observed at a time of 360 fs, which is longer than the duration of the cross-correlation of the two fs pulses (≈100 fs) and therefore indicates vibrational dynamics on the resulting ‘upper’ electronic state. The oscillatory Ag5+ signal is complex, suggesting that multiple frequency components, associated with different vibrational modes, contribute to the observed wave-packet dynamics. The oscillatory features in the Ag5+ signal are observed up to a time of ≈7 ps. The time-independent contribution remains constant and well above the non-oscillatory signal level observed at negative delay times. Recurrence of the oscillatory Ag5+ is not observed up to 40 ps. The reason is not clear, but it may be due to efficient coupling to the intramolecular ‘bath’ states that leads to intramolecular vibrational energy redistribution (IVR) and eventually vibrational decoherence.58,59
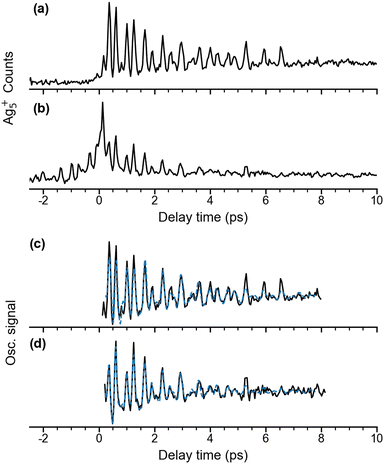 | ||
Fig. 2 Time-dependent Ag5+ cation counts over a delay time range from −2 to 10 ps with λprobe = 402 nm. (a) λpump = 510 nm, θ ≈ 55°; (b) λpump = 402 nm, θ ≈ 0°. Traces (c) and (d) show the extracted oscillatory Ag5+ signal (black) and a fit to this oscillation curve (blue dashed) in the delay time range 0.2 to 8 ps. The experimental oscillatory signal is fitted by a sum over cosine functions, 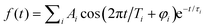 . The details are given in Fig. S3 and Table S1 (ESI†). . The details are given in Fig. S3 and Table S1 (ESI†). | ||
We also measured fs NeNePo transients using other relative polarization angles (see Fig. S2, ESI†). The largest oscillatory Ag5+ signal is observed for θ = 90°, while the oscillation is the weakest at θ = 0°. This indicates anisotropic electron photodetachment from Ag5−, reflecting the molecular-orbital symmetry of Ag5−.
The time-dependent Ag5+ yield obtained for λpump = 402 nm from −2 ps to 10 ps is shown in Fig. 2b. The relative polarization angle θ is set at 0°, which is the same condition as used in the previous study by Leisner et al.27 However, the present laser pulse energies (pump: 0.1 μJ, probe: 0.4 μJ) are nearly two orders of magnitude smaller than those used in the previous study. The present time-dependent cation yield shows similar transient features at time zero compared to the previous study.27 A substantial increase of the Ag5+ cation yield is seen at time zero owing to the interference from the two laser pulses, followed by a decay of the cation signal within 1 ps. Interestingly, the present result resolves temporal envelopes symmetrically in both negative and positive delay times, which was not observed in the previous study using the stronger laser pulse energies of 30 μJ.27 Similar to the time-dependence for λpump = 510 nm, more than a single frequency contributes to the oscillations.
3.2 Frequency analysis of the fs NeNePo transients
The oscillatory part of the transients, obtained for a pump wavelength of λpump = 510 nm (Fig. 2a) and λpump = 402 nm (Fig. 2b), is extracted for the delay times from 0.2 ps to 8 ps and shown in Fig. 2c and d. Both oscillations observed after 500 fs are similar with respect to the beating periods and amplitudes, suggesting similar frequency components. Their frequency spectra (black) are obtained by Fourier transform and shown in Fig. 3a and 3b, respectively. The resulting frequency resolution is ≈4.2 cm−1. Both FT spectra show the same three primary bands centered at 56 cm−1, 101 cm−1, and 157 cm−1 along with other weaker features below 300 cm−1, suggesting that they reflect wave-packet dynamics on the same electronic state. We assign those to the ground electronic state of neutral Ag5, previously characterized by vibrationally unresolved anion photoelectron spectra and electronic structure calculations,23–25 rather than to the dynamics on two different, resonantly excited electronic states of Ag5− anion at 2.4 eV and 3.1 eV.60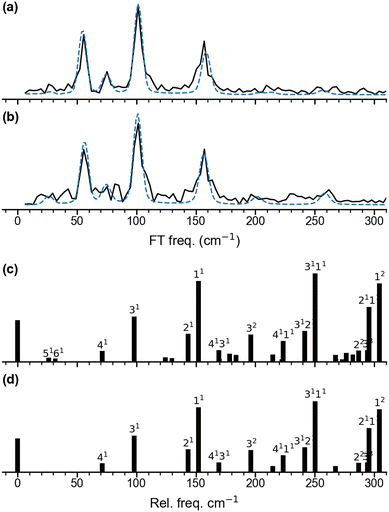 | ||
| Fig. 3 Fourier transform amplitude spectra for the oscillatory Ag5+ yield and the best fitting curves shown in Fig. 2c and d. (a) for λpump = 510 nm and (b) for λpump = 402 nm. The mean frequencies obtained for two pump wavelengths are listed in Table 1. (c) and (d) show the predicted population for the vibrational levels of planar Ag51 determined from Franck–Condon factors for the Ag5 (2A1) ← Ag5− (1A1) photodetachment transition at 20 K (c) and 0 K (d). | ||
To unravel weak and transient features in the frequency spectra, the short-time window Fourier transform (STFT) spectrograms are applied using a sliding window time of 4 ps (Fig. S3, ESI†), providing a frequency resolution of 9 cm−1. In addition to the three main bands, the STFT spectrogram for λpump = 510 nm (Fig. S3c, ESI†) shows a longer-lived (≈4 ps) weak feature at 75 cm−1 and shorter-lived (<2 ps) features at around 255 cm−1, 210 cm−1, 200 cm−1 and 26 cm−1. The STFT spectrogram for λpump = 402 nm (Fig. S3f, ESI†) shows comparable frequency features to the spectrogram of 510 nm, but more complex high-frequency components.
The frequencies identified in the FT spectrum and STFT spectrogram for λpump = 510 nm are then used as initial guesses for fitting the oscillations (see Methods section). The resulting curves and their FT spectra are plotted as blue dashed lines in Fig. 2c and d as well as Fig. 3a and b. More detailed fitting results and the residuals are given in Table S1 and Fig. S3 (ESI†). In addition to the primary frequencies at 158 cm−1, 101 cm−1, 75 cm−1 and 55 cm−1 shown in Fig. 3a, the 256 cm−1 band has a large amplitude of 23 a.u. with a relative short lifetime τ of 1.1 ps. The other three contributions of 213 cm−1, 203 cm−1 and 29 cm−1 only have weak amplitudes, suggesting minor contributions of these four frequency components to the time-dependences. Interestingly, six of the frequency components, except the bands at 213 cm−1 and 29 cm−1, have initial phases between 0 to π, which indicates that at positive delay times, the photoionization of Ag5 is more likely because of the better Franck–Condon factors in these vibrational modes. This reflects a delayed maximum of the Ag5+ signal at 360 fs in the time-dependences. The bands at 213 cm−1 and 29 cm−1 have phases larger than π, indicating worse photoionization Franck–Condon factors at positive delay times. The fitting parameters for λpump = 402 nm are similar to those for λpump = 510 nm. However, the amplitudes of the 201 cm−1 and of 258 cm−1 bands are two times larger than those for λpump = 510 nm, contributing to the high-frequency part of the oscillation (Fig. 2d) and the FT spectrum (Fig. 3b). Mean frequencies with amplitudes larger than 10 a.u. are listed in Table 1.
| Fs NeNePoa | Ramanb | Harm.c | Anharm.d | Mode Ass. |
|---|---|---|---|---|
| a Mean frequencies obtained for the two different pump wavelengths. b Raman spectroscopy of Ag5 in solid Ar matrix from ref. 15. c PBE/def2-TZVPP harmonic frequencies (present study). d VSCF/VCI anharmonic frequencies from ref. 56. | ||||
| 257 | ν 1 + ν3 | |||
| 202 | 2ν3 | |||
| 174 | 183 | 183 | ν 7(b2) | |
| 157 | 162 | 152 | 151 | ν 1(a1) |
| 136 | 143 | 143 | ν 2(a1) | |
| 126 | 117 | 118 | ν 8(b2) | |
| 101 | 105, 100 | 98 | 98 | ν 3(a1) |
| 80 | 77 | 78 | ν 9(b2) | |
| 75 | 68 | 71 | 71 | ν 4(a1) |
| 56 | ν 1 − ν3 | |||
| 31 | 32 | ν 6(b1) | ||
| 28 | 26 | 27 | ν 5(a2) | |
3.3 Vibrational normal mode assignment and Franck–Condon analysis
We performed DFT calculations (PBE/def2-TZVPP) to assign the observed frequencies and to determine which vibrational modes of Ag5 are excited. The calculated planar structures of the electronic ground states of Ag5− and Ag5 together with vibrational normal mode displacements are shown in Fig. 4. The harmonic vibrational frequencies are summarized in Table 1 and Table S2 (ESI†). The predicted populations for the vibrational levels of planar neutral Ag5 determined from the Franck–Condon factors of the Ag5 (2A1) ← Ag5− (1A1) photodetachment transition are shown in Fig. 3 and Fig. S5 (ESI†). The simulated spectrum at 0 K (Fig. 3d) reveals that all four totally symmetric vibrational modes of 1 at 152 cm−1, 143 cm−1, 98 cm−1 and 71 cm−1 (see Table 1) are excited upon photodetachment. The region below 160 cm−1 is dominated by the single quantum excitations 11 (ν1) and 31 (ν3). Interestingly, these are also the two modes that are most prominent in the FT spectra (Fig. 3a and b) at 157 cm−1 and 101 cm−1. The other totally symmetric mode (ν4) is assigned to the FT band at 75 cm−1. The three totally symmetric modes involved in the vibrational wave-packet dynamics are the five-membered ring breathing mode (ν1), the symmetric stretching (ν3) and the in-plane bending (ν4) modes of the linear Ag–Ag–Ag moiety (see Fig. 4). Furthermore, the FT band at 56 cm−1 corresponds to the difference frequency ν1 − ν3 and is therefore assigned accordingly. This observation of strong difference frequency band suggests the presence of coherent coupling between the ν1 and ν3 mode pair, yielding a relatively strong vibrational coherence from the superposition of the 11, 31 and 0 levels, as was observed previously for trapped ions.61–63 Excitation of the non-totally symmetric modes 51 and 61 at 26 cm−1 and 31 cm−1, respectively, is only possible from vibrationally hot anions, in which low-frequency modes are populated at non-zero temperatures (see Fig. 3c and Fig. S5 for simulated spectra at higher temperatures, ESI†). This explains why we also see weaker features at around 28 cm−1 in the transient measured at 20 K in a cryogenic ion trap. Above 160 cm−1, the combination bands 3111 and 2111 as well as the overtone excitations 32 and 12 are predicated to have substantial intensities. They agree with the observed small FT bands at 257 cm−1 and 202 cm−1, as listed in Table 1. The calculated harmonic frequencies of Ag5 are similar to the anharmonic frequencies (Table 1) calculated using the VSCF/VCI method,56 suggesting negligible anharmonic effects.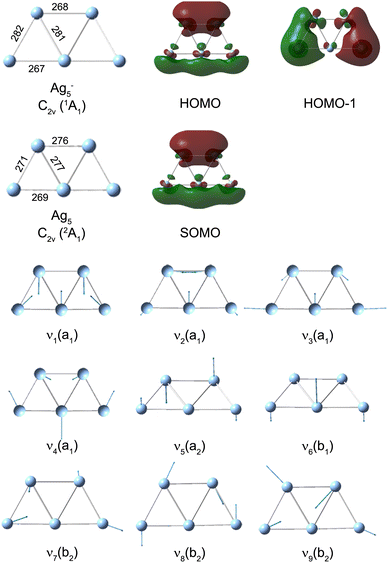 | ||
| Fig. 4 PBE/def2-TZVPP minimum-energy geometries of neutral Ag5 and anionic Ag5−, singly occupied molecular orbital (SOMO) of neutral Ag5, highest occupied molecular orbital (HOMO) of Ag5− and harmonic vibrational normal mode displacements (see Table 1 for the harmonic frequencies). Ag–Ag bond lengths are given in pm. | ||
The bipyramidal isomer 2 is calculated 41 kJ mol−1 higher in energy than the planar structure 1 using the CCSD(T) method.21 The harmonic frequencies for the totally symmetric modes of 2 (see Table S2 and Fig. S6, ESI†) are calculated at 180 cm−1, 106 cm−1, 83 cm−1, and 46 cm−1, showing less agreement with the observed FT bands. Moreover, the simulated population of the vibrational level of 2 shown in Fig. S7 (ESI†) cannot explain the experimental FT spectra shown in Fig. 3. This confirms the assignment to the planar structure 1.
The singly occupied molecular orbital (SOMO) of planar Ag51 and the highest occupied molecular orbital (HOMO) of Ag5− are shown in Fig. 4. Both MOs exhibit a nodal plane, which separates the upper Ag–Ag and the lower linear Ag–Ag–Ag moieties, similar to a ‘p-type’ orbital. This suggests that the photoelectron emitted from the Π ← Σ transition has a s and d partial wave character resulting in a negative anisotropy parameter.35,64,65 As a consequence, Ag5+ formed from neutral Ag5 should exhibit the largest signal when the probe pulse has a polarization perpendicular to that of the pump pulse. The larger delocalization of the Ag5 SOMO vs. the Ag5− HOMO (see Fig. 4) is mainly responsible for the geometry changes upon photodetachment. The increases of the bond lengths within the Ag–Ag and Ag–Ag–Ag moieties, as well as the decrease between the two moieties, results in the excitation of the ring breathing mode ν1 and the symmetric Ag–Ag–Ag stretching mode ν3.
Note, the initial geometry of Ag5 is prepared by vertical photodetachment of the precursor anion. In advance, there is no assurance that the geometry corresponds to the lowest-energy structure of Ag5. However, in the present case, the planar trapezoidal structure 1 lies within the vertical excitation window of the planar Ag5− anion, which allows us to investigate the vibrational wave-packet dynamics in the ground electronic state of Ag5. The so-obtained vibrational frequencies only agree with the prediction for the ground state structure of Ag5. Moreover, if there was a lower-energy structure of neutral Ag5, we might find evidence, since geometry relaxation typically occurs in a few ps for small silver clusters.36,42
The lowest-energy structure of Ag5+ has a three-dimensional twisted structure of D2d symmetry,66 which is significantly different from the planar neutral Ag5. Planar structures are predicted to be unstable in the positive charge state.54,66 To rationalize the influence of the ionization step on the fs NeNePo transients, we also calculated PBE/def2-TZVPP electronic transition energies for Ag5 (Fig. S8, ESI†). The UV-visible spectra of Ag5 deposited in different noble gas matrices have been reported previously.16–20 The strongest absorption of Ag5 in solid neon appears at around 3.27 eV with a small shoulder at around 3.11 eV.17 The wavelength of the probe laser in the present experiments is centered at 402 nm (3.08 eV) with a spectral width of 400 cm−1 (50 meV, see Fig. S9, ESI†). This transition at 3.11 eV is close to the photon energy of the probe pulse and therefore we assume that ionization proceeds via resonant excitation of this 2B2 excited electronic state, predicted at 3.06 eV (Fig. S8, ESI†). We therefore calculated the Franck–Condon factors for each individual vibrational mode of the Ag5 (2B2) ← Ag5 (2A1) transition (see Fig. S9, ESI†). It seems that these simple Franck–Condon simulations cannot reproduce the observed trends for the beating frequencies of the vibrational wave packet. Full quantum dynamic simulations would be helpful for disentangling these complex vibrational wave-packet dynamics.
3.4 Comparison with Raman spectra in solid argon
The FT spectra obtained in the present study reveal beating frequencies of neutral Ag5 in the gas phase without the perturbations from environment and can therefore be slightly different from the reported frequencies obtained by Raman spectroscopy of Ag5 in solid argon.15 Furthermore, previously reported fs NeNePo transients of Ag2 reveal FT bands at a lower wavenumber (red-shifted) compared to vibrational energies measured in the gas phase, due to the combination of vibrational anharmonicity and the population of higher-lying vibrational states.37,38 The frequency resolution of the present FT spectra is around 4.2 cm−1, given by the delay time range of the transient spectra of 8 ps. The reported ν1 frequency in solid argon (162 cm−1) is slightly higher that the FT band position (157 cm−1) obtained in the present study. For ν3 (present study: 101 cm−1) two frequencies (105 cm−1 and 100 cm−1) have been reported in the matrix study and attributed to different sites, indicating a strong matrix effect on the vibrational modes of Ag5. In contrast, the ν4 mode (75 cm−1) is observed at higher wavenumbers than in solid argon (68 cm−1). Such matrix effects on vibrational frequencies are well documented and understood.56,67,684. Conclusions
The vibrational wave-packet dynamics and frequency analysis of the fs NeNePo transients of Ag5 reveal three frequencies at 156 cm−1, 101 cm−1 and 56 cm−1 contributing to the observed quantum beating on the electronic ground state (2A1). Based on DFT calculations, the bands at 156 cm−1 and 101 cm−1 are attributed to the excitation of two totally symmetric vibrational normal modes of planar Ag5, namely, the ring breathing mode (ν1) and symmetric Ag3 stretching mode (ν3), respectively. The 56 cm−1 band is attributed to the difference frequency ν1 − ν3. The polarization dependence of the probe pulse reflects s and d partial wave character of the photoelectron, resulting from a ‘p-type’ molecular orbital of Ag5. The intensity of the observed beating frequencies is not only determined by Franck–Condon factors for the anion photodetachment step (first pulse), but also depends on the photoionization step (second pulse). The observed FT frequencies of Ag5 are similar to the vibrational frequencies measured by Raman spectroscopy in solid argon and differ only by minor shifts. The present studies demonstrate fs NeNePo spectroscopy as a powerful tool to study the vibrational wave-packet dynamics of neutral polyatomic metal clusters. The so-obtained far-IR frequency spectra allow to characterize the geometric structure of a fluxional metal cluster under a well-controlled environment.Author contributions
M. G., M. D. and J. J. performed the experimental works. M. G. curated and analysed the data. M. G. and J. J. prepared the figures and wrote the initial manuscript. All authors revised the manuscript. K. R. A. and J. J. designed the study. D. M. N., K. R. A. and J. J. coordinated the project, supervised the research and contributed to the data interpretations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft DFG as part of the major instrumentation grant INST 268/381-1. J. J. acknowledges the Alexander von Humboldt-Stiftung for a postdoctoral fellowship. M. G. gratefully acknowledges a doctoral scholarship from the Studienstiftung des deutschen Volkes. M. D. and D. M. N. were supported by the U.S. Air Force Office of Scientific Research under grant no. FA9550-19-1-0051.References
- D. Grandjean, E. Coutino-Gonzalez, N. T. Cuong, E. Fron, W. Baekelant, S. Aghakhani, P. Schlexer, F. DAcapito, D. Banerjee and M. B. J. Roeffaers, et al. , Science, 2018, 361(6403), 686 CrossRef CAS PubMed.
- S. Gao, D. Chen, Q. Li, J. Ye, H. Jiang, C. Amatore and X. Wang, Sci. Rep., 2014, 4, 4384 CrossRef PubMed.
- V. Porto, D. Buceta, B. Dominguez, C. Carneiro, E. Borrajo, M. Fraile, N. Davila-Ferreira, I. R. Arias, J. M. Blanco and M. C. Blanco, et al. , Adv. Funct. Mater., 2022, 32(29), 2113028 CrossRef CAS.
- L. Qin, F. Sun, Z. Gong, G. Ma, Y. Chen, Q. Tang, L. Qiao, R. Wang, Z.-Q. Liu and Z. Tang, ACS Nano, 2023, 17(13), 12747 CrossRef CAS PubMed.
- H. Zhai and A. N. Alexandrova, ACS Catal., 2017, 7(3), 1905 CrossRef CAS.
- Z. Zhang, B. Zandkarimi and A. N. Alexandrova, Acc. Chem. Res., 2020, 53(2), 447 CrossRef CAS PubMed.
- T. Imaoka, T. Toyonaga, M. Morita, N. Haruta and K. Yamamoto, Chem. Commun., 2019, 55(33), 4753 RSC.
- Z. Zhang, T. Masubuchi, P. Sautet, S. L. Anderson and A. N. Alexandrova, Angew. Chem., 2023, 135(20), e202218210 CrossRef.
- G. Liu, P. Poths, X. Zhang, Z. Zhu, M. Marshall, M. Blankenhorn, A. N. Alexandrova and K. H. Bowen, J. Am. Chem. Soc., 2020, 142(17), 7930 CrossRef CAS PubMed.
- D. Buceta, S. Huseyinova, M. Cuerva, H. Lozano, L. J. Giovanetti, J. M. Ramallo-López, P. López-Caballero, A. Zanchet, A. O. Mitrushchenkov, A. W. Hauser, G. Barone, C. Huck-Iriart, C. Escudero, J. C. Hernández-Garrido, J. J. Calvino, M. López-Haro, M. P. de Lara-Castells, F. G. Requejo and M. A. López-Quintela, Chemistry, 2023, 29(49), e202301517 CrossRef CAS PubMed.
- M. P. de Lara-Castells, C. Cabrillo, D. A. Micha, A. O. Mitrushchenkov and T. Vazhappilly, Phys. Chem. Chem. Phys., 2018, 20(28), 19110 RSC.
- P. López-Caballero, S. Miret-Artés, A. O. Mitrushchenkov and M. P. de Lara-Castells, J. Chem. Phys., 2020, 153(16), 164702 CrossRef PubMed.
- P. López-Caballero, J. M. Ramallo-López, L. J. Giovanetti, D. Buceta, S. Miret-Artés, M. A. López-Quintela, F. G. Requejo and M. P. de Lara-Castells, J. Mater. Chem. A, 2020, 8(14), 6842 RSC.
- J. A. Howard, R. Sutcliffe and B. Mile, J. Phys. Chem., 1983, 87(13), 2268 CrossRef CAS.
- T. L. Haslett, K. A. Bosnick and M. Moskovits, J. Chem. Phys., 1998, 108(9), 3453 CrossRef CAS.
- C. Yu, R. Schira, H. Brune, B. von Issendorff, F. Rabilloud and W. Harbich, Nanoscale, 2018, 10(44), 20821 RSC.
- S. Lecoultre, A. Rydlo, J. Buttet, C. Félix, S. Gilb and W. Harbich, J. Chem. Phys., 2011, 134, 18 Search PubMed.
- W. Harbich, S. Fedrigo and J. Buttet, Chem. Phys. Lett., 1992, 195(5–6), 613 CrossRef CAS.
- M. Harb, F. Rabilloud, D. Simon, A. Rydlo, S. Lecoultre, F. Conus, V. Rodrigues and C. Félix, J. Chem. Phys., 2008, 129(19), 194108 CrossRef CAS PubMed.
- S. Fedrigo, W. Harbich and J. Buttet, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(16), 10706 CrossRef CAS PubMed.
- M. Chen, J. E. Dyer, K. Li and D. A. Dixon, J. Phys. Chem. A, 2013, 117(34), 8298 CrossRef CAS PubMed.
- V. Bonačić-Koutecký, L. Češpiva, P. Fantucci and J. Koutecký, J. Chem. Phys., 1993, 98(10), 7981 CrossRef.
- J. Ho, K. M. Ervin and W. C. Lineberger, J. Chem. Phys., 1990, 93(10), 6987 CrossRef CAS.
- H. Handschuh, C.-Y. Cha, P. S. Bechthold, G. Ganteför and W. Eberhardt, J. Chem. Phys., 1995, 102(16), 6406 CrossRef CAS.
- K. Vetter, S. Proch, G. F. Ganteför, S. Behera and P. Jena, Phys. Chem. Chem. Phys., 2013, 15(48), 21007 RSC.
- D. Sucerquia, C. Parra, P. Cossio and O. Lopez-Acevedo, J. Chem. Phys., 2022, 156(15), 154301 CrossRef CAS PubMed.
- T. Leisner, S. Rutz, G. Sommerer, S. Vajda, S. Wolf, E. Schreiber and L. Wöste, Spectroscopy on mass-selected neutral clusters: Femtosecond dynamics of the ground state of Agn. AIP Conference Proceedings, 1996, pp. pp. 603–609.
- H. Heß, Femtosekunden-Spektroskopie an kalten Metallclustern, PhD thesis, Freie Universität, Berlin, 2000 Search PubMed.
- A. Fielicke, Chem. Soc. Rev., 2023, 52(11), 3778 RSC.
- M. A. Duncan, Int. J. Mass Spectrom., 2000, 200(1–3), 545 CrossRef CAS.
- K. R. Asmis, A. Fielicke, G. von Helden and G. Meijer, Chem. Phys. Solid Surf., 2007, 12, 327 CAS.
- G. Niedner-Schatteburg and M. M. Kappes, Chem. – Eur. J., 2021, 27(61), 15028 CrossRef PubMed.
- J. Roithová and J. M. Bakker, Mass Spectrom. Rev., 2022, 41(4), 513 CrossRef PubMed.
- A. Fielicke, I. Rabin and G. Meijer, J. Phys. Chem. A, 2006, 110(26), 8060 CrossRef CAS PubMed.
- D. M. Neumark, J. Phys. Chem. A, 2023, 127(19), 4207 CrossRef CAS PubMed.
- S. Wolf, G. Sommerer, S. Rutz, E. Schreiber, T. Leisner, L. Wöste and R. S. Berry, Phys. Rev. Lett., 1995, 74(21), 4177 CrossRef CAS PubMed.
- L. D. Socaciu-Siebert, J. Hagen, J. Le Roux, D. Popolan, M. Vaida, Š. Vajda, T. M. Bernhardt and L. Wöste, Phys. Chem. Chem. Phys., 2005, 7(14), 2706 RSC.
- J. Jin, M. Grellmann and K. R. Asmis, Phys. Chem. Chem. Phys., 2023, 25(36), 24313 RSC.
- H. Hess, S. Kwiet, L. Socaciu, S. Wolf, T. Leisner and L. Wöste, Appl. Phys. B, 2000, 71, 337 CrossRef CAS.
- H. Hess, K. R. Asmis, T. Leisner and L. Wöste, Eur. Phys. J. D, 2001, 16, 145 CrossRef CAS.
- D. W. Boo, Y. Ozaki, L. H. Andersen and W. C. Lineberger, J. Phys. Chem. A, 1997, 101(36), 6688 CrossRef.
- T. Leisner, S. Vajda, S. Wolf, L. Wöste and R. S. Berry, J. Chem. Phys., 1999, 111(3), 1017 CrossRef CAS.
- T. M. Bernhardt, J. Hagen, L. D. Socaciu, R. Mitrić, A. Heidenreich, J. Le Roux, D. Popolan, M. Vaida, L. Wöste and V. Bonačić-Koutecký, et al. , Chem. Phys. Chem., 2005, 6(2), 243 CrossRef CAS PubMed.
- F. Muntean, M. S. Taylor, A. B. McCoy and W. C. Lineberger, J. Chem. Phys., 2004, 121(12), 5676 CrossRef CAS PubMed.
- M. S. Taylor, J. Barbera, C.-P. Schulz, F. Muntean, A. B. McCoy and W. C. Lineberger, J. Chem. Phys., 2005, 122, 5 Search PubMed.
- J. Barbera, S. Horvath, V. Dribinski, A. B. McCoy and W. C. Lineberger, J. Chem. Phys., 2007, 126(8), 84307 CrossRef PubMed.
- C. Jackschath, I. Rabin and W. Schulze, Z. Phys. D - Atoms, Molecules and Clusters, 1992, 22, 517 CrossRef CAS.
- P. H. C. Eilers, Anal. Chem., 2003, 75(14), 3631 CrossRef CAS PubMed.
- H. F. M. Boelens, P. H. C. Eilers and T. Hankemeier, Anal. Chem., 2005, 77(24), 7998 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7(18), 3297 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8(9), 1057 RSC.
- K. Duanmu and D. G. Truhlar, J. Phys. Chem. C, 2015, 119(17), 9617 CrossRef CAS.
- S. Zhao, Z.-H. Li, W.-N. Wang, Z.-P. Liu, K.-N. Fan, Y. Xie and H. F. Schaefer, J. Chem. Phys., 2006, 124(18), 184102 CrossRef PubMed.
- L. A. Mancera and D. M. Benoit, Phys. Chem. Chem. Phys., 2016, 18(1), 529 RSC.
- S. Gozem and A. I. Krylov, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2022, 12(2), e1546 CrossRef CAS.
- M. Gruebele and A. H. Zewail, J. Chem. Phys., 1993, 98(2), 883 CrossRef CAS.
- D. M. Jonas, S. E. Bradforth, S. A. Passino and G. R. Fleming, J. Phys. Chem., 1995, 99(9), 2594 CrossRef CAS.
- S. Kawamura, M. Yamaguchi, S. Kono, M. Arakawa, T. Yasuike, T. Horio and A. Terasaki, J. Phys. Chem. A, 2023, 127(29), 6063 CrossRef CAS PubMed.
- Z. Ma, L. Chen, C. Xu and J. A. Fournier, J. Phys. Chem. Lett., 2023, 14(43), 9683 CrossRef CAS PubMed.
- L. Chen, Z. Ma and J. A. Fournier, J. Chem. Phys., 2023, 159(4), 041101 CrossRef CAS PubMed.
- L. Chen, J. L. S. Dean and J. A. Fournier, J. Phys. Chem. A, 2021, 125(47), 10235 CrossRef CAS PubMed.
- J. Cooper and R. N. Zare, J. Chem. Phys., 1968, 48(2), 942 CrossRef CAS.
- M. DeWitt, M. C. Babin, J. A. Lau, T. Solomis and D. M. Neumark, J. Phys. Chem. A, 2022, 126(43), 7962 CrossRef CAS PubMed.
- J. van der Tol, D. Jia, Y. Li, V. Chernyy, J. M. Bakker, M. T. Nguyen, P. Lievens and E. Janssens, Phys. Chem. Chem. Phys., 2017, 19(29), 19360 RSC.
- A. Fielicke, J. T. Lyon, M. Haertelt, G. Meijer, P. Claes, J. de Haeck and P. Lievens, J. Chem. Phys., 2009, 131(17), 171105 CrossRef PubMed.
- Y. Zhao and M. Zhou, Sci. China: Chem., 2010, 53, 327 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06229e |
| This journal is © the Owner Societies 2024 |

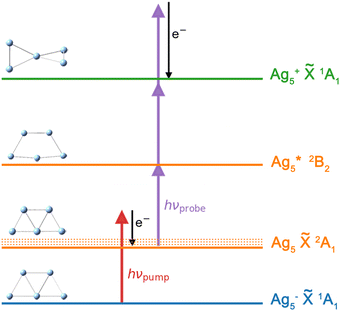
![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 1A1) by the first fs laser pulse (red arrow), populating vibrational excited levels (
1A1) by the first fs laser pulse (red arrow), populating vibrational excited levels (