Infrared spectra of Si_nH_4n−1⁺ ions (n = 2–8): inorganic H–(Si–H)_n−1 hydride wires of penta-coordinated Si in 3c–2e and charge-inverted hydrogen bonds

Abstract

Si_nH_m⁺ cations are important constituents in silane plasmas and astrochemical environments. Protonated disilane (Si₂H₇⁺) was shown to have a symmetric three-centre two-electron (3c–2e) Si–H–Si bond that can also be considered as a strong ionic charge-inverted hydrogen bond with polarity Si^δ+–H^δ−–Si^δ+. Herein, we extend our previous work to larger Si_nH_4n−1⁺ cations, formally resulting from adding SiH₄ molecules to a SiH₃⁺ core. Infrared spectra of size-selected Si_nH_4n−1⁺ ions (n = 2–8) produced in a cold SiH₄/H₂/He plasma expansion are analysed in the SiH stretch range by complementary dispersion-corrected density functional theory calculations (B3LYP-D3/aug-cc-pVTZ) to reveal their bonding characteristics and cluster growth. The ions with n = 2–4 form a linear inorganic H–(Si–H)_n hydride wire with adjacent Si–H–Si 3c–2e bridges, whose strength decreases with n, as evident from their characteristic and strongly IR active SiH stretch fundamentals in the range 1850–2100 cm⁻¹. These 3c–2e bonds result from the lowest-energy valence orbitals, and their high stability arises from their delocalization along the whole hydride wire. For Si_nH_4n−1⁺ with n ≥ 5, the added SiH₄ ligands form weak van der Waals bonds to the Si₄H₁₉⁺ chain. Significantly, because the Si_nH_4n−1⁺ hydride wires are based on penta-coordinated Si atoms leading to supersaturated hydrosilane ions, analogous wires cannot be formed by isovalent carbon.

---

Introduction

Hydrogen passivation converts reactive Si_n clusters into stable polysilanes nanostructures (Si_nH_m), with potential applications of their derivatives and ions in material science, inorganic chemistry, catalysis, plasma- and astrochemistry, and theoretical chemistry.^1–25 For example, polysilane oligomers and their radical ions reveal interesting electronic, photophysical, and optical properties arising from substantial σ-delocalization of the bonding Si–Si electrons.^1,26 Recently, higher-order silanes have been identified during monosilane pyrolysis by gas chromatography–mass spectrometry.²¹ From an astrochemical point of view, Si and H are amongst the ten most abundant elements in the universe, and thus Si_nH_m molecules and their ions are expected to occur in the interstellar medium, although so far only SiH₄ has been identified.²² In the laboratory, saturated Si_nH_2n+2 polysilanes up to n = 19 have been produced from bombarding SiH₄ ices with electrons and detected by mass spectrometry.²⁷ The discussed production mechanism involves radical–radical recombination and insertion reactions, although their structures have remained elusive. The structure and reactivity of Si_nH_m⁺ cations relevant for silane plasmas used in plasma-enhanced chemical vapor deposition for the industrial fabrication of Si-based microelectronic thin films and devices^17–20 have mostly been characterized by mass spectrometry.^15,16,28,29 However, firm identification of structure and bonding of Si_nH_m⁺ ions in plasma and astrochemical environments requires spectroscopic characterization, which is still rather scarce for ions with n ≥ 2.^30–33 In the condensed phase, silyl cations are highly reactive,^8,11 and only recently a SiH₃⁺ compound could be synthesized and characterized.¹⁴

Although Si and C are both group IV elements, their bonding properties differ substantially,³⁴ which partly arises from their different electronegativity with respect to H (EN = 1.90, 2.20, 2.55 for Si, H, C on the Pauling scale). Due to their weaker and less directional Si–Si and Si–H bonds, Si_nH_m molecules exhibit a larger variety of bonding motifs as compared to the corresponding C_nH_m molecules. For example, different from C_nH_m, Si_nH_m have more frequently Si–H–Si bridges, characterized by a three-center two-electron (3c–2e) bond.^35,36 In amorphous and crystalline silicon (a-Si:H and c-Si), used for example in commercial solar cells, linear Si–H–Si bridges are typical binding motifs for proton impurities. In c-Si, they form well-defined linear and symmetric Si–H–Si bonds.³⁷ The Si–H–Si 3c–2e bond was first detected in crystals of cyclic and linear silyl cations.^38–40 Subsequently, infrared photodissociation (IRPD) spectroscopy has been used in our group to characterize such 3c–2e bonds in a variety of Si_nH_m⁺ cations in the gas phase, i.e. free from any perturbation by matrix effects and counter ions. The studied ions include protonated disilane (Si₂H₇⁺),³¹ an isomer of trisilane (Si₃H₈⁺),³² and Si_nH_4n−4⁺ ions (n = 4–8)³³ which may formally be described as silane aducts of the unsaturated sylilene cation, Si₂H₄⁺(SiH₄)_n−2. The characteristic IR fingerprint of the Si–H–Si bond is its strongly IR active antisymmetric stretch fundamental (σ_SiHSi) occurring in the 1600–2100 cm⁻¹ range, whose frequency strongly depends on the structural and energetic details of the Si–H–Si bridges.³³ The strength of the Si–H–Si bonds can range from strong 3c–2e chemical bonds to very weak van der Waals contacts (5–150 kJ mol⁻¹).³³ In the covalent case, the molecular orbital describing the 3c–2e bond is the lowest-energy valence orbital, illustrating its high stability.^31,32 Because the EN of H is higher than that of Si, these 3c–2e bonds can also be considered as strong ionic charge-inverted hydrogen bonds (CIHB),^41,42 with polarity Si^δ+–H^δ−–Si^δ+ resulting in the limit of ionic bonding in a hydride (H⁻) bond. This is opposite to regular A^δ−–H^δ+–B^δ− hydrogen bonds (H-bonds) in which, according to the IUPAC definition,⁴³ a positive H atom (proton) is located between two basic atoms A (proton donor) and B (proton acceptor) with higher EN.

Herein, we extend our previous IRPD studies on silane cations to the Si_nH_4n−1⁺ series with n = 2–8 to probe their structure, bonding and cluster growth mechanism as a function of the cluster size, along with complementary calculations. The most stable structures of these supersaturated hydrosilane ions may formally be considered as SiH₃⁺(SiH₄)_n−1 clusters and exhibit unprecedented inorganic silicon hydride wires, H–(Si–H)_n with multiple 3c–2e Si–H–Si bonds of penta-coordinated Si atoms. These 3c–2e bonds get weaker as the chain grows and, starting from n = 5, the Si₄H₁₅⁺ wire is solvated by SiH₄ ligands via weak van der Waals bonds. The Si_nH_4n−1⁺ ions differ qualitatively from the previously studied Si_nH_4n−4⁺ series³³ because they do not contain any Si–Si and/or Si=Si bonds. While SiH₃⁺ and Si₂H₇⁺ (n = 1 and 2) have been well studied by IR spectroscopy,^31,44–46 mass spectrometry,^15,31,47,48 and calculations,^31,49,50 the only study available for n ≥ 3 utilizes high-pressure mass spectrometry to determine the binding enthalpies of SiH₃⁺(SiH₄)_n−1 as −ΔH₀ = >146, 37.7, and 13.8 kJ mol⁻¹ for n = 2–4, respectively.¹⁵ Although these data are not sensitive to structure, the authors concluded symmetric bonding of two SiH₄ ligands to the two sides of the 3p_z orbital of the planar SiH₃⁺ cation and thus closure of the first solvation shell at n = 3.

Results and discussion

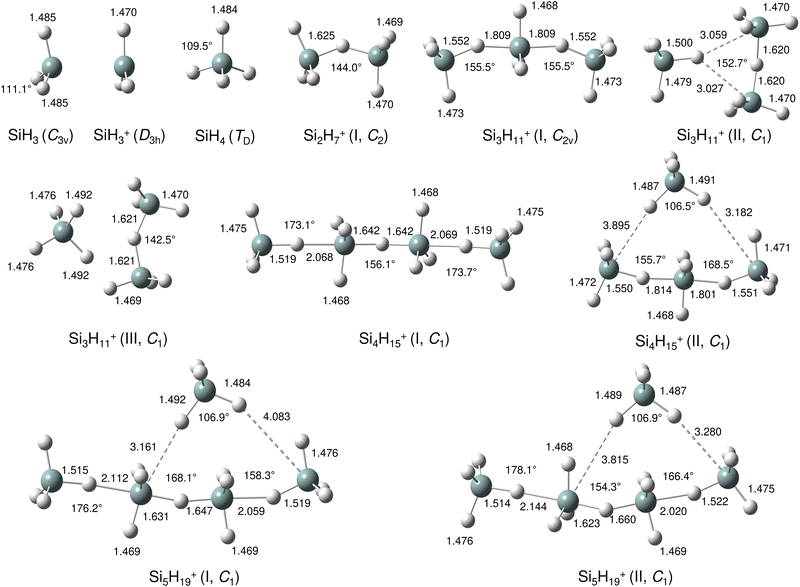
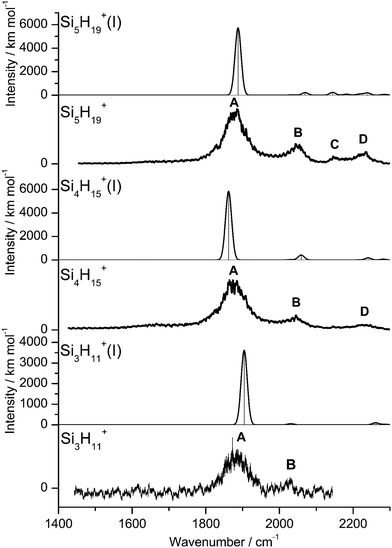
IRPD spectra of size-selected Si_nH_4n−1⁺ ions with n = 2–8 in the SiH stretch range (1400–2300 cm⁻¹, Fig. 1, Table 1) were obtained in a tandem quadrupole mass spectrometer coupled to an electron ionization source.^51,52 The ions were produced in a pulsed supersonic plasma expansion of a SiH₄/H₂/He gas mixture (ratio 1/1/38) at 3 bar stagnation pressure. This setup was used previously to record IRPD spectra of bare Si_nH_4n−4⁺ ions and Ar/Ne tagged Si₂H₆⁺,³⁰ Si₃H₈⁺,³² SiH₃OH₂⁺,⁵³ and Si₂H₇⁺.³¹ Chemical ionisation of this gas mixture causes silane polymerization reactions forming Si_nH_4n−1⁺ up to n = 8. They form in barrierless aggregation reactions of SiH₄ units to SiH₃⁺,^15,31,32 which is the major fragment of ionizing SiH₄. A typical mass spectrum of the ion source is shown in Fig. S1 in the ESI.† Si_nH_4n−1⁺ ions selected by the first quadrupole were irradiated with a tuneable IR laser pulse of an optical parametric oscillator (ν_IR, 2–5 mJ, 10 Hz repetition rate, 1 cm⁻¹ bandwidth). Resonant vibrational excitation by single-photon absorption resulted in the evaporation of either one (n = 3–4) or two (n ≥ 5) SiH₄ molecules, indicating a formal cluster composition of SiH₃⁺(SiH₄)_n−1 with decreasing SiH₄ binding energy as n increases. IRPD spectra were then obtained as a function of ν_IR by monitoring the fragment ions selected by the second quadrupole and normalization for laser intensity. Because the SiH₄ binding energy of Si₂H₇⁺ (ca. 150 kJ mol⁻¹) is much higher than the employed IR photon energy (<25 kJ mol⁻¹), its spectrum could only be obtained by Ne/Ar tagging.³¹ This spectrum was reported and analysed previously³¹ and is included in Fig. 1 only for comparison.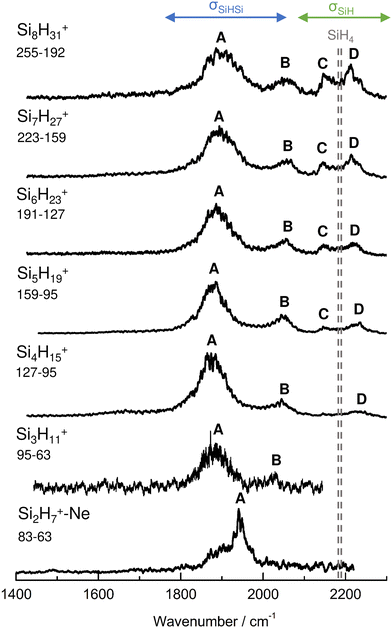

Fig. 1 IRPD spectra of Si_nH_4n−1⁺ (n = 3–8) in the SiH stretch range recorded in the SiH₄ or 2SiH₄ loss channel as indicated by the m/z values of parent and daughter ions. The Si₂H₇⁺Ne spectrum (n = 2) recorded in the Ne loss channel is included for comparison.³¹ The probed spectral range (1400–2300 cm⁻¹) covers σ_SiH fundamentals (C/D) of free Si–H bonds and σ_SiHSi modes (A/B) of 3c–2e bonds (Table 1). The dashed lines indicate the positions of the SiH stretch modes of bare SiH₄ at ν₁(a₁) = 2187 and ν₃(t₂) = 2191 cm⁻¹.⁵⁴

Table 1 Positions and widths (fwhm in parenthesis) in cm⁻¹ of the transitions observed in the IRPD spectra of Si_nH_4n−1⁺ (Fig. 1) compared to frequencies of SiH₄

Peak	Mode	SiH4^a	Si2H7^+Ne^b	Si3H11^+	Si4H15^+	Si5H19^+	Si6H23^+	Si7H27^+	Si8H31^+
a Ref. 54. b Ref. 31.
A	σ SiHSi(a)		1941 (30)	1886 (65)	1873 (70)	1877 (65)	1885 (70)	1893 (80)	1903 (100)
B	σ SiHSi(s)			2031 (15)	2045 (50)	2051 (45)	2055 (60)	2058 (60)	2060 (60)
C	σ SiH	2187				2144 (25)	2147 (30)	2144 (25)	2147 (35)
D	σ SiH	2191			2236 (45)	2235 (40)	2225 (40)	2216 (40)	2211 (45)

---

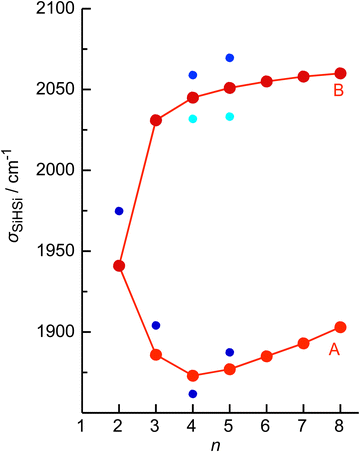
The four major peaks A–D observed in the IRPD spectra are readily assigned to the strongly IR active Si–H–Si stretch modes of the 3c–2e bond(s) between 1800 and 2100 cm⁻¹ (σ_SiHSi, A and B) and the much weaker SiH stretch modes of the free Si–H bonds between 2100 and 2300 cm⁻¹ (σ_SiH, C and D). For comparison, Fig. 1 also indicates the symmetric and triply degenerate antisymmetric SiH stretch frequencies of bare SiH₄ by dashed lines, ν₁(a₁)/ν₃(t₂) = 2187/2191 cm⁻¹.⁵⁴ Significantly, while ν₁ is IR forbidden in bare SiH₄, it becomes slightly allowed by the presence of the nearby positive charge and experiences shifts and splittings. The IRPD spectra are dominated by peak A, assigned to antisymmetric σ_SiHSi(a) modes of the Si–H–Si 3c–2e bonds by comparison to the previous analysis of the Si₂H₇⁺ and Si_nH_4n−4⁺ spectra. This band experiences a substantial monotonic red shift from 1941 to 1873 cm⁻¹ for n = 2–4 (by −55 to −13 cm⁻¹), while it shows smaller incremental blue shifts of +4, +8, +8, and +10 cm⁻¹ for n = 5–8, indicating a change in bonding at n = 5. Starting from n = 3, band B assigned to the corresponding symmetric σ_SiHSi(s) modes of the 3c–2e bonds grow in intensity. This mode exists only for n ≥ 3, indicating the appearance of a second Si–H–Si 3c–2e bond in Si₃H₁₁⁺. Band B experiences gradual monotonic blue shifts by +14, +6, +4, +3, and +2 cm⁻¹ for n = 4–8. The magnitude of the shifts drops for n ≥ 5, again indicating a change in bonding in this size regime. Bands C and D occur in the range of the free SiH stretch modes and grow roughly linearly in intensity starting from n = 5, again indicating a change in bonding at this size range. Their positions at around 2145 and 2225 cm⁻¹ hardly change as a function of n, although their widths get somewhat broader. Hence, the first rough analysis of the number and position of the IRPD bands, and their incremental shifts and changes in IR activity suggests a Si_nH_4n−1⁺ cluster growth with the formation of chemical 3c–2e bonds up to n = 4 and subsequent attachment of weakly bonded SiH₄ ligands attached to a Si₄H₁₅⁺ core ion by induction and dispersion forces. The weaker SiH₄ binding energy of the larger ions is also visible in the photofragmentation branching ratios measured at band A (Table S1 in the ESI†). While Si_nH_4n−1⁺ ions with n ≤ 4 evaporate only one SiH₄ ligand, those with n ≥ 5 can dissociate two ligands at an IR photon energy of around 2000 cm⁻¹. Neglecting kinetic energy release and assuming that the absorbed photon energy is merely used for ligand dissociation (and not for changes in internal energy) and all SiH₄ ligands have the same binding energy for n = 5–8, one can bracket their dissociation energy as D₀ = 850 ± 150 cm⁻¹ or 10.2 ± 1.8 kJ mol⁻¹. This value is consistent with the SiH₄ binding enthalpy of the somewhat stronger bonded n = 4 ion reported as −ΔH₀ = 13.8 ± 1.3 kJ mol⁻¹.¹⁵

For a more detailed structural and vibrational assignment and the analysis of chemical bonding (charge distributions, binding energies, molecular orbitals), quantum chemical calculations were performed at the dispersion-corrected B3LYP-D3/aug-cc-pVTZ level for Si_nH_4n−1⁺ ions with n ≤ 5 (Fig. 2, Fig. S2–S7 and Tables S2–S5 in ESI†). Reported relative energies (E₀) and binding energies (D₀) are corrected for harmonic zero-point vibrational energies. All calculated frequencies are scaled by a factor of 0.97878 to optimize the agreement between the calculated and measured ν_SiH frequencies of SiH₃ and SiH₄. The atomic charge distribution is evaluated using the natural bond orbital (NBO) analysis. We consider herein mainly the most stable structure for each cluster size, while information for less stable local minima is provided in the ESI.†

Fig. 2 Lowest energy structures of SiH₃, SiH₃⁺, SiH₄, Si₂H₇⁺, Si₃H₁₁⁺(I–III), Si₄H₁₅⁺(I,II) and Si₅H₁₉⁺(I,II) in their ground electronic states calculated at the B3LYP-D3/aug-cc-pVTZ level. Selected bond lengths and bond angles are given in Å and degree, respectively.

Our calculations yield a planar structure for SiH₃⁺ (D_3h) with a Si–H bond length and stretch frequencies (r_e = 1.470 Å, ν_1/3 = 2218/2295 cm⁻¹) in good agreement with previous experimental and computational data.^55,56 In line with the EN of Si and H, the partial charges are q_H = −124 and q_Si = +1371 me. The closed-shell SiH₃⁺ cation (¹A₁) has a vacant and thus rather electrophilic 3p_z orbital, which serves as attractive binding sites for neutral ligands, such as rare gas atoms,⁵⁷ H₂,^45,46 or H₂O.⁵³ Barrierless attachment of SiH₄ to this orbital results in protonated disilane, Si₂H₇⁺, forming a strong symmetric Si–H–Si 3c–2e bond characterized in detail previously.³¹ Our computed binding energy for SiH₄ loss (D₀ = 150.1 kJ mol⁻¹) agrees well with the measured bond enthalpy (−ΔH₀ > 146 kJ mol⁻¹)¹⁵ and our previous MP2 and CBS-QB3 calculations (148.2 and 150.1 kJ mol⁻¹).³¹ The SiH₄ ligand attacks the 3p_z orbital with one of the negative H atoms of SiH₄ (q_H = −161 and q_Si = +643 me) in a bent configuration with C₂ symmetry (θ = 144°), which is slightly more stable than the linear Si–H–Si structure (D_3h/3d) by only a few kJ mol⁻¹ (<5 kJ mol⁻¹),³¹ indicating a rather flat and anharmonic double minimum potential for H motion perpendicular to the Si–Si axis. The SiH₃ groups become slightly nonplanar (intermediate between sp² and sp³ hybridisation) and the barriers for hindered internal rotation are rather low (<3 kJ mol⁻¹).³¹ The corresponding molecular orbital (MO) describing the rather strong 3c–2e bond (1.625 Å) is delocalized along the Si–H–Si bridge and is the lowest valence MO (HOMO-6, Fig. 3). Although formally a proton is added to Si₂H₆, the bridging H atom has a negative charge of q_H = −304 me, while the two Si atoms carry most of the excess positive charge (q_Si = +954 me), and are thus attractive binding sites for both rare gas³¹ and further SiH₄ ligands. The alternating charge distribution in Si^δ+–H^δ−–Si^δ+ qualifies Si₂H₇⁺ as prototypical cationic example of a CIHB, and its formation causes charge transfer of 348 me from SiH₃⁺ to SiH₄. The strongly IR active antisymmetric SiH stretch mode is computed as σ_SiHSi = 1975 cm⁻¹ (I = 1314 km mol⁻¹), in good agreement with the value of the Ne-tagged complex (1941 cm⁻¹).

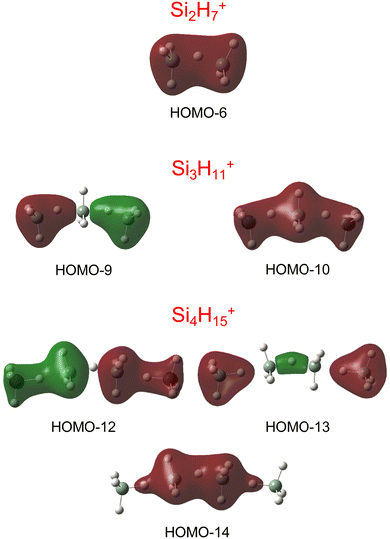Fig. 3 Visualisation of the lowest valence MOs of the most stable structures of Si₂H₇⁺, Si₃H₁₁⁺, and Si₄H₁₅⁺, representing the 3c–2e bonds.

By far, the most stable structure of Si₃H₁₁⁺ is obtained by barrierless attachment of SiH₄ to a Si atom of Si₂H₇⁺ (isomer I, Fig. 2). In this C₂ symmetric structure, two equivalent SiH₄ ligands bind to the 3p_z orbital of a central SiH₃⁺ cation forming two strongly asymmetric and bent 3c–2e bonds (1.809 and 1.552 Å, 155.5°). According to the much longer Si–H bond in the bridge (1.809 vs. 1.625 Å), the SiH₄ binding energy is computed to be much weaker than in Si₂H₇⁺ (40.8 vs. 150.0 kJ mol⁻¹) but again in excellent agreement with the measured bond enthalpy of −ΔH₀ = 37.7 ± 1.3 kJ mol⁻¹.¹⁵ The lower binding energy enables the IRPD spectrum of Si₃H₁₁⁺ to be recorded without tagging. This S_N2 like complex features one penta-coordinated Si atom and can be considered as a supersaturated hydrosilane molecule, because even protonated aliphatic trisilane would only have nine H atoms for three Si atoms (Si₃H₉⁺). Formation of the two CIHBs causes charge transfer of 433 me from SiH₃⁺ to the two SiH₄ ligands. The two negative H atoms in Si₃H₁₁⁺ carry a slightly more negative charge than in Si₂H₇⁺ (−306 vs. −304 me). The two MOs describing the two 3c–2e bonds are completely delocalized along the Si–H–Si–H–Si bridge and are again the two lowest valence MOs (HOMO-9/10, Fig. 3). The coupling of the two σ_SiHSi modes of the two 3c–2e bonds results in a splitting of the σ_SiHSi mode of 1975 cm⁻¹ of n = 2 in a rather weak symmetric and a rather strong antisymmetric normal mode at σ_SiHSi(s) = 2031 cm⁻¹ and σ_SiHSi(a) = 1904 cm⁻¹ for n = 3, respectively. These bands are in excellent agreement with the observed bands B and A predicted at 2031 and 1886 cm⁻¹ with respect to their absolute frequency, the frequency shifts with respect to band A of Si₂H₇⁺, and their relative IR activities (Fig. 4). We also calculated two further less stable Si₃H₁₁⁺ isomers (II and III), in which SiH₄ ligands are attached to the side of a Si₂H₇⁺ core ion by much weaker induction and dispersion forces (D₀ = 13.8 and 12.3 kJ mol⁻¹) and these feature only one 3c–2e bond. As a consequence, their predicted IR spectra are rather similar to that of Si₂H₇⁺ and in strong contradiction with the experiment (Fig. S3 in ESI†). Hence, we do not discuss them further here.

Fig. 4 Experimental IRPD spectra of Si₃H₁₁⁺, Si₄H₁₅⁺, and Si₅H₁₉⁺ compared to linear IR absorption spectra of the most stable isomers calculated at the B3LYP-D3/aug-cc-pVTZ level (Table S2 in ESI†).

The most stable structure of Si₄H₁₅⁺ (isomer I) is derived by barrierless addition of a further SiH₄ ligand to a terminal Si atom of the linear Si₃H₁₁⁺ wire. In this nearly symmetric structure, two almost equivalent SiH₄ ligands bind to the highly positive Si atoms of a central Si₂H₇⁺ cation forming a rather strong symmetric 3c–2e bond in the middle of the wire (1.642 Å, 156°) and two nearly equivalent and weaker asymmetric 3c–2e bonds at both ends (2.069 and 1.519 Å, 173°). (The C₂ symmetric structure is predicted as a transition state.) The MOs describing the three 3c–2e bonds are again completely delocalized along the Si–H–Si–H–Si bridge and these are again the three lowest valence MOs (HOMO-12/13/14, Fig. 3). The binding energy of the terminal SiH₄ units drops further down to D₀ = 14.6 kJ mol⁻¹, again in excellent agreement with the measured bond enthalpy of −ΔH₀ = 13.8 ± 1.3 kJ mol⁻¹.¹⁵ The lower binding energy is consistent with the smaller charge transfer from Si₃H₁₁⁺ to the added SiH₄ ligand (110 me). This linear inorganic hydride wire features two penta-coordinated Si atoms and is an even more supersaturated silane molecule than Si₃H₁₁⁺, because protonated aliphatic tetrasilane has eleven H atoms for four Si atoms (Si₄H₁₁⁺), i.e. four H atoms less than Si₄H₁₅⁺. Attachment of the two SiH₄ ligands at opposite ends of Si₂H₇⁺ changes its parameters with respect to both bond lengths and angle of the 3c–2e bridge (1.642 Å and 156° vs. 1.625 Å and 144°) and the negative charge on the central H atom (q_H = −317 vs. −304 me). The three 3c–2e bonds have their characteristic σ_SiHSi modes predicted at 1862 (very strong), 2032 (very weak), and 2059 (weak) cm⁻¹, with I = 5844, 34, and 423 km mol⁻¹, respectively. These predicted frequencies show again good agreement with the corresponding bands A and B at 1873 and 2045 cm⁻¹, where the latter band covers both weak σ_SiHSi modes (Fig. 4). Finally, the weak band D at 2236 cm⁻¹ can also be explained by unresolved σ_SiH modes with low IR activity in this spectral range. We also computed further less stable Si₄H₁₅⁺ isomers, in which either one SiH₄ ligand is attached to the side of Si₃H₁₁⁺ or two SiH₄ ligands attached to the side of Si₂H₇⁺, all with D₀ < 12 kJ mol⁻¹. As their predicted IR spectra do not match the measured IRPD spectrum recorded for Si₄H₁₅⁺, they are not considered further here (Fig. S4 in ESI†).

For the Si₅H₁₉⁺ ions, our calculations yield six low-energy isomers, all within an energy range of 4 kJ mol⁻¹. The binding energy for adding SiH₄ ligands to the Si_nH_4n−1⁺ wire drops with the length of the chain, and at n = 5 it is no longer favourable to extend the Si₄H₁₅⁺ chain further in a linear fashion. Indeed, we could not find a stable minimum for such a n = 5 chain, because the added SiH₄ ligand prefers to move closer to the central Si₂H₇⁺ unit, which carries a substantial amount of the positive excess charge. To this end, the global minimum identified for Si₅H₁₉⁺ has a SiH₄ unit attached to the side of the Si₄H₁₅⁺ wire, with D₀ = 10.6 kJ mol⁻¹ and very long SiH⋯Si contacts (3.161 and 4.083 Å). Further low-energy minima can be obtained for other isomers, with one SiH₄ attached to Si₄H₁₅⁺ or two SiH₄ ligands attached to the Si₃H₁₁⁺ core via induction and dispersion forces. The IR spectra predicted for Si₅H₁₉⁺ clusters with one or two SiH₄ ligands are quite different, because the core ions, Si₄H₁₅⁺ or Si₃H₁₁⁺, determine the coarse structure in the strongly IR active σ_SiHSi range. Comparison of these spectra with the measured IRPD spectrum suggests that the core in the observed Si₅H₁₉⁺ ions is the Si₄H₁₅⁺ wire. Depending on the exact position of the last weakly-bonded SiH₄ ligand in Si₅H₁₉⁺, the symmetry, structure, charge distribution, and IR spectrum changes slightly. Taking the computed global minimum, the charge transfer from Si₄H₁₅⁺ to SiH₄ is rather small (7 me). The intense σ_SiHSi transition predicted at 1887 cm⁻¹ agrees well with band A observed at 1877 cm⁻¹, while the two lower-intensity σ_SiHSi modes computed at 2033 and 2070 cm⁻¹ match with peak B at 2051 cm⁻¹. In the higher frequency range, the σ_SiH modes of the SiH₄ ligand and SiH₃ units predicted at 2144, 2182, 2214, 2224, 2238, 2239, and 2244 cm⁻¹ can be attributed to the weak broad and unresolved peaks C and D at 2144 and 2235 cm⁻¹, respectively.

No calculations have been performed for Si_nH_4n−1⁺ clusters with n ≥ 6, because of their multiple low-energy local minima, which differ from their global minimum merely by the different attachment of weakly-bonded SiH₄ ligands to the linear Si₄H₁₅⁺ core. The excellent agreement of the measured σ_SiHSi frequencies with those calculated for the global minima obtained for n ≤ 5 in Fig. 4 confirms the deduced cluster growth. The intense band A drops significantly in frequency for n = 2–4 and increases the monotonically for n ≥ 4 with a smaller slope, confirming the change in bonding mechanism from chemical to van der Waals between n = 4 and 5 (Fig. 5).

Fig. 5 Experimental σ_SiHSi frequencies of Si_nH_4n−1⁺ (bands A and B, red) as a function of n compared to computed values for the strongest (blue) and weaker (cyan) component, illustrating the change from strong chemical to weak van der Waals bonding between n = 4 and 5.

In the following, we analyse the binding properties in the identified H–(Si–H)_n wire in more detail. In general, Si–H–Si bridges are often formed by a 3c–2e bond in which two electrons in a bonding orbital establish two stable chemical bonds. These Si–H⋯Si H-bonds in Si_nH_m⁺ cations feature a cationic CIHB, because the EN of Si is lower than that of H, leading to a charge configuration (Si^δ+–H^δ−⋯Si^δ+) opposite from that of a conventional σ-type H-bond between a proton donor A and an acceptor B (A^δ−–H^δ+⋯B^δ−). However, in many aspects these CIHBs show similar features as the regular H-bonds, including the redshifts of the proton donor stretch frequency (σ_AH) observed in the IR spectrum. The adjacent Si–H–Si bridges observed in Si_nH_4n−1⁺ form an interesting inorganic hydride wire of the type H–(Si–H)_n in which the H atoms carry negative partial charges. A systematic characterization of individual Si–H–Si bridges as a function of the two Si–H bond lengths (R₁ and R₂) has been presented in our previous study of Si_nH_4n−4⁺.³³ In general, the more symmetric the Si–H–Si geometry, the stronger the 3c–2e bond. This can be observed in the H–(Si–H)_n wires with n = 2 and 4, in which the (inner) 3c–2e bond is rather strong and short with R₁ = R₂ = 1.625 and 1.642 Å, respectively, and D₀(n = 2) = 150 kJ mol⁻¹. On the other hand, the (outer) 3c–2e bonds for n = 3 and 4 are more asymmetric (R₁ = 1.552/1.519 Å and R₂ = 1.809/2.069 Å), reducing the bond strength to D₀(n = 3/4) = 41/15 kJ mol⁻¹, respectively. The correlation of the Si–H–Si bond angle with the 3c–2e bond strength is less strong, although it appears that they are more linear for weaker bonds. The observed trend is fully consistent with the analysis of Wiberg bond indices for the two bonds in the Si–H–Si bridge, yielding 0.44/0.44 for n = 2, 0.60/0.27 for n = 3, and 0.43/0.43 and 0.75/0.14 for the inner and outer bridges of n = 4. Clearly, for the weakly-bonded SiH₄ ligand in n = 5, the indices of 0.92/0.00 illustrate the situation of a bare van der Waals bond. In general, the H atoms in the 3c–2e bridges carry a substantially more negative partial charge (q_H = −290 to −320 me) than the free H atoms (−90 to −135 me). At the same time, the Si atoms carry nearly a full positive charge (q_Si = +800 to +960 me), justifying the view of a hydride bride in the limit of ionic bonding (e.g., Si⁺H⁻Si⁺).

In the following, we briefly compare the properties of the Si_nH_4n−1⁺ hydride wires to those of related systems. Overall, due to higher symmetry and the lack of any Si–Si/Si=Si bonds, the IRPD spectra of Si_nH_4n−1⁺ are much simpler and feature less bands than those of the previously studied Si_nH_4n−4⁺ ions,³³ which cannot form a regular hydride wire and lack supersaturation. The bonding of rare gas (Rg) atoms and H₂ ligands to the SiH₃⁺ cation is much weaker than that of SiH₄ ligands. Thus, while in SiH₃⁺Rg_1–2 and SiH₃⁺(H₂)_1–2 the ligands form weak van der Waals bonds to the 3p_z orbital of SiH₃⁺,^15,45,46,57 SiH₄ ligands form stronger covalent 3c–2e bonds in the SiH₃⁺(SiH₄)_1–2 hydride wires. The interaction of Rg atoms and H₂ with the related carbon analogue CH₃⁺ is much stronger than with SiH₃⁺, leading to covalent bonds in CH₃⁺Rg dimers with heavy Rg atoms and in CH₅⁺.^51,58–61 As (i) the EN of C is higher than that of H and (ii) C does not like to be penta-coordinated, the C_nH_4n−1⁺ ions do not form supersaturated hydride wires but instead form weakly-bonded van der Waals clusters of CH₄ ligands with a covalently-bonded C₂H₇⁺ core (Fig. S8–S10 in ESI†).^62,63 The linear H–(Si–H)_n hydride wires in Si_nH_4n−1⁺ differ in several aspects from the corresponding proton wires and networks frequently observed, for example in protonated water and ammonia clusters.^64–67 First, the H atoms in Si_nH_4n−1⁺ are negatively charged because EN(Si) < EN(H), while the H atoms in O–H–O and N–H–N bridges are positive because EN(O/N) > EN(H). Moreover, the H–(Si–H)_n hydride wires are essentially one-dimensional (1D), while H⁺(H₂O)_n and H⁺(NH₃)_n form 2D to 3D networks exhibiting proton transport via the Grotthuss mechanism.^68–70 Linear proton wires can be formed for example in protonated imidazole clusters, in which however a heterocyclic spacer is involved.^71–73

Conclusions

The interpretation of IRPD spectra of Si_nH_4n−1⁺ ions with n = 2–8 by complementary quantum chemical calculations reveals the formation of an inorganic H–(Si–H)_n hydride wire in the size range n = 2–4, with up three adjacent nonlinear covalent 3c–2e bonds involving penta-coordinated Si atoms. The binding energy with respect to SiH₄ elimination becomes weaker as the chain length (n) increases. As a result, starting from n = 5 further SiH₄ ligands bind weakly to the side of the linear Si₄H₁₅⁺ chain by induction and dispersion forces. The formation of such a wire is not favourable for the carbon analogue because penta-coordination is highly unfavourable and the EN order (Si < H < C), as illustrated by a comparison of the most stable structures of C_nH_4n−1⁺ and Si_nH_4n−1⁺ (Fig. S8–S9 in ESI†). As a result, the Si_nH_4n−1⁺ clusters are considered to be supersaturated with hydrogen when compared to carbon analogues. The adjacent 3c–2e bonds are associated with the lowest-lying valence MOs, due to their complete delocalization over the whole wire. Due to the relative EN values of Si and H, the Si_nH_4n−1⁺ hydride wires with negatively charged H atoms represent prototypical cationic examples for charge-inverted H-bonds (CIHB)^31–33,41 not yet covered by the IUPAC definition of H-bonds,⁴³ which thus should be revised for this aspect.⁴² Similar to SiH₃⁺ and Si₂H₇⁺, longer Si_nH_4n−1⁺ wires may be synthesized and stabilized in the condensed phase. Moreover, such Si_nH_4n−1⁺ ions may be observed in the future in SiH₄-rich interstellar regions. Finally, it may be interesting to investigate the effects of substitution of H atoms by functional groups on the properties of such hydride wires.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by Deutsche Forschungsgemeinschaft (project DO 729/9). The authors thank J. Langer, A. Lagutschenkov, and M. Savoca for support in the acquisition of the experimental data.

References

1. R. D. Miller and J. Michl, Chem. Rev., 1989, 89, 1359–1410.
2. V. Chandrasekhar, R. Boomishankar and S. Nagendran, Chem. Rev., 2004, 104, 5847–5910.
3. P. D. Lickiss, in Adv. Inorg. Chem., ed. A. G. Sykes, Academic Press, 1995, vol. 42, pp. 147–262.
4. J. Fischer, J. Baumgartner and C. Marschner, Science, 2005, 310, 825.
5. V. Kumar and Y. Kawazoe, Phys. Rev. Lett., 2003, 90, 055502.
6. F. Pichierri, V. Kumar and Y. Kawazoe, Chem. Phys. Lett., 2004, 383, 544–548.
7. R. Singh, J. Phys.: Condens. Matter, 2008, 20, 045226.
8. J. B. Lambert, L. Kania and S. Z. Zhang, Chem. Rev., 1995, 95, 1191–1201.
9. K. C. Kim, C. A. Reed, D. W. Elliott, L. J. Mueller, F. Tham, L. J. Lin and J. B. Lambert, Science, 2002, 297, 825–827.
10. H. F. T. Klare and M. Oestreich, Dalton Trans., 2010, 39, 9176–9184.
11. H. F. T. Klare, L. Albers, L. Süsse, S. Keess, T. Müller and M. Oestreich, Chem. Rev., 2021, 121, 5898–5985.
12. V. Y. Lee, Russ. Chem. Rev., 2019, 88, 351–369.
13. J. C. L. Walker, H. F. T. Klare and M. Oestreich, Nat. Rev. Chem., 2020, 4, 54–62.
14. Q. Wu, E. Irran, R. Müller, M. Kaupp, H. F. T. Klare and M. Oestreich, Science, 2019, 365, 168.
15. K. Hiraoka, J. Katsuragawa and A. Minamitsu, Chem. Phys. Lett., 1997, 267, 580.
16. T. P. Martin and H. Schaber, J. Chem. Phys., 1985, 83, 855–858.
17. H. Chatham and A. Gallagher, J. Appl. Phys., 1985, 58, 159–169.
18. M. L. Mandich and W. D. Reents, J. Chem. Phys., 1989, 90, 3121–3135.
19. M. J. Kushner, J. Appl. Phys., 1993, 74, 6538–6553.
20. G. Turban, Y. Catherine and B. Grolleau, Plasma Chem. Plasma Process., 1982, 2, 61–80.
21. G. M. Wyller, T. J. Preston, H. Klette, T. Mongstad and E. S. Marstein, J. Cryst. Growth, 2018, 498, 315–327.
22. D. M. Goldhaber and A. L. Betz, Astrophys. J., 1984, 279, L55–L58.
23. B. A. McGuire, Astrophys. J., Suppl. Ser., 2022, 259, 30.
24. M. C. McCarthy, C. A. Gottlieb and P. Thaddeus, Mol. Phys., 2003, 101, 697–704.
25. E. Herbst, T. J. Millar, S. Wlodek and D. K. Bohme, Astron. Astrophys., 1989, 222, 205–210.
26. F. Fang, Q. Jiang and R. S. Klausen, J. Am. Chem. Soc., 2022, 144, 7834–7843.
27. G. Tarczay, M. Förstel, P. Maksyutenko and R. I. Kaiser, Inorg. Chem., 2016, 55, 8776–8785.
28. N. Goldberg and H. Schwarz, in The Chemistry of Organic Silicon Compounds, ed. Z. Rappoport and Y. Apeloig, Wiley, 1998, ch. 18, vol. 2, pp. 1105–1142.
29. S. Fornarini, The Chemistry of Organic Silicon Compounds, 2001, ch. 18, pp. 1027–1057.
30. M. Savoca, M. A. R. George, J. Langer and O. Dopfer, Phys. Chem. Chem. Phys., 2013, 15, 2774–2781.
31. M. Savoca, J. Langer and O. Dopfer, Angew. Chem., Int. Ed., 2013, 52, 1568–1571.
32. M. A. R. George, M. Savoca and O. Dopfer, Chem. – Eur. J., 2013, 19, 15315–15328.
33. M. A. R. George and O. Dopfer, Int. J. Mass Spectrom., 2019, 435, 51–60.
34. S. Patai and Z. Rappoport, The Chemistry of Organic Silicon Compounds, Wiley, Chichester, 1989.
35. R. L. DeKock and W. B. Bosma, J. Chem. Educ., 1988, 65, 194–197.
36. J. E. McMurry and T. Lectka, Acc. Chem. Res., 1992, 25, 47–53.
37. S. K. Estreicher, Mater. Sci. Eng., R, 1995, 14, 319–412.
38. T. Müller, Angew. Chem., Int. Ed., 2001, 40, 3033–3036.
39. R. Panisch, M. Bolte and T. Müller, J. Am. Chem. Soc., 2006, 128, 9676–9682.
40. S. P. Hoffmann, T. Kato, F. S. Tham and C. A. Reed, Chem. Commun., 2006, 767–769.
41. M. Jablonski, Chem. Phys. Lett., 2009, 477, 374–376.
42. S. Civiš, M. Lamanec, V. Špirko, J. Kubišta, M. Špet’ko and P. Hobza, J. Am. Chem. Soc., 2023, 145, 8550–8559.
43. E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1637–1641.
44. D. M. Smith, P. M. Martineau and P. B. Davies, J. Chem. Phys., 1992, 96, 1741.
45. Y. B. Cao, J. H. Choi, B. M. Haas, M. S. Johnson and M. Okumura, J. Phys. Chem., 1993, 97, 5215–5217.
46. D. W. Boo and Y. T. Lee, J. Chem. Phys., 1995, 103, 514–519.
47. T. Y. Yu, T. M. H. Cheng, F. W. Lampe and V. Kempter, J. Phys. Chem., 1972, 76, 3321–3330.
48. A. Ding, R. A. Cassidy, L. S. Cordis and F. W. Lampe, J. Chem. Phys., 1985, 83, 3426–3432.
49. K. Raghavachari, J. Chem. Phys., 1990, 92, 452–465.
50. L. A. Curtiss, K. Raghavachari, P. W. Deutsch and J. A. Pople, J. Chem. Phys., 1991, 95, 2433–2444.
51. O. Dopfer, Int. Rev. Phys. Chem., 2003, 22, 437–495.
52. O. Dopfer, Z. Phys. Chem., 2005, 219, 125–168.
53. M. A. R. George, N. X. Truong, M. Savoca and O. Dopfer, Angew. Chem., Int. Ed., 2018, 57, 2919–2923.
54. T. Shimanouchi, Tables of Molecular Vibrational Frequencies, Consolidated Volume I, NSRDS-NBS, 1972.
55. P. Botschwina and M. Oswald, J. Chem. Phys., 1992, 96, 4044–4045.
56. J. Kapp, P. R. Schreiner and P. v R. Schleyer, J. Am. Chem. Soc., 1996, 118, 12154–12158.
57. S. Pan, D. Moreno, G. Merino and P. Chattaraj, Chem. Phys. Chem., 2014, 15, 3554–3564.
58. R. V. Olkhov, S. A. Nizkorodov and O. Dopfer, J. Chem. Phys., 1998, 108, 10046–10060.
59. D. W. Boo, Z. F. Liu, A. G. Suits, J. S. Tse and Y. T. Lee, Science, 1995, 269, 57–59.
60. S. P. Gnanasekar and E. Arunan, J. Phys. Chem. A, 2019, 123, 1168–1176.
61. O. Asvany, K. M. T. Yamada, S. Brunken, A. Potapov and S. Schlemmer, Science, 2015, 347, 1346–1349.
62. K. Hiraoka and P. Kebarle, J. Am. Chem. Soc., 1976, 98, 6119–6125.
63. L. I. Yeh, J. M. Price and Y. T. Lee, J. Am. Chem. Soc., 1989, 111, 5597.
64. M. Miyazaki, A. Fujii, T. Ebata and N. Mikami, Science, 2004, 304, 1134–1137.
65. J.-W. Shin, N. I. Hammer, E. G. Diken, M. A. Johnson, R. S. Walters, T. D. Jaeger, M. A. Duncan, R. A. Christie and K. D. Jordan, Science, 2004, 304, 1137–1140.
66. M. Park, I. Shin, N. J. Singh and K. S. Kim, J. Phys. Chem., 2007, 111, 10692–10702.
67. M. Katada, R. Shishido and A. Fujii, Phys. Chem. Chem. Phys., 2014, 16, 7595–7601.
68. C. J. D. Grotthuss, Ann. Chim. Phys., 1806, 58, 54–57.
69. N. Agmon, Chem. Phys. Lett., 1995, 244, 456.
70. D. Marx, Chem. Phys. Chem., 2006, 7, 1848–1870.
71. W. Münch, K. D. Kreuer, W. Silvestri, J. Maier and G. Seifert, Solid State Ionics, 2001, 145, 437–443.
72. H. K. Gerardi, G. H. Gardenier, U. Viswanathan, S. M. Auerbach and M. A. Johnson, Chem. Phys. Lett., 2011, 501, 172–178.
73. A. A. Adesokan, G. M. Chaban, O. Dopfer and R. B. Gerber, J. Phys. Chem. A, 2007, 111, 7374–7381.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05918a

---