Open Access Article
Open Access ArticleTwo-dimensional fullerene-based monolayer materials assembled by C80 and Sc3N@C80†
Yang
Zhao
a,
Yu
Guo
 a,
Yanyan
Zhao
a,
Xueke
Yu
a,
Nikolai
Cherenda
b,
Yan
Su
a,
Yanyan
Zhao
a,
Xueke
Yu
a,
Nikolai
Cherenda
b,
Yan
Su
 *a and
Jijun
Zhao
*a and
Jijun
Zhao
 *a
*a
aKey Laboratory of Materials Modification by Laser, Ion and Electron Beams (Dalian University of Technology), Ministry of Education, Dalian 116024, China. E-mail: su.yan@dlut.edu.cn; zhaojj@dlut.edu.cn
bPhysics Faculty, Belarusian State University, Minsk 220030, The Republic of Belarus
First published on 1st March 2024
Abstract
Construction of two-dimensional (2D) materials using fullerenes as building blocks has attracted particular attention, primarily due to their ability to integrate desired functionalities into devices. However, realization of stable 2D phases of polymerized fullerenes remains a big challenge. Here, we propose two stable 2D monolayer phases with covalently bridged C80 cages, namely α-C80-2D and β-C80-2D, which are semiconductors with strong absorption in the long wave range and appreciable carrier mobility, respectively. The high stability originates from the bond energy released by the [2+2] cycloaddition polymerization of C80 is greater than the deformation energy of a cage. Starting from α-C80-2D, endohedral incorporation of the Sc3N molecule into each C80 cage leads to 2D semiconductors of α-Sc3N@C80-2D and α′-Sc3N@C80-2D, which possess exceptional stability and diverse physical properties, including unique electronic band structures, strong optical absorption in the visible (VIS) to near-infrared (NIR) regime, and anisotropic optical characteristics. Remarkably, a temperature-induced order–disorder transition in the α-Sc3N@C80-2D phase has been observed at elevated temperatures above 600 K. These findings expand the family of 2D carbon materials and provide useful clue for the potential applications of fullerene-assembled monolayer networks.
1. Introduction
Owing to the stable cage structure and unique physical and chemical properties, carbon fullerenes are ideal building blocks of novel functional materials. To date, various fullerenes of different sizes, such as C60 and C70, have been successfully synthesized in bulk amounts.1–4 In addition, the interior cavity of fullerene cages provides ideal space for hosting atoms or small clusters, forming endohedral carbon fullerenes.5–7 To this end, the discovery of Sc3N@Ih–C80 with high yields and high stability marks a breakthrough in the study of endohedral metallofullerenes.8 The interaction between guest atoms or clusters and host carbon cages may give rise to novel properties and lead to potential applications in single-molecule electronics and information storage, quantum computing, biomedicine, nanocatalysis, and so on. For example, two electric dipole states switched by external electric fields and single-molecule ferroelectric effects have been observed in Gd@C82, which can be considered as a prototype of atomic-scale storage and logic devices.9 Sc2C2@Cs(hept)–C88 can be used as a two-terminal single-metallofullerene device achieving room-temperature logic-in-memory operations.10 U2C@C80–M (M = Cr, Mn, Mo, and Ru) chains, which exhibit intrinsic multiferroic behavior, are promising one-dimensional materials for the realization of a novel multifunctional device.11 Gd@C82 nanoparticles have been demonstrated to trigger robust cancer immunotherapy and relieve fatty liver disease without obvious toxicity.12,13 The 1T-MoS2/C60 heterostructure is an excellent electrocatalyst for the hydrogen evolution reaction.14Recently, two-dimensional (2D) polymerized C60 monolayer structures have been fabricated via covalent C–C bonds, which not only enrich the family of carbon fullerene derivatives but also bring new opportunities in fullerene-based materials and devices.15 This exciting breakthrough has led to boom of C60-based 2D structures. For instance, Zheng et al. synthesized a covalently bonded monolayer polymeric C60 with high crystallinity, good thermodynamic stability and moderate band gap.15 Using α-Li3N to catalyze C60 powder at ambient pressure, Zhu et al. obtained gram-scale long-range ordered porous carbon.16 At the same time, Roy et al. reported van der Waals C60 polymer materials with ultra-clean surfaces and found that their thermal conductivity was much higher than that of the C60 molecule.17 The unique geometric and electronic structures of 2D polymeric C60 monolayer materials endow them with great promise in optoelectronics, spintronics, information and energy storage, and photocatalysis.18–21
As the smallest fullerene obeying the isolated pentagonal ring (IPR) rule,22 C60 has relatively narrow interior space and can only enclose small guest species. In the fullerene family, C80 is the next member obeying the IPR rule and shares the same Ih point group symmetry with C60.23 Compared to C60, the larger cavity of Ih–C80 cages allows hosting a variety of molecules or clusters with up to seven atoms, e.g., Sc4CHN@Ih(7)–C80, Sc4C2H@Ih(7)–C80, and Sc4O3@Ih(7)–C80.24–28 Therefore, it would be desirable to assemble novel crystals of different dimensionality using Ih–C80 and its endohedral derivatives as building blocks, which are expected to possess tunable electronic, magnetic, and optical properties.
Inspired by the recent breakthrough in 2D polymeric C60 crystals, in this paper, we propose two thermodynamically and dynamically stable 2D phases of polymerized C80, i.e., central rectangular (α-C80-2D) and hexagonal porous (β-C80-2D) lattice structures, which are indirect semiconductors and direct semiconductors with appreciable carrier mobility and strong absorption in the long wave range, respectively. Covalent polymerization of endohedral fullerene Sc3N@C80 leads to two kinds of 2D semiconductors with central rectangular lattice structures (denoted as α-Sc3N@C80-2D and α′-Sc3N@C80-2D), which are bistable states with distinct electronic band structures. A temperature-controlled order–disorder transition is observed in α-Sc3N@C80-2D at high temperatures above 600 K. These theoretical findings provide valuable insights into the development of fullerene-based 2D materials and devices.
2. Computational details
All individual fullerenes and fullerene-based 2D networks were optimized using the Vienna ab initio simulation package29,30 (VASP) with the Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional.31 The electron–ion interaction was described using projector augmented wave (PAW) potential,32 and the plane-wave basis set was expanded to 500 eV. In order to account for the strong Coulomb interaction of 3d electrons in Sc atoms, an effective Hubbard parameter, Ueff = U − J = 3 eV, was applied to Sc atoms, where U represents the Coulomb repulsion and J is the exchange parameter (Table S1, ESI†).33–36 The introduction of Ueff parameters can more accurately describe the electronic properties of the system. A 30 × 30 × 30 Å3 supercell was utilized to simulate the isolated fullerene, and a Γ point was used to sample the Brillouin zone. Based on the PBE-optimized equilibrium structures, the more accurate electronic band structures and optical absorption spectra were calculated using the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional37 with VASP. The deformation energy (Ed) of C80 or Sc3N@C80 in the 2D polymeric phase (α-C80, β-C80 or α-Sc3N@C80 and α′-Sc3N@C80 cages) relative to the isolated one (C80 or Sc3N@C80) is defined as follows:| Ed = E2D-def-cage − EC80/Sc3N@C80 | (1) |
For fullerene-based 2D networks, a vacuum space with a 35 Å thickness was added to ensure separation between neighboring layers. A series of k-meshes of 2 × 3 × 1 (for central rectangular lattice), 2 × 2 × 1 (for hexagonal porous lattice), 4 × 4 × 1 (for rectangular lattice) and 4 × 1 × 2 (for α′-Sc3N@C80-2D) were used to sample the 2D Brillouin zones. During geometry optimization, atomic positions were allowed to relax until the maximum force was below 10−2 eV Å−1 and the change in total energy was less than 10−4 eV, respectively. The average C–C bond energy (Eb) is defined as follows:
| Eb = (E2D − N × E2D-cage)/n | (2) |
To further assess the thermal stability of these fullerene-based 2D networks, the formation energy (Ef) is calculated as follows:
| Ef = (E2D − N × Ecage)/N | (3) |
3. Results and discussion
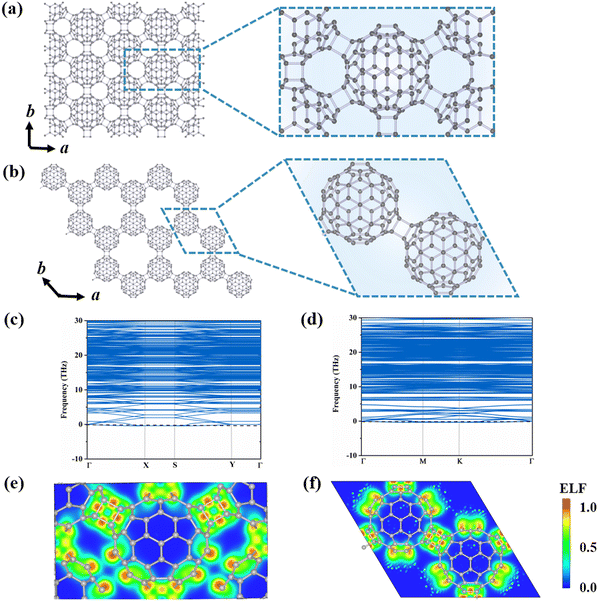
3.A. Structures and stabilities of 2D monolayer polymeric C80
To explore the possible stable configurations of 2D networks composed of C80 fullerenes, we consider three different connecting manners: a central rectangular lattice, a hexagonal porous lattice, and a rectangular lattice. The optimized structures are depicted in Fig. 1(a) and (b) and Fig. S1 (ESI†), and detailed geometrical parameters are provided in Table 1. Among these three constructed phases, the α-C80-2D monolayer with the Pmna (No. 53) space group and equilibrium lattice parameters of a = 17.76 Å and b = 10.25 Å is the most stable, in which each C80 cage is linked by six neighboring C80 cages through [2+2] cycloaddition bonds along the b direction and the diagonal lines of the rectangular unit cell. For comparison, the equilibrium structure of the β-C80-2D network exhibits the P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (No. 164) space group with lattice parameters of a = 17.64 Å and b = 17.64 Å, which is achieved through the formation of similar plane [2+2] cycloaddition bonds involving three adjacent fullerenes. For the γ-C80-2D network with the space group of P
m1 (No. 164) space group with lattice parameters of a = 17.64 Å and b = 17.64 Å, which is achieved through the formation of similar plane [2+2] cycloaddition bonds involving three adjacent fullerenes. For the γ-C80-2D network with the space group of P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (No. 2), the equilibrium lattice parameters are a = 10.19 Å and b = 9.90 Å, in which four fullerenes are connected by two [2+2] cycloaddition bonds along the a direction and C–C single bonds along the b direction.
(No. 2), the equilibrium lattice parameters are a = 10.19 Å and b = 9.90 Å, in which four fullerenes are connected by two [2+2] cycloaddition bonds along the a direction and C–C single bonds along the b direction.
| Monolayer | Space group | a (Å) | b/c (Å) | n | R C–C (Å) | E d (eV) | E b (eV) | E f (eV) | E g (eV) |
|---|---|---|---|---|---|---|---|---|---|
| qTP-C60 | Pmmm (47) | 8.70 | 9.00 | 8 | 1.58/1.58 | 4.75 | −0.89 | −2.39 | 1.68 |
| qHP-C60 | Pmna (53) | 15.70 | 8.50 | 8 | 1.58/1.59 | 5.30 | −1.95 | −2.49 | 1.43 |
| α-C80-2D | Pmna (53) | 17.76 | 10.25 | 12 | 1.59/1.60 | 7.41 | −2.01 | −4.66 | 0.14 |
| β-C80-2D |
P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1(164) m1(164) |
17.64 | 17.64 | 6 | 1.59/1.60 | 3.14 | −1.85 | −2.41 | 0.25 |
| γ-C80-2D |
P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (2) (2) |
10.19 | 9.90 | 8 | 1.62/1.76 | 5.59 | −0.97 | −2.16 | 0.73 |
| α-Sc3N@C80-2D | Pma2 (28) | 17.88 | 10.31 | 12 | 1.58/1.60 | 6.07 | −1.36 | −2.08 | 0.36 |
| α′-Sc3N@C80-2D | Pc (7) | 10.23 | 20.50 | 12 | 1.59/1.62 | 6.60 | −1.48 | −2.29 | 0.12 |
As summarized in Table 1, the calculated formation energies of the α-C80-2D, β-C80-2D, and γ-C80-2D monolayers are −4.66, −2.41, and −2.16 eV, respectively. These negative values indicate that synthesis of all three 2D structures from C80 cages is exothermic. For comparison, we have also calculated the formation energies of previously reported qTP-C60 and qHP-C60.18 Notably, our predicted α-C80-2D network has much lower formation energy than 2D polymeric C60 crystals, while β-C80-2D is only slightly less stable than qHP C60 by 0.08 eV per cage. Additionally, we also calculate the formation energy (Ef-atom) and deformation energy (Ed-atom) defined by atom-wise energies and compared with monolayer C60 (see Supplementary Note 2 of the ESI†). From Table S2 (ESI†), it can be seen that the thermodynamic stability of the C80-2D monolayer is comparable to that of the C60-2D monolayer. Therefore, these 2D networks composed of C80 fullerenes would be accessible under experimental conditions.
The phonon dispersions of the three C80-assembled 2D monolayers are computed and illustrated in Fig. 1(c) and (d) and Fig. S1 (ESI†). Among them, the α-C80-2D, β-C80-2D and γ-C80-2D monolayers exhibit dynamic stability without imaginary frequencies in the entire phonon spectra. Furthermore, AIMD simulations, as presented by Fig. S3 (ESI†), demonstrate that α-C80-2D and β-C80-2D monolayers maintain their lattice structures at temperatures as high as 600 K. However, in the γ-C80-2D monolayer, there is a noticeable increase in C–C distances along the b direction within the 2D structure (Fig. S4, ESI†). According to the aforementioned results, α-C80-2D and β-C80-2D monolayers exhibit excellent dynamic and thermal stabilities, making them viable candidates for experimental synthesis and excellent “host” materials for further endohedral doping.
To elucidate the exceptional stability of polymeric C80 monolayers, we analyze their bonding characteristic in terms of electron localization functions (ELFs), average inter-cage C–C bond energy (Eb), orbital-resolved partial density of state (PDOS) and deformation energy (Ed). Fig. 1(e) and (f) reveal high electron localization and strong covalent bonding between neighboring C80 cages in both α-C80-2D and β-C80-2D. This picture is further supported by the calculated Eb in Table 1. Fig. S5 (ESI†) presents the orbital-resolved partial density of states (PDOS) of C80-based 2D polymers. It is evident that the px, py, and pz orbitals of the C atoms all contribute equally to bonding, implying a transition of the part of the C atoms in C80 fullerenes from sp2 to sp3 hybridization. Intuitively, as more C atoms reach sp3 bonding saturation through inter-cage polymerization, a greater amount of surface tension is released in the originally unstable C80 cage,23,40 further increasing the stability of the entire system. As seen from Fig. 1(a) and (b) and Table 1, compared with C60 polymeric 2D materials like qTP-C60 and qHP-C60,18 each fullerene cage in α-C80-2D has 12 C atoms with sp3-hybridization by [2+2] cycloaddition with the surrounding six fullerenes. Although the deformation energy of the C80 cage is relatively larger (Ed) (Fig. S6, ESI†), this effect is compensated by the number of saturated bonds in the carbon cage, as signified by the amount of bond energy (nEb). As a consequence, α-C80-2D exhibits a significantly lower formation energy of −4.66 eV than C60-based 2D phases. For β-C80-2D, each carbon cage possesses 6 C atoms with sp3 hybridization, slightly less than the number in qTP-C60 or qHP-C60, while the deformation energy of the cage is also smaller. However, for the γ-C80-2D monolayer, each C80 cage contains 8 C atoms with sp3-hybridization, but the C–C bond length (1.76 Å) is 0.16 Å longer than that formed through [2+2] cycloaddition, resulting in a weaker average inter-cage C–C bond energy. While compared to the relatively large cage deformation energy, the bond energy release is only slightly increased, leading to the relative inferior stability of γ-C80-2D. According to the above analysis, the bond energy released by the [2+2] cycloaddition polymerization of C80 is consistently greater than the deformation energy of the cage, contributing to the stabilization of the resulting 2D phases. In summary, theoretical calculations suggest that C80 could serve as a promising building block to construct C60-2D-like monolayers. Additionally, we aspire for this study to inspire more theoretical and experimental efforts towards the synthesis of C80 monolayers.
3.B. Enclosing Sc3N into 2D C80 polymerized monolayers
The incorporation of endohedral units into C80 fullerene provides an extra opportunity for designing multifunctional nanodevices.11,41–43 According to previous reports, the Sc3N@Ih–C80 cluster shows great potential in various fields such as biomedicine and energy conversion.44,45 Based on the stable C80-assembled monolayer phases obtained above (i.e., central rectangular and hexagonal porous lattices), we select Sc3N as the guest species inside the C80 cage to further construct Sc3N@C80-2D monolayers.To determine the stable geometries of Sc3N@C80-2D monolayers, we have explored various possible orientations of the Sc3N cluster in α-C80-2D and β-C80-2D phases. As illustrated in Fig. 2(a) and (b), α′-Sc3N@C80-2D and α-Sc3N@C80-2D monolayers are the most stable and metastable phases, respectively. The phonon dispersions of these two phases are displayed in Fig. 2(c) and (d). Notably, in the α-Sc3N@C80-2D crystal (Fig. 2(a)), the central rectangular lattice is maintained after endohedral doping, with equilibrium lattice parameters of a = 17.88 Å and b = 10.31 Å, and a space group of Pma2 (No. 28). Intriguingly, the formation energy of this phase (−2.08 eV) is significantly lower than those of polymeric C80 and C60 crystals, suggesting that incorporation of the Sc3N cluster effectively passivates the surface activity of the fullerene cage and further reduces the average C–C bond energy (Table 1). These results demonstrate the experimental feasibility of synthesizing α-Sc3N@C80-2D and α′-Sc3N@C80-2D monolayers. In both the freestanding cage and α-Sc3N@C80-2D, the geometry of the endohedral Sc3N cluster retains a N-centered equilateral triangle with minor distortion (Fig. S7(a), ESI†). In the α-Sc3N@C80-2D phase, the Sc–N bond lengths are 2.04, 2.04, and 2.04 Å, slightly longer than those in isolated Sc3N@C80, i.e., 2.02, 2.02, and 2.02. All three Sc atoms are located over the [5, 6] junction of the Ih–C80 cage in α-Sc3N@C80-2D (Fig. S7(a), ESI†). For the α′-Sc3N@C80-2D crystal, the lattice parameters are a = 10.23 Å and c = 20.50 Å, with a space group of Pc (No. 7). The formation energy of −2.29 eV indicates slightly higher stability compared to the α-Sc3N@C80-2D phase. The enclosed Sc3N species in α′-Sc3N@C80-2D has Sc–N bond lengths of 1.98, 2.04, and 2.05 Å, and Sc–N–Sc angles of 126°, 136°, and 98°, respectively. In addition, the deformation energy (Ed) is 6.60 eV, which is larger than that of the α-Sc3N@C80-2D phase (6.07 eV). This is mainly due to the greater change in Sc–N bond lengths in a single distorted α′-Sc3N@C80 compared to isolated Sc3N@C80, resulting in a stronger interaction between Sc3N and C80. Moreover, the encapsulation of Sc3N clusters results in weaker inter-cage C–C bonds, reducing the distortion of the Sc3N@C80 cluster, resulting in Ed values of α-Sc3N@C80-2D and α′-Sc3N@C80-2D smaller than that of α-C80-2D. And its basal plane is perpendicular to the plane of the α-Sc3N@C80-2D monolayer (Fig. S7(b), ESI†).
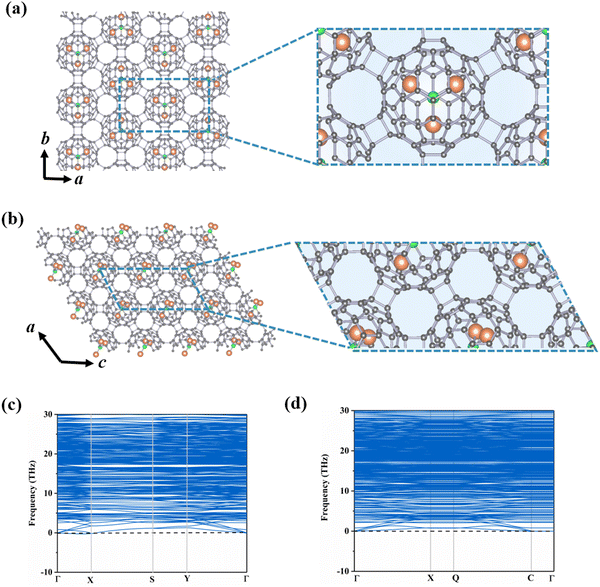 | ||
| Fig. 2 Crystal structures and phonon dispersions of monolayers (a) and (c) α-Sc3N@C80-2D and (b) and (d) α′-Sc3N@C80-2D, where grey, orange and green denote C, Sc and N atoms. | ||
Fig. S8 and S9 (ESI†) depict different β-Sc3N@C80-2D monolayers and their respective phonon dispersions. We have observed that the lowest energy β-Sc3N@C80-2D monolayer exhibits imaginary frequencies in the phonon dispersion calculations, suggesting that the Sc3N cluster cannot be enclosed within β-C80-2D. Taking the imaginary frequency of −1.70 THz at the Γ point as an example, the animation movie reveals complex vibrational modes in the β-Sc3N@C80-2D phase. Specifically, the carbon atoms on the C80 cage display two distinct vibration modes: stretching and swinging motions relative to the fullerene center, while the Sc–N bond in the Sc3N cluster belongs to a stretching–bending vibration mode. In addition, the lowest energy γ-Sc3N@C80-2D crystallizes in the space group P1 (No. 1) with lattice parameters a = 10.23 Å and b = 10.67 Å. The embedding of Sc3N into the γ-C80-2D phase significantly elongates the distance between the two C80 fullerenes along the b direction from 1.76 Å to 3.03 Å, surpassing the length of C–C single bonds, as displayed in Fig. S10 (ESI†). Meanwhile, compared to the isolated Sc3N@C80 (Fig. S6(d), ESI†), the deformation energy of the γ-Sc3N@C80 cage is relatively larger. Moreover, the formation energy of this phase is 4.71 eV, signifying an endothermic encapsulation process. Therefore, Sc3N also cannot stable the γ-C80-2D crystal.
It is important to observe the molecular behavior of metallofullerenes in the crystal lattice. Both previous computational and experimental studies have unraveled that the Sc3N cluster is freely rotating in single C80 fullerene.46–48 To probe the temperature dependent dynamics of the Sc3N cluster in α-Sc3N@C80-2D and α′-Sc3N@C80-2D phases, we performed molecular dynamics simulations and used spatial distribution maps to describe the detailed distribution of Sc atoms at the selected temperatures. Fig. 3 and Fig. S11, S12 and animation movies in the ESI† show the trajectories of 2D crystal structures from the AIMD simulation for 10 ps at different temperatures. For α-Sc3N@C80-2D (Fig. 3), the endohedral Sc3N cluster remains rigidly bonded to the adjacent pentagonal and hexagonal junctions up to 600 K, maintaining a well-ordered structure with the space group Pma2 (No. 28). However, as the temperature increases to 800 K, the Sc3N clusters undergo rotational motion along multiple directions, resulting in the loss of long-range order in the entire system. Such transformation can be considered as a temperature-induced order–disorder transition. In the case of α′-Sc3N@C80-2D, the Sc3N clusters exhibit unrestricted rotation at 300 K, inducing a disordered distribution of molecular orientations (Fig. S12, ESI†).
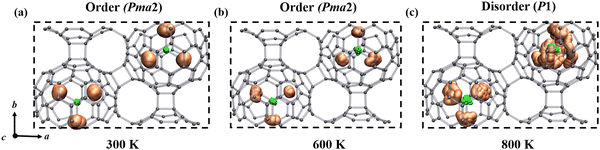 | ||
| Fig. 3 Schematic representation of order–disorder states of the α-Sc3N@C80-2D crystal driven by temperature at (a) 300 K, (b) 600 K, and (c) 800 K. The representative rotational operation of the Sc3N species for the α-Sc3N@C80-2D phase is available in the movies of the ESI.† | ||
3.C. Electronic structures, carrier mobility, and optical absorption properties
The electronic band structures of α-C80-2D, β-C80-2D, α-Sc3N@C80-2D, and α′-Sc3N@C80-2D are plotted in Fig. 4, and the 2D Brillouin region for the four types of crystal lattices is detailed in Fig. S2 (ESI†). One can see that α-C80-2D exhibits a small indirect band behavior with a band gap of 0.14 eV. In other words, the strong C–C bonding interaction (Eb = 2.01 eV) significantly changes the electronic structure of α-C80-2D assembly of semiconducting C80 fullerenes. Meanwhile, β-C80-2D still behaves as a semiconductor with a direct band gap of 0.25 eV at point K, which is close to the band gap of the freestanding C80 cage (0.28 eV), meaning that the coupling strength in such polymerization is relatively weaker (Eb = 1.85 eV). For comparison, the 2D networks of the C60 fullerene possess sizeable band gaps of 1.74 and 1.67 eV.18 Interestingly, the orientation of the Sc3N clusters in α-C80-2D monolayers has a notable effect on the band structure. Specifically, α-Sc3N@C80-2D has an indirect band gap of 0.36 eV, and α′-Sc3N@C80-2D exhibits distinctly different positions of the valence band maximum (VBM) and conduction band minimum (CBM) with an indirect band gap of 0.12 eV. Compared to individual metallofullerene Sc3N@C80, the band gaps of both α-Sc3N@C80-2D and α′-Sc3N@C80-2D phases are greatly reduced, primarily attributed to the inter-cage conjugated interaction. All these results demonstrate that self-assembling can generate richer electronic properties relative to those of individual clusters.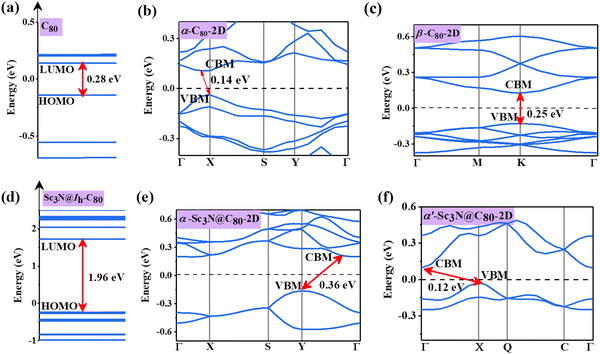 | ||
| Fig. 4 Electronic structures of (a) C80 fullerene, (b) α-C80-2D, (c) β-C80-2D, (d) Sc3N@Ih–C80 fullerene, (e) α-Sc3N@C80-2D, and (f) α′-Sc3N@C80-2D. The Fermi level is set to zero. | ||
Based on the deformation potential theory,49,50 the transport properties of semiconducting β-C80-2D, α-Sc3N@C80-2D, and α′-Sc3N@C80-2D monolayers are discussed in terms of effective mass and carrier mobility. The detailed results are described in the Supplementary Note 1 of the ESI.† As seen from Table S3 (ESI†), the electron effective masses of β-C80-2D are larger than those of holes, similar to the previously reported α-C60-2D.19 Owing to the disparities in the dispersion of valence and conduction bands of α-Sc3N@C80-2D and α′-Sc3N@C80-2D, significant variations are also observed in their effective masses of electrons and holes. In α-Sc3N@C80-2D, the effective masses of holes are considerably larger than those of electrons. Conversely, the hole effective masses in α′-Sc3N@C80-2D are smaller than the electron ones. Both the electron and hole effective masses of β-C80-2D are higher than those in α-Sc3N@C80-2D and α′-Sc3N@C80-2D materials. More importantly, the highest carrier mobility obtained in the β-C80-2D monolayer (5.57 × 103 cm2 V−1 s−1) is comparable to those of α-C60-2D (1.24 × 103 cm2 V−1 s−1)19 and black phosphorene (103 cm2 V−1 s−1).51 Such high electron mobility can be ascribed to small effective masses and deformation potential constants of the β-C80-2D monolayer.
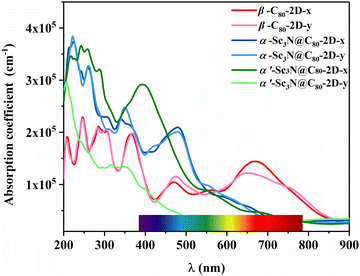
To explore potential optoelectronic applications, the absorption spectra of these three 2D semiconductors are simulated and show good absorption intensity from the near-infrared (NIR) to the ultraviolet (UV) regions, suggesting the usage as active layers in solar cells (Fig. 5). In particular, a high absorption coefficient (3.85 × 105 cm−1) is obtained in the ultraviolet region, which is comparable to that of the C60 2D crystal.52 Such strong ultraviolet absorption capability can not only be utilized in wearable devices to resist ultraviolet radiation and prevent tanning and sunburn, but also holds promise as potential photocatalysts. Excitingly, β-C80-2D exhibits a well-defined strong absorption characteristic in the wavelength range of 600–750 nm. It overcomes the limitation of the low absorption coefficient of conventional carbon nanomaterials in the longer wavelength regime53,54 and might be useful for future biomedical applications. In addition, for α′-Sc3N@C80-2D, the absorption peak along the x direction is stronger than that along the y direction, suggesting an inherent anisotropic characteristic in light absorption due to the symmetry of the 2D crystal. This phenomenon shows a pronounced linear dichroism and implies potential applications in the design of light detection and new-concept optoelectronic devices.
4. Conclusions
In summary, we have demonstrated that C80 and its endohedral derivatives can be used as versatile building blocks to assemble thermodynamically and dynamically stable 2D lattices via covalent bonding with each other. Further analysis indicates that the initially unstable pristine C80 cages can polymerize into two stable monolayer phases (namely, α-C80-2D and β-C80-2D), because the bond energy released by the [2+2] cycloaddition polymerization of C80 is greater than the deformation energy of the corresponding cage. Among them, α-C80-2D exhibits an indirect band behavior, while β-C80-2D is a direct semiconductor with appreciable carrier mobility and strong absorption in the long wave range. By incorporating Sc3N clusters into each C80 cage, we successfully obtain 2D semiconductors of α-Sc3N@C80-2D and α′-Sc3N@C80-2D, which exhibit bistable states with diverse physical properties, such as distinct band structures with bandgaps ranging from 0.36 to 0.12 eV, exceptional electron transport properties with a mobility from 0.31 × 103 cm2 V−1 s−1 to 0.17 × 103 cm2 V−1 s−1, broad optical absorption from the near-infrared to ultraviolet regimes, and remarkably strong anisotropic optical adsorption. Furthermore, a temperature-driven order–disorder transition is observed in the α-Sc3N@C80-2D lattice, offering an example of profound insight into the microscopic mechanism of order–disorder phase transition in 2D materials. In a word, such polymeric C80 monolayers can act as promising “host” materials for diverse endohedral doping, thereby contributing to the development of optical, ferroelectric, ferromagnetic and other functional materials. Furthermore, whether α-Sc3N@C80-2D and α′-Sc3N@C80-2D phases can be transformed through external fields, such as electric fields, photoexcitation, is also worthy of investigation, as this phenomenon holds promise in high-resolution fast data storage and in-memory computing devices.Author contributions
Yang Zhao: conceptualization, methodology, software, formal analysis, investigation, data curation, writing – original draft, writing – review and editing, and visualization; Yu Guo: formal analysis and funding acquisition; Yanyan Zhao: formal analysis; Xueke Yu: writing – review and editing; Nikolai Cherenda: writing – review and editing and funding acquisition; Yan Su and Jijun Zhao: conceptualization, software, resources, writing – review and editing, and funding acquisition. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (91961204 and 12174045), the Fundamental Research Funds for the Central Universities (DUT22RC(3)009), and the financial support of our International Cooperative Project (ICR2304). The computational resources utilized in this research were provided by the Supercomputing Center of the Dalian University of Technology and Shanghai Supercomputer Center.References
- H. W. Kroto, J. R. Heath, S. C. O’Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162 CrossRef CAS.
- W. Krätschmer, L. D. Lamb, K. Fostiropoulos and D. R. Huffman, Nature, 1990, 347, 354 CrossRef.
- J. W. Arbogast and C. S. Foote, J. Am. Chem. Soc., 1991, 113, 8886 CrossRef CAS.
- D. H. Parker, P. Wurz, K. Chatterjee, K. R. Lykke, J. E. Hunt, M. J. Pellin, J. C. Hemminger, D. M. Gruen and L. M. Stock, J. Am. Chem. Soc., 1991, 113, 7499 CrossRef CAS.
- Y. Chai, T. Guo, C. Jin, R. E. Haufler, L. P. F. Chibante, J. Fure, L. Wang, J. M. Alford and R. E. Smalley, J. Phys. Chem., 1991, 95, 7564 CrossRef CAS.
- J. R. Heath, S. C. O’Brien, Q. Zhang, Y. Liu, R. F. Curl, F. K. Tittel and R. E. Smalley, J. Am. Chem. Soc., 1985, 107, 7779 CrossRef CAS.
- A. A. Popov, S. Yang and L. Dunsch, Chem. Rev., 2013, 113, 5989 CrossRef CAS PubMed.
- S. Stevenson, G. Rice, T. Glass, K. Harich, F. Cromer, M. R. Jordan, J. Craft, E. Hadju, R. Bible, M. M. Olmstead, K. Maitra, A. J. Fisher, A. L. Balch and H. C. Dorn, Nature, 1999, 401, 55 CrossRef CAS.
- K. Zhang, C. Wang, M. Zhang, Z. Bai, F.-F. Xie, Y.-Z. Tan, Y. Guo, K.-J. Hu, L. Cao, S. Zhang, X. Tu, D. Pan, L. Kang, J. Chen, P. Wu, X. Wang, J. Wang, J. Liu, Y. Song, G. Wang, F. Song, W. Ji, S.-Y. Xie, S.-F. Shi, M. A. Reed and B. Wang, Nat. Nanotechnol., 2020, 15, 1019 CrossRef CAS PubMed.
- J. Li, S. Hou, Y.-R. Yao, C. Zhang, Q. Wu, H.-C. Wang, H. Zhang, X. Liu, C. Tang, M. Wei, W. Xu, Y. Wang, J. Zheng, Z. Pan, L. Kang, J. Liu, J. Shi, Y. Yang, C. J. Lambert, S.-Y. Xie and W. Hong, Nat. Mater., 2022, 21, 917 CrossRef CAS PubMed.
- Y. Zhao, Y. Guo, Y. Qi, X. Jiang, Y. Su and J. Zhao, Adv. Sci., 2023, 2301265 CrossRef CAS PubMed.
- L. Li, M. Zhen, H. Wang, Z. Sun, W. Jia, Z. Zhao, C. Zhou, S. Liu, C. Wang and C. Bai, Nano Lett., 2020, 20, 4487 CrossRef CAS PubMed.
- X. Li, M. Zhen, C. Zhou, R. Deng, T. Yu, Y. Wu, C. Shu, C. Wang and C. Bai, ACS Nano, 2019, 13, 8597 CrossRef CAS PubMed.
- A. R. Puente Santiago, T. He, O. Eraso, M. A. Ahsan, A. N. Nair, N. Chava, T. Zheng, S. Pilla, O. Fernandez-Delgado, A. Du, S. T. Sreenivasan and L. Echegoyen, J. Am. Chem. Soc., 2020, 142, 17923 CrossRef CAS PubMed.
- L. Hou, X. Cui, B. Guan, S. Wang, R. Li, Y. Liu, D. Zhu and J. Zheng, Nature, 2022, 606, 507 CrossRef CAS PubMed.
- F. Pan, K. Ni, T. Xu, H. Chen, Y. Wang, K. Gong, C. Liu, X. Li, M.-L. Lin, S. Li, X. Wang, W. Yan, W. Yin, P.-H. Tan, L. Sun, D. Yu, R. S. Ruoff and Y. Zhu, Nature, 2023, 614, 95 CrossRef CAS PubMed.
- E. Meirzadeh, A. M. Evans, M. Rezaee, M. Milich, C. J. Dionne, T. P. Darlington, S. T. Bao, A. K. Bartholomew, T. Handa, D. J. Rizzo, R. A. Wiscons, M. Reza, A. Zangiabadi, N. Fardian-Melamed, A. C. Crowther, P. J. Schuck, D. N. Basov, X. Zhu, A. Giri, P. E. Hopkins, P. Kim, M. L. Steigerwald, J. Yang, C. Nuckolls and X. Roy, Nature, 2023, 613, 71 CrossRef CAS PubMed.
- B. Peng, J. Am. Chem. Soc., 2022, 144, 19921 CrossRef CAS PubMed.
- L. Yu, J. Xu, B. Peng, G. Qin and G. Su, J. Phys. Chem. Lett., 2022, 13, 11622 CrossRef CAS PubMed.
- W. Li, R. Yang and M. Sun, J. Mater. Chem. A, 2023, 11, 3949 RSC.
- S. Zhao, X. Zhang, Y. Ni, Q. Peng and Y. Wei, Carbon, 2023, 202, 118 CrossRef CAS.
- H. W. Kroto, Nature, 1987, 329, 529 CrossRef CAS.
- A. R. Khamatgalimov and V. I. Kovalenko, Fullerenes, Nanotubes Carbon Nanostruct., 2011, 19, 599 CrossRef CAS.
- C. Zhao, K. Tan, M. Nie, Y. Lu, J. Zhang, C. Wang, X. Lu and T. Wang, Inorg. Chem., 2020, 59, 8284 CrossRef CAS PubMed.
- T. Wang and C. Wang, Acc. Chem. Res., 2014, 47, 450 CrossRef CAS PubMed.
- Y. Feng, T. Wang, J. Wu, Z. Zhang, L. Jiang, H. Han and C. Wang, Chem. Commun., 2014, 50, 12166 RSC.
- R. Valencia, A. Rodríguez-Fortea, S. Stevenson, A. Balch and L. J. M. Poblet, Inorg. Chem., 2009, 48, 5957 CrossRef CAS PubMed.
- B. Q. Mercado, M. M. Olmstead, C. M. Beavers, M. L. Easterling, S. Stevenson, M. A. Mackey, C. E. Coumbe, J. D. Phillips, J. P. Phillips, J. M. Poblet and A. L. Balch, Chem. Commun., 2010, 46, 279 RSC.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943 CrossRef CAS PubMed.
- A. Rohrbach, J. Hafner and G. Kresse, J. Phys.: Condens. Matter, 2003, 15, 979 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- M. Musa Saad H-E, Bull. Mater. Sci., 2022, 45, 69 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1 CrossRef CAS.
- A. R. Khamatgalimov, A. V. Luzhetskii and V. I. Kovalenko, Int. J. Quantum Chem., 2008, 108, 1334 CrossRef CAS.
- R. Nakanishi, J. Satoh, K. Katoh, H. Zhang, B. K. Breedlove, M. Nishijima, Y. Nakanishi, H. Omachi, H. Shinohara and M. Yamashita, J. Am. Chem. Soc., 2018, 140, 10955 CrossRef CAS PubMed.
- S. Sato, S. Seki, G. F. Luo, M. Suzuki, J. Lu, S. Nagase and T. Akasaka, J. Am. Chem. Soc., 2012, 134, 11681 CrossRef CAS PubMed.
- K. Jayanand, S. Chugh, N. Adhikari, M. Min, L. Echegoyen and A. B. Kaul, J. Mater. Chem. C, 2020, 8, 3970 RSC.
- J. R. Pinzon, M. E. Plonsk-Brzezinska, C. M. Cardona, A. J. Athans, S. S. Gayathri, D. M. Guldi, M. Á. Herranz, N. Martín, T. Torres and L. Echegoyen, Angew. Chem., Int. Ed., 2008, 47, 4173 CrossRef CAS PubMed.
- Y. Chai, X. Liu, B. Wu, L. Liu, Z. Wang, Y. Weng and C. Wang, J. Am. Chem. Soc., 2020, 142, 4411 CrossRef CAS PubMed.
- A. A. Popov and L. Dunsch, J. Am. Chem. Soc., 2008, 130, 17726 CrossRef CAS PubMed.
- T. Heine, K. Vietze and G. Seifert, Magn. Reson. Chem., 2004, 42, S199 CrossRef CAS PubMed.
- Y. Hao, Y. Wang, L. Spree and F. Liu, Inorg. Chem. Front., 2021, 8, 122 RSC.
- S. Takagi, A. Toriumi, M. Iwase and H. Tango, Electron Devices, 1994, 41, 2357 CrossRef CAS.
- S. Bruzzone and G. Fiori, Appl. Phys. Lett., 2011, 99, 222108 CrossRef.
- J. Qiao, X. Kong, Z. X. Hu, F. Yang and W. Ji, Nat. Commun., 2014, 5, 4475 CrossRef CAS PubMed.
- R. M. Tromer, L. A. Ribeiro and D. S. Galvão, Chem. Phys. Lett., 2022, 804, 139925 CrossRef CAS.
- X. Wang, L. Cao, S. T. Yang, F. S. Lu, M. J. Meziani, L. Tian, K. W. Sun, M. A. Bloodgood and Y. P. Sun, Angew. Chem., Int. Ed., 2010, 49, 5310 CrossRef CAS PubMed.
- P. Anilkumar, L. Cao, J. J. Yu, K. N. Tackett, P. Wang, M. J. Meziani and Y. P. Sun, Small, 2013, 9, 545 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04028c |
| This journal is © the Owner Societies 2024 |