Open Access Article
Open Access ArticleDiffuse reflectance spectroscopy for colorectal cancer surgical guidance: towards real-time tissue characterization and new biomarkers
Marcelo
Saito Nogueira
 *ab,
Siddra
Maryam
*ab,
Siddra
Maryam
 ab,
Michael
Amissah
ab,
Shane
Killeen
c,
Micheal
O'Riordain
c and
Stefan
Andersson-Engels
ab,
Michael
Amissah
ab,
Shane
Killeen
c,
Micheal
O'Riordain
c and
Stefan
Andersson-Engels
 ab
ab
aTyndall National Institute, Lee Maltings, Dyke Parade, Cork, T12 R5CP, Ireland. E-mail: marcelosaitonogueira@gmail.com; marcelo.nogueira@tyndall.ie
bDepartment of Physics, University College Cork, College Road, Cork, T12 K8AF, Ireland
cDepartment of Surgery, Mercy University Hospital, Cork, T12 WE28, Ireland
First published on 5th October 2023
Abstract
Colorectal cancer (CRC) is the third most common and second most deadly type of cancer worldwide, representing 11.3% of the diagnosed cancer cases and resulting in 10.2% (0.88 million) of the cancer related deaths in 2020. CRCs are typically detected at the late stage, which leads to high mortality and morbidity. Mortality and poor prognosis are partially caused by cancer recurrence and postoperative complications. Patient survival could be increased by improving precision in surgical resection using accurate surgical guidance tools based on diffuse reflectance spectroscopy (DRS). DRS enables real-time tissue identification for potential cancer margin delineation through determination of the circumferential resection margin (CRM), while also supporting non-invasive and label-free approaches for laparoscopic surgery to avoid short-term complications of open surgery as suitable. In this study, we have estimated the scattering properties and chromophore concentrations based on 2949 DRS measurements of freshly excised ex vivo specimens of 47 patients, and used this estimation to classify normal colorectal wall (CW), fat and tumor tissues. DRS measurements were performed with fiber-optic probes of 630 μm source–detector distance (SDD; probe 1) and 2500 μm SDD (probe 2) to measure tissue layers ∼0.5–1 mm and ∼0.5–2 mm deep, respectively. By using the 5-fold cross-validation of machine learning models generated with the classification and regression tree (CART) algorithm, we achieved 95.9 ± 0.7% sensitivity, 98.9 ± 0.3% specificity, 90.2 ± 0.4% accuracy, and 95.5 ± 0.3% AUC for probe 1. Similarly, we achieved 96.9 ± 0.8% sensitivity, 98.9 ± 0.2% specificity, 94.0 ± 0.4% accuracy, and 96.7 ± 0.4% AUC for probe 2.
Introduction
Colorectal cancer (CRC) represented 11.3% of the diagnosed cancer cases and resulted in 10.2% (0.88 million) of the cancer related deaths in 2020.1,2 High mortality and morbidity are caused by cancer recurrence, postoperative complications, and system complications typically associated with patients’ health even prior to surgery.3 The survival of patients tends to increase with complete resection enhanced by surgical guidance tools for real-time accurate intraoperative cancer margin delineation. In particular, tools for guidance of laparoscopic surgery (LS) could potentially reduce long-term surgical complications, as LS has already been shown to be an effective method to avoid short-term complications of open surgery (OS).4 However, one of the main drawbacks of LS compared with OS is its impaired accuracy due to the lack of tactile feedback. This reduction could potentially improve long-term outcomes including metastasis, recurrence-free survival, disease recurrence, mortality, and overall survival.4 Short-term outcomes already improved by LS include postoperative recovery parameters such as time-to-bowel function, time-to-food intake, time-to-mobilization and length of hospital stay and pain. Surgical parameters including size of surgical wound, positive tumor margin, blood loss, number of nodes removed, and duration of operation are also improved.4 Surgical long-term outcomes can be improved by increasing the accuracy of circumferential resection margin (CRM) determination. Currently, surgical decisions rely on tissue structural information, while higher accuracies could potentially be obtained by using molecular-sensitive methods of tissue identification. Preference in developing such methods is given to automated methods for intraoperative real-time surgical guidance. In this context, surgeons can obtain real-time probability scores for tissue types probed. Next, surgeons can use these scores to take biopsies from the most suspected locations containing cancer cells after resection, and ensure complete resection of every patient. Some of the most promising real-time and molecular-sensitive tools are based on optical spectroscopy methods combined with machine learning models.5 Our study uses diffuse reflectance spectroscopy (DRS).DRS uses the diffuse reflected light travelling inside the tissue to extract tissue structural and biochemical information based on light scattering and absorption properties, respectively. Scattering properties include reduced scattering amplitude α′, Mie scattering power bMie, and the percentage contribution of Rayleigh scattering fRay to the total Mie scattering in the tissue. These scattering properties can be associated with tissue microstructures including organelles (e.g., mitochondria) and other structures (e.g., cell and organelle membranes, collagen fibers and fibrils). Similarly, absorption properties consist of volume fractions of tissue chromophores (represented by fchromophore) including β-carotene, bile (fbile), bilirubin, ceroid, collagen, deoxyhemoglobin (fHb), oxyhemoglobin (fHbO2), methemoglobin (fmetHb), water (fwater), lipid (flipid), and melanin.6,7
Previous DRS and hyperspectral imaging studies on colorectal cancer detection focused on either endoscopic8–15 or surgical16–23 applications. Feasibility DRS studies have employed surgical guidance techniques based on machine learning (ML) approaches using either spectra collected from the outer surface of tissues through surface contact probes or spectra collected from interstitial tissues through needle-shaped probes.16–23 However, previous studies have several limitations. First, these studies explored only small tissue volumes determined by small source-to-detector distances (SDDs) employed in the fiber-optic probes used. Second, the only study determining tissue chromophore concentrations and scattering properties22 used analytical models based on the diffusion equation, which is known not to describe the reflectance at small SDDs well under the conditions in which DRS spectra were collected.5,6,10,11,14,24 Third, DRS surgical guidance studies analyzed visible and near-infrared wavelengths ranging up to 1600 nm only. Finally, the number of measurements collected in DRS studies ranges from 117 to 1273 per dataset (i.e., 117–1273 DRS measurements collected under the same conditions). Machine learning models considering thousands of wavelengths directly as predictors for validation in less than thousand measurements could lead to overfitting. Our study has overcome all of the above limitations.
In this study, we quantified tissue microstructural and biochemical parameters for potential clinical decision making in open surgery, laparoscopic surgery, and robotic surgery. Our study combined ML models with reflectance spectral fitting extraction of tissue chromophore concentrations and scattering properties from 2949 locations on fresh ex vivo tissue samples of 47 patients (1386 tissue locations with a 630 μm SDD probe and 1563 locations with a 2500 μm SDD probe). This extraction relied on a reflectance lookup table (LUT) built using MC simulations of light propagation in tissues10,24 and covering a wide range of optical properties (absorption coefficient from 0.01 to 300 cm−1 and scattering coefficient varying from 0.1 to 1000 cm−1 with the anisotropy factor g = 0.9). To train these ML models, we used a classification and regression tree (CART) algorithm to estimate thresholds of scattering properties and chromophore concentrations to classify normal colorectal wall (CW), fat and tumor tissues. All DRS measurements were performed in the extended wavelength range between 350 and 1920 nm by using fiber-optic probes of 630 μm SDD (probe 1) and 2500 μm SDD (probe 2) to measure tissue layers ∼0.5–1 mm and ∼0.5–2 mm deep, respectively.8
Compared to our previous studies focusing on investigating the potential of DRS for colorectal tissue diagnostics,8–10 this study is aimed at analyzing fat and CW tissues for LS and OS guidance applications instead of malignant and healthy surrounding tissues for endoscopic applications. With that in mind, please note that our study is novel based on the analysis of a different set of tissues for a completely different clinical application from those of our previous studies. We also emphasize that the analysis of this paper cannot be used to guide endoscopic microsurgery,8–10 since tissues have been measured from outside the colon and/or rectum.
Materials and methods
Study protocol and clinical data collection
In our study, we included 47 patients undergoing bowel resection at the Mercy University Hospital, Cork, Ireland. All experiments were performed in accordance with the Guidelines approved by the Clinical Research Ethics Committee of University College Cork under approval numbers ECM 4 (n) 07/03/18 and ECM 3 (hhh) 18/06/19. Informed consent was obtained from human participants of this study. Table 1 shows the patient demographics of our study. In total, 47 tumors were investigated, among which 5 were in the pT1 stage, 7 were pT2, 26 were pT3 and 9 were pT4. In addition, local lymph node metastases were found in 28 out of 47 patients.8–10| Number of patients | ||
|---|---|---|
| Gender | Female | 15 |
| Male | 32 | |
| Age (years) | Mean (± standard deviation) | 68 ± 11 |
| Range | 40–89 | |
We collected data from about 15 sites of freshly excised ex vivo CW tissues, 15 sites of fat tissues and 15 sites of tumor tissues on each colorectal specimen after surgical resection. To ensure sufficient representation of the tissue heterogeneity in our data collection, DRS measurements were performed over a typical area of 100 cm2. The measurement protocol consisted of first removing the colorectal specimen from the patient and transporting it to a measurement bench for DRS measurements. Next, we gently rinsed the specimen with water and cleaned it to remove any residual stool and excess of blood. Before starting DRS measurements, we placed the specimen on a measurement grid with the coordinates of the data collection locations. These locations were used to identify tissues based on demarcation by experienced surgeons and correlate tissue types with DRS spectra. On average, we took 40 minutes between specimen removal and the start of data collection, and about 1 hour after surgical resection for full data collection. We kept the tissue moist and preserved the physiological conditions to the best of our ability by putting a damp cloth on the specimen approximately every 7 measurements. Once we finished DRS data collection, we returned each specimen to the Pathology Department for processing and analysis according to standard protocols. The ground truth of our tissue types corresponding to our CRC DRS measurements was determined by histopathological analysis.
Diffuse reflectance spectroscopy (DRS) instrumentation
Our DRS system comprised a tungsten-halogen broadband light source with emission between 350 and 2400 nm (ref. 8) (HL-2000-HP, Ocean Optics, Edinburgh, United Kingdom), connected with fiber-optic probes of 630 μm SDD (probe 1) and 2500 μm SDD (probe 2) to send light from the source to the tissue and collect the tissue reflected light to be detected by two spectrometers. One spectrometer detected the reflected light intensity at the wavelength ranging between 350 and 1140 nm (QE-Pro, Ocean Optics, Edinburgh, United Kingdom) and another detected intensities in the wavelength range between 1090 and 1920 nm (NIR-Quest, Ocean Optics, Edinburgh, United Kingdom). We used the overlapping wavelengths between 1090 and 1140 nm to merge the two collected DRS spectra into one broadband (350–1920 nm) spectrum for each tissue site measured. More details of the instrumentation and data preprocessing are described elsewhere.8 The depth probed by probes 1 and 2 (i.e., ∼0.5–1 mm and ∼0.5–2 mm deep, respectively) was analyzed in detail in our earlier publications.8 Briefly, the tissue depth was estimated by using forward Monte Carlo (MC) simulations of light transport in multi-layered tissues (MCML)25 accelerated by a graphics processing unit (GPU).26,27 We considered a wide range of optical properties28,29 obtained from the analysis of our reflectance spectral fitting algorithm (described in detail elsewhere10,24) and in subsequent sections of this paper.Optical data collection
We collected background and reference DRS spectra by placing each probe within a dark enclosed holder that avoided ambient light and backscattered light, and fixed the distance between our reflectance standard (FWS-99-01c, Avian Technologies LLC, New London, USA) and the fiber-optic probes. Background spectra were taken with our broadband light source turned off, while reference spectra were taken with the light source turned on, before tissue measurements. We avoided probe contamination by covering our probes with a polyvinyl chloride (PVC) film. In addition, we cleaned all probes with ethanol 70% after each set of data collection. In this study, we analyzed a total of 1386 spectra for probe 1 and 1563 for probe 2.Data preprocessing
We obtained the tissue reflectance R(λ) by subtracting the background (IBackground) of each spectrometer from tissue intensity measurements (ITissue). Next, the subtracted intensity was divided by the reference measurements IReference taking into account its reflectivity: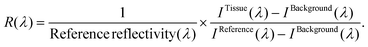 | (1) |
To merge the reflectance spectra and correct for any slight reflectance mismatch between spectra collected from the two spectrometers, we used the overlapping spectral range between 1090 and 1140 nm to perform an interpolation by using the weighted sum of eqn (2):
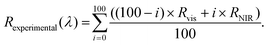 | (2) |
The resulting reflectance spectra Rexperimental(λ) were used for the estimation of chromophore concentrations and scattering parameters, as described in the next section.
Spectral fitting and extraction of biomolecule concentrations
The complete description of our reflectance spectral fitting algorithm can be found elsewhere.10,24 Briefly, we used the obtained reflectance spectra Rexperimental(λ) to obtain the scattering properties α′, bMie, and fRay and the tissue chromophore concentrations fchromophore of bile (fbile), deoxyhemoglobin (fHb), oxyhemoglobin (fHbO2), methemoglobin (fmetHb), water (fwater), and lipid (flipid). Blood-related chromophore concentrations were used to calculate the tissue total hemoglobin percentage (THb), total hemoglobin concentration (THC), tissue blood oxygen saturation (StO2) and the average blood vessel diameter Rvessel as indicated in the supplementary material of our previous publications.10,24 THC was calculated by using the equation from Jacques,29 which assumes the mass concentration within blood to be an average of 150 g L−1 and considers the molecular weight of 64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 458 g mol−1:
458 g mol−1: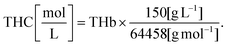 | (3) |
First, the spectral fitting used four types of input:
1. A measured reflectance spectrum Rexperimental(λ) to be fitted
2. The pure chromophore absorption spectra μa,chromophore(λ)
3. Wavelength-dependence of tissue scattering μ′s,tissue(λ) due to Rayleigh and Mie scattering (eqn (4))
4. A MC look-up table (LUT) of diffuse reflectance R(μa,μ′s) values generated with MC simulations
By associating the experimental reflectance of Rexperimental(λ) with a combination of (μa,tissue(λ), μ′s,tissue(λ)), we obtained Rtheoretical(λ) based on values of RMC(μa,tissue, μ′s,tissue) from the MC LUT. This association was only possible by using at least as many wavelengths as fitting parameters and allowed the extraction of fchromophore by using the equation:
 | (4) |
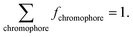 | (5) |
Similarly, the scattering properties α′, bMie, and fRay were extracted by calculating the optimum μ′s,tissue(λ)
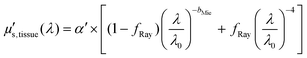 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Rexperimental(λ) transformation before fitting for the chromophore concentrations and scattering properties.
Rexperimental(λ) transformation before fitting for the chromophore concentrations and scattering properties.
It is worth noting that the tissue may contain traces of bilirubin found in blood at ranges between 5.8 and 40% in humans (based on bilirubin blood serum levels that vary between 10 and 50 mg dL−1 (ref. 30) and the total hemoglobin blood levels that vary between 121 and 172 mg dL−1 (ref. 29)). We did not include bilirubin as a chromophore with a significant contribution in our spectral fitting so that there is no contamination between the estimation of fbile and fbilirubin. Furthermore, we emphasize that the use of the bilirubin absorption spectrum in our reflectance spectral fitting would narrow the wavelength range of our fitting, since the bilirubin absorption spectrum was not reported over the broadband wavelength range used in our DRS measurements. Similarly, met-hemoglobin (metHb) has been taken into account not to interfere with the quantification of other chromophores due to absorption spectrum overlap and potential metHb formation in ex vivo tissues.
Machine learning for tissue classification
We used the estimated tissue chromophore concentrations and scattering properties as predictors to classify normal colorectal wall (CW), fat and tumor tissues. This classification involved building a decision tree model based on thresholds of predictor values defined by the classification and regression tree (CART) algorithm.10 We used 5-fold cross-validation to validate this model through its confusion matrix and evaluated classification performance metrics such as sensitivity, specificity, accuracy and area under the receiver operating characteristic curve (AUC). We also ensured that our tissue classification model was not overfitted by reporting the mean and standard deviation of the output of 20 iterations of 5-fold cross-validation with random sampling, as described in our previous publication.10Finally, we removed StO2 and fmetHb predictors with variations in ex vivo settings (and thus could not be translated to an in vivo setting from our study). Therefore, we considered only THb, Rvessel, flipid, fwater, fbile, α′, fRay and bMie as input predictors for tissue classification.
Statistical tests
Significant statistical differences between spectrally fitted parameters of CW, fat and tumor tissues were found by using one-way ANOVA with each fitted parameter. Every ANOVA test was performed with Tukey's honestly significant difference test (Tukey's HSD or Tukey–Kramer test) as the post-hoc test for pairwise comparison of means contributing to the overall significant difference. To evaluate the adequate use of one-way ANOVA, we assessed the normality of data distribution by using the Anderson–Darling normality test.Results and discussion
Tissue scattering properties and chromophore concentrations
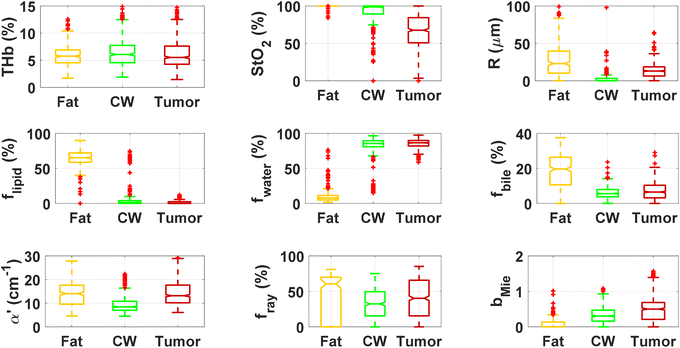
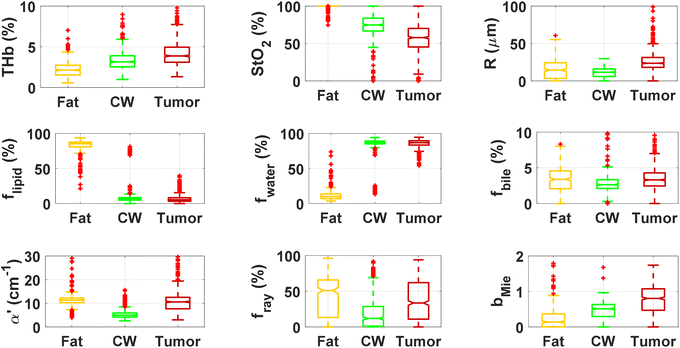
By using our reflectance spectral fitting method, we extracted relevant biochemical and microstructural parameters of tissues from superficial and deep tissue layers (∼0.5–1 mm and ∼0.5–2 mm deep, respectively). Fig. 1 and 2, and Table 2 show the THb, StO2, Rvessel, flipid, fwater, fbile, α′, fRay and bMie from probe 1 (i.e., the 630 μm source–detector distance probe) and probe 2 (2500 μm source–detector distance probe). As expected, fat tissues have higher flipid and StO2, and lower fwater in data from both probes. Since our measurements have been performed in ex vivo tissues, it is expected that fat tissues have higher StO2 since they have a lower metabolic rate compared to CW and tumor tissues and hence consume less O2 which is now replenished at slower rates since the blood flow has stopped. When using the small SDD probe, fat contained higher fbile, and exhibited larger Rvessel and lower bMie compared with CW and tumor tissues. When using probe 2, fat had slightly higher α′and lower bMie compared to normal colorectal wall (CW) and tumor tissues and exhibited smaller Rvessel compared to tumor tissues. Based on the findings of both probes, bile and large diameter blood vessels were only found in superficial fat tissues, whereas particle sizes tend to be larger throughout fat tissues up to 2 mm deep.| Small SDD probe (probe 1) | Large SDD probe (probe 2) | |||||
|---|---|---|---|---|---|---|
| Biochemical/microstructural parameters | Fat | Colorectal wall (CW) | Tumor | Fat | Colorectal wall (CW) | Tumor |
| THb (%) | 5.9 ± 2.0 | 6.5 ± 3.0 | 6.6 ± 3.9 | 2.3 ± 1.0 | 3.3 ± 1.3 | 4.8 ± 1.9 |
| THC (μmol L−1) | 136.6 ± 46.0 | 151.8 ± 69.1 | 154 ± 90 | 52.6 ± 22.3 | 77.7 ± 30.7 | 111 ± 45 |
| StO2 (%) | 99.8 ± 1.5 | 92.4 ± 13.7 | 66 ± 23 | 98.8 ± 3.7 | 73.3 ± 16.7 | 56 ± 18 |
| R (μm) | 29.8 ± 29.7 | 3.8 ± 14.8 | 14 ± 11 | 20.9 ± 75.7 | 11.3 ± 6.9 | 24 ± 13 |
| f lipid (%) | 64.9 ± 11.6 | 5.5 ± 14.0 | 1.4 ± 2.2 | 82.3 ± 9.5 | 10.6 ± 16.3 | 4.8 ± 3.0 |
| f water (%) | 10.4 ± 10.2 | 81.9 ± 15.4 | 84.9 ± 7.2 | 12.1 ± 9.0 | 83.1 ± 16.5 | 86.7 ± 4.0 |
| f bile (%) | 18.8 ± 9.2 | 6.1 ± 3.5 | 7.0 ± 4.8 | 3.3 ± 2.0 | 2.9 ± 1.5 | 3.7 ± 2.5 |
| f MetHb (%) | 1.4 ± 0.8 | 0.9 ± 0.6 | 1.1 ± 0.7 | 0.4 ± 0.2 | 0.3 ± 0.2 | 0.3 ± 0.5 |
| α′ (cm−1) | 14.2 ± 6.6 | 9.5 ± 3.7 | 15.9 ± 10.1 | 12.9 ± 12.2 | 5.7 ± 3.4 | 12.0 ± 5.6 |
| b Mie | 0.1 ± 0.1 | 0.3 ± 0.2 | 0.5 ± 0.3 | 0.2 ± 0.4 | 0.5 ± 0.3 | 0.9 ± 0.4 |
| f Ray (%) | 45.5 ± 30.2 | 32.0 ± 21.1 | 40 ± 27 | 42.5 ± 26.9 | 18.9 ± 21.3 | 36 ± 28 |
When comparing CW and tumor tissues, tumor has higher Rvessel, α′, and bMie, as well as slightly higher fwater and fbile, and slightly lower flipid. These results are valid for both probes, being more pronounced for probe 2 (2500 μm SDD probe). In particular, for probe 2, one can see that THb is slightly higher and the difference between StO2 of CW and tumor tissues is smaller compared to that in probe 1 (630 μm SDD probe). While this result may not be translated into in vivo colorectal tissues due to the study limitations described in subsequent sections,8 our results suggest that superficial tissue probed with probe 1 might be more sensitive to tissue metabolic rates once blood flow has been ceased. The higher difference in StO2 of ex vivo superficial tissues of the CW and tumor can be explained by the tumor higher metabolic rates leading to higher blood oxygen consumption, and the rates of replenishment of this oxygen through Hb exposure to atmospheric molecular oxygen forming HbO2 are significantly smaller than the blood oxygen consumption rates in tumors. On the other hand, rates of this replenishment seem to be comparable with blood oxygen consumption rates in the CW. Still, one should note that both blood oxygen consumption rates and oxygen replenishment rates change over time, as tissue cells die and Hb is converted to met-Hb which cannot bind to O2 molecules in its protein structure.
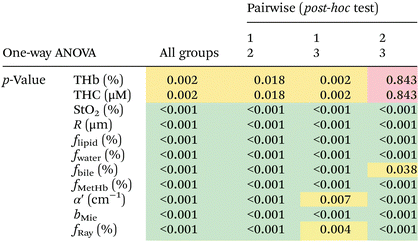
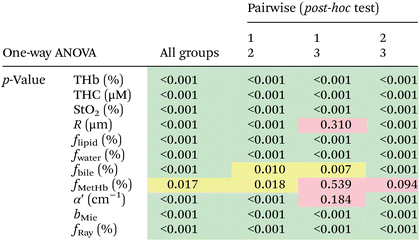
We found statistically significant differences between groups with one-way ANOVA p < 0.05 for all fitted parameters (Tables 3 and 4, column “All groups”). Pairwise comparison between groups did not show statistically significant differences (p < 0.05) between CW and tumor tissues by using the THb or THC of probe 1, between fat and tumor tissues by using R, fmetHb, α′ of probe 2, and between CW and tumor tissues by using the fmetHb of probe 2. All other parameters indicated statistically significant differences with p < 0.05 for pairwise comparisons of Tukey's HSD.
Tables 3 and 4 show the p-values corresponding to the one-way ANOVA test and post-hoc tests for all parameters listed in Table 2. These differences should be reliable for all parameters and tissue types, since all data distributions were considered normal by using the Anderson–Darling test (required for the reliability of the ANOVA test). It is worth noting that the choice of parameters for the most accurate tissue classification depends on the combination of parameters instead of the evaluation of each individual spectrally fitted parameter. With that in mind, such accuracy was evaluated by the CART analysis shown in the next section.
Tissue classification using decision trees
We built decision trees based on spectral fitting parameters of probes 1 and 2 in order to evaluate the accuracy of tissue identification in colorectal surgical applications and categorize tumors based on their particular ranges of chromophore concentrations and scattering properties.10 Based on the categories of tumor, fat and normal colorectal wall (CW) tissues, Table 5 shows the percentage of classified observations (samples) normalized by the total number of observations (true class) for each tissue type. Our results suggest that probe 2 can be used for more accurate tissue classification compared to probe 1. This result is valid for DRS measurements with a reasonable signal-to-noise ratio (SNR), and one should consider that miniaturized DRS instruments may have a less SNR due to less powerful light sources and/or less costly detectors.| % of classified observations/number of observations | Predicted class | |||||||
|---|---|---|---|---|---|---|---|---|
| Small SDD probe (probe 1) | Large SDD probe (probe 2) | |||||||
| Fat | Colorectal wall (CW) | Tumor | Fat | Colorectal wall (CW) | Tumor | |||
| True class | Fat (n = 318) | 96.3 ± 0.9 | 3.7 ± 0.9 | 0.1 ± 0.3 | Fat (n = 348) | 96.3 ± 0.5 | 3.4 ± 0.5 | 0.4 ± 0.3 |
| CW (n = 434) | 2.6 ± 0.5 | 86.2 ± 1.4 | 11.2 ± 1.3 | CW (n = 493) | 1.9 ± 0.6 | 92.7 ± 1.1 | 5.4 ± 1.0 | |
| Tumor (n = 635) | 0.3 ± 0.2 | 9.9 ± 0.6 | 89.8 ± 0.6 | Tumor (n = 722) | 0.3 ± 0.0 | 5.9 ± 0.5 | 93.8 ± 0.5 | |
A lower SNR may lead to a higher decrease in the accuracy for probe 2 measurements than that for probe 1 measurements because the amplitude of the reflected intensity is lower for probe 2. Therefore, to reproduce the results of this study, The SNR should be as high as possible to the current state-of-the-art DRS instruments and investigation should be conducted to confirm whether our results are translatable for in vivo colorectal tissues.
The SNR varies dramatically over the wide wavelength range between 350 nm and 1900 nm. For probe 1, the highest signal of a typical recorded spectrum is 1000 times stronger than the lowest signal, and the lowest signal is typically 10 times above the noise floor. Therefore, the dynamic range of the recorded spectra is 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. For probe 2, the highest signal is 100 times stronger than the lowest signal, and the lowest signal is typically twice above the noise floor for water-rich tissues (such as the CW and tumor), leading to a total dynamic range of 200
1. For probe 2, the highest signal is 100 times stronger than the lowest signal, and the lowest signal is typically twice above the noise floor for water-rich tissues (such as the CW and tumor), leading to a total dynamic range of 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The given dynamic range and noise of our measurements gave rise to the variations in the fitting parameters reported in Table 2. It is worth noting that the poor SNR in probe 2 occurs only between 1400 nm and 1600 nm of the fitted wavelength range, and that the spectral fitting algorithm may tend to consider fitting for the water concentration based on the wavelength range between 900 nm and 1300 nm for water-rich tissues, as the signal at the water absorption peaks is typically 50–100 times above the noise floor.
1. The given dynamic range and noise of our measurements gave rise to the variations in the fitting parameters reported in Table 2. It is worth noting that the poor SNR in probe 2 occurs only between 1400 nm and 1600 nm of the fitted wavelength range, and that the spectral fitting algorithm may tend to consider fitting for the water concentration based on the wavelength range between 900 nm and 1300 nm for water-rich tissues, as the signal at the water absorption peaks is typically 50–100 times above the noise floor.
Based on our experience on studies in colorectal tissues, we recommend having a bare minimum of 10 times higher reflectance signal compared to the noise (i.e., approximately 13 dB in the power ratio) for analyzing wavelengths below 1400 nm. Further scientific evidence is needed for the calculation of minimum SNR requirements and the impact of the SNR on the performance of the spectral fitting algorithm (SFA). Such evidence requires meticulous calculation that is out of the scope of our study. The calculation of minimum SNR requirements depends on factors including the combination of (1) the spectral shape difference due to the contribution of tissue chromophores at a given fitted wavelength range, (2) the amplitude of the reflectance signal at such a range, and (3) the homogeneity of optical properties over the tissue depth probed with light at each wavelength.
Our SFA will be more accurate when the sharper and more specific chromophore spectral features are at the selected wavelength range. Accuracy is also enhanced when the more homogeneous tissue layers are in terms of optical properties at the probed depth defined by the probe geometry (e.g., source–detector distance) and light wavelength used. If tissue is sufficiently homogeneous and has spectral features that can distinguish the contribution of each chromophore via spectral shape, the SNR helps to improve accuracy by facilitating the identification of chromophore spectral features. Future studies will explore the impact of the SNR on the performance of our SFA.
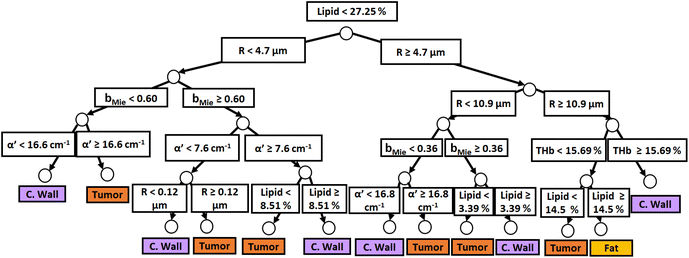
Fig. 3 and 4 show the two separate branches of a decision tree with parameters leading to the most accurate classification between fat (n = 318), CW (n = 434) and tumor (n = 634) tissues by using probe 1. These parameters were THb, Rvessel, flipid, α′, and bMie. By using the 5-fold cross-validation, we achieved 95.9 ± 0.7% sensitivity, 98.9 ± 0.3% specificity, 90.2 ± 0.4% accuracy, and 95.5 ± 0.3% AUC. Also, it is important to remember that parameters appearing close to the top of the decision trees (Fig. 3–6) are the most important for tissue classification. With this in mind, the parameters appearing at the top two layers of splits for probe 1 (Fig. 3 and 4), i.e., flipid, Rvessel, and bMie can be important parameters for laparoscopic CRC detection when using the 630 μm-SDD probe.
 | ||
| Fig. 3 Classification decision tree of fat, colorectal wall and tumor tissues based on parameter threshold values of probe 1 (630 μm-SDD probe) for flipid < 27.25%. | ||
 | ||
| Fig. 4 Classification decision tree of fat, colorectal wall and tumor tissues based on parameter threshold values of probe 1 (600 μm-SDD probe) for flipid ≥ 27.25%. | ||
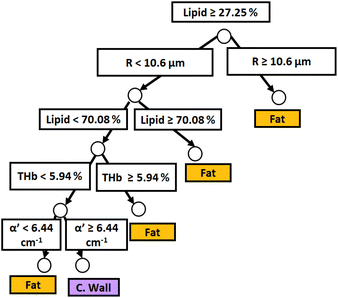
 | ||
| Fig. 5 Classification decision tree of fat, colorectal wall and tumor tissues based on parameter threshold values of probe 2 (2500 μm-SDD probe) for flipid < 33.12%. | ||
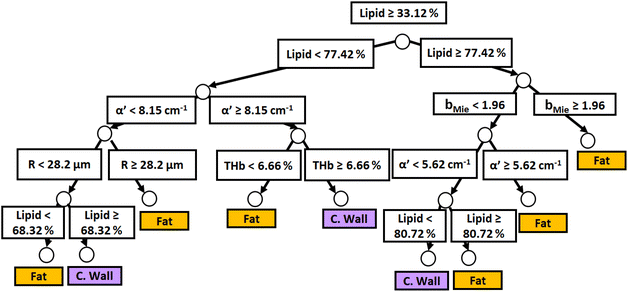 | ||
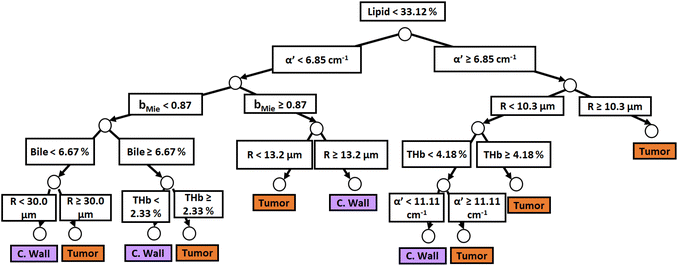
| Fig. 6 Classification decision tree of fat, colorectal wall and tumor tissues based on parameter threshold values of probe 2 (2500 μm-SDD probe) for flipid ≥ 33.12%. | ||
Similar to probe 1, Fig. 5 and 6 show that the two separate branches of a decision tree with parameters leading to the most accurate classification between fat (n = 348), CW (n = 493) and tumor (n = 722) tissues by using probe 2. These parameters were THb, Rvessel, flipid, fbile, α′, and bMie. By using 5-fold cross-validation, we achieved 96.9 ± 0.8% sensitivity, 98.9 ± 0.2% specificity, 94.0 ± 0.4% accuracy, and 96.7 ± 0.4% AUC. The parameters which appear on the top two layers of splits from probe 2 (flipid, Rvessel, α′, and bMie) were similar to those from probe 1. Since THb does not appear on the two layers of splits for neither probe, THb may not be an important parameter for classification of fat, CW and tumor tissues. Still, flipid, Rvessel, and bMie appear as important parameters for both probes and may be explored in future studies for laparoscopic CRC detection. These findings need to be confirmed by in vivo tissue measurements to overcome the limitations of data collection of ex vivo tissues.
Relevance of our work
Compared to previous studies with the intention to guide CRC resections, we have (1) extended the wavelength range of the collected DRS spectra to 350–1920 nm, (2) unveiled the tissue biochemistry and microstructure of superficial and deeper tissue layers (∼0.5–1 mm and ∼0.5–2 mm deep, respectively) with a real-time and non-invasive method, (3) collected more DRS measurements per dataset (2949 DRS spectra in total, 1386 with probe 1 and 1563 with probe 2) and (4) extracted tissue scattering properties and chromophore concentrations using probabilistic Monte Carlo models not restricted by the limitations of the diffusion theory used in previous studies.In a practical perspective, our study is the first step to overcome the limitations of prior DRS research on surgical CRC detection. By incorporating DRS into a flexible fiber-optic probe that can be either passed down a laparoscope working channel, or used with robotic surgery instruments, DRS surgical guidance can potentially increase the accuracy of surgical procedures, improve rates of complete resection and thereby decrease colorectal cancer (CRC) recurrence and mortality. If a side-firing fiber-optic probe31 can be directly integrated into the fingertip of a surgeon, open surgery could also be made more accurate.
In a research perspective, our work identified CRC categories based on the thresholds of biomarkers that may be associated with CRC recurrence and/or with patient prognosis. Prediction of treatment outcomes can potentially be achieved by future in vivo studies correlating surgical outcomes with CRC categories based on chromophore concentrations and scattering properties.
It is important to note that our approach combining spectral fitting with machine learning has a different purpose compared with approaches using only machine learning methods to identify colorectal cancer directly from reflectance spectral data. Our spectral fitting provides interpretable parameters with biological relevance while enabling tissue classification and future patient stratification based on parameters that can potentially be associated with other biochemical analysis of laboratory samples. Previous approaches using only machine learning methods used k-nearest neighbors (kNNs), support vector machines (SVMs), artificial neural networks, decision trees, and linear discriminant analysis (LDA) as methods to identify colorectal cancer in real-time without biologically/biochemically interpretable parameters.21 Future studies will include work on complementary approaches to ours including feature selection by excluding uncorrelated variables through ensembles of random forest classifiers (i.e., importance testing) and/or the maximum relevance minimum redundancy (MRMR).32
Validity and limitations of our study
Due to variations present in contact measurements and ex vivo tissues, our study has several limitations. First, the measured CRC locations were demarcated based on the palpation and naked eye feedback by experienced surgeons prior to confirmation with histopathology results. It is worth noting that this demarcation does not decrease the validity of our dataset and structural/biochemical analysis, as our dataset is sufficiently large to incorporate tissue spectral variations at larger areas (∼100 cm2) and within several time periods after surgery (which results in variation of tissue dehydration, blood concentration and blood oxygenation). In addition, we attempted to avoid dehydration by keeping tissue moist with damp cloth at every 7 DRS measurements.Our ex vivo measurements also could not control blood oxygenation, which could potentially be modeled by using data such as time after specimen excision, pH, and pCO2, among others in future studies. Still, in a pilot ex vivo observation of the DRS signal in 3 patients, we observed no significant variations in the average Hb and HbO2 of CRC tissues at 7 locations during the first 15 minutes of our measurements (data not shown).8–10 We are aware that, according to Baltussen et al.33fwater may decrease, and THb and StO2 may increase in ex vivo tissues compared to in vivo tissues within 1 hour after resection. Still, StO2 trends are controversial, since Salomatina et al.34 reported decreased StO2 in mouse ear tissues between 5 and 10 minutes after excision (ex vivo) of tissue and after 24 and 72 hours of storage. It is important to note that variations in THb, StO2 and fwater did not affect the results of our study because these parameters were not used to classify tissues.
We did not include non-cancer pathology in our study. Future inclusion of non-cancer pathologies such as inflammatory bowel disease, radiation-induced fibrosis, and scarring following local excision of cancers may change the classification performance of our CART model and categories of CRC to be considered on long-term follow up studies. It is worth noting that the lack of non-cancer pathology does not affect our tissue biochemical/structural parameters. Our analysis is valid and robust, considering that our dataset includes intra- and inter-patient variations (1386 + 1563 spectra of 47 patients) of both superficial and deeper tissue layers.
Also, our spectral fitting assumes homogeneous media to extract the average tissue chromophore concentrations and scattering properties. Inaccuracies may arise if the heterogeneity on the optical properties deviates significantly from the average properties estimated by assuming that tissue is homogeneous. These inaccuracies are only significant if the heterogeneity over tissue layers probed at each wavelength λ changes the spectral shape of Rexperimental(λ) at wavelength ranges pertinent to distinguish the contribution of different chromophores (e.g., heterogeneity at tissue probed between 520 nm and 560 nm when fitting primarily for Hb and HbO2). However, our results suggest that overfitting is not an issue in our study because uncertainties of fitted parameters are much smaller than uncertainties due to tissue heterogeneity.
For homogeneous medium simulating tissue optical properties, the typical coefficient of variation (COV, i.e., the ratio of the standard deviation to the mean) of each fitted parameter is about 1–10% of the true value of each parameter, except for bMie, which has typical standard deviations around 10–30% for tissue optical properties. When comparing COV in homogeneous media with COV values taken from Table 2, we can see that the average COV over all tissue types varies between 18% and 174%. The only parameters with a lower COV are StO2 (COV ranging from 2% and 35% with a mean of 18% over all tissue types) and water (COV ranging from 5% and 98% with a mean of 37% over all tissue types).
Further evidence indicating that fitted parameters may not be overfitted is that trends on lower COV values occur in the same tissue type, even when measured with different probes and using a different Monte Carlo Look-up Table for spectral fitting. We observed lower COV values only for StO2(%) in fat tissues and fwater (%) in tumor tissues, independent of the probe (or source–detector distance; SDD) used. Consistently lower COV values for independent spectral fitting procedures and probes suggest there was no overfitting even when COV values were approximately the minimum expected from the spectral fitting algorithm (SFA). Therefore, the uncertainty in the fitted parameters as evaluated by their COV should not affect our tissue classification.
In addition, StO2(%) and fwater (%) were not included in the list of the most important parameters for tissue classification and thus did not influence such a classification. This non-inclusion suggests that the tissue classification already excluded the contribution of fitted parameters with uncertainty comparable to the minimum expected from the SFA (i.e., parameters with potentially most of their uncertainties coming from the SFA instead of the tissue heterogeneity). Hence, only fitted parameters with uncertainty dictated primarily by tissue heterogeneity were considered as the most important parameters. With that in mind, our results suggest that the uncertainty on the fitted parameters did not influence our tissue classification.
Finally, previous studies have shown that reflectance measurements can accurately estimate optical properties based on the fitted parameters.35,36 A detailed study on the uncertainty on fitted parameters upon variations in reflectance is not within the scope of our study.
Conclusions
In this study, we evaluated the most important structural and biochemical parameters for surgical CRC delineation through broadband diffuse reflectance spectroscopy (DRS), as well as the categories of CW, fat and tumor tissues based on thresholds of these parameters. These parameters were flipid, Rvessel, α′, and bMie, since they appeared on the top of both decision trees of probe 1 and probe 2. Differences between probe 1 (for superficial tissues 0.5–1 mm deep) and probe 2 (for deeper tissue layers 0.5–2 mm deep) mainly rely on α′ being more important than Rvessel for tissue classification using probe 2. We have shown that classification performance metrics for tissue identification can be as high as 95.9 ± 0.7% sensitivity, 98.9 ± 0.3% specificity, 90.2 ± 0.4% accuracy, and 95.5 ± 0.3% AUC for probe 1, and 96.9 ± 0.8% sensitivity, 98.9 ± 0.2% specificity, 94.0 ± 0.4% accuracy, and 96.7 ± 0.4% AUC for probe 2. Future studies should validate these metrics for in vivo DRS and/or hyperspectral imaging during laparoscopy, open surgery and robotic surgery. Benefits of laparoscopic surgery and robotic surgery include real-time and accurate tissue identification when tactile feedback is not available to surgeons. Another benefit is the precise localization of cancer to obviate the need for multiple biopsies and accurately delineate cancer margins through personalized determination of the circumferential resection margin (CRM). The latter benefit also extends to open surgery.Author contributions
M. S. N.: conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing – original draft, writing – review & editing, visualization, supervision, project administration; S. M.: investigation; M. A.: investigation; S. K.: investigation, resources, data curation; M. O. R.: conceptualization, methodology, investigation, resources, writing – review & editing, supervision, project administration, funding acquisition; S. A. E.: conceptualization, methodology, resources, software, investigation, writing – original draft, writing – review & editing, supervision, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge Eduardo Moriyama for the advice and logistics of the project associated with this manuscript, Shree Krishnamoorthy for the discussions on the same project, Huihui Lu for the help with clinical research ethics documentation, Haiyang Li for the design and assembly of the holder of the DRS system, Noel Lynch and Andrew McGuire for the specimen retrieval of patients of this study and all the logistics related to it, and Vivienne Curran, Aoife Foyle, Una McAuliffe, Evelyn Flanagan, Shauni Fitzgerald, and Edmund Manning for all the logistics of clinical procedures, research ethics documents, and search for patient information. Shauni Fitzgerald and Edmund Manning were funded by the Mercy Hospital Foundation. This study received financial support from the Science Foundation Ireland (SFI): grant ID SFI/15/RP/2828.References
- F. Bray, J. Ferlay, I. Soerjomataram, R. L. Siegel, L. A. Torre and A. Jemal, Ca-Cancer J. Clin., 2018, 68, 394–424 CrossRef PubMed.
- J. Ferlay, M. Ervik, F. Lam, M. Colombet, L. Mery, M. Piñeros, A. Znaor, I. Soerjomataram and F. Bray, Global cancer observatory: cancer today, international agency for research on cancer, Lyon, France, 2018 Search PubMed.
- H. Pak, L. H. Maghsoudi, A. Soltanian and F. Gholami, Ann. Med. Surg., 2020, 55, 13–18 CrossRef.
- M. M. Reza, J. A. Blasco, E. Andradas, R. Cantero and J. Mayol, Br. J. Surg., 2006, 93, 921–928 CrossRef CAS.
- M. S. Nogueira, R. Matthews, S. Killeen, M. O'Riordain and S. Andersson-Engels, Colorectal cancer detection based on the extraction of scattering properties and biochemical concentrations from fluorescence spectroscopy measurements, Clinical and Translational Biophotonics, Optica Publishing Group, 2022, p. TS2B–5 Search PubMed.
- M. S. Nogueira, M. Raju, J. Gunther, K. Grygoryev, K. Komolibus, H. Lu and S. Andersson-Engels, in Proceedings of SPIE 10685 Biophotonics: Photonic Solutions for Better Health Care VI, 2018, vol. 10685, p. 106853G.
- C. T. de Andrade, M. S. Nogueira, S. C. Kanick, K. Marra, J. Gunn, J. Andreozzi, K. S. Samkoe, C. Kurachi and B. W. Pogue, in Proceedings of SPIE 9694 Optical Methods for Tumor Treatment and Detection: Mechanisms and Techniques in Photodynamic Therapy XXV, 2016, vol. 9694, p. 969410.
- M. S. Nogueira, S. Maryam, M. Amissah, H. Lu, N. Lynch, S. Killeen, M. O'Riordain and S. Andersson-Engels, Sci. Rep., 2021, 11, 798 CrossRef CAS PubMed , 1–17.
- M. Saito Nogueira, S. Maryam, M. Amissah, A. McGuire, C. Spillane, S. Killeen, S. Andersson-Engels and M. O'Riordain, Cancers, 2022, 14, 5715 CrossRef.
- M. S. Nogueira, M. Raju, J. Gunther, S. Maryam, M. Amissah, H. Lu, S. Killeen, M. O'Riordain and S. Andersson-Engels, J. Phys. D: Appl. Phys., 2021, 54, 454002 CrossRef CAS.
- M. S. Nogueira, M. Raju, J. Gunther, S. Maryam, M. Amissah, H. Lu, S. Killeen, M. O'Riordain and S. Andersson-Engels, Proc. SPIE 11943, Photonics West, 11943-4.
- M. S. Nogueira, S. Maryam, M. Amissah, N. Lynch, S. Killeen, H. Lu, M. O'Riordain and S. Andersson-Engels, Proc. SPIE 11954, Photonics West, 11954-15.
- M. S. Nogueira, S. Maryam, M. Amissah, N. Lynch, S. Killeen, M. O'Riordain and S. Andersson-Engels, in European Conference on Biomedical Optics, 2021, pp. EW4A–16.
- M. S. Nogueira, M. Raju, J. Gunther, S. Maryam, M. Amissah, S. Killeen, M. O'Riordain and S. Andersson-Engels, in European Conference on Biomedical Optics, 2021, pp. ETu3A–1.
- M. S. Nogueira, M. Amissah, S. Maryam, N. Lynch, S. Killeen, M. O'Riordain and S. Andersson-Engels, in European Conference on Biomedical Optics, 2021, pp. EW4A–17.
- E. J. M. Baltussen, P. Snæbjörnsson, S. G. B. De Koning, H. J. C. M. Sterenborg, A. G. J. Aalbers, N. Kok, G. L. Beets, B. H. W. Hendriks, K. F. D. Kuhlmann and T. J. M. Ruers, J. Biomed. Opt., 2017, 22, 106014 Search PubMed.
- E. J. M. Baltussen, E. N. D. Kok, S. G. B. de Koning, J. Sanders, A. G. J. Aalbers, N. F. M. Kok, G. L. Beets, C. C. Flohil, S. C. Bruin and K. F. D. Kuhlmann, et al. , J. Biomed. Opt., 2019, 24, 16002 Search PubMed.
- E. J. M. Baltussen, S. G. de Koning, J. Sanders, A. G. J. Aalbers, N. F. M. Kok, G. L. Beets, B. H. W. Hendriks, H. J. C. M. Sterenborg, K. F. D. Kuhlmann and T. J. M. Ruers, Lasers Surg. Med., 2020, 52, 604–611 CrossRef PubMed.
- E. J. M. Baltussen, S. G. B. De Koning, J. Sanders, A. G. J. Aalbers, N. F. M. Kok, G. L. Beets, B. H. W. Hendriks, H. J. C. M. Sterenborg, K. F. D. Kuhlmann and T. J. M. Ruers, J. Transl. Med., 2019, 17, 1–10 CrossRef.
- G. C. Langhout, T. M. Bydlon, M. van der Voort, M. Müller, J. Kortsmit, G. Lucassen, A. J. R. Balthasar, G.-J. van Geffen, T. Steinfeldt and H. J. C. M. Sterenborg, Lasers Surg. Med., 2018, 50, 253–261 CrossRef PubMed.
- E. J. M. Baltussen, H. J. C. M. Sterenborg, T. J. M. Ruers and B. Dashtbozorg, Biomed. Opt. Express, 2019, 10, 6096–6113 CrossRef CAS.
- G. C. Langhout, J. W. Spliethoff, S. J. Schmitz, A. G. J. Aalbers, M.-L. van Velthuysen, B. H. W. Hendriks, T. J. M. Ruers and K. F. D. Kuhlmann, Lasers Surg. Med., 2015, 47, 559–565 CrossRef CAS PubMed.
- G. C. Langhout, J. W. Spliethoff, A. G. J. Aalbers, V. J. Verwaal, B. H. W. Hendriks, T. J. M. Ruers and K. F. D. Kuhlmann, Ann. Oncol., 2014, 25, iv206 CrossRef.
- M. S. Nogueira, M. Raju, K. Komolibus, K. Grygoryev and S. Andersson-Engels, J. Phys. D: Appl. Phys., 2021, 54, 374003 CrossRef CAS.
- L. Wang, S. L. Jacques and L. Zheng, Comput. Methods Programs Biomed., 1995, 47, 131–146 CrossRef CAS.
- E. Alerstam, W. C. Y. Lo, T. D. Han, J. Rose, S. Andersson-Engels and L. Lilge, Biomed. Opt. Express, 2010, 1, 658–675 CrossRef PubMed.
- E. Alerstam, T. Svensson and S. Andersson-Engels, J. Biomed. Opt., 2008, 13, 60504 CrossRef.
- T. Valery, Tissue Optics: Light Scattering Methods and Instruments for Medical Diagnosis, SPIE Press, Bellingham, Washington, 2007 Search PubMed.
- S. L. Jacques, Phys. Med. Biol., 2013, 58(11), R37–R61 CrossRef PubMed.
- J. F. L. Cobbold and J. A. Summerfield, in Handbook of Liver Disease, Elsevier, 2012, pp. 297–307 Search PubMed.
- F. Geldof, M. Witteveen, H. J. C. M. Sterenborg, T. J. M. Ruers and B. Dashtbozorg, Biomed. Opt. Express, 2023, 14, 128–147 CrossRef PubMed.
- J. Ollesch, M. Zaczek, H. M. Heise, O. Theisen, F. Grosserueschkamp, R. Schmidt, K. Morgenroth, S. Philippou, M. Kemen and K. Gerwert, Vib. Spectrosc., 2017, 91, 99–110 CrossRef CAS.
- E. J. M. Baltussen, S. G. Brouwer De Koning, B. H. W. Hendriks, K. Jóźwiak, H. J. C. M. Sterenborg and T. J. M. Ruers, Transl. Biophotonics, 2019, 1, e201900008 CrossRef.
- E. Salomatina and A. N. Yaroslavsky, Phys. Med. Biol., 2008, 53, 2797 CrossRef CAS PubMed.
- G. M. Palmer and N. Ramanujam, Appl. Opt., 2006, 45, 1062–1071 CrossRef PubMed.
- R. J. Hennessy, S. L. Lim, M. K. Markey and J. W. Tunnell, J. Biomed. Opt., 2013, 18, 37003 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |