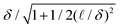Boundary design regulates the diffusion of active matter in heterogeneous environments†
Kevin J.
Modica
 a,
Ahmad K.
Omar
a,
Ahmad K.
Omar
 bc and
Sho C.
Takatori
bc and
Sho C.
Takatori
 *a
*a
aDepartment of Chemical Engineering, University of California, Santa Barbara, Santa Barbara, CA 93106, USA. E-mail: stakatori@ucsb.edu
bDepartment of Materials Science and Engineering, University of California, Berkeley, Berkeley, CA 94720, USA
cMaterials Sciences Division, Lawrence Berkeley National Laboratory, Berkeley, CA 94720, USA
First published on 9th February 2023
Abstract
Physical boundaries play a key role in governing the overall transport properties of nearby self-propelled particles. In this work, we develop dispersion theories and conduct Brownian dynamics simulations to predict the coupling between surface accumulation and effective diffusivity of active particles in boundary-rich media. We focus on three models that are well-understood for passive systems: particle transport in (i) an array of fixed volume-excluding obstacles; (ii) a pore with spatially heterogeneous width; and (iii) a tortuous path with kinks and corners. While the impact of these entropic barriers on passive particle transport is well established, we find that these classical models of porous media flows break down due to the unique interplay between activity and the microstructure of the internal geometry. We study the activity-induced slowdown of effective diffusivity by formulating a Smoluchowski description of long-time self diffusivity which contains contributions from the density and fluctuation fields of the active particles. Particle-based and finite element simulations corroborate this perspective and reveal important nonequilibrium considerations of active transport.
1 Introduction
Motile microorganisms self-propel and enhance their transport through complex, boundary-rich environments. The diffusion of living systems is crucial to public health; chronic infections can occur when pathogenic bacteria invade wound sites,1–3 whereas bioremediation requires bacterial penetration into soil sediments.4,5 In agriculture, rhizosphere bacteria move through soils and protect plant roots.6 Unfortunately, many biologically or industrially relevant porous materials are opaque and the details of the microstructure are challenging to resolve. Only recently have experiments been able to directly observe and track individual cell motion through a 3D porous domain;7 therefore, the development of theoretical models to predict boundary effects on self-propelled constituents is critical to our understanding of self-propelled (active) transport in complex physical environments.Porous media guides species transport through a combination of enthalpic and entropic interactions.8,9 In this work, we will focus our attention on entropic, excluded-volume interactions between diffusing particles and hard external boundaries. Introducing even a dilute concentration of immobile obstacles with purely excluded-volume interactions can provide a substantial slowdown to diffusive flux.10–12 While self-propelled bacteria move via nonequilibrium forcing, recent research has found success in describing swimmers as Brownian particles under a higher effective temperature and swim energy ksTs. This is then translated to a bulk diffusivity using the drag coefficient ζ by means of a modification to the Stokes–Einstein–Sutherland relation: D0 = (kBT + ksTs)/ζ.
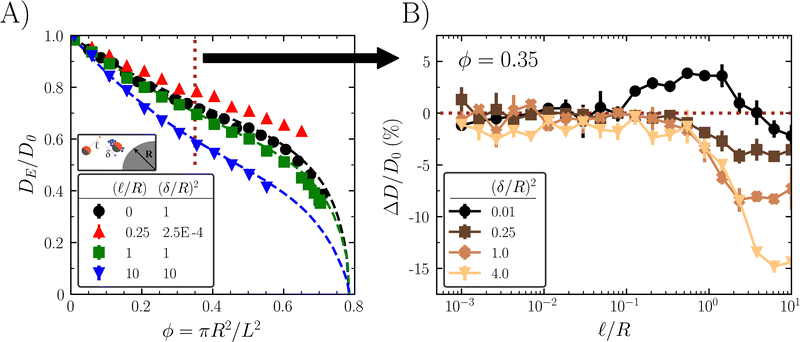
This effective temperature approach is an approximation of the true nonequilibrium behavior, but it has shown success in predicting swim pressure, bulk self-diffusivity, and the energy transferred to a tracer in an active bath.13–16 For an active Brownian particle (ABP), one can define the swim energy in 2D:17ksTs = ζU02τR/2. This corresponds to a long time self diffusivity of D0 = DT + U02τR/2, where DT = kBT/ζ is the thermal diffusivity, U0 is the self-propulsive velocity, τR is the reorientation time, and DR = 1/τR is the rotational diffusion coefficient.18 The effective temperature ansatz has been successful in describing the diffusivity of free suspensions; however, it may break down in the presence of excluded volume interactions or external boundaries. Boundaries are especially important for active matter systems due to their activity-induced enrichment along surfaces. Unlike passive (equilibrium) Brownian particles, active particles accumulate at boundaries due to their persistent motion, even in the absence of particle-boundary attraction.14,19–23
Many researchers have examined how confinement influences the behavior of self-propelled colloidal particles.7,12,24–29 In arrays of fixed obstacles, specific swimmer models and geometries allow one to observe subdiffusive30,31 and superdiffusive32 transport. Increased concavity and surface area enhances the partitioning of ABPs at boundaries and perturbs the microstructure further from Boltzmann statistics.33,34 We hypothesize that the transport properties of active matter can be tuned by the careful control of porous media microstructure, just as the steady-state properties can. We have recently determined that variations in boundary curvature reduces the mobility of nearby swimmers,34 but it is unclear how the design of porous materials reduces the macroscopic transport of swimmers from their well-known bulk diffusivity. Classical theories of diffusive transport in porous media rely on averaging over local degrees of freedom to find the effective diffusivity, DE. These theories are accurate for a dilute suspension of passive Brownian particles that exhibit no accumulation on surfaces; however, their applicability to self-propelled swimmers is unclear.
In this work, we demonstrate that existing theories of porous media transport fail due to the accumulation of active swimmers on boundaries. Boundaries create significant, long-ranged disturbances to the distribution of active particles; we show that these disturbances correspond to a reduced scaled diffusivity in boundary-rich media.
2 Model
We design three representative examples of distinct porous media to interrogate the accuracy of the corresponding equilibrium-based model with the transport of active Brownian particles (Fig. 1).First, in Fig. 1A, we consider a lattice array of circular 2D inclusions. For a dilute concentration of inclusions, the swimmers collide with the hard boundaries and then escape without difficulty, leading to a minor slowdown that depends on the obstacle density and size. Second, in Fig. 1B, we consider the transport across a narrow constriction. This constriction can be considered as the limit of dense packing for a lattice array of obstacles. Finally, in Fig. 1C, we consider the diffusion along a tortuous path that represents a simple model of a porous network. Each model system is designed to test how the geometry-dependent accumulation of active particles cause deviations in classical theories developed for passive Brownian systems. We focus on the transport of dilute ABPs in rigid, 2D porous media, such as swimmers in confined microfluidic devices, but our qualitative results and framework apply in 3D as well.
An ABP particle i follows the overdamped Langevin equation with a swim force of constant magnitude and white noise Brownian forces and torques.35–38 To simulate a dilute system, the ABPs interact with obstacles via a purely repulsive potential, but do not interact with each other (i.e., the particles are “ideal”).
 | (1a) |
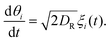 | (1b) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi, sin
θi, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θi] is the unit vector describing particle i's orientation in 2D. Finally, the thermal and rotational diffusion coefficients are DT and DR = 1/τR, with (ηi, ξi) as random variables obeying the zero mean and variance consistent with the fluctuation-dissipation theorem. The obstacle-particle repulsive force Fi,rep is implemented using the Weeks–Chandler–Andersen (WCA)39 potential on overlapping spheres defining the obstacle surface (see ESI† for details). We find the effective diffusivity tensor (DE) of an ABP in the porous medium from the slope of the mean squared displacement (MSD) at long times.
θi] is the unit vector describing particle i's orientation in 2D. Finally, the thermal and rotational diffusion coefficients are DT and DR = 1/τR, with (ηi, ξi) as random variables obeying the zero mean and variance consistent with the fluctuation-dissipation theorem. The obstacle-particle repulsive force Fi,rep is implemented using the Weeks–Chandler–Andersen (WCA)39 potential on overlapping spheres defining the obstacle surface (see ESI† for details). We find the effective diffusivity tensor (DE) of an ABP in the porous medium from the slope of the mean squared displacement (MSD) at long times. | (2) |
 | (3a) |
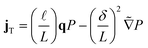 | (3b) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) = t/τR,
= t/τR, ![[R with combining tilde]](https://www.rsc.org/images/entities/b_char_0052_0303.gif) = R/L, and
= R/L, and  . We impose a no-flux boundary condition on all obstacle surfaces. Time is scaled by the reorientation time τR, and distance is scaled by a geometric feature of length L. In principle, Frep(R) should also appear, but we are using excluded volume interactions which can be implemented as boundary conditions. This form of nondimensionalization introduces two important length scales. The run length
. We impose a no-flux boundary condition on all obstacle surfaces. Time is scaled by the reorientation time τR, and distance is scaled by a geometric feature of length L. In principle, Frep(R) should also appear, but we are using excluded volume interactions which can be implemented as boundary conditions. This form of nondimensionalization introduces two important length scales. The run length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = U0τR is the average distance an ABP self-advects before reorienting and the microscopic length
= U0τR is the average distance an ABP self-advects before reorienting and the microscopic length  is the root mean squared distance an ABP travels by thermal motion before reorienting. These represent the strength of active and thermal forces, respectively.
is the root mean squared distance an ABP travels by thermal motion before reorienting. These represent the strength of active and thermal forces, respectively.
Taking orientational moments of the full Smoluchowski equation turns eqn (2) into an infinite series of coupled conservation equations.40 The density field  depends on the polar order,
depends on the polar order,  , which depends on the nematic order,
, which depends on the nematic order,  , and so on. We solve eqn (3) numerically and take orientational moments of the full solution to calculate the effective translational diffusivity using methods discussed in the following section. We will examine these equations using the list of relevant length scales shown in Table 1.
, and so on. We solve eqn (3) numerically and take orientational moments of the full solution to calculate the effective translational diffusivity using methods discussed in the following section. We will examine these equations using the list of relevant length scales shown in Table 1.
3 Case studies
3.1 Diffusion around rigid inclusions
For passive Brownian particles in a high porosity lattice (ϕ ≪ 1), as in Fig. 2A, the effective diffusivity decreases linearly with the area density of obstacles DE/DT = (1 − ϕ) + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (ϕ2),41,42 and has been solved to arbitrary order using series solutions.10 If the active particles are equivalent to passive Brownian particles at a higher effective temperature, their reduced diffusivity should track the series solution after replacing DT with D0 = DT + U02τR/2.
(ϕ2),41,42 and has been solved to arbitrary order using series solutions.10 If the active particles are equivalent to passive Brownian particles at a higher effective temperature, their reduced diffusivity should track the series solution after replacing DT with D0 = DT + U02τR/2.
In addition to Brownian dynamics simulations, we numerically solve eqn (3) using generalized Taylor dispersion theory.10,12,43–47 We obtain the effective velocity vector uE and diffusivity tensor DE of the active particles by splitting the full distribution into local and global contributions. The ABPs position vector R is defined as the sum of the global unit cell vector (X) and the local position inside the unit cell (r). For a particle that enters an L × L unit cell containing a central obstacle, the normalized probability density of finding a particle at position r and orientation q at time t is denoted as g0(r, q, t). Particle density fluctuations due to the presence of obstacles give rise to an effective diffusivity that is distinct from the bulk diffusivity D0. The strength and direction of these density fluctuations is measured by the fluctuation field d(r, q, t). Equations are kept in dimensional form for clarity. (See ESI† for full derivation):
 | (4a) |
 | (4b) |
We solve these equations at steady state subject to no-flux boundary conditions along the surface of the inclusion, periodic boundary conditions at the unit cell edges, and normalization constraints 〈g0〉q,r = 1,〈d〉q,r = 0 using the finite element method. Where  . We use the steady state solutions to compute the average effective velocity uE and diffusivity DE of the system:
. We use the steady state solutions to compute the average effective velocity uE and diffusivity DE of the system:
| uE = U0〈qg0〉q,r − DT〈∇rg0〉q,r | (5a) |
| DE = DTI − U0〈qd〉q,r + DT〈∇rd〉q,r. | (5b) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ≫ δ or
≫ δ or ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ≫ R). The effective temperature expression only holds for obstacles spaced far enough apart that the ABPs interact with at most one obstacle over many reorientation times. Therefore, as the activity increases, the effective temperature is restricted to a smaller and smaller ϕ.
≫ R). The effective temperature expression only holds for obstacles spaced far enough apart that the ABPs interact with at most one obstacle over many reorientation times. Therefore, as the activity increases, the effective temperature is restricted to a smaller and smaller ϕ.
As the obstacle density increases, the diffusivities diverge from those predicted by the effective temperature theory. At intermediate obstacle densities, ϕ ≈ 0.1–0.7, the relative microscopic length (δ) and run length (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ) become important predictors of scaled diffusivity. While each curve monotonically decreases with higher obstacle density, at high activities there can be large deviations from the effective temperature theory.
) become important predictors of scaled diffusivity. While each curve monotonically decreases with higher obstacle density, at high activities there can be large deviations from the effective temperature theory.
Finally, as the system approaches close packing, ϕ → π/4, the diffusivities rapidly decrease to zero due to particle transport being limited by a narrow escape through a small pore.
To further examine the effect of run length and microscopic length on active transport at intermediate obstacle densities, ϕ ≈ 0.1–0.7, we define the normalized deviation in measured diffusivity from the model's expected effective temperature diffusivity DModel as the quantity ΔD/D0:
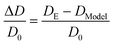 | (6) |
In Fig. 3B, we show the diffusivity deviation for a fixed obstacle density, ϕ = 0.35, while varying both the run length and microscopic length of the ABPs. For weak activity, ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /R ≪ 1, the scaled diffusivity matches the expected results from the passive limit, leading to minimal departure from DModel. As activity increases beyond
/R ≪ 1, the scaled diffusivity matches the expected results from the passive limit, leading to minimal departure from DModel. As activity increases beyond ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /R ≈ 1, the effective temperature theories no longer hold. Reductions in transport coefficients are reflected through the increased accumulation within the boundary layer. Strongly active particles are “trapped” within the boundary layer until they reorient or slide off. In contrast, when activity is weak, translational Brownian fluctuations dominate and carry the ABP away from the boundary layer before reorientation occurs. Inactive or weakly active particles “forget” the obstacle surface much faster than their reorientation time or sliding time. As
/R ≈ 1, the effective temperature theories no longer hold. Reductions in transport coefficients are reflected through the increased accumulation within the boundary layer. Strongly active particles are “trapped” within the boundary layer until they reorient or slide off. In contrast, when activity is weak, translational Brownian fluctuations dominate and carry the ABP away from the boundary layer before reorientation occurs. Inactive or weakly active particles “forget” the obstacle surface much faster than their reorientation time or sliding time. As ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) /R increases, more ABPs accumulate on the surface. While increasing (δ/R)2 may decrease the magnitude of surface accumulation, it also increases the boundary layer thickness, resulting in a net slowdown of scaled ABP diffusivity over the range of parameters studied.
/R increases, more ABPs accumulate on the surface. While increasing (δ/R)2 may decrease the magnitude of surface accumulation, it also increases the boundary layer thickness, resulting in a net slowdown of scaled ABP diffusivity over the range of parameters studied.
Interestingly, for very small values of the microscopic length [(δ/R)2 = 0.01 in Fig. 3B], we see an enhancement in scaled diffusivity beyond the passive theory. We suspect this is due to the unique geometry of the square lattice. When Brownian fluctuations are small in a square lattice, the particles exhibit sustained runs in the interstitial space, effectively lowering the number of obstacles an ABP runs into in a manner similar to the enhancement described by Pattanayak et al.48
The boundary-induced accumulation of ABPs occurs over a boundary layer19 of size λ−1:
 | (7) |
 | (8) |
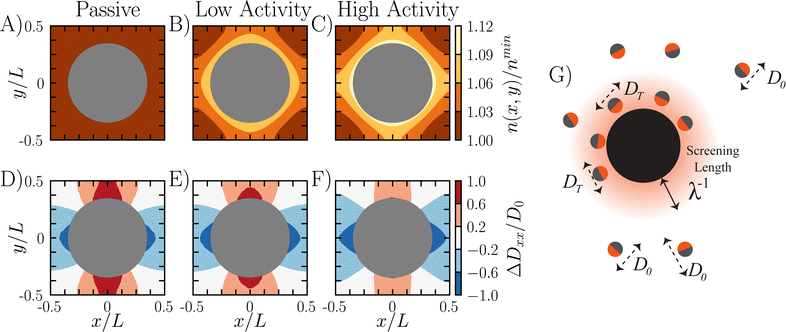 | ||
Fig. 4 Surface accumulation leads to slowdowns in scaled diffusivity. (A–C) Local number density of particles for different activity parameters. As the activity increases in strength, the particles experience larger accumulation near the obstacle surface as shown through the contours. (D–F) Pointwise diffusivity deviation along the x direction calculated numerically via dispersion theory (see ESI† for more details). The pointwise diffusivity deviation is ΔDxx/D0 = (Dxx(x,y) − DModel)/D0. The pointwise diffusivity has a quadrupolar form due to particles getting trapped in the leading and trailing wakes of the obstacles. (G) Cartoon demonstrating that ABPs within the boundary layer move with a reduced diffusivity compared to the ABPs in the bulk. Subplots (A and D) correspond to ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /R = 0 and δ2/R2 = N/A. Subplots (B and E) correspond to /R = 0 and δ2/R2 = N/A. Subplots (B and E) correspond to ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /R = 1 and δ2/R2 = 1. Subplots (C and F) correspond to /R = 1 and δ2/R2 = 1. Subplots (C and F) correspond to ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /R = 10 and δ2/R2 = 10. All data collected for ϕ = 0.38. /R = 10 and δ2/R2 = 10. All data collected for ϕ = 0.38. | ||
Fig. 4G is a schematic demonstrating the relationship between surface accumulation and transport reduction. For ABPs inside the boundary layer, their self-propulsive force is directed inward against the wall. These ABPs are trapped against the surface until they reorient, and are therefore only diffusing by thermal motion until they escape. This indicates that there are three domains relevant to ABP transport through a packed bed: the occupied area of obstacles ϕ, the boundary layer around obstacles ϕBL (which must be weighted by the fraction of ABPs partitioned inside the boundary layer), and then the bulk space ϕFree.
Within each of these domains, the ABP moves with a different effective diffusivity. Outside the boundary layer, an ABP in ϕFree does not feel any boundary effects and moves with bulk diffusivity D0. Inside the boundary layer ϕBL, an ABP is slowed by collisions with the obstacles, and moves with a local diffusivity approximately equal to DT. Finally, for impenetrable obstacles no transport can occur and therefore the diffusivity is zero.
3.2 Diffusion through a narrow pore
The Fick–Jacobs equation describes diffusion in a channel with a slowly varying cross section of width w(y), 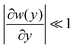 . Utilizing the methods described by Rubí and Reguera,51,52 we consider the flux of Brownian particles through a thin pore as a 1D problem, as shown in Fig. 5, with local variations in transverse width as an “entropic force”. For a Brownian particle, the Fick–Jacobs equation is:
. Utilizing the methods described by Rubí and Reguera,51,52 we consider the flux of Brownian particles through a thin pore as a 1D problem, as shown in Fig. 5, with local variations in transverse width as an “entropic force”. For a Brownian particle, the Fick–Jacobs equation is:
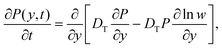 | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln(w) that reduce the axial flux. Rubí and Reguera51,52 show that the applicability of the 1D Fick–Jacobs equation can be extended via the introduction of a heuristically defined position dependent diffusion coefficient
ln(w) that reduce the axial flux. Rubí and Reguera51,52 show that the applicability of the 1D Fick–Jacobs equation can be extended via the introduction of a heuristically defined position dependent diffusion coefficient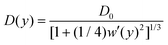 | (10) |
As shown earlier, if the self-propelled particles behave as Brownian particles at a higher effective temperature, one should be able to replace their thermal diffusivity with their bulk diffusivity, D0 = DT + U0τR/2. This expression can be used to find the one-dimensional axial effective diffusivity by using the Lifson–Jackson formula53 for motion in a periodic potential described by our entropic barrier
 | (11) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = U0τR; therefore, we expect the FJ model to be the most accurate when the pore width varies slowly compared to the run length.
= U0τR; therefore, we expect the FJ model to be the most accurate when the pore width varies slowly compared to the run length.
In Fig. 6A, we show the scaled diffusivity of several example active particle systems as a function of the nondimensional constriction. As the pore constricts [(H − b)/H → 1], transport through the small opening is blocked, rapidly reducing the diffusivity down to zero.
In Fig. 6B, we plot the scaled diffusivity deviation from the FJ theory as a function of run length and microscopic length. Over the range of parameters studied, FJ theories consistently overestimate the effective diffusivity past ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /Δy ≈ 0.2, with the exact deviation point depending on the pore amplitude and wavelength. Taylor dispersion theory is not used in Fig. 6 due to the high number of finite element meshing points needed to converge the solution at high activities. For example Taylor dispersion theory calculations of weakly active systems, see the ESI† for 3 contour plots of ABP concentration and local diffusivity deviation in a sinusoidal pore.
/Δy ≈ 0.2, with the exact deviation point depending on the pore amplitude and wavelength. Taylor dispersion theory is not used in Fig. 6 due to the high number of finite element meshing points needed to converge the solution at high activities. For example Taylor dispersion theory calculations of weakly active systems, see the ESI† for 3 contour plots of ABP concentration and local diffusivity deviation in a sinusoidal pore.
Our results corroborate the previous findings by Sandoval and Dagdug,54 who found that a similar overestimation of diffusivity occurred for a zig–zag and semicircular cavity as the swim speed increased. Their work focused on the impact of varying swim speed U0. However, our findings reveal this deviation is a result of geometric factors with ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) and δ providing the true measure of activity.
and δ providing the true measure of activity.
Axial diffusivity is reduced primarily through the high accumulation of active particles along the concave regions of the pore. As demonstrated in eqn (8), surface accumulation depends on the radius of curvature. For concave surfaces, the curvature κ is negative, causing surface accumulation to increase rapidly with more negative values of κ: nsurf ≈ 1 + ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 2/2δ2 −
2/2δ2 − ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 2λκ +
2λκ + ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) 2λκ)2. As the amplitude increases, the radius of curvature shrinks, leading to high accumulation at the concave valleys, away from the small convex pore, thus lowering scaled diffusivity further.
2λκ)2. As the amplitude increases, the radius of curvature shrinks, leading to high accumulation at the concave valleys, away from the small convex pore, thus lowering scaled diffusivity further.
3.3 Diffusion through a tortuous path
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) .
.
Assuming all motion is diffusive, the tortuosity can be determined using a tracer particle of known diffusivity. The relative reduction in measured diffusivity compared to bulk provides an estimate of the reduction factor. Following our definition provided in Fig. 7, the ratio of measured diffusivity in the pore to bulk diffusivity is the ratio in paths traveled in the same amount of time; therefore, one can define a nondimensional tortuosity:
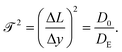 | (12) |
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) is system dependent and measured experimentally or via image analysis; however, many models and correlations exist for simple structures.55 In order to test the validity of the tortuosity effective temperature approach for active systems, we have designed a winding path that allows us to define the tortuosity directly from the geometry. Our system is made of 5 individual segments of length Li and width H. Covering a vertical displacement Δy = 3Li.
is system dependent and measured experimentally or via image analysis; however, many models and correlations exist for simple structures.55 In order to test the validity of the tortuosity effective temperature approach for active systems, we have designed a winding path that allows us to define the tortuosity directly from the geometry. Our system is made of 5 individual segments of length Li and width H. Covering a vertical displacement Δy = 3Li.
At low activity, the scaled diffusivity matches the prediction from the center-line path DE/D0 ≈ 1/![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 2 = 0.36. This indicates that the diffusion of ABPs roughly follows that of the center-line path, without extreme deviations due to backtracking or strong accumulation.
2 = 0.36. This indicates that the diffusion of ABPs roughly follows that of the center-line path, without extreme deviations due to backtracking or strong accumulation.
Our geometry informed tortuosity begins to fail when the run length ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = U0τR approaches the same size as either the segment length Li or pore width H. Motion is still diffusive over the unit cell, but the transport through each individual segment becomes increasingly ballistic. ABPs move along a segment until getting trapped in a corner. Eventually, the ABP reorients enough to hop across the next segment.
= U0τR approaches the same size as either the segment length Li or pore width H. Motion is still diffusive over the unit cell, but the transport through each individual segment becomes increasingly ballistic. ABPs move along a segment until getting trapped in a corner. Eventually, the ABP reorients enough to hop across the next segment.
At high activities (![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /H) ≫ 1, the ABPs move ballistically along a segment until colliding with the corner and then spend a significant amount of time trapped before turning. This ballistic motion leads to the concentration profile shown in Fig. 8B. Particles deplete from the convex regions, and accumulate in the highly concave corners. The ballistic motion also increases the effective path length, creating a long-tailed reduction in scaled diffusivity, as shown in Fig. 8A. Further exploration of the parameter space (such as Li/H ≫ 1 and full sweeps of
/H) ≫ 1, the ABPs move ballistically along a segment until colliding with the corner and then spend a significant amount of time trapped before turning. This ballistic motion leads to the concentration profile shown in Fig. 8B. Particles deplete from the convex regions, and accumulate in the highly concave corners. The ballistic motion also increases the effective path length, creating a long-tailed reduction in scaled diffusivity, as shown in Fig. 8A. Further exploration of the parameter space (such as Li/H ≫ 1 and full sweeps of ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /H at constant (δ/H)2) can be found in the ESI.† Those additional simulations justify our scaling by H instead of Li, as well as demonstrate that the solutions are relatively insensitive to (δ/H)2.
/H at constant (δ/H)2) can be found in the ESI.† Those additional simulations justify our scaling by H instead of Li, as well as demonstrate that the solutions are relatively insensitive to (δ/H)2.
Unlike the narrow pore and the fixed obstacle array, the tortuous path never exhibits a complete blockage of flow, meaning that for networks of the type described in this section, a nonzero diffusivity is possible, even for an arbitrarily large number of segments. Changing the channel boundary patterning from flat walls is expected to further decrease diffusivity. Small pockets of local curvature create an effect similar to that of the sinusoidal pore, providing an additional barrier to whatever maze the ABPs must diffuse through. While this work focuses on a design with only one possible path, the addition of concave “dead ends” should partition the ABPs away from the optimal path, resulting in a larger relative reduction in diffusivity.
4 Discussion
In this work, we test the validity of classical geometric scaling laws for diffusion in heterogeneous environments using analytical theory and Brownian dynamics simulations. We find that even mildly active particles have a scaled diffusivity that deviates from simple effective temperature arguments. The nonequilibrium nature of self-propelled particles needs to be carefully considered in transport calculations, just as it must be for phase behavior and surface accumulation.Through this work, we have examined the applicability (or lack thereof) of traditional porous media estimates for effective diffusivity in active matter. While Taylor dispersion theory is rigorous and accurate for all activities, numerical instabilities and analytic intractability create difficulty in practical use. Particle-based simulations allow for a micromechanical explanation of the decrease in scaled diffusivity due to accumulation. Both the Fick–Jacobs and tortuosity relationships are accurate in the weakly active limit (provided that one includes the swim diffusivity when calculating the bulk diffusivity), but the strong accumulation at boundary layers and ballistic transport on length scales commensurate with the geometry reduce scaled diffusivity beyond predicted amounts. Interestingly, for a packed bed/lattice, it is possible for ABPs to achieve scaled diffusivity above the passive predictions, and future work aims to understand this intriguing behavior.
Future work on this topic may look at modifications to the effective temperature theory when incorporating it into boundary rich environments. As a first correction, we can utilize the decreased local diffusivity in the boundary layer as DE ≈ D0ϕFree + αDTϕBL. With an unknown coefficient α related to the increased partitioning ABPs experience due to boundary curvature.
Previous research by Khatami et al. found that different models of active matter with the same bulk diffusivity have different transport rates when traversing through a maze.56 They report that run and tumble models have a smaller mean first passage time than active Brownian particles. Additionally, Kurzthaler et al.57 found that the introduction of a reorientation mechanism may lead to greater absolute diffusivity when the reversal run length is commensurate with the maximal chord length of a 3D porous medium. These results indicate that porous media may be used as a novel sorting method for mixtures of active particles utilizing different self-propulsion mechanisms.
This work focuses on the introduction of rigid, immobile obstacles and walls, similar to those found in soil sediments and etched microfluidic devices. However, soft porous materials present a rich opportunity for future study. Boundary fluctuations are important for passive transport in mucus, hydrogels, and other polymeric networks.8,58 For example, active particles can push through pores smaller than their diameter, if the pore or the particle can deform under thermal or swim forces.
Polymer networks are well-known to reduce the passive (non-motile) particle transport. Steric hindrance, nonspecific interactions (hydrophobicity, electrostatics), and specific interactions (ligand-receptor binding), all play a part to trap foreign debris.8,9 While this work focused only on the effect of the obstacle excluded volume, other forms of interactions can lead to controllable transport based on the swimmer and obstacle chemistry.
External torques also influence transport in a nontrivial matter. Rod-shaped bacteria can align with the boundaries and with other bacteria to create nematic ordering/flocking.59 Chemoattractants, repellents, light sources, and other external fields can influence the favored direction of bacteria in the absence of hard-wall interactions. For example, a random array of point-source repellents can lead to subdiffusive transport in closed spirals.30,31
Hydrodynamic interactions can provide qualitative or quantitative changes to active transport.60,61 Hydrodynamic coupling to walls leads to strong interactions between swimmers and surfaces, which would further alter the boundary-accumulation effect on transport.62 Pusher type active matter (like bacteria and sperm) are hydrodynamically driven to align parallel to the walls, while puller types align perpendicular to the walls.63 In addition, the surface-modified flow field creates a constant torque leading to motion via counterclockwise (for E. Coli.) spirals.64
Finally, in 3D there are additional degrees of freedom a swimmer can use to avoid obstacles. In 2D, close packing of disks precludes transport; however, a close packed bed of monodispersed spheres in 3D is permeable, resulting in a reduced but nonzero diffusivity. Future work in this space would benefit from mean field approximations for the network, in addition to a detailed analysis of the variance of pore sizes.
Author contributions
K. J. M. and S. C. T. conceived of the study; all authors designed research; K. J. M. performed simulations and analytical calculations; S. C. T. supervised the study; and all authors wrote the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This material is based upon work supported by the Air Force Office of Scientific Research under award number FA9550-21-1-0287. K. J. M. is supported by the National Science Foundation Graduate Research Fellowship under Grant No. 1650114. S. C. T. is supported by the Packard Fellowship in Science and Engineering. Use was made of computational facilities purchased with funds from the National Science Foundation (OAC-1925717) and administered by the Center for Scientific Computing (CSC). The CSC is supported by the California NanoSystems Institute and the Materials Research Science and Engineering Center (MRSEC; NSF DMR 1720256) at UC Santa Barbara.References
- D. Ribet and P. Cossart, Microbes Infect., 2015, 17, 173–183 CrossRef CAS PubMed.
- S. X. Gu and S. R. Lentz, J. Clin. Invest., 2018, 128, 3243–3245 CrossRef PubMed.
- C. Y. Kao, W. H. Lin, C. C. Tseng, A. B. Wu, M. C. Wang and J. J. Wu, Eur. J. Clin. Microbiol. Infect. Dis., 2014, 33, 2157–2162 CrossRef CAS PubMed.
- J. Gannon, U. Mingelgrin, M. Alexander and R. Wagenet, Soil Biol. Biochem., 1991, 23, 1155–1160 CrossRef.
- J. S. T. Adadevoh, S. Triolo, C. A. Ramsburg and R. M. Ford, Environ. Sci. Technol., 2016, 50, 181–187 CrossRef CAS PubMed.
- O. O. Babalola, Biotechnol. Lett., 2010, 32, 1559–1570 CrossRef CAS PubMed.
- T. Bhattacharjee and S. S. Datta, Nat. Commun., 2019, 10, 2075 CrossRef PubMed.
- L.-H. Cai, S. Panyukov and M. Rubinstein, Macromolecules, 2015, 48, 847–862 CrossRef CAS PubMed.
- J. Witten and K. Ribbeck, Nanoscale, 2017, 9, 8080–8095 RSC.
- M. Mangeat, T. Guérin and D. S. Dean, J. Chem. Phys., 2020, 152, 234109 CrossRef CAS PubMed.
- M. Saxton, Biophys. J., 1994, 66, 394–401 CrossRef CAS PubMed.
- R. Alonso-Matilla, B. Chakrabarti and D. Saintillan, Phys. Rev. Fluids, 2019, 4, 043101 CrossRef.
- D. Loi, S. Mossa and L. F. Cugliandolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77, 051111 CrossRef PubMed.
- S. C. Takatori and J. F. Brady, Curr. Opin. Colloid Interface Sci., 2016, 21, 24–33 CrossRef CAS.
- G. Szamel, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 012111 CrossRef PubMed.
- E. Fodor, C. Nardini, M. E. Cates, J. Tailleur, P. Visco and F. van Wijland, Phys. Rev. Lett., 2016, 117, 038103 CrossRef PubMed.
- S. C. Takatori and J. F. Brady, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 032117 CrossRef CAS PubMed.
- H. C. Berg, Random Walks in Biology, Princeton University Press, 1984 Search PubMed.
- W. Yan and J. F. Brady, J. Fluid Mech., 2015, 785, R1 CrossRef.
- F. Smallenburg and H. Löwen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 032304 CrossRef PubMed.
- S. C. Takatori, W. Yan and J. F. Brady, Phys. Rev. Lett., 2014, 113, 028103 CrossRef CAS PubMed.
- G. Volpe, S. Gigan and G. Volpe, Am. J. Phys., 2014, 82, 659–664 CrossRef.
- C. M. Kjeldbjerg and J. F. Brady, Soft Matter, 2022, 18, 2757–2766 RSC.
- L. J. Perez, T. Bhattacharjee, S. S. Datta, R. Parashar and N. L. Sund, Phys. Rev. E, 2021, 103, 012611 CrossRef CAS PubMed.
- N. A. Licata, B. Mohari, C. Fuqua and S. Setayeshgar, Biophys. J., 2016, 110, 247–257 CrossRef CAS PubMed.
- V. K. Truong, D. E. Mainwaring, P. Murugaraj, D. H. K. Nguyen and E. P. Ivanova, J. Mater. Chem. B, 2015, 3, 8704–8710 RSC.
- M. Brun-Cosme-Bruny, E. Bertin, B. Coasne, P. Peyla and S. Rafaï, J. Chem. Phys., 2019, 150, 104901 CrossRef PubMed.
- M. Kumar, J. S. Guasto and A. M. Ardekani, J. Rheol., 2022, 66, 375–397 CrossRef CAS.
- A. Martínez-Calvo, C. Trenado-Yuste and S. S. Datta, Active transport in complex environments, 2021, arxiv:2108.07011.
- O. Chepizhko and F. Peruani, Phys. Rev. Lett., 2013, 111, 160604 CrossRef PubMed.
- A. Morin, D. Lopes Cardozo, V. Chikkadi and D. Bartolo, Phys. Rev. E, 2017, 96, 042611 CrossRef PubMed.
- M. Zeitz, K. Wolff and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2017, 40, 23 CrossRef PubMed.
- W. Yan and J. F. Brady, Soft Matter, 2018, 14, 279–290 RSC.
- K. J. Modica, Y. Xi and S. C. Takatori, Frontiers Physics, 2022, 10, 869175 CrossRef.
- M. R. Shaebani, A. Wysocki, R. G. Winkler, G. Gompper and H. Rieger, Nat. Rev. Phys., 2020, 2, 181–199 CrossRef.
- C. Bechinger, R. Di Leonardo, H. Löwen, C. Reichhardt, G. Volpe and G. Volpe, Rev. Mod. Phys., 2016, 88, 045006 CrossRef.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- A. P. Solon, M. E. Cates and J. Tailleur, Eur. Phys. J.: Spec. Top., 2015, 224, 1231–1262 CAS.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- D. Saintillan and M. J. Shelley, Phys. Rev. Lett., 2008, 100, 178103 CrossRef PubMed.
- J. C. Maxwell, A Treatise on Electricity and Magnetism, Clarendon Press, 1881 Search PubMed.
- G. K. Batchelor, J. Fluid Mech., 1976, 74, 1–29 CrossRef.
- S. C. Takatori and J. F. Brady, Soft Matter, 2014, 10, 9433–9445 RSC.
- R. N. Zia and J. F. Brady, J. Fluid Mech., 2010, 658, 188–210 CrossRef CAS.
- S. C. Takatori and J. F. Brady, Phys. Rev. Lett., 2017, 118, 018003 CrossRef CAS PubMed.
- Z. Peng and J. F. Brady, Phys. Rev. Fluids, 2020, 5, 073102 CrossRef.
- E. W. Burkholder and J. F. Brady, Phys. Rev. E, 2017, 95, 052605 CrossRef PubMed.
- S. Pattanayak, R. Das, M. Kumar and S. Mishra, Eur. Phys. J. E: Soft Matter Biol. Phys., 2019, 42, 62 CrossRef PubMed.
- M. H. Jacobs, Diffusion Processes, Springer Berlin Heidelberg, Berlin, Heidelberg, 1967 Search PubMed.
- R. Zwanzig, J. Phys. Chem. C, 1992, 96, 3926–3930 CrossRef CAS.
- D. Reguera and J. M. Rubí, Phy. Rev. E, 2001, 64, 061106 CrossRef CAS PubMed.
- D. Reguera, G. Schmid, P. S. Burada, J. M. Rubí, P. Reimann and P. Hänggi, Phys. Rev. Lett., 2006, 96, 130603 CrossRef CAS PubMed.
- S. Lifson and J. L. Jackson, J. Chem. Phys., 1962, 36, 2410–2414 CrossRef CAS.
- M. Sandoval and L. Dagdug, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 062711 CrossRef PubMed.
- L. Shen and Z. Chen, Chem. Eng. Sci., 2007, 62, 3748–3755 CrossRef CAS.
- M. Khatami, K. Wolff, O. Pohl, M. R. Ejtehadi and H. Stark, Sci. Rep., 2016, 6, 37670 CrossRef CAS PubMed.
- C. Kurzthaler, S. Mandal, T. Bhattacharjee, H. Löwen, S. S. Datta and H. A. Stone, Nat. Commun., 2021, 12, 7088 CrossRef CAS PubMed.
- I. V. Bodrenko, S. Salis, S. Acosta-Gutierrez and M. Ceccarelli, J. Chem. Phys., 2019, 150, 211102 CrossRef PubMed.
- M. Bär, R. Großmann, S. Heidenreich and F. Peruani, Annu. Rev. Condens. Matter Phys., 2020, 11, 441–466 CrossRef.
- E. Lauga and T. R. Powers, Rep. Prog. Phys., 2009, 72, 096601 CrossRef.
- K. Drescher, J. Dunkel, L. H. Cisneros, S. Ganguly and R. E. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940–10945 CrossRef CAS PubMed.
- S. Rode, J. Elgeti and G. Gompper, New J. Phys., 2019, 21, 013016 CrossRef.
- A. P. Berke, L. Turner, H. C. Berg and E. Lauga, Phys. Rev. Lett., 2008, 101, 038102 CrossRef PubMed.
- R. G. Winkler and G. Gompper, Handbook of Materials Modeling, Springer International Publishing, Cham, 2018, pp. 1–21 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01421a |
| This journal is © The Royal Society of Chemistry 2023 |