Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Long term phase separation dynamics in liquid crystal-enriched microdroplets obtained from binary fluid mixtures†
Mehzabin
Patel
 a,
Seishi
Shimizu
a,
Seishi
Shimizu
 b,
Martin A.
Bates
b,
Martin A.
Bates
 b,
Alberto
Fernandez-Nieves
b,
Alberto
Fernandez-Nieves
 cde and
Stefan
Guldin
cde and
Stefan
Guldin
 *a
*a
aDepartment of Chemical Engineering, University College London, Torrington Place, London, WC1E 7JE, UK. E-mail: s.guldin@ucl.ac.uk
bDepartment of Chemistry, University of York, Heslington, York YO10 5DD, UK
cDepartment of Condensed Matter Physics, University of Barcelona, 08028 Barcelona, Spain
dICREA-Institució Catalana de Recerca i Estudis Avançats, 08010 Barcelona, Spain
eInstitute for Complex Systems (UBICS), University of Barcelona, 08028, Barcelona, Spain
First published on 9th January 2023
Abstract
The dynamics of long term phase separation in binary liquid mixtures remains a subject of fundamental interest. Here, we study a binary liquid mixture, where the minority phase is confined to a liquid crystal (LC)-rich droplet, by investigating the evolution of size, defect and mesogen alignment over time. We track the binary liquid mixture evolving towards equilibrium by visualising the configuration of the liquid crystal droplet through polarisation microscopy. We compare our experimental findings with computational simulations and elucidate differences between bulk phases and confined droplets based on the respective thermodynamics of phase separation. Our work provides insights on how phase transitions on the microscale can deviate from bulk phase diagrams with relevance to other material systems, such as the liquid–liquid phase separation of polymer and protein solutions.
1 Introduction
Binary fluid mixtures exhibit a miscibility gap for certain compositions and temperature ranges. A phase diagram may present a lower critical solution temperature (LCST) or upper critical solution temperature (UCST). Crossing the coexistence curve in the corresponding phase diagram of temperature T and composition x induces phase separation either by spinodal decomposition or by nucleation and growth.1 The dynamics of this liquid–liquid phase separation has been the subject of numerous investigations in food science, polymer physics and most recently, cell biology.2 In nucleation and growth processes, the spontaneous formation of nuclei upon cooling of binary fluid systems has been studied from the perspective of a phase ordering process.3–7 The dynamics in the late stage of phase separation has received considerable attention. In principle, after the initial processes of nucleation and coarsening, domain growth of the new phase proceeds through a sequence of physically distinct hydrodynamic, viscous or inertial effects, which ultimately lead to thermodynamic equilbrium.8–12Liquid crystals have been studied as one or both components of a binary liquid mixture. They offer unique characteristics for investigating mesophasic ordering and phase transitions.13 The surface anchoring of liquid crystal molecules, and unique optical and rheological properties, imply that they are strongly influenced by their local molecular composition.14,15 This effect is exacerbated when they are under curved confinement due to the introduction of defects. In droplet form they possess large interfacial area, defined director configurations, tunable optical properties and present stimuli response.16–23 To this end, the effect of confinement on the director configuration and in phase transitions is of fundamental interest. In particular, isotropic-to-nematic phase transitions have been studied extensively experimentally13,24,25 and theoretically26–28 over the years.
The effect of nonmesogenic species, in particular polymers, on the phase transition of liquid crystals is relevant for understanding mesogenic order and tuning viscoelastic properties.13,29–37 Thoen et al. found that solutes such as biphenyl and cyclohexane caused a linear decrease in the nematic-to-isotropic and the nematic–smectic-A transition temperature with increasing mole fraction. The nematic-to-isotropic transition was described as a first-order transition, where the latent heat did not change with mole fraction of the solute.36 Studies using hexane as a solute, however, found that the isotropic-to-nematic phase transition shifts toward lower temperatures nonlinearly with increasing mole fraction.13 It was deduced that the addition of a solvent diluted the liquid crystal, resulting in an impurity mechanism, which introduced a concentration fluctuation and softened the viscoelastic properties of the mixture with respect to that of pure liquid crystal.13
Serrano and Fornerod et al. investigated a binary liquid mixture of an isotropic liquid, methanol, with liquid crystal 4-cyano-4′-pentylbiphenyl (5CB).38 The dilution using methanol reduced and allowed to finely tune the isotropic-to-nematic transition temperature of 5CB.38 Methanol was miscible with 5CB below 10 vol%, but reduced the isotropic-to-nematic phase transition temperature from 35 °C with increasing volume fraction down to 7.8 ± 0.4 °C (at 10 vol% methanol). Above 10% methanol, the binary mixture displayed an isotropic–isotropic liquid phase separation with decreasing temperature, and an isotropic-to-nematic phase transition of the LC component as the temperature was lowered further. The partially miscible binary liquid mixture was later deployed for thermoresponsive microfluidics, where highly regular phase arrangements, namely droplets, plug, slug and annular flow, could be controlled by temperature manipulation.39 The phase behaviour of 5CB with ethanol as non-nematogenic component was subsequently studied by Reyes et al.40 While the study by Serrano and Fornerod et al. provided some indication over non-equilibrium phase separation aspects (see ESI in ref. 38 on isotropic–isotropic coexistence upon cooling), Reyes et al. developed a comprehensive picture over non-equilibrium phase separation aspects, in particular related to phase coexistence (isotropic–isotropic, isotropic–nematic) upon cooling and heating. Furthermore, they established a detailed phase diagram of 5CB and ethanol containing regions of both spinodal and binodal decomposition. Crucially, they found that the isotropic–isotropic phase coexistance within this mixture may be stable above room temperature (in fact, up to ≈60 °C) upon the addition of small traces of water (<5 vol%), which can be used to manipulate structure formation or mixing processes that make use of such LC-alcohol mixtures.
Building on the above work, a study by Patel et al. showed that cooling of an off-critical mixture of a binary fluid composed of liquid crystal 5CB and methanol led to nucleation and growth of liquid crystal-rich droplets, which were found isotropic or nematic depending on the temperature and could be tuned in size and number by temperature quench and cooling rate, respectively.41
Herein, we track the evolution of a nematic liquid crystal-enriched droplet that is obtained from a binary mixture with methanol. On the one hand, this offers a unique mode for investigating the phase separation of binary liquid mixtures evolving towards equilibrium, as the process can be tracked through changes in the texture of the liquid crystal-rich droplet. On the other hand, our work explicitly addresses whether droplet confinement affects phase equilibria. We examine both aspects experimentally using polarised optical microscopy, and deploy computer simulations and thermodynamic considerations to rationalize our results.
2 Results and discussion
Experimental results
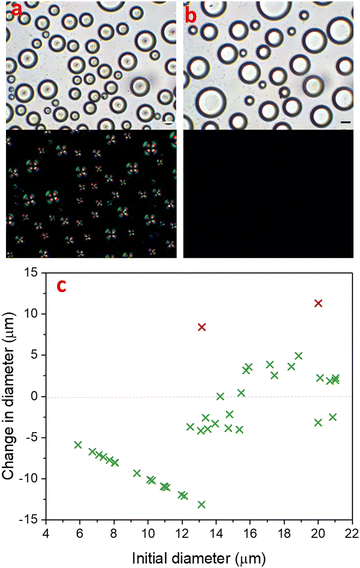
In a binary liquid mixture of 30% 4-cyano-4′-pentylbiphenyl (5CB) and 70% MeOH, isotropic 5CB-rich nucleated in the methanol-rich continuous phase upon cooling the mixture below the upper critical solution temperature (UCST) of 22 °C. Further cooling to −1 °C, resulted in an isotropic-to-nematic phase transition of 5CB-rich droplets. The phase diagram for this phenomenon was described by Serrano et al.,38 and we previously also investigated droplet formation by this process.41 The nematic 5CB-rich droplets initially adopted a radial configuration, with the single point defect at the centre of the droplet as described in Fig. 1a.Prior to isotropic-to-nematic transition of 5CB-rich droplets in the methanol-rich continuous phase, the phase separation of isotropic 5CB-rich droplets was dominated by coalescence. After adopting nematic order, 5CB-rich droplets no longer coalesced, even those in close proximity or even touching. Terentjev explained theoretically that the enhanced stability of nematic emulsions over their isotropic counterparts was due to the energy barrier that needs to be overcome due to the internal mesogen reorganization inside nematic droplets.42 Therefore, phase separation could only proceed further by other growth mechanisms.
Fig. 1 demonstrates how the partitioning of 5CB-rich droplets evolved during their nematic lifetime, from many smaller droplets (13.7 ± 4.9 μm) immediately after isotropic-to-nematic transition (Fig. 1a), to fewer droplets with a larger size distribution (19.5 ± 6.5 μm), 120 min later when the droplets had lost their nematic order (Fig. 1b). With increasing time t, the small droplets shrank as the solvent diffused through the majority phase into the larger droplets. This process is known as Ostwald ripening and occurs in order to reduce the total interfacial area of a system via a diffusional mass transfer process from regions of high interfacial curvature to regions of low interfacial curvature. The total interfacial area decreases and larger droplets grow with time in order for the system to reach thermodynamic equilibrium.43 In an off-critical partially miscible liquid mixture, the amount of each component dissolved in the other is expected to approach the equilibrium state. This amount is determined by the Lever rule.44,45
In order to understand the effect of Ostwald ripening in this system, we studied the shrinking and growth of droplets, and analysed their change in diameter and volume over time. Fig. 1c highlights the diameter change of each droplet in an image frame (with a green cross) from the isotropic–to-nematic transition point until 120 min later, i.e. after the transition back to the isotropic state occured. In the frame of the image, the sample size was 40 droplets. The two purple crosses represent droplets whose diameter change was largely related to coalescence. The graph shows many small droplets shrinking and being reabsorbed to increase the volume of fewer larger droplets. The graph shows a linear plot for droplets with diameter ≤13 μm, which ultimately disappeared completely into the methanol-rich phase. The remaining droplets with a diameter above ≈13 μm underwent a change in diameter of up to ±5 μm. Overall, there was a total increase in volume by 15%, which may be attributed to an increasing volume of methanol entering the droplet in order to reach equilibrium. In addition to a change in size over time, a clear change of the droplets can also be identified under cross-polarisation, as the radial point defect was no longer observed in Fig. 1b.
Further, we investigated the evolution of an individual 5CB-rich droplet in the methanol-rich phase at a constant temperature of −5 °C over time, as shown in Fig. 2. The first droplet image, Fig. 2a and b-left, was taken at the isotropic-to-nematic transition and the following images were acquired at characteristic intervals until the final image, which was taken after the nematic-to-isotropic transition, i.e. 120 minutes later. In the first 114 minutes, the radial defect in the centre of the LC moved gradually to the surface of the droplet, presenting the droplet in an escaped-radial configuration.46 After the defect reached the surface of the droplet, the nematic order in the droplet decreased by the formation of an isotropic shell on the outside of the drop, while the centre remained nematic. In the following 2 minutes, this nematic sphere shrunk and eventually disappeared completely, resulting in an entirely isotropic 5CB-rich droplet. While the total time for the evolution of initially nematic droplets back into the isotropic phase deviated by up to 10% between experiments, the observations on defect movement and phase transition were found consistent for all droplets in the field of view, regardless of their size. This is shown in the ESI† (Fig. S1).
The way in which the nematic-to-isotropic transition transpired inside the droplet is in contrast to research on a 5CB droplet immersed in silicone oil, where the nematic phase was found to disappear at several locations inside the droplet before the droplet transitioned to the isotropic phase.25,47 The radial to escaped-radial movement of a defect has been observed in previous studies during a topological transformation, often induced by an electric field, where a radial droplet transforms from a radial to an axial configuration.21 Other studies also identified morphological transitions when liquid crystal droplets passed a certain critical threshold radius, e.g., from bipolar, pre-radial to radial ordering with reducing size (for planar anchoring).17,48,49 However, this was typically seen in the sub-μm domain.
We observed the change in nematic order further through birefringence. Comparing the colours of the droplets to those on a Michel-Levy chart, Fig. 2c, the decreasing birefringence over time is evident, with the polarisation going from second to first order colours. Additionally, within each droplet, the order of interference colours seen in the isochromes decreased towards the melatope.
The occurrence of thermal gradients as a possible cause of the observed effect was investigated via thermal imaging of the sample and the surrounding area (Fig. S2, ESI†). The results demonstrate that the temperature of the stage remained constant and at least 2 °C below the nematic-isotropic temperature over the full period of investigation (90 min).
Computer simulations
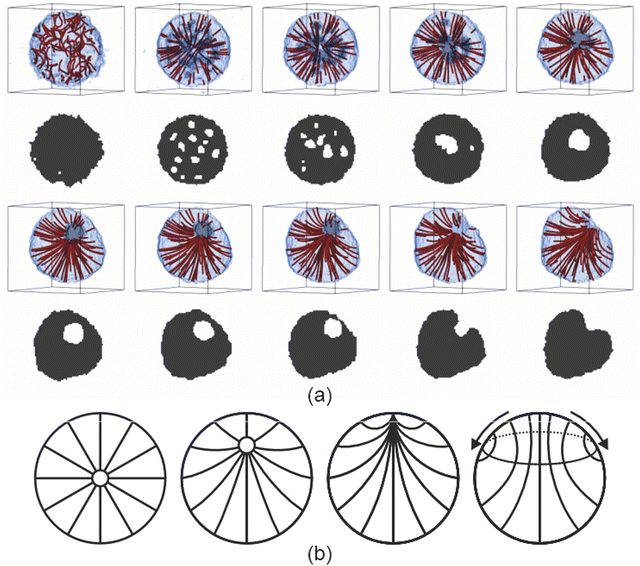
We deployed computer simulations to gain further insight into the formation and progression of the defect arrangement within a single two component droplet. We used a simple coarse grained model (see ESI†) to represent small volumes of the two components and tailored the interactions between these volumes to reproduce a phase diagram that is qualitatively similar to the experimental one and also presents homeotropic anchoring at the droplet surface.A small spherical droplet was prepared with the appropriate compositions of the minority and majority phases from the bulk phase diagram and equilibrated at a temperature just above the (bulk) transition to the nematic phase. The evolution of the small model droplet is shown in Fig. 3. On cooling the isotropic droplet into the nematic phase, the homeotropic surface anchoring rapidly induced a radial defect at the centre of the droplet. Due to the temperature change, and unlike pure LC droplets, the composition of the binary mixture droplet was no longer in equilibrium and the minority phase inside the droplet displayed an excess of solvent. Solvent molecules near the surface of the droplet were able to escape easily to the surrounding majority phase. Similarly, excess LC in the minority phase were absorbed into the droplet. However, the excess solvent that was found within the droplet but far enough away from the outer interface was observed to phase separate within the droplet forming many small methanol-rich droplets. To minimise the elastic energy of the nematic droplet, these internal phase-separated methanol droplets either left the droplet (if near the surface) or congregated near the radial defect observed in the director field; the high splay energy point defect was partially stabilised by becoming a virtual point defect within an inner droplet formed of excess solvent. As time progressed, both the virtual defect and the interior methanol droplet slowly moved towards the surface. As the interior solvent-rich droplet reached the exterior majority phase, this pinned a now escaped-radial defect at the surface of the droplet. Once the defect reached the surface, two different types of behaviour were observed. If quenched at lower temperatures, the escaped radial defect were prone to remain at the surface and appeared to be stable. At higher temperatures, the director configuration transformed from escaped radial into an axial configuration (as shown in the ESI†). In these simulations we did not observe the shrinking of the nematic region of the droplet as in the experiments. Of course, there are a number of assumptions that are necessarily made that could be responsible for differences between the experimental and simulated systems once the defect reached the surface.
To be computationally tractable, we assumed that each droplet can be investigated as a single small isolated system once the temperature is dropped. A relatively large temperature jump between the isotropic and nematic phase was used to examine the behaviour when the composition was out of equilibrium to be sure to identify changes in homogeneity of the composition. However, a similar time dependent behaviour of the director field was observed when using a smaller temperature difference either side of the phase transition, but the formation of an internal droplet in this case was less clear since the compositions of the two phases were much closer to each other. It was also necessary to make assumptions about the relative balance of the potential for nematic ordering compared to that of surface anchoring and that of immiscibility between the two components. The values chosen gave a qualitatively realistic bulk phase diagram and led to homeotropic anchoring at an interface. The observation that the director field was able change from escaped radial to axial was likely due to the surface anchoring being large compared to the bend bulk elastic constant combined with the small droplet size and hence the large surface to volume ratio.
It may also be that small deviations in the parameters could change the longer time behaviour once the radial defect reacheed the surface of the droplet, especially if the slow influx of individual methanol molecules across the interface, which was not accounted for in the coarse grained model, was responsible for the diminishing order at the surface. In both experiment and simulation, it was apparent that the size of the nematic region was reasonably constant while the defect core remained inside the droplet, and the formation and motion of the defect in the simulations appeared similar to that in the experiment. The observed behaviour deviated only once the defect reached the surface. We can therefore speculate that the existence of a region of disorder at the interface was responsible for the subsequent shrinkage of the nematic region. Since the defect itself represents a region of disorder, the composition within the defect region is likely to be different to that of the bulk majority and minority phases. This imperfection at the surface may allow methanol from the surrounding environment to enter the nematic region, causing the region around the defect to transform to the isotropic (minority) phase, with the droplet size remaining constant but the nematic region shrinking, while retaining the escaped radial defect at the interface between the nematic and isotropic regions of the droplet.
Simulations of the model also allowed us to run a control experiment not possible with the real droplets, where the starting isotropic droplet had the (bulk) composition of the final, lower temperature nematic phase. In this case, there should be no excess solvent inside the droplet when cooled. When simulations were run at this composition, the droplet was observed to either initially start to form a radial structure due to the surface anchoring, which rapidly transformed to axial as a central bulk-like nematic region grows, or, more frequently, the axial configuration formed directly on cooling. Therefore it seems likely that the presence of excess solvent inside the defect on cooling from the isotropic was responsible for inhomogeneity in composition within the droplet and helped to stabilise the overall radial director structure of the droplet by removing the highly strained splay defect region.
Discussion
Depending on the mixing composition, a binary mixture of 5CB and methanol may phase separate; the mixture composition of each phase is determined by the phase diagram, and the relative phase amounts can be evaluated by the Lever rule.44,45,50 For example, in a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 vol%
30 vol%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) vol% MeOH
vol% MeOH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5CB mixture, at −5 °C, the methanol-rich phase is composed of 76.6 vol% MeOH and 23.4 vol% 5CB, and the LC-rich minority phase is composed of 88.5 vol% 5CB and 11.5 vol% MeOH. The changing internal configuration of the LC-rich droplet described in Fig. 2 may be attributable to the shift in equilibrium of the binary mixture that accompanies the uptake of methanol in the 5CB-rich droplet; we will discuss this below. In return, this uptake of methanol may cause a deformation of the director due to the changing elastic energy of the LC, as explained by Sigdel and Denolf.13,36
5CB mixture, at −5 °C, the methanol-rich phase is composed of 76.6 vol% MeOH and 23.4 vol% 5CB, and the LC-rich minority phase is composed of 88.5 vol% 5CB and 11.5 vol% MeOH. The changing internal configuration of the LC-rich droplet described in Fig. 2 may be attributable to the shift in equilibrium of the binary mixture that accompanies the uptake of methanol in the 5CB-rich droplet; we will discuss this below. In return, this uptake of methanol may cause a deformation of the director due to the changing elastic energy of the LC, as explained by Sigdel and Denolf.13,36
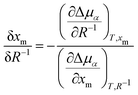
Thus, we have observed a loss of nematic order in the droplet over time, which we relate to an uptake of methanol. Such an observation could be supported by the drop size effect on the thermodynamics of phase equilibria. We note that a regular phase diagram will account for phase separation and nematic-to-isotropic phase transition in the bulk phase. However, the results found in micro-scale phase separation exhibited a deviation from the bulk phase diagram. Consequently, we must clarify thermodynamically how the droplet size affects the nematic-to-isotropic phase boundary. Such a scenario is consistent with our experiment (Fig. 2) and simulation (Fig. 3), in which we addressed how an unstable nematic droplet turns into an isotropic droplet. At the nematic-isotropic phase boundary, the chemical potentials of both components in the two phases are equal. Our goal is to clarify how this phase boundary is affected by the droplet size, composition, and temperature. The context of the problem invokes more degrees of freedom than are allowed from the standard Gibbs phase rule: a 2-component system forming 3 phases (the nematic droplet phase, the isotropic droplet phase, and the bulk isotropic phase that surrounds the droplet) has F = 2 − 3 + 2 = 1 degree of freedom. Hence, keeping the pressure constant would leave no degree of freedom. However, unlike an isotropic macroscopic system, the experimental microscopic system presented herein may present additional degrees of freedom. One is “the number of independent length scales influencing the free energy”3 that characterises the difference between the nematic and isotropic phases.1–3 Furthermore, an additional degree of freedom may be related to the boundary effect in microscopic systems,4 since the interfacial tension cannot be neglected for small droplet sizes. The problem is formulated in the ESI† as a deviation from the bulk phase diagram. The chemical potentials in the droplet are expressed as μ(i)5, μ(i)m, μ(n)5, and μ(n)m for 5CB and methanol in isotropic (denoted with the superscript (i)), and nematic (denoted with the superscript (n)) phases, respectively. Based on thermodynamic arguments (ESI†), how the methanol mole fraction at the nematic–isotropic phase boundary xm shifts (δxm) with the change in droplet size δR−1 can be expressed as:
 | (1) |
We now apply eqn (1) to understand the droplet effect on nematic stability. We observed the disappearance of the nematic phase in droplets, even though under the same conditions (mole fraction of methanol (xm), temperature (T)) the bulk nematic phase was observed to be stable. This suggests a decrease in nematic phase stability, or equivalently a shift of the nematic-to-isotropic boundary towards lower xm as R−1 increases, leading to 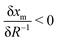 . Assuming that
. Assuming that 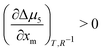 still holds true for droplets, we obtain
still holds true for droplets, we obtain 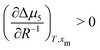 . This means that the relative stability of 5CB in the nematic phase decreases as the droplet becomes smaller. For methanol in droplets, assuming that
. This means that the relative stability of 5CB in the nematic phase decreases as the droplet becomes smaller. For methanol in droplets, assuming that 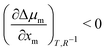 still holds true for a deviation from the bulk (R−1 = 0) (see ESI,† for details), we obtain
still holds true for a deviation from the bulk (R−1 = 0) (see ESI,† for details), we obtain 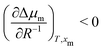 . As a result, the relative stability of methanol in the nematic phase increases as the droplet becomes smaller. Thus, the nematic phase is made less stable in smaller droplets by the destabilisation of 5CB and stabilisation of methanol, consistent with our findings from simulation.
. As a result, the relative stability of methanol in the nematic phase increases as the droplet becomes smaller. Thus, the nematic phase is made less stable in smaller droplets by the destabilisation of 5CB and stabilisation of methanol, consistent with our findings from simulation.
Furthermore, in a binary liquid mixture with partial miscibility, there is a diffuse interface barrier between the phases, which is defined by interfacial tension, and increases with temperature.3,39 Here, the diffuse interface barrier between the 5CB-rich phase and methanol-rich phase allowed exchange of individual molecules between the two components, and therefore, the amount of methanol in the 5CB-rich phase increased in order to eventually reach the equilibrium state. At equilibrium, there is no chemical potential difference across the phase boundary, and thus no net diffusive flux.51 In a similar manner, the increasing amount of an isotropic liquid in a liquid crystal droplet has been described in a study by Denolf and Sigdel as a dilution effect.13,36 The addition of a solvent to a liquid crystal influenced the isotropic-to-nematic transition and resulted in softening of the viscoelastic properties of the liquid crystal. Therefore, the change in nematic configuration and birefringence can be attributed to the uptake of methanol in the 5CB-rich droplet as it reached equilibrium, which caused a deformation of the director due to the changing elastic energy of the liquid crystal.
We note that after the nematic-to-isotropic transition of the 5CB-rich droplet, the temperature of the system was decreased further from −5 °C to −10 °C. With this cooling, the droplets transitioned back to the nematic phase. Thus, a change in temperature caused a shift in the equilibrium conditions. The system then worked again towards reaching equilibrium.
3 Conclusion
We have shown how the phase behaviour for a binary liquid mixture can deviate from the bulk for small droplets when interfacial tension is introduced. In a binary liquid mixture containing a LC-rich droplet phase at −5 °C, the internal configuration changed over time resulting in observable differences in the optical properties of the droplet. Droplets transformed from a nematic radial to an escaped-radial configuration and finally a nematic-to-isotropic transition took place after ≈2 hours. In contrast, the bulk system remained nematic at −5 °C indefinitely. The experimental evidence for defect formation and motion is also supported through simulations. Crucially, further lowering of the system temperature re-introduced an isotropic-to-nematic transition of the droplets, reinforcing the explanation that methanol uptake is responsible for the nematic-to-isotropic droplet phase transition. Our approach may have ramifications beyond liquid crystals in a generalised context of confinement-induced changes in phase stability,52 which ranges from small molecules (e.g., ethanol–water mixtures53–57) to biomolecular solutions58–60 and polymer blends,61 and also in crystallization of proteins in droplets.62,634 Experimental section
Reagents
The liquid crystal 4-cyano-4′-pentylbiphenyl (5CB) was obtained from Synthon Chemicals (99.5% (GC)). Methanol (HPLC grade) was purchased from Sigma Aldrich. All compounds were used without further purification.Sample preparation
5CB and methanol were mixed in a glass cuvette, which was enclosed by a Peltier-regulated sample compartment that allowed control over both temperature and stirring (Quantum Northwest, Qpod 2e). Unless stated otherwise, a 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 volume ratio of 5CB/RM257
70 volume ratio of 5CB/RM257![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeOH was used for all experiments. Samples were heated to 35 °C in the cuvette.
MeOH was used for all experiments. Samples were heated to 35 °C in the cuvette.
Sample analysis
For microscopic analysis, 10 μl of the homogeneous 5CB:MeOH mixture was deposited between a glass slide and cover slip and sealed with varnish (purchased from Rimmel: 15–40% ethyl acetate, 15–40% butyl acetate, 5–15% nitrocellulose, 1–10% isopropylalcohol) to prevent methanol evaporation.The slide was placed under an upright microscope (Zeiss, Axio Scope A1), which was operated in transmission and primarily in brightfield mode. Crossed polarisers were used to investigate anisotropic behaviour. A temperature controlled sample stage (Linkam, LTS120) was deployed for all experiments. Nitrogen was introduced into the chamber to prevent condensation at low temperatures. In situ droplet growth was recorded by time-resolved digital image acquisition using a Lumenera Infinity 3-3UR camera with a resolution of 1936 × 1456 pixels.
The sample stage was pre-heated to 35 °C, and then cooled at 20 °C min−1 to −5 °C. Quantitative droplet investigation was carried out by a bespoke computational image analysis code developed in Python. Droplets from the images were distinguished, and the number of droplets, the average diameter and standard deviation computed as a function of time.64 Calculation of volumes was carried out using Fiji.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. P. Acknowledges funding as part of the EPSRC Centre for Doctoral Training in Molecular Modelling and Materials Science (EP/L015862/1) in support of BASF SE. AFN is grateful for support by MCIN/AEI/10.13039/501100011033/FEDER, 289 (Grant No. PID2021-122369NB-100).Notes and references
- J. M. Gunton, M. San Miguel and P. S. Sahni, Phase Transit. Crit. Phenom., ed. J. L. Lebowitz, Academic, London, 8th edn, 1983, p. 267 Search PubMed.
- C. D. Keating and R. V. Pappu, J. Phys. Chem. B, 2021, 125, 12399–12400 CrossRef PubMed.
- J. W. Cahn and J. E. Hilliard, J. Chem. Phys., 1959, 31, 688–699 CrossRef.
- J. W. Gibbs, The Scientific Papers of J. Willard Gibbs, Dover, New York, 1961, vol. 1 Search PubMed.
- H. Reiss and M. Shugard, J. Chem. Phys., 1976, 65, 5280 CrossRef.
- A. J. Bray, Phys. A, 1993, 194, 41–52 CrossRef.
- J. Colombani and J. Bert, J. Non-Equilib. Thermodyn., 2004, 29, 389–395 Search PubMed.
- V. S. Nikolayev, D. Beysens and P. Guenoun, Phys. Rev. Lett., 1996, 76, 3144–3147 CrossRef PubMed.
- J. H. Yao, K. R. Elder, H. Guo and M. Grant, Phys. A Stat. Mech. its Appl., 1994, 204, 770–788 CrossRef.
- F. Cau and S. Lacelle, Phys. Rev. E, 1993, 47, 1429–1432 CrossRef CAS PubMed.
- T. Kalwarczyk, N. Ziebacz, M. Fiałkowski and R. Hołyst, Langmuir, 2008, 24, 6433–6440 CrossRef CAS PubMed.
- R. Limary and P. F. Green, Langmuir, 2003, 19, 2419–2424 CrossRef CAS.
- K. P. Sigdel and G. S. Iannacchione, J. Chem. Phys., 2010, 133, 044513 CrossRef CAS PubMed.
- P. S. Drzaic, J. Appl. Phys., 1986, 60, 2142–2148 CrossRef CAS.
- P. S. Drzaic, Liquid Crystal Dispersions, World Scientific, 1995 Search PubMed.
- G. P. Crawford and S. Zumer, Liquid Crystals In Complex Geometries: Formed by Polymer And Porous Networks, CRC Press, 1996 Search PubMed.
- J. Gupta, S. Sivakumar, F. Caruso and N. Abbott, Angew. Chem., Int. Ed., 2009, 48, 1652–1655 CrossRef CAS PubMed.
- M. I. Kinsinger, M. E. Buck, N. L. Abbott and D. M. Lynn, Langmuir, 2010, 26, 10234–10242 CrossRef CAS PubMed.
- W. Khan, J. H. Choi, G. M. Kim and S. Y. Park, Lab Chip, 2011, 11, 3493–3498 RSC.
- I. Lin, D. S. Miller, P. J. Bertics, C. J. Murphy, J. J. D. Pablo and N. L. Abbott, Science, 2011, 332, 1297–1300 CrossRef CAS PubMed.
- T. Lopez-Leon and A. Fernandez-Nieves, Colloid Polym. Sci., 2011, 289, 345–359 CrossRef CAS.
- A. Concellón, C. A. Zentner and T. M. Swager, J. Am. Chem. Soc., 2019, 141, 18246–18255 CrossRef PubMed.
- W. S. Wei, Y. Xia, S. Ettinger, S. Yang and A. G. Yodh, Nature, 2019, 576, 433–436 CrossRef PubMed.
- S. Bronnikov, V. Cozan and A. Nasonov, Phase Transitions, 2007, 80, 831–839 CrossRef.
- X. Chen, B. D. Hamlington and A. Q. Shen, Langmuir, 2008, 24, 541–546 CrossRef PubMed.
- A. Bhattacharya, M. Rao and A. Chakrabarti, Phys. Rev. E, 1996, 53, 4899–4903 CrossRef PubMed.
- A. J. Bray, Adv. Phys., 2002, 51, 481–587 CrossRef.
- Z. Kutnjak, S. Kralj, G. Lahajnar and S. Žumer, Phys. Rev. E, 2003, 68, 12 CrossRef PubMed.
- R. L. Humphries and G. R. Luckhurst, Proc. R. Soc. London, Ser. A, 1976, 352, 41–56 CAS.
- M. Mucha, Prog. Polym. Sci., 2003, 28, 837–873 CrossRef CAS.
- E. R. Soule and A. D. Rey, Mol. Simul., 2012, 38, 735–750 CrossRef CAS.
- R. Shimada and H. Watanabe, J. Soc. Rheol., Jpn, 2020, 48, 199–206 CrossRef CAS.
- R. Shimada, O. Urakawa, T. Inoue and H. Watanabe, Soft Matter, 2021, 17, 6259–6272 RSC.
- P. K. Mukherjee, J. Chem. Phys., 2002, 116, 9531–9536 CrossRef CAS.
- S. DasGupta and S. K. Roy, Phys. Lett. Sect. A Gen. At. Solid State Phys, 2001, 288, 323–328 CAS.
- K. Denolf, G. Cordoyiannis, C. Glorieux and J. Thoen, Phys. Rev. E, 2007, 76, 1–9 CrossRef PubMed.
- S. Thakur, P. A. Pullarkat and P. B. Kumar, Phys. Rev. E, 2009, 80, 1–7 CrossRef PubMed.
- L. A. Serrano, M. J. Fornerod, Y. Yang, F. Stellacci and S. Guldin, Soft Matter, 2018, 14, 4615–4620 RSC.
- M. J. Fornerod, E. Amstad and S. Guldin, Mol. Syst. Des. Eng., 2020, 5, 358–365 RSC.
- C. G. Reyes, J. Baller, T. Araki and J. P. F. Lagerwall, Soft Matter, 2019, 15, 6044–6054 RSC.
- M. Patel, A. N. Pallipurath Radhakrishnan, L. Bescher, E. Hunter-Sellars, B. Schmidt-Hansberg, E. Amstad, S. Ibsen and S. Guldin, Soft Matter, 2021, 17, 947–954 RSC.
- E. M. Terentjev, Europhys. Lett., 1995, 32, 607–612 CrossRef CAS.
- P. W. Voorhees, Annu. Rev. Mater. Sci., 1992, 22, 197–215 CrossRef CAS.
- D. A. Porter and K. E. Easterling, Phase Transformations in Metals and Alloys, 1992, pp. 1–227 Search PubMed.
- J. P. Erikson, J. Chem. Educ., 2017, 94, 75–78 CrossRef CAS.
- O. O. Prishchepa, V. Y. Zyryanov, A. P. Gardymova and V. F. Shabanov, Mol. Cryst. Liq. Cryst., 2008, 489, 84–93 CAS.
- Z. Bradač, S. Kralj and S. Žumer, Phys. Rev. E, 2002, 65, 1–10 CrossRef PubMed.
- V. Tomar, S. I. Hernandez, N. L. Abbott, J. P. Hernandez-Ortiz and J. J. de Pablo, Soft Matter, 2012, 8, 8679–8689 RSC.
- Z. Sumer and A. Striolo, Soft Matter, 2019, 15, 3914–3922 RSC.
- S. Puri, Phase Trans., 2004, 77, 407–431 CrossRef CAS.
- S. Mehta and J. Zhang, Nat. Rev. Cancer, 2022, 22, 239–252 CrossRef PubMed.
- S. Shimizu and N. Matubayasi, Phys. A, 2021, 563, 125385 CrossRef.
- A. Phan, D. R. Cole and A. Striolo, Langmuir, 2014, 30, 8066–8077 CrossRef PubMed.
- C.-H. Wang, P. Bai, J. I. Siepmann and A. E. Clark, J. Phys. Chem. C, 2014, 118, 19723–19732 CrossRef.
- X.-Y. Guo, T. Watermann and D. Sebastiani, J. Phys. Chem. B, 2014, 118, 10207–10213 CrossRef PubMed.
- M. Zhao and X. Yang, J. Phys. Chem. C, 2015, 119, 21664–21673 CrossRef.
- T. Muthulakshmi, D. Dutta, P. Maheshwari and P. K. Pujari, J. Condens. Matter Phys., 2018, 30, 025001 CrossRef CAS PubMed.
- L. Gelb, K. Gubbins, R. Radhakrishnan and M. Sliwinska-Bartkowiak, Rep. Prog. Phys., 1999, 62, 1573–1659 CrossRef CAS.
- Z. Fetahaj, L. Ostermeier, H. Cinar, R. Oliva and R. Winter, J. Am. Chem. Soc., 2021, 143, 5247–5259 CrossRef CAS PubMed.
- A. Villois, U. Capasso Palmiero, P. Mathur, G. Perone, T. Schneider, L. Li, M. Salvalaglio, A. deMello, S. Stavrakis and P. Arosio, Small, 2022, e2202606 CrossRef PubMed.
- R. Cherrabi, A. Saout-Elhak, M. Benhamou and M. Daoud, J. Chem. Phys., 1999, 111, 8174–8181 CrossRef CAS.
- S.-M. Yang, D. Zhang, W. Chen and S.-C. Chen, Lab Chip, 2015, 15, 2680–2687 RSC.
- F. Chen, G. Du, D. Yin, R. Yin, H. Zhang, W. Zhang and S.-M. Yang, Advances In Materials, Machinery, Electronics I, 2017 Search PubMed.
- A. N. Radhakrishnan, M. P. Marques, M. J. Davies, B. O'Sullivan, D. G. Bracewell and N. Szita, Lab Chip, 2018, 18, 585–594 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2sm01348g |
| This journal is © The Royal Society of Chemistry 2023 |