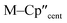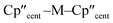Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Electronic structure comparisons of isostructural early d- and f-block metal(III) bis(cyclopentadienyl) silanide complexes†‡
Gemma K.
Gransbury§
 ,
Benjamin L. L.
Réant§
,
Benjamin L. L.
Réant§
 ,
Ashley J.
Wooles
,
Ashley J.
Wooles
 ,
Jack
Emerson-King
,
Jack
Emerson-King
 ,
Nicholas F.
Chilton
,
Nicholas F.
Chilton
 *,
Stephen T.
Liddle
*,
Stephen T.
Liddle
 * and
David P.
Mills
* and
David P.
Mills
 *
*
Department of Chemistry, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: nicholas.chilton@manchester.ac.uk; steve.liddle@manchester.ac.uk; david.mills@manchester.ac.uk
First published on 6th December 2022
Abstract
We report the synthesis of the U(III) bis(cyclopentadienyl) hypersilanide complex [U(Cp′′)2{Si(SiMe3)3}] (Cp′′ = {C5H3(SiMe3)2-1,3}), together with isostructural lanthanide and group 4 M(III) homologues, in order to meaningfully compare metal-silicon bonding between early d- and f-block metals. All complexes were characterised by a combination of NMR, EPR, UV-vis-NIR and ATR-IR spectroscopies, single crystal X-ray diffraction, SQUID magnetometry, elemental analysis and ab initio calculations. We find that for the [M(Cp′′)2{Si(SiMe3)3}] (M = Ti, Zr, La, Ce, Nd, U) series the unique anisotropy axis is conserved tangential to 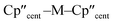 ; this is governed by the hypersilanide ligand for the d-block complexes to give easy plane anisotropy, whereas the easy axis is fixed by the two Cp′′ ligands in f-block congeners. This divergence is attributed to hypersilanide acting as a strong σ-donor and weak π-acceptor with the d-block metals, whilst f-block metals show predominantly electrostatic bonding with weaker π-components. We make qualitative comparisons on the strength of covalency to derive the ordering Zr > Ti ≫ U > Nd ≈ Ce ≈ La in these complexes, using a combination of analytical techniques. The greater covalency of 5f3 U(III) vs. 4f3 Nd(III) is found by comparison of their EPR and electronic absorption spectra and magnetic measurements, with calculations indicating that uranium 5f orbitals have weak π-bonding interactions with both the silanide and Cp′′ ligands, in addition to weak δ-antibonding with Cp′′.
; this is governed by the hypersilanide ligand for the d-block complexes to give easy plane anisotropy, whereas the easy axis is fixed by the two Cp′′ ligands in f-block congeners. This divergence is attributed to hypersilanide acting as a strong σ-donor and weak π-acceptor with the d-block metals, whilst f-block metals show predominantly electrostatic bonding with weaker π-components. We make qualitative comparisons on the strength of covalency to derive the ordering Zr > Ti ≫ U > Nd ≈ Ce ≈ La in these complexes, using a combination of analytical techniques. The greater covalency of 5f3 U(III) vs. 4f3 Nd(III) is found by comparison of their EPR and electronic absorption spectra and magnetic measurements, with calculations indicating that uranium 5f orbitals have weak π-bonding interactions with both the silanide and Cp′′ ligands, in addition to weak δ-antibonding with Cp′′.
Introduction
Transition metal (TM) silicon chemistry is well-established, with technological applications being actively developed1 for solid-state silicide materials used in microelectronics, ceramics and catalysis,2 and molecular silanide complexes that effect (hydro)silylation of unsaturated substrates.3–5 In comparison, f-block silicon chemistry is less well developed but shows promise,6 with lanthanide (Ln) silicides used to fortify low-alloy steels,7 Ln silanide catalysts employed in unsaturated hydrocarbon polymerisations,8,9 and actinide (An) silicides showing potential for use as high-density nuclear fuels.10–13 Given that the physicochemical properties of the f-elements have been exploited in numerous technologies,14,15 it follows that a deeper understanding of f-block silicon chemistry could lead to new applications that complement d-block silicon analogues.f-Block silicon chemistry has continued to slowly develop and now includes multiple examples of cyclopentadienyl (Cp)-supported M–Si bonds.6 Schumann reported the first Ln(III) examples, [Li(DME)3][Ln(Cp)2(SiMe3)2] (Ln = Dy, Ho, Er, Tm, Lu), in the late 1980s;16–18 since then, other Ln(III) Cp-supported silanide complexes have included [Ln(C5Me4R)2{SiH(SiMe3)2}] (R = Me; Ln = Sc, Y, Nd, Sm, R = Et; Ln = Nd, Sm) by Tilley and Rheingold,19,20 [Lu(Cp*)2{SiH2(o-MeOC6H4)}] (Cp* = {C5Me5}) by Castillo and Tilley,8 [K(2.2.2-crypt)][Y(C5H4Me)3(SiH2Ph)] by Evans,21 and a series of [Ln(Cp)3(SiR3)]− anions (Ln = La, Ce; SiR3 = Si(H)Mes2, Si(H)Ph2, Si(Me)Ph2, SiPh3; Mes = C6H2Me3-2,4,6) by Fang;22 Baumgartner and Marschner have reported a wide variety of this class of complex, including [K2(18-crown-6)2Cp][Ln(Cp)2{[Si(SiMe3)2SiMe2]2}] (Ln = Tm, Ho, Tb, Gd),23 [K(18-crown-6)][Ln(Cp)3{Si(SiMe3)3}] (Ln = Ho, Tm) and [{K(18-crown-6)}2Cp][Ln(Cp)3{Si(SiMe3)3}] (Ln = Ce, Sm, Gd, Tm),24 and the Y(III) complexes [K(DME)4][Y(Cp)2(L)] (L = {[Si(SiMe3)2SiMe2]2O}25 or {[Si(SiMe3)2SiMe2]2}).26 Reports of complexes that contain structurally authenticated Cp-supported An–Si bonds are currently limited to the U(III) silylenes [U(Cp′)3{Si(NMe2)[PhC(NtBu)2]}] (Cp′ = {C5H4SiMe3}) and [U(Cp′)3{Si[PhC(NiPr)2]2}] by Arnold,27 and the An(IV) silanides [An(Cp′)3{Si(SiMe3)3}] (An = Th, U) by some of us;28 Porchia,29 Tilley,30 and Marks31 have all reported examples of An silanide complexes that were not characterised in the solid state.
It has recently been demonstrated that the extent of covalency in f-block M–Si bonds can be established by a combination of 29Si NMR spectroscopy and density functional theory (DFT) calculations.32 However, this approach is currently limited to diamagnetic complexes and the vast majority of f-block complexes are paramagnetic; conversely, pulsed EPR spectroscopy has been applied to quantify An–C bond covalency in 5f3 U(III) and 6d1 Th(III) substituted Cp complexes.33 Although no U(III) silanide complex has been structurally authenticated to date, we posited that a substituted Cp-supported system could provide the necessary kinetic stabilisation. Ti(III) bis-Cp silanide complexes have been extensively studied by fluid solution continuous wave (CW) EPR spectroscopy, including mononuclear complexes with bidentate silanides,34,35 and monodentate silanides supported by a tethered donor atom or neutral co-ligand,34,36–38 as well as dinuclear Ti(III) complexes;39 however, powder and frozen solution spectra are rare.39 The only EPR spectra of nd1 Zr(III) and Hf(III) bis-Cp silanides reported to date are of [K(18-crown-6)][M(Cp)2{[Si(SiMe3)2SiMe2]2}].35
We reasoned that a series of early d- and f-block M(III) complexes containing M–Si bonds could be achieved by using two substituted Cp ligands and one bulky silanide. We decided to adapt our previous strategy where we prepared An(IV) silanide complexes with three Cp′ and one hypersilanide ligand, {Si(SiMe3)3};28 we were encouraged to continue using hypersilanide as this has provided the largest number of f-block silanide complexes to date,6 and to increase the size of the Cp′ ring to Cp′′ ({C5H3(SiMe3)2-1,3}) in an effort to maintain kinetic stabilization of the M–Si bonds when the number of coordinated ligands is reduced. The approach of using multiple silyl groups increases the number of signals to assign in 29Si NMR spectra, but this was preferred to the use of related alkyl-substituted silanide ligands that we have only previously found applicable to Ln(II) systems.32 Here we report the synthesis of an isostructural family of M(III) complexes, [M(Cp′′)2{Si(SiMe3)3}] (M = Ti, Zr, La, Ce, Nd, U), providing an opportunity to directly compare the electronic structures of early d- and f-block silanide bonds. This is predominantly achieved using a combination of CW EPR spectroscopy and complete active space self-consistent field-spin orbit (CASSCF-SO) calculations, complemented by supporting characterisation data including single crystal X-ray diffraction, elemental analysis, SQUID magnetometry, and NMR, UV-vis-NIR and ATR-IR spectroscopies. By comparing the electronic structures of 5f3 U(III) with 4f3 Nd(III), and nd1 Ti(III) and Zr(III) with 4f1 Ce(III), we rationalise differences in magnetic anisotropy, d-orbital splitting, orbital mixing, and covalency in the complexes reported herein, and observe clear differences between early d-block, Ln and An metal-silicon bonding regimes.
Results
Synthesis
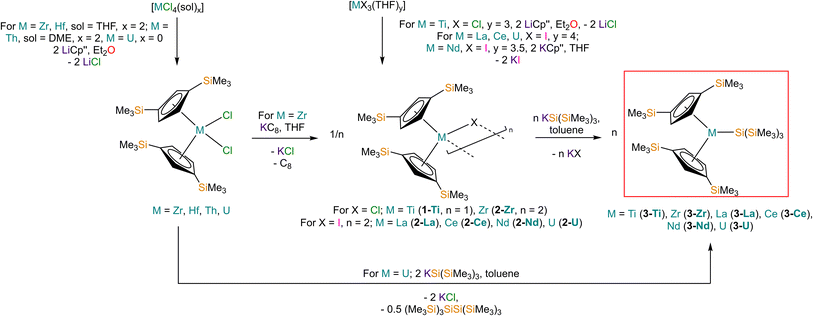
Salt elimination reactions between [Ti(Cp′′)2Cl] (1-Ti) or [{M(Cp′′)2(μ-X)}2] (X = Cl, M = Zr (2-Zr); X = I, M = La (2-La), Ce (2-Ce), Nd (2-Nd), U (2-U)) with one or two equivalents of [K{Si(SiMe3)3}],40 respectively, in toluene gave the heteroleptic M(III) silanide complexes [M(Cp′′)2{Si(SiMe3)3}] (3-M; M = Ti, Zr, La, Ce, Nd, U) in 34–77% yields following work-up and recrystallisation from pentane (Scheme 1). The Ti(III) starting material 1-Ti was prepared directly from the reaction of two equivalents of LiCp′′41,42 with [TiCl3(THF)3],43 whilst 2-Zr was synthesised by reduction of [Zr(Cp′′)2Cl2]44 using KC8.45 The f-block precursors 2-M were generated,45–47 by the reaction of two equivalents of KCp′′48 with [MI3(THF)y] (y = 4, M = La,49 Ce,49 U,50,51y = 3.5, M = Nd;49 see ESI for full Experimental details‡). Physical characterisation data of 1-3-M support the proposed formulations.We found that 3-U could also be prepared by the reaction of [U(Cp′′)2Cl2]52 with two equivalents of [K{Si(SiMe3)3}] in 77% yield following work-up and recrystallisation from pentane. The reaction of [U(Cp′′)2Cl2] with one equivalent of [K{Si(SiMe3)3}] exclusively resulted in reduction of the red U(IV) starting material to the dark green U(III) complex [{U(Cp′′)2(μ-Cl)}2], with oxidative coupling of the silanide to give colourless crystals of (Me3Si)3SiSi(SiMe3)3; addition of a second equivalent of [K{Si(SiMe3)3}] to the reaction mixture gave 3-U. The facile reduction of [U(Cp′′)2Cl2] by [K{Si(SiMe3)3}] was expected, given the accessible U(IV) → U(III) reduction potential (E0 = −0.63 V).53 We could not prepare Hf(III) and Th(III) homologues of 3-M using these procedures; although the M(IV) precursors [M(Cp′′)2Cl2] (M = Hf, Th,52 see ESI‡ for full Experimental details) can be prepared in appreciable yields. Lappert previously reported that the reduction of [Th(Cp′′)2Cl2] with Na/K alloy in THF gave [Th(Cp′′)3] by ligand scrambling;54 we found that some decomposition occurred when [M(Cp′′)2Cl2] (M = Hf, Th) were treated with KC8 in THF, and though no products could be identified from the Hf reaction, we identified crystals of [Th(Cp′′)3] by single crystal XRD.54
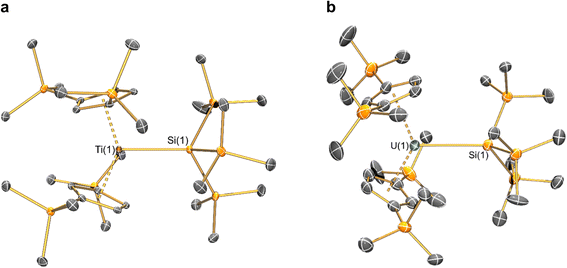
Structural characterisation
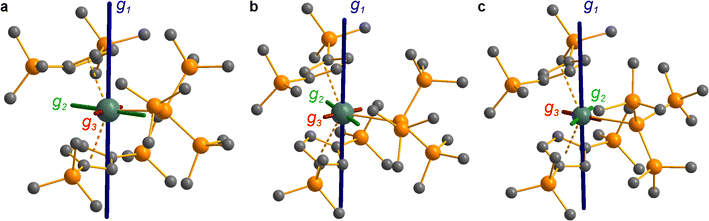
The solid-state molecular structures of [Hf(Cp′′)2Cl2], 2-Nd, 2-U and 3-M were verified by single crystal XRD, and only 3-M are discussed here for brevity; datasets for [Zr(Cp′′)2Cl2],44 [Th(Cp′′)2Cl2],52 [U(Cp′′)2Cl2],521-Ti,462-Zr,452-La47 and 2-Ce47 have previously been reported. As 3-M are isostructural only 3-Ti and 3-U are shown in Fig. 1 and key metrical parameters for all 3-M are compiled in Table 1 (see ESI Fig. S80–S86‡ for depictions of the solid-state structures of other complexes). Treating the Cp′′ centroids as coordination points, 3-M can be described as exhibiting distorted pseudo-trigonal planar geometries. The M–Si distances are consistently ∼0.20–0.40 Å longer than the sums of the respective M–Si single-bond covalent radii reported by Pyykkö55 of 2.52 (3-Ti), 2.70 (3-Zr), 2.96 (3-La), 2.79 (3-Ce), 2.90 (3-Nd) and 2.86 Å (3-U). We attribute this to the combination of sterically encumbered Cp′′ and hypersilanide ligands, together with the SiMe3 groups in the latter withdrawing a substantial amount of charge density from the silanide centre by negative hyperconjugation.56,57| Parameter | 1-Ti 46 | 1-Zr | 3-Ti | 3-Zr | 3-La | 3-Ce | 3-Nd | 3-U |
|---|---|---|---|---|---|---|---|---|
| a DFT-optimised structure. | ||||||||
| M–Si or M–Cl | 2.347(3) | 2.4534 | 2.7720(2) | 2.902(2) | 3.178(2) | 3.153(2) | 3.112(2) | 3.116(2) |
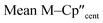
|
2.037(4) | 2.1801 | 2.0508(2) | 2.1841(4) | 2.5215(2) | 2.5005(2) | 2.4489(9) | 2.4726(2) |
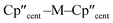
|
138.45(14) | 134.58 | 141.04(3) | 133.830(2) | 132.54(5) | 133.11(3) | 132.37(2) | 131.02(4) |
Complex 3-U (Fig. 1b) exhibits a relatively short U–Si distance of 3.116(2) Å compared to [U(Cp′)3{Si(NMe2)[PhC(NtBu)2]}] (3.1637(7) Å) and [U(Cp′)3{Si[PhC(NiPr)2]2}] (3.1750(6) Å),27 which contain dative silylene U(III)–Si bonds, in accord with the increased electrostatic attraction between the negatively charged hypersilanide and the U(III) centre in 3-U. Additionally, the U–Si bond length of 3-U is ca. 0.05 Å longer than the previously reported complex [U(Cp′)3{Si(SiMe3)3}] (3.0688(8) Å),28 consistent with the increased ionic radii of U(III) vs. U(IV) (six-coordinate U(III) = 1.025 Å, whilst U(IV) = 0.89 Å).58 There are essentially negligible changes to the 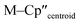 distances and
distances and 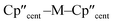 angles when comparing 3-M to 1-Ti and 2-M for the same metal. The orientation of the Cp′′ ligands with respect to each other are typically invariant within each series, with the ring trimethylsilyl substituents arranged to minimise inter-ligand steric repulsions;471-Ti and 3-Ti are outliers due to the high steric demands about the smaller Ti(III) centre (six-coordinate Ti(III) = 0.67 Å).58
angles when comparing 3-M to 1-Ti and 2-M for the same metal. The orientation of the Cp′′ ligands with respect to each other are typically invariant within each series, with the ring trimethylsilyl substituents arranged to minimise inter-ligand steric repulsions;471-Ti and 3-Ti are outliers due to the high steric demands about the smaller Ti(III) centre (six-coordinate Ti(III) = 0.67 Å).58
Previously reported neutral Ti(III) bis-Cp silanide complexes contain shorter Ti–Si bonds than that found for 3-Ti (Fig. 1a), though these all contain less sterically demanding Cp ligands and a PMe3 ancillary ligand: [Ti(Cp)2(SiH3)(PMe3)] (2.594(2) Å),34 [Ti(Cp)2(SiH2Ph)(PMe3)] (2.635(7) Å),59 and [Ti(Cp)2(SiHPh2)(PMe3)] (2.652(2) Å).36 However, the mean Ti–Si bond length of the anionic Ti(III) complex [K(18-crown-6)][Ti(Cp)2{[Si(SiMe3)2SiMe2]2}] (2.770(3) Å),60 which features a bidentate silanide ligand, is statistically equivalent to that of 3-Ti; similarly, the Zr–Si bond length of 3-Zr is comparable to those present in [K(18-crown-6)][Zr(Cp)2{[Si(SiMe3)2SiMe2]2}] (Zr–Si: 2.8503(11), 2.8950(10) Å)35 and the Ce–Si distance of 3-Ce is invariant to that of [{K(18-crown-6)}2Cp][Ce(Cp)3{Si(SiMe3)3}] (Ce–Si: 3.155(5) Å).24 Conversely, the La–Si distance in 3-La is intermediate to those seen in [La{μ-η:5κ1-SiC4(SiMe3)2-1,4-Ph2-2,3}(μ-η8:η8-C8H8)K(THF)3]2 for the η5 – (3.0888(5) Å) and κ1 – (3.2908(6) Å) bound silole.61 Complex 3-Nd contains the first structurally authenticated Nd–Si bond, precluding a literature comparison; however, the Ln–Si distances for the 3-Ln series vary in accord with the expected periodic trend for Ln(III) ionic radii.58
NMR spectroscopy
Multinuclear NMR spectroscopy was performed on 1-Ti, 2-M and 3-M (see ESI Fig. S1–S42‡ for annotated NMR spectra); we focus here on the spectra of 3-M. With the exception of diamagnetic 3-La, the collection of reliable NMR spectra for 3-M was challenging due to paramagnetism. C6D6 solutions of 3-Ti and 3-Zr also showed decomposition at ambient temperatures (t½ca. 2 h); δSi resonances at −116.11 and −11.97 ppm grew in intensity during data collection (see ESI Fig. S25 and S27‡) that were assigned to the organosilane HSi(SiMe3)3 by comparison with an authentic sample.62 An additional resonance observed in the 29Si NMR spectrum of 3-Ti at −21.83 ppm was attributed to silicone grease, whilst in 3-Zr a signal at δSi = −9.83 ppm could not be confidently assigned. Previous reports of complexes containing Ti(III)–Si and Zr(III)–Si bonds showed that solution decomposition processes are commonly observed by NMR spectroscopy.24,35,60 The rest of the 3-M series were stable in C6D6 solution at ambient temperature for a sufficient duration for multinuclear NMR spectra to be acquired (ca. 1 h; experiments had to be performed at relatively fast acquisition times to obtain data that are representative of freshly prepared solutions, e.g. 1D 29Si INEPT 128 scans).For diamagnetic 3-La the 1H NMR spectrum showed the four expected resonances: two inequivalent Cp-H signals for the 4,5- and 2-Cp-H positions at 7.17 and 7.46 ppm, respectively, and two resonances in a ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 for the chemically inequivalent trimethylsilyl environments, δH: 0.25 (Cp-SiCH3) and 0.55 ppm (Si(SiCH3)3); these correlated with five resonances in the 13C NMR spectrum. The 29Si NMR spectra of 3-La revealed three resonances; those at −6.57 and −10.32 ppm were respectively assigned as Si(SiCH3)3 and Cp-SiCH3via a 1H-29Si HMBC experiment, whilst a weak signal at −130.25 ppm correlated with the 1H resonances of the hypersilanide ligand; the latter signal can only be tentatively assigned as the quaternary metal-bound silicon atom due to quadrupolar broadening from coupling to 99.9% abundant I = 7/2 139La nuclei.
3 for the chemically inequivalent trimethylsilyl environments, δH: 0.25 (Cp-SiCH3) and 0.55 ppm (Si(SiCH3)3); these correlated with five resonances in the 13C NMR spectrum. The 29Si NMR spectra of 3-La revealed three resonances; those at −6.57 and −10.32 ppm were respectively assigned as Si(SiCH3)3 and Cp-SiCH3via a 1H-29Si HMBC experiment, whilst a weak signal at −130.25 ppm correlated with the 1H resonances of the hypersilanide ligand; the latter signal can only be tentatively assigned as the quaternary metal-bound silicon atom due to quadrupolar broadening from coupling to 99.9% abundant I = 7/2 139La nuclei.
The 1H NMR spectra of paramagnetic 3-M all exhibited signals for the two chemically inequivalent trimethylsilyl environments; resonances for the two Cp′′ ring proton environments were not observed due to paramagnetic line-broadening. As with 3-La, Cp-SiCH3 resonances in all cases are upfield of those assigned to Si(SiCH3)3, albeit paramagnetically shifted (Cp-SiCH3δH/ppm: 0.14 (3-Ti), 0.88 (3-Zr), −8.33 (3-Ce), −11.64 (3-Nd), −14.79 (3-U); Si(SiCH3)3δH/ppm: 1.60 (3-Ti), 2.97 (3-Zr), −1.11 (3-Ce), −2.02 (3-Nd), −5.90 (3-U)). Both of the trimethylsilyl environments were present in the 13C NMR spectrum of 3-U (δC/ppm: −28.48, Cp-SiMe3; 17.11, Si(SiMe3)), whilst only the hypersilanide resonances were seen for 3-Ce (8.39 ppm) and 3-Nd (19.79 ppm) and no signals could be assigned for 3-Ti and 3-Zr; in all cases assignments were confirmed by 1H-13C HSQC correlation experiments. Finally, only one signal was observed in the 29Si NMR spectrum of 3-Nd (22.18 ppm), whilst no 29Si NMR signals could be seen for 3-Ti, 3-Zr, 3-Ce or 3-U. The experimental parameters of the 1H-29Si HMBC experiment prohibited correlation with 1H NMR resonances, therefore we cannot confidently assign the 29Si NMR resonance observed for 3-Nd; however, this is unlikely to be due to the metal-bound silicon atom, as this resonance is not observed in the 1D29Si NMR spectra of diamagnetic 3-La. To the best of our knowledge there have not been any previous reports of 29Si NMR chemical shifts for paramagnetic M(III)–Si complexes in the literature for the metals studied here.63
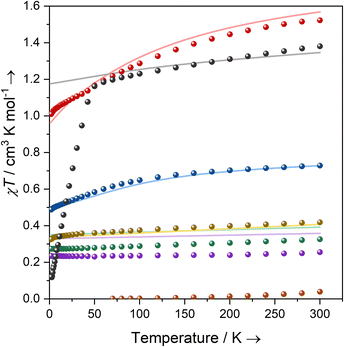
Magnetism
Solutions of 1-Ti, 2-Zr and 3-M (M = Ti, Zr, Ce, Nd, U) in C6D6 were prepared at 0 °C and the effective magnetic moments (μeff) and molar magnetic susceptibilities (χM) were measured by the Evans method immediately upon warming to 300 K (Table 2, ESI Fig. S43–S52‡).64 Solution magnetic susceptibilities for 1-Ti and 3-M are in good agreement with the corresponding data obtained from powdered samples examined by variable-temperature SQUID magnetometry, and CASSCF calculations (Table 2, Fig. 2 and ESI Fig. S94a–S99a‡). Magnetic susceptibility and field-dependent magnetisation data (ESI Table S5 and Fig. S94–S96‡) for 1-Ti, 3-Ti and 3-Zr indicate isolated S = 1/2 systems, as expected for mononuclear nd1 complexes. Previous studies of 2-Zr have reported that this complex is essentially diamagnetic based on NMR chemical shifts,65 but also that it exhibits an EPR spectrum in solution.45 We find near-zero magnetic susceptibility for a powder sample of 2-Zr, implying that the two S = 1/2 centres are strongly antiferromagnetically coupled in the solid state (Fig. 2). A solution of 2-Zr in C6D6 at 300 K was found to be paramagnetic by the Evans method, but less than expected for two uncoupled S = 1/2 (0.26 compared to 0.75 cm3 K mol−1), indicating weaker antiferromagnetic coupling than in the solid state, some minor sample decomposition, and/or the presence of some monomeric [Zr(Cp′′)2Cl] (1-Zr) in solution as proposed by Antiñolo et al.65 SQUID magnetometry and EPR spectra of 2-Ce, 2-Nd and 2-U showed extensive exchange interactions between the metal ions; these data are challenging to model,66 and will be communicated in a separate publication as they are outside the main focus of this study.| Complex | Solution | Powder | CASSCF calculations | Free ion14 | ||||
|---|---|---|---|---|---|---|---|---|
| μ eff | χ M T | μ eff | χ M T | μ eff | χ M T | μ eff | χ M T | |
| a CAS(3,7) active space averaging over all 5f3 configurations. | ||||||||
| 1-Ti | 1.63 | 0.33 | 1.61 | 0.33 | 1.77 | 0.39 | 1.73 | 0.38 |
| 2-Zr | 1.43 | 0.26 | 0.56 | 0.04 | — | — | — | — |
| 3-Ti | 1.93 | 0.47 | 1.83 | 0.42 | 1.81 | 0.41 | 1.73 | 0.38 |
| 3-Zr | 1.71 | 0.37 | 1.43 | 0.26 | 1.69 | 0.36 | 1.73 | 0.38 |
| 3-Ce | 2.34 | 0.69 | 2.41 | 0.73 | 2.41 | 0.73 | 2.54 | 0.81 |
| 3-Nd | 3.54 | 1.56 | 3.49 | 1.52 | 3.54 | 1.57 | 3.62 | 1.64 |
| 3-U | 3.16 | 1.25 | 3.33 | 1.38 | 3.28a | 1.35a | 3.62 | 1.64 |
Complexes 3-Ce and 3-Nd are more strongly magnetic than 3-Ti and 3-Zr due to the presence of orbital angular momentum; the smooth decrease in χMT with reducing temperature arises from crystal field splitting of the lowest total angular momentum multiplet. Assuming well-isolated ground Kramers doublets for 3-Ce and 3-Nd, the 2 K magnetisation data suggest |±5/2〉 and |±9/2〉 ground states, respectively (ESI Table S5, Fig. S97b and S98b;‡ in an axial crystal field, Msat = ½gJmJ, where gJ is the Landé g-factor67). For 3-U the μeff (χMT) of 3.32 μB (1.38 cm3 K mol−1) at 300 K is characteristic of a 4I9/2 U(III) ion;27 this value smoothly decreases to 3.05 μB (1.16 cm3 K mol−1) at 50 K, then rapidly decreases to 0.98 μB (0.12 cm3 K mol−1) at 1.8 K. The sharp decrease below 50 K occurs due to slow thermalisation of the sample on cooling (see ESI for details‡). The Msat value at 2 K and 7 T is diagnostic of a |±9/2〉 ground state (ESI Fig. S99b‡). Alternating current susceptibility measurements on 3-U show out-of-phase signals owing to slow relaxation of magnetisation below 5 K (ESI Fig. S102–S105‡), which modelling suggests arises due to Raman and quantum tunnelling of magnetisation (QTM) processes (ESI Fig. S106 and Tables S6, S7‡). Slow relaxation is common for U(III) complexes,68–75 however, as there is no effective barrier observed for the reversal of magnetisation and closed hysteresis loops around zero field (ESI Fig. S101‡), we do not refer to 3-U as a single-molecule magnet, following several literature definitions.76,77
UV-vis-NIR spectroscopy
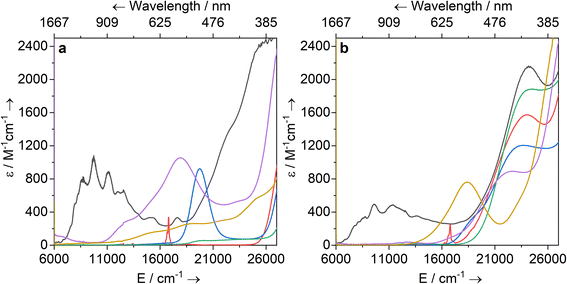
Solutions of 1-Ti, 2-M and 3-M were prepared at 0 °C in toluene (2 mM concentration for all complexes) and warmed to room temperature to immediately record UV-vis-NIR spectra (Fig. 3; see ESI Fig. S65–S79‡ for individual spectra). Some spectra, most notably 2-Nd and 2-U, contain several jagged features; this is attributed to a combination of the most intense absorption maxima being close to the detector limit at the concentrations used, and the spectral resolution of 1 nm. Intense charge transfer (CT) absorptions tailing in from the UV region are found for 3-Zr (![[small upsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d5.gif) max = 22
max = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 cm−1; ε = 890 M−1 cm−1), 3-La (
400 cm−1; ε = 890 M−1 cm−1), 3-La (![[small upsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d5.gif) max = 22
max = 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1; ε = 1880 M−1 cm−1), 3-Ce (
200 cm−1; ε = 1880 M−1 cm−1), 3-Ce (![[small upsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d5.gif) max = 23 500 cm−1; ε = 1200 M−1 cm−1), 3-Nd (
max = 23 500 cm−1; ε = 1200 M−1 cm−1), 3-Nd (![[small upsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d5.gif) max = 24
max = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1; ε = 1570 M−1 cm−1) and 3-U (
000 cm−1; ε = 1570 M−1 cm−1) and 3-U (![[small upsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d5.gif) max = 24
max = 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 cm−1; ε = 2160 M−1 cm−1) (Fig. 3b). These transitions were not observed for 1-Ti or 2-M (Fig. 3a), and therefore can be assigned to changes in CT upon replacing a halide with hypersilanide. Apart from this CT band, the spectra of 2-La, 3-Zr and 3-La are otherwise essentially featureless.
200 cm−1; ε = 2160 M−1 cm−1) (Fig. 3b). These transitions were not observed for 1-Ti or 2-M (Fig. 3a), and therefore can be assigned to changes in CT upon replacing a halide with hypersilanide. Apart from this CT band, the spectra of 2-La, 3-Zr and 3-La are otherwise essentially featureless.
Complex 3-Nd has an additional absorption in the visible region (![[small upsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d5.gif) max = 16
max = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1; ε = 260 M−1 cm−1), as does 2-Nd (
800 cm−1; ε = 260 M−1 cm−1), as does 2-Nd (![[small upsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d5.gif) max = 16
max = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 cm−1; ε = 330 M−1 cm−1; ESI Fig. S71 and S78‡), thus we propose these bands are Nd(III) f–f transitions of the 4I9/2 → 4G5/2 states.78,79 Complex 3-Ce is red and has a shoulder on the CT band at 18
800 cm−1; ε = 330 M−1 cm−1; ESI Fig. S71 and S78‡), thus we propose these bands are Nd(III) f–f transitions of the 4I9/2 → 4G5/2 states.78,79 Complex 3-Ce is red and has a shoulder on the CT band at 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1, while 2-Ce is bright pink and has an intense, broad absorption at
700 cm−1, while 2-Ce is bright pink and has an intense, broad absorption at ![[small upsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d5.gif) max = 19
max = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 (ε = 920 M−1 cm−1); these are assigned to 4f1 → 5d1 transitions, as observed for other Ce(III) complexes with Cp ligands.80–84 The NIR region of 3-U studied here (
700 (ε = 920 M−1 cm−1); these are assigned to 4f1 → 5d1 transitions, as observed for other Ce(III) complexes with Cp ligands.80–84 The NIR region of 3-U studied here (![[small upsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d5.gif) max > 6000 cm−1) is populated with a broad set of absorptions (ε = 200–500 M−1 cm−1) corresponding to normally Laporte-forbidden f–f transitions of significant intensity (Fig. 3a). The increased intensity is attributed to mixing of 5f orbitals with 6d and ligand orbitals allowing for intensity-stealing;53,85,86 similar transitions are observed in 2-U (Fig. 3b) and previously reported U(III) complexes.27,74,87
max > 6000 cm−1) is populated with a broad set of absorptions (ε = 200–500 M−1 cm−1) corresponding to normally Laporte-forbidden f–f transitions of significant intensity (Fig. 3a). The increased intensity is attributed to mixing of 5f orbitals with 6d and ligand orbitals allowing for intensity-stealing;53,85,86 similar transitions are observed in 2-U (Fig. 3b) and previously reported U(III) complexes.27,74,87
The UV-vis-NIR spectrum of 3-Ti features an intense CT band that tails into the visible region up to ca. 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 and a second broad absorption band at
000 cm−1 and a second broad absorption band at ![[small upsilon, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d5.gif) max = 18
max = 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 (ε = 760 M−1 cm−1) that is assigned to overlapping d–d transitions with substantial charge-transfer character, accounting for their higher than expected intensities.88 The spectrum for 1-Ti also exhibits multiple overlapping d–d transitions >14
300 cm−1 (ε = 760 M−1 cm−1) that is assigned to overlapping d–d transitions with substantial charge-transfer character, accounting for their higher than expected intensities.88 The spectrum for 1-Ti also exhibits multiple overlapping d–d transitions >14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1. Finally, the spectrum for 2-Zr shows a broad absorption at 17 900 cm−1 (ε = 1060 M−1 cm−1) with a weaker shoulder at 13 100 cm−1 (ε = 300 M−1 cm−1), and a broad low intensity NIR feature at ca. 6300 cm−1 (ε = 110 M−1 cm−1). We assign the former two absorptions as d–d transitions based on CASSCF calculations (see below), which also suggests the latter is not a 2-Zr d–d transition; this low-energy feature could arise from a fraction of 1-Zr in toluene solution, as suggested by the Evans method magnetic moment (see above).
000 cm−1. Finally, the spectrum for 2-Zr shows a broad absorption at 17 900 cm−1 (ε = 1060 M−1 cm−1) with a weaker shoulder at 13 100 cm−1 (ε = 300 M−1 cm−1), and a broad low intensity NIR feature at ca. 6300 cm−1 (ε = 110 M−1 cm−1). We assign the former two absorptions as d–d transitions based on CASSCF calculations (see below), which also suggests the latter is not a 2-Zr d–d transition; this low-energy feature could arise from a fraction of 1-Zr in toluene solution, as suggested by the Evans method magnetic moment (see above).
EPR spectroscopy
EPR spectra have been recorded at two frequencies where possible and simulations have modelled both spectra simultaneously in EasySpin;89 full details of simulations are included in the ESI (Tables S8–S12 and Fig. S107–S121‡). EPR spectra of 2-Ce, 2-Nd and 2-U show significant exchange interactions between the metal ions, and these will be studied in a separate publication.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene
1 toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hexane) that was pre-cooled to ca. 250 K, then frozen at 77 K and measured immediately. The g-values obtained for monomeric nd1 complexes (1-Ti, 3-Ti and 3-Zr) with this method are generally in excellent agreement with the powder spectra (Table 4).
hexane) that was pre-cooled to ca. 250 K, then frozen at 77 K and measured immediately. The g-values obtained for monomeric nd1 complexes (1-Ti, 3-Ti and 3-Zr) with this method are generally in excellent agreement with the powder spectra (Table 4).
The powder EPR spectrum of 2-Zr is isotropic with g = 1.9825 and a half-field transition, indicating that these transitions arise from a triplet state, reflecting the dimeric structure in the solid state (ESI Fig. S112–S114‡). There is one previous report of an EPR spectrum of 2-Zr with giso = 1.9506 and Aiso = 60 MHz in fluid toluene solution at 300 K.45 Measurement of a frozen solution sample of 2-Zr (see Section 12 of the ESI‡) gives clearly anisotropic spectra (g1 = 1.9961, g2 = 1.9834, g3 = 1.8618; the g3 resonance is at 360 and 1307 mT at X- and Q-band frequencies, respectively, far outside the spectral range of the powder spectrum of 2-Zr, ESI Fig. S115 cf. S112‡) and the half-field transition is absent (ESI Fig. S114‡). These data suggest that the dimer breaks apart in solution to form monomeric 1-Zr (S = 1/2), in accord with solution magnetic susceptibility and UV-vis-NIR data (see above); there may be some 2-Zr still present in the frozen solution; however, at 50 K the signal (arising from Boltzmann population of the triplet state) is dwarfed by the S = 1/2 spectrum. Thus, we henceforth discuss these frozen solution results as representing 1-Zr.
Ti(III) and Zr(III) are S = 1/2 and are expected to have anisotropic g-values (g1, g2, g3) close to the free electron value (ge ≈ 2.0023), with deviations from ge (Δgi = gi − ge) reflecting second order spin–orbit coupling with low energy crystal field states.92 X-band EPR spectra of frozen solutions of 1/3-Ti clearly show three g-features (47Ti/49Ti hyperfine coupling not resolved), while spectra of 1/3-Zr show a similar rhombic pattern superimposed with hyperfine coupling to the 91Zr nuclear spin (11% abundant I = 5/2; Table 4, Fig. 4, ESI Fig. S115 and S117‡). Superhyperfine coupling to α-29Si and β-29Si have been observed before,35 but are not resolved here. Complexes 1/3-Ti/Zr have a consistent axial pattern of g-values reflecting their similar structures; Δg1 is −0.003 to −0.017, Δg2 is −0.02 to −0.03, and Δg3 is −0.09 to −0.28 (Fig. 4, Table 3 and ESI Table S11‡). The g3 value is most sensitive to the different complexes, with larger Δg3 for 3-Ti/Zrvs.1-Ti/Zr, and also larger Δg3 for Zr(III) vs. Ti(III) in isostructural complexes. Complexes 3-Ti/Zr are significantly more anisotropic than previous reports of Ti(III) and Zr(III) bis-Cp silanide complexes, which are pseudo-tetrahedral: Δgave values (gave = (g1 + g2 + g3)/3) of 3-Ti/Zr are −0.076 to −0.109 compared to Δgiso = −0.004 to −0.021.34–39 The EPR spectra of 1/3-Ti/Zr are more comparable to pseudo-trigonal planar bent metallocenes [M(CpR)2X].88 The pattern of 91Zr hyperfine constants (Table 4; one large and two small) are typical for 4dz21 ground states with z aligned along g1,92 which also suggests an electronic structure tending to pseudo-trigonal planar environments.
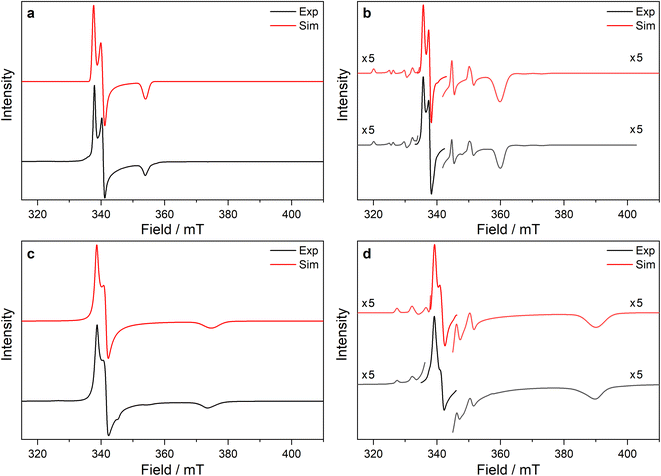 | ||
Fig. 4 Frozen solution CW X-band EPR spectra of (a) 1-Ti at 130 K and 5 mM, (b) 1-Zr at 50 K and 5 mM, (c) 3-Ti at 130 K and 1 mM, (d) 3-Zr at 130 K and 5 mM in 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene 1 toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hexane. Simulations using parameters from ESI Tables S9 and S10‡ are shown in red. hexane. Simulations using parameters from ESI Tables S9 and S10‡ are shown in red. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hexane (9
hexane (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) frozen solutions (FS). Band frequency: X = 9.37–9.47 GHz, K = 24 GHz, Q = 34 GHz
1) frozen solutions (FS). Band frequency: X = 9.37–9.47 GHz, K = 24 GHz, Q = 34 GHz
| Complex | State/temperature | Band(s) | g 1 | g 2 | g 3 |
|---|---|---|---|---|---|
| a Anisotropy in g-values not resolved. b Two species observed in solution, relative abundance given in brackets. | |||||
| 1-Ti | FS/130 K | X, Q | 1.9990 | 1.9818 | 1.9065 |
| Powder/50 K | X, K | 1.9957 | 1.9800 | 1.8964 | |
| CASSCF | — | 1.9994 | 1.9655 | 1.8370 | |
| 3-Ti | FS/130, 50 K | X, Q | 1.9955 | 1.9781 | 1.8030 |
| Powder/55, 50 K | X, Q | 1.9946 | 1.9778 | 1.7914 | |
| CASSCF | — | 1.9950 | 1.9595 | 1.7173 | |
| 1-Zr | FS/50 K | X, Q | 1.9961 | 1.9834 | 1.8618 |
| CASSCF | — | 1.9973 | 1.9524 | 1.8214 | |
| 2-Zr | Powder/50 K | X, Q | 1.9825a | 1.9825a | 1.9825a |
| CASSCF | — | 1.9944 | 1.9224 | 1.8262 | |
| 3-Zr | FS/130 K | X, Q | 1.9874 | 1.9728 | 1.7280 |
| Powder/130 K | X, Q | 1.9853 | 1.9758 | 1.7176 | |
| CASSCF | — | 1.9897 | 1.9438 | 1.6719 | |
| 3-Ce | FS/7 K | X | 3.907 | <0.4 | <0.4 |
| Powder/8, 5 K | X, Q | 3.884 | 0.888 | 0.493 | |
| CASSCF | — | 3.775 | 1.016 | 0.562 | |
| 3-Nd | FS/7 K | X | 5.225 | 0.360 | <0.4 |
| Powder/7, 5 K | X, Q | 5.490 | <0.4 | <0.4 | |
| CASSCF | — | 5.526 | 0.296 | 0.146 | |
| 3-U | FS/5 K | X | 5.949 (44%), 5.536 (56%)b | <0.4 | <0.4 |
| Powder/7, 5 K | X, Q | 6.055 | <0.4 | <0.4 | |
| CASSCF | — | 6.130 | 0.076 | 0.007 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hexane (9
hexane (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) frozen solutions (FS). Band frequency: X = 9.37–9.47 GHz, Q = 34 GHz
1) frozen solutions (FS). Band frequency: X = 9.37–9.47 GHz, Q = 34 GHz
Powder spectra of ground samples of 1-Ti, 3-Ti, 2-Zr and 3-Zr are considerably broadened relative to frozen solution spectra (likely owing to unresolved intermolecular dipolar interactions), resulting in overlap of the g1 and g2 features (see ESI Fig. S108, S110, S112 and S116‡).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hexane (9
hexane (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) has g1 of 3.907 and transverse g-values less than 0.4 (ESI Fig. S118c‡), indicating a geometry change in solution to form a more axial ground state.
1) has g1 of 3.907 and transverse g-values less than 0.4 (ESI Fig. S118c‡), indicating a geometry change in solution to form a more axial ground state.
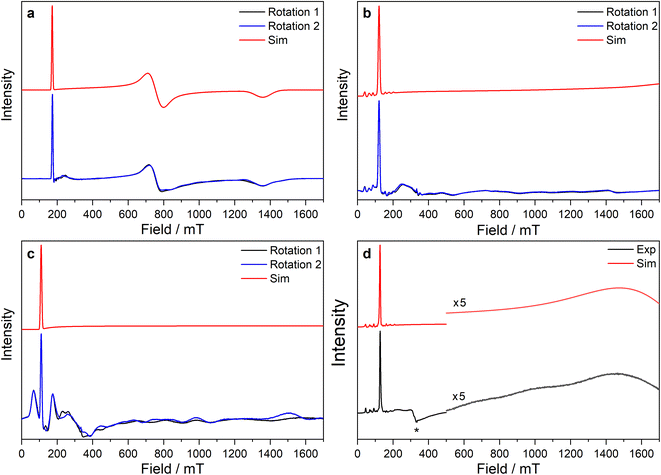 | ||
Fig. 5 CW X-band EPR spectra of (a) 3-Ce powder at 8 K, (b) 3-Nd powder at 7 K, (c) 3-U powder at 7 K, (d) 15 mM frozen solution of 3-Nd in 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 toluene 1 toluene![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hexane at 7 K. Two perpendicular orientations of powder spectra are shown in black and blue. Simulations using parameters from ESI Table S12‡ are shown in red. Asterisk (*) denotes feature intrinsic to cavity. hexane at 7 K. Two perpendicular orientations of powder spectra are shown in black and blue. Simulations using parameters from ESI Table S12‡ are shown in red. Asterisk (*) denotes feature intrinsic to cavity. | ||
The X-band powder EPR spectrum of 3-Nd at 7 K revealed only a single g1 feature of the ground Kramers doublet with resolved 143Nd and 145Nd hyperfine coupling within the accessible field range (Fig. 5b and ESI Fig. S119a–c‡). The g1 value of 5.490 is less than the value of 6.55 expected for a pure |±9/2〉, but is larger than the maximum g value for a pure |±7/2〉 state, implying a mixed |±9/2〉 ground doublet, consistent with the Msat value. Whilst g2 and g3 were not visible in the powder spectrum, a frozen solution X-band spectrum showed part of a g2 feature at the highest fields, estimated as g2 = 0.360 (Fig. 5d).
The powder X-band EPR spectrum of 3-U at 7 K exhibits a sharp feature at g = 6.055 (Fig. 5c), assigned as the g1 feature of an axial Seff = 1/2 ground state with g2, g3 < 0.4. This indicates a majority |±9/2〉 ground state, consistent with the Msat value. Two broader peaks were observed at 67 and 175 mT (g = 9.94 and 3.82), however, the Q-band EPR spectrum was too weak to establish whether these peaks behaved as true g-features. The extra features cannot be explained by dipolar interactions (ESI Fig. S121‡), and we have not been able to assign them. Solution X-band spectra of 3-U at 5 K showed two sharp g1 features at 5.949 and 5.536, indicating two very similar axial species present in solution (ESI Fig. S120c and d‡).
CASSCF calculations
We have investigated the electronic structures of 1-Ti/Zr, 2-Zr and 3-M by CASSCF-SO calculations (performed in OpenMolcas,93,94 see ESI for details‡). For discussion of the data we adopt the coordinate system of Petersen and Dahl, with x along the M–Si/Cl axis, y tangential to Cp′′–M–Cp′′ and z perpendicular to the plane defined by the Cp′′ centroids and coordinating Si/Cl atom.95,96Complexes 1/3-Ti/Zr showed similar results, with the nd1 electrons located in their respective ndz2 orbitals. A dz21 ground state is standard for bent metallocenes [M(CpR)2X] and is consistent with our analysis of the 91Zr hyperfine coupling (see above).88 The excited states place d–d transitions for 1-Ti and 3-Ti between 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 21
000 and 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (Fig. 6, ESI Tables S14 and S15‡), in reasonable agreement with experiment (Fig. 3). For 3-Zr, the d–d transitions are calculated at higher energies (23
000 cm−1 (Fig. 6, ESI Tables S14 and S15‡), in reasonable agreement with experiment (Fig. 3). For 3-Zr, the d–d transitions are calculated at higher energies (23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 224, 25
224, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 402 and 30
402 and 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 058 cm−1, ESI Table S18‡) and are thus obscured by the CT band in agreement with experiment (Fig. 3).
058 cm−1, ESI Table S18‡) and are thus obscured by the CT band in agreement with experiment (Fig. 3).
The dimeric structure of 2-Zr results in the lowest energy d–d transition calculated for 2-Zr′ shifting from below 5000 cm−1 for 1-Ti, 3-Ti and 3-Zr to 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 031 cm−1, with the other d–d transitions at 18
031 cm−1, with the other d–d transitions at 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 101, 20
101, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 609 and 22
609 and 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 362 cm−1 (Fig. 6 and ESI Table S17‡); the former band corresponds well with the low energy shoulder at 13
362 cm−1 (Fig. 6 and ESI Table S17‡); the former band corresponds well with the low energy shoulder at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 cm−1 (ε = 300 M−1 cm−1; Fig. 3), while the latter three agree well with the broad absorption at 17
100 cm−1 (ε = 300 M−1 cm−1; Fig. 3), while the latter three agree well with the broad absorption at 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 900 cm−1 (ε = 1060 M−1 cm−1; Fig. 3). There are no predicted d–d transitions in this region for 1-Zr, which has a low-energy band predicted at 7010 cm−1 and all other d–d transitions would be hidden beneath the CT band tailing from the UV region (ESI Table S16‡). These calculations agree with experimental data (see above) that both 1-Zr and 2-Zr are present in solution.
900 cm−1 (ε = 1060 M−1 cm−1; Fig. 3). There are no predicted d–d transitions in this region for 1-Zr, which has a low-energy band predicted at 7010 cm−1 and all other d–d transitions would be hidden beneath the CT band tailing from the UV region (ESI Table S16‡). These calculations agree with experimental data (see above) that both 1-Zr and 2-Zr are present in solution.
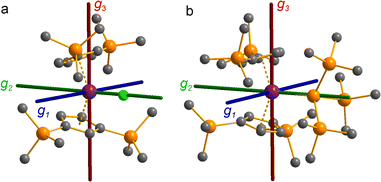
The pattern of calculated g-values for 1/3-Ti/Zr well-reproduces the experimental data (Table 3, ESI Tables S14–S16 and S18‡), while the absolute shifts in g2 and g3 are overestimated (ESI Table S11‡). The CASSCF calculations also give insight into the orientations of the g-values: for all 1/3-Ti/Zr, the largest value g1 is along the z direction (pseudo-three-fold), the intermediate value g2 is along x (M–Cl/Si bond), and the smallest value g3 is along y (tangential to Cp′′–M–Cp′′; Fig. 7 and ESI Fig. S134‡). While orbital energies do not strictly exist in a SA-CASSCF calculation, in this case the five states are each dominated by a single configuration with the unpaired electron located in one of the five d-orbitals, so approximate d-orbital energies can be determined by assigning the state energies to the energy of the singly occupied natural orbital for that state (Fig. 6, ESI Fig. S127, S128, S130–S132 and ESI Tables S14–S18‡).
We find that the dz2 orbital remains lowest in energy in all cases, followed by the dxz orbital, which varies significantly in energy between complexes. The dxy and dyz orbitals lie far higher in energy (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–26 000 cm−1) and are relatively close in energy to each other, whilst the dx2−y2 orbital is highest in energy as chloride and hypersilanide are both strong σ-donor ligands. This is consistent with the Lauher-Hoffmann bonding model of a naked bent metallocene,88,97 with an additional monodentate ligand. With these orbital energies we can rationalise the observed g-values. Spin–orbit coupling along z cannot mix in any excited state into a ground state with the electron in the dz2 orbital,92 and so Δgz is approximately zero which agrees well with experiment (ESI Table S11‡; small deviations away from ge are ascribed to mixing of dx2−y2 into the ground state95). Spin–orbit coupling along x (y) can mix in a state with an unpaired electron in dyz (dxz) into the ground state to shift gx (gy), where Δgx (Δgy) is inversely proportional to the energy of the excited orbital (ESI eqn (S4) and (S5)‡). As dxz is much lower in energy than dyz, Δgy is larger than Δgx, and as the d shell is less than half-filled all Δg are negative; hence g3 is along y and g2 is along x; this explains the obtained ab initio orientations (Fig. 7 and ESI Fig. S134‡).
000–26 000 cm−1) and are relatively close in energy to each other, whilst the dx2−y2 orbital is highest in energy as chloride and hypersilanide are both strong σ-donor ligands. This is consistent with the Lauher-Hoffmann bonding model of a naked bent metallocene,88,97 with an additional monodentate ligand. With these orbital energies we can rationalise the observed g-values. Spin–orbit coupling along z cannot mix in any excited state into a ground state with the electron in the dz2 orbital,92 and so Δgz is approximately zero which agrees well with experiment (ESI Table S11‡; small deviations away from ge are ascribed to mixing of dx2−y2 into the ground state95). Spin–orbit coupling along x (y) can mix in a state with an unpaired electron in dyz (dxz) into the ground state to shift gx (gy), where Δgx (Δgy) is inversely proportional to the energy of the excited orbital (ESI eqn (S4) and (S5)‡). As dxz is much lower in energy than dyz, Δgy is larger than Δgx, and as the d shell is less than half-filled all Δg are negative; hence g3 is along y and g2 is along x; this explains the obtained ab initio orientations (Fig. 7 and ESI Fig. S134‡).
The value of Δg3 reflects the energy of the dxz orbital and therefore the π-bonding character of the X ligand; this has been used previously to construct a π-donor spectrochemical series for [Ti(Cp*)2X].88 Between 1-Ti/Zr and 3-Ti/Zr Δg3 doubles, reflecting the dxz orbital being 40% lower in energy for 3-Ti/Zr; this is because chloride is a π-donor and dxz is formally π-antibonding in 1-Ti/Zr (the nominal dxz orbitals have 1.9% and 3.1% Cl 2pz character for 1-Ti and 1-Zr, respectively; ESI Fig. S127 and S130‡). In contrast, hypersilanide is a weak π-acceptor, and such interactions can be seen with a very low isosurface value (ESI Fig. S129 and S133‡). Upon moving from Ti to Zr there is more effective overlap of the 4d and ligand orbitals, leading to a larger crystal field splitting (Fig. 6), and a decrease in the metal contribution to the singly occupied natural orbitals (ESI Tables S14–S16 and S18‡). Spin–orbit coupling also increases moving from Ti to Zr, which acts to increase |Δg|, whilst increased d-orbital splitting and ligand–metal mixing oppose this; as all Δg become more negative upon going from 1/3-Ti to 1/3-Zr, spin–orbit coupling is the dominant effect.
CASSCF calculations on 3-U averaging over all 5f3 states reproduce well the experimental susceptibility and g1 value, and suggest a 95% |±9/2〉 ground state. Like 3-Ce and 3-Nd, the oblate spheroidal electron density of |±9/2〉 in 3-U is orientated with g1 tangential to Cp′′–M–Cp′′ (Fig. 8c).98,99 However, this CASSCF calculation overestimates Msat; averaging instead over only the 4I9/2 ground term (13 spin quartets) gives a more accurate reproduction of Msat but underestimates g1 and the magnetic susceptibility (ESI Fig. S99 and ESI Table S22‡), suggesting a slightly more mixed ground state of 89% |±9/2〉 + 6% |±5/2〉. The true ground state composition of 3-U is likely between these values, but it is certainly less mixed than that of 3-Nd.
The CAS(3,7)SCF averaged orbitals for 3-U (35 quartets and 112 doublets) showed small 6d orbital contributions (∼5%), so we extended the active space to also include two low-lying 6d orbitals (6dz2 and 6dxz, ESI Fig. S136,‡ in accordance with 3-Ti and 3-Zr, see above). Averaging over all f3 and f2d1 configurations in this active space, the f2d1 states lie at ∼7000 cm−1 (ESI Fig. S138‡), suggesting that spin- and Laporte-allowed f → d transitions contribute to the broad band from 6000 to 17 000 cm−1 in the UV-vis-NIR spectrum (Fig. 3). Examining the averaged molecular orbitals with a low isosurface value showed that the 5f orbitals participate in weak δ-antibonding and π-bonding with Cp′′, and weak π-bonding with low lying vacant orbitals on Si (ESI Fig. S137‡).
Discussion
From the single crystal X-ray diffraction and DFT-optimised structural data it can be seen that the M–Si bonds are 0.26–0.30 Å longer than the corresponding M–Cl bonds in 1/3-Ti/Zr after correcting for the difference in single-bond covalent radii (Table 1).55 The steric bulk of the hypersilanide ligand imposes the longer M–Si bonds, which leads to weaker M–Si bonding interactions through reduced orbital overlap. The bonding in the {M(Cp′′)2}+ fragments are expected to be similar in 1-Mvs.3-M. Whilst the orientation of Cp′′ rings changes, the key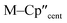 distances and
distances and 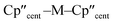 angles for Zr(III) are virtually unchanged, and for Ti(III) there are only modest respective increases of these metrics of 0.014 Å and 2.6°.
angles for Zr(III) are virtually unchanged, and for Ti(III) there are only modest respective increases of these metrics of 0.014 Å and 2.6°.
The 3d1 and 4d1 systems 3-Ti and 3-Zr exhibit ndz21 ground state occupancies, with spin density perpendicular to the 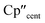 ,
, 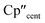 , Si plane. The ndz21 ground state is non-bonding and is favoured by strong anti-bonding interactions of the remaining nd-orbitals with the two Cp′′ ligands as well as with the hypersilanide ligand, which acts as a σ-donor. The hypersilanide ligand also acts as a weak π-acceptor, giving rise to a low energy ndxz1 excited state in both cases (<10
, Si plane. The ndz21 ground state is non-bonding and is favoured by strong anti-bonding interactions of the remaining nd-orbitals with the two Cp′′ ligands as well as with the hypersilanide ligand, which acts as a σ-donor. The hypersilanide ligand also acts as a weak π-acceptor, giving rise to a low energy ndxz1 excited state in both cases (<10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1). The stabilisation of ndz2 and ndxz orbitals is echoed in 3-U, where low energy f3 → f2d1 transitions are seen above 6000 cm−1. However, for 3-Ce and 3-Nd the fn → fn−1d1 transitions are not proximate to the ground states, as expected.
000 cm−1). The stabilisation of ndz2 and ndxz orbitals is echoed in 3-U, where low energy f3 → f2d1 transitions are seen above 6000 cm−1. However, for 3-Ce and 3-Nd the fn → fn−1d1 transitions are not proximate to the ground states, as expected.
Due to the orbitally non-degenerate ground state, the anisotropy of the g-tensors in 3-Ti and 3-Zr are dominated by second-order spin–orbit coupling with the ndxz1 excited state. This results in a large shift of gy away from ge, where y is tangential to Cp′′–M–Cp′′. In f-block complexes with near-complete f-orbital degeneracy, anisotropy in the ground state is dictated by electrostatics, and we find that the bis-Cp′′ crystal field dominates over the hypersilanide contribution. This favours oblate f-electron density in the ground state, giving ground states dominated by |±5/2〉, |±9/2〉 and |±9/2〉, for 3-Ce, 3-Nd and 3-U, respectively, with the magnetic easy axis tangential to Cp′′–M–Cp′′. These data indicate that the M–Si bonds in 3-Ti and 3-Zr are both more covalent than the M–Si bonds in 3-Ln and 3-U, whilst the greater covalency of the M–Si bonds in 3-Zrvs.3-Ti is also evident from the respective magnitudes of 4d vs. 3d crystal field splitting.
The presence of slow magnetic relaxation for 3-U and the lack of such behaviour for 3-Nd is an outlier compared to literature examples, where analogous f3 compounds tend to show more similar behaviour.75,100 It is likely that faster magnetic relaxation occurs for 3-Nd due to the lower purity of the ground state, which itself is likely to arise due to mixing with low energy spin–orbit states at 65 and 176 cm−1: the more-pure ground state in 3-U on the other hand, is well-separated from the lowest excited states at 330 and 524 cm−1, which likely arises from a larger crystal field effect due to 5f vs. 4f orbitals. This is in accord with the UV-vis-NIR spectrum of 3-U, where the f → d transitions are low energy for U(III),53 and are a hallmark of polarised covalent metal–ligand bonding.15 The greater involvement of 5f vs. 4f orbitals in M–Si bonds was also seen in ab initio calculations. It follows that the M–Si bond in 3-U has greater covalency than that of 3-Nd, with the M–Si bonds of 3-La, 3-Ce and 3-Nd assumed to show similar predominantly electrostatic character due to their valence 4f orbitals.
Conclusions
We have reported the synthesis and characterisation of a series of isostructural early d- and f-block M(III) bis(cyclopentadienyl) hypersilanide complexes, providing the first structurally authenticated examples of U(III) and Nd(III) silanides. By using a combination of CW EPR spectroscopy and CASSCF calculations we have shown that the d-block complexes herein have 3/4dz21 ground states aligned perpendicular to the coordination plane, with the hypersilanide ligand acting as a strong σ-donor and weak π-acceptor to impart axial anisotropy through π-bonding with low-lying ndxz orbitals; as expected, the orbital splitting is greater for 4dz21 Zr(III) vs. 3dz21 Ti(III). In contrast, the early f-block Ln/U(III) silanide 4/5fn complexes exhibit predominantly ionic bonding, with the dominant crystal field imparted by the Cp′′ ligands favouring oblate spheroidal f-electron densities and magnetic easy axes tangential to Cp′′–M–Cp′′.The uranium silanide complex was found to exhibit increased covalency over Ln congeners, with calculations showing weak π-bonding between the 5f orbitals and both the silanide and Cp′′ ligands, and weak δ-antibonding between 5f orbitals and Cp′′. The greater crystal field imposed for 5f3 U(III) vs. 4f3 Nd(III) gave a purer ground state due to the energies of low-lying excited states being raised to the extent that they can no longer mix, switching on slow magnetic relaxation in the former complex below 5 K. The U(III) congener additionally displayed low energy 5f3 → 5f26d1 electronic transitions from 6000 to 17 000 cm−1, signifying that the ndz2 and ndxz orbitals have been stabilised in a similar manner to Ti(III) and Zr(III) homologues. Together, the combination of data acquired herein show the qualitative ordering of the extent of covalency to be Zr > Ti ≫ U > Nd ≈ Ce ≈ La, and reveal clear differences between the compositions of early d-block, Ln and An M–Si bonds.
Data availability
Research data files supporting this publication are available from FigShare at: https://doi.org/10.6084/m9.figshare.20459439.Author contributions
B. L. L. R., S. T. L. and D. P. M. provided the original concept. B. L. L. R. synthesised and characterised the compounds and solved and refined the crystal structures. G. K. G. collected and interpreted EPR and magnetic data and performed calculations. A. J. W. further refined the crystallographic data and finalised CIFs. J. E.-K. carried out supporting synthetic and characterisation work. N. F. C. supervised the EPR, magnetism and calculations components. D. P. M. and S. T. L. supervised the synthetic component and directed the research. B. L. L. R., G. K. G., D. P. M., S. T. L. and N. F. C. wrote the manuscript, with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the University of Manchester for a PhD studentship for B. L. L. R. (Nuclear Endowment) and access to the Computational Shared Facility, and the European Research Council (StG-851504, CoG-816268 and CoG-612724) and the UK EPSRC (EP/M027015/1, EP/P001386/1, and EP/S033181/1) for funding. We thank Ivana Borilovic for collecting preliminary EPR data, and Adam Brookfield for supporting EPR measurements. We acknowledge the EPSRC UK National Electron Paramagnetic Resonance Service for access to the EPR facility and the SQUID magnetometer. S. T. L. thanks the Alexander von Humboldt Foundation for a Friedrich Wilhelm Bessel Research Award and N. F. C. thanks the Royal Society for a University Research Fellowship (URF191320).References
- R. Waterman, P. G. Hayes and T. D. Tilley, Acc. Chem. Res., 2007, 40, 712–719 CrossRef CAS PubMed.
- X. Chen and C. Liang, Catal. Sci. Technol., 2019, 9, 4785–4820 RSC.
- W. Gao, X. Zhang, X. Xie and S. Ding, Chem. Commun., 2020, 56, 2012–2015 RSC.
- A. Walczak, H. Stachowiak, G. Kurpik, J. Kaźmierczak, G. Hreczycho and A. R. Stefankiewicz, J. Catal., 2019, 373, 139–146 CrossRef CAS.
- V. Srinivas, Y. Nakajima, K. Sato and S. Shimada, Org. Lett., 2018, 20, 12–15 CrossRef CAS PubMed.
- B. L. L. Reánt, S. T. Liddle and D. P. Mills, Chem. Sci., 2020, 11, 10871–10886 RSC.
- F. Pan, J. Zhang, H.-L. Chen, Y.-H. Su, C.-L. Kuo, Y.-H. Su, S.-H. Chen, K.-J. Lin, P.-H. Hsieh and W.-S. Hwang, Materials, 2016, 9, 417 CrossRef PubMed.
- I. Castillo and T. D. Tilley, Organometallics, 2001, 20, 5598–5605 CrossRef CAS.
- A. D. Sadow and T. D. Tilley, J. Am. Chem. Soc., 2005, 127, 643–656 CrossRef CAS PubMed.
- J. T. White, A. T. Nelson, J. T. Dunwoody, D. D. Byler, D. J. Safarik and K. J. McClellan, J. Nucl. Mater., 2015, 464, 275–280 CrossRef CAS.
- T. L. Wilson, E. E. Moore, D. Adorno Lopes, V. Kocevski, E. Sooby Wood, J. T. White, A. T. Nelson, J. W. McMurray, S. C. Middleburg, P. Xu and T. M. Besmann, Adv. Appl. Ceram., 2018, 117, S76–S81 CrossRef CAS.
- U. E. Humphrey and M. U. Khandaker, Renewable Sustainable Energy Rev., 2018, 97, 259–275 CrossRef CAS.
- S. He and J. Cai, Ann. Nucl. Energy, 2020, 140, 107303 CrossRef CAS.
- D. A. Atwood, The Rare Earth Elements: Fundamentals and Applications, John Wiley & Sons, Ltd, Chichester, UK, 2012 Search PubMed.
- I. Grenthe, J. Drożdżynński, T. Fujino, E. C. Buck, T. E. Albrecht-Schmitt and S. F. Wolf, in The Chemistry of the Actinide and Transactinide Elements, ed. L. R. Morss, N. M. Edelstein and J. Fuger, Springer, Dordrecht, 3rd edn, 2006, pp. 253–698 Search PubMed.
- H. Schumann, S. Nickel, E. Hahn and M. J. Heeg, Organometallics, 1985, 4, 800–801 CrossRef CAS.
- H. Schumann, S. Nickel, J. Loebel and J. Pickardt, Organometallics, 1988, 7, 2004–2009 CrossRef CAS.
- H. Schumann, J. A. Meese-Marktscheffel and F. E. Hahn, J. Organomet. Chem., 1990, 390, 301–308 CrossRef CAS.
- N. S. Radu, T. D. Tilley and A. L. Rheingold, J. Organomet. Chem., 1996, 516, 41–49 CrossRef CAS.
- N. S. Radu, T. D. Tilley and A. L. Rheingold, J. Am. Chem. Soc., 1992, 114, 8293–8295 CrossRef CAS.
- D. H. Woen, D. N. Huh, J. W. Ziller and W. J. Evans, Organometallics, 2018, 37, 3055–3063 CrossRef CAS.
- X. Pan, C. Wu, H. Fang and C. Yan, Inorg. Chem., 2022, 61, 14288–14296 CrossRef CAS PubMed.
- R. Zitz, H. Arp, J. Hlina, M. Walewska, C. Marschner, T. Szilvási, B. Blom and J. Baumgartner, Inorg. Chem., 2015, 54, 3306–3315 CrossRef CAS PubMed.
- R. Zitz, J. Hlina, H. Arp, D. Kinschel, C. Marschner and J. Baumgartner, Inorg. Chem., 2019, 58, 7107–7117 CrossRef CAS PubMed.
- A. Pöcheim, C. Marschner and J. Baumgartner, Inorg. Chem., 2021, 60, 8218–8226 CrossRef PubMed.
- A. Pöcheim, R. Zitz, J. Hönigsberger, C. Marschner and J. Baumgartner, Inorg. Chem., 2022, 61, 17527–17536 CrossRef PubMed.
- I. J. Brackbill, I. Douair, D. J. Lussier, M. A. Boreen, L. Maron and J. Arnold, Chem.–Eur. J., 2020, 26, 2360–2364 CrossRef CAS PubMed.
- B. L. L. Reánt, V. E. J. Berryman, J. A. Seed, A. R. Basford, A. Formanuik, A. J. Wooles, N. Kaltsoyannis, S. T. Liddle and D. P. Mills, Chem. Commun., 2020, 56, 12620–12623 RSC.
- M. Porchia, N. Brianese, U. Casellato, F. Ossola, G. Rossetto, P. Zanella and R. Graziani, J. Chem. Soc. Dalton Trans., 1989, 677–681 RSC.
- N. S. Radu, M. P. Engeler, C. P. Gerlach, T. D. Tilley and A. L. Rheingold, J. Am. Chem. Soc., 1995, 117, 3621–3622 CrossRef CAS.
- W. A. King and T. J. Marks, Inorg. Chim. Acta, 1995, 229, 343–354 CrossRef CAS.
- B. L. L. Réant, V. E. J. Berryman, A. R. Basford, L. E. Nodaraki, A. J. Wooles, F. Tuna, N. Kaltsoyannis, D. P. Mills and S. T. Liddle, J. Am. Chem. Soc., 2021, 143, 9813–9824 CrossRef PubMed.
- A. Formanuik, A.-M. Ariciu, F. Ortu, R. Beekmeyer, A. Kerridge, F. Tuna, E. J. L. McInnes and D. P. Mills, Nat. Chem., 2016, 9, 578–583 CrossRef PubMed.
- L. Hao, A.-M. Lebuis and J. F. Harrod, Chem. Commun., 1998, 35, 1089–1090 RSC.
- H. Arp, M. Zirngast, C. Marschner, J. Baumgartner, K. Rasmussen, P. Zark and T. Müller, Organometallics, 2012, 31, 4309–4319 CrossRef CAS PubMed.
- E. Samuel, Y. Mu, J. F. Harrod, Y. Dromzee and Y. Jeannin, J. Am. Chem. Soc., 1990, 112, 3435–3439 CrossRef CAS.
- L. Hao, A.-M. Lebuis, J. F. Harrod, H.-G. Woo and E. Samuel, Chem. Commun., 1998, 229, 2013–2014 RSC.
- A. Sauermoser, T. Lainer, G. Glotz, F. Czerny, B. Schweda, R. C. Fischer and M. Haas, Inorg. Chem., 2022, 61, 14742–14751 CrossRef CAS PubMed.
- C. T. Aitken, J. F. Harrod and E. Samuel, J. Am. Chem. Soc., 1986, 108, 4059–4066 CrossRef CAS.
- C. Marschner, Eur. J. Inorg. Chem., 1998, 221–226 CrossRef CAS.
- P. Jutzi and R. Sauer, J. Organomet. Chem., 1973, 50, C29–C30 CrossRef CAS.
- Y. A. Ustynyuk, Y. N. Luzikov, V. I. Mstislavsky, A. A. Azizov and I. M. Pribytkova, J. Organomet. Chem., 1975, 96, 335–353 CrossRef CAS.
- N. A. Jones, S. T. Liddle, C. Wilson and P. L. Arnold, Organometallics, 2007, 26, 755–757 CrossRef CAS.
- A. Antiñolo, M. F. Lappert, A. Singh, D. J. W. Winterborn, L. M. Engelhardt, C. L. Raston, A. H. White, A. J. Carty and N. J. Taylor, J. Chem. Soc. Dalton Trans., 1987, 1463–1472 RSC.
- P. B. Hitchcock, M. F. Lappert, G. A. Lawless, H. Olivier and E. J. Ryan, J. Chem. Soc. Chem. Commun., 1992, 474–476 RSC.
- M. F. Lappert, W. P. Leung, R. A. Bartlett and P. P. Power, Polyhedron, 1989, 8, 1883 CrossRef CAS.
- F. Ortu, J. M. Fowler, M. Burton, A. Formanuik and D. P. Mills, New J. Chem., 2015, 39, 7633–7639 RSC.
- M. J. Harvey, T. P. Hanusa and M. Pink, J. Chem. Soc., Dalton Trans., 2001, 1128–1130 RSC.
- K. Izod, S. T. Liddle and W. Clegg, Inorg. Chem., 2004, 43, 214–218 CrossRef CAS PubMed.
- L. R. Avens, S. G. Bott, D. L. Clark, A. P. Sattelberger, J. G. Watkin and B. D. Zwick, Inorg. Chem., 1994, 33, 2248–2256 CrossRef CAS.
- A. J. Gaunt, A. E. Enriquez, S. D. Reilly, B. L. Scott and M. P. Neu, Inorg. Chem., 2008, 47, 26–28 CrossRef CAS PubMed.
- P. C. Blake, M. F. Lappert, R. G. Taylor, J. L. Atwood, W. E. Hunter and H. Zhang, J. Chem. Soc., Dalton Trans., 1995, 3335–3341 RSC.
- S. T. Liddle, Angew. Chem., Int. Ed., 2015, 54, 8604–8641 CrossRef CAS PubMed.
- P. C. Blake, M. F. Lappert, J. L. Atwood and H. Zhang, J. Chem. Soc., Chem. Commun., 1986, 1148–1149 RSC.
- P. Pyykkö and M. Atsumi, Chem.–Eur. J., 2009, 15, 186–197 CrossRef PubMed.
- A. Bande and J. Michl, Chem.–Eur. J., 2009, 15, 8504–8517 CrossRef CAS PubMed.
- C. Marschner, in Functional Molecular Silicon Compounds I, Structure and Bonding, ed. D. Scheschkewitz, Springer, Cham, 2014, vol. 155, pp. 163–228 Search PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Adv., 1976, 32, 751–767 CrossRef.
- J. Britten, Y. Mu, J. F. Harrod, J. Polowin, M. C. Baird and E. Samuel, Organometallics, 1993, 12, 2672–2676 CrossRef CAS.
- M. Zirngast, U. Flörke, J. Baumgartner and C. Marschner, Chem. Commun., 2009, 5538–5540 RSC.
- X. Sun, L. Münzfeld, D. Jin, A. Hauser and P. W. Roesky, Chem. Commun., 2022, 58, 7976–7979 RSC.
- S. Kyushin, H. Sakurai and H. Matsumoto, Chem. Lett., 1998, 107–108 CrossRef CAS.
- C. J. Windorff and W. J. Evans, Organometallics, 2014, 33, 3786–3791 CrossRef CAS.
- S. K. Sur, J. Magn. Reson., 1989, 82, 169–173 CAS.
- A. Antiñolo, M. F. Lappert, G. A. Lawless and H. Olivier, Polyhedron, 1989, 8, 1882 CrossRef.
- J. Mayans, L. Tesi, M. Briganti, M.-E. Boulon, M. Font-Bardia, A. Escuer and L. Sorace, Inorg. Chem., 2021, 60, 8692–8703 CrossRef CAS PubMed.
- J.-L. Liu, Y.-C. Chen and M.-L. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453 RSC.
- F. Moro, D. P. Mills, S. T. Liddle and J. van Slageren, Angew. Chem., Int. Ed., 2013, 52, 3430–3433 CrossRef CAS PubMed.
- S. T. Liddle and J. van Slageren, Chem. Soc. Rev., 2015, 44, 6655–6669 RSC.
- J. D. Rinehart and J. R. Long, J. Am. Chem. Soc., 2009, 131, 12558–12559 CrossRef CAS PubMed.
- J. D. Rinehart, K. R. Meihaus and J. R. Long, J. Am. Chem. Soc., 2010, 132, 7572–7573 CrossRef CAS PubMed.
- K. R. Meihaus, J. D. Rinehart and J. R. Long, Inorg. Chem., 2011, 50, 8484–8489 CrossRef CAS PubMed.
- M. A. Antunes, L. C. J. Pereira, I. C. Santos, M. Mazzanti, J. Marçalo and M. Almeida, Inorg. Chem., 2011, 50, 9915–9917 CrossRef CAS PubMed.
- D. P. Mills, F. Moro, J. McMaster, J. van Slageren, W. Lewis, A. J. Blake and S. T. Liddle, Nat. Chem., 2011, 3, 454–460 CrossRef CAS PubMed.
- J. D. Rinehart and J. R. Long, Dalton Trans., 2012, 41, 13572–13574 RSC.
- M. J. Giansiracusa, G. K. Gransbury, N. F. Chilton and D. P. Mills, in Encyclopedia of Inorganic and Bioinorganic Chemistry, ed. R. A. Scott, John Wiley, Chichester, 2021, DOI:10.1002/9781119951438.eibc2784.
- N. F. Chilton, Annu. Rev. Mater. Res., 2022, 52, 79–101 CrossRef.
- J. Liu, D. Reta, J. A. Cleghorn, Y. X. Yeoh, F. Ortu, C. A. P. Goodwin, N. F. Chilton and D. P. Mills, Chem.–Eur. J., 2019, 25, 7749–7758 CrossRef CAS PubMed.
- V. A. Volkovich, A. B. Ivanov, S. M. Yakimov, D. V. Tsarevskii, O. A. Golovanova, V. V. Sukhikh and T. R. Griffiths, AIP Conf. Proc., 2016, 1767, 020023 CrossRef.
- R. J. Lang, Can. J. Res. A, 1936, 14, 127–130 CrossRef.
- P. N. Hazin, C. Lakshminarayan, L. S. Brinen, J. L. Knee, J. W. Bruno, W. E. Streib and K. Folting, Inorg. Chem., 1988, 27, 1393–1400 CrossRef CAS.
- W. K. Kot, PhD thesis, University of California, Berkeley, 1991.
- G. Blasse and A. Bril, J. Chem. Phys., 2004, 47, 5139–5145 CrossRef.
- M. Suta, N. Harmgarth, M. Kühling, P. Liebing, F. T. Edelmann and C. Wickleder, Chem.–Asian J., 2018, 13, 1038–1044 CrossRef CAS PubMed.
- D. E. Morris, R. E. Da Re, K. C. Jantunen, I. Castro-Rodriguez and J. L. Kiplinger, Organometallics, 2004, 23, 5142–5153 CrossRef CAS.
- C. R. Graves, P. Yang, S. A. Kozimor, A. E. Vaughn, D. L. Clark, S. D. Conradson, E. J. Schelter, B. L. Scott, J. D. Thompson, P. J. Hay, D. E. Morris and J. L. Kiplinger, J. Am. Chem. Soc., 2008, 130, 5272–5285 CrossRef CAS PubMed.
- A. J. Wooles, D. P. Mills, F. Tuna, E. J. L. McInnes, G. T. W. Law, A. J. Fuller, F. Kremer, M. Ridgway, W. Lewis, L. Gagliardi, B. Vlaisavljevich and S. T. Liddle, Nat. Commun., 2018, 9, 2097 CrossRef PubMed.
- W. W. Lukens, M. R. Smith and R. A. Andersen, J. Am. Chem. Soc., 1996, 118, 1719–1728 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- M. Křižan, J. Honzíček, J. Vinklárek, Z. Růžičková and M. Erben, New J. Chem., 2015, 39, 576–588 RSC.
- C. E. Housecroft and A. G. Sharpe, Inorganic Chemistry, 5th edn, Pearson, Harlow, 2018 Search PubMed.
- F. E. Mabbs and D. Collison, Electron Paramagnetic Resonance of d Transition Metal Compounds, Elsevier Science, Amsterdam, 1992 Search PubMed.
- I. F. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. L. Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P. O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964 CrossRef PubMed.
- F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey, I. F. Galván, N. Ferré, L. Freitag, M. Garavelli, X. Gong, S. Knecht, E. D. Larsson, R. Lindh, M. Lundberg, P. Å. Malmqvist, A. Nenov, J. Norell, M. Odelius, M. Olivucci, T. B. Pedersen, L. Pedraza-González, Q. M. Phung, K. Pierloot, M. Reiher, I. Schapiro, J. Segarra-Martí, F. Segatta, L. Seijo, S. Sen, D. C. Sergentu, C. J. Stein, L. Ungur, M. Vacher, A. Valentini and V. Veryazov, J. Chem. Phys., 2020, 152, 214117 CrossRef CAS PubMed.
- J. L. Petersen and L. F. Dahl, J. Am. Chem. Soc., 1975, 97, 6416–6422 CrossRef CAS.
- J. L. Petersen and L. F. Dahl, J. Am. Chem. Soc., 1975, 97, 6422–6433 CrossRef CAS.
- J. W. Lauher and R. Hoffmann, J. Am. Chem. Soc., 1976, 98, 1729–1742 CrossRef CAS.
- J. Sievers, Z. Phys. B: Condens. Matter, 1982, 45, 289–296 CrossRef CAS.
- J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085 RSC.
- J. J. Le Roy, S. I. Gorelsky, I. Korobkov and M. Murugesu, Organometallics, 2015, 34, 1415–1418 CrossRef CAS.
Footnotes |
| † Dedicated to Professor Peter Junk on the occasion of his 60th birthday. |
| ‡ Electronic supplementary information (ESI) available. CCDC 2195632–2195640. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2sc04526e |
| § Contributed equally as co-first authors. |
| This journal is © The Royal Society of Chemistry 2023 |