Exploring the intra-4f and the bright white light upconversion emissions of Gd₂O₃:Yb³⁺,Er³⁺-based materials for thermometry

Abstract

Upconversion broadband white light emission driven by low-power near-infrared (NIR) lasers has been reported for many materials, but the mechanisms and effects related to this phenomenon remain unclear. Herein, we investigate the origin of laser-induced continuous white light emission in synthesized nanoparticles (Gd_0.89Yb_0.10Er_0.01)₂O₃ and a mechanical mixture of commercial oxides with the same composition 89% Gd₂O₃, 10% Yb₂O₃, and 1% Er₂O₃. We report their photophysical features with respect to sample compactness, laser irradiation (wavelength, power density, excitation cycles), pressure, temperature, and temporal dynamics. Despite the sensitizer (Yb³⁺) and activator (Er³⁺) being in different particles for the mechanical mixture, efficient discrete and continuous upconversion emissions were observed. Furthermore, the synthesized nanoparticles were developed as primary luminescent thermometers (upon excitation at NIR) in the 299–363 K range, using the Er³⁺ upconversion ²H_11/2 → ⁴I_15/2/⁴S_3/2 → ⁴I_15/2 intensity ratio. They were also operating as secondary ones in the 1949–3086 K, based on the blackbody distribution of the observed white light emission. Our findings provide important insights into the mechanisms and effects related to the transition from discrete to continuous upconversion emissions with potential applications in remote temperature sensing.

---

Introduction

Over the past decades, an unusual type of anti-Stokes (or upconversion, UC) broadband white light emission under near-infrared (NIR) laser excitation has been reported for organometallic complexes,¹ organic–inorganic hybrid nanostructures,² carbon nanotubes,³ graphene,⁴ and oxides, with^5,6 or without^7,8 activator ions (trivalent lanthanides, Ln³⁺, and transition metals). A common and distinguishing feature of this unusual type of UC is the continuous emission from the visible to the IR spectral regions, in contrast to the usual discrete UC emissions observed particularly in Ln³⁺-based materials.⁹ Although the continuous white light emission was reported in vacuum in many of these examples, there are several works showing results at ambient pressure.^8,10–18 This emission has attracted much attention due to intriguing and exciting applications in luminescence thermometry,¹⁹ pressure detection,^19,20 high-performance and low-energy solid-state lighting,^1,21 increased efficiency of solar panels,²² and optoelectronic devices.^4,7 It depends on several factors related either to the materials (e.g., chemical composition, dopant/co-dopant ion concentration, particle size, phonon energy, absorption coefficient, thermal conductivity, bandgap) or to the excitation process (e.g., energy, power density, on/off cycles, exposure time, pressure).^4,18,23–26 However, as far as we know, there are no systematic studies describing the impact of these effects on the anti-Stokes continuous white light emission, as well as on the transition from discrete to continuous UC emissions. Moreover, the origin of this continuous emission is still under debate and different processes have been invoked to describe it such as photon avalanche,²⁷ blackbody radiation/incandescence,^12,28 thermal avalanche,¹⁰ structural defects,^11,29 or charge transfer.^30,31

Here, we investigated the transition of discrete (Er³⁺ transitions in the red and green spectral regions) to continuous white light UC emissions to gain insights into their nature in a Yb³⁺/Er³⁺ co-doped nanopowder, (Gd_0.89Yb_0.10Er_0.01)₂O₃ (1), and a simple mechanical mixture of Gd₂O₃, Yb₂O₃, and Er₂O₃ oxides (2). For that, the impact on both white light emissions of the compactness of the materials, excitation power density, wavelength and exposure time (808 or 980 nm), pressure, temperature, on–off cycles of irradiation, humidity, as well as their risetime and halftime decays, was analysed in detail. Gd₂O₃ was selected as a host material because it is the only example reported thus far where both discrete and continuous UC white light emission under NIR laser excitation have been discussed.^12,32 Moreover, oxide materials offer advantages such as low thermal conductivity and physical and chemical resistance to high temperatures (>1500 K) being also readily available for use as a “mixed powder sample”. Sample 2 mimics the composition of 1 but with the Yb³⁺ and Er³⁺ ions separated in individual particles permitting, thus, understanding the spatial dependence of both UC emissions, particularly the range-dependent nonradiative energy transfer processes. We reported a colour modulation of the discrete UC emission with an increase in the excitation source intensity and under reduced pressure. To comprehend and quantify this colour modulation, we developed a luminescence primary thermometer based on the ²H_11/2 → ⁴I_15/2 and ⁴S_3/2 → ⁴I_15/2Er³⁺ transitions^33,34 for 1. For the first time, we established a relationship between the local temperature and the excitation power density. Additionally, we developed a thermometer based on the blackbody radiation distribution of the observed white light emission for high-temperature sensing. We anticipate that the results reported here will provide a deeper understanding of the transition from discrete to continuous white light UC emissions, as well as the nature and underlying nanoscale features of the latter.

Experimental

Materials

Er(NO₃)₃·5H₂O (99.9%), Yb(NO₃)₃·5H₂O (99.9%), Gd(NO₃)₃ 6H₂O (99.9%) were purchased from Sigma-Aldrich and NH₂CH₂COOH (glycine) (>99%) from Alfa Aesar and used as received. A modified co-precipitation procedure reported by Bilir et al.³² was used to prepare the (Gd_0.89Yb_0.10Er_0.01)₂O₃ nanoparticles, denoted as 1. The starting reagents were dissolved in 1 mL of deionized water under vigorous stirring for 15 min. The solution was heated at 500 °C for 1 hour at 10 °C·min⁻¹. After cooling to room temperature, the precursor was calcined at 1000 °C for 24 hours with heating and cooling rates at 1.6 °C·min⁻¹. The particles were obtained as a white powder and pellets were prepared with 150 mg compressed at 8 × 10⁶ kg for 1 min. A simple mechanical mixture of commercial oxides purchased from Sigma-Aldrich (>99.9%) Gd₂O₃ (89%), Yb₂O₃ (10%), and Er₂O₃ (1%), denoted as 2, was also prepared.

Methods

Structural and morphological characterization. X-ray diffraction (XRD) patterns were collected on a Panalytical (Almelo, Netherlands, model X'Pert PRO3). The X-ray diffractometer operates at 45 kV and 40 mA, with CuKα radiation at 1.5406 Å, in the 2 θ range 5°–89° with a 0.01° step size and 40 s acquisition time per step, in the reflection scanning mode. The samples were placed inside a thermal chamber (Anton Paar HTK 16N) with a Platinum heater. The data were treated considering the instrumental broadening factor measured with a LaB₆ (NIST 660a) standard. The reference data were taken from the International Centre for Diffraction Data (ICDD) database. The structural features like lattice parameters have been investigated using Rietveld refinement with High Score Plus software. The crystallite size was estimated by applying the Scherrer equation to the main peak of the diffractograms. The observed full width at half maximum (FWHM) of the peak was corrected from the instrumental and strain broadening factors using the NIST 660a standard. A shape factor characteristic of spherical particles was used (0.94), although the observed agglomerated nanostructures have irregular shapes, as shown by scanning transmission electron microscopy (STEM) images acquired on a Jeol JEM-2200FS (200 kV). Energy-dispersive X-ray spectroscopy (EDS, Oxford) was performed in a Hitachi H-9000 (300 kV) microscope.

Photoluminescence. The upconversion emission spectra were recorded under vacuum and in air using a Fluorolog-3 Horiba Scientific (ModelFL3-2T) spectrofluorometer, with a TRIAX 320 single-emission monochromator (fitted with 1200 grooves·mm⁻¹ grating, blazed at 500 nm) coupled to an R928 Hamamatsu photomultiplier, using the lateral face acquisition mode. The samples were placed inside a helium-closed cycle cryostat coupled to a vacuum system formed by a rotary pump (2 × 10⁻⁵ bar) and a turbo molecular pump (7 × 10⁻⁵ bar). The spectra were corrected for the detection and optical spectral response of the spectrofluorometer using a photodiode as a reference. The samples were placed on a smaller Cu plate (1.0 × 0.5 cm²) attached to the holder by a thermal conductive paste (WLP 500, Fischer Elektronik) and coupled to a temperature controller (IES-RD31). The temperature was measured with a Barnant thermocouple 100 (model 600–2820) with a temperature accuracy of 0.1 K, accordingly to the manufacturer. The excitation sources are NIR continuous-wave laser diodes (CrystaLaser LC DL980-3W0-TO and CrystaLaser LC DL808-3WO-T), emitting a nearly Gaussian beam centred at 980 ± 5 nm and 808 ± 5 nm (TEM00 mode, accordingly to the manufacturer), respectively. The laser power was quantified using a power meter (Coherent, Field MaxII- TOP) coupled to a high-sensitivity silicon photodiode optical sensor (Coherent OP-2 VIS). The laser power density, P_D, was computed by dividing the excitation power by the illuminated area. The laser beams were focused using a C230TM-B aspheric lens (Thorlabs). For 808 nm excitation, neutral density filters (NE02B-B, NE05B-B, and NE10B-B, Thorlabs) were placed between the laser and the sample to change the power density from 73.8 to 310 W·cm⁻². To get reliable data, each time before starting the measurements the samples were irradiated by the laser for one minute to stabilize temperature at a given pressure value. Temporal analysis was performed using an Ocean Optics spectrometer (200–1100 nm), with an optical resolution of 2.39 pixels (FWHM), a maximum scan rate of 4500 scans·s⁻¹, and integration times between 10 μs and 10 s. Laser irradiation cycles were conducted to assess the stability, uniformity, repeatability, and hysteresis of white light emission as a function of P_D. Cycle 1 involved measuring the UC emission spectra at a single spot of the sample while increasing P_D, whereas cycle 2 involved measuring the UC emission spectra decreasing P_D at the same spot. Cycle 3 involved measurements at multiple points on the sample. The effect of humidity on the P_D dependence of the white light emission was studied performing two irradiation cycles in 1 after exposing the sample to a saturated water atmosphere for three days.

Fitting procedure. A spectral deconvolution procedure was applied to the emission spectra to calculate Δ and ΔE parameters.³⁴ The procedure starts with a baseline subtraction to remove the spectrometer electric noise, followed by the conversion of the signal of each emission spectrum from wavelength to energy units by applying the Jacobian transformation.^35,36 For ΔE determination, the 17 500–19 500 cm⁻¹ spectral region was fitted using a multiparametric Gaussian function by peak analyser routine of the OriginLab© software. Good fits to the experimental data (R² > 0.99) were obtained with six and four Gaussian functions describing the ²H_11/2 → ⁴I_15/2 and ⁴S_3/2 → ⁴I_15/2 and transitions, respectively. The intensities of the transitions were estimated by the sum of the fitted areas of the respective Gaussian functions. For the calculus of Δ, the ²H_11/2 → ⁴I_15/2 and ⁴S_3/2 → ⁴I_15/2 transitions were integrated between 510–542 nm (I_H) and 543–573 nm (I_S), respectively.

Results and discussion

Synthesis and morphological characterization

The XRD patterns of 1 and 2 shown in Fig. 1 reveal the presence of the Gd₂O₃ and Yb₂O₃ cubic phases.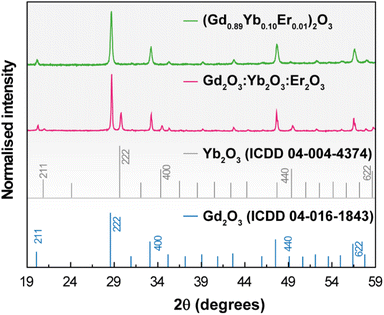

Fig. 1 X-ray diffraction patterns of 1 (green line) and 2 (red line) (powders). The reflections of cubic Gd₂O₃ and Yb₂O₃ are also depicted.

No diffraction peaks associated with the Er₂O₃ phase could be discerned in the pattern of 2 because the concentration lies below the experimental detection limit of the technique. Under different conditions of pressure and temperature (ambient conditions, 1273 K, and 10⁻⁵ bar), the patterns remain nearly identical indicating that no phase transitions occur in the samples in the tested temperature and pressure cycles (Fig. S1† for the illustrative example of 1). The average crystallite size was estimated as 63 ± 3 nm and 157 ± 3 nm for 1 and 2, respectively, applying the Scherrer equation to the main diffraction peak. STEM images show that both samples exhibit similar agglomerated nanostructures with irregular shapes and EDS reveals the majority presence of Gd atoms and concentration values of Er and Yb one order of magnitude smaller (Fig. S2†), in accord with the proposed stoichiometry of 1 and the relative proportion used in 2. The elemental distributions of the two samples show, despite aggregation, microstructural uniformity, supporting chemical homogeneity (Fig. S2(e)† for 2). This is also supported by identical emission spectra acquired at different spots and under different cycles of laser irradiation in both samples (see below).

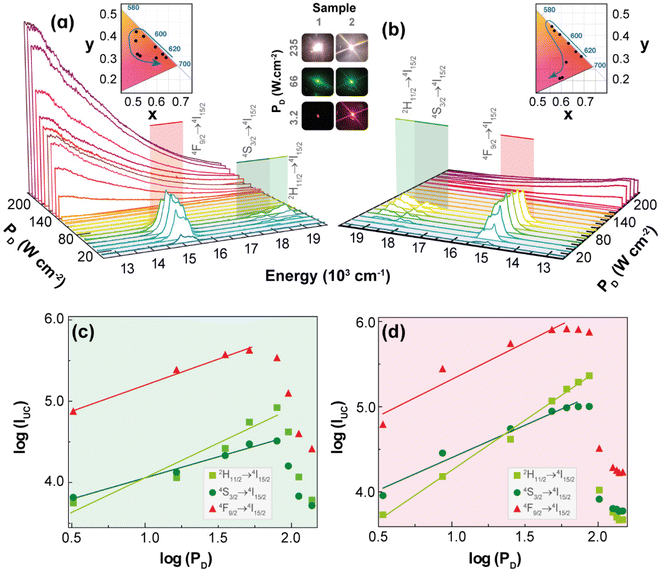
Intra-4f upconversion emission and primary thermometry

Fig. 2 shows the UC emission spectra of 1 and 2 (980 nm excitation) as a function of P_D. Given that the absorption cross-section of Yb³⁺ (ca. 10⁻²⁰ cm²) is approximately one order of magnitude larger than that of Er³⁺ (ca. 10⁻²¹ cm²) under NIR excitation,^37,38 the energy transfer upconversion (ETU) sensitization of Er³⁺ ions by Yb³⁺ is the likely mechanism for the discrete UC emissions. Accordingly, the well-known relationship between the integrated UC emission, I_UC, and P_D: I_UC ∝ Pⁿ_D, where the exponent n can be interpreted as the number of photons involved in the upconversion process,^39,40 should be observed. However, the values of n obtained as the slope of the linear fit of the plot of the logarithm of the integrated intensities of the ²H_11/2 → ⁴I_15/2 (I_H, 510–542 nm), ⁴S_3/2 → ⁴I_15/2 (I_S, 543–573 nm), and ⁴F_9/2 → ⁴I_15/2 (I_F, 626–714 nm) Er³⁺ transitions versus the logarithm of P_D are smaller than 2.0 and most are near to 1.0 (Table S1†). This unusual behaviour is most likely due to the heating of the excitation region as indicated by the increase in the ratio I_H/I_S (the so-called thermometric parameter Δ) with P_D (see discussion in the next section). Because the transition rates, namely the nonradiative ones and the back-ET rates, are temperature dependent, the increase of P_D affects unevenly these rates and the populations of thermally coupled levels, so the interpretation of the exponent n as being the number of photons involved in the UC process is no longer valid. This reasoning is more likely than invoking the competition of different processes (e.g., cross-relaxation between excited states, avalanche process, energy transfer between three ions, and energy transfer to other impurity ions) or possible oscillations of the excitation source.³⁹

Fig. 2 Emission spectra as a function of the excitation power density, P_D, for (a) 1 and (b) 2, both samples in powders, normalized to the ⁴F_9/2 → ⁴I_15/2 transition. A short pass filter (cut-off at 850 nm) was used. The insets show photographs of the samples at selected P_D values together with the CIE-1935 chromaticity diagrams with the colour coordinates for increasing P_D values between 3 and 235 W·cm⁻². The corresponding double-log plots of the integrated intensities, I_UC, of selected Er³⁺ transitions as a function of P_D are presented in (c) and (d), respectively. The lines are the best fits to the data using straight lines (r² > 0.99).

The differences in the slopes obtained for powders of 1 and 2 are probably due to the dynamics of ETU pathways involving ions within the same particle, for 1, contrasted to ions in different particles, for 2. Because the ETU pathways become less efficient as the distances between ions increase, it is expected that ETU in 1 would be more efficient than in 2, thus causing a lesser dependence of the integrated intensity on P_D. Notice that for 1 the slopes n, of log I_UCvs. log P_D plots, in the pellets are larger than in powder (Table S1†), which suggests that the higher thermal conductivities of pellets hinder the temperature increase, so the transition rates become almost constant with P_D and the slopes n tend to be the number of photons involved in the UC process. On the other hand, when the 1 pellet is placed at low-pressure atmospheres, the thermal conductivity decreases, and the temperature drastically increases with P_D, so the slopes n are no longer related to the number of photons, and they become smaller than those at ambient pressure (Table S1†).

The temperature increase within the excitation region with P_D,³² can also explain the decrease of the integrated UC emission intensities above a given value of P_D (see Fig. 2(c and d)), the so-called absorption saturation regime. The threshold of P_D for which the saturation regime of the integrated intensities I_H, I_S, and I_F is observed in 2 (140, 112, and 65.0 W·cm⁻², respectively) is higher compared with those of 1 (79.1, 79.1, and 51.4 W·cm⁻², respectively). Indeed, this is consistent with the ETU pathways in 2 (sensitizer-activator ions in different particles) being less efficient than in 1 (ions within the same particle), so the former would require a higher P_D to reach the saturation regime. The energy transfer rates between Yb³⁺–Er³⁺ pairs located in the same particle can be calculated by quantitative models;^41,42 however, for ions located in different particles are still a challenging problem, so the UC emissions results reported here for 2 (mechanical mixture) are quite relevant for developing quantitative models.

The insets in Fig. 2(a and b) display the 1931 CIE chromaticity diagram of the UC emission for increasing P_D, where the x,y coordinates were calculated based on the emission spectra. The modulation of the UC emission colour by the excitation intensity is an intriguing feature because of its simplicity compared to other strategies of modulation (e.g., co-doping).^43–46 Previous example of colour modulation by P_D has been achieved in the UC emissions of Ho³⁺, Tm³⁺, and Yb³⁺ tri-doped Gd₂(MoO₄)₃ phosphors,⁴⁷ which was ascribed to the different dependence of the blue, green, and red UC emissions upon P_D. However, explanations and details of these distinct dependencies were not provided.

UC emission colour modulation by P_D was also observed in upconverting Y₂O₃:Yb³⁺/Er³⁺ microrods coated by silver nanoparticles (Ag-NPs).⁴⁸ In this case, the Ag-NPs absorb energy from the excitation beam causing a local increase in temperature that leads to changes in UC emission from red to green upon increasing the excitation intensity. Employing luminescence thermometry, it was shown that local temperature varied from 418 to 1458 K upon increasing P_D, which was responsible for the colour modulation.⁴⁸ Based on this example, and the increase in the thermometric parameter Δ with P_D, the colour modulation of the UC emissions observed for 1 and 2 was ascribed to the increase of the temperature within the excitation region, which affected mainly the nonradiative transition rates within each Ln³⁺ ion and between two ions.

A possible explanation could be the increase of the phonon-assisted ET transfer rate Yb³⁺ → Er³⁺ with the increase in temperature, which rises the population of the green emitting levels (²H_11/2 and ⁴S_3/2), thus modulating the colour change from red to green. However, a detailed and definite explanation for this colour change requires a model based on the rate equations that employs temperature dependent transition rates, which is still unavailable. To obtain information regarding the dependence of the local temperature increase with P_D, it is relevant to determine reliable temperature values that can be achieved with Δ involving the thermally-coupled ²H_11/2 and ⁴S_3/2 levels, whose populations are described by the Boltzmann distribution.^49,50

The thermometric performance of 1 as a primary thermometer is then based on these two thermally coupled levels with temperature, T, being determined as:³³

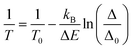where ΔE is the energy gap between the barycenters of the ²H_11/2 and ⁴S_3/2 levels, Δ₀ is the value of the thermometric parameter at the reference temperature T₀, and k_B is the Boltzmann constant. The quantities I_H, I_S, and ΔE are determined by the spectral deconvolution of the ²H_11/2,⁴S_3/2 → ⁴I_15/2 transitions (Fig. S3(a)† and Experimental section for details).

The thermometric parameter increases with the laser power density (Fig. S3(b)†), indicating that the laser-induced local temperature increase causes a rise in the population of the thermally governed ²H_11/2 level, at the expense of the ⁴S_3/2 lower energy level, according to the Boltzmann distribution. These levels are thermally coupled with an energy difference of 795 ± 25 cm⁻¹, which is in very good agreement with the values reported in the literature for Gd₂O₃:Yb³⁺,Er³⁺ samples (700 cm⁻¹ ≤ ΔE ≤ 856 cm⁻¹).^{12,43,51–53} The value of Δ₀ is determined by extrapolating the value of Δ to the low-power limit at T₀.⁵² This consists of recording emission spectra at the temperature T₀ upon different excitation laser power densities. In the limit of null power density (usually extrapolated using a linear function), the heating due to the irradiation is zero and so the temperature on the luminescent material is T₀ (Fig. S3(b)†). Fig. 3(a) presents the temperature dependence in the 297–364 K range of the emission spectra of 1. The temperature dependence of the integrated areas of the I_H and I_S transitions and the corresponding thermometric parameter, Δ, are presented in Fig. 3(b and c). The experimental values of the reference temperatures were obtained directly through a thermocouple in contact with the sample. Replacing the values of T₀, ΔE, Δ, and Δ₀ in eqn (1), the predicted temperature, the solid line in c, is in excellent agreement with the reference, indicating that 1 can work as a luminescent primary thermometer (Fig. 3(d)).

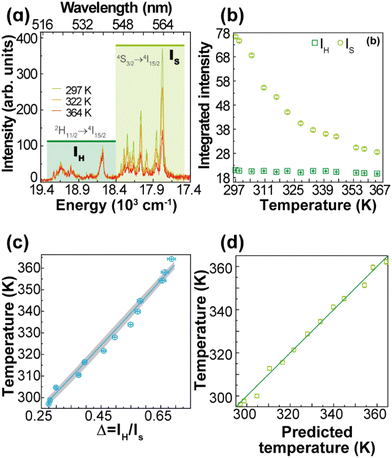Fig. 3 (a) Upconversion emission spectra of 1 (pellet) under 980 nm excitation at selected temperatures (P_D = 16.4 W·cm⁻²). Temperature dependence of (b) I_H and I_S integrated emission intensities and (c) Δ = I_H/I_S. The temperature uncertainty (shadowed in grey) is given by eqn (S6),† whereas the line represents the predicted temperature using eqn (1). (d) The reference temperature (y) versus the predicted temperature (eqn (1), x). The line is a guide for the eyes corresponding to y = x.

The performance of the thermometer is estimated by the relative thermal sensitivity, S_r, (eqn (S4) and (S5)†) and temperature uncertainty, δT, (eqn (S6)†), Fig. 4. These parameters (figures-of-merit) allow the comparison between thermometers of different natures and applied in different chemical environments. The calculated S_r and δT are 1.3–0.9% K⁻¹ and 0.03–0.08 K, respectively, for the 299–363 K range. As it can be verified in Fig. S4 and Table S2,† the maximum value of S_r reported in this work is higher than most of the other reports on Gd₂O₃:Yb³⁺,Er³⁺ discussed in the literature, especially in the physiological range. The calculated temperature uncertainty for 1 (Fig. 4(b)) corresponds to the lowest values reported up to now for Gd₂O₃:Yb³⁺,Er³⁺ samples (Table S2†). The temperatures measured by the luminescent thermometer present a linear dependence with the excitation power density, T = αP_D + β, with α = 4.1 ± 0.2 K (W·cm⁻²)⁻¹ and β = 299 ± 10 K (Fig. 4(c)). This is consistent, for instance, with the linear behaviour of the temperature with P_D inferred from the increase of the thermometric parameter for NaYF₄:20%Yb,2%Er nanocrystals (NCs).⁵⁴ For the unmodified NaYF₄:20%Yb,2%Er NCs, and modified NCs with thioglycollic acid, the slopes are 0.116 and 0.175 K (W·cm⁻²)⁻¹, respectively,⁵⁴ which are much smaller than that found for 1, most likely due to the differences in the thermal conductivities and absorption coefficients.

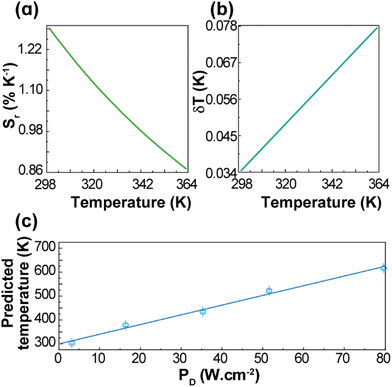Fig. 4 Temperature dependence of (a) S_r and (b) δT of 1 (pellet). (c) Dependence of the predicted temperatures on P_D for 1 (pellet). The line is the best linear fit to the data (r² > 0.985).

Bright white light upconversion emission

Although several works reported the white light emission, characterized as discrete spectra, by Gd₂O₃:Yb³⁺/Er³⁺,^55–57 only two works^12,32 discussed the white light UC emission as a continuous broadband under NIR excitation. Based on the results of the UC emission colour modulation and the temperature increase measured by the luminescent thermometer, it is proposed that the absorbed excitation radiation is converted into heat that causes a significant temperature increase within the excitation region that leads to thermal or blackbody radiation emission.

The excitation intensity has to be high enough to balance the heat dissipation, so the internal energy can rise, causing the temperature to increase. When the heat cannot be dissipated fast enough, especially at the interface of the sample with the atmosphere, the temperature within the excitation region continues to rise until it reaches the Draper point (ca. 800 K), where the thermal emission of typical solids becomes visible (reddish) to the human eye. As P_D increases, so does the local temperature, which causes a significant intensification of the UC emission as well as an increase in the fraction of emitted light in the visible region. This process culminates into a highly bright white light emission, with a continuous spectrum, under excitation at the NIR region (photographs in the insets of Fig. 2(a)). This description relies on several properties of the materials such as the absorption coefficient at the excitation wavelength interval, energy transfer, and thermal conductivity. Thus, because of the higher concentration of Yb³⁺(10%) and their larger absorption cross section at 980 nm, compared to the lower concentration of Er³⁺ (1%) and smaller cross section at 808 nm, the white light UC emission under 980 nm should be much more pronounced according to the description just proposed. Indeed, the observed emissions at these excitation wavelengths corroborate this assertion. For comparison, to obtain similar white light UC emission, P_D needs to be larger than 310 W·cm⁻² at 808 nm compared to 240 W·cm⁻² at 980 nm, Fig. S5.†

The dependence of the integrated intensity of the white light emission, I_WL, with P_D (980 nm) is also investigated via log (I_WL) versus log (P_D). The slopes of these plots are usually larger than 4, so they should also have a different interpretation from that of discrete UC emissions. For 1 and 2, these slopes are within 4 to 7 (Fig. 5(a) and Table S3†), which agree with the behaviour of rare-earth oxides.^5,7,12,24,27

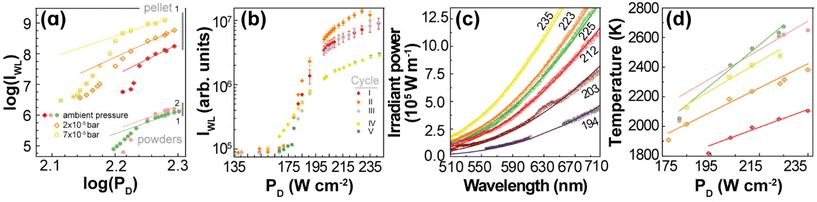Fig. 5 (a) Log–log plot of the P_D dependence of I_WL for 1 and 2 in powder and at ambient pressure (green and pink dots, respectively), and for 1 in pellet at ambient pressure (red), 2 × 10^–5 bar (orange), and 7 × 10^–5 bar (yellow). The lines are the best linear fits to the saturation regime data (Table S3†). (b) P_D dependence of I_WL for 1 (pellet) recorded in different cycles of irradiation before (I, II, and III) and after (IV and V) exposing the sample to a water saturated atmosphere (see the Experimental section for details). (c) Emission spectra of 1 (pellet at ambient pressure) acquired between 194 and 235 W· cm⁻². The lines represent the fits to the blackbody radiation distribution with a proportionality constant of 4.2 × 10⁻²¹ (Table S4†). (d) P_D dependence of the fitted temperatures for 1 and 2 in powder and pellet at different pressure values (Tables S5–S8†). The colour code is the one used in (a). The lines are the best linear fits to the data (Table S9†).

The continuous white light emission was analysed for repeated cycles of laser irradiation with both 1 (Fig. 5(b)) and 2 (Fig. S6†) showing remarkable stability under repeated excitation cycles. Notice that the excitation cycles were performed at different spots on the sample and their similarities indicate the homogeneity of the materials for white light UC emission. The effect of the humidity was also analysed exposing the samples to a water-saturated atmosphere (details in the Experimental section). The humidity significantly decreased the intensity of the white light UC emissions (indeed, 2 showed no white light emission), which is consistent with the increase of the thermal conductivity of the samples upon exposure to air saturated with water as well as the presence of high energy O–H oscillators that affect the nonradiative transitions. The effects of the thermal conductivity can be ascertained by the compactness of the sample,²⁸ which can explain the lower P_D threshold (to observe white light emission) for 1 powder (140 W·cm⁻², Fig. 2(a)) compared to 1 pellet (200 W·cm⁻², Fig. S7†).

As the thermal conductivity of the sample decreases when it becomes more porous²⁸ (e.g., from pellet to nanopowder), the volume able to sustain high temperatures enlarges, so the number of emitters increases. As a result, the white light emission becomes brighter for the powder compared to the pellet or the powder emits the same white light intensity as the pellet, but at a lower excitation power density. Indeed, for Gd₂O₃, the effective thermal conductivity decreases ca. 3-fold when the effective porosity increases from 0.4 to 0.8 for consolidated and unconsolidated nanopowders of similar materials²⁸ (see ESI†). Another relevant aspect is the large difference in the thermal conductivity of the (solid) sample and the atmosphere surrounding it. In fact, due to this difference, the UC thermal emission is likely a surface phenomenon, constrained to the excitation region and a few particle layers determined by the effective thermal conductivity of the solid. Hence, the thermal conductivity of the atmosphere plays a determining role in establishing the steady-state temperature that can be achieved during the white light UC emission. It is expected that the efficiency of this process depends on the nature of the atmosphere and its pressure, because together with the temperature they determine the thermal conductivity. This explains the significant increase of bright white emission at low pressures.^{11,12,25,58–60} Indeed, Fig. 5(a) shows that the integrated intensity of the UC emission increases ca. 100 times when the pressure is reduced from 1 bar to 2 × 10⁻² mbar, which can be explained simply by the decrease of the thermal conductivity of the environment and there is no need to invoke structural changes with the pressure as previously proposed.^59,60 It is noteworthy that the thermal conductivity of gases at very low pressures (for Knudsen number larger than 1) becomes dependent on the pressure. For white light UC processes, the thermal conductivity of air can decrease ca. 50-fold at pressures of 2 × 10⁻⁵ bar compared to that at atmospheric pressure (see ESI†), which could explain the significant enhancement of the integrated emission.

The effects of the pressure, hence the thermal conductivity, are significant on the power density of the excitation source, for instance, P_D decreases from ca. 190 to 165 to 150 W·cm⁻² upon vacuum (1 bar to 7 × 10⁻⁵ bar to 2 × 10⁻⁵ bar) to produce the same bright white light UC emission (Fig. S7–S9†).

The broadband emission extends from the visible to the infrared spectral range and is well described by the Planck distribution of blackbody radiation,^22,24,28

L_bb(λ,T) = Aλ⁻⁵(e^B(T)/λ − 1)⁻¹ (2)

where L_bb is the spectral radiance proportional to the intensity of radiation, A = 2πhc², B(T) = hc/(k_BT), λ the wavelength, h the Planck constant, and c the speed of light.

The temperatures of 1 (Fig. 5(c) and Fig. S10(b)†) and 2 (Fig. S10(a)†) at different P_D values were estimated by fitting the emission spectrum to eqn (2). However, the emission intensity was measured, I_obs, as photon counting per second onto an unspecified area of the detector, so L_bb ∝ I_obs. Because the proportionality constant of this relationship is unknown, the quantities A and B(T) in eqn (2) were initially treated as adjustable parameters for each P_D. Then, an average of the fitted values of A was employed in a final fitting, keeping A constant (at 4.2 × 10⁻²¹), and considering B(T) the only adjustable parameter from which the temperature was determined. Notice that once the proportionality constant in L_bb ∝ I_obs is known, the thermometric parameter Δ = I_obs becomes a primary thermometer. For the emission spectra of 1 (Fig. 5(c)), the estimated temperatures increased systematically from 1818 to 2106 K as P_D raised from 194 to 235 W·cm⁻² (Fig. 5(d) and Table S4†). Indeed, this temperature dependence on P_D is approximately linear (r² = 0.940) with a slope of 6 ± 1 K· (W·cm⁻²)⁻¹. This dependence was also observed for 1 at different conditions (vacuum and powder) as well as for 2 (powder at ambient pressure), however, with different slopes (Fig. 5(d) and Table S9†), which is a relevant result for testing and validating new models for describing the bright white light UC emissions. In addition, this observed behaviour is consistent with the observations in the literature for (Gd_0.89Yb_0.10Er_0.01)₂O₃-Au nanorods.¹² The estimated temperatures at the steady-state regime of the white light emission are consistent with those available in the literature^22,24 (e.g., 1910 K for Y₂O₃:Yb³⁺,Er³⁺)²⁸ and are below the melting point of Yb₂O₃ (ca. 3000 K)¹⁰ or Gd₂O₃ (2698 K).⁶¹ It is noteworthy that the temperature within the excitation region has the same linear dependence with P_D for both discrete Er³⁺ UC and the continuous white light emission regimes, although with different slopes, ca. 4 and 6 K·(W·cm⁻²)⁻¹, respectively. This similar behaviour suggests that the heating process by the excitation source is the same in both regimes; however, different heat losses at these regimes are indicated by the distinct slopes. This is another relevant result for developing quantitative models to describe laser heating white light emission.

Temporal dynamics of bright white light emission

For Yb³⁺/Er³⁺-codoped materials, the UC emissions were characterized either as a discrete spectrum or as a continuous structureless spectrum described as thermal emission. In addition to these distinct spectra, these UC processes have different dependences on the integrated emission intensity with respect to the excitation power. Because of the distinct nature of these UC processes, it is expected that other behaviours would also be different, particularly, the temporal dependence of the UC emission such as risetime and decay lifetime. The dynamics and kinetics of the discrete UC emissions have already been investigated in different systems and conditions. For instance, Er³⁺-typical lifetime values associated with a photon avalanche process range from 51 to 231 μs,⁶² whereas the risetimes of the Er^{3+ 4}S_3/2 and ⁴F_9/2 levels in Gd₂O₃:10%Yb³⁺,1%Er³⁺ nanocrystals are 99 and 104 μs, respectively.⁴⁵ On the other hand, the lifetimes of the red (656 nm) and green (540 nm) UC emissions for NaYF₄ doped with 20%Yb³⁺ and 2%Er³⁺ are 443 and 194 μs, respectively, which increase to 495 and 210 μs upon doping with 30%Gd³⁺.⁶³ Other upconverting systems Gd₂O₃:Yb³⁺,Er³⁺ have been investigated, under laser excitation at ca. 980 nm, showing typical emission lifetimes within 10–425 μs,^64,65 for the ⁴S_3/2 → ⁴I_15/2 transition, and from 30 to 180 μs^65,66 for the ⁴F_9/2 → ⁴I_15/2 one. However, studies regarding the temporal behaviour of the continuous UC emissions are scarce, so it is presented here the temporal behaviour of the white light UC emission for 1 (pellet) under 980 nm excitation, Fig. 6.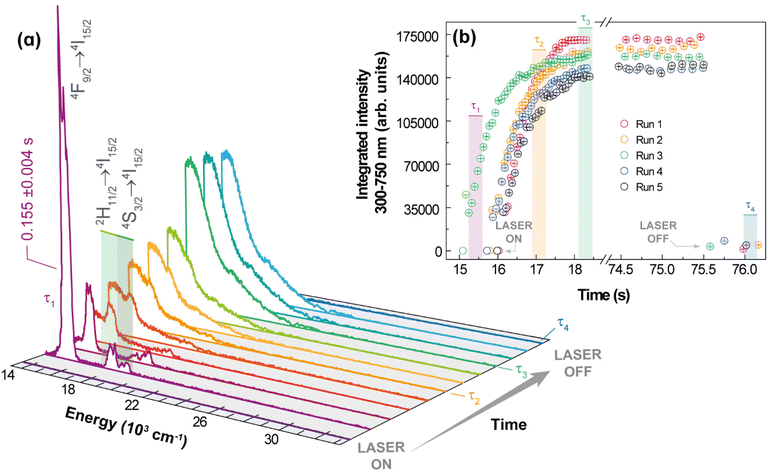

Fig. 6 Emission spectra of 1 acquired at 102 W·cm⁻² under ambient conditions. (b) Transient integrated intensity over 300 at 750 nm (see text for the meaning of τ₁, τ₂, τ₃, and τ₄).

The experimental procedure used to study the dynamics of the white light generation process is described in the ESI.† However, two aspects should be emphasized: there is a shutter between the laser source and the sample, so the source is initially stabilized, and the excitation is started when the shutter is open, thus unambiguously characterizing the initial time, and the spectra were acquired during a minimum time interval (integration time) of 0.1 ms. The temporal behaviour of the white light emission can be characterized by four relevant events: (i) the period for heating the sample up to the white light emission τ₁, which is defined as the time interval between the opening of the shutter and the transition between the discrete UC spectrum to the continuum spectrum; (ii) the time related to the sudden increase of the UC emission intensity, denoted as risetime of white light emission τ₂, defined as the time interval between τ₁ and the time at which the integrated intensity is half of the steady-state intensity; (iii) the interval for which the UC emission remains constant, denoted as the steady-state regime, τ₃, which is controlled by the operator and quantifies the stability of the emission; and (iv) the decaying of the UC emission after the shutter is closed (or excitation source is switched off), characterized by a decaying emission τ₄, defined as the time required for the intensity to decrease half of its steady-state value. It was noticed in the initial heating of the sample by the excitation source a short-lived (τ₁ = 0.155 ± 0.004 s) green emission due to the discrete UC emission, while the risetime was longer (τ₂ = 0.47 ± 0.01 s), as can be observed in Fig. 6. The average value over 5 runs of the risetime τ₂ is 0.5 s, which is a hundred to a thousand times longer than the typical risetime of the discrete ETU emissions and photon avalanche UC emissions. This result corroborates the assumption of the different nature of the continuous white light UC emission (thermal or blackbody-type emission), which involves non-quantized heat transfer processes, compared to the discrete UC emissions that are based on transitions between discrete (quantized) energy levels obeying specific selections rules. The risetime of white light UC emissions represents a balance between the energy absorbed from the radiation beam and the energy losses such as heat conduction, increase of internal energy, and thermal irradiation. Thus, high excitation intensities are required to achieve bright white light emissions, which because of the several effective pathways for energy losses would require longer times than those involved in transitions (non-radiative, radiative, energy transfer) between discrete quantum states. There are reports in the literature of much longer risetimes related to the white light UC emission,^11,13,67 which should be interpreted with care because the time required for stabilization and focusing of the excitation source must be removed from the determination of the risetime.

Regarding the temporal behaviour of the intensity decay of the white light emission, τ₄, it was shorter than the spectral acquisition time, which yields a lower limit to τ₄ of a fraction of μs, τ₄ ≲ 1 μs. This can be rationalized by considering that after the excitation source is switched off, the heated spot rapidly cools down due to efficient energy loss pathways (heat conduction, release of internal energy due to temperature decrease, and thermal irradiation), which are not bounded by selection rules and transition probabilities, as are the usual decays from excited quantum levels to lower discrete states.

Conclusions

The upconversion (UC) features of a mechanical mixture of commercial oxides (89% Gd₂O₃, 10% Yb₂O₃, and 1% Er₂O₃), 2, in comparison to a synthesized sample with the same stoichiometry (Gd_0.89Yb_0.10Er_0.01)₂O₃, 1, were investigated and reported. Both materials 1 and 2 presented colour modulation of the UC emission simply by varying the excitation source power density, which was ascribed to the effects of the laser on the population dynamics of the ²H_11/2 and ⁴S_3/2 Er³⁺ excited levels. We expect that this colour modulation is unaffected by small changes in environmental conditions. At ambient pressure, the thermal conductivity of air is relatively constant with respect to humidity. Different initial temperatures should be compensated by different temperature gradients, which could compensate for changes in heat losses by conduction.

It is noteworthy that efficient energy transfer between ions (Yb³⁺ to Er³⁺) in different particles was observed in 2. This study provides a step forward in the understanding of the mechanism behind the white light emission characterized by continuous broadband, under NIR excitation, and describes the relationship between this emission and several factors (e.g., sample compactness, wavelength excitation, power density, temperature, pressure, humidity, and time). The results reported indicate the thermal nature of this emission that shows repeatability, homogeneity, and stability over cycles of excitation. Cooling down to cryogenic temperatures could decrease its brightness, which might be compensated by increasing the excitation power density. Furthermore, the brightness is affected by humidity that, however, does not completely suppress the continuous white light emission. Thus, depending on the application, it would only require recalibration for significant changes in humidity.

As an added benefit, it was demonstrated that 1 is a luminescent thermometer upon 980 nm CW laser excitation over a very broad range (ca. 300–3100 K). Within 299 to 363 K, 1 is a luminescent primary thermometer with a relative thermal sensitivity within 1.28–0.87% K⁻¹ and temperature uncertainty of 0.03–0.08 K.

The emission modulation observed for 1 and 2 under pump power could provide a great opportunity to develop efficient, cheap, and environment-friendly solid-state lighting. We foresee the application of 1, and possibly the simpler material 2, as a temperature sensor with unprecedented range coupled with vacuum detection.

Author contributions

L. C., O. M., and R. L. conceived the project. T. R. synthesized the samples, performed the structural, morphological, and photoluminescence characterization and analysed the data under the supervision of L. C. and R. F. C. B. checked the thermometric performance of the materials and design the final figures. The manuscript was written through contributions of all authors. All authors have approved the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was developed within the scope of the project CICECO-Aveiro Institute of Materials, UIDB/50011/2020, UIDP/50011/2020 & LA/P/0006/2020, financed by national funds through the FCT/MEC (PIDDAC). The Brazilian Agencies FACEPE, CNPq, CAPES, and FINEP are acknowledged for providing partial financial support under grants (FACEPE: BFD 0020-1.05/22, PRONEX APQ-0675-1.06/14, APQ-1007-1.06/15), (CNPq: GD 870024/2001-9, PQ 309177/2018-9), (CAPES PDSE: 88881.623514/2021-01).

References

1. N. W. Rosemann, J. P. Eussner, A. Beyer, S. W. Koch, K. Volz, S. Dehnen and S. Chatterjee, Science, 2016, 352, 1301–1304.
2. H. Q. Ye, V. Bogdanov, S. Liu, S. Vajandar, T. Osipowicz, I. Hernandez and Q. H. Xiong, J. Phys. Chem. Lett., 2017, 8, 5695–5699.
3. K. Mizuno, J. Ishii, H. Kishida, Y. Hayamizu, S. Yasuda, D. N. Futaba, M. Yumura and K. Hata, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 6044–6047.
4. W. Strek, B. Cichy, L. Radosinski, P. Gluchowski, L. Marciniak, M. Lukaszewicz and D. Hreniak, Light: Sci. Appl., 2015, 4, e237.
5. A. K. Soni, S. Mathur and B. P. Singh, ChemistrySelect, 2019, 4, 3408–3415.
6. L. Li, Y. Pan, W. X. Chang, Z. S. Feng, P. Chen, C. Li, Z. Y. Zeng and X. J. Zhou, Mater. Res. Bull., 2017, 93, 144–149.
7. S. Xu, Y. S. Zhu, W. Xu, B. Dong, X. Bai, L. Xu, C. Miao and H. W. Song, Appl. Phys. Express, 2012, 5, 102701.
8. M. Cesaria, J. Collins and B. Di Bartolo, J. Lumin., 2016, 169, 574–580.
9. F. Auzel, J. Lumin., 2020, 223, 116900.
10. J. Wang and P. A. Tanner, J. Am. Chem. Soc., 2010, 132, 947–949.
11. S. Tabanli, G. Eryurek and B. Di Bartolo, Opt. Mater., 2017, 69, 207–213.
12. M. L. Debasu, D. Ananias, I. Pastoriza-Santos, L. M. Liz-Marzán, J. Rocha and L. D. Carlos, Adv. Mater., 2013, 25, 4868–4874.
13. J. H. Wu, C. Xu, J. R. Qiu and X. F. Liu, J. Mater. Chem. C, 2018, 6, 7520–7526.
14. M. Erdem and B. Sitt, Opt. Mater., 2015, 46, 260–264.
15. S. A. Khrushchalina, P. A. Ryabochkina, V. M. Kyashkin, A. S. Vanetsev, O. M. Gaitko and N. Y. Tabachkova, JETP Lett., 2016, 103, 302–308.
16. G. Bilir, G. Ozen, J. Collins, M. Cesaria and B. Di Bartolo, IEEE Photonics J., 2014, 6, 8200518.
17. G. Bilir, G. Ozen, M. Bettinelli, F. Piccinelli, M. Cesaria and B. Di Bartolo, IEEE Photonics J., 2014, 6, 2201211.
18. S. Tabanli, H. C. Yilmaz, G. Bilir, M. Erdem, G. Eryurek, B. Di Bartolo and J. Collins, ECS J. Solid State Sci. Technol., 2018, 7, R3199–R3210.
19. M. Runowski, P. Wozny, S. Lis, V. Lavin and I. R. Martin, Adv. Mater. Technol., 2020, 5, 1901091.
20. M. Runowski, P. Wozny and I. R. Martin, J. Mater. Chem. C, 2021, 9, 4643–4651.
21. W. Strek, R. Tomala and M. Lukaszewicz, Opt. Mater., 2018, 78, 335–338.
22. J. Wang, T. Ming, Z. Jin, J. Wang, L. D. Sun and C. H. Yan, Nat. Commun., 2014, 5, 5669.
23. Y. J. Zheng, Q. Lu, J. L. Wang, G. H. Zhang, Y. Gao and Z. B. Liu, Opt. Laser Technol., 2014, 63, 39–44.
24. C. I. Silva, A. L. Oliveira, S. C. F. Pereira, G. F. de Sa, L. L. da Luz and S. Alves, Dalton Trans., 2019, 48, 2574–2581.
25. W. Strek, R. Tomala, M. Lukaszewicz, B. Cichy, Y. Gerasymchuk, P. Gluchowski, L. Marciniak, A. Bednarkiewicz and D. Hreniak, Sci. Rep., 2017, 7, 41281.
26. F. Qin, H. Zhao, Y. Zheng, Z. Cheng, P. Wang, C. Zheng, Y. Yu, Z. Zhang and W. Cao, Opt. Lett., 2011, 36, 1806–1808.
27. M. Stefanski, M. Lukaszewicz, D. Hreniak and W. Strek, J. Chem. Phys., 2017, 146, 104705.
28. S. Redmond, S. C. Rand, X. L. Ruan and M. Kaviany, J. Appl. Phys., 2004, 95, 4069–4077.
29. W. Xu, B. T. Chen, W. Yu, Y. S. Zhu, T. Liu, S. Xu, X. L. Min, X. Bai and H. W. Song, Dalton Trans., 2012, 41, 13525–13532.
30. W. Strek, L. Marciniak, D. Hreniak and A. Lukowiak, J. Appl. Phys., 2012, 111, 024305.
31. W. Strek, L. Marciniak, A. Bednarkiewicz, A. Lukowiak, R. Wiglusz and D. Hreniak, Opt. Express, 2011, 19, 14083–14092.
32. G. Bilir and O. Erguzel, Mater. Res. Express, 2016, 3, 106201.
33. S. Balabhadra, M. L. Debasu, C. D. S. Brites, R. A. S. Ferreira and L. D. Carlos, J. Phys. Chem. C, 2017, 121, 13962–13968.
34. J. C. Martins, A. R. N. Bastos, R. A. S. Ferreira, X. Wang, G. Chen and L. D. Carlos, Adv. Photonics Res., 2021, 2, 2000169.
35. J. Mooney and P. Kambhampati, J. Phys. Chem. Lett., 2013, 4, 3316–3318.
36. J. Mooney and P. Kambhampati, J. Phys. Chem. Lett., 2014, 5, 3497–3497.
37. X. D. Wang, R. R. Valiev, T. Y. Ohulchanskyy, H. Agren, C. H. Yang and G. Y. Chen, Chem. Soc. Rev., 2017, 46, 4150–4167.
38. S. A. Saleem, T. Sasikala, A. M. Babu, L. R. Moorthy, B. C. Jamalaiah and M. Jayasimhadri, Int. J. Appl. Glass Sci., 2011, 2, 215–221.
39. M. Pollnau, D. R. Gamelin, S. R. Luthi, H. U. Gudel and M. P. Hehlen, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 3337–3346.
40. J. C. Wright, in Radiationless Processes in Molecules and Condensed Phases: in Molecules and Condensed Phases, ed. D. J. Diestler, F. K. Fong, K. F. Freed, R. Kopelman and J. C. Wright, Springer Berlin Heidelberg, Berlin, Heidelberg, 1976, vol. 15, pp. 239–295.
41. X. Qin, A. N. C. Neto, R. L. Longo, Y. M. Wu, O. L. Malta and X. G. Liu, J. Phys. Chem. Lett., 2021, 12, 1520–1541.
42. A. N. Carneiro Neto, R. T. Moura, J. A. A. Coelho, M. E. Silva-Junior, J. L. Costa, O. L. Malta and R. L. Longo, Chin. J. Lumin., 2022, 43, 1871–1891.
43. Y. Lei, H. Song, L. Yang, L. Yu, Z. Liu, G. Pan, X. Bai and L. Fan, J. Chem. Phys., 2005, 123, 174710–174715.
44. A. M. Pires, O. A. Serra, S. Heer and H. U. Gudel, J. Appl. Phys., 2005, 98, 063529.
45. K. Z. Zheng, D. S. Zhang, D. Zhao, N. Liu, F. Shi and W. P. Qin, Phys. Chem. Chem. Phys., 2010, 12, 7620–7625.
46. G. Tian, Z. J. Gu, X. X. Liu, L. J. Zhou, W. Y. Yin, L. Yan, S. Jin, W. L. Ren, G. M. Xing, S. J. Li and Y. L. Zhao, J. Phys. Chem. C, 2011, 115, 23790–23796.
47. H. Y. Hao, H. Y. Lu, G. H. Ao, Y. L. Song, Y. X. Wang and X. R. Zhang, Dyes Pigm., 2018, 148, 298–305.
48. H. R. Tuxun, Z. F. Cai, M. Ji, B. B. Zhang, C. Y. Zhang, J. P. Li, X. D. Yu, Z. K. Fu, Z. L. Zhang and H. R. Zheng, Nanophotonics, 2022, 11, 979–986.
49. S. A. Wade, S. F. Collins and G. W. Baxter, J. Appl. Phys., 2003, 94, 4743.
50. C. D. S. Brites, S. Balabhadra and L. D. Carlos, Adv. Opt. Mater., 2019, 7, 1801239.
51. S. K. Singh, K. Kumar and S. Rai, Appl. Phys. B: Lasers Opt., 2010, 100, 443–446.
52. Y. Tian, B. N. Tian, C. E. Cui, P. Huang, L. Wang and B. J. Chen, RSC Adv., 2015, 5, 14123–14128.
53. W. Zheng, B. Y. Sun, Y. M. Li and R. Wang, ACS Appl. Nano Mater., 2021, 4, 3922–3931.
54. D. Li, B. A. Dong, X. Bai, Y. Wang and H. W. Song, J. Phys. Chem. C, 2010, 114, 8219–8226.
55. H. Guo, N. Dong, M. Yin, W. P. Zhang, L. R. Lou and S. D. Xia, J. Phys. Chem. B, 2004, 108, 19205–19209.
56. P. K. Yadaw, R. K. Padhi, V. Dubey, M. Rao and N. K. Swamy, Inorg. Chem. Commun., 2022, 143, 109736.
57. T. Pang and W. H. Lu, Ceram. Int., 2017, 43, 1061–1065.
58. H. Cinkaya, G. Eryurek, G. Bilir, M. Erdem and B. Di Bartolo, J. Lumin., 2017, 181, 321–326.
59. M. Erdem, G. Eryurek and B. Di Bartolo, J. Alloys Compd., 2015, 639, 483–487.
60. G. Bilir and B. Di Bartolo, Opt. Mater., 2014, 36, 1357–1360.
61. M. Lukaszewicz, R. Tomala and R. Lisiecki, J. Mater. Chem. C, 2020, 8, 1072–1082.
62. T. Liu, Y. P. Song, S. S. Wang, Y. J. Li, Z. Y. Yin, J. B. Qiu, Z. W. Yang and Z. G. Song, J. Alloys Compd., 2019, 779, 440–449.
63. H. Qin, D. Y. Wu, J. Sathian, X. Y. Xie, M. Ryan and F. Xie, Sci. Rep., 2018, 8, 12683.
64. S. Singh, Kanika, G. Kedawat, J. H. Park, B. Ghorai, U. K. Ghorai, C. Upadhyay, B. A. Kaipparettu and B. K. Gupta, J. Photochem. Photobiol., 2021, 8, 100081.
65. K. Z. Zheng, Z. Y. Liu, Y. Liu, W. Y. Song and W. P. Qin, J. Appl. Phys., 2013, 114, 183109.
66. X. Q. Zhao, H. Suo, Z. Y. Zhang and C. F. Guo, Ceram. Int., 2018, 44, 2911–2918.
67. G. Bilir and G. Eryurek, Ceram. Int., 2016, 42, 6065–6071.

---

Footnote

† Electronic supplementary information (ESI) available: Structural characterization, energy gap determination, thermometric analysis, white-light emission, estimating the thermal conductivity, experimental procedure to temporal analysis. See DOI: https://doi.org/10.1039/d3nr01764h

---