Open Access Article
Open Access ArticleMolecular insights into the temperature and pressure dependence of mechanical behavior and dynamics of Na-montmorillonite clay†
Sarah
Ghazanfari
 a,
Amirhadi
Alesadi
a,
Yangchao
Liao
a,
Amirhadi
Alesadi
a,
Yangchao
Liao
 a,
Yida
Zhang
a,
Yida
Zhang
 b and
Wenjie
Xia
b and
Wenjie
Xia
 *ac
*ac
aDepartment of Civil, Construction and Environmental Engineering, North Dakota State University, Fargo, ND 58108, USA. E-mail: wenjie.xia@ndsu.edu
bDepartment of Civil, Environmental, Architectural Engineering, University of Colorado Boulder, Boulder, CO 80309, USA
cDepartment of Aerospace Engineering, Iowa State University, Ames, IA 50011, USA. E-mail: wxia@iastate.edu
First published on 3rd August 2023
Abstract
Sodium montmorillonite (Na-MMT) clay mineral is a common type of swelling clay that has potential applications for nuclear waste storage at high temperatures and pressures. However, there is a limited understanding of the mechanical properties, local molecular stiffness, and dynamic heterogeneity of this material at elevated temperatures and pressures. To address this, we employ all-atomistic (AA) molecular dynamics (MD) simulation to investigate the tensile behavior of Na-MMT clay over a wide temperature range (500 K to 1700 K) and pressures (200 atm to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atm). The results show that increasing the temperature significantly reduces the tensile modulus, strength, and failure strain, while pressure has a minor effect compared to temperature, as seen in the normalized pressure–temperature plot. Mean-square displacement (MSD) analysis reveals increased molecular stiffness with increasing pressure and decreasing temperature, indicating suppressed atomic mobility. Our simulations indicate temperature-dependent dynamical heterogeneity in the Na-MMT model, supported by experimental studies and quantified local molecular stiffness distribution. These findings enhance our understanding of the tensile response and dynamical heterogeneity of Na-MMT clay under extreme conditions, aiding the development of clay minerals for engineering applications such as nuclear waste storage and shale gas extraction.
000 atm). The results show that increasing the temperature significantly reduces the tensile modulus, strength, and failure strain, while pressure has a minor effect compared to temperature, as seen in the normalized pressure–temperature plot. Mean-square displacement (MSD) analysis reveals increased molecular stiffness with increasing pressure and decreasing temperature, indicating suppressed atomic mobility. Our simulations indicate temperature-dependent dynamical heterogeneity in the Na-MMT model, supported by experimental studies and quantified local molecular stiffness distribution. These findings enhance our understanding of the tensile response and dynamical heterogeneity of Na-MMT clay under extreme conditions, aiding the development of clay minerals for engineering applications such as nuclear waste storage and shale gas extraction.
1 Introduction
Clay minerals are fine-grained soils that consist of a group of layered aluminum silicates or magnesium silicates, also known as phyllosilicates. Clay minerals have attracted widespread attention due to their diverse applications in industries such as catalyst supports,1 drug-delivery systems,2 nuclear waste disposal,3 and wastewater treatment.4 Hence, understanding and modeling these minerals is a topic of great interest among researchers, especially in multidisciplinary fields such as engineering, physics, chemistry, and earth sciences.Among different clay minerals, montmorillonite (MMT) is a type of smectite (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) clay mineral with the chemical formula Al2Si4O10(OH)2.5,6 These MMT clay minerals have a significant impact on nuclear waste disposal,7,8 shale gas formation or extraction,9,10 and carbon dioxide geologic sequestration.11 For example, bentonite, consisting mostly of MMT minerals, is a feasible buffer material for deep geological disposal of nuclear wastes because of its low permeability, excellent self-healing capability, and adsorption potential of radionuclides.12,13 In addition, the barrier material should be able to dissipate excessive heat produced by high-level radioactive waste onto the host rock. A previous study14 has shown that surrounding temperature could increase to a peak of 90 °C.
1) clay mineral with the chemical formula Al2Si4O10(OH)2.5,6 These MMT clay minerals have a significant impact on nuclear waste disposal,7,8 shale gas formation or extraction,9,10 and carbon dioxide geologic sequestration.11 For example, bentonite, consisting mostly of MMT minerals, is a feasible buffer material for deep geological disposal of nuclear wastes because of its low permeability, excellent self-healing capability, and adsorption potential of radionuclides.12,13 In addition, the barrier material should be able to dissipate excessive heat produced by high-level radioactive waste onto the host rock. A previous study14 has shown that surrounding temperature could increase to a peak of 90 °C.
Although there are numerous studies available on the physical behavior of clay minerals at room temperature,15–21 the molecular and mechanical characteristics of MMT clay minerals at elevated temperatures and pressures are not well understood, especially for their optimization as nuclear waste buffer materials. Several experimental22–26 and theoretical derivation methods27,28 have been developed to study the swelling, structural, and mechanical properties of clay minerals, such as high energy synchrotron X-ray methods,29 acoustic measurement,30 and the Brillouin scattering method.31 These studies have demonstrated that as the water content of clay minerals increases, their mechanical strength decreases, and they become more prone to failure. Swelling pressures can also be affected by temperature, with some clay types experiencing an increase while others experience a decrease. The exact outcome depends on factors such as experimental conditions and isomorphic substitution of exchangeable cation types.22,32 However, these experimental methods can be time-consuming and expensive, which has led researchers to turn to computational approaches. In particular, molecular dynamics (MD) simulations33–35 have been extensively utilized to study the different physical properties of clay minerals, including MMT.36–38 For instance, utilizing the Grand Canonical Monte Carlo (GCMC) method, in conjunction with MD, it was found that temperature moderately lessens the range of swelling pressure of clay with a d-spacing smaller than 16 Å.39 In another work, using steered molecular dynamics (SMD),40 Faisal and coworkers37 have measured interaction energies between clays and cations during loading, enabling the evaluation of the mechanical behavior of Na-MMT tactoid under compression, tension, and shear at normal temperature and pressure.
In the present study, an all-atomistic MD (AA-MD)41 modeling approach was utilized to investigate the mechanical behavior and dynamics of Na-MMT clay minerals at elevated temperatures and pressures. Tensile responses including the tensile modulus, tensile strength, and failure strain at elevated temperatures from 300 K to 1700 K and pressures from 200 atm to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atm were reported from the simulations. The relationship between the tensile modulus and pressure/temperature was clearly depicted and explained, with pressures normalized by temperature for better understanding. By evaluating local molecular stiffness and its distribution from mean-square displacement (MSD) analysis, one can obtain valuable insights into the dynamical heterogeneity of Na-MMT models at a fundamental level. These findings improve one's understanding of the mechanical properties and dynamical heterogeneity of Na-MMT, paving the way for the development of advanced clay buffer materials optimized for nuclear waste isolation purposes.
000 atm were reported from the simulations. The relationship between the tensile modulus and pressure/temperature was clearly depicted and explained, with pressures normalized by temperature for better understanding. By evaluating local molecular stiffness and its distribution from mean-square displacement (MSD) analysis, one can obtain valuable insights into the dynamical heterogeneity of Na-MMT models at a fundamental level. These findings improve one's understanding of the mechanical properties and dynamical heterogeneity of Na-MMT, paving the way for the development of advanced clay buffer materials optimized for nuclear waste isolation purposes.
2 Methods
In this study, AA-MD simulations were carried out using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)42 software package and visualized by Visual Molecular Dynamics (VMD).43 Interatomic interactions were calculated through the CLAYFF force field.44–46 A combination of both Mulliken47 and electrostatic charge48,49 determinations derived from single point electronic structure calculations of the unit cells were employed to start allocating partial charges. Partial charges and van der Waals parameters were assigned to each atom type in the model, where only a single physical bond stretch parameter for the O–H groups was considered. In this force field, the total non-bonded energy consists of coulombic energy and van der Waals energy which are represented by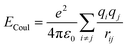 and
and 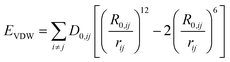 , respectively, where e is the electron charge, ε0 is the vacuum dielectric permittivity, q is the partial charge of atoms, and D0,ij and R0,ij are empirical parameters obtained from the fitting of the model to observed physical and structural properties. Utilizing the General Utility Lattice Program GULP50 computer package, optimized values for the Lennard–Jones parameters (D0,ij and R0,ij) were attained and by employing a Newton–Raphson algorithm,51 the predicted structure of a model was fitted to the observed compound. Previous studies have shown that the CLAYFF force field was not parametrized for clay edge surface calculation. Hence, they proposed a CLAYFF-compatible partial charge for oxygen atoms located on clay edges according to an algorithm that considers cation charge, charge saturation and bond valence.45 Using the following equation, the partial charge of any oxygen atom type in the CLAYFF45,52 force field can be calculated:
, respectively, where e is the electron charge, ε0 is the vacuum dielectric permittivity, q is the partial charge of atoms, and D0,ij and R0,ij are empirical parameters obtained from the fitting of the model to observed physical and structural properties. Utilizing the General Utility Lattice Program GULP50 computer package, optimized values for the Lennard–Jones parameters (D0,ij and R0,ij) were attained and by employing a Newton–Raphson algorithm,51 the predicted structure of a model was fitted to the observed compound. Previous studies have shown that the CLAYFF force field was not parametrized for clay edge surface calculation. Hence, they proposed a CLAYFF-compatible partial charge for oxygen atoms located on clay edges according to an algorithm that considers cation charge, charge saturation and bond valence.45 Using the following equation, the partial charge of any oxygen atom type in the CLAYFF45,52 force field can be calculated: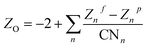 | (1) |
To construct a well-ordered structure file with proper atom typing, an open-source library of modular MATLAB routines called atomistic topology operations in MATLAB (atom) was employed.56 This library facilitated several functions, including model building, manipulation, and structural analysis. Moreover, it enabled the use of the bond valence method and a neighbor-distance analysis to determine various chemical properties of inorganic molecules. The atom library can generate topology files that incorporate bonding and angle information by considering periodic boundary conditions. It also supports multiple topology file formats, such as LAMMPS, NAMD, GROMACS, and RASPA2. Furthermore, in addition to reading and writing several topology files and trajectory formats, this library supports CLAYFF46 and INTERFACE force fields57,58 for GROMACS and NAMD as well.
Smectite (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) clay minerals, also known as phyllosilicates, consist of one alumina octahedral (O) sheet sandwiched between two silica tetrahedral (T) sheets, i.e., T-O-T.59 These T-O-T layers are stacked in the z direction by relatively weak attractive van der Waals forces.60 Several isomorphic substitutions, such as Si4+ by Al3+ or Fe3+ in tetrahedral sheets and Al3+ by Mg2+ or Fe3+ in octahedral sheets, can lead to the negative charge of layers. Different interlayer counterions such as Na, Mg, K, Ca, and Cs balance the negative charges induced by isomorphic substitution.59,61–63 The generic Wyoming type Na-MMT64 with the structural formula Na0.66[Al3.33Mg0.66][Si8]O20[OH]4 and random isomorphic substitutions of Al3+ by Mg2+ in the octahedral sheet was utilized in this study. The periodically replicated model consisting of 6 × 4 unit cells (extending 30.96 Å and 35.86 Å in the lateral x and y directions, respectively) had overall 1952 atoms (including Na+ counter ions). The model was first minimized using the iterative conjugate gradient algorithm65 and then equilibrated at 300 K in a canonical (NVT) ensemble for 100 ps. Subsequently, the systems were brought up to various temperatures (between 300 K and 1700 K) and pressures (between 200 atm and 100
1) clay minerals, also known as phyllosilicates, consist of one alumina octahedral (O) sheet sandwiched between two silica tetrahedral (T) sheets, i.e., T-O-T.59 These T-O-T layers are stacked in the z direction by relatively weak attractive van der Waals forces.60 Several isomorphic substitutions, such as Si4+ by Al3+ or Fe3+ in tetrahedral sheets and Al3+ by Mg2+ or Fe3+ in octahedral sheets, can lead to the negative charge of layers. Different interlayer counterions such as Na, Mg, K, Ca, and Cs balance the negative charges induced by isomorphic substitution.59,61–63 The generic Wyoming type Na-MMT64 with the structural formula Na0.66[Al3.33Mg0.66][Si8]O20[OH]4 and random isomorphic substitutions of Al3+ by Mg2+ in the octahedral sheet was utilized in this study. The periodically replicated model consisting of 6 × 4 unit cells (extending 30.96 Å and 35.86 Å in the lateral x and y directions, respectively) had overall 1952 atoms (including Na+ counter ions). The model was first minimized using the iterative conjugate gradient algorithm65 and then equilibrated at 300 K in a canonical (NVT) ensemble for 100 ps. Subsequently, the systems were brought up to various temperatures (between 300 K and 1700 K) and pressures (between 200 atm and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atm) using an isothermal-isobaric (NPT) ensemble in the z direction for 1 ns. The electrostatic interactions were calculated using the Ewald summation method66 with a precision of 10−4 and 12 Å cutoff distances, and an integration timestep of 1 fs was used. To ensure the equilibration and stability of the simulation, the total potential energy decay was checked before measuring mechanical and dynamics properties.
000 atm) using an isothermal-isobaric (NPT) ensemble in the z direction for 1 ns. The electrostatic interactions were calculated using the Ewald summation method66 with a precision of 10−4 and 12 Å cutoff distances, and an integration timestep of 1 fs was used. To ensure the equilibration and stability of the simulation, the total potential energy decay was checked before measuring mechanical and dynamics properties.
2.1 Property calculations
The strain-controlled uniaxial tensile deformation was applied to the Na-MMT clay system in the x direction. To this end, a constant engineering strain rate of 0.5 ns−1, which is consistent with previous studies,67,68 ensured reliability, and computational efficiency was imposed for all simulations. The lateral directions (i.e., y and z directions) were kept fixed throughout the tensile deformation simulations. The tensile direction (x) stress component was calculated using the atomic virial stress tensor,69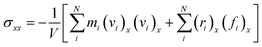 | (2) |
To evaluate the dynamical heterogeneity, the local molecular stiffness of the Na-MMT clay system was calculated. Specifically, the Debye–Waller factor (DWF)70 〈u2〉, an important short-time fast dynamics property at a picosecond to nanosecond timescale, was quantified. Here, the 〈u2〉 was determined from the mean-square displacement (MSD) 〈r2(t)〉 of the center of mass of all atoms excluding Na counter ions and H atoms. 〈u2〉 was defined as the average value of the 〈r2(t)〉 curves within two fixed time ranges, specifically from ∼148 ps to 885 ps for a temperature range of 300 K to 1500 K at zero pressure and from 5 ps to 46 ps for a pressure range of 200 atm to 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atm at a temperature of 300 K, respectively. These time ranges corresponded to the estimated caging time for a given temperature and pressure, respectively. MSD 〈r2(t)〉 can be calculated as
000 atm at a temperature of 300 K, respectively. These time ranges corresponded to the estimated caging time for a given temperature and pressure, respectively. MSD 〈r2(t)〉 can be calculated as
| 〈r2(t)〉 = 〈|rj(t) − rj(0)|2〉 | (3) |
3 Results and discussion
3.1 Tensile deformation analysis
To explore the tensile behavior of the Na-MMT system, a uniaxial non-equilibrium tensile deformation at different elevated temperatures and pressures was carried out. Fig. 1a shows a snapshot of the AA Na-MMT clay model box after minimization and equilibration at zero pressure and 300 K temperature, just prior to tensile deformation. Fig. 1b shows the simulation box under a maximum tensile strain of 10% deformation along the x-direction where the system still preserves the crystalline structure of MMT. In contrast, Fig. 1c depicts a critical tensile strain of 11% where the system no longer has the well-ordered clay structure. One can note that the tensile strain response was calculated as the ratio of change (ΔLx) relative to the original box length (L0x). Using Lx(t) = L0x(1 +![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a1.gif) × Δt), the box length variation (Lx) as a function of time was measured (where one can use a constant engineering strain rate
× Δt), the box length variation (Lx) as a function of time was measured (where one can use a constant engineering strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a1.gif) of 0.5 ns−1 and timestep of Δt = 1 fs).
of 0.5 ns−1 and timestep of Δt = 1 fs).
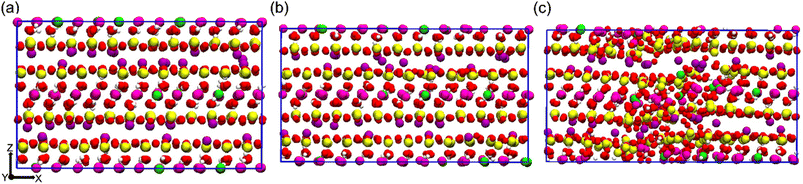 | ||
| Fig. 1 Simulation box snapshots of an all-atomistic Na-MMT model under uniaxial tension at (a) zero tensile strain, (b) ten percent tensile strain and (c) eleven percent tensile strain (side view). | ||
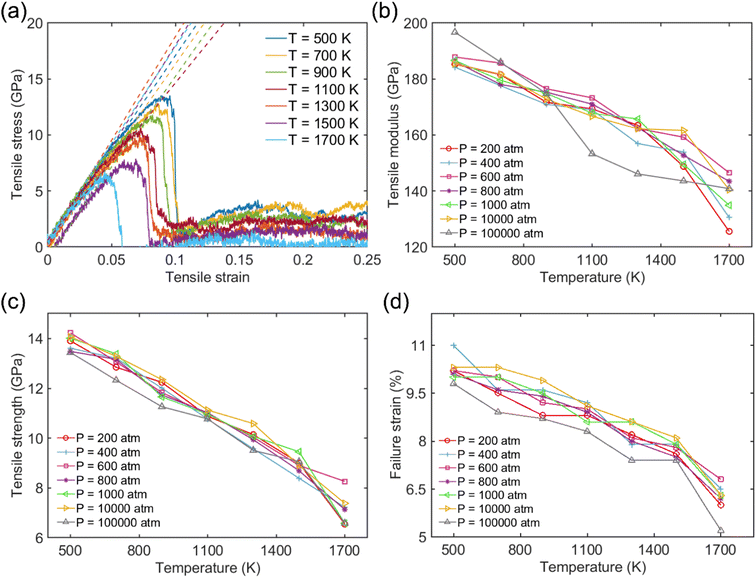
Fig. 2a shows the typical tensile stress–strain curve for the Na-MMT clay system at elevated temperatures from 500 K to 1700 K at a pressure of 1000 atm. The elastic modulus of tension was determined by fitting the stress–strain data of the linear regime within 3% strain, as indicated using the dashed lines. The obtained tensile modulus varied between 197 GPa and 125 GPa and the tensile strength lied between 6.2 GPa and 14.5 GPa. It was observed that stress increases almost linearly with strain from the initial state to maximum during the stretching process along the x direction which was consistent with previous studies.71–73 Subsequently, there was a sharp drop in stress from the maximum value to a lower value, indicating instantaneous brittle failure. The final tensile strength (σtoverall) was calculated by taking the maximum stress on the stress–strain curve in the tensile direction.
The tensile modulus, tensile strength, and failure strain were found to decrease as T increased, while pressure didn't significantly affect tensile responses (see Fig. 2b–d). Using a normalized pressure by temperature relation, the role of pressure on the mechanical performance of the clay system will be discussed in more detail later. The results of the tensile modulus, tensile strength, and failure strain of the Na-MMT model at room temperature and pressure were in good agreement with previously published literature.27,73–75 Chen and coworkers27 reported that the MMT tensile modulus lies within the range of 178–265 GPa based on an empirical modulus-density relation. Using MD simulations based on CLAYFF, Wei et al.73 reported a tensile modulus of 208 GPa along the x-direction for a similar model system. It should be emphasized that to evaluate the effectiveness of the simulation outside of the selected ranges, additional tensile tests have been conducted. As shown in Fig. S1 in the ESI,† the clay doesn't exhibit a normal stress–strain response and any noticeable tensile strength at temperatures above 1900 K. We have tested these temperatures at different pressures and observed similar behavior. Therefore, we expect that the simulations are no longer effective in capturing the reliable mechanical response of clay beyond this range of temperature.
The tensile modulus as a function of pressure normalized by temperature (P/T) was plotted to better understand their relationship. This was inspired by Xu and coworkers,76 who recently studied the influence of cohesive energy on the bulk thermodynamic properties of a glass-forming polymer melt. They found that the dimensionless thermodynamic properties (i.e., cohesive energy density) are a universal function of the cohesive energy scaled by temperature. It has also been demonstrated that the pressure and cohesive energy are closely correlated where increasing the pressure tends to enhance cohesive energy.77 Similarly, Goyal et al.78 reported the close correlation of pressure and cohesive energy by reconciling a fundamental comprehension in studying the cement hydration mechanism. Fig. 3 presents a clear depiction of the relationship between pressure, temperature, and tensile modulus. It demonstrated that the pressure alone doesn't play a significant role in the tensile modulus, and only the highest pressure of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atm can lead to a slightly higher tensile modulus. The fitted dashed lines to data in Fig. 3 further show apparent power-law scaling relationships between the modulus and P/T. It should be mentioned that CLAYFF17 relies on fixed connectivity between atoms and cannot simulate bond rupture, thereby preventing the modeled failure of MMT at ultra-high pressures. Therefore, more sophisticated reactive potentials are necessary to properly capture the mechanisms and dynamics of tensile failure. We intend to employ quantum-accurate reactive MD simulations on localized regions to accurately represent bond dissociation and failure as future work.
000 atm can lead to a slightly higher tensile modulus. The fitted dashed lines to data in Fig. 3 further show apparent power-law scaling relationships between the modulus and P/T. It should be mentioned that CLAYFF17 relies on fixed connectivity between atoms and cannot simulate bond rupture, thereby preventing the modeled failure of MMT at ultra-high pressures. Therefore, more sophisticated reactive potentials are necessary to properly capture the mechanisms and dynamics of tensile failure. We intend to employ quantum-accurate reactive MD simulations on localized regions to accurately represent bond dissociation and failure as future work.
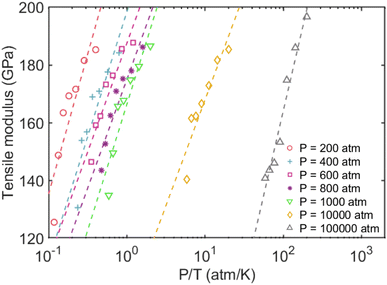 | ||
| Fig. 3 Tensile modulus vs. normalized pressures by temperatures. The dashed lines represent the power-law fitting to the data. | ||
3.2 Molecular stiffness evaluation through Debye–Waller factor 〈u2〉
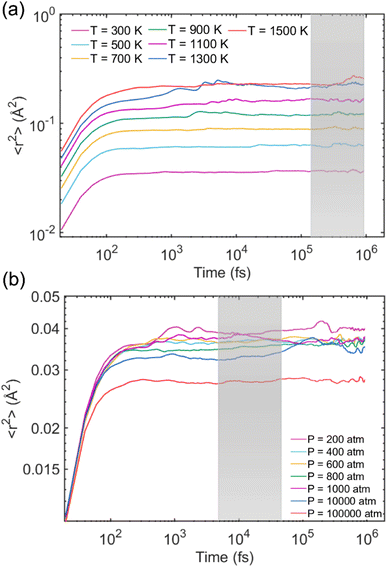
In order to calculate the Debye–Waller factor 〈u2〉, the model systems underwent another 1 ns after equilibration to ensure that the simulated Na-MMT had reached a stable state before collecting data for MSD 〈r2(t)〉 calculation. The MSD was defined as the mean square of the atom's position change with reference to its initial position at different times, which can reflect the change of atom offset with time evolution. In the first set of simulations, seven elevated temperatures including 300, 500, 700, 900, 1100, 1300, and 1500 K were considered while the pressure was zero. For the second calculation, MSD 〈r2(t)〉 was measured at several elevated pressures comprising 200, 400, 600, 800, 1000, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atm, and 100
000 atm, and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atm where the temperature was 300 K.
000 atm where the temperature was 300 K.
Fig. 4a shows how 〈r2(t)〉 changes over time for all atoms, excluding Na and H, in the Na-MMT model at different elevated temperatures when the pressure is zero. As expected, the MSD 〈r2(t)〉 of the system increased noticeably by increasing the temperature due to enhanced atoms’ mobility. The caging time region was highlighted in the shadowed gray region, where one can determine the 〈u2〉 of the model. Similarly, Fig. 4b shows the MSD r2(t) of the clay model for all constituent atoms except for Na and H atoms at varying pressures. As pressure increases, 〈r2(t)〉 of the model decreases significantly; this indicates that increasing the pressure, similar to increasing the cohesive energy, will increase the molecular stiffness by suppressing atoms’ mobility. A similar pattern can be observed for 〈r2(t)〉 as T decreases. The MSD 〈r2(t)〉 curve patterns were also in good agreement with previous studies. Li and co-workers70 explored the microstructure and dynamics of nanocrystal cellulose thin films utilizing CG-MD simulations. They reported the MSD curves of CG beads for different packing densities where the results showed that increasing density leads to a remarkable decrease in 〈r2(t)〉. Moreover, they found that as tensile strain increases, the 〈r2(t)〉 enhances, indicating an increase in mobility when subjecting nanocellulose to a particular deformation.
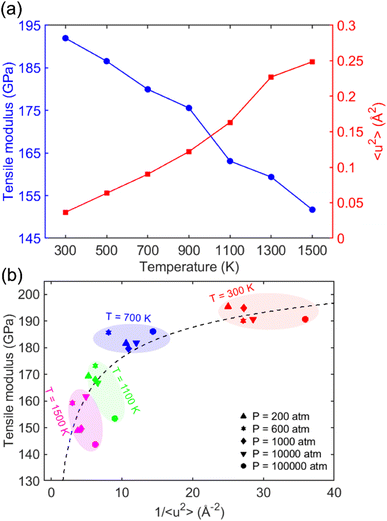
Fig. 5 presents a summary of the results for the tensile modulus, the Debye–Waller factor 〈u2〉, and molecular stiffness 1/〈u2〉 at elevated temperatures and pressures. Fig. 5a shows a double-axis plot of the tensile modulus on the left-y axis and 〈u2〉 on the right-y axis as a function of temperature. This plot revealed that increasing the temperature T leads to 1/〈u2〉 enhancement and tensile modulus reduction because of enhanced atoms' mobility. This observation was consistent with the findings of other crystalline materials. Wei et al.79 utilized AA-MD simulations to explore the effect of temperature and pressure on the tensile behavior of ice-Ih on a simple point charge (SPC)80 water model. They found that both the tensile modulus and ultimate strength of the system decrease linearly with increasing temperature, indicating that raising temperature reduces the stability of the molecular structure.
Fig. 5b depicts the relationship between the tensile modulus and molecular stiffness 1/〈u2〉 for different pressures at different temperatures T, with each color corresponding to a specific temperature. In this plot, the red, blue, green, and magenta colors represent temperatures of 300, 700, 1100, and 1500 K, respectively. As the temperature decreased from 1500 K to 300 K, both the tensile modulus and local molecular stiffness 1/〈u2〉 tended to increase, where a nonlinear relationship can be observed. Moreover, it was observed that pressure doesn't appear to have a noticeable effect on the tensile modulus values, with the results being similar for each particular temperature.
3.3 Dynamical heterogeneity of the Na-MMT model
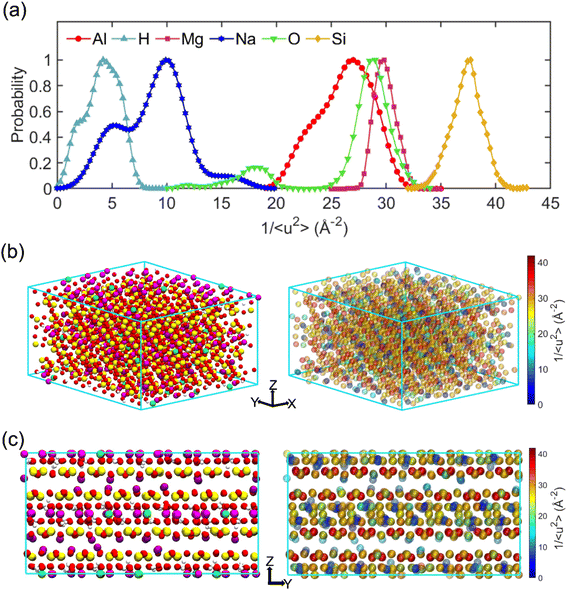
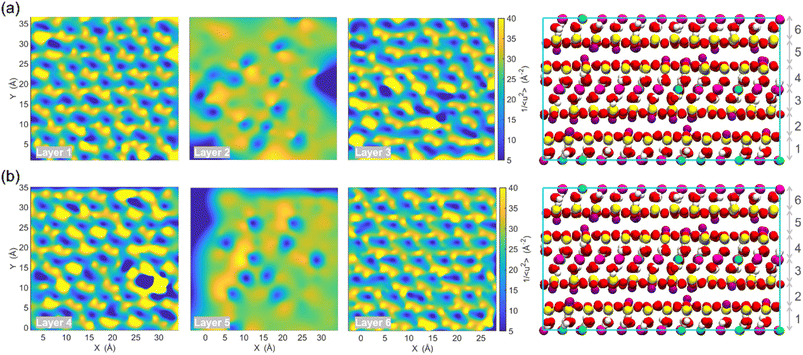
The term “dynamics heterogeneity” refers to the occurrence of non-uniform motion of particles or molecules in a system. Due to the great diversity in particle motion, amorphous material systems, which have a disorganized arrangement of particles, often exhibit dynamical heterogeneity.33,68 On the other hand, dynamical heterogeneity is less common in crystalline systems with a regular pattern of particle arrangement. Nevertheless, clay's layered and sandwich-like structure, despite being crystalline, can still exhibit dynamics heterogeneity, as the imperfect alignment of clay particles can create local regions of disorder with the presence of surface.First, the probability distribution of the local molecular stiffness 1/〈u2〉 of the atoms was evaluated to measure the dynamical heterogeneity of the Na-MMT system as shown in Fig. 6a. The kernel probability distribution81 for each atom type indicated that atoms with higher atomic mass exhibited higher local molecular stiffness or lower mobility. In the simulation box, hydrogen and sodium counterions had the highest mobility in comparison to other types of atoms because they have lower atomic masses and do not form covalent bonds with the clay structure, respectively. The probability distribution for atoms at 1700 K showed a significant decrease in molecular stiffness compared to that at room temperature (see Fig. S2, ESI†), while Fig. S3 in the ESI† shows an insignificant change in stiffness for the Na-MMT model undergoing 1000 atm pressure. For instance, at a temperature of 300 K, the local molecular stiffness of Al atoms ranged from 20 to 35 Å−2, whereas at 1700 K, this range dropped to 1 and 4 Å−2. In the meantime, increasing the temperature led to a noticeable suppression in the degree of dynamical heterogeneity as manifested by the narrowing of the probability distribution (Fig. S2†). On the other hand, increasing pressure only led to an insignificant change or a slight decrease in the degree of dynamical heterogeneity. Afterwards, for improved comprehension of the Na-MMT clay dynamics, an investigation into the spatial distribution of local molecular stiffness 1/〈u2〉 for each individual atom was conducted. This offers a comprehensive gauge of dynamic heterogeneity in crystals. The local molecular stiffness 1/〈u2〉 was specifically determined by computing the local mean squared displacement (MSD) of each atom type at zero pressure and 300 K at a relevant caging time. A higher molecular stiffness corresponded to a lower mobility of the particles, and vice versa. The right panels of Fig. 6b and c show the three-dimensional (3D) color maps of the local molecular stiffness 1/〈u2〉 of the individual atom within the clay model system, while the left panels represent the Corey–Pauling–Koltun (CPK)82 atom colors in the simulation box.
To gain better insights into the spatial dynamic heterogeneity of the Na-MMT clay system, the local molecular stiffness 1/〈u2〉 distribution in two-dimensions (2D) at different z elevations was plotted. As depicted in the rightmost panels of Fig. 7, the simulation box in the z direction is divided into six sublayers (with a thickness of almost ∼2 Å). The MSD 〈r2(t)〉 was calculated for each individual layer from which the 1/〈u2〉 values of mobile and immobile atoms within a given layer are determined. Note that the blueish regions corresponded to the atoms with lower stiffness or higher local mobility and the yellowish regions corresponded to the atoms with higher stiffness or lower local mobility. It can be observed that layers 2 and 6 correspond to interlayer spaces, where the sodium counterions with the highest mobility were located (the blueish points correspond to the Na ions). The remaining four layers exhibited relatively similar patterns of local molecular stiffness 1/〈u2〉 distribution within the x–y plane. Overall, Fig. 7 clearly shows the heterogeneous distribution of the local 1/〈u2〉 of the Na-MMT model which agrees with other experimental studies.83–86 McAtee and co-workers showed that montmorillonite has a heterogeneous nature, based on X-ray diffraction patterns and cation-exchange data. They showed that montmorillonite can be divided into two fractions: one phase includes sodium montmorillonite, and the other phase contains basically calcium–magnesium montmorillonite. The dissimilarities are thought to be due to differences in the isomorphous substitutions that occur inside the montmorillonite crystal lattice.86 These findings align with the present results and further support the dynamical heterogeneity of the Na-MMT clay systems.
4 Conclusion
In this study, the tensile response and dynamical heterogeneity of Na-MMT clay at elevated temperatures and pressures were investigated by employing AA-MD simulations. By carrying out tensile deformation simulations, it was demonstrated that pressure does not play a significant role in the tensile modulus, while increasing the temperature leads to a significant decrease in the tensile modulus/strength and failure strain. The mean-square displacement (MSD) calculations had revealed that molecular stiffness increased at elevated pressure due to suppressed atoms’ mobility, which was particularly noticeable at lower temperatures. Finally, current analysis of the distribution of local molecular stiffness, as measured using the inverse Debye–Waller factor 1/〈u2〉, confirmed the dynamically heterogeneous nature of the system, consistent with prior studies. Present simulations uncovered the scaling relationship between pressure, temperature, and tensile modulus for Na-MMT clay over a wide range of thermodynamic conditions. These results have significant implications for the development of clay-based materials in diverse engineering and technological applications, particularly for nuclear waste storage where a considerable temperature and pressure increase may arise.Conflicts of interest
There are no conflicts to declare.Acknowledgements
W. X. acknowledges the support of the National Science Foundation (NSF) under NSF CMMI Award No. 2113558 and No. 2331017. Y. Z. acknowledges the support of NSF CMMI Award No. 2113474. S. G. acknowledges the ND-ACES Doctoral STEM Teaching Assistantship Award from ND EPSCoR. W. X., A. A., L. Yang and S. G. also acknowledge the support of NSF OIA ND-ACES Award No. 1946202. This work used the resources of the Center for Computationally Assisted Science and Technology (CCAST) at North Dakota State University, which were made possible in part by NSF MRI Award No. 2019077.References
- K. Peng, L. Fu, H. Yang and J. Ouyang, Perovskite LaFeO3/montmorillonite nanocomposites: synthesis, interface characteristics and enhanced photocatalytic activity, Sci. Rep., 2016, 6, 1–10 CrossRef PubMed.
- S.-S. Feng, L. Mei, P. Anitha, C. W. Gan and W. Zhou, Poly (lactide)–vitamin E derivative/montmorillonite nanoparticle formulations for the oral delivery of Docetaxel, Biomaterials, 2009, 30, 3297–3306 CrossRef CAS PubMed.
- P. Sellin and O. X. Leupin, The use of clay as an engineered barrier in radioactive-waste management – a review, Clays Clay Miner., 2013, 61, 477–498 CrossRef CAS.
- N. Rong, C. Chen, K. Ouyang, K. Zhang, X. Wang and Z. Xu, Adsorption characteristics of directional cellulose nanofiber/chitosan/montmorillonite biomimetic aerogel as adsorbent for wastewater treatment, Sep. Purif. Technol., 2021, 1–13 Search PubMed.
- H. Man-Chao, F. Zhi-Jie and Z. Ping, Atomic and electronic structures of montmorillonite in soft rock, Chin. Phys. B, 2009, 18, 2933–2937 CrossRef.
- S. Ghazanfari, Y. Han, W. Xia and D. S. Kilin, First-Principles Study on Optoelectronic Properties of Fe-Doped Montmorillonite Clay, J. Phys. Chem. Lett., 2022, 13, 4257–4262 CrossRef CAS PubMed.
- D. Savage, J. Wilson, S. Benbow, H. Sasamoto, C. Oda, C. Walker, D. Kawama and Y. Tachi, Natural systems evidence for the effects of temperature and the activity of aqueous silica upon montmorillonite stability in clay barriers for the disposal of radioactive wastes, Appl. Clay Sci., 2019, 179, 105146 CrossRef CAS.
- F. Bergaya and G. Lagaly, Handbook of Clay Science, Newnes, 2013 Search PubMed.
- X. Du, D. Pang, Y. Cheng, Y. Zhao, Z. Hou, Z. Liu, T. Wu and C. Shu, Adsorption of CH4, N2, CO2, and their mixture on montmorillonite with implications for enhanced hydrocarbon extraction by gas injection, Appl. Clay Sci., 2021, 210, 106160 CrossRef CAS.
- D. J. K. Ross and R. M. Bustin, The importance of shale composition and pore structure upon gas storage potential of shale gas reservoirs, Mar. Pet. Geol., 2009, 26, 916–927 CrossRef CAS.
- V. N. Romanov, Evidence of irreversible CO2 intercalation in montmorillonite, Int. J. Greenhouse Gas Control, 2013, 14, 220–226 CrossRef CAS.
- S. Tashiro, A. Fujiwara and M. Senoo, Study on the permeability of engineered barriers for the enhancement of a radioactive waste repository system, Nucl. Technol., 1998, 121, 14–23 CrossRef CAS.
- Y. Yang, R. Qiao, Y. Wang and S. Sun, Swelling pressure of montmorillonite with multiple water layers at elevated temperatures and water pressures: a molecular dynamics study, Appl. Clay Sci., 2021, 201, 105924 CrossRef CAS.
- B. Pastina, P. Hellä, Expected evolution of a spent nuclear fuel repository at Olkiluoto, Posiva Oy, 2006 Search PubMed.
- L. Brochard, Swelling of Montmorillonite from Molecular Simulations: Hydration Diagram and Confined Water Properties, J. Phys. Chem. C, 2021, 125, 15527–15543 CrossRef CAS.
- M. Chávez-Páez, K. Van Workum, L. De Pablo and J. J. de Pablo, Monte Carlo simulations of Wyoming sodium montmorillonite hydrates, J. Chem. Phys., 2001, 114, 1405–1413 CrossRef.
- R. T. Cygan, V. N. Romanov and E. M. Myshakin, Molecular simulation of carbon dioxide capture by montmorillonite using an accurate and flexible force field, J. Phys. Chem. C, 2012, 116, 13079–13091 CrossRef CAS.
- J. A. Greathouse, R. T. Cygan, J. T. Fredrich and G. R. Jerauld, Molecular dynamics simulation of diffusion and electrical conductivity in montmorillonite interlayers, J. Phys. Chem. C, 2016, 120, 1640–1649 CrossRef CAS.
- S. Karaborni, B. Smit, W. Heidug, J. Urai and E. Van Oort, The swelling of clays: molecular simulations of the hydration of montmorillonite, Science, 1996, 271, 1102–1104 CrossRef CAS.
- K. B. Thapa, K. S. Katti and D. R. Katti, Influence of the fluid polarity on shear strength of sodium montmorillonite clay: A steered molecular dynamics study, Comput. Geotech., 2023, 158, 105398 CrossRef.
- Y. Zheng, A. Zaoui and I. Shahrour, Evolution of the interlayer space of hydrated montmorillonite as a function of temperature, Am. Mineral., 2010, 95, 1493–1499 CrossRef CAS.
- S. Tripathy, H. R. Thomas and R. Bag, Geoenvironmental application of bentonites in underground disposal of nuclear waste: characterization and laboratory tests, J. Hazard., Toxic Radioact. Waste, 2017, 21, D4015002 CrossRef.
- T. Húlan, A. Trnik, I. Štubňa, P. Bačík, T. Kaljuvee and L. Vozar, Development of Young's modulus of illitic clay during heating up to 1100 C, Mater. Sci., 2015, 21, 429–434 CrossRef.
- S. Hedan, F. Hubert, D. Pret, E. Ferrage, V. Valle and P. Cosenza, Measurement of the elastic properties of swelling clay minerals using the digital image correlation method on a single macroscopic crystal, Appl. Clay Sci., 2015, 116, 248–256 CrossRef.
- C. Bobko and F.-J. Ulm, The nano-mechanical morphology of shale, Mech. Mater., 2008, 40, 318–337 CrossRef.
- N. H. Mondol, J. Jahren, K. Bjørlykke and I. Brevik, Elastic properties of clay minerals, Lead. Edge, 2008, 27, 758–770 CrossRef.
- B. Chen and J. R. G. Evans, Elastic moduli of clay platelets, Scr. Mater., 2006, 54, 1581–1585 CrossRef CAS.
- J. A. Ortega, F.-J. Ulm and Y. Abousleiman, The effect of the nanogranular nature of shale on their poroelastic behavior, Acta Geotech., 2007, 2, 155–182 CrossRef.
- H.-R. Wenk, I. Lonardelli, H. Franz, K. Nihei and S. Nakagawa, Preferred orientation and elastic anisotropy of illite-rich shale, Geophysics, 2007, 72, E69–E75 CrossRef.
- T. Vanorio, M. Prasad and A. Nur, Elastic properties of dry clay mineral aggregates, suspensions and sandstones, Geophys. J. Int., 2003, 155, 319–326 CrossRef CAS.
- L. E. McNeil and M. Grimsditch, Elastic moduli of muscovite mica, J. Phys.: Condens. Matter, 1993, 5, 1681 CrossRef CAS.
- W.-M. Ye, Z. J. Zheng, B. Chen, Y.-G. Chen, Y.-J. Cui and J. Wang, Effects of pH and temperature on the swelling pressure and hydraulic conductivity of compacted GMZ01 bentonite, Appl. Clay Sci., 2014, 101, 192–198 CrossRef CAS.
- A. Alesadi, Z. Cao, Z. Li, S. Zhang, H. Zhao, X. Gu and W. Xia, Machine learning prediction of glass transition temperature of conjugated polymers from chemical structure, Cell Rep. Phys. Sci., 2022, 100911 CrossRef CAS.
- A. B. Croll, Y. Liao, Z. Li, W. M. A. Jayawardana, T. Elder and W. Xia, Sticky crumpled matter, Matter, 2022, 5(6), 1792–1805 CrossRef.
- Y. Liao, Z. Li, S. Ghazanfari, Fatima, A. B. Croll and W. Xia, Understanding the role of self-adhesion in crumpling behaviors of sheet macromolecules, Langmuir, 2021, 37(28), 8627–8637 CrossRef CAS PubMed.
- D. R. Katti, K. S. Katti, K. B. Thapa, H. M. Faisal, M. P. Consortium, Development of Models for the Prediction of Shear Strength of Swelling Clays, Mountain Plains Consortium, 2019 Search PubMed.
- H. M. N. Faisal, K. S. Katti and D. R. Katti, Molecular mechanics of the swelling clay tactoid under compression, tension and shear, Appl. Clay Sci., 2021, 200, 105908 CrossRef CAS.
- S. Ghazanfari, H. M. N. Faisal, K. S. Katti, D. R. Katti and W. Xia, A Coarse-Grained Model for the Mechanical Behavior of Na-Montmorillonite Clay, Langmuir, 2022, 38(16), 4859–4869 CrossRef CAS PubMed.
- T. Honorio, L. Brochard and M. Vandamme, Hydration phase diagram of clay particles from molecular simulations, Langmuir, 2017, 33, 12766–12776 CrossRef CAS PubMed.
- S. Izrailev, S. Stepaniants, B. Isralewitz, D. Kosztin, H. Lu, F. Molnar, W. Wriggers and K. Schulten, in Computational molecular dynamics: Challenges, methods, ideas, Springer, 1999, pp. 39–65 Search PubMed.
- L. Ruiz Pestana, K. Kolluri, T. Head-Gordon and L. N. Lammers, Direct exchange mechanism for interlayer ions in non-swelling clays, Environ. Sci. Technol., 2017, 51, 393–400 CrossRef CAS PubMed.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- M. Holmboe and I. C. Bourg, Molecular dynamics simulations of water and sodium diffusion in smectite interlayer nanopores as a function of pore size and temperature, J. Phys. Chem. C, 2014, 118, 1001–1013 CrossRef CAS.
- L. N. Lammers, I. C. Bourg, M. Okumura, K. Kolluri, G. Sposito and M. Machida, Molecular dynamics simulations of cesium adsorption on illite nanoparticles, J. Colloid Interface Sci., 2017, 490, 608–620 CrossRef CAS PubMed.
- R. T. Cygan, J.-J. Liang and A. G. Kalinichev, Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field, J. Phys. Chem. B, 2004, 108, 1255–1266 CrossRef CAS.
- R. S. Mulliken, Electronic population analysis on LCAO–MO molecular wave functions. II. Overlap populations, bond orders, and covalent bond energies, J. Chem. Phys., 1955, 23, 1841–1846 CrossRef CAS.
- L. E. Chirlian and M. M. Francl, Atomic charges derived from electrostatic potentials: A detailed study, J. Comput. Chem., 1987, 8, 894–905 CrossRef CAS.
- C. M. Breneman and K. B. Wiberg, Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis, J. Comput. Chem., 1990, 11, 361–373 CrossRef CAS.
- J. D. Gale, GULP: a computer program for the symmetry-adapted simulation of solids, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- J. D. Gale, Empirical potential derivation for ionic materials, Philos. Mag. B, 1996, 73, 3–19 CrossRef CAS.
- C. Tournassat, I. C. Bourg, M. Holmboe, G. Sposito and C. I. Steefel, Molecular dynamics simulations of anion exclusion in clay interlayer nanopores, Clays Clay Miner., 2016, 64, 374–388 CrossRef CAS.
- R. E. Grim and G. Kulbicki, Montmorillonite: high temperature reactions and classification, Am. Mineral., 1961, 46, 1329–1369 CAS.
- B. K. Benazzouz and A. Zaoui, Melting Behaviour under Pressure of Kaolinite Clay: A Nanoscale Study, Minerals, 2023, 13, 679 CrossRef CAS.
- E. V Tararushkin, V. V Pisarev and A. G. Kalinichev, Equation of State, Compressibility, and Vibrational Properties of Brucite over Wide Pressure and Temperature Ranges: Atomistic Computer Simulations with the Modified ClayFF Classical Force Field, Minerals, 2023, 13, 408 CrossRef.
- M. Holmboe, atom: A MATLAB package for manipulation of molecular systems, Clays Clay Miner., 2019, 67, 419–426 CrossRef.
- H. Heinz, H. Koerner, K. L. Anderson, R. A. Vaia and B. L. Farmer, Force field for mica-type silicates and dynamics of octadecylammonium chains grafted to montmorillonite, Chem. Mater., 2005, 17, 5658–5669 CrossRef CAS.
- H. Heinz, T.-J. Lin, R. Kishore Mishra and F. S. Emami, Thermodynamically consistent force fields for the assembly of inorganic, organic, and biological nanostructures: the INTERFACE force field, Langmuir, 2013, 29, 1754–1765 CrossRef CAS PubMed.
- F. Bergaya and G. Lagaly, General introduction: clays, clay minerals, and clay science, Dev. Clay Sci., 2006, 1, 1–18 CAS.
- E. Akalin, S. Akyuz and T. Akyuz, Adsorption and interaction of 5-fluorouracil with montmorillonite and saponite by FT-IR spectroscopy, J. Mol. Struct., 2007, 834, 477–481 CrossRef.
- A. Jha, A. C. Garade, M. Shirai and C. V Rode, Metal cation-exchanged montmorillonite clay as catalysts for hydroxyalkylation reaction, Appl. Clay Sci., 2013, 74, 141–146 CrossRef CAS.
- D. Zhang, C.-H. Zhou, C.-X. Lin, D.-S. Tong and W.-H. Yu, Synthesis of clay minerals, Appl. Clay Sci., 2010, 50, 1–11 CrossRef CAS.
- F. Uddin, Montmorillonite: an introduction to properties and utilization, IntechOpen, London, 2018 Search PubMed.
- B. R. Bickmore, K. M. Rosso, K. L. Nagy, R. T. Cygan and C. J. Tadanier, Ab initio determination of edge surface structures for dioctahedral 2:1 phyllosilicates: Implications for acid-base reactivity, Clays Clay Miner., 2003, 51, 359–371 CrossRef CAS.
- Y. Liao, Z. Li and W. Xia, Size-dependent structural behaviors of crumpled graphene sheets, Carbon, 2021, 174, 148–157 CrossRef CAS.
- S. Plimpton, R. Pollock, M. Stevens, Particle-Mesh Ewald and rRESPA for Parallel Molecular Dynamics Simulations, PPSC, 1997, pp. 1–13 Search PubMed.
- Y. Wang, Z. Li, K. Niu and W. Xia, Energy renormalization for coarse-graining of thermomechanical behaviors of conjugated polymer, Polymer, 2022, 256, 125159 CrossRef CAS.
- A. Alesadi and W. Xia, Understanding the Role of Cohesive Interaction in Mechanical Behavior of a Glassy Polymer, Macromolecules, 2020, 53, 2754–2763 CrossRef CAS.
- A. P. Thompson, S. J. Plimpton and W. Mattson, General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions, J. Chem. Phys., 2009, 131, 154107 CrossRef PubMed.
- Z. Li, Y. Liao, Y. Zhang, Y. Zhang and W. Xia, Microstructure and dynamics of nanocellulose films: Insights into the deformational behavior, Extreme Mech. Lett., 2022, 50, 101519 CrossRef.
- H. Yang, M. He, C. Lu and W. Gong, Deformation and failure processes of kaolinite under tension: Insights from molecular dynamics simulations, Sci. China: Phys., Mech. Astron., 2019, 62, 1–9 CrossRef.
- L.-L. Zhang, Y.-Y. Zheng, P.-C. Wei, Q.-F. Diao and Z.-Y. Yin, Nanoscale mechanical behavior of kaolinite under uniaxial strain conditions, Appl. Clay Sci., 2021, 201, 105961 CrossRef CAS.
- P. Wei, Y.-Y. Zheng, Y. Xiong, S. Zhou, K. Al-Zaoari and A. Zaoui, Effect of water content and structural anisotropy on tensile mechanical properties of montmorillonite using molecular dynamics, Appl. Clay Sci., 2022, 228, 106622 CrossRef CAS.
- G. D. Zartman, H. Liu, B. Akdim, R. Pachter and H. Heinz, Nanoscale tensile, shear, and failure properties of layered silicates as a function of cation density and stress, J. Phys. Chem. C, 2010, 114, 1763–1772 CrossRef CAS.
- D. R. Katti, S. R. Schmidt, P. Ghosh and K. S. Katti, Modeling the response of pyrophyllite interlayer to applied stress using steered molecular dynamics, Clays Clay Miner., 2005, 53, 171–178 CrossRef CAS.
- W.-S. Xu, J. F. Douglas and K. F. Freed, Influence of cohesive energy on the thermodynamic properties of a model glass-forming polymer melt, Macromolecules, 2016, 49, 8341–8354 CrossRef CAS.
- H. R. Jappor, M. A. Abdulsattar and A. M. Abdul-Lettif, Electronic structure of AlP under pressure using semiempirical method, Open Condens. Matter Phys. J., 2010, 3, 1–7 CrossRef CAS.
- A. Goyal, I. Palaia, K. Ioannidou, F.-J. Ulm, H. Van Damme, R. J.-M. Pellenq, E. Trizac and E. Del Gado, The physics of cement cohesion, Sci. Adv., 2021, 7, eabg5882 CrossRef CAS PubMed.
- P. Wei, D. Zhuang, Y.-Y. Zheng, A. Zaoui and W. Ma, Temperature and pressure effect on tensile behavior of ice-Ih under low strain rate: a molecular dynamics study, J. Mol. Liq., 2022, 355, 118945 CrossRef CAS.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, The missing term in effective pair potentials, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- S. Węglarczyk, in ITM Web of Conferences, EDP Sciences, 2018, vol. 23, p. 37 Search PubMed.
- B. A. Baldo, Perioperative reactions to sugammadex, Curr. Treat. Options Allergy, 2020, 7, 43–63 CrossRef.
- N. Kaur and D. Kishore, Montmorillonite: an efficient, heterogeneous and green catalyst for organic synthesis, J. Chem. Pharm. Res., 2012, 4, 991–1015 CAS.
- E. Tombácz and M. Szekeres, Surface charge heterogeneity of kaolinite in aqueous suspension in comparison with montmorillonite, Appl. Clay Sci., 2006, 34, 105–124 CrossRef.
- P. H. Hsu, Heterogeneity of montmorillonite surface and its effect on the nature of hydroxy-aluminum interlayers, Clays Clay Miner., 1968, 16, 303–311 CrossRef.
- J. L. McATEE, Heterogeneity in montmorillonite, Clays Clay Miner., 1956, 5, 279–288 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Probability distribution of local molecular stiffness 1/〈u2〉 of the Na-MMT system for different atom types at zero pressure and 1700 K temperature; probability distribution of local molecular stiffness 1/〈u2〉 of the Na-MMT system for different atom types at 1000 atm pressure and 300 K temperature. See DOI: https://doi.org/10.1039/d3na00365e |
| This journal is © The Royal Society of Chemistry 2023 |