 Open Access Article
Open Access ArticleCurrent rectification by nanoparticles in bipolar nanopores†
Andrés
Córdoba
 ad,
Joan M.
Montes de Oca
ad,
Joan M.
Montes de Oca
 ad,
Johnson
Dhanasekaran
ad,
Johnson
Dhanasekaran
 ad,
Seth B.
Darling
ad,
Seth B.
Darling
 abd and
Juan J.
de Pablo
abd and
Juan J.
de Pablo
 *acd
*acd
aPritzker School of Molecular Engineering, University of Chicago, Chicago, Illinois 60637, USA. E-mail: depablo@uchicago.edu
bChemical Sciences and Engineering Division, Argonne National Laboratory, Lemont, Illinois 60439, USA
cMaterials Science Division, Argonne National Laboratory, Lemont, Illinois 60439, USA
dAdvanced Materials for Energy-Water Systems (AMEWS) Energy Frontier Research Center, Argonne National Laboratory, Lemont, Illinois 60439, USA
First published on 25th October 2022
Abstract
Bipolar nanochannels comprising two domains of positively and negatively charged walls along the pore axis are known to rectify current when exposed to an electric potential bias. We find that addition of charged nanoparticles can increase rectification considerably, by approximately one order of magnitude. Two bipolar channel geometries are considered here; their behavior is examined at rest and under the influence of a negative bias and a positive bias, respectively. We do so by relying on a molecular-level model of the electrolyte solution in the channels. The large increase in current rectification can be explained by the inherent electric field that charged nanoparticles generate within the channel. This effect is found to be largely dependent on the pore's geometry, its charge distribution, and the sign of the nanoparticles' charge, thereby offering new opportunities for design of engineered nanopore membrane-nanoparticle systems for energy storage.
Design, System, ApplicationBipolar nanopores with at least two regions of opposite charge along the pore axis can rectify electric current when exposed to an electric potential bias. An important application of bipolar nanopores is in membranes used in reverse electrodialysis (RED) processes. In RED, an electric current is harvested due to the asymmetric concentration of ions that arises in an electrolyte when held in two reservoirs connected by a membrane system. Bipolar nanopores have recently been shown to increase the efficiency of RED processes. Our work utilizes coarse-grained simulations to study the effect of adding small quantities of nanoparticles on the current rectification properties of bipolar nanopores. Charged nanoparticles can significantly increase rectification, but this effect is largely dependent on the pore's geometry, its charge distribution, and the sign of the nanoparticles' charge. Therefore our computational and theoretical results provide a framework to guide the molecular design of systems containing bipolar nanopores and nanoparticles. |
1 Introduction
Permselective-media-based bipolar diodes consist of pores with at least two regions of opposite charge. These bipolar nanopores are interesting from both a fundamental point of view and from a technological perspective. Bipolar nanopores can exhibit powerful rectification properties due to the asymmetry of a charge pattern along the wall of the pore. In this context, rectification refers to the nanopores' ability to generate a preferred direction in the transport of electric current. For the particular case of bipolar pores having separate positive and negative surface charge domains along the pore axis, rectification is significant if the radius of the nanopore is small compared to the screening length of the electrolyte. This ionic rectification is accompanied by the formation of depletion zones for both cations and anions along the main axis of the pore, whose extent depends on the magnitude and sign of the applied external voltage.1 A bipolar diode comprises a negatively charged region and a positively charged region; when their surface charge densities have the same absolute value, one has a so-called nanofluidic diode. By modifying the surface charge density in the middle section of the channel, one can form a nanofluidic bipolar transistor.2 Experimental work on bipolar nanopores has examined a range of properties, including ionic current rectification, breakdown, and switching in heterogeneous oxide nanofluidic devices.3,4Janus membranes composed of bipolar nanopores have recently been used to increase the efficiency of reverse electrodialysis (RED). In RED, an electric current is harvested due to the asymmetric concentration of ions that arises in an electrolyte when held in two reservoirs connected by a membrane system.5,6 At large scales this can be accomplished by placing RED membranes at river mouths where river water mixes with sea water. In the typical membrane-based RED process, the practical power output is limited by non-ohmic mass-transfer resistances. These resistances are caused by the accumulation of ions inside the membrane's charged nanopores near the side that interfaces with the low concentration reservoir.5,7 This accumulation lowers the concentration difference across the membrane and suppresses ionic transport. This is a common limitation in traditional RED but it can be eliminated with an asymmetric bipolar membrane, which considerably increases the output power density.8–11 In this work we do not impose a concentration difference across the nanopores, we instead apply a voltage bias, and therefore we do not explicitly model a RED process. However, with the approach employed here the effect of small concentrations of charged nanoparticles in the current–voltage relationship of bipolar nanopores can be examined.
While important theoretical and experimental advances have led to a better understanding of the fundamental physics at work in bipolar nanopores, the coupled roles of nanopore geometry and the addition of small concentrations of charged nanoparticles on ion transport and electric current rectification have not been considered before. In previous work,12 we calculated and analyzed the cation and anion concentration profiles and current–voltage relationship of dilute electrolytes in bipolar nanopores at rest and under applied biases of +2 V and −2 V, respectively. In this work we discuss the effect of adding small quantities of nanoparticles on the concentration profiles and current rectification properties of bipolar nanopores. Our results indicate that rectification can be increased considerably, raising distinct opportunities for development of practical devices for energy storage.
Several theoretical studies of the current–voltage relationship have been reported for membranes consisting of two fixed charge regions of opposite sign. That body of work has relied on solution of the underlying diffusion equations in conjunction with the Poisson–Boltzmann equation.13,14 An analysis of four 1D permselective membranes adjacent to each other has also been presented.15 Due to the complexity of such systems, however, a number of simplifications have generally been made, such as assuming linear concentration and electric potential profiles within the permselective regions.15 A simple theory for multi-ionic transport, non-equilibrium water dissociation, and space-charge effects in bipolar membranes was developed on the basis of some of the concepts used to describe solid-state P–N junctions;16 specifically, ion transport was modeled in terms of the Nernst–Planck flux equation and non-equilibrium water dissociation was accounted for by the Onsager theory of the second Wien effect.16 An important finding of that study was the concept of rectification, whereby a preferred direction in the transport of current can be achieved.
Analytical expressions for the current–voltage, or I–V response of bipolar nanopores have been derived under a set of ad hoc assumptions. With these expressions,17 it has been proposed that, in theory, the surface charge asymmetry could lead to simple nanofluidic-based diodes whose rectification (depending on geometry) can be as large as 102–103. This means that the electric current generated by, for example, a positive voltage can be up to a thousand times larger than the current generated by a voltage of the same magnitude but negative sign. Other work has investigated the effects of a single non-ideal permselective region (three-layers system),7 and a complete theoretical model of a bipolar diode consisting of a four-layered model (two microchambers and two permselective regions) has also been derived under the assumption of cross-sectional local electroneutrality.17 More recently, the possibility of nano-fluidic RED for energy harvesting from salinity gradients has been evaluated by considering ion transport in bilayer cylindrical nanochannels consisting of different sized nanopores, connected to two large reservoirs having different NaCl concentrations. In that work, numerical simulations at the level of coupled Poisson–Nernst–Planck and Navier–Stokes equations have been used to describe the electrokinetic behavior over asymmetric sub-pore lengths, and to predict the effects of surface charge on transference number, osmotic current, diffusive voltage, maximum power and maximum power efficiency.18
Multiscale modeling approaches have also been used before to study charged nanopores.19–21 The validity of the mean-field approximation in Poisson–Nernst–Planck theory has been established by contrasting its predictions with those of Brownian dynamics simulations in both model cylindrical channels and in a more realistic potassium channel. However, in simple cylindrical channels, considerable differences arise between these two levels of description with regards to the concentration profiles in the channel and the corresponding conductance properties. These differences are more pronounced in narrow channels having a radius smaller than the Debye length, and gradually diminish with increasing radius. Convergence occurs when the channel radius is over two Debye lengths.19,20
In recent years, the ability to fabricate carefully designed nanopores has renewed interest in such systems. Bipolar nanochannels have been studied using three modeling levels1,21 that include (1) an all-atom explicit-water model studied with molecular dynamics, and reduced models with implicit water containing (2) hard-sphere ions studied through a “local equilibrium Monte Carlo” simulation method (which determines ionic correlations accurately), and (3) point ions studied with Poisson–Nernst–Planck theory (mean-field approximation). It has been shown that reduced models are able to reproduce key device functionalities (e.g. rectification and selectivity) for a wide variety of charge patterns; that is, reduced models are useful in understanding the mesoscale physics of the device (e.g. how the current is produced). Multiscale approaches have also been used to examine the relationship of reduced implicit-water models to explicit-water models, and have proposed that diffusion coefficients in reduced models can be treated as adjustable parameters for comparisons between explicit- and implicit-water models.21 It has also been reported that the values of the diffusion coefficients are sensitive to the net charge of the pore, but are relatively transferable to different voltages and charge patterns with the same total charge.21
In this work we employ molecular dynamics simulations with explicit ions and an implicit solvent. The parameters for the ion–ion effective potentials are obtained from systematically coarse-graining all-atom interactions. The use of an implicit solvent does not allow to account for electroconvective mechanisms in the ionic transport inside the bipolar nanopores.22–24 However in charged nanopores there is a regime where a decoupling of the electrodiffusive problem from the electroconvective problem occurs. This decoupling is determined by the smallness of the electroconvective Péclet number.25,26 In bipolar nanopores the assumption of Pé ≪ 1 holds in the low-voltage ohmic region of the I–V curve, at voltages beyond the ohmic region convection effects can become important. Models of charged nanopores based on the Poisson–Nernst–Planck theory7,17,26,27 are based on the Pé ≪ 1 assumption. The MD simulations presented here are valid in that same regime. Moreover the discrete nature of the simulation method allows us to study the effect that nanoparticles with a surface charge distribution have on the rectification properties of bipolar nanopores.
2 Methods
2.1 Ions model
The coarse-grained, CG, parameters of the ion–ion effective potentials were obtained using relative entropy coarse-graining, RE-CG,28 which provides a systematic approach to obtaining effective potentials for use in CG simulations, given a mapping function from all-atom, AA, to CG coordinates.29 The CG non-bonded effective potentials between ions are represented as the sum of a coulombic interaction and a correction term, Ucorr, as follows,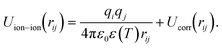 | (1) |
2.2 Nanopores model
The nanopores considered here are channels with a slit geometry that is periodic in the x and y coordinates. The total size of the simulation box is set to 70 nm × 20 nm × 30.1 nm. The height of the channels and the wall charge density as a function of length, [h(x), σ(x)], is given by, | (2) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 5 nm in eqn (2). In this channel for −30 nm ≤ x ≤ −5 nm the wall charge density is σ1 = +0.1 C m−2 and the surface area of the wall in this section is S1 = 1000 nm2. For −5 nm ≤ x ≤ 20 nm the wall charge density is σ2 = −0.1 C m−2, and the surface area of the wall in this section is also S2 = 1000 nm2. The wall charge density is σ≠1,2 = 0 C m−2 for the rest of the walls, including the walls between sections of different height and walls that are perpendicular to the x axis. The sections at the end of the channel, where the wall charge is zero, are intended to act as reservoirs. The total volume of C1 is VC1 = 25
= 5 nm in eqn (2). In this channel for −30 nm ≤ x ≤ −5 nm the wall charge density is σ1 = +0.1 C m−2 and the surface area of the wall in this section is S1 = 1000 nm2. For −5 nm ≤ x ≤ 20 nm the wall charge density is σ2 = −0.1 C m−2, and the surface area of the wall in this section is also S2 = 1000 nm2. The wall charge density is σ≠1,2 = 0 C m−2 for the rest of the walls, including the walls between sections of different height and walls that are perpendicular to the x axis. The sections at the end of the channel, where the wall charge is zero, are intended to act as reservoirs. The total volume of C1 is VC1 = 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 nm3.
500 nm3.
The second channel is denoted C2 and in it the negatively charged section is four times longer than the positively charged section. Therefore ![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) = 20 nm in eqn (2). And for −30 nm ≤ x ≤ −20 nm the wall charge density is σ1 = +0.24 C m−2 and the surface area of the wall in this section is S1 = 400 nm2. For −20 nm ≤ x ≤ 20 nm the wall charge density is σ2 = −0.08 C m−2, and the surface area of the wall in this section is S2 = 1600 nm2. The wall charge density is σ≠1,2 = 0 C m−2 for the rest of the walls, including the walls between sections of different height and walls that are perpendicular to the x axis. The sections at the end of the channel, where the wall charge is zero, are intended to act as reservoirs. The total volume of C2 is VC2 = 23
= 20 nm in eqn (2). And for −30 nm ≤ x ≤ −20 nm the wall charge density is σ1 = +0.24 C m−2 and the surface area of the wall in this section is S1 = 400 nm2. For −20 nm ≤ x ≤ 20 nm the wall charge density is σ2 = −0.08 C m−2, and the surface area of the wall in this section is S2 = 1600 nm2. The wall charge density is σ≠1,2 = 0 C m−2 for the rest of the walls, including the walls between sections of different height and walls that are perpendicular to the x axis. The sections at the end of the channel, where the wall charge is zero, are intended to act as reservoirs. The total volume of C2 is VC2 = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 nm3.
400 nm3.
The systems are always globally neutral, i.e., S1σ1 + S2σ2 = zcenc + zaena + zpenp. Where na is the total number of anions (chloride) in the simulation box and eza = −e is the charge of each anion. e ≈ 1.6 × 10−19 C is the elementary charge. nc is the total number of cations (sodium) and ezc = +e is the charge of each cation. np is the total number of nanoparticles in the simulation box and ezp is the charge of each nanoparticle. The Debye length which is used to estimate the size of the electrical double layer is 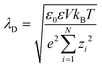 . Where V is the volume of the pore and N is the total number of charged particles in the solution that flows through the pore. In all the simulations presented in this work λD ≈ 0.95 nm.
. Where V is the volume of the pore and N is the total number of charged particles in the solution that flows through the pore. In all the simulations presented in this work λD ≈ 0.95 nm.
In our coarse grained MD simulations the channel walls are modeled with a combination of neutral and charged sites that are kept fixed in space at their initial position. The charged wall sites are placed at random positions along the walls. The proportion of charged to neutral sites in a (charged) wall is determined by the wall charge density, the surface area of the wall, and by the charge of the wall charged sites. Each charged wall site is assigned a charge of ±0.25e and interacts with the ions through Coulomb interactions.
Additionally, all wall sites, charged and uncharged, interact with the ions in solution through a repulsive Lennard-Jones potential,
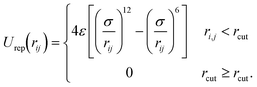 | (3) |
To apply the electric potential bias between the two ends of the bipolar nanopores we use a method commonly employed in MD simulations and that has been previously shown to be a valid approach.30 The method consists of applying a uniform electric field throughout the entire simulated periodic cell containing the nanopore. The external electric field E(r) is related to the external electric potential, ψE(r), by E(r) = −∇ψE(r). In our simulations the external electric field is applied in the x direction, E(r) = Exδx, where δx is the unit vector in the x direction and Ex = ±0.0286 V nm−1. The total length of the pores in the x direction is L = 70 nm. The voltage bias is defined as ΔV = ψE(x = 30 nm) − ψE(x = −40 nm). Therefore when Ex = −0.0286 V nm−1, ΔV = −Ex/L = +2 V. And when Ex = +0.0286 V nm−1, ΔV = −Ex/L = −2 V.
2.3 Dynamics
The coarse grained MD simulations were performed using LAMMPS31 in the NVT ensemble using the Grønbench-Jensen–Farago (G-J–F) Langevin thermostat,32,33 with a damping factor of τionsm = 10 × 10−15 s. The value of τionsm has been chosen such that the electric currents in our simulations are of a similar magnitude to what has been measured experimentally in nanofluidic diodes for the same applied voltage biases.4 A time step Δt = 2 × 10−15 s and a temperature of 297 K were used in all simulations. All the coulombic interactions were calculated using the particle mesh Ewald solver, which splits the calculation into a real space sum for the short-range forces and a Fourier space sum for the long-range forces. The real space cutoff was set to 1.2 nm and for the Fourier space sum we used a modification of the three-dimensional Ewald summation technique for calculation in systems with a slab geometry that are periodic in two dimensions and have a finite length in the third dimension.342.4 Nanoparticle model
Each nanoparticle is modeled by placing eight charged sites in the corners of a cube with sides of length 0.8 nm. Each site in the nanoparticle is assigned a charge of ±e, therefore the total charge of each nanoparticle is ezp = ±8e. In our simulations, the relative distance between these sites is held approximately constant by using stiff harmonic springs. More specifically, adjacent sites are bonded by a spring with an equilibrium length of 0.8 nm and a spring constant of 1.2 × 105kBT/nm2. Sites in opposite corners of the cube are bonded by a harmonic potential with equilibrium length of 1.39 nm and an energy barrier of 1.2 × 105kBT/nm2. Triplets of adjacent sites in the nanoparticles are also constrained with an angle potential with equilibrium value of 90° and an energy barrier of 5.1 × 102kBT. The nanoparticle model used here is intended as a simple representation of a nano-scale object with a surface charge distribution. To estimate the charge density of the nanoparticles we consider a cube of side length 0.8 nm. Therefore each nanoparticle has a surface area of 3.84 nm2. Since each nanoparticle has eight charged sites with a charge of ±e the surface charge density is ±0.33 C m−2. The total mass of each nanoparticle is mnp = 305.6 × 10−23 g (i.e. 1839 g mol−1). The same damping factor used for the ions is employed for the nanoparticles in the Langevin thermostat, τnpm = τionsm. Additional replicas of some of the simulations were performed with a larger τnpm, details on these are given in subsection 2.8 below. The nanoparticle sites as well as the charged wall sites interact with the ions and with each other through Coulomb's law. All wall sites, charged and uncharged, as well as the nanoparticle sites also interact with the ions and with each other through the repulsive Lennard-Jones potential given in eqn (3).2.5 Diffusion coefficients
The diffusion coefficient of anions, cations and nanoparticles inside the confined environment of the nanopores are calculated from the mean-squared displacement, 〈Δr2(t)〉eq, of each species inside the nanopores. This calculation is done without a voltage bias applied and therefore 〈…〉eq indicates an average at equilibrium. Specifically the diffusion constants are obtained from the relation![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) eff = 〈Δr2(t)〉eq/(6t). See Fig. S7 of the ESI† for plots of the mean-squared displacements and see Table S2 also in the ESI† with the diffusion coefficients for each species in each system. The diffusion coefficient for each species does not change significantly from one system to another. The average values are,
eff = 〈Δr2(t)〉eq/(6t). See Fig. S7 of the ESI† for plots of the mean-squared displacements and see Table S2 also in the ESI† with the diffusion coefficients for each species in each system. The diffusion coefficient for each species does not change significantly from one system to another. The average values are, 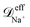 ≈ 9.05 × 10−10 m2 s−1,
≈ 9.05 × 10−10 m2 s−1, 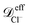 ≈ 5.85 × 10−10 m2 s−1 and
≈ 5.85 × 10−10 m2 s−1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) effnp ≈ 0.24 × 10−10 m2 s−1.
effnp ≈ 0.24 × 10−10 m2 s−1.
The effective diffusion coefficients inside the nanopores observed in the simulations can be compared with the values obtained from a simple hydrodynamic calculation. The simple hydrodynamic calculation assumes that ions and nanoparticles can be treated as spheres. For this estimate the diffusion coefficients are calculated from the relation ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) hyd = kBT/ζhyd, with ζhyd = 6πRη where η is the viscosity of the solvent and R is the hydrodynamic radius of each species. For the nanoparticles we consider that the eight sites that compose it are at a distance 0.69 nm from its center. Also since each site interacts with other species through eqn (3) we add 0.4 × 21/6 = 0.44 nm to the previous value. Therefore Rp ≈ 1.14 nm. The soft-core repulsion radii given above in the ions model subsection are used for the ions. Then, using η ≈ 1 mPa s, the diffusion coefficients given by this calculation are
hyd = kBT/ζhyd, with ζhyd = 6πRη where η is the viscosity of the solvent and R is the hydrodynamic radius of each species. For the nanoparticles we consider that the eight sites that compose it are at a distance 0.69 nm from its center. Also since each site interacts with other species through eqn (3) we add 0.4 × 21/6 = 0.44 nm to the previous value. Therefore Rp ≈ 1.14 nm. The soft-core repulsion radii given above in the ions model subsection are used for the ions. Then, using η ≈ 1 mPa s, the diffusion coefficients given by this calculation are 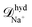 ≈ 8.7 × 10−10 m2 s−1 and
≈ 8.7 × 10−10 m2 s−1 and 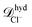 ≈ 4.8 × 10−10 m2 s−1 and
≈ 4.8 × 10−10 m2 s−1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) hydnp ≈ 1.9 × 10−10 m2 s−1. The effective diffusion coefficients for the ions inside the nanopore agree well with the simple hydrodynamic calculation. For the nanoparticles the effective diffusivity in the simulations is about 7.9 times smaller than the one obtained in the simple hydrodynamic calculation. Moreover, below we show that the current rectification results can also be replicated when a smaller friction coefficient is used for the nanoparticles in the simulations.
hydnp ≈ 1.9 × 10−10 m2 s−1. The effective diffusion coefficients for the ions inside the nanopore agree well with the simple hydrodynamic calculation. For the nanoparticles the effective diffusivity in the simulations is about 7.9 times smaller than the one obtained in the simple hydrodynamic calculation. Moreover, below we show that the current rectification results can also be replicated when a smaller friction coefficient is used for the nanoparticles in the simulations.
2.6 Electric current
The electric current that flows through the nanopore as a function of time, is calculated using a commonly employed method,35–37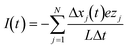 , where the sum is over all the ions and nanoparticles, N, and ezj is the charge of each species. Δxj(t) is the displacement in the x direction of charged species j on the time interval Δt and L is the total length of the channel. Plots of I(t) during 24 ns of our production runs are given in Fig. S5 of the ESI† for all the different systems considered in here. Moreover, in Fig. 3 we have reported the time average of I(t) over those 24 ns of our production runs for all the systems considered in this work. The statistical uncertainties for the electric currents plotted in Fig. 3 and also given in Table S1 in the ESI† were calculated using the blocking transformation method of Flyvbjerg and Petersen,38 specifically eqn (28) in that reference. The blocking transformation method is applicable to estimating statistical error in averages of time series data and properly accounts for the correlation in the data.
, where the sum is over all the ions and nanoparticles, N, and ezj is the charge of each species. Δxj(t) is the displacement in the x direction of charged species j on the time interval Δt and L is the total length of the channel. Plots of I(t) during 24 ns of our production runs are given in Fig. S5 of the ESI† for all the different systems considered in here. Moreover, in Fig. 3 we have reported the time average of I(t) over those 24 ns of our production runs for all the systems considered in this work. The statistical uncertainties for the electric currents plotted in Fig. 3 and also given in Table S1 in the ESI† were calculated using the blocking transformation method of Flyvbjerg and Petersen,38 specifically eqn (28) in that reference. The blocking transformation method is applicable to estimating statistical error in averages of time series data and properly accounts for the correlation in the data.
2.7 Electric potential
To calculate the total electric potential of the nanopores as a function of length, ψ(x), shown in Fig. 4 we use the Poisson equation integrated over the y and z coordinates, i.e.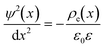 . Where
. Where 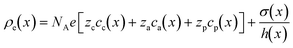 is the charge density as a function of the channel's length (i.e. averaged over the channel's width and depth). Where NA is Avogadro's number, σ(x) and h(x) were defined in eqn (2). cc(x), ca(x) and cp(x) are molar concentration profiles of cations, anions and nanoparticles respectively. Each concentration profile is obtained by averaging 106 simulation frames taken during 24 ns of simulation after the systems have reached steady-state. In each frame the simulation box is divided into cubic bins of (0.8 × 20 × 0.2) nm3. The number of particles of each species inside each bin are counted to calculate the concentrations. The steady-state molar concentration profiles are given in Fig. 2 and S3 and S4 in the ESI.† The Poisson equation is solved with boundary conditions, ψ(x = −40 nm) = 0 and ψ(x = 30 nm) = −Ex/L.
is the charge density as a function of the channel's length (i.e. averaged over the channel's width and depth). Where NA is Avogadro's number, σ(x) and h(x) were defined in eqn (2). cc(x), ca(x) and cp(x) are molar concentration profiles of cations, anions and nanoparticles respectively. Each concentration profile is obtained by averaging 106 simulation frames taken during 24 ns of simulation after the systems have reached steady-state. In each frame the simulation box is divided into cubic bins of (0.8 × 20 × 0.2) nm3. The number of particles of each species inside each bin are counted to calculate the concentrations. The steady-state molar concentration profiles are given in Fig. 2 and S3 and S4 in the ESI.† The Poisson equation is solved with boundary conditions, ψ(x = −40 nm) = 0 and ψ(x = 30 nm) = −Ex/L.
2.8 Reproducibility
To check for reproducibility of the rectification results presented here we have performed additional replicas of the simulations for the system that shows the largest rectification ratio. Moreover we have also performed those replicas using a damping factor for the nanoparticles about 8 times larger than the specified in subsection 2.3. More precisely, a damping factor of τnpm = 7.9τionsm was used for the nanoparticles in the additional replicas. Where the damping factor for the ions is kept the same as that given in subsection 2.3. The damping factor is related to the friction coefficient by ζ = m/τm therefore increasing τnpm by a factor of 7.9 decreases the friction coefficient of the nanoparticles in the Langevin thermostat by a factor of 7.9. Snapshots of the orthographic projections of the initial conditions and steady-state configurations of these replicas are shown in Fig. S8 of the ESI.† The steady-state nanoparticle concentration as a function of the channel length obtained from averaging the four replicas done for C1 with positively charged nanoparticles are shown in the bottom row of Fig. S8.† The mean-squared displacement at equilibrium, 〈Δr2(t)〉eq, of each species inside the nanopores for the replicas with a larger τnpm are given in Fig. S9.† The average values of the diffusion coefficients obtained from these 〈Δr2(t)〉eq are,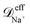 ≈ 9.1 × 10−10 m2 s−1,
≈ 9.1 × 10−10 m2 s−1, 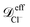 ≈ 6.1 × 10−10 m2 s−1 and
≈ 6.1 × 10−10 m2 s−1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) effnp ≈ 1.0 × 10−10 m2 s−1. Note that for the nanoparticles this diffusion coefficient is about 4 times larger than the one obtained in the simulations with the larger friction coefficient. Fig. S10 and Table S3 in the ESI† show comparisons of the electric currents and the rectification ratios obtained in the different replicas performed.
effnp ≈ 1.0 × 10−10 m2 s−1. Note that for the nanoparticles this diffusion coefficient is about 4 times larger than the one obtained in the simulations with the larger friction coefficient. Fig. S10 and Table S3 in the ESI† show comparisons of the electric currents and the rectification ratios obtained in the different replicas performed.
3 Results and discussion
3.1 Effect of nanoparticle addition on the concentration distributions
Two bipolar nanopore geometries are examined in what follows, namely a pore in which the two oppositely charged sections have the same length and wall charge density, and another in which the section with positive wall charges is four times shorter and has a wall charge density three times larger than the section with negative wall charges. In the first nanopore, referred to as C1, the section with positively charged walls has a charge density of σ1 = +0.1 C m−2. The section with negatively charged walls has a wall charge density of σ2 = −0.1 C m−2. The wall charge density is σ≠1,2 = 0 C m−2 for the rest of the walls. In the second channel, which is referred to as C2, the region with positively charged walls has a wall charge density of σ1 = +0.24 C m−2, and the section with negatively charged walls has a wall charge density of σ2 = −0.08 C m−2. In C2 the wall charge density is also σ≠1,2 = 0 C m−2 for the rest of the walls. The magnitudes of the surfaces charges adopted here are comparable to those found in experimental studies with Janus membranes.8–11 Both geometries feature changes in the height as a function of channel length. In both channels, the section with positively charged walls has a height of 17 nm and the section with negatively charged walls has a height of 10 nm. When nanoparticles are added to the nanopores, the ionic strength of the solution (≈0.1 M) is kept constant. The Debye length of the electrolytic solution is λD ≈ 0.95 nm. Which is an order of magnitude smaller than the height in the narrowest section of the nanochannels considered here. Plots of the ionic concentrations as a function of the channel's height in the wide and narrow sections of the nanopore are given in Fig. S1 in the ESI.†We consider the addition of 10 nanoparticles in both channels. Moreover the effect of changing the surface charge of the nanoparticles from positive to negative is also studied here. Each nanoparticle has a hydrodynamic radius of about 1.14 nm and a surface charge density of about ±0.33 C m−2. See the Methods section above for more details on the nanoparticle model used here. The contributions to the ionic strength from the cations, anions and nanoparticles for the different cases considered here are summarized in Table 1.
| Additive | n c z c e | n a z a e | n w z w e | n p z p e | ||||
|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C1 | C2 | C1 | C2 | C1 | C2 | |
| None | +1535e | +1609e | −1535e | −1409e | 0e | −200e | 0e | 0e |
| Negatively charged | ||||||||
|---|---|---|---|---|---|---|---|---|
| 10 particles | +1535e | +1609e | −1455e | −1329e | 0e | −200e | −80e | −80e |
| Positively charged | ||||||||
|---|---|---|---|---|---|---|---|---|
| 10 particles | +1455e | +1529e | −1535e | −1409e | 0e | −200e | +80e | +80e |
Fig. 1 shows steady state orthographic projections of the two bipolar nanopores as predicted by the coarse-grained molecular dynamics (MD) simulations. Sodium ions are represented as red spheres and chlorine ions as blue spheres and the black spheres represent the interaction sites that make up the channel walls and the nanoparticles. The cases shown in Fig. 1 correspond to nanopores where positively charged nanoparticles have been added. The same channels but with negatively charged nanoparticles can be found in Fig. S2 of the ESI.†Fig. 1A and D correspond to C1 and C2, respectively, when no voltage bias is applied. It can be observed that there is an obvious excess of anions in the wider sections of the nanopores, where the wall has a positive charge. In the narrow section of the nanopores, where the wall charge is negative, a excess of cations is evident. In C1 the nanoparticles are distributed more or less evenly between the wide and narrow sections of the pore. In C2 the nanoparticles mostly remain in the long narrow section. With respect to the height of the channels, the location of the nanoparticles does not exhibit major differences between C1 and C2. The positively charged nanoparticles reside near the wall in the section of the pores with negative wall charge. In the section of the pores with positive wall charge the positively charged nanoparticles tend to stay near the center of the channels. As expected, the negatively charged nanoparticles do the opposite.
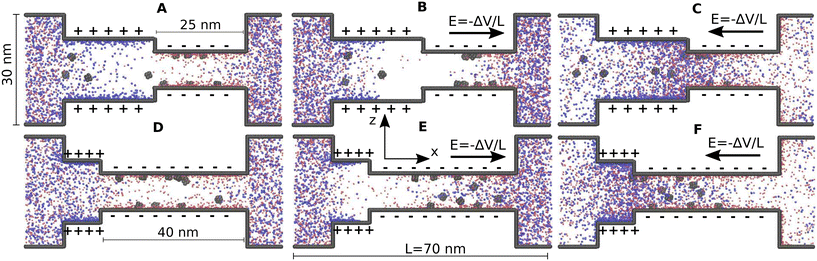 | ||
| Fig. 1 Orthographic projections of steady-state configurations for the two bipolar slit nanopores considered in this work. The top row shows nanopore C1 and the bottom row nanopore C2. Sodium ions are represented as red spheres and chlorine ions as blue spheres. Black spheres represent the interaction sites that make up the nanoparticles and the channel walls. The cases shown correspond to positively charged nanoparticles. The cases with negatively charged nanoparticles are shown in the ESI.† In A and D no bias is applied (i.e. equilibrium). B and E have a negative bias, −2 V, applied. And C and F have a positive bias, +2 V, applied. | ||
Fig. 1B and E show C1 and C2, respectively, when a negative bias, −2 V, is applied. The details on how the voltage bias between the two ends of the nanopores is applied in the simulations are given in the Methods section above. Also note that the magnitude of the voltage bias used here is what has been commonly used in experiments with Janus membranes.8–11 In the −2 V case, a pronounced depletion zone, where the amount of both anions and cations drops, is observed around the transition from the narrow to the wide section of the nanopores. For this negative bias the general location of the nanoparticles inside the channels is not significantly changed compared to the equilibrium cases. However, in C1 it is more apparent that, similarly to what the ions do, the nanoparticles also stay away from the aforementioned depletion zone. Fig. 1C and F show C1 and C2, respectively, when a positive bias +2 V, is applied. Here, contrary to what happens in the negative bias case, anions and cations appear to concentrate around the transition zone between the narrow and wide sections of the channels. For the positive bias, the positively charged nanoparticles move towards the wide section of the nanopores. They tend to concentrate around the transition zone between the narrow and wide sections of the channels. As can be seen in Fig. S2 in the ESI,† the negatively charged nanoparticles move towards the narrow section when the positive bias is applied.
The top row of Fig. 2 shows concentration profiles as a function of the channel's length (i.e. averaged over the channel's width and depth). For (A) cations and (B) anions in C1 without nanoparticles (lines) and in C1 with positively charged nanoparticles (symbols). The background colors in Fig. 2 indicate the different sections of the nanopores. Light gray for the reservoirs, light blue for the positively charged section and light red for the negatively charged section. The insets with the drawings of the nanopores also show to which section each color corresponds. The bottom row of Fig. 2 shows concentration profiles as a function of the channel's length for (A) cations and (B) anions in C2 without nanoparticles and in C2 with positively charged nanoparticles (symbols). The same plots but for the cases where the nanoparticles have a negative surface charge are provided in Fig. S3 in the ESI.† As expected, the concentration of cations is larger in the narrow section of the slits, where the walls are negatively charged. In the wide section of the slits, where the wall is positively charged, the concentration of cations is smaller. A depletion zone is observed where the concentration of cations drops nearly to zero in the transition region between the narrow and wide sections of the nanopores. This depletion zone is larger for the −2 V bias case, and is also present in the equilibrium case. However, it is almost non-existent in the +2 V bias case. It has been previously reported that both cations and anions exhibit depletion zones in bipolar nanochannels, and that the depth of these depletion zones is sensitive to the sign of the external voltage.1 The presence of either the negatively or the positively charged nanoparticles increases the length and depth of this depletion zone for the cations in both channels. It is also evident from Fig. 2 that the cation depletion zone is longer and deeper in C1. Furthermore, it is the longest and deepest for C1 with a −2 V applied bias. For the +2 V applied bias no depletion zone is observed for the cations, and the maximum concentration occurs in the transition region between the narrow section and the wide section of the nanopores.
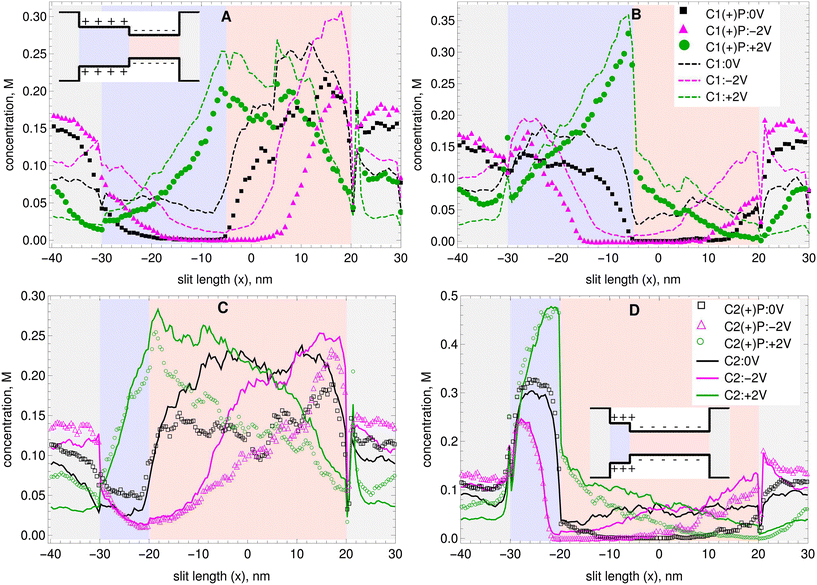 | ||
| Fig. 2 Average concentration as a function of channel length of A) cations and B) anions in C1 at equilibrium and for two different applied voltages with (symbols) and without (dashed lines) the addition of positively charged nanoparticles. Concentration of C) cations and D) anions in C2 at equilibrium and for two different applied voltages with (symbols) and without (lines) the addition of positively charged nanoparticles. The background colors indicate the different sections of the nanopores. The insets with the drawings of the nanopores show to which section each color corresponds. The concentration profiles with addition of negatively charged nanoparticles are given in the ESI.† | ||
As can be seen in Fig. 2B and D, the concentration of anions is larger in the wide section of the slits, where the walls are positively charged. In the narrow section of the slits, where the wall is negatively charged, the concentration of anions is smaller. A depletion zone is also observed where the concentration of anions drops nearly to zero in the transition region between the narrow section and the wide section of the pore. This depletion zone again is observed at equilibrium, but is most pronounced in the −2 V case. As before, nanoparticles make the anion depletion zone significantly longer and deeper, specially in the C1 nanopore. The highest concentrations of anions occur for a +2 V bias applied, and they concentrate near the transition area between the narrow and wide sections of the slit. Note that they stay primarily on the side where the wall is positively charged.
3.2 Electric current rectification
From a practical perspective, the purpose of computer simulations is to design bipolar nanopores that can produce a usable current for a given applied voltage bias. Several theoretical and computational works have proposed current–voltage relationships for bipolar nanopores.1,16–21,39Fig. 3 shows the current–voltage relationship for the two slit pores considered here, as predicted by our coarse-grained MD calculations. Details on how the electric current is calculated are given in the Methods section above. In particular, Fig. 3A shows the effect of adding nanoparticles (positive or negative) on the current–voltage relationship for the C1 nanopore. It can be observed that, for the −2 V applied bias, the electric current is suppressed by the presence of positive and negative charged nanoparticles. For the +2 V bias case, the effect of nanoparticles on the current is minor, and falls within the uncertainty of the calculations. The electric current rectification for C1 with positively charged nanoparticles is 22.3, which is about 13 times larger than without nanoparticles. The electric current rectification for C1 with negatively charged nanoparticles is 12.3, which is about 7 times larger than without nanoparticles.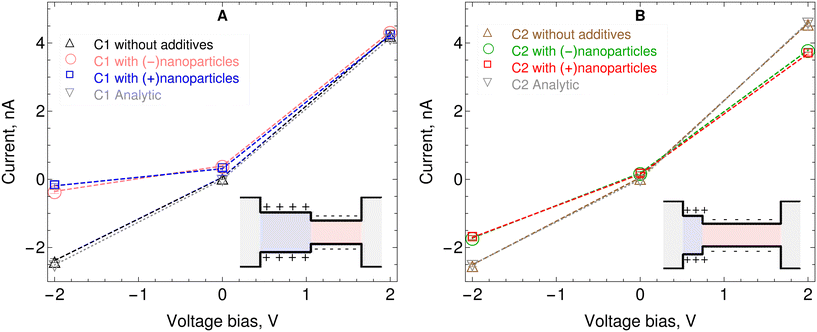 | ||
| Fig. 3 Current–voltage relationship for the two nanochannels considered here with and without nanoparticles. A) Channel where the two charged sections have the same length, C1 B) channel where the negatively charged section is longer than the positively charged section, C2. The statistical uncertainties for the electric currents are calculated using the blocking transformation method38 which is applicable to estimating statistical error in averages of time series data by properly accounting for the correlation in the data. The bipolar pore model of Green et al.17 is used for the analytical predictions. | ||
Fig. 3B shows the effect of adding nanoparticles, positively or negatively charged on the current–voltage relationship for the C2 nanopore. First, note that without nanoparticles the rectification ratios in C2, |IC2+2V|/|IC2−2V| = 1.82, and C1 |IC1+2V|/|IC1−2V| = 1.78 are very similar. However, when nanoparticles (either positively or negatively charged) are added to C2, the rectification ratio increases only by a factor of about 1.2. This represents a much smaller increase than the factor of 13 that is observed in C1 when positively charged nanoparticles are added. A summary of the rectification factors is given in Table 2.
| Additive | Electric current rectification (|I+2V|/|I−2V|) | |
|---|---|---|
| C1 | C2 | |
| None | 1.78 ± 0.05 | 1.82 ± 0.035 |
| Negatively charged | ||
|---|---|---|
| 10 particles | 12.3 ± 2.05 | 2.20 ± 0.076 |
| Positively charged | ||
|---|---|---|
| 10 particles | 22.3 ± 7.3 | 2.16 ± 0.08 |
Fig. 3 also shows comparisons of the current–voltage relation from the MD simulations used here with predictions obtained using the analytic model for bipolar nanopores proposed by Green et al.17 The analytic model is based on the Poisson–Nernst–Planck (PNP) equations. It's main assumptions are local electroneutrality in the reservoirs, cross-sectional local electroneutrality in the permselective regions and equal concentration of the electrolyte in the two reservoirs. The analytic predictions of that model have been verified by solving the fully coupled PNP equations using the finite elements numerical method. The analytic expression for the electric current has three distinct terms, one term accounts for the reservoirs' ohmic resistors, which also account for field focusing into the permselective interfaces. Another term describes the electric potential drop over the permselective regions. A third term describes the Donnan potential jumps at all three interfaces. The only adjustable parameter of the model is a diffusion coefficient for the ions.
For the predictions shown in Fig. 3 the value obtained from fitting the analytic model to the electric currents obtained in the simulations is ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) = 1.0 × 10−10 m2 s−1. This value can be contrasted with the diffusion coefficients of the ions inside the nanopores measured in the simulations. These are
= 1.0 × 10−10 m2 s−1. This value can be contrasted with the diffusion coefficients of the ions inside the nanopores measured in the simulations. These are ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) Na+ ≈ 9.05 × 10−10 m2 s−1 and
Na+ ≈ 9.05 × 10−10 m2 s−1 and ![[scr D, script letter D]](https://www.rsc.org/images/entities/i_char_e523.gif) Cl− ≈ 5.85 × 10−10 m2 s−1. See the Methods section above for details on how these diffusion coefficients are calculated. This means that to predict similar currents the diffusion coefficient in the analytic model has to be about 5 to 9 times smaller than the diffusion coefficients in the MD simulations. The difference is reasonable given the different levels of description of the two models; the less detailed level of the continuum analytical model and the more detailed level of the MD simulations. Note that the analytical model is only applicable in the cases where there are no nanoparticles added. But in those cases the electric current shows agreement with the results obtained with the MD simulations employed here.
Cl− ≈ 5.85 × 10−10 m2 s−1. See the Methods section above for details on how these diffusion coefficients are calculated. This means that to predict similar currents the diffusion coefficient in the analytic model has to be about 5 to 9 times smaller than the diffusion coefficients in the MD simulations. The difference is reasonable given the different levels of description of the two models; the less detailed level of the continuum analytical model and the more detailed level of the MD simulations. Note that the analytical model is only applicable in the cases where there are no nanoparticles added. But in those cases the electric current shows agreement with the results obtained with the MD simulations employed here.
We have also examined the effect of the nanoparticle's friction coefficient on the electric current. This was done by performing additional replicas of the simulations but using a friction coefficient for the nanoparticles about 8 times smaller than the one used for the results shown in Fig. 3. See the Methods section above for details. Fig. S10 and Table S3 in the ESI† show comparisons of the electric currents and the rectification ratios obtained in the different replicas performed for nanopore C1 with positively charged nanoparticles. To within the statistical uncertainty of the simulations all the replicas give the same electric currents and rectification ratios. The bottom row of Fig. S8 in the ESI† shows the steady-state nanoparticle concentration as a function of channel length obtained from averaging the four replicas done for C1 with positively charged nanoparticles. For the −2 V case the nanoparticles stay within the charged regions of the nanopore, exhibiting a higher concentration in the section with negative wall charges. For the +2 V bias the nanoparticles are more evenly distributed between the uncharged (i.e. reservoirs) and charged sections of the nanopore.
3.3 Mechanism of current rectification
In the simulations presented here, the ionic strength of the solutions has been kept constant when adding the nanoparticles. Therefore one can immediately rule out that the observed increases in current rectification are due to an increase or decrease in the concentration of the total charges in the systems. Also, the concentration of particles has been kept very low, at about 0.7 mM, and their mobility is about ten times smaller than the mobility of the ions (see the Methods section above). Therefore the contribution of the nanoparticles to the total electric current flowing through the nanopores is always less than 1% (see Tables S4–S6 in the ESI† for the individual contributions of each charged species to the total electric currents). Moreover, decreasing the friction coefficient of the nanoparticles by a factor of 8 does not have a significant effect on the observed rectification ratios. Nevertheless, the nanoparticles can have a significant effect on the charge distribution inside the nanopores and therefore can produce significant changes in the nanopore's electric potential.Several theoretical studies based on the PNP equations,7,13–15,17,27,40 have shown that in a bipolar nanopore, the asymmetric and diode-like behavior of the current is due to the system layout. When the voltage is applied in a direction that coincides with the inherent electric field of the nanopore, then the current is enhanced. When the voltage is applied in the opposite direction, a so-called reverse bias, then the applied electric field operates against the inherent electric field, leading to a reduction in the resultant current.17 The effects of adding positively charged nanoparticles or negatively charged nanoparticles on the electric field are shown in Fig. 4A and B, respectively. Results are shown for the electric potential in C1 as a function of channel length, ψ(x). Here again the background colors in the plot indicate the different sections of the nanopore. The inset with the drawing of the nanopore shows to which section each color corresponds. The details on how the electric field of the nanopores as a function of length, ψ(x), is calculated are given in the Methods section above. Results for C2 are given in Fig. S6 of the ESI.†
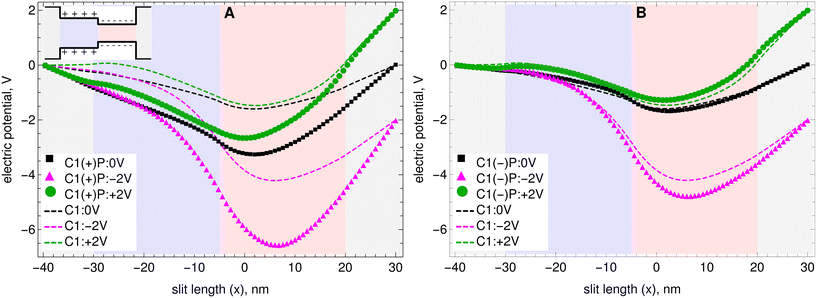 | ||
| Fig. 4 Effect on the electric potential of C1 as a function of channel length when A) positively charged nanoparticles are added and B) negatively charged nanoparticles are added. The electric potential in the channels where nanoparticles are added is shown with symbols. The background colors indicate the different sections of the nanopore. The inset with the drawing of the nanopore shows to which section each color corresponds. The electric potentials in the channels without nanoparticles are shown with lines. The electric potentials in nanopore C2 are given in the ESI.† | ||
One can clearly observe that the nanoparticles have a large effect on the electric potential. More specifically, in C1 negatively charged nanoparticles increase the depth of the minimum from −1.6 V to −1.7 V, and positively charged nanoparticles increase the depth of the minimum from −1.6 V to −3.3 V. For the −2 V applied bias case, negatively charged nanoparticles increase the depth of the minimum from −4.2 V to −4.8 V. For this negative bias case, positively charged nanoparticles increase the depth of the minimum from −4.2 V to −6.5 V. For the +2 V applied bias case, negatively charged nanoparticles decrease the depth of minimum in the electric potential from −1.5 V to −1.3 V. For this positive bias case, positively charged nanoparticles increase the depth of the minimum from −1.5 V to −2.6 V. In Tables S4–S6 of the ESI† it can be observed that the deeper minimum in the electric potential observed for −2 V bias in the presence of nanoparticles significantly reduces the fluxes of anions and cations in that case. The rectification ratio is increased more by the positively charged nanoparticles because these produce a much deeper minimum in the electric potential for the −2 V bias, thereby causing the current to be diminished for that bias while maintaining the current enhancement for the +2 V bias.
In C2, nanoparticles do not have a significant effect on the inherent electric field of the nanopore. Overall, they tend to slightly increase the depth of the minimum in the electric potential. This leads to a slight overall reduction in the electric current that is observed in that pore upon addition of nanoparticles.
4 Conclusions
While recent work has produced significant theoretical and experimental progress in our understanding of the fundamental physics that govern bipolar nanopores, important design challenges still remain with regards to the role of nanopore geometry and the addition of nanoparticles on current rectification. In this paper, we have considered two channel geometries, one in which the two oppositely charged sections have the same length, and one in which the negatively charged section is about twice the length of the negatively charged section. Both of these geometries include changes in the height as a function of channel length. The cation and anion concentration profiles and current–voltage relationship of dilute electrolytes (0.1 M) were determined for neutral, positive, and negative applied biases, respectively, and we examined the role of nanoparticles on current rectification.Our simulations with explicit ions in an implicit solvent have revealed that the current rectification ratio in the bipolar nanochannel with a longer negatively charged section is 1.82. Negatively charged nanoparticles can raise the rectification to 2.2. In a channel with that geometry, positively charged nanoparticles also increase the rectification to 2.2. In the channel where the negatively and positively charged sections have the same length, the current rectification without nanoparticles is 1.78. However, adding negatively charged nanoparticles increases the rectification to 12.3. In this latter channel, positively charged nanoparticles increase the current rectification to 22.3. These considerable increases in current rectification can be explained by the large effect that positively charged nanoparticles have in the inherent electric field of the nanopore. Moreover, this effect is strongly dependent on the pore geometry, its charge distribution and the sign of the nanoparticles' charge. These findings could have significant implications for design of improved current rectification systems based on nanopore diodes, and we hope that they will stimulate experimental work.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Department of Energy, Basic Energy Sciences, through the AMEWS EFRC Center. The development of advanced sampling codes is supported by the Department of Energy, Basic Energy Sciences, through MiCCoM. We also acknowledge computational resources provided by the University of Chicago Research Computing Center.Notes and references
- D. Fertig, M. Valiskó and D. Boda, Phys. Chem. Chem. Phys., 2020, 22, 19033–19045 RSC.
- H. Daiguji, Y. Oka and K. Shirono, Nano Lett., 2005, 5, 2274–2280 CrossRef CAS PubMed.
- L.-J. Cheng and L. J. Guo, ACS Nano, 2009, 3, 575–584 CrossRef CAS PubMed.
- I. Vlassiouk and Z. S. Siwy, Nano Lett., 2007, 7, 552–556 CrossRef CAS.
- J. W. Post, H. V. Hamelers and C. J. Buisman, Environ. Sci. Technol., 2008, 42, 5785–5790 CrossRef CAS PubMed.
- D. Brogioli, Phys. Rev. Lett., 2009, 103, 058501 CrossRef.
- V. Chinaryan, M. Z. Bazant, I. Rubinstein and B. Zaltzman, et al. , Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 012302 CrossRef.
- J. Gao, W. Guo, D. Feng, H. Wang, D. Zhao and L. Jiang, J. Am. Chem. Soc., 2014, 136, 12265–12272 CrossRef CAS.
- Z. Zhang, X.-Y. Kong, K. Xiao, Q. Liu, G. Xie, P. Li, J. Ma, Y. Tian, L. Wen and L. Jiang, J. Am. Chem. Soc., 2015, 137, 14765–14772 CrossRef CAS PubMed.
- Z. Zhang, X. Sui, P. Li, G. Xie, X.-Y. Kong, K. Xiao, L. Gao, L. Wen and L. Jiang, J. Am. Chem. Soc., 2017, 139, 8905–8914 CrossRef CAS.
- X. Zhu, J. Hao, B. Bao, Y. Zhou, H. Zhang, J. Pang, Z. Jiang and L. Jiang, Sci. Adv., 2018, 4, eaau1665 CrossRef CAS PubMed.
- J. M. Montes de Oca, J. Dhanasekaran, A. Córdoba, S. B. Darling and J. J. de Pablo, ACS Nano, 2022, 16, 3768–3775 CrossRef CAS PubMed.
- A. Mauro, Biophys. J., 1962, 2, 179–198 CrossRef CAS.
- H. Coster, Biophys. J., 1965, 5, 669 CrossRef CAS.
- A. A. Sonin and G. Grossman, J. Phys. Chem., 1972, 76, 3996–4006 CrossRef CAS.
- S. Mafé, J. Manzanares and P. Ramrez, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 42, 6245 CrossRef.
- Y. Green, Y. Edri and G. Yossifon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 033018 CrossRef PubMed.
- R. Long, Z. Kuang, Z. Liu and W. Liu, Phys. Chem. Chem. Phys., 2018, 20, 7295–7302 RSC.
- G. Moy, B. Corry, S. Kuyucak and S.-H. Chung, Biophys. J., 2000, 78, 2349–2363 CrossRef CAS.
- B. Corry, S. Kuyucak and S.-H. Chung, Biophys. J., 2000, 78, 2364–2381 CrossRef CAS PubMed.
- M. Valiskó, B. Matejczyk, Z. Ható, T. Kristóf, E. Mádai, D. Fertig, D. Gillespie and D. Boda, J. Chem. Phys., 2019, 150, 144703 CrossRef.
- I. Rubinstein and B. Zaltzman, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 2238 CrossRef CAS.
- B. Zaltzman and I. Rubinstein, J. Fluid Mech., 2007, 579, 173–226 CrossRef.
- A. Gubbiotti, M. Baldelli, G. Di Muccio, P. Malgaretti, S. Marbach and M. Chinappi, Adv. Phys.: X, 2022, 7, 2036638 Search PubMed.
- I. Rubinstein, Phys. Fluids A, 1991, 3, 2301–2309 CrossRef CAS.
- Y. Green and G. Yossifon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 013024 CrossRef.
- Y. Green and G. Yossifon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 063001 CrossRef.
- M. S. Shell, J. Chem. Phys., 2008, 129, 108 CrossRef.
- D. M. Hinckley and J. J. de Pablo, J. Chem. Theory Comput., 2015, 11, 5436–5446 CrossRef CAS.
- J. Gumbart, F. Khalili-Araghi, M. Sotomayor and B. Roux, Biochim. Biophys. Acta, Biomembr., 2012, 1818, 294–302 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- N. Grønbech-Jensen and O. Farago, Mol. Phys., 2013, 111, 983–991 CrossRef.
- N. Grønbech-Jensen, N. R. Hayre and O. Farago, Comput. Phys. Commun., 2014, 185, 524–527 CrossRef.
- I.-C. Yeh and M. L. Berkowitz, J. Chem. Phys., 1999, 111, 3155–3162 CrossRef CAS.
- P. S. Crozier, D. Henderson, R. L. Rowley and D. D. Busath, Biophys. J., 2001, 81, 3077–3089 CrossRef CAS.
- A. Aksimentiev and K. Schulten, Biophys. J., 2005, 88, 3745–3761 CrossRef CAS PubMed.
- G. Di Muccio, B. Morozzo della Rocca and M. Chinappi, ACS Nano, 2022, 16, 8716–8728 CrossRef CAS PubMed.
- H. Flyvbjerg and H. G. Petersen, J. Chem. Phys., 1989, 91, 461–466 CrossRef CAS.
- D. Fertig, B. Matejczyk, M. Valiskó, D. Gillespie and D. Boda, J. Phys. Chem. C, 2019, 123, 28985–28996 CrossRef.
- Y. Green, S. Shloush and G. Yossifon, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 043015 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Versions of Fig. 1 and 2 when the particles are negatively charged; the version of Fig. 4 for pore C2; figures with the concentration of the ions as a function of the channel height in the positively and negatively charged regions of the nanopores; figures with the concentration of nanoparticles as a function of the channel length; plots of the electric current as a function of time; a table with the averages and uncertainties of the electric currents; mean-squared displacements of ions and nanoparticles in the nanopores at equilibrium; a table with the diffusion coefficients of ions and nanoparticles in the different nanopores considered here. See DOI: https://doi.org/10.1039/d2me00187j |
| This journal is © The Royal Society of Chemistry 2023 |
