Open Access Article
Open Access ArticleThe removal efficiency of emerging organic contaminants, heavy metals and dyes: intrinsic limits at low concentrations
Sara
Khaliha
,
Derek
Jones
,
Alessandro
Kovtun
 *,
Maria Luisa
Navacchia
*,
Maria Luisa
Navacchia
 ,
Massimo
Zambianchi
,
Massimo
Zambianchi
 ,
Manuela
Melucci
,
Manuela
Melucci
 and
Vincenzo
Palermo
and
Vincenzo
Palermo

Consiglio Nazionale delle Ricerche – Istituto per la Sintesi Organica e la Fotoreattività, CNR-ISOF, via Gobetti 101, 40129 Bologna, Italy. E-mail: alessandro.kovtun@isof.cnr.it
First published on 13th April 2023
Abstract
In this work, we exploit Langmuir adsorption isotherms to compare the performance of different materials (adsorbents) in removing organic contaminants (adsorbates) from water. The removal efficiency observed reaches an intrinsic limit at low concentrations. We also demonstrate quantitatively how multi-step adsorption processes achieve better purification efficiency than single-step adsorption performed using much smaller amounts of adsorbent material. We demonstrate how such performance is strongly affected by adsorbent concentration. Only the use of both the parameters obtained from Langmuir adsorption isotherm (Qm and KL) modelling allows one to compare materials tested under different experimental conditions by different groups, whereas most published reviews focus only on Qm which is rather limited for comparing the performance of different materials studied under different conditions. Finally, we present some guidelines for data reporting in future work and reviews.
Water impactFor materials science applied to water purification, it is strategic to compare the performances of different adsorbents, the use of appropriate parameters is an open question. In the present work we show how a widely used and intuitive parameter as removal efficiency is not suitable for such purpose, while the isotherm's parameters, i.e. Langmuir model, are the effective ones. |
Introduction
More than 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chemicals including drugs, pesticides, additives etc. are used every day for domestic and industrial purposes, and over 21
000 chemicals including drugs, pesticides, additives etc. are used every day for domestic and industrial purposes, and over 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chemicals have been registered under the European procedures of registration, evaluation, authorisation and restriction of chemicals (REACH).† Thus fast and reliable tests are required for comparing how different materials can remove from water a large and continually increasing number of organic contaminants.1
000 chemicals have been registered under the European procedures of registration, evaluation, authorisation and restriction of chemicals (REACH).† Thus fast and reliable tests are required for comparing how different materials can remove from water a large and continually increasing number of organic contaminants.1
Adsorption is one of the most important water treatment technologies, particularly for the removal of organic contaminants from waste water, drinking water and industrial effluents.2 In many published works the removal efficiency is reported as a simple percentage (weight of molecules adsorbed/total weight of molecules in the original solution), measured at a specific concentration, which is the most intuitive approach for waste water treatment (WWT) plants and prototypes.1a There is, however, no scientific evidence that removal efficiency values measured at different concentrations, or under different experimental conditions (adsorbent, pH, adsorbate, temperature, etc.) can be compared directly.
The most common method used for modelling the adsorption of different contaminants on a given material is based on a semi-empirical equation which takes into consideration the octanol–water partition coefficient of a target adsorbate molecule (Kow).3 After finding the partition coefficient, this approach is able to model experimental adsorption data for many organic molecules2 including pesticides,4 but shows significant deviation for bisphenols,5 some active pharmaceutical ingredients6 and water soluble organics.2 An alternative approach measures the weight of contaminant adsorbed at equilibrium (qe, in mg g−1) for different equilibrium concentrations of the adsorbate molecule in solution (ce, in mg L−1). Some reviews compare the performance of different materials by reporting removal efficiency, but considering that the data was acquired under different experimental conditions, the usefulness of these data is questionable.
The aim of this communication is to compare results based on isotherm approaches to calculate unambiguously the removal efficiency (R). Most work reported so far focusses on the calculation of adsorption capacity assuming a monolayer of adsorbate forms on the material, yielding a quantity Qm. This value can be estimated theoretically using Langmuir7 or similar adsorption models, as well as by extrapolation of the experimental isotherm curve. The extensive literature on adsorption phenomena has been used to validate our approach and show the consistency of our model of removal efficiency prediction.
Materials and methods
The vast majority of papers studying adsorption report the data as adsorption isotherms and test different theoretical models to obtain the main physical parameters. In the present work we have considered only the Langmuir isotherms and have collected from the literature parameters obtained experimentally for validation purposes.Many previous works report data giving the removal efficiency at low concentrations, since for practical purposes the adsorption is carried out at low concentration and R is usually reported as a parameter changing as a function of pH or other external parameters. Here we have considered only the papers where the isotherms are presented graphically, in order to allow verification of overall data quality.
The experimental data of the isotherm shown as an example in Fig. 1 is taken from our previous publication.8
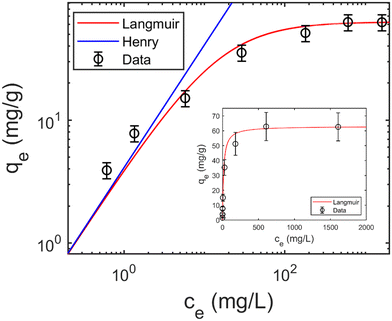 | ||
| Fig. 1 Adsorption isotherm with Langmuir fit, plotted in logarithmic scale (log–log plot), Qm = 63.0 mg g−1, KL = 65.2 mL mg−1, V = 25 mL, M = 50 mg. Inset: Isotherm plot in linear scale. | ||
Results and discussion
Fig. 1 shows a typical isotherm obtained for rhodamine B adsorption on a polysulfone support coated with graphene oxide.8 We see that qe at high concentrations corresponds approximately to the theoretical value estimated from the Langmuir isotherm model Qm (continuous red line in Fig. 1) assuming the formation of a single monolayer of molecules on the available adsorbent surface.The Langmuir isotherm equation, which should ideally contain all the information about the adsorption mechanism, is:
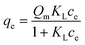 | (1a) |
| qe = QmKLce when ce < 1/KL | (1b) |
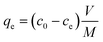 | (2) |
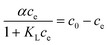 | (3a) |
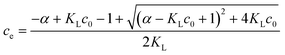 | (3b) |
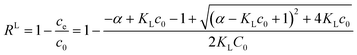 | (4) |
| αce = c0 − ce | (5a) |
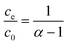 | (5b) |
Thus, the removal efficiency becomes:
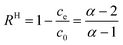 | (6) |
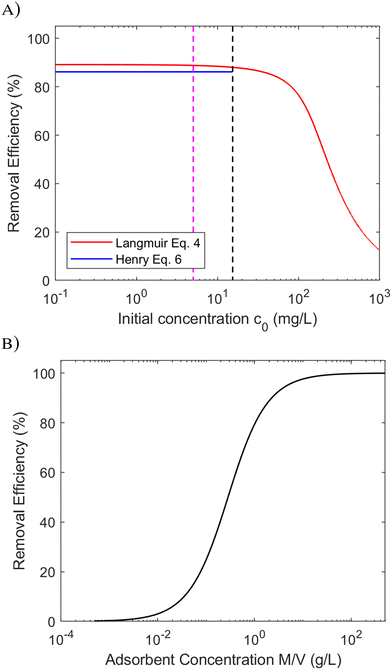
In this work we have chosen to focus the attention to Langmuir isotherms, since it is the most used model for describe the monolayer adsorption on an homogenous surface, but with the consideration developed here above the multilayer adsorption can be considered: the Brunauer–Emmett–Teller (BET) isotherm can be approximated to the Henry isotherm as well, by substituting KL = CBET/CS, where CBET is the thermodynamic equilibrium BET constant and CS the solubility of adsorbate, both obtained from BET fit. While the Freundlich model has no analytical approximation at low C, since the derivate of the Freundlich isotherm is a singularity at zero concentration, thus cannot be used for a similar comparison at low concentration. In a practical case was reported that for low concentration – when often the isotherms is well described by Henry (linear) model – the fit of Freundich equation (qe = KF·c1/ne) can be performed with n = 1,10 but in this specific case no advantages can be found by using Freundlich instead of Henry.
We tested the accuracy of eqn (6) using a wide range of data published in the literature, since the parameter α can be calculated from such data. Different adsorbate groups were chosen: organic molecules, arsenic and other heavy metals. In order to understand how α influences the removal efficiency, Fig. 3 shows the experimental values available in the literature together with those calculated using eqn (6). The points with R > 90% are nicely aligned along the plateau of the curve, and the best accuracy is obtained for α > 10. Fig. 3 can be considered as a different way of visualizing the isotherm in Fig. 1, providing an intuitive validation of the Langmuir fit at low concentrations. It should be stressed that, for a good fit, a consistent set of measurements is required over a wide range of concentrations: in the example reported in Fig. 1, 7 different concentration values are reported, correctly spaced along a logarithmic scale. In other works, however, a good fit was obtained by acquiring more points at only at low concentrations.15
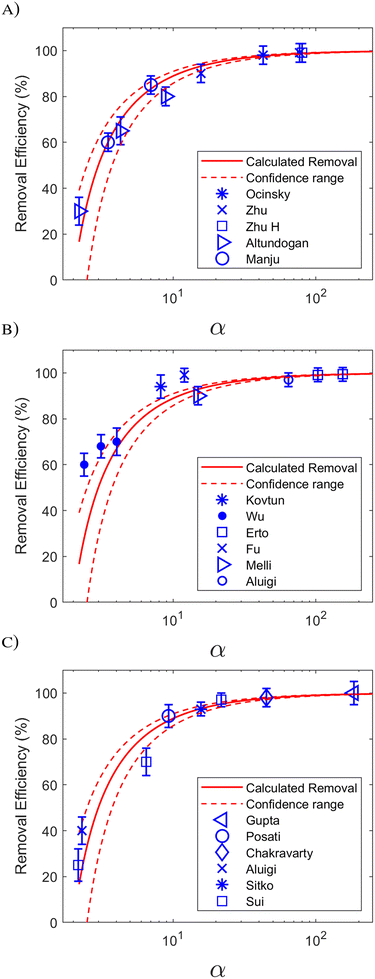 | ||
| Fig. 3 Removal efficiency (%) as a function of parameter α = QmKLM/V: the experimental points from the literature are compared to the expected behaviour of eqn (6) (red line). Upper and lower confidence ranges, calculated by assuming a 20% relative error in the determination of α, are shown as red dotted lines. The experimental points are from papers reported in Table 1. Different adsorbates were considered: (A) arsenic. (B) Organic molecules and (C) other heavy metals. | ||
The previously published data show that the relative experimental error in KL is the most influential factor in the overall uncertainty in the removal efficiency, R: typically, this error reaches 20%, and in some cases even 50%.8Fig. 3 shows how a 20% error could lead to considerable uncertainty in the determination of R at low α.
Once the single parameter approach for calculating R is validated these results can be used to solve a more practical problem, the optimization of adsorbent mass. The amount of adsorbent necessary to achieve a target removal efficiency R can be calculated from eqn (6):
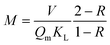 | (7) |
Taking as an example, the need to decrease the concentration of a pollutant from 500 ppb (μg L−1) to 5 ppb (i.e. removal efficiency 99%), for a given material (Qm and KL) and solution volume V, we can calculate the necessary mass of adsorbent required,16,17Msingle using eqn (7). However, a value of R = 99% can also be achieved by two sequential purification steps, each having R = 90%: the first step decreases the concentration from 500 to 50 ppb and the second from 50 to 5 ppb. As can be seen from eqn (7), the same removal efficiency using a single step would require ≈4.5 times the material (Msingle = 4.5Mdouble) used for the two-step approach. The better efficiency of multi-step processes is due to the weak dependence of R on α (proportional to the amount of adsorbent used), as clearly shown in Fig. 2B. Taking another example, in order to increase R from 90% to 99% it would be necessary to increase α (i.e. the mass of adsorbent) by a whole order of magnitude.
In a more demanding example, we can reduce the concentration of a test contaminant from 50 ppm to 5 ppb (corresponding to a removal efficiency 99.99%) with either four purification steps (each step having R = 90%) or one single purification step, using a large excess of adsorbent. The single step will, in fact, require ≈227 times more adsorbent (in mass) than the four-step process. Practical considerations such as the cost per purification step may influence decisions on optimisation of the contaminant removal in question.
Concluding, we would like to point out some aspects of the extensive literature on adsorption for pollutant removal purposes and especially, contrary to common assumptions made there, the value of R, removal efficiency, cannot be used for a direct comparison between different adsorbents under different conditions. In fact, some papers and reviews (other examples are given in Table 2) report only the removal for one specific case, rendering such data clearly pointless for any realistic comparison of performance with other systems. While most of the reviews focus on the value of Qm, this is not enough for comparing different materials, often giving only a partial view of adsorption performance for a given adsorbate. One example, for arsenic removal (of those given in Table 1) reports that As(III) removal has a larger Qm with respect to As(V) removal, but As(V) removal shows a larger KL, and thus the product QmKL is similar for both As species and their removal under the same conditions are usually similar too. Here, our model provides a simple explanation of the phenomena observed and described in the literature.
| Ref. | Adsorbate | Adsorbent | Q m (mg g−1) | K L (mL mg−1) | M (g) | V (mL) | α | R H (%) | R m (%) |
|---|---|---|---|---|---|---|---|---|---|
| Gupta (ref. 12) | Cr(IV) | Sawdust | 42 | 438 | 1 | 100 | 184 | 99 | 100 |
| Posati (ref. 18) | Cu(II) | Polydopamine + polysulfone | 4.5 | 1100 | 0.015 | 8 | 9.3 | 88 | 90 |
| Aluigi (ref. 19) | Cu(II) | Wool keratin nanofiber | 18 | 130 | 1 | 1000 | 2.3 | 25 | 40 |
| Chakravarty (ref. 20) | Cd(II) | Heartwood powder | 10.6 | 857 | 0.5 | 100 | 45.4 | 98 | 97 |
| Sitko (ref. 21) | Pb(II) | Graphene oxide | 1119 | 140 | 0.1 | 1000 | 15.7 | 93 | 95 |
| Sui (ref. 22) | Cu(II) | Graphene oxide + polyethylenimine | 157 | 69 | 2 | 1000 | 21.7 | 95 | 97 |
| 157 | 69 | 0.6 | 1000 | 6.5 | 82 | 70 | |||
| 157 | 69 | 0.2 | 1000 | 2.2 | 14 | 25 | |||
| Ociński (ref. 23) | As(V) | Chitosan + MnFe oxides | 27 | 395 | 4 | 1000 | 43 | 98 | 99 |
| Zhou (ref. 24) | As(III) | Reduced graphene oxide + MnFe oxides | 22.4 | 3500 | 0.2 | 1000 | 15.7 | 93 | 90 |
| As(V) | 22.2 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
0.2 | 1000 | 76.8 | 99 | 99 | ||
| Zhu H. (ref. 25) | As(III) | Activated carbon | 18 | 8900 | 0.5 | 1000 | 80.1 | 99 | 99 |
| Altundoğan (ref. 13) | As(III) | Red mud | 0.664 | 334 | 10 | 1000 | 2.2 | 18 | 30 |
| As(III) | 0.664 | 334 | 20 | 1000 | 4.4 | 71 | 65 | ||
| As(III) | 0.664 | 334 | 40 | 1000 | 8.9 | 87 | 80 | ||
| As(V) | 0.513 | 1642 | 100 | 1000 | 84.4 | 99 | 99 | ||
| Manju (ref. 11) | As(III) | Husk carbon | 146 | 24 | 2 | 1000 | 7.0 | 83 | 85 |
| As(III) | 146 | 24 | 0.05 | 50 | 3.5 | 60 | 60 | ||
| Wu (ref. 5) | BPA | Polyvinyl chloride | 0.923 | 1721 | 1.5 | 1000 | 2.4 | 28 | 60 |
| BPB | 0.993 | 2101 | 1.5 | 1000 | 3.1 | 53 | 68 | ||
| BPAF | 1.05 | 2574 | 1.5 | 1000 | 4.1 | 67 | 70 | ||
| Kovtun (ref. 8) | RhB | Graphene oxide + polysulfone | 63.2 | 65.2 | 0.05 | 25 | 8.2 | 86 | 94 |
| Erto (ref. 9) | 203 | 127 | 0.6 | 100 | 155 | 99.3 | 99.4 | ||
| TCE | Activated carbon | 203 | 127 | 0.4 | 100 | 103 | 99.0 | 99.1 | |
| 203 | 127 | 0.45 | 200 | 58.1 | 98.2 | 97.6 | |||
| Melli (ref. 26) | MB | Agroindustrial wastes | 17.4 | 171 | 0.5 | 100 | 14.9 | 93 | 90 |
| Aluigi (ref. 27) | MB | Keratin nanofibrous membrane | 167 | 385 | 1.0 | 1000 | 64.3 | 98 | 97 |
| Fu (ref. 28) | MB | Polydopamine | 89 | 272 | 0.01 | 20 | 12.1 | 91 | 99 |
| Ref. | Adsorbate | Adsorbent | Q m | K L | Comment |
|---|---|---|---|---|---|
| Wu (ref. 29), 2010 | HM | Chitosan | Y | Y | All data reported correctly |
| Bhatnagar (ref. 30), 2011 | Fluoride | Various materials | Y | N | Removal is used in text for comparison |
| Gupta (ref. 31), 2013 | Dyes | Nanotubes | Y | N | — |
| Hua (ref. 32), 2012 | HM | Various materials | Y | N | Removal used in text for comparison |
| Gupta (ref. 33), 2008 | Dyes | Various materials | Y | N | Removal used in tables for comparison |
| Ngah (ref. 34), 2011 | Dyes & HM | Chitosan composites | Y | N | Removal used in text for comparison |
| Ngah (ref. 35), 2008 | HM | Plants wastes | Y | N | Removal used in text for comparison |
| Bailey (ref. 36), 1999 | HM | Low cost adsorbent | Y | N | Does not use removal |
| Crini (ref. 37), 2006 | Dyes | Low cost adsorbent | Y | N | Does not use removal |
| Mohan (ref. 38), 2007 | As | Various materials | Y | N | Removal used in text for comparison |
| Sağ (ref. 39), 2001 | HM | Fungal biomass | Y | N | Does not use removal |
| Anastopoulos (ref. 40), 2014 | Dyes | Agricultural peels | Y | N | Removal used in text for comparison |
| Kyzas (ref. 41), 2015 | EOCs | Various materials | N | N | Uses only removal values for comparison |
| Sousa (ref. 42), 2022 | EOCs | Microalgal | N | N | Uses only removal values for comparison |
| Ahmad (ref. 43), 2021 | EOCs | Biochar-Iron | N | N | Uses only removal values for comparison |
| Zheng (ref. 44), 2022 | EOCs | Metal organic frameworks and graphene oxide | Y | N | Removal used in text for comparison |
| Gogoi (ref. 45), 2018 | EOCs | Various materials | N | N | Uses only removal values for comparison |
Thus, as supported by the above equations and considerations, the performance of materials (removal efficiency) depends on the product of Qm and KL. Only these two main parameters allow a direct comparison between different adsorbents at the same concentration. Qm and KL should always be reported correctly when comparing different adsorbents, only one review was found in such form.
It should become a basic requirement when publishing scientific work, whether reviews or individual studies, on the comparison of removal performance of different materials that Qm and KL values be reported instead of using the value of removal efficiency, since the latter can not provide valid comparisons for choosing, in practice, the most effective and inexpensive approach. Removal efficiency should be considered as a target value, which can be potentially reached by any adsorbent by tuning suitable concentrations of M/V, and which should be the effective cost parameter.
Conclusions
The removal efficiency R of contaminants through adsorption depends critically upon isotherm parameters (Qm and KL) and adsorbent concentration (M/V), and can be modelled at low concentration as a function of the combined parameter α = QmKLM/V. The removal efficiency R reaches its largest value at low contaminant concentration (c < 1/KL); at these levels, removal efficiency can be considered constant. An increase in single-step removal efficiency from 90% to 99% requires an increase in the quantity of adsorbent materials of one order of magnitude. Compared to single-step adsorption processes, multi-step processes allow greater removal of contaminants with lower quantities of adsorbent material, and such increased efficiency should thus be preferred and encouraged whenever possible. Future reviews comparing the adsorption performances of different materials must be encouraged, if not obliged, to report both the parameter isotherms Qm and KL.Author contributions
The manuscript was written with contributions from all authors. All authors have given approval to the final version of the manuscript. A. K. conceptualization, data curation, validation, writing original draft. S. K. and D. J. literature research, review, editing. M. M. writing and founding acquisition. V. P., M. Z., M. L. N. contributed during discussion and manuscript writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research leading these results has received funding from the European Union Horizon 2020 research and innovation programme under GrapheneCore3 No 881603 – Graphene Flagship; SH1 Graphil project, and from the FLAG-ERA III project GOFOR-WATER, No 825207.References
- (a) R. Mailler, J. Gasperi, Y. Coquet, S. Deshayes, S. Zedek, C. Cren-Olivé, N. Cartiser, V. Eudes, A. Bressy, E. Caupos, R. Moilleron, G. Chebbo and V. Rocher, Study of a large scale powdered activated carbon pilot: Removals of a wide range of emerging and priority micropollutants from wastewater treatment plant effluents, Water Res., 2015, 72, 315–330 CrossRef CAS PubMed; (b) C. E. Cowan, R. J. Larson, T. C. J. Feijtel and R. A. Rapaport, An improved model for predicting the fate of consumer product chemicals in wastewater treatment plants, Water Res., 1993, 27(4), 561–573 CrossRef CAS.
- G. Byrns, The fate of xenobiotic organic compounds in wastewater treatment plants, Water Res., 2001, 35(10), 2523–2533 CrossRef CAS PubMed.
- S. W. Karickhoff, Organic Pollutant Sorption in Aquatic Systems, J. Hydraul. Eng., 1984, 110(6), 707–735 CrossRef.
- V. Petit, R. Cabridenc, R. P. J. Swannell and R. S. Sokhi, Review of strategies for modelling the environmental fate of pesticides discharged into riverine systems, Environ. Int., 1995, 21(2), 167–176 CrossRef CAS.
- P. Wu, Z. Cai, H. Jin and Y. Tang, Adsorption mechanisms of five bisphenol analogues on PVC microplastics, Sci. Total Environ., 2019, 650, 671–678 CrossRef CAS PubMed.
- (a) P. D. Anderson, V. J. D'Aco, P. Shanahan, S. C. Chapra, M. E. Buzby, V. L. Cunningham, B. M. Duplessie, E. P. Hayes, F. J. Mastrocco, N. J. Parke, J. C. Rader, J. H. Samuelian and B. W. Schwab, Screening analysis of human pharmaceutical compounds in U.S. surface waters, Environ. Sci. Technol., 2004, 38(3), 838–849 CrossRef CAS PubMed; (b) K. I. Andersson, M. Eriksson and M. Norgren, Removal of Lignin from Wastewater Generated by Mechanical Pulping Using Activated Charcoal and Fly Ash: Adsorption Isotherms and Thermodynamics, Ind. Eng. Chem. Res., 2011, 50(13), 7722–7732 CrossRef CAS.
- I. Langmuir, The adsorption of gases on plane surfaces of Glass, Mica and Platinum, J. Am. Chem. Soc., 1918, 40(9), 1361–1403 CrossRef CAS.
- A. Kovtun, M. Zambianchi, C. Bettini, A. Liscio, M. Gazzano, F. Corticelli, E. Treossi, M. L. Navacchia, V. Palermo and M. Melucci, Graphene oxide–polysulfone filters for tap water purification, obtained by fast microwave oven treatment, Nanoscale, 2019, 11(47), 22780–22787 RSC.
- A. Erto, Adsorbimento di composti organici volatili (VOCs) in soluzione acquosa su materiali sorbenti granulari, Ph. D. Thesis, Università degli studi di Napoli “Federico II”, Napoli, Italy, 2007 Search PubMed.
- M. Tagliavini, F. Engel, P. G. Weidler, T. Scherer and A. I. Schäfer, Adsorption of steroid micropollutants on polymer-based spherical activated carbon (PBSAC), J. Hazard. Mater., 2017, 337, 126–137 CrossRef CAS PubMed.
- G. N. Manju, C. Raji and T. S. Anirudhan, Evaluation of coconut husk carbon for the removal of arsenic from water, Water Res., 1998, 32(10), 3062–3070 CrossRef CAS.
- S. Gupta and B. V. Babu, Removal of toxic metal Cr(VI) from aqueous solutions using sawdust as adsorbent: Equilibrium, kinetics and regeneration studies, Chem. Eng. J., 2009, 150(2), 352–365 CrossRef CAS.
- H. S. Altundoğan, S. Altundoğan, F. Tümen and M. Bildik, Arsenic removal from aqueous solutions by adsorption on red mud, Waste Manage., 2000, 20(8), 761–767 CrossRef.
- A. Sahu, K. Blackburn, K. Durkin, T. B. Eldred, B. R. Johnson, R. Sheikh, J. E. Amburgey and J. C. Poler, Green synthesis of nanoscale anion exchange resin for sustainable water purification, Environ. Sci.: Water Res. Technol., 2018, 4(10), 1685–1694 RSC.
- (a) L. Sellaoui, M. Kehili, E. C. Lima, P. S. Thue, A. Bonilla-Petriciolet, A. B. Lamine, G. L. Dotto and A. Erto, Adsorption of phenol on microwave-assisted activated carbons: Modelling and interpretation, J. Mol. Liq., 2019, 274, 309–314 CrossRef CAS; (b) B.-Y. Zhu and T. Gu, Surfactant adsorption at solid-liquid interfaces, Adv. Colloid Interface Sci., 1991, 37(1), 1–32 CrossRef CAS.
- C. D. Palmer and P. R. Wittbrodt, Processes affecting the remediation of chromium-contaminated sites, Environ. Health Perspect., 1991, 92, 25–40 CrossRef CAS PubMed.
- M. Owlad, M. K. Aroua, W. A. W. Daud and S. Baroutian, Removal of Hexavalent Chromium-Contaminated Water and Wastewater: A Review, Water, Air, Soil Pollut., 2009, 200(1), 59–77 CrossRef CAS.
- T. Posati, M. Nocchetti, A. Kovtun, A. Donnadio, M. Zambianchi, A. Aluigi, M. L. Capobianco, F. Corticelli, V. Palermo, G. Ruani, R. Zamboni, M. L. Navacchia and M. Melucci, Polydopamine Nanoparticle-Coated Polysulfone Porous Granules as Adsorbents for Water Remediation, ACS Omega, 2019, 4(3), 4839–4847 CrossRef CAS PubMed.
- A. Aluigi, C. Tonetti, C. Vineis, C. Tonin, R. Casasola and F. Ferrero, Wool Keratin Nanofibres for Copper(II) Adsorption, J. Biobased Mater. Bioenergy, 2012, 6(2), 230–236 CAS.
- P. Chakravarty, N. S. Sarma and H. P. Sarma, Biosorption of cadmium(II) from aqueous solution using heartwood powder of Areca catechu, Chem. Eng. J., 2010, 162(3), 949–955 CrossRef CAS.
- R. Sitko, E. Turek, B. Zawisza, E. Malicka, E. Talik, J. Heimann, A. Gagor, B. Feist and R. Wrzalik, Adsorption of divalent metal ions from aqueous solutions using graphene oxide, Dalton Trans., 2013, 42(16), 5682–5689 RSC.
- N. Sui, L. Wang, X. Wu, X. Li, J. Sui, H. Xiao, M. Liu, J. Wan and W. W. Yu, Polyethylenimine modified magnetic graphene oxide nanocomposites for Cu2+ removal, RSC Adv., 2015, 5(1), 746–752 RSC.
- D. Ociński and P. Mazur, Highly efficient arsenic sorbent based on residual from water deironing – Sorption mechanisms and column studies, J. Hazard. Mater., 2020, 382, 121062 CrossRef PubMed.
- J. Zhu, Z. Lou, Y. Liu, R. Fu, S. A. Baig and X. Xu, Adsorption behavior and removal mechanism of arsenic on graphene modified by iron–manganese binary oxide (FeMnOx/RGO) from aqueous solutions, RSC Adv., 2015, 5(83), 67951–67961 RSC.
- H. Zhu, Y. Jia, X. Wu and H. Wang, Removal of arsenic from water by supported nano zero-valent iron on activated carbon, J. Hazard. Mater., 2009, 172(2), 1591–1596 CrossRef CAS PubMed.
- L. Meili, P. V. S. Lins, M. T. Costa, R. L. Almeida, A. K. S. Abud, J. I. Soletti, G. L. Dotto, E. H. Tanabe, L. Sellaoui, S. H. V. Carvalho and A. Erto, Adsorption of methylene blue on agroindustrial wastes: Experimental investigation and phenomenological modelling, Prog. Biophys. Mol. Biol., 2019, 141, 60–71 CrossRef CAS PubMed.
- A. Aluigi, F. Rombaldoni, C. Tonetti and L. Jannoke, Study of Methylene Blue adsorption on keratin nanofibrous membranes, J. Hazard. Mater., 2014, 268, 156–165 CrossRef CAS PubMed.
- J. Fu, Z. Chen, M. Wang, S. Liu, J. Zhang, J. Zhang, R. Han and Q. Xu, Adsorption of methylene blue by a high-efficiency adsorbent (polydopamine microspheres): Kinetics, isotherm, thermodynamics and mechanism analysis, Chem. Eng. J., 2015, 259, 53–61 CrossRef CAS.
- F.-C. Wu, R.-L. Tseng and R.-S. Juang, A review and experimental verification of using chitosan and its derivatives as adsorbents for selected heavy metals, J. Environ. Manage., 2010, 91(4), 798–806 CrossRef CAS PubMed.
- A. Bhatnagar, E. Kumar and M. Sillanpää, Fluoride removal from water by adsorption—A review, Chem. Eng. J., 2011, 171(3), 811–840 CrossRef CAS.
- V. K. Gupta, R. Kumar, A. Nayak, T. A. Saleh and M. A. Barakat, Adsorptive removal of dyes from aqueous solution onto carbon nanotubes: A review, Adv. Colloid Interface Sci., 2013, 193–194, 24–34 CrossRef CAS PubMed.
- M. Hua, S. Zhang, B. Pan, W. Zhang, L. Lv and Q. Zhang, Heavy metal removal from water/wastewater by nanosized metal oxides: A review, J. Hazard. Mater., 2012, 211–212, 317–331 CrossRef CAS PubMed.
- V. K. Gupta, Suhas, Application of low-cost adsorbents for dye removal – A review, J. Environ. Manage., 2009, 90(8), 2313–2342 CrossRef CAS PubMed.
- W. S. Wan Ngah, L. C. Teong and M. A. K. M. Hanafiah, Adsorption of dyes and heavy metal ions by chitosan composites: A review, Carbohydr. Polym., 2011, 83(4), 1446–1456 CrossRef CAS.
- W. S. Wan Ngah and M. A. K. M. Hanafiah, Removal of heavy metal ions from wastewater by chemically modified plant wastes as adsorbents: A review, Bioresour. Technol., 2008, 99(10), 3935–3948 CrossRef CAS PubMed.
- S. E. Bailey, T. J. Olin, R. M. Bricka and D. D. Adrian, A review of potentially low-cost sorbents for heavy metals, Water Res., 1999, 33(11), 2469–2479 CrossRef CAS.
- G. Crini, Non-conventional low-cost adsorbents for dye removal: A review, Bioresour. Technol., 2006, 97(9), 1061–1085 CrossRef CAS PubMed.
- D. Mohan and C. U. Pittman, Arsenic removal from water/wastewater using adsorbents—A critical review, J. Hazard. Mater., 2007, 142(1), 1–53 CrossRef CAS PubMed.
- Y. Sağ, Biosorption of heavy metals by fungal biomass and modeling of fungal biosorption: a review, Sep. Purif. Methods, 2001, 30(1), 1–48 CrossRef.
- I. Anastopoulos and G. Z. Kyzas, Agricultural peels for dye adsorption: A review of recent literature, J. Mol. Liq., 2014, 200, 381–389 CrossRef CAS.
- G. Z. Kyzas, J. Fu, N. K. Lazaridis, D. N. Bikiaris and K. A. Matis, New approaches on the removal of pharmaceuticals from wastewaters with adsorbent materials, J. Mol. Liq., 2015, 209, 87–93 CrossRef CAS.
- H. Sousa, C. A. Sousa, L. C. Simões and M. Simões, Microalgal-based removal of contaminants of emerging concern, J. Hazard. Mater., 2022, 423, 127153 CrossRef CAS PubMed.
- S. Ahmad, X. Liu, J. Tang and S. Zhang, Biochar-supported nanosized zero-valent iron (nZVI/BC) composites for removal of nitro and chlorinated contaminants, Chem. Eng. J., 2022, 431, 133187 CrossRef CAS.
- M. Zheng, L. Xu, C. Chen, L. Labiadh, B. Yuan and M.-L. Fu, MOFs and GO-based composites as deliberated materials for the adsorption of various water contaminants, Sep. Purif. Technol., 2022, 294, 121187 CrossRef CAS.
- A. Gogoi, P. Mazumder, V. K. Tyagi, G. G. Tushara Chaminda, A. K. An and M. Kumar, Occurrence and fate of emerging contaminants in water environment: A review, Groundw. Sustain. Dev., 2018, 6, 169–180 CrossRef.
Footnote |
| † European Chemicals Agency, ECHA, https://echa.europa.eu/universe-of-registered-substances retrieved July 27, 2020. |
| This journal is © The Royal Society of Chemistry 2023 |