Open Access Article
Open Access ArticleAb initio rate coefficients for the reaction of OH and H2O2 under upper troposphere and lower stratosphere conditions†
Thanh Lam
Nguyen
 * and
John F.
Stanton
*
* and
John F.
Stanton
*
Quantum Theory Project, Departments of Chemistry and Physics, University of Florida, Gainesville, FL 32611, USA. E-mail: tlam.nguyen@chem.ufl.edu; johnstanton@chem.ufl.edu
First published on 25th October 2023
Abstract
The reaction between hydrogen peroxide (H2O2) and hydroxyl radical (OH) plays an important role in the upper troposphere and lower stratosphere (UTLS). However, direct experimental studies are lacking for this UTLS regime for a temperature range of 190–250 K. In this work, mechanism and kinetics for the title reaction were studied using high-level theoretical methods to provide highly accurate rate coefficients for the UTLS regime. The reaction was found to proceed via a van der Waals (vdW) complex at low temperatures, but to undergo a direct H-abstraction via a well-skipping mechanism at higher temperature to yield products HO2 + H2O. The ab initio rate coefficients are pressure-independent under terrestrial atmospheric conditions (T = 180–350 K and P ≤ 1 atm) and agree well to within 20% with most experimental data available for T = 165–500 K.
Environmental significanceHOx (OH/HO2) radicals participate in catalytic cycles involving ozone in the upper troposphere and lower stratosphere (UTLS) regime. Hydrogen peroxide (H2O2) is an important HOx reservoir in the atmosphere. Therefore, the reaction of OH and H2O2 plays an important role in the UTLS. Because the vapor pressure of H2O2 is extremely low at temperatures below 250 K, direct experimental studies are lacking for this UTLS regime for a temperature range of 190–250 K. To provide highly accurate rate coefficients that are useful for kinetics modeling, we have studied mechanism and kinetics for the title reaction using high-level theoretical calculations. |
Introduction
Hydrogen peroxide (H2O2) is an important OH/HO2 (HOx) reservoir in the atmosphere.1 It is principally produced from a self-reaction of HO2 radicals viaeqn (1).2,3 The atmospheric fate of H2O2 is sensitively dependent on altitude.4 On the Earth's surface where the humidity is often high, H2O2 is mostly taken up into aerosols (or condensed phases) or rained out. In the upper stratosphere where ultraviolet sunlight is highly intense, H2O2 is generally photolyzed to yield two hydroxyl radicals viaeqn (2). The oxidation of H2O2 by OH radicals (eqn (3)) is believed to be a major sink of H2O2 in the upper troposphere and lower stratosphere (UTLS) regime.5| HO2 + HO2 → H2O2 + O2 | (1) |
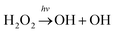 | (2) |
| H2O2 + OH → HO2 + H2O | (3) |
| HO2 + OH → O2 + H2O | (4) |
A combination of eqn (1) and (3) gives eqn (4), which represents a chain-termination step of two highly reactive radicals (OH and HO2). It is well established that HOx radicals participate in catalytic cycles involving ozone in the UTLS,5 the title reaction is therefore believed to play an important role. Because of these considerations, the mechanism and kinetics for the title reaction needs to be determined to provide reliable data for atmospheric modeling.
The reaction has been studied experimentally4–15 and found to have a small positive activation energy of about 0.32 kcal mol−1 over the T = 300–500 K range.1 However, the proposed reaction mechanism is somewhat complicated.5 It is presumed to go through a pre-reaction (van der Waals) complex at low temperatures and to become a direct H-abstraction at higher temperatures.5 The reaction rate constants were measured, mostly for T ≥ 250 K because the vapor pressure of H2O2 is extremely low at temperatures below this.5 There is only one experimental study reported for T ≤ 165 K down to 98 K.5 However, there are no direct rate measurements5 for T = 190–250 K relevant to the UTLS regime where the title reaction plays its most important role.
The title reaction was studied theoretically16–19 using various levels of theory including CASPT2//CASSCF,16 CCSD(T)/6-31G*//MP2,17 DFT-MPW1K/6-31G**,18 and CCSD(T)/CBS(aD,aT,aQ)//MP2/aug-cc-pVDZ19 (here A//B means A single-point energy calculations at B geometries). The effect of a single water molecule on the mechanism and kinetics was investigated and found to be negligible.19 The reaction rate coefficients were computed for T = 250–500 K by assuming a thermal equilibrium between the pre-reaction complex (PRC) and the initial reactants. Such an assumption is only fulfilled at the high-pressure limit, which cannot be attained under atmospheric conditions on Earth, thus is inappropriate for the PRC having a binding energy less than 4 kcal mol−1. The title reaction proceeding via a vibrationally excited intermediate (i.e. pre-reaction complex) is obvious to be pressure-dependent, thus a master equation analysis must be done to obtain rate constants as a function of both temperature and pressure. To the best of our knowledge, there are no theoretical results reported for T = 190–250 K, which is the relevant range of T for the UTLS regime.
In this work, we use a higher accuracy composite method20 to characterize the title reaction mechanism. We then compute reaction rate coefficients for a wide range of temperature (50–1500 K) using E,J-resolved two-dimensional master equation (2DME) techniques21–24 in combination with semiclassical transition state theory (SCTST),25–29 which is used to obtain microcanonical rate constants, k(E,J). Theoretical results will be compared with experimental ones where they are available to validate methodologies used in this work. Finally, we provide accurate results for k(T) with T = 190–250 K – where direct experimental data is absent – which are expected to be useful for atmospheric modeling in the UTLS region.
Theoretical methodologies
High accuracy coupled cluster calculations
In this paper, energies of all stationary points were computed using a composite method, namely the amHEAT-345(Q) protocol,20 which bases on all-electron (ae) CCSD(T)/cc-pVQZ geometries. Relative energies (to the initial reactants) include anharmonic zero-point vibration energy (ZPE) corrections. Anharmonic ZPEs of all stationary points are obtained using second-order vibration perturbation theory (VPT2), in which harmonic vibrational frequencies and anharmonic constants are computed with ae-CCSD(T)/aug-cc-pCVTZ and ae-CCSD(T)/aug-cc-pCVDZ levels of theory, respectively. As detailed elsewhere,20 the amHEAT protocol includes sequences of single-point energy calculations using coupled cluster methods. The CCSD(T) method is used to recover a large portion of electron correlation while a smaller portion of electron correlation is recovered using full single, double, and triple excitation (CCSDT) and non-iterative (perturbative) quadruple excitation (CCSDT(Q)) methods. Furthermore, smaller corrections including core-valence correlation effects, scalar relativity, spin–orbit couplings, and the diagonal Born–Oppenheimer correction (DBOC) are also added. The total energy calculated with the amHEAT protocol20 can be expressed as:| EamHEAT = ESCF(∞) + δE(T)−SCF + δET−(T) + δE(Q)−T + δEZPE + δECore + δESO + δERel + δEDBOC | (5) |
As seen in Fig. 1, the amHEAT reaction enthalpies and the benchmark ATcT30 are generally in excellent agreement (better than 0.1 kcal mol−1). However, a conservative accuracy of ca. 0.4 kcal mol−1 can be expected for the calculated barrier heights. Table S1 in the ESI† shows a comparison of the amHEAT energies in this work with other results that were calculated using lower levels of theory reported in the literature. To the best of our knowledge, the amHEAT method is the highest level of theory that has yet been applied to the title reaction. The CFOUR program31 was used for all CCSD(T) and CCSDT calculations (and also CCSDT(Q) for closed-shell systems) while the CCSDT(Q) calculations for open-shell species were done with MRCC,32 which is interfaced to CFOUR.
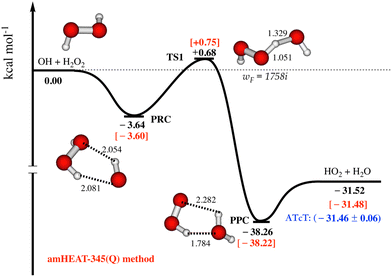 | ||
| Fig. 1 Most important part of the lowest-lying doublet state potential energy surface for the OH + H2O2 reaction is constructed using amHEAT-345(Q) method (see text, values in red and black are with and without the HIR treatment, respectively). Benchmark ATcT values30 (in blue) are also included for comparison. | ||
E,J-Resolved two-dimensional master equation calculations
The association of OH and H2O2 forms a vibrationally excited adduct (PRC†), after that it carries out an H-abstraction to yield the products (see Fig. 1). Therefore, the reaction rate is pressure-dependent. We solve a master equation to obtain rate coefficients as a function of both pressure and temperature using energies, rovibrational parameters, and anharmonic constants calculated with the amHEAT protocol as described above. Solutions of a master equation were well described and provided in detail in our previous studies.21–24 So, they need not to be repeated again here. Collisional parameters, a ceiling internal energy, a maximum total angular momentum, and others used in the E,J-resolved 2DME model are given in Table S2.† To solve a master equation, microcanonical rate coefficients k(E,J) must be provided as input data. For the tight TS1, Miller's SCTST theory25–29 as implemented in the Multiwell program33 is used to compute k(E,J). For a loosely variational TS0, microvariational TST theory34–37 is used to find a kinetic bottleneck. As explained in detail below, hindered internal rotations in H2O2 and TS1 are separated from the remaining vibrations, and they are independently treated as one-dimensional hindered internal rotations. As seen below, the calculated rate coefficients in this work are expected to have an estimated uncertainty of about 20%.Results and discussion
Reaction mechanism
The most important part of the lowest-lying doublet state PES for the title reaction calculated with the amHEAT-345(Q) method is displayed in Fig. 1. As seen, the association of OH and H2O2 is a barrierless process leading to formation of a vibrationally excited pre-reaction complex (PRC†). PRC is formed by two (weak) hydrogen bonds and has a binding energy of 3.60 kcal mol−1; therefore, PRC is highly unlikely to be thermally stabilized by collisions unless at an extremely high pressure and very low temperature. There are two possible reaction pathways from PRC: it can either re-dissociate back to the initial reactants (OH + H2O2) via a loose, variational TS0 (not shown) or undergo an H-abstraction via a tight (well-defined) TS1 leading to formation of pre-product complex (PPC). TS1 lies slightly above the initial reactants, thus the title reaction has an overall positive barrier height of 0.75 kcal mol−1, in good agreement with a (proposed) experimental activation energy of 0.32 kcal mol−1.1 As a result, the former pathway is enthalpically and entropically favored while the latter pathway is controlled by quantum tunneling effects, which play an important role at low temperature. So, kinetic analysis is necessary to resolve this competition. PPC† when formed has a highly internal energy of (ca. 39–40 kcal mol−1), so it instantaneously decomposes to yield HO2 and H2O.Reaction rate coefficient calculations
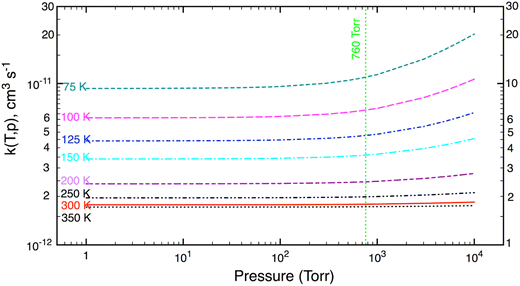
The SCTST results heavily depend on VPT2 calculations, which are used to obtain anharmonic constants, Xij, for small amplitude vibrations. It is well established that the VPT2 approach may not be satisfactory for hindered internal rotations (HIRs), which are large amplitude motions, especially at high temperatures (or high energies). As usual, these HIRs are assumed to be separable from the remaining vibrations and treated individually as (uncoupled) one-dimensional (1D) HIR. To see the effects of the HIR treatment on k(T,p), in this work both chemical kinetic models (namely, K1 model including the HIR treatment and K2 model without any HIR treatment) were used to compute reaction rate coefficients.Fall-off curves computed as a function of pressure (P = 1–104 torr) and a fixed temperature (T = 75–350 K) are exhibited in Fig. 2. Inspection of Fig. 2 shows that the calculated k(T) decreases with increasing temperature, as expected for this temperature range where the reaction rate has a negative T-dependence. The reaction rate depends only slightly on pressure; and the effects of pressure (due to quantum tunneling effects) are only important at very low temperature and very high pressure. Such characteristics can also be seen for other (similar) reactions.23,24,38–40 Under terrestrial atmospheric conditions (T = 180–350 K and P = 0–1 atm), the reaction rate is practically pressure-independent. This remains true at higher temperatures in combustion environment (with P < 10 atm).
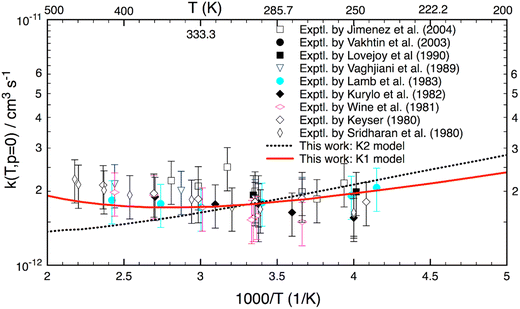
Fig. 3 shows the reaction rate coefficients calculated for T = 200–500 K relevant to the terrestrial atmospheric conditions. Experimental data (given in symbols) are also included for comparison. As seen, the calculated k(T) with the K1 model agree well (better than 20%) with almost all experimental results. Particularly, the theoretical K1 results are in line with the experimental values reported by Lamb et al.9 However, there is a difference of the shape between theory and experiment in this temperature range. Experimental results (excluding the results of Lamb et al.9) show a positive T-dependence (because of a positive activation energy), whereas the theoretical K1 model yields a concave-shaped curve. At low T, it decreases with increasing temperature and reaches a minimum at about 340 K, and only then is positively T-dependent. Unlike the K1 model, the K2 yields a negative T-dependence for k(T). Although the K2 model yields good results up to 350 K, it diverges at higher temperatures. Because of the different ZPE corrections, there are small differences between the K1 and K2 models at the lower temperatures. Overall all (combined) experimental results also show a similar concave-shaped curve to that predicted by theory. More importantly, the K1 results with the hindered rotor treatment are more accurate than the K2 model over the T = 200–500 K range.
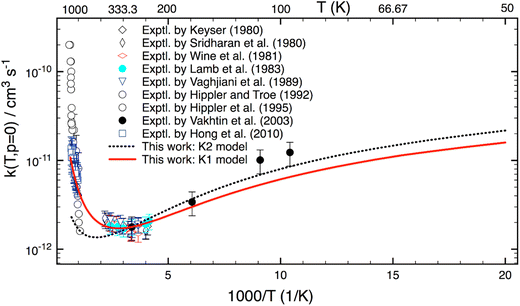
Although this work mainly focuses on computing k(T,p) at atmospheric UTLS conditions, it is of importance to compare theory with experiment at high combustion temperatures. There are only three experimental studies13–15 reported for T > 900 K, as shown in Fig. 4. Two studies agree well with one another for T = 1000–1300 K, but they disagree by a factor of 2–3 at higher temperature. A reason for the difference is unknown. As compared to experiment,13–15 the calculation is in good agreement (within 20–30%) with a recent study of Hong et al.,15 but it underestimates the results of Hippler et al.14 at T > 1300 K and overestimates below 1000 K. Further experimental studies appear to be warranted.
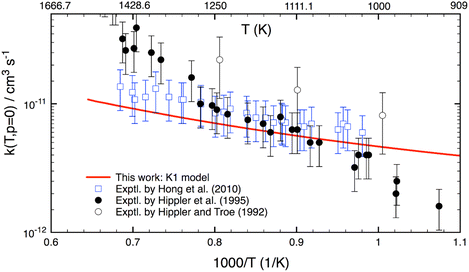 | ||
| Fig. 4 Thermal rate coefficients calculated at T = 900–1500 K and the low-pressure limit for the OH + H2O2 reaction. Experimental data (in symbols) are included for comparison. | ||
Fig. 5 reveals the calculated k(T) for a wide range of T = 50–1500 K. As seen, rate coefficients have a concave shape. Starting at T = 50 K, it decreases with increasing temperature, then it passes through a minimum at about 340 K; and finally, it rises with T at higher T. This characteristic can be explained as follows: the reaction mechanism depends sensitively on temperature. At low-T the reaction proceeds via a van der Waals complex (PRC), thus it is negatively T-dependent; whereas at high-T the formation of PRC is unimportant, therefore the reaction undergoes a direct H-abstraction process (i.e. “well-skipping”41 PRC) to yield products. As a result, it displays a positive dependence of temperature.
Fig. 5 also shows that the K2 model (which does not include any HIR treatment) works rather well at low-T. This implies that VPT2 approach may be sufficient and anharmonic constants (Xij) associated with these HIRs play an important role at low-T. The difference between the K1- and K2 model at low-T is mainly due to changes of ZPE. However, the K2 model fails at high-T, indicating that the HIR treatment is very essential in this range.
Conclusions
The mechanism and kinetics of the OH + H2O2 reaction were re-investigated using the amHEAT composite method and an E,J-resolved two-dimensional master equation approach. At low temperatures, the reaction proceeds via an energized pre-reaction complex, followed by an H-abstraction step to yield products HO2 + H2O. At higher temperatures, however the reaction skips the PRC well and directly withdraws a hydrogen atom (through a well-skipping mechanism) to yield products. This finding verifies the mechanism earlier proposed from an experimental study.5 The amHEAT reaction enthalpy agrees well (within 0.1 kcal mol−1) with the benchmark ATcT value. The calculated barrier height has a positive value of 0.7 ± 0.4 kcal mol−1, which is in close agreement with a (recommended) experimental activation energy. The reaction rate coefficients were found to be pressure-independent under terrestrial atmospheric conditions (T = 180–350 K and P ≤ 1 atm) and in excellent agreement (better than 20%) with experimental results for T = 165–500 K. However, at high combustion temperatures the agreement is rather good, within 30%. For T = 180–250 K relevant to the UTLS regime where direct rate measurements are not available, we provide a mathematic expression of k(T) = 8.5 × 10−13 × exp(206 K/T) in cm3 s−1 (with an estimated uncertainty of 20%), which is expected to be useful for atmospheric modeling.Data availability
The data that support the findings of this study are available within the article and its ESI.† Detailed theoretical data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
TLN and JFS conceived the presented ideas. TLN performed the computations. All authors discussed the results, wrote the manuscript, and contributed to the final manuscript.Conflicts of interest
There is no conflict to declare.Acknowledgements
The work at UF was supported by the U.S. Department of Energy, Office of Basic Energy Sciences under Award DE-SC0018164. We would like to thank Prof. John R. Barker (University of Michigan) for helpful discussion. We thank two anonymous reviewers who provided helpful comments that helped to improve the presentation and the quality of this work.References
- J. B. Burkholder, S. P. Sander, J. P. D. Abbatt, J. R. Barkeri, C. Cappa, J. D. Crounse, T. S. Dibble, R. E. Huie, C. E. Kolbi, M. J. Kurylo, V. L. Orkin, C. J. Percival, D. M. Wilmouth and P. H. Wine, Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies, Evaluation No. 19, JPL Publication 19-5, Jet Propulsion Laboratory, Pasadena, 2019, http://jpldataeval.jpl.nasa.gov Search PubMed.
- H. Hippler, J. Troe and J. Willner, Shock-Wave Study of the Reaction HO2+HO2->H2O2+O2 – Confirmation of a Rate-Constant Minimum near 700-K, J. Chem. Phys., 1990, 93, 1755–1760 CrossRef CAS.
- P. D. Lightfoot, B. Veyret and R. Lesclaux, The Rate-Constant for the HO2+HO2 Reaction at Elevated-Temperatures, Chem. Phys. Lett., 1988, 150, 120–126 CrossRef CAS.
- L. F. Keyser, Absolute Rate-Constant of the Reaction OH + H2O2->HO2 + H2O from 245-K to 423-K, J. Phys. Chem., 1980, 84, 1659–1663 CrossRef CAS.
- A. B. Vakhtin, D. C. McCabe, A. R. Ravishankara and S. R. Leone, Low-temperature kinetics of the reaction of the OH radical with hydrogen peroxide, J. Phys. Chem. A, 2003, 107, 10642–10647 CrossRef CAS.
- U. C. Sridharan, B. Reimann and F. Kaufman, Kinetics of the Reaction OH + H2O2->HO2 + H2O, J. Chem. Phys., 1980, 73, 1286–1293 CrossRef CAS.
- P. H. Wine, D. H. Semmes and A. R. Ravishankara, A laser flash photolysis kinetics study of the reaction OH + H2O2 -> HO2 + H2O, J. Chem. Phys., 1981, 75, 4390–4395 CrossRef CAS.
- M. J. Kurylo, J. L. Murphy, G. S. Haller and K. D. Cornett, A Flash-Photolysis Resonance Fluorescence Investigation of the Reaction OH + H2O2->HO2 + H2O, Int. J. Chem. Kinet., 1982, 14, 1149–1161 CrossRef CAS.
- J. J. Lamb, L. T. Molina, C. A. Smith and M. J. Molina, Rate-Constant of the OH + H2O2 -> HO2 + H2O Reaction, J. Phys. Chem., 1983, 87, 4467–4470 CrossRef CAS.
- G. L. Vaghjiani, A. R. Ravishankara and N. Cohen, Reactions of OH and OD with H2O2 and D2O2, J. Phys. Chem., 1989, 93, 7833–7837 CrossRef CAS.
- E. R. Lovejoy, T. P. Murrells, A. R. Ravishankara and C. J. Howard, Oxidation of CS2 by Reaction with OH2. Yields of HO2 and SO2 in Oxygen, J. Phys. Chem., 1990, 94, 2386–2393 CrossRef CAS.
- E. Jimenez, T. Gierczak, H. Stark, J. B. Burkholder and A. R. Ravishankara, Reaction of OH with HO2NO2 (peroxynitric acid): Rate coefficients between 218 and 335 K and product yields at 298 K, J. Phys. Chem. A, 2004, 108, 1139–1149 CrossRef CAS.
- H. Hippler and J. Troe, Rate Constants of the Reaction HO+H2O2->HO2+H2O at T-Greater-Than-or-Equal-to-1000-K, Chem. Phys. Lett., 1992, 192, 333–337 CrossRef CAS.
- H. Hippler, H. Neunaber and J. Troe, Shock Wave-Studies of the Reactions HO+H2O2->H2O+HO2 and HO+HO2->H2O+O2 between 930 and 1680 K, J. Chem. Phys., 1995, 103, 3510–3516 CrossRef CAS.
- Z. K. Hong, R. D. Cook, D. F. Davidson and R. K. Hanson, A Shock Tube Study of OH + H2O2 -> H2O + HO2 and H2O2 + M -> 2OH+M using Laser Absorption of H2O and OH, J. Phys. Chem. A, 2010, 114, 5718–5727 CrossRef CAS PubMed.
- M. Bahri, Y. Tarchouna, N. Jaidane, Z. Ben Lakhdar and J. P. Flament, Ab initio study of the hydrogen abstraction reaction H2O2+OH -> HO2+H2O, J. Mol. Struct.: THEOCHEM, 2003, 664, 229–236 CrossRef.
- F. Atadinc, H. Gunaydin, A. S. Ozen and V. Aviyente, A quantum mechanical approach to the kinetics of the hydrogen abstraction reaction H2O2+OH -> HO2+H2O, Int. J. Chem. Kinet., 2005, 37, 502–514 CrossRef CAS.
- B. Ginovska, D. M. Camaioni and M. Dupuis, Reaction pathways and excited states in H2O2+OH -> HO2+H2O: A new ab initio investigation, J. Chem. Phys., 2007, 127, 084309 CrossRef PubMed.
- R. J. Buszek, M. Torrent-Sucarrat, J. M. Anglada and J. S. Francisco, Effects of a Single Water Molecule on the OH+H2O2 Reaction, J. Phys. Chem. A, 2012, 116, 5821–5829 CrossRef CAS PubMed.
- J. H. Thorpe, C. A. Lopez, T. L. Nguyen, J. H. Baraban, D. H. Bross, B. Ruscic and J. F. Stanton, High-accuracy extrapolated ab initio thermochemistry. IV. A modified recipe for computational efficiency, J. Chem. Phys., 2019, 150, 224102 CrossRef PubMed.
- T. L. Nguyen and J. F. Stanton, Pragmatic Solution for a Fully E,J-Resolved Master Equation, J. Phys. Chem. A, 2020, 124, 2907–2918 CrossRef CAS PubMed.
- T. L. Nguyen and J. F. Stanton, A Steady-State Approximation to the Two-Dimensional Master Equation for Chemical Kinetics Calculations, J. Phys. Chem. A, 2015, 119, 7627–7636 CrossRef CAS PubMed.
- T. L. Nguyen and J. F. Stanton, Ab Initio Thermal Rate Calculations of HO + HO = O(3P) + H2O Reaction and Isotopologues, J. Phys. Chem. A, 2013, 117, 2678–2686 CrossRef CAS PubMed.
- T. L. Nguyen and J. Peeters, The CH(X2Pi) + H2O reaction: two transition state kinetics, Phys. Chem. Chem. Phys., 2021, 23, 16142–16149 RSC.
- W. H. Miller, Semiclassical Theory for Non-Separable Systems – Construction of Good Action-Angle Variables for Reaction-Rate Constants, Faraday Discuss., 1977, 62, 40–46 RSC.
- W. H. Miller, R. Hernandez, N. C. Handy, D. Jayatilaka and A. Willetts, Abinitio Calculation of Anharmonic Constants for a Transition-State, with Application to Semiclassical Transition-State Tunneling Probabilities, Chem. Phys. Lett., 1990, 172, 62–68 CrossRef CAS.
- R. Hernandez and W. H. Miller, Semiclassical Transition-State Theory - a New Perspective, Chem. Phys. Lett., 1993, 214, 129–136 CrossRef CAS.
- T. L. Nguyen, J. F. Stanton and J. R. Barker, A practical implementation of semi-classical transition state theory for polyatomics, Chem. Phys. Lett., 2010, 499, 9–15 CrossRef CAS.
- T. L. Nguyen, J. F. Stanton and J. R. Barker, Ab Initio Reaction Rate Constants Computed Using Semiclassical Transition-State Theory: HO+H2 -> H2O+H and Isotopologues, J. Phys. Chem. A, 2011, 115, 5118–5126 CrossRef CAS PubMed.
- B. Ruscic and D. H. Bross, Active Thermochemical Tables (ATcT) Values Based on Ver. 1.148 of the Thermochemical Network, 2023 Search PubMed.
- D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T. C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, Coupled-cluster techniques for computational chemistry: The CFOUR program package, J. Chem. Phys., 2020, 152, 214108 CrossRef CAS PubMed.
- M. Kalley, et al., MRCC, a quantum chemical program suite written by M. Kallay and co-workers, J. Chem. Phys., 2013, 139, 094105 CrossRef PubMed ), as well as: www.mrcc.hu.
- J. R. Barker, T. L. Nguyen, J. F. Stanton, C. Aieta, M. Ceotto, F. Gabas, T. J. D. Kumar, C. G. L. Li, L. L. Lohr, A. Maranzana, N. F. Ortiz, J. M. Preses, J. M. Simmie, J. A. Sonk and P. J. Stimac, MULTIWELL Program Suite, Climate and Space Sciences and Engineering, University of Michigan, Ann Arbor, MI, 48109-2143, 2022 Search PubMed.
- H. Eyring, The activated complex in chemical reactions, J. Chem. Phys., 1935, 3, 107–115 CrossRef CAS.
- M. G. Evans and M. Polanyi, Some applications of the transition state method to the calculation of reaction velocities, especially in solution, Trans. Faraday Soc., 1935, 31, 0875–0893 RSC.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, Current status of transition-state theory, J. Phys. Chem., 1996, 100, 12771–12800 CrossRef CAS.
- W. L. Hase, Variational Unimolecular Rate Theory, Acc. Chem. Res., 1983, 16, 258–264 CrossRef CAS.
- T. L. Nguyen and J. F. Stanton, Pressure-Dependent Rate Constant Caused by Tunneling Effects: OH + HNO3 as an Example, J. Phys. Chem. Lett., 2020, 11, 3712–3717 CrossRef CAS PubMed.
- T. L. Nguyen, B. Ruscic and J. F. Stanton, A master equation simulation for the OH + CH3OH reaction, J. Chem. Phys., 2019, 150, 084105 CrossRef PubMed.
- T. L. Nguyen, A. Perera and J. Peeters, High-accuracy first-principles-based rate coefficients for the reaction of OH and CH3OOH, Phys. Chem. Chem. Phys., 2022, 24, 26684–26691 RSC.
- J. A. Miller, S. J. Klippenstein, S. H. Robertson, M. J. Pilling, R. Shannon, J. Zador, A. W. Jasper, C. F. Goldsmith and M. P. Burke, Comment on "When Rate Constants Are Not Enough", J. Phys. Chem. A, 2016, 120, 306–312 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Optimized geometries, ro-vibrational parameters, anharmonic constants, the calculated rate coefficients, and additional figures and tables. See DOI: https://doi.org/10.1039/d3ea00143a |
| This journal is © The Royal Society of Chemistry 2023 |