Open Access Article
Open Access ArticleSize-dependent shape distributions of platinum nanoparticles†
Ruikang
Ding
 *a,
Ingrid M.
Padilla Espinosa
*a,
Ingrid M.
Padilla Espinosa
 *b,
Dennis
Loevlie
c,
Soodabeh
Azadehranjbar
a,
Andrew J.
Baker
*b,
Dennis
Loevlie
c,
Soodabeh
Azadehranjbar
a,
Andrew J.
Baker
 a,
Giannis
Mpourmpakis
a,
Giannis
Mpourmpakis
 c,
Ashlie
Martini
c,
Ashlie
Martini
 b and
Tevis D. B.
Jacobs
b and
Tevis D. B.
Jacobs
 a
a
aDepartment of Mechanical Engineering and Materials Science, University of Pittsburgh, Pittsburgh, PA 15261, USA. E-mail: tjacobs@pitt.edu
bDepartment of Mechanical Engineering, University of California, Merced, Merced, CA 95343, USA
cDepartment of Chemical and Petroleum Engineering, University of Pittsburgh, Pittsburgh, PA 15261, USA
First published on 26th August 2022
Abstract
While it is well established that nanoparticle shape can depend on equilibrium thermodynamics or growth kinetics, recent computational work has suggested the importance of thermal energy in controlling the distribution of shapes in populations of nanoparticles. Here, we used transmission electron microscopy to characterize the shapes of bare platinum nanoparticles and observed a strong dependence of shape distribution on particle size. Specifically, the smallest nanoparticles (<2.5 nm) had a truncated octahedral shape, bound by 〈111〉 and 〈100〉 facets, as predicted by lowest-energy thermodynamics. However, as particle size increased, the higher-energy 〈110〉 facets became increasingly common, leading to a large population of non-equilibrium truncated cuboctahedra. The observed trends were explained by combining atomistic simulations (both molecular dynamics and an empirical square-root bond-cutting model) with Boltzmann statistics. Overall, this study demonstrates experimentally how thermal energy leads to shape variation in populations of metal nanoparticles, and reveals the dependence of shape distributions on particle size. The prevalence of non-equilibrium facets has implications for metal nanoparticles applications from catalysis to solar energy.
Introduction
Nanoparticle shape plays a critical role in determining the physical properties of functional nanoparticles, including their plasmonic resonance,1 catalytic activity,2 adhesion strength3 and interactions with biological systems.4 A variety of different shapes have been observed in metal nanoparticles as synthesized using equilibrium or growth-controlled methods.5–7 In many cases, the particle shape is governed by thermodynamics, where the most stable (lowest-energy) shape can be determined by the Wulff construction,8 in which the distance of the facets to the geometric center varies in proportion to the surface energy of the facets. This approach applied to a face-centered-cubic (FCC) crystal predicts a cuboctahedral or truncated octahedral shape, bound by the two lowest-energy facets, 〈111〉 and 〈100〉, whose energy ratio is about 0.866 according to the broken-bond rule.9–12 These shapes are also commonly observed in experiments on nanoparticles of various materials, including Au13 and Pd.14 Other polyhedral shapes, which are thermodynamically less stable than the Wulff-predicted truncated octahedron, are also commonly observed, including cubes, truncated cubes, octahedra, truncated octahedra, tetrahedra, truncated tetrahedra, and even highly non-equilibrium shapes like nanorods.6,15,16 These shapes can be obtained by manipulating growth kinetics, especially in cases where the surface is passivated or ligand-capped, such that the particle cannot readily relax to its equilibrium shape.Following the core idea of the Wulff construction, that nanoparticles tend to form shapes that minimize the energy of the system, simulation studies point out that the stability of different shapes is also influenced by nanoparticle size.17 In these simulations, nanoparticles are typically modeled as polyhedral atomic clusters. The total excess surface energy is computed as the difference between the total potential energy of the particle and the total potential energy of a bulk system containing the same number of atoms. For example, molecular dynamics simulations with two different semiempirical many-body potentials were used to calculate excess energies of three polyhedral shapes of Ag, Cu, Au, Pd, and Pt nanoparticles containing up to 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms and showed that different size ranges had different stable shapes.18 For Au, Pd, and Pt, larger particles had lowest-energy shapes of decahedra and truncated octahedra while, for small particles, the lowest-energy equilibrium shapes were icosahedra. The transition typically happened at 100–1000 atoms, corresponding to a size of 1–3 nm. Icosahedra and decahedra can compete with conventional stable Wulff polyhedra because their surface is enveloped uniquely by low-energy 〈111〉 facets, though twin boundaries contribute to the excess energy. Another simulation study characterized the size-dependence of surface energy of gold nanoparticles with different Wulff shapes, including cubes, truncated cubes, octahedra, truncated octahedra, and cuboctahedra, by examining the size-dependent surface-to-volume ratio and surface-stress-induced volume dilation.13 The results showed that twinned structures (icosahedra and decahedra) were favored below 3 nm, while truncated octahedra were favored at larger sizes. A summary of previous simulations reporting size-dependent nanoparticle shapes is given in the ESI, Section S1.†
000 atoms and showed that different size ranges had different stable shapes.18 For Au, Pd, and Pt, larger particles had lowest-energy shapes of decahedra and truncated octahedra while, for small particles, the lowest-energy equilibrium shapes were icosahedra. The transition typically happened at 100–1000 atoms, corresponding to a size of 1–3 nm. Icosahedra and decahedra can compete with conventional stable Wulff polyhedra because their surface is enveloped uniquely by low-energy 〈111〉 facets, though twin boundaries contribute to the excess energy. Another simulation study characterized the size-dependence of surface energy of gold nanoparticles with different Wulff shapes, including cubes, truncated cubes, octahedra, truncated octahedra, and cuboctahedra, by examining the size-dependent surface-to-volume ratio and surface-stress-induced volume dilation.13 The results showed that twinned structures (icosahedra and decahedra) were favored below 3 nm, while truncated octahedra were favored at larger sizes. A summary of previous simulations reporting size-dependent nanoparticle shapes is given in the ESI, Section S1.†
Recent investigations have suggested that, while lowest-energy computational analyses are useful for understanding the energetics, they provide an incomplete description of nanoparticle shapes in practice. Indeed, while simulations accurately predict the shape of the lowest-energy particle, they do not explain the coexistence of a variety of shapes for similarly sized particles observed experimentally.19–21 One potential explanation for this variety of stable shapes is thermal energy and Boltzmann statistics.22–26 At any temperature above absolute zero, there will be a distribution of thermal energy, given by the Boltzmann equation, leading to a distribution of shapes. The fraction of each shape is determined by the energy difference between the possible shapes.
Due to the importance of controlling nanoparticle shape in functional applications, many investigations have focused on using stabilizers or surface capping agents to controllably synthesize specific nanoparticle shapes. However, few investigations have explored the shape distributions of nanoparticles that arise without the use of such stabilizers. The purpose of this study is to explore shape distributions of uncapped metal nanoparticles with sizes less than 15 nm, a size range in which Boltzmann statistics are predicted to play a significant role.27 Platinum nanoparticles are used as a representative FCC material, and synthesized using common wet impregnation (WI) methods in which no surface capping agents or stabilizers are added to control size and shape of nanoparticles. The nanoparticle shapes are then characterized using transmission electron microscopy (TEM). Since the influence of environmental species is minimized, the effect of thermodynamics and thermal energy can be explicitly assessed.
Materials & methods
Synthesis
We used WI methods to synthesize platinum nanoparticles, similar to standard protocols in, for example, ref. 28. Four different synthesis recipes were used (Table 1) to ensure that trends in behavior were not dependent on the synthesis approach. The general procedure is as follows. First, microfabricated silicon TEM wedges (<200 nm-plateau silicon wedges, Bruker, Billerica, MA) were plasma-cleaned and then annealed in air at 800 °C with a flow rate of 0.05 cm3 min−1 and a heating rate of 10 °C min−1 for 30 min. As a result, the surface was oxidized to form a silica layer. Second, 2.5 mg of ionic metal precursors of tetraamineplatinum(II) hydroxide hydrate Pt(NH3)4(OH)2·xH2O (Sigma-Aldrich, Burlington, MA) were added to 10 mL of deionized water. Third, the silicon wedges were impregnated with the solution for 4 h. For nanoparticles synthesized by SEA recipes (rows 3 and 4 in Table 1), the solution's pH was adjusted to 12 by the addition of NaOH, and the silicon wedges were impregnated with the solution for just 1 h. Fourth, the impregnated silicon wedges were dried overnight and then, for the high-temperature recipes (rows 2 and 4 in Table 1), calcined in air at 675 °C with a flow rate of 0.05 cm3 min−1 and heating rate of 10 °C min−1 for 3 h in a tube furnace (Lindberg/Blue M, Thermo Electron, Waltham, MA). Calcination at high temperature disrupted the strong metal complex–substrate interactions and led to larger nanoparticle sizes.29 Finally, the impregnated silicon wedges were hydrogenated in an atmosphere of 10% H2/Ar at 250 °C with a flow rate of 0.50 cm3 min−1 and a heating rate of 5 °C min−1 for 2 h. The purpose of this hydrogenation step was to reduce the platinum from the ionic metal precursors, this temperature was chosen based on prior literature describing this synthesis approach,28 and temperatures much higher than this were shown to cause significant particle growth. Because no special surface capping agent or stabilizer was added during synthesis, the synthesized nanoparticles were regarded as bare and free of surface ligands that would favor certain shapes.| Route | Method | Concentration | pH | Calcination | Hydrogenation |
|---|---|---|---|---|---|
| 1 | Low temperature WI | 2.5 mg/10 ml | — | — | 250 °C |
| 2 | High temperature WI | 2.5 mg/10 ml | — | 675 °C | 250 °C |
| 3 | Low temperature SEA | 2.5 mg/10 ml | 12 | — | 250 °C |
| 4 | High temperature SEA | 2.5 mg/10 ml | 12 | 675 °C | 250 °C |
Characterization
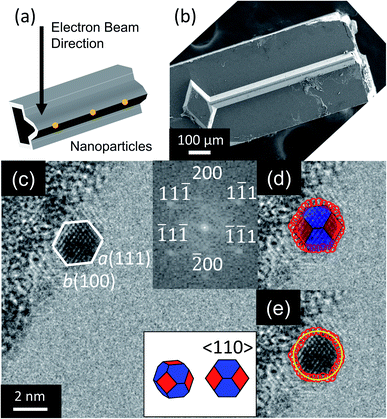
Nanoparticles were observed by TEM (2100F, JEOL, Tokyo, Japan) as illustrated in Fig. 1a and b. A total of 224 nanoparticles were randomly selected, imaged, and analyzed (with an example shown in Fig. 1c). Their outer contours were manually traced using custom Matlab scripts (Fig. 1d), and their crystallographic orientations were determined using Fast Fourier Transforms (FFT) of the images (inset of Fig. 1c). While scanning electron microscopy is more commonly used to assess nanoparticle shape, its few-nm resolution could not accurately discern the shape of particles below approximately 20 nm in diameter. The small size of these applications-relevant nanoparticles (most of which had single-digit-nanometer diameters) required the use of TEM. The overall approach of extracting shape from TEM is well-established in prior literature.13,30–32 Here, the three-dimensional nanoparticle shape was determined by fitting the outer contour to the orientation-matched contour of a polyhedron bound by one of the three lowest-energy facets, namely 〈111〉, 〈100〉 and 〈110〉. Nanoparticle size was defined as the average diameter of the traced nanoparticle shape (Fig. 1e). This process was repeated with the four different synthesis recipes to verify the reproducibility of results. The 224 nanoparticles characterized were randomly selected from the four synthesis recipes for analysis: 35 from low-temperature WI, 76 from high-temperature WI, 36 from low-temperature SEA, and 77 from high-temperature SEA. The difference in the number of particles from the different techniques reflects the fact that larger size ranges were obtained from the high-temperature synthesis methods. The full range of nanoparticle sizes (1–15 nm) was divided into six subranges, each spanning 2.5 nm, and it was ensured that at least 10 nanoparticles were sampled from each subrange.The shape-matching procedure compared the two-dimensional profile of the experimental particle against the corresponding profile of different shapes when viewed along the same crystallographic orientation. More specifically, a wide variety of possible polyhedra were considered at various orientations, as shown in Fig. S1 and Tables S2–S4 (ESI, Section S2†). Based on this analysis, it was determined that the 〈110〉 viewing direction had the greatest variation in two-dimensional profile between different shapes; and therefore provided the least ambiguity about possible shapes (as explained in more detail in ESI, Section 2†). Therefore, only nanoparticles with their 〈110〉 crystallographic direction oriented parallel to the electron beam were selected for analysis in this investigation. Because the substrate was amorphous oxide-coated silicon (with no preferred crystallographic orientation), this selection criterion did not bias the orientation of the particle relative to the substrate.
Simulation
Atomistic simulations were performed using the large-scale atomic/molecular massively parallel simulator (LAMMPS).33 Six different sizes (2–12 nm) of truncated octahedron and truncated cuboctahedron nanoparticles were created. The degree of truncation of the model particles (before equilibration) was chosen to match, as closely as possible, the experimentally observed averaged shapes. The area fractions of observed particles on which these were modeled were 0.58 ± 0.12 and 0.42 ± 0.12 for the 〈111〉 and 〈100〉 facets, respectively, for truncated octahedra. The truncated cuboctahedra had area fractions of 0.30 ± 0.07, 0.28 ± 0.13, and 0.41 ± 0.13, for the 〈111〉, 〈100〉, and 〈110〉 facets, respectively. The size of the model particles was defined analogously to the experimental measurement as the equivalent diameter of the shape as observed along the 〈110〉 viewing direction. The relationship between size and number of atoms for these shapes is plotted in Fig. S2a.† The relative surface-area fraction of these shapes is plotted in Fig. S2b.† The surface-area is defined as the number of atoms belonging to a given facet times the area per atom of that facet. The model nanoparticles were created by carving planes from a platinum crystal oriented in 〈100〉 using LAMMPS and the visualization software Ovito.34 The energy of these shapes was calculated using two distinct approaches, molecular dynamics (MD) simulation and the square-root bond-cutting (SRB) model, to confirm and co-validate the simulation results.In MD simulation, shrink-wrapped boundary conditions were imposed in all directions of the rectangular cuboid simulation box. The atomic energy interactions were defined by the embedded atom method (EAM),35 where the energy is given by:
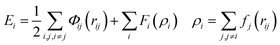 | (1) |
The nanoparticles were geometrically optimized using the conjugate gradient method until the energy difference between successive iterations divided by the energy magnitude was less than 1 × 107 eV/eV. Once the structures were geometrically optimized, the temperature of the simulation was increased to room temperature. The system was equilibrated for 300 ps using a timestep of 1 fs, within a canonical ensemble with a Langevin thermostat and a damping parameter of 0.1 ps. For completeness, the MD simulations were also equilibrated at the two other temperatures involved in synthesis, 250 °C and 675 °C, (as described in the ESI, Section 3, Fig. S3†) to check for structural changes. The energy per atom for each nanoparticle size and shape was taken as the average over the last 30 ps of the equilibration simulations. The standard deviation of the calculated energies was less than 1 × 10−3 eV per atom, confirming thermal equilibrium was reached within the simulation time (Fig. S4†).
In addition to MD simulations, the energy of the nanoparticle shapes was also computed using the SRB model. In this model, the average bond energy, i.e., cohesive energy (CE), of the nanoparticles was estimated from the coordination number (CN) of each atom:40,41
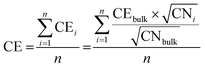 | (2) |
Results & discussion
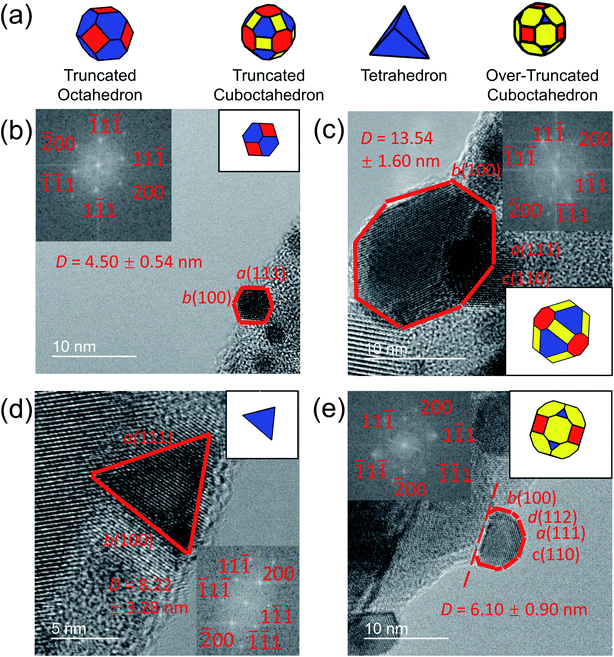
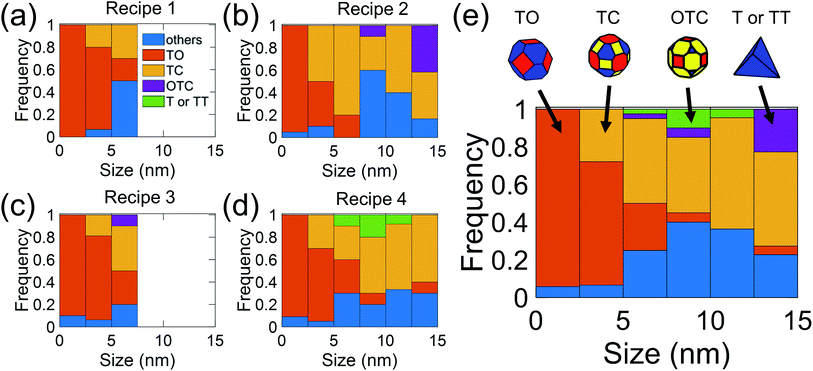
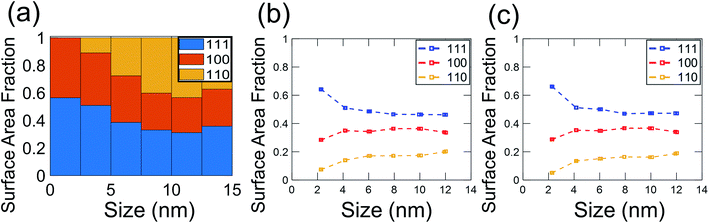
In the present investigation, four kinds of shapes were observed (Fig. 2a), and two particle locations were considered: some particles were located on the side surface of the wedge (not the plateau) such that the substrate-contacting surface was not visible in the image (Fig. 2b–d); other particles were located on the apex of the wedge, such that the contact between the particle and wedge was observed (Fig. 2e). For the former location, the particle contour was matched as observed; for the latter location, the boundary in contact with the substrate (dashed line in Fig. 2e) was explicitly ignored during the shape-matching process to identify the free-particle shape, rather than the substrate-truncated particle shape. Based on Wulff–Kaishew theory,42 the shape of a particle on a substrate can be defined as a truncation of the free-particle shape, with the degree of truncation serving as a measurement of the adhesion energy. Because this investigation was not focused on the adhesion energy of the particle to the substrate, but rather on the free-particle shape, the effect of the substrate was excluded.Fig. 3a–d show the shape distribution analysis for the observed nanoparticles. The most commonly observed shapes were truncated octahedra and truncated cuboctahedra; other shapes observed were over-truncated cuboctahedra, tetrahedra, and truncated tetrahedra. The low-temperature recipes tended to yield smaller particles (Fig. 3a and c), while the high-temperature recipes yielded a wider variety of particle sizes (Fig. 3b and d). For all recipes, the overall trends in distribution of different shapes were similar. The data from all four recipes is combined into a single plot to show the trends for the entire population of nanoparticles (Fig. 3e). All recipes demonstrated a mix of shapes, with truncated octahedra being most common at small sizes, while the prevalence of non-lowest-energy shapes increased with increasing size. In particular, the frequency of truncated cuboctahedra, which has 〈110〉 facets, increased with particle size. Many nanoparticles were grouped into the category “other,” which included irregular shapes that could not be categorized as any of the considered polyhedra (examples include spherical particles or irregular polyhedra, like elongated rods). Tetrahedra and over-truncated cuboctahedra were observed, but infrequently. Overall, these results demonstrate that there is a distribution of particle shapes rather than a single lowest-energy shape and that there is a strong size-dependence of shape distributions.
As described in the introduction, the most commonly used approaches to understand these nanoparticle shapes would be to assume either lowest-energy thermodynamics (Wulff construction) or to assume that they are metastable states that are locked in by the growth kinetics. Neither of these explanations can satisfactorily explain results. A Wulff-construction approach would predict that the truncated octahedron would be most prevalent at all sizes, since it is bound by the lowest-energy facets, 〈111〉 and 〈100〉. A growth-kinetics analysis can easily explain the prevalence of 〈110〉 facets by assuming that they were kinetically favored during particle synthesis. But neither can quantitatively explain the size-dependent distribution of shapes, with its steadily increasing prevalence of non-lowest-energy truncated cuboctahedra. To explain this behavior, we turn to atomistic models to determine the size-dependent energy of different shapes, and Boltzmann statistics to compute the predicted distributions of shapes as a function of particle size. We recognize that the temperatures used in synthesis (523 K and 948 K) are low relative to the bulk melting temperature of platinum (2041 K), however prior work26 has suggested that distributions of shapes can result even at these temperatures.
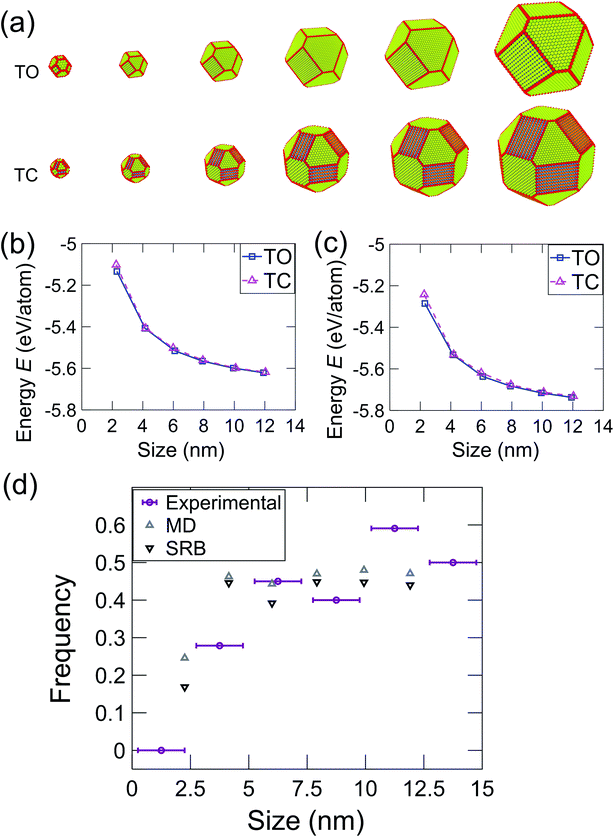
The most common shapes (Fig. 3e) were truncated octahedra and truncated cuboctahedra. To understand the expected relative prevalence of these shapes, atomistic models were created of these two shapes with crystallographic orientations and degrees of truncation that matched the average shapes of the particles observed in experiments (see Materials & methods section). Model particles with six different sizes were created ranging from 2 nm to 12 nm, as shown in Fig. 4. The energy of these particles was determined using an intensive form, i.e., computed on a per-atom basis, to facilitate comparison across different nanoparticle sizes. In the MD simulations, the energy was averaged during equilibration from the EAM potential in eqn (1); for the SRB model, the energy was computed using eqn (2). The energy difference between truncated octahedra and truncated cuboctahedra was small using either MD (Fig. 4b) or SRB (Fig. 4c). As the size increased, this energy difference became even smaller, and the energy approached the bulk value for both shapes. While the results indicated that the truncated octahedron was more stable than the truncated cuboctahedron at every size, the relative difference between them diminished with increasing particle size. This is because the majority of atoms in both shapes lie in the body of the nanoparticles, resulting in similar per-atom-energies at large sizes.
To compute expected shape distributions, Boltzmann statistics were applied to the MD- and SRB-computed energies. Specifically, the population pi,N of the ith shape for a particle with N atoms was computed from the energy of the corresponding shape, as follows:
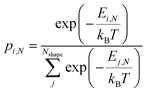 | (3) |
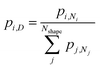 | (4) |
Because of the technological importance of different crystal facets in, for example, catalysis applications, we also computed the area fraction of 〈111〉, 〈100〉, and 〈110〉 facets in experiments and simulations. For a given facet, the surface area fraction Fhkl was computed by dividing the area of the target facet by the total area of all facets for all nanoparticles of that size:
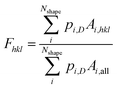 | (5) |
These results demonstrate the critical role of nanoparticle size in determining the distribution of nanoparticle shapes, as well as the fraction of different crystallographic facets present on those particles. As the size of a nanoparticle decreases to the range of a few nanometers, the fraction of surface atoms increases, with significant predicted effects on, for instance, the catalytic activity of the particles.43 The present results demonstrate experimentally how the increasing importance of surface atoms in small nanoparticles affects the shape distributions. In small particles, there are large differences in the energy per atom for particles between different shapes; this diminishes the role of Boltzmann statistics and leads to a greater population of lowest-energy shapes. However, as the nanoparticle size increases, more atoms are in the body of the particle (bulk sites), so the relative importance of surface atoms decreases. This enhances the role of Boltzmann statistics for larger particles, leading to a greater diversity of shapes and a larger population of higher-energy facets. We have used energy terms on a per-atom basis so that the energy can be compared consistently between different particle sizes. While this intensive energy value does not represent the total nanoparticle energy, it represents the averaged energies of atoms at different particle sizes. Thus, it reflects the thermodynamic tendency of atoms to form nanoparticles of different shapes and thus, different facets.
Finally, these results do not claim to describe the universal shapes of all platinum nanoparticles; indeed, a wide variety of shapes have been observed in prior literature, and the final shape depends sensitively on various factors such as synthesis conditions or surface passivation. Instead, these results indicate that, when the shape of bare nanoparticles is not explicitly controlled, the resulting nanoparticles will take on a distribution of shapes, which is consistent with predictions based on thermal fluctuations and the Boltzmann distribution.
Conclusions
In summary, this study investigated the size-dependence of nanoparticle shape for FCC platinum nanoparticles using experiments and simulations. Nanoparticles with diameters from 1 to 15 nm were synthesized using four variants of a simple wet impregnation method without added surface-capping agents, and then the particle shape was characterized using a transmission electron microscope. For particles smaller than 2.5 nm, the experimentally measured nanoparticles were almost exclusively composed of truncated octahedra, and only the lowest-energy 〈111〉 and 〈100〉 facets were observed. As the particle size increased, other shapes such as truncated cuboctahedra became increasingly common, along with higher-energy 〈110〉 facets. These trends plateaued as the nanoparticle size increased above approximately 7.5 nm. These size-dependent-shape trends were consistent with an analysis based on statistical thermodynamics and Boltzmann statistics. This analysis was applied to model nanoparticles whose energies were computed using two separate simulation approaches: molecular dynamics and the square-root bond cutting model. The results of this investigation demonstrate the critical role of particle size on both shape distribution and area-fraction of higher-energy facets.Data availability
Data are available from the corresponding authors upon reasonable request.Author contributions
R. Ding did the experiments, performed associated analysis, and led the writing. I. M. Padilla Espinosa performed MD simulations and wrote the associated content. D. Loevlie did the work related to SRB model and wrote associated content. S. Azadehranjbar and A. J. Baker contributed to some of the experimental work. G. Mpourmpakis guided the Boltzmann statistical analysis. A. Martini guided the MD simulation work. T. D. B. Jacobs guided the overall experiments and analysis and also the writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy, in the Office of Basic Energy Sciences, under Award No. DE-SC0021155. DL and GM acknowledge support by the National Science Foundation (NSF, CBET-CAREER program) under Grant No. 1652694. Use of the NanoFabrication and Characterization Facility (NFCF) in the Petersen Institute for Nano Science and Engineering (PINSE) is acknowledged. The authors also thank Götz Veser and Sanjana Karpe at the University of Pittsburgh for providing guideline for nanoparticle synthesis.References
- E. Ringe, M. R. Langille, K. Sohn, J. Zhang, J. Huang, C. A. Mirkin, R. P. Van Duyne and L. D. Marks, J. Phys. Chem. Lett., 2012, 3, 1479–1483 CrossRef CAS PubMed.
- H. Lee, RSC Adv., 2014, 4, 41017–41027 RSC.
- M. C. Arno, M. Inam, A. C. Weems, Z. Li, A. L. A. Binch, C. I. Platt, S. M. Richardson, J. A. Hoyland, A. P. Dove and R. K. O'Reilly, Nat. Commun., 2020, 11, 1–9 CrossRef PubMed.
- C. Kinnear, T. L. Moore, L. Rodriguez-Lorenzo, B. Rothen-Rutishauser and A. Petri-Fink, Chem. Rev., 2017, 117, 11476–11521 CrossRef CAS PubMed.
- Y. Xia, Y. Xiong, B. Lim and S. E. Skrabalak, Angew. Chem., Int. Ed., 2009, 48, 60–103 CrossRef CAS PubMed.
- Y. Xiong and Y. Xia, Adv. Mater., 2007, 19, 3385–3391 CrossRef CAS.
- Y. Xiong, H. Cai, Y. Yin and Y. Xia, Chem. Phys. Lett., 2007, 440, 273–278 CrossRef CAS.
- G. Wulff, Z. Kristallogr., 1901, 34, 449–530 CAS.
- R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Perssion and S. P. Ong, Sci. Data, 2016, 3, 1–13 Search PubMed.
- A. Mayoral, H. Barron, R. Estrada-Salas, A. Vazquez-Duran and M. José-Yacamán, Nanoscale, 2010, 2, 335–342 RSC.
- J. L. Elechiguerra, J. Reyes-Gasga and M. J. Yacaman, J. Mater. Chem., 2006, 16, 3906–3919 RSC.
- I. Galanakis, G. Bihlmayer, V. Bellini, N. Papanikolaou, R. Zeller, S. Blügel and P. H. Dederichs, Europhys. Lett., 2002, 58, 751–757 CrossRef CAS.
- A. S. Barnard, X. M. Lin and L. A. Curtiss, J. Phys. Chem. B, 2005, 109, 24465–24472 CrossRef CAS PubMed.
- C. R. Henry, Prog. Surf. Sci., 2005, 80, 92–116 CrossRef CAS.
- F. Kim, S. Connor, H. Song, T. Kuykendall and P. Yang, Angew. Chem., Int. Ed., 2004, 43, 3673–3677 CrossRef CAS PubMed.
- H. Song, F. Kim, S. Connor, G. A. Somorjai and P. Yang, J. Phys. Chem. B, 2005, 109, 188–193 CrossRef CAS PubMed.
- M. M. Blazhynska, A. Kyrychenko and O. N. Kalugin, Mol. Simul., 2018, 44, 981–991 CrossRef CAS.
- F. Baletto, R. Ferrando, A. Fortunelli, F. Montalenti and C. Mottet, J. Chem. Phys., 2002, 116, 3856–3863 CrossRef CAS.
- A. R. Tao, S. Habas and P. Yang, Small, 2008, 4, 310–325 CrossRef CAS.
- J. Chen, B. Lim, E. P. Lee and Y. Xia, Nano Today, 2009, 4, 81–95 CrossRef CAS.
- C. Y. Chiu, Y. Li, L. Ruan, X. Ye, C. B. Murray and Y. Huang, Nat. Chem., 2011, 3, 393–399 CrossRef CAS PubMed.
- R. Cheula, M. Maestri and G. Mpourmpakis, ACS Catal., 2020, 10, 6149–6158 CrossRef CAS.
- M. A. Ha, J. Dadras and A. Alexandrova, ACS Catal., 2014, 4, 3570–3580 CrossRef CAS.
- E. T. Baxter, M. A. Ha, A. C. Cass, A. N. Alexandrova and S. L. Anderson, ACS Catal., 2017, 7, 3322–3335 CrossRef CAS.
- G. Sun and P. Sautet, J. Am. Chem. Soc., 2018, 140, 2812–2820 CrossRef CAS PubMed.
- A. S. Barnard, Nanoscale, 2014, 6, 9983–9990 RSC.
- R. V. Chepulskii and S. Curtarolo, ACS Nano, 2011, 5, 247–254 CrossRef CAS PubMed.
- L. Jiao and J. R. Regalbuto, J. Catal., 2008, 260, 329–341 CrossRef CAS.
- J. T. Miller, M. Schreier, A. J. Kropf and J. R. Regalbuto, J. Catal., 2004, 225, 203–212 CrossRef CAS.
- L. Y. Chang, A. S. Barnard, L. C. Gontard and R. E. Dunin-Borkowski, Nano Lett., 2010, 10, 3073–3076 CrossRef CAS PubMed.
- W. Gao, J. Wu, A. Yoon, P. Lu, L. Qi, J. Wen, D. J. Miller, J. C. Mabon, W. L. Wilson, H. Yang and J. M. Zuo, Sci. Rep., 2017, 7, 1–10 CrossRef CAS PubMed.
- J. Wu, W. Gao, H. Yang and J. M. Zuo, ACS Nano, 2017, 11, 1696–1703 CrossRef CAS PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- X. W. Zhou, R. A. Johnson and H. N. G. Wadley, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 144113 CrossRef.
- S. Nasiri, C. Greff, K. Wang, M. Yang, Q. Li, P. Moretti and M. Zaiser, Adv. Eng. Mater., 2020, 22, 1–11 CrossRef.
- Y. Feng, Z. Zhao, F. Li, L. Bu, Q. Shao, L. Li, J. Wu, X. Zhu, G. Lu and X. Huang, Nano Lett., 2021, 21, 5075–5082 CrossRef CAS PubMed.
- J. Li, Y. Hu, Y. Zhang and R. Xia, Microporous Mesoporous Mater., 2022, 331, 111656 CrossRef CAS.
- I. M. Padilla Espinosa, T. D. B. Jacobs and A. Martini, J. Chem. Theory Comput., 2021, 17, 4486–4498 CrossRef CAS PubMed.
- Z. Yan, M. G. Taylor, A. Mascareno and G. Mpourmpakis, Nano Lett., 2018, 18, 2696–2704 CrossRef CAS PubMed.
- D. Tománek and S. Mukherjee, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 28, 665–673 CrossRef.
- S. Stankic, R. Cortes-Huerto, N. Crivat, D. Demaille, J. Goniakowski and J. Jupille, Nanoscale, 2013, 5, 2448–2453 RSC.
- M. G. Taylor, N. Austin, C. E. Gounaris and G. Mpourmpakis, ACS Catal., 2015, 5, 6296–6301 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: There are three sections. In the first section, previous studies reporting size and shape of nanoparticles are summarized. In the second section, the candidate polyhedral models and associated analysis are described in detail. In the third section, additional information is provided about the nanoparticle model construction and equilibration. See https://doi.org/10.1039/d2na00326k |
| This journal is © The Royal Society of Chemistry 2022 |