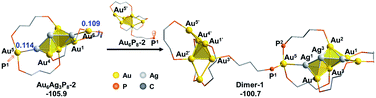Open Access Article
Open Access ArticleMechanistic insights into Ag+ induced size-growth from [Au6(DPPP)4]2+ to [Au7(DPPP)4]2+ clusters†
Ying
Lv
a,
Xiaohang
Wu
 a,
Shuping
He
a and
Haizhu
Yu
a,
Shuping
He
a and
Haizhu
Yu
 *ab
*ab
aDepartment of Chemistry and Centre for Atomic Engineering of Advanced Materials, Anhui Province Key Laboratory of Chemistry for Inorganic/Organic Hybrid Functionalized Materials, Key Laboratory of Structure and Functional Regulation of Hybrid Materials of Ministry of Education, Anhui University, Hefei 230601, Anhui, P. R. China. E-mail: yuhaizhu@ahu.edu.cn
bInstitute of Energy, Hefei Comprehensive National Science Center, Hefei, 230031, Anhui, P. R. China
First published on 4th July 2022
Abstract
The size conversion of atomically precise metal nanoclusters lays the foundation to elucidate the inherent structure–activity correlations on the nanometer scale. Herein, the mechanism of the Ag+-induced size growth from [Au6(dppp)4]2+ to [Au7(dppp)4]3+ (dppp is short for 1,3-bis(diphenylphosphino)propane) is studied via density functional theory (DFT) calculations. In the absence of extra Au sources, the one “Au+” addition was found to be regulated by the Ag+ doping induced Au-activation, i.e., the formation of formal Au(I) blocks via the Ag+ alloying processes. The Au(I) blocks could be extruded from the core structure in the formed Au–Ag alloy clusters, triggering a facile Au+ migration to the Au6 precursor to form the Au7 product. This study sheds light on the structural and stability changes of gold nanoclusters upon the addition of Ag+ and will hopefully benefit the development of more metal ion-induced size-conversion of metal nanoclusters.
Introduction
The stimuli response upon exposure to extra metal ions represents an attractive characteristic of metal nanoclusters.1–8 The structural response may be reflected in the complexation of the metal ion(s) with the surface ligands,9–11 the doping/exchange/addition of the metal ion(s) into the metallic framework of the cluster,12–15 the slightly changed structure with a different charge state16 or the re-arrangement of the entire cluster structure.17–20 Moreover, enhanced physicochemical properties (such as thermostability) and novel applications21–23 could be achieved due to the synergistic effect.Associated with the experimental outcomes, the atomic precision, spectroscopic characterization, and theoretical simulations have greatly improved our mechanistic understanding on these reactions. For example, the [M+] − Cl (M = Ag/Cu) interactions of the M+ with the vertex AuCl moiety of the rod-shaped Au24(SR)5(PR3)10Cl2 were found to be a dominating effect to initiate the single atom addition, and thus, the formation of the rod-shaped Au24M(SR)5(PR3)10Cl2 clusters.24 The Cs–S/O and cation–π interactions are pivotal to the Cs+ induced one-dimensional linear assembly of Ag29(SSR)12(PPh3)4.25 In addition, the anti-galvanic mechanism was proposed to account for the cation-stimulated alloying.26–28 Nevertheless, the reported mechanistic study mainly focuses on the metal ion-induced alloying/assembly, while the mechanistic details on the ion “catalyzed” size conversion of nanoclusters (Ag+ induced [Au6(dppp)4]2+ to [Au7(dppp)4]3+ and Cu2+ induced Au25(PET)18 → Au44(PET)18)18,23 have been largely unknown.
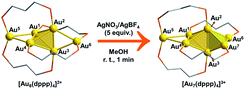
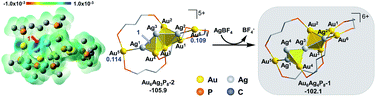
Intrigued by the fantastic foreign metal effect,29–31 we sought to perform a detailed mechanistic study on the Ag+ induced reaction of [Au6(dppp)4]2+ → [Au7(dppp)4]3+ with density functional theory (DFT) calculations. According to Konishi's experiments,18 [Au6(dppp)4]2+ transformed into [Au7(dppp)4]3+ within one minute after 5 molars equivalent AgBF4 was added. According to single-crystal structure analysis, [Au6(dppp)4]2+ comprises a bi-capped tetrahedral skeleton. The tetrahedral Au atoms (Au1–4) are each protected by one P hand of the dppp ligand, while the two-terminal Au atoms (Au5,6) are each protected by two P hands from two dppp ligands. The framework of [Au7(dppp)4]3+ is similar to that of [Au6(dppp)4]2+, except for the addition of one formal Au+, and the re-arrangement of one dppp ligand (one P coordination on the Au6 atom migrates to coordinate to Au7).
According to the DFT calculation results, the addition of Ag+ on clusters favorably generates the alloy structure with higher nucleation (i.e. with more tetrahedral and triangular blocks in the core structure). The incorporated Ag+ induced activation of the exterior Au atoms in the metal framework, resulting in an easy structural tautomerization therein. This proposal correlates with the heavily doping-induced size-rearrangement of metal nanoclusters in recent studies27,32 and will be hopefully applicable to other alloying systems (Scheme 1).18
Results and discussion
Throughout this study, the experimentally used dppp ligands (i.e. bis(diphenylphosphino)propane) were simplified with dmpp (i.e. bis(dimethylphosphino)propane ligands) to reduce computational costs. Similar structural simplification has also been used in recent studies.33,34The doping of Ag+ in Au6P8 clusters
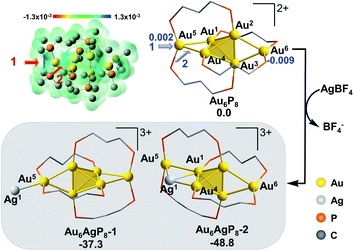
The formula of Au6P8 is differentiated from Au7P8 by only one Au+, which is unlikely to be released directly from the Au6P8 precursor. To this end, the dissociation of Au+ is anticipated to be induced by the Ag+ doping of Au6P8. Given the high activity of the mono-nuclear, cationic Au+ species, the generation of Au+ from the gold cluster precursors is designated as the activation of the Au atom. Of note, the Ag+ alloying-induced activation of the “Au” site(s) correlates with the general concept of anti-galvanic reduction.26 Using Ag+ as a dopant, we considered the possible configurations and energy demands for successive doping procedures.Considering the structural symmetry and the Fukui function analysis (f−, Fig. 1)35 of the Au6P8 precursor, the terminal Au5/6 atom, Au1/4-Au5 bond, and Au2/3-Au6 bond are the most labile sites for the electrophilic attack of the first Ag+. In this study, the isodesmic reaction of NCn+ + AgBF4 → [NCAg](n+1)+ + BF4−] (NC denotes the reaction precursor for the Ag+ addition steps) was used to determine the reaction energy of the Ag+ addition steps. As shown in Fig. 1, the addition of the first Ag+ could possibly generate Au6AgP8-1 and Au6AgP8-2, and the suffix of −1/−2 denotes the isomeric products via adding Ag+ on different sites. Both two doping processes are thermodynamically highly feasible. Nevertheless, adding an exterior Ag+ makes little perturbation on the Au6 skeleton in the former case, but results in a stretched core structure in the latter case (Fig. 1 and S1†). From Fig. 1, the Au4–Au5 bond insertion is significantly more feasible than the Au5-binding mode (−48.8 vs. −37.3 kcal mol−1). Alternatively, Ag+ is more likely to be reduced by Au6; that is, Ag+ is incorporated into the core sites to form a highly coordinated structure (the coordination number36 of Ag1 in Au6AgP8-1 and Au6AgP8-2 is 1 and 3; please see ESI† for more details), and thus Au6AgP8-2 is preferentially formed.
According to the Hirshfeld charge analysis, the charge state of the terminal Au5/6 in Au6P8 (0.002/−0.009, Table S1†) is slightly higher than that of the tetrahedral Au (avg. −0.030). By contrast, the charge of Au5 in Au6AgP8-1 and Au6AgP8-2 (0.055 and 0.057) is significantly more positive than that of tetrahedral Au atoms (avg. −0.012) and becomes closer to the charge of Au in the Au2(dppp)2Cl237 complex (0.082). The results unambiguously demonstrate the improved positive charge of the Au5 atom after Ag+ incorporation, and thus the higher reactivity for bond dissociation (due to the increased electrostatic repulsion between the cationic metal centers). In other words, the incorporation of Ag+ activates the core Au atoms, particularly in the corner sites.38 Of note, compared to the aforementioned Ag+-addition processes, the metal exchange of Ag with Au in Au6P8 is thermodynamically much more disfavored (Scheme S1†). Therefore, the metal exchange pathways were not examined in the following section.
According to the Fukui function analysis, the most nucleophilic sites of Au6AgP8-2 are located in the region nearby Au5 and Au6 atoms (Fig. 2). Accordingly, we examined four possible binding modes of the second Ag+.
As shown in Fig. 2, the activation of the terminal Au5 could occur via the addition of Ag+ on the site 1 of Au5 or site 2 of attacking the Au2–Ag1 bond to form the isomeric Au6Ag2P8-1 and Au6Ag2P8-2, respectively. Similarly, the corner Au6 could be possibly activated via Ag+ insertion into the space behind (site 3) or in front (site 4) of the butterfly-like Au1/4-Au2-Au3-Au6 structure to form Au6Ag2P8-3 or Au6Ag2P8-4.
The results indicate that the binding of second Ag+ (i.e. Ag2) directly on Au5 makes little perturbation on the framework, correlating with the results of Au6P8 + AgBF4 → Au6AgP8-1 + BF4− (Fig. 1). Nevertheless, the reaction energy is remarkably higher (−5.4 kcal mol−1 in Au6AgP8-2 + AgBF4 → Au6Ag2P8-1vs. −37.3 kcal mol−1 in Au6P8 + AgBF4 → Au6AgP8-1 + BF4−), implying that the structure of the precursor is pivotal to the facilitation of alloying. Moreover, the attack of Ag2 to Ag1 resembles a synergistic bi-molecular electrophilic reaction mechanism as the Au1 atom migrates from cis-to trans-configuration (refer to Au4) around the Au2–Au3 bond spontaneously during the geometry optimization (see Fig. S2† for the details). The formation of Au6Ag2P8-2 from Au6AgP8-2 is exothermic by 30.7 kcal mol−1. Besides, the approaching of Ag2 to either Au1–Au2–Au3–Au6 or Au4–Au2–Au3–Au6 results in a core-structure re-organization, predominantly via incorporating Ag1 into the tetrahedral blocks and forming the face-sharing tri-tetrahedral structure. Due to the meta-orientation of the two Ag+ and the symmetry of the tri-tetrahedral core structure, the relative energy and the M-P framework of the formed Au6Ag2P8-3 are almost the same as those of Au6Ag2P8-4. Both steps are highly exothermic (−44.8 and −45.1 kcal mol−1). Through the structural re-organization, the reduced coordination number of Au5 and Au6 (compared to the related one in the precursor) is overwhelmed by the extra stability associated with the formation of a larger metallic core structure. Therefore, the formation of Au6Ag2P8-3/4 is favored over that of Au6Ag2P8-1/2.
Comparing the optimized geometries of Au6AgP8-2 and Au6Ag2P8-3/4, we found that the bond distance between the Au5/Au6 and the core metal atoms is significantly lengthened after incorporating the second Ag+. Moreover, the charge on Au5/Au6 atoms becomes more positive (Au6AgP8-2: 0.057/0.035 → Au6Ag2P8-2: 0.086/0.083, Table S1†), and is comparable to that of the aforementioned Au(I) complex (0.082). The results indicate the formation of a formal Au(I) center on the cluster, and thus, the enhanced activity for the nucleophilic coordination and Au–Au dissociation (the charge of the other Au atoms also becomes more positive, Table S1†). Nevertheless, the alloying with Ag+ remains thermodynamically feasible, and therefore, we examined the energetics for further doping of Ag+ in the target system.
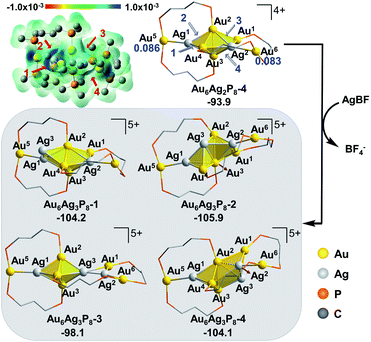
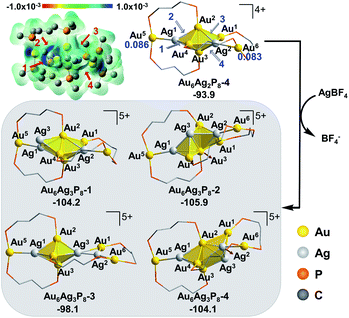
In view of the preferential core expansion via Ag+ doping (over the Ag addition steps), we mainly examined the core-expansion pathways from Au6Ag2P8-4. As shown in Fig. 3, the third Ag-doping process leads to four possible Au6Ag3P8 isomers. The third Ag+ (i.e. Ag3) could possibly attack site 1 of the Ag1–Au4 bond, site 2 of the Au2–Ag1 bond, site 3 of the Au2–Ag2 bond, and site 4 of the Ag2–Au3 bond, forming Au6Ag3P8-1, Au6Ag3P8-2, Au6Ag3P8-3, and Au6Ag3P8-4, respectively. The approaching of Ag3 into the Ag1–Au4 bond internalizes Ag3 into the left tetrahedral Ag1Au2,3,4 block, forming a square pyramid (Ag1,3Au2,3,4) therein. Moreover, the approaching of Ag3 to the Au2–Ag1 bond results in the enlargement of the Au2–Au3–Ag1/Au4 bond angle, and the incorporation of Ag3 to form two vertex-sharing tetrahedral blocks (see Fig. S3† for the partial optimization energy profile). The approaching of Ag3 to the Au2–Ag2 bond leads to the extrusion of the Au1–Au2 bond from the metallic core structure, resulting in the formation of a face-sharing bi-tetrahedral block with a vertex-sharing triangular Au1Ag2,3 unit (Au6Ag3P8-3). The attack of Ag3 on the Ag2-Au3 bond results in the formation of a distorted square-pyramid Au2,3Ag2,3,4 block, and the cleavage of the Au1/Ag2–Au3 bonds. In the formed Au6Ag3P8-4, the new-formed square-pyramid shares one facet with the original left tetrahedron. According to the calculation results, the four types of Ag+ insertion steps are exothermic by 10.3, 12.0, 4.2, and 10.2 kcal mol−1, respectively.
The slightly higher energy of Au6Ag3P8-3 than the other isomers is predominantly caused by the lower cohesive degree of the whole metal skeleton39 (the average coordination number of the metal atoms is 3.4/3.4/3.1/3.3 for Au6Ag3P8-1/2/3/4, see details in Table S2†).36 In addition, the comparable energies of Au6Ag3P8-1, Au6Ag3P8-2, and Au6Ag3P8-4 indicate the competitive Ag+ doping sites. For clarity reasons, the following analysis and discussions mainly refer to the most stable intermediate Au6Ag3P8-2.
According to Hirshfeld charge analysis, the doping with the third Ag+ further enhances the electron deficiency of the Au5/Au6 atoms (with the charge of 0.114/0.109, compared to the charge of 0.086/0.083 in Au6Ag2P8-4, Table S1†). Moreover, the average charge of the Au4Agn (Au4 denotes the tetrahedral Au4 block in the Au6 reactant, and n = 1–4) blocks also significantly increases with the doping with the third Ag+ (Au6P8: −0.030 → Au6AgP8-2: −0.012 → Au6Ag2P8-4: 0.019 → Au6Ag3P8-4: 0.070), resulting in critically increased electrostatic repulsion within the metal skeleton and the reduced stability. This is also the reason why the Ag+ doping becomes less feasible after each doping process (the first, second, and third Ag+ doping steps are exothermic by −48.8, −45.1, and −12.0 kcal mol−1).
Starting from Au6Ag3P8-2, the fourth Ag+ (i.e. Ag4) could be capped on the Ag1,3Au4 facet as the maximum of f− appears above the Ag1,3Au4 facet, and then the four-Ag+-doped product Au6Ag4P8-1 was formed.
The incorporation of Ag4 also resembles a synergistic bi-molecular electrophilic reaction mechanism, similar to the reaction of Au6AgP8-2 + AgBF4 → Au6Ag2P8-2. When the Ag4 atom is capped on the bare Ag1,3Au4 facet, the Au3 atom leaves the back capping site (on the Ag1,3Au4 facet) with the right part of the face-sharing bi-tetrahedron remaining. Distinct from the aforementioned exothermic doping processes in the 1–3 Ag+ incorporation steps, adding the fourth Ag+via this pathway was endothermic by 3.8 kcal mol−1 (Fig. 4). In other words, the incorporation of the fourth Ag+ is thermodynamically disfavored. The reason is mainly ascribed to the significantly enhanced electrostatic repulsion among the metal atoms (the average Hirshfeld charge of the metal atoms in the Au4Agn core is 0.112 for Au6Ag4P8-1). Throughout the Ag-doping pathway, Ag+ favors the core site of Au6Agn and leads to the oxidation of Au atoms (i.e. Au5,6). As shown in Scheme S2,† the contribution of Ag+ to the HOMO of Au6Agn (n = 0, 1, 2, and 3) increased remarkably with the increased doping number of Ag+ (Au6: 0.00%, Au6Ag: 21.74%, Au6Ag2: 41.27%, and Au6Ag3: 43.05%). In combination with the Fukui function analysis (Fig. 1–4), the Au sites adjacent to Ag atoms are the active sites for the electrophilic attack of the incoming-Ag+.
Size-growth by the dimerization of Au6Ag3P8-2
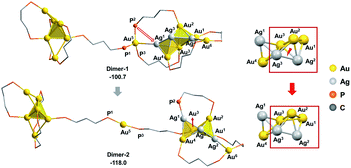
According to the aforementioned results and discussion, the successive addition of Ag+ on Au6P8 favorably generates the alloy structure with a higher degree of nucleation (i.e. with more tetrahedral and triangular blocks in the core structure).40 Meanwhile, the most plausible doping number of Ag+ is 3 (Au6P8 + 3 AgBF4 → Au6Ag3P8-2 + 3 BF4−), wherein the metallic core has been largely activated due to the strong electrostatic repulsion therein (most Au atoms show Au(I) character, Table S1†). In this context, the terminal Au5 and Au6 atoms are the most labile sites for the subsequent reactions because of the relatively lower steric hindrance and the higher electron deficiency (compared to all other metal sites). For this reason, the Au5 (or Au6) in Au6Ag3P8-2 is used as the [Au]+ source to react with the Au6P8 cluster precursor to form Au7P8.Of note, the direct approaching of Au6Ag3P8-2 to Au6P8 is precluded due to the high inter-cluster steric hindrance (see Fig. S4;† note: the steric hindrance would be much higher for the experimental dppp protected system). In this context, a prior Au5–P dissociation on Au6P8 (Au6P8 → Au6P8-2, see Fig. S5†) might occur first to release the steric hindrance.34 After that, the nucleophilic attack of P1 to Au5 occurs with the formation of Dimer-1 (Fig. 5), and this step is slightly endothermic by 5.2 kcal mol−1. By contrast, the coordination of P1 to the Au6 atom is thermodynamically slightly less disfavored (6.7 kcal mol−1, Scheme S3†); thus, its subsequent transformations were omitted for clarity reasons. The P–Au bonding makes no obvious influence on the framework of both cluster precursors. To this end, the endothermicity might be caused by the high steric hindrance around the over-protected Au5 (coordination number: 4, with three P-coordination).
Given the high steric hindrance around Au5, the adjacent bare Ag1 in Dimer-1, and the easiness for 1,2 P migration in cluster systems,41–43 we examined the possibility of a 1,2-P2 migration from Au5 to Ag1. The kinetic analysis by partial optimization (via gradually shortening the P2–Ag1 bond distance; see Fig. S6† for details) demonstrates the gradual bond cleavage of Au5–Ag1 and Au3–Ag2 bonds. As a result, the triangular bi-pyramidal block of Au1,2,3Ag2,3 (Fig. 6, inset) tautomerizes into a twisted square pyramid. The energy curve indicates a low energy barrier (12.4 kcal mol−1, Fig. S6†), which could be easily overcome under the experimental condition (i.e. room temperature).18 Meanwhile, due to the released steric hindrance around the Au5 atom, the concerned P2-migration from Dimer-1 to Dimer-2 is exothermic by 17.3 kcal mol−1.
 | ||
| Fig. 6 The energy (in kcal mol−1) and structural changes after the P2-migration of Dimer-1, and the details of the tautomerized core structure. | ||
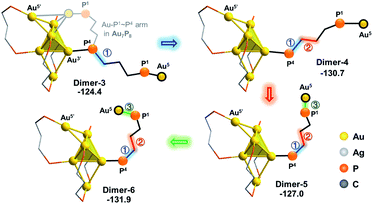
As the square pyramid block has been found to be less stable than the triangular bipyramid block (Au6Ag3P8-1vs.Au6Ag3P8-2, Fig. 3), we further examined an isomerization of Dimer-2via changing the square pyramidal block into a triangular bi-pyramidal one (Dimer-3 in Fig. 7).40 This isomerization was found to occur easily via lengthening the Au1–Au3 bond distance, with a barrier of 8.0 kcal mol−1 (Fig. S7†). The relative energy of Dimer-3 is lower than that of Dimer-2 by 6.4 kcal mol−1, demonstrating the thermodynamic facility of this step.
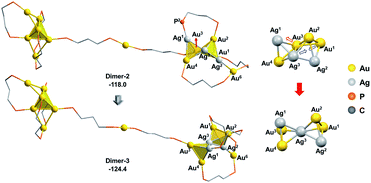 | ||
| Fig. 7 The isomerization of the alloy core in Dimer-2. The relative energies are given in kcal mol−1. The methyl groups on the dmpp ligands and all H atoms are omitted for clarity reasons. | ||
From Dimer-3, the approaching of the Au5 atom to the Au6 block is requisite to forming the target Au7 structure, which could be regulated by a series of single bond rotation processes of the related dmpp ligand (Dimer-3 → Dimer-6 in Scheme 2; see Fig. S8† for the details). Throughout the transformations, the structure of the alloy moiety is preserved, and the system energy is decreased by 7.5 kcal mol−1.
From Dimer-6, the target Au7 block of Au7P8 could be formed via the binding of Au5 to the Au1’,4’,5’ facet of the Au6 block, and the dissociation of the Au5–P3 bond (Fig. 8). According to the calculation results, the binding of Au5 is exothermic by 3.2 kcal mol−1 and occurs with a very low barrier of <5 kcal mol−1 (Fig. S9†). From Dimer-7, the Au5–P3 cleavage occurs to generate Au7P8 and a by-product Au5Ag3P8. In contrast, the progress of moving an Ag+ from Au6Ag3P8-3 to Au6P8 to generate Au6AgP8 is thermodynamically less feasible (−18.7 kcal mol−1, see exothermic by only 2.3 kcal mol−1. The total reaction energy of Au6P8 + Au6Ag3P8-3 → Au7P8 + Au5Ag3P8 is −31.4 kcal mol−1. See Scheme S3† for more details), demonstrating that the alloy cluster after Ag+ doping is a good [Au]+ donor, but not a good [Ag]+ donor.
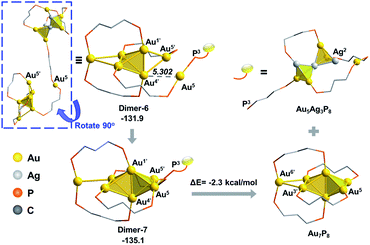 | ||
| Fig. 8 The formation of the Au7 skeleton from Dimer-6 to Dimer-7 and the subsequent Au5–P3 cleavage step. The relative energies are given in kcal mol−1. | ||
Due to the lack of experimental evidence and the complexity of the reaction system, we are not able to confirm the final state of Ag at this stage. However, in view of the bare Ag2 atom and the dangling P3 atom, we assumed that Au5Ag3P8 could possibly undergo the P3–Ag2 coordination to generate a more stable intermediate. The calculation results (Au5Ag3P8 → Au5Ag3P8-2, Scheme S4†) indicate this step to be highly feasible (exothermic by 26.8 kcal mol−1). In particular, after the Au–P coordination, the Au6 atom was further extruded from the metallic core and could possibly act as the second “[Au]+” source to regulate the second Au6P8 → Au7P8 conversion. The formed Au4Ag3P8 could undergo further Ag–P coordination (Scheme S4†) or comprehensive nucleation/decomposition processes. Due to the complexity of the target reaction system, the details for the conversion of Au5Ag3P8 are still ambiguous and deserve more studies.
Experimentally, AgBF4 was not largely excessive, and thus, the transformation from Au6P8 to Au7P8 might deviate from a pseudo-first-order reaction. Hence, the reaction pathways using Au6AgP8-2 and Au6Ag2P8-4 as [Au+] sources were also examined. As shown in Scheme S5,† the Au+ migration from Au6AgP8-2 or Au6Ag2P8-3 to the Au6 skeleton was as feasible as that from Au6Ag3P8-3 (energy demands are all lower than 15 kcal mol−1). According to the aforementioned results and discussion, the Ag+ induced size conversion from Au6P8 to Au7P8 could occur via a series of competitive pathways. For clarity, the most feasible pathway deduced in this study is shown in Scheme 3 (the relative energies are given with the reference states of Au6P8 and AgBF4).
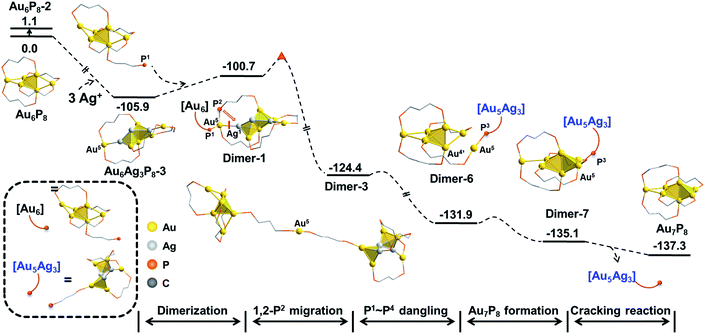 | ||
| Scheme 3 The total energy profile of Ag+ catalyzed size-growth of Au6P8 to Au7P8. The relative energies are given in kcal mol−1. | ||
In this mechanism, the continuous doping of Au6P8 clusters with Ag+ (dominant doping product: Au6Ag3P8-2) activates the terminal Au atoms and generates the [Au]+ source for subsequent size conversion. After that, Au–P coordination between the dangling phosphine ligand of the Au6 precursor and the formal [Au+] occurs, followed by the intramolecular migration of [Au+] through a series of isomerization steps (on the diphosphine ligand). Finally, the Au7P8 product is formed via the Au–P dissociation and the release of the alloy cluster block. Albeit the comprehensive calculations, the experimental evidence for the proposed mechanism is still lacking, predominantly due to the rapid reaction rate and the lability of the formed [Au7(dppp)4](BF4)3 to convert to [Au8(dppp)4Cl2].33,34 Moreover, some other mechanistic possibilities, such as the formation of the target Au7 products via the reaction of one alloy intermediate with another one, could not be excluded.
Computational details
The modeling clusters were constructed by simplifying the dppp ligands with dmpp ligands. Geometry optimization of all species was performed with Dmol3 software44 with the generalized gradient approximation45–47 Perdew–Burke–Ernzerhof functional.48–50 Effective core potentials and double numerical orbital basis group + orbital polarization function (DNP) base groups (Basic 4.4) were chosen with the values of 2 × 10−5 Ha for total energy, 0.004 Ha Å−1 for force, 0.05 Å for displacement, and 1 × 10−5 Ha for the self-consistent field (SCF) computation criterion. Following the recent studies,51–54 the constrained structural optimization strategy is used in evaluating the barrier of the elementary steps. Based on the optimized structures, the solution-phase single point energy calculations were conducted with the COSMO55,56 model, using methanol as the solvent (corresponding to Konishi's experimental conditions18). Unless otherwise specified, the solution-phase binding energy (in kcal mol−1) was used to determine the energy changes of all steps. The Fukui function of the f− evaluated using finite difference approximations and the orbital composition analysis of the metal skeleton was calculated with Multiwfn version 3.8.35,57,58Conclusions
Herein, a plausible mechanism for the Ag+ induced conversion from [Au6(dppp)4]2+ to [Au7(dppp)4]3+ was proposed with DFT calculations. The size growth starts with the successive doping of Ag+ (preferentially adopts high nucleation), associated with the gradual formation of formal Au(I) on terminal sites and the weakened metal–metal bonding interactions. In this context, the release of the terminal Au atom (i.e. the activated Au(I) atom) to the Au6 precursor occurs easily to generate the Au7 cluster product, while the alloy cluster could further function as a “Au(I)” donor to regulate another group of the Au6P8 → Au7P8 conversion. Due to the complexity of the target reaction system, the full details on the overall size growth remain to be established. Nevertheless, the mechanism insights, such as the preferential doping site of Ag+ on the cluster precursor (on the most nucleophilic site, and favorably forms structures with a higher degree of nucleation), the activation of exterior Au atom(s) via the gradual incorporation of Ag+ (i.e. formation of formal Au(I) and its subsequent dissociation, re-assembly, etc.), and the easy structure tautomerization in the metallic core and the diphosphine ligands, will be helpful for understanding the inherent correlation between different nanoclusters and their alloying reactivity in future studies.Author contributions
H. Y. conceived and supervised the project. Y. L. carried out the experimental planning, simulations, and data analysis. X. W. and S. H. provided constructive suggestions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from National Science Foundation of Anhui Province (2108085J08), The University Synergy Innovation Program of Anhui Province (GXXT-2021-023), 2021 university scientific research projects of Anhui Province (YJS20210031), and the technical support of high-performance computing platform of Anhui University. Supercomputing facilities were provided by the Hefei Advanced Computing Center.Notes and references
- A. George, A. Sundar, A. S. Nair, M. P. Maman, B. Pathak, N. Ramanan and S. Mandal, J. Phys. Chem. Lett., 2019, 10, 4571–4576 CrossRef CAS PubMed
.
- S. Li, Z. Y. Wang, G. G. Gao, B. Li, P. Luo, Y. J. Kong, H. Liu and S. Q. Zang, Angew. Chem., Int. Ed., 2018, 57, 12775–12779 CrossRef CAS PubMed
.
- Z. J. Guan, F. Hu, J. J. Li, Z. R. Wen, Y. M. Lin and Q. M. Wang, Isomerization in Alkynyl-Protected Gold Nanoclusters, J. Am. Chem. Soc., 2020, 142, 2995–3001 CrossRef CAS PubMed
.
- L. L. Yan, L. Y. Yao, M. Ng and V. W. Yam, J. Am. Chem. Soc., 2021, 143, 19008–19017 CrossRef CAS PubMed
.
- J. M. Lopez-de-Luzuriaga, M. Monge, M. E. Olmos, J. Quintana and M. Rodriguez-Castillo, Inorg. Chem., 2019, 58, 1501–1512 CrossRef CAS PubMed
.
- Y. Zhao, M. Yu, C. Liu, S. Li, Z. Li, F. Jiang, L. Chen and M. Hong, J. Mater. Chem. C, 2021, 9, 2890–2897 RSC
.
- Y. Yuan, K. Sheng, S. Zeng, X. Han, L. Sun, I. Loncaric, W. Zhan and D. Sun, Inorg. Chem., 2020, 59, 5456–5462 CrossRef CAS PubMed
.
- N. Yan, L. Liao, J. Yuan, Y.-j. Lin, L.-h. Weng, J. Yang and Z. Wu, Chem. Mater., 2016, 28, 8240–8247 CrossRef CAS
.
- N. Yan, N. Xia and Z. Wu, Small, 2021, 17, 2000609 CrossRef CAS PubMed
.
- Z. Liu, X. Jing, S. Zhang and Y. Tian, Anal. Chem., 2019, 91, 2488–2497 CrossRef CAS PubMed
.
- Q. Zhou, Y. Lin, M. Xu, Z. Gao, H. Yang and D. Tang, Anal. Chem., 2016, 88, 8886–8892 CrossRef CAS PubMed
.
- J. Lin, Q. Zhang, L. Wang, X. Liu, W. Yan, T. Wu, X. Bu and P. Feng, J. Am. Chem. Soc., 2014, 136, 4769–4779 CrossRef CAS PubMed
.
- C. Yao, J. Chen, M. B. Li, L. Liu, J. Yang and Z. Wu, Nano Lett., 2015, 15, 1281–1287 CrossRef CAS PubMed
.
- M. Kim, K. L. D. M. Weerawardene, W. Choi, S. M. Han, J. Paik, Y. Kim, M.-G. Choi, C. M. Aikens and D. Lee, Chem. Mater., 2020, 32, 10216–10226 CrossRef CAS
.
- R. P. B. Silalahi, Q. Wang, J. H. Liao, T. H. Chiu, Y. Y. Wu, X. Wang, S. Kahlal, J. Y. Saillard and C. W. Liu, Angew. Chem., Int. Ed., 2022, 61, e202113266 CAS
.
- M. Zhu, G. Chan, H. Qian and R. Jin, Nanoscale, 2011, 3, 1703–1707 RSC
.
- P. K. Liao, C. S. Fang, A. J. Edwards, S. Kahlal, J. Y. Saillard and C. W. Liu, Inorg. Chem., 2012, 51, 6577–6591 CrossRef CAS PubMed
.
- Y. Shichibu, M. Zhang, Y. Kamei and K. Konishi, J. Am. Chem. Soc., 2014, 136, 12892–12895 CrossRef CAS PubMed
.
- C. Yao, Y. J. Lin, J. Yuan, L. Liao, M. Zhu, L. H. Weng, J. Yang and Z. Wu, J. Am. Chem. Soc., 2015, 137, 15350–15353 CrossRef CAS PubMed
.
- S. Lee, M. S. Bootharaju, G. Deng, S. Malola, H. Hakkinen, N. Zheng and T. Hyeon, J. Am. Chem. Soc., 2021, 143, 12100–12107 CrossRef CAS PubMed
.
- R. Jiang, Y. Zhang, Q. Zhang, L. Li and L. Yang, ACS Appl. Nano Mater., 2021, 4, 9760–9767 CrossRef CAS
.
- L. Liao, S. Zhou, Y. Dai, L. Liu, C. Yao, C. Fu, J. Yang and Z. Wu, J. Am. Chem. Soc., 2015, 137, 9511–9514 CrossRef CAS PubMed
.
- M. B. Li, S. K. Tian, Z. Wu and R. Jin, Chem. Commun., 2015, 51, 4433–4436 RSC
.
- S. Wang, H. Abroshan, C. Liu, T.-Y. Luo, M. Zhou, H. J. Kim, N. L. Rosi and R. Jin, Shuttling single metal atom into and out of a metal nanoparticle, Nat. Commun., 2017, 8, 848 CrossRef PubMed
.
- X. Wei, X. Kang, Q. Yuan, C. Qin, S. Jin, S. Wang and M. Zhu, Chem. Mater., 2019, 31, 4945–4952 CrossRef CAS
.
- Z. Wu, Anti-Galvanic Reduction of Thiolate-protected Gold and Silver Nanoparticles, Angew. Chem., Int. Ed., 2012, 51, 2934–2938 CrossRef CAS PubMed
.
- M. Zhu, P. Wang, N. Yan, X. Chai, L. He, Y. Zhao, N. Xia, C. Yao, J. Li, H. Deng, Y. Zhu, Y. Pei and Z. Wu, Angew. Chem., Int. Ed., 2018, 57, 4500–4504 CrossRef CAS PubMed
.
- X. Liu, J. Yuan, J. Chen, J. Yang and Z. Wu, Part. Part. Syst. Charact., 2019, 36, 1900003 CrossRef
.
- X. Lin, W. Ma, K. Sun, B. Sun, X. Fu, X. Ren, C. Liu and J. Huang, J. Phys. Chem. Lett., 2021, 12, 552–557 CrossRef CAS PubMed
.
- F. Tian and R. Chen, J. Am. Chem. Soc., 2019, 141, 7107–7114 CrossRef CAS PubMed
.
- A. K. Das, S. Mukherjee, S. R. Sreehari, A. S. Nair, S. Bhandary, D. Chopra, D. Sanyal, B. Pathak and S. Mandal, ACS Nano, 2020, 14, 16681–16688 CrossRef CAS PubMed
.
- Y. Negishi, T. Iwai and M. Ide, Chem. Commun., 2010, 46, 4713–4715 RSC
.
- Y. Kamei, Y. Shichibu and K. Konishi, Angew. Chem., Int. Ed., 2011, 50, 7442–7445 CrossRef CAS PubMed
.
- Y. Lv, R. Zhao, S. Weng and H. Yu, Chem. – Eur. J., 2020, 26, 12382–12387 CrossRef CAS PubMed
.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1874 CrossRef CAS PubMed
.
- C. Liu, Y. Pei, H. Sun and J. Ma, J. Am. Chem. Soc., 2015, 137, 15809–15816 CrossRef CAS PubMed
.
- W. Kaim, A. Dogan, A. Klein and S. Záliš, Z. Anorg. Allg. Chem., 2005, 631, 1355–1358 CrossRef CAS
.
- J. H. Stenlid and T. Brinck, J. Am. Chem. Soc., 2017, 139, 11012–11015 CrossRef CAS PubMed
.
- M. G. Taylor and G. Mpourmpakis, Nat. Commun., 2017, 8, 15988–15995 CrossRef CAS PubMed
.
- W. W. Xu, B. Zhu, X. C. Zeng and Y. Gao, Nat. Commun., 2016, 7, 13574–13581 CrossRef CAS PubMed
.
- D. S. Matteson, Chem. Rev., 1989, 89, 1535–1551 CrossRef CAS
.
- J. Q. Wang, Z. J. Guan, W. D. Liu, Y. Yang and Q. M. Wang, J. Am. Chem. Soc., 2019, 141, 2384–2390 CrossRef CAS PubMed
.
- X. Wu, Y. Lv, Y. Bai, H. Yu and M. Zhu, Dalton Trans., 2021, 50, 10113–10118 RSC
.
- B. Delley, J. Chem. Phys., 1990, 92, 508–517 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS
.
- K. Weerawardene, P. Pandeya, M. Zhou, Y. Chen, R. Jin and C. M. Aikens, J. Am. Chem. Soc., 2019, 141, 18715–18726 CrossRef CAS PubMed
.
- Q. Li, M. A. Mosquera, L. O. Jones, A. Parakh, J. Chai, R. Jin, G. C. Schatz and X. W. Gu, ACS Nano, 2020, 14, 11888–11896 CrossRef CAS PubMed
.
- J. V. Rival, P. Mymoona, R. Vinoth, A. M. V. Mohan and E. S. Shibu, ACS Appl. Mater. Interfaces, 2021, 13, 10583–10593 CrossRef CAS PubMed
.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans., 1993, 2, 799–805 RSC
.
- M. F. Matus, S. Malola, E. Kinder Bonilla, B. M. Barngrover, C. M. Aikens and H. Hakkinen, Chem. Commun., 2020, 56, 8087–8090 RSC
.
- S. Malola and H. Hakkinen, J. Am. Chem. Soc., 2019, 141, 6006–6012 CrossRef CAS PubMed
.
- A. Fernando and C. M. Aikens, J. Phys. Chem. C, 2015, 119, 20179–20187 CrossRef CAS
.
- C. L. Heinecke, T. W. Ni, S. Malola, V. Makinen, O. A. Wong, H. Hakkinen and C. J. Ackerson, J. Am. Chem. Soc., 2012, 134, 13316–13322 CrossRef CAS PubMed
.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS
.
- A. Klamt and V. Jonas, J. Chem. Phys., 1996, 105, 9972–9981 CrossRef CAS
.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed
.
- T. Lu and F. Chen, Acta Chim. Sin., 2011, 69, 2393–2406 CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2na00301e |
| This journal is © The Royal Society of Chemistry 2022 |