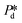Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Capillary pressure-based measurement of dynamic interfacial tension in a spontaneous microfluidic sensor†
Boxin
Deng
 *a,
Karin
Schroën
a,
Maartje
Steegmans
b and
Jolet
de Ruiter
*a,
Karin
Schroën
a,
Maartje
Steegmans
b and
Jolet
de Ruiter
 a
a
aWageningen University, Food Process Engineering Group, Bornse Weilanden 9, 6708, WG, Wageningen, The Netherlands. E-mail: boxin.deng@wur.nl
bFrieslandCampina, Stationsplein 4, 3818 LE, Amersfoort, The Netherlands
First published on 8th September 2022
Abstract
The size of droplets and bubbles, and the properties of emulsions and foams strongly depend on dynamic interfacial tension (γd) – a parameter that is often inaccessible due to the very short time scales for droplet and bubble formation, and the inaccessibility of (e.g., food) production lines. To solve this challenge, we developed a microfluidic tensiometer that can measure γd by monitoring the formation time of both droplets and bubbles. Our tensiometer is a pressure-driven microfluidic device that operates based on the principle of a pressure balance: the formation of a droplet (or a bubble) is initialized when the Laplace pressure of the interface is decreased below the externally applied pressure, and this decrease is caused by a reduction in γd that can be calculated from the applied pressure and the Young–Laplace equation. The decay of γd due to surfactant adsorption can be followed at the characteristic time scale, which is dependent on surfactant type and concentration. For 0.05–1% wt sodium dodecyl sulfate (SDS), we were able to measure γd at time scales down to 1 ms and 0.1 ms for droplet and bubble interfaces, respectively, at increasing applied pressures and SDS concentrations. Our tensiometer proves to be a simple, robust method that inherently allows access to nearly the full range of dynamic interfacial tension at relevant time scales.
Introduction
Emulsions and foams are common forms of products in the food, cosmetics, and pharmaceutical industries and are dispersions of two (semi-)immiscible fluids that are stabilised by surface-active components (surfactants). Two competing processes occur during emulsification, namely droplet formation and coalescence, and both are influenced by surfactant adsorption through the resulting interfacial tension and interfacial layer formation. The same applies to foaming, during which the dispersed fluid is a gas, thus forming bubbles, and the air–water tension is also referred to as surface tension.Given the critical role of surfactant adsorption, it is not surprising that often in emulsification and foaming research, an excess of surfactant is used to dampen the effects of dynamic adsorption and induce a situation that is less affected by the dynamics of surfactant adsorption and thus requires less tight control of the system.1 In general, it is assumed that because of the high dosage the interfacial tension does not change throughout the process, and it is expected to be at its equilibrium value. Yet, real systems are often more complex with a wide variety of dispersed phase properties and types of surfactant that may invalidate this assumption. For example, for slow-adsorbing whey protein isolate, we have demonstrated the role of dynamic adsorption (i.e., dynamic surface tension) on bubble formation and coalescence.2 In addition, the interfacial tension controls macroscopic properties of emulsions and foams, such as their rheology and morphology. The measurement of the interfacial tension is thus both scientifically and practically important and must be assessed at the relevant time scales at which the dynamic interfacial tension decreases due to surfactant adsorption. This characteristic time scale provides an indication of how fast the emulsion or foam will become stable.
The application of microfluidic technology has grown rapidly for the controllable production and the in-depth characterisation of emulsions and foams. Microfluidic tensiometers resting on manipulation of liquid–liquid or gas–liquid interfaces have been proposed for the measurement of dynamic interfacial tension – through so-called microtensiometry. With these methods, the dynamic interfacial tension can be measured at (sub)millisecond time scales, which agree with the formation time scales as would occur in industrial-scale emulsification processes. Typically 0.1–30 ms is in high-pressure homogenisers and 0.1–100 s in colloid mills.3 Mostly, shear-based T-junction, Y-junction and co-axial geometries are used to study dynamic interfacial tension based on offline analysis of droplet properties, which are, typically, the shape representing the time-evolving deformability (i.e., droplet rheology)4–8 or the size determined by a force balance between the interfacial tension force and the viscous drag force in the dripping regime of droplet formation.9–15 The dynamic interfacial tension can be measured also during droplet formation in the transition or squeezing regime, based on a force balance between the interfacial tension force and the externally controllable pressure drop, which is called the ‘pressure drop-based’ measurement.11,16,17 For all the above-mentioned scenarios, the dynamic interfacial tension is a result of surfactant adsorption and linked to the (droplet) size-dependent droplet formation time. A third measurement principle relies on monitoring the movement of an interface in a microfluidic channel or a microcapillary as driven by surfactant adsorption, and the dynamic interfacial tension can be calculated from the Young–Laplace equation (i.e., capillary pressure). In this case, the dynamic interfacial tension can be linked to a surfactant-dependent droplet formation time.18,19
To widen the applicability of microfluidic tensiometers, it is crucial to improve their measurement accuracy and consolidate their measurement at (sub)millisecond time scales that are relevant to industrial processes. Though various measurement principles have been exploited, the aforementioned studies have been conducted either in shear-based devices that rely on very tight control of the flow fields and the physiochemical properties of the two phases (e.g., viscosity) to precisely control droplet formation (e.g., frequency and size), or in microcapillaries that require a highly accurate pressure sensor. In addition, complex theoretical models with fitting parameters through calibration curves are usually needed to describe the relationship between the droplet properties and the dynamic interfacial tension.20 Moreover, the microfluidic tensiometers have been mainly characterised for droplet interfaces, yet, the characterisation for bubble interfaces has received less attention.8,13,18,21
In this study, we introduced a spontaneous microfluidic tensiometer, which can be used for the measurement of dynamic interfacial tension in both droplet (i.e., o/w interface) and bubble (i.e., a/w interface) formation systems. In this microfluidic device, droplet and bubble formation occurs at the exit of an array of pores; formation initiation is determined by a force balance between the Laplace pressure of the confined interface (in the pores) and the applied pressure, while the formation frequency is determined by surfactant adsorption rate that lowers the dynamic interfacial tension (and thus the Laplace pressure) until the force balance is reached. This method has three strong points: first, the dynamic surface tension is directly calculated from the Young–Laplace equation, which avoids possible compressibility effects associated with bubble formation.5 Second, the surfactant-dependent time scales are determined from the formation frequency of droplets and bubbles, which is a fast and unambiguous analysis. Third, and most importantly, the measurements are independent of the formation processes of individual droplets and bubbles. Thus, the method does not require tight control of continuous phase velocity and physiochemical properties of the two phases – only a tight control of the pressure drop across the meniscus in the pores, which sets the formation frequency and thus the time scale. Our tensiometer was tested for the dynamic interfacial and surface tension for both o/w and a/w interfaces, for 0.05–1% wt sodium dodecyl sulfate (SDS). To prove the robustness of our tensiometer, the results of dynamic interfacial tension versus surfactant-dependent time scales were compared with those obtained by Muijlwijk et al. (2016)9 with both a shear-based microfluidic tensiometer (Y-junction) and a macroscopic automatic drop tensiometer (ADT).
Experimental
Materials
Air and anhydrous hexadecane (>99% purity, Sigma-Aldrich, USA) were used as the dispersed phase for bubble and droplet formation, respectively. Aqueous solutions of 0.05–1% wt sodium dodecyl sulfate (SDS; >99% purity, Sigma-Aldrich, USA) were prepared in ultrapure water (Milli-Q, Merck Millipore) and used as the continuous phase. For the microfluidic experiments, all aqueous solutions were filtered using 0.22 μm PES filters (Merck, Germany) before use.Microchips and set-up
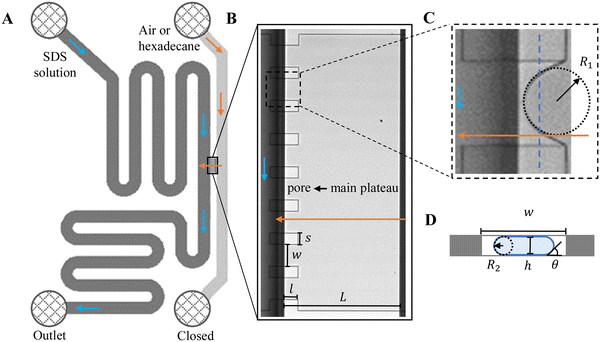
Custom-designed Edge-based Droplet GEneration microchips with partitioned plateaus (partitioned-EDGE) were produced by Micronit Microtechnologies B.V. (Enschede, The Netherlands). They were previously used to study droplet formation,22 as well as the formation and coalescence of bubbles.2 In this study, the partitioned-EDGE microchip is further developed as a sensor for dynamic interfacial tension measurements, based on Laplace-pressure driven formation of droplets and bubbles in this device. The Young–Laplace pressure of a meniscus (ΔPL) is defined in eqn (1), where γ is the interfacial tension, R1 and R2 the principal radii of curvature, and θ the contact angle outside the meniscus (the walls of the device are wetted by the continuous phase).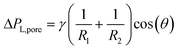 | (1) |
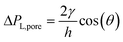 due to w ≫ h.
due to w ≫ h.
The microchip was put in a chip holder (Fluidic Connect 4515, Micronit Microfluidics) and connected to the dispersed and continuous phases using PEEK tubing (0.75 mm, BGB®, Switzerland). The dispersed and continuous phases were pressurized at Pd and Pc using a digital pressure controller via Smart Interface Software (Elveflow®, France). The resulting effective pressure difference across the shallow region (main plateau with pores) is 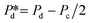 with Pc/2 representing the pressure halfway through the meandering channel. When the outlet of the dispersed phase is closed, the dispersed phase flows onto the main plateau and into the pores, and forms droplets or bubbles in the continuous phase. When operating the sensor,
with Pc/2 representing the pressure halfway through the meandering channel. When the outlet of the dispersed phase is closed, the dispersed phase flows onto the main plateau and into the pores, and forms droplets or bubbles in the continuous phase. When operating the sensor, 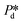 is varied while Pc is kept constant at 100 mbar to transfer the generated droplets or bubbles away from the pores, avoiding any effects related to variations in shear flow.
is varied while Pc is kept constant at 100 mbar to transfer the generated droplets or bubbles away from the pores, avoiding any effects related to variations in shear flow.
Data analysis
Videos and images were recorded with a high-speed camera (FASTCAM SA-Z, Photron Limited, Japan) connected to an inverted microscope (Axiovert 200 MAT, Carl Zeiss B.V., The Netherlands). In each experiment, two videos were recorded (at a frame rate of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fps and 700
000 fps and 700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 fps, respectively) for the measurement of formation frequency (f0) at each pore, and the analysis of time scales, for instance, the pore filling time (tfill) and the neck thinning time (tn) during bubble and droplet formation. Typically, f0 was obtained by counting the number of bubbles or droplets formed at the pore within a set period of time, and 1/f0 = tfill + tn; the f0 value was averaged over three independent recordings and thereafter the eight pores on the plateau. tn was obtained by counting the number of frames taken by the neck thinning process, and tfill represents the lag time between two consecutive neck thinning processes as will be discussed below.
000 fps, respectively) for the measurement of formation frequency (f0) at each pore, and the analysis of time scales, for instance, the pore filling time (tfill) and the neck thinning time (tn) during bubble and droplet formation. Typically, f0 was obtained by counting the number of bubbles or droplets formed at the pore within a set period of time, and 1/f0 = tfill + tn; the f0 value was averaged over three independent recordings and thereafter the eight pores on the plateau. tn was obtained by counting the number of frames taken by the neck thinning process, and tfill represents the lag time between two consecutive neck thinning processes as will be discussed below.
Results
General formation behaviour of bubbles and droplets
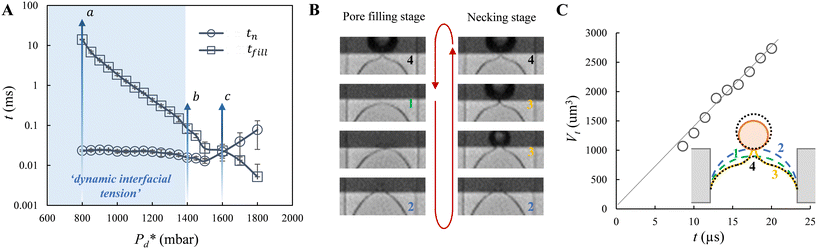
Furthermore, we zoomed in on bubble formation dynamics at the pore, and typically, a single bubble formation cycle can be divided into two stages, which are the pore filling stage and the subsequent bubble necking stage. Each stage has a typical time scale, and they are tfill and tn, respectively. In the low-pressure regime (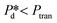 ), the pore filling stage further consists of two sub-processes: first, surfactant adsorption to the static meniscus (Fig. 2B, left, location 1) and, second, pore flow. Dynamic adsorption occurring during the former sub-process is required to lower the surface tension and thus reduce the Laplace pressure across the static meniscus, resulting in a lag period (with a corresponding time scale – τ). When the Laplace pressure reduces to the applied pressure (i.e.,
), the pore filling stage further consists of two sub-processes: first, surfactant adsorption to the static meniscus (Fig. 2B, left, location 1) and, second, pore flow. Dynamic adsorption occurring during the former sub-process is required to lower the surface tension and thus reduce the Laplace pressure across the static meniscus, resulting in a lag period (with a corresponding time scale – τ). When the Laplace pressure reduces to the applied pressure (i.e., 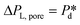 ), pore flow (i.e., the forward motion of the meniscus) is initiated, followed by the subsequent bubble necking stage. Specifically, the (partially-) covered meniscus advances towards the edge of the pore during the pore flow process (Fig. 2B, left, location 1 → 2); during the subsequent bubble necking stage, the meniscus leaps over the edge, and forms a bulb that expands with a linear volume increase in time (Fig. 2C) while the neck that connects the bulb to the supplying pore narrows and in the meantime, the meniscus moves backwards (Fig. 2B, right, location 2 → 3). When the neck width decreases below the pore's height, the neck quickly snaps off (Fig. 2B, right, location 4) and a bubble (with V0) is released into the continuous phase. Simultaneously, the meniscus stops moving further backwards, instead, relaxes rapidly (which benefits from the small surface area of the meniscus constricted in the pore) and returns to an approximately half-circular shape in less than 10 μs (i.e., returns from location 4 to 1). During the consecutive formation of bubbles at the pore, the meniscus moves in a loop, repeating the profile 4 → 1 → 2 → 3 → 4 as sketched in the inset in Fig. 2C. The pore filling time tfill is typically much larger than the bubble necking time tn; tfill markedly decreases with the applied pressure
), pore flow (i.e., the forward motion of the meniscus) is initiated, followed by the subsequent bubble necking stage. Specifically, the (partially-) covered meniscus advances towards the edge of the pore during the pore flow process (Fig. 2B, left, location 1 → 2); during the subsequent bubble necking stage, the meniscus leaps over the edge, and forms a bulb that expands with a linear volume increase in time (Fig. 2C) while the neck that connects the bulb to the supplying pore narrows and in the meantime, the meniscus moves backwards (Fig. 2B, right, location 2 → 3). When the neck width decreases below the pore's height, the neck quickly snaps off (Fig. 2B, right, location 4) and a bubble (with V0) is released into the continuous phase. Simultaneously, the meniscus stops moving further backwards, instead, relaxes rapidly (which benefits from the small surface area of the meniscus constricted in the pore) and returns to an approximately half-circular shape in less than 10 μs (i.e., returns from location 4 to 1). During the consecutive formation of bubbles at the pore, the meniscus moves in a loop, repeating the profile 4 → 1 → 2 → 3 → 4 as sketched in the inset in Fig. 2C. The pore filling time tfill is typically much larger than the bubble necking time tn; tfill markedly decreases with the applied pressure 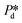 (Fig. 2A) since increasingly higher surface tension is sufficient to enable
(Fig. 2A) since increasingly higher surface tension is sufficient to enable 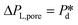 . Next to that, tfill decreases as SDS concentration increases (Fig. SI 1B†).
. Next to that, tfill decreases as SDS concentration increases (Fig. SI 1B†).
In the high-pressure regime (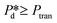 ), pore flow is instantaneously initiated upon applying pressure, since lowering the Laplace pressure of the meniscus and thus surfactant adsorption is not required. Accordingly, tfill continues to decrease as function of
), pore flow is instantaneously initiated upon applying pressure, since lowering the Laplace pressure of the meniscus and thus surfactant adsorption is not required. Accordingly, tfill continues to decrease as function of 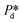 and converges to tn. These two time scales overlap at Pcross (i.e., the so-called cross-over pressure, see point c in Fig. 2A), above which an increase in both bubble size and polydispersity can be observed, indicating the ‘dripping-jetting’ transition.23 Although this regime is interesting for the extremely fast bubble formation,2 and the rich behaviour of possible coalescence events and dripping-jetting transition,23 it cannot be used for tensiometry due to absence of surfactant adsorption to a static meniscus.
and converges to tn. These two time scales overlap at Pcross (i.e., the so-called cross-over pressure, see point c in Fig. 2A), above which an increase in both bubble size and polydispersity can be observed, indicating the ‘dripping-jetting’ transition.23 Although this regime is interesting for the extremely fast bubble formation,2 and the rich behaviour of possible coalescence events and dripping-jetting transition,23 it cannot be used for tensiometry due to absence of surfactant adsorption to a static meniscus.
To conclude, in the current study, we only focus on the low-pressure regime – irrespective of the nature of this transition – to measure the dynamic interfacial tension as function of the surfactant-dependent lag time. We have studied the formation of bubbles to measure dynamic surface tension at an a/w interface, and the formation of droplets to measure dynamic interfacial tension at an o/w interface. Our microfluidic tensiometer is termed after the microfluidic device – ‘EDGE tensiometer’.
EDGE tensiometer for dynamic interfacial tension measurement
In this section, the results are discussed following this sequence: (1) the method definition, focusing on the measurement principles and the accuracy analysis of the EDGE tensiometer; 2) the method validation, comparing the dynamic interfacial tension decay versus the surfactant-dependent time scale with known dynamics reported in the literature.Measurement principles
In the low-pressure regime of the partitioned-EDGE device, the time scale for one droplet or bubble formation is dominated by the lag time for surfactant adsorption to the meniscus in the pore to lower the (dynamic) interfacial or surface tension. The applied pressure sets the ‘final goal’, namely the (dynamic) interfacial or surface tension γd that allows the, initially static, meniscus to start moving towards the pore edge. While the necessary γd value is independent of the composition of the continuous phase, namely the type and concentration of the surfactant, it is obtained via dynamic adsorption during the lag time τ that is surfactant-dependent (τ ≤ tfill) and not directly measurable. However, τ can be well approximated by the droplet or bubble formation time 1/f0, with f0 the formation frequency. In doing so we neglect the time scales for the pore flow (Fig. SI 2-1†) and the neck thinning (Fig. SI 2-2†), both of which are much shorter than the lag time in our device. Thus, we stress here that the tensiometer operates on a static meniscus (the situation indicated by location 1 in Fig. 2B) and we can ignore viscous stresses and dynamics of bubble or droplet snap-off. The tension that initiates pore flow can be derived from a balance between applied pressure and Laplace pressure, as discussed above, and can be expressed as eqn (2):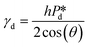 | (2) |
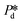 is varied and the corresponding time scale τ = 1/f0 is measured. As
is varied and the corresponding time scale τ = 1/f0 is measured. As 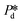 increases gradually, an increasingly higher γd already allows pore flow to be initiated, which results in a shorter lag time τ. These experiments yield (
increases gradually, an increasingly higher γd already allows pore flow to be initiated, which results in a shorter lag time τ. These experiments yield (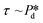 ) plots, which are shown in Fig. SI 3,† and can be replotted as the (γd ∼ τ) plots shown below by inverting the axes and using eqn (2) to derive γd. It is assumed that after one necking stage, during which the meniscus expands significantly and a droplet or a bubble is released, an essentially clean meniscus is created for the next cycle of droplet or bubble formation.
) plots, which are shown in Fig. SI 3,† and can be replotted as the (γd ∼ τ) plots shown below by inverting the axes and using eqn (2) to derive γd. It is assumed that after one necking stage, during which the meniscus expands significantly and a droplet or a bubble is released, an essentially clean meniscus is created for the next cycle of droplet or bubble formation.
Measurement accuracy analysis
For accurately known channel height h, there are two variables in eqn (2) that might influence the accuracy of the calculated γd values, which are the applied pressure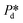 and the contact angle θ. First, the accuracy of the applied pressures, determined by the resolution of the pressure control system, is as low as 0.1 mbar in this study. Accordingly, the dynamic interfacial tension can be measured at a resolution of 0.005 mN m−1. It is also important to realise that our applied pressures are not influenced by additional dynamics, for example, the equilibration of the interface as was reported for other pressure methods (e.g., a micropipette interfacial area-expansion method).18 The second source of error is the contact angle, which we assume to be 15° for our systems with non-wetting dispersed phase (for both droplet and bubble systems), in line with similar fluid systems in hydrophilic glass devices.24,25 For a variation of 5° or 10° around this contact angle of 15°, the maximum variation in the dynamic interfacial tension is approximately 1.2 mN m−1 or 2.8 mN m−1, respectively. This would represent a systematic shift up or down, while the rate of change of dynamic interfacial tension remains unchanged. The best measurement accuracy of γd can be obtained if the contact angle can be measured for each experimental condition, however, this is not straightforward as the out-of-plane contact angle cannot be observed and the in-plane contact angle may not be representative due lack of resolution and possible pinning at the pore entrance. Hence it is best to work with a system with low contact angle of the continuous phase as cos(θ) is less sensitive to variations in θ when θ is closer to zero.
and the contact angle θ. First, the accuracy of the applied pressures, determined by the resolution of the pressure control system, is as low as 0.1 mbar in this study. Accordingly, the dynamic interfacial tension can be measured at a resolution of 0.005 mN m−1. It is also important to realise that our applied pressures are not influenced by additional dynamics, for example, the equilibration of the interface as was reported for other pressure methods (e.g., a micropipette interfacial area-expansion method).18 The second source of error is the contact angle, which we assume to be 15° for our systems with non-wetting dispersed phase (for both droplet and bubble systems), in line with similar fluid systems in hydrophilic glass devices.24,25 For a variation of 5° or 10° around this contact angle of 15°, the maximum variation in the dynamic interfacial tension is approximately 1.2 mN m−1 or 2.8 mN m−1, respectively. This would represent a systematic shift up or down, while the rate of change of dynamic interfacial tension remains unchanged. The best measurement accuracy of γd can be obtained if the contact angle can be measured for each experimental condition, however, this is not straightforward as the out-of-plane contact angle cannot be observed and the in-plane contact angle may not be representative due lack of resolution and possible pinning at the pore entrance. Hence it is best to work with a system with low contact angle of the continuous phase as cos(θ) is less sensitive to variations in θ when θ is closer to zero.
On the other hand, the accuracy of the lag time τ (via the formation time) depends on the magnitude of time scales of pore flow and neck thinning that we neglect with respect to the lag time. tn only becomes comparable to the lag time at applied pressure just below the transition pressure (for droplet system) – when the dynamic interfacial tension approaches the equilibrium value of the pure interface. In this case, to improve the accuracy of the lag time τ, it should be approximated as tfill, namely by subtracting the tn from 1/f0.
The uncertainty of the measured formation time (i.e., τ = 1/f0) across multiple recordings obtained under the same experimental conditions is shown in Fig. SI 4,† and as an example, error bars are shown in Fig. 3B and 4 for one representative data set (0.15% wt SDS).
 | ||
| Fig. 4 Dynamic surface tension versus the adsorption lag time at the a/w interface for a series of SDS concentrations (same as shown in Fig. 3B). Dashed lines: interfacial tension for the bare (upper) and saturated (lower) interfaces with SDS concentrations above ccmc. Error bars indicate the uncertainty in bubble formation time for repeated recordings (for the data points obtained at 0.15% wt); mostly, the error bars are smaller than the symbols. | ||
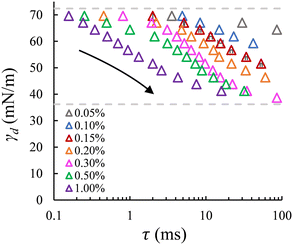
Dynamic interfacial tension at the o/w interface. The dynamic interfacial tension, γd, is plotted against the droplet formation time for SDS concentrations in the range of 0.05–1% wt. Fig. 3A clearly demonstrates that the number of droplets formed within a set period of time, and thus the droplet formation frequency, increases as the applied pressure increases. In Fig. 3B, as the applied pressure decreases (following the direction of the arrow), a lower dynamic interfacial tension is required to push the Laplace pressure below the applied pressure (
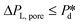 ) and thus a longer lag time is needed for surfactant adsorption to take place.
) and thus a longer lag time is needed for surfactant adsorption to take place.
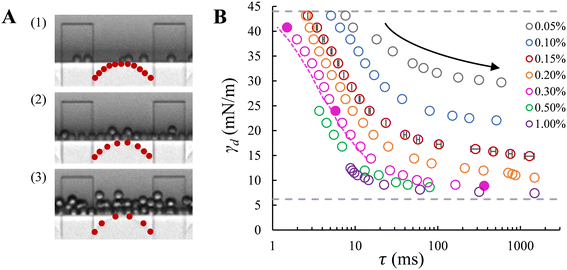
With the EDGE tensiometer, we retrieve the well-known dynamics of SDS adsorption in the hexadecane–water (o/w) system. The γd values are between the interfacial tension for the bare (γ0 = 44 mN m−1) and that for the saturated hexadecane–water interface, with the latter depending on surfactant concentrations. In the rapid fall region typically below 10 ms in Fig. 3B, the adsorption kinetics increase with SDS concentration,4 and as a result, the dynamic interfacial tension at a fixed lag time decreases as the SDS concentration increases up to 1% wt. This is ascribed to the increased number density and fast disaggregation of SDS micelles,12,14,17 which results in increasingly higher availability of SDS monomer as SDS concentration increases above ccmc. After the initial decrease γd converges to a plateau phase due to the fact that the interface gradually approaches saturation and the activation barrier for adsorption increases.26 At the end of this plateau phase, an equilibrium interfacial tension (γeq) is assumed to be reached. Fig. 3B shows that γeq decreases with the SDS concentration, and levels off for SDS concentrations above 0.3% wt, which is just above the critical micelle concentration, ccmc = 0.28% wt. This is in good agreement with literature, where a constant interfacial tension was obtained for SDS concentrations with c/ccmc > 1.4.14 In terms of measurement accuracy, it is good to mention that on the high end of the monitored tensions, the much higher viscosity of the hexadecane phase leads to a slight overestimation of the lag time τ when using the approximation of 1/f0 since the necking process is relatively slow with this more viscous dispersed phase. This can be solved by an additional analysis step, namely by measuring and subtracting the necking time (e.g., the pink dashed line in Fig. 3B). Lastly, in the droplet formation system, for high SDS concentrations above ccmc (i.e., 0.5 and 1% wt, shown in Fig. 3B) a transition from monodisperse to polydisperse droplet formation occurs at applied pressures that approach the maximum γd of the bare interface, and the latter thus cannot be measured due to this instability.
Dynamic surface tension at the a/w interface. The dynamic surface tension is plotted against the bubble formation time for the same range of SDS concentrations. Like the case of droplet formation, as the applied pressure decreases (indicated by the arrow), a longer lag time is needed for surfactant adsorption to lower the γd and thus the Laplace pressure to lower values; and at a fixed lag time, γd decreases as the SDS concentration increases (Fig. 4). We also retrieve the well-known dynamics of SDS for the air–water (a/w) system. The dynamic surface tension decreases from 72.4 mN m−1 for the bare air–water interface to the value for the saturated air–water interface, which varies for SDS concentrations below ccmc. Yet, although γd tends to level off at low applied pressures for SDS concentrations above 0.3% wt, an obvious plateau phase is not (yet) observed.
The minimum γd on the low end of the monitored tensions depends on the minimum applied pressure that can keep the meniscus constricted in the pore, and thus still allow for the pore flow and the subsequent bubble or droplet necking process to take place. In the a/w system, the meniscus retracts from the pore when the applied pressure reduces to a critical value, which increases significantly with decreasing SDS concentration (below ccmc). In this case, the minimum γd that can be measured is higher than the equilibrium surface tension of a saturated interface; for example, for 0.5% wt SDS, γd reaches approximately 41 mN m−1 (Fig. 4) in comparison to 31 mN m−1 that was reported in literature.27 However, in the o/w system, the applied pressure can be reduced very closely to the Laplace pressure that corresponds to the equilibrium interfacial tension of a saturated interface, and this allows us to monitor nearly the full range of γd. This discrepancy is likely due to contact line pinning, or the lack thereof, which is a resisting force (against the retraction) that is proportional to the dispersed phase viscosity and thus 100 times lower for air than hexadecane.28
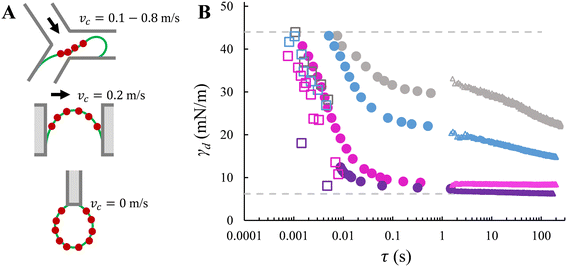 | ||
| Fig. 5 Method comparison. A. Schematics of adsorption locations in Y-junction, EDGE tensiometer and ADT technique. The red dots represent surfactant molecules. From top to bottom: the characteristic (i.e., smallest) dimension is tens of micrometres, one micrometre, and a few millimetres. The schematics are not drawn to scale. B. Dynamic interfacial tension versus time obtained with Y-junction (squares), EDGE tensiometer (circles), and ADT technique (triangles). The comparison is illustrated with four SDS concentrations: 0.05% wt (grey), 0.1% wt (blue), 0.3% wt (pink), and 1% wt (purple). The data sets for Y-junction and ADT are adapted from Muijlwijk et al. (2016), with permission from Elsevier.9 | ||
Fig. 5B clearly highlights that nearly the full range of the dynamic interfacial tension decay from γ0 to γeq can be accessed in the EDGE tensiometer and Y-junction; moreover, the EDGE tensiometer allows the assessment of dynamic interfacial tension of a saturating interface (which corresponds to the plateau phase), which is beyond the range accessible by the Y-junction. In the EDGE tensiometer, the dynamic interfacial tension is measured at time scales that are inherently needed for surfactant adsorption. In the Y-junction, the time scale is determined by the force balance (i.e., which determines the droplet snap-off), and γd at higher time scales (>10 ms) are inaccessible due to the limitation of the dripping regime. Using the ADT technique, the accessible time scale is simply the rate of data capture; and γd values at lower time scales are inaccessible as the concentration-dependent decrease of γd is much faster than the time required to refresh the interface, and the data capture is started, typically, after 1 second (i.e., experimental resolution).
In terms of time scales, the EDGE tensiometer data set overlaps with the extremities of the other two data sets. At the lower end of the time scales accessible with the EDGE tensiometer (τ < 10 ms), an agreement is observed with the Y-junction data in terms of the decreasing trend in γd as function of time (Fig. 5B). In the Y-junction, the obtained γd values are consistently lower than those obtained with the EDGE tensiometer at the same time scale. This is due to the continuous phase flow and the resulted (stronger) convective transfer of SDS towards the dilute interface.14,29 At the upper end of the time scales accessible with the EDGE tensiometer (τ ∼ 1 s), the EDGE tensiometer data stitches together with the ADT data, for SDS concentrations in the range of 0.1–1% wt. In the presence of only the lowest concentration that is 0.05% wt SDS, a lower γd is obtained with the EDGE tensiometer. This discrepancy suggests that surfactant adsorption is likely dominated by distinct mass transfer mechanisms, depending on the surfactant concentration used. When the surfactant concentration is low (e.g., 0.05% wt), the dynamic interfacial tension decay follows a diffusion-controlled mass transfer mechanism and the radius of the curved interface is a key parameter.30 In the EDGE tensiometer, dynamic adsorption is enhanced since the mass transfer distance (i.e., the depletion depth) is shorter for a highly-curved interface (i.e., the meniscus is confined in a micrometre-sized pore).6,31 This results in a faster decay in the dynamic interfacial tension and thus a lower γd at τ ≈ 1 s, compared to the ADT data. On the other hand, when the surfactant concentration is higher (i.e., >0.1% wt in this study), dynamic adsorption is enhanced by the bulk concentration and the kinetics of surfactant adsorption at the interface plays an important role. We have calculated the characteristic time scales for mass transfer (Fig. SI 5†), and it is found that the adsorption time (at the interface) is longer than the diffusion time (from the bulk phase to the sub-interface), which is in line with literature.10 This indicates that at these higher concentrations, surfactant mass transfer is either mixed diffusion-kinetic controlled32 or purely kinetic-controlled.11 Besides, as the interface gradually approaches saturation (e.g., at τ ≈ 1 s), the free energy barrier for adsorption may also slow down the adsorption rate of SDS monomers, which also gives rise to the transition from diffusion- to kinetic-controlled mass transfer mechanism.26 For 0.1% wt, surfactant mass transfer is likely mixed diffusion-kinetic controlled; γd continues to decrease at τ > 1 s and reaches an equilibrium value that is lower than the γd values obtained with the EDGE tensiometer.
The EDGE tensiometer stands out from the existing microfluidic tensiometers in multiple aspects. First, the EDGE tensiometer is simple and universal since no complex theoretical models or sophisticated calculations are needed. Second, the dynamic interfacial tension is linked to the adsorption lag time – which can be approximated as droplet or bubble formation time in this device – which makes the method insensitive to produced droplet or bubble size and continuous phase properties (e.g., velocity and viscosity23). Third, the adsorption lag time inherently covers the full decrease of dynamic interfacial tension from γ0 to γeq, as the low-pressure regime in this device is bounded by the Laplace pressures of the (nearly) empty and saturated interfaces. Fourth, both o/w and a/w interfaces can be characterised; in the latter case, the dynamic surface tension can be estimated without any correction for compressibility. Last but not least, the geometrical characteristics of the partitioned-EDGE device allow us to work with multiple tensiometers (i.e., multiple pores) at the same time: the time scale obtained from a single experiment is an averaged value (here, from eight parallel tensiometers) leading to a high accuracy and a high statistical efficiency.
Conclusion
In the partitioned-EDGE device, bubbles and droplets are formed in two pressure regimes.2,22 The low-pressure regime is typically bounded by the Laplace pressures of the empty and saturated interfaces, and therefore suitable for tensiometry. To initiate the formation of bubbles and droplets, the Laplace pressure needs to be decreased below the applied pressure, and this is caused by a reduction in the dynamic interfacial tension due to surfactant adsorption. The dynamic interfacial tension can be calculated from the Young–Laplace equation and linked to the adsorption lag time τ, which can be estimated from the – easily monitored – formation frequency.We studied droplet and bubble formation in the presence of 0.05–1% wt SDS, and for the first time introduced a microfluidic tensiometer based on a spontaneous device – the EDGE tensiometer, where the continuous phase flow is only used for carrying the generated droplets and bubbles away from the sensor. In the EDGE tensiometer, τ is surfactant-dependent (i.e., the type and concentration); surfactant adsorption is enhanced due to the highly-curved interface and the high bulk concentration. It is found that τ varies in the range of 1–1500 ms and 0.1–90 ms in terms of droplet and bubble interfaces, respectively, with increasing applied pressures and SDS concentrations. This range of time scales intersects with that encountered in industrial scale high-pressure homogenisers (0.1–30 ms),3 which implies that the EDGE tensiometer provides insights that not only help scientists understand the effect of dynamic adsorption on droplet and bubble formation (and coalescence), but also can be applied to design industrial processes in a more efficient way, for instance making better use of surfactant materials.
Author contributions
Boxin Deng: conceptualization, methodology, investigation, validation, formal analysis, visualization, writing – original draft. Karin Schroën: conceptualization, methodology, supervision, writing – review & editing. Maartje Steegmans: conceptualization, writing – review & editing. Jolet de Ruiter: conceptualization, methodology, visualization, supervision, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the China Scholarship Council (grant number 201806790006) and FrieslandCampina for financial support.References
- K. Schroën, J. de Ruiter and C. Berton-Carabin, ChemEngineering, 2020, 4, 1–22 CrossRef.
- B. Deng, K. Schroën and J. De Ruiter, J. Colloid Interface Sci., 2021, 602, 316–324 CrossRef CAS PubMed.
- S. Schultz, G. Wagner, K. Urban and J. Ulrich, Chem. Eng. Technol., 2004, 27, 361–368 CrossRef CAS.
- Q. Brosseau, J. Vrignon and J. C. Baret, Soft Matter, 2014, 10, 3066–3076 RSC.
- R. D. Apolito, A. Perazzo, M. D. Antuono, V. Preziosi, G. Tomaiuolo, R. Miller and S. Guido, Langmuir, 2018, 34, 4991–4997 CrossRef PubMed.
- Y. Chen and C. S. Dutcher, Soft Matter, 2020, 16, 2994–3004 RSC.
- S. D. Huston, J. T. Cabral, J. William, J. Goodrum, K. L. Beers and E. J. Amis, Appl. Phys. Lett., 2005, 87, 081905 CrossRef.
- S. Liu and C. S. Dutcher, J. Phys. Chem. B, 2021, 125, 13916–13927 CrossRef CAS.
- K. Muijlwijk, E. Hinderink, D. Ershov, C. Berton-Carabin and K. Schroën, J. Colloid Interface Sci., 2016, 470, 71–79 CrossRef CAS.
- M. Kalli, L. Chagot and P. Angeli, J. Colloid Interface Sci., 2022, 605, 204–213 CrossRef CAS PubMed.
- X. Liang, M. Li, K. Wang and G. Luo, J. Colloid Interface Sci., 2022, 617, 106–117 CrossRef CAS PubMed.
- J. H. Xu, P. F. Dong, H. Zhao, C. P. Tostado and G. S. Luo, Langmuir, 2012, 28, 9250–9258 CrossRef CAS.
- P. Pawliszak, B. H. Bradshaw-hajek, C. Greet, W. Skinner, D. A. Beattie and M. Krasowska, Colloids Interfaces, 2021, 5, 1–12 Search PubMed.
- K. Wang, Y. C. Lu, J. H. Xu and G. S. Luo, Langmuir, 2009, 25, 2153–2158 CrossRef CAS PubMed.
- M. L. J. Steegmans, A. Warmerdam, K. G. P. H. Schroen and R. M. Boom, Langmuir, 2009, 25, 9751–9758 CrossRef CAS PubMed.
- H. Gu, M. H. G. Duits and F. Mugele, Colloids Surf., A, 2011, 389, 38–42 CrossRef CAS.
- X. Wang, A. Riaud, K. Wang and G. Luo, Microfluid. Nanofluid., 2015, 18, 503–512 CrossRef CAS.
- K. Kinoshita, E. Parra and D. Needham, J. Colloid Interface Sci., 2017, 504, 765–779 CrossRef CAS PubMed.
- M. J. Geerken, R. G. H. Lammertink and M. Wessling, J. Colloid Interface Sci., 2007, 312, 460–469 CrossRef CAS PubMed.
- T. M. Ho, A. Razzaghi, A. Ramachandran and K. S. Mikkonen, Adv. Colloid Interface Sci., 2022, 299, 102541 CrossRef CAS.
- N. Nguyen, S. Lassemono, F. Chollet, C. Yang, I. Tension, N. Nguyen, S. Lassemono, F. A. Chollet and C. Yang, IEEE Sens. J., 2007, 7, 692–697 CAS.
- S. Sahin and K. Schroën, Lab Chip, 2015, 15, 2486–2495 RSC.
- B. Deng, K. Schroën and J. De Ruiter, J. Colloid Interface Sci., 2022, 622, 218–227 CrossRef CAS PubMed.
- K. Van Dijke, R. De Ruiter, K. Schroën and R. Boom, Soft Matter, 2010, 6, 321–330 RSC.
- K. C. Van Dijke, K. C. P. G. H. Schroën and R. M. Boom, Langmuir, 2008, 24, 10107–10115 CrossRef CAS PubMed.
- J. Eastoe and J. S. Dalton, Adv. Colloid Interface Sci., 2000, 85, 103–144 CrossRef CAS.
- J. H. Xu, S. W. Li, G. G. Chen and G. S. Luo, AIChE J., 2006, 52, 2254–2259 CrossRef CAS.
- V. Pratap, N. Moumen and R. S. Subramanian, Langmuir, 2008, 91, 5185–5193 CrossRef PubMed.
- K. Muijlwijk, W. Huang, J. E. Vuist, C. Berton-Carabin and K. Schroën, Soft Matter, 2016, 12, 9025–9029 RSC.
- N. J. Alvarez, L. M. Walker and S. L. Anna, Langmuir, 2010, 26, 13310–13319 CrossRef CAS PubMed.
- N. J. Alvarez, L. M. Walker and S. L. Anna, Phys. Rev. E, 2010, 82, 011604 CrossRef.
- Y. Jiang, T. Geng, Q. Li, G. Li and H. Ju, J. Mol. Liq., 2015, 204, 126–131 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2lc00545j |
| This journal is © The Royal Society of Chemistry 2022 |