Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Determining overpotentials for the oxidation of alcohols by molecular electrocatalysts in non-aqueous solvents†
Amy L.
Speelman
 a,
James B.
Gerken
b,
Spencer P.
Heins
a,
Eric S.
Wiedner
a,
James B.
Gerken
b,
Spencer P.
Heins
a,
Eric S.
Wiedner
 a,
Shannon S.
Stahl
a,
Shannon S.
Stahl
 b and
Aaron M.
Appel
b and
Aaron M.
Appel
 *a
*a
aCenter for Molecular Electrocatalysis, Pacific Northwest National Laboratory, Richland, WA 99352, USA. E-mail: aaron.appel@pnnl.gov
bDepartment of Chemistry, University of Wisconsin–Madison, Madison, Wisconsin 53706-1322, USA
First published on 17th August 2022
Abstract
Molecular electrocatalysts for energy-related transformations offer unique opportunities to elucidate mechanistic principles that contribute to improved rates and energy efficiency. New catalysts for electrochemical alcohol oxidation in non-aqueous conditions have been developed recently, but it is difficult to make meaningful performance comparisons between them because the different conditions used for each catalyst result in unquantified differences in driving force. The present report outlines an approach to determine the equilibrium potential for the oxidation of alcohols in organic solvents or solvent mixtures. These equilibrium potentials are then used to determine the overpotentials for a series of molecular electrocatalysts. Overall, the methodology outlined herein provides a foundation for future advances in this field and enables comparison of electrocatalyst performance under aqueous and non-aqueous reaction conditions.
Broader contextElectrocatalytic alcohol oxidation is a key process in direct methanol fuel cells and is the focus of growing attention in biomass conversion and electrochemical synthesis. Significant effort has therefore been directed toward the design of molecular electrocatalysts for alcohol oxidation. Reactions with these catalysts are often performed in non-aqueous solvents and under different reaction conditions, which complicates quantitative comparisons of catalyst performance and thereby impedes progress in this field. This perspective outlines an approach to assess overpotentials for catalytic reactions under any conditions, enabling meaningful comparison of different catalysts and providing a foundation to establish criteria for the design of new catalytic systems. |
Introduction
Alcohol oxidation is a fundamental functional group transformation that is of interest in both synthetic and energy-related contexts. As an anode reaction in fuel cells, it is imperative that oxidation takes place at an electrode potential close to the thermodynamic potential of the reaction. Although this is less critical in the context of synthetic alcohol oxidation, the energetic requirements for a process can impact reaction selectivity and, potentially, economic viability. Thus, it is important to know not only the operating potential of an alcohol oxidation catalyst, but also how that potential is related to the thermodynamic potential of the overall reaction under the catalytic conditions.Overpotential (η) is generally defined as the difference between the equilibrium potential of the reaction being catalyzed and the potential at which a catalyst operates at a specific current.1 In other words, overpotential is an indicator of the excess electrochemical driving force for catalysis at a given rate. It is therefore essential to report the electrocatalytic rate and the corresponding overpotential together since each can be improved at the cost of the other.
To determine an overpotential, both the catalytic potential and equilibrium potential must be well-defined. For molecular electrocatalysts, the catalytic wave typically occurs near a redox couple of the parent complex and reaches a steady-state current (icat) at sufficiently anodic potentials (or cathodic potentials, for reduction reactions). The selection of a catalytic potential can be somewhat subjective because similar values of icat are observed over a range of potentials. The overpotential of a molecular catalyst is therefore frequently reported at the catalytic half-wave potential (Ecat/2), defined as the potential at which the current of the catalytic wave reaches half of icat.1,2 This concept is illustrated in Fig. 1 for the electrocatalytic oxidation of 1-butanol to butanal using 4-acetamido-TEMPO (ACT, TEMPO = 2,2,6,6-tetramethylpiperidine-N-oxyl).3 By using this approach, the current and potential are well-defined and coupled to each other. The equilibrium potential for a catalytic reaction (E°′) is determined from the standard potential (E°) by accounting for non-standard state reaction conditions, specifically for temperatures other than 298 K and any reactant or product that does not have a solution concentration of 1 M (or 1 atm for gases). Buffering is recommended any time an overpotential is determined in order to provide a stable, well-defined thermodynamic potential, but is particularly important when the overpotential is low.1
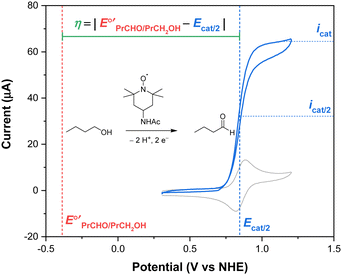 | ||
Fig. 1 Overpotential is the difference between the thermodynamic potential  and the potential for catalysis (Ecat/2), as illustrated for the oxidation of 1-butanol to butanal catalyzed by ACT in water at pH 10. Data from ref. 3. and the potential for catalysis (Ecat/2), as illustrated for the oxidation of 1-butanol to butanal catalyzed by ACT in water at pH 10. Data from ref. 3. | ||
The ability to accurately define the thermodynamic potential for a reaction under each set of catalytic conditions is crucial to enable meaningful comparisons of overpotentials with different catalysts. Direct experimental measurement of E° requires an electrode that can reversibly and rapidly perform the electrochemical reaction of interest. In cases like alcohol oxidation where no such electrode exists, E° may be calculated from the free energies of formation of the substrate(s) and product(s). Using this method, the standard potentials of many redox reactions have been reported in aqueous solution.4 However, molecular electrocatalysts are often studied in organic solvents or solvent mixtures in which standard potentials are not known.
In this manuscript, we report a method for determining the thermodynamic potentials for the oxidation of alcohols under non-aqueous conditions, including the 2e−/2H+ interconversion of several common aldehydes and ketones with the corresponding alcohol, the 4e−/4H+ oxidations of primary alcohols to esters and carboxylic acids, and the 6e−/6H+ oxidation of methanol to CO2. These potentials allow, for the first time, a direct quantification of the overpotential for alcohol oxidation with molecular electrocatalysts in organic solvents.
Calculation of standard potentials for the oxidation of alcohols
A crucial advance in evaluating overpotentials in organic solvents and solvent mixtures came with the application of open-circuit potential (OCP) measurements for the direct determination of the equilibrium potentials for the hydrogen evolution reaction (eqn (1)) in organic solvents, measured vs. the ferrocenium/ferrocene (Fc+/0) couple (EBH+/H2(org)).5| 2HBase(org)+ + 2e−(Fc+/0) ⇌ H2(g) + 2Base(org) | (1) |
In this method, EBH+/H2(org) is determined by measuring the OCP of buffered mixtures of an acid and its conjugate base under 1 atm H2 using a Pt electrode freshly annealed in a H2 flame. In solvents with an established absolute pKa scale, the OCP method can also be used to determine the standard hydrogen couple 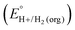 viaeqn (2).
viaeqn (2).
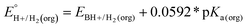 | (2) |
Using this approach, values of 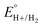 have been reported in several solvents (see Table S3, ESI†), including MeCN
have been reported in several solvents (see Table S3, ESI†), including MeCN 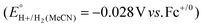 .5 We note that the value reported in THF6
.5 We note that the value reported in THF6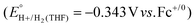 was calculated using an absolute pKa scale7 which is different from the most commonly used pKa scale in THF (sometimes referred to the pKα scale).8 Although only a few absolute pKa values have been directly determined, pKα values, which have been reported for a wide variety of bases, can be used to calculate approximate pKa values (see ESI,† Section 2a for a more detailed discussion).
was calculated using an absolute pKa scale7 which is different from the most commonly used pKa scale in THF (sometimes referred to the pKα scale).8 Although only a few absolute pKa values have been directly determined, pKα values, which have been reported for a wide variety of bases, can be used to calculate approximate pKa values (see ESI,† Section 2a for a more detailed discussion).
Based on EBH+/H2(org), thermochemical cycles can be constructed to determine the thermodynamic potentials for reactions involving transfer of H2 equivalents. This approach has been previously used to establish standard potentials for reduction of gaseous small molecules (O2, CO2, and N2) in organic solvents9,10 as well as for oxidation of a limited number of alcohols in water or MeCN.11–13
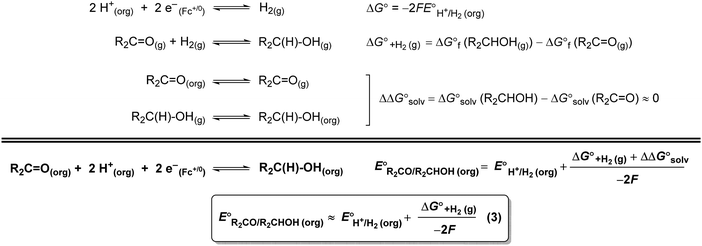
A thermochemical cycle for determination of standard potentials for 2-electron oxidation of alcohols 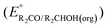 is shown in Fig. 2.14 The cycle starts from
is shown in Fig. 2.14 The cycle starts from 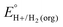 and the gas-phase free energy for aldehyde or ketone hydrogenation
and the gas-phase free energy for aldehyde or ketone hydrogenation 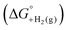 , which can be calculated from the difference in the gas-phase free energies of formation
, which can be calculated from the difference in the gas-phase free energies of formation 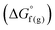 of the pure aldehyde or ketone and alcohol. It also involves the difference in solvation free energy between the alcohol and aldehyde or ketone
of the pure aldehyde or ketone and alcohol. It also involves the difference in solvation free energy between the alcohol and aldehyde or ketone 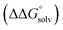 . Although solvation free energies for common alcohols, aldehydes, and ketones are known in aqueous solution, few have been reported in the organic solvents commonly used in electrochemical studies of alcohol oxidation. However, since an alcohol and the corresponding aldehyde or ketone have nearly identical sizes and only modest differences in polarity,
. Although solvation free energies for common alcohols, aldehydes, and ketones are known in aqueous solution, few have been reported in the organic solvents commonly used in electrochemical studies of alcohol oxidation. However, since an alcohol and the corresponding aldehyde or ketone have nearly identical sizes and only modest differences in polarity, 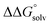 is likely to be a relatively small contributor to the potential. In support of this assumption, the contributions of solvation free energy terms to the aqueous standard potentials for the oxidation of ethanol, 2-propanol, and benzyl alcohol are between 20 and 50 mV (see ESI† Section 4a for the complete analysis). In the solvents typically used in electrochemical experiments with organometallic and inorganic complexes, the magnitude of
is likely to be a relatively small contributor to the potential. In support of this assumption, the contributions of solvation free energy terms to the aqueous standard potentials for the oxidation of ethanol, 2-propanol, and benzyl alcohol are between 20 and 50 mV (see ESI† Section 4a for the complete analysis). In the solvents typically used in electrochemical experiments with organometallic and inorganic complexes, the magnitude of 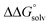 is likely to be similar to or smaller than the value in water (see ESI† Section 4b). Based on its very limited contribution to the potential,
is likely to be similar to or smaller than the value in water (see ESI† Section 4b). Based on its very limited contribution to the potential, 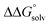 can be omitted when solvation free energies are not available. In these cases,
can be omitted when solvation free energies are not available. In these cases, 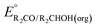 is calculated using eqn (3), shown at the bottom of Fig. 2. Values of
is calculated using eqn (3), shown at the bottom of Fig. 2. Values of 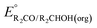 in water, MeCN, and THF are provided in Table 1 for several common alcohols.
in water, MeCN, and THF are provided in Table 1 for several common alcohols.
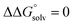 , except where noted
, except where noted
| Reaction | Alcohol | |||
|---|---|---|---|---|
| Water (V vs. SHE) | MeCN (V vs. Fc+/0) | THF (V vs. Fc+/0) | ||
a Literature value for oxidation of methanol to methanediol.15 See ESI Section 4a for further discussion.
b These values correspond to the standard potential for the oxidation of methanol to formaldehyde. As discussed in more detail in ESI Section 4a, significant additional driving force for methanol oxidation is likely provided by condensation and oligomerization. Values calculated using this standard potential therefore correspond to a lower limit on the overpotential.
c Values were calculated including an estimate for 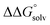 . See ESI Sections 5, 6, and 7 for more details.
d Under basic conditions where pKa(HBase+) > pKa(RCO2H), the thermodynamic potential for the carboxylate/alcohol pair is calculated as . See ESI Sections 5, 6, and 7 for more details.
d Under basic conditions where pKa(HBase+) > pKa(RCO2H), the thermodynamic potential for the carboxylate/alcohol pair is calculated as 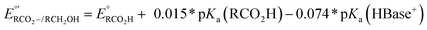 . See ESI Section 6 for complete analysis. . See ESI Section 6 for complete analysis.
|
||||
| R2CO(solv) + 2H(solv)+ + 2e− ⇌ R2CHOH(solv) | MeOH | 0.23a | 0.28b | −0.03b |
| EtOH | 0.21 | 0.15 | −0.16 | |
| i PrOH | 0.13 | 0.08 | −0.24 | |
| BnOH | 0.18 | 0.10 | −0.21 | |
| RC(O)OCH2R(solv) + 4H(solv)+ + 4e− ⇌ 2RCH2OH(solv) | MeOH | — | 0.04 | −0.28 |
| EtOH | — | 0.01c | −0.33 | |
| RCO2H(solv) + 4H(solv)+ + 4e− ⇌ RCH2OH(solv) + H2O(solv)d | MeOH | 0.11 | 0.08 | −0.24 |
| EtOH | 0.06 | 0.04c | −0.29 | |
| BnOH | 0.06 | 0.03 | −0.28 | |
| CO2(g) + 6H(solv)+ + 6e− ⇌ MeOH(solv) + H2O(solv) | MeOH | 0.03 | 0.00c | −0.31c |
The same approach can be used for the 4 e− oxidation of alcohols to esters or carboxylic acids (see ESI† Sections 5 and 6 for complete analysis).16 We note that there is a greater degree of uncertainty in the values for carboxylic acids and carboxylates because in organic solvents these species are prone to aggregation, including homoconjugation, dimerization, and ion pairing, which perturbs solution equilibria and changes the driving force for the overall reaction. The impact of aggregation can be included if all of the relevant equilibrium constants are known. When they are not known, the influence of aggregation can be minimized by conducting measurements of Ecat/2 in buffered solutions containing the acid, base, alcohol, and carboxylic acid.1
An analogous thermochemical scheme for determination of the standard potential for the 6 e− oxidation of methanol to CO2 is discussed in the ESI† (Section 7). Because CO2 has a gas-phase standard state, a correction for its solvation free energy is not included. The solvation free energy term for the alcohol therefore makes a slightly larger contribution to the potential compared to the 2-electron and 4-electron cases. When solvation free energies are not available, a better estimate of 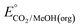 can be obtained based on
can be obtained based on 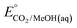 (see ESI,† Section 7c) following the approach described in ref. 9.
(see ESI,† Section 7c) following the approach described in ref. 9.
We note that the thermodynamic potentials calculated using the above schemes involve several approximations. In addition to neglecting the contribution from solvation free energies, the analysis described above assumes ideal solutions (i.e., that the activities of all species are equal to their nominal concentrations). While the impacts on the thermodynamic potentials are expected to be small, the resulting overpotentials, particularly when they are low, should be interpreted with these sources of uncertainty in mind.
Calculation of equilibrium potentials under catalytic conditions
The values of E° discussed above correspond to standard-state conditions of 1 M solvated H+, 1 M alcohol, and 1 M oxidized product at 298 K. Electrochemical experiments are rarely performed under standard-state conditions, however, and it is necessary to determine the equilibrium potential (E°′) under the conditions employed in the experiment. The following discussion explains how to calculate E°′ for 2 e− oxidation of alcohols. The same approach may be used for 4 e− and 6 e− oxidations of alcohols.Under non-aqueous conditions, alcohol oxidation is generally conducted in the presence of an organic base. In solvents with an established pKa scale, the value of E°′ can be calculated from E° and the pKa of the protonated form of the organic base using eqn (4), shown at the bottom of Fig. 3. In solvents or solvent mixtures in which a pKa scale has not been established or 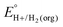 is not known, E°′ can instead be calculated from EBH+/H2(org) (determined via OCP measurements using the same acid/base pair employed in the catalytic conditions) and
is not known, E°′ can instead be calculated from EBH+/H2(org) (determined via OCP measurements using the same acid/base pair employed in the catalytic conditions) and 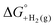 (see ESI,† Section 2b).
(see ESI,† Section 2b).
 | ||
Fig. 3 Calculation of the thermodynamic potential for 2 e− oxidation of an alcohol in the presence of an acid/base pair 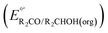 from from 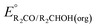 (see Fig. 2) and pKa(HBase+). (see Fig. 2) and pKa(HBase+). | ||
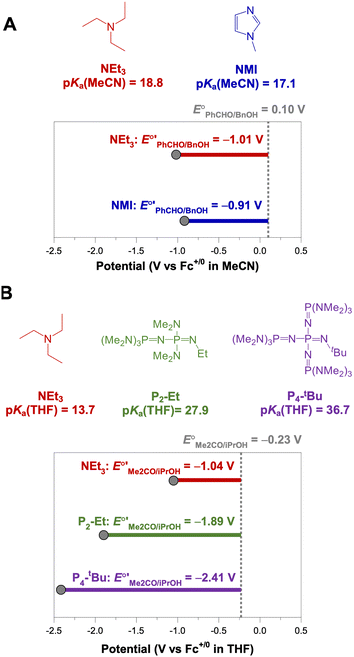
The analysis in Fig. 3 indicates that the choice of base has a substantial impact on the value of 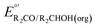 . Fig. 4 shows the range of thermodynamic potentials for bases that have been used in reports of electrocatalytic oxidation of benzyl alcohol in MeCN and 2-propanol in THF. Use of the organic bases triethylamine (NEt3) and N-methyl imidazole (NMI) in MeCN, rather than standard-state conditions (i.e., solvated H+), results in an ∼1 V shift in the thermodynamic potential for the PhCHO/BnOH redox equilibrium. Studies in THF have used even stronger phosphazene bases, leading to shifts of up to 2.2 V from standard-state potentials.
. Fig. 4 shows the range of thermodynamic potentials for bases that have been used in reports of electrocatalytic oxidation of benzyl alcohol in MeCN and 2-propanol in THF. Use of the organic bases triethylamine (NEt3) and N-methyl imidazole (NMI) in MeCN, rather than standard-state conditions (i.e., solvated H+), results in an ∼1 V shift in the thermodynamic potential for the PhCHO/BnOH redox equilibrium. Studies in THF have used even stronger phosphazene bases, leading to shifts of up to 2.2 V from standard-state potentials.
 | ||
| Fig. 4 Calculation of E°′ for 2-electron oxidation of benzyl alcohol in MeCN (A) and 2-electron oxidation of 2-propanol to acetone in THF (B) with different bases from the standard potential (see Table 1) and pKa(HBase+) using eqn (4). | ||
Electrocatalytic measurements are also often performed on solutions containing only alcohol and base. Under these conditions, the thermodynamic potential is ill-defined because the ln(Q) term in the Nernst equation contains terms with initial values of zero. Therefore, the solution composition at the electrode surface, and the corresponding electrode potential, change substantially as soon as electrocatalysis begins. If the measurement is instead performed using a buffered solution (containing a base, its conjugate acid, an alcohol, and the corresponding aldehyde or ketone), the relative change in ln(Q) and correspondingly in the thermodynamic potential will be small. The most straightforward method for establishing a stable potential is to perform electrocatalytic reactions in solutions containing 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratios of base to conjugate acid and alcohol to conjugate aldehyde or ketone. The resulting potential is the same as that calculated from eqn (4), despite the deviation from standard state conditions. If ratios other than 1
1 ratios of base to conjugate acid and alcohol to conjugate aldehyde or ketone. The resulting potential is the same as that calculated from eqn (4), despite the deviation from standard state conditions. If ratios other than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 are used,
1 are used, 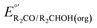 must be modified via the Nernst equation (eqn (5)) to account for the non-standard state concentrations.
must be modified via the Nernst equation (eqn (5)) to account for the non-standard state concentrations.
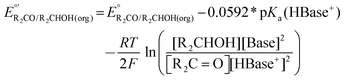 | (5) |
Evaluation of overpotential for known electrocatalysts for oxidation of alcohols
Molecular catalysts for electrochemical alcohol oxidation have been reviewed recently.17–19 Here, we focus on a subset of catalysts for which electrochemical two-electron oxidation of alcohols was performed in THF or MeCN using bases with known pKa values, which allows the determination of overpotentials (Fig. 5 and Table 2).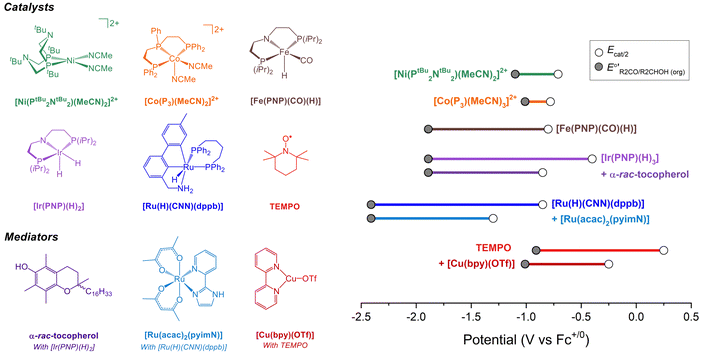 | ||
Fig. 5 (Left) Molecular catalysts for oxidation of alcohols in organic solution. (Right) Illustration of the overpotentials for oxidation of alcohols by molecular catalysts. The grey circles represent 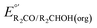 (see Fig. 4) and the white circles represent Ecat/2. The length of the colored bars corresponds to the overpotential (see also Table 2). (see Fig. 4) and the white circles represent Ecat/2. The length of the colored bars corresponds to the overpotential (see also Table 2). | ||
| Catalyst | Solvent | ROH | Base (pKa)a | η (V) | k obs (s−1) | Ref. |
|---|---|---|---|---|---|---|
| a pKa refers to the conjugate acid of the indicated base. pKa values in MeCN were taken from the literature.8,28 pKα values in THF8 were converted7 to absolute pKa values (see ESI section 2a). b Measurements were conducted on buffered solutions (see ESI Section 9). c No electrocatalytic activity was observed on the CV timescale, but bulk electrolysis at an applied potential of −0.63 V produced PhCHO with 97% Faradaic efficiency. η was estimated based on the Co(II/I) E1/2 (−0.78 V vs. Fc+/0). d Measurements were not conducted under buffered conditions which increases the uncertainty in η. Values are therefore reported to the nearest 100 mV. e Rate not determined due to overlap of catalytic wave with background base oxidation by the electrode. | ||||||
| [Ni(PtBu2NtBu2)(MeCN)2][BF4]2b | MeCN | i PrOH | NEt3 (18.8) | 0.32b | 2.1 | 20 and 21 |
| [Ni(PtBu2NtBu2)(MeCN)2][BF4]2b | MeCN | BnOH | NEt3 (18.8) | 0.39b | 4.5 | 20 and 21 |
| [Co(P3)(MeCN)2][BF4]2 | MeCN | BnOH | NEt3 (18.8) | ∼0.2c | <0.1c | 22 |
| [Fe(PNP)(CO)(H)] | THF | i PrOH | P2-Et (27.9) | 1.1d | 1.7 | 23 |
| [Ir(PNP)(H)2] | THF | i PrOH | P2-Et (27.9) | 1.5d | n.d. | 24 |
| [Ir(PNP)(H)2] with α-rac-tocopherol | THF | i PrOH | P2-Et (27.9) | 1.0d | 14.6 | 24 |
| [Ru(H)(CNN)(dppb)] | THF | i PrOH | P4-tBu (36.7) | 1.6d | 0.6 | 25 and 26 |
| [Ru(H)(CNN)(dppb)] with [Ru(acac)2(pyimN)] | THF | i PrOH | P4-tBu (36.7) | 1.1d | 0.3 | 25 and 26 |
| TEMPO | MeCN | BnOH | NMI (17.1) | 1.2d | 2.3 | 27 |
| TEMPO with [Cu(bpy)(OTf)] | MeCN | BnOH | NEt3 (18.8) | 0.8d | 11.6 | 27 |
As discussed in the previous section, catalyst performance should be evaluated under buffered conditions. Such conditions are rarely employed in practice, and it is difficult to accurately predict what impact buffering will have on the observed catalytic rate and potential. To illustrate the impact of buffering, the oxidations of BnOH and iPrOH catalyzed by [Ni(PtBu2NtBu2)(MeCN)2][BF4]2 were examined under unbuffered conditions (only alcohol and Et3N) and buffered conditions (alcohol, PhCHO or Me2CO, Et3N, and Et3NH+). As shown in Fig. S7 and S8 (ESI†), for this specific catalyst buffering results in a small (∼50 mV) positive shift in Ecat/2 and an approximately two-fold decrease in rate. The precise changes will not be generalizable across catalysts, but this example shows that measuring under buffered conditions can result in a change in catalytic performance in some cases. This approach has not been used for the other systems in Fig. 5; the reported performance for these catalysts should be interpreted with this discrepancy in mind, especially for the values in THF that are expected to be more significantly impacted by the effects of ion pairing. To illustrate how the catalyst properties contribute to both overpotential and rate, the proposed catalytic cycles for several of these systems are discussed in detail below.
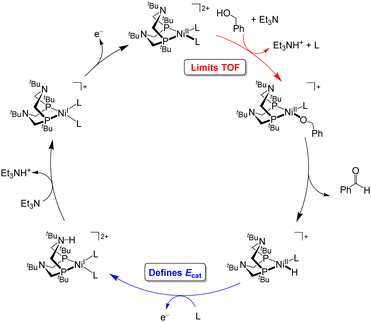
Under the buffered conditions described above, [Ni(PtBu2NtBu2)(MeCN)2]2+ catalyzes the oxidation of BnOH at Ecat/2 = −0.71 V vs. Fc+/0, corresponding to an overpotential of 0.39 V. As shown in Fig. 6, the catalytic cycle is proposed to involve generation of an alkoxide complex as the rate-limiting step.21 This species undergoes β-hydride elimination to release benzaldehyde. Oxidation of the resulting Ni(II) hydride, which is the potential determining step, occurs at a mild potential because of the presence of the pendant amine, which provides a pathway for intramolecular proton transfer.29,30 Although the Ni(II) hydride could not be isolated, this hypothesis is supported by comparison to related bis(diphosphine) Ni(II)–H complexes. For example, the oxidation of [HNi(depp)2]+ (depp = 1,3-bis(diethylphosphino)propane) occurs 0.6 V more positive than the oxidation of a corresponding complex that contains a pendant amine ([HNi(Et2PCH2NMeCH2PEt2)2]+).31 The presence of the pendant amine is therefore crucial to achieving a low overpotential in this system. An analogous catalytic cycle was proposed for [Co(P3)(MeCN)2]2+, but the Co(II)–H is oxidized at a mild potential without the need for a pendant amine.22 This complex has a similar overpotential to [Ni(PtBu2NtBu2)(MeCN)2]2+ but a much lower catalytic rate.
Waymouth and co-workers have reported several electrocatalysts for the oxidation of 2-propanol based on thermal catalysts that were originally used for acceptorless alcohol dehydrogenation and transfer hydrogenation reactions.32–35 The proposed catalytic cycle for [Ir(PNP)(H)2] is shown as a representative example in Fig. 7A. This complex dehydrogenates 2-propanol via a mechanism involving proton transfer to the PNP ligand amide group and hydride transfer to the Ir center to produce acetone and [Ir(PN(H)P)(H)3].24,35 This species is oxidized at −0.65 V vs. Fc+/0 and then deprotonated by phosphazene P2-Et. The strong base makes a large contribution to E°′, which results in a high overpotential of 1.5 V. Oxidation of 2-propanol by [Fe(PNP)(CO)(H)] follows an analogous mechanism.23 Although the Ecat/2 is slightly more modest for the Fe complex, the use of a strong base (phosphazene P2-Et) results in a high overpotential of 1.1 V.
 | ||
| Fig. 7 Proposed catalytic cycle for oxidation of 2-propanol by [Ir(PNP)(H)2] in the absence (A) and presence (B) of a phenoxyl radical mediator. | ||
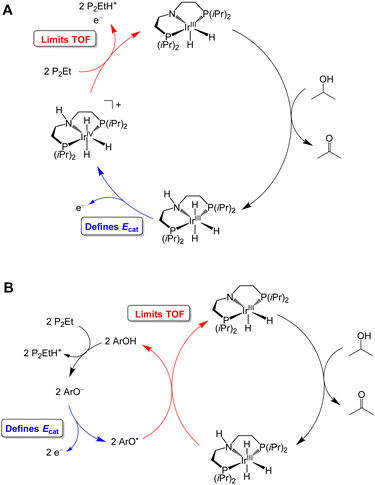
The overpotential of the Ir catalyst can be decreased by addition of a phenol/phenoxyl radical electron–proton transfer mediator,36 which performs two successive formal H-atom abstractions to regenerate [Ir(PNP)(H)2] (Fig. 7B).24 The mediator is then regenerated electrochemically through deprotonation of the phenol by P2-Et and oxidation of the phenoxide at −1.07 V vs. Fc+/0. Since this oxidation occurs at a milder potential than the oxidation of [Ir(PN(H)P)(H)3], the overpotential is decreased to 1.0 V. Similarly, the addition of [Ru(acac)2(pyimN)] to [Ru(H)(CNN)(dppb)] lowers the overpotential for 2-propanol oxidation from 1.6 V to 1.1 V with phosphazene P4-tBu as the base.25,26 The origin of the decrease in overpotential is less clear in this case, but has been proposed to involve H-atom abstraction by [Ru(acac)2(pyimN)].
Organic aminoxyls, such as TEMPO and ACT, have been widely used as molecular electrocatalysts for alcohol oxidation.37 As a representative example, the oxidation of benzyl alcohol occurs via reaction of the alcohol with TEMPO+ (Fig. 8A) to give TEMPOH and benzaldehyde.27,38 TEMPOH is then deprotonated and re-oxidized to TEMPO+ at a potential of +0.24 V vs. Fc+/0 in MeCN. The overpotential for this reaction is 1.2 V when NMI is used as the base. The addition of a Cu co-catalyst, which was originally developed to support aerobic alcohol oxidation,39 has also been shown to enhance electrocatalytic alcohol oxidation. In this case, [Cu(bpy)]2+ and TEMPO mediate alcohol oxidation by a different mechanism in which the CuII and TEMPO˙ species act cooperatively to achieve net hydride abstraction from a Cu-coordinated alkoxide (Fig. 8B). Formation of the Cu-alkoxide complex is the rate-limiting step in this reaction. The [Cu(bpy)]2+ species also promotes proton-coupled oxidation of TEMPOH to regenerate TEMPO˙; oxidation of [Cu(bpy)]+ is the potential-determining step of the electrocatalytic reaction. This redox step occurs at a more moderate potential than the oxidation of TEMPO˙ to TEMPO+, resulting in a lower overpotential of 0.8 V.
 | ||
| Fig. 8 Proposed catalytic cycle for oxidation of benzyl alcohol by TEMPO in the absence (A) and presence (B) of [Cu(bpy)]2+. | ||
Comparison of overpotentials for the oxidation of alcohols
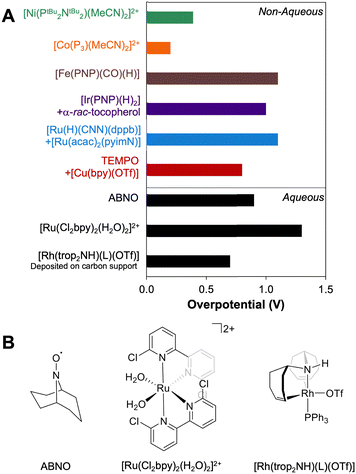
Using the approach described above, overpotentials for electrocatalytic alcohol oxidation can be meaningfully compared across solvents and conditions, as illustrated in Fig. 9A. Among the catalysts discussed so far, [Co(P3)(MeCN)2]2+ exhibits the lowest overpotential for alcohol oxidation, but it is significantly slower than the other catalysts. [Ni(PtBu2NtBu2)(MeCN)2]2+ also has a relatively low overpotential of 0.3–0.4 V while maintaining a similar rate to most of the catalysts. Other systems have η ≥ 0.8 V. Although mediators can be used to decrease the operating potential for 2-propanol oxidation by [Ir(PNP)(H)2] and [Ru(H)(CNN)(dppb)], the overpotentials remain high because strong bases are still used. Likewise, although the addition of [Cu(bpy)]2+ lowers Ecat/2 for TEMPO-catalyzed BnOH oxidation, the overpotential remains high because a relatively high potential is still needed to oxidize [Cu(bpy)]+.The well-defined overpotentials discussed above for catalysts that operate in organic solvents also provide a basis for clearer comparison with catalysts operating under aqueous conditions. Fig. 9B shows examples of catalysts from different classes that operate in aqueous solution. TEMPO and its analogues catalyze the oxidation of a variety of alcohols in water, although the reactions generally occur at high overpotential. For example, the overpotential for ABNO-catalyzed oxidation of 1-butanol to butanal is 0.9 V at pH 9.3 By modifying the pH and the identity of the nitroxyl, the overpotential can be lowered by 0.15 V, but at a cost to the rate.40 A variety of polypyridyl Ru complexes can also catalyze oxidation of alcohols, but generally require high overpotentials (η ≥ 1 V) because their mechanisms involve electrochemical generation of a Ru-oxo species at high potential.41–47 As a representative example, [Ru(Cl2bpy)2(H2O)2]2+ catalyzes the 2-electron oxidations of methanol, ethanol, 2-propanol, and benzyl alcohol at pH 1.1 with overpotentials of 1.3–1.4 V.41 Organometallic complexes immobilized on carbon supports have also been used for electrochemical alcohol oxidation under aqueous conditions.48–51 For example, [Rh(trop2NH)(PPh3)(OTf)] catalyzes oxidation of ethanol to acetate with overpotentials >0.7 V at pH 12 when deposited on carbon black.50,51
For comparison, Pt/Ru alloys are among the most active heterogeneous catalysts for oxidation of alcohols and have been widely studied in direct methanol fuel cells.52–55 Under the acidic conditions typical for proton-exchange membrane fuel cells, these alloys exhibit overpotentials as low as 0.3 V for conversion of MeOH to CO2.53 Unfortunately, these catalysts are poisoned by aldehydes and carboxylic acids, limiting their utility with alcohol substrates containing C–C bonds.54 At high pH, metal oxides such as NiOOH have been used to promote electrocatalytic alcohol oxidation, and exhibit good activity, stability, and selectivity for oxidation of primary alcohols to carboxylates. However, these reactions require potentials approaching those capable of supporting water oxidation, resulting in overpotentials for alcohol oxidation of up to 1.3 V.56–59
Conclusions
The methodology outlined herein provides an important foundation for future advances in the field of electrocatalytic alcohol oxidation by enabling comparisons of catalyst performance across different reaction conditions. Compared to previous studies in water, studies of reactivity and catalytic properties in organic solvents can be performed under a wider range of conditions. To date, overpotentials have not been reported for molecular electrocatalysts for the oxidation of alcohols in non-aqueous solvents because of the lack of established thermodynamic potentials, and this gap has hindered meaningful comparisons between catalysts studied under different conditions. The analysis above highlights the crucial role of both solvent and base strength on the thermodynamic potential of alcohol oxidation and shows how these two features combine with the electrochemical properties of the catalyst to establish the overpotential for electrocatalytic alcohol oxidation.To summarize briefly, the overpotential for alcohol oxidation with a catalyst corresponds to the difference between the thermodynamic potential for the reaction under the conditions used for catalysis and the potential at which catalysis occurs at a given rate. Estimation of thermodynamic potentials for the 2 e−, 4 e−, and 6 e− oxidation of alcohols in organic solvents requires three values:
(1) The equilibrium potential for the hydrogen evolution reaction (EBH+/H2(org)) in organic solvent with the acid-base pair used in the catalytic reaction.
(2) Values for the gas-phase free-energies of formation 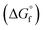 of the alcohol and oxidized product.
of the alcohol and oxidized product.
(3) An approximation for the difference in solvation free energies of the alcohol and oxidized product 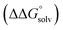 .
.
In solvents with an established pKa scale, EBH+/H2(org) can be determined from 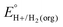 and pKa(HBase+). OCP measurements can also be used to directly determine this benchmark value when there is no established pKa scale for a solvent or
and pKa(HBase+). OCP measurements can also be used to directly determine this benchmark value when there is no established pKa scale for a solvent or 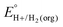 is not known. For the remaining two values,
is not known. For the remaining two values, 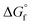 is known for the common species of interest, and
is known for the common species of interest, and 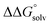 is expected to be small (ca. 1–2 kcal mol−1) based on known values for relevant species.60 The resulting uncertainty (≲50 mV) is often small relative to the operating overpotentials and
is expected to be small (ca. 1–2 kcal mol−1) based on known values for relevant species.60 The resulting uncertainty (≲50 mV) is often small relative to the operating overpotentials and 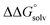 can therefore be reasonably omitted in most cases.
can therefore be reasonably omitted in most cases.
The approach provided here has enabled comparison of the overpotentials for the oxidation of alcohols by molecular electrocatalysts in organic solvents. From this analysis, [Ni(PtBu2NtBu2)(MeCN)2]2+ is noteworthy for its combination of good rate and comparatively low overpotential for catalysis. The lower overpotential is a result of a less positive potential for oxidation of the catalytically relevant species and the ability of the catalyst to operate with a modest base, resulting in a mild thermodynamic potential. As this field of research grows, the approach outlined here provides a basis for quantitative comparisons of catalyst performance, thereby facilitating the identification of catalyst properties that contribute to higher activities and lower overpotentials.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported as part of the Center for Molecular Electrocatalysis, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences.Notes and references
- A. M. Appel and M. L. Helm, ACS Catal., 2014, 4, 630–633 CrossRef CAS.
- B. M. Stratakes, J. L. Dempsey and A. J. M. Miller, ChemElectroChem, 2021, 8, 4161–4180 CrossRef CAS.
- M. Rafiee, K. C. Miles and S. S. Stahl, J. Am. Chem. Soc., 2015, 137, 14751–14757 CrossRef CAS PubMed.
- J. E. Nutting, J. B. Gerken, A. G. Stamoulis, D. L. Bruns and S. S. Stahl, J. Org. Chem., 2021, 86, 15875–15885 CrossRef CAS PubMed.
- J. A. Roberts and R. M. Bullock, Inorg. Chem., 2013, 52, 3823–3835 CrossRef CAS PubMed.
- R. G. Agarwal, S. C. Coste, B. D. Groff, A. M. Heuer, H. Noh, G. A. Parada, C. F. Wise, E. M. Nichols, J. J. Warren and J. M. Mayer, Chem. Rev., 2022, 122, 1–49 CrossRef CAS PubMed.
- G. Garrido, E. Koort, C. Rafols, E. Bosch, T. Rodima, I. Leito and M. Roses, J. Org. Chem., 2006, 71, 9062–9067 CrossRef CAS PubMed.
- S. Tshepelevitsh, A. Kütt, M. Lõkov, I. Kaljurand, J. Saame, A. Heering, P. G. Plieger, R. Vianello and I. Leito, Eur. J. Org. Chem., 2019, 6735–6748 CrossRef CAS.
- M. L. Pegis, J. A. Roberts, D. J. Wasylenko, E. A. Mader, A. M. Appel and J. M. Mayer, Inorg. Chem., 2015, 54, 11883–11888 CrossRef CAS PubMed.
- B. M. Lindley, A. M. Appel, K. Krogh-Jespersen, J. M. Mayer and A. J. M. Miller, ACS Energy Lett., 2016, 1, 698–704 CrossRef CAS.
- Y. Wang, S. Gonell, U. R. Mathiyazhagan, Y. Liu, D. Wang, A. J. M. Miller and T. J. Meyer, ACS Appl. Energy Mater., 2018, 2, 97–101 CrossRef.
- While this manuscript was in preparation, standard potentials in acetonitrile were reported (ref. 13) for a subset of the couples discussed in this manuscript. That work followed a similar approach to the one described here and the resulting values are within expected error of those reported here (see ESI† Section S8).
- I. Fokin, K.-T. Kuessner and I. Siewert, Synthesis, 2021, 295–314 Search PubMed.
- Two alternative thermochemical cycles are discussed in ESI† Section S4c.
- A. J. Bard, R. Parsons and J. Jordan, Standard Potentials in Aqueous Solution, Marcel Dekker, Inc., New York, 1985 Search PubMed.
- An alternative thermochemical scheme for calculation of E°HCO2H/MeOH can also be constructed based on the hydricity of formate in acetonitrile (see ESI† Section S6d). This scheme requires E°CO2/MeOH in acetonitrile, but avoids the requirement for the solvation free energy of formic acid in acetonitrile. The E°HCO2H/MeOH calculated from this cycle is identical to the value calculated from ΔG°+2H2.
- A. W. Cook and K. M. Waldie, ACS Appl. Energy Mater., 2019, 3, 38–46 CrossRef.
- N. Wolff, O. Rivada-Wheelaghan and D. Tocqueville, ChemElectroChem, 2021, 8, 4019–4027 CrossRef.
- M. Bellini, M. Bevilacqua, A. Marchionni, H. A. Miller, J. Filippi, H. Grützmacher and F. Vizza, Eur. J. Inorg. Chem., 2018, 4393–4412 CrossRef CAS.
- C. J. Weiss, E. S. Wiedner, J. A. Roberts and A. M. Appel, Chem. Commun., 2015, 51, 6172–6174 RSC.
- T. Gunasekara, Y. Tong, A. L. Speelman, J. D. Erickson, A. M. Appel, M. B. Hall and E. S. Wiedner, ACS Catal., 2022, 12, 2729–2740 CrossRef CAS.
- S. P. Heins, P. E. Schneider, A. L. Speelman, S. Hammes-Schiffer and A. M. Appel, ACS Catal., 2021, 11, 6384–6389 CrossRef CAS.
- E. A. McLoughlin, B. D. Matson, R. Sarangi and R. M. Waymouth, Inorg. Chem., 2020, 59, 1453–1460 CrossRef CAS PubMed.
- C. M. Galvin and R. M. Waymouth, J. Am. Chem. Soc., 2020, 142, 19368–19378 CrossRef CAS PubMed.
- K. M. Waldie, K. R. Flajslik, E. McLoughlin, C. E. Chidsey and R. M. Waymouth, J. Am. Chem. Soc., 2017, 139, 738–748 CrossRef CAS PubMed.
- E. A. McLoughlin, K. C. Armstrong and R. M. Waymouth, ACS Catal., 2020, 10, 11654–11662 CrossRef CAS.
- A. Badalyan and S. S. Stahl, Nature, 2016, 535, 406–410 CrossRef CAS PubMed.
- E. J. Nurminen, J. K. Mattinen and H. Lönnberg, J. Chem. Soc., Perkin Trans. 2, 2001, 2159–2165 RSC.
- S. Horvath, L. E. Fernandez, A. V. Soudackov and S. Hammes-Schiffer, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 15663–15668 CrossRef CAS PubMed.
- L. E. Fernandez, S. Horvath and S. Hammes-Schiffer, J. Phys. Chem. C, 2012, 116, 3171–3180 CrossRef CAS.
- C. J. Curtis, A. Miedaner, R. Ciancanelli, W. W. Ellis, B. C. Noll, M. Rakowski DuBois and D. L. DuBois, Inorg. Chem., 2003, 42, 216–227 CrossRef CAS PubMed.
- W. Baratta, G. Chelucci, S. Gladiali, K. Siega, M. Toniutti, M. Zanette, E. Zangrando and P. Rigo, Angew. Chem., Int. Ed., 2005, 44, 6214–6219 CrossRef CAS PubMed.
- P. J. Bonitatibus, Jr., S. Chakraborty, M. D. Doherty, O. Siclovan, W. D. Jones and G. L. Soloveichik, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 1687–1692 CrossRef PubMed.
- S. Chakraborty, P. O. Lagaditis, M. Förster, E. A. Bielinski, N. Hazari, M. C. Holthausen, W. D. Jones and S. Schneider, ACS Catal., 2014, 4, 3994–4003 CrossRef CAS.
- Z. E. Clarke, P. T. Maragh, T. P. Dasgupta, D. G. Gusev, A. J. Lough and K. Abdur-Rashid, Organometallics, 2006, 25, 4113–4117 CrossRef CAS.
- F. Wang and S. S. Stahl, Acc. Chem. Res., 2020, 53, 561–574 CrossRef CAS PubMed.
- J. E. Nutting, M. Rafiee and S. S. Stahl, Chem. Rev., 2018, 118, 4834–4885 CrossRef CAS PubMed.
- B. J. Taitt, M. T. Bender and K.-S. Choi, ACS Catal., 2020, 10, 265–275 CrossRef CAS.
- B. L. Ryland and S. S. Stahl, Angew. Chem., Int. Ed., 2014, 53, 8824–8838 CrossRef CAS PubMed.
- D. P. Hickey, D. A. Schiedler, I. Matanovic, P. V. Doan, P. Atanassov, S. D. Minteer and M. S. Sigman, J. Am. Chem. Soc., 2015, 137, 16179–16186 CrossRef CAS PubMed.
- C.-M. Che and W.-O. Lee, J. Chem. Soc., Chem. Commun., 1988, 881–882 RSC.
- H. Ozawa, T. Hino, H. Ohtsu, T. Wada and K. Tanaka, Inorg. Chim. Acta, 2011, 366, 298–302 CrossRef CAS.
- C. Sens, M. Rodriguez, I. Romero, A. Llobet, T. Parella and J. Benet-Buchholz, Inorg. Chem., 2003, 42, 8385–8394 CrossRef CAS PubMed.
- X. Sala, A. Poater, I. Romero, M. Rodríguez, A. Llobet, X. Solans, T. Parella and T. M. Santos, Eur. J. Inorg. Chem., 2004, 612–618 CrossRef CAS.
- M. Rodriguez, I. Romero, A. Llobet, A. Deronzier, M. Biner, T. Parella and H. Stoeckli-Evans, Inorg. Chem., 2001, 40, 4150–4156 CrossRef CAS PubMed.
- N. Chanda, B. Mondal, V. G. Puranik and G. K. Lahiri, Polyhedron, 2002, 21, 2033–2043 CrossRef CAS.
- V. J. Catalano, R. A. Heck, C. E. Immoos, A. Ohman and M. G. Hill, Inorg. Chem., 1998, 37, 2150–2157 CrossRef CAS PubMed.
- K. R. Brownell, C. C. McCrory, C. E. Chidsey, R. H. Perry, R. N. Zare and R. M. Waymouth, J. Am. Chem. Soc., 2013, 135, 14299–14305 CrossRef CAS PubMed.
- S. Yamazaki, M. Yao, N. Fujiwara, Z. Siroma, K. Yasuda and T. Ioroi, Chem. Commun., 2012, 48, 4353–4355 RSC.
- S. P. Annen, V. Bambagioni, M. Bevilacqua, J. Filippi, A. Marchionni, W. Oberhauser, H. Schonberg, F. Vizza, C. Bianchini and H. Grutzmacher, Angew. Chem., Int. Ed., 2010, 49, 7229–7233 CrossRef CAS PubMed.
- M. Bevilacqua, C. Bianchini, A. Marchionni, J. Filippi, A. Lavacchi, H. Miller, W. Oberhauser, F. Vizza, G. Granozzi, L. Artiglia, S. P. Annen, F. Krumeich and H. Grützmacher, Energy Environ. Sci., 2012, 5, 8608–8620 RSC.
- S. Najafishirtari, K. Friedel Ortega, M. Douthwaite, S. Pattisson, G. J. Hutchings, C. J. Bondue, K. Tschulik, D. Waffel, B. Peng, M. Deitermann, G. W. Busser, M. Muhler and M. Behrens, Chem. – Eur. J., 2021, 27, 16809–16833 CrossRef CAS PubMed.
- H. Lei, P. Atanassova, Y. Sun and B. Blizanac, State-of-the-Art Electrocatalysts for Direct Methanol Fuel Cells, in Electrocatalysis of Direct Methanol Fuel Cells, ed. H. Liu and J. Zhang, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2009, ch. 5, pp. 197–226 Search PubMed.
- S. L. Blair and W. L. Law, Electrocatalysis in Other Direct Liquid Fuel Cells, in Electrocatalysis of Direct Methanol Fuel Cells, ed. H. Liu and J. Zhang, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2009, pp. 527–566 Search PubMed.
- N. Kakati, J. Maiti, S. H. Lee, S. H. Jee, B. Viswanathan and Y. S. Yoon, Chem. Rev., 2014, 114, 12397–12429 CrossRef CAS PubMed.
- H. Huang, C. Yu, X. Han, H. Huang, Q. Wei, W. Guo, Z. Wang and J. Qiu, Energy Environ. Sci., 2020, 13, 4990–4999 RSC.
- M. T. Bender, Y. C. Lam, S. Hammes-Schiffer and K. S. Choi, J. Am. Chem. Soc., 2020, 142, 21538–21547 CrossRef CAS PubMed.
- W.-J. Liu, L. Dang, Z. Xu, H.-Q. Yu, S. Jin and G. W. Huber, ACS Catal., 2018, 8, 5533–5541 CrossRef CAS.
- M. T. Bender, X. Yuan and K. S. Choi, Nat. Commun., 2020, 11, 4594 CrossRef CAS PubMed.
- In other work (ref. 10), solvation free energies have been estimated computationally. This approach required benchmarking, and still resulted in uncertainty on the order of 1–2 kcal mol−1. For alcohol oxidation, computationally estimated values are therefore unlikely to provide a substantial improvement in accuracy compared to neglecting solvation free energies.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ee01458k |
| This journal is © The Royal Society of Chemistry 2022 |