Open Access Article
Open Access ArticleReactivation of chromia poisoned oxygen exchange kinetics in mixed conducting solid oxide fuel cell electrodes by serial infiltration of lithia†
Han Gil
Seo‡
 a,
Anna
Staerz‡
a,
Anna
Staerz‡
 a,
Dennis S.
Kim
a,
Dennis S.
Kim
 a,
Dino
Klotz
a,
Dino
Klotz
 ab,
Clement
Nicollet
ab,
Clement
Nicollet
 c,
Michael
Xu
a,
James M.
LeBeau
a and
Harry L.
Tuller
c,
Michael
Xu
a,
James M.
LeBeau
a and
Harry L.
Tuller
 *a
*a
aDepartment of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: tuller@mit.edu
bInternational Institute for Carbon-Neutral Energy Research (I2CNER), Kyushu University, Fukuoka, 819-0385, Japan
cUniversité de Nantes, CNRS, Institut des Matériaux Jean Rouxel, IMN, F-44000 Nantes, France
First published on 11th August 2022
Abstract
Solid oxide fuel cells have the potential to render the conversion from fuel to electrical energy more efficienct while lowering emissions. The technology, however, suffers from performance degradation due to cathode poisoning by chromia from metal interconnects. We confirm the deleterious impact of chromia on the performance of the model mixed conducting cathode material Pr0.1Ce0.9O2−δ by examining the oxygen exchange coefficient (kchem) via electrical conductivity relaxation measurements, and the area-specific resistance (ASR) by electrochemical impedance spectroscopy. Liquid Cr-infiltration decreases kchem 20-fold and the oxygen exchange component of ASR increases 20-fold while maintaining the same activation energy. We then demonstrate the ability to not only recover initial kchem and ASR values, but improve properties above those exhibited by the pristine specimen through subsequent Li-infiltration, leading to enhancement of kchem by more than three orders of magnitude and reduction in oxygen exchange component of the ASR by over a factor 100. We attribute these dramatic changes to the depletion of electrons induced by the acidic Cr-infiltrant on the Pr0.1Ce0.9O2−δ surface and the recovery to accumulation of electrons from the basic Li-infiltrant. These results point to acidity as a key descriptor in addressing the long-standing challenge of reactive surface poisoning in applications reliant on rapid oxygen exchange and recovery behavior. The ability to achieve remarkable levels of recovery of electrocatalytic surfaces by controlling the relative acidity of surface species is demonstrated for the first time.
Broader contextMetal oxides are an important class of functional materials for a wide array of applications, ranging from energy storage and conversion and catalysis to sensors. In many of these cases, the reaction of oxygen with the metal oxide surface plays a central role. A great deal of effort is invested in optimizing the metal oxide's initial performance. Nevertheless, the commercial viability of such devices is often markedly depressed as a result of unacceptable performance degradation rates with operating time, e.g. due to chromia poisoning of mixed ionic electronic conducting (MIEC) solid oxide fuel cell cathodes or silica poisoning of gas sensors. In the literature most studies addressing long term stability aim to render the surface more robust against poisons, while others propose methods to limit poison exposure. In this study, we demonstrate not only the ability to recover the initial performance of a chromia-poisoned cathode material by subsequent infiltration with a Li-source binary oxide with high basicity, but enhance its performance (faster oxygen exchange kinetics and lower area specific resistance) above that of the pristine specimen. This study serves as a proof of concept, that through systematic control of the relative acidity of the surface, it is possible to regenerate poisoned metal oxide surfaces. |
Introduction
The chemical degradation of surfaces due to both internal and external poisoning sources limits the long-term performance of metal oxides in a variety of application fields ranging from energy storage and conversion to sensors.1–8 Degradation in performance is often associated with decreased oxygen surface exchange kinetics. Many studies have focused on optimizing the initial surface exchange kinetics, e.g. in solid oxide fuel and electrolysis cells (SOFCs/SOECs), permeation membranes and solar thermochemical reactors.9–17 While the initial reactivity is important, maintaining performance over time is critical and often less examined. Today acceptable performance and degradation values (0.2–0.5% per 1000 h) are attained with single cells, but reliability and endurance must be increased in stacks where degradation rates are 2–4 times higher, due to e.g. Cr-poisons.18 The US Department of Energy has set the ambitious goal of reaching a stack voltage degradation rate target of 0.2%/1000 hours by 2035–2050.18 Assuming degradation targets can be met, a global SOFC market size of $5.3 billion by 2028 is projected.19 Identifying means for recovering the degraded performance of poisoned metal oxide electrodes would thus have great value in rendering this technology commercially viable.As an example, in SOFCs and SOECs, mixed ionic electronic conducting (MIEC) perovskite oxides, such as (La,Sr)(Co,Fe)O3 (LSCF), provide high oxygen surface exchange rates, making them efficient air electrodes.20–25 While their initial performance is very promising, they remain susceptible to surface poisoning upon prolonged cell operation. Extensive non-active cation segregation, primarily Sr, to the electrode surface is well-documented as leading to blocking of the active surface with a charge transfer barrier (e.g. SrO layer) resulting in reduced reaction rates e.g. for the oxygen reduction reaction (ORR) in SOFCs.26–29 Furthermore, segregated SrO has been found to be a preferred nucleation site for chromium species, resulting in the formation of SrCrO4.30 Chromium is well known to be the most pervasive extrinsic surface poison for SOFCs and is inherent to the operation of fuel cell stacks.31–35 Ferritic steels with a chromium content between 18 and 25% are well suited interconnect materials, given their need to be simultaneously electronically conducting, oxidation resistant, impermeable to gas diffusion, stable and compatible with the other fuel cell materials, as well as being inexpensive.36 Unfortunately, Cr inevitably finds its way from the interconnect to the cathode during operation via vapor phase or surface diffusion. The vapor pressures of the various volatile chromium oxide sources including CrO3(g), CrO2(g), and CrO(g) over Cr2O3(s) increase with increasing oxygen partial pressure characteristic of the cathode environment. Additionally, the rate of degradation is increased in humidity attributed to CrO2(OH)2(g).37,38 While barrier coatings (e.g. (Mn,Cr)3O4 spinel) have been applied to the Cr containing metal interconnects with the objective of reducing Cr volatility, they have not succeeded in completely mitigating long-term Cr induced cathode electrochemical degradation.37
In addition to limiting exposure to impurity sources, strategies to make air electrodes more robust through, e.g. the addition of getters,1,39–43 and other surface modifications40,44–46 have been investigated. Two notable examples are the work of Zhao et al. in which the addition of a thin La2O3 layer was found to recover, to a significant extent, the degradation in the oxygen exchange rate resulting from silica,43 and Niu et al. who found enhanced tolerance of LSCF against Cr poisoning through infiltration with a multiphase additive.42 In the latter case, the authors attribute the increased tolerance specifically to the BaCO3 phase of the additive. In both cases the rationale for selecting the additive is based on empirical findings, i.e. the gettering ability of La2O3 or previous success with a multiphase additive. However, no comprehensive model was found in the literature that allows one to predict, a priori, the efficacy of additives in compensating degradation.
In our recent work, we showed that the Smith acidity scale for binary oxides can be used as a powerful descriptor for predicating their effect on the oxygen exchange coefficient (kchem) of MIEC oxides.47 As a result, infiltration with binary oxides, ranging from strongly basic (Li2O) to strongly acidic (SiO2), onto the surface of Pr0.1Ce0.9O2−δ (PCO), a chemically stable fluorite, free of inherent poison sources (e.g. segregated Sr), systematically varied kchem by over 6 orders of magnitude. Li2O increased kchem by nearly 1,000 times over that of pristine PCO, while SiO2 depressed kchem by nearly the same factor.47 Interestingly, both Cr2O3 and SiO2 were determined to be acidic by Smith,48 suggesting that this feature could likely be the primary reason that these compounds serve to poison the ORR on SOFC cathodes.47 With this insight, we hypothesized that not only could the Smith acidity be used to determine the influence of a single additive, but that the surface exchange kinetics could be tuned by adding multiple infiltrants and thereby controlling the relative surface acidity. In this study, we systematically examine the effect of serial infiltration of acidic and basic oxides on the exchange coefficient using electrical conductivity relaxation experiments on porous PCO bulk specimens. Indeed, we found that serial infiltration with Li2O compensates the initial degradation caused by acidic Cr2O3, resulting in even better performance than pristine PCO. We further verified the relevance of these findings by examining changes in area-specific resistance (ASR) associated with the oxygen exchange reaction in a symmetric cell and gained insight into the surface additive chemistry using microscopy. In addition to the importance of predicting and optimizing SOFC cathode performance and durability, this same concept can be applied to other applications in which extrinsic surface poisoning limits long-term operation, e.g. electrolyzers, oxygen permeation membranes and gas sensors.1–8
Results and discussion
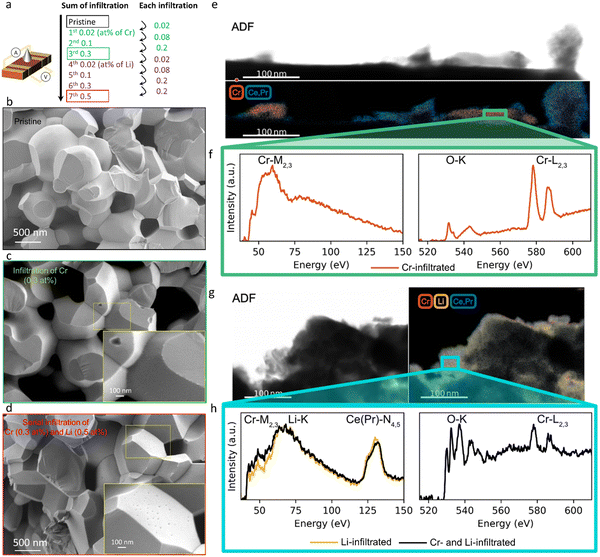
Here we study how the addition of a basic infiltrate affects surface oxygen exchange kinetics degraded by Cr poisoning. The electrical conductivity of mixed conducting oxides varies with oxygen stoichiometry i.e. with variation in the surrounding oxygen partial pressure. By monitoring the electrical conductivity transient after a rapid step change in oxygen partial pressure, the kinetics associated with the uptake or release of oxygen by the oxide can be determined.49 There are a number of factors to consider in insuring the correct interpretation of electrical conductivity relaxation measurements in porous specimens. One must ensure that neither gas phase diffusion inside the pores nor bulk oxygen diffusion within the solid materially impact the kinetics, but rather that only the surface oxygen exchange kinetics are limiting.50,51 In our preceding study,47 we verified that the overall kinetics of the prepared porous PCO specimen are not limited by gas phase diffusion inside the pores under the measurement conditions (see Supplementary Note 1-1, Table S1 and Fig. S1, S2 in the ESI†). While the oxygen equilibration kinetics in general depend on both bulk oxygen diffusivity and the surface exchange reaction, by selecting a microstructure characterized by a physical oxygen diffusion length (∼1 μm based on grain size) much shorter than the critical thickness of PCO (3.6 × 103 μm at 670 °C,52 above which bulk oxygen diffusion becomes dominant), readily ensures that the reduction/oxidation kinetics are solely determined by surface oxygen exchange, consistent with the report by M.W. Den Otter et al.50 (see Supplementary Note 1-2 in the ESI†). Thus, a porous specimen of PCO with a grain size of approximately 1 μm, and a geometrically determined porosity of 26%, was selected to ensure surface limited oxygen exchange kinetics. An additional benefit of this measurement is that the surface can be easily infiltrated with ethanol-based solutions of Cr(NO3)3 and LiNO3. The nitrates fully decompose following in situ calcination in synthetic air at 600 °C. The PCO specimen is measured once, prior to infiltration, to provide a reference data set of kchem. Then, the specimen is infiltrated with chromium, starting with low loading (0.02 at% with respect to PCO) and re-measured. In order to determine the dependence of the degradation level on Cr-concentration, the infiltration was repeated three times to increase Cr loading incrementally (up to 0.3 at%). The sample was re-measured by conductivity relaxation following each subsequent infiltration. In an attempt to reactivate the exchange rate of oxygen, the same porous PCO specimen was then infiltrated a total of four additional times (up to 0.5 at%) with Li-species and re-measured after each infiltration step. A schematic illustrating the sequence of infiltrations of Cr- and Li-based nitrate solutions into the porous PCO specimen is shown in Fig. 1a, with the infiltration notation used hereafter described as the sum of the infiltration amount. In the low resolution scanning electron microscopy (SEM) images, no significant microstructural change of the PCO specimen was observed following all seven infiltration steps; compare Fig. 1b–d. In order to gain more detailed chemical information about surface chemistry and to examine the structure of the additives, scanning transmission electron microscopy with electron energy loss spectroscopy (STEM-EELS) was used. The energy loss near-edge fine structure (ELNES) is based on the number of unoccupied states and highly dependent on the local chemical environment that creates a unique “fingerprint” for each element and phase that is used to determine the spatial distribution of atomic species.53Fig. 1e (Fig. S3a, ESI†) presents an image of the 0.3 at% Cr-infiltrated PCO surface. The top panel shows the annular dark field (ADF) image and bottom the elemental mapping of Cr-rich regions in red and PCO regions in blue. The spectra for the Cr-M2,3 and O-K and Cr-L2,3 edges are shown in Fig. 1f. Based on the EELS white-line ratios between Cr-L2 and Cr-L3 the Cr-rich regions are crystalline Cr2O3 (alpha).54 This indicates, in line with the SEM image (see Fig. 1c), that the infiltration forms tens of nm scale Cr2O3 crystallites on the surface of PCO. In the case of perovskite electrodes, in addition to the formation of Cr2O3 crystallites, authors often report the formation of chromates with intrinsic poisons, e.g. segregated Sr on the surface. For more information see the comprehensive review by Jiang et al.3 Given that PCO is free of intrinsic poison sources, such products are not expected here.In the images of the 0.3 at% Li-infiltrated PCO surface, no crystalline Li2O phase is visible. Instead, the Li-species are finely dispersed on the PCO surface. These spectra taken of the pure Cr- and Li-infiltrated PCO specimens will be used as a reference for the serial Cr- and Li-infiltrated samples. Fig. 1g shows the ADF image (top) and elemental mapping of Li-K, Cr-M2,3, and Ce(Pr)-N4,5 edges in yellow, red and blue, respectively (bottom). Similar to the pure Li-infiltrated sample, we find the infiltrated species are uniformly distributed on PCO in the serial infiltrated samples (Fig. 1g and Fig. S3b, ESI†). Although the presence of Cr can be confirmed by the Cr-L2,3 edge intensities in the right panel of Fig. 1h, there are no regions with only Cr-species (Fig. S3c, ESI†). Instead, the Cr signal is accompanied by those for Li, Ce and Pr, and therefore greatly reduced in intensity. This finding, and the changes in the white-line ratio in the serial infiltrated PCO compared to the Cr-infiltrated PCO (Fig. 1f and h) from the EELS spectra, suggest that crystalline Cr2O3 reacts with the Li-species forming mixed amorphous phases composed of Cr, Li, Ce, Pr and O. Based on the STEM observations, the Li-species chemically react with the surface oxide and dissolve both Cr2O3 and PCO into an amorphous mixed oxide. This process is likely driven by the strong reactivity of Li with ceria, consistent with the reported use of Li2O as a sintering aid in the densification of ceria.55,56
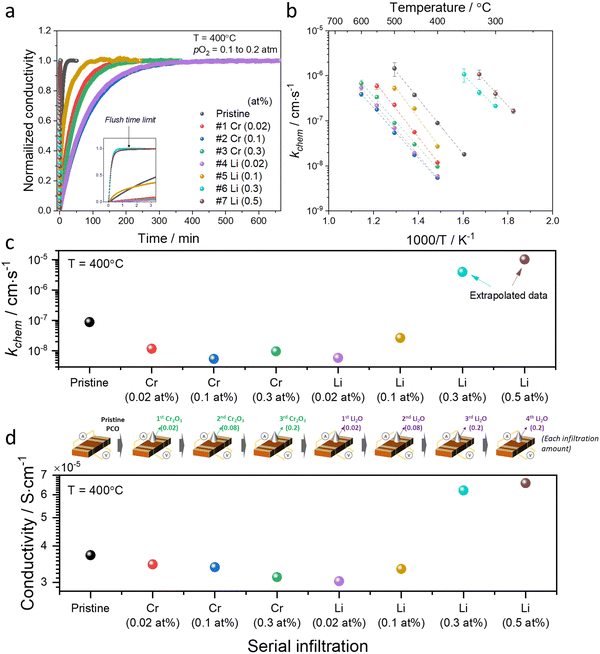
Conductivity relaxation experiments were used to extract the oxygen chemical surface exchange coefficients kchem of both the pristine PCO specimen and those serially infiltrated with Cr- and Li-species. Fig. 2a presents the normalized transient conductivity response to a step change in oxygen partial pressure from 0.1 atm to 0.2 atm of the pristine, Cr- and subsequently Li-infiltrated PCO specimen measured at 400 °C. The oxygen exchange coefficient, kchem, was calculated by fitting the conductivity transients with the following equation:
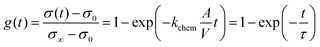 | (1) |
 | ||
| Fig. 2 (a) Normalized conductivity relaxation profile in response to pO2 step (0.1 to 0.2 atm) beginning with a pristine PCO specimen and following successive Cr- and Li-infiltration, measured at 400 °C. (b) Arrhenius plot of log surface oxygen exchange coefficient (kchem) vs. reciprocal temperature. Error bars in (b) were derived from fitting transient profiles with and without the flush time correction, see Supplementary Note 1-1 (ESI†). Comparison of (c) kchem and (d) conductivity values obtained at 400 °C of pristine PCO followed by subsequent Cr- and Li-infiltrations, respectively. Inset of illustration between (c) and (d) shows the concentrations associated with the serial infiltrations of Cr (from 0.02 to 0.3 at%) and then Li (0.02 to 0.5 at%). The cartoon between (c) and (d) indicates each infiltration amount. | ||
An Arrhenius plot of the kchem values extracted by fitting the normalized conductivity transient profiles at a series of temperatures is presented in Fig. 2b. The initial 0.02 at% Cr-infiltration already substantially impedes the rate of response to the step change in pO2. Additional Cr-infiltration further degrades the exchange kinetics. Above 0.1 at%, the sample appears saturated, as further loading with 0.3 at% does not lead to further decreases in kchem (Fig. 2b and c). Subsequent low concentration Li-infiltration (0.02 at%) leads to little change in kchem values. At higher concentrations, however, significant recovery in exchange rate was observed. For Li-infiltration at levels of 0.3 and 0.5 at%, the relaxation becomes too rapid, in the same temperature regime (400–600 °C), to enable the evaluation of kchem values from the transient response, given that the time constants drop below the flush time limit of the reactor. They could, however, be determined by repeating the transient studies at lower temperatures, and then extrapolating to 400 °C for comparison. This explains why different temperature windows for the various samples, presented in Fig. 2b, were employed.
The exchange kinetics exhibit an extremely strong dependence on the serial Cr- and Li-infiltration sequence, with kchem values varying by more than three orders of magnitude between Cr-species (0.1 at%) and Li-species (0.5 at%). Cr-infiltration at the 0.1 at% level resulted in a roughly 20-fold decrease in kchem as compared to pristine PCO, while serial Li-infiltration of 0.5 at% led to a boost in kchem by >1000 fold, more than fully recovering the initial value of the pristine PCO specimen, as shown in Fig. 2b and c. Although measurements were repeated seven times following serial Cr- and Li-infiltrations, the activation energy (Ea) of kchem showed little dependence on infiltration, in contrast to the very dramatic changes in magnitude observed for kchem (Fig. 2c and Fig. S6, ESI†), consistent with similar observations in our earlier study that was limited to infiltration of individual binary oxides with controlled acidity into PCO.47 The relatively larger error bars in the activation energy may be connected to the increasing co-existence of mixed Cr-rich and Li-rich regions, with some varying distributions in these mixed regions. Notwithstanding these observations, there is no obvious trend in activation energy with infiltration of either Cr- or Li-species.
In concert with our earlier findings,47 we also found that the overall electrical conductivity (σ) of the PCO specimens was impacted by infiltration with the steady state conductivity decreasing upon acidic Cr-infiltration, while increasing under subsequent basic Li-infiltration. Fig. 2d shows that acidic 0.3 at% Cr-infiltration decreased the conductivity values of PCO by 19% at 400 °C, while a 117% improvement of the poisoned specimen's conductivity was observed following serial Li-infiltration at 0.5 at%. Note the correlation between the trend in kchem with that of conductivity (Fig. 2c and d). Although the conductivity changes show a similar tendency, percent changes in conductivity are much lower than those for kchem. This is not surprising given that any accumulation or depletion of electrons induced by additives should only affect the near-surface conductivity of PCO, and not the bulk as a whole. Thus, the smaller changes in overall conductivity are expected and are in line with the previously reported results.47 The dramatic changes of several orders of magnitude in kchem that are directly controlled by the surface can also be interpreted. Acidic Cr-species result in surface electron depletion, while basic Li-species lead to surface electron accumulation, in turn decreasing or increasing the conductivity of PCO upon serial infiltration. Previously, we attributed the reduction/enhancement of kchem to the depletion/accumulation of surface electrons that facilitate oxygen exchange47,57 With this insight, it is now possible to argue that the ability of additives to mitigate the poisoning behavior of acidic oxides can be predicted using the Smith acidity descriptor.
All specimens exhibited similar Ea values for the electrical conductivity (taken from the in-plane resistance measurements) of approximately 1.1–1.2 eV for temperatures between 500 °C and 350 °C (Fig. S7, ESI†) except for those with high levels of Li-infiltration that show a lower value of approximately 0.9 eV. In this temperature and pO2 range, the electronic conductivity σe is given by:58–60
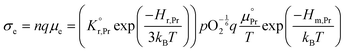 | (2) |
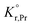 the prefactor of the PCO reduction reaction, Hr,Pr the reduction enthalpy, pO2 the oxygen partial pressure, kB & T taking on their normal meanings. The obtained activation energy values match well with the sum of the electron small polaron hopping energy (Hr,Pr = 0.56 eV) and one third of the reduction enthalpy
the prefactor of the PCO reduction reaction, Hr,Pr the reduction enthalpy, pO2 the oxygen partial pressure, kB & T taking on their normal meanings. The obtained activation energy values match well with the sum of the electron small polaron hopping energy (Hr,Pr = 0.56 eV) and one third of the reduction enthalpy 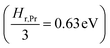 that together equal 1.19 eV.58 The dominant conduction pathway is via small polaron hopping in the Pr 4f band. Acidic Cr-species deplete the electrons from this Pr 4f band, decreasing the conductivity without affecting the activation energy. Interestingly, for high Li-loadings, not only does the conductivity increase, but the activation energy is approximately 0.2 eV lower than in pristine PCO. In their theoretical work on PCO, Elm et al. conclude that following full reduction of Pr(IV) to Pr(III), the next state to become occupied is the higher lying Ce(4f)-state.61 Following electron transfer from Li containing species to the PCO surface, and subsequent electron accumulation, the near surface Pr 4f levels are expected to become fully occupied, leading to occupation of the higher lying Ce 4f levels. Given the lower reported activation energy associated with small polaron hopping via the Ce 4f band of 0.39 eV,59 this would explain the reduction in overall activation of conduction by ∼0.17 eV. On the other hand, the reduction enthalpy of PCO is a bulk characteristic and therefore should not be expected to vary with surface infiltration.
that together equal 1.19 eV.58 The dominant conduction pathway is via small polaron hopping in the Pr 4f band. Acidic Cr-species deplete the electrons from this Pr 4f band, decreasing the conductivity without affecting the activation energy. Interestingly, for high Li-loadings, not only does the conductivity increase, but the activation energy is approximately 0.2 eV lower than in pristine PCO. In their theoretical work on PCO, Elm et al. conclude that following full reduction of Pr(IV) to Pr(III), the next state to become occupied is the higher lying Ce(4f)-state.61 Following electron transfer from Li containing species to the PCO surface, and subsequent electron accumulation, the near surface Pr 4f levels are expected to become fully occupied, leading to occupation of the higher lying Ce 4f levels. Given the lower reported activation energy associated with small polaron hopping via the Ce 4f band of 0.39 eV,59 this would explain the reduction in overall activation of conduction by ∼0.17 eV. On the other hand, the reduction enthalpy of PCO is a bulk characteristic and therefore should not be expected to vary with surface infiltration.
Our conductivity relaxation measurements in this, and in our previous study,47 show a clear inverse correlation between the relative acidity of the infiltrated oxides and the oxygen exchange reaction rate, kchem. In an electrochemical cell, the polarization resistance of the cathode (i.e. area-specific resistance, ASR) reflects contributions from a number of sources including the oxygen exchange kinetics, gas diffusion limitations, contact resistance, effective in-plane conductivity, and ion transfer processes across the electrolyte–cathode interfaces.62–66 The fraction of the ASR responsible for the oxygen exchange kinetic limitations, which we define by RS, should follow the inverse relationship to kel given by:
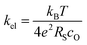 | (3) |
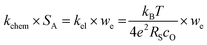 | (4) |
To test if this relationship between kchem and RS holds true here as well, the ASR of pristine and infiltrated PCO electrodes were examined using electrochemical impedance spectroscopy (EIS). Symmetrical cells with two nominally identical PCO electrodes, screen printed onto both sides of an YSZ single-crystal substrate were used (Fig. 3a). Similar to the procedure followed in the conductivity relaxation measurements, a reference PCO symmetric cell was first characterized by impedance spectroscopy, and then again after successive infiltration with Cr (0.15 at%) and subsequently Li (0.4 at%). To ensure the ability to reactivate a Cr-poisoned cell even after exposure to high Cr concentrations, 0.15 at% Cr-species (over four times the concentrations found by Menzler et al. after 3000 hours of stack operation68) were added to each side of a symmetric cell. Impedance spectra were fitted with three serial R–Q circuit elements (inset in Fig. 3b). The total ASR (sum of R2, R3 and R4) obtained from Nyquist plots at 575 °C (Fig. 3b) increased nearly nine-fold as a result of the Cr-infiltration. Reactivation of a cell initially infiltrated with Cr-species by subsequent Li-infiltration (0.4 at%) resulted in more than a 22-fold decrease in total ASR below its initial value. The Nyquist plots of the impedance spectra, however, are distorted as a result of several overlapping processes in the frequency regime of interest. In order to better differentiate the different sources of losses in the cell, the distribution of relaxation times (DRT) approach was utilized in which the characteristic peaks can be more readily distinguished as observed in Fig. 3c.69–71 Using the DRT method shows that the infiltration significantly affects the lower frequency peak (P1), which correlates to R4. R2 and R3 show little dependence on infiltration (Fig. S8, ESI†) and are likely associated with ion transfer processes across the electrolyte–cathode interface.64,65 These losses will therefore not be examined in further detail. Only R4 exhibits a strong dependence on infiltration, changing by orders of magnitude. In this frequency region, the losses are commonly attributed to surface oxygen exchange processes including oxygen adsorption and dissociation, as well as mass transfer processes i.e., gas diffusion within the cathode pores.65,66 The resistance of P1 obtained from DRT, determined via peak fitting, is however thermally activated (thus not controlled by gas diffusion). One can correlate R4 and the resistance associated with P1, given that both exhibit similar magnitudes and activation energies (here only the detailed evaluation of R4 is included (for analog evaluation of P1 see Fig. S9, ESI†). R4 values were converted to kchem × SA with the aid of eqn (4). As SA is not trivial to determine, but should remain largely constant between the samples, it is considered an arbitrary constant that does not influence Ea. In Fig. 3d, we observe that the activation energies of 1.0–1.2 eV, match well with those obtained for kchem, further indicating that R4 reflects losses directly associated with the oxygen exchange processes. Based on the thermal activation and relatively high pO2 power law dependence (ca. 0.34) (Fig. 3e), which is consistent with the previously reported values (ranging from −0.3 to −0.7), we attribute R4 to oxygen exchange processes (Rs) on the PCO surface.47,52,67,72–74 For the pristine cell, and after the serial Li-infiltration, it was difficult to clearly discern the surface oxygen exchange resistance (Rs) at high temperatures and high pO2. In these cases, the oxygen dependence, was therefore determined at 475 °C. The surface exchange resistance increases by a factor of almost 20 upon Cr-infiltration and shifts to lower frequencies. Interestingly, after the serial Li-infiltration, Rs significantly decreases by over two orders of magnitude (see Fig. 3d and Fig. S9 in the ESI†).
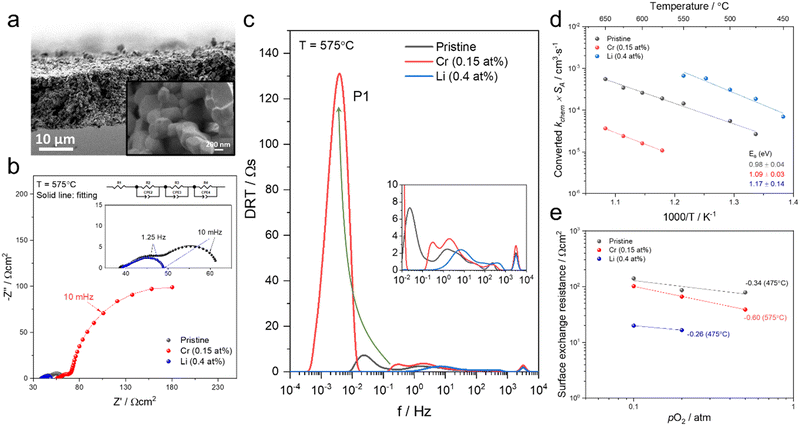 | ||
| Fig. 3 (a) SEM image of screen printed PCO electrode/electrolyte interface in prepared PCO/YSZ/PCO symmetric cell at two levels of magnification. (b) Nyquist plots and (c) distribution of relaxation time (DRT) plots of the pristine, Cr-infiltrated, and Cr- and Li-infiltrated symmetric cells obtained at 575 °C with pO2 = 0.1 atm. Three serial R–Q circuit elements were used. (d) Temperature dependence of converted kchem × SA by using eqn (4) based on extraction of the surface exchange resistance and (e) pO2 dependence of the surface exchange resistance obtained from fitting the Nyquist plot. | ||
The corresponding capacitance (C4) was calculated by fitting results from the Nyquist plot. The resulting high C4 values of the cells at 575 °C (for Li-infiltration at 475 °C) fall in the range of 200 and 600 F cm−3 and exhibit −1/6 slope dependence of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C4 on log pO2 (Fig. S10, ESI†), which are in line with those previously reported for the chemical capacitance of PCO thin films,75 further confirming that C4 corresponds to surface oxygen exchange processes that dominate Rs (see eqn (3)). Given that the chemical capacitance is associated with the volumetric characteristic of the electrode, we do not expect it to change dramatically with infiltration, while the surface exchange resistance does. The rate-determining step on the PCO surface remains under debate in the literature47,57,72 and based on the findings in this work, it is not possible to draw a concrete mechanism for the detailed rate-determining step (e.g. oxygen adsorption, diffusion, charge transfer). Nonetheless, it is noteworthy that infiltrants strongly impact the surface oxygen exchange reaction.
C4 on log pO2 (Fig. S10, ESI†), which are in line with those previously reported for the chemical capacitance of PCO thin films,75 further confirming that C4 corresponds to surface oxygen exchange processes that dominate Rs (see eqn (3)). Given that the chemical capacitance is associated with the volumetric characteristic of the electrode, we do not expect it to change dramatically with infiltration, while the surface exchange resistance does. The rate-determining step on the PCO surface remains under debate in the literature47,57,72 and based on the findings in this work, it is not possible to draw a concrete mechanism for the detailed rate-determining step (e.g. oxygen adsorption, diffusion, charge transfer). Nonetheless, it is noteworthy that infiltrants strongly impact the surface oxygen exchange reaction.
Discussion and conclusions
Comparing the pristine, Cr-infiltrated and serially Cr-/Li-infiltrated samples using microscopy analysis, conductivity relaxation and electrochemical impedance measurements provides important insights into the mechanism responsible for the remarkable compensation of Cr-species by Li-species. As expected from our earlier study,47 acidic Cr-infiltration decreases the oxygen surface reaction rate of PCO. Although in the STEM-EELS results, relatively large (tens of nm) Cr2O3 crystallite form, leaving a substantial amount of PCO surface free of readily visible Cr-species (although highly dispersed species are likely47), the oxygen exchange coefficient (by a factor of 20) and overall conductivity (by 19%) decrease significantly for 0.3 at% Cr. Moreover, Cr-infiltration severely degrades the surface exchange resistance (R4 increases 20 times with 0.15 at%). Regardless of these large changes, the corresponding activation energies remain unchanged. Based on this finding and those of the previous report,47 we attribute the degradation to the depletion of surface electrons in PCO as a result of the hetero-junction with Cr2O3. Through the serial Li-infiltration, it is not only possible to regenerate the oxygen surface reaction rate, but enhance it above that of the untreated PCO surface. The oxygen exchange rate (by a factor of 1000) and overall conductivity (by 117%) increase for 0.5 at% Li, while the surface exchange resistance decreases over 100 fold with 0.4 at% Li. After serial infiltration of Li, no crystalline lithia phase was observed, and crystalline Cr2O3 was no longer visible in the STEM-EELS results. Although no crystalline lithia phase remains, the Li-rich amorphous phase apparently retains its basicity, as indicated by its ability to recover rapid oxygen exchange rates. This hypothesis is further supported by the observations in Fig. 2d of increased conductivity of PCO when serial-infiltrated with Li-species, suggestive of electron transfer from the amorphous phase to PCO. The decomposition of the crystalline Cr2O3 phase, and its incorporation into an amorphous Li-rich phase, likely enhances the ability of the Li-infiltrate to more readily compensate for the chromia acidity and contribute to the regeneration of the oxygen exchange rate. Taken together, the positive impact of Li-infiltration on the exchange kinetics appears to originate from two features: (1) recovering the fraction of the PCO surface poisoned by Cr2O3 due to Li-induced decomposition of Cr2O3 and (2) increasing the overall surface electron concentration which facilitates oxygen exchange.The ability to tune the oxygen exchange kinetics of metal oxides through the addition of surface additives, utilizing relative acidity as a guide, is demonstrated to be a powerful tool. This work serves as a proof of concept that the performance degradation of a mixed conducting oxide (PCO) induced by acidic poisons e.g. chromia, can be compensated through the serial addition of basic additives e.g. lithia. Strikingly, even using chromia concentrations over 10 times higher than expected after 3000 hours of stack operation, not only does one achieve the complete regeneration of the oxygen exchange kinetics through Li-infiltration, but also improvements above those found in the pristine sample. These findings are not only significant for insuring extended operation of SOFCs with reduced performance degradation rates, but for all applications where the oxygen exchange reaction at metal oxide surfaces plays a central role e.g. electrolyzers, oxygen permeation membranes and gas sensors. It thus offers insight into how the operation lifetimes of a variety of devices can be extended through the compensation of acidic poisons in general.
Author contributions
H. G. S., C. N. and H. L. T. conceived the original ideas. H. G. S., A. S., C. N. and H. L. T. designed the experimental protocol. H. G. S. prepared the porous structure specimen, built the experimental set-up, examined the microstructures and performed the conductivity relaxation measurements. A. S. prepared the PCO symmetric cells and performed the electrochemical impedance spectroscopy measurements. D. S. K. performed the STEM-EELS analysis with assistance of M. X. D. K. assisted in the interpretation of DRT and C. N. proposed the modeling of the electrical conductivity relaxation results. J. M. L. interpreted the STEM-EELS results. H. L. T. supervised the work and provided guidance throughout the project. H. G. S., A. S. and H. L. T. wrote the manuscript with inputs from all the co-authors. All the co-authors contributed to discussing the results and helped to revise the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was initially supported by the US Department of Energy (DOE), National Energy Technology Laboratory (NETL), Office of Fossil Energy under Award No. DE-FE0031668—Robust highly durable solid oxide fuel cell cathodes – Improved materials compatibility & self-regulating surface chemistry. Additional funding included support in part for H. G. S by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (No. 2021R1A6A3A03044464) and for H. G. S, A. S. and H. L. T with funds provided by the MIT Department of Materials Science and Engineering via the R. P. Simmons Professor of Ceramics and Electronic Materials Chair. D. S. K., M. X. and J. M. L. acknowledge support for STEM characterization from the Air Force Office of Scientific Research (FA9550-20-0066).References
- M. Reisert, A. Aphale and P. Singh, Materials., 2018, 11, 2169 CrossRef.
- M. Lankin, Y. Du and C. Finnerty, J. Fuel Cell Sci. Technol., 2011, 8, 1–7 CrossRef.
- S. P. Jiang and X. Chen, Int. J. Hydrogen Energy, 2014, 39, 505–531 CrossRef CAS.
- M. Schüler, T. Sauerwald and A. Schütze, J. Sens. Sens. Syst., 2015, 4, 305–311 CrossRef.
- D. E. Williams and K. F. E. Pratt, J. Chem. Soc., Faraday Trans., 1998, 94, 3493–3500 RSC.
- M. van Essen, P. Visser, S. Gersen and H. Levinsky, SAE Int. J. Fuels Lubr., 2018, 11, 35–42 CrossRef CAS.
- M. M. Viitanen, R. G. V. Welzenis, H. H. Brongersma and F. P. F. Van Berkel, Solid State Ionics, 2002, 150, 223–228 CrossRef CAS.
- B. W. Holleboom, S. W. Hawes and E. L. Ker, SAE Tech. Pap. Ser., Technical Paper 860478, 1986 Search PubMed.
- A. Steinfeld, Sol. Energy, 2005, 78, 603–615 CrossRef CAS.
- W. C. Chueh, C. Falter, M. Abbott, D. Scipio, P. Furler, S. M. Haile and A. Steinfeld, Science, 2010, 330, 1797–1801 CrossRef CAS PubMed.
- J. Sunarso, S. S. Hashim, N. Zhu and W. Zhou, Prog. Energy Combust. Sci., 2017, 61, 57–77 CrossRef.
- C. Graves, S. D. Ebbesen, S. H. Jensen, S. B. Simonsen and M. B. Mogensen, Nat. Mater., 2015, 14, 239–244 CrossRef CAS PubMed.
- S. Y. Gómez and D. Hotza, Renewable Sustainable Energy Rev., 2016, 61, 155–174 CrossRef.
- M. A. Laguna-Bercero, J. Power Sources, 2012, 203, 4–16 CrossRef CAS.
- J. H. Myung, D. Neagu, D. N. Miller and J. T. S. Irvine, Nature, 2016, 537, 528–531 CrossRef CAS PubMed.
- J. Sunarso, S. Baumann, J. M. Serra, W. A. Meulenberg, S. Liu, Y. S. Lin and J. C. Diniz da Costa, J. Membr. Sci., 2008, 320, 13–41 CrossRef CAS.
- A. A. Plazaola, A. C. Labella, Y. Liu, N. B. Porras, D. A. P. Tanaka, M. V. S. Annaland and F. Gallucci, Processes, 2019, 7(3), 128 CrossRef CAS.
- S. D. Vora, U.S. DOE Office of Fossil Energy Solid Oxide Fuel Cell Program, 2018, Proceedings – 19TH Annual Solid Oxide Fuel Cell (Sofc) Project Review Meeting, https://netl.doe.gov/node/7801.
- Fortune Bus. Insights, 2021, https://www.fortunebusinessinsights.com/industry-reports/solid-oxide-fuel-cell-market-101306.
- J. A. Kilner and M. Burriel, Annu. Rev. Mater. Res., 2014, 44, 365–393 CrossRef CAS.
- A. Esquirol, N. P. Brandon, J. A. Kilner and M. Mogensen, J. Electrochem. Soc., 2004, 151, A1847 CrossRef CAS.
- J. Hwang, H. Lee, K. J. Yoon, H.-W. Lee, B.-K. Kim, J.-H. Lee and J.-W. Son, J. Electrochem. Soc., 2012, 159, F639–F643 CrossRef CAS.
- Z. Shao and S. M. Halle, Nature, 2004, 431, 170–173 CrossRef CAS PubMed.
- Y. Chen, S. Yoo, Y. Choi, J. H. Kim, Y. Ding, K. Pei, R. Murphy, Y. Zhang, B. Zhao, W. Zhang, H. Chen, Y. Chen, W. Yuan, C. Yang and M. Liu, Energy Environ. Sci., 2018, 11, 2458–2466 RSC.
- Y. Chen, Y. Bu, Y. Zhang, R. Yan, D. Ding, B. Zhao, S. Yoo, D. Dang, R. Hu, C. Yang and M. Liu, Adv. Energy Mater., 2017, 7, 1601890 CrossRef.
- H. Tellez, J. Druce, Y. Shi, M. Kubicek, N. J. Simrick, J. L. M. Rupp, T. Ishihara and J. A. Kilner, ECS Trans., 2015, 66, 69–77 CrossRef CAS.
- W. Jung and H. L. Tuller, Energy Environ. Sci., 2012, 5, 5370–5378 RSC.
- B. Koo, K. Kim, J. K. Kim, H. Kwon, J. W. Han and W. C. Jung, Joule, 2018, 2, 1476–1499 CrossRef CAS.
- B. Koo, H. Kwon, Y. Kim, H. G. Seo, J. W. Han and W. Jung, Energy Environ. Sci., 2018, 11, 71–77 RSC.
- S. P. Jiang and Y. Zhen, Solid State Ionics, 2008, 179, 1459–1464 CrossRef CAS.
- S. P. S. Badwal, R. Deller, K. Foger, Y. Ramprakash and J. P. Zhang, Solid State Ionics, 1997, 99, 297–310 CrossRef CAS.
- M. Kornely, N. H. Menzler, A. Weber and E. Ivers-Tiffée, Fuel Cells, 2013, 13, 506–510 CrossRef CAS.
- A. Beez, K. Schiemann, N. H. Menzler and M. Bram, Front. Energy Res., 2018, 6, 1–8 CrossRef.
- J. Tallgren, O. Himanen, M. Bianco, J. Mikkola, O. Thomann, M. Rautanen, J. Kiviaho and J. Van Herle, Fuel Cells, 2019, 19, 570–577 CrossRef CAS.
- M. Bianco, J. P. Ouweltjes and J. Van herle, Int. J. Hydrogen Energy, 2019, 44, 31406–31422 CrossRef CAS.
- J. G. Grolig, J. Froitzheim and J. E. Svensson, J. Power Sources, 2014, 248, 1007–1013 CrossRef CAS.
- H. Kurokawa, C. P. Jacobson, L. C. DeJonghe and S. J. Visco, Solid State Ionics, 2007, 178, 287–296 CrossRef CAS.
- R. Sachitanand, M. Sattari, J. E. Svensson and J. Froitzheim, Int. J. Hydrogen Energy, 2013, 38, 15328–15334 CrossRef CAS.
- A. Aphale, J. Hong, B. Hu and P. Singh, J. Visualized Exp., 2019, 147, e59623 Search PubMed.
- K. Chen, N. Ai, K. M. O’Donnell and S. P. Jiang, Phys. Chem. Chem. Phys., 2015, 17, 4870–4874 RSC.
- S. R. Bishop, J. Druce, J. A. Kilner, T. Ishihara and K. Sasaki, ECS Trans., 2013, 57, 2003–2007 CrossRef.
- Y. Niu, Y. Zhou, W. Lv, Y. Chen, Y. Zhang, W. Zhang, Z. Luo, N. Kane, Y. Ding, L. Soule, Y. Liu, W. He and M. Liu, Adv. Funct. Mater., 2021, 31, 1–11 Search PubMed.
- L. Zhao, N. H. Perry, T. Daio, K. Sasaki and S. R. Bishop, Chem. Mater., 2015, 27, 3065–3070 CrossRef CAS.
- D. Ding, M. Liu, Z. Liu, X. Li, K. Blinn, X. Zhu and M. Liu, Adv. Energy Mater., 2013, 3, 1149–1154 CrossRef CAS.
- Y. Chen, S. Yoo, X. Li, D. Ding, K. Pei, D. Chen, Y. Ding, B. Zhao, R. Murphy, B. deGlee, J. Liu and M. Liu, Nano Energy, 2018, 47, 474–480 CrossRef CAS.
- D. Ding, X. Li, S. Y. Lai, K. Gerdes and M. Liu, Energy Environ. Sci., 2014, 7, 552–575 RSC.
- C. Nicollet, C. Toparli, G. F. Harrington, T. Defferriere, B. Yildiz and H. L. Tuller, Nat. Catal., 2020, 3, 913–920 CrossRef CAS.
- D. W. Smith, J. Chem. Educ., 1987, 64, 480–481 CrossRef CAS.
- C. B. Gopal and S. M. Haile, J. Mater. Chem. A, 2014, 2, 2405–2417 RSC.
- M. W. den Otter, H. J. M. Bouwmeester, B. A. Boukamp and H. Verweij, J. Electrochem. Soc., 2001, 148, J1 CrossRef CAS.
- Y. Zhang, F. Yan, B. Hu, C. Xia and M. Yan, J. Mater. Chem. A, 2020, 8, 17442–17448 RSC.
- D. Chen, S. R. Bishop and H. L. Tuller, J. Electroceram., 2012, 28, 62–69 CrossRef CAS.
- R. P. Ferrier, Energy-Loss Spectroscopy in the Electron Microscope: Theoretical Considerations, Springer, 3rd edn, 1981 Search PubMed.
- S. P. McBride and R. Brydson, J. Mater. Sci., 2004, 39, 6723–6734 CrossRef CAS.
- S. Le, S. Zhu, X. Zhu and K. Sun, J. Power Sources, 2013, 222, 367–372 CrossRef CAS.
- C. Nicollet, J. Waxin, T. Dupeyron, A. Flura, J.-M. Heintz, J. P. Ouweltjes, P. Piccardo, A. Rougier, J.-C. Grenier and J.-M. Bassat, J. Power Sources, 2017, 372, 157–165 CrossRef CAS.
- R. A. De Souza, J. Mater. Chem. A, 2017, 5, 20334–20350 RSC.
- D. Chen, A. Groß, D. C. Bono, J. Kita, R. Moos and H. L. Tuller, Solid State Ionics, 2014, 262, 914–917 CrossRef CAS.
- S. R. Bishop, T. S. Stefanik and H. L. Tuller, Phys. Chem. Chem. Phys., 2011, 13, 10165–10173 RSC.
- S. R. Bishop, T. S. Stefanik and H. L. Tuller, J. Mater. Res., 2012, 27, 2009–2016 CrossRef CAS.
- K. Michel, T. S. Bjørheim, T. Norby, J. Janek and M. T. Elm, J. Phys. Chem. C, 2020, 124, 15831–15838 CrossRef CAS.
- S. B. Adler, Chem. Rev., 2004, 104, 4791–4844 CrossRef CAS PubMed.
- T. M. Huber, E. Navickas, K. Sasaki, B. Yildiz, H. Hutter, H. L. Tuller and J. Fleig, J. Electrochem. Soc., 2018, 165(9), F702–F709 CrossRef CAS.
- P. Caliandro, A. Nakajo, S. Diethelm and J. Van herle, J. Power Sources, 2019, 436, 226838 CrossRef CAS.
- J. Hayd and E. Ivers-Tiffée, J. Electrochem. Soc., 2013, 160, F1197–F1206 CrossRef CAS.
- H. G. Seo, Y. Choi and W. C. Jung, Adv. Energy Mater., 2018, 8, 1–7 Search PubMed.
- J. J. Kim, Defect Equilibria and Electrode Kinetics in PrxCe1-xO2-δ Mixed Conducting Thin Films: An in-situ Optical and Electrochemical Investigation, PhD thesis, Massachusetts Institute of Technology, Cambridge, MA, 2015 Search PubMed.
- N. Menzler, F. Tietz, M. Bram, I. Vinke and L. Haart, in Ceramic Engineering and Science Proceedings, 2009, vol. 29, pp. 93–104 Search PubMed.
- E. Ivers-Tiffée and A. Weber, J. Ceram. Soc. Japan, 2017, 125, 193–201 CrossRef.
- T. H. Wan, M. Saccoccio, C. Chen and F. Ciucci, Electrochim. Acta, 2015, 184, 483–499 CrossRef CAS.
- F. Ciucci and C. Chen, Electrochim. Acta, 2015, 167, 439–454 CrossRef CAS.
- D. Chen, Z. Guan, D. Zhang, L. Trotochaud, E. Crumlin, S. Nemsak, H. Bluhm, H. L. Tuller and W. C. Chueh, Nat. Catal., 2020, 3, 116–124 CrossRef CAS.
- M. Schaube, R. Merkle and J. Maier, J. Mater. Chem. A, 2019, 7, 21854–21866 RSC.
- P. Simons, H.-I. Ji, T. C. Davenport and S. M. Haile, J. Am. Ceram. Soc., 2017, 100, 1161–1171 CrossRef CAS.
- D. Chen, S. R. Bishop and H. L. Tuller, Adv. Funct. Mater., 2013, 23, 2168–2174 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d1ee03975j |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2022 |