Open Access Article
Open Access ArticleThe promoter role of sulfur in carbon nanotube growth†
Balázs
Orbán
a and
Tibor
Höltzl
 *abc
*abc
aBudapest University of Technology and Economics, Department of Inorganic and Analytical Chemistry, Műegyetem rkp. 3, H-1111, Budapest, Hungary
bMTA-BME Computation Driven Research Group, Műegyetem rkp. 3, H-1111, Budapest, Hungary
cFurukawa Electric Institute of Technology, Késmárk utca 28/A, H-1158, Budapest, Hungary. E-mail: tibor.holtzl@furukawaelectric.com
First published on 30th May 2022
Abstract
We investigate the effect of sulfur on the interaction of iron catalyst nanoparticles and carbon nanotubes (CNTs), typically present in a floating catalyst chemical vapor deposition (FCCVD) process. As a reference, the interaction of graphene with the Fe fcc(111) surface is used. In both systems we performed a systematic density functional theory (DFT) study on the interaction with different sulfur contents. We found that the presence of sulfur changes the nature and strength of interaction between graphene and the iron surface from strong chemisorption to weak physisorption. Furthermore, sulfur significantly reduces the CNT–iron binding, indicating a beneficial effect on the CNT growth and its promoter role. We believe that these results induce further experimental studies and optimization of the CNT synthesis process.
1. Introduction
Since the discovery of carbon nanotubes (CNTs),1 their synthesis has become one of the central goals in nanotechnology, due to their outstanding electrical, mechanical and optical properties with various potential applications.2–5 In the last few decades, several synthesis methods have been developed for this purpose such as arc discharge,1,6 laser ablation7 and chemical vapor deposition.8–10 Among these, catalytic chemical vapor deposition (CCVD) is the most generally applicable method as it shows high throughput and controllability and hence allows production scale-up. The growth of CNTs by CCVD originates from the dissociation of carbon-containing gas on the surface of transition metal catalyst nanoparticles at elevated temperature.The hitherto developed CCVD methods differ in the form of the catalyst nanoparticles. Application of substrate-supported nanoparticles leads to the formation of surface anchored nanotubes or nanotube forests.11,12 On the other hand, the catalyst nanoparticles can also be formed by in situ gas flow; this process is commonly denoted as floating catalyst chemical vapor deposition (FCCVD).13–18 Typically, ferrocene is introduced as the iron source. It has been observed that addition of a small amount of a promoter improves considerably the FCCVD process.14,19–21 Several additives have been applied successfully as promoters in the FCCVD method such as chlorine,22 phosphorus23 and even selenium.24 Also, the presence of oxygen has been shown to have a great influence on CNT growth.25 However, the most commonly used is sulfur16–18,26–30 that has outstanding promoter activity in CNT synthesis, despite the fact that it is a well-known transition metal catalyst poison in many chemical processes.31 Sulfur can be added as powder or in the form of a sulfur-containing compound such as thiophene or carbon disulfide.32
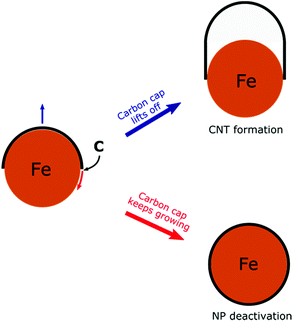
To develop a controllable and scalable FCCVD technique, it is important to understand the growth mechanism and how the different synthesis parameters (type of carbon source, composition, size and structure of the catalyst nanoparticles, growth temperature, carrier gas composition, pressure, growth time, etc.) influence the process.17,33 Computational methods based on density functional theory (DFT), density functional tight-binding (DFTB), reactive force-field (ReaxFF)34 or reactive empirical bond order (REBO)35,36 have been applied successfully. The CNT growth mechanism has been extensively investigated using molecular dynamics (MD),37–47 hybridized molecular dynamics and basin-hopping optimization (H-MD-BH),48,49 Monte Carlo simulations50 and also the combination of MD with force-bias Monte Carlo simulations (MD/tfMC).51–54 Although it is still the subject of active research on both experimental and computational sides, it is already known that the growth process consists of five main stages. First, ferrocene (catalyst source) thermally decomposes and the catalyst nanoparticles form through collision and coalescence along the furnace reactor. The precursor molecules decompose on the catalyst nanoparticle surface and active carbon species, e.g. C atoms, C2 dimers or hydrocarbon radicals are formed. The active carbon species dissolve in the nanoparticle and create a liquid or surface-molten metal carbide phase. After supersaturation, carbon polyyne chains (up to 10–15 C atoms) begin to grow in which Y-junctions can form. These carbon chains partially close into five- and six-membered rings. With the attachment of more carbon species, the number of rings increases and these rings aggregate into a graphitic cap on the nanoparticle. This is the initial structure of CNT formation. Finally, the tubular structure of CNTs begins to grow if the carbon cap lifts off the nanoparticle. On the other hand, if the cap lift-off is hindered, the nanoparticle deactivates due to the complete carbon encapsulation (Scheme 1).55 Recent computations show that the key factor in the two competitive processes (cap lift-off and NP deactivation) is the interfacial energy of the CNT–catalyst interface and its contact angle dependency.56
Sulfur has been found to be an indispensable co-catalyst to avoid the catalyst deactivation in FCCVD, which also affects the morphology,57,58 wall number16 and even the conductivity of the synthesized CNTs.26 Interestingly, sulfur is also known to be beneficial for the supported catalyst CVD of CNTs.59,60
However, the detailed promoter mechanism is still an open question. Based on the HRTEM images, the sulfur shell surrounds the iron nanoparticle.28 This forms a liquid iron-sulfide shell at high temperature, and thus it clearly influences the nanoparticle growth. On the other hand, the sulfur-rich layer also obstructs the diffusion of the gaseous carbon source to the catalytic surface where the decomposition takes place. This can decrease the carbon cap formation rate which gives more time for the nanoparticles to grow by collision.27,29 It has been suggested that the formation of transient S–C bonds stabilizes the graphitic cap edge while the Fe–S–C molten catalyst does not wet the graphitic plane, facilitating the carbon cap lift-off at the onset of tube formation.27
Here, we investigate the role of sulfur in the interaction of the metal catalyst and carbon nanotube cap and its impact on the efficiency of CNT growth.
2. Methods of computations
All computations were carried out using the GPAW package61,62 in the Atomic Simulation Environment.63 Weak interactions such as van der Waals forces play a crucial role in the studied systems. As the dispersion effects are important, we used the C09 corrected version of the first generation van der Waals density functional (C09-vdW-DF) which is shown to yield accurate adsorption energies on metal surfaces.64–66 The Kohn–Sham equations were solved using the projector-augmented wave method (PAW)67 in which the Kohn–Sham orbitals were expanded in plane-waves (PWs) up to a cutoff energy of 500 eV. An electronic Fermi smearing of 0.1 eV was used and the total energies were extrapolated to 0 K. The SCF energy convergence limit was set to 10−6 eV per valence electron and the geometry optimization was performed using the FIRE algorithm68 until the force on every atom was less than 0.01 eV Å−1. Monkhorst–Pack k-point meshes of 10 × 10 × 1 (the first two are the periodic directions) were applied to sample the Brillouin zone in metal–graphene systems. A vacuum of 15 Å was applied in the non-periodic direction to avoid the interaction between the replicas of the system. In finite nanoparticle–CNT computations, only a single k-point and a box with sizes of 15 × 15 × 25 Å and 20 × 20 × 30 Å were considered for M13 and M55 based systems, respectively.69We performed spin-polarized computations. It must be noted that the typical temperature applied in the FCCVD process is above the Curie point of iron (770 °C), and thus the nanoparticle is expected to be non-magnetic under the synthesis conditions, while the computations can converge to several different magnetic states. Thus, we investigated the role of magnetism and our computations showed that the binding energies depend slightly on the magnetism (see Fig. S2 and Table S4 in the ESI†). Thus, the static density functional theory (DFT) computations performed at 0 K can be used to draw conclusion at the high temperature applied in FCCVD.
Further details of the computations are described in the ESI.†
3. Results and discussion
We apply two different model systems: a graphene layer adsorbed on the Fe fcc(111) surface with different sulfur coverages, and then small CNT segments and carbon caps binding to icosahedral Fe13 and Fe55 nanoparticles. Both zigzag ((5,0) and (10,0)) and armchair ((3,3) and (6,6)) nanotubes were considered in the computations. While the first system (metal slab–graphene) serves as a reference and focuses on how sulfur affects the long-range interactions such as van der Waals forces between the graphitic layer and the metal, the second system (metal nanoparticle–CNT) gives a more accurate insight into the nature of interaction in CNT growth.3.1. Graphene–iron surface interaction
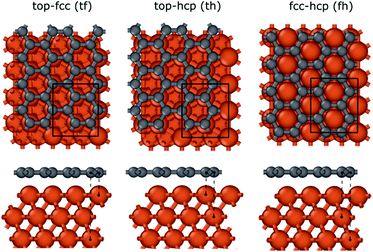
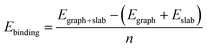
To investigate the interaction between the metal surfaces and graphene a (2 × 2) orthogonal cell of a metal slab with 6 atomic layers was used. First, we optimized the Fe cell with a face-centered cubic (fcc) structure. The choice of the fcc structure for Fe is motivated by its thermodynamic stability over 900 °C, which is similar to the temperature range that is often used in the synthesis of carbon nanotubes by FCCVD.15,27,29 The computed and the experimental lattice constants are 3.44 Å and 3.63 Å, respectively.70 The fcc structure of iron is only stable at high temperature where the anharmonicity of the potential energy surface and the thermal expansion cannot be neglected which leads to a significantly larger experimental lattice constant than the one calculated at 0 K using DFT.Although the binding energy of graphene on several different transition metals has been computed,66 the fcc iron (111) surface is only considered recently.56 Here we investigated three different configurations of graphene on the fcc(111) surface (Fig. 1); in two of them every second carbon atom resides on top of the Fe surface (top–fcc hollow site and top–hcp hollow site) while in the third all carbon atoms are located above the hollows of the surface (fcc–hcp hollow site). During geometry optimization the bottom layer of the Fe slab was fixed to model the effect of the bulk crystal. The binding energy per carbon atom was calculated as
 | (1) |
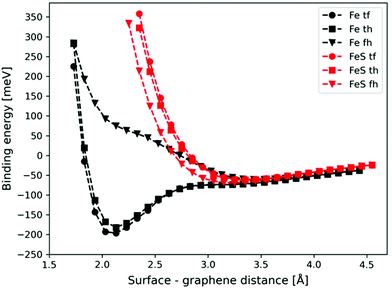
The potential energy curves corresponding to the graphene–metal surface distance are shown in Fig. 2 (black lines). In the case of top–fcc and top–hcp structures the equilibrium graphene–metal surface distance is 2.13 Å and the binding energies are −196 and −182 meV, respectively. These results imply the chemisorption of the graphene layer on the iron surface.71 However, the binding is considerably weaker if no carbon atoms are above iron (−61 meV for fcc–hcp configuration) with a longer equilibrium graphene–metal distance of 3.45 Å.
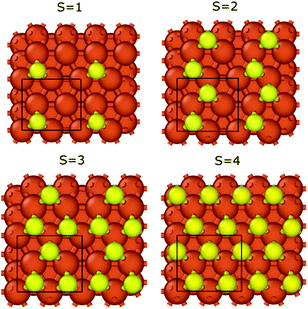
We calculated the binding energies with different sulfur coverages. As four surface atoms are present in the (2 × 2) orthogonal cell of the fcc structure we calculated the binding energy with 1 to 4 sulfur atoms (S = 1–4) placed in the hollow sites between the surface iron atoms (Fig. 3). Our computations showed that anchoring more than 4 sulfur atoms on our 2 × 2 model surface leads to an unstable structure where the sulfur atoms desorb.
In the case of S = 4, the four surface sulfur atoms form a new top layer, and thus, it is possible to compare the binding energy to the clean fcc(111) iron surface without any structural differences. The calculated potential energy curves of graphene binding to the S = 4 surface are shown in Fig. 2 (red lines). Instead of the stronger chemisorption observed in the top–fcc and top–hcp structures on a clean iron surface, diagrams show much weaker interaction for all configurations with the most negative binding energy of −69 meV in the case of the fcc–hcp structure. It is also well visible that the equilibrium distance increases from 2.13 Å (clean iron surface) to 3.1–3.25 Å in the presence of sulfur which suggests the van der Waals force-based physisorption of graphene on the sulfur covered iron surface. Therefore, sulfur considerably reduces the graphene binding energy, implying a weak physisorption.
The binding energy of graphene to the sulfur covered iron surfaces (S = 0–4) is presented in Table 1. Even low sulfur coverage weakens the graphene binding to the iron surface and the binding energy decreases from −39 meV (in the case of S = 1) to −71 meV (the highest sulfur coverage with S = 4). Therefore, the interaction is stronger with increasing sulfur content but is still significantly weaker than that on bare surface (the binding energy is −196 meV for S = 0). The binding energy per sulfur atom in Table 1 clearly shows the non-additive effect of the sulfur coverage on the interaction energies. Thus, relatively low sulfur coverage already shows a great effect on reducing the graphene–iron interaction strength. We observed a small corrugation of the sulfur-covered iron bound graphene (see section 3 and Fig. S4 in the ESI†). Thus, even a relatively low sulfur coverage greatly reduces the metal–carbon interaction, as the sulfur atoms can effectively suspend the graphene layer above the iron surface, also in the bare metal regions between the sulfur atoms. This leads to decreased metal–carbon interaction.
| Sulfur coverage (S) | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Binding energy [meV] | −196 | −39 | −50 | −61 | −71 |
| Binding energy per S atom [meV] | — | −39 | −25 | −20 | −18 |
These results show the significant effect of sulfur on the adsorption of graphene to the iron surface as it drastically reduces the strength of interaction. The iron–graphene system can be considered as an idealistic model of the nanoparticle–nanocap structure without a curvature, a model representing large nanoparticles. It allows us to investigate the interaction between the nanoparticle surface and carbon cap without the binding edge which remains intact during the cap lift-off and CNT growth. Thus, it shows the part of interaction which considerably determines the occurrence of the cap lift-off. Without sulfur the carbon cap binds to the surface strongly which hinders the detachment of the cap and carbon encapsulation would rather occur in further growth. However, the presence of sulfur can significantly reduce the interaction with the surface which helps in lifting off the nanocap more easily. Therefore, the reduction in the adhesion of the carbon cap can favour tube formation in CNT synthesis.56
3.2. Interaction of iron nanoparticles with carbon nanotubes
Typically, nanoparticles of ∼1 nm to a few nanometres are applied for the CNT synthesis. Thus it is important to consider the curvature of the nanoparticle and the cap. The interaction between the icosahedral nanoparticles and the hydrogen terminated CNT segments has been widely studied using DFT computations for all transition metals.69,72 Thus, we selected the icosahedral Fe13 and Fe55 nanoparticles with diameters of 0.47 and 0.94 nm, respectively. For CNTs the zigzag (5,0) and (10,0)-tubes and the armchair (3,3) and (6,6)-tubes were selected as their diameters of 0.40/0.41 nm (for (5,0)/(3,3)) and 0.79/0.83 (for (10,0)/(6,6)) are compatible with those of the Fe13 and Fe55 nanoparticles, respectively. We investigated the binding of the carbon caps and capped CNT segments to the nanoparticles. The Fe55 based model has been previously used to investigate the effect of carbon encapsulation on the nanoparticle by fullerene.73 The binding energy per Fe–C bond is calculated using the equation below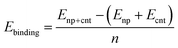 | (2) |
In the case of Fe13 we considered three different sulfur substitution patterns: top/bottom belongs to the substitution of the atom which is closest to/furthest from the carbon nanocap (Fe12S Top/Bottom) while the edge refers to the substitution of a bonding iron (Fe12S Edge). We also calculated the binding energies in the absence of the top iron atom (Fe12). The results are presented in Table 2 and the geometries of the optimized structures are shown in Fig. 4. For all systems the negative binding energies suggest significant stabilization both for the nanocap and for the CNT segment.
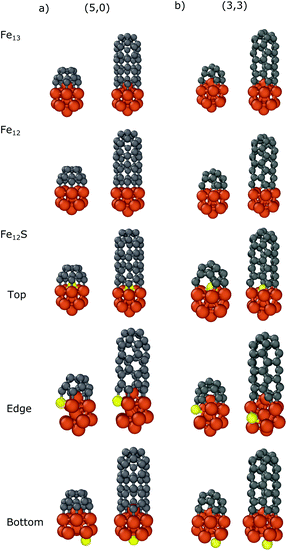 | ||
| Fig. 4 Optimized structures of the carbon nanocap and CNT segment with chirality of (a) (5,0) and (b) (3,3) binding to Fe12X (X = Fe, -, S) nanoparticles. | ||
| Binding energy [eV] | |||||
|---|---|---|---|---|---|
| Nanoparticle | cap(5,0) | CNT(5,0) | cap(3,3) | CNT(3,3) | |
| Fe13 | −3.17 | −2.74 | −2.42 | −2.09 | |
| Fe12 | −2.80 | −2.22 | −2.26 | −1.97 | |
| Fe12S | Top | −2.05 | −1.54 | −1.72 | −1.23 |
| Edge | −2.84 | −2.39 | −2.20 | −1.87 | |
| Bottom | −3.00 | −2.46 | −2.31 | −2.01 | |
Comparing the binding energies in the cases of Fe13 and Fe12, the top iron atom makes a significant contribution to the interaction, both with the nanocaps (−3.17/−2.42 and −2.80/−2.26 eV for (5,0)/(3,3), respectively) and with the CNT segments (−2.74/−2.09 and −2.22/−1.97 eV for (5,0)/(3,3), respectively). This shows that there is a significant interaction between the top iron atom and the CNT edge.
The sulfur substitution of the top iron atom (Fe12S top) strongly decreases the interaction strength. The binding energies of the nanocaps and the CNT segments with Fe12S are −2.05/−1.72 and −1.54/−1.23 eV, respectively. If sulfur substitutes a bonding iron (denoted by the Fe12S Edge in Table 2 and in Fig. 4) the reduction in the interaction is smaller; the binding energies change to −2.84/−2.20 eV for the carbon caps and −2.39/−1.87 eV for the CNTs. As the sulfur atom binds to a carbon atom, the structure of the nanoparticle distorts to reduce the number of bonds with iron atoms around it. Anchoring the sulfur atom to a site opposite of the caps or CNT segments (denoted by the Fe12S Bottom in Table 2 and in Fig. 4) only slightly modifies the binding energy, decreasing to −3.00/−2.31 eV for the nanocaps and to −2.46/−2.01 eV for the CNT segments. These results show that in CNT growth the sulfur atoms significantly decrease the interaction strength between the iron nanoparticle and CNT segment considering both zig-zag and armchair configurations. Although this effect has been observed in all configurations, the sulfur atoms under the nanotube cap have the largest effect.
We also investigated the dependence of the binding energy on the sulfur content using the Fe55 icosahedral nanoparticle with the CNT(10,0) nanocap and CNT segment. There are 6 iron atoms on the surface inside the nanocap or CNT, and thus we substituted the top iron atom (Fe54S1), three iron atoms (Fe52S3) or all the six (Fe49S6) surface atoms corresponding to the sulfur coverages of 1/6, 3/6 and 6/6, respectively. Here we use static models to systematically investigate the effect of sulfur on the carbon-nanotube growth. Preliminary molecular dynamics simulations (see section 6 in the ESI† for details) suggest that sulfur can migrate along the molten surface layer of the NP during cap growth, and thus the sulfur content under the cap depends on the sulfur coverage of the whole nanoparticle.
The results are summarized in Table 3, while the optimized structures are depicted in Fig. 5. The strongest interaction is observed in the case of bare iron nanoparticle (Fe55) with binding energies of −3.17/−2.21 and −3.21/−2.16 eV for the nanocaps and CNT segments of (10,0)/(6,6), respectively. The top-substituted sulfur (Fe54S1) has a small effect on the binding energy (−3.16/−2.20 and −3.21/−2.14 eV, respectively) because in this position the atom is too far from the edge of the carbon structures to modify its Fe–C bonds with the nanoparticle. However, increasing the sulfur content increases its effect, as the sulfur atoms are closer to the CNT binding region. In the case of Fe52S3, the binding energies are −2.45/−1.64 (with nanocaps) and −2.58/−1.62 (with CNTs) eV while these values increase to −1.80/−1.15 and −1.89/−1.03 eV for Fe49S6, respectively. This indicates that the interaction of the nanoparticle with the carbon structures weakens with the number of sulfur atoms under the nanocap. This effect of sulfur on the binding is observed for both zigzag and armchair CNTs and is also supported by our non-covalent interaction (NCI) computations (see the ESI†).75,76
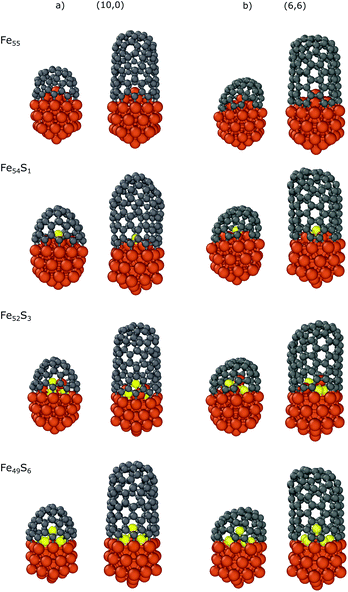 | ||
| Fig. 5 Optimized structures of the carbon nanocaps and CNT segments with chirality indices of (a) (10,0) and (b) (6,6) binding to Fe55−xSx (x = 0,1,3,6) nanoparticles. | ||
| Binding energy [eV] | ||||
|---|---|---|---|---|
| Nanoparticle | cap(10,0) | CNT(10,0) | cap(6,6) | CNT(6,6) |
| Fe55 | −3.17 | −3.21 | −2.21 | −2.16 |
| Fe54S1 | −3.16 | −3.21 | −2.20 | −2.14 |
| Fe52S3 | −2.45 | −2.58 | −1.64 | −1.62 |
| Fe49S6 | −1.80 | −1.89 | −1.15 | −1.03 |
Our results show that sulfur modifies the nanoparticle–cap binding and imply how this affects the growth efficiency of the CNTs. As it is shown in Scheme 1, at the onset of the CNT growth process the carbon cap must lift off from the catalyst nanoparticle surface. This process depends strongly on the strength of nanoparticle–cap binding. Although iron is an appropriate catalyst to realize CNT growth based on the strength of NP–CNT binding69 it can still lead to carbon encapsulation due to the strong interaction with the carbon cap.55 We found that, in the presence of sulfur, the binding weakens significantly which facilitates the cap lift-off. This favours tube formation and prevents nanoparticle deactivation. This effect on the interaction strength has been investigated in the case of oxygen25 but has never been studied for sulfur before. Furthermore, our computations showed that sulfur also reduces the CNT binding to the nanoparticle which can influence the growth of the tubular structure, as the weakened NP–CNT interaction leads to easier addition of carbon atoms to the edge of the growing tube. This may increase the growth rate which can lead to the formation of longer CNTs. The reduction in the NP–CNT interaction may also enhance the defect healing at the edge of the tube. Although sulfur is generally applied in the floating CCVD technique, these results may also explain its beneficial effect on the supported catalyst CCVD of CNTs.59,60
4. Conclusions
We systematically investigated the effect of sulfur on the interaction between iron catalyst and carbon structures using density functional theory (DFT) computations. Two types of systems were considered in the simulations that are relevant in the onset of CNT growth. Computations based on the adsorption of the graphene layer on the iron surface indicate that the presence of sulfur significantly reduces the strength of interaction. The increase in the metal–graphene distance (from 2.13 Å to 3.25 Å) and in the binding energy (from −196 meV to −71 meV in regard to the clean and sulfur covered iron surfaces with the same structure) suggests the change in the nature of interaction from strong chemisorption to weak physisorption. We also investigated the binding of small CNT segments and carbon caps to Fe13/Fe55 icosahedral nanoparticles in which iron atoms in different positions were substituted by sulfur. We observed a significant reduction of the interaction strength in the case of sulfur located under the carbon cap or CNT fragment while the interaction slightly changed in other configurations. Also, upon increasing the amount of sulfur under the cap or CNT fragment, the interaction becomes weaker which is highly visible in Fe55−xSx (x = 0,1,3, and 6) nanoparticles. These results show that sulfur enables both the detachment of the carbon cap at the onset of CNT formation and the further growth of the tubular structure. By reducing the interaction between the nanoparticle and the growing carbon structure, new carbon atoms can connect to the edge of CNTs more easily which can enhance both the growth efficiency and rate. We believe that this effect of sulfur could be a part of its promoter role in the floating and substrate supported catalyst CVD process which helps achieve a better CNT yield for large scale production.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the members of the Nanomaterials Science Group of Furukawa Electric Institute of Technology for the valuable discussions. T. H. is grateful for the János Bolyai Research Scholarship of the Hungarian Academy of Sciences (grant number BO/00642/21/7).Notes and references
- S. Iijima, Helical microtubules of graphitic carbon, Nature, 1991, 354, 56–58 CrossRef CAS.
- D. Sun, M. Y. Timmermans, Y. Tian, A. G. Nasibulin, E. I. Kauppinen, S. Kishimoto, T. Mizutani and Y. Ohno, Flexible high-performance carbon nanotube integrated circuits, Nat. Nanotechnol., 2011, 6, 156–161 CrossRef CAS PubMed.
- P. Avouris, M. Freitag and V. Perebeinos, Carbon-nanotube photonics and optoelectronics, Nat. Photonics, 2008, 2, 341–350 CrossRef CAS.
- Y. Liang, Y. Li, H. Wang and H. Dai, Strongly Coupled Inorganic/Nanocarbon Hybrid Materials for Advanced Electrocatalysis, J. Am. Chem. Soc., 2013, 135, 2013–2036 CrossRef CAS PubMed.
- Q. Zhang, J. Huang, W. Qian, Y. Zhang and F. Wei, The Road for Nanomaterials Industry: A Review of Carbon Nanotube Production, Post-Treatment, and Bulk Applications for Composites and Energy Storage, Small, 2013, 9, 1237–1265 CrossRef CAS PubMed.
- N. Arora and N. N. Sharma, Arc discharge synthesis of carbon nanotubes: Comprehensive review, Diam. Relat. Mater., 2014, 50, 135–150 CrossRef CAS.
- R. A. Ismail, M. H. Mohsin, A. K. Ali, K. I. Hassoon and S. Erten-Ela, Preparation and characterization of carbon nanotubes by pulsed laser ablation in water for optoelectronic application, Phys. E, 2020, 119, 113997 CrossRef CAS.
- H. Dai, A. G. Rinzler, P. Nikolaev, A. Thess, D. T. Colbert and R. E. Smalley, Single-wall nanotubes produced by metal-catalyzed disproportionation of carbon monoxide, Chem. Phys. Lett., 1996, 260, 471–475 CrossRef CAS.
- M. L. Terranova, V. Sessa and M. Rossi, The world of carbon nanotubes: An overview of CVD growth methodologies, Chem. Vap. Depos., 2006, 12, 315–325 CrossRef CAS.
- Y. Manawi, I. Ihsanullah, A. Samara, T. Al-Ansari and M. Atieh, A Review of Carbon Nanomaterials’ Synthesis via the Chemical Vapor Deposition (CVD) Method, Materials, 2018, 11, 822 CrossRef PubMed.
- A. Magrez, J. W. Seo, R. Smajda, M. Mionić and L. Forró, Catalytic CVD Synthesis of Carbon Nanotubes: Towards High Yield and Low Temperature Growth, Materials, 2010, 3, 4871–4891 CrossRef CAS PubMed.
- P. Li and J. Zhang, CVD Growth of Carbon Nanotube Forest with Selective Wall-Number from Fe-Cu Catalyst, J. Phys. Chem. C, 2016, 120, 11163–11169 CrossRef CAS.
- A. Oberlin, M. Endo and T. Koyama, Filamentous growth of carbon through benzene decomposition, J. Cryst. Growth, 1976, 32, 335–349 CrossRef CAS.
- H. M. Cheng, F. Li, G. Su, H. Y. Pan, L. L. He, X. Sun and M. S. Dresselhaus, Large-scale and low-cost synthesis of single-walled carbon nanotubes by the catalytic pyrolysis of hydrocarbons, Appl. Phys. Lett., 1998, 72, 3282–3284 CrossRef CAS.
- Y. L. Li, I. A. Kinloch and A. H. Windle, Direct Spinning of Carbon Nanotube Fibers from Chemical Vapor Deposition Synthesis, Science, 2004, 304, 276–278 CrossRef CAS PubMed.
- L. Ci, Z. Rao, Z. Zhou, D. Tang, X. Yan, Y. Liang, D. Liu, H. Yuan, W. Zhou, G. Wang, W. Liu and S. Xie, Double wall carbon nanotubes promoted by sulfur in a floating iron catalyst CVD system, Chem. Phys. Lett., 2002, 359, 63–67 CrossRef CAS.
- Y. Jung, J. Song, W. Huh, D. Cho and Y. Jeong, Controlling the crystalline quality of carbon nanotubes with processing parameters from chemical vapor deposition synthesis, Chem. Eng. J., 2013, 228, 1050–1056 CrossRef CAS.
- H. M. Duong, T. Q. Tran, R. Kopp, S. M. Myint and L. Peng, Direct spinning of horizontally aligned carbon nanotube fibers and films from the floating catalyst method, Elsevier Inc., 2nd edn, 2019 Search PubMed.
- H. M. Cheng, F. Li, X. Sun, S. D. M. Brown, M. A. Pimenta, A. Marucci, G. Dresselhaus and M. S. Dresselhaus, Bulk morphology and diameter distribution of single-walled carbon nanotubes synthesized by catalytic decomposition of hydrocarbons, Chem. Phys. Lett., 1998, 289, 602–610 CrossRef CAS.
- M. S. Kim, N. M. Rodriguez and R. T. K. Baker, The Interplay Between Sulfur Adsorption and Carbon Deposition on Cobalt Catalysts, J. Catal., 1993, 143, 449–463 CrossRef CAS.
- G. G. Tibbetts, C. A. Bernardo, D. W. Gorkiewicz and R. L. Alig, Role of sulfur in the production of carbon fibers in the vapor phase, Carbon, 1994, 32, 569–576 CrossRef CAS.
- C. Ghemes, A. Ghemes, M. Okada, H. Mimura, T. Nakano and Y. Inoue, Study of Growth Enhancement of Multiwalled Carbon Nanotubes by Chlorine-Assisted Chemical Vapor Deposition, Jpn. J. Appl. Phys., 2013, 52, 035202 CrossRef.
- L. Ci, H. Zhu, B. Wei, J. Liang, C. Xu and D. Wu, Phosphorus - a new element for promoting growth of carbon filaments by the floating catalyst method, Carbon, 1999, 37, 1652–1654 CrossRef CAS.
- B. Mas, B. Alemán, I. Dopico, I. Martin-Bragado, T. Naranjo, E. M. Pérez and J. J. Vilatela, Group 16 elements control the synthesis of continuous fibers of carbon nanotubes, Carbon, 2016, 101, 458–464 CrossRef CAS.
- M. C. Diaz and P. B. Balbuena, On the role of surface oxygen during nascent single-walled carbon nanotube cap spreading and tube nucleation on iron catalysts, Carbon, 2021, 184, 470–478 CrossRef CAS.
- R. M. Sundaram, K. K. K. Koziol and A. H. Windle, Continuous Direct Spinning of Fibers of Single-Walled Carbon Nanotubes with Metallic Chirality, Adv. Mater., 2011, 23, 5064–5068 CrossRef CAS PubMed.
- B. Alemán, M. M. Bernal, B. Mas, E. M. Pérez, V. Reguero, G. Xu, Y. Cui and J. J. Vilatela, Inherent predominance of high chiral angle metallic carbon nanotubes in continuous fibers grown from a molten catalyst, Nanoscale, 2016, 8, 4236–4244 RSC.
- R. Rao, N. Pierce, X. Zhang, R. Wheeler, B. Maruyama and S. Talapatra, Understanding the Role of Sulfur in Tuning the Diameter and Morphology in the Chemical Vapor Deposition Growth of Carbon Nanotubes, Mater. Express, 2011, 1, 160–166 CrossRef CAS.
- T. S. Gspann, F. R. Smail and A. H. Windle, Spinning of carbon nanotube fibres using the floating catalyst high temperature route: purity issues and the critical role of sulphur, Faraday Discuss., 2014, 173, 47–65 RSC.
- L. Zhang, P. X. Hou, S. Li, C. Shi, H. T. Cong, C. Liu and H. M. Cheng, In situ TEM observations on the sulfur-assisted catalytic growth of single-wall carbon nanotubes, J. Phys. Chem. Lett., 2014, 5, 1427–1432 CrossRef CAS PubMed.
- P. Forzatti, Catalyst deactivation, Catal. Today, 1999, 52, 165–181 CrossRef CAS.
- M. D. Yadav and K. Dasgupta, Role of sulfur source on the structure of carbon nanotube cotton synthesized by floating catalyst chemical vapour deposition, Chem. Phys. Lett., 2020, 748, 137391 CrossRef CAS.
- V. Jourdain and C. Bichara, Current understanding of the growth of carbon nanotubes in catalytic chemical vapour deposition, Carbon, 2013, 58, 2–39 CrossRef CAS.
- J. E. Mueller, A. C. T. van Duin and W. A. Goddard, Development and Validation of ReaxFF Reactive Force Field for Hydrocarbon Chemistry Catalyzed by Nickel, J. Phys. Chem. C, 2010, 114, 4939–4949 CrossRef CAS.
- D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons, J. Phys.: Condens. Matter, 2002, 14, 783–802 CrossRef CAS.
- A. Martinez-Limia, J. Zhao and P. B. Balbuena, Molecular dynamics study of the initial stages of catalyzed single-wall carbon nanotubes growth: Force field development, J. Mol. Model., 2007, 13, 595–600 CrossRef CAS PubMed.
- F. Ding, K. Bolton and A. Rosén, Nucleation and growth of single-walled carbon nanotubes: A molecular dynamics study, J. Phys. Chem. B, 2004, 108, 17369–17377 CrossRef CAS.
- F. Ding, A. Rosén and K. Bolton, Molecular dynamics study of the catalyst particle size dependence on carbon nanotube growth, J. Chem. Phys., 2004, 121, 2775 CrossRef CAS PubMed.
- F. Ding, A. Rosén and K. Bolton, The role of the catalytic particle temperature gradient for SWNT growth from small particles, Chem. Phys. Lett., 2004, 393, 309–313 CrossRef CAS.
- F. Ding, A. Rosén and K. Bolton, Dependence of SWNT growth mechanism on temperature and catalyst particle size: Bulk versus surface diffusion, Carbon, 2005, 43, 2215–2217 CrossRef CAS.
- Y. Ohta, Y. Okamoto, S. Irle and K. Morokuma, Density-functional tight-binding molecular dynamics simulations of SWCNT growth by surface carbon diffusion on an iron cluster, Carbon, 2009, 47, 1270–1275 CrossRef CAS.
- Y. Ohta, Y. Okamoto, S. Irle and K. Morokuma, Single-walled carbon nanotube growth from a cap fragment on an iron nanoparticle: Density-functional tight-binding molecular dynamics simulations, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 1–7 Search PubMed.
- Y. Ohta, Y. Okamoto, A. J. Page, S. Irie and K. Morokuma, Quantum chemical molecular dynamics simulation of single-walled carbon nanotube cap nucleation on an iron particle, ACS Nano, 2009, 3, 3413–3420 CrossRef CAS PubMed.
- A. J. Page, S. Minami, Y. Ohta, S. Irle and K. Morokuma, Comparison of single-walled carbon nanotube growth from Fe and Ni nanoparticles using quantum chemical molecular dynamics methods, Carbon, 2010, 48, 3014–3026 CrossRef CAS.
- Y. Wang, X. Gao, H. J. Qian, Y. Ohta, X. Wu, G. Eres, K. Morokuma and S. Irle, Quantum chemical simulations reveal acetylene-based growth mechanisms in the chemical vapor deposition synthesis of carbon nanotubes, Carbon, 2014, 72, 22–37 CrossRef CAS.
- R. Yoshikawa, K. Hisama, H. Ukai, Y. Takagi, T. Inoue, S. Chiashi and S. Maruyama, Molecular Dynamics of Chirality Definable Growth of Single-Walled Carbon Nanotubes, ACS Nano, 2019, 13, 6506–6512 CrossRef CAS PubMed.
- S. Fukuhara and Y. Shibuta, Free energy surface of initial cap formation in carbon nanotube growth, Nanoscale Adv., 2021, 3, 6191–6196 RSC.
- Z. Xu, T. Yan and F. Ding, Atomistic simulation of the growth of defect-free carbon nanotubes, Chem. Sci., 2015, 6, 4704–4711 RSC.
- Z. Xu and F. Ding, Catalyst particle size dependent carbon nanotube cloning, Carbon, 2021, 175, 69–76 CrossRef CAS.
- M. Diarra, A. Zappelli, H. Amara, F. Ducastelle and C. Bichara, Importance of carbon solubility and wetting properties of nickel nanoparticles for single wall nanotube growth, Phys. Rev. Lett., 2012, 109, 1–5 CrossRef PubMed.
- E. C. Neyts, A. C. T. van Duin and A. Bogaerts, Changing Chirality during Single-Walled Carbon Nanotube Growth: A Reactive Molecular Dynamics/Monte Carlo Study, J. Am. Chem. Soc., 2011, 133, 17225–17231 CrossRef CAS PubMed.
- E. C. Neyts, A. C. T. van Duin and A. Bogaerts, Insights in the Plasma-Assisted Growth of Carbon Nanotubes through Atomic Scale Simulations: Effect of Electric Field, J. Am. Chem. Soc., 2012, 134, 1256–1260 CrossRef CAS PubMed.
- U. Khalilov, A. Bogaerts and E. C. Neyts, Microscopic mechanisms of vertical graphene and carbon nanotube cap nucleation from hydrocarbon growth precursors, Nanoscale, 2014, 6, 9206–9214 RSC.
- U. Khalilov, A. Bogaerts and E. C. Neyts, Atomic scale simulation of carbon nanotube nucleation from hydrocarbon precursors, Nat. Commun., 2015, 6, 10306 CrossRef CAS PubMed.
- Y. Xu, Y. Ma, Y. Liu, S. Feng, D. He, P. Haghi-Ashtiani, A. Dichiara, L. Zimmer and J. Bai, Evolution of Nanoparticles in the Gas Phase during the Floating Chemical Vapor Deposition Synthesis of Carbon Nanotubes, J. Phys. Chem. C, 2018, 122, 6437–6446 CrossRef CAS.
- L. P. Ding, B. McLean, Z. Xu, X. Kong, D. Hedman, L. Qiu, A. J. Page and F. Ding, Why Carbon Nanotubes Grow, J. Am. Chem. Soc., 2022, 144, 5606–5613 CrossRef CAS PubMed.
- C. Wang, L. Zhan, Y. Wang, W.-M. Qiao, X. Liang and L.-C. Ling, Effect of sulfur on the growth of carbon nanotubes by detonation-assisted chemical vapor deposition, Appl. Surf. Sci., 2010, 257, 932–936 CrossRef CAS.
- J. M. Romo-Herrera, B. G. Sumpter, D. A. Cullen, H. Terrones, E. Cruz-Silva, D. J. Smith, V. Meunier and M. Terrones, An Atomistic Branching Mechanism for Carbon Nanotubes: Sulfur as the Triggering Agent, Angew. Chem., Int. Ed., 2008, 47, 2948–2953 CrossRef CAS PubMed.
- S. Suzuki and S. Mori, Promoted growth of carbon nanotubes by sulfur addition in chemical vapor deposition shown via Arrhenius law, Diam. Relat. Mater., 2018, 89, 74–83 CrossRef CAS.
- S. Suzuki and S. Mori, The role of sulfur in promoted growth of carbon nanotubes in chemical vapor deposition proposed through the characterizations on catalytic nanoparticles, Appl. Surf. Sci., 2019, 471, 587–594 CrossRef CAS.
- J. J. Mortensen, L. B. Hansen and K. W. Jacobsen, Real-space grid implementation of the projector augmented wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Møller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. H. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, Electronic structure calculations with GPAW: a real-space implementation of the projector augmented-wave method, J. Phys.: Condens. Matter, 2010, 22, 253202 CrossRef CAS PubMed.
- A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- V. R. Cooper, van der Waals density functional: An appropriate exchange functional, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 161104 CrossRef.
- I. Hamada and M. Otani, Comparative van der Waals density-functional study of graphene on metal surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 1–4 CrossRef.
- K. Toyoda, K. Nozawa, N. Matsukawa and S. Yoshii, Density Functional Theoretical Study of Graphene on Transition-Metal Surfaces: The Role of Metal d-Band in the Potential-Energy Surface, J. Phys. Chem. C, 2013, 117, 8156–8160 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Structural Relaxation Made Simple, Phys. Rev. Lett., 2006, 97, 170201 CrossRef PubMed.
- F. Silvearv, P. Larsson, S. L. T. Jones, R. Ahuja and J. A. Larsson, Establishing the most favorable metal–carbon bond strength for carbon nanotube catalysts, J. Mater. Chem. C, 2015, 3, 3422–3427 RSC.
- M. Onink, C. M. Brakman, F. D. Tichelaar, E. J. Mittemeijer, S. van der Zwaag, J. H. Root and N. B. Konyer, The lattice parameters of austenite and ferrite in Fe-C alloys as functions of carbon concentration and temperature, Scr. Metall. Mater., 1993, 29, 1011–1016 CrossRef CAS.
- X. Zhang and S. Wang, First-principles investigation of the microscopic mechanism of the physical and chemical mixed adsorption of graphene on metal surfaces, RSC Adv., 2019, 9, 32712–32720 RSC.
- C. S. T. Peraça, G. R. Nagurniak, R. P. Orenha, R. L. T. Parreira and M. J. Piotrowski, A theoretical indicator of transition-metal nanoclusters applied in the carbon nanotube nucleation process: A DFT study, Dalton Trans., 2020, 49, 492–503 RSC.
- S. Taubert and K. Laasonen, The molecular and magnetic structure of carbon-enclosed and partially covered Fe55 particles, Phys. Chem. Chem. Phys., 2014, 16, 3648–3660 RSC.
- X. Li, J. Feng, E. Wang, S. Meng, J. Klime and A. Michaelides, Influence of water on the electronic structure of metal-supported graphene: Insights from van der Waals density functional theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 1–10 Search PubMed.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, Revealing Noncovalent Interactions, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, NCIPLOT: A Program for Plotting Noncovalent Interaction Regions, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Verification of computation methods, further analysis and atomic coordinates. See DOI: https://doi.org/10.1039/d2dt00355d |
| This journal is © The Royal Society of Chemistry 2022 |