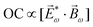Open Access Article
Open Access ArticleUltrafast chirality: the road to efficient chiral measurements
David
Ayuso
 ab,
Andres F.
Ordonez
ab,
Andres F.
Ordonez
 ac and
Olga
Smirnova
ac and
Olga
Smirnova
 *ad
*ad
aMax-Born-Institut, 12489 Berlin, Germany
bImperial College London, SW7 2AZ London, UK. E-mail: d.ayuso@imperial.ac.uk
cICFO-Institut de Ciencies Fotoniques, The Barcelona Institute of Science and Technology, 08860 Barcelona, Spain. E-mail: andres.ordonez@icfo.eu
dTechnische Universität Berlin, 10623 Berlin, Germany. E-mail: olga.smirnova@mbi-berlin.de
First published on 7th November 2022
Abstract
Today we are witnessing the electric–dipole revolution in chiral measurements. Here we reflect on its lessons and outcomes, such as the perspective on chiral measurements using the complementary principles of “chiral reagent” and “chiral observer”, the hierarchy of scalar, vectorial and tensorial enantio-sensitive observables, the new properties of the chiro-optical response in the ultrafast and non-linear domains, and the geometrical magnetism associated with the chiral response in photoionization. The electric–dipole revolution is a landmark event. It has opened routes to extremely efficient enantio-discrimination with a family of new methods. These methods are governed by the same principles but work in vastly different regimes – from microwaves to optical light; they address all molecular degrees of freedom – electronic, vibrational and rotational, and use flexible detection schemes, i.e. detecting photons or electrons, making them applicable to different chiral phases, from gases to liquids to amorphous solids. The electric–dipole revolution has also enabled enantio-sensitive manipulation of chiral molecules with light. This manipulation includes exciting and controlling ultrafast helical currents in vibronic states of chiral molecules, enantio-sensitive control of populations in electronic, vibronic and rotational molecular states, and opens the way to efficient enantio-separation and enantio-sensitive trapping of chiral molecules. The word “perspective” has two meanings: an “outlook” and a “point of view”. In this perspective article, we have tried to cover both meanings.
1 Introduction
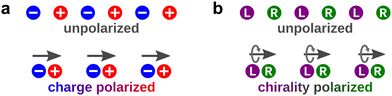
Chirality is a fundamental concept of geometrical origin ubiquitous in nature, from elementary particles to molecules to macroscopic objects. Chiral molecules are characterised by the spatial arrangement of their nuclei, which makes them non-superimposable on their mirror image. The two mirror-reflected versions of a chiral molecule are called enantiomers. Two opposite enantiomers of the same molecule interact differently with other chiral objects, such as chiral light or another chiral molecule.† This property underlies their important function in chemistry and biology: chiral structure facilitates recognition at the molecular level, which is a key component of metabolic reactions in biological organisms.Most biologically relevant molecules are chiral, and many appear in nature only in one of their two possible forms.1 Whereas the amino acids found in living beings are essentially left-handed, sugars are right-handed. While the origin of biological homochirality, i.e. the single-handedness of key biomolecules, is still debated,2–12 its importance could be related to the fact that this geometrically protected quantity – handedness – carries a single bit of information10 – left or right, i.e. “true” or “false”. Then, to enable such information processing in biological systems, the balance between left and right must be broken. The measure of such imbalance, the enantiomeric excess, is maximized in homochiral systems, making them ideal for chirality-based information processing in living organisms.
Since handedness is a key element in molecular recognition, it is both fundamentally interesting and important to learn how it is encoded in interactions between chiral molecules and light.
Many applications use chirality for characterizing molecular structures via linear light-matter interaction. For example, absorption circular dichroism (CD)‡ measurements are routinely used to characterize the helical structures of DNA, RNA, and some proteins. The results are typically interpreted on a phenomenological basis, e.g. by comparing to benchmark structures. The physical understanding of chirality at the molecular level, i.e. at the level of the relevant properties of electronic structure and dynamics, is challenging. Indeed, little is known about the dynamics of chirality in terms of concepts such as electronic ring currents13–15 and the fields they may generate inside molecules,16,17 ultrafast charge migration18–27 or nonlinear electronic response.28 Yet, the dynamical response provides a different and independent access to the physical mechanisms underlying the chiral function.
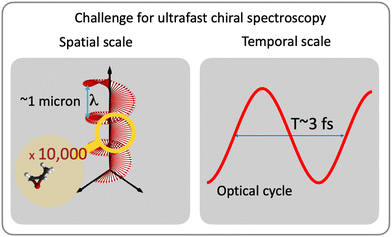
While understanding chiral interactions and time-resolving chiral electronic or vibronic dynamics are much desired, most of the existing ultrafast methods are restricted to weak interactions with the magnetic component of the light field (e.g. ref. 29–38). In the IR-VUV range, such restriction severely limits their efficiency for medium-size molecules or chiral moieties, with useful time-resolved signals often just above the noise. A recent experiment35 graphically demonstrates the challenges: the time-resolved CD signal is only a few percent of the static CD and is on the order of the baseline stability of the setup. While standard CD signal relying on interaction with the magnetic field can be improved e.g. by using broadband ultrafast circular dichroism spectroscopy in the deep ultraviolet in combination with transient absorption measurements,39 or using short-wavelength light,31–33,40,41 developing ultrafast and highly enantio-sensitive approaches, which track electronic/vibronic dynamics without relying on magnetic interactions, is an important challenge. This challenge has been taken on by the electric–dipole revolution in chiral measurements. It began decades ago,42–44 but is steadily picking up the pace now, just as we are writing these words. It involves several extremely efficient enantio-sensitive methods that rely on purely electric–dipole interactions and address electronic,42–83 vibrational57,72,80,84 and rotational85–99 degrees of freedom in molecules. Importantly, the analysis of the already existing methods allows one to identify the key common principles underlying all these schemes and formulate general requirements for experimental setups,88 which should help one to create new efficient enantio-sensitive approaches, tailored to the needs, tasks and means of a given laboratory.
Here we formulate the key principles underlying efficient and ultrafast chiral measurements operating in the electric–dipole approximation. We also describe where we see future challenges and frontiers in developing such methods. Throughout the paper we discuss several enantio-sensitive phenomena. We introduce several rules characterizing the interaction of chiral molecules with light, and present new fundamental concepts relevant for enantio-sensitive optical measures.
Our perspectives include not only an outlook for the future, but also a general view on the basic principles underlying various chiral measurements and on how these principles can be used to develop new measurement approaches and increase their efficiency. We begin our analysis with a tutorial-style introduction into the basic principles underlying chiral measurements. This analysis is presented in Section 2 and focuses on the interaction of chiral molecules with light (or electromagnetic, EM, fields). We introduce the concepts of chiral reagent and chiral observer as two fundamental principles that allow one to construct and analyse chiral measurements and establish a generalized perspective on chiral measurements common to different observation regimes.
These two principles offer complementary approaches. The principle of chiral reagent involves enantio-sensitive interactions of electromagnetic fields with molecules, whereas the chiral observer, does not. We show how both approaches can be upgraded in their efficiency, i.e. realized within the electric–dipole approximation (Sections 3 and 4), enabling extremely efficient enantio-sensitive signals from gas-phase molecules and creating new opportunities for efficient probes of chiral liquids. Section 2 includes a generalized vision of the structure of generic chiral observables, and of how they map onto the ultrafast response of molecules to light. We shall see that there exists a hierarchy of chiral observables encompassing scalar, vectorial and tensorial quantities. That is, there are infinitely many of them, allowing for significant flexibility in constructing chiral measurements, an important asset for future experiments.
In Section 3, we show that we do not need to rely on light's chirality to probe the chirality of matter. It can be substituted by the chirality of an experimental setup. The flexibility in designing chiral experimental setups offers additional flexibility for efficient enantio-discrimination. We shall see that there is a chirality measure for experimental setups, which serves as a guideline for optimizing their enantio-sensitivity.
In Section 4, we show how light can be chiral already in the electric–dipole approximation.100–102 We shall see that the chirality measures for matter, light, or experimental setups have an identical structure, and that there are arrays of these measures with an identical hierarchy, from scalars to vectors to tensors of various ranks. We also describe how, in the outcome of an experiment, the chirality measure of matter couples to the chirality measure of light, or to the chirality measure of the experimental setup, to produce enantio-sensitive observables.
Section 5 describes how the handedness of light can be structured in space, and how such chirality-structured light can be used for efficient enantio-discrimination. Section 6 outlines our perspectives on efficient control and manipulation of chiral molecules with light, and charts the roads for new and highly enantio-sensitive approaches. In Section 7, we discuss how we can imprint the chirality of light onto objects which are initially achiral, such as atoms, driving achiral-to-chiral transitions in matter.
Section 8 discusses a geometric perspective on enantio-sensitive observables in photoionization of chiral molecules, and on how geometry affects the physical mechanism of a chiral response. In condensed matter physics it has been recently realized that the manner in which geometric properties of nuclear configurations in solids map onto the geometrical properties of the Hilbert space is very important. This mapping leads to the concepts of Berry phase103 and Berry curvature, topological phases,104,105 and the general concept of geometrical magnetism in solids, providing a novel framework for understanding electronic response.106 About 20% of all materials known today have electronic properties dictated by the topology of their electronic wave functions,107 and quantified by the Berry curvature. Therefore, we expect that geometry and topology should also play a prominent role in the electronic response of chiral molecules and should lead to new enantio-sensitive phenomena,108,109 especially in the non-linear response.
Our expectations are based on our recent finding of the parallels between the Berry curvature in solids and a geometric ‘propensity’ field generated by electronic dynamics in chiral molecules.108 This field maps the geometric properties of nuclear arrangements sensed by chiral electron currents onto chiral observables in photoionization. In particular, it controls the strength of the enantio-sensitive photoionization current110 orthogonal to the polarization plane of the circularly polarized driving laser field, known as the photoelectron circular dichroism (PECD) in one photon ionization.42,43,45–57 This control is formally similar108 to how the Berry curvature controls, e.g. the current in circular photogalvanic effect in 3D materials lacking inversion symmetry, or the anomalous current in 2D two-band topological materials. We expect that PECD is but a tip of the iceberg: the geometric propensity field (Section 8.6) provides a guiding principle for uncovering new enantio-sensitive observables in photoionization.108
Section 9 provides a unified perspective on the hierarchy of chiral measures. We review how the chirality of matter couples to the chirality of light or the chirality of an experimental setup to produce enantio-sensitive observables. Section 10 concludes the paper.
2 Probing chirality: introducing the concepts of chiral observer and chiral reagent
How do we find out if an object is chiral or not, and how do we probe its handedness? In the macro-world, we can compare the object with its mirror image. This detection principle uses the concept of “chiral observer”; the rigorous definition will follow.Probing chirality can also involve interaction between two chiral objects. One example is a proper handshake, which requires the two enantiomers – the two hands – to have the same handedness. This detection principle uses a “chiral reagent”, which interacts differently with left- and right-handed objects.
In the micro-world, a chiral reagent can simply be another chiral molecule. The basic reason for the different outcome of a chemical reaction involving chiral molecules is the key difference in their shape.
Light can also act as a chiral reagent. It is well known that the electric-field vector of a circularly polarized wave draws a basic chiral structure in space: a helix (Fig. 1). Thus, circularly polarized light is a chiral photonic reagent, which interacts differently with left- and right-handed molecules. The most prominent example being that left- and right-handed molecules absorb different amounts of circularly polarized light of a given handedness, a phenomenon known as photo-absorption circular dichroism (CD).
Absorption CD is still the method of choice (e.g. ref. 34, 35 and 111) among all-optical methods. Unfortunately, the CD signal is very weak (three to five orders of magnitude smaller than light absorption at the same frequency), as it scales with the ratio of the molecular size to the light's wavelength (i.e. pitch of the helix). Optical rotation is a complementary approach based on detecting the rotation of the polarization of a linearly polarized pulse propagating through a chiral medium. It has the same unfavourable scaling,29,30 especially in the IR-UV range and for small and medium-size molecules. This makes time-resolved measurements very challenging, especially in optically thin media, unless one uses X-ray light to match the pitch of the helix to the molecular size40,41,112,113 or very intense fields36,114–118 to generate and record high harmonic spectra. Both routes can enhance the chiral dichroism from 0.01% to a few percent level. There are also new measurement regimes, such as e.g. broadband ultrafast circular dichroism spectroscopy in the deep ultraviolet in combination with transient absorption measurements,39 or ingenious field configurations that rely on suppression of the electric–dipole interaction (e.g. ref. 119–122) to maximise the contribution of “traditional” magnetic–dipole terms, emerging due to the light helix. Further improvements require one to abandon weak magnetic interactions and rely exclusively on electric–dipole transitions.
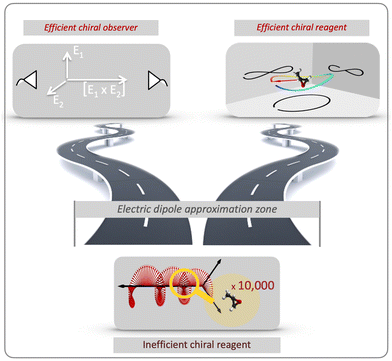
There are two roads that one can take (Fig. 2). The first option is to develop new approaches that do not rely on the chiral properties of light. Along this road we will meet a chiral observer. The second option is to replace the inefficient (non-local) chiral reagent – the helix drawn by the light's polarization vector in space – with an efficient (local) chiral reagent – a helix, or any other chiral structure, drawn by light's electric vector in time. We shall see that these two roads will take us to fundamentally different observables. But let us first recall how one can characterize the handedness of a chiral object.
2.1 Chiral observables
Let us consider left-chewing and right-chewing cows123,124 as prototypical carriers of chiral dynamics,§ and define a number that characterizes its handedness. While the jaws of a cow make a rotating motion, the food moves in the direction orthogonal to the plane of this rotation, see Fig. 3. The chiral dynamics emerging in this process is associated with two directions. The first is the direction in which food goes, which is a vector![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) . The second is the pseudo-vector of the angular momentum
. The second is the pseudo-vector of the angular momentum ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) associated with the rotation of the jaw. An example of a chiral observable, h, is a number incorporating these two key directions: the scalar product of
associated with the rotation of the jaw. An example of a chiral observable, h, is a number incorporating these two key directions: the scalar product of ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) and
and ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) ,
,h = ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) · ·![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) . . | (1) |
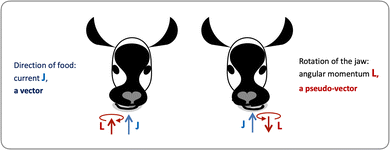 | ||
Fig. 3 Left- and right-chewing (chiral) cows convert in-plane rotation of the jaw, characterized by the pseudo-vector ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) , into out-of-plane food motion, characterized by the vector , into out-of-plane food motion, characterized by the vector ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) . . | ||
As ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) is a pseudo-vector and
is a pseudo-vector and ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) is a vector, h is a pseudoscalar. Note that a pseudovector can be generated by taking the vector product of two vectors, e.g.
is a vector, h is a pseudoscalar. Note that a pseudovector can be generated by taking the vector product of two vectors, e.g. ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) = [
= [![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ×
× ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) ], and thus the chiral observable can also be given by a triple product of three vectors. Pseudo-scalars change sign upon mirror reflection and are, therefore, ideally suited to distinguish opposite enantiomers.
], and thus the chiral observable can also be given by a triple product of three vectors. Pseudo-scalars change sign upon mirror reflection and are, therefore, ideally suited to distinguish opposite enantiomers.
An important conclusion from the above example is that a chiral system can convert in-plane rotation into linear motion orthogonal to this plane. We shall see that this can lead to helical electron currents excited in molecules by circularly polarized electric fields. It is this coupling that “merges” the pseudovector ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) with the vector
with the vector ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) into a chiral molecular pseudoscalar h. Often the pseudovector component
into a chiral molecular pseudoscalar h. Often the pseudovector component ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) is responsible for encoding the in-plane rotation induced, e.g. by a circularly polarized electric field, while the vectorial component
is responsible for encoding the in-plane rotation induced, e.g. by a circularly polarized electric field, while the vectorial component ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) can be used to read out the enantio-sensitive signal, provided that a chiral reference frame (chiral observer) is defined by the experimental set-up.
can be used to read out the enantio-sensitive signal, provided that a chiral reference frame (chiral observer) is defined by the experimental set-up.
2.2 Hierarchy of scalar, vectorial and tensorial observables
Experiments always measure “clicks”, which are scalars. Then, how are pseudoscalars encoded in experimental observables? Let us consider the two oldest and most common optical techniques of chiral discrimination, photo-absorption circular dichroism and optical rotation, from this perspective.How does the situation change if we have a setup that allows us to measure vectorial observables, such as the polarization of light transmitted through a medium of randomly oriented chiral molecules? The canonical example of such a setup is the detection of chirality via optical rotation. Optical rotation, observed by Biot in 1815, was the first experiment that revealed molecular chirality, but its deep lessons have become especially pertinent now in the light of the electric–dipole revolution. Namely, optical rotation does not use chiral light: it uses linearly polarized light and detects the rotation of its polarization.
![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) and (ii) the ability to distinguish positive from negative rotations around the polar vector
and (ii) the ability to distinguish positive from negative rotations around the polar vector ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) . Since rotations are characterized by pseudovectors, this ability requires the definition of a unitary rotation pseudovector
. Since rotations are characterized by pseudovectors, this ability requires the definition of a unitary rotation pseudovector ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) such that
such that ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ·
·![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ≠ 0. A polarizer rotating in the plane orthogonal to the light propagation vector defines such a pseudovector, because the direction of polarizer rotation defines an oriented plane.
≠ 0. A polarizer rotating in the plane orthogonal to the light propagation vector defines such a pseudovector, because the direction of polarizer rotation defines an oriented plane.
When taken together, the vector ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) associated with light and the pseudovector
associated with light and the pseudovector ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) associated with the rotation of the polarizer in the laboratory reference frame form a chiral setup. The handedness of this setup is given by a pseudoscalar
associated with the rotation of the polarizer in the laboratory reference frame form a chiral setup. The handedness of this setup is given by a pseudoscalar ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ·
·![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) .
.
This handedness of the setup emerges naturally within a formal description of the phenomenon. Indeed, such a description yields an angle of rotation 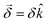 , where
, where 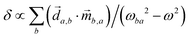 is a molecular pseudoscalar with opposite signs for opposite enantiomers, a and b denote the ground and excited states, respectively, the sum is taken over all excited states,
is a molecular pseudoscalar with opposite signs for opposite enantiomers, a and b denote the ground and excited states, respectively, the sum is taken over all excited states, ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) a,b and
a,b and ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) b,a are the transition matrix elements for the electric- and magnetic-dipole operators
b,a are the transition matrix elements for the electric- and magnetic-dipole operators ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) and
and ![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) , respectively, ω is the light frequency and ωab ≡ ωb − ωa. In writing
, respectively, ω is the light frequency and ωab ≡ ωb − ωa. In writing 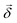 vectorially, we have explicitly indicated that the rotation of the plane of polarization (measured by the polarizer
vectorially, we have explicitly indicated that the rotation of the plane of polarization (measured by the polarizer ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ) is defined with respect to
) is defined with respect to ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) .
.
As for any vectorial measurement, what the experiment reveals are its components with respect to some reference frame. In our case, the relevant unitary (pseudo) vector in our reference frame is ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) so that the measurement yields the scalar quantity
so that the measurement yields the scalar quantity 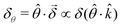 . That is, the rotation angle δθ measured in the chosen reference frame is the product of two pseudoscalars, one associated with the molecule (δ) and the other associated with the setup (
. That is, the rotation angle δθ measured in the chosen reference frame is the product of two pseudoscalars, one associated with the molecule (δ) and the other associated with the setup (![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) ·
·![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) ). If either the handedness of the molecules or of the setup is reversed, δθ changes sign.
). If either the handedness of the molecules or of the setup is reversed, δθ changes sign.
Neither the linearly polarized light, nor the polarizer are chiral on their own. Separately, they are not suited to detect chirality, but together they form the chiral setup, or the chiral reference frame of the observer. Thus, vectorial observables allow one to substitute a chiral reagent by a chiral observer, i.e. a chiral setup formed by any chiral combination of achiral fields and achiral detectors.
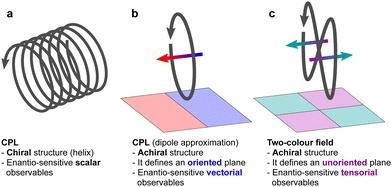
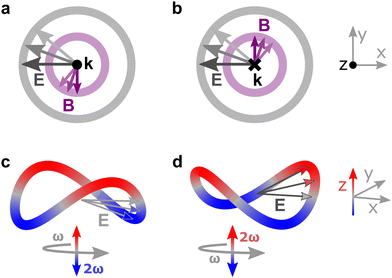
Importantly, circularly polarized light in the electric–dipole approximation is not chiral: the spatial helix drawn by the rotating electric-field vector as the light propagates in space (Fig. 4a) is lost in the electric–dipole approximation. Geometrically, in this approximation, the rotation of the electric-field vector only defines an oriented plane (Fig. 4b). The light supplies a pseudovector, which defines the plane's orientation and is the vector product of the two orthogonal components of the light's polarization. To compose a chiral observer, one needs to complement this pseudovector with a vector orthogonal to the polarization plane. This vector can be supplied by the detector axis.
When the light field can provide a pseudovector, such as the vector product of its two orthogonal polarization components, the enantio-sensitive and dichroic signal will be a vector collinear with the light pseudovector. But what if the light field does not define an oriented plane, and therefore it cannot provide a pseudovector?
A two-color field with orthogonal ω and 2ω polarizations is one example of such a field (Fig. 4c). Its Lissajous figure changes the direction of rotation twice per laser period. Such a field does not define an oriented plane and therefore it does not provide a pseudovector. Yet, it can still be employed for enantio-discrimination76–78 using a chiral observer. In this case, the chiral observer has to supply not one, but two detector axes. The first one should be along the direction orthogonal to the polarization plane; the second one should break the symmetry between the two counter-rotating parts of the figure eight (see Fig. 4c), i.e. should be directed along the polarization of the fundamental field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω. Thus, the chiral observer can employ two axes defined by the detector. These two axes define a quadrupolar detector, which allows one to correlate measurements in two detection directions. The quadrupolar detector identifies positive or negative correlations between the observables measured along two orthogonal axes. Such a correlation of different detection directions results in tensorial chiral observables.125
ω. Thus, the chiral observer can employ two axes defined by the detector. These two axes define a quadrupolar detector, which allows one to correlate measurements in two detection directions. The quadrupolar detector identifies positive or negative correlations between the observables measured along two orthogonal axes. Such a correlation of different detection directions results in tensorial chiral observables.125
The concept of chiral observer embodies a powerful principle of detecting chirality. It allows one to detect chirality using a collection of two (or more) non-chiral objects, which are able to collectively form a single chiral object – a chiral reference frame, which is used to detect a vectorial (or tensorial) observable. Of course, none of these objects interacts with a chiral molecule in an enantio-sensitive way, as a chiral reagent does.
The power of the chiral observer comes from the freedom to compose this observer from any vectors available in the experiment, and the general framework for designing such measurements. The measurement no longer has to rely on light's magnetic field to probe chiral molecules, eschewing the need to focus on weak non-electric–dipole effects and taking maximum advantage of available tools and experimental specifics.
2.3 Two electric–dipole revolutions in chiral measurements
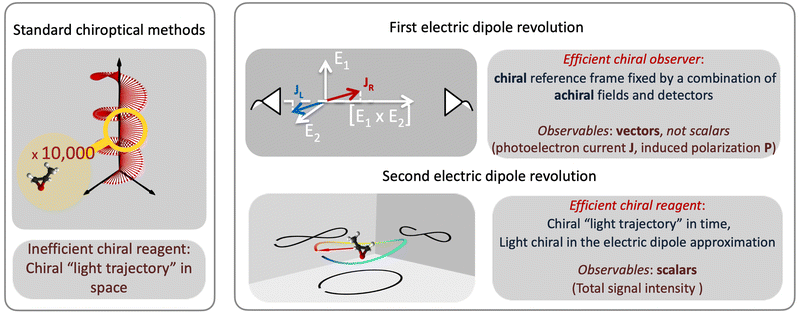
Revolutions often come in sequence. The first electric–dipole revolution (Fig. 5) in chiral measurements has “revolutionized” the observer: non-chiral light, interacting with matter in the electric–dipole approximation, in combination with the detection system, has become a very efficient tool for chiral discrimination.42–87 Since the concept of chiral observer is completely general, it can be applied in a variety of experiments. Such experiments can detect photo-electrons,42,43,45–79 or molecular fragments,126,127 or photons, such as optical light,44,80 microwave emission,85–87etc. Below we shall briefly outline several “chiral observer” methods developed so far, from photoionization to microwave detection to non-linear optics.Yet, there is one thing that a chiral observer cannot do: it cannot detect enantio-sensitive scalar observables. This is where the second electric dipole revolution comes into play (Fig. 5). It aims to revolutionize the chiral reagent, i.e. to create and use light100,128–136 or a combination of electric fields89,90,95,99,101,102 that is chiral already in the electric-dipole approximation. This means that the electric-field vector of such light, at any given point in space, should draw a chiral Lissajous figure during its oscillation period. We shall refer to it as “synthetic chiral light”100 to distinguish it from standard chiral light, i.e. standard light helix in space.
Since synthetic chiral light (or chiral combination of electric fields including static or microwave electric fields) possesses its own pseudoscalar, it can provide access to scalar observables such as enantio-sensitive populations of molecular electronic, vibronic and rotational states.90,95,99 Enantio-sensitive control of populations opens a way to extremely efficient manipulation of chiral molecules such as e.g. enantio-separation, enantio-sensitive trapping, and possibly even to enantio-sensitive cooling if (or when) the huge challenges in cooling large molecules are resolved.
The pseudoscalar of synthetic chiral light does not include its magnetic-field component: it is constructed from at least three non-coplanar electric-field components. Thus, the electric-field vector of such light needs to be 3D, a property that may arise in non-collinear configurations,81,100,128–131 in tightly focused laser beams83,132 or inside nano-photonic structures,137 thanks to the emergence of longitudinal components.138 What's more, it has to be multi-color, since the three electric-field vectors have to be distinguishable. It also means that such light can sense the chirality of matter only via non-linear interactions, as it has to encode the three field components into the light-induced transition.
Importantly, the pseudoscalar – the chirality measure h of synthetic chiral light – is local, because it is defined in the electric–dipole approximation. To control total enantio-sensitive absorption in the entire sample, synthetic chiral light should maintain its handedness globally, across the whole interaction region. That is, its pseudoscalar should maintain its sign from one spatial point to another, or at the very least be non-zero on average in space. This can be achieved in different ways, one of them is discussed in Section 4.
If the light field is not globally chiral, i.e. its pseudoscalar h = h(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) is zero on average,
) is zero on average, 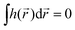 , higher multipoles of light's handedness will start to play a key role. For example, we shall see that the presence of the chirality dipole
, higher multipoles of light's handedness will start to play a key role. For example, we shall see that the presence of the chirality dipole 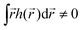 , which characterizes the spatial distribution of local handedness in a locally chiral field with
, which characterizes the spatial distribution of local handedness in a locally chiral field with 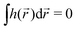 , would lead to enantio-sensitive emission direction of light generated from the molecular sample via non-linear processes such as even harmonic generation.128
, would lead to enantio-sensitive emission direction of light generated from the molecular sample via non-linear processes such as even harmonic generation.128
Looking broadly, sculpting multi-color light beams in three dimensions and applying them to chiral molecules appears as a natural next step for the rapidly developing field of generating and using vector beams. This step is compelled by the rich opportunities arising from the interaction of such synthetic chiral light with chiral matter.
3 The first electric–dipole revolution in chiral measurements: efficient chiral observer
The “chiral observer” is a concept of chiral measurement in which the detection relies not on the interaction of two chiral objects, but rather on the interaction of a chiral object with two or more achiral objects arranged in such a way that together they form a chiral experimental setup, i.e. the experimental setup becomes a chiral object. A chiral observer can detect enantio-sensitive vectorial88 and tensorial125 observables. In the simplest case of vectorial observables, the chiral setup provides a reference frame, right or left, defined by three non-coplanar vectors. The chiral measurement has to be resolved in this reference frame. Tensorial chiral observables couple to chiral tensorial detectors, correlating two or more detection directions in an enantio-sensitive way. Enantio-sensitive scalar observables, such as the total intensity of a signal, cannot be produced or measured in such a setup, since the interaction of two chiral objects is not involved.A chiral observer does not require chiral light, and therefore the chiral optical enantio-sensitive response can be induced via strong electric–dipole interactions, leading to highly efficient enantio-sensitive signals. This is the essence of the first electric–dipole revolution: strong enantio-sensitive response without chiral light. It has brought a family of new methods benefiting from highly-efficient enentio-sensitive signals based on detecting electrons or photons: PECD in one-photon42,43,45–57 and multi-photon regimes,58–71 PXECD and PXCD,72 three wave mixing80,84,139–141 and enantio-sensitive microwave spectroscopy.85–87 The relevant vectorial observables are the induced polarization or photoelectron current. Tensorial observables related to multipolar bound polarizations142 or multipolar photoelectron currents have been predicted in the two-photon regime76,77 and measured in the multiphoton regime.78
The concept of chiral observer provides a set of rules to find new vectorial or tensorial enantio-sensitive observables, and to design the experimental setup required for their observation. These rules may also allow us to adapt the setup to the specifics of the experimental tools available in each laboratory. Let us formulate these simple rules.
Rule 1. The enantio-sensitive vectorial signal excited by the light field in a randomly oriented ensemble of chiral molecules and detected by a chiral observer has the following general form:
〈![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) 〉 = g 〉 = g![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) , , | (2) |
![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) is a field pseudovector.
is a field pseudovector.
The lowest-order field pseudovector that can be constructed without the help of the magnetic component of the light field is the vector product of the two orthogonal, phase-delayed electric-field components. Such a vector product arises naturally in elliptically polarized fields, maximizing in circularly polarized fields. The respective molecular pseudoscalar is a triple product of three vectors: the first two are the non-collinear dipole moments responsible for the coupling with each of the two field components present in the light pseudoscalar. The third is a vector ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) representing the desired vectorial observable.
representing the desired vectorial observable.
The two types of vectorial observables outlined so far require observation of light generated due to the induced dipole ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) if,
if, ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) =
= ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) if (e.g. PXCD, see below), or ejected photoelectrons with momentum
if (e.g. PXCD, see below), or ejected photoelectrons with momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ,
, ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) =
= ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) (e.g. PECD, see below). Thus, the molecular pseudoscalar g includes the triple product of dipoles [
(e.g. PECD, see below). Thus, the molecular pseudoscalar g includes the triple product of dipoles [![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) ik ×
ik × ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) ki]·
ki]·![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) if for detecting light and a similar construct in the case of detecting photoelectrons [
if for detecting light and a similar construct in the case of detecting photoelectrons [![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) ik ×
ik × ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) ki]·
ki]·![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) . The two pseudoscalars differ by a single vector – the one characterizing the type of observation.
. The two pseudoscalars differ by a single vector – the one characterizing the type of observation.
To illustrate Rule 1, consider the phenomenon that heralded the electric–dipole revolution, photoelectron circular dichroism (PECD) in one-photon ionization by circularly polarized light.
3.1 Photoelectron circular dichroism (PECD)
PECD was predicted by Ritchie,42 Cherepkov143 and Powis43 and first detected by Böwering et al.45 It has now been extended to the multiphoton58–60 and strong-field ionization regimes,71,144 to liquid targets,145 is being adopted for industrial applications146 and proposed as a key mechanism in a photophysical astrophysical scenario for the origin of life’s homochirality.12In PECD, the circularly polarized field
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (t) = (t) = ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ωe−iωt + c.c. ωe−iωt + c.c. | (3) |
The PECD current can be written as88
![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) = g = g![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) , , | (4) |
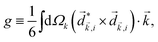 | (5) |
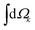 indicates integration over all directions of the photoelectron momentum
indicates integration over all directions of the photoelectron momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ,
, ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif)
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ,i
,i ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) 〈
〈![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) |
|![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) |i〉 is the transition dipole matrix element between the ground state |i〉 and the continuum state |
|i〉 is the transition dipole matrix element between the ground state |i〉 and the continuum state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉, and
〉, and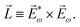 | (6) |
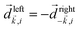 , one can show that g has opposite values for opposite enantiomers,88i.e. it is responsible for the enantio-sensitivity of
, one can show that g has opposite values for opposite enantiomers,88i.e. it is responsible for the enantio-sensitivity of ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) . Using the standard expression for the amplitude of an elliptically polarized field
. Using the standard expression for the amplitude of an elliptically polarized field 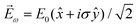 , we can obtain the respective light's pseudovector:
, we can obtain the respective light's pseudovector: ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) = i|E0|2σẑ. It is proportional to the photon spin (spin angular momentum of light) σẑ, therefore it vanishes for linearly polarized fields (σ = 0) and points in opposite directions for opposite circular polarizations (σ = ±1). Thus,
= i|E0|2σẑ. It is proportional to the photon spin (spin angular momentum of light) σẑ, therefore it vanishes for linearly polarized fields (σ = 0) and points in opposite directions for opposite circular polarizations (σ = ±1). Thus, ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) is responsible for the circular dichroism of
is responsible for the circular dichroism of ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) . Moreover, since the observable
. Moreover, since the observable ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) is perpendicular to the polarization plane, the corresponding detector must be able to distinguish between the two opposite directions perpendicular to the polarization plane, i.e. it must define a reference vector (e.g. ẑ), on which the vector of photoelectron current
is perpendicular to the polarization plane, the corresponding detector must be able to distinguish between the two opposite directions perpendicular to the polarization plane, i.e. it must define a reference vector (e.g. ẑ), on which the vector of photoelectron current ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) can be projected. Otherwise, the detector will not have the capacity of recording the circular dichroism or the enantio-sensitivity encoded in
can be projected. Otherwise, the detector will not have the capacity of recording the circular dichroism or the enantio-sensitivity encoded in ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) . Indeed, one can show that the coefficient b1,0 usually measured in PECD satisfies b1,0 ∝ ẑ·
. Indeed, one can show that the coefficient b1,0 usually measured in PECD satisfies b1,0 ∝ ẑ·![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) = gS, which is a product of the molecular handedness encoded in g and the handedness of the chiral setup encoded in S ≡ ẑ·
= gS, which is a product of the molecular handedness encoded in g and the handedness of the chiral setup encoded in S ≡ ẑ·![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) .88 Due to the purely electric–dipole nature of PECD, the enantio-sensitive and dichroic signal recorded in b1,0 ∝ jz reaches several tens of percent of the total photoionization signal.42,43,45–75
.88 Due to the purely electric–dipole nature of PECD, the enantio-sensitive and dichroic signal recorded in b1,0 ∝ jz reaches several tens of percent of the total photoionization signal.42,43,45–75
Importantly, the vector product of the two photoionization dipoles is equal to zero for the “flat” (plane wave) continuum: the formation of an enantio-sensitive electron current in the continuum upon photoionization from a stationary state requires electron scattering from the molecular potential. This scattering imparts angular momentum on the electron, which, together with its linear momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) , characterizes chirality of the electron dynamics in the continuum, i.e. the chirality of the photoelectron current. Eqn (5) points to the physical origin of PECD and its connection to the concept of geometric fields (see Section 8.6).
, characterizes chirality of the electron dynamics in the continuum, i.e. the chirality of the photoelectron current. Eqn (5) points to the physical origin of PECD and its connection to the concept of geometric fields (see Section 8.6).
Rule 2. A chiral observer can detect enantio-sensitive signals in the electric–dipole approximation due to even-order non-linear optical processes, such as those described by even-order electric susceptibilities81,82,147χ(2), χ(4),…
It is easy to understand this rule. Here we deal with excitation or detection of induced polarization ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) . From Rule 1, we already know that any vectorial enantio-sensitive signal, such as
. From Rule 1, we already know that any vectorial enantio-sensitive signal, such as ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) , must be proportional to a pseudovector coming from the electromagnetic field. Let us look at all available pseudovectors.
, must be proportional to a pseudovector coming from the electromagnetic field. Let us look at all available pseudovectors.
In the first order with respect to the field, there is only one pseudovector ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) ω – the magnetic component of EM wave. In the second order, we have the first opportunity to construct the field pseudovector from the vector product of the electric fields,
ω – the magnetic component of EM wave. In the second order, we have the first opportunity to construct the field pseudovector from the vector product of the electric fields, 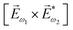 . In the third order, to construct a field pseudovector, we have to use the magnetic field again, e.g.
. In the third order, to construct a field pseudovector, we have to use the magnetic field again, e.g.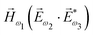 . Here we have used the pseudovector
. Here we have used the pseudovector ![[H with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0048_20d1.gif) ω1 and multiplied it by a scalar
ω1 and multiplied it by a scalar 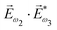 . In the fourth order, we can use the field pseudovector in the electric–dipole approximation
. In the fourth order, we can use the field pseudovector in the electric–dipole approximation 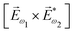 and combine it with the scalar
and combine it with the scalar 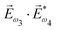 . The rest is clear: in even orders, the pseudovector can be constructed from electric field vectors, but in odd orders there is no such an opportunity and we have to use the magnetic field instead. Thus, non-linear optical processes of even order can be enantio-sensitive in the electric–dipole approximation, while the enantio-sensitivity of odd-order processes relies on magnetic interactions. The same conclusion can be obtained using symmetry arguments.81,148
. The rest is clear: in even orders, the pseudovector can be constructed from electric field vectors, but in odd orders there is no such an opportunity and we have to use the magnetic field instead. Thus, non-linear optical processes of even order can be enantio-sensitive in the electric–dipole approximation, while the enantio-sensitivity of odd-order processes relies on magnetic interactions. The same conclusion can be obtained using symmetry arguments.81,148
To illustrate Rules 1 and 2, we shall consider several phenomena which arise in different fields of research, but have identical mechanisms of enantio-sensitive response.
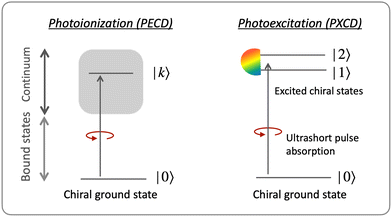
3.2 Photo-excitation circular dichroism: helical currents in bound molecular states
Consider first the phenomenon of photo-excitation circular dichroism (PXCD), introduced recently by Beaulieu et al.72 It shows that chiral photoelectron currents, which underlie the photoionization circular dichroism (PECD) discussed above, can also be excited in bound states (Fig. 6).In PXCD72,88 a short pulse
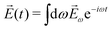 | (7) |
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 〉 in the direction perpendicular to the polarization plane.72 In the frequency domain, this dipole is:
〉 in the direction perpendicular to the polarization plane.72 In the frequency domain, this dipole is:〈![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 〉(ω2,1) = g 〉(ω2,1) = g![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) , , | (8) |
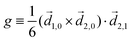 | (9) |
![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) ≡ ≡ ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) *(ω1,0) × *(ω1,0) × ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (ω2,0). (ω2,0). | (10) |
![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) . The excited dipole is indeed a result of the conversion of the initial in-plane rotation, excited in the electronic or vibrational degrees of freedom by the circularly polarized pump field, into motion orthogonal to this plane. The phase of these oscillations is determined not only by
. The excited dipole is indeed a result of the conversion of the initial in-plane rotation, excited in the electronic or vibrational degrees of freedom by the circularly polarized pump field, into motion orthogonal to this plane. The phase of these oscillations is determined not only by ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) but also by the sign of the molecular pseudoscalar g. Thus, oscillations excited in opposite enantiomers will have opposite phases. Observing an enantio-sensitive response requires detecting the phase of the oscillating signal, or equivalently the direction of the respective vectorial observable.
but also by the sign of the molecular pseudoscalar g. Thus, oscillations excited in opposite enantiomers will have opposite phases. Observing an enantio-sensitive response requires detecting the phase of the oscillating signal, or equivalently the direction of the respective vectorial observable.
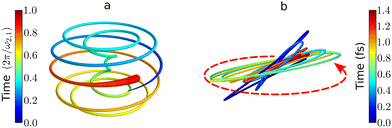 | ||
| Fig. 7 Chiral electronic currents in molecules: trajectories traced by the tip of the induced dipole in randomly oriented chiral molecules. (a) Helical attosecond electron current in PXCD72 for a model chiral molecule. Time is in units of the period set by the energy difference between the excited states. (b) Time-dependent polarization driven in randomly oriented propylene oxide by of an elliptically polarized field with intensity 5 × 1013 W cm−2, wavelength 1770 nm and 5% of ellipticity (see ref. 82 for details of the calculations). The polarization of the driving field is depicted by the dashed red ellipse. The ultrafast polarization response is 3D, chiral, and enantio-sensitive: the in-plane (achiral) polarization components are identical in left- and right-handed molecules, whereas the (chiral) out-of plane component is out of phase in opposite enantiomers. | ||
While PXCD is similar to PECD, the conversion of in-plane rotation into motion orthogonal to the plane happens in bound states and requires at least two excited states (instead of one continuum state in PECD). Therefore, we are now dealing with the Fourier components of the field at two different frequencies. This aspect opens more options for the pump pulse polarizations which lead to a non-zero ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) . For example, one can use an elliptically polarized broadband pulse, e.g.
. For example, one can use an elliptically polarized broadband pulse, e.g.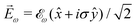 , which yields
, which yields 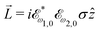 , or two linearly polarized pulses at an angle with respect to each other, e.g.
, or two linearly polarized pulses at an angle with respect to each other, e.g. ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω1,0 =
ω1,0 = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) ω1,0
ω1,0![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and
and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω2,0 =
ω2,0 = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) ω2,0ŷ, which yields
ω2,0ŷ, which yields 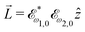 .
.
The PXCD signal is an attractive new enantio-senstive molecular observable. It depends on molecular properties (dipoles) and hence it is molecule specific. It relies on coherence between the states and, hence, it tracks coherence, electronic or vibronic. For example, in the experiment72 such vibronic coherence, excited in Rydberg states of fenchone and camphor by a circularly polarized femtosecond pulse, gave rise to chiral vibronic currents lasting for 1.2 ps. Its evolution reflected significant variations of molecular chirality when probed via photoionization (see PXECD below). Finally, since the emission associated with the PXCD dynamics is a parametric process, signals from all molecules in the ensemble will add coherently to form a macroscopic dipole. This opens an opportunity to control the enantio-sensitive response not only on a single-molecule level, but also at the macroscopic level. We will consider such macroscopic control of chiral emitters later, developing the concept of light with structured chirality in Section 5.
3.3 Enantio-sensitive microwave spectroscopy
A phenomenon analogous to PXCD exists in the microwave domain. Known as enantio-sensitive microwave spectroscopy (EMWS), it occurs in the case of purely rotational transitions, was discovered by Patterson et al.85 and recently further developed in ref. 89 and 91, 94. Indeed, as shown in ref. 88, the rotational problem can be formulated in a way mathematically similar to PXCD in electronic or vibrational states, with the only difference that the expression for the molecular pseudoscalar includes a sum over all magnetic quantum numbers Mi of the asymmetric rotor states in each energy level i = 0, 1, 2: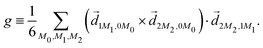 | (11) |
3.4 Enantio-sensitive non-linear wave-mixing
PXCD and EMWS are not the only two relatives in the family of enantio-sensitive phenomena which occur in the electric–dipole approximation and follow Rule 1. Although PXCD and EMWS are resonant processes, and oscillations take place in the absence of the driving field, the pseudoscalar g can loosely be interpreted as a second order susceptibility χ(2). Indeed, PXCD and EMWS are closely related to the original predictions of Giordmaine44 for sum- and difference-frequency generation in chiral liquids. The expression for the second-order induced polarization at, e.g. the difference frequency can be rewritten in the form dictated by our Rule 1:![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) (2)(ω2,1) = χ(2) (2)(ω2,1) = χ(2)![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) , , | (12) |
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) i,0 ×
i,0 × ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) j,0)·
j,0)·![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) j,i;
j,i; ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) is given by eqn (10).
is given by eqn (10).
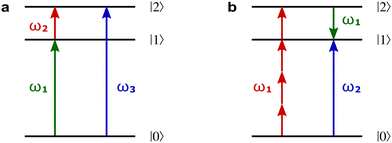
Fig. 8a shows non-linear optics-type diagrams for PXCD, EMWS, and difference frequency generation (DFG), which unify all three processes. The arrows directed up describe amplitudes of photon absorption, while the arrows directed down describe conjugated amplitudes corresponding to photon emission. These amplitudes are excited by the respective (conjugated or not) components of the incident field: the conjugated field is associated with the arrow directed down. Further advances in enantio-sensitive perturbative non-linear optics are described in the review by Fisher et al.80
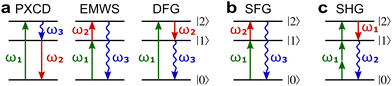 | ||
Fig. 8 Diagrams for various nonlinear enantio-sensitive or chiral-sensitive processes. Different colors mark different directions of light polarization (e.g. green – x, red – y, blue – z). Straight up and down arrows indicate photon absorption and photon emission, wavy arrows indicate induced polarization. (a) Diagrams for photo-excitation circular dichroism (PXCD), enantio-sensitive microwave spectroscopy (EMWS), and difference-frequency generation (DFG); (b) sum-frequency generation (SFG). For SFG, the field pseudovector is given by ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) = = ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (ω1) × (ω1) × ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (ω2)44,139 and thus it vanishes when ω1 = ω2, i.e. second harmonic generation requires more than two photons. (c) Second harmonic generation (SHG) is indeed possible for higher-order processes because these are associated with field pseudovectors such as (ω2)44,139 and thus it vanishes when ω1 = ω2, i.e. second harmonic generation requires more than two photons. (c) Second harmonic generation (SHG) is indeed possible for higher-order processes because these are associated with field pseudovectors such as ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) = [ = [![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (ω1)· (ω1)·![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (ω1)][ (ω1)][![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) *(ω1) × *(ω1) × ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (ω1)], which are non-zero for elliptically polarized light and record its rotation direction. (ω1)], which are non-zero for elliptically polarized light and record its rotation direction. | ||
Similarly, in the context of highly non-linear interactions, symmetry arguments81,82,148 show that the interaction between a periodic (but not necessarily monochromatic) electric field and an isotropic chiral medium can lead to enantio-sensitive polarization at even multiples of the fundamental frequency ω of the field. That is, while ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) (2n+1)ω is identical for both enantiomers,
(2n+1)ω is identical for both enantiomers, ![[P with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0050_20d1.gif) 2nω has opposite signs for the opposite enantiomers. Analogously to the perturbative case, this means that there are electric-field configurations for which even-order high harmonics are possible only if the medium is chiral.81,82 Interestingly, while second harmonic generation is symmetry-forbidden in the lowest-order perturbative regime (sum-frequency generation, Fig. 8b, vanishes for ω1 = ω2), it becomes symmetry-allowed in the strong-field regime, as the medium can efficiently absorb additional photons from the intense laser field. Fig. 8c shows that chiral second harmonic generation in the non-perturbative regime involves additional up-down arrows corresponding to virtual emission/absorption of photons.
2nω has opposite signs for the opposite enantiomers. Analogously to the perturbative case, this means that there are electric-field configurations for which even-order high harmonics are possible only if the medium is chiral.81,82 Interestingly, while second harmonic generation is symmetry-forbidden in the lowest-order perturbative regime (sum-frequency generation, Fig. 8b, vanishes for ω1 = ω2), it becomes symmetry-allowed in the strong-field regime, as the medium can efficiently absorb additional photons from the intense laser field. Fig. 8c shows that chiral second harmonic generation in the non-perturbative regime involves additional up-down arrows corresponding to virtual emission/absorption of photons.
In all of these methods, the ability to distinguish between opposite enantiomers requires access to the phase of the induced polarization. Thus, intensity measurements of the even order polarizations can distinguish chiral media from achiral media or different chiral media from each other, but cannot distinguish between opposite enantiomers.
In the next section, we shall see how enantio-sensitive information can be mapped on the polarization ellipse of the nonlinear optical response.
3.5 Chiral high harmonic generation in the electric–dipole approximation (cHHGd)
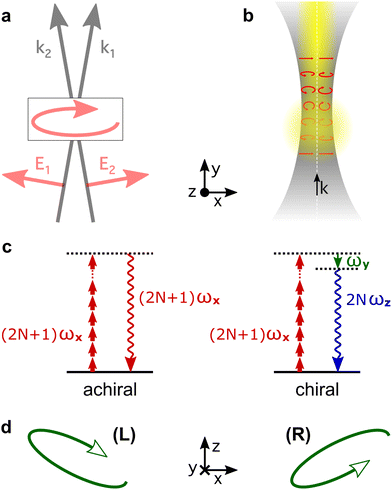
High harmonic generation (HHG) is an extremely nonlinear process that converts intense radiation, usually in the IR domain, into high-energy photons with frequencies that are high-integer multiples of the incident field frequency.150 It can be understood semi-classically as a sequence of three steps, starting with strong-field ionization.151 In the second step, the laser electric field takes the liberated electron away from the core, driving its oscillations in the continuum. Note that the laser field can also interact with the ionic core, driving rich multi-electron dynamics.152 The third step is the electron-core recombination, resulting in the emission of the harmonic light. A typical HHG spectrum contains information about both the structure of the atomic/molecular system and of the ultrafast dynamics between ionization and recombination.The third step of HHG, radiative electron-core recombination, is the inverse of photoionization. Therefore, just like in the photoionization current in PECD, the recombination dipole responsible for HHG driven by an elliptically polarized field in isotropic chiral media can develop a component which is orthogonal to the polarization of the driving field, i.e. along the direction of light propagation, as show in Fig. 7b. This component oscillates out of phase in media of opposite handedness. However, unlike the photoelectron current in PECD, this chiral dipole component escapes direct observation in standard HHG measurements: the dipole component oscillating along the light propagation direction radiates orthogonal to it. This means that the chiral component of the induced polarization cannot be observed in the macroscopic HHG signal. Indeed, the macroscopic HHG signal requires coherent addition of the light emitted from different positions in the chiral medium, which is only possible if the harmonic light co-propagates with the driver. For this reason, in the first chiral HHG experiments36 and subsequent setups114–116,118 this enantio-sensitive dipole component could not be observed, and the enantio-sensitive response relied on the interaction of chiral molecules with the magnetic component of the laser field.
The fact that the electric-field vector of the intense laser field driving HHG is orthogonal to its propagation direction stops us from imprinting the strong chiral response shown in Fig. 7b into the macroscopic HHG signal, severely limiting the potential of HHG spectroscopy. This problem can be overcome by creating light with “forward” ellipticity, or transverse spin138 (spin angular momentum of light), and using it to drive chiral HHG.
Consider two laser beams that propagate non-collinearly at a small angle, both carrying the same fundamental frequency and linearly polarized in the propagation plane. In the overlap region, the total electric field becomes elliptically polarized in the plane of propagation (x, y), with the minor ellipticity component in the propagation direction (y-axis), see Fig. 9a. Now the chiral dipole component has adequate orientation to generate harmonic light that co-propagates with the driving field. Thus, it can be mapped onto the macroscopic HHG signal.82
Non-collinear optical setups are not the only way of creating electric-field vector components along the propagation direction which lead to forward ellipticity. Such longitudinal components naturally arise when light is confined in space, as it happens in a tightly focused laser beam, see Fig. 9b.
The HHG signal driven by light with forward ellipticity has two orthogonally polarized components: the (standard) component in the propagation plane, which is not sensitive to chirality, and the enantio-sensitive component orthogonal to it, Fig. 9b, which is out of phase in media of opposite handedness. One might think that the harmonic light would be elliptically polarized, but this is not necessarily the case. Indeed, Rule 2 dictates that the enantio-sensitive and non-enantio-sensitive components of the induced polarization carry different harmonic frequencies: the non-enantio-sensitive component carries odd harmonics, the enantio-sensitive component carries even harmonics, Fig. 9c. Hence, for relatively long pulses, the non-collinear setup in Fig. 9 generates non-overlapping even and odd harmonics, polarized orthogonal to each other. Only the phase of the even harmonics records the medium's handedness82 as it follows from Rules 1 and 2. But, what if the driving pulse is only a few cycles long, and therefore has a broad spectrum?
3.6 Ultrafast nonlinear optical rotation
In chiral HHG driven by a few-cycle laser pulse which has forward ellipticity, the chiral (even-order) and achiral (odd-order) harmonics can spectrally overlap. Then, the emitted harmonic light becomes elliptically polarized83 in the overlap region. Since the chiral components of the nonlinear-optical response are out of phase in opposite enantiomers, both the spin angular momentum (ellipticity) and the rotation of the polarization ellipse of the nonlinear-optical response in the spectral overlap region will be opposite in opposite enantiomers.Fundamentally, using the ultra-broad spectrum of a tightly focused few-cycle pulse83 is akin to using a two-colour non-collinear setup. Such a setup allows one to tailor the polarization of the driver in two and three dimensions and maps the molecular handedness onto the polarization properties of the emitted harmonic light.
A polarizer placed before the high harmonic detector and rotated by an angle 0 < α < 90° with respect to the linearly polarized driving field can convert the enantio-sensitive orientations of the harmonic polarization ellipse into different signal intensities.83 Just like traditional optical rotation, its nonlinear analogue does not require chiral light (see Section 2.2.2). As a result, the total number of photons that reach the detector does not depend on the medium's handedness. Note that the rotation of the polarization ellipse of the emitted light83 is analogous to the rotation of the linear polarization in standard optical rotation. Indeed, in the non-linear optical rotation,83 the chiral setup is formed by the pseudovector defining rotations of the polarization ellipse and by the vector defining the propagation direction ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) of the light.
of the light. ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) is relevant in this electric–dipole effect not only because of phase-matching conditions along
is relevant in this electric–dipole effect not only because of phase-matching conditions along ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) but also because
but also because ![[k with combining circumflex]](https://www.rsc.org/images/entities/i_char_006b_0302.gif) is encoded in the pattern of forward ellipticities of the driving field, a phenomenon known as transverse spin-momentum locking.138
is encoded in the pattern of forward ellipticities of the driving field, a phenomenon known as transverse spin-momentum locking.138
Rule 3. A chiral observer allows the detection of enantio-sensitive tensorial observables, e.g. quadrupolar currents and quadrupolar polarizations.
Tensorial observables are particularly relevant in two-color fields, such as a laser beam carrying ω and 2ω frequencies, arranged so that enantio-sensitivity at the level of vectorial observables is symmetry forbidden. The two-color aspect of these fields naturally brings perspectives of coherent control into the discussion. Let us consider some examples.
3.7 Photoionization in two-color fields without spin angular momentum
The light pseudovector in many electric–dipole-based methods is proportional to the field's spin angular momentum. In the absence of spin angular momentum, there can be no vectorial enantio-sensitive observables. For example, laser beams carrying ω and 2ω frequencies, linearly polarized and orthogonal to each other, do not carry spin angular momentum: their vector product changes direction during the laser cycle and is equal to zero on average. Hence, they cannot excite vectorial enantio-sensitive observables in randomly oriented ensembles. Yet, enantio-sensitive photoionization signals triggered by such fields have been predicted,76,77 detected,78 and interpreted in terms of the instantaneous spin angular momentum of the field.78,153The fundamental reason underlying the possibility of such a detection is that in addition to vectorial observables such as induced polarization (ESMW, PXCD, difference- and sum-frequency generation, cHHGd) and photoelectron current (PECD, PEXCD), chiral measurements can also yield tensorial observables. The two-color arrangement described above takes advantage of such observables.
A simple way to introduce tensorial observables is to consider photoionization.125,154 Indeed, any photo-electron angular distribution W(θ, ϕ) can be decomposed in spherical harmonics as
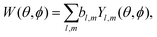 | (13) |
Since vectors are tensors of rank one, for l = 1 we obtain the vectorial observables we have already discussed. In PECD, for example, where W(k, θ, ϕ) is the photoelectron angular distribution at photoelectron energy k2/2, the three coefficients b1,m describe the vector of the photoelectron current; b1,±1 = 0 due to symmetry and b1,0 ≠ 0 is responsible for the so-called forward–backward asymmetry. In the case of chiral dynamics in bound states, e.g. in PXCD, one could employ W(r, θ, ϕ) to describe bound electron density. In this case the b1,m coefficients describe the expectation value of the electric–dipole operator coupling the two states excited by the pump pulse.
Just like the b1,m coefficients encode vectorial properties, the b2,m coefficients describe the quadrupolar part of W(θ, ϕ). In the context of photoionization with circularly polarized light, it is well known that these coefficients are not enantio-sensitive. However, they become enantio-sensitive and correspond to excitation of an enantio-sensitive quadrupolar photoelectron current resulting from the interference between a two-ω-photon and a one-2ω-photon ionization pathways when the ω and 2ω fields are linearly polarized perpendicular to each other, as predicted in ref. 76 and 77. These predictions have been supported by the observation of similar enantio-sensitive multipolar signals with l ≥ 2 in strong-field ionization of fenchone and camphor.78 The analysis of the symmetry properties of this electric-field configuration reveals that, together with an appropriately oriented quadrupolar detector, it yields a chiral setup (see Fig. 4c), and its handedness emerges naturally in the expressions for the enantio-sensitive response.125
Let us consider interference of the one-photon ionization pathway of the initial state |0〉 triggered by the 2ω-field with the two-photon ionization pathway via an intermediate state |1〉, triggered by the ω field. The fields are defined as
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (t) = (t) = ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ωe−iωt + ωe−iωt + ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2ωe−2iωt + c.c., 2ωe−2iωt + c.c., | (14) |
![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω = Eω
ω = Eω![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and
and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2ω = E2ωe−iϕẑ. One can show that the coefficient describing an xy quadrupole in the photoionization distribution is125
2ω = E2ωe−iϕẑ. One can show that the coefficient describing an xy quadrupole in the photoionization distribution is125![[b with combining tilde]](https://www.rsc.org/images/entities/i_char_0062_0303.gif) 2,−2 = A(1)*A(2)gS + c.c., 2,−2 = A(1)*A(2)gS + c.c., | (15) |
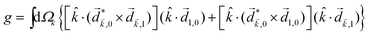 | (16) |
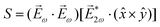 | (17) |
![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) and ŷ, in the expression for S. They highlight the role of the detector (see Fig. 4c) in defining a reference frame that distinguishes directions for which the product xy is positive from directions for which it is negative (see also discussion related to Fig. 4). Note that S depends on the two-color phase ϕ, which can be used as a control parameter. The phase ϕ is analogous to the relative phase between
and ŷ, in the expression for S. They highlight the role of the detector (see Fig. 4c) in defining a reference frame that distinguishes directions for which the product xy is positive from directions for which it is negative (see also discussion related to Fig. 4). Note that S depends on the two-color phase ϕ, which can be used as a control parameter. The phase ϕ is analogous to the relative phase between ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) *(ω1,0) and
*(ω1,0) and ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (ω2,0) in PXCD and to the relative phase between the two perpendicular components of circularly polarized light in PECD.
(ω2,0) in PXCD and to the relative phase between the two perpendicular components of circularly polarized light in PECD.
Just like the vectorial enantio-sensitive electron current in photoionization (PECD) has its counterpart in bound states (PXCD), the quadrupolar current found in photoionization76–78 has a quadrupolar analogue in the context of bound excitation. That is, the same field configuration and the same interference scheme translated to the context of bound excitation leads to the emergence of an enantio-sensitive quadrupole.142 There is, however, an important difference from the induced bound-state dipole in PXCD: the interreference here arises from the two pathways, one-photon and two-photon, and no longer requires coherent population of two electronic or vibronic states: a single final bound electronic state is sufficient. Consequently, the generated quadrupole is permanent: it does not oscillate and is associated with uniaxial orientation of the (initially isotropic) molecular sample.
Note that, in all phenomena considered in this section, the total intensity of the nonlinear-optical or photoelectron signal is not enantio-sensitive because the driving fields are not chiral. Achieving enantio-sensitivity in the total signal intensity requires an efficient chiral photonic reagent: synthetic chiral light.
4 The second electric–dipole revolution in chiral measurements: efficient chiral reagent
A chiral reagent provides access to fundamentally different enantio-sensitive observables upon interaction with chiral matter: scalar enantio-sensitive observables, such as populations of states or total intensity of emitted or absorbed light, not accessible by a chiral observer. Circularly polarized light, the standard chiral photonic reagent, owes its handedness to the (chiral) helix that the electric-field vector draws in space, which can either be left- or right-handed. Its chirality is, however, non-local – at any given point in space, the electric-field vector draws a planar circle, see Fig. 10a and b. A fundamentally different way of endowing light with chirality is to encode it in time, making the trajectory that the tip of the electric field vector traces in time chiral.100 In contrast to the (standard) handedness of circularly polarized light, this new type of chirality is defined locally, at each point in space. It arises already in the electric–dipole approximation.Concept 1. Locally chiral light is chiral within the electric–dipole approximation: the tip of the electric field vector draws a (three-dimensional) chiral Lissajous figure in time. The generation of this light requires three orthogonal polarization components and, at least, two colours.
An example of a locally chiral field100 is shown in Fig. 10c. The combination of a fundamental field, which is elliptically polarized in the propagation (xy) plane, and an orthogonally polarized second harmonic generates a chiral Lissajous figure. Indeed, if we reflect the field's trajectory, e.g. through the xy plane, the elliptically polarized ω-field remains the same, but the z-polarized 2ω component flips sign, see Fig. 10d. These mirror-reflected Lissajous figures cannot be superimposed by any rotation and/or translation.
Such locally chiral light can drive strongly enantio-sensitive optical signals in isotropic chiral matter via purely electric–dipole interactions. Control over the temporal structure of the light field enables efficient control over the enantio-sensitive response of chiral matter.100 For the field presented in Fig. 10c, three key parameters enable such control (for a given total intensity): the ellipticity of the fundamental field, the amplitude of the second harmonic, and the two-colour phase delay.
As we know from Section 2, a chiral “object”, such as locally chiral light, must have at least one pseudoscalar which characterizes its handedness. What is the chirality measure (pseudoscalar) of this locally chiral light?
Concept 2. Chiral correlation functions characterize the local handedness of synthetic chiral light by recording the correlated interplay between the different frequency components of the light wave, which encodes the handedness of the Lissajous figure. Chiral correlation functions characterize the strength of non-linear enantio-sensitive light-matter interaction in the electric–dipole approximation.
To characterize the handedness of the light's Lissajous figure, one can take three snapshots of the electric-field vector ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (t) at three successive instants of time t1, t2 and t3, and construct a triple product of these three vectors
(t) at three successive instants of time t1, t2 and t3, and construct a triple product of these three vectors ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (t1)·[
(t1)·[![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (t2) ×
(t2) × ![[F with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0046_20d1.gif) (t3)]. If such a product is non-zero, it means that between t1 and t3 the tip of the electric field vector traced a chiral trajectory in the space of Fx, Fy, Fz. To make sure that not only a section, but the entire Lissajous curve is chiral, one can average the triple product over time:
(t3)]. If such a product is non-zero, it means that between t1 and t3 the tip of the electric field vector traced a chiral trajectory in the space of Fx, Fy, Fz. To make sure that not only a section, but the entire Lissajous curve is chiral, one can average the triple product over time:
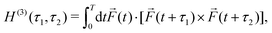 | (18) |
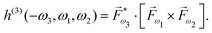 | (19) |
Rule 4. The scalar enantio-sensitive response of chiral matter to locally chiral light is nonlinear and results from the interference between a chiral even-order process and an achiral odd-order process. Thus, it involves an odd number of photons, leading to chiral light correlation functions of odd order.
For example, h(3) characterizes the interference of two pathways leading to enantio-sensitive absorption and emission in a 3-level system with chiral states 0, 1 and 2. Let us consider a locally chiral field with frequencies ω1, ω2 and ω3 = ω1 + ω2, polarized along x, y and z, respectively.90,95,97,99,101,102,109,132 The first (achiral) pathway is associated with the linear response at frequency ω3, which is not sensitive to chirality, and leads to polarization at ω3 along z. The second (chiral) pathway corresponds to sum-frequency generation, a second-order process that records the molecular handedness: the medium absorbs one ω1 photon and one ω2 photon from the field components polarized in the xy plane, generating polarization at frequency ω3 along z (Fig. 8b). In contrast, randomly oriented ensembles of achiral molecules cannot generate a polarization response in the direction orthogonal to the driving field polarization because these systems are symmetric with respect to reflections in the polarization plane. That is, this second pathway is unique to chiral media, and the induced polarization is out of phase in media of opposite handedness. The two pathways interfere, making absorption (Fig. 11a) and emission (ω3 photon emitted via the enantio-sensitive process depicted in Fig. 8b interferes with the linear response at ω3) at frequency ω3 strongly enantio-sensitive. In a randomly oriented ensemble of chiral molecules, the enantio-sensitive contribution to absorption is ℑ[χ(2)h(3)]. The physical meaning of h(3) is clear from Table 1, comparing standard absorption CD and non-linear absorption CD in the electric–dipole approximation: h(3) plays the role of optical chirality, which characterizes the strength of enantio-sensitive absorption in the linear response.119 Thus, chiral light correlation functions characterize the strength of enantio-sensitive light matter interaction in the electric-dipole approximation. Likewise, in the non-linear regime, the molecular pseudoscalar formed by the triple product of the three relevant dipoles replaces the one typical for the linear response – the scalar product between the electric and magnetic dipoles.
4.1 Synthetic chiral light with two colors
For a two-colour field, such as the one in Fig. 10c, h(3) = 0 simply because the field does not contain three frequencies. It means that nonlinear 3-photon processes driven by this field are not enantio-sensitive, but it does not necessarily mean that the field is achiral. If the field is locally chiral, its handedness can be recorded in higher-order processes, which are characterized and controlled by higher-order correlation functions. They involve additional dot products of the electric field vectors, evaluated at different times. The next-order chiral correlation function is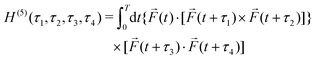 | (20) |
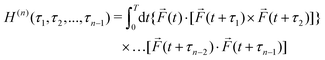 | (21) |
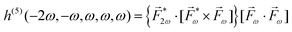 | (22) |
4.2 Locally chiral light vs. globally chiral light
While locally chiral light and the concept of local chirality have been introduced100 very recently, the second electric–dipole revolution started almost two decades ago. Using quantum control strategies, Král, Thanopulos, Shapiro, and Cohen102 and Gerbasi, Brumer, Saphiro and co-workers101 proposed a two-step optical scheme for enantio-purification of randomly oriented mixtures of opposite enantiomers, which works in the electric–dipole approximation.101 In the first step, a combination of three laser pulses with mutually orthogonal linear polarizations was used to selectively excite one of the two enantiomers to a selected vibrational state. In the second step, the photo-excited molecules were forced to flip handedness by a sequence of two linearly polarized pulses. Their simulations predicted 95% of enantio-purity when starting from a racemic mixture of dimethylallene.101 By controlling the relative phases between the laser fields in the first step, they were able to control whether the left-handed molecules were turned into right-handed or vice versa. This is probably the earliest example of application of locally chiral light to enantio-manipulation of molecules. The relative phases between the colors fully control the shape of light's Lissajous figure and its handedness, controlling the outcome of the interference in Fig. 11.Yet, there is an important caveat to this scheme. Locally chiral fields carrying three orthogonally polarized colours can be realized in the overlap region of two (or more) laser beams that propagate in different directions. However, the phase delay between the non-collinear beams, i.e. the relative time at which their wavefronts reach a specific point in space, is space-dependent. As a result, the handedness of the generated locally chiral field changes periodically in space, and so does the enantio-sensitive response of chiral matter.
For example, for the laser parameters proposed in ref. 101, considering cross-propagating beams, the field's handedness would change in space with periodicities on the order of a few micrometers. The application of such a field to a racemic mixture of isotropically distributed left- and right-handed molecules would create a non-homogeneous distribution of left- and right-handed molecules, which would be periodically distributed in space. This structured distribution would be, on average, still racemic, unless using extremely tight laser focusing or thin media.
This problem is alleviated in the case of the longer wavelengths associated with the microwave radiation, which leads to significantly wider spatial regions where the field maintains its local handedness, on the order of a few tens of centimeters. Eibenberger, Doyle and Patterson pioneered enantio-selective population of rotational states using phase-controlled microwave fields90 (see also ref. 99) together with Schnell and co-workers,95 who demonstrated an alternative implementation. Leibscher, Koch and co-workers97,98,157 are developing optimal control protocols of enantio-sensitive state transfer in chiral microwave fields.
Unfortunately, if one tries to apply an equivalent scheme to achieve enantio-sensitive populations of electronic states, one has to face the above problem: the field's local handedness changes rapidly in space, destroying the enantio-sensitivity in the total (global) integrated response of the macroscopic medium. To translate the huge enantio-sensitivity enabled by locally chiral fields to the macroscopic response of the medium, at the level of total signal intensities, the field also needs to be globally chiral.
Concept 3. Synthetic chiral light is globally chiral if its handedness, characterized by the nth-order chiral correlation function, survives integration in space, i.e. if  .
.
The standard circularly polarized light is either left- or right-handed everywhere in space. Since the handedness of synthetic chiral light can be controlled locally in every point in space, such light may or may not be globally chiral. In particular, if the field's handedness is maintained in space, one can achieve the highest possible degree of control over the enantio-sensitive response of chiral matter: quench it in one enantiomer while maximizing it in its mirror twin.100
The locally chiral field in Fig. 10c can be created in a way that maintains the same handedness globally in space100 using a non-collinear setup, see Fig. 12. It contains two laser beams that propagate at a small angle, with each beam carrying two cross-polarized phase-locked colors: the fundamental and its second harmonic. By controlling the ω, 2ω phase delays in the two beams, one achieves full control over the field's local handedness globally in space. This field enables complete discrimination between left- and right-handed randomly oriented chiral molecules via high harmonic generation spectroscopy.100
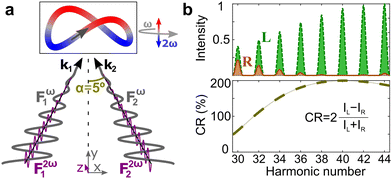 | ||
| Fig. 12 Locally and globally chiral light. (a) Synthetic chiral light that is locally and globally chiral can be created with two non-collinear beams carrying cross polarized ω and 2ω colours.100 In the overlap region, the total ω field is elliptical in the xy plane, the 2ω field is z-polarized, generating the chiral Lissajous curve in the inset. (b) Even harmonic intensity emitted by randomly oriented left- and right-handed propylene oxide and the chiral response, see ref. 100 for details. The field's chirality, and thus the enantio-sensitive response of the medium, is fully controlled by the ω, 2ω phase delays in the two beams. | ||
5 New enantio-sensitive observables via structuring light's chirality
Synthetic chiral light that is locally and globally chiral makes an extremely efficient chiral photonic reagent.100 Yet, the first dipole revolution taught us that we do not need to rely on the (global) handedness of light to detect the chirality of matter efficiently. Can we apply these lessons to synthetic chiral light? Can we measure strongly enantio-sensitive signals using light that is locally chiral (h(n)(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) ≠ 0), but globally achiral
) ≠ 0), but globally achiral  ? The answer is yes. Applying the concepts from the first dipole revolution leads to new enantio-sensitive observables, which arise upon structuring light's local handedness.
? The answer is yes. Applying the concepts from the first dipole revolution leads to new enantio-sensitive observables, which arise upon structuring light's local handedness.
Concept 4. Chirality-structured light is light whose handedness is non-trivially structured in space.
The possibility of structuring the local properties of light in space,40,158 including both its intensity and phase,159 creates unique opportunities for imaging160 and manipulating161 properties of matter. Likewise, structuring light's chirality119,162–165 could open new efficient routes for enantio-sensitive imaging and control of chiral matter. With structuring of light performed locally, the control extends to the level of individual molecules. One example of the new type of structured locally chiral light is chirality polarized light.128
The concept of polarization of chirality applies to both light and matter and is somewhat analogous to polarization of charge. A periodic distribution of alternating positive (+q) and negative (−q) charges in one dimension is unpolarized if the particles are uniformly distributed, and polarized if this distribution is periodically modified (Fig. 13a). Likewise, a periodic distribution of chiral units of alternating handedness can have polarization of chirality if the units are not uniformly distributed, see Fig. 13b. Here, we find dipoles of chirality ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) c = h
c = h![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0, where
0, where ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 0 is the vector connecting two nearby chiral units and h = hR = −hL is the handedness of one chiral unit. Note that, regardless the value of
0 is the vector connecting two nearby chiral units and h = hR = −hL is the handedness of one chiral unit. Note that, regardless the value of ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) c, the medium is racemic and achiral, just like the medium of alternating negative and positive charges is neutral.
c, the medium is racemic and achiral, just like the medium of alternating negative and positive charges is neutral.
This concept can immediately be applied to synthetic chiral light using the same non-collinear setup as in Fig. 12a. Now, however, we can control the ω, 2ω delays in each beam so that the field's handedness, characterized by its fifth-order chiral correlation function, is not maintained globally in space as in ref. 100 but periodically alternates in space creating dipoles of chirality, see Fig. 14a, polarized along x.
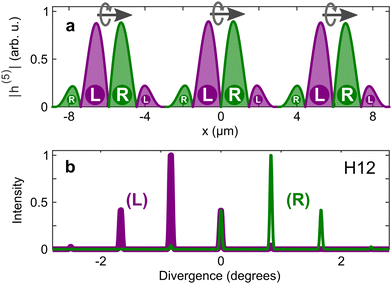 | ||
| Fig. 14 Chirality polarized light can be created using the setup of Fig. 12a, but adjusting the ω, 2ω phase delays so that the field's handedness, characterized by its 5th-order chiral correlation function h(5), is not maintained globally in space, in contrast to ref. 100. Here, it creates a periodic structure of dipoles of chirality. (a) h(5), its phase (i.e. the field's handedness) is encoded in the colours. The arrows indicate the direction of polarization of chirality, which is imprinted in the nonlinear response of chiral matter. (b) 12th-harmonic emission from randomly oriented left- and right-handed fenchone, see ref. 128 for λ = 1030 nm, F(1)ω = F(2)ω = 0.015 a.u. and F2ω = Fω/10. | ||
The non-linear parametric processes resulting from interaction of this light with randomly oriented chiral molecules, effectively “ignite” chiral emitters with handedness modulated in space. The mapping of this near-field nonlinear optical response into the far-field image will be sensitive to the chirality dipole of the light.
Fig. 14b shows the far-field harmonic intensity emitted from randomly oriented fenchone as a function of the emission angle. The total (angle-integrated) signal is the same for left- and right-handed molecules, as the overall field is achiral. However, the emission direction is highly enantio-sensitive: while the left-handed molecules emit light to the left (towards negative angles), the right-handed molecules emit light to the right (positive angles).
By looking into a specific emission direction, a chiral observer will allow us to distinguish between left- and right-handed molecules. Note that neither the light field, nor the detector are chiral on their own. However, by selecting a specific emission direction in the far field, the measurement setup, created by the (achiral) light field and the detector, becomes chiral.
Enantio-sensitive light bending is not limited to high harmonic generation, it is pertinent to any non-linear parametric emission. Enantio-sensitive light bending in free induction decay has been recently demonstrated by Khokhlova et al.132 Exciting opportunities for enantio-sensitive imaging arise from structuring light's handedness by combining locally chiral light with vortex beams.166
6 Towards efficient control, imaging and manipulation of chiral molecules with light
We now outline some of the new opportunities offered by substituting concepts and tools of enantio-sensitive molecular imaging and control, which use linear response and require the magnetic field component of the light wave, by concepts and tools that rely on non-linear response and do not require the magnetic field component. In terms of imaging, in this section we address the opportunities for photon-based spectroscopies. The next section will focus on new opportunities arising in photoelectron spectroscopy.6.1 Enantio-sensitive and molecular specific spectroscopy with synthetic chiral light
In this subsection we describe the fundamental origins of enantio– and molecular sensitivity in the interaction of synthetic chiral light with chiral matter. Possible applications of these ideas to enantio-separation are discussed in the subsequent subsection.The next step is to develop spectroscopy, which would provide access to molecule-specific information recorded in this interference, such as the relative amplitude and phase between the chiral and the achiral non-linear responses. The latter should be naturally sensitive to the type of the molecule and its conformation.129 As a result, the handedness of the light field that maximizes enantio-sensitivity in the optical response should also be molecule-specific, opening new opportunities for efficient molecular recognition and enabling the design of molecular markers: molecule-specific “fingerprints” of chiral molecules and their ultrafast light-driven dynamics, based on the relative amplitude and phase of chiral and achiral non-linear responses.
For example, the intensity of the enantio-sensitive emission at frequency 2ω driven by the locally chiral field (Fig. 10c) is
I = Iach + Ich + a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϕM + ϕω,2ω) cos(ϕM + ϕω,2ω) | (23) |
One example are few-cycle pulses, where the temporal structure of the electric field vector E(t) = E0a(t)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt + ϕCEP) depends on the carrier-envelope phase (CEP) ϕCEP. The sensitivity of the electronic dynamics to the instantaneous value of the oscillating electric field leads to strong CEP dependence of the nonlinear response.167–170 For our purposes, the CEP acts as an additional spectroscopic parameter somewhat equivalent to the two-colour phase delay in long laser pulses, which carry two well-defined frequency components such as ω and 2ω. In fact, changing the relative phase between these two colors shapes the individual oscillations of the total laser field on the sub-cycle scale. Along this route, one can use intense, linearly polarized light pulses to drive the nonlinear analogue of optical rotation, now induced by purely electric–dipole interactions.83 Importantly, such pulses should be confined both in space and in time.
cos(ωt + ϕCEP) depends on the carrier-envelope phase (CEP) ϕCEP. The sensitivity of the electronic dynamics to the instantaneous value of the oscillating electric field leads to strong CEP dependence of the nonlinear response.167–170 For our purposes, the CEP acts as an additional spectroscopic parameter somewhat equivalent to the two-colour phase delay in long laser pulses, which carry two well-defined frequency components such as ω and 2ω. In fact, changing the relative phase between these two colors shapes the individual oscillations of the total laser field on the sub-cycle scale. Along this route, one can use intense, linearly polarized light pulses to drive the nonlinear analogue of optical rotation, now induced by purely electric–dipole interactions.83 Importantly, such pulses should be confined both in space and in time.
Confinement in space can be achieved by tightly focusing the beam into a medium of randomly oriented chiral molecules, as depicted in Fig. 9b. Thanks to tight focusing, the field acquires ellipticity in the direction of light propagation, i.e. “forward ellipticity”. The chiral medium converts this forward ellipticity into the enantio-sensitive response orthogonal to the propagation plane (the plane of the figure).
Confinement in time, arising in nearly single-cycle pulses with controlled CEP, ensures that the pulse has ultra-broad spectral bandwidth. The latter enables the interference of the odd-order achiral response in the polarization plane and the even-order chiral response orthogonal to it.
As a result, the generated nonlinear polarization becomes elliptically polarized and enantio-sensitive: the ellipticity and the rotation angle of the non-linear optical response will have opposite signs in media of opposite handedness, signifying the non-linear optical activity (rotation).83 The rotation angle is controlled by the CEP of the laser pulse. In contrast to conventional optical rotation, this nonlinear effect is driven by purely electric–dipole interactions and leads to giant rotation angles (and ellipticities) already at the single-molecule level, enabling the possibility of highly efficient chiral discrimination in optically thin media. Since the CEP of the pulse controls the enantio-sensitive response in this non-linear optical activity, the value of the CEP that maximizes the enantio-sensitive response of a chiral molecule may constitute a molecular marker. The enantio-sensitive signal plotted vs. frequency and the CEP phase presents a two-dimensional set of data, which may be perceived as a “molecular QR-code”, sensitive to both the molecule and possibly its conformer. While the uniqueness of such measure is yet to be proven, the respective investigation is interesting in its own right, as it may result in a new interesting path in ultrafast non-linear spectroscopy. Adding additional spectroscopic parameters to a few-cycle laser pulse, such as a frequency-dependent phase delay,171 may increase the dimensionality and consequently the sensitivity of this approach, extending opportunities for ultrafast enantio-sensitive imaging and control in the electric–dipole approximation.
6.2 Enantio-sensitive manipulation
Locally and globally chiral electric fields create opportunities for excitation of only one of the two enantiomers of a chiral molecule to rotational, vibrational or electronic states and open routes to achieving efficient enantio-manipulation. Enantio-sensitive excitations to rotational states have already been demonstrated using microwave fields with three orthogonally polarized components90,95,99 including opportunities for its optimal control.97,98,157A recent experiment94 demonstrated an alternative path to enantio-sensitive control over rotational excitations. This experiment realises the concept of chiral observer and combines the optical centrifuge172–174 with Coulomb explosion imaging. The chiral experimental setup consists of an optical centrifuge, i.e. a linearly polarised laser field rotating (with acceleration) at the slow, rotational, time scale around the propagation direction. The additional axis is provided by the Coulomb explosion imaging detector. The respective molecular pseudoscalar should include the projection of the total angular momentum (transferred from the field to the molecule and recorded in its rotational excitation) on the detector axis, i.e. on the direction of the Coulomb explosion. Note that the control of rotational degrees of freedom resulting in enantio-sensitive molecular orientation in space is also an observer type approach: it can be achieved with achiral optical pulses with shaped polarizations.92–94,175,176
Alternatively, one can also project the total angular momentum supplied by the optical centrifuge on a different axis, e.g. the direction of an additional external static field. This setup has recently been proposed by Yachmenev et al.89 The combination of strong infrared fields forming the optical centrifuge and static electric field polarized along the centrifuge rotational axis is an example of a locally and globally chiral electric field arrangement.
Synthetic chiral light in the optical domain enables control over the electronic degrees of freedom, and thus the possibility of exciting a selected molecular enantiomer to a desired electronic or vibronic state. Enantio-sensitive coherent control over such chiral electronic clouds opens additional routes for enantio-selective manipulation, since the properties of the photo-excited molecules, e.g. their dipole moments or polarizabilities, can be substantially different from those in the ground state.
Synthetic chiral light may also allow one to measure strongly enantio-sensitive photo-absorption signals, with the ambitious goal of enhancing the enantio-sensitivity of standard photo-absorption circular dichroism by several orders of magnitude. Along this route, introducing synthetic chiral light to attosecond transient absorption spectroscopy (ATAS) may allow one to induce and measure strongly enantio-sensitive dynamics with attosecond time resolution using photon-based measurements.
6.3 Enantio-separation
Intense laser beams allow one to manipulate, accelerate, decelerate and trap particles.177–179 Enantio-sensitive optical potentials, which could be applied for selective manipulation, trapping and sorting of chiral particles with specific handedness have recently been demonstrated in the linear light-matter interaction regime.162,180–187 A promising route to efficient enantio-separation was proposed by Cameron and co-workers,165,188 who suggested creating gratings of chiral light of alternating handedness, which could then send opposite molecular enantiomers in opposite directions. They found strongly enantio-sensitive deflection angles in chiral molecules with strong magnetic dipoles, such as helicene, demonstrating the feasibility of the method. A recent theoretical proposal showed that optical gratings could also be used to generate quantum superpositions of opposite enantiomers.189 However, in these works, the proposed optical setups are chiral only beyond the electric–dipole approximation, and thus the sensitivity of these methods to smaller molecules and localized chiral structures such as due to an asymmetric carbon, could be limited by the weakness of the non-electric–dipole interactions. Synthetic chiral light may allow one to overcome this limitation, enhancing these opportunities even further.7 Synthetic chiral matter: imprinting chirality on achiral matter
Synthetic chiral light can also be used to endow achiral matter with chiral properties. Achiral matter excited with such locally chiral light becomes “synthetic chiral matter”. That is, one can aim to imprint chirality on atoms,190 achiral molecules,191 and solids, and read it out on ultrafast scales. In molecules, Owens et al.191 showed that a chiral arrangement of a DC field and an optical centrifuge172,173 produces PH3 molecules that rotate around a P–H bond in a direction determined by the centrifuge, with the P–H bond oriented along the DC field. Formally, in this case the chirality of the electric field is imprinted on the molecular rotational states, which can be detected using e.g. ESMW spectroscopy.In the case of electronic states, relatively simple superpositions of angular momentum eigenstates suffice to form chiral electronic wave functions in atomic hydrogen,190i.e. synthetic chiral atoms, which are already oriented in space. These chiral atoms can also display PECD upon ionization with a circularly polarized field.130,131,190,192 The experimental demonstration of PECD on chiral atoms will require efficient excitation schemes. Such schemes have recently been proposed in the first theoretical works on using locally chiral light to imprint chirality on atomic ensembles,130,131 supporting our general expectation that the non-perturbative interaction of locally chiral light with atoms will in general lead to chiral superpositions of states.
Interesting opportunities may arise for imprinting chirality on atoms in optical lattices and on electrons in solids. Recently, the spatial symmetry of the light's Lissajous figure has been used to imprint topological properties onto a trivial two-dimensional hexagonal material.193 Analogously, the longitudinal components emerging in tightly focused few-cycle pulses can be used to make locally chiral light, which can break the symmetry of a cubic lattice, by introducing “forward–backward” asymmetry in the field-modified hopping coefficients and thus turning the cubic lattice into a chiral object. Strongly correlated systems may provide an opportunity to maintain such laser induced modifications194 after the end of the pulse. Chiral crystals have been shown to possess interesting topological properties.195 Therefore, imprinting chirality on lattices might offer a way to induce light-driven ultrafast topology.
Looking broadly, the outcome of the interaction between such synthetic chiral matter and either ‘natural’ matter or light (chiral or not) has not been explored and raises many interesting questions. How and to what extent will the chirality of synthetic chiral matter influence the outcome of its interaction with ‘natural’ chiral matter or light? Is synthetic chiral matter useful for enantio-selective chemical synthesis? Can we design efficient catalysts for asymmetric synthesis based on synthetic chiral matter? Is it possible to implement ultra-sensitive chirality detectors based on chiral Rydberg atoms? How will many-body effects influence the dynamics of chiral Rydberg atoms trapped in optical lattices? And can we perform quantum simulations of phenomena unique to chiral crystals196 using chiral Rydberg atoms in optical lattices?
8 Opportunities for imaging and controlling chiral molecules via photoionization
Photoelectrons are extremely sensitive structural probes of matter in gas and condensed phase. In molecules, electron scattering on the nuclei during photoionization provides information about their spatial arrangements. This information is recorded in the key photoionization observable: the angular and energy resolved photoelectron distribution; angle-resolved photo-electron spectroscopy can be viewed as “diffraction from within.”PECD and PXCD (see Section 3) are two important milestones in understanding the chiral electronic and vibronic response of molecules to light. PECD in photoionization from a stationary state is generated by chiral continuum currents, while PXCD in photoexcitation is generated by chiral bound currents. Probing PXCD via photoionization with a circularly polarized field would inevitably “mix” these two types of chiral dynamics and such time-resolved probe could be understood in terms of “synchronisation” of chiral bound and continuum currents. Controlling the interplay of pump and probe pulses can be interpreted in terms of controlling this synchronisation. Thus, formulating standard photoionization observables in terms of the currents and fields they generate154 may provide a helpful physical picture and a language for communicating the observations.
Since standard photoionization observables are defined in momentum space, the continuum electron currents and the fields they generate should also be defined in momentum space.154
Such a perspective is customary in condensed matter physics, where one analyzes the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -dependent fields generated by electrons photo-excited from a valence to a conduction band. Electron scattering on the lattice sites may lead to swirling electron trajectories. These, in turn, generate a geometric magnetic field, known as Berry curvature. The geometric magnetic field in solids plays an important role in understanding the electronic response, especially in materials with non-trivial topological properties.
-dependent fields generated by electrons photo-excited from a valence to a conduction band. Electron scattering on the lattice sites may lead to swirling electron trajectories. These, in turn, generate a geometric magnetic field, known as Berry curvature. The geometric magnetic field in solids plays an important role in understanding the electronic response, especially in materials with non-trivial topological properties.
Can the perspective offered by analysing the electronic response in molecular photoionization via a geometric magnetic field generated by swirling electron photoionization currents be fruitful, especially for chiral molecules? Could it allow us to uncover new enantio-sensitive observables in photoionization? What can we learn from the topology of field lines? How does this field reflect information about molecular dynamics prior to ionization? Interestingly, the standard photoionization observables formulated in terms of local, i.e. ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -dependent currents and the fields they generate, provide some answers to these questions (see Section 8.6 below).
-dependent currents and the fields they generate, provide some answers to these questions (see Section 8.6 below).
As an extremely sensitive probe of molecular chirality, PECD has already given rise to a family of time-resolved methods which use various pump-probe setups and detect angularly resolved photoelectron spectra. All these methods involve two- or higher-order multiphoton processes. An important player in such setups is the polarization of the pump and probe pulses. For example, two-photon ionization of a chiral molecule can be performed in many different ways: linearly polarized pump – circularly polarized probe (TD PECD70), circularly polarized pump – linearly polarized probe (PXECD72), circularly polarized pump – circularly polarized probe co-rotating (coherent control of PECD79,154) or counter-rotating to each other.
Interestingly, chiral properties can also be probed using linearly polarized pump and probe pulses, but conditions apply.88 What are these conditions? What is the difference in the photoionization observables detected using these different schemes?
In this section, we first provide the perspective on such two-photon measurements, which demonstrates that each of these schemes addresses different molecular properties, because it relies on different molecular pseudoscalars and therefore exposes a different and independent aspect of molecular chirality. Next, we discuss the physical picture behind these schemes and perspectives for imaging and control of chiral molecular dynamics inspired by these schemes. Finally, we discuss the geometric magnetic field and the physical origin of PECD using the language of currents and fields generated by electrons during photoionization. At this point we would also like to address the X-ray community, which identifies imaging of molecular currents as an important milestone.
8.1 Chiral molecular fingerprints in the two-photon angular resolved photoionization
In this subsection we are dealing with methods of chiral detection relying on the principle of the chiral observer, just like the PECD and PXCD methods considered in Section 3. However, there is an important difference. While PECD and PXCD are one-photon processes and involve two light field vectors that form a single light pseudovector![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) (see eqn (2)), PEXCD is a two-photon process. In two-photon and, in general, multiphoton processes, more than two light vectors may be relevant. Therefore, different pseudovectors {
(see eqn (2)), PEXCD is a two-photon process. In two-photon and, in general, multiphoton processes, more than two light vectors may be relevant. Therefore, different pseudovectors {![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) 1,
1, ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) 2,…} can be formed. This gives rise to a hierarchy of chiral measures (see Section 9). Analogously, more than three molecular vectors may be relevant, and thus several different molecular pseudoscalars {g1, g2,…} can be formed. The availability of multiple light pseudovectors and multiple molecular pseudoscalars is reflected in a generalization of eqn (2) according to
2,…} can be formed. This gives rise to a hierarchy of chiral measures (see Section 9). Analogously, more than three molecular vectors may be relevant, and thus several different molecular pseudoscalars {g1, g2,…} can be formed. The availability of multiple light pseudovectors and multiple molecular pseudoscalars is reflected in a generalization of eqn (2) according to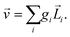 | (24) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) is given by a sum of several such products, involving all possible combinations of all available vectors. Rule 5 in Section 9 provides the most general expression and points to its formal origins.
is given by a sum of several such products, involving all possible combinations of all available vectors. Rule 5 in Section 9 provides the most general expression and points to its formal origins.
The array of different molecular pseudoscalars simply reflects the fact that the description of a complex chiral object requires the specification of more than one pseudoscalar. For example, while a simple helix has just one helicity, a compound helix where a loosely wound helix is formed from a tightly wound helix requires the specification of two independent helicities: one for the loose helix and one for the tight helix, see Fig. 15. In this sense, the coupling between molecular pseudoscalars and light pseudovectors in eqn (24) reveals how each of the ‘helicities’ of a chiral molecule (a rather complex ‘compound helix’) couples to the light field. Similar situations with “nested” chiral structures can occur due to the presence of several chiral centers with different handedness in a chiral molecule.
 | ||
| Fig. 15 An object displaying compound chirality in the form of two independent handedness: a helix made of a more tightly bound helix. | ||
Two photon pump–probe processes are a perfect example illustrating eqn (24). Suppose that the pump ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 1 induces a transition from the ground state |g〉 into a bound excited state |j〉 and the probe
1 induces a transition from the ground state |g〉 into a bound excited state |j〉 and the probe ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2 induces a transition from the state |j〉 into the continuum |
2 induces a transition from the state |j〉 into the continuum |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉. For pulses and time delays short compared to the rotational dynamics, the photoelectron current is given in ref. 88
〉. For pulses and time delays short compared to the rotational dynamics, the photoelectron current is given in ref. 88
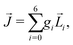 | (25) |
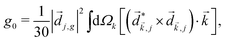 | (26) |
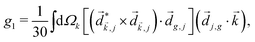 | (27) |
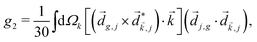 | (28) |
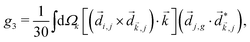 | (29) |
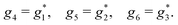 | (30) |
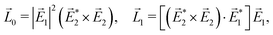 | (31) |
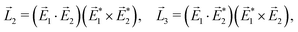 | (32) |
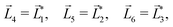 | (33) |
For example, the g0![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) 0 term is associated with PECD from the excited state |j〉 and requires only an elliptically polarized probe field (eqn (4), (5) and (6)). The pseudovector formed by the photoionization vectors
0 term is associated with PECD from the excited state |j〉 and requires only an elliptically polarized probe field (eqn (4), (5) and (6)). The pseudovector formed by the photoionization vectors 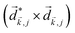 is important in its own right, since it can be understood as a propensity field
is important in its own right, since it can be understood as a propensity field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) )110 associated with photoionization of chiral molecules, which is related to geometric fields in molecular photoionization190 (see Section 8.6). Note that g0 and g1 encode different components of
)110 associated with photoionization of chiral molecules, which is related to geometric fields in molecular photoionization190 (see Section 8.6). Note that g0 and g1 encode different components of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ): g0 encodes the radial field component and g1 encodes the field component along the direction of the bound dipole connecting the ground and excited states.
): g0 encodes the radial field component and g1 encodes the field component along the direction of the bound dipole connecting the ground and excited states.
Accessing g1![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) 1 requires a different and more sophisticated arrangement of pump and probe polarizations. Indeed,
1 requires a different and more sophisticated arrangement of pump and probe polarizations. Indeed, ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) 1 is non-zero only when
1 is non-zero only when ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2 is elliptically polarized and in addition
2 is elliptically polarized and in addition ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 1 has a component perpendicular to the plane defined by
1 has a component perpendicular to the plane defined by ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 2. In contrast,
2. In contrast, ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) 2 and
2 and ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) 3 are non-zero even if both the pump and the probe are linearly polarized, as long as they are neither parallel nor perpendicular to each other, suggesting a connection to some recent works using such an arrangement of pump and probe pulses to excite rotational states of chiral molecules and inducing enantio-sensitive molecular orientation.91,92,175 Note also that while
3 are non-zero even if both the pump and the probe are linearly polarized, as long as they are neither parallel nor perpendicular to each other, suggesting a connection to some recent works using such an arrangement of pump and probe pulses to excite rotational states of chiral molecules and inducing enantio-sensitive molecular orientation.91,92,175 Note also that while ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) 2 vanishes for co-rotating circularly polarized pump and probe,
2 vanishes for co-rotating circularly polarized pump and probe, ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) 3 vanishes for counter-rotating pump and probe. These simple rules together with eqn (25)–(33), specifying the coupling between molecular pseudoscalars and field pseudovectors, can be combined to determine the values of each molecular pseudoscalar gi.
3 vanishes for counter-rotating pump and probe. These simple rules together with eqn (25)–(33), specifying the coupling between molecular pseudoscalars and field pseudovectors, can be combined to determine the values of each molecular pseudoscalar gi.
In the case where the final state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 can be reached via two different intermediate states, additional molecular pseudoscalars and field pseudovectors (see ref. 88) resulting from the two-path interference contribute to the generation of the photoelectron current. Importantly, they also can be expressed88 in a compact form similar to eqn (26)–(33). Unlike the direct terms, these terms oscillate with the time delay between the pump and probe and record the dynamics excited by the pump. One example of such dynamics are the helical currents excited in bound states by ultrashort circularly polarized pulses (PXCD). Below we provide a perspective on their detection.
〉 can be reached via two different intermediate states, additional molecular pseudoscalars and field pseudovectors (see ref. 88) resulting from the two-path interference contribute to the generation of the photoelectron current. Importantly, they also can be expressed88 in a compact form similar to eqn (26)–(33). Unlike the direct terms, these terms oscillate with the time delay between the pump and probe and record the dynamics excited by the pump. One example of such dynamics are the helical currents excited in bound states by ultrashort circularly polarized pulses (PXCD). Below we provide a perspective on their detection.
8.2 Nonlinear photo-ionization probes of molecular chirality: probing helical currents in bound states (PXECD)
In the previous section we gave the formal description of the two-photon pump–probe setups for probing chiral molecular structure and dynamics. Here we discuss the underlying physical picture describing two-photon photoionization as an interplay of chiral bound and continuum currents. This interplay can be disentangled in PXECD,72 which induces photoionization using linearly polarized light to decrease the influence of continuum currents.The helical currents excited in chiral molecules by short circularly polarized pulses (PXCD, see Section 3) can be probed by photoionization. Since induced polarization oscillates out of phase in opposite enantiomers, the respective electron currents flow in opposite directions. Photoionization by a linearly polarized short pulse can reveal this direction of the bound current: the liberated electron should typically continue to move in the same direction as it was moving in the bound states. Thus, two photoelectron detectors placed along the propagation direction (along the direction of spin angular momentum of the field) of the pump pulse will show the forward-backward asymmetry: more forward electrons in one enantiomer and more backward electrons in the opposite enantiomer.
The interference of two photoionization signals originating from the two excited PXCD states (see Fig. 6) records the coherence between these states and also its time evolution as a function of the delay between the exciting (pump) and photoionizing (probe) pulses. Since both pulses are short, the interference of the photoionization signals coming from the two intermediate states excited by the pump may cover a considerable range of photoelectron energies. In this range, one can observe that the photoelectron current oscillates with the time-delay between the two pulses and has opposite directions for opposite enantiomers, or for opposite spins of the pump pulse. That is, thanks to the molecular chirality, the spin of the pump photon can be read out from the photoelectron angular distribution even though the ionizing step is carried out with linearly polarized light.
Indeed, one can show72 that the photoelectron current is proportional to two terms:
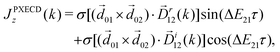 | (34) |
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 01 and
01 and ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 02 are the transition dipoles from the ground state to the excited states, and
02 are the transition dipoles from the ground state to the excited states, and ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) 12(k) = Dr12(k) + iDi12(k) is a complex Raman-type photoionization vector that connects the excited bound states via the common continuum. Since
12(k) = Dr12(k) + iDi12(k) is a complex Raman-type photoionization vector that connects the excited bound states via the common continuum. Since ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) 12(k) encodes coherence between the excited states, it plays the role of
12(k) encodes coherence between the excited states, it plays the role of ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 12 in eqn (8)–(10) for PXCD. The two triple products in eqn (34) are the molecular pseudoscalars characterizing the enantio-sensitive signal in PEXCD. The photoionization vector
12 in eqn (8)–(10) for PXCD. The two triple products in eqn (34) are the molecular pseudoscalars characterizing the enantio-sensitive signal in PEXCD. The photoionization vector ![[D with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0044_20d1.gif) 12 in eqn (34) is given by
12 in eqn (34) is given by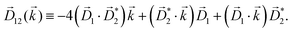 | (35) |
Note that this general expression shows that every available vector  can be used to “complete” the triple product in eqn (34). Physically, the appearance of the second and third term in eqn (35) is due to partial alignment of the molecules by the pump pulse. To validate this statement it is sufficient to consider an isotropic probe pulse, which cannot be sensitive to the initial alignment by the pump. One can show (see SI of ref. 72) that only the first term in eqn (35) survives in this case.
can be used to “complete” the triple product in eqn (34). Physically, the appearance of the second and third term in eqn (35) is due to partial alignment of the molecules by the pump pulse. To validate this statement it is sufficient to consider an isotropic probe pulse, which cannot be sensitive to the initial alignment by the pump. One can show (see SI of ref. 72) that only the first term in eqn (35) survives in this case.
How accurately can the continuum current image the current in the bound states? The difficulties here are similar to those encountered in the so-called tomographic imaging of molecular orbitals in high harmonic spectroscopy.197 Namely, the bound-continuum mapping is only exact in the case of the plane wave continuum: in this case, the total photoelectron current ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) PXECDtot, integrated over all photoelectron energies
PXECDtot, integrated over all photoelectron energies 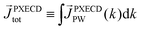 is indeed proportional to the bound current
is indeed proportional to the bound current 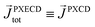 , since one can show that
, since one can show that 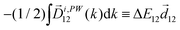 . However, the structure of the continuum in chiral molecules is a lot more complex than simple plane waves. Perhaps, the connection between the bound and continuum currents can be established by introducing an additional unknown function f(k), such that
. However, the structure of the continuum in chiral molecules is a lot more complex than simple plane waves. Perhaps, the connection between the bound and continuum currents can be established by introducing an additional unknown function f(k), such that 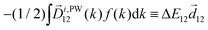 . This function will then have to be reconstructed together with the bound current, e.g. iteratively, starting with f(k) = 1 for the plane wave continuum, similar to the efforts in tomographic reconstruction of molecular orbitals in high harmonic spectroscopy.198
. This function will then have to be reconstructed together with the bound current, e.g. iteratively, starting with f(k) = 1 for the plane wave continuum, similar to the efforts in tomographic reconstruction of molecular orbitals in high harmonic spectroscopy.198
The first PEXCD images72 were recorded via excitation of Rydberg bands in fenchone and camphor molecules using a circularly polarized femtosecond pump pulse carried at 201 nm (with 80 meV 1/e2 bandwidth) and probing it using a time-delayed, linearly polarized probe pulse carried at 405 nm (with 85 meV at 1/e2 bandwidth). Although the results demonstrate excitation of a chiral vibronic wave-packet in these molecules, detailed information about the specific nature of these dynamics requires further analysis. Such an analysis could provide much desired insight into chiral molecular dynamics at femtosecond time-scales and presents one of the exciting future opportunities for this field.
8.3 Two-color coherent control
Another interesting aspect of chiral molecular dynamics may result from the interplay of bound and continuum chiral currents. Both currents are present if both the pump and probe pulses are circularly polarized. Indeed, the spin angular momentum carried by the pump can be transferred to the current excited in bound states. At the same time, the spin angular momentum carried by the probe pulse can lead to chiral continuum currents. This combination of pump and probe polarizations has been recently explored by Goetz et al.79 and used for two-photon coherent control of the chiral photoelectron current associated with the coefficient b1,0 and multipolar currents associated with the coefficient b3,0. Goetz et al.79 achieved very significant enhancement of enantio-sensitivity of photoionization observables by optimizing the arrival of each frequency in the pump and probe pulses. Since the scheme involves the absorption of two circularly polarized photons, the optimization could have been related to achieving the best synchronization between the bound and continuum currents. Whether the control has been associated with such synchronisation remains to be seen, but exploring and exploiting the interplay of bound and continuum currents for enhancing the chiral photoelectron signal may present an interesting future direction.8.4 Time-dependent PECD
Time-dependent PECD implies exciting molecular vibronic dynamics by a linearly polarized pump pulse and probing it with a circularly polarised pulse.70 As we have seen from previous examples, excitation with a circularly polarized pump imprints the spin angular momentum of light onto the bound states dynamics and excites helical currents in chiral molecules. At first glance one may think that a linearly polarized pump cannot excite chiral dynamics, because the spin angular momentum is required to define the “helicity” of the excited bound current. Indeed, since a linearly polarized pump is a superposition of two counter-rotating circular pulses, we should expect the excitation of two PXCD currents of opposite handedness in a given enantiomer. However, the probe – a circularly polarized pulse, will break this symmetry between left and right helical PXCD currents. Indeed, two co-rotating photons and two counter-rotating photons produce different photoionization signals, because they correspond to different molecular pseudoscalars [see e.g.eqn (28) and (29) for g2 and g3 in case of a single intermediate state; eqn (35) of ref. 88 generalizes this result for two intermediate states]. Thus, the time-dependent PECD is a probe highlighting the synchronisation of bound and continuum chiral currents pondered above. It presents a differential measure encoding two chiral currents of opposite handedness with different amplitudes. The results of time-dependent PECD experiments could be re-interpreted as the images of such an interplay.708.5 Enantio-separation via photoionization
The possibility of selectively exciting only one of the two enantiomers of a chiral molecule to an electronic state opens several routes for enantio-separation that we chart below.One option is to use synthetic chiral light100 (see Section 4) to selectively excite one of the two enantiomers of a chiral molecule to a desired state, tuning the frequencies of the light field in (possibly multi-photon) resonance with a specific electronic or vibronic transition. Next, the photo-excited molecules could be photoionized with a second laser pulse, yielding enantio-selective ionization. These molecular ions with well-defined handedness could then be extracted with a static field.
Another option is to use achiral light without spin angular momentum to achieve enantio-sensitive uniaxial orientation of chiral molecules on the electronic time-scale142 due to orientation-dependent excitation.
It is often assumed that molecular orientation can only occur on rotational time-scales. However, in chiral molecules, this does not have to be the case. Our analysis142 in the perturbative regime predicts that phase-locked, orthogonally polarized fields with frequencies ω and 3ω can induce field-free permanent electronic dipoles in initially isotropic samples of chiral molecules via resonant electronic excitation. The dipole's orientation is enantio-sensitive and it is controlled by the relative phase between ω and 3ω fields, which determines the sub-cycle direction of rotation of the total electric field. In contrast to the photo-excited circular dichroism (PXCD),72 here not only the excited electron but also the molecule correlated to the excitation acquires orientation.
This effect is fundamentally multi-photon. In the frequency domain, the interference between the two pathways, 3 × ħ ω vs. 1 × 3ħ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ω, is sensitive to the molecular orientation and handedness. This leads to orientation-dependent excitation and thus uniaxial orientation of the excited molecules, on the electronic excitation time scale. The orientation is perpendicular to the polarization plane and is reflected in the emergence of a field-free permanent dipole.
ω, is sensitive to the molecular orientation and handedness. This leads to orientation-dependent excitation and thus uniaxial orientation of the excited molecules, on the electronic excitation time scale. The orientation is perpendicular to the polarization plane and is reflected in the emergence of a field-free permanent dipole.
This fundamental phenomenon points to interesting opportunities for creating enantio-sensitive permanent dipoles via orientation-dependent excitation of Rydberg states upon resonance-enhanced multiphoton ionization (REMPI). The non-perturbative ω and 3ω fields should also be explored, since in such regime hitting resonances does not necessarily require carefully tuning the light frequency to specific molecular transitions. Indeed, in the non-perturbative regime one can take advantage of light-induced energy shifts of excited states. These are known as Freeman resonances199 and are virtually inevitable at intensities I ∼ 1013 W cm−2 and above. They will also lead to orientation of molecular ions after orientation-selective resonantly enhanced multi-photon ionization. By selectively depleting randomly oriented neutrals, preferential orientation in the neutral ensemble is also created. After that, a static field can be used to spatially separate opposite enantiomers.
8.6 Geometric magnetism in chiral molecules
The excitation of enantio-sensitive photoelectron currents (PECD) in the electric–dipole approximation can be linked to the concept of geometric magnetism introduced by Berry.103 One of its manifestations is the Berry curvature in solids, which links electronic response to EM fields to topological properties of bands and underlies a class of phenomena in condensed-matter systems enabled by their topological properties.106 A geometric magnetic field also appears in photoionization of chiral molecules by circularly polarized fields.108 This field arises due to “curly” or “twisted” polarization in vibronic states or due to “curly” or “twisted” currents. The “twist” originates from the chiral arrangements of the nuclei and does not vanish upon averaging over the random molecular orientations. The geometric magnetic field arising in chiral molecules underlies several classes of chiral photoionization observables.108 It is related to the so-called propensity field that we have introduced recently.110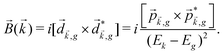 | (36) |
![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif)
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ,g and
,g and ![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif)
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ,g = i(Ek − Eg)
,g = i(Ek − Eg)![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif)
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ,g are transition dipoles in the length and velocity gauges, respectively, and Ek and Eg are the energies of the photoelectron and of the ground state, respectively.
,g are transition dipoles in the length and velocity gauges, respectively, and Ek and Eg are the energies of the photoelectron and of the ground state, respectively.
As usual for photoionization observables, the propensity field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) is a function of the photoelectron momentum
) is a function of the photoelectron momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) .
. ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) quantifies the absorption circular dichroism (CD) for a specific state |
) quantifies the absorption circular dichroism (CD) for a specific state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉. The direction of
〉. The direction of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) indicates a preferred direction in the molecular frame: circularly polarized light propagating along this direction maximizes the CD for a transition from the ground state into a specific final state |
) indicates a preferred direction in the molecular frame: circularly polarized light propagating along this direction maximizes the CD for a transition from the ground state into a specific final state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉. Loosely speaking, the direction of
〉. Loosely speaking, the direction of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) defines the axis in the molecular frame along which the rotational symmetry of the molecule is broken to the highest extent, for a given final state |
) defines the axis in the molecular frame along which the rotational symmetry of the molecule is broken to the highest extent, for a given final state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉.
〉.
The magnitude of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) is proportional to the corresponding CD, i.e. it is proportional to the difference between the populations of the state |
) is proportional to the corresponding CD, i.e. it is proportional to the difference between the populations of the state |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 obtained with left and right circularly polarized light propagating along
〉 obtained with left and right circularly polarized light propagating along ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ). Indeed, if we denote the direction of
). Indeed, if we denote the direction of ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) by
) by 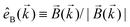 , we obtain110,154
, we obtain110,154
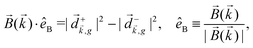 | (37) |
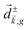 are the photoionization dipoles for ionization by left or right circularly polarized fields propagating along the direction specified by
are the photoionization dipoles for ionization by left or right circularly polarized fields propagating along the direction specified by ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ). Thus, the vector field
). Thus, the vector field ![[B with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0042_20d1.gif) (
(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) provides the molecule-specific
) provides the molecule-specific ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -resolved map of maximal possible photoionization CD.
-resolved map of maximal possible photoionization CD.
One can show that the propensity field is similar to the Berry curvature in two band solids,108,110 which is responsible for the circular photogalvanic effect in chiral solids200 in the same way as the propensity field is responsible for PECD in gas phase chiral molecules. The geometric magnetic field introduced in ref. 108 provides a generalization of the propensity field.
The geometric magnetic field108 reflects the geometry of the molecular photoionization dipoles and gives rise to three classes of enantio-sensitive observables, relying on various quadratures of the geometric field. The new enantio-sensitive observables of Class I have been completely overlooked so far. Class I observables can only appear if the current in molecular bound states was excited prior to photoionization. Thus, Class I observables can serve as messengers of charge-directed reactivity: chemical reactivity driven by ultrafast chiral electron dynamics. The first member of Class I observables is molecular orientation circular dichroism in photoionization. Observables of Class II and III include the PECD (and time-dependent PECD) current and an infinite array of its multipolar versions. Most of these observables have not been studied so far.
Concept 5. The geometric field108 underlies vectorial and tensorial enantio-sensitive observables in photoionization, in the electric–dipole approximation. Its flux in photoelectron momentum space quantifies the PECD, its integral over all photoelectron momenta quantifies chiral current excited in bound states, its multipole moments characterize multipolar currents, which can be excited by light fields without net spin angular momentum. The geometric field in photoionization can be linked to the Berry curvature.
The geometric field so far served for us as a heuristic principle for discovering and classifying new enantio-sensitive observables. Future directions can include identification of new members of Classes I-III, establishing the connection between the topology of the geometric field and the topology of the respective molecular bound and continuum states, and the application of enantio-sensitive molecular orientation,108 which occurs in neural molecules and molecular ions, for enantio-separation and ultrafast molecular imaging. Other possibilities include exploiting the analogy between chiral effects in photoionization and a broad class of topological phenomena in solids, aiming to create observables which encode both chiral and topological properties of matter,108,109 such as quantized circular dichroism.
9 The hierarchy of chiral measures
This section concludes the paper by offering a unified view on chiral measurements and chiral observables as a cornerstone of such measurements, ultimately defining their efficiency. In chiral measurements performed with electromagnetic fields we usually deal with the following objects: a chiral molecule and either chiral light (or a combination of electric fields), or a chiral setup. An enantio-sensitive measurement couples the pseudoscalars of the two objects: the chiral molecule and the chiral light and/or electric fields (the “chiral reagent” type of interaction), or the chiral molecule and the chiral setup (the “chiral observer” type of interaction). Remarkably, not only the pseudoscalars of all these chiral objects have very similar structure, but they also form a very similar hierarchy associated with the increasing order of non-linear interactions.A graphical example of such structural similarity of chiral measures emerges from the comparison of the laser and the setup pseudoscalars. Table 2 shows that in every order of non-linearity the structure of these two pseudoscalars is the same, only the specific vectors are different. Namely, the setup pseudoscalar always contains vectors associated with the detector axes, which “substitute” one or more light vectors of the light pseudoscalar.
| Phenomenon | Molecular pseudoscalar | Light/setup pseudoscalar |
|---|---|---|
| Linear CD | [![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) f,i· f,i·![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) f,i]119 f,i]119 |
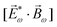 119
119
|
| PECD |
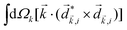 88
88
|
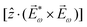 88
88
|
| Non-linear CD (2) | [![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 2,0·( 2,0·(![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 2,1 × 2,1 × ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 1,0)] or 1,0)] or 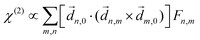 44,140 44,140 |
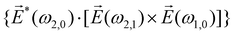 100
100
|
| PXCD/ESMW | [![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 2,0·( 2,0·(![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 2,1 × 2,1 × ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 1,0)]72,88 1,0)]72,88 |
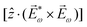 88
88
|
| Non-linear CD (4) | (![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 0,1· 0,1·![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 1,2)[ 1,2)[![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 0,2·( 0,2·(![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 2,4 × 2,4 × ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) 4,3)] or χ(4) 4,3)] or χ(4) |
 100
100
|
| Quadrupole currents |
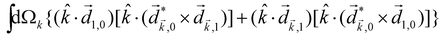 125
125
|
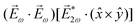 125
125
|
| Permanent quadrupoles |
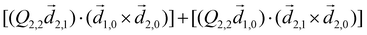 142
142
|
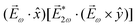 142
142
|
| PECD (2) (circ. pump - circ. probe) |
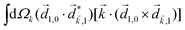 88
88
|
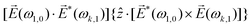 88
88
|
| TD-PECD (linear pump - circ. probe) |
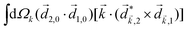 88
88
|
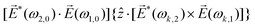 88
88
|
| PEXCD (circ. pump - linear probe) |
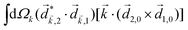 88
88
|
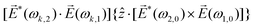 88
88
|
The first two rows of Table 2 show the linear chiral measures involving the light and the setup pseudoscalars, respectively. Comparing them shows that in PECD the light pseudovector 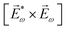 substitutes the light pseudovector
substitutes the light pseudovector  in absorption CD, while the detector axis ẑ substitutes the light vector
in absorption CD, while the detector axis ẑ substitutes the light vector ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω.
ω.
The second-order phenomena involving the light and setup pseudoscalars are shown in the third and fourth rows of the table. Here non-linear absorption CD(2) and PXCD/ESMW use the same light pseudovector, which is given by the cross product of the electric fields at two different frequencies, but the third vector necessary to form the desired triple product has a very different nature. Indeed, the light vector contributing to the light pseudoscalar in absorption CD(2) is substituted by the detector axis ẑ in PXCD/ESMW. The fifth and sixth rows show that the same happens in the fourth order of nonlinearity: the setup pseudoscalar pertinent for tensorial observables such as, e.g. the quadrupole current, substitutes the two laser vectors employed in absorption CD(4) by the detector axes. The presence of the two detector axes reflects the tensorial nature of the required detection scheme.
Thus, the overall structure of any chiral measure contributing to experimental observables is encoded in pseudoscalar expressions formed by dot and cross products between appropriate vectors. In particular, the chiral measures in the electric dipole approximation in Table 2 involve a triple product of three vectors in the lowest order and are subsequently complemented by one scalar product of two vectors per each subsequent order of non-linearity. For example, the two-photon pump–probe photoionization of randomly oriented chiral molecules leads to the appearance of one additional (with respect to PECD) scalar product of light fields in the setup pseudoscalar (see the last row of Table 2).
Table 2 reveals not only the common overall structure of pseudoscalars but also the flexibility in addressing various molecular properties for distinguishing opposite enantiomers. The interchangeability of molecular, light and setup vectors is a great asset for chiral experiments, provided that the vectors are chosen wisely. Depending on the type of observation, the enantio-sensitive response of a given molecular sample can have different strengths and require different light pseudovectors.
For example, let us compare molecular pseudoscalars for the linear CD and the non-linear absorption circular dichroism CD(2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 in Table 2 (note that pseudoscalars of CD(2) also describe three-level enantio-sensitive population transfer90,95). We see that in the latter case, instead of relying on the molecular magnetic transition dipole, one can rely on the cross product of two electric transition dipoles; instead of relying on the magnetic field one can rely on the cross product of the electric field at two different frequencies.
100 in Table 2 (note that pseudoscalars of CD(2) also describe three-level enantio-sensitive population transfer90,95). We see that in the latter case, instead of relying on the molecular magnetic transition dipole, one can rely on the cross product of two electric transition dipoles; instead of relying on the magnetic field one can rely on the cross product of the electric field at two different frequencies.
One also has freedom in choosing the setup vectors. They can be constructed not only by introducing detectors for electrons, as done in PECD, but also by using additional electronic or vibrational/rotational degrees of freedom introduced via molecular alignment or coincidence detection involving other electrons, fragments, etc.
Formally, different dot and cross products in light/molecular/setup pseudoscalars appear as a result of the orientation averaging procedure. Indeed, the isotropy of the molecular sample is the reason why these expressions do not depend on the relative orientations between molecular and setup vectors (e.g. through the terms of the form ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) f,i·
f,i·![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) ω), but instead only on the relative orientations between either molecular vectors among themselves (e.g.
ω), but instead only on the relative orientations between either molecular vectors among themselves (e.g. ![[d with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0064_20d1.gif) f,i·
f,i·![[m with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006d_20d1.gif) f,i), or the setup vectors among themselves (e.g.
f,i), or the setup vectors among themselves (e.g. ).
).
In general, if e.g. the process involves several photons, more vectors become available and the simple Rule 1 requires generalization.
Rule 5. Enantio-sensitive observables pertinent to randomly oriented molecular ensembles can be written in the general form:154,201
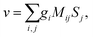 | (38) |
The gi's result from different possible contractions of Levi–Civita and Kronecker delta tensors with molecular tensors, which then lead to the dot and cross products discussed above. The same applies to the Sj's but using the setup (or light) instead of molecular tensors. In the simplest cases there is a single possible contraction so that the sum over i and j reduces to a single term. This is precisely what occurs in the case of Rule 1 in Section 3: the measured click, a scalar v, corresponding to the projection of the respective vectorial observable ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) if onto the detector axis ẑ, converts the laser pseudovector
if onto the detector axis ẑ, converts the laser pseudovector ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) into the setup pseudoscalar S by projecting
into the setup pseudoscalar S by projecting ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) on the detector axis: S =
on the detector axis: S = ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) · ẑ. The resulting expression v =
· ẑ. The resulting expression v = ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) if · ẑ = gS is indeed the simplest case of Rule 5.
if · ẑ = gS is indeed the simplest case of Rule 5.
10 Conclusions
Our perspective on ultrafast chirality presented here offers a unifying framework for understanding and quantifying enantio-sensitive phenomena emerging in the interaction between chiral molecules and electromagnetic fields. This framework is applicable to all frequency regimes, from microwaves to infrared, to visible, to X-rays and underlies spectroscopic tools probing electronic, vibronic or rotational states of chiral molecules and detecting photons or photo-electrons. We have described the new concepts of synthetic and locally chiral light, light with handedness structured in space, polarization of chirality, and geometric field in chiral molecules. These concepts lead to new applications in ultrafast optics and molecular photoionization with intense mid-infrared fields or X-rays. The perspective on synthetic chiral light in confined environments and its applications in nanophotonics will be discussed separately.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Discussions with Prof. M. Ivanov, Prof. A. Steinberg, Prof. M. Stockman and Dr. I. Nowitzki were extremely important at different stages of this work and are gratefully acknowledged. A. F. O. and O. S. gratefully acknowledge the MEDEA Project, which has received funding from the European Union's Horizon 2020 Research and Innovation Programme under the Marie Skłodowska-Curie Grant Agreement No. 641789. A. F. O. and O. S. gratefully acknowledge support from the DFG SPP 1840 “Quantum Dynamics in Tailored Intense Fields” and DFG Grant No. SM 292/5-2. A. F. O. gratefully acknowledges grants supporting his research at ICFO: Agencia Estatal de Investigación (the R&D project CEX2019-000910-S, funded by MCIN/AEI/10.13039/501100011033, Plan Nacional FIDEUA PID2019-106901GB-I00, FPI), Fundació Privada Cellex, Fundació Mir-Puig, Generalitat de Catalunya (AGAUR Grant No. 2017 SGR 1341, CERCA program), and EU Horizon 2020 Marie Skłodowska-Curie grant agreement No. 101029393. D. A. acknowledges funding from the Royal Society URF\R1\201333 and RF\ERE\210358. O. S. gratefully acknowledges funding Horizon Europe ERC-2021-ADG 101054696 ULISSES.Notes and references
- L. G. Wade, Chirality in Drug Research, Prentice Hall, 2003 Search PubMed.
- W. A. Bonner, Origins Life Evol. Biosphere, 1991, 21, 59–111 CrossRef CAS PubMed.
- J. Cohen, Science, 1995, 267, 1265–1266 CrossRef CAS PubMed.
- R. M. Hazen, T. R. Filley and G. A. Goodfriend, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 5487–5490 CrossRef CAS PubMed.
- D. G. Blackmond, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 5732–5736 CrossRef CAS.
- R. Breslow and Z.-L. Cheng, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 9144–9146 CrossRef CAS PubMed.
- I. Weissbuch and M. Lahav, Chem. Rev., 2011, 111, 3236–3267 CrossRef CAS PubMed.
- J. E. Hein and D. G. Blackmond, Acc. Chem. Res., 2012, 45, 2045–2054 CrossRef CAS PubMed.
- J. E. Hein, D. Gherase and D. G. Blackmond, in Chemical and Physical Models for the Emergence of Biological Homochirality, ed. P. Cintas, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 83–108 Search PubMed.
- A. Brewer and A. P. Davis, Nat. Chem., 2014, 6, 569 CrossRef CAS PubMed.
- F. Jafarpour, T. Biancalani and N. Goldenfeld, Phys. Rev. Lett., 2015, 115, 158101 CrossRef.
- R. Hadidi, D. Bozanic, G. A. Garcia and L. Nahon, Adv. Phys.: X, 2018, 3(1), 21477530 Search PubMed.
- T. Bredtmann and J. Manz, Angew. Chem., Int. Ed., 2011, 50, 12652–12654 CrossRef CAS PubMed.
- I. Barth and J. Manz, Angew. Chem., Int. Ed., 2006, 45, 2962–2965 CrossRef CAS PubMed.
- O. Neufeld and O. Cohen, Phys. Rev. Lett., 2019, 123, 103202 CrossRef CAS PubMed.
- I. Barth and J. Manz, Phys. Rev. A: At., Mol., Opt. Phys., 2007, 75, 012510 CrossRef.
- K.-J. Yuan and A. D. Bandrauk, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 013417 CrossRef.
- L. Cederbaum and J. Zobeley, Chem. Phys. Lett., 1999, 307, 205–210 CrossRef CAS.
- J. Breidbach and L. S. Cederbaum, J. Chem. Phys., 2003, 118, 3983–3996 CrossRef CAS.
- A. I. Kuleff and L. S. Cederbaum, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124002 CrossRef.
- S. Lünnemann, A. I. Kuleff and L. S. Cederbaum, Chem. Phys. Lett., 2008, 450, 232–235 CrossRef.
- F. Remacle, R. D. Levine, E. W. Schlag and R. Weinkauf, J. Phys. Chem. A, 1999, 103, 10149–10158 CrossRef CAS.
- F. Remacle and R. D. Levine, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 6793–6798 CrossRef CAS PubMed.
- F. Calegari, D. Ayuso, A. Trabattoni, L. Belshaw, S. De Camillis, S. Anumula, F. Frassetto, L. Poletto, A. Palacios, P. Decleva, J. B. Greenwood, F. Martn and M. Nisoli, Science, 2014, 346, 336–339 CrossRef CAS.
- F. Calegari, G. Sansone, S. Stagira, C. Vozzi and M. Nisoli, J. Phys. B: At., Mol. Opt. Phys., 2016, 49, 062001 CrossRef.
- M. Nisoli, P. Decleva, F. Calegari, A. Palacios and F. Martín, Chem. Rev., 2017, 117, 10760–10825 CrossRef CAS PubMed.
- D. Ayuso, A. Palacios, P. Decleva and F. Martín, Phys. Chem. Chem. Phys., 2017, 19, 19767–19776 RSC.
- S. Mukamel, Principles of nonlinear optical spectroscopy, Oxford University Press, New York, 1995 Search PubMed.
- J. Meyer-Ilse, D. Akimov and B. Dietzek, Laser Photonics Rev., 2013, 7, 495–505 CrossRef CAS.
- S. Ghosh, G. Herink, A. Perri, F. Preda, C. Manzoni, D. Polli and G. Cerullo, ACS Photonics, 2021, 8, 2234–2242 CrossRef CAS PubMed.
- J. R. Rouxel, A. Rajabi and S. Mukamel, J. Chem. Theory Comput., 2020, 16, 5784–5791 CrossRef CAS PubMed.
- L. Ye, J. R. Rouxel, S. Asban, B. Rösner and S. Mukamel, J. Chem. Theory Comput., 2019, 15, 4180–4186 CrossRef CAS PubMed.
- J. R. Rouxel, Y. Zhang and S. Mukamel, Chem. Sci., 2019, 10, 898–908 RSC.
- H. Rhee, Y.-G. June, J.-S. Lee, K.-K. Lee, J.-H. Ha, Z. H. Kim, S.-J. Jeon and M. Cho, Nature, 2009, 458, 310–313 CrossRef CAS PubMed.
- M. Oppermann, J. Spekowius, B. Bauer, R. Pfister, M. Chergui and J. Helbing, J. Phys. Chem. Lett., 2019, 10, 2700–2705 CrossRef CAS PubMed.
- R. Cireasa, A. E. Boguslavskiy, B. Pons, M. C. H. Wong, D. Descamps, S. Petit, H. Ruf, N. Thiré, A. Ferré, J. Suarez, J. Higuet, B. E. Schmidt, A. F. Alharbi, F. Légaré, V. Blanchet, B. Fabre, S. Patchkovskii, O. Smirnova, Y. Mairesse and V. R. Bhardwaj, Nat. Phys., 2015, 11, 654–658 Search PubMed.
- M. Cho, Nat. Phys., 2015, 11, 621–622 Search PubMed.
- D. Baykusheva, D. Zindel, V. Svoboda, E. Bommeli, M. Ochsner, A. Tehlar and H. J. Wörner, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 23923–23929 CrossRef CAS PubMed.
- M. Oppermann, F. Zinna, J. Lacour and M. Chergui, Nat. Chem., 2022, 14, 739–745 CrossRef CAS PubMed.
- J. R. Rouxel and S. Mukamel, Molecular chirality and its monitoring by ultrafast X-ray pulses, arXiv, 2022, preprint, arXiv:2209.08808.
- J. R. Rouxel, B. Rösner, D. Karpov, C. Bacellar, G. F. Mancini, F. Zinna, D. Kinschel, O. Cannelli, M. Oppermann, C. Svetina, A. Diaz, J. Lacour, C. David and M. Chergui, Nat. Photonics, 2022, 16(8), 570–574 CrossRef CAS.
- B. Ritchie, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 1411–1415 CrossRef.
- I. Powis, J. Chem. Phys., 2000, 112, 301–310 CrossRef CAS.
- J. A. Giordmaine, Phys. Rev., 1965, 138, A1599–A1606 CrossRef.
- N. Böwering, T. Lischke, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Phys. Rev. Lett., 2001, 86, 1187–1190 CrossRef PubMed.
- T. Lischke, N. Böwering, B. Schmidtke, N. Müller, T. Khalil and U. Heinzmann, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 022507 CrossRef.
- S. Turchini, N. Zema, G. Contini, G. Alberti, M. Alagia, S. Stranges, G. Fronzoni, M. Stener, P. Decleva and T. Prosperi, Phys. Rev. A: At., Mol., Opt. Phys., 2004, 70, 014502 CrossRef.
- M. Stener, G. Fronzoni, D. D. Tommaso and P. Decleva, J. Chem. Phys., 2004, 120, 3284–3296 CrossRef CAS PubMed.
- S. Stranges, S. Turchini, M. Alagia, G. Alberti, G. Contini, P. Decleva, G. Fronzoni, M. Stener, N. Zema and T. Prosperi, J. Chem. Phys., 2005, 122, 244303 CrossRef CAS PubMed.
- D. Di Tommaso, M. Stener, G. Fronzoni and P. Decleva, ChemPhysChem, 2006, 7, 924–934 CrossRef CAS PubMed.
- S. Turchini, D. Catone, G. Contini, N. Zema, S. Irrera, M. Stener, D. Di Tommaso, P. Decleva and T. Prosperi, ChemPhysChem, 2009, 10, 1839–1846 CrossRef CAS PubMed.
- L. Nahon, G. A. Garcia and I. Powis, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 322–334 CrossRef CAS.
- A. Ferré, C. Handschin, M. Dumergue, F. Burgy, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, L. Merceron, E. Mével, L. Nahon, S. Petit, B. Pons, D. Staedter, S. Weber, T. Ruchon, V. Blanchet and Y. Mairesse, Nat. Photonics, 2015, 9, 93–98 CrossRef.
- S. Turchini, J. Phys.: Condens. Matter, 2017, 29, 503001 CrossRef CAS PubMed.
- K. Fehre, N. M. Novikovskiy, S. Grundmann, G. Kastirke, S. Eckart, F. Trinter, J. Rist, A. Hartung, D. Trabert, C. Janke, G. Nalin, M. Pitzer, S. Zeller, F. Wiegandt, M. Weller, M. Kircher, M. Hofmann, L. P. H. Schmidt, A. Knie, A. Hans, L. B. Ltaief, A. Ehresmann, R. Berger, H. Fukuzawa, K. Ueda, H. Schmidt-Böcking, J. B. Williams, T. Jahnke, R. Dörner, M. S. Schöffler and P. V. Demekhin, Phys. Rev. Lett., 2021, 127, 103201 CrossRef CAS PubMed.
- P. Krüger and K.-M. Weitzel, Angew. Chem., Int. Ed., 2021, 60, 17861–17865 CrossRef PubMed.
- G. A. Garcia, L. Nahon, S. Daly and I. Powis, Nat. Commun., 2013, 4, 2132 CrossRef PubMed.
- C. Lux, M. Wollenhaupt, T. Bolze, Q. Liang, J. Köhler, C. Sarpe and T. Baumert, Angew. Chem., Int. Ed., 2012, 51, 5001–5005 CrossRef CAS PubMed.
- C. S. Lehmann, N. B. Ram, I. Powis and M. H. M. Janssen, J. Chem. Phys., 2013, 139, 234307 CrossRef PubMed.
- N. Bhargava Ram, C. S. Lehmann and M. H. M. Janssen, EPJ Web Conf., 2013, 41, 02029 CrossRef CAS.
- M. M. Rafiee Fanood, I. Powis and M. H. M. Janssen, J. Phys. Chem. A, 2014, 118, 11541–11546 CrossRef CAS PubMed.
- M. M. R. Fanood, N. B. Ram, C. S. Lehmann, I. Powis and M. H. M. Janssen, Nat. Commun., 2015, 6, 7511 CrossRef CAS PubMed.
- C. Lux, M. Wollenhaupt, C. Sarpe and T. Baumert, ChemPhysChem, 2015, 16, 115–137 CrossRef CAS PubMed.
- C. Lux, A. Senftleben, C. Sarpe, M. Wollenhaupt and T. Baumert, J. Phys.B: Atom., Mol. Opt. Phys., 2015, 49, 02LT01 CrossRef.
- S. Beaulieu, A. Comby, B. Fabre, D. Descamps, A. Ferré, G. Garcia, R. Géneaux, F. Légaré, L. Nahon, S. Petit, T. Ruchon, B. Pons, V. Blanchet and Y. Mairesse, Faraday Discuss., 2016, 194, 325–348 RSC.
- A. Kastner, C. Lux, T. Ring, S. Züllighoven, C. Sarpe, A. Senftleben and T. Baumert, ChemPhysChem, 2016, 17, 1119–1122 CrossRef CAS PubMed.
- J. Miles, D. Fernandes, A. Young, C. Bond, S. Crane, O. Ghafur, D. Townsend, J. Sá and J. Greenwood, Anal. Chim. Acta, 2017, 984, 134–139 CrossRef CAS PubMed.
- A. Kastner, T. Ring, H. Braun, A. Senftleben and T. Baumert, ChemPhysChem, 2019, 20, 1416–1419 CAS.
- S. T. Ranecky, G. B. Park, P. C. Samartzis, I. C. Giannakidis, D. Schwarzer, A. Senftleben, T. Baumert and T. Schäfer, Phys. Chem. Chem. Phys., 2022, 24, 2758–2761 RSC.
- A. Comby, S. Beaulieu, M. Boggio-Pasqua, D. Descamps, F. Légaré, L. Nahon, S. Petit, B. Pons, B. Fabre, Y. Mairesse and V. Blanchet, J. Phys. Chem. Lett., 2016, 7, 4514–4519 CrossRef CAS PubMed.
- S. Beaulieu, A. Ferré, R. Géneaux, R. Canonge, D. Descamps, B. Fabre, N. Fedorov, F. Légaré, S. Petit, T. Ruchon, V. Blanchet, Y. Mairesse and B. Pons, New J. Phys., 2016, 18, 102002 CrossRef.
- S. Beaulieu, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, A. G. Harvey, F. Légaré, Z. Mašín, L. Nahon, A. F. Ordonez, S. Petit, B. Pons, Y. Mairesse, O. Smirnova and V. Blanchet, Nat. Phys., 2018, 14, 484–489 Search PubMed.
- I. Powis, in Photoelectron Circular Dichroism in Chiral Molecules, John Wiley & Sons, Ltd, 2008, ch. 5, pp. 267–329 Search PubMed.
- M. H. M. Janssen and I. Powis, Phys. Chem. Chem. Phys., 2014, 16, 856–871 RSC.
- R. Hadidi, D. K. Bozanic, G. A. Garcia and L. Nahon, Adv. Phys.: X, 2018, 3, 1477530 Search PubMed.
- P. V. Demekhin, A. N. Artemyev, A. Kastner and T. Baumert, Phys. Rev. Lett., 2018, 121, 253201 CrossRef CAS PubMed.
- P. V. Demekhin, Phys. Rev. A, 2019, 99, 063406 CrossRef CAS.
- S. Rozen, A. Comby, E. Bloch, S. Beauvarlet, D. Descamps, B. Fabre, S. Petit, V. Blanchet, B. Pons, N. Dudovich and Y. Mairesse, Phys. Rev. X, 2019, 9, 031004 CAS.
- R. E. Goetz, C. P. Koch and L. Greenman, Phys. Rev. Lett., 2019, 122, 013204 CrossRef CAS PubMed.
- P. Fischer and F. Hache, Chirality, 2005, 17, 421–437 CrossRef CAS PubMed.
- O. Neufeld, D. Ayuso, P. Decleva, M. Y. Ivanov, O. Smirnova and O. Cohen, Phys. Rev. X, 2019, 9, 031002 CAS.
- D. Ayuso, A. F. Ordonez, P. Decleva, M. Ivanov and O. Smirnova, Opt. Express, 2022, 30, 4659–4667 CrossRef CAS PubMed.
- D. Ayuso, A. F. Ordonez, M. Ivanov and O. Smirnova, Optica, 2021, 8, 1243–1246 CrossRef.
- M. A. Belkin, T. A. Kulakov, K.-H. Ernst, L. Yan and Y. R. Shen, Phys. Rev. Lett., 2000, 85, 4474–4477 CrossRef CAS PubMed.
- D. Patterson and J. M. Doyle, Phys. Rev. Lett., 2013, 111, 023008 CrossRef PubMed.
- D. Patterson, M. Schnell and J. M. Doyle, Nature, 2013, 497, 475–477 CrossRef CAS PubMed.
- K. K. Lehmann, in Frontiers and Advances in Molecular Spectroscopy, ed. J. Laane, Elsevier, 2018, pp. 713–743 Search PubMed.
- A. F. Ordonez and O. Smirnova, Phys. Rev. A: At., Mol., Opt. Phys., 2018, 98, 063428 CrossRef CAS.
- A. Yachmenev, J. Onvlee, E. Zak, A. Owens and J. Küpper, Phys. Rev. Lett., 2019, 123, 243202 CrossRef CAS PubMed.
- S. Eibenberger, J. Doyle and D. Patterson, Phys. Rev. Lett., 2017, 118, 123002 CrossRef PubMed.
- A. Yachmenev and S. N. Yurchenko, Phys. Rev. Lett., 2016, 117, 033001 CrossRef PubMed.
- E. Gershnabel and I. S. Averbukh, Phys. Rev. Lett., 2018, 120, 083204 CrossRef CAS PubMed.
- I. Tutunnikov, J. Floß, E. Gershnabel, P. Brumer, I. S. Averbukh, A. A. Milner and V. Milner, Phys. Rev. A, 2020, 101, 021403 CrossRef CAS.
- A. A. Milner, J. A. M. Fordyce, I. MacPhail-Bartley, W. Wasserman, V. Milner, I. Tutunnikov and I. S. Averbukh, Phys. Rev. Lett., 2019, 122, 223201 CrossRef CAS PubMed.
- C. Pérez, A. L. Steber, S. R. Domingos, A. Krin, D. Schmitz and M. Schnell, Angew. Chem., Int. Ed., 2017, 56, 12512–12517 CrossRef PubMed.
- V. A. Shubert, D. Schmitz, C. Pérez, C. Medcraft, A. Krin, S. R. Domingos, D. Patterson and M. Schnell, J. Phys. Chem. Lett., 2016, 7, 341–350 CrossRef CAS PubMed.
- M. Leibscher, E. Pozzoli, C. Pérez, M. Schnell, M. Sigalotti, U. Boscain and C. P. Koch, Commun. Phys., 2022, 5, 1–16 CrossRef.
- M. Leibscher, T. F. Giesen and C. P. Koch, J. Chem. Phys., 2019, 151, 014302 CrossRef PubMed.
- J. Lee, J. Bischoff, A. O. Hernandez-Castillo, B. Sartakov, G. Meijer and S. Eibenberger-Arias, Phys. Rev. Lett., 2022, 128(17), 173001 CrossRef CAS PubMed.
- D. Ayuso, O. Neufeld, A. F. Ordonez, P. Decleva, G. Lerner, O. Cohen, M. Ivanov and O. Smirnova, Nat. Photonics, 2019, 13, 866–871 CrossRef CAS.
- D. Gerbasi, P. Brumer, I. Thanopulos, P. Král and M. Shapiro, J. Chem. Phys., 2004, 120, 11557–11563 CrossRef CAS PubMed.
- P. Král, I. Thanopulos, M. Shapiro and D. Cohen, Phys. Rev. Lett., 2003, 90(3), 033001 CrossRef PubMed.
- M. V. Berry, Proc. R. Soc. Lond. A, 1984, 392, 45–57 Search PubMed.
- C. L. Kane and E. J. Mele, Phys. Rev. Lett., 2005, 95, 226801 CrossRef CAS PubMed.
- B. A. Bernevig, T. L. Hughes and S.-C. Zhang, Science, 2006, 314, 1757–1761 CrossRef CAS PubMed.
- R. Resta, Rev. Mod. Phys., 1994, 66, 899–915 CrossRef CAS.
- C. Felser and J. Gooth, arXiv, 2022, preprint, arXiv:2205.05809 DOI:10.48550/arXiv.2205.05809.
- A. F. Ordonez, D. Ayuso, P. Decleva and O. Smirnova, 2021, arXiv:2106.14264 [physics].
- K. Schwennicke and J. Yuen-Zhou, J. Phys. Chem. Lett., 2022, 13, 2434–2441 CrossRef CAS PubMed.
- A. F. Ordonez and O. Smirnova, Phys. Rev. A, 2019, 99, 043417 CrossRef CAS.
- N. Berova, P. L. Polavarapu, K. Nakanishi and R. W. Woody, Comprehensive Chiroptical Spectroscopy, Wiley, 2013 Search PubMed.
- Y. Zhang, J. R. Rouxel, J. Autschbach, N. Govind and S. Mukamel, Chem. Sci., 2017, 8, 5969–5978 RSC.
- J. R. Rouxel, M. Kowalewski and S. Mukamel, Struct. Dyn., 2017, 4, 044006 CrossRef PubMed.
- O. Smirnova, Y. Mairesse and S. Patchkovskii, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 234005 CrossRef.
- D. Ayuso, P. Decleva, S. Patchkovskii and O. Smirnova, J. Phys. B: Atom., Mol. Opt. Phys., 2018, 51, 06LT01 CrossRef.
- D. Ayuso, P. Decleva, S. Patchkovskii and O. Smirnova, J. Phys. B: At., Mol. Opt. Phys., 2018, 51, 124002 CrossRef.
- Y. Harada, E. Haraguchi, K. Kaneshima and T. Sekikawa, Phys. Rev. A, 2018, 98, 021401 CrossRef CAS.
- D. Baykusheva and H. J. Wörner, Phys. Rev. X, 2018, 8, 031060 CAS.
- Y. Tang and A. E. Cohen, Phys. Rev. Lett., 2010, 104, 163901 CrossRef PubMed.
- Y. Tang and A. E. Cohen, Science, 2011, 332, 333–336 CrossRef CAS PubMed.
- C. Rosales-Guzmán, K. Volke-Sepulveda and J. P. Torres, Opt. Lett., 2012, 37, 3486–3488 CrossRef PubMed.
- K. A. Forbes and D. L. Andrews, J. Phys.: Photon., 2021, 3, 022007 CAS.
- P. Jordan and R. d L. Kronig, Nature, 1927, 120, 807 CrossRef.
- T. Bungo, Y. Nakano, K. Okano, M. Hayashida, H. Kawagoe, H. Furusawa, K. Yasukochi, T. Matsuishi, K. Izumi, M. Shimojo, M. Furuse and Y. Masuda, Appl. Anim. Behav. Sci., 1999, 64, 227–232 CrossRef.
- A. F. Ordonez and O. Smirnova, Phys. Chem. Chem. Phys., 2022, 24, 7264 RSC.
- M. Pitzer, M. Kunitski, A. S. Johnson, T. Jahnke, H. Sann, F. Sturm, L. P. H. Schmidt, H. Schmidt-Böcking, R. Dörner, J. Stohner, J. Kiedrowski, M. Reggelin, S. Marquardt, A. Schießer, R. Berger and M. S. Schöffler, Science, 2013, 341, 1096–1100 CrossRef CAS PubMed.
- M. Pitzer, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 153001 CrossRef.
- D. Ayuso, A. F. Ordonez, P. Decleva, M. Ivanov and O. Smirnova, Nat. Commun., 2021, 12, 3951 CrossRef CAS PubMed.
- D. Ayuso, Phys. Chem. Chem. Phys., 2022, 24, 10193 RSC.
- N. Mayer, M. Ivanov and O. Smirnova, 2021, arXiv:2112.02658 [physics].
- G. P. Katsoulis, Z. Dube, P. Corkum, A. Staudte and A. Emmanouilidou, arXiv:2112.02670 [physics], 2021.
- M. Khokhlova, E. Pisanty, S. Patchkovskii, O. Smirnova and M. Ivanov, Sci. Adv., 2022, 8, eabq1962 CrossRef PubMed.
- O. Neufeld, M. Even Tzur and O. Cohen, Phys. Rev. A, 2020, 101, 053831 CrossRef CAS.
- O. Neufeld, H. Hübener, A. Rubio and U. De Giovannini, Phys. Rev. Res., 2021, 3, L032006 CrossRef CAS.
- O. Neufeld, O. Wengrowicz, O. Peleg, A. Rubio and O. Cohen, Opt. Express, 2022, 30, 3729–3740 CrossRef CAS PubMed.
- O. Neufeld and O. Cohen, Phys. Rev. A, 2022, 105, 023514 CrossRef CAS.
- P. Lodahl, S. Mahmoodian, S. Stobbe, A. Rauschenbeutel, P. Schneeweiss, J. Volz, H. Pichler and P. Zoller, Nature, 2017, 541, 473–480 CrossRef CAS PubMed.
- K. Y. Bliokh and F. Nori, Phys. Rep., 2015, 592, 1–38 CrossRef.
- P. Fischer, K. Beckwitt, F. W. Wise and A. C. Albrecht, Chem. Phys. Lett., 2002, 352, 463–468 CrossRef CAS.
- P. Fischer, A. D. Buckingham and A. C. Albrecht, Phys. Rev. A: At., Mol., Opt. Phys., 2001, 64, 053816 CrossRef.
- P. Fischer, A. D. Buckingham, K. Beckwitt, D. S. Wiersma and F. W. Wise, Phys. Rev. Lett., 2003, 91, 173901 CrossRef CAS PubMed.
- A. F. Ordonez and O. Smirnova, in Molecular Beams in Physics and Chemistry: From Otto Stern's Pioneering Exploits to Present-Day Feats, ed. B. Friedrich and H. Schmidt-Böcking, Springer International Publishing, 2021, pp. 335–352 Search PubMed.
- N. A. Cherepkov, Chem. Phys. Lett., 1982, 87, 344 CrossRef CAS.
- K. Fehre, S. Eckart, M. Kunitski, C. Janke, D. Trabert, J. Rist, M. Weller, A. Hartung, L. Schmidt, T. Jahnke, R. Dörner and M. Schöffler, J. Phys. Chem. A, 2019, 123, 6491 CrossRef CAS PubMed.
- M. N. Pohl, S. Malerz, F. Trinter, C. Lee, C. Kolbeck, I. Wilkinson, S. Thürmer, D. M. Neumark, L. Nahon and I. Powis, et al. , Phys. Chem. Chem. Phys., 2022, 24, 8081–8092 RSC.
- I. Powis and M. H. M. Janssen, LCGC, 2017, 15, 16 Search PubMed , https://www.chromatographyonline.com/view/direct-enantiomer-selective-mass-spectrometry-chiral-mixtures-mass-selected-photoelectron-circular-0.
- R. Boyd, Nonlinear Optics, Elsevier, 3rd edn, 2008 Search PubMed.
- O. Neufeld, D. Podolsky and O. Cohen, Nat. Commun., 2019, 10, 405 CrossRef PubMed.
- E. Hollander, E. O. Kamenetskii and R. Shavit, J. Appl. Phys., 2017, 122, 034901 CrossRef.
- F. Krausz and M. Ivanov, Rev. Mod. Phys., 2009, 81, 163–234 CrossRef.
- P. B. Corkum, Phys. Rev. Lett., 1993, 71, 1994 CrossRef CAS PubMed.
- O. Smirnova and M. Ivanov, Multielectron High Harmonic Generation: Simple Man on a Complex Plane, John Wiley & Sons, Ltd, 2014, ch. 7, pp. 201–256 Search PubMed.
- O. Neufeld and O. Cohen, Phys. Rev. Lett., 2018, 120, 133206 CrossRef CAS PubMed.
- A. F. Ordonez and O. Smirnova, Phys. Chem. Chem. Phys., 2022, 24, 13605 RSC.
- D. M. Brink and G. R. Satchler, Angular Momentum, Clarendon Press, Oxford, 2nd edn., 1968 Search PubMed.
- P. Fischer, D. S. Wiersma, R. Righini, B. Champagne and A. D. Buckingham, Phys. Rev. Lett., 2000, 85, 4253–4256 CrossRef CAS PubMed.
- M. Leibscher, J. Kalveram and C. Koch, Symmetry, 2022, 14, 871 CrossRef.
- H. Rubinsztein-Dunlop, A. Forbes, M. V. Berry, M. R. Dennis, D. L. Andrews, M. Mansuripur, C. Denz, C. Alpmann, P. Banzer, T. Bauer, E. Karimi, L. Marrucci, M. Padgett, M. Ritsch-Marte, N. M. Litchinitser, N. P. Bigelow, C. Rosales-Guzmán, A. Belmonte, J. P. Torres, T. W. Neely, M. Baker, R. Gordon, A. B. Stilgoe, J. Romero, A. G. White, R. Fickler, A. E. Willner, G. Xie, B. McMorran and A. M. Weiner, J. Opt., 2016, 19, 013001 CrossRef.
- E. Pisanty, G. J. Machado, V. Vicuña-Hernández, A. Picón, A. Celi, J. P. Torres and M. Lewenstein, Nat. Photonics, 2019, 13, 569–574 CrossRef CAS.
- S. W. Hell, Angew. Chem., Int. Ed., 2015, 54, 8054–8066 CrossRef CAS PubMed.
- M. Padgett and R. Bowman, Nat. Photonics, 2011, 5, 343–348 CrossRef CAS.
- F. Patti, R. Saija, P. Denti, G. Pellegrini, P. Biagioni, M. A. Iatì and O. M. Maragò, Sci. Rep., 2019, 9, 1 CrossRef CAS PubMed.
- M. Li, S. Yan, Y. Zhang, P. Zhang and B. Yao, J. Opt. Soc. Am. B, 2019, 36, 2099–2105 CrossRef CAS.
- D. S. Bradshaw and D. L. Andrews, Opt. Lett., 2015, 40, 677–680 CrossRef PubMed.
- R. P. Cameron, A. M. Yao and S. M. Barnett, J. Phys. Chem. A, 2014, 118, 3472–3478 CrossRef CAS PubMed.
- N. Mayer, D. Ayuso, M. Ivanov and O. Smirnova, Control of achiral and chiral media with synthetic chiral vortex beams, in The International Conference on Ultrafast Phenomena (UP), ed. F. Légaré, T. Tahara, J. Biegert, T. Brixner and N. Dudovich, Optica Publishing Group, Technical Digest Series, 2022, paper W4A.26, https://opg.optica.org/abstract.cfm?URI=UP-2022-W4A.26 Search PubMed.
- G. G. Paulus, F. Grasbon, H. Walther, P. Villoresi, M. Nisoli, S. Stagira, E. Priori and S. De Silvestri, Nature, 2001, 414, 182–184 CrossRef CAS PubMed.
- A. Baltuška, T. Udem, M. Uiberacker, M. Hentschel, E. Goulielmakis, C. Gohle, R. Holzwarth, V. S. Yakovlev, A. Scrinzi, T. W. Hänsch and F. Krausz, Nature, 2003, 421, 611–615 CrossRef PubMed.
- A. Schiffrin, T. Paasch-Colberg, N. Karpowicz, V. Apalkov, D. Gerster, S. Mühlbrandt, M. Korbman, J. Reichert, M. Schultze, S. Holzner, J. V. Barth, R. Kienberger, R. Ernstorfer, V. S. Yakovlev, M. I. Stockman and F. Krausz, Nature, 2013, 493, 70–74 CrossRef PubMed.
- T. T. Luu, M. Garg, S. Y. Kruchinin, A. Moulet, M. T. Hassan and E. Goulielmakis, Nature, 2015, 521, 498–502 CrossRef CAS PubMed.
- G. L. Yudin, A. D. Bandrauk and P. B. Corkum, Phys. Rev. Lett., 2006, 96, 063002 CrossRef CAS PubMed.
- J. Karczmarek, J. Wright, P. Corkum and M. Ivanov, Phys. Rev. Lett., 1999, 82, 3420–3423 CrossRef CAS.
- D. M. Villeneuve, S. A. Aseyev, P. Dietrich, M. Spanner, M. Y. Ivanov and P. B. Corkum, Phys. Rev. Lett., 2000, 85, 542–545 CrossRef CAS PubMed.
- L. Yuan, S. W. Teitelbaum, A. Robinson and A. S. Mullin, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6872–6877 CrossRef CAS.
- I. Tutunnikov, J. Floß, E. Gershnabel, P. Brumer and I. S. Averbukh, Phys. Rev. A, 2019, 100, 043406 CrossRef CAS.
- I. Tutunnikov, E. Gershnabel, S. Gold and I. S. Averbukh, J. Phys. Chem. Lett., 2018, 9(5), 1105–1111 CrossRef CAS PubMed.
- H. L. Bethlem, G. Berden and G. Meijer, Phys. Rev. Lett., 1999, 83, 1558–1561 CrossRef CAS.
- S. Y. T. van de Meerakker, H. L. Bethlem and G. Meijer, Nat. Phys., 2008, 4, 595–602 Search PubMed.
- C. Maher-McWilliams, P. Douglas and P. F. Barker, Nat. Photonics, 2012, 6, 386–390 CrossRef.
- R. J. Hernández, A. Mazzulla, A. Pane, K. Volke-Sepúlveda and G. Cipparrone, Lab Chip, 2013, 13, 459–467 RSC.
- A. Canaguier-Durand, J. A. Hutchison, C. Genet and T. W. Ebbesen, New J. Phys., 2013, 15, 123037 CrossRef.
- G. Tkachenko and E. Brasselet, Nat. Commun., 2014, 5, 3577 CrossRef PubMed.
- G. Tkachenko and E. Brasselet, Nat. Commun., 2014, 5, 4491 CrossRef CAS PubMed.
- A. Hayat, J. P. B. Mueller and F. Capasso, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 13190–13194 CrossRef CAS PubMed.
- I. D. Rukhlenko, N. V. Tepliakov, A. S. Baimuratov, S. A. Andronaki, Y. K. Gun'ko, A. V. Baranov and A. V. Fedorov, Sci. Rep., 2016, 6, 36884 CrossRef CAS PubMed.
- R. Ali, F. A. Pinheiro, R. S. Dutra, F. S. S. Rosa and P. A. Maia Neto, Nanoscale, 2020, 12, 5031–5037 RSC.
- G. Pellegrini, M. Finazzi, M. Celebrano, L. Duò, M. A. Iatì, O. M. Maragò and P. Biagioni, J. Phys. Chem. C, 2019, 123, 28336–28342 CrossRef CAS.
- R. P. Cameron, S. M. Barnett and A. M. Yao, New J. Phys., 2014, 16, 013020 CrossRef.
- B. A. Stickler, M. Diekmann, R. Berger and D. Wang, Phys. Rev. X, 2021, 11, 031056 CAS.
- A. F. Ordonez and O. Smirnova, Phys. Rev. A, 2019, 99, 043416 CrossRef CAS.
- A. Owens, A. Yachmenev, S. N. Yurchenko and J. Küpper, Phys. Rev. Lett., 2018, 121, 193201 CrossRef CAS PubMed.
- A. F. Ordonez and O. Smirnova, Phys. Chem. Chem. Phys., 2022, 24, 5720 RSC.
- A. Jiménez-Galán, R. E. F. Silva, O. Smirnova and M. Ivanov, Nat. Photonics, 2020, 14, 728–732 CrossRef.
- V. Valmispild, E. Gorelov, M. Eckstein, A. Lichtenstein, H. Aoki, M. Katsnelson, M. Ivanov and O. Smirnova, Sub-cycle multidimensional spectroscopy of strongly correlated materials, arXiv, 2022, preprint, arXiv:2208.04647.
- G. Chang, B. J. Wieder, F. Schindler, D. S. Sanchez, I. Belopolski, S.-M. Huang, B. Singh, D. Wu, T.-R. Chang, T. Neupert, S.-Y. Xu, H. Lin and M. Z. Hasan, Nat. Mater., 2018, 17, 978 CrossRef CAS PubMed.
- D. S. Sanchez, I. Belopolski, T. A. Cochran, X. Xu, J.-X. Yin, G. Chang, W. Xie, K. Manna, V. Süβ, C.-Y. Huang, N. Alidoust, D. Multer, S. S. Zhang, N. Shumiya, X. Wang, G.-Q. Wang, T.-R. Chang, C. Felser, S.-Y. Xu, S. Jia, H. Lin and M. Z. Hasan, Nature, 2019, 567, 500–505 CrossRef CAS PubMed.
- J. Itatani, J. Levesque, D. Zeidler, H. Niikura, H. Pépin, J. C. Kieffer, P. B. Corkum and D. M. Villeneuve, Nature, 2004, 432, 867–871 CrossRef CAS PubMed.
- C. Vozzi, M. Negro, F. Calegari, G. Sansone, M. Nisoli, S. De Silvestri and S. Stagira, Nat. Phys., 2011, 7, 822–826 Search PubMed.
- R. R. Freeman, P. H. Bucksbaum, H. Milchberg, S. Darack, D. Schumacher and M. E. Geusic, Phys. Rev. Lett., 1987, 59, 1092–1095 CrossRef CAS PubMed.
- F. de Juan, A. G. Grushin, T. Morimoto and J. E. Moore, Nat. Commun., 2017, 8, 15995 CrossRef CAS PubMed.
- D. L. Andrews and T. Thirunamachandran, J. Chem. Phys., 1977, 67, 5026–5033 CrossRef CAS.
Footnotes |
| † The word enantio-sensitive is used throughout this article in its most general meaning, to describe phenomena which are sensitive to the molecular handedness. |
| ‡ The CD quantifies the difference in intensity of absorbed left and right circularly polarized light by a chiral medium; CD is usually given in relative units, such that the enantio-sensitive difference is normalized to the non-enantio-sensitive signal, CD = 2(IL − IR)/(IL + IR), where IL and IR are the light intensities absorbed from the left- and right-handed fields, respectively. |
| § We gratefully acknowledge Prof. D. Herschbach, who brought to our attention the idea of chiral cows and its graphical illustration by E. Heller during one of his visits to Fritz-Haber Institute. |
| ¶ Interestingly, the overall chirality of the helical trajectory traced by the induced dipole in PXCD (see Fig. 7) is evident, since the two helices of opposite chirality (inner and outer) have different size. It means that, in the near-field, the light generated by this dipole via the free induction decay at three frequencies would be chiral in the electric-dipole approximation. |
| This journal is © the Owner Societies 2022 |