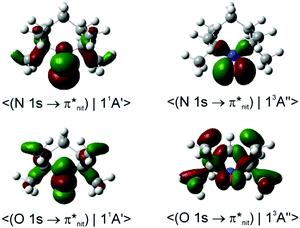Frontier orbital stability of nitroxyl organic radicals probed by means of inner shell resonantly enhanced valence band photoelectron spectroscopy†
R.
Totani
 *a,
I.
Ljubić
*a,
I.
Ljubić
 *b,
A.
Ciavardini
c,
C.
Grazioli
*b,
A.
Ciavardini
c,
C.
Grazioli
 d,
F.
Galdenzi
c,
M.
de Simone
d,
F.
Galdenzi
c,
M.
de Simone
 d and
M.
Coreno
d and
M.
Coreno
 a
a
aISM-CNR, LD2 Unit, Basovizza Area Science Park, 34149 Trieste, Italy. E-mail: roberta.totani@elettra.eu
bDivision of Physical Chemistry, Ruđer Bošković Institute, Bijenička cesta 54, HR-10000 Zagreb, Croatia. E-mail: iljubic@irb.hr
cUniversity of Nova Gorica, Vipavska 13, SI-5000 Nova Gorica, Slovenia
dIOM-CNR, Laboratorio TASC, Basovizza SS-14, km 163.5, 34149 Trieste, Italy
First published on 22nd December 2021
Abstract
We have investigated the frontier orbitals of persistent organic radicals known as nitroxyls by resonant photoelectron spectroscopy (ResPES) under inner shell excitation. By means of this site-specific technique, we were able to disentangle the different atomic contributions to the outer valence molecular orbitals and examine several core–hole relaxation pathways involving the singly occupied molecular orbital (SOMO) localized on the nitroxyl group. To interpret the ResPES intensity trends, especially the strong enhancement of the SOMO ionized state at the N K-edge, we computed the Dyson spin orbitals (DSOs) pertaining to the transitions between the core-excited initial states and several of the singly ionized valence final states. We found that the computed vertical valence ionization potentials and norms of the DSOs are reasonably reliable when based on the long-range corrected CAM-B3LYP density functional. Thanks to their unpaired electrons, nitroxyls have recently found application in technological fields implying a spin control, such as spintronics and quantum computing. The present findings on the electronic structure of nitroxyl persistent radicals furnish important hints for their implementation in technological devices and, more in general, for the synthesis of new and stable organic radicals with tailored properties.
Introduction
Resonant photoelectron spectroscopy (ResPES) under core excitation is a powerful spectroscopic technique that profits from modern synchrotron radiation sources (see the ESI† for more details). It combines the site-specificity of core hole electron spectroscopies with the sensitivity of outer valence photoelectron spectroscopy to reveal fine details of the electronic structure of frontier molecular orbitals. This inner-shell photoexcitation technique is complementary to the studies of Powis and co-workers of valence shell and photoionization dynamics employing synchrotron radiation1–4 and laser resonance-enhanced-multiphoton-ionization.5,6 ResPES has already been employed to perform experiments on several gas phase systems,7–16 revealing the importance of tuneable and controlled core excitation in the study of the de-excitation channels. In this study, we apply ResPES to a specific category of persistent organic radicals known as nitroxyls. Organic radicals are usually highly reactive compounds, because of an open-shell electronic configuration. Obtaining persistent organic radicals is possible if the paramagnetic centre is screened by bulky substituents,17 preventing them from undesired reactions but at the expense of a decreased reactivity. Polychlorinated trityl radicals, for example, are sterically protected, as the spin-bearing atoms are the central methyl sp2 carbon.18Alternatively, one can obtain stable organic radicals and, at the same time, preserve the reactivity, by increasing the delocalization of the unpaired electrons. This is the case of verdazyls,19 phenylhydrazyls,20 galvinoxyl21 and nitroxyl free radicals (NRs)19 such as (2,2,6,6-tetramethylpiperidin-1-yl)oxyl (TEMPO, Fig. 1) and its analogues. NRs present the unpaired electron located in the antibonding π* singly occupied molecular orbital (SOMO)22 and delocalized between the nitrogen and oxygen atoms.23 This stabilizes the SOMO and thereby the entire radical. Thanks to these peculiar properties, NRs find implementation in several hi-tech fields, such as catalysis,24 chemical synthesis as initiators in radical-chain polymerization, redox reactions,25 and biological imaging agents.26 As often replacing heavy metals, they represent a greener choice in the context of more sustainable and environmentally friendly technological development.25 Moreover NRs were the first radicals to be employed in molecular materials.27 As the unpaired electrons give rise to a magnetic moment, NRs are also employed in quantum computing, spintronics28 and molecular magnetism.29
Considering the important role played by the unpaired electron, a thorough study of its behaviour in the photoionized and photoexcited molecules is of paramount importance in the design and synthesis of new organic radicals with targeted functionalities and in their technological implementation. By combining the techniques of X-ray photoelectron spectroscopy (XPS) and near edge X-ray absorption fine structure (NEXAFS) we have already characterized in the gas phase the electronic valence and core-hole properties of TEMPO and two pyrrolidine NRs, nit8 and nit9 (adopting the previous nomenclature).30–32 As a computational aid in rationalizing and assigning these spectra, we have thus far mainly tested the methods based on density functional theory (DFT).32,33 Specifically, the spin-unrestricted and restricted open ΔDFT method was used to model XPS33 while the short-range corrected DFT in the time-dependent formalism (TD-DFT) was used for NEXAFS.32 In each of these studies we witnessed a good performance of both these approaches and hence established them as a generally useful tool for the interpretation of the core-ionized and core-excited spectral features in free radicals32–34 and other organic molecules with a challenging electronic structure.35,36 In this way, the delocalization of the spin density, the long-range interactions governing the conformation, the fine vibrational structure, and the effects of the different functional groups have been rationalized.31–36
To further advance our studies on the gas phase photoexcited states of NRs, we performed a ResPES investigation on TEMPO, di-tert-butyl nitroxyl (DTBN), nit8, and nit9 (Fig. 1), at O and N K-edge resonant photon energies. These are the elements carrying most information about the unpaired electrons localized in the nitroxyl group and, additionally for nit8 and nit9, in the amide functional group. DTBN can be considered as an open-ring fragment of TEMPO, and so can furnish further insights into the influence of the open/closed ring configurations and the introduction of the amide functional group as the second chromophore in nit8 and nit9. At the same time the systematic theoretical and experimental characterization of the different N and O contributions to the valence spectra should assist in clarifying the role of the SOMO in the through-bond effects in the photoexcited isolated molecules.
To the best of our knowledge, the only ResPES studies thus far realized on open shell systems regard small inorganic molecules such as NO2,12 O2,13 NO,37–40 CF,41 OH42 and OD.42 Indeed, because of their complexity, spectroscopic investigations on TEMPO and its derivatives, both in the gas phase and as thin films, are still rare despite their peculiar properties and the promising technological scenario they open. As a first approximation to the description of the de-excitation channels connecting the core-to-valence (CV) excited states of the four NRs with the manifold of their singly ionized valence states, we intend to make use of the concept of Dyson spin–orbitals (DSOs).43,44 Evaluated as the overlap between N and (N − 1) electron wave functions, the DSOs capture essential information about the ionization process, and so provide a valuable aid in the interpretation of data obtained via a number of spectroscopic and scattering experimental techniques.44 Considering the size of the four NRs and the difficulties in computing the initial and final states via high-level ab initio quantum chemistry, our analysis of the core-level spectra and the DSO formalism will presently be restricted to the framework of DFT.45–47
Experimental methods
Measurements were performed at the Gas Phase Photoemission beamline of the Elettra Synchrotron in Trieste,48 using a Scienta SES-200 electron analyzer49 mounted at the magic angle with respect to the electric vector of the linearly polarized incident light.Commercially available Merck TEMPO (99%), DTBN (90%), nit8 (99%) and nit9 (99%) were used for measurements. As TEMPO and DTBN evaporated already at room temperature and under room pressure conditions, they were kept in an evacuated glass tube outside the analysis chamber and then introduced by means of an appropriate gas inlet system. In order to have a more controlled sublimation, TEMPO was slightly cooled down to 13–14 °C by means of a water chiller. Nit8 and nit9 were sublimated in a vacuum using a custom built resistively heated furnace, up to temperatures between 90 °C and 100 °C, in order to obtain a high enough vapour pressure. For all molecules, the pressure during measurements was kept at about 5–6 × 10−6 mbar (a base pressure of the experimental chamber at about 10−8 mbar). Valence band photoelectron spectra (VBs) were acquired with a photon energy of hν = 50 eV, with an overall resolution of about 50 meV. The Ar 3p peaks were collected to calibrate the binding energy (BE) scale (3p3/2 at 15.760 eV50). TEMPO and nit9 NEXAFS spectra were measured by recording the total ion yield collected using a time-of-flight (TOF) detector. DTBN NEXAFS spectra were recorded by measuring the ion yield recorded using a channel electron multiplier, while for nit8 NEXAFS we measured the Auger yield using a SES200 electron analyzer in a fixed kinetic energy window mode. All the NEXAFS spectra were normalized by the transmitted photon flux measured using a calibrated Si photodiode. The energy scales of the O and N K-edge NEXAFS spectra were calibrated by taking simultaneous spectra of the samples of CO2 and N2, with the characteristic transitions at 535.30 eV (O 1s → π*, CO2)51 and 401.2 eV (N 1s → π, v = 1).52 The photon energy resolution was approximately 200 meV for the O K-edge NEXAFS and 140 meV for the N K-edge NEXAFS. The ResPES spectra were recorded by varying the incident photon energy to match it with the O and N K-edge resonances previously measured via NEXAFS and detecting the electrons from the outer VB region (BE ≈ 4–20 eV). Each resonant VB was acquired by employing a SES200 in a fixed BE window, with an overall resolution of ≈600 meV.
Computational methods
To check if the changes in the used minimum geometry have a significant effect on the calculated CV excitation energies, we presently re-optimized the geometries of the four NRs at the spin-unrestricted (U) B3LYP-D3/aug-cc-pVTZ level (see Table S1 (ESI†) for the Cartesian coordinates; previously for TEMPO, nit8, and nit9, UB3LYP/6-31+G(d) minima were used31–33). At these geometries the vertical core electron binding energies (CEBEs) and the CV excited states were calculated using the ΔU-DFT method.33 The higher lying valence ionized singlet monocation states were modelled using the spin-restricted Tamm–Dancoff TD-DFT formalism53 while the lowest singlet and triplet were simply computed as the difference between the U-DFT energies of the doublet ground state (GS) and the monocations with the singlet (or triplet) multiplicity. The standard B3LYP density functional (comprising the 5th formula from the VWN study)54 and its long-range corrected version CAM-B3LYP55 were used throughout. In all cases the mixed basis set approach (abbreviated as//mixed) was employed which was originally proposed in the context of calculating CEBEs using the ΔMP2 method.56 This approach is currently based on the model core potential basis set of the triple-ζ quality supplemented by the d and f polarization functions (denoted as mcp-tzp)57 and contracted to 3s3p2d1f for the second-row atoms (previously mcp-dzp with the 2s2p1d contraction was used).31–33 On the core-excited (or core-ionized) N or O atom we used the Peterson–Dunning all-electron weighted core-valence-correlating triple-ζ polarized basis set (cc-pwCVTZ)58 while on the remaining second-row atoms mcp-tzp was used, and the standard double-ζ polarized cc-pVDZ basis set on the H atoms. This resulted in the still feasibly sized mixed basis sets of 479, 445, 542, and 532 basis functions for TEMPO, DTBN, nit8 and nit9, respectively. The key advantage of the//mixed approach is that only one 1s core orbital is retained in the basis set (the one originating from cc-pwCVTZ). This precludes linear combinations of the core orbitals thus giving rise to a unique core-hole localized strictly to the atom of interest while also significantly alleviating the SCF convergence. The maximum overlap method (MOM)59 was applied to prevent the variational collapse and preserve a desired CV electron configuration. As an aid in the assignment of the valence PE spectra, the ionization energies of the four radicals were computed up to ca. 20 eV in the electron propagator formalism using the partial third-order P3+ approximation (EPT-P3+)60,61 and the cc-pVTZ basis set. The GAMESS-US, version June 2021,62 software was used for the ΔDFT and TD-DFT calculations, and the Gaussian 16, Rev. C01,63 software was used for the EPT-P3+ calculations.To help rationalize the intensity trends observed in the ResPES spectra, we computed the DSOs as the overlap functions between the initial N-electron N 1s and O 1s CV states (doublets) and 12 (N − 1)-electron (cationic) final states, viz. 11 singlets and 1 triplet in total. The latter states include the lowest singlet and triplet cations calculated via U-DFT, in addition to the 10 singlet-coupled spin-restricted TD-DFT excited states computed on top of the lowest singlet cation. If one formally considers a determinant wave function constructed as the anti-symmetrized product of the optimized Kohn–Sham molecular orbitals (MOs), the DSO φDys(x) within the DFT framework can be defined as:64
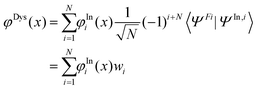 | (1) |
In the atomic orbital (AO) basis the overlap of the two determinant wave functions can be computed as:
| 〈ΨFi|ΨIn,i〉 = det[C†FiSCIn] | (2) |
Finally, the ratio of the intensities of transitions from a common initial CV state to the final valence ionized states Fi and Fi’ was approximated by the ratio of the norms of DSOs (the so-called probability factors P, where 0 ≤ P ≤ 1):
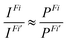 | (3) |
Results and discussion
Experimental results
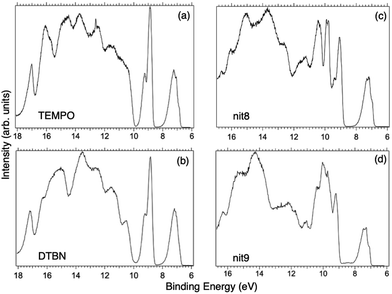
Fig. 2 displays the high-resolution VBs acquired for the four NRs. Our results are compatible with previous studies on TEMPO, nit8 and nit9.30,31,66 From a first look we can notice several resemblances between TEMPO and DTBN (Fig. 2a and b, respectively) and between nit8 and nit9 (Fig. 2c and d, respectively). TEMPO and DTBN VBs are characterized by three bands in the SOMO and SOMO−1 regions, between 6 and 10 eV BE, very similar in relative intensity and line shape. The peak at ≈17 eV is also common to both molecules, while the two spectra show more important differences in the region between 10 and 17 eV. The SOMOs of nit8 and nit9 are very similar and also resemble those of TEMPO and DTBN. The two spectra are substantially different for the remaining part, though. The small peak visible for all molecules at 12.6 eV is due to a residual amount of water released upon sublimation.Previous studies on TEMPO, nit8 and nit9 and new calculations on DTBN allow the assignment of the main VBs structures30 and XAS resonances.32 In TEMPO and DTBN VBs (Fig. 3a and b), the SOMO at 7.2 eV is due to the ionization from the antibonding orbital located at the NO moiety (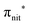 , nit = nitroxyl), while the SOMO−1 is due to the ionizations from the oxygen lone pair of the NO group (nnit) in a triplet (8.8 eV) or a singlet (9.2 eV) state. In nit8 and nit9 VBs, as for TEMPO and DTBN, there are the contributions of the ionizations from
, nit = nitroxyl), while the SOMO−1 is due to the ionizations from the oxygen lone pair of the NO group (nnit) in a triplet (8.8 eV) or a singlet (9.2 eV) state. In nit8 and nit9 VBs, as for TEMPO and DTBN, there are the contributions of the ionizations from 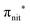 (SOMO, 7.3 and 7.4 eV, respectively) and the nnit triplet and singlet in the SOMO−1 region at 9 and 9.4 eV (nit8) and 9.2 and 9.7 eV (nit9), respectively. Furthermore, in the SOMO−1 band we see the contributions of the ionizations from amide group orbitals: nCO (9.8 eV) and nNH2 (10.4 eV) orbitals for nit8 and nO (10 eV) and nN (10.4 eV) orbitals for nit9. We did not aim to resolve the fine structure of the intramolecular vibrations of such bands. However, an appropriate fitting analysis taking into account the vibrational envelopes via the skewed Gaussian line shapes (see Fig. S2, ESI†) reveals that the triplet/singlet area ratio is 2.9, reasonably close to the theoretically expected value.
(SOMO, 7.3 and 7.4 eV, respectively) and the nnit triplet and singlet in the SOMO−1 region at 9 and 9.4 eV (nit8) and 9.2 and 9.7 eV (nit9), respectively. Furthermore, in the SOMO−1 band we see the contributions of the ionizations from amide group orbitals: nCO (9.8 eV) and nNH2 (10.4 eV) orbitals for nit8 and nO (10 eV) and nN (10.4 eV) orbitals for nit9. We did not aim to resolve the fine structure of the intramolecular vibrations of such bands. However, an appropriate fitting analysis taking into account the vibrational envelopes via the skewed Gaussian line shapes (see Fig. S2, ESI†) reveals that the triplet/singlet area ratio is 2.9, reasonably close to the theoretically expected value.
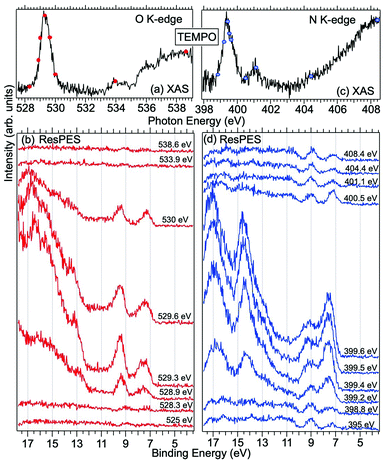 | ||
| Fig. 3 NEXAFS and ResPES spectra of the gas phase TEMPO molecules at O (a and b) and N (c and d) K-edges. The photon energies selected for ResPES are marked by dots in the NEXAFS spectra at the top. | ||
The first consideration we can draw from the comparison of the VBs is that in all four NRs examined SOMO photoionization involves the NO group. This is consistent with the very similar shape of the lowest BE peak in our valence photoionization spectra. The lack of the closed ring in DTBN has an effect only on the inner valence region, where few differences can be noted in the shape of the bands at highest ionization energies, whereas the SOMO−1 band in DTBN is still due to contributions from NO singlet and triplet ionized states. The amide functional group determines the more structured shape of the SOMO−1 band in nit8 and nit9, where it is responsible for the appearance of two additional peaks. These peaks are also different in the two molecules, being originated from different molecular orbitals. We can likely assume that the double bond, characterizing only the nit9 pyrrole ring, can be the cause of the different molecular orbital contributions to the SOMO−1 and of the different s peaks observed in the remaining VB region.
Fig. 3 and 4 show TEMPO and DTBN O and N K-edge NEXAFS, together with the corresponding ResPES spectra acquired across the observed NEXAFS resonances. TEMPO NEXAFS is in agreement with the already published results32 and NEXAFS spectra of TEMPO and DTBN are very similar. We observe main resonances for O (Fig. 4a and 5a) and N (Fig. 4c and 5c) K-edges at ≈529.3 eV and 399.4 eV photon energy, due to 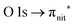 and
and 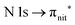 excitations, respectively.32 These are strong core-to-valence transitions, well separated from the Rydberg manifold starting at around 533 eV and 403 eV. The small features appearing at around 534 and 536 eV photon energy in the O K-edge spectra of TEMPO are most likely due to photoexcitation from residual water present in the sample. The second main resonance visible in the TEMPO N K-edge NEXAFS at around 401.1 eV is ascribable to the N 1s → π* band of N2,52 likely due to a small leak in the vacuum system.‡ In order to perform ResPES measurements, we acquired VBs at photon energies below, at and above the core edge resonances, selected from NEXAFS. In TEMPO ResPES at the N K-edge (Fig. 3d), we see a clear increase in the SOMO intensity when photon energies are scanned across the
excitations, respectively.32 These are strong core-to-valence transitions, well separated from the Rydberg manifold starting at around 533 eV and 403 eV. The small features appearing at around 534 and 536 eV photon energy in the O K-edge spectra of TEMPO are most likely due to photoexcitation from residual water present in the sample. The second main resonance visible in the TEMPO N K-edge NEXAFS at around 401.1 eV is ascribable to the N 1s → π* band of N2,52 likely due to a small leak in the vacuum system.‡ In order to perform ResPES measurements, we acquired VBs at photon energies below, at and above the core edge resonances, selected from NEXAFS. In TEMPO ResPES at the N K-edge (Fig. 3d), we see a clear increase in the SOMO intensity when photon energies are scanned across the 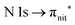 transition with respect to the off-resonance and high-resolution VBs discussed above (Fig. 3a). Differently, in ResPES at the O K-edge we notice an enhancement in both SOMO and SOMO−1 intensities across the
transition with respect to the off-resonance and high-resolution VBs discussed above (Fig. 3a). Differently, in ResPES at the O K-edge we notice an enhancement in both SOMO and SOMO−1 intensities across the 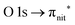 transition (Fig. 3b), with a change in the SOMO/SOMO−1 intensity ratio. The same behaviour is observed for the DTBN O and N K-edge ResPES results (Fig. 4).
transition (Fig. 3b), with a change in the SOMO/SOMO−1 intensity ratio. The same behaviour is observed for the DTBN O and N K-edge ResPES results (Fig. 4).
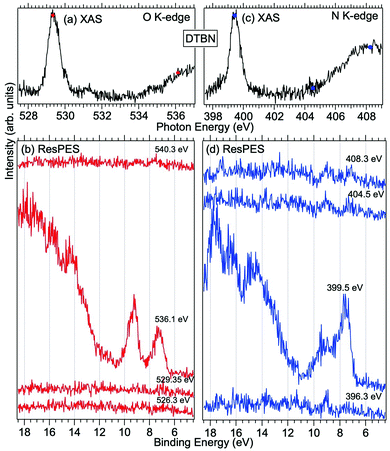 | ||
| Fig. 4 NEXAFS and ResPES spectra of gas phase DTBN molecules at O (a and b) and N (c and d) K-edges. The photon energies selected for ResPES are marked by dots in the NEXAFS spectra at the top. | ||
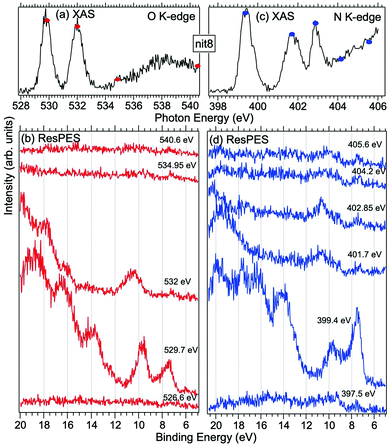 | ||
| Fig. 5 NEXAFS and ResPES spectra of gas phase nit8 molecules at O (a and b) and N (c and d) K-edges. The photon energies selected for ResPES are marked by dots in the NEXAFS spectra at the top. | ||
Fig. 5 and 6 show nit8 and nit9 O and N K-edge NEXAFS, together with the corresponding ResPES spectra, acquired across the observed NEXAFS resonances. Also in this case the NEXAFS spectra are in agreement with the already published results32 and are mutually very similar.
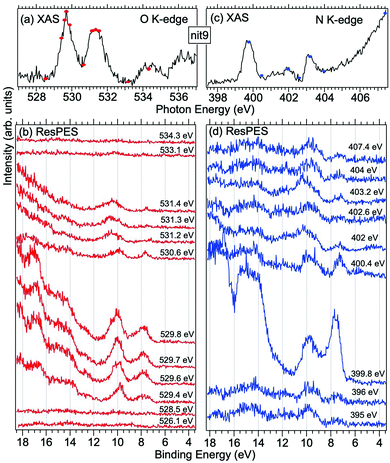 | ||
| Fig. 6 NEXAFS and ResPES spectra of gas phase nit9 molecules at O (a and b) and N (c and d) K-edges. The photon energies selected for ResPES are marked by dots in the NEXAFS spectra at the top. | ||
O K-edge spectra consist of two main resonances at 529.7 and 532 eV for nit8 (Fig. 5a) and 529.7 and 531.3 eV for nit9 (Fig. 6a). They correspond to 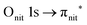 and (amd = amide)
and (amd = amide) 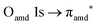 and 3s orbital transitions, respectively.32 N K-edge spectra consist of three main clearly distinguishable resonances at 399.4, 401.7 and 402.85 eV for nit8 (Fig. 5c) and at 398.5, 402 and 403.2 eV for nit9 (Fig. 6c). In both cases, the first transition corresponds to the
and 3s orbital transitions, respectively.32 N K-edge spectra consist of three main clearly distinguishable resonances at 399.4, 401.7 and 402.85 eV for nit8 (Fig. 5c) and at 398.5, 402 and 403.2 eV for nit9 (Fig. 6c). In both cases, the first transition corresponds to the 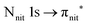 excitation. The second transition stems from excitations from
excitation. The second transition stems from excitations from 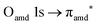 and
and 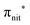 . Moreover, there are contributions from the excitations to 3s orbitals of the α and β spin sets for nit8 and excitations to 3s, 3p, 4s and 4p orbitals of the α spin set for nit9. The latter cases are a valence–Rydberg mix of excitations.
. Moreover, there are contributions from the excitations to 3s orbitals of the α and β spin sets for nit8 and excitations to 3s, 3p, 4s and 4p orbitals of the α spin set for nit9. The latter cases are a valence–Rydberg mix of excitations.
Finally, the third transition is due to the excitations from Namd to p and d type Rydberg orbitals for nit8 and to np and nd Rydberg orbitals (n ≥ 3) for nit9.32
For N K-edge ResPES (Fig. 5d and 6d), for both nit8 and nit9, the SOMO becomes more intense than SOMO−1, when the photon energy is scanned across the first XAS resonance at 399.8 eV, corresponding to the 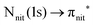 excitation. This is different to what is observed in the off-resonance and in the high-resolution VBs, but is analogous to TEMPO and DTBN N K-edge ResPES. Excitations localized at the amide nitrogen do not produce any relevant resonant enhancement in the ResPES of the outer VB orbitals.
excitation. This is different to what is observed in the off-resonance and in the high-resolution VBs, but is analogous to TEMPO and DTBN N K-edge ResPES. Excitations localized at the amide nitrogen do not produce any relevant resonant enhancement in the ResPES of the outer VB orbitals.
In the ResPES at the O K-edge (Fig. 5b and 6b) we can notice for nit8 and nit9 an enhancement of both the SOMO and SOMO−1 peaks, with respect to the off-resonance VB, when Onit 1s electrons are excited into 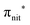 empty orbitals. Moreover there is a change in the SOMO/SOMO−1 intensity ratio, analogously to what is observed for TEMPO and DTBN O K-edge ResPES. Both the SOMO and SOMO−1 are quenched on the second resonance, when excitations occur from Oamd 1s into the amide π* orbitals. In the former case, we can as well notice that the SOMO band almost disappears and that the SOMO−1 broadens and shifts towards a higher BE.
empty orbitals. Moreover there is a change in the SOMO/SOMO−1 intensity ratio, analogously to what is observed for TEMPO and DTBN O K-edge ResPES. Both the SOMO and SOMO−1 are quenched on the second resonance, when excitations occur from Oamd 1s into the amide π* orbitals. In the former case, we can as well notice that the SOMO band almost disappears and that the SOMO−1 broadens and shifts towards a higher BE.
The reason for the SOMO/SOMO−1 intensity ratio inversion when comparing O and N K-edge resonant VBs can be found in different contributions of the vibrational modes and in the new NO singlet/doublet electronic configuration associated with the final states. Indeed, the 8–15 eV BE region of the VB is interspersed with the vibrational bands associated with the X 1Σ+ (2π0) final state of NO O 1s and N 1s → 2π core excitations.38 We can also observe the appearance of intense features in the inner VB, i.e. from roughly 12 eV BE. In this region, we find the structures due to the electronic final states and vibrational sub-levels.38 Here we can also find the main change due to the photoexcitation of a Namd or Oamd 1s core electron into the amide unoccupied orbitals. In general we can conclude that the resemblance of TEMPO, DTBN, nit8 and nit9 resonant SOMO and SOMO−1 indicates a negligible contribution of the amide functional groups and of C–C single and double bonds to the outermost VB structures. Indeed, these mainly originated from the interaction of the photoexcited electron with the NO localized SOMO.
Computational results
Tables 1–4 collect the computed (spin-unrestricted EPT-P3+ and (TD-)CAM-B3LYP), and measured vertical ionization potentials (IPs) of the four NRs up to ca. 13 eV, in addition to the norms of the DSOs between the N 1s/O 1s → π* CV states and the valence ionized states. The α-spin orbital EPT-P3+ values are assumed to approximate the singlet IPs, and the lowest β-spin orbital value is assumed for the IP of the 13A1 (13A′′) triplet state. The corresponding results obtained with the B3LYP density functional are given in the ESI† (Table S2). Except for a few lowest IPs, the experimental assignments of the PES spectra in Tables 1–4 are only tentative, and are mainly based on the superimposed experimental and EPT-P3+ stick spectra shown in Fig. S3 (ESI†).| State | EPT-P3+ | (TD-)DFT | Expt. | O | N |
|---|---|---|---|---|---|
| 11A′ | 7.42 | 7.53 | 7.3 | 1.35 | 10.13 |
| 13A′′ | 9.06 | 8.73 | 8.9 | 1.35 | 9.63 |
| 11A′′ | 9.63 | 9.70 | 9.3 | 0.80 | 7.37 |
| 21A′ | 10.99 | 10.95 | 11.1 | 1.52 | 7.49 |
| 31A′ | 11.34 | 11.41 | 0.97 | 7.38 | |
| 21A′′ | 11.43 | 11.62 | 11.4 | 0.98 | 7.44 |
| 31A′′ | 11.57 | 11.69 | 11.7 | 0.92 | 7.10 |
| 41A′′ | 12.26 | 12.21 | 1.02 | 6.54 | |
| 41A′ | 12.46 | 12.39 | 0.96 | 6.90 | |
| 51A′′ | 12.76 | 12.56 | 12.6 | 0.95 | 7.18 |
| 61A′′ | 12.90 | 12.69 | 1.02 | 7.45 | |
| 51A′ | 13.18 | 13.06 | 1.62 | 8.75 |
| State | EPT-P3+ | (TD-)DFT | Expt. | O | N |
|---|---|---|---|---|---|
| 11A1 | 7.33 | 7.47 | 7.2 | 1.13 | 9.19 |
| 13A1 | 9.01 | 8.70 | 8.8 | 1.18 | 8.77 |
| 21A1 | 9.58 | 9.71 | 9.2 | 0.80 | 7.48 |
| 31A1 | 11.28 | 11.32 | 11.3 | 0.76 | 4.30 |
| 41A1 | 11.71 | 11.66 | 11.6 | 2.35 | 7.62 |
| 51A1 | 11.79 | 11.72 | 1.04 | 6.92 | |
| 61A1 | 11.83 | 12.22 | 1.22 | 5.80 | |
| 71A1 | 12.76 | 12.54 | 12.7 | 0.94 | 6.40 |
| 81A1 | 12.89 | 12.56 | 1.23 | 6.50 | |
| 91A1 | 13.02 | 12.66 | 0.87 | 6.05 | |
| 101A1 | 13.25 | 13.20 | 1.95 | 7.19 | |
| 111A1 | 13.45 | 13.26 | 13.6 | 0.95 | 6.56 |
| State | EPT-P3+ | (TD-)DFT | Expt. | Oamd | Namd | Onit | Nnit |
|---|---|---|---|---|---|---|---|
| 11A1 | 7.35 | 7.42 | 7.2 | 0.19 | 1.41 | 0.14 | 0.96 |
| 13A1 | 9.44 | 8.91 | 9.1 | 0.20 | 2.75 | 0.15 | 0.96 |
| 21A1 | 9.67 | 9.81 | 0.14 | 1.15 | 0.74 | 2.28 | |
| 31A1 | 9.82 | 10.06 | 9.8 | 0.14 | 1.23 | 0.67 | 1.02 |
| 41A1 | 10.16 | 10.48 | 9.9 | 0.14 | 1.01 | 0.15 | 0.68 |
| 51A1 | 11.58 | 11.54 | 11.3 | 0.16 | 0.88 | 0.25 | 0.99 |
| 61A1 | 11.67 | 11.72 | 0.15 | 1.03 | 0.14 | 0.79 | |
| 71A1 | 12.01 | 12.02 | 0.15 | 0.96 | 0.74 | 0.90 | |
| 81A1 | 12.13 | 12.42 | 0.14 | 0.96 | 0.22 | 0.65 | |
| 91A1 | 12.79 | 12.60 | 12.6 | 0.11 | 1.25 | 0.10 | 1.59 |
| 101A1 | 13.08 | 12.94 | 0.17 | 0.70 | 0.38 | 0.79 | |
| 111A1 | 13.12 | 13.12 | 0.24 | 0.89 | 0.65 | 0.58 |
| State | EPT-P3+ | (TD-)DFT | Expt. | Oamd | Namd | Onit | Nnit |
|---|---|---|---|---|---|---|---|
| 11A1 | 7.85 | 7.55 | 7.3 | 1.04 | 7.10 | 0.65 | 4.29 |
| 13A1 | 9.30 | 9.02 | 9.2 | 1.04 | 7.43 | 0.65 | 4.07 |
| 21A1 | 9.59 | 9.93 | 9.7 | 0.65 | 5.61 | 0.46 | 3.21 |
| 31A1 | 9.99 | 10.06 | 0.77 | 5.60 | 0.44 | 3.37 | |
| 41A1 | 10.04 | 10.26 | 0.84 | 4.67 | 0.48 | 3.13 | |
| 51A1 | 10.07 | 10.64 | 10.0 | 0.76 | 5.25 | 0.49 | 3.00 |
| 61A1 | 11.81 | 11.89 | 11.8 | 0.76 | 4.12 | 0.45 | 3.10 |
| 71A1 | 12.18 | 12.18 | 12.2 | 0.79 | 5.08 | 0.47 | 2.92 |
| 81A1 | 12.46 | 12.24 | 0.48 | 11.07 | 0.00 | 0.14 | |
| 91A1 | 12.55 | 12.39 | 0.67 | 4.81 | 0.95 | 3.45 | |
| 101A1 | 13.07 | 12.62 | 0.77 | 5.46 | 0.43 | 2.75 | |
| 111A1 | 13.22 | 13.11 | 0.67 | 4.80 | 0.58 | 2.73 |
For Tables 1–4 and Table S2 (ESI†) we choose to show the results obtained with the cc-pwCVTZ basis set placed on the O (TEMPO and DTBN) and Oamd (nit8 and nit9) atoms. The results with the other variants of the mixed basis, such as with the all-electron basis set on the N, Namd, Nnit or Onit atoms, are very similar. The general electronic configurations envisaged for the CV states, the lowest singlet and triplet states, and the lowest TD-DFT singlet state are schematically depicted in Fig. S4 (ESI†).
Core and valence ionized, and core-to-valence states
The ΔB3LYP//mixed values for the lowest N 1s and O 1s CV excitation energies (ECV), currently obtained at the B3LYP-D3/aug-cc-pVTZ minima and with the mcp-tzp basis set, generally agree within 0.1 eV with the earlier values (the B3LYP/6-31+G(d) minima and the smaller mcp-dzp basis).36 This confirms that the small changes in the used geometries are of minor significance in this context. We also tested the performance of the diffuse functions in the basis set via mcp-dzp++ but found no benefits relative to mcp-dzp that would justify the significantly aggravated SCF convergence.The similar performances of mcp-dzp and mcp-tzp indicate that the key component in the//mixed approach is the quality of the basis set on the core-ionized (core-excited) atom, which has been kept the same in our studies (cc-pwCVTZ).32–36 This is comparable with the previous finding that resorting to only the minimal STO-3G basis set on hydrogens may likewise yield reasonable ΔDFT//mixed results and substantially improve the SCF convergence in larger molecules.34,35
The ECV values obtained with ΔB3LYP and ΔCAM-B3LYP are virtually identical (Table S3, ESI†); therefore, the inclusion of the long-range correction plays a minor role in these observables. Importantly, however, the singlet valence IPs and the probability factors obtained from the DSOs (vide infra) observe significant improvements with CAM-B3LYP (Tables 1–4 and S2, ESI†).
The N 1s and O 1s CEBEs and the ECV values for DTBN, here measured and calculated for the first time (Table S3, ESI†), are closely similar to those for TEMPO.31,33 The similarity of their radical centres is also anticipated from the experimental data; viz. the differences in their structures affect the local properties of the N–O bond and the 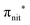 antibonding orbital only negligibly.
antibonding orbital only negligibly.
The TD-DFT computations on the low-lying excited states of cations are sometimes able to provide an acceptable inexpensive alternative to the more sophisticated treatments for computing molecular IPs.67 The reason is that formally the same electron configurations as in singly ionized (doublet) radicals can be realized by considering the single excitations from the (inner) valence MOs to the LUMO of the corresponding (singlet) monocations (Fig. S4, ESI†). Considering specifically the 10 lowest excited states of the four NR singlet cations, such a simple orbital picture, i.e. the one in which unique excitation to the LUMO dominates a given excited state, is generally not seen with the canonical MOs (with a partial exception of the Cs symmetric TEMPO). However, precisely, this picture is recovered upon the transformation to the natural transition orbitals (NTO).68
The EPT-P3+ values for the first three ionizations in TEMPO (7.4; 9.1; 9.6 eV; Table 1) can be compared to the values obtained using the IP-UADC(3) method (7.2; 9.0; and 9.3 eV after shifting by −0.3 eV).69 Comparing the TD-DFT and EPT-P3+ vertical valence singlet IPs (the TD-DFT IPs are obtained by adding the IP of the 11A1 state to the TD-DFT singlet excitation energies; Tables 1–4 and Table S2, ESI†), it is seen that TD-CAM-B3LYP convincingly outperforms TD-B3LYP. While the correlation coefficients between the TD-DFT and EPT-P3+ values are high for both density functionals (≥0.98–0.99), the TD-B3LYP values are systematically much lower, on average by 1.5 eV. This is confirmed by the detailed comparison between the TD-B3LYP, TD-CAM-B3LYP, EPT-P3+, and IP-UADC(3)69 vertical IPs given in Table S4 (ESI†). From the calculated average absolute deviations (AADs), we conclude that the TD-CAM-B3LYP values for the singlet states are very similar to the EPT-P3+ ones, and that both methods are much closer to the benchmark IP-UADC(3) values than TD-B3LYP. The good agreement seen with TD-CAM-B3LYP lends support to the attribution of the TD-DFT CIS wave functions to the wave functions of the singlet valence ionized states.
Another issue with B3LYP is the considerably underestimated lowest triplet 13A1 (13A′′ in TEMPO) states of the NR cations, by 0.4–0.6 eV (Table S2, ESI†). This issue can likewise be partially rectified by switching to CAM-B3LYP although the triplets remain underestimated by 0.2 eV. On the other hand, the B3LYP results for the 11A1 state (11A′ in TEMPO) are surprisingly better than the CAM-B3LYP ones since the latter functional systematically overshoots (by 0.2–0.3 eV) the measured vertical IPs (Tables 1–4 and Table S2, ESI†).
With regard to the triplet-to-singlet intensity ratios observed for the SOMO−1 peaks in the VBs (see also the discussion of Fig. 2), the EPT-P3+ pole strengths (the quantities equivalent to the norms of the DSOs44) come out virtually identical for the 13A1 (13A′′) and 21A1 (11A′′) states in all four NRs. We emphasize, however, that in the case of TEMPO the more sophisticated IP-UADC(3) approach significantly favours the ionization to the triplet state predicting the 0.86![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.68 ratio of the 13A′′
0.68 ratio of the 13A′′![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11A′′ spectroscopic factors.69
11A′′ spectroscopic factors.69
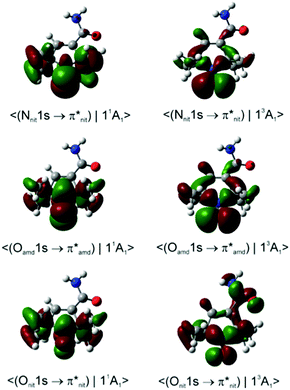
Dyson spin–orbitals
The DSOs between the N 1s and O 1s CV states and the lowest singlet and triplet monocation states of TEMPO and nit9 are shown in Fig. 7 and 8.From Tables 1–4 and Table S2, ESI† it is seen that the probability factors for the transitions between the CV and the valence ionized states are very small, on the order of magnitude of 10–4–10–5. The reason is in the very small overlap between the β-spin orbital sets due to the promotion of the β core electron to the π* LUMO in the initial CV state (Fig. S4, ESI†). In each of the DFT DSOs computed as per eqn (1) we detect the participation of several Kohn–Sham MOs with non-negligible weights; hence the relaxation effects extend significantly beyond the single orbital picture inherent to the Koopmans' approximation.64
We note that the probability factors for the transitions from the N 1s CV initial state are in the general order of magnitude larger than for the O 1s counterparts. In the case of the singlet final states this occurrence is due to the larger overlap between the β-spin orbital sets while in the case of the triplet final state it is due to the larger weight of the β HOMO in the DSO. The latter orbital mainly comprises the in-ring-plane lone pair on the O atom conjugated to the vicinal C–N bonds. This shows that the properties of the MOs in the β-spin sets of the initial and final states effectively govern the magnitude of the norm. Relative to the O 1s core-hole, the presence of the N 1s core-hole gives rise to a more efficient delocalization of the DSO owing to the stronger involvement of the C–C and C–H σ-bonds further away from the nitroxide radical centre.
Within the framework of the DFT DSOs and the approximations implied by eqn (3), we next compare the B3LYP and CAM-B3LYP performances with regard to the most significant experimental finding, viz. in all four NRs the Nnit 1s CV initial state exhibits a clear preference for de-excitation to the 11A1 (11A′) final state; conversely, the Onit 1s CV initial state decays with comparable probabilities to either of the 11A1 or 13A1 (13A′′) states.
In the case of TEMPO and DTBN, the predicted P(11A1)/P(13A1) ratios of the probability factors are virtually the same for the two functionals (Tables 1, 2 and Table S2, ESI†). These ratios are generally in agreement with the observed trends although the N 1s CV state de-excitation to 11A1 (11A′) is favoured only mildly (P(11A1)/P(13A1) ≈ 1.05). The present CV DSOs exhibit several differences relative to the DSOs that pertain to the ionization transitions from the ground state TEMPO.69 The CV DSOs are in general much more delocalized into the C–C σ-skeleton, and show a greater involvement of the out-of-plane O density in the case of the 11A′ final state (Fig. 7).
Importantly, with the introduction of the amide functionality the B3LYP and CAM-B3LYP probability factors begin to diverge significantly. Thus, in both nit8 and nit9 B3LYP erroneously predicts P(11A1)/P(13A1) < 1 for the Nnit 1s CV initial state, especially in nit8 where this ratio is as low as 0.55 (Table S2, ESI†). CAM-B3LYP is successful in rectifying these values but, as in TEMPO and DTBN, the two P(11A1)/P(13A1) ratios are only slightly larger than 1, up to 1.05 in nit9 (Tables 3 and 4). The CAM-B3LYP trends thus correspond much better to the measured data, which indicates that the long-range correction becomes increasingly important with the introduction of the second chromophore distant from the nitroxide group. Indeed, Fig. 8 illustrates how the DSOs in nit9 can delocalize over the entire molecule, including the significant participation of both chromophores, in particular for the 13A1 final state.
In contrast, the de-excitation channels of the Namd and Oamd 1s CV states are both predicted to show preference for the 13A1 final state (P(11A1)/P(13A1) < 1), significantly more so for nit8. This possibly finds some support in the ResPES spectra (Fig. 5 and 6) although the spectral features and intensity trends are here considerably more difficult to discern than with the Nnit and Onit 1s CV initial states.
With regard to the possibility of the de-excitations to the higher-lying singlet monocations described via TD-DFT (Tables 1–4), for the 10 such states studied, the probability factors generally do not show signs of decrease towards the higher BEs. Indeed, one finds among these states some of the largest probability factors, which may be indicative of the amassing of the spectral intensity seen in the >12 eV region (Fig. 3–6), in particular considering that the entire spectra exhibit shift towards higher BE values.
Finally, we investigated how changes in the geometry affect the DSOs and probability factors in order to assess the possibility of long-lived CV states having a sufficient time for the structural relaxation. To this end, in the case of DTBN, we calculated the probability factors at the geometries pertaining to the N 1s and O 1s CV minima, which were optimized at the B3LYP//mixed level (Tables S5 and S6, ESI†). The most important structural difference relative to the GS DTBN minimum concerns the significant elongation of the nitroxide bond, by almost 0.2 Å, owing to the population of the π*(N-O) SOMO by the N (or O) 1s electron. It is found, however, that the ratios of the probability factors at the CV minima diverge more from the observed intensity trends (Table S6, ESI†); hence we consider the presently used GS minima to be more pertinent to the current ResPES data.
Conclusions
The ResPES results indicate a very similar behaviour of all the investigated molecules. In particular, when O 1s and N 1s core electrons are promoted into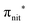 unoccupied orbitals, we notice a remarkable change in the SOMO/SOMO−1 intensity ratio, with respect to the non-resonant VBs. The modification with respect to the non-resonant VBs is particularly enhanced for the
unoccupied orbitals, we notice a remarkable change in the SOMO/SOMO−1 intensity ratio, with respect to the non-resonant VBs. The modification with respect to the non-resonant VBs is particularly enhanced for the 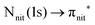 transition, where the de-excitation channels cause an intensity inversion, with the SOMO getting more intense than SOMO−1. An explanation of this behaviour could be found in the new NO singlet/doublet configurations accessible after the relaxation of the photoexcited molecule. The photoexcitation of a Namide (1s) or Oamide (1s) core electron into the amide unoccupied orbitals mainly provokes changes in the inner valence structures. The resemblances of TEMPO, DTBN, nit8 and nit9 resonant SOMO and SOMO−1 indicate a negligible contribution of the amide functional groups, the open/closed ring configuration and C–C single and double bonds on the outermost VBs structures, mainly influenced by the interaction of the photoexcited electron with the SOMO.
transition, where the de-excitation channels cause an intensity inversion, with the SOMO getting more intense than SOMO−1. An explanation of this behaviour could be found in the new NO singlet/doublet configurations accessible after the relaxation of the photoexcited molecule. The photoexcitation of a Namide (1s) or Oamide (1s) core electron into the amide unoccupied orbitals mainly provokes changes in the inner valence structures. The resemblances of TEMPO, DTBN, nit8 and nit9 resonant SOMO and SOMO−1 indicate a negligible contribution of the amide functional groups, the open/closed ring configuration and C–C single and double bonds on the outermost VBs structures, mainly influenced by the interaction of the photoexcited electron with the SOMO.
The de-excitation channels of the N and O 1s CV states to several valence ionized monocations were studied in the framework of density functional theory. Thus, the ΔDFT and TD-DFT methods were used to obtain the initial and final state determinant wave functions built from the Kohn–Sham MOs while the probability factors computed from the DFT DSO were used to model the transition intensities. The comparison of the two related density functionals, B3LYP and CAM-B3LYP, shows that the long-range correction implemented in the latter is essential for obtaining more reliable results. This is in particular true for the lowest triplet state of the NR monocations, the singlet vertical IPs, and the DSO probability factors. For example, unlike the case with TD-B3LYP, the TD-CAM-B3LYP 10 lowest singlet excitation energies of the NR monocations are in a good absolute agreement with the singlet valence IPs computed via the EPT-P3+/cc-pVTZ method.
From the theoretical standpoint, the main conclusion is that the intensity trends seen in the ResPES spectra can be accounted for reasonably well in terms of the properties and norms of CAM-B3LYP DSOs. Still, it has to be noted that while the ratios of the probability factors are predicted largely correctly upon including the long-range correction, they are in general only mildly indicative of the observed rather pronounced spectral effects. This particularly applies to the strong enhancement of the 11A1 (11A′) absorption seen in the N K-edge spectra. It would be of interest to see if the use of a high-level ab initio method to compute the DSOs could furnish additional explanatory power, or instead if consideration of the continuum states of the Auger electron39 and/or the vibronic effects36 (e.g. lifetime vibrational interference37,38) are the conditio sine qua non for improving the results.
Finally, our ResPES study allowed us to conclude that the presence of different bonds and/or different functional groups does not affect the SOMO character, which shows a great persistency keeping its properties. These results will help us to pave the way to a more rational and functional NR technological implementation, such as a tailored synthesis of new organic radicals or an appropriate functionalization of a ligand in a coordination compound for an efficient design of new transition metal complex catalysts.
Author contributions
R. Totani: investigation, formal analysis, visualization, and writing – original draft. I. Ljubić: formal analysis, software, computational methodology, visualization, and writing – original draft. A. Ciavardini: investigation, and writing – review and editing. C. Grazioli: investigation and writing – review and editing. F. Galdenzi: investigation and writing – review and editing. M. de Simone: investigation, data curation, software, and writing – review and editing. M. Coreno: conceptualization, data curation, funding acquisition, project administration, supervision, and writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank F. Zuccaro (CNR-ISM) for his technical support during the beamtimes and C. Puglia (Uppsala University, Sweden) and the Carl Tygger Foundation for making available the VGScienta SES-200 photoelectron analyser at the Gas Phase beamline, Elettra Synchrotron, Italy. The work of I. Lj. is supported in full by the Croatian Science Foundation under the project number IP-2020-02-9932. He also gratefully acknowledges the computational time at the Isabella cluster administered by the University of Zagreb Computing Centre (SRCE).Notes and references
- D. M. P. Holland, S. Nandi, C. Nicolas, J. D. Bozek, M. Patanen and I. Powis, Chem. Phys., 2021, 542, 111050 CrossRef CAS.
- R. Forbes, A. De Fanis, D. Rolles, S. T. Pratt, I. Powis, N. A. Besley, A. R. Milosavljević, C. Nicolas, J. D. Bozek and D. M. P. Holland, J. Phys. B: At. Mol. Opt. Phys., 2020, 53, 155101 CrossRef CAS.
- I. Powis, A. B. Trofimov, I. L. Bodzuk, D. M. P. Holland, A. W. Potts and L. Karlsson, Chem. Phys., 2013, 415, 291 CrossRef CAS.
- G. A. Garcia, L. Nahon and I. Powis, Int. J. Mass Spectrom., 2003, 225, 261 CrossRef CAS.
- D. P. Singh, N. De Oliveira, G. A. Garcia, A. Vredenborg and I. Powis, ChemPhysChem, 2020, 21, 2468 CrossRef CAS PubMed.
- M. M. Rafiee Fanood, M. H. M. Janssen and I. Powis, Phys. Chem. Chem. Phys., 2015, 17, 8614 RSC.
- S. L. Sorensen, S. J. Osborne, A. Ausmees, A. Kikas, N. Correia, S. Svensson, A. Naves de Brito, P. Persson and S. Lunell, J. Chem. Phys., 1996, 105, 10719 CrossRef CAS.
- E. E. Rennie, U. Hergenhahn, O. Kugeler, A. Rüdel, S. Marburger and A. M. Bradshaw, J. Chem. Phys., 2002, 117, 6524–6532 CrossRef CAS.
- U. Hergenhahn, A. Rüdel, K. Maier, A. M. Bradshaw, R. F. Fink and A. T. Wen, Chem. Phys., 2003, 289, 57 CrossRef CAS.
- M. N. Piancastelli, T. Lischke, G. Prümper, X. J. Liu, H. Fukuzawa, M. Hoshino, T. Tanaka, H. Tanaka, J. Harries, Y. Tamenori, Z. Bao, O. Travnikova, D. Céolin and K. Ueda, J. Electron Spectrosc. Relat. Phenom., 2007, 156, 259 CrossRef.
- A. Kivimäki, P. Norman, M. Coreno, M. de Simone, C. Grazioli, R. Totani, B. Ressel, H. Ottosson and C. Puglia, Phys. Rev. A, 2013, 88, 062502 CrossRef.
- M. N. Piancastelli, V. Carravetta, I. Hjelte, A. De Fanis, K. Okada, N. Saito, M. Kitajima, H. Tanaka and K. Ueda, Chem. Phys. Lett., 2004, 399, 426 CrossRef CAS.
- R. Feifel, Y. Velkov, V. Carravetta, C. Angeli, R. Cimiraglia, P. Sałek, F. Gel'mukhanov, S. L. Sorensen, M. N. Piancaśtelli, A. De Fanis, K. Okada, M. Kitajima, T. Tanaka, H. Tanaka and K. Ueda, J. Chem. Phys., 2008, 128, 064304 CrossRef CAS PubMed.
- X.-J. Liu, C. Nicolas, M. Patanen and C. Miron, Sci. Rep., 2017, 7, 2898 CrossRef PubMed.
- S. Stranges, M. Y. Adam, C. Cauletti, M. de Simone, C. Furlani, M. N. Piancastelli, P. Decleva and A. Lisini, J. Chem. Phys., 1992, 97, 7 CrossRef.
- S. Stranges, M. Y. Adam, M. De Simone, P. Decleva, A. Lisini, C. Cauletti, M. N. Piancastelli and C. Furlani, J. Chem. Phys., 1995, 102, 9 Search PubMed.
- A. Caneschi, D. Gatteschi and P. Rey, Prog. Inorg. Chem., ed. S. J. Lippard, John Wiley & Sons, Inc., 1991, vol. 39 Search PubMed.
- O. Armet, J. Veciana, C. Rovira, J. Riera, J. Castañer, E. Molins, J. Rius, C. Miravitlles, S. Olivella and J. Brichfeus, J. Phys. Chem., 1987, 91, 5608 CrossRef CAS.
- R. Kuhn, F. A. Neugebauer and H. Trischmann, Monatsch., 1966, 97, 525 CrossRef CAS.
- (a) A. L. Buchachenko, Stable Radicals, Consultants Bureau,New York, NY, 1965 Search PubMed; (b) G. W. Wheland, Resonance in Organic Chemistry, John Wiley and Sons, Inc., New York, NY, 1955, p. 381 ff Search PubMed; (c) W. E. Bachmann, in Organic Chemistry, An Advanced Treatise, 2nd edn, ed. H. Gilman, John Wiley and Sons, Inc., New York, NY, 1943, ch. 6, Vol. I Search PubMed.
- G. Coppinger, Tetrahedron, 1962, 18, 61 CrossRef CAS.
- I. Ratera and J. Veciana, Chem. Soc. Rev., 2012, 41, 303 RSC.
- J. H. Osiecki and E. F. Ullman, J. Am. Chem. Soc., 1968, 90(4), 1078 CrossRef CAS.
- Z. Ma, K. T. Mahmudov, V. A. Aliyeva, A. V. Gurbanov and A. J. L. Pombeiro, Coord. Chem. Rev., 2020, 423, 213482 CrossRef CAS.
- K. Zhang, M. J. Monteiro and Z. Jia, Polym. Chem., 2016, 7, 5589 RSC.
- M. A. Sowers, J. R. McCombs, Y. Wang, J. T. Paletta, S. W. Morton, E. C. Dreaden, M. D. Boska, M. F. Ottaviani, P. T. Hammond, A. Rajca and J. A. Johnson, Nat. Commun., 2014, 5, 5460 CrossRef PubMed.
- T. Ishida, K. Shinozuka, M. Kubota, M. Ohashi and T. Nogami, Chem. Commun., 1995, 1841 RSC.
- T. Sugawara, H. Komatsu and K. Suzuki, Chem. Soc. Rev., 2011, 40, 3105 RSC.
- Y. Borozdina, E. Mostovich, V. Enkelmann, B. Wolf, P. T. Cong, U. Tutsch, M. Lang and M. Baumgarten, J. Mater. Chem. C, 2014, 2, 6618 RSC.
- I. Novak, L. J. Harrison, B. Kovač and L. M. Pratt, J. Org. Chem., 2004, 69, 7628 CrossRef CAS PubMed.
- B. Kovač, I. Ljubić, A. Kivimäki, M. Coreno and I. Novak, Phys. Chem. Chem. Phys., 2014, 16, 10734 RSC.
- I. Ljubić, A. Kivimäki and M. Coreno, Phys. Chem. Chem. Phys., 2016, 18, 10207 RSC.
- I. Ljubić, J. Chem. Theory Comput., 2014, 10, 2333 CrossRef PubMed.
- I. Ljubić, A. Kivimäki, M. Coreno, S. Kazazić and I. Novak, Phys. Chem. Chem. Phys., 2018, 20, 2480 RSC.
- B. Kovač, I. Ljubić, A. Kivimäki, M. Coreno and I. Novak, Phys. Chem. Chem. Phys., 2015, 17, 10656 RSC.
- I. Ljubić, M. T. Cvitaš, C. Grazioli, M. Coreno, S. Kazazić and I. Novak, Phys. Chem. Chem. Phys., 2020, 22, 25396 RSC.
- E. Kukk, G. Snell, J. D. Bozek, W.-T. Cheng and N. Berrah, Phys. rev. A, 2001, 63, 062702 CrossRef.
- H. Wang, R. F. Fink, M. N. Piancastelli, M. Bässler, I. Hjelte, O. Björneholm, F. Burmeister, R. Feifel, A. Giertz, C. Miron, S. L. Sorensen, K. Wiesner and S. Svensson, Chem. Phys., 2003, 289, 31 CrossRef CAS.
- A. Rüdel, U. Hergenhahn, K. Maier, E. E. Rennie, O. Kugeler, J. Viefhaus, P. Lin, R. R. Lucchese and A. M. Bradshaw, New J. Phys., 2005, 7, 189 CrossRef.
- F. Innocenti, M. L. Costa, A. A. Dias, M. Goubet, A. Morris, R. I. Oleriu, S. Stranges, N. Zema and J. M. Dyke, Mol. Phys., 2007, 105, 771 CrossRef CAS.
- F. Innocenti, L. Zuin, M. L. Costa, A. A. Dias, M. Goubet, A. Morris, R. I. Oleriu, S. Stranges and J. M. Dyke, Mol. Phys., 2007, 105, 755 CrossRef CAS.
- J. D. Barr, A. De Fanis, J. M. Dyke, S. D. Gamblin, N. Hooper, A. Morris, S. Stranges, J. B. West and Y. G. Wright, J. Chem. Phys., 1999, 110, 1 CrossRef.
- C. M. Oana and A. I. Krylov, J. Chem. Phys., 2007, 127, 234106 CrossRef PubMed.
- J. V. Ortiz, J. Chem. Phys., 2020, 153, 070902 CrossRef CAS PubMed.
- N. A. Besley, M. J. G. Peach and D. A. Tozer, Phys. Chem. Chem. Phys., 2009, 11, 10350 RSC.
- N. A. Besley, Acc. Chem. Res., 2020, 53, 1306 CrossRef CAS PubMed.
- N. A. Besley, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1527, DOI:10.1002/wcms.1527.
- R. Blyth, R. Delaunay, M. Zitnik, J. Krempasky, R. Krempaska, J. Slezak, K. C. Prince, R. Richter, M. Vondracek, R. Camilloni, L. Avaldi, M. Coreno, G. Stefani, C. Furlani, M. de Simone, S. Stranges and M.-Y. Adam, J. Electron Spectrosc. Relat. Phenom., 1999, 101, 959 CrossRef.
- N. Mårtensson, P. Baltzer, P. A. Brühwiler, J. O. Forsell, A. Nilsson, A. Stenborg and B. Wannberg, J. Electron Spectrosc. Relat. Phenom., 1994, 70, 117 CrossRef.
- C. b. E. Moore, Atomic energy levels as derived by the analysis of optical spectra, Vol I, II, III, reissued 1971, US Govt Printing Office, Washington, DC, 1971 Search PubMed.
- G. R. Wight and C. E. Brion, J. Electron Spectrosc. Relat. Phenom., 1974, 3, 191–205 CrossRef CAS.
- R. N. S. Sodhi and C. E. Brion, J. Electron Spectrosc. Relat. Phenom., 1984, 34, 363 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291 CrossRef CAS.
- (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed; (c) S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200 CrossRef CAS; (d) P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623 CrossRef CAS.
- T. Yanai, D. Tew and N. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS.
- J. Shim, M. Klobukowski, M. Barysz and J. Leszczynski, Phys. Chem. Chem. Phys., 2011, 13, 5703 RSC.
- E. Miyoshi, H. Mori, R. Hirayama, Y. Osanai, T. Noro, H. Honda and M. Klobukowski, J. Chem. Phys., 2005, 122, 074104 CrossRef PubMed.
- K. A. Peterson and T. H. Dunning Jr, J. Chem. Phys., 2002, 117, 10548 CrossRef CAS.
- A. T. B. Gilbert, N. A. Besley and P. M. W. Gill, J. Phys. Chem. A, 2008, 112, 13164 CrossRef CAS PubMed.
- J. V. Ortiz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 123 CAS.
- J. V. Ortiz, Int. J. Quantum Chem., 2005, 105, 803 CrossRef CAS.
- G. M. J. Barca, et al. , J. Chem. Phys., 2020, 152, 154102 CrossRef CAS PubMed.
- M. J. Frisch, et al., Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2019 Search PubMed.
- M. Dauth, M. Wiessner, V. Feyer, A. Schöll, P. Puschnig, F. Reinert and S. Kümmel, New J. Phys., 2004, 16, 103005 CrossRef.
- R. Manne and T. Åberg, Chem. Phys. Lett., 1970, 7, 282 CrossRef CAS.
- D. Kubala, K. Regeta, R. Janečková, J. Fedor, S. Grimme, A. Hansen, P. Nesvadba and M. Allan, Mol. Phys., 2013, 111, 2033 CrossRef CAS.
- V. Lemierre, A. Chrostowska, A. Dargelos and H. Chermette, J. Phys. Chem. A, 2005, 109, 8348 CrossRef CAS PubMed.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775 CrossRef CAS.
- S. Banerjee and A. Y. Sokolov, J. Chem. Phys., 2021, 154, 074105 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Details of the ResPES technique; fitting analysis of TEMPO SOMO−1, Fig. S1–S4, and Tables S1–S6. See DOI: 10.1039/d1cp05264k |
| ‡ This contamination affected neither the observation of the observed absorption features, nor the subsequently acquired resonant spectra. On the contrary, it represented a further help for the NEXAFS photon energy calibration. |
| This journal is © the Owner Societies 2022 |