3D printed architected conducting polymer hydrogels

Abstract

Conducting polymer hydrogels combine electrical conductivity and tunable water content, rendering them strong candidates for a range of applications including biosensors, cell culture platforms, and energy storage devices. However, these hydrogels are mechanically brittle and prone to damage, prohibiting their use in emerging applications involving dynamic movement and large mechanical deformation. Here, we demonstrate that applying the concept of architecture to conducting polymer hydrogels can circumvent these impediments. A stereolithography 3D printing method is developed to successfully fabricate such hydrogels in complex lattice structures. The resulting hydrogels exhibit elastic compressibility, high fracture strain, enhanced cycling stability, and damage-tolerant properties despite their chemical composition being identical to their brittle, solid counterparts. Furthermore, concentrating the deformation to the 3D geometry, rather than polymer microstructure, effectively decouples the mechanical and electrical properties of the hydrogel lattices from their intrinsic properties associated with their chemical composition. The confluence of these new physical properties for conducting polymer hydrogels opens broad opportunities for a myriad of dynamic applications.

---

Introduction

Conducting polymer hydrogels are typically comprised of a cationic conducting polymer and an anionic, insulating polymer or small molecule with multiple anionic groups.¹ The anionic moieties serve as p-type dopants to the conducting polymers, enhancing their electrical conductivity. The polymer chains are physically or chemically crosslinked, creating a network that enables high water retention. The resulting hydrogels possess electrical conductivity, ionic conductivity, tunable water content, low stiffness, and biocompatibility.^1,2 This unique combination of properties renders them widely used materials in human–machine interfaces,⁵ culture platforms for electroresponsive cells,³ tissue engineering,⁴ bio-sensors,^2,5,6 drug delivery,⁷ solar water evaporation,^8,9 supercapacitors,⁹ and batteries.⁹ Unfortunately, conventional conducting polymer hydrogels are mechanically brittle and weak, precluding their usage from applications that involve dynamic movement.¹⁰

A number of approaches that revolve around manipulating the chemistry of conducting polymer hydrogels have been developed to circumvent this challenge. Combining conducting polymers with an insulating polymer possessing desirable mechanical characteristics leads to composite hydrogels with high stretchability.^11,12 Another powerful approach is to create double network hydrogels, wherein a soft and ductile neutral polymer forms an interpenetrated network with a brittle, anionic dopant polymer to provide tough hydrogels. Conducting polymers are typically added as a third component to the network to add electrical conductivity.^10,13 The resulting hydrogel exhibits drastically enhanced ductility and toughness as a result of the unique deformation mechanism of interpenetrated polymer networks.

However, these chemical approaches share the same limitation: the physical properties of the hydrogels are inevitably coupled to the chemical properties of the formative polymers. For instance, changing the chemical structures in an effort to enhance certain mechanical characteristics often leads to a decrease in electrical conductivity.¹⁴ Also, the strain-resistance correlation of a conducting polymer hydrogel is heavily dependent on the pathway of polymer chain deformation under mechanical stress, which offers little control for deliberate tuning of physical properties. Developing a strategy that can decouple a material's bulk mechanical and electrical properties from those prescribed by its chemical compositions can offer new opportunities for applications such as wearable (bio)electronics or soft robotics, where achieving stable, predictable device performance under dynamic movement is crucial. Informed architectural design provides an avenue to achieve this goal.

Integrating architectural design at multiple length scales with material design has led to revolutionary materials possessing traditionally contradictory properties, such as low density and high strength.^15,16 They are considered metamaterials because their macroscopic mechanical properties diverge from the intrinsic properties associated with their chemical composition. This effective decoupling of these traditionally interdependent properties occurs because the mechanical deformations of the architectures are predominantly controlled by geometry at various length scales instead of by chemical composition alone. Commonly explored lattices are comprised of 3D-tessellated unit cells of Kelvin, octet, Kagome, octahedron and dodecahedron with uniform truss diameter and aspect ratio.¹⁷ Such complex lattice structures are conventionally challenging to fabricate at micro or nanoscopic scales but have been enabled in recent years by advancement in 3D printing technologies. The structural regularity, precision and topological complexity offered by 3D printed architected structures also led them to significantly outperform their stochastic foam counterparts, which are prone to damage at the weaker sites due to the lack of structural uniformity.¹⁸

We envisage that applying the powerful concept of architecture to conducting polymer hydrogels can serve as a new strategy to imbue elasticity and pliability in these conventionally brittle materials, thus decoupling the mechanical and electrical properties from the underlying chemical structures. The ability to independently determine these functionalities a priori through structural design can open new opportunities in dynamic applications such as soft electronics, artificial organs, soft robotics, and stretchable energy storage devices. This architectural route is hitherto unexploited for this class of materials partly because the 3D printing of conducting polymers and their hydrogels is still in its infancy due to a number of complications including slow reaction kinetics and thermal instability.^19–22 A number of recent reports offer a hopeful glimpse into the successful 3D printing of conducting polymer hydrogels via direct ink write (DIW)^23–26 and vat photopolymerization methods including digital light processing (DLP)^27–31 and stereolithography (SLA).³² However, the resulting prints are limited to geometries with the same 2D pattern extending along the height direction or 3D structures with simple topography, which is far from the structural complexity required for architected lattices. Here, we describe an SLA-based method for realizing conducting polymer hydrogels with complex lattice structures. We demonstrate that their mechanical and electrical properties under strain are tunable via architecture and decoupled from the bulk properties imbued by their chemical compositions, overcoming impediments associated with previous approaches.

Results and discussion

The 3D printing and processing of conducting polymer hydrogels are illustrated in Fig. 1a. SLA is chosen as the 3D printing technique here due to its ability to create freeform, complex 3D architectures. In this process, a laser (usually 405 nm) is rastered in a 2D pattern to cure a thin layer of precursor solution (usually <100 μm) between the UV-transmittable window and the growing structure adhered to the build plate. This process is repeated layer by layer until the 3D object is formed. Direct photopolymerization of conducting polymers is not feasible due to (1) the slow reaction kinetics compared to the laser raster speed, (2) the lack of long-range connectivity and flexibility of conducting polymer chains, which prohibits the formation of a standalone, mechanically robust entity, and (3) the strong UV absorption of the growing conducting polymer outcompeting the photoinitiator for the incident UV light.^19,29 Due to these constraints, we print the architected structures with the anionic dopant polymer network first, which serves as a template for the subsequent growth of the cationic conducting polymers via interfacial polymerization (Fig. 1a). We chose polyaniline (PANI) as the conducting polymer here due to its usefulness in artificial muscle, biosensors, soft electronics, and energy storage devices.^1,33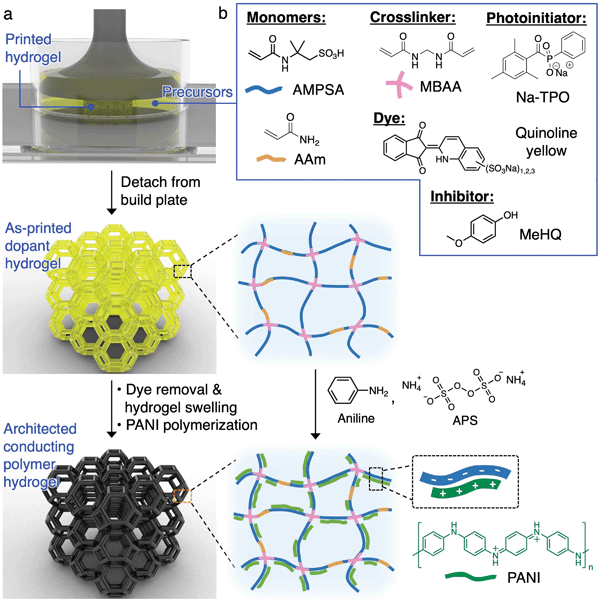

Fig. 1 (a) Schematic diagram illustrating the printing and synthesis of architected PANI hydrogels. (b) Chemical structures for the components in the aqueous precursor solution.

SLA precursor solution development

In order to successfully execute this fabrication strategy, an appropriate precursor solution for the photopolymerization of the dopant polymer needs to be developed. Our design is guided by the following key factors: (1) incorporation of an anionic monomer which allows for the templated growth of conductive networks and serves as dopant to the conducting polymer, (2) monomer(s) which allow for significant swelling ratios to provide enough free volume within the gels for the growth of conducting polymers, and (3) a hydrogel composition that provides adequate mechanical toughness for the beams in the lattices, to rotate and bend, when the architected structures are under compression. 2-Acrylamido-2-methyl-1-propanesulfonic acid (AMPSA) monomers are well-known to provide a large equilibrium swelling ratio while serving as a structural template and dopant for the growth of a number of conducting polymers including polyaniline.³⁴ One major downside to AMPSA hydrogels is that they are extremely brittle and typically rupture even during gentle manual handling. Therefore, a 3 : 1 molar ratio of AMPSA and acrylamide (AAm) are used as co-monomers. Incorporation of AAm to the hydrogels provides adequate mechanical toughness for physical manipulation of the hydrogel lattices. The co-monomers are chemically crosslinked by N,N′-methylenebis(acrylamide) (MBAA) to form a 3D polymer network that is swellable by water.

Pivotal to the success of 3D printing was the choice of a photoinitiator that was soluble in mildly acidic (pH 3–4) aqueous solutions because of the acidity of AMPSA. We identified sodium phenyl(2,4,6-trimethylbenzoyl)phosphinate (Na-TPO) as a photoinitiator with good solubility within our aqueous precursor mixture and also a fast curing rate appropriate for SLA printing.³⁵ TPO nanoparticle is another possibility for the SLA printing of aqueous resins when the necessary processing equipment are available.³⁶ Additionally, we incorporated a commercially available dye, quinoline yellow, that displayed an absorbance with suitable overlap with Na-TPO. The dye effectively reduces the penetration depth of the laser and allows for finer control over the crosslinking activities within the set layer height, thus reduces line width spreading in the lateral direction. A commonly used inhibitor for acrylamides, 4-methoxyphenol (MeHQ), was added for oxygen inhibition.³⁷ The contents of the optimized precursor solution are shown in Fig. 1b and tabulated in Table S1 (ESI†).

3D printing of architected hydrogels

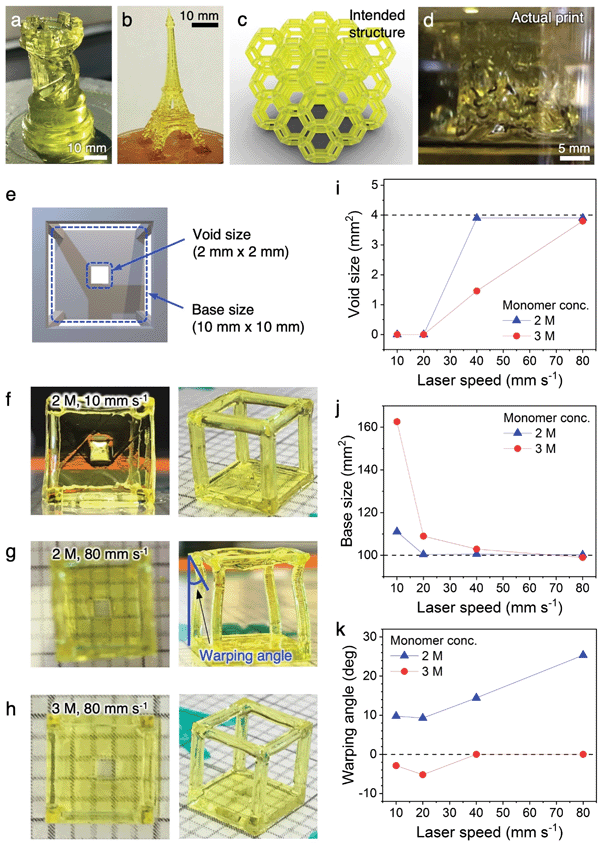
To begin the development of our 3D printing platform, Moai (Peopoly Inc.) was chosen as the commercially available, open source stereolithography printer due to its affordability and ease of physical modification. Our customization to the printer is described in Fig. S1 and associated text (ESI†).

We started the printing optimization using monolithic, centimeter-scale 3D structures such as a rook and an Eiffel Tower without the fine beam structures. The precursor solution had a combined monomer concentration of 1 M. In combination with low laser raster speed (5–10 mm s⁻¹), the intended structures were successfully printed (Fig. 2a and b). They exhibit complexities that rival, or exceed, those from previous reports on conducting polymer hydrogels. However, the structures visibly tilt under their own weight along the vertical axis and do not appear stiff. These minor distortions are exacerbated during the printing of complex 3D lattices with sub-millimeter beam diameters. The distorted printed structure attached to the build plate shown in Fig. 2d is in stark contrast to the intended structure shown in Fig. 2c. The printed lattice crumbled under its own weight once detached from the build plate.

Fig. 2 Printing parameter optimization. As-printed parts of (a) a rook and (b) Eiffel Tower without the fine beam structures. (c) CAD illustration showing the intended lattice structure for printing and (d) the actual print. (e) Structure designed for parameter optimization. (f–h) Photographs of the printed structures with different monomer concentration and laser raster speed. The dimension of the smallest grid on the substrate is 2 mm (length) by 2 mm (width) and is used as a reference for size. (i–k) Void size, base size and warping angle, respectively, plotted against laser speed at different monomer concentrations (conc.) for identifying the conditions optimal for printing complex lattices with high resolution. The dashed line on each plot represents the theoretical dimension/angle for each quantification parameter.

These initial results highlighted the challenges of printing complex conducting polymer hydrogel lattices with sub-millimeter beam dimensions, and the importance of optimizing hydrogel stiffness through the tuning of precursor solution composition and printing parameters. The hydrogel stiffness can be enhanced by increasing the crosslinking density per unit volume, either by increasing the concentration of the reactive precursor species or by increasing the laser exposure time per unit volume. However, both of the possible approaches could lead to a “bleeding” effect where the precursors not in the direct laser pathway, but within close proximity, also get crosslinked, leading to a loss of resolution. A near-maximum laser intensity has already been used here, which left little room for further tuning. In order to achieve the balance between hydrogel stiffness and printing resolution, both critical parameters for complex 3D lattices, we designed a wireframe structure with a solid base containing a 2 mm (length) by 2 mm (width) void (Fig. 2e and Fig. S3, ESI†). If the stiffness of the hydrogel is inadequate, the long and narrow beams of the wireframe would buckle or warp due to the weight of the frame on top. If the precursor or laser parameters result in a “bleeding” effect and a loss of resolution, the void on the solid base would occlude. The effect of different combinations of precursor concentrations and laser raster speeds were systematically studied and summarized in Fig. 2f–k and Fig. S4 (ESI†). In short, increasing the monomer concentration from 1 M to 2 M (concentration of all other species scaled accordingly to maintain relative ratio) while maintaining a low laser speed of 10 mm s⁻¹ provided sufficient stiffness for the wireframe, but led to the complete occlusion of the void due to overcuring (Fig. 2f). Retaining the 2 M monomer concentration while increasing the laser speed to 80 mm s⁻¹ provided good resolution for the void, but resulted in warping of the wireframe beams because the fast laser movement does not provide a sufficient exposure for complete curing (Fig. 2g). A balance between the two factors can be found by further increasing the monomer concentration to 3 M while maintain the 80 mm s⁻¹ laser speed. Using this combination, a suitable amount of monomers are crosslinked within the short laser exposure time (Fig. 2h) to provide structures that are sufficiently stiff with high resolution. The dimensions of the void and the solid base, along with the warping angle of the beams, are quantified against laser speed and monomer concentration in Fig. 2i–k. The correlations reveal that high structural fidelity and high resolution can be achieved with an optimal monomer concentration of 3 M and laser speed of 80 mm s⁻¹. These parameters were used for the printing of all complex hydrogel lattices in this work. A typical printing process is shown in Video S1 (ESI†). We employ the two most widely used architectures for this study: open cell Kelvin lattice and octet lattice.

PANI:PAMPSA–PAAm hydrogel fabrication

PANI-infiltrated PAMPSA–PAAm hydrogels, termed PANI:PAMPSA–PAAm from here on, were created by first rinsing and swelling the as-printed hydrogel lattices, followed by the interfacial polymerization of aniline. During each stage of processing, environmental scanning electron microscopy (ESEM) was employed to monitor the morphological changes of the hydrogels directly in their hydrated state.

The as-printed PAMPSA–PAAm Kelvin or octet hydrogel lattices have a dimension (length, width, and height) of ∼18 mm with an average beam diameter of ∼800 μm when printed (Fig. 3c). They have a light yellow tint due to the presence of quinoline yellow dye (Fig. 3a, left). ESEM images of a cleaved section of an as-printed Kelvin lattice show clear layering along the printing direction, characteristic of 3D printed structures (Fig. 3d). The surface of the beams appear to be non-porous, but it is possible that small pores with dimension beyond the resolution of our ESEM are present due to the high water content of the precursor solution. Repeatedly rinsing the as-printed hydrogel in water removes the dye and other impurities, leading to a transparent appearance (Fig. 3a, middle). The hydrogel also swelled significantly during the process, with the average lattice dimension increasing to ∼27 mm, and average beam diameter to ∼900 μm, accompanied by an increase in the length of the beam (Fig. 3e). The swelling of the hydrogel led to much higher uptake of water within the polymer network, resulting in a highly porous morphology with water-filled pores ranging ∼10–40 μm in diameter (Fig. 3f).

Fig. 3 Morphology and mechanical characteristics of the printed lattices. (a) Photograph of the as-printed PAMPSA–PAAm hydrogel (yellow lattice), swelled PAMPSA–PAAm hydrogel (clear lattice), and PANI:PAMPSA–PAAm hydrogel (dark green/black lattice). The dimension of the smallest grid on the substrate is 2 mm × 2 mm. (b) Photograph of several hydrogel lattices at different stages of PANI growth. (c–h) ESEM images of as-printed PAMPSA–PAAm hydrogel lattice (c and d), swelled PAMPSA–PAAm hydrogel lattice (e and f), and PANI:PAMPSA–PAAm hydrogel lattice (g and h). Photograph series showing the compression behavior of (i) solid and (j) lattice of PANI:PAMPSA–PAAm hydrogels.

PANI was infiltrated into the swelled PAMPSA–PAAm hydrogels via interfacial polymerization (described in Experimental and Fig. S5, ESI†) similarly to previously reported processes.³¹ During the polymerization process, the initially transparent PAMPSA–PAAm hydrogels gradually adopt the characteristic green color of PANI in the doped, emeraldine salt oxidation state (Fig. 3b). The purified PANI:PAMPSA–PAAm hydrogel has a dark green color that almost appears black (Fig. 3a, right). The incorporation of PANI in the hydrogel is spectroscopically confirmed by UV-vis-NIR (Fig. S6a, ESI†) and ATR-IR (Fig. S6b, ESI†).^38–40 The hydrogel swells further during the polymerization process, with the average lattice dimension increases to ∼30 mm, and average beam diameter to ∼1100 μm, accompanied by additional increase in the length of the beams (Fig. 3g). A change in microscopic pore structure is also observed, where many of the pores in the swelled PAMPSA–PAAm hydrogels are now covered by sheet-like structures that are likely PANI (Fig. 3h).

The purified PANI:PAMPSA–PAAm hydrogels have a water content of ∼98 wt%, a slight decrease from the ∼99 wt% water content of the swelled PAMPSA–PAAm hydrogels, possibly due to the more hydrophobic nature of PANI compared to PAMPSA. The high water content of these hydrogels render them excellent candidates for potential applications that require additional material loading, including cells or electrochemically active materials for energy storage applications.

The PANI:PAMPSA–PAAm hydrogels have a conductivity of ∼0.53 S m⁻¹, which can be further increased to ∼8 S m⁻¹ by additional doping through soaking in an HCl solution. These values are consistent with control hydrogels made using bulk chemical polymerization with identical precursor composition. The conductivities are also similar to those in literature reports of conducting polymer hydrogels synthesized by various conventional chemical methods.² The doping step not only increases conductivity but also the acidity of the hydrogels, which is likely acceptable for applications in soft electronics or stretchable energy storage devices (e.g., supercapacitors or batteries), but might not be suitable for biological applications such as cell culture.

Stress–strain behavior

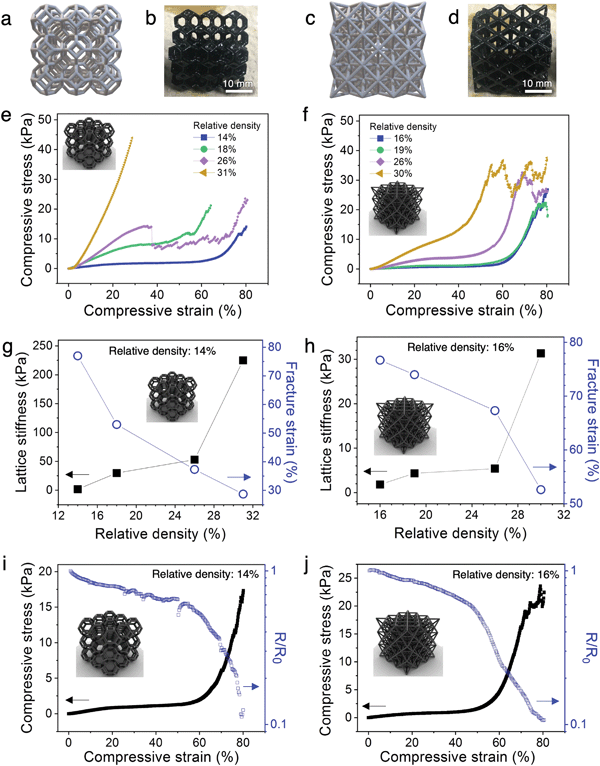
The architected PANI:PAMPSA–PAAm lattices exhibit drastically different mechanical properties from the solid counterparts. The 3D printed solid PANI:PAMPSA–PAAm hydrogel is compressible at low strain, but undergoes sudden brittle fracture at strain above 20% (Fig. 3i and Fig. S7a, Video S2, ESI†). In contrast, low relative density, architected PANI:PAMPSA–PAAm lattices with identical chemical composition can be elastically compressed to 60% strain with the hydrogel recovering to its original height upon unloading (Fig. 3j and Video S3, ESI†). This drastically different compressive behavior illustrates the potential and benefit of exploring the concept of architecture as an alternative avenue to incorporate new mechanical properties in conducting polymer hydrogels with existing chemical compositions. In our case, the 3D architecture successfully suppressed brittle fracture of the hydrogel, an intrinsic mechanical characteristic, and provided ductility.

To better understand the structure–property relationships of the 3D printed hydrogel lattices, we focus our investigation on the two most widely studied architectures: open cell Kelvin and octet lattices (Fig. 4a–d). Kelvin is a compression-dominated lattice whereas octet is a stretching-dominated lattice.¹⁵ The relative density of a cellular matter is defined as the ratio of the density of porous structure to the density of solid.¹⁸ To explore the effect of changing the ratio of polymer to free volume of the lattices, we systematically varied the relative density from ∼10-30%. Because of the post-printing swelling and PANI polymerization steps, the relative densities calculated by CAD software were typically not preserved at the end of the process. The density values indicated on figures are the experimentally measured values for the PANI:PAMPSA–PAAm hydrogel lattices. For both lattice structures with relative density less than 20%, the compressive stress–strain behavior between 0–80% strain exhibits typical characteristics of cellular materials.^18,41 Three distinct regions are observed: an initial Hookean region, a plateau region where the lattice deforms through the rotation and buckling of beams which led to only mild increases in lattice stiffnesses, and a densification region at high strain where the stress rises rapidly (Fig. 4e and f). At relative densities above 20%, lattices are typically not expected to abide to mechanical characteristics of cellular materials.¹⁵ This is the case for the Kelvin lattices: the stress–strain behavior for lattices with 26 and 31% relative density start to resemble that of the corresponding bulk materials (Fig. 4e). However, at similar relative densities, the octet lattices still retain some of the cellular material properties, evidenced by the three distinct regions in its stress–strain curves (Fig. 4f). This difference appears surprising because compression-dominated structures such as Kelvin lattices are typically more compressible than stretching-dominated structures such as octet at the same relative density.¹⁸ Previous reports showed that a number of factors can cause the stress–strain behavior to deviate away from the typical trend, including variation in beam aspect ratios.¹⁷ As shown by ESEM images in Fig. 3, the post-printing steps including polymer network swelling and PANI growth significantly change the aspect ratio of the beams compared to the as-printed hydrogels. Due to the nature of the architectures, the beams are longer in octet than Kelvin lattices at the same relative density. Therefore, it is possible that after the post-printing steps, the aspect ratio of the beams in octet remains high enough for buckling to occur easily, whereas those in Kelvin lattice cannot. We would like to emphasize that quantifying the scaling laws of stiffness or strength versus density is not a focus of this work. Doing so will require developing new procedures for retaining consistent beam aspect ratios and other parameters through the various processing and polymerization steps, and may be the subject of future studies.

Fig. 4 Mechanical and electrical behavior of architected PANI hydrogel lattices. CAD illustration (a and c) and photographs (b and d) of PANI:PAMPSA–PAAm hydrogel in the form of Kelvin and octet lattices, respectively. (e and f) Stress–strain behavior of Kelvin and octet PANI:PAMPSA–PAAm hydrogel lattices, respectively. (g and h) Plots showing relationship between relative density and lattice stiffness (i.e., stiffness of the plateau region) and fracture strains for the lattice structures as indicated. (i and j) Correlation between the mechanical and electrical properties for the hydrogel lattices (identifications labeled on plots). A loading rate of 100% min⁻¹ was used for all compression studies.

In addition to the three-region stress–strain behavior of cellular materials, the hydrogel lattices exhibit step-wise rupture where the stress continues to rise after each dip (Fig. 4e and f), as opposed to the catastrophic failure mechanism observed in solid PANI:PAMPSA–PAAm hydrogels (Fig. 3i and Fig. S7a, Video S2, ESI†). Such macroscopic structural resilience is common in hierarchical structures where the beams form cracks and fracture at different strains, during which process the macroscopic lattice remains partially intact.^15,42

The correlation between relative density and the lattice stiffness (defined as the stiffness of the plateau region) and fracture strain (defined by the onset of the first dip in stress) are summarized in Fig. 4g and h. For both architectures, the lattice stiffness increases while fracture strain decreases with increasing relative density. We chose the lowest density lattices from both architectures (14% for Kelvin and 16% for octet) for further analyses because they possess (1) the most tunable stress–strain behavior with plateau region lasting from ∼5–60% strain for Kelvin and ∼5–55% strain for octet lattices, (2) lowest stiffness values of 1.9 kPa for Kelvin and 1.8 kPa for octet lattices, and (3) highest fracture strain of ∼77% for both Kelvin and octet lattices. This collective combination of properties are highly desirable for dynamic applications that involve biological interfaces such as soft electronics or soft robotics.^43,44

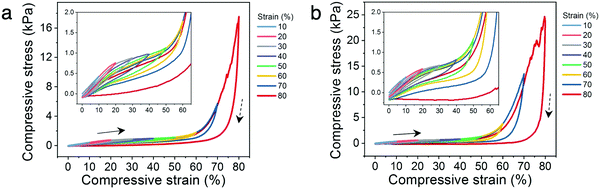
In addition, the cyclic compressibility of the architected hydrogels were investigated by cyclically loading-unloading the lattices through incrementally stepped strain amplitude of 10% in sequence. For each architecture, representative relative densities below and above the 20% threshold were analyzed. The lattices with low relative densities (14% for Kelvin and 16% for octet) exhibit excellent cyclic compressibility where the lattices recover elastically even after cycling to strains as high as 80% (Fig. 5a and b). The presence of hysteresis loops indicate energy dissipation, which can be attributed to dissociation of ionic bonds or the sliding or buckling of the polymer microstructures observed in ESEM (Fig. 3h).^41,45 When comparing a loading curve to that from the preceding loading cycle, only a slight decrease in stress at the same strain is observed (insets to Fig. 5a and b). This suggests that the mechanisms leading to energy dissipation during loading are largely recoverable during the time scale of the experiments.

Fig. 5 Cyclic compression behavior of PANI hydrogels. Stress–strain curves during loading–unloading to various strains for (a) Kelvin lattice with 14% relative density, and (b) octet lattice with 16% relative density. Arrows and dashed arrows represent the loading and unloading directions, respectively. A loading and unloading rate of 100% min⁻¹ was used.

Mechanical–electrical property relations

In order to understand the correlation between the resistance–strain and stress–strain behavior of low density PANI:PAMPSA–PAAm hydrogel lattices (14% for Kelvin and 16% for octet), we monitored the resistance of the hydrogels in situ under compression. The measurement geometry is depicted in Fig. S8a (ESI†). For both architectures, resistance–strain curves loosely resemble the mirror image of their corresponding stress–strain curves (Fig. 4i and j). The change in resistance for the hydrogels is mild in the plateau region of the stress–strain curves, but the resistance decreases rapidly when the hydrogel transitions into the densification region due to the formation of additional conductive pathways. Also note that when the lattice starts to fracture at above 70% strain for the octet lattice, the resistance does not increase or fluctuate rapidly. This electrical stability is possible in lattice structures because sufficient charge transport pathways remain available through the vast number of beams despite the fracture of a few of them, offering enhanced damage–resistance properties compared to their solid counterparts. These results highlight the distinct advantages of manipulating material properties via architecture as opposed to chemical means. By applying an architectural approach to conducting polymer hydrogels, their electrical property–strain relationship is now controlled by the lattice deformation behavior rather than chemical composition. Hence, this approach effectively decouples the electrical properties of hydrogels from their intrinsic chemical characteristics. Potentially, complex, pre-determined resistance–strain behaviors may be achieved by introducing architectural variations within the same lattice without changing the chemical composition of the hydrogels, offering new opportunities to tune various physical properties independently for tailored applications.

Cycling stability

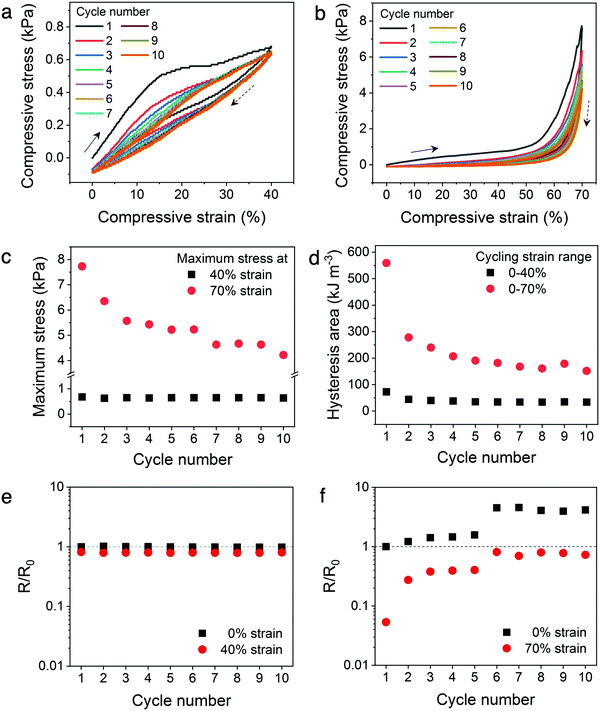
To establish the mechanical and electrical stability of the architected conducting polymer hydrogels through repeated cycling, Kelvin lattices with 14% relative density were cyclically loaded and unloaded to 40% and 70% strains (Fig. 6a and b). The cycling stability of the hydrogel lattices to the plateau region was represented by the 40% strain cycles, whereas that to the densification region was represented by the 70% strain cycles. For both cycling experiments, the biggest decrease in peak stress and hysteresis were observed between the first and second cycles, indicating some of the energy dissipation mechanisms, including ionic bond dissociation, sliding or buckling of polymer microstructures, or formation of microscopic cracks, were not reversible during the experimental time scale.^41,45 After the initial cycle(s), the mechanical stability of the lattices is significantly higher with repeated loading and unloading to the plateau region (40% strain), evidenced by the nearly constant maximum stress and hysteresis area with increasing cycle number (Fig. 6c and d). On the contrary, this high mechanical cycling stability is not observed when the lattices are cyclically loaded to the densification region (70% strain), where both peak stress and hysteresis area decrease consistently with increasing cycle number.

Fig. 6 Mechanical and electrical cycling stability of the Kelvin lattices (14% relative density). (a and b) Stress–strain curves for 10 cycles of loading–unloading the lattices between 0–40% strain and 0–70% strain, respectively. Arrows and dashed arrows represent the loading and unloading directions, respectively. A loading and unloading rate of 100% min⁻¹ was used. (c) Maximum stress for the 10 compression cycles to different strains. (d) Area of the hysteresis loop for the 10 compression cycles to different strain ranges. (e and f) Electrical resistance changes of the lattices when loaded–unloaded to 40% strain and 70% strain, respectively. The dashed line indicates no change in electrical resistance from the initial, uncompressed hydrogel.

Similar to the in situ resistance–stress–strain correlations, the electrical stability of the hydrogel lattices display a direct correlation to their mechanical stability (Fig. 6e and f). Fig. 6e illustrates the resistance–strain relation when the hydrogel lattices are cyclically loaded to 40% strain, which is within the plateau region of the stress–strain curve. The resistance values of the hydrogel lattices at 0% versus 40% do not differ significantly and remain constant throughout repeated cyclic loading within this plateau regime. On the contrary, the resistance values varied considerably when cyclically compressed to the densification region (70% strain), indicating poor electrical stability (Fig. 6f). In addition, the resistance values at both 0% and 70% strains increased with increasing compression cycles. This suggests the hydrogel lattices experienced incremental loss in conduction pathways with additional compression cycles to the densification region, similarly to the mechanism leading to the sizable decrease in maximum stress and hysteresis area. This set of experiments illustrates the possibility of designing materials with enhanced electrical and mechanical cycling stability through architectural design. Creating architectures with a stress–strain plateau region that overlaps with the operational strain range for tailored devices can potentially enhance their long-term stability without changing the chemical composition of conducting polymer hydrogels.

Conclusions

We have demonstrated a 3D printing strategy for creating architected conducting polymer hydrogels with complex lattice structures. Key factors for success include customized precursor composition for SLA photopolymerization, printing parameter optimization, and tailored post-processing steps. Addressing these facets has led to architected lattice structures of conducting polymer hydrogels with similar chemical composition as their solid counterparts, but drastically different mechanical and electrical properties. The mechanical properties of the lattices at low relative densities are controlled by the 3D geometry, rather than chemical composition alone, enabling the rational tuning of various mechanical characteristics including stress–strain behavior, stiffness, fracture strain, and damage–resistance. Most significantly, the plateau region in the stress–strain curves, a distinctive characteristic of cellular materials, induces the successful decoupling of electrical resistance–strain pathways from the intrinsic characteristics of the conducting polymer hydrogels, properties that are traditionally interdependent. Only mild changes in electrical resistance are present when the lattice hydrogels are compressed in the plateau region, and the material exhibits high electrical and mechanical stability when cyclically loaded–unloaded to this plateau region. This work illustrates that applying the concept of architecture to conducting polymer hydrogels can give rise to pre-determined, non-interdependent structure–property relationships that are hitherto unavailable through existing chemical composition-based approaches. We focused on a specific chemical composition: PANI as the conducting polymer and PAMPSA–PAAm as the dopant and structural polymer network due to their established biocompatibility. For instance, PANI hydrogel have been used for drug release⁴⁶ and nerve regeneration,⁴⁷ and PAMPSA–PAAm hydrogels are excellent candidates for cell migration⁴⁸ and cartilage regeneration.^49,50 However, the 3D printing platform and general strategies presented here can be widely applied to many other conducting polymers such as polypyrrole and poly(3,4-ethylenedioxythiophene), each in combination with various dopant polymers, producing hydrogels with desired mechanical, biological, or stimuli-responsive functionalities. The 3D printed hydrogel lattices can also serve as the structural template for complex architectures of solid-state conducting polymers by isotropic dehydration and conducting polymer aerogels by freeze or supercritical drying, providing additional functionalities through structural hierarchy at different length scales. Collectively, the new processes, materials, and knowledge established by this work can open new opportunities for a broad range of emerging applications operating under dynamic conditions, including wearable or implantable electronics and bioelectronics, soft robotics, stretchable energy storage devices, and cell culture platforms.

Experimental section

CAD and slicing

Computer-aided design (CAD) models of the architected structures were created using Rhinoceros 3D and the integrated graphical algorithm editor, Grasshopper. Ultimaker Cura was used for slicing the 3D CAD models into printable 2D layers.

SLA printer modification and printing parameters

A Peopoly Moai stereolithography (SLA) printer was used for this work. It has a laser wavelength of 405 nm and maximum power of 150 mW. The open source feature of the printer allowed a number of project-specific modifications to be carried out, which were detailed in Fig. S1 (ESI†) and associated text.

3D printing and post-processing

Precursor solution preparation. The precursor solution contains sodium 2-acrylamido-2-methyl-1-propanesulfonic acid (AMPSA) and acrylamide (AAm) as co-monomers, N,N′-methylenebis(acrylamide) (MBAA) as crosslinker, sodium phenyl(2,4,6-trimethylbenzoyl)phosphinate (Na-TPO) as photoinitiator, quinoline yellow as dye, 4-methoxyphenol (MeHQ) as inhibitor, and nitrogen-purged deionized (DI) water as solvent. The precursor solution was prepared using the following procedure. To a 500 mL 3-neck round bottom flask (RBF), 100 mL of N₂-purged DI water and a Teflon-coated stir bar were added. The solution was magnetically stirred at 300 rpm and kept under a N₂ atmosphere. After 10 minutes, 9 grams (225.1 mmol) of sodium hydroxide (NaOH) was added and allowed to dissolve for 30 minutes. The RBF was placed in an ice water bath to cool the solution to ∼0 °C. Subsequently, 68 mg (0.548 mmol) of MeHQ was added and allowed to fully dissolve. After 1 hour, 46.6 g (225.1 mmol) of the first monomer (AMPSA) was slowly added in portions to avoid large solution temperature fluctuation (solution remains under 8 °C during the process). After complete dissolution, the flask was removed from the ice bath and returned to room temperature. Next, 5.4 g (75.97 mmol) of the second monomer (AAm), 1.9 g (12.32 mmol) of the crosslinker (MBAA), and 31.25 mg (0.065 mmol) of the quinoline yellow dye were added in succession and allowed to dissolve for 5 hours. The RBF was then moved to a UV-filtered room, to protect content from UV light, followed by the addition of 3 g (9.67 mmol) of the photoinitiator (Na-TPO) in one portion. The synthetic procedure for Na-TPO is discussed in the next section. The RBF was purged with N₂ again, sealed, and allowed to stir overnight. The next morning, 1 pellet of NaOH (∼120 mg, 3 mmol) was added to aid the dissolution of Na-TPO. The flask was purged with N₂ and sealed again. Upon complete dissolution of all contents in the flask, the pH of the solution was carefully monitored and adjusted to 3–4 by slowly adding additional AMPSA. The final mixture was allowed to stir for 2 hours followed by gravitational filtration through a cotton plug into a jar covered with aluminum foil. The filtrate in the light-protected jar was purged with N₂ one more time and stored in the dark, protected from UV light, until used.

Synthesis of Na-TPO. The reaction vessel was protected against light during the entirety of this reaction. First, 20 g (63.2 mmol) of ethyl(2,4,6-trimethylbenzoyl)phenylphosphinate (TPO-L) was added to a 250 mL round bottom flask, equipped with a reflux condenser, and dissolved in 35 mL of acetone. The round bottom flask was then placed in an oil bath at 50 °C under a N₂ protected atmosphere and stirred at 150 rpm. 10.42 g (69.5 mmol) of sodium iodide (NaI) was added to the flask and the mixture was allowed to stir overnight. The next morning, the reaction mixture was cooled to room temperature and 25 mL of acetone was added to the flask. The precipitate was filtered and washed with fresh acetone 3 times. The material was dried under vacuum, protected from light, at room temperature for 48 hours. Once dried, Na-TPO was stored in a tightly sealed jar and covered with aluminum foil. The chemical reaction scheme and ¹H NMR characterization are shown in Fig. S2 (ESI†).

Dopant architected hydrogel lattice (PAMPSA–PAAm) printing. All SLA printing experiments were carried out in a UV-filtered room created by installing a Lithoprotect® self-adhesive UV-protection yellow foil over the ceiling light panel. Fig. 1 illustrates the printing and processing steps. Fig. S5 (ESI†) shows the architected hydrogel lattices during each of the printing and processing steps.

In a typical experiment, approximately 120 mL of precursor solution was poured into the homebuilt vat (diameter: 750 mm, height: 370 mm) as shown in Fig. S1c and d (ESI†). The 405 nm laser in the SLA printer was operated at a laser power setting of 60 with an X–Y movement speed of 80 mm s⁻¹ unless otherwise stated. A 100 μm layer height was used for all prints. Four hydrogels could be printed at a time on a single build plate, which typically takes approximately 30–35 min to complete. A razor blade was used to carefully delaminate the hydrogels from the glass build plate surface. The hydrogels were then placed in DI water for 30 min, and the rinsing process was repeated 8 times with fresh DI water. During the process, the hydrogels lose their light yellow tint and become optically transparent, indicating the complete removal of quinoline yellow dye. The sizes of the hydrogels also increased during the process as a result of polymer network swelling.

PANI-loaded architected hydrogel lattice (PANI:PAMPSA–PAAm) synthesis. An interfacial polymerization procedure was adopted for infiltrating the PANI network into hydrogels.³¹ In a typical reaction, the rinsed and swelled gels were placed into a 1 M HCl_(aq.) solution containing 0.08 M ammonium persulfate (APS) for 16 hours to absorb the oxidant into the hydrogel interior. Subsequently, the hydrogels were removed from the solution and rinsed with hexane to eliminate excess APS solution trapped in lattice void spaces. The hydrogels were then submerged in a hexane solution containing 0.16 M aniline and left unagitated for 4 hours for aniline to diffuse into the APS-containing hydrogels and polymerize. The hydrogels transitioned from transparent to the characteristic green color of PANI during the process, and appeared dark green/black at the end of the process (Fig. S5, ESI†). The PANI hydrogels were transferred to a DI water bath and soaked for 2 hours to remove low molecular weight oligomers and other impurities. The process was repeated 6 times with fresh DI water. Then, the PANI hydrogels were placed in a 1 M HCl solution for 16 hours to fully dope the PANI network, followed by another round of soaking in DI water for 16 hours to remove excess HCl.

Chemical characterization

¹H nuclear magnetic resonance (NMR) spectra were collected on a Bruker 600 MHz NMR and data was processed using Topspin. UV-vis-NIR spectra were collected on a Shimadzu UV-3600 Plus. Samples for the UV-vis-NIR experiments were prepared by blending Kelvin lattice hydrogels (14% relative density) with 200 mL of deionized water using a Hamilton hand blender (Model 59762) at its lowest power setting for 5 s. The homogenized dispersion was transferred to a 4 mL quartz vial for UV-vis-NIR measurements. ATR-IR spectra were obtained on a Bruker Vertex 70 spectrometer (ATR mode, diamond window). Each spectrum was collected with 120 scans within the wavenumber range of 200 to 4000 cm⁻¹ at a 4 cm⁻¹ resolution. The hydrogel lattices were dehydrated at 60 °C overnight in a convection oven. The dried structures were then crushed into powder for ATR-IR measurements.

Environmental scanning electron microscopy (ESEM)

An FEI Quanta 200 ESEM was used to image the hydrogels in their hydrated state. Samples were kept in a sealed container prior to imaging to retain their degree of hydration. They were cut into approximately 5 mm × 5 mm × 5 mm chunks followed by immediate loading into the ESEM chamber. The low-vacuum operation mode (pressure range of 0.1 to 106 Pa) was used for imaging the hydrogels. The chamber pressure was maintained at 60 Pa under room temperature. The images were acquired using the low vacuum secondary electron detector (LFD) with an accelerating voltage of 20 kV, a spot size of 3, and a working distance of 12–14 mm.

Mechanical and electrical characterization

Hydrogels were kept in tightly sealed containers prior to mechanical and electrical testing to retain their degree of hydration. A universal testing machine (Instron 3369) with a 1000 N load cell was used to characterize the compressive properties of PANI hydrogels. A loading rate of 100% min⁻¹ was used. Due to the high degree of hydration, the hydrogel/compression plate interface has very low friction, frequently causing the testing specimen to slip out from the gap between compression plates. To overcome this issue, a hydrated piece of Kimwipe was placed between the hydrogel/compression plate interface to provide adequate friction and prevent significant specimen movement during compression. Resistance of the hydrogels under compression were collected in situ using a Keithley 2450 sourcemeter. The measurement configuration is illustrated in Fig. S8a (ESI†). The conductivity of the hydrogels was measured using solid pucks in a parallel plate geometry, as depicted in Fig. S8b (ESI†).

Author contributions

R. S. J. and Y. W. conceived the project. R. S. J., J. F., V. H., N. A., I. P. M. F.-M. carried out most experiments. A. G. created most CAD models. K. S. and B. X. conducted morphological characterization. I. M. H. performed ATR-IR spectroscopy. All authors contributed to data analysis and manuscript preparation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank John Misiaszek for assistance with machine building in the early stages of the project. This work is funded by the National Science Foundation-CAREER (DMR-1945664), Beckman Young Investigator Award from the Arnold and Mabel Beckman Foundation, and the University of California, Merced startup fund. I. P. and M. F.-M. acknowledge support from the ACS SEED and UC LEADS fellowships, respectively. ESEM access was provided by the Imaging and Microscopy Facility (IMF) at UC Merced.

References

1. F. Zhao, Y. Shi, L. Pan and G. Yu, Acc. Chem. Res., 2017, 50, 1734–1743.
2. M. Tomczykowa and M. Plonska-Brzezinska, Polymers, 2019, 11, 350.
3. D. Mawad, A. Artzy-Schnirman, J. Tonkin, J. Ramos, S. Inal, M. M. Mahat, N. Darwish, L. Zwi-Dantsis, G. G. Malliaras, J. J. Gooding, A. Lauto and M. M. Stevens, Chem. Mater., 2016, 28, 6080–6088.
4. D. Mawad, E. Stewart, D. L. Officer, T. Romeo, P. Wagner, K. Wagner and G. G. Wallace, Adv. Funct. Mater., 2012, 22, 2692–2699.
5. B. Guo, Z. Ma, L. Pan and Y. Shi, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 1606–1621.
6. D. Zhai, B. Liu, Y. Shi, L. Pan, Y. Wang, W. Li, R. Zhang and G. Yu, ACS Nano, 2013, 7, 3540–3546.
7. C. Ma, Y. Shi, D. A. Pena, L. Peng and G. Yu, Angew. Chem., 2015, 127, 7484–7488.
8. F. Zhao, X. Zhou, Y. Shi, X. Qian, M. Alexander, X. Zhao, S. Mendez, R. Yang, L. Qu and G. Yu, Nat. Nanotechnol., 2018, 13, 489–495.
9. Y. Guo, J. Bae, Z. Fang, P. Li, F. Zhao and G. Yu, Chem. Rev., 2020, 120, 7642–7707.
10. R. Kishi, K. Hiroki, T. Tominaga, K.-I. Sano, H. Okuzaki, J. G. Martinez, T. F. Otero and Y. Osada, J. Polym. Sci., Part B: Polym. Phys., 2012, 50, 790–796.
11. G. Kaur, R. Adhikari, P. Cass, M. Bown and P. Gunatillake, RSC Adv., 2015, 5, 37553–37567.
12. Y. Zhao, B. Zhang, B. Yao, Y. Qiu, Z. Peng, Y. Zhang, Y. Alsaid, I. Frenkel, K. Youssef, Q. Pei and X. He, Matter, 2020, 3, 1196–1210.
13. V. R. Feig, H. Tran, M. Lee and Z. Bao, Nat. Commun., 2018, 9, 2740.
14. A. T. Kleinschmidt and D. J. Lipomi, Acc. Chem. Res., 2018, 51, 3134–3143.
15. J. R. Greer and V. S. Deshpande, MRS Bull., 2019, 44, 750–757.
16. J. U. Surjadi, L. Gao, H. Du, X. Li, X. Xiong, N. X. Fang and Y. Lu, Adv. Eng. Mater., 2019, 21, 1800864.
17. Y. Jiang and Q. Wang, Sci. Rep., 2016, 6, 34147.
18. S. J. Yeo, M. J. Oh and P. J. Yoo, Adv. Mater., 2019, 31, 1803670.
19. R. S. Jordan and Y. Wang, J. Polym. Sci., Part B: Polym. Phys., 2019, 57, 1592–1605.
20. A. W. Rinaldi, M. H. Kunita, M. J. L. Santos, E. Radovanovic, A. F. Rubira and E. M. Girotto, Eur. Polym. J., 2005, 41, 2711–2717.
21. K. Yamada, M. Watanabe and J. Sone, Opt. Rev., 2014, 21, 679–682.
22. K. Yamada, Y. Yamada and J. Sone, Thin Solid Films, 2014, 554, 102–105.
23. C. A. Mire, A. Agrawal, G. G. Wallace, P. Calvert and M. in het Panhuis, J. Mater. Chem., 2011, 21, 2671.
24. H. Yuk, B. Lu, S. Lin, K. Qu, J. Xu, J. Luo and X. Zhao, Nat. Commun., 2020, 11, 1604.
25. J. R. Aggas, S. Abasi, J. F. Phipps, D. A. Podstawczyk and A. Guiseppi-Elie, Biosens. Bioelectron., 2020, 168, 112568.
26. F. B. Holness and A. D. Price, Smart Mater. Struct., 2018, 27, 015006.
27. X. Ding, R. Jia, Z. Gan, Y. Du, D. Wang and X. Xu, Mater. Res. Express, 2020, 7, 055304.
28. E. Fantino, I. Roppolo, D. Zhang, J. Xiao, A. Chiappone, M. Castellino, Q. Guo, C. F. Pirri and J. Yang, Macromol. Mater. Eng., 2018, 303, 1700356.
29. A. T. Cullen and A. D. Price, Synth. Met., 2018, 235, 34–41.
30. Y. Wu, Y. X. Chen, J. Yan, D. Quinn, P. Dong, S. W. Sawyer and P. Soman, Acta Biomater., 2016, 33, 122–130.
31. Y. Wu, Y. X. Chen, J. Yan, S. Yang, P. Dong and P. Soman, J. Mater. Chem. B, 2015, 3, 5352–5360.
32. D. N. Heo, S.-J. Lee, R. Timsina, X. Qiu, N. J. Castro and L. G. Zhang, Mater. Sci. Eng., C, 2019, 99, 582–590.
33. D. Li, J. Huang and R. B. Kaner, Acc. Chem. Res., 2009, 42, 135–145.
34. M. Sezen-Edmonds and Y.-L. Loo, J. Phys. Chem. Lett., 2017, 8, 4530–4539.
35. M. G. Neumann, W. G. Miranda, C. C. Schmitt, F. A. Rueggeberg and I. C. Correa, J. Dent., 2005, 33, 525–532.
36. B. Zhang, S. Li, H. Hingorani, A. Serjouei, L. Larush, A. A. Pawar, W. H. Goh, A. H. Sakhaei, M. Hashimoto, K. Kowsari, S. Magdassi and Q. Ge, J. Mater. Chem. B, 2018, 6, 3246–3253.
37. H. Becker and H. Vogel, Chem. Eng. Technol., 2006, 29, 1227–1231.
38. Y. Wang, H. D. Tran, L. Liao, X. Duan and R. B. Kaner, J. Am. Chem. Soc., 2010, 132, 10365–10373.
39. J.-W. Jeon, Y. Ma, J. F. Mike, L. Shao, P. B. Balbuena and J. L. Lutkenhaus, Phys. Chem. Chem. Phys., 2013, 15, 9654.
40. Z. D. Zujovic, Y. Wang, G. A. Bowmaker and R. B. Kaner, Macromolecules, 2011, 44, 2735–2742.
41. C. Zhu, T. Y.-J. Han, E. B. Duoss, A. M. Golobic, J. D. Kuntz, C. M. Spadaccini and M. A. Worsley, Nat. Commun., 2015, 6, 6962.
42. G. E. Fantner, T. Hassenkam, J. H. Kindt, J. C. Weaver, H. Birkedal, L. Pechenik, J. A. Cutroni, G. A. G. Cidade, G. D. Stucky, D. E. Morse and P. K. Hansma, Nat. Mater., 2005, 4, 612–616.
43. Z. Rao, F. Ershad, A. Almasri, L. Gonzalez, X. Wu and C. Yu, Adv. Mater. Technol., 2020, 5, 2000233.
44. Y. Ling, T. An, L. W. Yap, B. Zhu, S. Gong and W. Cheng, Adv. Mater., 2020, 32, 1904664.
45. T. L. Sun, T. Kurokawa, S. Kuroda, A. B. Ihsan, T. Akasaki, K. Sato, Md. A. Haque, T. Nakajima and J. P. Gong, Nat. Mater., 2013, 12, 932–937.
46. C. J. Pérez-Martínez, S. D. M. Chávez, T. del Castillo-Castro, T. E. L. Ceniceros, M. M. Castillo-Ortega, D. E. Rodríguez-Félix and J. C. G. Ruiz, React. Funct. Polym., 2016, 100, 12–17.
47. V. Guarino, M. A. Alvarez-Perez, A. Borriello, T. Napolitano and L. Ambrosio, Adv. Healthcare Mater., 2013, 2, 218–227.
48. X. Ren, Q. Yang, D. Yang, Y. Liang, J. Dong, Y. Ren, X. Lu, L. Xue, L. Li and L. Xu, Colloids Surf., A, 2018, 549, 50–57.
49. Z. P. Gu, K. Huang, Y. Luo, L. Zhang, T. Kuang, Z. Chen and G. Liao, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2018, 10, e1520.
50. T. Nonoyama and J. P. Gong, Annu. Rev. Chem. Biomol. Eng., 2021, 12, 7.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1tb00877c

‡ Equal contribution.

---