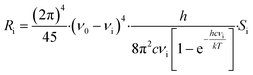Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
New insights into the biphasic “CO-free” Pauson–Khand cyclisation reaction through combined in situ spectroscopy and multiple linear regression modelling†
Robert
Geitner‡
 *a,
Tianbai
Huang
b,
Stephan
Kupfer
*a,
Tianbai
Huang
b,
Stephan
Kupfer
 b,
Stefanie
Gräfe
b,
Stefanie
Gräfe
 b,
Florian
Meirer
a and
Bert M.
Weckhuysen
b,
Florian
Meirer
a and
Bert M.
Weckhuysen
 *a
*a
aInorganic Chemistry and Catalysis Group, Debye Institute for Nanomaterials Science, Utrecht University, Universiteitsweg 99, 3584 CG Utrecht, The Netherlands. E-mail: robert.geitner@uni-jena.de; b.m.weckhuysen@uu.nl
bInstitute for Physical Chemistry and Abbe Center of Photonics, Friedrich Schiller University Jena, Helmholtzweg 4, 07743, Jena, Germany
First published on 6th January 2021
Abstract
“CO-free” carbonylations are catalytic reactions, which strive to replace toxic synthesis gas with less harmful surrogate molecules like formaldehyde. This study sheds light on the mechanism of the biphasic, Rh-catalysed Pauson–Khand type cyclisation reaction by applying in situ Raman spectroscopy together with NMR, dynamic light scattering measurements, and quantum chemical calculations. The reaction is particularly challenging to analyse as the Rh-catalyst features different ligands in the aqueous and organic phase. To tackle this challenge, a novel approach was designed, coupling in situ Raman spectroscopy with an advanced data analysis model in the form of multiple linear regression. This fruitful combination of highly specific vibrational spectroscopy with state-of-the-art data analysis allowed not only identification of a new reaction mechanism, but also identification of parameters to accelerate the “CO-free” Pauson–Khand cyclisation, i.e. using mononuclear Rh–phosphine complexes with labile ligands, small organic micelles formed by an increased surfactant concentration, low formaldehyde concentration, and elevated temperature. This novel knowledge-driven optimisation protocol is superior to simple qualitative optimization routines and can be transferred to other reactions and spectroscopy techniques.
1. Introduction
Carbonylation reactions are cornerstones of pharmaceutical and chemical industry employed for the production of highly relevant synthetic products, such as methyl propionate,1 ibuprofen,2 and vanillin,3 at the multi-million tonnes scale annually. Usually, carbonylation reactions take place in the liquid phase employing a homogeneous catalyst. This makes, to the best of our knowledge, carbonylation reactions one of the most important applications of homogeneous catalysis in industry.4On an industrial level, carbonylation reactions are conducted using a synthesis gas feedstock – a mixture of CO and H2 gas.5 This feedstock is easily generated via steam reforming, but requires adequate safety measures to handle the toxic and flammable gas mixture. These properties render synthesis gas unattractive for carbonylations in the scope of pharmaceutical products and intermediates as well as speciality chemicals, as small chemical plants or laboratories do not always have the proper infrastructure to safely handle a synthesis gas stream.
As carbonylation reactions are very useful transformations in organic synthesis, considerable efforts have been directed towards the development of “CO-free” carbonylation reactions where the synthesis gas is replaced by less harmful surrogate molecules that are safe to handle on a laboratory scale.6 The most interesting CO surrogate molecules are formaldehyde, formed from paraformaldehyde (PFA),7,8 and formic acid9 as they are very atom efficient and can be formally seen as CO + H2 or H2O, respectively. The role of the utilized transition metal catalysts is thus twofold. Firstly, they decompose the surrogate molecule into a CO (equivalent) species, and secondly, they insert this species into the organic product.9 The concept of “CO-free” carbonylations has e.g. been successfully applied in the carbonylation of alkenes,10 the carbonylations of aryl bromides,11 or the synthesis of 9-fluorenones.12
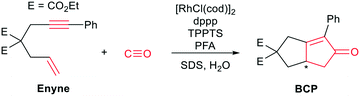
One of the earliest works on “CO-free” carbonylations was published by Morimoto et al., describing the use of Rh–phosphine complexes in a biphasic Pauson–Khand type reaction for the production of bicyclopentenone compounds (see Scheme 1).13 This reaction features many interesting concepts, such as the use of two different phosphine ligands (i.e., 1,3-bis(diphenylphosphino)propane (dppp) and 3,3′,3′′-phosphanetriyltris(benzenesulfonic acid)trisodium salt (TPPTS)) to separate the formaldehyde decomposition and the carbonylation reaction by using water and the organic substrate to form a biphasic reaction mixture. The suspension is further stabilized by sodium dodecyl sulphate (SDS), which acts as a surfactant and enhances the reaction rate. However, the underlying reaction mechanism has not been investigated in detail.
Recently, we have studied Pd-catalysed “CO-free” carbonylation reactions and found that, to our own surprise, no CO is formed during this reaction, and postulated a new formyl group-based mechanism.14 The Rh-catalysed Pauson–Khand type reaction, reported by Morimoto et al.,13 caught our attention as it can be compared to the previously studied Pd-catalysed reaction. Hence, in this work, we investigate the reaction mechanism of the “CO-free” Pauson–Khand type reaction to gain new insight into “CO-free” carbonylation reactions and to enable a knowledge-driven optimisation of the Rh-catalysed reaction. However, its biphasic nature and the application of phase-specific phosphine ligands makes it in particular challenging to characterise intermediates by in situ spectroscopy. In order to tackle this obstacle, we have developed a new analysis approach, which is based on in situ bulk Raman spectroscopy coupled with advanced data analysis and a multiple linear regression model. This allowed us to evaluate the influence of the reaction conditions (i.e., temperature, metal precursor, ligand, (co)-substrate and surfactant concentration) on the reaction kinetics. Furthermore, the molecular origin of the influencing parameters was studied using NMR spectroscopy as well as dynamic light scattering (DLS). Finally, a new reaction mechanism is proposed that was verified by density functional theory (DFT) calculations. In what follows, we present our novel analytical approach and illustrate our new mechanistic findings for the “CO-free” Rh-catalysed Pauson–Khand type cyclisation.
2. Methods
2.1 Chemicals and materials
All reactions were carried out under Ar atmosphere using standard Schlenk technique. [Rh(cod)Cl]2 (cod = 1,5-cyclooctadiene), 1,3-bis(diphenylphosphino)propane (dppp), 3,3′,3′′-phosphanetriyltris(benzenesulfonic acid)trisodium salt (TPPTS), 37 w% formaldehyde solution in H2O with 10–15 w% MeOH, sodium dodecyl sulphate (SDS), diethylallylmalonate and 3-phenyl-2-propyne-1-ol were purchased from Sigma Aldrich and used without further purification. Paraformaldehyde was obtained from ACROS Chemicals, 13C-paraformaldehyde was purchased from Eurisotope. Both were used without further purification. 3-Bromo-1-phenyl-1-propyne,15 diethyl-2-allyl-2-(3-phenylprop-2-yn-1-yl)malonate (enyne),16 [Rh(TPPTS)3Cl]17 and [Rh(dppp)2Cl]18 were synthesized according to known or slightly modified procedures. H2O was purified by an ion exchanger and degassed with argon for 2 h. DCCl3 and D2O were purchased from Sigma Aldrich. DCCl3 was degassed via freeze–pump–thaw cycles and dried over molsieves (3 Å).2.2 Raman spectroscopy
Raman spectra were recorded using a Renishaw InVia Raman microscope (Renishaw, UK), a 532 nm diode laser, a 50× objective (0.75 NA, Leica, Germany) and a grid with 1200 lines mm−1.For reference purposes and the subsequent data analysis, 32 Raman spectra with an integration time of 10 s were taken of 3-phenyl-2-propyne-1-ol, diethylallylmalonate, H2O, H2O in a microwave tube, enyne, diethyl-5-oxo-6-phenyl-3,3a,4,5-tetrahydropentalene-2,2(1H)-dicarboxylate (BCP), dppp, TPPTS, SDS, [Rh(cod)Cl]2, [Rh(PPh3)3Cl], [Rh(TPPTS)3Cl], [Rh(dppp)2Cl] and formaldehyde in H2O (37 w%) (Fig. S1–S14†) The reference spectra were recorded between 250 and 4000 cm−1.
For a typical in situ Raman experiment, a microwave vial (Biotage, Cardiff, United Kingdom) was charged with [Rh(cod)Cl]2, dppp, TPPTS, paraformaldehyde, SDS and a stirring bar before being evacuated and flushed with argon three times. Degassed H2O (5 mL) and enyne were added to the microwave vial under argon atmosphere before the vial was sealed. The utilized amounts for each individual in situ experiment are summarized in Table S1.† The microwave vial was heated to the intended measurement temperature while Raman spectra were recorded before (3 spectra), during and after the heating period. The samples were heated using a sand bath on a feedback-controlled heating plate (IKA, Germany). Care should be taken as the vial auto pressurizes at elevated temperatures!
For each in situ measurement, 340 Raman spectra between 250–3400 cm−1 with an integration time of 30 s were recorded. The power at the samples was 30.1 mW. To validate the linear relationship between the enyne concentration and its Raman signal at 2238 cm−1, a calibration experiment was performed. For this experiment, 9 Raman spectra with an integration time of 10 s, each were collected from different enyne/H2O suspensions (0.00, 0.04, 0.11, 0.22, 0.37, 0.54, 0.81 mmol L−1). The result is depicted in Fig. S21.†
The description of the subsequent data analysis procedure is summarized in Scheme 2 as well as in Fig. S15 and described in detail in the ESI.†
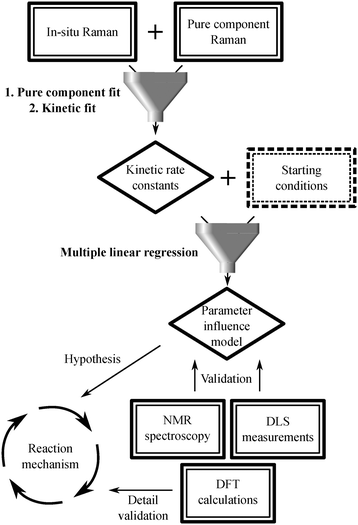 | ||
| Scheme 2 Scheme representing how the different measurement techniques funnel into the data analysis procedure. | ||
2.3 NMR spectroscopy
The NMR spectra were recorded on an Agilent MRF400 and on a Varian VNMR-S-400 400 MHz NMR spectrometer. 1H-NMR spectra were recorded with 8 scans, 31P-NMR spectra with 128 scans and 13C-NMR spectra with 256 scans. The NMR spectra were processed with MestReNova (10.0.2–15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 465).19 The 1H-NMR spectra were referenced to the residual solvent signal (DCCl3: 7.26 ppm, D2O: 4.87 ppm).20 All NMR spectra were background corrected with a third order Bernstein polynomial.21
465).19 The 1H-NMR spectra were referenced to the residual solvent signal (DCCl3: 7.26 ppm, D2O: 4.87 ppm).20 All NMR spectra were background corrected with a third order Bernstein polynomial.21
For the coordination experiments between [Rh(cod)Cl]2 and dppp or TPPTS, [Rh(cod)Cl]2 (10.00 or 5.50 mg) was mixed with different amounts of dppp in 0.5 mL DCCl3 (0.5, 1, 2, 3, 4, 5 equivalents of dppp) or TPPTS in 0.5 mL D2O (0.5, 1, 2, 3, 4, 5 equivalents of TPPTS) under inert conditions, respectively (see Fig. 2b and d, S26 and S27†).
For an ex situ NMR study [Rh(cod)Cl]2 (1.62 mg), dppp (3.34 mg) and 13C-paraformaldehyde (10.01 mg) were suspended in a quick pressure valve 5 mm OD NMR sample tube (Wilmad-LabGlass, Vineland, New Jersey) in DCCl3 (0.5 mL) before D2O (50 μL) was added. 1H, 13C and 31P NMR spectra were recorded before the yellow suspension was heated to 100 °C and after heating for 990 min. The NMR spectra prove the quantitative conversion of the initial Rh–dppp complexes into [Rh(dppp)(CO)2]Cl (see Fig. S28†).
All NMR spectra show small contributions from the oxidized phosphine ligands and trace amounts of water. These contributions are unfortunately unavoidable and stem from the sample preparation process.
A complete NMR signal assignment for 3-bromo-1-phenyl-1-propyne, enyne and BCP is given as they were previously not provided:
13C{1H}-NMR 100 MHz (d-HCCl3): 15.4 (CH2), 84.4 (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C), 86.8 (C
C), 86.8 (C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C), 122.2 (i-C–Ph), 128.4 (C–Ph), 128.9 (C–Ph), 131.9 (o/m-C–Ph) ppm.
C), 122.2 (i-C–Ph), 128.4 (C–Ph), 128.9 (C–Ph), 131.9 (o/m-C–Ph) ppm.
Enyne. 1H-NMR 400 MHz (d-HCCl3): 1.16 (t, J = 7 Hz, 6H, CH3), 2.83 (d, J = 8 Hz, 2H, CH2–CH
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), 2.97 (s, 2H, CH2–C
CH2), 2.97 (s, 2H, CH2–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C), 4.12 (q, J = 7 Hz, 4H, CH2–O), 5.07 (dd, J = 10, 2 Hz, 1H, CH2–CH
C), 4.12 (q, J = 7 Hz, 4H, CH2–O), 5.07 (dd, J = 10, 2 Hz, 1H, CH2–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2–(E)), 5.15 (dd, J = 17, 2 Hz, 1H, CH2–CH
CH2–(E)), 5.15 (dd, J = 17, 2 Hz, 1H, CH2–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2–(Z)), 5.64 (ddt, J = 17, 10, 8 Hz, 1H, CH2–CH
CH2–(Z)), 5.64 (ddt, J = 17, 10, 8 Hz, 1H, CH2–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), 7.17 (m, 3H, CH–Ph), 7.29 (m, 2H, o/m-CH–Ph) ppm.
CH2), 7.17 (m, 3H, CH–Ph), 7.29 (m, 2H, o/m-CH–Ph) ppm.
13C{1H}-NMR 100 MHz (d-HCCl3): 14.0 (CH3), 23.5 (CH2–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C), 36.6 (CH2–CH
C), 36.6 (CH2–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), 56.9 (C–(C
CH2), 56.9 (C–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)2), 61.4 (CH2–O), 83.5 (CH2–C
O)2), 61.4 (CH2–O), 83.5 (CH2–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C), 84.4 (CH2–C
C), 84.4 (CH2–C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C), 119.5 (CH2–CH
C), 119.5 (CH2–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), 123.2 (i-C–Ph), 127.9 (p-C–Ph), 128.1 (o/m-C–Ph), 131.5 (o/m-C–Ph), 132.0 (CH2–CH
CH2), 123.2 (i-C–Ph), 127.9 (p-C–Ph), 128.1 (o/m-C–Ph), 131.5 (o/m-C–Ph), 132.0 (CH2–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2), 169.5 ((C
CH2), 169.5 ((C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O) ppm.
O)O) ppm.
BCP. 1H-NMR 400 MHz (d-HCCl3): 1.22 (t, J = 7 Hz, 3H, CH3), 1.31 (t, J = 7 Hz, 3H, C′H3), 1.76 (m, 1H, C–CH2–C*H), 2.31 (dd, J = 18, 3 Hz, 1H, C*H–CH2–C
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 2.83 (m, 1H, C–CH2–C*H), 2.83 (m, J = 18, 3 Hz, 1H, C*H–CH2–C
O), 2.83 (m, 1H, C–CH2–C*H), 2.83 (m, J = 18, 3 Hz, 1H, C*H–CH2–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 3.14 (m, 1H, C*H), 3.29 (d, J = 18 Hz, 1H, C–CH2–C
O), 3.14 (m, 1H, C*H), 3.29 (d, J = 18 Hz, 1H, C–CH2–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 3.65 (d, J = 18 Hz, 1H, C–CH2–C
C), 3.65 (d, J = 18 Hz, 1H, C–CH2–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 4.16 (q, J = 7 Hz, 2H, O–CH3), 4.28 (q, J = 7 Hz, 2H, O–C′H2), 7.33 (m, 1H, p-CH–Ph), 7.40 (m, 2H, m-CH–Ph), 7.56 (m, 2H, o-CH–Ph) ppm.
C), 4.16 (q, J = 7 Hz, 2H, O–CH3), 4.28 (q, J = 7 Hz, 2H, O–C′H2), 7.33 (m, 1H, p-CH–Ph), 7.40 (m, 2H, m-CH–Ph), 7.56 (m, 2H, o-CH–Ph) ppm.
13C{1H}-NMR 100 MHz (d-HCCl3): 14.1 (CH3), 14.2 (C′H3), 36.0 (C–CH2–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C), 38.9 (C–CH2–C*H), 42.8 (C*H–CH2–C
C), 38.9 (C–CH2–C*H), 42.8 (C*H–CH2–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 43.0 (C*H), 61.4 (C–(C
O), 43.0 (C*H), 61.4 (C–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)2), 62.1 (CH2–O), 62.3 (C′H2–O), 128.3 (p-C–Ph), 128.6 (m-C–Ph), 128.6 (o-C–Ph), 131.0 (i-C–Ph), 135.6 (C
O)2), 62.1 (CH2–O), 62.3 (C′H2–O), 128.3 (p-C–Ph), 128.6 (m-C–Ph), 128.6 (o-C–Ph), 131.0 (i-C–Ph), 135.6 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C6H5), 170.8 ((C′
C–C6H5), 170.8 ((C′![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O), 171.7 ((C
O)O), 171.7 ((C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O), 179.1 (C
O)O), 179.1 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C6H5), 207.3 (C
C–C6H5), 207.3 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) ppm.
O) ppm.
A tentative assignment for [Rh(dppp)(CO)2]Cl is given:
31P{1H}-NMR 161 MHz (d-HCCl3): 203.3 (1JRh–P = 127.5 Hz, 2JP–C = 7.2 Hz) ppm.
2.4 Dynamic light scattering
Dynamic light scattering (DLS) was measured on a Zetasizer Nano-S from Malvern Panalytical (Malvern, United Kingdom). The accompanying Zetasizer Software (version 7.13) automatically controlled the measurement volume as well as the light intensity. The subsequent autocorrelation and fitting procedure were also done via the measurement software. The samples were prepared by mixing enyne (0.08 mL) with H2O (2.0 mL) and different amounts of SDS (0, 37.22, 72.47, 111.01, 146.69, 216.27 and 288.16 mg). The samples were heated to 100 °C for 30 min and stirred at 800 rounds per minute. The samples were subsequently diluted at a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 with H2O before being measured at 25.0 °C.
6 with H2O before being measured at 25.0 °C.
2.5 Quantum chemical simulations
All quantum chemical simulations were performed using the Gaussian16 software.22 The ground state equilibrium structures and electronic properties of the rhodium complexes, i.e. [Rh(TPPTS)3]8− (I.1, fully deprotonated), [Rh(TPPTS)3(H2O)]8−, [Rh(TPPTS)3(HCHO)]8−, [Rh(TPPTS)3(CHO)(H)]8− (I.2), mer-cis-[Rh(TPPTS)3(CO)(H)2]8− (I.3), [Rh(TPPTS)3(CO)]8− (I.4), [Rh(dppp)2]+ (II.1 and III.1), [Rh(dppp)2(CHO)(H)]+ (II.2a), mer-cis-[Rh(dppp)(κ1-dppp)(CHO)(H)]+ (II.2b), mer-cis-[Rh(dppp)(κ1-dppp)(CO)(H)2]+ (II.3), square-[Rh(dppp)(κ1-dppp)(CO)]+ (II.4a), bipy-[Rh(dppp)2(CO)]+ (II.4b), mer-[Rh(dppp)(κ1-dppp)(enyne)]+ (III.2b), mer-cis-[Rh(dppp)(κ1-dppp)(enyne)(CO)]+ (III.3) and mer-[Rh(dppp)(κ1-dppp)(CO–enyne)]+ (III.4) as well as of enyne, BCP, dppp, TPPTS, CO, H2 and HCHO were obtained at the density functional (DFT) level of theory utilizing the B3LYP XC functional.23 The def2-SVP basis set as well as the respective core potentials were applied for all atoms.24 A subsequent vibrational analysis was carried out for each optimized ground state structure to verify that a minimum on the potential energy (hyper-)surface (PES) was obtained. To correct for the lack of anharmonicity and for the approximate description of electron correlation, the harmonic frequencies were scaled by a factor of 0.95.25 All calculations were performed including D3 dispersion correction with Becke–Johnson damping.26An analogous computational setup was applied for the optimisation of transition states (TSs) and the intrinsic reaction coordinate (IRC) calculations, accordingly. For the TS search, an initial guess in the vicinity of the saddle point was at first obtained via the nudged elastic band (NEB)27 method as implemented in physisphus28 with xtb.29 Thereafter, the TSs were obtained in Gaussian16 via the Berny algorithm,30 followed by a vibrational analysis to verify that a first-order saddle point on the PES was obtained. From the optimized TS structures, the IRC calculations based on a local quadratic approximation (LQA) algorithm31 were performed, in order to verify that the TSs were located in the minimal energy path (MEP) connecting the desired educt and product states.
Raman intensities were obtained based on the calculated Raman activities using the following expression:32
3. Results and discussion
3.1 In situ Raman spectroscopy
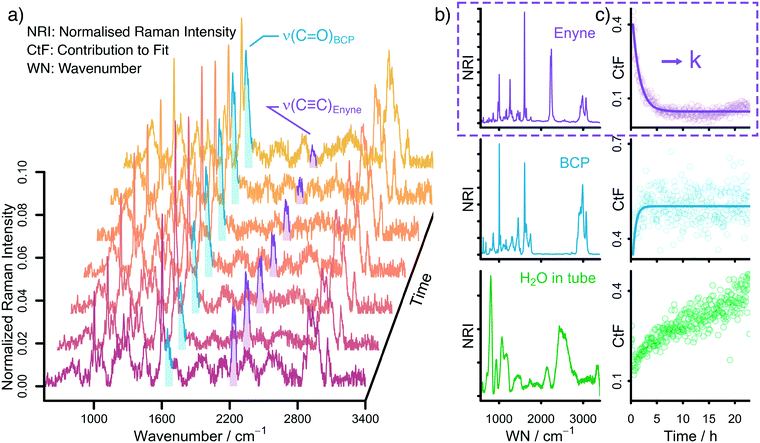
Raman spectroscopy is ideally suited to follow the changing concentrations during the transformation of an enyne into a bicyclopentenone. The substrate features a distinct alkynyl group that gives a strong Raman signal at 2238 cm−1. The product includes a newly formed carbonyl group, which exhibits a vibrational band at 1690 cm−1. A set of in situ Raman spectra with the aforementioned bands highlighted can be seen in Fig. 1.During the data acquisition it became clear that the Raman spectra, due to the complex nature of the reaction process, suffered from poor signal-to-noise ratios (SNRs). Thus, a simple single band integration was susceptible to errors and consequently featured large standard errors. To overcome this problem, a new and more advanced data analysis scheme was developed. Each individual time-dependent in situ Raman spectrum was linearly fitted by using the Raman spectra of the pure components. Initially, all compounds (Rh salt, phosphine ligands, enyne, BCP, H2O, SDS, PFA and formaldehyde) were considered for the fit (see Fig. S16†). However, most components did not contribute significantly to the overall Raman signal, therefore we analysed which components could be neglected from the fitting procedure without significantly influencing the quality of the final fit (see Fig. S18†). It was found that only the substrate (enyne), the product (BCP) and the solvent (H2O) were necessary to reliably reproduce the in situ Raman spectra (see Fig. 1, Fig. S17 and S19†). This finding was to be expected as these three components feature the largest concentration in the reaction solution. The remaining components are merely present as traces, therefore their contribution to the in situ Raman spectra is marginal.
The fitting approach was cross validated by principal component analysis (PCA) (see Fig. S20†) and multivariate curve resolution (MCR). The first two pure component spectra extracted by MCR are very similar to the Raman spectra of enyne and BCP (see Fig. S23 and S24†) while the PCA revealed that the majority of the variance in the datasets is described by three components.
The linear fitting procedure results in time-dependent coefficient profiles that are linked to the concentration of enyne, BCP, and H2O (see Fig. 1 and S22†). As the reaction proceeds, the contribution of enyne to the fit decreases while simultaneously the contribution from BCP increases. Thus, the extracted fit coefficients can be used to follow the reaction progress. Interestingly the contribution of H2O also increases. This is effect does not stem from a change in water concentration but is rather associated with the change in Raman cross scattering section of the reaction solution when enyne is consumed in favour of BCP. The Raman cross scattering section of enyne is higher than the one of BCP. Thus, at first the organic molecules contribute more to the Raman signal of the reaction solution than H2O but as the reaction proceeds the Raman cross section of the organic molecules decreases as enyne is transformed into BCP and therefore the contribution of water to the overall Raman signal increases. Nevertheless, the fit coefficients of the organic molecules are proportional to their concentration.
For further analysis, the coefficient profiles of enyne were fitted with a first-order kinetic exponential function to extract a kinetic rate constant k from each in situ measurement (see ESI† for details). The first-order kinetic of the reaction was cross validated by integrating the ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C) band at 2238 cm−1 by summing up the relevant Raman channel intensities to follow the concentration of enyne (see Fig. S22†).
C) band at 2238 cm−1 by summing up the relevant Raman channel intensities to follow the concentration of enyne (see Fig. S22†).
3.2 Multiple linear regression
With the kinetic rate constants k at hand, the influence of the initial reaction conditions on the reaction rate was analysed, i.e. how to tune the experimental conditions to accelerate the investigated Pauson–Khand type cyclisation. Morimoto et al. performed some basic optimisation and found: i) a combination of dppp/TPPTS is more effective than dppp alone, ii) TPPTS alone is not able to catalyse the carbonylation, and iii) an increased SDS concentration is favourable for the reaction.13 However, the molecular origin associated to the altered reactivity was not investigated in-depth.To enable a knowledge-driven optimisation procedure, we used a multiple linear regression model to predict the kinetic rate constants k from the reaction conditions. The basic idea behind the approach is to vary the reaction conditions and evaluate their impact on the reaction's rate constant. In physical chemistry, this increase in reaction rate is described by an increase in the associated kinetic rate constant k which is available from the in situ Raman measurements. By using a multiple linear regression model, multiple experiments can be evaluated at the same time, making it possible to vary multiple reaction conditions in one experiment while still being able to extract the influence of each individual reaction condition on the kinetic rate constant k. Thus, the multiple linear regression model enables an overarching multi-parameter evaluation on the reaction conditions via in situ Raman experiments.
The seven reaction conditions considered for the multiple linear regression model are the reaction temperature as well as the starting molar concentrations (in units of L mmol−1) of [Rh(cod)Cl]2, dppp, TPPTS, SDS, PFA and enyne. Formally, the model is described by the following equation:
| k = aT·T + aRh·[Rh]0 + adppp·[dppp]0 + aTPPTS·[TPPTS]0 + aSDS·[SDS]0 + aPFA·[PFA]0 + aEnyne·[Enyne]0 |
The obtained parameters ax for each reaction condition are summarized in Table 1. The sign of ax indicates if an increased or decreased reaction rate is observed under the altered conditions, i.e. temperature or concentrations, respectively.
| Name | Value/unit |
|---|---|
| a T | +7.71 10−9/s−1 K−1 |
| a Rh | +6.54 10−3/L s−1 mmol−1 |
| a dppp | −4.22 10−3/L s−1 mmol−1 |
| a TPPTS | −1.06 10−3/L s−1 mmol−1 |
| a SDS | +1.19 10−4/L s−1 mmol−1 |
| a Enyne | −2.97 10−5/L s−1 mmol−1 |
| a PFA | −1.91 10−4/L s−1 mmol−1 |
The influence of the temperature on the reaction is straight forward: a higher temperature results in a faster reaction rate (aT > 0). The influence of the remaining reaction conditions is not quite as obvious. Increasing the Rh concentration has a positive influence on the reaction rate (aRh > 0) while an increasing phosphine ligand concentration has a negative effect (adppp < 0, aTPPTS < 0). An increased SDS concentration accelerates the reaction (aSDS > 0), while large amounts of enyne substrate and paraformaldehyde slow the reaction down (aEnyne < 0, aPFA < 0,).
When comparing the linear influence parameters in a quantitative fashion, it becomes evident that [Rh(cod)Cl]2, dppp and TPPTS concentrations have a major impact as the rate constant is increased by one or even two orders of magnitudes, while the influence of the SDS, enyne and PFA concentrations is less prominent. This is not surprising, as the formed Rh–phosphine complexes play the key role in enabling the reaction.
It is very remarkable that this type of information can be extracted from bulk in situ Raman measurements. This was only possible due to the introduced advanced data analysis procedure which allowed to rationalise the kinetic rate constant k by a linear fit of in situ Raman measurements followed by a multiple linear regression – linking the experimental reaction conditions with the reaction rate. This analysis approach is a clear improvement over the simple qualitative variation of experimental parameters without in situ spectroscopy. The presented approach is not limited to the Rh-catalysed Pauson–Khand cyclisation or tied to the use of Raman spectroscopy presented here but can be extend to other reactions and spectroscopic techniques – as long as the rate of the reaction of interest can be linked to its experimental conditions.
3.3 Nuclear magnetic resonance and dynamic light scattering
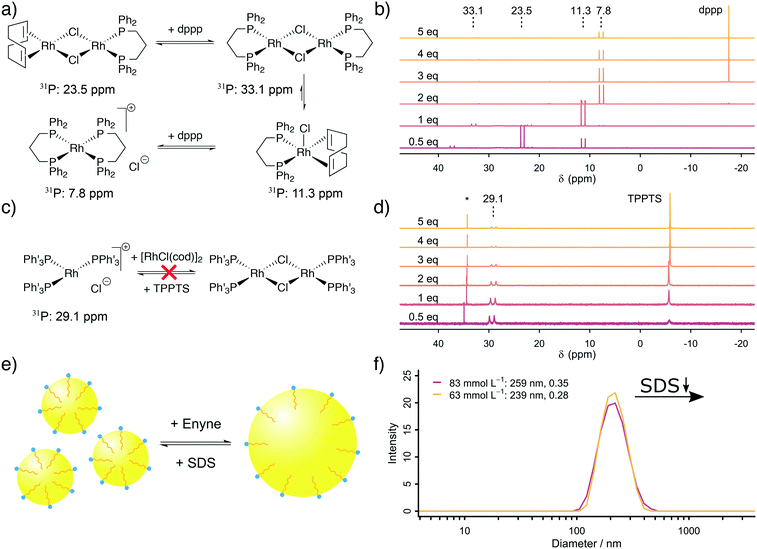
The next step was to address the molecular origin for the observed influence of the reaction conditions on the reaction rate. The influencing parameters can be grouped as follows: firstly, the Rh, TPPTS and dppp concentration are associated with the active catalytic species, secondly, the substrate and SDS concentrations are linked with the exchange rate between the organic and aqueous phase and finally, the formaldehyde and substrate concentrations are important for the ratio between CO formation and Pauson–Khand type carbonylation.Firstly, our explanation on the positive influence of an increasing Rh concentration and the negative influence of increased phosphine ligand concentrations on the reaction rate is the existence of multiple equilibria between mono- and dinuclear Rh–phosphine complexes. We further studied the Rh–dppp equilibria by using 31P NMR spectroscopy (see Fig. 2a and b). The NMR spectra reveal a signal at 23.5 ppm (1JRh–P = 112 Hz) at sub-stochiometric dppp concentrations, which changes into a signal at 11.3 ppm (1JRh–P = 121 Hz) with a small signal at 33.1 ppm (1JRh–P = 135 Hz) at a Rh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) dppp ratio of 1
dppp ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which transforms into a signal at 7.8 ppm (1JRh–P = 131 Hz) at higher dppp concentrations. In accordance with Heller et al.,34 the signals are assigned to [Rh(cod)(dppp)(μ2-Cl)2], [Rh(cod)(dppp)(Cl)], [Rh(dppp)(μ2-Cl)]2 and [Rh(dppp)2]Cl, respectively. Therefore, the NMR spectra clearly show how an increasing dppp concentration forces the formation of more stable Rh–dppp complexes. Our interpretation of the kinetic results and the NMR experiments is that a lower dppp concentration enables the coordination of labile cod ligands, which can be easily displaced when either HCHO or enyne approach the complex.
1, which transforms into a signal at 7.8 ppm (1JRh–P = 131 Hz) at higher dppp concentrations. In accordance with Heller et al.,34 the signals are assigned to [Rh(cod)(dppp)(μ2-Cl)2], [Rh(cod)(dppp)(Cl)], [Rh(dppp)(μ2-Cl)]2 and [Rh(dppp)2]Cl, respectively. Therefore, the NMR spectra clearly show how an increasing dppp concentration forces the formation of more stable Rh–dppp complexes. Our interpretation of the kinetic results and the NMR experiments is that a lower dppp concentration enables the coordination of labile cod ligands, which can be easily displaced when either HCHO or enyne approach the complex.
A similar experiment with TPPTS was conducted (see Fig. 2c and d). Surprisingly, only the mononuclear complex [Rh(TPPTS)3]Cl at 29.1 ppm (1JRh–P = 150.0 Hz)17 is visible in the 31P NMR spectra, independent of the TPPTS concentration. This finding can be explained by the observation that excess [Rh(cod)Cl]2 is not soluble in D2O. Thus, only as much Rh+ is present in the aqueous phase as there is TPPTS to form [Rh(TPPTS)3]Cl. Consequently, the negative influence of an increasing TPPTS concentration can be explained by an increasing tendency to leech Rh+ from the organic phase into the aqueous phase, which, in turn, reduces the amount of catalytically active Rh–dppp complexes. We conclude from our kinetic analysis based on in situ Raman spectroscopy and the supporting NMR experiments that [Rh(cod)(dppp)(Cl)] is more active than the [Rh(dppp)2]Cl in the Pauson–Khand type carbonylation reaction, and that the mononuclear complex [Rh(TPPTS)3]Cl is the catalytically active species in the decomposition of formaldehyde in the aqueous phase.
Secondly, an increased SDS concentration leads to the formation of smaller organic micelles in the aqueous phase. This hypothesis was proven based on DLS measurements. The DLS experiments reveal that at high SDS concentrations, micelles with an average diameter of 250 nm are formed from the organic substrate in the aqueous environment (see Fig. 2e and f). Below a critical SDS concentration, which lays between 42.4 and 62.5 mmol L−1, the micelles are instable, causing them to aggregate and form larger bubbles which are too large (d > 10 μm) to be measured by DLS. The same effect is observed when the relative enyne concentration increases, leading to larger bubbles. This change in average micelle diameter from >10 μm to 250 nm with increasing SDS concentration leads to an increase in the aqueous–organic exchange surface by a factor of >40. The positive influence of an increased SDS concentration was also observed by Morimoto et al. although they did not explore its origin.13 In line with their proposed mechanism (formaldehyde decomposition in the aqueous phase, carbonylation in the organic phase), we propose a molecular exchange across the aqueous–organic interface, which is enhanced by a larger micellular surface.
Finally, a large formaldehyde concentration – stemming from a large initial PFA concentration7 – is competitively hindering the carbonylation reaction by blocking Rh–dppp complexes. As Rh–dppp complexes are able to catalyse the Pauson–Khand cyclisation and the HCHO decomposition while Rh–TPPTS complexes can only catalyse the HCHO decomposition, the availability of Rh–dppp complexes is crucial for the overall reaction progress. NMR experiments on the decomposition of formaldehyde reveal that not merely [Rh(TPPTS)3]Cl is forming CO from HCHO but [Rh(dppp)2]Cl yields [Rh(dppp)(CO)2]+ (ref. 35) when CO is formed from HCHO (see Fig. S28† for 13C and 31P NMR spectra). Thus, an excess of formaldehyde can suppress the desired carbonylation reaction by reacting more efficiently with Rh–dppp complexes in comparison to the enyne substrate. Based on the NMR spectra, we propose that the structure of [Rh(dppp)(CO)2]+ is either trans-square planar – which seems unlikely with dppp as a ligand – or the structure is labile on the NMR time scale. Both hypotheses allow to explain the origin of triplets observed in the 13C and 31P NMR spectra.
In conclusion, the Rh-catalysed Pauson–Khand type reaction can be improved by i) an elevated temperature, ii) an excess of Rh+ favouring the formation of catalytically active complexes, iii) the formation of small micelles by an excess of SDS and iv) avoiding an excess of HCHO, which would block all active Rh centres.
3.4 Proposed mechanism and quantum chemical simulations
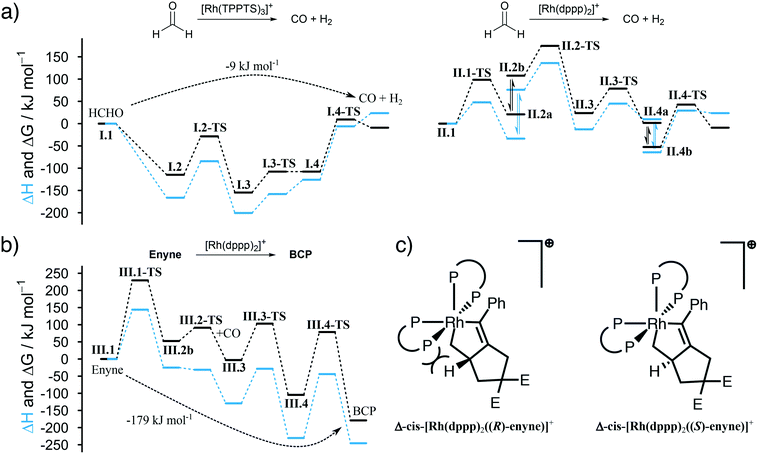
We summarize the results, obtained by in situ Raman spectroscopy, NMR and DLS, in a newly proposed mechanism, which is illustrated in Scheme 3. The catalytic reaction is initiated with the decomposition of formaldehyde at either [Rh(TPPTS)3]+ (I.1, cycle I in Scheme 3) or [Rh(dppp)2]+ (II.1, cycle II). Both complexes activate the C–H bond in HCHO during an oxidative addition (I.2 and II.2). The resulting formyl group subsequently decomposes into CO and a hydride, resulting in octahedral Rh(III) complexes I.3 and II.3. These complexes reductively eliminate H2 (I.4 and II.4) and finally release a CO molecule. Both cycles predominately proceed in the aqueous phase. Therefore, it shall be noted that the open coordination sites shown in Scheme 3 are most likely occupied by H2O molecules, as also suggested by DFT simulations comparing the stabilisation on the respective Rh species with vacant coordination in the presence of H2O, HCHO or CO (ΔG = −85, −83 and −23 kJ mol−1 respectively vs. [Rh(TPPTS)3]+ with a vacant coordination side, ΔH = −114, −97 and −56 kJ mol−1).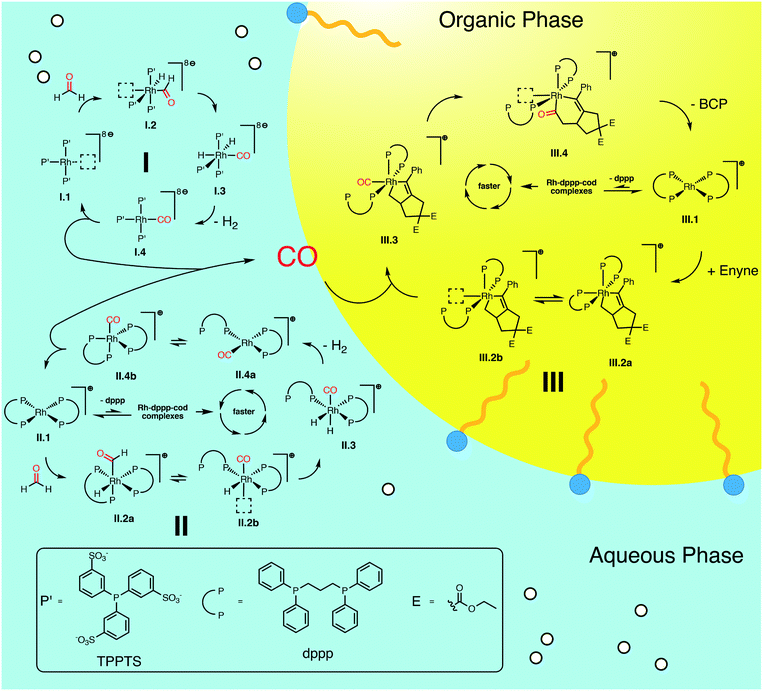 | ||
| Scheme 3 Proposed catalytic cycles for the Rh-catalysed Pauson–Khand type “CO-free” carbonylation. Cycle I and II happen preferably in the aqueous phase and decompose HCHO to CO. Cycle III happens in the organic phase and uses the released CO to form BCP from enyne. For Rh–dppp–cod complexes see Fig. 2a. | ||
The released CO molecules diffuse into the organic phase where they are consumed during the Pauson–Khand type reaction. The carbonylation will most likely be catalysed by [Rh(dppp)2]+ (III.1, cycle III) as it is the dominate species according to the NMR experiments described above. Initially, the complex adds the enyne substrate in an oxidative Pauson–Khand type addition reaction forming the five-membered rhodacycle III.2. In [Rh(dppp)2(enyne)]+ one of the coordinated phosphorous dissociates to yield an open coordination site (equilibrium III.2a and III.2b), which can be occupied by CO (III.3). Subsequently, CO inserts into the Rh–C bond in cis position, expanding the rhodacycle by one carbon atom (III.4). Finally, [Rh(dppp)2]+ is regenerated by a reductive elimination of BCP. Here it is important to note that in the present case, a chiral molecule is formed from an achiral substrate. Thus, the initial formation of the rhodacycle can potentially be influenced by chiral phosphine ligands favouring the formation of a specific enantiomer.
For cycle II and III we favour the idea that all Rh–dppp–cod complexes identified by NMR spectroscopy (see Fig. 2a) are able to catalyse the decomposition and cyclisation reactions but that the reactions are of different speeds due to the fact that dppp ligands dissociate from the Rh centre much slower than chloride and cod ligands. This is especially important for the equilibria II.2 and III.2. Nevertheless NMR experiments show that [Rh(dppp)2]+ is the dominant Rh–dppp species under the present conditions. Thus we assume that it is the main active species as shown in Scheme 3. This does not rule out the fact that [Rh(cod)(dppp)(μ2-Cl)2], [Rh(cod)(dppp)(Cl)] and [Rh(dppp)(μ2-Cl)]2 will also contribute to the catalytic reaction when they are present. This assumption is consistent with our earlier kinetic analysis which revealed the decelerating effect of added dppp.
Finally, the proposed reaction mechanism was studied in detail using DFT. All structures and TSs were calculated in the gas phase. It is therefore important to keep in mind that solvent interactions – either explicit or implicit – are neglected which play an important role especially in the aqueous phase. Therefore, activation energies related to intermediates featuring a vacant coordination are likely overestimated as such species would be stabilised by the surrounding solvent (or reactants). Unfortunately, including an explicit solvent environment without a biased preselection of specific structures comprising one water molecule interacting with the catalyst are computationally to demanding to be applied along the entire reaction profile. Nevertheless, the DFT calculations provide a solid foundation to qualitatively rationalise our experimental findings.
The first question we tried to answer was why [Rh(TPPTS)3]+ is better than [Rh(dppp)2]+ in decomposing HCHO into CO (see Fig. 3a). From an energetic point of view, both reactions are possible, which is in line with the experimental observations. The energy profile for [Rh(TPPTS)3]+ shows that the addition and decomposition of HCHO at the complex is favoured when compared to the pure complex. This is not the case when [Rh(dppp)2]+ is used. Here, the intermediate steps are all higher in energy than the initial complex. As the activation energies for all steps are comparable, the main reason why [Rh(TPPTS)3]+ is better than [Rh(dppp)2]+ in decomposing HCHO is that the intermediary complexes are lower in energy than the starting complex which is not the case for [Rh(dppp)2]+.
Furthermore, we were interested in the geometry of the Rh complexes throughout the reaction. The findings can be seen in Scheme 3. The HCHO activation at [Rh(TPPTS)3]+ and [Rh(dppp)2]+ in both cases results, as expected, in a cis coordination of the resulting hydride and formyl group. Both complexes reorganize into a square-pyramidal geometry with a vacancy in trans position opposed to the formyl group. This is expected as formyl groups are known for their strong trans effect. An important information is that the necessary dissociation of a dppp phosphorus from the Rh centre in [Rh(dppp)2(CHO)(H)]+ (II.2a to II.2b in Scheme 3) seems to be an endergonic reaction step. This is in line with the NMR experiments discussed earlier, which revealed that [Rh(cod)(dppp)(Cl)] is a better complex for the HCHO decomposition due to the easier displacement of cod. Subsequently, the formyl group decomposes into CO and a second hydride. [Rh(TPPTS)3(CO)(H)2]+ as well as [Rh(dppp) (κ1-dppp)(CO)(H)2]+ feature a meridional coordination geometry regarding the phosphine ligands while the hydride ions can be found in cis position to each other. Finally, first H2 then CO is eliminated from the complexes. Overall, the decomposition of HCHO into CO and H2 is slightly exergonic at ΔG = −9 kJ mol−1 (ΔH = 24 kJ mol−1).
The Pauson–Khand type carbonylation (cycle III in Scheme 3), starts with the oxidative addition of enyne to [Rh(dppp)2]+ (III.1-TS). Subsequently, the Rh–P bond trans to the alkenyl carbon breaks (III.2a to III.2b). Again, this behaviour can be rationalised by the trans effect. The open coordination site is occupied by a CO molecule, which is located trans to the alkenyl carbon but cis to the alkyl carbon (III.3). Thus, the following CO insertion can only proceed at the alkyl Rh–C bond, as shown by structure III.4. Finally, the catalyst is regenerated by the reductive elimination of BCP. The formation of BCP from enyne and CO is thermodynamically highly favoured by ΔG = −179 kJ mol−1 (ΔH = −246 kJ mol−1).
It is worth noting that the Pauson–Khand cyclisation is susceptible to enantioselective induction. The calculations show that the right-handed isomer Δ-cis-[Rh(dppp)2(enyne)]+ slightly favours the (S)-enantiomer of enyne by about 10 kJ mol−1 when compared to the (R)-enantiomer. This is due to steric constraints enforced by the two dppp ligands (see Fig. 3c). Of course, dppp is not a chiral ligand and, therefore, the formation of Δ-cis-[Rh(dppp)2(enyne)]+ and Λ-cis-[Rh(dppp)2(enyne)]+, which favours the (R)-enantiomer of enyne, is equally likely and, thus, it comes to no surprise that a racemate of BCP is formed. Our calculations indicate that it is possible to perform an enantioselective “CO-free” Pauson–Khand cyclisation when a chiral bisphosphine ligand is used. This is an improvement over the Ti-catalysed approach for the synthesis of chiral bicyclopentones36 and in line with the results from Kim et al.37
4. Conclusions
We have investigated the mechanism of one of the oldest and most challenging “CO-free” carbonylation reactions using in situ Raman spectroscopy, nuclear magnetic resonance (NMR) and dynamic light scattering (DLS) coupled with advanced data analysis and density functional theory (DFT) calculations. Our data analysis approach revealed, and is able to predict, how the studied catalytic reaction can be accelerated in quantitative fashion. Furthermore, all influencing reaction conditions (i.e., temperature, metal precursor, ligand, (co)-substrate and surfactant concentration) were studied on the molecular level revealing a series of relevant Rh–phosphine equilibria and the formation of micelles in the biphasic system. Finally, the newly proposed catalytic cycles take into consideration the biphasic nature of the reaction and explain all experimental findings. DFT calculations unravelled how the reaction can be performed in an enantioselective way by the utilization of chiral bisphosphines which is a subject of great interest in asymmetric catalysis.Overall, the presented approach of combining in situ spectroscopy and advanced data analysis enables a knowledge-driven optimisation and improvement of not only the studied “CO-free” Pauson–Khand type cyclisation but of catalytic reactions in general. Our findings encourage us to investigate how our analysis scheme can be used as a building block to enhance automated high throughput experiments.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
R.G. gratefully acknowledges a Research Scholarship from the German Research Foundation (DFG) under the grant number GE3112/2-1. The authors would like to thank Johann Jastrzebski (Utrecht University, UU) for assistance during the advanced NMR measurements and the Organic Chemistry and Catalysis (OCC) group for providing NMR measurement time. Mies van Steenbergen (UU) is acknowledged for help during the DLS measurements and the Department of Pharmaceutical Sciences is acknowledged for DLS measurement time.References
- U.-R. Samel, W. Kohler, A. O. Gamer and U. Keuser, in Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH, Weinheim, 2000, vol. 30, pp. 295–312 Search PubMed.
- G. Papadogianakis, L. Maat and R. A. Sheldon, J. Chem. Technol. Biotechnol., 1997, 70, 83 CrossRef CAS.
- D. J. Rowe, Chemistry and Technology of Flavors and Fragrances, Blackwell Publishing Ltd, Oxford, UK, 2004 Search PubMed.
- M. Beller, Catalytic Carbonylation Reactions, Topics in Organometallic Chemistry, Springer, 2006, vol. 18 Search PubMed.
- R. Franke, D. Selent and A. Börner, Chem. Rev., 2012, 112, 5675 CrossRef CAS.
- (a) T. Morimoto and K. Kakiuchi, Angew. Chem., Int. Ed., 2004, 43, 5580 CrossRef CAS; (b) L. Wu, Q. Liu, R. Jackstell and M. Beller, Angew. Chem., Int. Ed., 2014, 53, 6310 CrossRef CAS.
- R. Geitner and B. M. Weckhuysen, Chem. – Eur. J., 2020, 26, 5297 CrossRef CAS.
- W. Li and X.-F. Wu, Adv. Synth. Catal., 2015, 357, 3393 CrossRef CAS.
- J. Cao, Z.-J. Zheng, Z. Xu and L.-W. Xu, Coord. Chem. Rev., 2017, 336, 43 CrossRef CAS.
- Q. Liu, K. Yuan, P.-B. Arockiam, R. Franke, H. Doucet, R. Jackstell and M. Beller, Angew. Chem., Int. Ed., 2015, 54, 4493 CrossRef CAS.
- K. Natte, A. Dumrath, H. Neumann and M. Beller, Angew. Chem., Int. Ed., 2014, 53, 10090 CrossRef CAS.
- H. Konishi, S. Futamata, X. Wang and K. Manabe, Adv. Synth. Catal., 2018, 360, 1805 CrossRef CAS.
- K. Fuji, T. Morimoto, K. Tsutsumi and K. Kakiuchi, Angew. Chem., Int. Ed., 2003, 42, 2409 CrossRef CAS.
- R. Geitner, A. Gurinov, T. Huang, S. Kupfer, S. Graefe and B. M. Weckhuysen, Angew. Chem., Int. Ed., 2020 DOI:10.1002/anie.202011152.
- C. M. Marson, U. Grabowska, T. Walsgrove, D. S. Eggleston and P. W. Baures, J. Org. Chem., 1994, 59, 284 CrossRef CAS.
- T. Morimoto, K. Fuji, K. Tsutsumi and K. Kakiuchi, J. Am. Chem. Soc., 2002, 124, 3806 CrossRef CAS.
- W. A. Herrmann and C. W. Kohlpaintner, in Inorganic Syntheses, ed. M. Y. Darensbourg, John Wiley & Sons, New York, 32nd edn, 1998, vol. 32, pp. 8–25 Search PubMed.
- B. R. James and D. Mahajan, Can. J. Chem., 1979, 57, 180 CrossRef CAS.
- Mestrelab Research S. L., MestReNova (10.0.2-15465), Mestrelab Research S.L., Santiago de Compostela, Spain, 2015 Search PubMed.
- G. R. Fulmer, A. J. M. Miller, N. H. Sherden, H. E. Gottlieb, A. Nudelman, B. M. Stoltz, J. E. Bercaw and K. I. Goldberg, Organometallics, 2010, 29, 2176 CrossRef CAS.
- S. N. Bernstein, Communications of the Kharkov Mathematical Society, 1912, 12, 1 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 (Revision B.01), Gaussian, Inc, Wallingford, CT, USA, 2016 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- J. P. Merrick, D. Moran and L. Radom, J. Phys. Chem. A, 2007, 111, 11683 CrossRef CAS.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901 CrossRef CAS.
- J. Steinmetzer, S. Kupfer and S. Gräfe, Int. J. Quantum Chem., 2020, e26390 Search PubMed.
- (a) S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989 CrossRef CAS; (b) C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652 CrossRef CAS.
- H. B. Schlegel, J. Comput. Chem., 1982, 3, 214 CrossRef CAS.
- (a) M. Page and J. W. McIver, J. Chem. Phys., 1988, 88, 922 CrossRef CAS; (b) M. Page, C. Doubleday and J. W. McIver, J. Chem. Phys., 1990, 93, 5634 CrossRef CAS.
- P. L. Polavarapu, J. Phys. Chem., 1990, 94, 8106 CrossRef CAS.
- J. J. Olivero and R. L. Longbothum, J. Quant. Spectrosc. Radiat. Transfer, 1977, 17, 233 CrossRef.
- (a) A. Meissner, A. König, H.-J. Drexler, R. Thede, W. Baumann and D. Heller, Chem. – Eur. J., 2014, 20, 14721 CrossRef CAS; (b) A. Meißner, A. Preetz, H.-J. Drexler, W. Baumann, A. Spannenberg, A. König and D. Heller, ChemPlusChem, 2015, 80, 169 CrossRef.
- (a) P. Barbaro, C. Bianchini, V. Dal Santo, A. Meli, S. Moneti, C. Pirovano, R. Psaro, L. Sordelli and F. Vizza, Organometallics, 2008, 27, 2809 CrossRef CAS; (b) T. A. Betley and J. C. Peters, Angew. Chem., Int. Ed., 2003, 42, 2385 CrossRef CAS.
- F. A. Hicks and S. L. Buchwald, J. Am. Chem. Soc., 1996, 118, 11688 CrossRef CAS.
- D. E. Kim, V. Ratovelomanana-Vidal and N. Jeong, Adv. Synth. Catal., 2010, 352, 2032 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cy02267e |
| ‡ Present address: Institute for Organic and Macromolecular Chemistry, Friedrich Schiller University Jena, Philosophenweg 7, 07743, Jena, Germany. |
| This journal is © The Royal Society of Chemistry 2021 |