Understanding the mechanism of plasmon-driven water splitting: hot electron injection and a near field enhancement effect†
Jiaquan
Huang
a,
Xinyi
Zhao
b,
Xunkun
Huang
a and
WanZhen
Liang
 *a
*a
aState Key Laboratory of Physical Chemistry of Solid Surfaces, Fujian Provincial Key Laboratory of Theoretical and Computational Chemistry, and Department of Chemistry, College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, Fujian Province, China. E-mail: liangwz@xmu.edu.cn
bXiamen Huaxia University, Ximen 361005, Fujian Province, China
First published on 26th October 2021
Abstract
Utilizing plasmon-generated hot carriers to drive chemical reactions has currently become an active area of research in solar photocatalysis at the nanoscale. However, the mechanism underlying exact transfer and the generation dynamics of hot carriers, and the strategies used to further improve the quantum efficiency of the photocatalytic reaction still deserve further investigation. In this work, we perform a nonadiabatic excited-state dynamics study to depict the correlation between the reaction rate of plasmon-driven water splitting (PDWS) and the sizes of gold particles, the incident light frequency and intensity, and the near-field spatial distribution. Four model systems, H2O and Au20@H2O separately interacting with the laser field and the near field generated by the Au nanoparticle (NP) with a few nanometers in size, have been investigated. Our simulated results clearly unveil the mechanism of PDWS and hot-electron injection in a Schottky-free junction: the electrons populated on the antibonding orbitals of H2O are mandatory to drive the OH bond breaking and the strong orbital hybridization between Au20 and H2O creates the conditions for direct electron injection. We further find that the linear dependence of the reaction rate and the field amplitude only holds at a relatively weak field and it breaks down when the second OH bond begins to dissociate and field-induced water fragmentation occurs at a very intensive field, and that with the guarantee of electron injection, the water splitting rate increases with an increase in the NP size. This study will be helpful for further improving the efficiency of photochemical reactions involving plasmon-generated hot carriers and expanding the applications of hot carriers in a variety of chemical reactions.
1 Introduction
Plasmonic metal (typically Au, Ag, and Cu) nanoparticles (MNPs) have extremely important applications in many fields due to their characteristic optical properties1–3 such as localized surface plasmon resonance (LSPR). When the incident light induces the collective oscillation of metal free electrons, LSPR occurs in those MNPs.4,5 However, this coherent electron oscillation can dephase quickly by nonradiative decay,6–9 generating electron–hole pairs with higher energy in a non-equilibrium state (i.e., hot carriers) at the timescale of 1–100 fs.10 During dephasing, the collective dipole moment decreases along with the near-field interaction and scattering probabilities, with the incident energy converted into a hot carrier distribution.1,11When molecules are adsorbed on the metal nanostructure surface, the hot electrons can be transferred to the empty states of adsorbates before thermalization and create a transient negative ion (TNI).12–15 With the response of molecular geometry, the TNI moves on the excited-state potential energy surface, and therefore their reactive capability is mediated. The plasmon-induced photochemical reactions have different properties from thermal activation, and have the potential to efficiently convert solar energy into chemical energy.2,8,16
In general, there exist two pathways for hot electron transfer, the conventional indirect transfer and the recently proposed direct transfer.14,17–19 In the indirect electron transfer process,20 hot electrons are first generated in the plasmonic metal nanoparticle, and are then injected into the adsorbate. For direct electron transfer,18,21 in the presence of empty hybridized orbitals due to the strong metal–adsorbate coupling, chemical interface damping22,23 can induce the plasmon dephasing directly and generate nonthermalized electrons in the empty hybridized orbitals. The plasmon-induced hot carrier transfer has been utilized to foster various photochemistry processes, such as the dissociation of H2,24–26 N2,27 and O2,28,29 CO2 reduction,15,30 water splitting31–33 and organic transformations.34
Solar photocatalytic water splitting is a promising method for hydrogen production. This process usually takes place in metal-semiconductor heterojunctions where plasmons enhance photoconversion in the semiconductor via three mechanisms, including light trapping, hot electron/hole transfer, and plasmon-induced resonance energy transfer.16,35 The solar water splitting in a Schottky-free junction has been recently found by Robatjazi et al.,36 who observed large photocurrents as a result of direct injection of hot electrons from plasmonic Au NPs to molecules. Many theoretical studies started to explore the mechanism by investigating the effect of laser intensity and frequency on photocatalytic activity. For example, Meng's group31 simulated the H2O splitting dynamics on Au nanospheres using a TDDFT/Ehrenfest dynamics scheme and found a strong correlation between laser intensity, hot electron transfer, and reaction rates. Zhang et al.25 focused on the H2 dissociation induced by Au spheres and found that the dissociation rate of H2 was closely related to the molecular initial positions. In the above two studies, the Au particles were identified by the jellium spheres. The jellium model is the simplest physical model for the valence electrons, it replaces the real geometry of the metal ionic core by a featureless positively charged background in a finite volume and treats only delocalized electrons explicitly in the mean-field approximation, such as the Hartree–Fock or the local density approximations. The jellium model neglects the lattice structures of metal spheres, and hardly describes the interaction between the metal and adsorbates, and the effect of lattice vibration. Furthermore, the LSPRs of MNPs are largely dependent on the MNP shapes and sizes. It is essential to involve those effects in describing plasmon-mediated chemical reactions.
In this work, we investigate the dynamic process of water splitting driven by an Au cluster and NPs with a few nanometers in size under a femtosecond laser pulse. We explore the related mechanisms of H2O splitting and hot electron injection, and reveal the relationships between the reaction rate and the incident light intensity and frequency, and NP sizes. The real-space real-time TDDFT/Ehrenfest dynamics scheme is adopted. Four model systems, H2O and Au20@H2O interacting with the laser field and the near field generated by different sized NPs, have been investigated. The initial geometry of the water molecule is set to be adjacent to the one of the vertexes of Au20. Au20 has a tetrahedral structure and is highly stable and chemically inert.37,38 The tetrahedral Au20 is a fragment of the face-centered cubic lattice of bulk gold with a small structural relaxation, a unique molecule with atomic packing similar to that of bulk gold.38 For H2O and Au20@H2O systems, their electronic degrees of freedom were treated quantum mechanically within the real-space real-time implementation of time-dependent density functional theory (TDDFT), while their nuclei were handled classically.
Currently, it is still a great challenge to describe the excited-state dynamics of the hybrid system of molecule–MNPs with large sizes without using the jellium approximation to the MNPs. Here, we thus divide the nanosized tetrahedron into two parts: the tetrahedral cluster Au20 and the residue, where Au20 is described by TDDFT and the interaction of the residue to Au20@H2O is identified by the near field to which Au20@H2O is subjected. The near field is obtained by the numerical solution of Maxwell's equations using the classical computational electrodynamics finite-difference time-domain (FDTD) technique. With this regard, the interaction of metal–molecule is described at the atomic level and the strong near-field enhancement effect of NPs can also get involved.
2 Theoretical and computational details
The real-space real-time TDDFT calculations reported in this work were carried out using the open-source OCTOPUS code (version 9.2).39,40,41 The simulation grid is localized spherically around each atom with a radius of 8.00 Å, and the grid point is set to be 0.20 Å which is considered as the balance of simulation accuracy and time consumption. The core electrons are approximate by the Troullier–Martins pseudopotentials42 with 11, 6 and 1 valence electrons for Au, O and H atoms. Therefore, the Au20@H2O system has 228 valence electrons and 114 occupied orbitals, and 30 unoccupied states are included in all the calculations. The general gradient approximation exchange–correlation functional Perdew–Burke–Ernzerhof (PBE)43 with Average-density self-interaction correction44 is adopted in all DFT/TDDFT calculations. The time-dependent evolution is performed using the approximated enforced time-reversal symmetry algorithm45 with a time step of 1.5 as. To obtain the optical absorption spectrum, a δ function electric field is used.Nonadiabatic dynamics of Au20@H2O is treated by the TDDFT/Ehrenfest dynamics scheme46 with temperature fluctuating at around 300 K. The set of equations to be solved for the electron and ion dynamics of Au20@H2O are
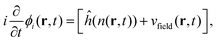 | (1) |
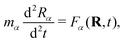 | (2) |
The laser field is assumed to polarize along the +z direction with the function form: 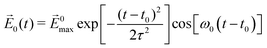 , where |E0max| denotes the amplitude of the external electric field, ω0 is the excitation frequency, t0 = 6.60 fs is the center of the Gauss-type laser and τ = 1.60 fs is the width of the laser pulse. When the water molecule is in the proximity of the nanosized Au tetrahedron, the field E(r, t), interacting with Au20@H2O, includes the incident laser field
, where |E0max| denotes the amplitude of the external electric field, ω0 is the excitation frequency, t0 = 6.60 fs is the center of the Gauss-type laser and τ = 1.60 fs is the width of the laser pulse. When the water molecule is in the proximity of the nanosized Au tetrahedron, the field E(r, t), interacting with Au20@H2O, includes the incident laser field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) 0(t) and the scattered field
0(t) and the scattered field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) sca(r, t) generated by the truncated tetrahedron (Au20 is cut off from this nanosized tetrahedron). This inhomogeneous near field can be expressed as E(r, t) = Es(r)Et(t), where Es(r) is the spatial function that represents the non-uniform distribution of fields and Et(t) is the temporal function which matches the incident laser pulse. In order to describe the non-uniformity of the enhanced near-field, we need to obtain the expression of the spatial function Es(r). In this work, we applied a fifth-order polynomial to fit the spatial function Es(r) via a geodesic Levenberg–Marquardt (LM) algorithm,47,48 namely,
sca(r, t) generated by the truncated tetrahedron (Au20 is cut off from this nanosized tetrahedron). This inhomogeneous near field can be expressed as E(r, t) = Es(r)Et(t), where Es(r) is the spatial function that represents the non-uniform distribution of fields and Et(t) is the temporal function which matches the incident laser pulse. In order to describe the non-uniformity of the enhanced near-field, we need to obtain the expression of the spatial function Es(r). In this work, we applied a fifth-order polynomial to fit the spatial function Es(r) via a geodesic Levenberg–Marquardt (LM) algorithm,47,48 namely, 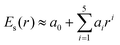 , where r represents the coordinate of the space grid and ai is the fitting parameters.
, where r represents the coordinate of the space grid and ai is the fitting parameters.
The classical electromagnetic simulations to the Au NPs are performed using the FDTD++ package.49,50 The Maxwell's equations are solved using Yee's algorithm.51,52 Considering that Au20 is a fragment of the face-centered cube lattice of bulk gold, or a part of the whole large-sized tetrahedron, we chose the shape of the Au NP to be tetrahedral. The other reason for our choice is that we know that a weak laser field can induce an intensive near field near the apex of an Au tetrahedron, even when the size of the NP is small. The dielectric function of an Au tetrahedron is described by the Drude–Lorentz model53 in the form of
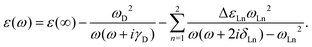 | (3) |
| ε ∞ | Drude | Lorentz | |||
|---|---|---|---|---|---|
| ω D | γ D | ω Ln | ΔεLn | δ Ln | |
| 5.513 | 9.013 | 0.000 | 3.658 | 1.857 | 0.714 |
| 2.833 | 1.004 | 0.399 | |||
The excited-state population is computed by using orbital projections. The occupation at time t of the static orbital ϕm(r) is given by projecting all occupied time-dependent orbitals onto the static unoccupied ones58
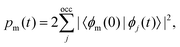 | (4) |
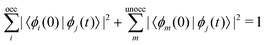 .
.
3 Results and discussion
3.1 Electronic structure and optical properties of Au20@H2O
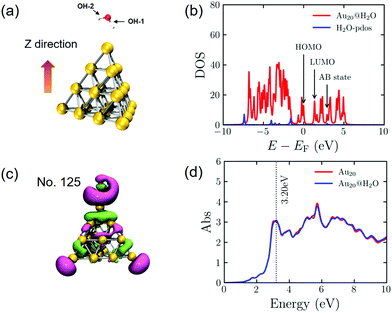
Before investigating the dynamic processes of PDWS, we calculate the electronic and geometric structures of an isolated H2O molecule and the Au20@H2O system. The energy gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) for the isolated H2O molecule is 8.74 eV, much larger than the energy of the visible light photon, indicating that it is difficult to excite H2O to drive water splitting.During the geometry optimization, H2O and Au20 are initially optimized separately, then they are combined to form the hybrid system of Au20@H2O, which is re-optimized with all Au atoms frozen. The optimized distance between O and the apex of Au20 is 3.03 Å as shown in Fig. 1a. The calculated density of state (DOS) shown in Fig. 1b indicates that the energy gap between the AB state and the HOMO of the hybrid system is 2.95 eV, which is much smaller than the HOMO–LUMO gap of H2O, opening the possibility of excitation-induced electron transfer from the Au cluster to the AB state. In addition, we plot the wavefunction of the AB state of the Au20@H2O system and the optical absorption spectrum of Au20@H2O. For comparison, the absorption spectrum of isolated Au20 is also plotted. The major absorption peak in the low energy band of Au20@H2O lies at 3.20 eV, and this peak is considered to be the plasmon resonance excitation. The spectral difference between Au20 and Au20@H2O manifests the strong orbital coupling between the two components, which can be thought to be caused by the charge transfer excitations and the interface metal/adsorbate hybrid states.25,29,59
3.2 Electronic/nuclear dynamics of Au20@H2O
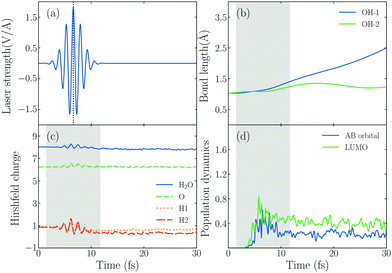
In order to explore the hot electrons transfer mechanism of water splitting reaction, we show the dynamic process of H2O splitting in atomic sight by TDDFT/Ehrenfest dynamics in Fig. 2, where we set ω0 = 3.07 eV and E0max = 1.80 V Å−1 (the corresponding laser intensity is 4.30 × 1013 W cm−2).Fig. 2b shows the time-dependent evolution of the OH bond length (dOH) of the hybrid system under an intensive external laser field. The initial lengths of two OH bonds are 1.03 Å, and during the active time window of the field, one of OH bonds denoted by dOH−1, which is the one with an H atom pointing to the Au20 apex, increases from 1.03 Å to 1.41 Å, and finally dOH−1 keeps increasing until it reaches 2.49 Å after 30 fs, and the corresponding OH bond splits. However, the other OH bond doesn't break, dOH−2 increases at first and reaches the maximum value of 1.35 Å in t = 17.16 fs, then it decreases and oscillates until t = 30 fs. In other words, the water splitting reaction is asymmetric. The OH bond near the apex of Au20 is prone to breaking firstly, attributed to the initial structural arrangement. As Fig. 1 shows, we set one of the H atoms of H2O to bind with an Au atom in the apex of Au20 and the other to be away from the apex. With this structural arrangement, the symmetry of H2O breaks down. As the MO of No. 125 in Fig. 1(c) shows, the wavefunction overlap between two OH bonds of H2O and Au20 will be different, indicating that their ability to accept electrons will be different. With this regard, the asymmetric dissociation appears in the PDWS process.
To obtain the information of products of water splitting, we compute the Hirshfeld charge60 of H and O atoms in real time. The amount of Hirshfeld charge may be underestimated because of the electron loss when they reach the absorbing boundary.61 The results in Fig. 2c show that the Hirshfeld charge of an H2O molecule oscillates with the change in the external field, and the total charge number of H and O atoms fluctuates around 1 and 8 after the laser is switched off. This result indicates that the H2O molecule in the Au20@H2O system splits into a hydrogen (H) and hydroxyl group (OH) under this laser field.
In order to understand the reaction mechanism, we calculate the time-evolved population of the AB state of the H2O molecule and LUMO of the hybrid system in Fig. 2d. We observe that the photo-induced electron transfer takes place from the metal to the AB states of the H2O molecule, indicating that the water splitting occurs when the AB states are populated by the electrons.
To further confirm this, we set a new system of an isolated H2O molecule interacting with the same laser field. From the result shown in Fig. S2 (ESI†), we observe that the first OH bond oscillates with a period of 8.62 fs and the maximum bond length reaches 0.94 Å, with no signs of bond breaking. The population dynamics on the HOMO and LUMO of an isolated H2O molecule also indicate that there are rarely electron populations in H2O's AB orbital, namely, this laser doesn't excite the electrons to the unoccupied orbitals of H2O, so the isolated H2O molecule doesn't split. These results suggest that the OH bond breaking in Au20@H2O is attributed to the photon-induced intermolecular electronic transfer from the metal to the H2O.
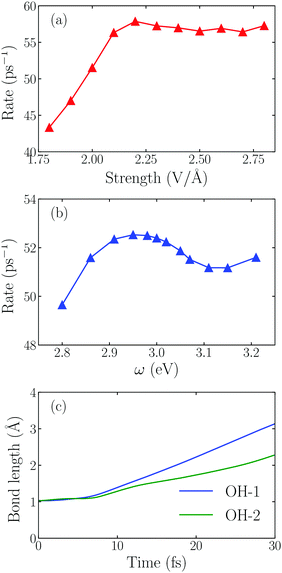
Next we examine the dependence of the dissociation rate on the laser intensity and frequency. The dissociation rate of an H2O molecule is defined as the inverse of the time required for the first OH bond length to reach 2.00 Å. As shown in Fig. 3a, initially, the splitting rate increases linearly as E0max increases from 1.80 V Å−1 to 2.20 V Å−1. A maximum rate appears at 2.20 V Å−1. When the field intensity is further increased, the rate doesn't change obviously. To gain insight into this phenomenon, we plot the time-evolution of the OH bond length at E0max = 2.80 V Å−1 in Fig. 3c, and find that both OH bonds are dissociated in this case. The intensive laser field can drive two OH bonds to break one after another though the reaction rate doesn't change obviously. As the light field increases from 1.80 V Å−1 to 2.80 V Å−1, there is a transition from water splitting to water fragmenting, and the dissociation rate of the OH bond even decreases.
To unveil the possibility of water fragmentation, we perform a calculation of the absorption spectra of Au20@H2O with varied laser intensity. Fig. S4 in the ESI† shows the calculated results. We observe that as the field intensity continuously increases, the intensities of the high-energy absorption bands with excitation energies ≥2.9 eV decrease and their peak locations blue-shift while the intensities of low-energy absorption bands continually increase. These phenomena manifest that the intensive laser fields couple with the system Au20@H2O nonlinearly.64 The decrease of the high-energy absorption and the integrated energy shift are attributed to the absorption saturation and the field dressing during the excitation. The appearing and continually increasing intensity of low-energy bands confirms that multiphoton absorption occurs. This nonlinear coupling between the system and laser field definitely affects the dynamics of water splitting and may lead to the water fragmentation.
Fig. 3b shows that the splitting rate varies with the laser frequency. The maximum rate appears at ω0 = 2.95 eV, not at 3.20 eV, indicating that more hot electrons are transferred when the frequency of the incident field matches the energy gap between the Fermi-level and AB orbital, namely, the hot electron injection mechanism in the water splitting reaction follows the direct one.11,25
3.3 Electronic/nuclear dynamics of nanosized tetrahedron@H2O
To simulate the plasmon-induced water splitting reaction with an Au particle at the nanometer scale with a mixed TDDFT/FDTD method, we firstly calculate the time-dependent spatial inhomogeneous scattering field generated by the truncated Au tetrahedron via the FDTD++ package, then describe the time evolution trajectory dynamics of the Au20@H2O system under the intensive near field by the TDDFT/Ehrenfest scheme. With this treatment, the hot electron injection is assumed to always appear around the interface between the metal cluster and the adsorbate, and the different sized NPs provide the near field with different intensity to which Au20@H2O is subjected, as Fig. 4 shows.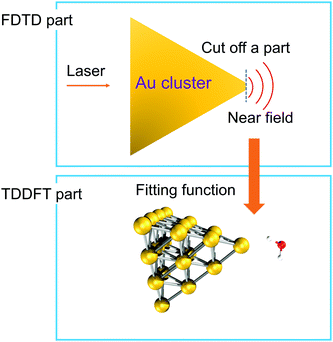 | ||
| Fig. 4 A schematic diagram showing the mixed FDTD/TDDFT scheme for the PDWS reaction with large-sized NPs. | ||
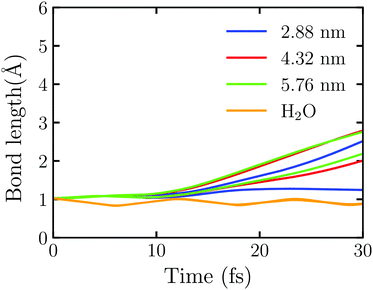
Fig. 5 shows the time evolution of the OH bond length in Au20@H2O under the intensive near field which is generated by the truncated Au tetrahedrons with different sizes. Here the laser field with E0max = 0.50 V Å−1 and ω0 = 3.07 eV is set. We observe that one of the OH bonds breaks at 25.12 fs under the field enhancement by the truncated Au tetrahedron with L = 2.88 nm. In this case, the disassociation reaction takes place at E0max < 1.80 V Å−1. Furthermore, we observe that the larger the NP's size, the faster the disassociation reaction. For example, at L = 4.32 nm, the two OH bond dissociation times are 21.47 fs and 27.80 fs while at L = 5.76 nm, they are 21.03 fs and 25.88 fs, respectively. For comparison, we also calculate the splitting dynamics of an isolated H2O molecule which interacts with the near field generated by the whole Au tetrahedron of L = 2.88 nm obtained by FDTD. In this case, no electron is injected to H2O, and only the field enhancement effect of Au NPs is involved. As Fig. 5 shows, the OH bond oscillates at a certain frequency, and there is no sign of splitting. These numerical simulations suggest that the near field can enhance the reaction rate of water splitting and one can adjust the size of a metal NP to control the plasmon-assisted photochemistry via the field enhancement effect. However, without the injection of hot electrons, the water splitting reaction will not take place, which highlights the decisive factor to drive the water splitting.
To show the field enhancement effect, we calculate the absorption spectra and near fields of the truncated Au tetrahedrons with different side lengths of 2.88 nm, 4.32 nm, and 5.76 nm in Fig. S5 and S6 (ESI†). The major low-energy absorption bands locate at 1.92–2.16 eV, deviating largely from the major low-energy absorption peak of Au20, manifesting the quantum size effect of the optical responses of NPs with a few nanometers in size. The larger the NP's size, the stronger the absorption. And then, we calculate the strong scattered field generated by the truncated Au tetrahedrons. The incident laser is set to match the one used in TDDFT calculations. Fig. S6 (ESI†) clearly shows the strong field enhancement effect near the ‘tip’ of the tetrahedron, and the ‘hot spots’ are formed close to the Au particles. In addition, it is clear that the field enhancement ratio increases with the size of NPs.
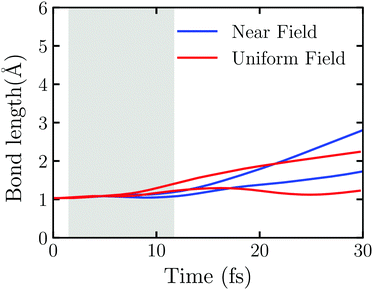
The near field decays rapidly with the surface separation as Fig. S6 (ESI†) shows. To have a clear picture on the effect of the near field's inhomogeneity on the water splitting, we perform the TDDFT/Ehrenfest dynamics of Au20@H2O interacting with the real near field generated by the truncated Au tetrahedron with L = 2.88 nm and the uniform electric field taken from the center of mass of Au20@H2O generated by the same NP, respectively. In this case, a very weak laser field with ω0 = 3.07 eV and E0max = 0.65 V Å−1 is applied. As Fig. S7 (ESI†) shows, the duration of the scattered field at the center of mass of Au20@H2O is much longer than the incident field, and the scattered field's amplitude is magnified about three-fold so that the OH bond disassociates even with a weak laser field. Fig. 6 displays the evolution of OH bonds in Au20@H2O which is interacting with the two kinds of fields, respectively. In the laser activity window, in the case with a uniform field, the change of OH bond length shows an “upward arc”, while in the real near field case, it shows as a “downward arc”. The near field generated from LSPR is a very short-range electromagnetic field with a strong intensity gradient which may generate a gradient force to affect the molecule.62,63
To explain why the field's spatial distribution can affect the evolution of OH bonds with time, we compare the forces acting on the H2O molecule in Fig. S8 and S9 (ESI†). During the laser activity window (from 6.60 fs to 6.84 fs), the results with the uniform field and the near field are quite dissimilar. In the uniform field, the force vectors in the XZ plane acting on the H2O molecule are affected by the field and electron injection, and its direction and magnitude change rapidly. While in the near field, the force vectors in the XZ plane always point to the ‘tips’ of Au20, especially the force acting on the O atom. It is known that this direction is also the negative gradient direction of the field. We thus suggest that the inhomogeneous near field affects the water splitting reaction through the gradient force and causes a different reaction during the field active window.
4 Concluding remarks
We have presented a theoretical study on the PDWS via TDDFT/Ehrenfest nonadiabatic dynamics. By comparing the calculated results of four model systems: H2O and Au20@H2O separately interacting with the laser field and the near fields, we clearly reveal the microscopic mechanism of PDWS and the interface electron transfer, and the correlation of the reaction rate with the laser field frequency and intensity, the NP sizes, and the field's spatial distribution. A multiscale scheme has been applied to describe PDWS dynamics. For H2O and Au20@H2O systems, its electronic degrees of freedom were treated quantum mechanically within the real-space real-time implementation of TDDFT, while their ions were handled classically. For the system with a larger sized NP, we divided this NP into Au20 + residue, where Au20 was described by TDDFT and the truncated NP was described by FDTD.The main conclusions are summarized as follows:
(1) The electrons populated on the AB orbitals of H2O are mandatory to drive the OH bond breaking. The strong orbital hybridization between Au20 and H2O creates the condition for photo-induced direct electron injection.
(2) The dynamic results under different laser intensities unveil that the linear dependence of the reaction rate of PDWS and the incident field amplitude holds only at a relatively weak field, however the linear correlation breaks down by the participation of other reactions such as water fragmenting in the intensive field regime. The splitting rate varies with the laser frequency, and the maximum rate appears when the laser frequency matches the energy gap between the metal Fermi-level and AB orbital.
(3) To describe the effect of field enhancement induced by large-sized Au NPs, the mixed FDTD/TDDFT method is used. By dividing the large sized NPs into the Au20 + residue, the requirement of near-field enhancement and hot-electron injection in the water splitting reaction can be simultaneously satisfied. Setting the water near the apex of the large-sized tetrahedron, OH bonds can be disassociated by a very weak laser field.
(4) The intensive electric field can make two OH bonds in the Au20@H2O system break successively, attributed to the nonlinear coupling between the system and the applied field. When the intensity of the incident field reaches a certain degree, the field couples with the system nonlinearly, opening the possibility of multiphoton absorption. These hot electrons excited by multiphoton absorption can give important contributions in H2O splitting reactions.
(5) The influence of the field's spatial distribution on water splitting is significant. The gradient force caused by the strong intensity gradient of the near field makes the distinction of force vectors in the XZ plane compared to those in the uniform field case, leading to the different OH bond evolution dynamics.
This work is useful for understanding hot electron induced reactions at ambient conditions by plasmonic excitations and can provide a reference for the development of a related mixed quantum-classical method in describing large-sized plasmonic systems.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The financial support from the National Natural Science Foundation of China with Grant No. 21833006 and 22173074 is appreciated.References
- M. Bernardi, J. Mustafa, J. B. Neaton and S. G. Louie, Nat. Commun., 2015, 6, 1–9 CrossRef PubMed.
- V. Giannini, A. I. Fernández-Domnguez, S. C. Heck and S. A. Maier, Chem. Rev., 2011, 111, 3888–3912 CrossRef CAS PubMed.
- G. V. Hartland, Chem. Rev., 2011, 111, 3858–3887 CrossRef CAS PubMed.
- N. J. Halas, S. Lal, W.-S. Chang, S. Link and P. Nordlander, Chem. Rev., 2011, 111, 3913–3961 CrossRef CAS PubMed.
- K. A. Willets and R. P. Van Duyne, Annu. Rev. Phys. Chem., 2007, 58, 267–297 CrossRef CAS PubMed.
- L. D. Landau, Zh. Eksp. Teor. Fiz., 1946, 10, 25 Search PubMed.
- D. Ryutov, Plasma Phys. Controlled Fusion, 1999, 41, A1 CrossRef CAS.
- M. L. Brongersma, N. J. Halas and P. Nordlander, Nat. Nanotechnol., 2015, 10, 25–34 CrossRef CAS PubMed.
- X. Li, D. Xiao and Z. Zhang, New J. Phys., 2013, 15, 023011 CrossRef CAS.
- C. Voisin, N. Del Fatti, D. Christofilos and F. Vallée, J. Phys. Chem. B, 2001, 105, 2264–2280 CrossRef CAS.
- H. Tang, C.-J. Chen, Z. Huang, J. Bright, G. Meng, R.-S. Liu and N. Wu, J. Chem. Phys., 2020, 152, 220901 CrossRef CAS PubMed.
- J. S. DuChene, B. C. Sweeny, A. C. Johnston-Peck, D. Su, E. A. Stach and W. D. Wei, Angew. Chem., Int. Ed., 2014, 53, 7887–7891 CrossRef CAS PubMed.
- S.-F. Hung, F.-X. Xiao, Y.-Y. Hsu, N.-T. Suen, H.-B. Yang, H. M. Chen and B. Liu, Adv. Energy Mater., 2016, 6, 1501339 CrossRef.
- M. J. Kale, T. Avanesian, H. Xin, J. Yan and P. Christopher, Nano Lett., 2014, 14, 5405–5412 CrossRef CAS PubMed.
- S. Yu, A. J. Wilson, J. Heo and P. K. Jain, Nano Lett., 2018, 18, 2189–2194 CrossRef CAS PubMed.
- S. K. Cushing and N. Wu, J. Phys. Chem. Lett., 2016, 7, 666–675 CrossRef CAS PubMed.
- Q. Wei, S. Wu and Y. Sun, Adv. Mater., 2018, 30, 1802082 CrossRef PubMed.
- C. Boerigter, U. Aslam and S. Linic, ACS Nano, 2016, 10, 6108–6115 CrossRef CAS PubMed.
- C. Boerigter, R. Campana, M. Morabito and S. Linic, Nat. Commun., 2016, 7, 1–9 Search PubMed.
- Y. Tian and T. Tatsuma, J. Am. Chem. Soc., 2005, 127, 7632–7637 CrossRef CAS PubMed.
- Q. Xiao, S. Sarina, E. R. Waclawik, J. Jia, J. Chang, J. D. Riches, H. Wu, Z. Zheng and H. Zhu, ACS Catal., 2016, 6, 1744–1753 CrossRef CAS.
- H. Hövel, S. Fritz, A. Hilger, U. Kreibig and M. Vollmer, es, 1993, 48, 18178 Search PubMed.
- B. Foerster, A. Joplin, K. Kaefer, S. Celiksoy, S. Link and C. Sönnichsen, ACS Nano, 2017, 11, 2886–2893 CrossRef CAS PubMed.
- L. Yan, Z. Ding, P. Song, F. Wang and S. Meng, Appl. Phys. Lett., 2015, 107, 083102 CrossRef.
- Y. Zhang, T. Nelson, S. Tretiak, H. Guo and G. C. Schatz, ACS Nano, 2018, 12, 8415–8422 CrossRef CAS PubMed.
- Q. Wu, L. Zhou, G. C. Schatz, Y. Zhang and H. Guo, J. Am. Chem. Soc., 2020, 142, 13090–13101 CrossRef CAS PubMed.
- O. A. Hull, D. B. Lingerfelt, X. Li and C. M. Aikens, J. Phys. Chem. C, 2020, 124, 20834–20845 CrossRef CAS.
- P. Christopher, H. Xin, A. Marimuthu and S. Linic, Nat. Mater., 2012, 11, 1044–1050 CrossRef CAS PubMed.
- B. Seemala, A. J. Therrien, M. Lou, K. Li, J. P. Finzel, J. Qi, P. Nordlander and P. Christopher, ACS Energy Lett., 2019, 4, 1803–1809 CrossRef CAS.
- H. Robatjazi, H. Zhao, D. F. Swearer, N. J. Hogan, L. Zhou, A. Alabastri, M. J. McClain, P. Nordlander and N. J. Halas, Nat. Commun., 2017, 8, 1–10 CrossRef CAS PubMed.
- L. Yan, F. Wang and S. Meng, ACS Nano, 2016, 10, 5452–5458 CrossRef CAS PubMed.
- K. Ueno, T. Oshikiri and H. Misawa, ChemPhysChem, 2016, 17, 199–215 CrossRef CAS PubMed.
- L. Yan, J. Xu, F. Wang and S. Meng, J. Phys. Chem. Lett., 2018, 9, 63–69 CrossRef CAS PubMed.
- H. Kisch, Angew. Chem., Int. Ed., 2013, 52, 812–847 CrossRef CAS PubMed.
- Z. Zheng, W. Xie, B. Huang and Y. Dai, Chem. – Eur. J., 2018, 24, 18322–18333 CrossRef CAS PubMed.
- H. Robatjazi, S. M. Bahauddin, C. Doiron and I. Thomann, Nano Lett., 2015, 15, 6155–6161 CrossRef CAS PubMed.
- R. W. Burgess and V. J. Keast, J. Phys. Chem. C, 2014, 118, 3194–3201 CrossRef CAS.
- J. Li, X. Li, H.-J. Zhai and L.-S. Wang, Science, 2003, 299, 864–867 CrossRef CAS PubMed.
- A. Castro, H. Appel, M. Oliveira, C. A. Rozzi, X. Andrade, F. Lorenzen, M. A. Marques, E. Gross and A. Rubio, Phys. Status Solidi B, 2006, 243, 2465–2488 CrossRef CAS.
- X. Andrade, D. Strubbe, U. De Giovannini, A. H. Larsen, M. J. Oliveira, J. Alberdi-Rodriguez, A. Varas, I. Theophilou, N. Helbig and M. J. Verstraete, et al. , Phys. Chem. Chem. Phys., 2015, 17, 31371–31396 RSC.
- N. Tancogne-Dejean, M. J. Oliveira, X. Andrade, H. Appel, C. H. Borca, G. Le Breton, F. Buchholz, A. Castro, S. Corni and A. A. Correa, et al. , J. Chem. Phys., 2020, 152, 124119 CrossRef CAS PubMed.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- C. Legrand, E. Suraud and P. Reinhard, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, 1115 CrossRef CAS.
- A. Castro, M. A. Marques and A. Rubio, J. Chem. Phys., 2004, 121, 3425–3433 CrossRef CAS PubMed.
- J. L. Alonso, X. Andrade, P. Echenique, F. Falceto, D. Prada-Gracia and A. Rubio, Phys. Rev. Lett., 2008, 101, 096403 CrossRef CAS PubMed.
- M. K. Transtrum, B. B. Machta and J. P. Sethna, Phys. Rev. Lett., 2010, 104, 060201 CrossRef PubMed.
- M. K. Transtrum, B. B. Machta and J. P. Sethna, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 036701 CrossRef PubMed.
- A. L. Atkinson, J. M. McMahon and G. C. Schatz, SelfOrganization of Molecular Systems, Springer, 2009, pp. 11–32 Search PubMed.
- J. M. McMahon, Y. Wang, L. J. Sherry, R. P. Van Duyne, L. D. Marks, S. K. Gray and G. C. Schatz, J. Phys. Chem. C, 2009, 113, 2731–2735 CrossRef CAS.
- K. Yee, IEEE Trans. Antennas Propag., 1966, 14, 302–307 Search PubMed.
- E. Miller, J. Electromagnet. Wave., 1994, 8, 1125–1172 CrossRef.
- P. Drude, Ann. Phys., 1900, 308, 369–402 CrossRef.
- J. M. McMahon, G. C. Schatz and S. K. Gray, Phys. Chem. Chem. Phys., 2013, 15, 5415–5423 RSC.
- J. M. McMahon, S. K. Gray and G. C. Schatz, Nano Lett., 2010, 10, 3473–3481 CrossRef CAS PubMed.
- C. Cirac, R. Hill, J. Mock, Y. Urzhumov, A. Fernández-Domnguez, S. Maier, J. Pendry, A. Chilkoti and D. Smith, Science, 2012, 337, 1072–1074 CrossRef PubMed.
- P. Zhang, J. Jing and W. Z. Liang, J. Phys. Chem. C, 2018, 122, 10545 CrossRef CAS.
- J. Krumland, A. M. Valencia, S. Pittalis, C. A. Rozzi and C. Cocchi, J. Chem. Phys., 2020, 153, 054106 CrossRef CAS PubMed.
- R. L. Gieseking, M. A. Ratner and G. C. Schatz, Frontiers of Plasmon Enhanced Spectroscopy Volume 1, ACS Publications, 2016, pp. 1–22 Search PubMed.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- A. Castro, E. Räsänen, A. Rubio and E. Gross, Europhys. Lett., 2009, 87, 53001 CrossRef.
- C. Zhan, G. Wang, J. Yi, J.-Y. Wei, Z.-H. Li, Z.-B. Chen, J. Shi, Y. Yang, W. Hong and Z.-Q. Tian, Matter, 2020, 3, 1350–1360 CrossRef.
- T. Iwasa and K. Nobusada, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 043411 CrossRef.
- J. Sun, Z. Ding, Y. Yu and W. Liang, Phys. Chem. Chem. Phys., 2021, 23, 15994–16004 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: The DOS of an isolated H2O molecule, the evolution of an OH bond when an isolated H2O molecule interacts with the laser field, the time evolution of OH bonds in an Au20@H2O system under the laser field with Emax = 1.60 V Å−1 and Emax = 1.70 V Å−1, the absorption spectra of Au20@H2O vary with the intensity of the incident field, the absorption spectra of Au tetrahedrons with L = 2.88 nm, 4.32 nm, and 5.76 nm calculated by FDTD, the contour plot of near fields, and the time evolution of the forces acting on the H2O molecule in the XZ plane under a uniform field and the real near field, respectively. See DOI: 10.1039/d1cp03509f |
| This journal is © the Owner Societies 2021 |