Time-resolved relaxation and cage opening in diamondoids following XUV ultrafast ionization
Alexie
Boyer
 ,
Marius
Hervé
,
Marius
Hervé
 ,
Audrey
Scognamiglio
,
Vincent
Loriot
,
Audrey
Scognamiglio
,
Vincent
Loriot
 and
Franck
Lépine
and
Franck
Lépine
 *
*
Univ Lyon, Université Claude Bernard Lyon 1, CNRS, Institut Lumière Matière, F-69622, Villeurbanne, France. E-mail: franck.lepine@univ-lyon1.fr
First published on 29th November 2021
Abstract
Unraveling ultrafast processes induced by energetic radiation is compulsory to understand the evolution of molecules under extreme excitation conditions. To describe these photo-induced processes, one needs to perform time-resolved experiments to follow in real time the dynamics induced by the absorption of light. Recent experiments have demonstrated that ultrafast dynamics on few tens of femtoseconds are expected in such situations and a very challenging task is to identify the role played by electronic and nuclear degrees of freedom, charge, energy flows and structural rearrangements. Here, we performed time-resolved XUV-IR experiments on diamondoids carbon cages, in order to decipher the processes following XUV ionization. We show that the dynamics is driven by two timescales, the first one is associated to electronic relaxation and the second one is identified as the redistribution of vibrational energy along the accessible modes, prior to the cage opening that is involved in all fragmentation mechanisms in this family of molecules.
1. Introduction
Diamondoids are molecules composed by one or several unit carbon cage of diamond surrounded by hydrogens. On Earth, diamondoids can be isolated from hydrocarbon-rich materials such as natural gas. Recently, large diamondoids (∼1 to 2 nm) were extracted from petroleum.1 The possibility to access a wide range of sizes and shapes of diamondoids has attracted the attention of several scientific communities,2 from nanotechnologies towards medical applications. Indeed, diamondoids combine the properties of nanomaterials together with the ones of bulk diamonds. They exhibit remarkable strength, rigidity, thermal stability and tunable optical gaps, pushed towards UV range, due to quantum confinement.3,4 Moreover, recent results show that diamondoids have negative electron affinities (NEA),5,6 which brings new opportunities in the development of electron emitter devices. Small diamondoids are also easy to functionalize, an essential condition to push for further applications7 for instance in medicine thanks to their non-toxicity. As an example, adamantane derivatives are currently used for pharmaceutical applications in the treatment of various viral diseases and parkinsonism.8With the discovery of small nano-diamondoids in meteorites,9 diamondoids also gained a lot of attention from the astrophysical community. Due to isotope anomaly, these diamondoids are considered to have presolar origin9 and are even considered as the most abundant component of presolar grains.10 Regarding their high stability, they are also expected to be abundant in the interstellar medium. However, compared to polycyclic aromatic hydrocarbon (PAH) emission bands that dominate most of the mid-IR emission from astronomical objects, only few astronomical objects show spectroscopic evidences of the presence of diamondoids. For example, they are thought to be responsible for two broad emission bands (at 3.43 and 3.53 μm), observed in the spectrum of circumstellar disks around the stars Elias 1 and HD 97048 but their size is still a matter of debate.11–13 Regarding the strength of these bands, diamondoids are thought to represent 1–2% of the amount of cosmic carbon.14,15 The difficulty to detect emission spectra associated to diamondoids have been partially explained by the specific local conditions for their formation.16 However, the presolar origin of the diamondoids found in meteorites indicates sources of diamondoids outside the solar system. To understand the paucity of diamondoids in the interstellar medium, a large number of laboratory experiments and theoretical calculations have been developed, in particular to investigate the photostability of these molecules. Indeed, in space and for instance in Photo-Dissociation Regions, molecules are exposed to extreme ultraviolet (XUV) radiations above 10 eV. In that case, a low photostability could also explain the low detection of spectroscopic features. It was shown that upon ionization small diamondoids have low photostability, with efficient H-loss channels to form a stable closed-shell cation17 or fragmentation following the opening of the cage structure.18 The photostability of the doubly charged adamantane was investigated using XUV excitation, showing that the dissociation is driven by Coulomb repulsion.19 Although, these processes are expected to occur on ultrafast timescales, ranging from attosecond to picosecond, we note that no experiment has been able to investigate in a time-resolved fashion, the photoinduced evolution of diamondoids.
In this work, we investigate the electronic and vibrational relaxation dynamics of the two smallest diamondoids, adamantane (C10H16) and diamantane (C14H20), following XUV ionization. We use an ultrashort XUV pulse to ionize and excite the molecules and the induced dynamics is probe using an ultrashort IR pulse. The observed dynamics are associated to the electronic relaxation of the correlation bands (CBs), features created by electron correlation, and the following vibrational redistribution of the energy to lower electronic states. Similar temporal dynamics have been observed previously in polycyclic aromatic hydrocarbons (PAHs).20,21 Here, we investigate the effect of the 3D structure of these nanoscale diamonds on the energy redistribution and discuss its implication in understanding cage opening.
2. Experimental set-up
The experimental set-up has been described in details in previous paper.20 It consists of a Mach-Zehnder interferometer seeded with an amplified laser delivering 25 fs pulses at 2 mJ, centered around 800 nm with a repetition rate of 5 kHz. The first arm is focused into a gas cell using a f = 30 cm lens in order to generate XUV light through high harmonic generation process (HHG). In our experiment, Xenon, Krypton and Argon were used to generate the XUV pulses, giving access to an energy range of the corresponding pulses of 17 to 35 eV. After the HHG, the residual IR is removed by a Nb2O5 dichroic mirror and an aluminum filter that removes the harmonics below the 11th one. A toroidal mirror is used to focus the XUV pulses in the interaction region of a velocity map imaging (VMI) spectrometer.22 The second part of the IR beam, the probe arm, goes through a half-wave plate and a polarizer to control the intensity. A refractive delay line made of two wedges is used to control the delay between the pump and the probe pulses with an attosecond accuracy. The delayed beam is focused using a f = 1 m lens before being recombined with the pump arm using a drilled mirror. The molecular effusive jet is created through sublimation. In the case of adamantane, the vapor pressure at room temperature is enough to sublimate the sample (from Sigma-Aldrich, purity ≥99%). In the case of diamantane, the sample (from Tokyo Chemical Industry, purity >98%) is heated up to 80 °C by an oven. The results of the interaction of the neutral molecules in gas phase and the XUV and IR pulses is then recorded with the VMI operating as a time-of-flight (TOF) spectrometer. Mass spectra are recorded at each pump–probe delay in order to obtain the time dependent signals. The zero delay t0, corresponding to the temporal overlap of the two laser pulses, is determined by measuring the IR pump–IR probe time-dependent signal of the photoelectrons emitted from the ionization of argon targets. All the experiments have been performed using several XUV and IR conditions.3. Experimental results
3.1. Fragmentation mechanisms
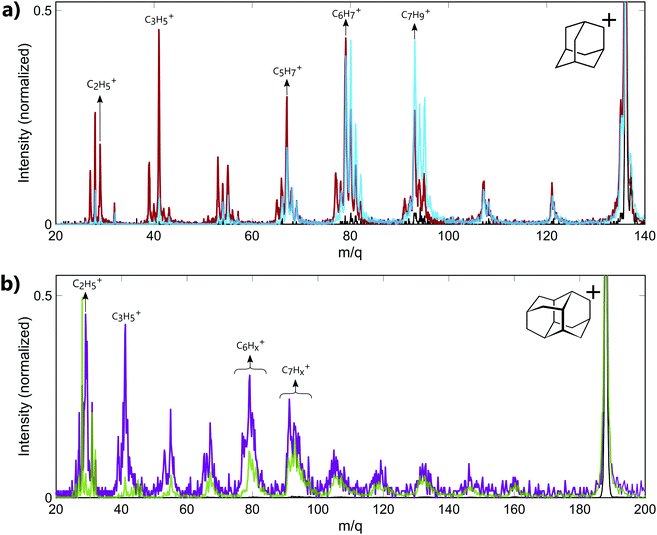
The experiments have been performed on the two smallest diamondoids, adamantane (C10H16, m/q = 136, IP = 9.2 eV,23 IP2 = 23.9 eV19) and diamantane (C14H20, m/q = 188, IP = 9.2 eV23). In both cases, the energy of the XUV pulse (>17 eV) is sufficient to ionize the molecules and create highly excited cations with internal energy of approximately 10 eV. Moreover, calculations performed on adamantane using RRKM model have shown that the fragmentation thresholds for large fragment ion (m/q ≥ 78) lie between 10.5 eV and 10.83 eV.18 Thus, the energy of the XUV pulse used in our experiment is also sufficient to produce cations resulting from the fragmentation of the parent ion.Mass spectra recorded from the interaction of neutral adamantane with either XUV or IR pulses are shown in Fig. 1a. These measurements were obtained with XUV photons energy centered around 17–23 eV or 30–33 eV and an IR intensity of about 5.5 TWcm−2. The spectra show a fragmentation pattern corresponding to the loss of CnHx groups. Similar patterns have been observed in collision induced dissociation (CID)24 or electron impact experiments.25,26 In CID experiments, the kinetic energy of the ions is converted into internal energy due to the collision, resulting in statistical fragmentation. Here, the main statistical fragments observed in CID correspond to the dominant peaks at groups of masses C6Hx+ (m/q ≈ 79) and C7Hx+ (m/q ≈ 93). The same behavior is observed in infra-red multi photon ionization (MPI) as shown in the mass spectrum measured with IR only (black line), where the number of photon is not sufficient to double ionize the molecule but the internal energy left in the monocation is sufficiently high to produce the same two groups of fragments. The same dominant peaks are also observed following the absorption of XUV photons of 17–23 eV (blue line). Since the absorption of 17–23 eV is not sufficient to double ionize the molecule, we conclude that most of the fragment ions observed in the corresponding mass spectrum are coming from the fragmentation of the excited monocation. In particular, some fragments such as the groups of masses C6Hx+ (m/q ≈ 79) and C7Hx+ (m/q ≈ 93) can be identify as statistical fragments. For the absorption of XUV photons of 30–33 eV (red line), the energy is sufficient to lead to the second ionization of the molecule. We note that no signature of the stable dication is measured at mass m/q = 68. This illustrates the low stability of the doubly charged adamantane. Indeed, one can see in Fig. 1a that some of the fragments detected in the mass spectrum at energy above IP2 (red line) are significantly different from the mass spectrum obtained at energy lower than the (blue line). For instance, the dominant peak for higher energy photons corresponds to the mass m/q = 41 (C3H5+). No significant amount of this fragment is observed in the statistical fragmentation of the monocation while it has been identified as part of the 2 and 3-body break-up channels of the dication.19 Some low masses can therefore be identified as coming mainly from the dissociation of the dication. Overall, the measured fragment ions in our experiment can come from two different mechanisms: statistical fragmentation of the monocation or dissociation of the unstable dication.
In the case of diamantane, only few experiments have been performed on the ionized molecule.27 To our knowledge, no study on the photostability of the doubly charged diamantane has been reported in literature. Its double ionization potential is also not known. However, regarding the similarity of adamantane and diamantane,2 it can be assumed to similar to IP2 of adamantane. The mass spectra recorded in diamantane are shown in Fig. 1b. The mass spectrum recorded from the interaction of the neutral diamantane with XUV photons energy centered around 20–23 eV (green line) exhibits the same fragmentation pattern than the one obtained in electron impact experiment.27 The dominant peaks are similar and correspond to the mass C7Hx+ (m/q ≈ 93). It means that the energy used in this experiment is probably not sufficient to significantly double ionize the molecule. Thus, the observed fragments mainly come from the statistical fragmentation of the monocation. When the XUV photon energy increases up to 33–39 eV, a significant number of small masses appears (purple line). Among these fragments, the masses m/q = 29 (C2H5+) and 41 (C3H5+) become dominant and correspond to fragments involved in the 2-body and 3-body break-up channels of the doubly charged adamantane. One can assume that, similarly to adamantane, these fragments come from the dissociation of the dication. Thus, the different fragments observed in the mass spectra arise either from statistical fragmentation of the monocation or from the dissociation of the dication. We also note that in the case of diamantane, the internal energy left in the monocation after the multi photon ionization by the IR is not sufficient to reach the fragmentation threshold of the monocation. Indeed, only the parent ion is observed in the IR only mass spectrum (black line).
3.2. Time-resolved dynamics
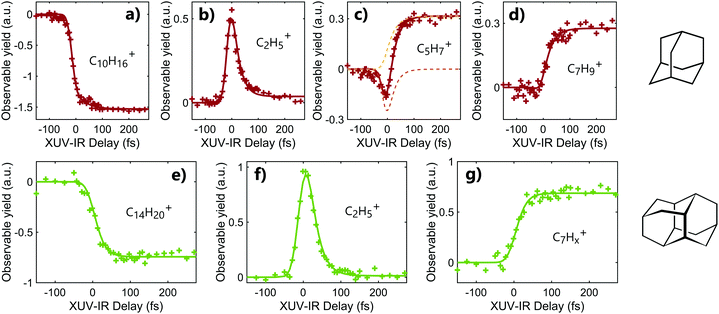
Following the absorption of the XUV pulse, cations are formed with an internal energy up to approximately 10 eV. In that case, the IR pulse probes the dynamics induced by the absorption of XUV light by leading to a second ionization step or to the statistical fragmentation of the cation. As discussed in the previous section, the double ionization of adamantane and diamantane may also lead to fragmentation due to the low photostability of the dications. Thus, the time-dependent fragmentation signals contain the information on the dynamics following XUV ionization, namely in excited cations.Time-dependent signals are shown in Fig. 2. for adamantane (a–d) and diamantane (e–g). The signals were obtained using XUV pulses of 30–33 eV for adamantane and 20–23 eV for diamantane. The contribution from the XUV and IR pulses only are subtracted from the two color signal. Different temporal behaviors can be observed depending on the measured fragments. In the case of a fragment coming from the dissociation of the doubly charged molecules, C2H5+ (m/q = 29), the time-dependent signal exhibits a fast increase of the signal around the zero delay followed by an exponential decay of the yield (see Fig. 2b and f). In the case of major statistical fragments of the monocations, C7Hx+ (m/q ≈ 93), one can observe a population behavior with an increase of the signal after the zero delay following an exponential increase of the yield (see Fig. 2d and g). Thus, probing the dynamics by statistical fragmentation of the monocation gives access to a population timescale while probing the dynamics by the dissociation of the dication gives access to a decay dynamics. Depending on the observable, different ultrafast processes can be investigated.
In the case of diamantane, most of the studied fragments exhibit either a decay dynamics or a population dynamics as shown in Fig. 2f and g. In the case of adamantane, the number of fragments that exhibit both dynamics is high. The example of C5H7+ is given in Fig. 2c. However, despite the apparent complexity of these dynamics, our analysis led to the conclusion that only two time scales, τdecay and τpop, for the decay and population, respectively, are sufficient to describe the dynamics observed in all the fragments for adamantane and diamantane. This conclusion arises from a multistep procedure in our analysis starting from the use of free parameters (each transient is considered independently) to constrained parameters. Here we describe only the last step of our analysis. A multi-dimensional fitting procedure using the convolution between the cross-correlation of the XUV and IR pulses Icc and an exponential decay plus an exponential increase has been used:
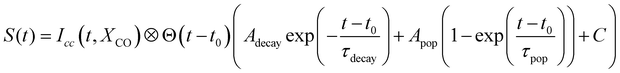 | (1) |
| τ decay (fs) | τ pop (fs) | |
|---|---|---|
| Adamantane | 22 ± 5 | 28 ± 4 |
| Diamantane | 29 ± 7 | 19 ± 6 |
The experiment was performed for different XUV photon energies and different IR intensities and no significant XUV and IR dependency of the timescales was observed. However, the amplitudes of the decay component Adecay and the population component Apop can change depending on the observed fragments, even going from positive to negative value in the case of adamantane. Moreover, the ratio of these two amplitudes also change with the XUV photon energy (without altering the measured timescales). This can be understood as a change in internal energy deposited into the molecule and the competition between statistical fragmentation of the monocation and direct dissociation of the dication. For instance, in the case of C5H7+ (m/q = 67) (Fig. 2c), the time-dependent signal is composed by a negative Adecay (orange dashed line) and a positive Apop (yellow dashed line). Since the two dynamics are measured from different observables, the negative Adecay means that the absorption of the IR pulse depopulated the states that should have led to the statistical fragmentation of the monocation towards C5H7+ to lead to the creation of dication. The formed dication later dissociates into other fragments.
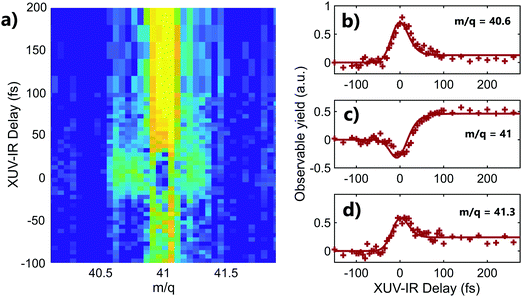
A striking example of the two origins of the fragments is observed in the mass m/q = 41 (C3H5+) of adamantane. The 2D time-dependent mass spectrum is shown in Fig. 3a. One can see that signals surrounding mass 41 appear at the zero delay. It corresponds to the C3H5+ ions with high kinetic energy. Indeed, the presence of translational kinetic energy affects the arrival time of the ion on the detector, arriving earlier or later than the ion with low initial kinetic energy. This leads to the detection of signal around the m/q values. The corresponding time-dependent signals obtained by integrating the map at masses m/q = 40.6 ± 0.1, m/q = 41 ± 0.1 and m/q = 41.3 ± 0.1 are shown respectively in Fig. 3b–d. One can see that the signals of the fragments with high kinetic energy exhibit decay dynamics. Their high kinetic energy allows to identify them as purely coming from the dissociation of the dication following Coulomb repulsion. The signal at the central mass (ion with low kinetic energy) corresponds to mass 41 coming from statistical fragmentation only. It exhibits a negative amplitude of the decay, corresponding to a depletion of the statistical fragmentation channel towards the creation of dication. This shows that a given fragment can be reached following different pathways that can be separated as a function of the kinetic energy of the ions.
4. Discussion
4.1. Dynamics of correlation bands
We first consider the case of fragments coming from the dissociation of the dication following Coulomb repulsion. These fragments show a characteristic decay process with a common timescale for all the fragments. When neutral molecules are ionized by an XUV pulse, highly excited cationic states are created. These cationic states have a strong multielectronic character as they are composed by a large number of electronic configurations. These states form dense electronic structures just below the second ionization potential, named the correlation bands (CBs) that are features resulting from electron correlation effects. Although these structures were predicted and described theoretically in the 90's,28 it is only recently that their intrinsic relaxation dynamics was observed experimentally. This first experimental demonstration was performed on PAHs by measuring the variation of the dication yield as a function of the XUV-IR delay.20 In this article, the relaxation dynamics of CBs in adamantane and diamantane is also presented. Here, we have extracted the CBs relaxation timescale from the time-dependent fragmentation signals (see for example Fig. 2b and f). Indeed, due to the instability of the dications, the dynamics observed in fragments coming from the dication dissociation are equivalent to the dynamics observed in the stable dication time-dependent signal of the PAHs. Thus, we associate the decay timescales of τdecay = 22 ± 5 fs for adamantane and τdecay = 29 ± 7 fs for diamantane to the electronic relaxation of the CBs. We note that these values are in good agreement with the results presented in ref.20 (τdecay = 22 ± 2 fs for adamantane, τdecay = 25 ± 7 fs for diamantane).4.2. Vibrational dynamics in 3D molecules
Here we consider fragments coming from statistical dissociation. Dynamics extracted from time-dependent signal of statistical fragments show a population behavior and a common population timescale for all the fragments. During the relaxation of the CBs, the molecules evolves from highly excited electronic states toward lower-lying electronic states with higher vibrational energy in specific modes. These initially populated modes relax towards other vibrational modes eventually leading to complete intramolecular vibrational energy redistribution and fragmentation on longer timescale. Here, the time-dependent population measured in all the fragments is interpreted as the population of all accessible vibrational modes (τpop), prior to any fragmentation processes which are not probed in our experiment. In order to understand the measured timescale, it is essential to determine the modes involved in the CBs relaxation.We note that the vibrational dynamics described above has been observed in PAHs in recent experiments. In PAHs, the population timescales were substantially longer than in the case of diamandoids. For instance, pyrene whose number of valence electron (N = 74) is similar to diamantane, has a population timescale of τpop = 101 ± 27 fs, while diamantane (N = 76) has a population timescale of τpop = 19 ± 6 fs. In the case of PAHs, ab initio calculations show that following CBs relaxation, mainly symmetric normal modes are excited. For instance, ab initio calculations performed on the smallest PAH, naphthalene, show that the frequency of the symmetric normal modes responsible for the electron-vibration energy redistribution are 514.30, 771.15 and 1050.83 cm−1 [ref. 20]. Since the normal modes are very sensitive to the geometrical structure of the system, one can expect that higher frequency modes (compared to PAHs) will be involved in the electronic relaxation of carbon cages such as diamondoids. For instance, the three lowest symmetric modes of adamantane have frequencies of 759.0, 1057.0 and 1496.0 cm−1 [ref. 29]. Consequently, we can assume that the initially populated vibrational modes have higher frequency in the case of diamondoids compared to PAHs. These higher frequency modes are considered as the starting point of the subsequent vibrational dynamics and therefore one can expect the redistribution of energy to occur faster. This could explain the shorter timescales measured in the case of diamondoids compared to PAHs.
We conclude that in the case of diamondoid cations, the vibrational energy is spread in few tens of fs over the vibrational degrees of freedom. With high energy in the nuclear degrees of freedom, diamondoids are unstable and fragment on longer timescales. Although there is not detailed theoretical or experimental investigations about these fragmentation mechanisms, any fragmentation of diamondoids starts with an essential first step of the molecular reorganization that is the opening of the carbon cage.18,19 Cage and ring openings are a general feature in organic molecules that recently attracted the attention of the ultrafast community.30 The energy barrier corresponding to the cage opening in adamantane was found to be 1.71 eV above the ionization potential of the molecule18 and therefore could be easily overcome in our experiment. Since the population dynamics is associated with the energy flow towards nuclear degrees of freedom and prior to dissociation, one can try to interrogate the link between τpop and the timescale of cage opening.
To answer this question, one should consider that the complete cage opening is expected to occur on femtosecond timescale and our measurements are rather connected to the first steps of this structural change. The comparison between the timescales measured in adamantane and diamantane provides a direct information on the size dependence of the process. One expects that the cage opening will take more time for a larger diamondoid (diamantane). However, the population timescales in diamantane is about 10 fs faster than in adamantane. This decrease of τpop with the size of the molecules is similar to what was observed in our previous work on PAHs.21 It is associated with the larger number of accessible degrees of freedom for a larger system, which leads to faster dynamics. We conclude that in our XUV-IR experiment the extracted timescale reveals the first instants of energy flow towards all accessible vibrational modes, which gives birth to the cage opening and subsequent fragmentation. Thus, our experiment is neither sensible to the cage opening of the molecule, neither to the fragmentation process itself which should occur on longer (picosecond) timescale. The vibrational dynamics we are measuring is an initial step of energetic relaxation, prior to any structural change and occurs in the intact parent ion. The larger the molecule, the faster this initial step even if the complete structural change itself is slower.
5. Conclusion
In this work, we performed time-resolved experiments to investigate dynamics induced by XUV ionization in diamondoids. We show that, similarly to what has been observed previously in PAHs, two dynamics can be observed using XUV-IR pump–probe scheme: a decay dynamics associated to the electronic relaxation of correlation bands (CBs) and a population dynamics associated to energy redistribution through vibrational degrees of freedom.In contrast to the case of PAHs, the CBs dynamics was not observed by measuring the stable dication signal, but using fragments arising from the dissociation of unstable dications. We showed that the fast vibrational dynamics measured in diamondoids could be understood by the high frequency vibrational modes involved in the relaxation of the CBs in the case of 3D molecules. We show that in our experiment, the timescales are associated to the initial step of cage opening that is a general feature of diamondoid fragmentation. Our experimental results show that XUV induced ultrafast electronic and vibrational dynamics in diamondoids occurs on very short timescales of few tens of fs, reaching a threshold from where the molecule dissociates through complex structural rearrangements. Further time-resolved experiments, for instance using coulomb explosion imaging, could allow to measure XUV induced structural changes on longer timescales overall providing a multiscale “movie” of photoinduced processes in diamondoids.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Pablo Castellanos Nash and Alexander Tielens for fruitful discussion. We acknowledge financial support from CNRS, ANR Circé ANR-16-CE30-0012.References
- J. E. Dahl, S. G. Liu and R. M. K. Carlson, Isolation and structure of higher diamondoids, nanometer-sized diamond molecules, Science, 2003, 299(5603), 96–99 CrossRef CAS PubMed.
- W. A. Clay, J. E. P. Dahl, R. M. K. Carlson, N. A. Melosh and Z.-X. Shen, Physical properties of materials derived from diamondoid molecules, Rep. Prog. Phys., 2015, 78(1), 016501 CrossRef CAS PubMed.
- J.-Y. Raty, G. Galli, C. Bostedt, T. van Buuren and L. Terminello, Quantum confinement and fullerenelike surface reconstructions in nanodiamonds, Phys. Rev. Lett., 2003, 90(3), 037401 CrossRef PubMed.
- Y. K. Chang, H. H. Hsieh, W. F. Pong, M.-H. Tsai, F. Z. Chien and P. K. Tseng, et al., Quantum confinement effect in diamond nanocrystals studied by X-Ray-absorption spectroscopy, Phys. Rev. Lett., 1999, 82(26), 5377–5380 CrossRef CAS.
- N. D. Drummond, A. J. Williamson, R. J. Needs and G. Galli, Electron emission from diamondoids: A diffusion quantum Monte Carlo study, Phys. Rev. Lett., 2005, 95(9), 096801 CrossRef CAS.
- W. L. Yang, J. D. Fabbri, T. M. Willey, J. R. I. Lee, J. E. Dahl and R. M. K. Carlson, et al., Monochromatic electron photoemission from diamondoid monolayers, Science, 2007, 316(5830), 1460–1462 CrossRef CAS PubMed.
- R. C. Fort and P. v. R. Schleyer, Adamantane: consequences of the diamondoid structure, Chem. Rev., 1964, 64(3), 277–300 CrossRef CAS.
- A. A. Spasov, T. V. Khamidova, L. I. Bugaeva and I. S. Morozov, Adamantane derivatives: Pharmacological and toxicological properties (review), Pharm. Chem. J., 2000, 34(1), 1–7 CrossRef CAS.
- R. S. Lewis, T. Ming, J. F. Wacker, E. Anders and E. Steelt, Interstellar diamonds in meteorites, Nature, 1987, 326(12), 160–162 CrossRef CAS.
- E. Anders and E. Zinner, Interstellar grains in primitive meteorites: diamond, silicon carbide, and graphite, Meteoritics, 1993, 28(4), 490–514 CrossRef CAS.
- O. Guillois, G. Ledoux and C. Reynaud, Diamond infrared emission bands in circumstellar media, Astrophys. J., 1999, 521(2), L133–L136 CrossRef CAS.
- C. Van Kerckhoven, A. G. G. M. Tielens and C. Waelkens, Nanodiamonds around HD 97048 and Elias 1, Astron. Astrophys., 2002, 384(2), 568–584 CrossRef CAS.
- O. Pirali, M. Vervloet, J. E. Dahl, R. M. K. Carlson, A. G. G. M. Tielens and J. Oomens, Infrared spectroscopy of diamondoid molecules: New insights into the presence of nanodiamonds in the interstellar medium, Astrophys. J., 2007, 661(2), 919–925 CrossRef CAS.
- C. W. Bauschlicher, Y. Liu, A. Ricca, A. L. Mattioda and L. J. Allamandola, Electronic and vibrational spectroscopy of diamondoids and the interstellar infrared bands between 3.35 and 3.55 m, Astrophys. J., 2007, 671(12), 458–469 CrossRef CAS.
- T. Henning and F. Salama, Carbon in the universe, Science, 1998, 282(5397), 2204–2210 CrossRef CAS PubMed.
- M. Goto, T. Henning, A. Kouchi, H. Takami, Y. Hayano and T. Usuda, et al., Spatially resolved 3 micron spectroscopy of Elias 1: Origin of diamonds in protoplanetary disks, Astrophys. J., 2009, 693(1), 610–616 CrossRef CAS.
- M. Steglich, F. Huisken, J. E. Dahl and R. M. K. Carlson, Henning Th. Electronic spectroscopy of fuv-irradiated diamondoids: a combined experimental and theoretical study, Astrophys. J., 2011, 729(2), 91 CrossRef.
- A. Candian, J. Bouwman, P. Hemberger, A. Bodi and A. G. G. M. Tielens, Dissociative ionisation of adamantane: a combined theoretical and experimental study, Phys. Chem. Chem. Phys., 2018, 20(8), 5399–5406 RSC.
- S. Maclot, J. Lahl, J. Peschel, H. Wikmark, P. Rudawski and F. Brunner, et al., Dissociation dynamics of the diamondoid adamantane upon photoionization by XUV femtosecond pulses, Sci. Rep., 2020, 10(1), 2884 CrossRef CAS PubMed.
- M. Hervé, V. Despré, P. Castellanos Nash, V. Loriot, A. Boyer and A. Scognamiglio, et al., Ultrafast dynamics of correlation bands following XUV molecular photoionization, Nat. Phys., 2021, 17(3), 327–331 Search PubMed.
- A. Boyer, M. Hervé, V. Despré, P. Castellanos Nash, V. Loriot and A. Marciniak, et al., Ultrafast vibrational relaxation dynamics in XUV-excited polycyclic aromatic hydrocarbon molecules, Phys. Rev. X, 2021, 11(4), 041012 Search PubMed.
- A. T. J. B. Eppink and D. H. Parker, . Velocity map imaging of ions and electrons using electrostatic lenses: Application in photoelectron and photofragment ion imaging of molecular oxygen, Rev. Sci. Instrum., 1997, 68(9), 3477–3484 CrossRef CAS.
- K. Lenzke, L. Landt, M. Hoener, H. Thomas, J. E. Dahl and S. G. Liu, et al., Experimental determination of the ionization potentials of the first five members of the nanodiamond series, J. Chem. Phys., 2007, 127(8), 084320 CrossRef CAS PubMed.
- C. Aubry, J. L. Holmes and J. C. Walton, 1- and 2-Adamantyl radicals and cations in the gas phase: Thermochemistry and mass spectrometry, J. Phys. Chem. A, 1998, 102(8), 1389–1393 CrossRef CAS.
- W. E. Wallace, “Mass Spectra” by NIST Mass Spectrometry Data Center in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, ed. P. J. Linstrom and W. G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 019, p. 20899).
- J. Bouwman, S. Horst and J. Oomens, Spectroscopic Characterization of the product ions formed by electron ionization of adamantane, ChemPhysChem., 2018, 19(23), 3211–3218 CrossRef CAS PubMed.
- R. J. Waltman and A. C. Ling, Mass spectrometry of diamantane and some adamantane derivatives, Can. J. Chem., 1980, 58(20), 2189–2195 CrossRef CAS.
- M. S. Deleuze and L. S. Cederbaum, Formation of satellite bands in the ionization spectra of extended systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53(20), 13326–13339 CrossRef CAS PubMed.
- NIST Computational Chemistry Comparison and Benchmark Database (http://cccbdb.nist.gov/).
- O. Schalk, J. Galiana, T. Geng, T. L. Larsson, R. D. Thomas and I. Fdez Galván, et al., Competition between ring-puckering and ring-opening excited state reactions exemplified on 5H-furan-2-one and derivatives, J. Chem. Phys., 2020, 152(6), 064301 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2021 |