Ultrafast “end-on”-to-“side-on” binding-mode isomerization of an iron–carbon dioxide complex†
Steffen
Straub
and
Peter
Vöhringer
 *
*
Lehrstuhl für Molekulare Physikalische Chemie, Institut für Physikalische und Theoretische Chemie Rheinische Friedrich-Wilhelms, Universität Wegelerstraße 12, 53115 Bonn, Germany. E-mail: p.voehringer@uni-bonn.de
First published on 29th July 2021
Abstract
Carbon dioxide (CO2) binding by transition metals is a captivating phenomenon with a tremendous impact in environmental science and technology, most notably, for establishing circular economies based on greenhouse gas emissions. The molecular and electronic structures of coordination compounds containing CO2 can be studied in great detail using photochemical precursors bearing the photolabile oxalato-ligand. Here, we study the photoinduced elementary dynamics of the ferric complex, [FeIII(cyclam)(C2O4)]+, in dimethyl sulfoxide solution using femtosecond mid-infrared spectroscopy following oxalate-to-iron charge transfer excitation with 266 nm pulses. The pump–probe response in the ν3-region of carbon dioxide gives unequivocal evidence that a CO2-molecule is detached from the metal within only 500 fs and with a primary quantum yield of 38%. Simultaneously, a primary ferrous product is formed that carries a carbon dioxide radical anion ligand absorbing at 1649 cm−1, which is linked to the metal in a bent-O-“end-on” fashion. This primary ηO,bent1-product is formed with substantial excess vibrational energy, which relaxes on a time scale of several picoseconds. Prior to full thermalization, however, a fraction of the ferrous primary product can structurally isomerize at a rate of 1/(3.5 ps) to a secondary ηCO2-product absorbing at 1727 cm−1, which features a bent carbon dioxide ligand that is linked to the metal in a “side-on” fashion. The ηO,bent1-to-ηCO2 isomerization requires an intersystem crossing from the sextet to the quartet state, which rationalizes a partial trapping of the system in the metastable bent-O-“end-on” geometry. Finally, a fraction (62%) of the initially photoexcited complexes can return without structural changes to the parent's electronic ground state, but dressed with excess kinetic energy, which relaxes again on a time scale of several picoseconds.
1. Introduction
The binding of carbon dioxide to transition metal (TM) centers is an area of intense research, in particular, in the fields of coordination chemistry and chemical catalysis.1–5 The scientific activities are thrusted primarily by the pressing societal challenge to alleviate the environmental consequences of anthropogenic greenhouse gas emissions.6 Not surprisingly, the development of technologies utilizing CO2 as an abundant carbon-containing raw material for chemical processes appears to be an intriguing strategy that may become, in the future, an important cornerstone for addressing this formidable task.7–11Much progress has been made in the recent past in the preparation of mononuclear TM–CO2 complexes and in understanding their molecular and electronic structures. These species can be classified formally based on the mode of binding of the carbonaceous triatomic ligand to the TM-center.12 In the “side-on” binding mode,13–22 the molecular O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O axis is oriented perpendicular to that of the metal–ligand binding vector, very much like the classical π-complexes of TMs containing dihaptic (η2) olefin ligands.23–25 In contrast, the CO2-molecule can also interact with a TM through its central carbon atom only, i.e. in a monohaptic (η1) fashion, thereby forming a TM–carbon σ-bond.16–18,26 In both cases, the binding involves some back transfer of electron density from the metal to the low-lying antibonding π-orbitals of the heterocumulene, which in turn, gives rise to the lowering of the CO-bond order and a significant angular distortion of the otherwise linear O
O axis is oriented perpendicular to that of the metal–ligand binding vector, very much like the classical π-complexes of TMs containing dihaptic (η2) olefin ligands.23–25 In contrast, the CO2-molecule can also interact with a TM through its central carbon atom only, i.e. in a monohaptic (η1) fashion, thereby forming a TM–carbon σ-bond.16–18,26 In both cases, the binding involves some back transfer of electron density from the metal to the low-lying antibonding π-orbitals of the heterocumulene, which in turn, gives rise to the lowering of the CO-bond order and a significant angular distortion of the otherwise linear O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety. In a third binding mode, CO2 can also weakly couple to the metal through its terminal oxygen atom mostly via electrostatic interactions without much back-donation, in which case, the ligand retains its heterocumulenic character and linear geometry.27
O moiety. In a third binding mode, CO2 can also weakly couple to the metal through its terminal oxygen atom mostly via electrostatic interactions without much back-donation, in which case, the ligand retains its heterocumulenic character and linear geometry.27
Very recently, unexpected novel insight into the molecular and electronic structure of TM–CO2 complexes has been gained from time-resolved vibrational spectroscopy and its application to the photochemistry and photophysics of coordination compounds containing an oxalate moiety.28–32 When embedded into the ligand sphere of a TM, the oxalate dianion becomes susceptible to photo-induced fragmentation, which generates a neutral carbon dioxide molecule along with a doubly negatively charged carbonite ion33 according to C2O42− + hν → CO2 + CO22−. Femtosecond mid-infrared (MIR) spectroscopy could demonstrate that the neutral CO2-fragment is rapidly expelled from the coordination sphere whereas CO22− is retained by the metal as a redox-active ligand.32 As such, it can bind not only as a dianion, but also as a monoanionic carbon dioxide radical, CO2˙−,34,35 or as a neutral carbon dioxide, CO2, depending on the number of electrons transferred to the metal. Indeed, it is this fascinating redox-non-innocence of the carbonite ligand, i.e. its capacity to reduce the metal by one or two equivalents, which rationalizes the fascinating complexity of the molecular and electronic structure of the TM–CO2 complexes.32
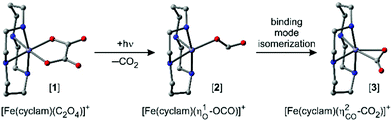
Along these lines of thought and in an effort to leverage the spin for controlling the TM–CO2-binding mode, we recently studied the photochemical product distribution of the oxalato species, [Fe(cyclam)(C2O4)]+ ([1]), containing an iron center at the oxidation state +III (cf.Fig. 1).32 Optical excitation leads indeed to CO2-loss and the primary product was shown to feature an unusual monohaptic O-“end-on” binding mode with the original carbonite fragment being held to an iron(II) center as a genuine radical anion, CO2˙−, that adopts a bent, rather than a linear geometry. Yet, a fraction of the primary products continued to evolve into the more ubiquitous dihaptic “side-on” binding mode as evidenced by the time-gated infrared spectra at 500 fs and at 1 ns.32
In this paper, we now wish to address the molecular dynamical aspects of this system; that is, we wish to qualitatively understand and quantitatively simulate the full spectro-temporal response in the infrared region of [1] in terms of the nature of the underlying elementary processes and of course their associated time scales.
2. Methods
2.1 Synthesis
The hexafluoroborate salt of cis-oxalato-(1,4,8,11-tetraazacyclotetradecane)iron(III) ([Fe(cyclam)(C2O4)][BF6]), [1][BF6], was prepared according to ref. 32. Oxalic acid (1.14 g, 12.6 mmol, 1.5 eq.) was dissolved in 180 mL of deionized water and 3.08 g of cis-[Fe(cyclam)Cl2]Cl was added. The solution was then stirred for 2 h at room temperature while keeping it in the dark, whereupon the color changed from yellow to orange. Next, 18 mL of an aqueous solution of NH4PF6 (2.14 mol L−1, 4.5 eq.) was added and the mixture was kept at 3 °C over night. The precipitate was filtered off, washed with cold water and diethyl ether, and finally dried for 4 h at room temperature under vacuum. [1][PF6] was obtained as an orange-brown powder (3.88 g, 7.99 mmol, 94% yield) and was used without further recrystallization. Anal. calcd for C12H24N4O4FePF6: 11.45% N, 29.47% C, 4.95% H; found: 11.23% N, 29.17% C, 5.01% H.2.2 Spectroscopic techniques
Stationary Fourier-transform infrared (FTIR) spectra were recorded using a Thermo Fisher Nicolet 5700 FTIR-spectrometer operating with a spectral resolution of 0.5 cm−1. Stationary UV/Vis absorption spectra were obtained using a Shimadzu UV-160 dual-beam spectrophotometer. Femtosecond ultraviolet-pump/mid-infrared-probe (UV/MIR) spectroscopy was conducted using an ultrafast laser system described previously.36 Briefly, 266 nm-pump-pulses with a duration of 60 fs were generated by frequency tripling a fraction of the fundamental output of an ultrafast front-end system (Solstice Ace, Newport/Spectra-Physics). MIR-probe pulses were generated through difference frequency mixing of the temporally synchronized signal and idler pulses of an optical parametric amplifier, which in turn was driven by another fraction of the front-end's output. The pump–probe setup enabled a frequency-resolved detection of the pump-induced absorbance (or differential optical density, ΔOD) of the sample using probe and reference beams that were steered into an imaging spectrometer (Horiba, iHR 320), which in turn was equipped with a 2 × 32 pixel HgCdTe-array detector (Infrared Associates). Further details are given in ref. 36. The pump-induced signals were recorded under magic angle conditions to remove signal contributions arising from rotational dynamics of the molecules. Using a gear pump, the sample solution was circulated at a flow rate of roughly 100 mL min−1 through a home-built transmission flow cell. The latter featured two CaF2 windows, which were kept at a distance of 100 μm using a lead spacer. The entire pump–probe setup was purged continually with N2 to avoid deteriorating atmospheric absorptions of the probe pulses.3. Results and discussion
3.1 Stationary spectroscopy
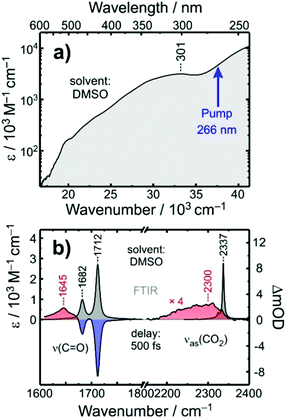
The stationary electronic absorption spectrum of [1] in liquid dimethyl sulfoxide (DMSO) solution at room temperature is depicted in Fig. 2a. It features a very strong band at 301 nm with an extinction coefficient of ca. 3 × 104 M−1 cm−1. According to ref. 32 this band can be attributed to an oxalate-to-cobalt charge transfer (LMCT) involving the oxygen-pz and the cobalt-dxz-orbitals. The onset of another charge transfer band can be seen for wavelengths shorter than 289 nm, which can be traced back to a complementary LMCT that includes transfer of electron density either from py(O) to dz2(Co) or from the nitrogen-pz-orbital to the same dz2-orbital at the metal. The pump-pulses used here were tuned to the onset of this high-energy LMCT-band.32The FTIR-spectrum of [1] in liquid DMSO at room temperature is displayed in Fig. 2b (gray spectrum, left abscissa). It consists of two pronounced resonances peaking at 1712 cm−1 and 1682 cm−1, respectively, whose amplitude ratio is roughly 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The two bands can be assigned to the in-phase and out-of-phase stretching vibrations of the two dangling C
1. The two bands can be assigned to the in-phase and out-of-phase stretching vibrations of the two dangling C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups of the oxalato ligand. Magnetometry and electron spin resonance data suggest that at room temperature the system is considerably spin-mixed with energetically nearly degenerate doublet and sextet ground states.32 In the neat powder, the low-spin configuration, (S = 1/2), is energetically favored, whereas in DMSO solution, it is the high-spin configuration (S = 5/2). A careful vibrational analysis of temperature-dependent FTIR spectra together with a normal-mode analysis of the two states based on density functional theory (DFT) demonstrates that the 1712 cm−1 band is indeed purely due to the in-phase dangling C
O groups of the oxalato ligand. Magnetometry and electron spin resonance data suggest that at room temperature the system is considerably spin-mixed with energetically nearly degenerate doublet and sextet ground states.32 In the neat powder, the low-spin configuration, (S = 1/2), is energetically favored, whereas in DMSO solution, it is the high-spin configuration (S = 5/2). A careful vibrational analysis of temperature-dependent FTIR spectra together with a normal-mode analysis of the two states based on density functional theory (DFT) demonstrates that the 1712 cm−1 band is indeed purely due to the in-phase dangling C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode of the high-spin state. In contrast, the 1682 cm−1 band is a mixture of the corresponding out-of-phase mode of the S = 5/2 state and the in-phase C
O stretching mode of the high-spin state. In contrast, the 1682 cm−1 band is a mixture of the corresponding out-of-phase mode of the S = 5/2 state and the in-phase C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibration of the low-spin state. The out-of-phase mode of the low-spin state contributes to the low-frequency tail of the 1682 cm−1 band, and builds up upon heating (see ref. 32 for details).
O vibration of the low-spin state. The out-of-phase mode of the low-spin state contributes to the low-frequency tail of the 1682 cm−1 band, and builds up upon heating (see ref. 32 for details).
3.2 UV/MIR-spectrum at early delay and quasi-prompt CO2-release
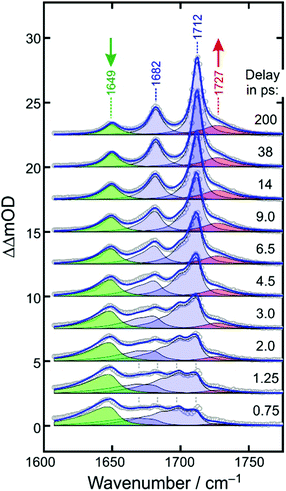
A time-resolved 266 nm-pump/MIR-probe spectrum recorded in the oxalate-C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching region at a time delay of 500 fs is also shown in Fig. 2b (colored spectrum, left abscissa). Two prominent negative bands (shaded in blue) are detected at exactly the same spectral locations of the two stationary FTIR-absorptions of [1]. These signals arise clearly from the pump-induced depletion of population in the electronic ground state(s). At the same time, an additional third band is detected (shaded in red), which peaks at 1645 cm−1 and is undoubtedly due to a nascent species that is generated by the pump pulse upon its interaction with the complex.
O stretching region at a time delay of 500 fs is also shown in Fig. 2b (colored spectrum, left abscissa). Two prominent negative bands (shaded in blue) are detected at exactly the same spectral locations of the two stationary FTIR-absorptions of [1]. These signals arise clearly from the pump-induced depletion of population in the electronic ground state(s). At the same time, an additional third band is detected (shaded in red), which peaks at 1645 cm−1 and is undoubtedly due to a nascent species that is generated by the pump pulse upon its interaction with the complex.
To clarify the nature of this nascent species, complementary pump–probe experiments were conducted in the spectral region corresponding to the anti-symmetric stretching vibration, ν3, of carbon dioxide. In liquid DMSO solution, the stationary FTIR-resonance of this mode peaks at 2337 cm−1 (cf. gray spectrum in Fig. 2b, right abscissa) and any absorption in the spectral vicinity of this feature can be taken as unequivocal evidence of the photo-induced release of a CO2 fragment by complex [1]. Indeed, even for a time delay as short as 500 fs, a weak but very broad induced absorption is detected, which appears around 2300 cm−1, i.e. a slightly frequency-downshifted with respect to the stationary ν3-band. Thus, we can conclude here that the photochemical conversion
| [Fe(cyclam)(C2O4)]+ + hν → [Fe(cyclam)(CO2)]+ + CO2 | (1) |
Based on a meticulous in silico analysis published earlier,32 we could demonstrate that the induced 1645 cm−1-absorption can be assigned to the anti-symmetric OCO-stretching vibration of a bent carbon dioxide radical anion ligand that is ferromagnetically coupled to a high-spin (S = 2) iron(II) center. At the same time, it is bound to the metal in an “end-on”-fashion via one of its two terminal O-atoms, i.e. the electronic structure of the primary product is best described as [FeII(cyclam)(–OCO˙)]+ ([2], ηO,bent1-binding mode, for its molecular structure, see Fig. 1, middle). To reiterate, the 266 nm LMCT-excitation of [1] leads to the cleavage of a neutral CO2-molecule within 500 fs and gives rise to a primary ferrous product, [2], featuring a ηO1-bound carbon dioxide radical anion (CO2˙−) ligand that absorbs at 1645 cm−1.
3.3 Time-dependent UV/MIR-spectrum in the ν3-region of CO2
To determine a primary photochemical quantum yield for CO2-release, (1), it is important to understand in the first place why the 500 fs-UV/MIR-spectrum in the ν3-band region of the neutral CO2-fragment differs so markedly from the corresponding stationary FTIR-spectrum. To this end, we investigated the full delay-dependence of the pump–probe spectrum between 2100 cm−1 and 2400 cm−1. Fig. 3 displays a series of such spectra for various time delays ranging between 750 fs and almost 1 ns. The most glaring features of these data are the dynamic loss of spectral bandwidth and the concomitant frequency-upshift of the CO2-absorption from ∼2300 cm−1 to 2337 cm−1, i.e. towards the exact spectral position of the stationary FTIR band (cf.Fig. 2). This peculiar spectro-temporal evolution is an unambiguous fingerprint that the triatomic fragment is initially born in a highly vibrationally excited fashion and that it undergoes vibrational energy relaxation on a time scale of tens of picoseconds.37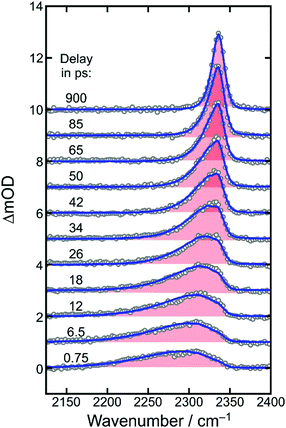 | ||
| Fig. 3 Femtosecond UV-pump/MIR-probe spectra of [1] in liquid DMSO solution at room temperature. The experimental data (open circles) were collected in the spectral region of the anti-symmetric stretching mode (ν3) of CO2 for various pump–probe delays as indicated by the numbers. The solid curves are simulated spectra using the anharmonic coupling model described in detail in ref. 32. | ||
To quantify the dynamics of CO2 vibrational relaxation, the experimental data can be simulated with the anharmonic coupling model originally introduced by Zinth and coworkers38 and later applied to the special case of CO2 by Reichardt et al.37 and by ourselves.29 In this model, the triatomic molecule's internal energy is assumed to be canonically distributed over all four vibrational modes; namely, the symmetric stretching vibration, ν1, the two degenerate bending vibrations, ν2, and the anti-symmetric stretch, ν3 – the mode that is actually probed in Fig. 3. The anharmonic coupling constants between ν3 and the other modes are taken from the literature (x13 = −19.14 cm−1 and x23 = −12.54 cm−1).39 A harmonic frequency of 2377 cm−1 together with a diagonal anharmonicity, x33, of the anti-symmetric stretch of −12.50 cm−1 was used to spectrally align the calculated ν3-fundamental transition with the experimentally measured band at 2337 cm−1.
With the above assumption of a canonical redistribution of the excess energy one can specify a vibrational temperature, which in turn is allowed to relax in a simple mono-exponential fashion, [T(t) − T(∞)]/[T(0) − T(∞)] = exp(−kVERt). Here, t is the time delay, kVER is the relaxation rate, and T(0) and T(∞) are the initial and final temperatures, respectively. Using an inverse relaxation rate of 38 ps together with an initial temperature of 2200 K and a residual heating29 of the pump focal volume of T(∞) = 350 K, a simulation is obtained that is in excellent agreement with the experimental data (cf. solid curves in Fig. 3, and Fig. S1 of the ESI†).
Importantly, the simulated spectra do not need any delay-dependent scaling, indicating that the number of CO2 absorbers is conserved during the course of vibrational relaxation and for delays as long as 1 ns. Thus, we can dismiss any geminate recombination of the primary products emerging from reaction (1).
Having established that the number density of CO2 product molecules remains constant from 500 fs onwards, the primary photochemical quantum yield, Φ (i.e. the number of product molecules produced in the reaction (i) divided by the number of photoexcited parent molecules), can now be deduced. As can be observed in Fig. 2b, the peak extinction coefficient of [1] at 1712 cm−1 is nearly identical to the peak extinction coefficient of CO2 at 2337 cm−1. Therefore, Φ is simply given by the ratio between the differential optical density recorded at the ν3-band of CO2 at infinite delays and that of the symmetric C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode of [1] at zero delay. Neglecting the convolution effects due to the finite time and frequency resolution of the pump–probe setup, a lower limit for this ratio can be estimated by Φ = ΔOD(2337 cm−1, t = 1 ns)/|ΔOD(1712 cm−1, t = 500 fs)|. Inspecting Fig. 1b and 3, we find Φ ≈ 3/8 ≈ 38%.
O stretching mode of [1] at zero delay. Neglecting the convolution effects due to the finite time and frequency resolution of the pump–probe setup, a lower limit for this ratio can be estimated by Φ = ΔOD(2337 cm−1, t = 1 ns)/|ΔOD(1712 cm−1, t = 500 fs)|. Inspecting Fig. 1b and 3, we find Φ ≈ 3/8 ≈ 38%.
3.4 Time-dependent UV/MIR-spectra in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) O stretching region
O stretching region
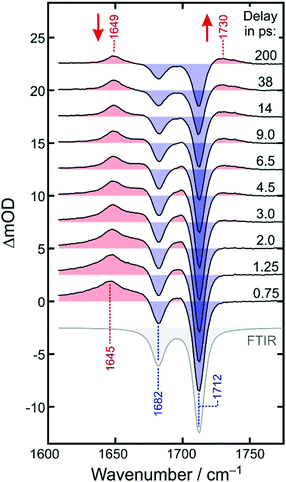
Fig. 4 displays the UV-pump/MIR-probe spectra in the oxalate C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O-region of [1] for various representative time delays ranging between 750 fs and 200 ps. No significant spectral changes were detected on longer times of up to 1 ns. In this series of spectra, the following observations can be made as the time delay increases: (i) the amplitudes of the two negative bleaching bands continuously decrease indicating a dynamic recovery of population in the electronic ground-state of [1]. (ii) The frequency-downshifted induced absorption of [2] initially peaking at 1645 cm−1 gradually decays and simultaneously shifts to higher wavenumbers to approach an asymptotic value of 1649 cm−1. (iii) Another induced absorption, which is located in between the two bleaching bands, builds up and subsequently decays on a time scale of a few picoseconds. (iv) A third induced absorption builds up, which is maximal at ∼1730 cm−1 and is thus, frequency-upshifted with respect to the two bleaching bands. (v) The build-up of the upshifted absorption seems to mirror the decay of the down-shifted absorption as both components evolve on roughly the same time scale.
O-region of [1] for various representative time delays ranging between 750 fs and 200 ps. No significant spectral changes were detected on longer times of up to 1 ns. In this series of spectra, the following observations can be made as the time delay increases: (i) the amplitudes of the two negative bleaching bands continuously decrease indicating a dynamic recovery of population in the electronic ground-state of [1]. (ii) The frequency-downshifted induced absorption of [2] initially peaking at 1645 cm−1 gradually decays and simultaneously shifts to higher wavenumbers to approach an asymptotic value of 1649 cm−1. (iii) Another induced absorption, which is located in between the two bleaching bands, builds up and subsequently decays on a time scale of a few picoseconds. (iv) A third induced absorption builds up, which is maximal at ∼1730 cm−1 and is thus, frequency-upshifted with respect to the two bleaching bands. (v) The build-up of the upshifted absorption seems to mirror the decay of the down-shifted absorption as both components evolve on roughly the same time scale.
Based on previously published extensive DFT calculations,32 we could unequivocally assign the upshifted absorption at 1730 cm−1 to a secondary metal-containing product, [3], that features a bent CO2–ligand, which is bound to the metal in a “side-on” fashion (ηCO2-binding mode, for its molecular structure, see Fig. 1, right). When adopting an overall spin doublet (S = 1/2) configuration, this species can be described by two mesomeric forms; namely, as a carbonite dianion, CO22−, bound to a low-spin iron(III) center and a neutral CO2 bound to a low-spin iron(I) center. Alternatively, when adopting an overall spin quartet (S = 3/2) configuration, the species may also be described either as a carbon dioxide radical anion, CO2˙−, that is antiferromagnetically coupled to a high-spin (S = 5/2) iron(II) center or as a neutral CO2 bound to a high-spin (S = 3/2) iron(I) center. Regardless of the total spin, this structure is IR-spectroscopically reminiscent of a carbonyl compound with a C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O frequency in excess of 1700 cm−1, which is why this binding mode can also be viewed as a heterocyclic ketone, and more specifically, a ferraoxacylcopronanone (FOCP).32
O frequency in excess of 1700 cm−1, which is why this binding mode can also be viewed as a heterocyclic ketone, and more specifically, a ferraoxacylcopronanone (FOCP).32
Obtaining a more comprehensive understanding of the full spectro-temporal evolution of the UV/MIR spectrum in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching region is the subject of the remainder of this paper.
O stretching region is the subject of the remainder of this paper.
3.5 UV-pump/MIR-kinetic traces in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) O stretching region
O stretching region
Equipped with knowledge about the nature of both the primary product at early delay and the secondary product at 1 ns, we are now tasked with extracting the dynamics of the underlying chemical transformation| [FeII(cyclam)(ηO1-OCO˙)]+ → [FeI/II/III(cyclam)(ηCO2-CO2)]+ | (2) |
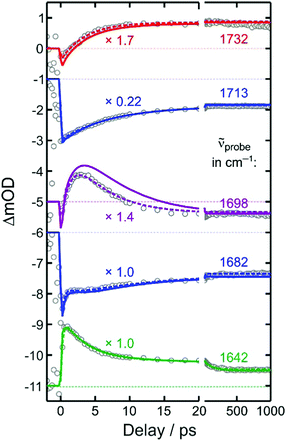
To this end, we inspect in a first step kinetic traces recorded at representative probe wavenumbers (cf.Fig. 5). All traces, ΔmOD(t), could be reproduced in a satisfactory manner using a multi-exponential fit to which a constant offset is added, i.e. ΔmOD(t) = A0 + ΣiAi![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kit). The amplitudes, Ai, and inverse rate constants, τi = 1/ki, are listed in Table 1 for the probe wavenumbers chosen in Fig. 5. It can be seen that the upshifted transient absorption builds up in a monoexponential fashion with a characteristic time constant of 3.6 ps. Almost the same time constant is obtained for an intermediate, decaying component, when the downshifted transient absorption is probed (last row in Table 1). This gives us again a hint that the upshifted band appears at the expense of the downshifted counterpart and that the two different binding modes are connected by the simple unimolecular isomerization expressed in reaction (2).
exp(−kit). The amplitudes, Ai, and inverse rate constants, τi = 1/ki, are listed in Table 1 for the probe wavenumbers chosen in Fig. 5. It can be seen that the upshifted transient absorption builds up in a monoexponential fashion with a characteristic time constant of 3.6 ps. Almost the same time constant is obtained for an intermediate, decaying component, when the downshifted transient absorption is probed (last row in Table 1). This gives us again a hint that the upshifted band appears at the expense of the downshifted counterpart and that the two different binding modes are connected by the simple unimolecular isomerization expressed in reaction (2).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−k1t) + A2
exp(−k1t) + A2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−k2t), where t is the pump probe delay
exp(−k2t), where t is the pump probe delay
![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) probe/cm−1
probe/cm−1 |
A 0 | A 1 | k 1 −1/ps | A 2 | k 2 −1/ps | A 3 | k 3 −1/ps |
|---|---|---|---|---|---|---|---|
| 1732 | 0.48 | −0.72 | 3.6 | ||||
| 1713 | −4.01 | −5.05 | 7.4 | ||||
| 1698 | −0.26 | 2.19 | 4.8 | −2.53 | 1.3 | ||
| 1682 | −1.38 | −0.8 | 11 | 0.40 | 2.0 | −2.00 | 0.30 |
| 1642 | 0.5 | 0.35 | 100 | 1.50 | 3.5 | −2.00 | 0.30 |
However, additional dynamics also affects the spectro-temporal evolution in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O region as up to two more exponential components are required to properly represent the kinetic traces. This becomes most apparent when comparing the two bleaching traces at 1713 cm−1 and 1682 cm−1. Both traces decay to about 40% of their initial bleaching amplitude. Yet, whereas the in-phase C
O region as up to two more exponential components are required to properly represent the kinetic traces. This becomes most apparent when comparing the two bleaching traces at 1713 cm−1 and 1682 cm−1. Both traces decay to about 40% of their initial bleaching amplitude. Yet, whereas the in-phase C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching band of [1] recovers smoothly in a simple single-exponential fashion within 7.4 ps, the complementary out-of-phase band recovers initially on an ultrafast, 300 fs time scale, then remains almost constant during the next 5 ps, and finally decays rather slowly within a few tens of picoseconds. In between the two bleaching bands, kinetic traces are observed, which feature initially a net bleach (cf.Fig. 5, data at 1698 cm−1). This negative signal quickly turns over into an induced absorption within 2 ps, but only to switch sign yet again to become a net residual bleach within about 10 ps.
O stretching band of [1] recovers smoothly in a simple single-exponential fashion within 7.4 ps, the complementary out-of-phase band recovers initially on an ultrafast, 300 fs time scale, then remains almost constant during the next 5 ps, and finally decays rather slowly within a few tens of picoseconds. In between the two bleaching bands, kinetic traces are observed, which feature initially a net bleach (cf.Fig. 5, data at 1698 cm−1). This negative signal quickly turns over into an induced absorption within 2 ps, but only to switch sign yet again to become a net residual bleach within about 10 ps.
3.6 Simulating the spectro-temporal evolution in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h3_char_e001.gif) O stretching region
O stretching region
For understanding the nature of the additional dynamics contributing to the UV/MIR-response in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching region of [1], it is advantageous to remove the two dominating ground-state bleaching bands. To this end, we add the properly weighted stationary FTIR spectrum of the sample to the raw UV/MIR-data.40 The resultant so-called purely absorptive product spectra41 are depicted in Fig. 6 for the same representative time delays chosen in Fig. 4.
O stretching region of [1], it is advantageous to remove the two dominating ground-state bleaching bands. To this end, we add the properly weighted stationary FTIR spectrum of the sample to the raw UV/MIR-data.40 The resultant so-called purely absorptive product spectra41 are depicted in Fig. 6 for the same representative time delays chosen in Fig. 4.
At early delay, the product spectrum is extremely broad ranging from 1600 cm−1 all the way up to 1710 cm−1. Nonetheless, the downshift induced absorption at 1645 cm−1 is again recognized as the spectroscopic fingerprint of the primary ferrous fragment. It appears to be riding on top of a broader, more continuous background absorption, which features an additional distinct spectral modulation with a wavenumber spacing of ca. 13 cm−1. At the earliest delay, the background absorption is maximal around 1680 cm−1 but as the time delay increases, it redistributes drastically along the wavenumber axis to evolve gradually into the two stationary absorption bands of the equilibrated parent at 1682 cm−1 and 1712 cm−1. Therefore, we attribute the background absorption including its subtle modulation to the fraction of complexes, which returns via internal conversion to the structurally intact electronic ground state. However, immediately after electronic relaxation, the parent's ground state is dressed with substantial vibrational excess energy and the vibrational cooling manifests itself in the complex dynamic spectral redistribution.42 Finally, the upshifted absorption arising from the secondary product exhibiting the “side-on”-bound CO2–ligand is also evident as a pronounced shoulder building up on the high-frequency edge of the equilibrated in-phase C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching band of the thermalized parent.
O stretching band of the thermalized parent.
To simulate the full MIR-response shown in Fig. 6 in both the time domain and the frequency domain, four components are needed; namely, the absorptions of the primary and secondary products (shaded in green and red) and the in-phase and out-of-phase combinations of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching mode of the vibrationally excited parent ground sate (both shaded in blue).
O stretching mode of the vibrationally excited parent ground sate (both shaded in blue).
The ground-state contribution was modeled using a simplified anharmonic coupling model for the two C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O modes having harmonic fundamental wavenumbers,
O modes having harmonic fundamental wavenumbers, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0a and
0a and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0b, and diagonal anharmonicities of xaa and xbb. Both degrees of freedom can couple to a fictitious bath mode with a harmonic frequency,
0b, and diagonal anharmonicities of xaa and xbb. Both degrees of freedom can couple to a fictitious bath mode with a harmonic frequency, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0c, by virtue of the off-diagonal anharmonicities, xac and xbc. The absorption spectrum of the vibrationally excited electronic ground state is then written as38,42
0c, by virtue of the off-diagonal anharmonicities, xac and xbc. The absorption spectrum of the vibrationally excited electronic ground state is then written as38,42
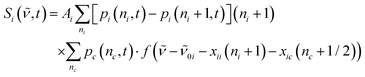 | (3) |
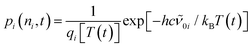 | (4) |
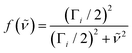 | (5) |
To reproduce the spectral modulation seen at early delays (marked in Fig. 6 by dashed vertical lines) in a satisfactory manner and, at the same time, to minimize the number of free adjustable parameters, we chose equal diagonal anharmonicities, i.e. xaa = xbb= −13 cm−1. Furthermore, a harmonic bath frequency, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0c, of 600 cm−1 together with equal off-diagonal anharmonicities, xac = xbc= −4 cm−1, was required to mimic the modulation depth and the broad background at early delay in a reasonable fashion. Then, with these numbers, harmonic fundamental wavenumbers,
0c, of 600 cm−1 together with equal off-diagonal anharmonicities, xac = xbc= −4 cm−1, was required to mimic the modulation depth and the broad background at early delay in a reasonable fashion. Then, with these numbers, harmonic fundamental wavenumbers, ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0a and
0a and ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0b, of 1727 cm−1 and 1697 cm−1, are necessary to spectrally align the two equilibrated C
0b, of 1727 cm−1 and 1697 cm−1, are necessary to spectrally align the two equilibrated C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O resonances (i = a, b) at late delays with the experimentally observed FTIR-bands at 1717 cm−1 and 1682 cm−1.
O resonances (i = a, b) at late delays with the experimentally observed FTIR-bands at 1717 cm−1 and 1682 cm−1.
Next, for modeling of the spectro-temporal evolution of the relaxing hot ground-state, an ansatz for the time-dependent temperature is needed. It was realized that a single-exponential decay of T(t) was incapable of reproducing the complex reappearance of the thermalized ground-state features for all delays equally well, e.g. if the fit provided a good description for the evolution at short times, it failed completely to describe the long-time dynamics, and vice versa. Therefore, the more flexible bi-exponential decay from an initial temperature, T(0), to a final temperature, T(∞) = 300 K,
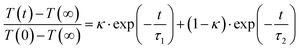 | (6) |
Having found an excellent representation of the ground-state spectral features, we can finally turn our attention to the modeling of the spectroscopic fingerprints of the metal-containing carbon dioxide product complexes. The downshifted primary product absorption is also highly asymmetric at early delays with a very long low-frequency tail. As the delay increases, this band decays and simultaneously, it becomes more symmetrical while slightly blue-shifting by 5 cm−1. It is important to stress that at delays as short as 500 fs, the CO2 fragment is likely to reside in close proximity of the metal-containing fragment. Thus, the subtle frequency upshift from 1645 cm−1 to 1649 cm−1 and the concurrent symmetrization of the band profile may be interpreted as the escape of the triatomic carbonaceous fragment from the mutual solvent shell, the concomitant structural relaxation of the inner coordination sphere of its geminate partner, and the vibrational relaxation.
This peculiar evolution due to the coupled structural/vibrational relaxation can be simulated again using eqn (3)–(6), but now in a purely phenomenological fashion. To this end we use ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) 0i = 1649 cm−1, arbitrarily set xii = 0 and xic = −6 cm−1, and increase the intrinsic linewidth to Γi = 12 cm−1 while keeping the same time-dependent temperature from above. The kinetics (i.e. the delay-dependent amplitude) of the primary product band is best described by a double-exponential decay to which a constant offset is added. The faster 3.5 ps-component accounts for 63%, the slower 100 ps-component for 15% of the total decay with the remaining 22% of the downshifted absorption persisting for quasi-infinite delays. With these parameters, the green-shaded spectra in Fig. 6 are obtained, and together with the ground-state spectral components from above, a near perfect simulation for the dynamically evolving product spectrum is obtained for the low wavenumber portion from ca. 1600 cm−1 all the way down to 1710 cm−1.
0i = 1649 cm−1, arbitrarily set xii = 0 and xic = −6 cm−1, and increase the intrinsic linewidth to Γi = 12 cm−1 while keeping the same time-dependent temperature from above. The kinetics (i.e. the delay-dependent amplitude) of the primary product band is best described by a double-exponential decay to which a constant offset is added. The faster 3.5 ps-component accounts for 63%, the slower 100 ps-component for 15% of the total decay with the remaining 22% of the downshifted absorption persisting for quasi-infinite delays. With these parameters, the green-shaded spectra in Fig. 6 are obtained, and together with the ground-state spectral components from above, a near perfect simulation for the dynamically evolving product spectrum is obtained for the low wavenumber portion from ca. 1600 cm−1 all the way down to 1710 cm−1.
Finally, a model must be built for the upshifted absorption of the secondary product. For simplicity, a Lorentzian profile (cf.eqn (5)) was used that is centered at 1727 cm−1 and that builds up single-exponentially with a time constant of 3.5 ps. The resultant contribution is displayed in Fig. 6 by the red-shaded spectrum and it provides an excellent fit for the remaining high wavenumber portion (>1710 cm−1) of the time-dependent product spectrum. As displayed in Fig. 6 by the blue curve, all four components, i.e. in-phase and out-of-phase C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretches of the vibrationally hot ground state of [1], the anti-symmetric OCO-stretch of the primary product, [2], and the dangling C
O stretches of the vibrationally hot ground state of [1], the anti-symmetric OCO-stretch of the primary product, [2], and the dangling C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch of the secondary FOCP-product, [3], add up to provide a remarkably accurate representation of time- and frequency-dependent MIR-response. Simulated kinetic traces are reproduced in Fig. 5 by the solid curves. Except for the probe wavenumber, located in between the two ground-state bleaches, the global model is practically indistinguishable from the phenomenological biexponential fit and is, hence, also of excellent quality in the time-domain. A comparison of the full global simulation with the entire experimental data set obtained for probe wavenumbers from 1610 cm−1 to 1790 cm−1 and for time delays from 500 fs up to 1 ns is given in the ESI,† as an animation.
O stretch of the secondary FOCP-product, [3], add up to provide a remarkably accurate representation of time- and frequency-dependent MIR-response. Simulated kinetic traces are reproduced in Fig. 5 by the solid curves. Except for the probe wavenumber, located in between the two ground-state bleaches, the global model is practically indistinguishable from the phenomenological biexponential fit and is, hence, also of excellent quality in the time-domain. A comparison of the full global simulation with the entire experimental data set obtained for probe wavenumbers from 1610 cm−1 to 1790 cm−1 and for time delays from 500 fs up to 1 ns is given in the ESI,† as an animation.
3.7 Elementary dynamics and binding-mode isomerization
As was already mentioned in Section 3.5, the decay of the downshifted absorption of [2] and the growth of the upshifted absorption of [3] are highly correlated, both sharing the same (dominant) time constant of 3.5 ps. Since our global fit further corroborates this observation, we now firmly attribute this time constant to the inverse rate of the O-“end-on”-to-“side-on” isomerization reaction stated in eqn (2).The elementary dynamics following the 266 nm-excitation of [1] can now be sketched as follows (see Fig. 7). Starting from a sextet ground-state of the parent and its intact oxalate ligand, the initial absorption of the UV-photon prepares a high-spin LMCT excited state. Whether or not this excited state is dissociative with regard to CO2 loss remains unclear from the recorded data because of the finite time resolution of our experiments. However, within only 500 fs, an unmistakable spectroscopic fingerprint of a neutral carbon dioxide molecule emerges around 2300 cm−1. This distinctive absorption in the ν3-region of CO2 is accompanied by an additional induced absorption peaking near 1645 cm−1. Together, these two signals are indicative of significant structural and electronic rearrangements within the parent's ligand sphere, which involve a carbon–carbon bond breakage and ultimately a full one-electron transfer to the metal center. Owing to the very short time scale, it is highly likely that the neutral CO2 fragment remains loosely attached to the immediate ligand sphere, which in turn, now features a bent OCO-radical anion ligand bound to an iron(II) center via one of its terminal oxygens. Neglecting any changes of the ν3-transition dipole that may be caused by the residual interactions with the nearby metal, a primary quantum yield for Fe(II)/CO2-formation of 38% can be derived from the MIR-response.
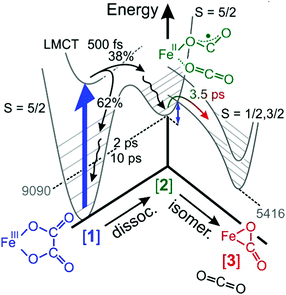 | ||
| Fig. 7 Sketch of the elementary dynamics following the 266 nm-LMCT-excitation (blue vertical arrow) of [1] in liquid DMSO solution. The gray numbers indicate the energies of the primary and secondary products, [2] and [3], in units of cm−1 and were determined through quantum chemical calculations described in ref. 32. The blue double-headed arrow indicates an energy barrier associated with intersystem crossing and the binding-mode isomerization. | ||
The initial UV-photon imparts an excitation of 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 cm−1 to the system and as a result, the primary products are dressed with substantial excess vibrational energy. This holds true for not only the neutral CO2 and its cationic metal-containing geminate partner, but also for the remaining fraction of 62% of all photoexcited parent complexes that return within 500 fs back to the structurally intact electronic ground state in a non-adiabatic fashion. While the neutral CO2 fragment undergoes vibrational cooling on a time scale of 38 ps, the ferric parent, [1], and the ferrous primary product, [2], relax similarly fast with characteristic time constants of 2 ps and 10 ps (cf. wavy arrows in Fig. 7). The observation that the CO2 fragment relaxes independently from its geminate partner is suggestive of a rather weak residual inter-fragment interaction as compared to the interactions of the positively charged (parent and primary product) complexes with their surrounding DMSO solvent.
700 cm−1 to the system and as a result, the primary products are dressed with substantial excess vibrational energy. This holds true for not only the neutral CO2 and its cationic metal-containing geminate partner, but also for the remaining fraction of 62% of all photoexcited parent complexes that return within 500 fs back to the structurally intact electronic ground state in a non-adiabatic fashion. While the neutral CO2 fragment undergoes vibrational cooling on a time scale of 38 ps, the ferric parent, [1], and the ferrous primary product, [2], relax similarly fast with characteristic time constants of 2 ps and 10 ps (cf. wavy arrows in Fig. 7). The observation that the CO2 fragment relaxes independently from its geminate partner is suggestive of a rather weak residual inter-fragment interaction as compared to the interactions of the positively charged (parent and primary product) complexes with their surrounding DMSO solvent.
Importantly, a pronounced spectral modulation with a spacing of 4 cm−1 was observed in the purely absorptive hot ground-state absorption (see Fig. 6). We attributed this feature to the coupling of the oxalate CO-stretching modes to a bath mode having a frequency of 600 cm−1. The origin of the bath mode (low-frequency solvent mode vs. intramolecular vibration) is unclear at this stage. However, the DFT-normal mode analysis of the parent, [1], predicts that this region is governed by the in-plane OOC–COO stretching and shearing modes of the oxalate ligand with only little activity from the cyclam moiety. If the spectral modulation is indeed caused by the excitation of these two oxalate modes; this would suggests that the systems moves initially along the C–C dissociation coordinate on the LMCT-excited state potential. However, prior to decomposing fully into neutral CO2 and species, [2], a fraction, 62%, of the complexes returns back to the ground state, which strongly advocates for a diminishing energy gap between the ground and excited states as the structure evolves on the LMCT-state toward the dissociation products (cf.Fig. 7). In other words, motion along the C–C dissociation coordinate is also required for the system to relax electronically, which is why the structurally intact ground state exhibits vibrational excitation particularly in the low-frequency oxalate modes around 600 cm−1.
The formation of the secondary “side-on”-product, [3], is observed as a MIR-absorption building up around 1730 cm−1 with a time-constant of 3.5 ps, and it is undeniably born from the O-“end-on”-primary product serving as its direct precursor. As judged by the band area ratio between downshifted and upshifted absorptions, the two products, [2] and [3], are formed in about equal amounts within a maximal time delay of 1 ns.32 Their fate on longer time scales is not known at this stage. We rationalize this product distribution by the kinetic competition between vibrational relaxation and intersystem crossing from the sextet electronic manifold into the doublet and quartet manifold. The electronic structure calculations suggest32 that the FOCB-structure is unstable in the high-spin configuration. Species, [3], occupies an intermediate-spin ground-state, which is 3674 cm−1 below the high-spin ground-state of species, [2]. Thus, based on energetic arguments, one would expect the ηCO2-binding mode to prevail, quite in contrast to the experimental product spectrum recorded after 1 ns. This discrepancy between experimental observation and theoretical prediction is indicative of a substantial energy barrier inhibiting the binding-mode isomerization. Here, this barrier is traced back to the sextet-to-quartet intersystem crossing, which kinetically traps the ηO,bent1-binding mode quite efficiently (see Fig. 7).
4. Conclusions
In summary, we have studied the primary processes of the ferric complex, [FeIII(cyclam)(C2O4)]+, featuring the photolabile oxalato ligand. Following an initial oxalate-to-iron charge-transfer excitation, the departure of a neutral carbon dioxide from the ligand sphere is monitored, which results in the formation of a ferrous primary product that exhibits an O-“end-on”-bound CO2˙−-ligand. The open-shell carbonaceous ligand reveals itself by its asymmetric OCO-stretching mode, which appears downshifted relative to the oxalate-C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O absorptions of the parent complex. As the product complex vibrationally cools, a secondary structural relaxation occurs, which transforms a fraction of the primary ferrous complexes into a cyclic ferraoxacyclopropanone. This O-“end-on”-to-“side-on” or, equivalently, ηO,bent1-to-ηCO2-binding-mode isomerization is formally spin–forbidden since it necessitates a high-spin to intermediate-spin intersystem crossing. As a result, the non-adiabatic transition has to compete with the rapid vibrational cooling, thereby leading to a partial trapping of the system in the metastable high-spin state of [Fe(cyclam)(CO2)]+ and hence in the unusual ηO,bent1-binding mode. Its fate and that of its “side-on” companion on time scales in excess of 1 ns will be the subject of further step-scan-FTIR-spectroscopic investigations that are currently ongoing in our laboratories.
O absorptions of the parent complex. As the product complex vibrationally cools, a secondary structural relaxation occurs, which transforms a fraction of the primary ferrous complexes into a cyclic ferraoxacyclopropanone. This O-“end-on”-to-“side-on” or, equivalently, ηO,bent1-to-ηCO2-binding-mode isomerization is formally spin–forbidden since it necessitates a high-spin to intermediate-spin intersystem crossing. As a result, the non-adiabatic transition has to compete with the rapid vibrational cooling, thereby leading to a partial trapping of the system in the metastable high-spin state of [Fe(cyclam)(CO2)]+ and hence in the unusual ηO,bent1-binding mode. Its fate and that of its “side-on” companion on time scales in excess of 1 ns will be the subject of further step-scan-FTIR-spectroscopic investigations that are currently ongoing in our laboratories.
We conclude this paper by emphasizing that, to our knowledge, such ultrafast binding mode isomerization dynamics have not yet been reported. We believe, however, that such processes hold the key to a thorough understanding of and successful control over the molecular and electronic structures of transition metal complexes featuring the carbon dioxide ligand. Importantly, the two distinct binding modes may actually feature quite distinct chemical reactivities. While the spin density of the bent-O-“end-on” species is mostly located at the central carbon atom, that of the “side-on” species resides primarily at the metal. Furthermore, in the bent-O-“end-on” mode, the C-atom of the triatomic ligand is quite exposed and readily accessible for possible reaction partners, whereas in the bent-O-“end-on” mode, the same atom is heavily involved in metal–ligand bonding. Thus, it would not come as a total surprise if the ηO,bent1-motif would pave the way toward a carbon-centered reactivity, while the ηCO2-motif would facilitate proton/electron transfer reactivity and C–O bond fission.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the financial support by the Deutsche Forschungsgemeinschaft through the grant VO 593/7-1.Notes and references
- D. H. Gibson, Chem. Rev., 1996, 96, 2063–2095 CrossRef CAS PubMed.
- D. H. Gibson, Coord. Chem. Rev., 1999, 185–186, 335–355 CrossRef CAS.
- W. Leitner, Coord. Chem. Rev., 1996, 153, 257–284 CrossRef CAS.
- A. Paparo and J. Okuda, Coord. Chem. Rev., 2017, 334, 136–149 CrossRef CAS.
- X. L. Yin and J. R. Moss, Coord. Chem. Rev., 1999, 181, 27–59 CrossRef CAS.
- H. Arakawa, M. Aresta, J. N. Armor, M. A. Barteau, E. J. Beckman, A. T. Bell, J. E. Bercaw, C. Creutz, E. Dinjus, D. A. Dixon, K. Domen, D. L. DuBois, J. Eckert, E. Fujita, D. H. Gibson, W. A. Goddard, D. W. Goodman, J. Keller, G. J. Kubas, H. H. Kung, J. E. Lyons, L. E. Manzer, T. J. Marks, K. Morokuma, K. M. Nicholas, R. Periana, L. Que, J. Rostrup- Nielson, W. M. H. Sachtler, L. D. Schmidt, A. Sen, G. A. Somorjai, P. C. Stair, B. R. Stults and W. Tumas, Chem. Rev., 2001, 101, 953–996 CrossRef CAS PubMed.
- M. Cokoja, C. Bruckmeier, B. Rieger, W. A. Herrmann and F. E. Kuhn, Angew. Chem., Int. Ed., 2011, 50, 8510–8537 CrossRef CAS PubMed.
- M. Aresta, in Activation of Small Molecules. Organometallic and Bioinorganic Perspectives, ed. W. B. Tolman, Wiley-VCH, Weinheim, 2006, pp. 1–41 Search PubMed.
- M. Aresta, Carbon Dioxide as a Chemical Feedstock, Wiley-VCH Verlag, Weinheim, 2010 Search PubMed.
- Q. Liu, L. P. Wu, R. Jackstell and M. Beller, Nat. Commun., 2015, 6, 5933 CrossRef PubMed.
- M. Aresta and A. Dibenedetto, Dalton Trans., 2007, 2975–2992 RSC.
- S. Sakaki and A. Dedieu, Inorg. Chem., 1987, 26, 3278–3284 CrossRef CAS.
- M. Aresta, C. F. Nobile, V. G. Albano, E. Forni and M. Manassero, J. Chem. Soc., Chem. Commun., 1975, 636–637 RSC.
- M. Aresta and C. F. Nobile, J. Chem. Soc., Dalton Trans., 1977, 708–711 RSC.
- M. G. Mason and J. A. Ibers, J. Am. Chem. Soc., 1982, 104, 5153–5157 CrossRef CAS.
- M. Aresta and C. F. Nobile, Inorg. Chim. Acta, 1977, 24, L49–L50 CrossRef CAS.
- T. Herskovitz, J. Am. Chem. Soc., 1977, 99, 2391–2392 CrossRef CAS.
- H. H. Karsch, Chem. Ber., 1977, 110, 2213–2221 CrossRef CAS.
- S. Komiya, M. Akita, N. Kasuga, M. Hirano and A. Fukuoka, J. Chem. Soc., Chem. Commun., 1994, 1115–1116 RSC.
- M. Sakamoto, I. Shimizu and A. Yamamoto, Organometallics, 1994, 13, 407–409 CrossRef CAS.
- C. Jegat, M. Fouassier and J. Mascetti, Inorg. Chem., 1991, 30, 1521–1529 CrossRef CAS.
- C. Jegat, M. Fouassier, M. Tranquille and J. Mascetti, Inorg. Chem., 1991, 30, 1529–1536 CrossRef CAS.
- M. A. Bennett, Chem. Rev., 1962, 62, 611–652 CrossRef CAS.
- M. J. S. Dewar and G. P. Ford, J. Am. Chem. Soc., 1979, 101, 783–791 CrossRef CAS.
- Y. Jean, Molecular Orbitals of Transition Metal Complexes, Oxford University Press, New York, 2005 Search PubMed.
- J. C. Calabrese, T. Herskovitz and J. B. Kinney, J. Am. Chem. Soc., 1983, 105, 5914–5915 CrossRef CAS.
- I. Castro-Rodriguez, H. Nakai, L. N. Zakharov, A. L. Rheingold and K. Meyer, Science, 2004, 305, 1757–1759 CrossRef CAS PubMed.
- D. M. Mangiante, R. D. Schaller, P. Zarzycki, J. F. Banfield and B. Gilbert, ACS Earth Space Chem., 2017, 1, 270–276 CrossRef CAS.
- S. Straub, P. Brünker, J. Lindner and P. Vöhringer, Phys. Chem. Chem. Phys., 2018, 20, 21390–21403 RSC.
- S. Straub, P. Brünker, J. Lindner and P. Vöhringer, Angew. Chem., Int. Ed., 2018, 57, 5000–5005 CrossRef CAS PubMed.
- F. H. Pilz, J. Lindner and P. Vöhringer, Phys. Chem. Chem. Phys., 2019, 21, 23803–23807 RSC.
- S. Straub and P. Vöhringer, Angew. Chem., Int. Ed., 2021, 60, 2519–2525 CrossRef CAS PubMed.
- A. Paparo and J. Okuda, J. Organomet. Chem., 2018, 869, 270–274 CrossRef CAS.
- M. F. Zhou and L. Andrews, J. Chem. Phys., 1999, 110, 2414–2422 CrossRef CAS.
- K. O. Hartman and I. C. Hisatsune, J. Chem. Phys., 1966, 44, 1913–1918 CrossRef CAS.
- B. Wezisla, J. Lindner, U. Das, A. C. Filippou and P. Vöhringer, Angew. Chem., Int. Ed., 2017, 56, 6901–6905 CrossRef CAS PubMed.
- C. Reichardt, J. Schroeder and D. Schwarzer, J. Phys. Chem. A, 2007, 111, 10111–10118 CrossRef CAS PubMed.
- P. Hamm, S. M. Ohline and W. Zinth, J. Chem. Phys., 1997, 106, 519–529 CrossRef CAS.
- W. D. Allen, Y. Yamaguchi, A. G. Csaszar, D. A. Clabo, R. B. Remington and H. F. Schaefer, Chem. Phys., 1990, 145, 427–466 CrossRef CAS.
- The weight is found from the data collected at the shortest time delay, at which the coherent artefact becomes negligibly small. In our pump–probe setup, this delay is typically 500 fs or less, depending upon the sample. We then compute the difference spectrum, ΔOD(ν,500 fs) − c·FTIR(ν), and systematically vary the factor, c, until the negative signals disappear for all ν. The purely absorptive product spectrum is then calculated from ΔOD(ν,t) – c·FTIR(ν) using the same weight, c, for all delays, t.
- H. Vennekate, D. Schwarzer, J. Torres-Alacan and P. Vöhringer, J. Am. Chem. Soc., 2014, 136, 10095–10103 CrossRef CAS PubMed.
- S. Straub, J. Stubbe, J. Lindner, B. Sarkar and P. Vöhringer, Inorg. Chem., 2020, 59, 14629–14642 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Kinetic traces in the CO2-ν3-region, movie of the absorptive UV/MIR-response. See DOI: 10.1039/d1cp02300d |
| This journal is © the Owner Societies 2021 |