Interfacial photoinduced carrier dynamics tuned by polymerization of coronene molecules encapsulated in carbon nanotubes: bridging type-I and type-II heterojunctions†
Xiao-Ying
Xie
a,
Jia-Jia
Yang
b,
Xiang-Yang
Liu
c,
Qiu
Fang
b,
Wei-Hai
Fang
b and
Ganglong
Cui
 *b
*b
aThe Laboratory of Theoretical and Computational Chemistry, School of Chemistry and Chemical Engineering, Yantai University, Yantai, 264005, China
bKey Laboratory of Theoretical and Computational Photochemistry, Ministry of Education, College of Chemistry, Beijing Normal University, Beijing 100875, China. E-mail: ganglong.cui@bnu.edu.cn
cCollege of Chemistry and Material Science, Sichuan Normal University, Chengdu 610068, China
First published on 24th May 2021
Abstract
Carbon nanomaterials play important roles in modern scientific research. Integrating different carbon-based building blocks into nano-hybrid architectures not only takes full advantage of each component, but also brings in novel interfacial properties. Herein, we have employed density functional theory (DFT) calculations to investigate the effects of polymerization degree of coronene molecules encapsulated in single-walled carbon nanotubes (SWNTs) (19,0) on their interfacial properties. The present results reveal that the interfacial properties of the formed heterojunctions are remarkably regulated by the polymerization degree. For example, monomer- and dimer-encapsulated SWNTs are type-I heterojunctions in which interfacial excitation energy transfer is preferred, whereas interfacial charge carrier transfer is favorable in trimer- and polymer-encapsulated SWNTs because they are type-II heterojunctions. On the other hand, we have employed the time-domain nonadiabatic dynamics simulation approach to explore the interfacial carrier dynamics in type-II polymer-encapsulated SWNT heterojunctions. It is found that the electron and hole transfer processes are asymmetric and occur in opposite directions and at different rates. The former takes place from polymers to SWNTs in an ultrafast way (ca. 370 fs), whereas the latter occurs slowly from SWNTs to polymers (ca. 24 ps). A closer analysis uncovers the fact that the different carrier transfer rates mainly originate from the different densities of the acceptor states, energy differences and inter-state couplings between the donor and acceptor states. Finally, the present work demonstrates that the polymerization degree could act as a new regulating strategy to tune the interfacial properties of molecule-encapsulated SWNT heterojunctions.
Introduction
Since the discovery of C60 in 1985,1 a rich family of carbon-based nanoscale materials, including carbon nanotubes (CNTs),2,3 graphene,4 graphene nanoribbons (GNRs)5,6 and so on, has been emerging and flourishing in the nanomaterials science society.7 In recent years, the exploration of combining different carbon-based nanoscale materials to fabricate novel carbon nano-hybrid architectures has further broadened the scope of materials science. Their potential applications in the fields of photovoltaics, photodetectors, photocatalysts, etc. are investigated experimentally and theoretically due to their intrinsic unique interfacial properties.8–12 For instance, studies on inserting C6013,14 or GNRs15,16 into CNTs, placing single-walled carbon nanotubes (SWNTs) among graphene planes,17 have been reported. On one hand, carbon-based hybrid architectures formed by encapsulating SWNTs with GNRs (GNR@SWNT) are expected to achieve high photo-to-electrical conversion via effective charge separation between the two components; on the other hand, SWNTs can act as protectors of enclosed GNRs to prevent them from being destroyed.18,19Polymerization of polycyclic aromatic hydrocarbon (PAH) molecules is a facile and efficient method to construct hydrogen-terminated GNRs encapsulated in SWNTs.20–27 In the fusion reaction, a SWNT serves as a one-dimensional reactor, compelling the PAH molecules to align edge-to-edge and be polymerized step by step. Coronene is a typical PAH molecule, while the encapsulation products with SWNTs are extremely sensitive to the preparation conditions. Talyzin and coauthors demonstrated the formation of H-terminated GNRs inside SWNTs through thermally induced coronene precursor fusion.28 However, Okazaki et al. observed coaxially columnar stacked coronene molecules inside nanometer-scale SWNTs instead of GNRs.29 Later, Anoshkin and co-workers pointed out that the difference between these two experiments is ascribed to the choice of synthesis conditions: dimeric coronene (dicoronylene) and molecular stacking columns are obtained under high vacuum; in contrast, under an argon atmosphere (0.17 MPa), the molecular blocks are polymerized and fused to form GNRs.30 Notably, Talyzin et al. identified coronene dimers and trimers during the step-by-step polymerization process.28 So, a cornucopia of encapsulation products can be obtained by controlling the synthesis conditions.26–33 Concomitant with the various encapsulation products are the different interfacial properties and promising applications of the corresponding nano-encapsulation systems.
The photophysical properties of polymer@SWNT nanocomposites are closely related to photoinduced charge and energy transfer processes. Uncovering the photoinduced interfacial carrier dynamics is of great importance to targeted-design optoelectronic devices with improved performance. More recently, Nakamura et al. explored the charge transfer process and relaxation dynamics in coronene–polymer@SWNT composites using a series of techniques.34 With the aid of energy band structures calculated by local density approximation (LDA), the authors ascribed the optical absorption at ∼1.7 and 3.4 eV in the differential absorption spectra to the electron transitions originating from the coronene polymer. After photoirradiation with an excitation energy of 1.59 eV, a photoinduced electron–hole pair is created in the encapsulated polymer coronene, and then the electron is transferred to the SWNT on a timescale of ∼0.38 ps. As mentioned above, one would obtain various encapsulating systems via inserting coronene molecules into SWNTs, e.g., monomer@SWNT, dimer@SWNT, trimer@SWNT, and polymer@SWNT. However, as far as our knowledge extends, systematic studies on the correlations between the distinct polymerization degree of inserted coronenes and the photoinduced carrier dynamics of integrated hybrid nanosystems are scarce. Efforts are still desirable to map out more details of the polymerization effects, which will lead to suitable applications of integrated systems.
In this work, we aim at computationally exploring the effects of the polymerization degree of coronenes encapsulated within a specific (19,0) SWNT on their interfacial electronic structures by using periodic DFT calculations. It is known that the band alignment of heterojunctions is mainly classified into two types (type I and type II) according to the relative position of both the valence band maximum (VBM) and the conduction band minimum (CBM) states of the two relevant components (see Fig. S1 for the schematic diagram, ESI†). The results show that the hybrid structures of SWNTs encapsulated with the monomer and dimer coronene molecules, i.e., monomer@SWNT and dimer@SWNT, belong to type-I heterojunctions, which are beneficial for interfacial excitation energy transfer dynamics. In obvious contrast, those encapsulated with the coronene trimer and polymer, i.e., trimer@SWNT and polymer@SWNT, are type-II heterojunctions. Their interfaces favor interfacial charge carriers, i.e., electron or hole transfer. In addition to static electronic structure calculations, we also simulate light-induced charge carrier relaxation dynamics of the polymer@SWNT heterojunction using the recently developed DFT-based time-domain nonadiabatic dynamics simulation approach implemented with localized atomic orbital basis sets. It is found that the interfacial electron transfer is two orders of magnitude faster than the hole transfer upon photoexcitation at the polymer@SWNT heterojunction. The origin leading to this difference stems from the different densities of the acceptor states, energy differences and inter-state couplings between the donor and acceptor states (see below).
Simulation details
A semi-conducting zigzag (19,0) SWNT with a diameter of 14.87 Å is chosen according to a previous study.34 Furthermore, the adsorption energy indicating the binding strength between the SWNT and polymer coronene is also calculated. The results show that the larger the diameter is, the weaker the adsorption is. This is due to the reduced van der Waals interactions between the polymer coronene and SWNT.28 Meanwhile, if the diameter of the SWNT is smaller than that of the (19,0) SWNT, the semi-conducting nanotube would deform due to the strong repulsion interactions between the coronene and SWNT. Taken together, the zigzag (19,0) SWNT is selected as our research model. Monomer and polymer coronenes are placed flat inside the SWNTs to model a coronene–monomer-encapsulated SWNT (containing 340 atoms) and coronene–polymer-encapsulated SWNT (containing 368 atoms), respectively. To avoid the arbitrary intermolecular interactions, the SWNTs are elongated twice to integrate the dimer and trimer coronenes to construct a coronene–dimer-encapsulated SWNT (containing 668 atoms) and coronene–trimer-encapsulated SWNT (containing 696 atoms), respectively. A vacuum layer of 10 Å is applied along the directions normal to the axis of the SWNTs to avoid spurious interactions between the two images. The density functional theory (DFT) method implemented in the Quickstep/CP2K package is employed to optimize the geometries and perform adiabatic molecular dynamics simulations.35,36 The energy cutoff for the real space grid is set to 400 Ry. The Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA) is selected to deal with exchange–correlation interactions.37 At the same time, the optimized double-ζ Gaussian basis sets together with the Goedecker–Teter–Hutter (GTH) pseudopotentials are used.38–42 The van der Waals (vdW) interactions are taken into consideration by means of the empirical dispersion correction method proposed by Grimme et al.43 The Heyd–Scuseria–Ernzerhof (HSE06) functional with the auxiliary density matrix method (ADMM) is used to recalculate the density of states (DOS) and projected DOS (PDOS).44–46 Only the gamma point is included in the calculations owing to the rather large simulation models.With respect to molecular dynamics simulations, a 1 ps canonical molecular dynamics simulation is first performed to heat the optimized geometry from 0 K to 300 K using the Nosé–Hoover chain thermostat with a chain length of five.47,48 The atomic time-step of nuclear propagation is set to 1.0 fs. Then, 100 initial conditions are randomly selected from a 5 ps microcanonical trajectory.49–51 1000 surface-hopping trajectories are propagated for each initial condition. Therefore, a total of 100 × 1000 trajectories are prepared for subsequent nonadiabatic dynamics simulations (see Fig. S2 for the convergence test, ESI†). For electron transfer, each trajectory propagates for 1 ps. For hole transfer, the previous 5 ps microcanonical trajectory is sequentially iterated three times resulting in a 15 ps trajectory and then all the trajectories propagate for 6 ps.52,53 The empirical quantum decoherence correction (0.1 a.u.) proposed by Granucci et al. is adopted for surface-hopping dynamics simulations.54 The reported dynamical results are averaged over all the prepared trajectories. More theoretical backgrounds and simulation details can be found in the ESI† and our previous studies.55–58
It is worth emphasizing that the present nonadiabatic carrier dynamics simulation method is different from the linear-response time-dependent density functional theory (LR-TDDFT)-based nonadiabatic dynamics simulation method, which has been widely used to simulate the excited-state dynamics of isolated molecules.59–61 In the LR-TDDFT-based nonadiabatic dynamics simulation, the total electronic wavefunction is linearly expanded with relevant adiabatic electron states that are further linearly expanded with Slater determinants from the LR-TDDFT calculations and an equation of motion (EOM) is finally obtained based on the time-dependent Schrödinger equation. However, such kind of nonadiabatic dynamics simulations are not affordable computationally for periodic systems. Instead, photoinduced nonadiabatic carrier (hole or electron) dynamics simulations are adopted for extended systems. In this situation, the total electron or hole wavefunction is expanded linearly by relevant electron or hole states (corresponding to the Kohn–Sham orbitals from the DFT calculations). Similarly, an EOM turns out based on the time-dependent Kohn–Sham equation from the TDDFT theory. Of course, these two EOMs are mathematically the same, but the associated quantities are different physically. The former needs the energies of the electronic states and the relevant nonadiabatic couplings between the electronic states, whereas the latter needs the energies of the electron or hole states (i.e. Kohn–Sham orbital energies) and the nonadiabatic couplings between these orbitals. This scheme was proposed by Prezhdo and coworkers62,63 and extensively applied to simulate the photoinduced carrier dynamics of periodic systems.64,65
Results and discussion
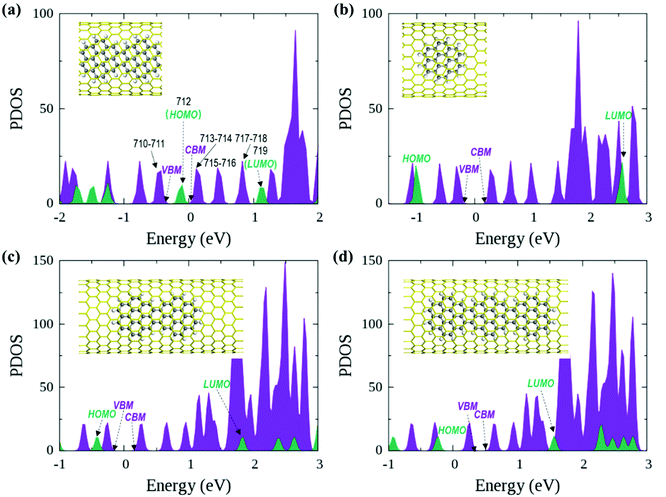
In the optimized polymer@SWNT model, the coronene polymer is coaxial with the SWNT and planar at the optimized minimum-energy structure (see Fig. 1a). After heating to 300 K, the backbone of the coronene polymer distorts much more significantly than that of the SWNT due to the weaker rigidity (see Fig. S3, ESI†), which is in accordance with Zhou's results.66 Then, we have studied the relative energies of the corresponding band states that are involved in the charge transfer processes. Fig. 1a and Fig. S3 (ESI†) detail the projected density of states (PDOS) of polymer@SWNT at 0 K and 300 K calculated at the HSE06 level (see Fig. S4 for PBE + D3, ESI†). The conduction band minimum state, referred to as CBM in Fig. 1, and the five conduction states of the SWNT (referred to as 714–718 in Fig. 1a) are lower than the lowest unoccupied molecular orbital (LUMO) of the polymer in the view of energy. In addition, HOMO is higher than the valence band maximum (VBM) state. Clearly, the CBM state and the higher five states of the SWNT are located between the HOMO and LUMO of the polymer. In the same way, its HOMO is located between the VBM and CBM states of the SWNT. The above results corroborate that polymer@SWNT is a type-II heterojunction. That is, the charge transfer takes place after a suitable photon is absorbed. To be more specific, when the polymer is photoirradiated, an electron is excited into the LUMO and a hole is simultaneously left in the HOMO (see Fig. 1a). Subsequently, the excited electron that transferred from the polymer component to the SWNT component is facile because this process is thermodynamically exothermic. Alternatively, the hole at the VBM state of the SWNT can move to the HOMO of the polymer after the SWNT is photoexcited. In general, the PDOS calculated by the HSE06 functional has larger energy gaps compared to the PDOS obtained at the PBE + D3 level. For example, the PBE + D3 calculated HOMO–LUMO gap of the polymer is 0.83 eV versus 1.25 eV at the HSE06 level. Nonetheless, these two methods share similar results and lead to the same conclusion that the intrinsic force can drive the electron or hole transfer process that occurs efficiently between the polymer and the SWNT components depending on the different light-harvesting components. The PDOS of polymer@SWNT at 300 K, calculated based on one snapshot, is also provided in Fig. S3 (ESI†), which looks very similar to the one shown in Fig. 1a. As mentioned above, the polymer@SWNT model is a type-II heterojunction, which makes it crucial to attain considerable open-circuit voltages. But, what will happen if the encapsulated coronene molecules are not well polymerized in the SWNT? Do the different polymerization degrees affect their interfacial properties?To answer these questions, we further construct monomer@SWNT, dimer@SWNT, and trimer@SWNT models in which all the encapsulated monomer, dimer, and trimer are parallel to the tube axis inside the SWNT. Note that for all the constructed systems, the centroids of the embedded species well coincided with that of the zigzag (19,0) SWNT used. The optimized structures are presented in Fig. 1b–d. We also calculate the DOS and PDOS of each heterojunction at the HSE06 and PBE + D3 levels (see Fig. 1 and Fig. S4, ESI†). Evidently, the energy-level alignment of monomer@SWNT between its two components is different from that of polymer@SWNT (see Fig. 1bvs.Fig. 1a). Both the VBM and CBM states of the SWNT are located between the HOMO and LUMO of the encapsulated monomer, indicating that monomer@SWNT is a type-I heterojunction, unlike the type-II polymer@SWNT heterojunction. In such a situation, upon photoexcitation, an interfacial excitation energy transfer is preferred to occur from the monomer to the SWNT component since the LUMO and HOMO states of the monomer are higher and lower than the CBM and VBM states of the SWNT component, respectively. Similarly, dimer@SWNT is still a type-I heterojunction (see Fig. 1c). But the HOMO state of the dimer is up-shifted a lot to get close to the VBM state of the SWNT component. Meanwhile, the LUMO state is slightly down-shifted. Thus, the HOMO–LUMO gap of the dimer becomes narrower than that in monomer@SWNT. The previous studies also illustrate that the fusion of coronene molecules in a free molecular phase can reduce the energy gap between HOMO and LUMO.27,67 By extrapolating the energies of the VBM, HOMO, CBM, and LUMO states, as shown in Fig. 2, one can easily find that the HOMO state remains up-shifted and the LUMO state remains down-shifted with the increase of the polymerization degree. This may result from the elongation of the conjugated carbon chain.
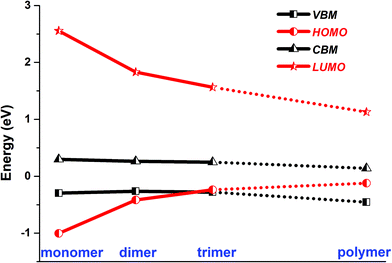 | ||
| Fig. 2 HSE06 calculated energies of the VBM and CBM states of SWNT, and the HOMO and LUMO states of monomer, dimer, trimer, and polymer encapsulated within SWNT. | ||
The turning point appears when the trimer is encapsulated inside the SWNT used. The HOMO state of the trimer becomes a little higher than the VBM state of the SWNT component, which is qualitatively different from those observed in the preceding monomer@SWNT and dimer@SWNT models, although the LUMO state still stays above the CBM state of the SWNT component. In other words, trimer@SWNT is changed to a type-II heterojunction and its HOMO–LUMO gap is reduced to 1.80 eV at the HSE06 level.
Upon further increasing the polymerization degree, the energy of the HOMO state remains up-shifted and finally becomes higher than the VBM state of the SWNT component leading to a type-II heterojunction. At the same time, the energy gap between HOMO and LUMO continues to shrink to 1.25 eV at the HSE06 level. Furthermore, the energy gap between the LUMO state of the polymer and the CBM state of the SWNT component continues to decrease, thereby further accelerating the interfacial electron transfer from the former to the latter. Differently, the energy gap between the HOMO state of the polymer and the VBM state of the SWNT component becomes larger than that at the turning point, i.e., trimer@SWNT. Hence, the interfacial hole transfer from the SWNT component to the polymer component should become slower than that in trimer@SWNT (see Fig. 2).
Overall speaking, the present study has computationally demonstrated that the polymerization degree of coronene molecules embedded in a SWNT can tune the interfacial and optoelectronic properties of a coronene-based SWNT heterojunction. First, the heterojunction changes from type-I to type-II. This is mainly originated from the significant up-shifting and down-shifting of the energies of the HOMO and LUMO states from the monomer via dimer and trimer to the polymer embedded in the SWNT used. The different alignment of energy levels of the two components will completely change the interfacial charge carrier dynamical behaviors. In type-I heterojunctions, that is, monomer@SWNT and dimer@SWNT, the excitation energy transfer from the monomer or dimer to the SWNT is favorable in the view of energy.
In contrast, the interfacial hole and electron transfer processes are preferred to occur between the trimer or polymer and the SWNT in the trimer@SWNT or polymer@SWNT heterojunction. On the other hand, the band gaps of the entire heterojunction and its individual components also vary greatly upon increasing the polymerization degree of the coronene molecules embedded in the SWNT (Table 1). These differences should lead to distinct optoelectronic properties, which is worthy of further experimental exploration.
| Band gap | HOMO | LUMO | VBM | CBM | |
|---|---|---|---|---|---|
| a VBM/CBM and HOMO/LUMO represent the highest occupied and lowest unoccupied states of the SWNT and coronene-based components, respectively; band gap is calculated based on the highest occupied and lowest unoccupied levels of the whole heterojunction system. | |||||
| Monomer@SWNT | 0.60 | −1.00 | 2.56 | −0.30 | 0.30 |
| Dimer@SWNT | 0.52 | −0.42 | 1.83 | −0.26 | 0.26 |
| Trimer@SWNT | 0.52 | −0.24 | 1.56 | −0.28 | 0.25 |
| Polymer@SWNT | 0.58 | −0.12 | 1.13 | −0.46 | 0.14 |
Recently, the experiments by Nakamura et al. demonstrated that the interfacial charge carrier transfer across the interface of polymer@SWNT occurs on an ultrafast timescale (∼0.38 ps).34 But, only the electron transfer process through exciting polymer coronene is studied by the experimental group.34 However, as discussed above, the hole transfer from the SWNT to the polymer coronene is facile when the SWNT acts as a light-harvesting species. Even though the ends of these two plots are the same, the involved rates of charge transfer could be quite different.68,69 What's more, it is desirable to establish an in-depth understanding of the mechanisms and key factors that regulate the complicated carrier dynamics driven by photoexcitation in polymer@SWNT. To delve into this issue, the photoinduced charge transfer processes between the SWNT and the polymer coronene based on the coronene–polymer-encapsulated SWNT hybrid system are further quantitatively investigated employing the nonadiabatic molecular dynamics (NAMD) simulations. This approach has been applied to tackle many photoinduced charge transfer processes of carbon nanotube-related systems before.66,69–77
It is clear from the preceding discussion that polymer@SWNT is a type-II heterojunction. If the photoexcitation takes place within the polymer component, the excited electron and hole will occupy its LUMO and HOMO states, respectively. When considering the band-edge excitation, the HOMO and LUMO states will be occupied correspondingly. Since the LUMO state of the embedded polymer is much higher than the CBM state of the SWNT, the electron transfer from the former to the latter is allowed in the view of energy. However, the corresponding hole transfer process is inhibited because the HOMO state is higher than the VBM state. Differently, if the SWNT is photoexcited with the near-bandgap energy, the hole transfer process from the SWNT component to the polymer component opens up, whereas the electron transfer process is suppressed because the CBM state of the SWNT is lower than the LUMO state of the polymer. Taken together, one can find that the dynamics of the interfacial electron and hole transfer is asymmetric. Specifically, the SWNT excitation benefits the hole transfer to the polymer while the polymer excitation drives the electron transfer to the SWNT. This asymmetric feature might be exploited to control the direction of the interfacial charge carrier dynamics in the SWNT–coronene-based hybrid heterojunctions. Next, we will employ the DFT-based time-domain nonadiabatic carrier dynamics simulation approach to explore these two asymmetric interfacial carrier processes.
First, we focus on the interfacial electron transfer to the SWNT from the photoexcited polymer. As discussed above, upon the band-edge excitation energy, ca. 1.25 eV at the HSE06 level, the excited electron will occupy the LUMO state, which is hence selected as the initial electron state. As seen from Fig. S5 and S6 (ESI†), this state is of obvious π character and its spatial distribution is completely localized within the polymer itself without any residual wavefunction on the SWNT. Below this electron donor state, there are six acceptor states available (index: 713 to 718). So, there are seven electron states included in the electron transfer simulation. The population of each considered state with time evolution over the electron transfer simulation is presented in Fig. S7a (ESI†). The electron population of the LUMO state decreases to 0.2 within 1 ps. Meanwhile, the population of state-718 first increases to its maximum value at ca. 220 fs and soon starts to decrease. However, the population of state-717 keeps increasing within 1 ps. As mentioned above, both state-717 and state-718 are energetically close to each other (see Fig. 1a and 3). So, the electron populated on state-718 that transferred from the LUMO state quickly evolves into state-717. It can be seen from Fig. S7a (ESI†) that only a small number of electrons successively decay to lower states, i.e., state-715, state-714, and state-713 within the 1 ps dynamics simulation. The electron trapped in state-717 is mainly caused by the large energy gap between state-717 and state-716 as shown in Fig. 3. Because the inter-state couplings are reversely proportional to the energy gaps involved, one can see small nonadiabatic couplings between state-717 and state-716, which is estimated to be 0.52 kcal mol−1 averaged over the 5 ps trajectory. Therefore, the large energy gap and small couplings block the further electron cooling process to the lower conduction bands of the SWNT.
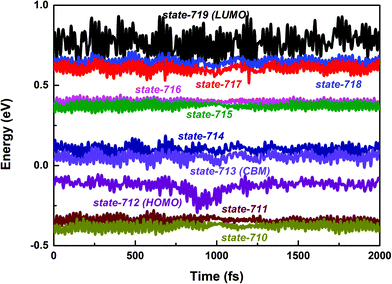 | ||
| Fig. 3 PBE + D3 calculated time-dependent energies of adiabatic states from 710 to 719 along the 2 ps molecular dynamics trajectory of the polymer@SWNT model. | ||
The time-dependent population of the number of electrons survived in the polymer due to the interfacial electron transfer process is projected out in Fig. 4a. The electron transfer process is completed within 0.37 ps attained through a single-exponential function fitting of the remaining electrons in the polymer. The timescale agrees well with the time constant of 0.38 ps obtained experimentally.34
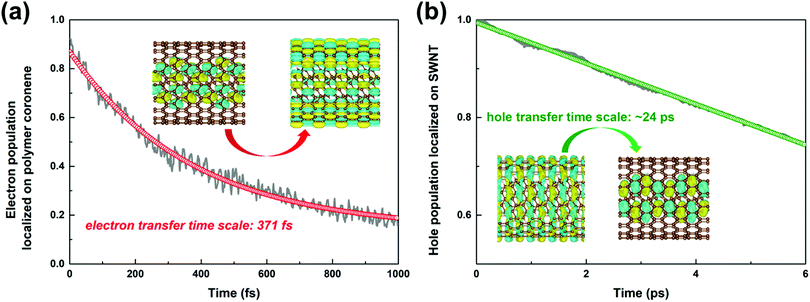 | ||
| Fig. 4 Time-dependent population of the electrons remaining on the polymer coronene moiety (a), and the holes on the SWNT moiety (b) in the nonadiabatic dynamics simulations. | ||
The interfacial hole transfer process is due to the SWNT excitation, as discussed before. Although this process is not explored explicitly in the experiments by Nakamura and colleagues,34 it is still worthy of in-depth nonadiabatic dynamics simulations, which are expected to provide valuable insights into near-future experimental exploration. Clearly, the E11 excitation of the SWNT, ca. 0.60 eV at the HSE06 level, will promote an electron to its lowest conduction band and leave a hole in its highest valence band. According to the PDOS results in Fig. 1a, it is evident that the highest valence band has two close states, i.e., state-710 and state-711, both of which are lower than the HOMO state of the polymer. Consequently, these three states are included in the hole transfer simulation and state-710 is chosen as the initial hole state.
As shown in Fig. S7b (ESI†), the intra-band hole transfer dynamics is very fast because both state-710 and state-711 are energetically close to each other. The hole population of state-710 quickly decays to state-711 within ca. 10 fs. However, the subsequent inter-band hole transfer from state-711 to state-712 takes a much longer time. The number of holes left in the SWNT as a function of time is shown in Fig. 4b. By fitting the residual holes in the SWNT, the inter-band hole decay time, i.e., from the SWNT component to the polymer component, is estimated to be 24 ps, which is about two orders of magnitude higher than that of the corresponding electron transfer process discussed above.
It is evident that the interfacial electron and hole transfer processes in the coronene-based polymer-encapsulated-SWNT hybrid system are not only opposite spatially but also have quite different carrier transfer rates, which is similar to the previous studies.68,69 The above simulations show that the electron transfer process is driven by polymer excitation and takes place from the polymer to the SWNT in an ultrafast way, which is estimated to be 371 fs. In contrast, the hole transfer process is two orders of magnitude slower, i.e., 24 ps, after the SWNT photoexcitation. To uncover the underlying reasons leading to such different rates, we first analyze the densities of the acceptor states. In the electron transfer process, there are six acceptor states from the SWNT, which are below the LUMO state of the polymer as demonstrated by the calculated PDOS in Fig. 1a, whereas there is essentially one acceptor state, i.e., the HOMO state, for the interfacial hole transfer from the VBM state of the SWNT. This could somewhat induce a faster electron transfer. Furthermore, inter-state couplings and energy gaps are also two vital factors to control the nonadiabatic transition in the electron and hole transfer dynamics according to the equation of motion of Tully's fewest surface-hopping approaches. Thus, it is insightful to analyze the distribution of these two important quantities in the trajectory. Fig. 5 shows the 2-dimensional distribution of the energy differences between the LUMO and state-718 (electron transfer), and between state-711 and state-712 (hole transfer). It is apparent that the overwhelming majority of the energy differences in the electron transfer process is smaller than 2 kcal mol−1 although there is a wide distribution of up to 8 kcal mol−1. This point is also seconded by the calculated averaged energy difference of 2.5 kcal mol−1. In stark contrast, the energy differences in the hole transfer are relatively larger although there is a similar distribution width like that in the electron transfer. The corresponding averaged value is predicted to be 5.0 kcal mol−1 along the trajectory. It is known that the inter-state couplings are reversely proportional to the energy gaps involved. Thus, one can see large nonadiabatic couplings in the electron transfer dynamics with an estimated averaged coupling value of 4.1 kcal mol−1. However, the couplings are very smaller in the hole transfer with an averaged coupling value of 0.2 kcal mol−1. Taking these three factors together, it is reasonable that the electron transfer is quite faster than the hole transfer as observed in the dynamics simulations.
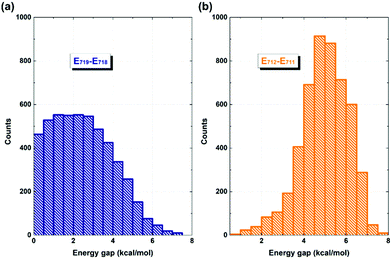 | ||
| Fig. 5 Distribution of energy differences between state-719 and state-718 (a), and between state-711 and state-712 (b) along the 5 ps NVE dynamics. | ||
Conclusions
In summary, we have used DFT calculations to study the effects of different polymerization degrees of coronene molecules encapsulated in a (19,0) SWNT on the interfacial properties of the formed heterojunctions. The present results show that polymerization can be used as an efficient regulating strategy to tune appropriately the energy-level alignment of the individual components of heterojunctions. For example, the constructed monomer- and dimer-encapsulated SWNTs belong to type-I heterojunctions, in which the interfacial excitation energy is more likely to occur. However, upon increasing the polymerization degree, type-II heterojunctions appear, for instance, trimer- and polymer-encapsulated SWNTs. In these type-II ones, it is obvious that interfacial charge carrier transfer processes are more likely to occur. In addition, we have explored the light-induced interfacial carrier dynamics of the polymer-encapsulated SWNT heterojunctions with DFT-based time-domain nonadiabatic carrier dynamics simulations. It is found that the interfacial electron and hole transfer processes occur in opposite directions and at different rates. The electron transfer from the polymer component to the SWNT component is ultrafast and is completed within ca. 370 fs. In contrast, the SWNT-to-polymer hole transfer is two orders of magnitude slower, which is mainly ascribed to the fewer acceptor states, larger energy differences and smaller inter-state couplings between the donor and the acceptor states. Finally, the present work suggests a new avenue to regulate the interfacial properties of molecular-encapsulated SWNT heterojunctions, e.g., from type-I to type-II. These interesting findings could provide significant information for developing high-quality photovoltaic and optoelectronic devices based on carbon-based hybrid nanomaterials.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the NSFC grants 21688102, 21590801, 21520102005, and 21421003 (G. C. and W. F.), the Sichuan Science and Technology Program grant 2020YJ0161 (X. L.) and the High Performance Computing Center of Sichuan Normal University.References
- H. W. Kroto, J. R. Heath, S. C. O’Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- T. W. Ebbesen and P. M. Ajayan, Nature, 1992, 358, 220–222 CrossRef CAS.
- S. Iijima, Nature, 1991, 354, 56–58 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- X. Li, X. Wang, L. Zhang, S. Lee and H. Dai, Science, 2008, 319, 1229–1232 CrossRef CAS PubMed.
- B. Özyilmaz, P. Jarillo-Herrero, D. Efetov and P. Kim, Appl. Phys. Lett., 2007, 91, 192107 CrossRef.
- P. M. Ajayan, Nature, 2019, 575, 49–50 CrossRef CAS PubMed.
- B. Chitara, L. S. Panchakarla, S. B. Krupanidhi and C. N. R. Rao, Adv. Mater., 2011, 23, 5419–5424 CrossRef CAS PubMed.
- X. Yu, Z. Dong, J. K. W. Yang and Q. J. Wang, Optica, 2016, 3, 979–984 CrossRef CAS.
- C. M. Isborn, C. Tang, A. Martini, E. R. Johnson, A. Otero-de-la-Roza and V. C. Tung, J. Phys. Chem. Lett., 2013, 4, 2914–2918 CrossRef CAS.
- H. Zheng, C. Y. Neo and J. Ouyang, ACS Appl. Mater. Interfaces, 2013, 5, 6657–6664 CrossRef CAS PubMed.
- L. Qiu, X. Yang, X. Gou, W. Yang, Z.-F. Ma, G. G. Wallace and D. Li, Chem. – Eur. J., 2010, 16, 10653–10658 CrossRef CAS PubMed.
- S. Okada, S. Saito and A. Oshiyama, Phys. Rev. Lett., 2001, 86, 3835–3838 CrossRef CAS PubMed.
- B. W. Smith, M. Monthioux and D. E. Luzzi, Nature, 1998, 396, 323–324 CrossRef CAS.
- Y. Jiang, H. Li, Y. Li, H. Yu, K. M. Liew, Y. He and X. Liu, ACS Nano, 2011, 5, 2126–2133 CrossRef CAS PubMed.
- A. I. Chernov, P. V. Fedotov, H. E. Lim, Y. Miyata, Z. Liu, K. Sato, K. Suenaga, H. Shinohara and E. D. Obraztsova, Nanoscale, 2018, 10, 2936–2943 RSC.
- M.-Q. Zhao, X.-F. Liu, Q. Zhang, G.-L. Tian, J.-Q. Huang, W. Zhu and F. Wei, ACS Nano, 2012, 6, 10759–10769 CrossRef CAS PubMed.
- T. Takenobu, T. Takano, M. Shiraishi, Y. Murakami, M. Ata, H. Kataura, Y. Achiba and Y. Iwasa, Nat. Mater., 2003, 2, 683–688 CrossRef CAS PubMed.
- K. Yanagi, Y. Miyata and H. Kataura, Adv. Mater., 2006, 18, 437–441 CrossRef CAS.
- H. E. Lim, Y. Miyata, M. Fujihara, S. Okada, Z. Liu, Arifin, K. Sato, H. Omachi, R. Kitaura, S. Irle, K. Suenaga and H. Shinohara, ACS Nano, 2015, 9, 5034–5040 CrossRef CAS PubMed.
- J. Wu, W. Pisula and K. Müllen, Chem. Rev., 2007, 107, 718–747 CrossRef CAS PubMed.
- K. Müllen and J. P. Rabe, Acc. Chem. Res., 2008, 41, 511–520 CrossRef PubMed.
- C. Yu, S. C. Wang, M. Sosnowski and Z. Iqbal, Synth. Met., 2008, 158, 425–429 CrossRef CAS.
- J. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh, X. Feng, K. Müllen and R. Fasel, Nature, 2010, 466, 470–473 CrossRef CAS PubMed.
- M. Treier, C. A. Pignedoli, T. Laino, R. Rieger, K. Müllen, D. Passerone and R. Fasel, Nat. Chem., 2011, 3, 61–67 CrossRef CAS PubMed.
- A. I. Chernov, P. V. Fedotov, A. V. Talyzin, I. S. Lopez, I. V. Anoshkin, A. G. Nasibulin, E. I. Kauppinen and E. D. Obraztsova, ACS Nano, 2013, 7, 6346–6353 CrossRef CAS PubMed.
- M. Fujihara, Y. Miyata, R. Kitaura, Y. Nishimura, C. Camacho, S. Irle, Y. Iizumi, T. Okazaki and H. Shinohara, J. Phys. Chem. C, 2012, 116, 15141–15145 CrossRef CAS.
- A. V. Talyzin, I. V. Anoshkin, A. V. Krasheninnikov, R. M. Nieminen, A. G. Nasibulin, H. Jiang and E. I. Kauppinen, Nano Lett., 2011, 11, 4352–4356 CrossRef CAS PubMed.
- T. Okazaki, Y. Iizumi, S. Okubo, H. Kataura, Z. Liu, K. Suenaga, Y. Tahara, M. Yudasaka, S. Okada and S. Iijima, Angew. Chem., Int. Ed., 2011, 50, 4853–4857 CrossRef CAS PubMed.
- I. V. Anoshkin, A. V. Talyzin, A. G. Nasibulin, A. V. Krasheninnikov, H. Jiang, R. M. Nieminen and E. I. Kauppinen, ChemPhysChem, 2014, 15, 1660–1665 CrossRef CAS PubMed.
- B. Verberck, T. Okazaki and N. V. Tarakina, Phys. Chem. Chem. Phys., 2013, 15, 18108–18114 RSC.
- F. Furuhashi and K. Shintani, AIP Adv., 2013, 3, 092103 CrossRef.
- B. Botka, M. E. Füstös, G. Klupp, D. Kocsis, E. Székely, M. Utczás, B. Simándi, Á. Botos, R. Hackl and K. Kamarás, Phys. Status Solidi B, 2012, 249, 2432–2435 CrossRef CAS.
- A. Nakamura, K.-i. Yamanaka, K. Miyaura, H. E. Lim, K. Matsuda, B. Thendie, Y. Miyata, T. Kochi, S. Okada and H. Shinohara, J. Phys. Chem. C, 2018, 122, 16940–16949 CrossRef CAS.
- J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25 CAS.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- M. Krack, Theor. Chem. Acc., 2005, 114, 145–152 Search PubMed.
- C. Hartwigsen, S. Goedecker and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 3641–3662 CrossRef CAS.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2010, 6, 2348–2364 CrossRef CAS PubMed.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- W. Chu, W. A. Saidi, Q. Zheng, Y. Xie, Z. Lan, O. V. Prezhdo, H. Petek and J. Zhao, J. Am. Chem. Soc., 2016, 138, 13740–13749 CrossRef CAS PubMed.
- Q. Zheng, W. A. Saidi, Y. Xie, Z. Lan, O. V. Prezhdo, H. Petek and J. Zhao, Nano Lett., 2017, 17, 6435–6442 CrossRef CAS PubMed.
- Q. Zheng, Y. Xie, Z. Lan, O. V. Prezhdo, W. A. Saidi and J. Zhao, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 205417 CrossRef CAS.
- Z. S. Zhang, W.-H. Fang, M. V. Tokina, R. Long and O. V. Prezhdo, Nano Lett., 2018, 18, 2459–2466 CrossRef CAS PubMed.
- L. Q. Li, R. Long, T. Bertolini and O. V. Prezhdo, Nano Lett., 2017, 17, 7962–7967 CrossRef CAS PubMed.
- G. Granucci, M. Persico and A. Zoccante, J. Chem. Phys., 2010, 133, 134111 CrossRef PubMed.
- J.-J. Yang, X.-Y. Liu, W.-H. Fang, D. Q. Xiao and G. L. Cui, J. Phys. Chem. A, 2019, 123, 10019–10029 CrossRef CAS PubMed.
- X.-Y. Liu, X.-Y. Xie, W.-H. Fang and G. L. Cui, J. Phys. Chem. A, 2018, 122, 9587–9596 CrossRef CAS PubMed.
- X.-Y. Liu, W.-K. Chen, W.-H. Fang and G. L. Cui, J. Phys. Chem. Lett., 2019, 10, 2949–2956 CrossRef CAS PubMed.
- X.-Y. Xie, X.-Y. Liu, Q. Fang, W.-H. Fang and G. L. Cui, J. Phys. Chem. A, 2019, 123, 7693–7703 CrossRef CAS PubMed.
- D. B. Lingerfel, D. B. Williams-Young, A. Petrone and X. Li, J. Chem. Theory Comput., 2016, 12, 935–945 CrossRef PubMed.
- R. Send and F. Furche, J. Chem. Phys., 2010, 132, 044107 CrossRef PubMed.
- Q. Ou, S. Fatehi, E. Alguire, Y. Shao and J. E. Subotnik, J. Chem. Phys., 2014, 144, 069903 CrossRef.
- C. F. Craig, W. R. Duncan and O. V. Prezhdo, Phys. Rev. Lett., 2005, 95, 163001 CrossRef PubMed.
- S. A. Fischer, B. F. Habenicht, A. B. Madrid, W. R. Duncan and O. V. Prezhdo, J. Chem. Phys., 2011, 134, 024102 CrossRef PubMed.
- Q. Zheng, W. Chu, C. Zhao, L. Zhang, H. Guo, Y. Wang, X. Jiang and J. Zhao, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1411 CAS.
- L. Wang, R. Long and O. V. Prezhdo, Annu. Rev. Phys. Chem., 2015, 66, 549–579 CrossRef CAS PubMed.
- G. Zhou, C. Cen, S. Wang, M. Deng and O. V. Prezhdo, J. Phys. Chem. Lett., 2019, 10, 7179–7187 CrossRef CAS PubMed.
- K. Narita and S. Okada, Jpn. J. Appl. Phys., 2016, 55, 06GF02 CrossRef.
- R. Long and O. V. Prezhdo, Nano Lett., 2014, 14, 3335–3341 CrossRef CAS PubMed.
- R. Sarkar, M. Habib, S. Pal and O. V. Prezhdo, Nanoscale, 2018, 10, 12683–12694 RSC.
- J.-J. Yang, Z.-W. Li, X.-Y. Liu, W. H. Fang and G. L. Cui, Phys. Chem. Chem. Phys., 2020, 22, 19542–19548 RSC.
- H. Mehdipour, B. A. Smith, A. T. Rezakhani, S. S. Tafreshi, N. H. de Leeuw, O. V. Prezhdo, A. Z. Moshfegh and A. V. Akimov, Phys. Chem. Chem. Phys., 2019, 21, 23198–23208 RSC.
- S. Pal, D. Casanova and O. V. Prezhdo, Nano Lett., 2018, 18, 58–63 CrossRef CAS PubMed.
- W. Li, R. Long, Z. Hou, J. Tang and O. V. Prezhdo, J. Phys. Chem. Lett., 2018, 9, 4006–4013 CrossRef CAS PubMed.
- V. V. Chaban, S. Pal and O. V. Prezhdo, J. Am. Chem. Soc., 2016, 138, 15927–15934 CrossRef CAS PubMed.
- O. Postupna, H. M. Jaeger and O. V. Prezhdo, J. Phys. Chem. Lett., 2014, 5, 3872–3877 CrossRef CAS PubMed.
- B. F. Habenicht and O. V. Prezhdo, J. Am. Chem. Soc., 2012, 134, 15648–15651 CrossRef CAS PubMed.
- R. Sarkar, M. Habib, S. Pal and O. V. Prezhdo, J. Appl. Phys., 2021, 129, 025501 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Theoretical background and additional figures. See DOI: 10.1039/d1cp01008e |
| This journal is © the Owner Societies 2021 |