Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The F + HD(v = 0, 1; j = 0, 1) reactions: stereodynamical properties of orbiting resonances
V.
Sáez-Rábanos
 *a,
J. E.
Verdasco
*a,
J. E.
Verdasco
 b,
F. J.
Aoiz
b,
F. J.
Aoiz
 b and
V. J.
Herrero
b and
V. J.
Herrero
 *c
*c
aDepartamento de Sistemas y Recursos Naturales, E.T.S. de Ingeniería de Montes, Forestal y del Medio Natural, Universidad Politécnica de Madrid, 28040, Madrid, Spain. E-mail: v.saez@upm.es
bDepartamento de Química Física, Facultad de Química, Universidad Complutense de Madrid (Unidad Asociada CSIC), 28040, Madrid, Spain. E-mail: verdasco@ucm.es; aoiz@ucm.es
cInstituto de Estructura de la Materia (IEM-CSIC), Serrano 123, 28006, Madrid, Spain. E-mail: vherrero@iem.cfmac.csic.es
First published on 5th January 2021
Abstract
The excitation functions (reaction cross-section as a function of collision energy) of the F + HD(v = 0, 1; j = 0, 1) benchmark system have been calculated in the 0.01–6 meV collision energy interval using a time-independent hyperspherical quantum dynamics methodology. Special attention has been paid to orbiting resonances, which bring about detailed information on the three-atom interaction during the reactive encounter. The location of the resonances depends on the rovibrational state of the reactants HD(v,j), but is the same for the two product channels HF + D and DF + H, as expected for these resonances that are linked to the van der Waals well at the entrance. The resonance intensities depend both on the entrance and on the exit channels. The peak intensities for the HF + D channel are systematically larger than those for DF + H. Vibrational excitation leads to an increase of the peak intensity by more than an order of magnitude, but rotational excitation has a less drastic effect. It deceases the resonance intensity of the F + HD(v = 1) reaction, but increases somewhat that of F + HD(v = 0). Polarization of the rotational angular momentum with respect to the initial velocity reveals intrinsic directional preferences in the F + HD(v = 0, 1; j = 1) reactions that are manifested in the resonance patterns. The helicities (Ω = 0, Ω = ±1) possible for j = 1 contribute to the resonances, but that from Ω ± 1 is, in general, dominant and in some cases exclusive. It corresponds to a preferential alignment of the HD internuclear axis perpendicular to the initial direction of approach and, thus, to side-on collisions. This work also shows that external preparation of the reactants, following the intrinsic preferences, would allow the enhancement or reduction of specific resonance features, and would be of great help for their eventual experimental detection.
I. Introduction
Scattering resonances play a major role in reaction dynamics and provide detailed information on the interactions of all the atoms during the early or final stages of the collision. They usually show up as distinct maxima in the integral cross-section, and they are ubiquitous at low collision energies (<1 meV ⇔ <11.6 K). Indeed, with the advent of sophisticated experimental techniques, such as merged beams, scattering resonances in collision processes are amenable to direct experimental detection.Scattering resonances are the result of trapping of the intermolecular complex in a well. If there is a transfer of energy between the different degrees of freedom, they are called Feshbach resonances, which arise from the coupling of scattering states to a bound state belonging to a different scattering channel. The shape or orbiting resonances, in contrast, are the result of tunneling through a barrier in a single potential, usually associated with a centrifugal barrier that leads to the formation of quasi-bound rotational states. They are observed at low energies (typically <1 meV), constitute a sensitive probe of the attractive potential between approaching collision partners,1 and can also play an important role in many dynamical processes.1,2 They were experimentally observed in elastic scattering in the seventies3,4 and, more recently, also in inelastic5–10 and reactive11–13 scattering using merged beam techniques.14–16 In collisions involving molecules, rotational excitation can give rise to stereodynamical effects associated with the polarization of the rotational angular momentum in the scattering frame, which is defined by the relative velocity vectors of the reactants and products (see, for instance, ref. 17, 18 and the references cited therein). At the low collision energies, Ecoll, typical of orbiting resonances, the number of partial waves implied in the dynamics is relatively small and this circumstance facilitates the performance of precise fundamental calculations, as a consequence there is growing interest, both experimentally and theoretically, in the stereodynamics of collisions in this low Ecoll range.19–26
The pioneering work of Balakrishnan and Dalgarno27 on reactivity at ultra-low temperatures was performed for the F + H2 system and, at temperatures down to a few K, the reaction is also of interest in astrophysics, where the HF molecule is used to estimate the depletion of fluorine from ice mantles in dense clouds, and as a tracer of H2 in the diffuse interstellar medium.28,29 This reaction, which has been a prototype in the field of reaction dynamics since the seventies, is very well known in many respects. In particular the F + H2 system and isotopic variants have been used as a benchmark for the experimental and theoretical study of Feshbach resonances30–36 associated with quasibound states of the transition state. These resonances are very sensitive to the topography of the potential energy surface (PES) and, consequently, much effort has been invested over decades on the derivation of a PES of high accuracy for the system. Dynamical calculations performed on the latest generation potential energy surfaces (PESs)37–40 account well for the experimental features associated with the mentioned Feshbach resonances (see ref. 41 for a review).
Studies of the dynamics at lower Ecoll have not been so exhaustive. The pioneering calculations of Balakrishnan and Dalgarno on F + H2 were performed on the SW PES42 and were focused on the Wigner regime, exploring the limiting value of the rate coefficient when the temperature tends to zero. The calculations were restricted to the ground ro-vibrational state of H2 and to a total angular momentum J = 0. These calculations were later extended by the same authors to F + HD43 and by Bodo and Gianturco44 to F + D2 and to the j = 2 and v = 1 excited states of F + H2 and F + D2. In the latter work, values of the angular momentum up to J = 2 were included in the calculations for the rotationally excited molecules. These calculations are accurate in the ultracold regime, but for collision energies beyond ≈0.01 meV, which is the region of interest for orbiting resonances, angular momenta J > 2 are required for convergence. Aldegunde et al.19 investigated the mechanism and stereodynamical properties of the F + H2(v = 0, j = 2) reaction at low and ultralow collision energies. The study, performed on the SW PES, unveiled interesting directional properties of the reaction and suggested a considerable extent of control by suitable preparation of the reagents. It was found, for instance, that at Ecoll = 0.1 meV, the reaction was enhanced by side-on collisions for the F + H2(v = 0, j = 2). Orbiting resonances were not investigated in the just mentioned low-temperature works since they require a more dense grid of energies in the scattering calculations.
In recent studies, De Fazio et al.45,46 and Sáez-Rábanos et al.47 reported dynamical calculations for the range of energies relevant to orbiting resonances. The calculations of De Fazio et al.45,46 were carried out for F + H2(v = 0, j = 0), F + D2(v = 0, j = 0) and F + HD(v = 0, j = 0) on the SW42 and PES-II48,49 surfaces, and those of Sáez-Rábanos et al. were performed for F + HD(v = 0, 1; j = 0) on the LWA-5 PES.37 The latter, constructed at a very high ab initio level with a larger basis set, is highly accurate in the entrance channel, and correlates with the ground spin–orbit level. In all these studies, narrow orbiting resonances in the integral reaction cross-sections were found in the near cold regime (close to 1 K ⇔ 0.086 meV). In contrast to Feshbach resonances, which are associated with a specific output channel, orbiting resonances, whose properties are largely given by the characteristics of the van der Waals well at the entrance, are common to both exit pathways. Although the energies and J values associated with the individual resonances depend on the specific PES and the isotopomer considered, the qualitative resonance pattern is similar in all the mentioned studies.45–47 In all these works, the orientational properties of reactive scattering were not considered.
The stereodynamics of the F + HD(v = 0, j = 1) system was investigated by Aldegunde et al. at higher energies.50 These authors carried out calculations on the SW PES up to 160 meV and studied the alignment preferences of the reaction with special emphasis on the properties of the much studied Feshbach resonance at Ecoll = 22 meV,30,31 close to the classical reaction threshold, which is only found in the HF + D channel. The strereodynamical analysis showed that the large decrease in the resonance intensity upon rotational excitation predicted by QM calculations30,31 could be traced back to the intrinsic directional properties of the reaction. It was found that the intensity of the resonance is enhanced when the HD internuclear axis is aligned along the initial relative velocity vector, and this polarization corresponds to the mechanism observed for the reaction with j = 0. Rotational excitation to j = 1 allows for additional non-resonant polarizations and dilutes the effect of the resonance. In principle, the polarization of the internuclear axis could be externally controlled, which would offer the possibility of switching on or off the resonance. The generalization of this scheme to other systems would provide more insight into the dynamics. In fact, similar stereo-selective effects have been found for resonances in inelastic collisions at very low energies,21–26 but as far as we know, they have not been studied for orbiting resonances in reactive collisions.
In this work we address the effects of rotational excitation on the orbiting resonances of the F + HD(v = 0,1) reactions, with special attention to the stereodynamical properties of reactive collisions. To this aim, we have performed detailed QM calculations of integral reaction cross-sections over the 0.01–6 meV energy range on the LWA-5 PES.37 In Section II, the details of the QM method are presented along with the relevant expressions to determine cross-sections, reaction probabilities and polarization parameters. In Section III, we have revisited our previous results for F + HD(v = 0, 1; j = 0) using a finer energy grid, which allows the identification of new resonances. Then, we have explored the changes in the resonance patterns observed upon rotational excitation and have identified the angular momenta responsible for the resonant features. Finally, we have studied the directional preferences of the collisions leading to resonant scattering and have considered the possibility of influencing the resonance structure through an external control of the polarization of the rotational angular momentum of the reactants. The summary and conclusions of this work are presented in Section IV.
II. Theoretical method
QM scattering calculations were performed for the F + HD(v = 0, j = 0,1) and F + HD(v = 1, j = 0,1) reactions using the coupled-channel hyperspherical coordinate method as implemented in ABC code developed by Skouteris et al.51 All calculations were carried out on the LWA-5 PES of Li et al.,37 which was shown to accurately reproduce the broad resonance that peaks at Ecoll = 20–25 meV, found experimentally by Liu and coworkers for F + HD(v = 0),30,31 and the energy dependence of backward scattering as measured by by Wang et al.36 for the F + HD(v = 0,1) reactions.47 Calculations for F + HD(v = 0, 1; j = 1) were carried out in two energy grids: 30 total energies with a spacing of 0.2 meV, and a finer grid to capture the low energy regime in more detail, consisting of 40 total energies with a spacing of 0.02 meV. The starting total energy was 0.24581 eV for v = 0, j = 1, and 0.6974 eV for v = 1, j = 1, which correspond to a collision energy Ecoll/kB ≈ 0.1 K. The rest of input parameters were identical for all the calculations. The basis set included all diatomic levels up to a cutoff energy of 3.0 eV and comprised all possible helicity quantum numbers, Ω. The propagation of the integration was extended in 150 sectors up to a maximum hyperradius of 18a0. To determine the integral cross-sections, all partial waves till Jmax = 16 (coarse grid) and Jmax = 8 (finer grid) were considered for the v = 1 level, whereas partial waves up to Jmax = 9 (coarse and finer grids) were considered for the v = 0 level of the HD molecule.With the scattering matrices in the helicity representation, the reaction probabilities summed over all final states for a given total angular momentum as a function of the collision energy were calculated for each reaction channel as:52
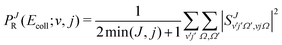 | (1) |
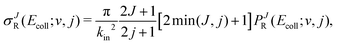 | (2) |
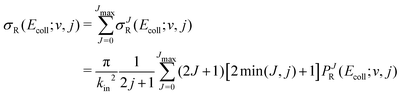 | (3) |
It is also possible to define the Ω-resolved cross-section as
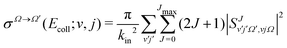 | (4) |
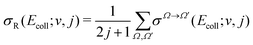 | (5) |
We will next revise the most relevant expressions for the alignment-dependent cross-sections. The scattering frame is defined as that with the z axis along the initial relative velocity, kin, and the xz plane determined by the initial and final relative velocities. The polar angle that defines the direction of the polarization vector (or, in general terms, of the relevant field used for the reactant preparation) in the scattering frame will be denoted by β; that is, the angle between the initial relative velocity and the polarization vector. Following ref. 18, the cross-sections for a given β is given by:
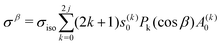 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) are the Legendre polynomials, and s(k)0 are the intrinsic polarization parameters.18 The A(k)0 coefficients are the extrinsic polarization parameters (external preparation) with respect to the polarization vector. For a pure directed state |j0〉, A(k)0 is given by the 〈j0,k0|j0〉 Clebsch–Gordan coefficients.
β) are the Legendre polynomials, and s(k)0 are the intrinsic polarization parameters.18 The A(k)0 coefficients are the extrinsic polarization parameters (external preparation) with respect to the polarization vector. For a pure directed state |j0〉, A(k)0 is given by the 〈j0,k0|j0〉 Clebsch–Gordan coefficients.
The intrinsic polarization parameters, s(k)0, can be calculated from the S-matrix as:26,53
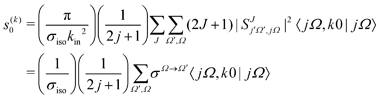 | (7) |
After some algebra, it can be shown that for a pure state preparation, eqn (6) can be recast as
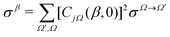 | (8) |
Collisions prepared with β = 0° only involve the Ω = 0 contribution, as can be immediately inferred from eqn (8). In particular, for j = 1
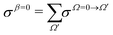 | (9) |
Similarly, when β = 90°
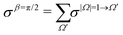 | (10) |
III. Results and discussion
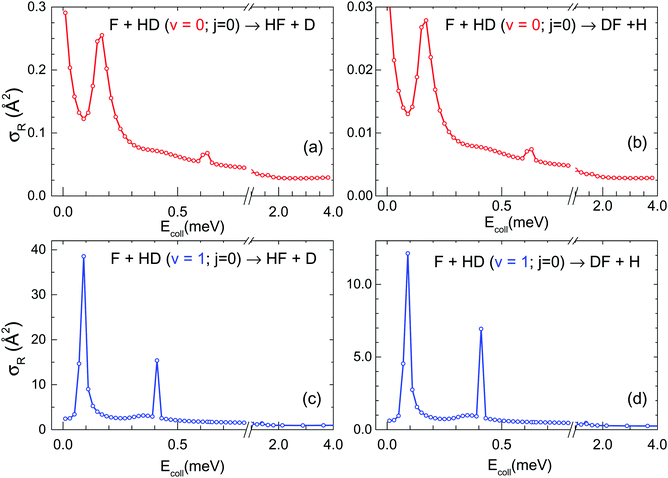
Fig. 1 shows the excitation functions for the reaction of F atoms with HD molecules in j = 0 and in their ground and first excited vibrational states. These calculations extend and supersede our previous results47 by using a finer energy grid below Ecoll = 0.80 meV which discloses new resonances below Ecoll = 0.2 meV. Within each vibrational state, the resonance pattern is the same for the two isotopic exit channels, as expected for orbiting resonances, but the intensity of the resonance peaks is much higher for HF + D. With increasing collision energy, the intensity of the resonance peaks decreases. Beyond the resonance region, the cross-sections show a smooth decay tending to a plateau. The upper panels show the results for F + HD(v = 0, j = 0). Two resonances, at Ecoll = 0.17 meV (large) and Ecoll = 0.63 meV (small), are seen in the excitation function. As discussed in ref. 47, the small peak at 0.63 meV is due to J = 7, which is the highest J participating in the reaction at that energy. A similar analysis shows that the larger peak at 0.17 meV corresponds to J = 3. The resonance peaks for HF + D are larger by an order of magnitude than those for DF + H. Between 0.01 and 0.09 meV, the cross-section decreases sharply with growing Ecoll and this sharp fall suggests the existence of another resonance, below Ecoll = 0.01 meV, but the present calculations cannot confirm this point. The resonance picture just described for F + HD(v = 0, j = 0) is qualitatively similar to that recently reported by De Fazio et al.46 from their calculations on the SW PES42 and on the PES-II surface of Aquilanti et al.,48,49 which is derived from the SW PES, but has a modified van der Waals well. Orbiting resonances are also found in the integral cross-sections calculated on these two surfaces in the ≈0.05–2 meV range, and the resonance peaks are much larger for the HF + D channel. The most intense resonances found by these authors correspond to J = 2 and J = 6 for the SW PES, and J = 4 and J = 8 for the PES-II surface. The difference in the specific resonance patterns for the different potential surfaces considered reveals the high sensitivity of resonances to the characteristics of the attractive potential well at the entrance. Although the present work is focused on the properties of orbiting resonances, it should be briefly mentioned that they are not the only kind of resonance that can be associated with van der Waals wells in the F + H2 system. Specifically, resonances related to the H(D)–F van der Waals well in the exit channel have also been reported by Takayanagi et al.,54,55 and more recently by Lique et al.39 They are associated with specific exit channel states and are not related to the orbiting resonances considered in this article. A recent study of H + HF(v = 0, j = 1,2) inelastic collisions in the 1 mK to 100 K Ecoll/kB range on the LWA-78 PES37 revealed a whole series of shape resonances in the exit channel which have a marked effect on the inelastic transitions at low temperatures.26 However, there is no evident correspondence with the shape resonances discussed in this work and attributed to the entrance channel. A discussion of exit channel resonances is beyond the scope of this work.The effect of vibrational excitation is seen in the lower panels of Fig. 1, where the cross-sections for F + HD(v = 1, j = 0) are represented. The resonance features are narrower and much more intense (typically a factor 30–100) than those for F + HD(v = 0, j = 0). The resonance peaks for the HF + D channel are bigger by a factor of 2–3 than those for DF + H; this difference is smaller than that found for the reaction with HD(v = 0, j = 0). Two sharp and intense resonances are evident at Ecoll = 0.09 meV and Ecoll = 0.41 meV. Besides these two resonances, there is a small bulge at Ecoll = 0.35 meV and a very small bump at Ecoll = 1.41 meV, barely discernible at the scale of the figure. As discussed in ref. 47 the peak at 0.41 meV corresponds to J = 7 and the small features at 0.35 and 1.41 meV to J = 4 and J = 8, respectively. The most intense resonance, associated with J = 3 and with a remarkable cross-section value of 39 Å2 for the HF + D channel, was not seen in our previous work,47 due to the coarser energy grid used. The calculations extend to Ecoll = 4 meV, but beyond 0.6 meV the cross-section shows just a smooth structureless decline.
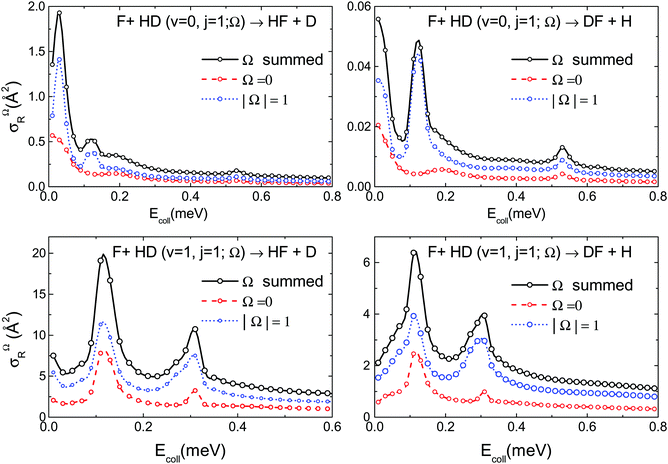
Fig. 2 shows the effect of rotational excitation. The promotion of the HD molecule to the j = 1 rotational state transforms the resonance pattern. At first sight the close resemblance between the resonance structure in the two exit channels, observed in the cases commented on thus far, is not maintained for F + HD(v = 0, j = 1) (see panels (a) and (b)). The σR(Ecoll) for the HF + D channel seems to be dominated by a sharp peak at Ecoll = 0.03 meV, and has a small maximum at Ecoll = 0.12 meV and a bump at Ecoll = 0.53 meV that also appear in the DF + H channel. Although the cross-section seems to grow monotonically below 0.01 meV in the D + HF channel, in contrast to the maximum in the H + DF channel at 0.03 meV, a maximum at slightly lower collision cannot be ruled out. The similarities in the J resolved cross-sections (see below) underpin a similar origin for the peaks observed in both channels in spite of their differnt intensities. It is worth noting that the resonance maxima for F + HD(v = 0, j = 1) are larger than those for F + HD(v = 0, j = 0) (upper panel of Fig. 1).
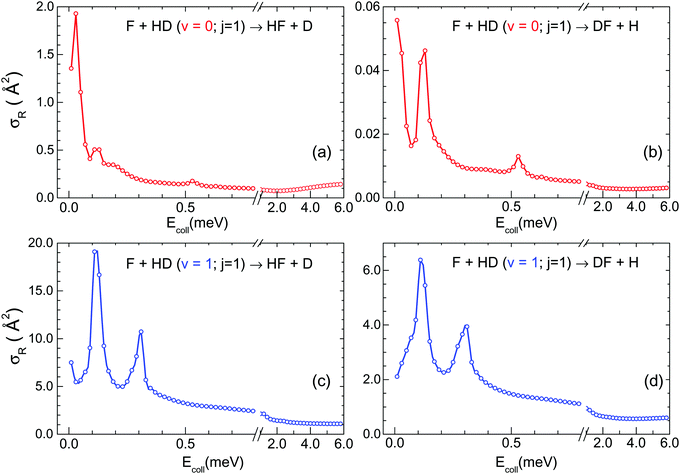 | ||
| Fig. 2 The same as Fig. 1 but for reaction with initial rotational j = 1 state. Top panels: F + HD(v = 0, j = 1) reaction. Bottom panels: F + HD(v = 1, j = 1) reaction. | ||
In the F + HD(v = 1, j = 1) reaction (lower panels) the resonance pattern is again similar for the two isotopic output channels. Two peaks appear at Ecoll = 0.12 meV and Ecoll = 0.31 meV, but although the peaks appear at the same energy for HF + D and DF + H, there are appreciable differences in their shapes. In comparison with the resonances for F + HD(v = 0, j = 1), these peaks are broader, shifted in energy, and 2–3 times less intense. It should be stressed that the collision energies considered in Fig. 1 and 2 lie below the vibrationally adiabatic barrier for reaction and, under these conditions all the reactivity is due to tunneling. Although a more detailed analysis is required to establish the lifetimes of the resonances, it is noteworthy that the peaks for the reaction in j = 1 are consistently broader than those for j = 0, especially for v = 1, suggesting that the lifetimes are somewhat shorter for j = 1.
In all cases, not only the resonance peaks but also the background scattering is considerably more intense for the HF + D than for the DF + H channel. The comparison between cross-sections for the HF and DF channels was already discussed in quasi-classical trajectory calculations above the classical threshold.56 At lower energies, the larger cross-sections in the HF channel was also discussed in ref. 50. Although a more detailed analysis would be pertinent, this effect is probably caused by the longer arm of the H-end due to the mass asymmetry of the HD molecule.
To shed more light into the characteristics of the resonances in the F + HD(v = 0, 1; j = 1) reactions, the partial cross-section σJ(Ecoll) for individual values of the angular momentum are displayed in Fig. 3 in the Ecoll = 0.01–0.6 meV energy interval. Inspection of this figure shows that several J participate always in the total reaction cross-section over the energy range considered, but only some of them lead to resonance peaks. For the reaction in the ground-state vibrational level (upper panels), resonance peaks are found for J = 1 at Ecoll = 0.03 meV, J = 3, at Ecoll = 0.12 meV and J = 6 Ecoll = 0.53 meV in both arrangement channels, but the relative contribution of the various J to the total cross-section is indeed very different. In the HF + D channel (upper left panel) there is a very large peak for J = 1, a small one for J = 3 and an even smaller one for J = 6, and these peaks define the resonance structure in the total cross-section shown in Fig. 2. Note that, for energies below that of the 0.12 meV peak, the σJ=3(Ecoll) goes through a valley and then grows sharply with decreasing energy until the lowest energy studied. In the DF + H channel (upper right panel), the relative contribution of J = 1 is much smaller and J = 3 dominates the global picture. The J = 3 peak stands out as the absolute maximum, and the low energy contribution of J = 3 obliterates the J = 1 peak in the total cross-section.
In the reaction with vibrationally excited HD (lower panels of Fig. 3), there are resonance maxima for J = 2, at Ecoll = 0.09 meV, J = 4 at Ecoll = 0.12 and 0.29 meV, and J = 6 at Ecoll = 0.31 meV in the two exit channels. Again, the contribution of the different J to the total cross-section is different for HF + D and DF + H, but here the differences are not so large, and J = 4 is always dominant. Note the dual peak shape of σJ=4(Ecoll). There is a significant overlap between the maxima corresponding to different J values that results in the broadening of the resonance peaks observed in the total cross-section (see Fig. 2). Specifically J = 2 and J = 4 contribute to the resonance peak at Ecoll 0.12 meV and J = 4 and J = 6 contribute to the peak at Ecoll = 0.31 meV. The different peak shapes observed in Fig. 2 depend on the proportion of the individual J resonances contributing to them.
To further investigate the properties of the resonances, we analyze now the directional characteristics of the F + HD(v = 0, 1; j = 1) reactions. Fig. 4 shows the Ω-partial cross-sections for the different helicity values possible for j = 1. In the figure, the Ω dependent excitation functions have been multiplied by a factor indicating their relative weight so that: σR(Ecoll) = (1/3)σΩ=0(Ecoll) + (2/3)σ|Ω|=1(Ecoll). In the F +HD(v = 0, j = 1) reaction (upper panels) most of the reactivity over the energy range relevant to orbiting resonances corresponds to Ω = ±1. Notably, the J = 3 resonance peak at Ecoll = 0.12 meV is exclusively due to this helicity value and Ω = ±1 is also the largest component of the J = 1 resonance at Ecoll = 0.03 for the HF + D channel. The predominance of Ω = ±1 indicates that the main reaction mechanism favors a perpendicular alignment of the internuclear axis of the molecule with respect to the direction of the initial velocity vector, kin, which reflects a preference for side-on, non collinear, collisions. The small J = 6 resonance at Ecoll = 0.53 meV has a more balanced contribution of the different helicities. In the F + HD(v = 1, j = 1) reaction (lower panels), the Ω = ±1 helicity is also dominant, but here, the resonance peaks in the total cross-sections have always a contribution from Ω = 0, which means that head-on collisions, in which the internuclear axis of the molecule is parallel to kin, also participate in the resonant scattering. However, the weight of Ω = 0 in the second resonance peak (Ecoll = 0.31 meV) is small, especially in the DF + H exit channel. This resonance includes contributions from J = 4 and J = 6, with J = 6 defining the peak position at Ecoll = 0.31 meV as shown in Fig. 3. The location of the small Ω = 0 peak precisely at this energy suggests that it is due to J = 6. In any case, most of the reactive scattering for this resonance corresponds again to Ω = ±1 and thus to side-on collisions.
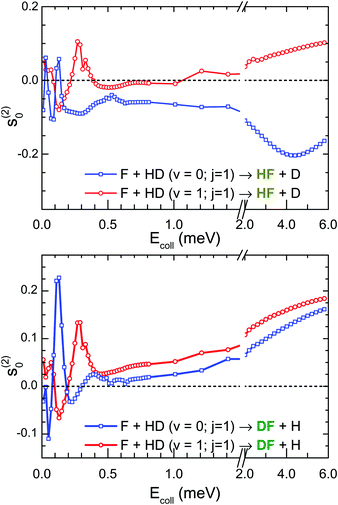
Additional information on the directional properties of the F + HD(v = 0, 1; j = 1) reactions is provided by the intrinsic s(2)0 polarization parameter,17,18 which is displayed in Fig. 5 as a function of collision energy. Positive values of this parameter indicate an alignment of j parallel to kin, and thus an alignment of the internuclear axis perpendicular to kin (side-on collisions), whereas negative values of s(2)0 correspond to a perpendicular alignment between j and kin (head-on collisions). The limits of this parameter are 0.316 and −0.632, respectively.17 Over most of the Ecoll range, s(2)0 undergoes a smooth variation but has marked oscillations below 0.5 meV, which are indicative of abrupt changes of mechanism around the resonances. Three positive maxima stand out in the figure. In the upper panel, there is a peak at Ecoll = 0.29 meV in the HF + D channel of the F + HD(v = 1, j = 1) reaction. In the lower panel there are maxima at Ecoll = 0.12 and Ecoll = 0.29 meV corresponding to the DF + H channel of the F + HD(v = 0, j = 1) and F + HD(v = 1, j = 1) reactions, respectively. Note that these positive maxima coincide in location with three of the resonances (see Fig. 2 and 3) and that precisely for these resonances the helicity analysis of Fig. 4 indicated a preference for side-on collisions, especially pronounced for the resonance at Ecoll = 0.12 meV, which corresponds to the highest s(2)0 maximum. Beyond the energy range of the resonances, the evolution of s(2)0 is smooth and remains initially close to zero, indicating that there are no marked directional preferences. With growing collision energy, the predominance of side-on collisions in the reaction mechanism increases gradually, except for the HF + D channel of the F + HD(v = 0, j = 1) reaction, where s(2)0 has a negative minimum close to Ecoll = 4 meV.
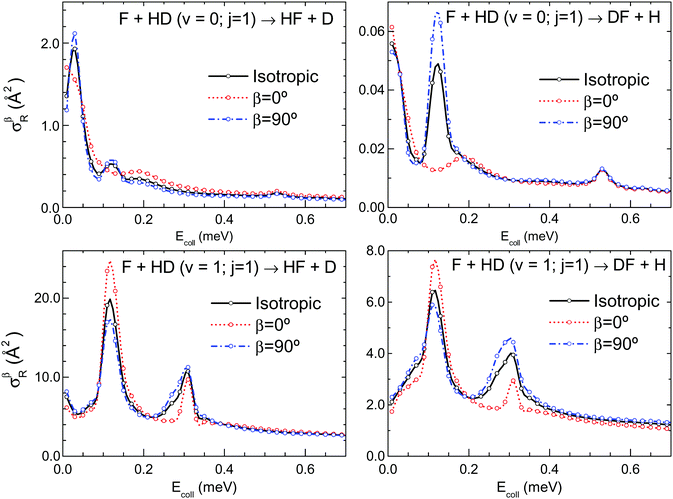
After the analysis of the intrinsic stereodynamical characteristics, we explore the possibility of external control of the F + HD(v = 0, 1; j = 1) reactions, and especially of their orbiting resonances. To achieve that, we will consider a hypothetical experiment in which the internuclear HD axis is preferentially aligned along a (laboratory) direction, Z, that may represent the radiation polarization vector or an external field. The angle between Z and k is denoted as β and relates the laboratory and scattering frames.50 With this definition, β = 0° corresponds to head-on collisions and β = 90° to side-on collisions. The results of the calculations for these two extreme orientations are represented in Fig. 6, together with the reaction cross-sections for isotropic collisions. The selected reactant preparations have a pronounced effect on the large resonances, but not on the flat region of the excitation functions or in the small resonance at Ecoll = 0.53 meV. The largest effect is observed for the J = 3 resonance (Ecoll = 0.12 meV) in the F + HD(v = 0, j = 1) reaction, which is much enhanced for β = 90° (side-on collisions) and is suppressed for β = 0° (head-on collisions). This is best seen in the DF + H channel (upper right panel), however, note the small absolute magnitude of this peak. The second resonance in the F + HD(v = 1, j = 1) reaction, located at Ecoll = 0.31 meV, and having contributions from J = 4 and 6 (see Fig. 3), is also favored by β = 90°. The effect is seen in the two exit channels, but is more marked for DF + H (lower right panel). Both, the F + HD(v = 0, j = 1) resonance at 0.12 meV and the F + HD(v = 1, j = 1) resonance at 0.31 meV, could be switched on and off (the latter not completely) by orientating the HD internuclear axis parallel or perpendicular to kin. Finally, the F + HD(v = 1, j = 1) resonance peak at Ecoll = 0.12 meV, with contributions from J = 2 and J = 4, is enhanced for β = 0° (head-on collisions), but it is also pronounced for β = 90°. The effects of β on the resonances are not so clear-cut for F + HD(v = 1, j = 1) as for F + HD(v = 0, j = 1), but from an experimental point of view it would be probably easier to investigate the reaction with vibrationally excited HD, due to its much larger cross-sections. The effects produced by the specific preparations of the reactants illustrated in Fig. 6 mirror those described for the different helicities (see Fig. 4), which is not surprising. It has been shown in Section II, that Ω = 0 is the sole contribution to the cross-section for the β = 0° polarization, and likewise, only Ω = ±1 helicities contribute to the cross-section for for j = 1 and β = 90°. This coincidence between the corresponding Ω and β cross-sections shows that the best control of the stereodynamics is achieved when the external preparation matches the intrinsic directional properties of the reaction. Among all the resonances observed, the highest streodynamical selectivity is found for the peak at Ecoll = 0.12 meV, which is found in both channels of the F + HD(v = 0, j = 1) reaction. The fact that this peak is practically suppressed with β = 0° preparation (or equivalently with Ω = 0) is also related to the parity. As seen in Fig. 3, this peak can be attributed to J = 3 partial waves. Of the two possible parities for a given J, (−1)J and (−1)J+1, Ω = 0 only contributes to the former.51 Therefore the parity associated with the J = 3 resonance is (−1)J+1 = + as it has no contribution from Ω = 0. On the other hand, the parity is also given by (−1)L+j, which should be positive in this case. For j = 1 and J = 3, the three possible values of the orbital angular momentum quantum number are L = 2, 3, and 4. Of these values, only L = 3 may lead to a positive parity. Consequently, it can be concluded that the main contribution to this specific resonance proceeds from L = 3. For other resonance peaks, there are contributions from Ω = 0 and |Ω| = 1, to a more or less extent, and this analysis cannot be carried out.
Significant differences are found between the stereodynamical properties of the orbiting resonances discussed thus far and those of the Ecoll = 22 meV Feshbach resonance for the HF + D channel of the F + HD(v = 0) reaction.30,31 Promotion of the HD molecule to j = 1 does not have a drastic effect on the orbiting resonances (Fig. 1 and 2). They decrease by a factor of 2–3 for the HF + D channel, but increase somewhat for DF + H. However rotational excitation causes a large decrease in the intensity of the Feshbach resonance.30,31 All the orbiting resonances for F + HD(v = 0, 1; j = 1) have a significant (in some cases almost exclusive) contribution from side-on collisions, in which the HD internuclear axis is preferentially aligned perpendicular to the direction of approach (Ω = ±1, β = 90°). In contrast, in the Feshbach resonance, head-on collisions (Ω = 0, β = 0°) are dominant.50 Finally, it should be stressed that, thanks to the recent development of sophisticated experimental techniques (see, for instance, ref. 14 and 20 and the references cited therein), the results of this work should be in principle amenable to experimental investigation, especially those for the F + HD(v = 1) reaction, where the resonances are very intense.
IV. Summary and conclusions
The effects of rotational excitation and the stereodynamics of the F + HD(v = 0, 1; j = 0,1) system have been investigated in the near cold regime (0.01–6 meV or 0.12–70 K) by means of QM calculations. By determining the excitation functions (integral cross-section as a function of the collision energy) for the respective initial states, it was found that they exhibit a series of peaks that can be attributed to shape resonances. For the reactions with j = 0, these calculations extend our previous work, and allow the identification of new resonances. In all cases, the intensity of the resonance peaks for the reactions with HD(v = 1) is more than one order of magnitude larger than that for their HD(v = 0) counterparts. For the F + HD(v = 0, 1; j = 0) reactions, a very similar resonance pattern is found in the two exit channels, as expected for orbiting resonances, which depend on the van der Waals well at the entrance. For the reactions with rotationally excited molecules, F + HD(v = 0, 1; j = 1), resonances are still found at the same collision energies for the HF and DF product channel, but the intensity and shape of the peaks vary appreciably. Rotational excitation decreases the intensity of the resonance peaks of F + HD(v = 1, j = 1) by a factor of 2–3 with respect to those of F + HD(v = 1, j = 0).The integral cross-sections were analyzed in terms of the total angular momentum contributions. It was found that most of the resonances are due to one or two J-partial waves. The same partial waves contribute to each of the resonance peaks for the two product channels although with different intensities. This seems to corroborate the assumption that the observed peaks are indeed shape resonances occurring in the entrance channel.
The influence of the rotational angular momentum polarization was also investigated to determine the intrinsic directional properties of the reactive collisions leading to the observed orbiting resonances. The calculations showed that the reactant's helicity components, Ω = 0 and Ω = ±1, possible for j = 1 contribute in general to resonant scattering. However, the contribution of |Ω| = 1 is more important for the two exit arrangement channels of the F + HD(v = 0, j = 1) reaction, indicating the preference of the internuclear axis to be perpendicular to the relative velocity vector, and thus a preference for side-on collisions. The most extreme case is the resonance at 0.12 meV due to J = 3, which is furnished almost exclusively by |Ω| = 1. By conservation of parity argument, it is possible to assign this resonance to the orbital angular momentum partial wave L = 3. In contrast, for the vibrationally excited reaction, F + HD(v = 1, j = 1), Ω = 0 and Ω = ±1 helicities contribute to all the resonances although with different weights. In addition, the participation of the helicity components in the two product channels is basically the same and so is expected their respective stereodynamical response. The fact that for the reactions with HD(v = 0, 1) the contributions from the helicity components are the same for the two channels lends further support to the assertion that the observed peaks are indeed shape resonances.
Using the calculated polarization parameters, it is possible to corroborate the stereodynamical effects and control that can be achieved by varying the external preparation of the HD rotational angular momentum and consequently of the internuclear axis alignment. In almost all cases, to a more or less extent, there is clear influence of the alignment on the intensity of the various resonant peaks. The most extreme case is for the resonance associated with the J = 3 partial wave in the two channels of the F + HD(v = 0, j = 1), in which aligning the internuclear axis perpendicular to the incoming direction causes the practical switch off of the resonance.
The stereodynamical properties of the orbiting resonances for the F + HD reaction are in contrast with those of the well-known Feshbach resonance at Ecoll = 22 meV for the HF + D channel of this system, which is much diminished by rotational excitation.30,31 In addition, no resonance of this type is found in the DF + H product channel in the 10–40 meV energy range. While the Feshbach resonance is largely suppressed by side-on encounters and strongly enhanced by head-on attacks,50 this type of collision tends to dominate in the orbiting resonances.
The resonance patterns found in this work, and their variation with vibrational and rotational excitation, are amenable in principle to experimental investigation at least for the j = 2 initial state. In this respect, the external preparation of the reactants following the intrinsic directional preferences just described could be of great help in the identification of specific resonances by enhancing or diminishing, sometimes even suppressing, their intensity. As shown in the present work, it is worth noting that this effect that has been found in inelastic collisions is also present in reactive collisions. Recent works have proved that the stereodynamical control achieved by suitable external preparation has become a powerful tool to investigate the directional properties of inelastic and reactive collisions.57–59
Conflicts of interest
There are no conflicts to declare.Note added after first publication
This article replaces the version published on 22 Jan 2020, which contained errors in eqn (7).Acknowledgements
This work has been funded by the MINECO and by the the Ministry of Science and innovation of Spain under grants FIS2016-77726-C3-1P and PGC2018-096444-B-I00 respectively. VJH acknowledges also the funding from the EU project ERC-2013-Syg610256 (Nanocosmos). The research was conducted within the Unidad Asociada between the Department of Physical Chemistry of the UCM and the CSIC of Spain.References
- D. W. Chandler, J. Chem. Phys., 2010, 132, 110901 CrossRef.
- N. Balakrishnan, J. Chem. Phys., 2016, 145, 150901 CrossRef CAS.
- A. Schutte, G. Scoles, F. Tomassini and D. Bassi, Phys. Rev. Lett., 1972, 29, 979 CrossRef CAS.
- J. P. Toennies, W. Weltz and G. Wolff, J. Chem. Phys., 1979, 71, 614 CrossRef CAS.
- S. Chefdeville, T. Stoecklin, A. Bergeat, K. M. Hickson, C. Naulin and M. Costes, Phys. Rev. Lett., 2012, 109, 023201 CrossRef.
- S. Chefdeville, Y. Kalugina, S. van de Meerakker, C. Naulin, F. Lique and M. Costes, Science, 2013, 341, 1094 CrossRef CAS.
- C. Naulin and M. Costes, Int. J. Phys. Chem., 2014, 33, 427 CAS.
- A. Bergeat, J. Onvlee, C. Naulin, A. van der Avoird and M. Costes, Nat. Chem., 2015, 7, 349 CrossRef CAS.
- M. Costes and C. Naulin, Chem. Sci., 2016, 7, 2462 RSC.
- N. S. Vogels, T. Karman, J. Klos, M. Besmer, J. Onvlee, A. van der Avoird, G. C. Groenenboom and S. Y. T. van de Meerakker, Nat. Chem., 2018, 10, 435 CrossRef.
- A. B. Henson, S. Gersten, Y. Shagam, J. Narevicius and E. Narevicius, Science, 2012, 338, 234 CrossRef CAS.
- E. Lavert-Ofir, Y. Shagam, A. B. Henson, S. Gersten, J. Klos, P. S. Zuchowski, J. Narevicius and E. Narevicius, Nat. Chem., 2014, 6, 332 CrossRef CAS.
- J. Jankunas, K. Jachymsky, M. Hapk and A. Osterwalder, J. Chem. Phys., 2015, 142, 164305 CrossRef.
- A. Osterwalder, EPJ Tech. Instrum., 2015, 2, 10 CrossRef.
- B. Margulis, J. Narevicius and E. Narevicius, Nat. Commun., 2020, 11, 3553 CrossRef CAS.
- P. Paliwal, N. Deb, D. M. Reich, A. van der Avoird, C. P. Koch and E. Narevicius, Nat. Chem., 2021, 13, 94–98 CrossRef CAS.
- M. P. De Miranda, F. J. Aoiz, L. Bañares and V. Sáez-Rábanos, J. Chem. Phys., 1999, 111, 5368 CrossRef CAS.
- J. Aldegunde, M. P. de Miranda, J. M. Haigh, B. K. Kendrick, V. Sáez-Rábanos and F. J. Aoiz, J. Phys. Chem. A, 2005, 109, 6200 CrossRef CAS.
- J. Aldegunde, J. M. Alvariño, M. P. de Miranda, V. Saez-Rabanos and F. J. Aoiz, J. Chem. Phys., 2006, 125, 133104 CrossRef CAS.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Science, 2017, 359, 356 CrossRef.
- W. E. Perreault, N. Mukherjee and R. N. Zare, Nat. Chem., 2018, 10, 561 CrossRef CAS.
- W. E. Perreault, N. Mukherjee and R. N. Zare, J. Chem. Phys., 2019, 150, 174301 CrossRef.
- W. E. Perreault, N. Mukherjee and R. N. Zare, J. Chem. Phys., 2020, 152, 209901 CrossRef CAS.
- P. G. Jambrina, J. F. E. Croft, H. Guo, M. Brouard, N. Balakrishnan and F. J. Aoiz, Phys. Rev. Lett., 2019, 123, 043401 CrossRef CAS.
- M. Morita and L. Balakrishnan, J. Chem. Phys., 2020, 153, 5368 Search PubMed.
- P. G. Jambrina, L. González-Sánchez, M. Lara, M. Menéndez and F. J. Aoiz, Phys. Chem. Chem. Phys., 2020, 22, 24943–24950 RSC.
- N. Balakrishnan and A. Dalgarno, Chem. Phys. Lett., 2001, 341, 652 CrossRef CAS.
- M. Tizniti, S. D. L. Picard, F. Lique, C. Berteloite, A. Canosa, M. H. Alexander and I. R. Sims, Nat. Chem., 2014, 6, 141 CrossRef CAS.
- M. Gerin, D. A. Neufeld and J. R. Goicoechea, Annu. Rev. Astron. Astrophys., 2016, 54, 181 CrossRef CAS.
- R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S.-H. Lee, F. Dong and K. Liu, J. Chem. Phys., 2000, 112, 4536 CrossRef CAS.
- R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S.-H. Lee, F. Dong and K. Liu, Phys. Rev. Lett., 2000, 85, 1206 CrossRef CAS.
- T. I. Yakovitch, E. Garand, J. B. Kim, C. Hock, T. Theis and D. M. Neumark, Faraday Discuss., 2012, 157, 399 RSC.
- J. B. Kim, M. L. Weichman, T. F. Sjolander, D. M. Neumark, J. Kos, M. H. Alexander and D. E. Manolopoulos, Science, 2015, 349, 510 CrossRef CAS.
- M. Qiu, Z. Ren, L. Che, D. Dai, S. A. Harich, X. Wang, C. Xu, D. Dai, M. Gustafsson, R. T. Skodje, Z. Sun and D. H. Zhang, Science, 2006, 311, 1440 CrossRef CAS.
- Z. Ren, L. Che, M. Qiu, X. Wang, W. Dong, D. Dai, X. Wang, X. Yang, Z. Sun, B. Fu, S.-Y. Lee, X. Xu and D. H. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12662 CrossRef CAS.
- T. Wang, J. Chen, T. Yang, C. Xiao, Z. Sun, L. Huang, D. Dai, X. Yang and D. H. Zhang, Science, 2013, 342, 1499 CrossRef CAS.
- G. Li, H.-J. Werner, F. Lique and M. H. Alexander, J. Chem. Phys., 2007, 127, 174302 CrossRef.
- B. Fu, X. Xu and D. H. Zhang, J. Chem. Phys., 2008, 129, 011103 CrossRef.
- G. Lique, G. Li, H.-J. Werner and M. H. Alexander, J. Chem. Phys., 2011, 134, 231101 CrossRef.
- J. Chen, Z. G. Sun and D. H. Zhang, J. Chem. Phys., 2015, 142, 024303 CrossRef.
- T. Wang, T. Yang, C. Xiao, Z. Sun, D. H. Zhang, X. Yang, M. L. Weichman and D. M. Neumark, Chem. Soc. Rev., 2018, 47, 6744 RSC.
- K. Stark and H.-J. Werner, J. Chem. Phys., 1996, 104, 6515 CrossRef CAS.
- N. Balakrishnan and A. Dalgarno, J. Phys. Chem. A, 2003, 107, 7101 CrossRef CAS.
- E. Bodo and F. A. Gianturco, Eur. Phys. J. D, 2004, 31, 423 CrossRef CAS.
- D. De Fazio, V. Aquilanti and S. Cavalli, Front. Chem., 2019, 7, 328 CrossRef CAS.
- D. De Fazio, V. Aquilanti and S. Cavalli, J. Phys. Chem. A, 2020, 124, 12 CrossRef CAS.
- V. Sáez-Rábanos, J. E. Verdasco and V. J. Herrero, Phys. Chem. Chem. Phys., 2019, 21, 15177 RSC.
- V. Aquilanti, S. Cavalli, D. de Fazio, A. Volpi, A. Aguilar and M. J. Lucas, Chem. Phys. Lett., 2003, 371, 504 CrossRef CAS.
- V. Aquilanti, S. Cavalli, D. de Fazio, A. Volpi, A. Aguilar and M. J. Lucas, Chem. Phys. Lett., 2005, 308, 237 CAS.
- J. Aldegunde, P. G. Jambrina, M. P. de Miranda, V. Sáez-Rábanos and F. J. Aoiz, Phys. Chem. Chem. Phys., 2011, 13, 8345 RSC.
- D. Skouteris, J. F. Castillo and D. E. Manolopoulos, Comput. Phys. Commun., 2000, 133, 128 CrossRef CAS.
- F. J. Aoiz, V. Saez-Rabanos, B. Martinez-Haya and T. Gonzalez-Lezana, J. Chem. Phys., 2005, 123, 094101 CrossRef CAS.
- J. Aldegunde, D. Herréz-Aguilar, P. Jambrina, F. J. Aoiz, J. Jankunas and R. N. Zare, J. Phys. Chem. Lett., 2012, 3, 2959 CrossRef CAS.
- T. Takayanagi and Y. Kurosaki, J. Chem. Phys., 1998, 109, 8929 CrossRef CAS.
- T. Takayanagi, Chem. Phys. Lett., 2006, 433, 15 CrossRef CAS.
- F. J. Aoiz, L. Banares, V. J. Herrero, V. Saez-Rabanos, K. Stark, I. Tanarro and H.-J. Werner, Chem. Phys. Lett., 1996, 262, 175 CrossRef CAS.
- F. Wang, K. Liu and T. P. Rakitzis, Nat. Chem., 2012, 4, 636–641 CrossRef CAS.
- F. Wang and K. Liu, J. Chem. Phys., 2016, 145, 144305 CrossRef.
- C. G. Heid, V. Walpole, M. Brouard, P. G. Jambrina and F. J. Aoiz, Nat. Chem., 2019, 11, 662–668 CrossRef CAS.
| This journal is © the Owner Societies 2021 |