Probing transport limitations in thick sintered battery electrodes with neutron imaging†
Ziyang
Nie
a,
Samuel
Ong
a,
Daniel S.
Hussey
 b,
Jacob M.
LaManna
b,
David L.
Jacobson
b and
Gary M.
Koenig
Jr.
b,
Jacob M.
LaManna
b,
David L.
Jacobson
b and
Gary M.
Koenig
Jr.
 *a
*a
aDepartment of Chemical Engineering, University of Virginia, 102 Engineers Way, Charlottesville, 22904-4741, VA, USA. E-mail: gary.koenig@virginia.edu
bNational Institute of Standards and Technology Physical Measurements Laboratory, Gaithersburg, 20899-8461, MD, USA
First published on 16th October 2019
Abstract
Lithium-ion batteries have received significant research interest due to their advantages in energy and power density, which are important to enabling many devices. One route to further increase energy density is to fabricate thicker electrodes in the battery cell; however, careful consideration must be taken when designing electrodes as to how increasing the thickness impacts the multiscale and multiphase molecular transport processes, which can limit the overall battery operating power. Design of these electrodes necessitates probing the molecular processes when the battery cell undergoes electrochemical charge/discharge. One tool for in situ insights into the cell is neutron imaging, because neutron imaging can provide information of where electrochemical processes occur within the electrodes. In this manuscript, neutron imaging is applied to track the lithiation/delithiation processes within electrodes at different current densities for a full cell with a thick sintered Li4Ti5O12 anode and LiCoO2 cathode. The neutron imaging reveals that the molecular distribution of Li+ during discharge within the electrode is sensitive to the current density, or equivalently discharge rate. An electrochemical model provides additional insights into the limiting processes occurring within the electrodes. In particular, the impact of tortuosity and molecular transport in the liquid phase within the interstitial regions in the electrodes are considered, and the influence of tortuosity was shown to be highly sensitive to the current density. Qualitatively, the experimental results suggest that the electrodes behave consistent with the packed hard sphere approximation of Bruggeman tortuosity scaling, which indicates that the electrodes are largely mechanically intact but also that a design that incorporates tunable tortuosity could improve the performance of these types of electrodes.
Design, System, ApplicationLithium-ion batteries are a leading energy storage technology. Higher energy density batteries are desired, and one route to achieve this at the system level is through using thicker electrodes and removing inactive materials – with both attributes shared by the “sintered electrodes” in this study. Thick electrodes increase the molecular transport path distances, limiting charge/discharge rates. This work uses a combination of in situ neutron imaging experiments during electrochemical discharge and calculations to provide insight into the processes and operating conditions that limit sintered electrodes. It was found that the electrodes in this study have tortuosity and molecular transport consistent with hard sphere packing, and that gains in battery performance are possible with improvements to the electrode tortuosity. These results will impact researchers by demonstrating 1) limitations for high energy thick battery electrodes, 2) neutron imaging to probe battery processes under different operating conditions, and 3) the net impact of efforts to modify electrode tortuosity. This design framework is valuable not just for lithium-ion batteries with thick electrodes, but for electrochemical systems operating under designs and conditions where molecular transport through interstitial regions in the electrode architecture is rate limiting. |
1. Introduction
Lithium-ion (Li-ion) batteries have received great interest due to their high energy and power density.1 In researching improved Li-ion batteries, a common area of focus is new materials (e.g., active electrode materials or electrolyte chemistry),2–5 but another route is to increase the energy density through electrode or cell design, for example, by increasing the relative fraction of the active electrode in the cell or minimizing inactive additives within the electrode.6,7 Recently, towards the goal of improving battery energy density, researchers have designed electrodes composed of only active materials.8–10 Compared to conventional composite electrodes, sintered electrodes consist of pure active materials without conductive carbon additives and polymer binders. In addition, these electrodes can be made much thicker than composite electrodes. The combination of reducing the amount of inactive components in the electrode and making thicker electrodes results in high energy density and areal capacities at the electrode and cell levels.8–10 When making electrodes composed of only electroactive materials, there is often a sintering step to improve the mechanical robustness of the porous thin film; thus we refer to them as “sintered electrodes”.While sintered electrodes have very high energy density, the fraction of the electrochemical energy delivered at increasing rates of charge/discharge (or equivalently current densities) decreases quickly relative to many conventional composite electrodes; thus cells with sintered electrodes have low rate capability. This limitation results in the need to better understand the molecular processes limiting the electrochemical performance of the electrodes. Li-ion batteries have a number of different multiscale and multiphase processes which can limit the performance of the cell, including solid phase, liquid phase, and interphase ion transport with relevant length scales ranging from a few nanometers to hundreds of micrometers depending on the specific materials and cell designs employed.11,12 Two major differences between conventional composite electrodes and sintered electrodes that would be expected to impact rate capability are the electrical conductivity and the Li+ mass transport through the electrode microstructure. The electrical transport for composite electrodes is primarily facilitated by the carbon black/binder matrix within the interstitial regions between the active material particles, while for sintered electrodes the electrical conductivity must be provided by the active material particles themselves and their connections. The electrical conductivity for the electrode matrix is orders of magnitude higher for the conventional composite electrode than it is for active materials used in sintered electrodes.13,14 However, previous reports have suggested that the greater contributor to limitations of rate capability for porous electrodes is the mass transport of Li+ through the electrode microstructure.15 Sintered electrodes are much thicker (typically >500 μm) than composite electrodes (often <100 μm),16,17 and thus the Li+ must traverse much greater distances through the liquid phase of the tortuous electrode microstructure with sintered electrodes. Increased molecular transport paths result in increased cell polarization and can result in the cell quickly reaching a mass transport limiting current density.16,17 To better understand the limitations of sintered electrodes and the mass transport through the electrode architecture, an in situ technique is needed that provides information on the Li+ concentration within the cell as a function of time and at different rates/current densities. In this study, neutron imaging will be used to provide in situ information on Li+ concentration in the direction of the molecular Li+ flux throughout the battery thickness at different discharge rates to provide insights into the transport limitations of sintered electrodes.
Neutron imaging involves passing a low energy neutron beam through a sample and detecting the relative intensity of the transmitted beam through the sample via a scintillation detector. Neutrons that do not pass through the sample are either scattered or absorbed, and the combination of these interactions of an element or isotope with the neutrons is the attenuation provided by that species. A highly attenuating isotope is 6Li (7Li is nearly transparent), and thus the intensity of individual pixels in a neutron radiograph is highly sensitive to the concentration of Li which the neutrons must pass through before reaching the detector.18 During charge/discharge of a Li-ion battery, the only species that is expected to substantially change in concentration throughout the cell is Li+, and the changes of Li+ at a given depth within the electrode can change in excess of 10 mol L−1.19 The combination of the sensitivity of neutron imaging to Li concentration, Li being the only elemental or molecular species expected to change in concentration significantly within the cell during operation, and the large changes in Li concentration within the electrode makes neutron imaging a promising nondestructive in situ tool to probe lithiation/delithiation as a function of electrode depth during electrochemical cycling, improving the rational design of the electrode architecture and other battery cell components.19–21 While neutron imaging has been used previously for conventional composite electrodes, the relatively large pixel size (in some cases >30 μm)20 limits the number of depth locations that can be mapped for the Li+ concentration gradient within the cell.20,21 The relatively large thickness of sintered electrodes makes them ideal for probing the Li+ concentration gradient throughout the thickness of the cell and subsequently correlating to electrode transport characteristics.
In a previous report,19 we applied neutron imaging on battery coin cells where both the anode and cathode were thick sintered electrodes and explored how the electrode thickness impacted the lithiation/delithiation processes within the cells. Different lithiation processes were observed in each electrode, with the relatively thinner cathode having a relatively uniform lithiation throughout the thickness during discharge and the relatively thicker anode having a front of delithiation that propagated from the separator side of the electrode to the current collector side of the electrode. However, in the previous work only a single and relatively slow rate of discharge was used. In this report, increasing rates of discharge and their impact on the lithiation/delithiation processes within the electrodes in a sintered full cell will be investigated. The electrochemical performance becomes limited at higher current densities, and thus greater insights into the limiting processes within the electrode were expected at higher current densities. Specifically, electrode design elements such as tortuosity in the cell, which impacts the molecular mobility in the liquid phase and the possibility of mechanical fracture or cracking of the electrodes, will be discussed to interpret combined calculation and experimental results with implication for future design improvements of the cells.
2. Materials and methods
2.1 Active material powder preparation
The cathode material used in this study was LiCoO2 (LCO). The material was synthesized via CoC2O4·2H2O precursor coprecipitation and subsequent calcination with Li2CO3 salt in a furnace exposed to an air environment.10,22 To prepare the CoC2O4·2H2O precursor, 1800 mL of 62.8 mM Co(NO3)2·6H2O (Fisher Reagent Grade)‡ and 1800 mL of 87.9 mol m−3 (NH4)2C2O4·H2O (Fisher Certified ACS) were prepared separately and dissolved in deionized water. After heating to 50 °C, the solutions were mixed together all at once by pouring the Co(NO3)2·6H2O solution into the (NH4)2C2O4·H2O solution. A Teflon stir bar set at 83.9 rad s−1 (800 rpm) was used to maintain solution mixing, and the coprecipitation proceeded at 50 °C for 30 min. Then, the solid precipitate was collected using vacuum filtration and rinsed with 4 L of deionized water. The powder was dried in an oven with an air atmosphere at 80 °C for 24 h.To prepare the LCO active material, the oxalate precursor powder was mixed with Li2CO3 (Fisher Chemical) powder with an excess of lithium salt (Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Co ratio of 1.02
Co ratio of 1.02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) using a mortar and pestle. The powder mixture was heated to 800 °C at a ramp rate of 1 °C min−1 under an air atmosphere in a Carbolite CWF 1300 box furnace. The product was cooled to ambient temperature in the furnace without control over the cooling rate. The LCO material was ground using a mortar and pestle. To further reduce the particle size, the LCO was milled in a Fritsch Pulverisette 7 planetary ball mill using 5 mm diameter zirconia beads at 31.4 rad s−1 (300 rpm) for 5 hours.
1) using a mortar and pestle. The powder mixture was heated to 800 °C at a ramp rate of 1 °C min−1 under an air atmosphere in a Carbolite CWF 1300 box furnace. The product was cooled to ambient temperature in the furnace without control over the cooling rate. The LCO material was ground using a mortar and pestle. To further reduce the particle size, the LCO was milled in a Fritsch Pulverisette 7 planetary ball mill using 5 mm diameter zirconia beads at 31.4 rad s−1 (300 rpm) for 5 hours.
The anode material used in this study, Li4Ti5O12 (LTO), was purchased from a commercial supplier (NANOMYTE BE-10 from NEI Corporation) and used without any additional treatment. The characterization and electrochemical performance of both LCO and LTO materials used in this study were reported previously.10,22–24
2.2 Electrode preparation and battery fabrication
Sintered electrodes which were composed of only active materials were used in this study. The same procedure was used to make both cathode and anode pellets. First, active powder was mixed with 1% by weight polyvinyl butyral (Pfaltz & Bauer) dissolved in ethanol (Acros). 2 mL of solution was blended with 1 g of active material using a mortar and pestle and the solvent was allowed to evaporate in air. Next, 0.2 g of the powder and binder mixture was loaded into a 13 mm diameter Carver pellet die and then pressed with about 5443 kg (12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 lbf) for 2 minutes in a Carver hydraulic press. After that, the pellets were heated in a Carbolite CWF 1300 box furnace. The furnace heating was carried out in an air atmosphere with a ramping rate of 1 °C min−1 from 25 °C to 600 °C. After holding at 600 °C for 1 hour, the pellets were cooled to 25 °C at 1 °C min−1.
000 lbf) for 2 minutes in a Carver hydraulic press. After that, the pellets were heated in a Carbolite CWF 1300 box furnace. The furnace heating was carried out in an air atmosphere with a ramping rate of 1 °C min−1 from 25 °C to 600 °C. After holding at 600 °C for 1 hour, the pellets were cooled to 25 °C at 1 °C min−1.
The sintered electrodes were assembled into full cells within a CR2032 coin cell. LCO and LTO pellets were pasted onto the bottom plate and the stainless steel spacer of the cell, respectively. A carbon paste of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 weight ratio of Super P carbon black (Alfa Aesar) to polyvinylidene difluoride (PVDF, Alfa Aesar) binder dissolved in N-methyl pyrrolidone (NMP, Sigma-Aldrich) was used to attach the pellets to the metal components. Then, the pellets were dried at 80 °C in an oven in air for 12 hours. Next, the pellets were transferred into a glove box (Ar atmosphere, O2 and H2O both <1 μL L−1). In the glove box, LTO and LCO electrodes were assembled into a coin cell. The anode and cathode were separated by a Celgard 2325 polymer separator (25 μm thick) and 16 drops of electrolyte (1.2 M LiPF6 in 3
1 weight ratio of Super P carbon black (Alfa Aesar) to polyvinylidene difluoride (PVDF, Alfa Aesar) binder dissolved in N-methyl pyrrolidone (NMP, Sigma-Aldrich) was used to attach the pellets to the metal components. Then, the pellets were dried at 80 °C in an oven in air for 12 hours. Next, the pellets were transferred into a glove box (Ar atmosphere, O2 and H2O both <1 μL L−1). In the glove box, LTO and LCO electrodes were assembled into a coin cell. The anode and cathode were separated by a Celgard 2325 polymer separator (25 μm thick) and 16 drops of electrolyte (1.2 M LiPF6 in 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 ethylene carbonate
7 ethylene carbonate![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethyl methyl carbonate, BASF) were added into the cell. Other parts of the CR2032 coin cell used in this study include a stainless steel wave spring, a stainless steel top cap, and a Teflon gasket. The LCO pellet used in the study had a thickness of 0.468 mm and the thickness of the LTO pellet was 0.691 mm. More information about the structure of the coin cell that contained the sintered electrodes can be found in a previous report.19 The internal resistance for the coin cells containing sintered electrodes was determined from the high frequency intercept from an electrochemical impedance spectroscopy measurement (amplitude 10 mV).
ethyl methyl carbonate, BASF) were added into the cell. Other parts of the CR2032 coin cell used in this study include a stainless steel wave spring, a stainless steel top cap, and a Teflon gasket. The LCO pellet used in the study had a thickness of 0.468 mm and the thickness of the LTO pellet was 0.691 mm. More information about the structure of the coin cell that contained the sintered electrodes can be found in a previous report.19 The internal resistance for the coin cells containing sintered electrodes was determined from the high frequency intercept from an electrochemical impedance spectroscopy measurement (amplitude 10 mV).
The LTO/LCO coin cell was cycled galvanostatically at different C rates on a MACCOR battery cycler and Bio-Logic SP-50 potentiostat, with the latter used during the neutron imaging experiments. The C rate was based on the assumed capacity of 150 mA h g−1 for the LCO mass in the coin cell, where 1C was assumed to correspond to 150 mA g−1 LCO. The cut off voltages were set to be 1.0–2.8 V (cell voltage, vs. LTO anode) for all cells and C rates evaluated. The cycling capacity data before neutron imaging tests for three cells nominally identical to the one used in this study can be found in the ESI,† Fig. S1.
2.3 Neutron imaging
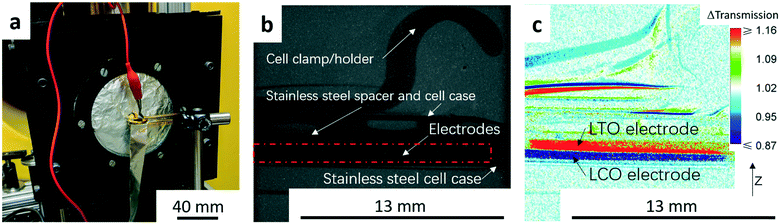
The neutron imaging experiment was carried out at the thermal Neutron Imaging Facility (NIF) beamline BT-2 at the National Institute for Standards and Technology (NIST) Center for Neutron Research.25 The experimental setup with the coin cell in front of the detector is shown in Fig. 1a. The scintillator was Gd2O2S:Tb for converting the incident neutrons into visible light. The visible light was then captured with an Andor NEO scientific complementary metal-oxide semiconductor detector coupled with a 105 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Nikon f2.8 lens and PK13 extension tube, which provided a pixel pitch of 6.5 μm. Radiographs were collected every minute from the initiation of the experiment. An example of a raw radiograph is shown in Fig. 1b. To reduce non-statistical noise, three radiographs were combined through a median operation. Images were also dark image corrected. The goal of this study was to track changes in Li+ concentration throughout the thickness of the cell during electrochemical discharge. Therefore, pixel intensities in radiographs at all time points were normalized relative to the image taken before starting the cycling (the “no current” image). The change in the pixel intensity relative to the “no current” image (Δtransmission) will be depicted using a color scale in this manuscript (Fig. 1c). The movement of Li+ results in most of the changes in neutron transmission observed in the radiographs, and thus the differences in transmission were attributed to the net movement of Li+ in the cell. In the color scale images, blue regions correspond to lower transmission and higher Li+ concentration than the beginning state of the experiment while red regions correspond to higher transmission and lower Li+ concentration. The image in Fig. 1c was taken at the end of the C/20 discharge to highlight the contrast between the anode and cathode regions. In Fig. 1c, the dark blue region represents the LCO electrode which had a higher Li+ concentration (lower neutron transmission) at the end of discharge and the red region represents the LTO electrode which had a lower Li+ concentration (higher neutron transmission).
1 Nikon f2.8 lens and PK13 extension tube, which provided a pixel pitch of 6.5 μm. Radiographs were collected every minute from the initiation of the experiment. An example of a raw radiograph is shown in Fig. 1b. To reduce non-statistical noise, three radiographs were combined through a median operation. Images were also dark image corrected. The goal of this study was to track changes in Li+ concentration throughout the thickness of the cell during electrochemical discharge. Therefore, pixel intensities in radiographs at all time points were normalized relative to the image taken before starting the cycling (the “no current” image). The change in the pixel intensity relative to the “no current” image (Δtransmission) will be depicted using a color scale in this manuscript (Fig. 1c). The movement of Li+ results in most of the changes in neutron transmission observed in the radiographs, and thus the differences in transmission were attributed to the net movement of Li+ in the cell. In the color scale images, blue regions correspond to lower transmission and higher Li+ concentration than the beginning state of the experiment while red regions correspond to higher transmission and lower Li+ concentration. The image in Fig. 1c was taken at the end of the C/20 discharge to highlight the contrast between the anode and cathode regions. In Fig. 1c, the dark blue region represents the LCO electrode which had a higher Li+ concentration (lower neutron transmission) at the end of discharge and the red region represents the LTO electrode which had a lower Li+ concentration (higher neutron transmission).
To obtain quantitative information of the Li+ movement, a 1000 pixel wide line scan was used across the electrode area from the bottom to the top (z-direction in Fig. 1c). An example showing the line scan region in this study can be found in the ESI,† Fig. S2. The LTO/LCO cell used in the neutron imaging was charged to 2.8 V at a rate of C/20 before travelling to NIST. At NIST, after the cell was set up for the experiment (Fig. 1a), the cell was charged again at a rate of C/20 to 2.8 V to compensate for any capacity potentially lost during the shipment.
2.4 Model analysis
To aid in interpretation of the experimental results, an electrochemical mathematical model developed by Newman et al.26 was used to calculate the discharge curves and Li+ concentration in both the solid and electrolyte phases within the cell as a function of depth within the cell and time. These results were compared in relation to the experimentally measured discharge curve and change in neutron transmission in the neutron radiographs. Details of the model can be found in previous publications.27–293. Results and discussion
3.1 Neutron radiographs before and after discharge at different rates
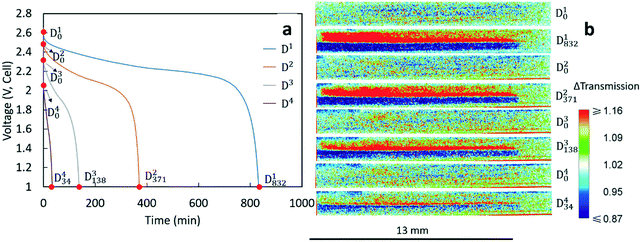
After being charged to 2.8 V, the cell was cycled at different rates. The procedure and capacity for each charge/discharge step are listed in Table 1. The charge rates for each cycle were the same (C/20, corresponding to 1.46 mA and 1.10 mA cm−2), while the discharge rate varied for each cycle. Since discharge processes were the focus of this study, Di is used to represent the ith discharge in the experiment. The discharge rate for D1 was the same as the charge rate (C/20). The discharge rates for D2, D3 and D4 were C/10 (corresponding to 2.92 mA and 2.20 mA cm−2), C/5 (corresponding to 5.85 mA and 4.40 mA cm−2) and C/2.5 (corresponding to 11.70 mA and 8.80 mA cm−2), respectively. Between each cycle, there was a 10 min rest to allow the voltage to stabilize. Inspection of Table 1 reveals that each charge capacity after the first discharge (D1) matched well with the capacity of the preceding discharge process, indicating that each discharge process initiated from a similar state of charge for the cell. The capacities in Table 1 were also consistent with experimental results for nominally equivalent sintered LTO/LCO coin cells not used in neutron imaging experiments (Fig. S1†).| Charge/discharge | C rate | Capacity (mA h g−1 LCO) |
|---|---|---|
| a Capacity charged at NIST before the first discharge. The charge capacity before travelling to NIST was 100.0 mA h g−1 LCO. b Label Di is used to represent the ith discharge in the test. | ||
| Charge | C/20 | 7.5a |
| Discharge (D1)b | C/20 | 104.0 |
| Charge | C/20 | 101.8 |
| Discharge (D2)b | C/10 | 92.5 |
| Charge | C/20 | 92.1 |
| Discharge (D3)b | C/5 | 69.0 |
| Charge | C/20 | 69.6 |
| Discharge (D4)b | C/2.5 | 34.0 |
The voltage profiles for the four discharges conducted during the neutron imaging experiment are displayed in Fig. 2a. A higher discharge rate resulted in a lower final capacity and more significant polarization in the discharge profile. Although these outcomes are generally observed with Li-ion batteries, the capacity fade was relatively large for the sintered electrode cell. To gain further insights into how the Li+ ions distributed within the cell at the different rates of discharge, the neutron images with changes in neutron intensity were analyzed for the 4 beginning of discharge points and 4 end of discharge points shown in Fig. 2a. These points are labeled as Dix, which indicates the neutron image at the xth minute of the ith discharge. The corresponding neutron imaging radiographs are displayed in Fig. 2b. The first important result in Fig. 2b is that all images taken at the beginning of discharge (the Di0 images) were very similar, suggesting that each discharge process started with a similar Li+ distribution in both electrodes. However, neutron images at the end of discharge revealed redistribution of Li+ in the electrode that was highly dependent on the rate. For all rates, the bottom electrode (LCO) had regions which were blue due to a higher Li+ concentration (and lower relative neutron transmission) after discharging and the top electrode (LTO) had regions which were red due to a lower Li+ concentration (and higher relative neutron transmission). This overall result was consistent with the expected flux of Li+ from the anode to the cathode during discharge. In addition, with the color scale, the darker the blue the higher the Li+ concentration in the LCO electrode and the brighter the red the lower the Li+ concentration for the LTO electrode. On comparing the end state of different discharge processes, D1832 showed the darkest blue and the brightest red in the cathode and anode area, respectively. This implies that greater amounts of Li+ were transferred from LTO to LCO while discharging at a rate of C/20, consistent with D1 having the highest discharge capacity (Table 1). With increasing rates of discharge, the blue regions are both not as dark and do not go as deep into the cathode and the red regions are not as bright and also do not go as deep into the anode, consistent with the lower capacities and lower amounts of net Li+ exchanged at increasing rates (Table 1). Qualitatively, the C/20 discharge (D1832) and C/10 discharge (D2371) appear to have lithiation/delithiation of the entire electrode regions but the capacity difference primarily appeared to result in changes in color intensity, or equivalently differences in extents of lithiation, within the electrodes. However, at the highest rates of C/5 (D3138) and C/2.5 (D434), the lithiation/delithiation becomes more localized near the separator region as a function of increasing rate/current density. This outcome indicated much lower utilization of the electrode thickness at increasing rate and the Li+ redistribution being highly localized near the separator region within the cell. This observation suggested limitations in the availability and transport of Li+ in the cell, which will be discussed in detail in section 3.3.
3.2 Numerical calculations of discharge profiles with different Bruggeman exponents
To gain insight into the discharge process at different rates, a 1-D porous electrode model was used to calculate the discharge curves and Li+ compositional profile in the sintered electrode full cell. The model was developed by Newman et al. and has been adopted in a number of previous reports.27–31 The parameters used in this study are listed in Table 2. These values were either from experimental measurement, reported in the literature,3,13,22,23,32–38 provided by the commercial material supplier or assumed using approximations previously developed for the model, as indicated in the table.| Parameters | Value | Source |
|---|---|---|
| Thickness of the negative electrode/LTO (m) | 6.91 × 10−4 | Measured |
| Thickness of the separator (m) | 2.5 × 10−5 | Manufacturer |
| Thickness of the positive electrode/LCO (m) | 4.68 × 10−4 | Measured |
| Bulk LiPF6 concentration (mol m−3) | 1200 | Manufacturer |
| Initial stoichiometric parameter, y for the anode (y in Li(4/3+y)Ti(5/3)O4) | 0.64 | Estimate from experimental capacities |
| Initial stoichiometric parameter, x for the cathode (x in LixCoO2) | 0.57 | Estimate from experimental capacities |
| Solid-state Li+ diffusion coef. in the anode (m2 s−1) | 1 × 10−12 | Experimental data and Zaghib et al.32 |
| Solid-state Li+ diffusion coef. in the cathode (m2 s−1) | 5 × 10−19 | Geng et al.33 |
| Radius of anode active particles (m) | 1.0 × 10−7 | Qi et al.23 |
| Radius of cathode active particles (m) | 1.5 × 10−7 | Qi et al.22 |
| Volume fraction of electrolyte in the negative electrode | 0.42 | Based on measured porosity using pellet dimensions and material density |
| Volume fraction of electrolyte in the separator | 0.39 | Manufacturer |
| Volume fraction of electrolyte in the positive electrode | 0.38 | Based on measured porosity using pellet dimensions and material density |
| Conductivity of the negative matrix (S m−1) | 2 | Young et al.34 |
| Conductivity of the positive matrix (S m−1) | 0.3 | Ménétrier et al.13 |
| Coulombic gravimetric capacity of the negative material (mA h g−1) | 175 | Nitta et al.3 |
| Coulombic gravimetric capacity of the positive material (mA h g−1) | 274 | Nitta et al.3 |
| Density of the negative insertion material (kg m−3) | 3485 | Theoretical crystal density, Kataoka et al.35 |
| Density of the positive insertion material (kg m−3) | 5010 | Theoretical crystal density, Takahashi et al.36 |
| Rate constant for the negative reaction | 8.7 × 10−6 | Calculated based on He et al.37 |
| Rate constant for the positive reaction | 4.3 × 10−7 | Zhang et al.38 |
| Internal resistance (Ω m2) | 5.8 × 10−3 | Experimental data |
In this study, tortuosity (τ) was investigated in greater detail to better understand the effects of molecular transport in the liquid phase through the interconnected electrode pores on the sintered electrode battery performance. For the calculations using the electrochemical model, the tortuosity was accounted for using a Bruggeman exponent (α), where by using the measured porosity of the electrode, ε, the tortuosity of the electrode was determined by τ = ε1−α.39 Typically, the value assumed for α in porous electrode calculations is 1.5, a value which would be consistent with close packing of uniform hard spheres.39 Though the particles used in the sintered electrodes were not monodisperse, experimentally it was determined that α ≈ 1.5 was a reasonable approximation for the sintered electrodes. The experimental determination of the tortuosity of the sintered electrodes was done by measuring the effective ionic conductivity in symmetric Li/Li coin cells.27,39 Details of the tortuosity measurements can be found in the ESI† and include Fig. S3 and S4 and Table S1, and the method was adapted from ref. 39. Also included in this section are further details on electrolyte properties used in calculations.26,40,41
It is noted that for the tortuosity measurements performed it is assumed that the LTO electronic conductivity could be neglected. While pristine LTO has been reported to have an electronic conductivity of ∼10−5 mS cm−1 which could safely be neglected for the tortuosity determination,34 the lithiation profiles and polarization during discharge (presented later in the manuscript) suggested that the electronic conductivity of LTO was likely much greater. The contributions from the electronic conductivity of LTO would result in the measured resistance in the experiments being lower than that provided by just the ion transport through the electrode microstructure, which means that the measured values of tortuosity described below should be considered as lower bounds for the actual tortuosity and Bruggeman exponent for the electrodes.
While assembling the pellets into a coin cell, some cracking may occur during the crimping process. These cracks would create vertical channels though the electrode. Assuming the channels were perfectly aligned, within the channel region the tortuosity would be 1, corresponding to the Bruggeman exponent α being 1.0. Taking the whole pellet into consideration, the cracks would result in a tortuosity between the packed hard sphere Bruggeman tortuosity (α = 1.5) and no tortuosity (α = 1). Therefore, in this work, the behavior of both α = 1.5 and α = 1 was calculated and compared with the experimental results. Note that for the α = 1.5 case that τ = 1.62 for the LCO electrode and τ = 1.54 for the LTO electrode, which was relatively low compared to values of >3 reported for composite electrodes.42 Note that the composite electrodes have higher tortuosity due to additional restrictions to ion transport by the binder and carbon black additives in the interstitial regions between active material particles. Consideration of these two extremes of α also was expected to provide insights into the potential value of designing cells with template structures to improve tortuosity and/or improve molecular transport through the electrode pores. Note that the α values were applied to both electrodes in the calculations. The value of α used for the separator in calculations was 2.2 (and thus a τ of 3.10), which was determined experimentally from tortuosity measurements using a symmetric cell with only separators.
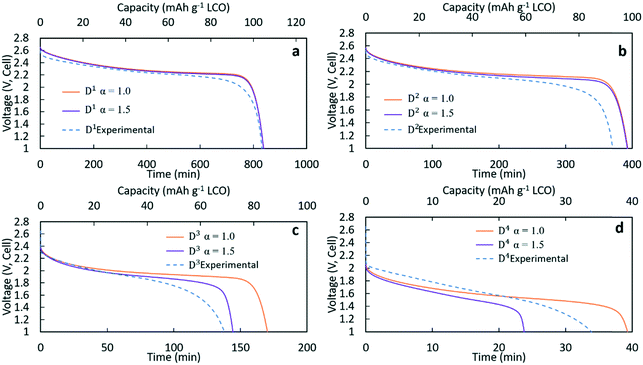
Fig. 3 contains the experimental discharge profiles for the coin cell at the four different rates and the calculated discharge profiles using Bruggeman exponent values of α = 1.0 and α = 1.5. As can be seen in Fig. 3a and b, at low discharge rates (C/20 (D1) and C/10 (D2)), the calculated profiles for the two different tortuosity exponents were almost the same, suggesting that limitations to Li+ transport through the electrode were not significantly impacted by the tortuosity of the microstructure. The experimental agreement with the calculated profiles was also very good at the two lowest discharge rates, although the C/10 discharge ended slightly before the calculated profiles. For D1 (Fig. 3a) the capacity for both calculated discharge profiles was 105 mA h g−1 LCO, which was a <1% difference compared to the experimental value (104 mA h g−1 LCO, Table 1). In Fig. 3b, the calculated capacity was 99 mA h g−1 LCO, which was a ∼7% difference from the experimental value (92.5 mA h g−1 LCO, Table 1). At the two higher rates of discharge, the two calculated profiles had significant differences in the final discharge capacity and time. In Fig. 3c, the calculated capacity for D3 with α = 1.0 was 86 mA h g−1 LCO while the calculated capacity for α = 1.5 was 72 mA h g−1 LCO. Compared with the experimental result which had a capacity of 69 mA h g−1 LCO, the result of α = 1.5 showed better agreement, although all profiles had similar polarization at early times of the discharge. For D4 in Fig. 3d, the calculated final capacities for α = 1.0 and α = 1.5 were significantly different, with values of 39 mA h g−1 LCO and 24 mA h g−1 LCO, respectively. The experimental capacity was 34 mA h g−1 LCO, which was between the two calculated values. The increasing differences in total delivered capacity for the two values of α reflect the increasing limitations to Li+ transport through the electrode microstructure dictating the performance of the battery, consistent with previous studies of the impacts of tortuosity on Li-ion battery capacity at high discharge rates.43 There was only a slight difference in the two extremes of tortuosity at the lower rates of D1 and D2 because the necessary flux of Li+ to maintain those rates was low enough that the differences in tortuosity did not impact the Li+ transport significantly. At higher rates, the impact of tortuosity started to limit Li+ transport at the higher flux necessary to accommodate the increased current density and resulted in significant differences in the calculated total capacity that could be delivered. At C/5 (D3), compared to the no tortuosity condition, the pellet with α = 1.5 lost 16% capacity (14 mA h g−1 LCO), while at C/2.5 nearly 40% capacity (16 mA h g−1 LCO) was lost.
3.3 Comparison of experimental and calculated Li+ composition profiles
To gain further insights into the Li+ transport behavior during lithiation/delithiation processes, the calculated Li+ concentration profiles within the cell, based on the model, were compared to the neutron images collected during discharge. Note that both the liquid and solid phase Li+ concentrations were calculated, but in most cases when Li+ concentration is discussed it is the volume weighted sum of these two concentrations (or the net change of this concentration) because the neutrons will be attenuated by all the Li+ ions in the region they pass through. For this analysis, 5 time points were analyzed: the beginning of discharge, the end of discharge, and 25%, 50%, and 75% of the discharge time. Due to the different total discharge times, the specific time points were at different values for each rate. The selected time points in the discharge profile and the corresponding neutron images can be found in the ESI,† Fig. S5–S8. To obtain a more quantitative comparison between the neutron images and calculated Li+ concentration profiles, a 1000 pixel line scan was applied for each image analyzed. The direction of the scan is from bottom to top (z-direction as noted in Fig. 1). The scan was done from a position slightly below the LCO electrode to a position slightly above the LTO electrode to ensure that all electrode regions were included (example of the scan region can be found in the ESI,† Fig. S2). All neutron radiographs were originally normalized by the no current image; thus, the line scan results were the change in transmission relative to the initiation of the experiment (these profiles for all discharge rates can be found in the ESI,† Fig. S9a, S10a, S11a and S12a). As the focus of the work was to observe the net Li+ movement for each discharge process, all the transmission profiles were normalized again by subtracting the transmission profiles at the initiation of each cycle. The resulting profiles were Δtransmission relative to the initiation of each discharge process and thus every Dx0 profile (x = 1, 2, 3, 4) became a horizontal line with a value of 0 (these profiles can be found in the ESI,† Fig. S9b, S10b, S11b and S12b). In addition, to facilitate a more direct comparison with the calculated Li+ concentration profiles, the electrode region in the neutron images was defined (this region is labeled in Fig. S9b, S10b, S11b and S12b in the ESI†). Details and discussion about selection of the electrode region can be found in the ESI,† including Fig. S13. The total depth of the selected region was 1.248 mm, which was 5% greater than the 1.184 mm total measured thickness of the combined electrodes and separator. The cause of this difference was likely due to image magnification and a slight misalignment of the sample relative to the neutron beam. The final resulting profiles of Δtransmission relative to the beginning of discharge and with the normalized electrode depth for the 4 different rates of discharge can be found in Fig. 4a and 5a (for D1 and D3) and in the ESI,† Fig. S14a and S15a (for D2 and D4).The calculated Li+ concentration profiles of the same time points chosen for each discharge process were also extracted. The concentration profiles included the sum of the Li+ concentrations in both the electrolyte and solid phases and accounted for their relative volume fraction in the electrode. The changes in Li+ concentration were dominated by changes due to lithiation/delithiation of the solid phase. To maintain charge neutrality, the PF6− anion would also be expected to have a corresponding gradient that matched the Li+ liquid phase gradient, however, for discussion of consequences to neutron transmission PF6− was not taken into account. Due to the relatively low attenuation of P and F compared to Li, as well as the primary influence on neutron attenuation being changes in solid phase composition, neglecting the PF6− gradient was not expected to impact the interpretation of results. The detailed Li+ concentration profiles for the individual solid and electrolyte phases using both α = 1.0 and α = 1.5 for the Bruggeman exponent can be found in the ESI,† Fig. S16–S23. For comparison with the Δtransmission profiles from neutron imaging experiments, the concentration profiles were also normalized by subtracting the initial concentration profile for each discharge process (Dx0 profiles (x = 1, 2, 3, 4)). In neutron imaging experiments, a lower transmission corresponded to a higher Li+ concentration. Thus, for calculated results, the y-axis of concentration was reversed for easier comparison (e.g., increasing concentration is down instead of up in the y-axis). The final results of concentration profiles for each discharge process with different tortuosity values are displayed in Fig. 4b and c and 5b and c, and in the ESI† in Fig. S14b and c and S15b and c.
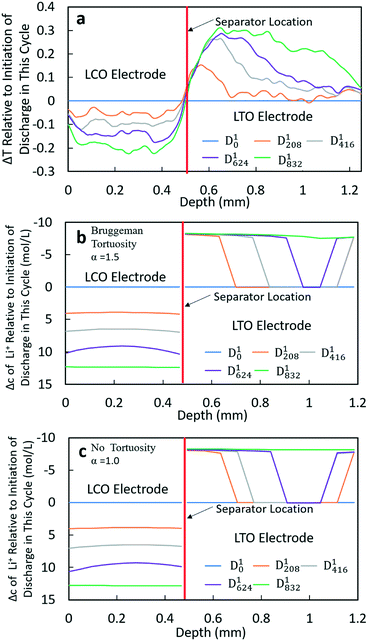
The Δtransmission (ΔT) and Δconcentration (Δc) profiles for D1 and D2 processes were similar; thus only D1 will be discussed in detail (Fig. 4). The corresponding information for D2 can be found in the ESI,† Fig. S14. From the transmission profiles, it can be clearly seen that the lithiation of LCO was uniform during the discharge process, i.e. the extent of lithiation increased gradually for all LCO material throughout the thickness of the electrode. The less negative ΔT towards the edges of the electrode near the separator and current collector/stainless steel was interpreted as being due to those regions having contributions from both the LCO material and stainless steel (near the current collector electrode edge) or separator/LTO (near the separator electrode edge). In contrast, the LTO electrode did not have as uniform of a delithiation process throughout the anode thickness. At 208 min (D1208), it can be clearly observed that the delithiation first occurred at the position near the separator, and there was a region within LTO where there was a sharp transition from completely delithiated to almost completely lithiated – although not obvious in the figure there was slight delithiation in all regions of the electrode. Then, the location of this delithiation front propagated towards the LTO current collector as the discharge proceeded. At the end of discharge, a nearly uniform distribution of Li+ was achieved. This qualitative behavior was consistent for both the neutron imaging and calculation results using both Bruggeman exponents. The similarity between the two calculations (Fig. 4b and c) suggested that at low rates (C/20 and C/10 for this cell) tortuosity would not be expected to influence the Li+ distribution, at least within the range of 1.0–1.5 considered. One noticeable difference between both calculated results and the neutron ΔT profile was that in the calculations there was a second delithiation front which initiated from the current collector and there was no evidence for this second front in the ΔT profile. There does appear to be some delithiation that occurs near the current collector even as early as at D1208, however, there was not a delithiation front that proceeded towards the separator. It was suspected that the difference between calculations and experiments with regards to the second delithiation front may have been due to the assumption of a single value for the electronic conductivity for the matrix conductivity of the electrode, although LTO and LCO both had electronic conductivity which was dependent on the extent of lithiation.13,34 It was expected that this simplification of the electronic conductivity using a single value for each electrode as opposed to a lithiation-dependent value was also a major contributor to differences in the experimental and calculated discharge potentials as a function of time (Fig. 3). The electrodes will have differences in extent of lithiation not just as a function of time/discharge extent but also as a function of depth within the electrode, thus the electronic conductivity varied with both time and electrode depth. The calculated potential during discharge and the presence and propagation of the second delithiation front were highly sensitive to the electronic conductivity, and a future research direction will include incorporating an electronic conductivity in calculations which is a function of the state of lithiation and measuring this conductivity for the materials used in the cells.
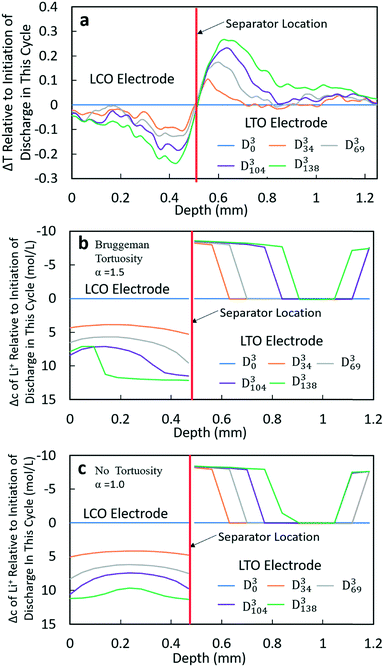
At higher rates, both the experimental and calculated results showed a different lithiation/delithiation trend. The ΔT and Δc profiles for D3 and D4 processes can be found in Fig. 5 and S15,† respectively. Both discharge rates resulted in significant limitations in the extent and propagation of lithiation/delithiation in the electrodes, and only one of these (D3) will be discussed in greater detail here. Inspection of the ΔT profiles for the LCO electrode during D3 (Fig. 5a) revealed that the lithiated region was primarily between 0.3 mm and 0.5 mm while the delithiated region for LTO was primarily between 0.5 mm and 0.9 mm. Beyond these regions, relatively low lithiation/delithiation was observed for both electrodes. However, in the lithiated region of LCO, the profiles still followed the same trend as that observed for the lower discharge rate (D1 process in Fig. 4a), where the lithiation distribution as a function of depth in the electrode was relatively uniform within the region of the electrode undergoing lithiation. For LTO, the delithiation front was still observed, but in contrast to the lower discharge rate the delithiation did not propagate as deep into the electrode and the peak in ΔT grew larger during discharge, indicating that the regions closer to the separator were more gradually lithiated during discharge relative to lower discharge rates. At higher rates of discharge (D3 at C/5 and D4 at C/2.5), the calculated concentration profiles for α = 1.0 and α = 1.5 had significant differences (Fig. 5b and c and S15b and c†). In the LTO region in Fig. 5b and c, the concentration profiles were qualitatively similar, and in both cases a delithiation front can be observed. The difference was the extent and depth of delithiation, which would be expected because the calculated capacity was different for these two cases as shown in Fig. 3c. In the LCO region for α = 1.5 a relatively uniform distribution of Li+ could still be observed at 34 minutes, but a gradient of lithiation started to build up in the electrode. At later times the gradient of Li+ concentration within LCO was clearly observed with a higher Li+ concentration in regions near the separator and a lower concentration in regions near the current collector. Inspection of the last two time points (D3104 and D3138) revealed that the Li+ concentration still went up near the separator while there was no further lithiation near the current collector. This outcome was consistent with the higher discharge rate resulting in a higher concentration gradient in the electrolyte phase in which there was much greater Li+ in the electrolyte within the LTO electrode and fewer Li+ ions in LCO electrolyte regions (Fig. S20a†). Near the end of discharge, Li+ was driven to zero in LCO regions near the current collector, and this lack of Li+ transport to the regions of the cathode still with lithium capacity resulted in the end of the discharge process. For α = 1.0, the distribution of Li+ showed a different pattern. The overall trend for LCO was similar to the calculated results for lower discharge rates where lithiation occurred across all depths of the LCO electrode, although at 69 min (D369), 104 min (D3104) and 138 min (D3138) the Li+ concentration was higher in both the regions near the separator and near the current collector with the middle region having a slightly lower concentration. The more uniform LCO electrode lithiation was due to the lack of tortuosity in the calculation, resulting in a smaller Li+ concentration gradient in the electrolyte. There was not a large limitation of Li+ availability in the electrolyte phase even at the highest discharge rate (Fig. S21a†). The electrode then was lithiated both on the current collector and separator ends, due to favorable electronic polarization near the current collector and ionic polarization near the separator.19,44
Comparing the experimental and calculated results, the tortuosity condition with α = 1.5 (Bruggeman hard sphere packing) had better agreement with the transmission profiles, particularly with regard to both demonstrating a confined lithiation/delithiation in both electrodes at high rates of discharge. The lithiation/delithiation profiles and discharge polarization curves (Fig. 3c) suggested that the transport in the liquid phase through the pore volume in the sintered electrodes was consistent with a thin film of close packed spheres, and that any cracks that may have formed during cell processing did not significantly impact the average transport experienced by liquid molecular species within the cell. Comparisons to calculations with the no tortuosity scaling (α = 1.0) revealed that at low rates of discharge the tortuosity did not significantly impact the electrochemical performance or the ability of Li+ to redistribute within the cell. At high rates, however, the lithiation/delithiation profiles were qualitatively different, with no tortuosity enabling more uniform lithiation of LCO, greater penetration of the Li+ front into the LTO electrode towards the current collector, and enabling the liquid phase Li+ concentration to not drop to values which resulted in the discharge process stopping earlier in the cell. This outcome suggested that improvements to tortuosity could result in gains in electrochemical performance with thick electrodes at high current densities.
It is noted that at the highest rate of discharge investigated in this study (Fig. 3d), for the simulation of the best case with regard to tortuosity (α = 1.0) only ∼40% of the available discharge capacity could be accessed. The limitation with regard to extracting that additional ∼60% of the capacity still remaining in the cell was attributed to limited ionic transport in the electrolyte phase. This result suggested that modifying tortuosity can play a role in improving the electrochemical performance of thick electrodes (extracting ∼40% compared to ∼23% for the simulation example in Fig. 3d), but that there are limits where the intrinsic transport properties of the electrolyte itself must be modified to further increase the electrode capacity.
The tortuosity in the electrodes represented a combination of many processes occurring which limited the transport of molecules in the liquid phase relative to their transport in the bulk electrolyte. Several strategies may be employed to reduce the tortuosity and/or the transport limitations of Li+ in the electrolyte phase to improve the electrochemical performance of the cells. First, it is important to note that the use of sintered electrodes without inactive materials already improved the transport relative to composite electrodes of equivalent thickness. While for the electrodes in this study the tortuosity scaling was consistent with α = 1.5, in studies with conventional composite electrodes reported values have ranged from 1.9 to 3.2.45 This increased tortuosity was due to the pore volume not just being filled with electrolyte, but also with carbon and polymeric binders which further restricted the transport of molecules through the liquid phase which filled the pores. Second, reductions in tortuosity could be achieved by controlling the electrode architecture to direct the pore alignment in the direction of Li+ flux. A few strategies have been reported in the literature, including using magnetic fields to align the pores and/or the particles themselves.46,47 Third, molecular approaches could be developed to modify the interactions between the liquid phase within the pores and the solid active material. Many of the pores would have regions of high confinement, which may provide an opportunity for modifying the particle interface or the solvent molecules to design the solvent–solid interactions to facilitate enhanced transport. Finally, increasing the Li+ concentration and/or the conductivity of the electrolyte itself will improve overcoming the transport limitations without modifying the tortuosity. Changes in the electrolyte are not trivial due to the many metastable interfaces in within Li-ion batteries, however, such improvements would improve the prospects for utilizing more of the capacity of thick battery electrodes at high rates of charge/discharge.
Conclusions
In this manuscript, neutron imaging was used to probe the Li+ transport in LTO/LCO battery full cells with sintered electrodes at different discharge rates. More Li+ was transferred from LTO to LCO at lower rates, resulting in higher discharge capacity. At higher rates, neutron imaging provided confirmation that the lithiation/delithiation only occurred in the region near the separator, limiting the delivered discharge capacity. This outcome was consistent with the discharge process being limited by the transport of Li+ through the porous electrode architecture. A numerical model was also used to calculate the discharge profiles and Li+ concentration profiles under different discharge conditions. Tortuosity scaling considering either hard sphere packing or the absence of tortuosity was used for the calculations. The calculations indicated that within the limits considered the tortuosity had only a slight impact on the discharge performance and expected Li+ compositional profiles within the cell at lower discharge rates. However, at higher discharge rates, the discharge capacities and Li+ compositional profiles were significantly different depending on the tortuosity scaling used. Compared with the experimental results, all calculations had good agreement at low discharge rates regardless of the tortuosity scaling. However, at higher discharge rates, the tortuosity scaling for hard spheres had much closer agreement with the experimental results, indicating that assuming the pellets as packed hard spheres was an appropriate assumption for electrolyte transport processes even though the particles were polydisperse and there were likely some cracks within the electrode pellets. The calculations also revealed that at higher discharge rates the limited region for lithiation/delithiation and subsequently much lower delivered electrochemical capacity were due to the limited access of Li+ from the electrolyte phase. These results thus provide insights into the significant quantitative impact that could result from improving transport within the porous electrode architecture. For example, molecular designs to improve the performance of these electrodes could be achieved through either templating the electrode pores to decrease tortuosity or by modifying the electrolyte properties to increase the conductivity of Li+ in the liquid phase within these cells.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Research funding support provided by the National Science Foundation grant CMMI-1825216. We acknowledge the use of the neutron research facilities of the National Institute of Standards and Technology in providing the neutron imaging used in this work. NIST authors acknowledge the efforts of Mr. Elias Baltic in the conduct of the measurements and support from the U.S. Department of Commerce, the NIST Radiation Physics Division, the Director's office of NIST, and the NIST Center for Neutron Research.References
- V. Etacheri, R. Marom, R. Elazari, G. Salitra and D. Aurbach, Energy Environ. Sci., 2011, 4, 3243–3262 RSC.
- J. B. Goodenough and K. S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- N. Nitta, F. Wu, J. T. Lee and G. Yushin, Mater. Today, 2015, 18, 252–264 CrossRef CAS.
- H. Pan, S. Zhang, J. Chen, M. Gao, Y. Liu, T. Zhu and Y. Jiang, Mol. Syst. Des. Eng., 2018, 3, 748–803 RSC.
- W. Weng, J. Lin, Y. Du, X. Ge, X. Zhou and J. Bao, J. Mater. Chem. A, 2018, 6, 10168–10175 RSC.
- H. Zheng, J. Li, X. Song, G. Liu and V. S. Battaglia, Electrochim. Acta, 2012, 71, 258–265 CrossRef CAS.
- Z. Chen and J. R. Dahn, J. Electrochem. Soc., 2002, 149, A1184–A1189 CrossRef CAS.
- C. J. Bae, C. K. Erdonmez, J. W. Halloran and Y. M. Chiang, Adv. Mater., 2013, 25, 1254–1258 CrossRef CAS.
- L. L. Lu, Y. Y. Lu, Z. J. Xiao, T. W. Zhang, F. Zhou, T. Ma, Y. Ni, H. B. Yao, S. H. Yu and Y. Cui, Adv. Mater., 2018, 30, 1706745 CrossRef PubMed.
- J. P. Robinson, J. J. Ruppert, H. Dong and G. M. Koenig, J. Appl. Electrochem., 2018, 48, 1297–1304 CrossRef CAS.
- S. P. Sheu, C. Y. Yao, J. M. Chen and Y. C. Chiou, J. Power Sources, 1997, 68, 533–535 CrossRef CAS.
- J. H. Pikul, H. G. Zhang, J. Cho, P. V. Braun and W. P. King, Nat. Commun., 2013, 4, 1732 CrossRef.
- M. Ménétrier, I. Saadoune, S. Levasseur and C. Delmas, J. Mater. Chem., 1999, 9, 1135–1140 RSC.
- H. Ji, L. Zhang, M. T. Pettes, H. Li, S. Chen, L. Shi, R. Piner and R. S. Ruoff, Nano Lett., 2012, 12, 2446–2451 CrossRef CAS.
- K. X. Wang, X. H. Li and J. S. Chen, Adv. Mater., 2015, 27, 527–545 CrossRef CAS PubMed.
- M. Singh, J. Kaiser and H. Hahn, J. Electrochem. Soc., 2015, 162, A1196–A1201 CrossRef CAS.
- G. F. Yang, K. Y. Song and S. K. Joo, RSC Adv., 2015, 5, 16702–16706 RSC.
- N. Kardjilov, I. Manke, A. Hilger, M. Strobl and J. Banhart, Mater. Today, 2011, 14, 248–256 CrossRef.
- Z. Nie, P. McCormack, H. Z. Bilheux, J. C. Bilheux, J. P. Robinson, J. Nanda and G. M. Koenig Jr, J. Power Sources, 2019, 419, 127–136 CrossRef CAS.
- H. Zhou, K. An, S. Allu, S. Pannala, J. Li, H. Z. Bilheux, S. K. Martha and J. Nanda, ACS Energy Lett., 2016, 1, 981–986 CrossRef CAS.
- J. B. Siegel, X. Lin, A. G. Stefanopoulou, D. S. Hussey, D. L. Jacobson and D. Gorsich, J. Electrochem. Soc., 2011, 158, A523–A529 CrossRef CAS.
- Z. Qi and G. M. Koenig Jr, ChemistrySelect, 2016, 1, 3992–3999 CrossRef CAS.
- Z. Qi and G. M. Koenig, J. Power Sources, 2016, 323, 97–106 CrossRef CAS.
- Z. Qi, A. L. Liu and G. M. Koenig Jr, Electrochim. Acta, 2017, 228, 91–99 CrossRef CAS.
- D. S. Hussey, D. L. Jacobson, M. Arif, K. J. Coakley and D. F. Vecchia, J. Fuel Cell Sci. Technol., 2010, 7, 021024 CrossRef.
- P. Albertus and J. Newman, Introduction to dualfoil 5.0, University of California Berkeley, Berkeley, CA, Tech. Rep., 2007 Search PubMed.
- M. Doyle, T. F. Fuller and J. Newman, J. Electrochem. Soc., 1993, 140, 1526–1533 CrossRef CAS.
- T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 1994, 141, 1–10 CrossRef CAS.
- T. F. Fuller, M. Doyle and J. Newman, J. Electrochem. Soc., 1994, 141, 982–990 CrossRef CAS.
- M. Rashid, A. Sahoo, A. Gupta and Y. Sharma, Electrochim. Acta, 2018, 283, 313–326 CrossRef CAS.
- S. Allu, S. Kalnaus, W. Elwasif, S. Simunovic, J. A. Turner and S. Pannala, J. Electrochem. Soc., 2014, 246, 876–886 CAS.
- K. Zaghib, M. Simoneau, M. Armand and M. Gauthier, J. Power Sources, 1999, 81, 300–305 CrossRef.
- L. Geng, M. E. Denecke, S. B. Foley, H. Dong, Z. Qi and G. M. Koenig, Electrochim. Acta, 2018, 281, 822–830 CrossRef CAS.
- D. Young, A. Ransil, R. Amin, Z. Li and Y. M. Chiang, Adv. Energy Mater., 2013, 3, 1125–1129 CrossRef CAS.
- K. Kataoka, Y. Takahashi, N. Kijima, J. Akimoto and K. I. Ohshima, J. Phys. Chem. Solids, 2008, 69, 1454–1456 CrossRef CAS.
- Y. Takahashi, N. Kijima, K. Dokko, M. Nishizawa, I. Uchida and J. Akimoto, J. Solid State Chem., 2007, 180, 313–321 CrossRef CAS.
- Z. He, Z. Wang, F. Wu, H. Guo, X. Li and X. Xiong, J. Alloys Compd., 2012, 540, 39–45 CrossRef CAS.
- Q. Zhang, Q. Guo and R. E. White, J. Power Sources, 2007, 165, 427–435 CrossRef CAS.
- I. V. Thorat, D. E. Stephenson, N. A. Zacharias, K. Zaghib, J. N. Harb and D. R. Wheeler, J. Power Sources, 2009, 188, 592–600 CrossRef CAS.
- C. Capiglia, Y. Saito, H. Kageyama, P. Mustarelli, T. Iwamoto, T. Tabuchi and H. Tukamoto, J. Power Sources, 1999, 81, 859–862 CrossRef.
- C. M. Doyle, PhD Thesis, Lawrence Berkeley Laboratory, 1995.
- J. Landesfeind, M. Ebner, A. Eldiven, V. Wood and H. A. Gasteiger, J. Electrochem. Soc., 2018, 165, A469–A476 CrossRef CAS.
- M. Ebner, D. W. Chung, R. E. García and V. Wood, Adv. Energy Mater., 2014, 4, 1301278 CrossRef.
- J. Nanda, H. Bilheux, S. Voisin, G. M. Veith, R. Archibald, L. Walker, S. Allu, N. J. Dudney and S. Pannala, J. Phys. Chem. C, 2012, 116, 8401–8408 CrossRef CAS.
- D. Kehrwald, P. R. Shearing, N. P. Brandon, P. K. Sinha and S. J. Harris, J. Electrochem. Soc., 2011, 158, A1393–A1399 CrossRef CAS.
- L. Li, R. M. Erb, J. Wang, J. Wang and Y. M. Chiang, Adv. Energy Mater., 2019, 9, 1802472 CrossRef.
- J. Billaud, F. Bouville, T. Magrini, C. Villevieille and A. R. Studart, Nat. Energy, 2016, 1, 16097 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9me00084d |
| ‡ Certain trade names and company products are mentioned in the text or identified in an illustration in order to adequately specify the experimental procedure and equipment used. In no case does such identification imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the products are necessarily the best available for the purpose. |
| This journal is © The Royal Society of Chemistry 2020 |