Predicting Cr(VI) adsorption on soils: the role of the competition of soil organic matter

Abstract

Cr(VI) has posed a serious risk for the environment and human beings because of its pollution and toxicity. It is essential to understand the equilibrium behavior of Cr(VI) in soils. In this study, the adsorption of Cr(VI) on fourteen soils was studied with batch experiments and quantitative modeling. The batch experiments included the adsorption edge and adsorption isotherm experiments, investigating the adsorption of Cr(VI) with varying soil properties, solution pH, and initial Cr(VI) concentrations. The experimental data were then modeled using the surface complexation models in Visual MINTEQ of CD-MUSIC by considering the adsorption of Cr(VI) and ions onto Fe (hydr)oxides and Al (hydr)oxides, and the Stockholm Humic Model and the fixed charge site model by accounting for the adsorption of the cations to soil organic matter and clay, respectively. Particularly, the modeling method of this study introduced an important parameter RO⁻ to account for the amount of soil organic matter irreversibly adsorbed on soil minerals. Overall, the model predicted reasonably well for the equilibrium partition of Cr(VI) under various conditions with a root-mean-square-error of 0.35 for the adsorption edge data and 0.19 for the adsorption isotherm data. According to the model calculations, ferrihydrite dominated the binding of Cr(VI) at pH of 3.0–7.0. The content of ferrihydrite and reactive soil organic matter was found to be the main factor influencing RO⁻. The modeling results help to understand and predict Cr(VI) adsorption on different soils and are beneficial to environmental risk assessment and pollution remediation.

---

Environmental significance

Chromium (Cr) has been a lasting risk to the environment and human health. Predicting the equilibrium speciation of Cr(VI) is essential for understanding the fate and bioavailability of Cr(VI) in soil and is of great environmental interest. The modeling method developed in this study incorporated several surface complexation models implemented in Visual MINTEQ, which can account for the variations of soil properties and reaction chemistry conditions. Our results highlight the importance of organic matter sorption to minerals in controlling Cr(VI) adsorption in soils. This study helps us to understand the partition equilibrium of Cr(VI) in soils and also provides a useful tool to evaluate the equilibrium behavior, bioavailability, and environmental risk of Cr(VI) in Cr contaminated soils.

1. Introduction

Chromium (Cr) has been a lasting risk to the environment and human health. Soluble in water, hexavalent chromium (Cr(VI)) exists in the environment mainly as the anionic forms of CrO₄²⁻ and HCrO₄⁻,¹ which are easily absorbed by humans and then may cause genetic defects and cancer. In soils, Cr(VI) can be adsorbed by soil minerals, such as Fe (hydr)oxides due to their strong binding abilities.² Predicting the equilibrium speciation of Cr is essential for understanding the fate and bioavailability of Cr(VI) in soil. Furthermore, understanding the equilibrium partition behavior of Cr(VI) provides a basis for the study of its kinetic behavior in soil.^3,4

Surface complexation models (SCMs) have been developed and widely used to predict the adsorption equilibrium of heavy metals in soils or soil adsorbents, such as soil organic matter (SOM), metal oxides, and clay minerals.^5–10 The Charge Distribution and Multisite Surface Complexation Model (CD-MUSIC) is among the widely used SCMs¹¹ and has been shown to successfully describe the adsorption of metals on Fe minerals. The complexation of ions to Al (hydr)oxides can be modelled by the Diffuse Layer Model (DLM).¹² For the complexation between cations and soil organic matter (SOM), several SCMs were developed, including the Stockholm Humic Model (SHM),¹³ the Humic Ion-Bonding Models,^14,15 and the NICA-Donnan model.^5,16 The fixed-charge site model can be used to calculate the adsorption of heavy metals onto clay minerals.¹⁷

For the individual soil minerals, the surface complexation reactions and theoretical models for Cr(VI) binding to natural or synthesized minerals have been developed, including Cr(VI) adsorption on ferrihydrite,^18–23 goethite,^2,24–27 and gibbsite.²⁸ Adsorption of Cr(VI) to other kinds of metal oxides and clay minerals has also been investigated with both experimental and modeling approaches.^29–32 Studies have found that soil organic matter could adsorb onto the surface of soil minerals, blocking some of the binding sites of minerals.³³ To account for such an effect, Gustafsson (2006)³⁴ has introduced a component RO⁻ as the irreversibly adsorbed SOM on minerals to predict As(V) adsorption on soil. Other models have also been developed to specifically consider the interactions between organic matter and minerals, such as the Ligand and Charge Distribution model^35,36 and the Natural Organic Matter-Charge Distribution model.^37,38

In this study, Cr(VI) adsorption edge and adsorption isotherm experiments were carried out with 14 soils and surface complexation models in Visual MINTEQ were used to predict the Cr(VI) partition in soils, with the consideration of the RO⁻ component. The model performances were assessed, the major factors affecting RO⁻ were analyzed, and the roles of individual soil components in influencing the Cr(VI) adsorption were elucidated. The results presented in this study would help us to understand the distribution behavior of Cr(VI) in soils and provide guidance for environmental risk assessment and remediation of Cr(VI) contaminated soils.

2. Materials and methods

2.1. Soil properties and batch experiments

The 14 soils used in this study were collected in New Jersey, US. All soils were non-calcareous and were sieved with a 2 mm-screen after they were air-dried. The background Cr(VI) concentration in each soil was negligible. The main properties of the 14 selected New Jersey soils are summarized in Table 1, and the detailed analysis methods for each soil can be found in the previous study.⁸ The dissolved cations in the solution were analyzed using a PerkinElmer Model 5000 atomic absorption spectrophotometer. Dissolved anions were not analyzed since nitrate ions were the major anions.

Table 1 Soil properties and related model input parameters

Soil name	pH	Fe-DCB (%)	Fe-oxalate (%)	Al-oxalate (%)	Ca–BaCl2 (mg kg^−1)	Mg–BaCl2 (mg kg^−1)	SOC (%)	Ferrihydrite (g L^−1)	Goethite (g L^−1)	ROC (%)	Humic acid (g L^−1)	Fulvic acid (g L^−1)	Clay (g L^−1)	RO^− (μmol L^−1)
Birdsboro slit loam	5.7	1.12	0.73	0.38	769	196	1.38	0.22	0.06	0.77	0.10	0.03	0.18	704
Boonton loam (Bergen County)	5.1	1.46	1.09	0.7	405	60	3.34	0.38	0.06	1.27	0.17	0.06	0.13	1126
Boonton loam (Union County)	5.1	1.42	0.54	0.76	394	58	7.15	0.31	0.14	2.15	0.29	0.10	0.16	883
Downer loamy sand	4.7	0.45	0.05	0.06	5	4	0.74	0.02	0.06	0.45	0.06	0.02	0.08	54
Dunellen sandy loam	5.6	0.90	0.31	0.19	573	149	1.25	0.10	0.09	0.71	0.10	0.03	0.14	312
Freehold sandy loam (A horizon)	5.2	0.90	0.13	0.03	66	25	0.18	0.03	0.12	0.12	0.02	0.01	0.06	74
Freehold sandy loam (B horizon)	6.4	1.27	0.36	0.23	671	141	1.06	0.13	0.14	0.61	0.08	0.03	0.21	379
Hazen gravelly loam	6	1.04	0.78	0.3	1590	281	2.32	0.21	0.04	1.14	0.15	0.05	0.23	666
Lakewood sand	4.2	1.12	0.24	0.05	1	2	0.69	0.05	0.14	0.42	0.06	0.02	0.06	145
Penn silt loam	4.7	1.16	0.52	0.31	268	64	1.13	0.17	0.10	0.65	0.09	0.03	0.27	546
Rockaway stony loam	4.7	2.69	0.58	0.62	143	21	2.99	0.27	0.33	1.25	0.17	0.06	0.16	863
Sassafras sandy loam	5.8	1.38	0.49	0.24	384	81	0.62	0.15	0.14	0.38	0.05	0.02	0.18	482
Washington loam	6	1.27	0.63	0.36	1461	215	2.14	0.20	0.10	1.08	0.15	0.05	0.31	664
Whippany silty clay loam	6.2	1.04	0.52	0.21	1508	382	1.67	0.14	0.08	0.89	0.12	0.04	0.37	407

---

In all adsorption experiments, 1.0 g of individual soil samples were added in 100 mL 0.01 M NaNO₃ background electrolyte. For the batch adsorption edge experiments, a certain amount of potassium chromate was added into the suspension, reaching final concentrations of 1 × 10⁻⁵ and 1 × 10⁻⁴ M. The suspensions were adjusted to a range of pH values from 3.0 to 7.0 with NaOH or HNO₃. The suspension samples were shaken at 150 rpm at room temperature (25 °C) for 24 hours and then filtered through 0.45 μM membrane filters. After 24 h shaking, the pH values of the samples were measured and were denoted as the reaction pH. The concentration of Cr(VI) in the filtered solution was determined by UV-visible spectrophotometry (Bausch & Lomb Spectronic 21 UVD spectrophotometer) after adding 1,5-diphenylcarbohydrazide under acidic conditions. The amount of the adsorbed Cr(VI) on soil was calculated according to the mass balance. For the adsorption isotherm experiments, potassium chromate was added into the suspension with concentrations ranging from 1 × 10⁻⁵ to 2 × 10⁻³ M. During the adsorption experiments, the pHs of the samples were monitored and adjusted to 4.5 and 6.0 by adding NaOH or HNO₃. Then the samples were shaken, filtered, and determined for the aqueous and adsorbed Cr(VI) following the methods described for adsorption edge experiments.

2.2. Modelling methods

In this study, Visual MINTEQ 3.1 was used for adsorption equilibrium calculations. It is a free software with several implemented surface complexation models that can be used to calculate the equilibrium partition of heavy metals under varying solution chemistry.³⁹ We utilized CD-MUSIC for the adsorption of ions to amorphous and crystalline Fe (hydr)oxides, represented by ferrihydrite and goethite, respectively. In Visual MINTEQ 3.1, there was a surface complex model for ion binding to gibbsite but no appropriate models for ion binding to amorphous Al (hydr)oxides. Since gibbsite was quite different from the amorphous Al (hydr)oxides, for ion binding to amorphous Al (hydr)oxides, they were considered as ferrihydrite in model calculations as proposed previously.⁴⁰ Crystalline Al (hydr)oxides were not considered due to the low binding ability based on preliminary model calculations. Under our experimental conditions, SOM functional groups were most likely negatively charged. The clay contents in the studied soils were also low (Table 1). Therefore, compared with Cr(VI) binding to Fe and Al (hydr)oxides, adsorption of Cr(VI) on SOM and clay was likely to be small and not considered in the modeling. Although Cr(VI) adsorption on SOM was not considered, adsorption of cations onto SOM and clay minerals was considered and modelled by SHM and the fixed-charge site model based on the default parameters. Binding of cations to SOM and clay will affect the dissolved cation concentrations, and thus the ionic strength and cation adsorption on minerals.

SOM contains acidic functional groups, such as carboxylic and phenolic groups, which can adsorb on soil minerals. Adsorption of SOM on minerals made the surface charges of soil minerals more negative and also reduced the binding sites available for Cr(VI) complexation. Therefore, we introduced a component RO⁻ as part of SOM complexation on metal oxides in this study, an approach used previously.³⁴ RO⁻ is used to represent the reactive portion of SOM adsorbed on the soil mineral surfaces. We added the component RO⁻ into the CD-MUSIC model in order to describe the SOM complexation on the mineral surfaces. The logarithm of the binding constants between metal oxides and RO⁻ were all set to 25 to ensure complete complexation under all conditions, as used in the previous studies.^34,41 The surface complexation reactions between RO⁻ and Fe oxides are presented in Tables S2 and S3 of the ESI.† In Visual MINTEQ calculations, we specified the pH, temperature, solution and solid phase components when inputting the model parameters. Specifically, for the solution phase, we considered cations Al³⁺, Fe³⁺, Ca²⁺, Mg²⁺, K⁺, Na⁺, and anions NO₃⁻ and RO⁻ for ionic strength, charge balance, and adsorption competition. The concentrations of Cr(VI), K, and Na were input as used in the experiments. The BaCl₂ extractable Ca and Mg were input as total Ca and Mg. For Al³⁺, the ion activity was calculated from the solubility of Al oxides with log K_so = 8.3 at pH > 5.5, and from the linear regression equation at pH < 5.5.⁸ The ion activity of Fe³⁺ was assumed to be controlled by the solubility of Fe oxides with log K_so = 2.7 at the selected pH range. The concentrations of NO₃⁻ were adjusted to balance the charges. For the solid phases, Fe (hydr)oxides, Al (hydr)oxides, SOM and clay were considered. The amorphous and crystalline Fe (hydr)oxides were input as ferrihydrite and goethite, respectively. Amorphous Al (hydr)oxides were input as ferrihydrite. Only a portion of SOM was considered as reactive soil organic matter (ROM), which was calculated based on the method proposed previously to obtain the reactive organic carbon (ROC).⁸ The ROM was quantified by multiplying a factor of 1.8 with ROC. It was assumed that ROM contained 75% HA and 25% FA when using the SHM.^6,8

In Visual MINTEQ, the default model parameters were used with some modifications from the previous study.³⁴ The reactions of Cr(VI) with goethite were based on the previous study.²⁶ Detailed information of surface complexation reactions and related model parameters can be found in Tables S1–S4.† Only one parameter, the RO⁻ concentration, needed to be determined in the prediction of Cr(VI) adsorption in each soil. Since pH edge data covered different pH values, we first optimized the RO⁻ concentration for each soil based on the adsorption edge data and then used the determined RO⁻ concentrations to predict the adsorption isotherms for all soils. By varying the RO⁻ concentrations, model predicted Cr(VI) adsorption can be acquired at different RO⁻ concentrations. Then we calculated Cr(VI) equilibrium partition coefficient (K_p, L g⁻¹), which was calculated as adsorbed Cr(VI) concentration divided by the solution Cr(VI) concentration, based on model calculations and experimental data. To get the optimal RO⁻ concentration, we calculated the minimum root-mean-square-error (RMSE) of the logarithm of Cr(VI) equilibrium partition coefficient with a trial-and-error procedure. The optimized RO⁻ amount was then input into the corresponding model calculations for the adsorption isotherms.

3. Results and discussion

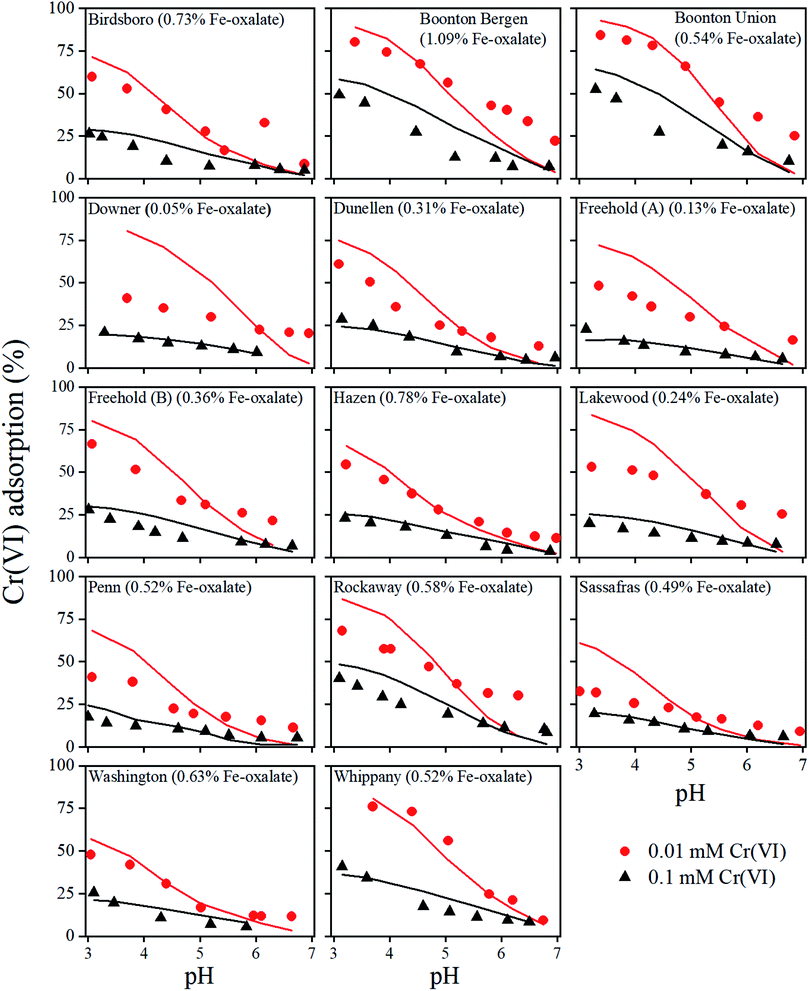
3.1. Modeling Cr(VI) adsorption edges

The influence of pH on Cr(VI) adsorption with two different initial Cr(VI) concentrations are presented in Fig. 1 for all 14 soils. According to the experimental results, the adsorption of Cr(VI) decreased with the increase of pH. As pH went up, the concentrations of OH⁻ increased, which resulted in the increasing competition between CrO₄²⁻ and OH⁻ and the decrease of CrO₄²⁻ adsorption. The increase in pH also made the surface charges of Fe oxides more negative, which inhibited CrO₄²⁻ adsorption. The percentages of Cr(VI) adsorbed with the initial Cr(VI) concentration of 0.1 mM were significantly lower than that with the initial Cr(VI) concentration of 0.01 mM, due to the limited soil binding sites and steric hindrance of adsorbed Cr(VI). Furthermore, there were no consistent effects of amorphous Fe oxides on Cr(VI) adsorption, although ferrihydrite was considered to be the major adsorbent for Cr(VI). This suggested that the concentrations of the ferrihydrite alone did not control Cr(VI) adsorption. This could be due to the different binding abilities of Fe oxides among different soil samples. Other factors such as the competing ligands including RO⁻ also affected Cr(VI) adsorption, which will be discussed in the following sections.

Fig. 1 Modeling adsorption edges for Cr(VI) adsorption on 14 soils at two initial Cr(VI) concentrations. Symbols are experimental data and solid lines are model fits. The soil names, Fe concentrations extracted by oxalate, and initial Cr(VI) concentrations are indicated in the figure.

Generally, the model reasonably described the experimental data given the different soil properties, varying solution pH, and initial Cr(VI) concentrations. Some large deviations were also observed for a few soils such as the Boonton Bergen, Downer, Lakewood, and Sassafras soils (Fig. 1). In those cases, model calculations were higher than the experimental data at low pHs but lower than the experimental data at high pHs. The exact reasons were not clear yet but were likely due to both the uncertainties of the model parameters and some factors not considered in the current model (e.g., dissolved organic matter or other competing anions). Further studies with more data are needed to elucidate those uncertainties. The optimized RO⁻ values ranged from 54 to 1126 μmol L⁻¹ (Table 1), indicating a varying competition effect of organic matter on Cr(VI) adsorption. This is consistent with the previous observations of the varying RO⁻ in different soils.³⁴

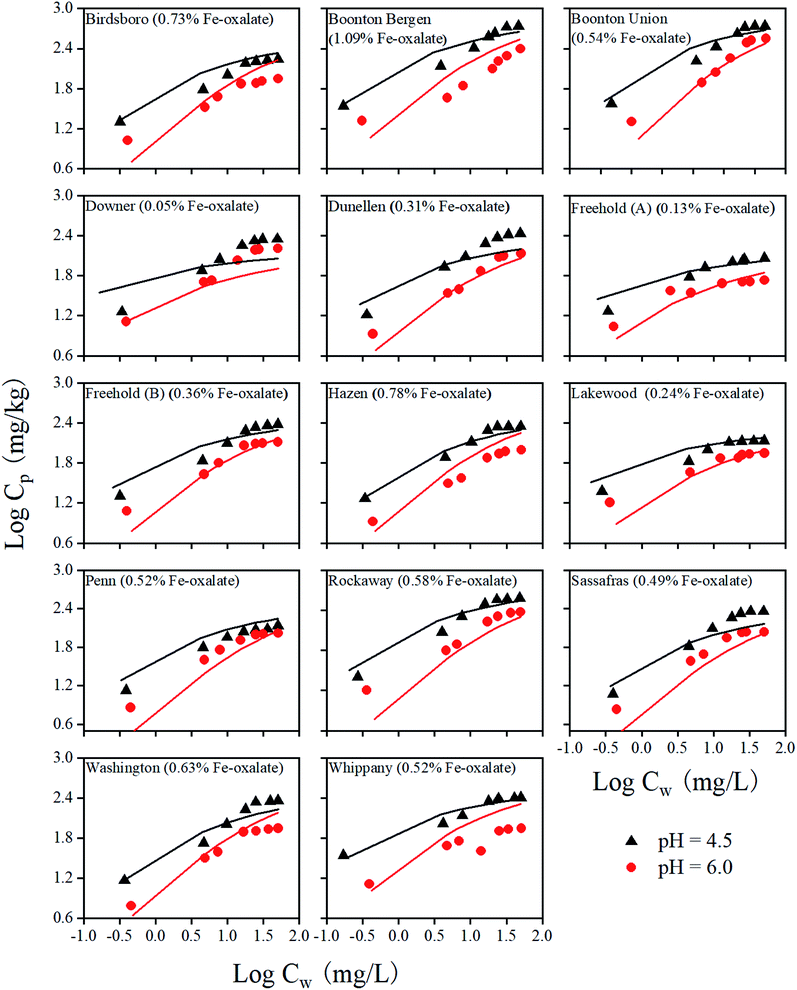
3.2. Predicting Cr(VI) adsorption isotherms

With the pre-determined RO⁻ values for all 14 soils, we predicted Cr(VI) adsorption isotherms without any other model adjustments. The experimental and model predicted Cr(VI) adsorption isotherms at pH 4.5 and 6.0 are represented in Fig. 2 for all 14 soils. At adsorption equilibrium, the adsorbed Cr(VI) concentrations increased with increasing concentrations of the aqueous Cr(VI). Consistent with the adsorption edge results, Cr(VI) adsorption was higher at pH = 4.5 than at pH = 6.0. Overall, the model predicted the adsorption isotherm data well (see the Model assessment section), which indicated that the modeling method was applicable to conditions with varying total Cr(VI) concentrations. Therefore, a single RO⁻ value for each soil appeared to reasonably account for the competition effect of organic matter on Cr(VI) adsorption in soil.

Fig. 2 Predicting adsorption isotherms of Cr(VI) adsorption on 14 soils at pH 4.5 and 6.0. Symbols are experimental data and solid lines are model predictions. The soil names, Fe concentrations extracted by oxalate, and reaction pHs are indicated in the figure. C_p represents the adsorbed Cr(VI) and C_w represents the dissolved Cr(VI).

Similar to the adsorption edge results, the amount of Cr(VI) adsorption on soils did not directly depend on the contents of the oxalate extractable Fe due to the competition of the organic matter in soils. Some deviations between experimental data and model predictions were observed. Those deviations could be due to the uncertainties related to RO⁻ concentrations and competition from the phosphate ions that were not considered. In addition, although cations do not directly compete with Cr(VI) for surface binding sites, it was found that adsorbed cations such as Ca²⁺ on the mineral surfaces may affect the surface charges and thus Cr(VI) adsorption.^42,43 All those factors, collectively, may contribute to the observed deviations between the experimental results and model calculations.

3.3. Impact of RO⁻ on Cr(VI) adsorption and the relationship between RO⁻ and soil properties

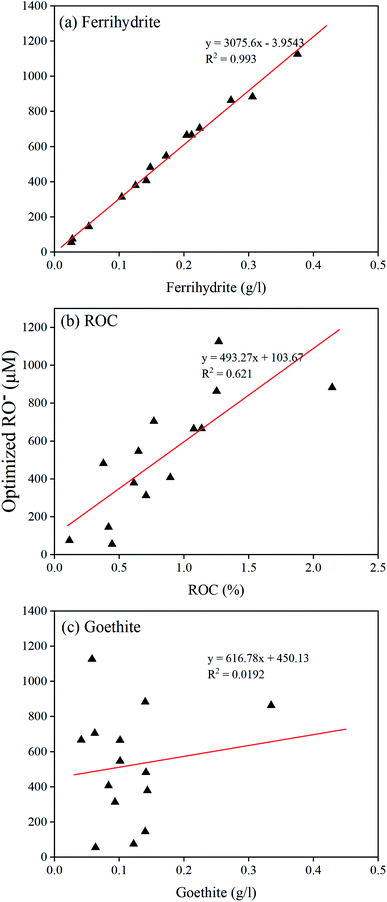
To assess the significance of RO⁻ on competing Cr(VI) binding to soils, we have simulated Cr(VI) adsorption edges on four selected soils without considering the competition of RO⁻ in model calculations (Fig. S1†). As shown in the model simulations, without considering the competition effect of RO⁻, Cr(VI) adsorption on soils was too high compared with the experimental data, which suggested that SOM binding to minerals (the competition of RO⁻) could significantly reduce Cr(VI) adsorption on soil minerals. In our study, the optimized RO⁻ concentrations were all virtually adsorbed on soil minerals since the binding constant of RO⁻ was set to a high value. Therefore, the adsorbed RO⁻ concentrations were much higher than the adsorbed Cr(VI) concentrations on soil minerals, indicating that RO⁻ effectively competed with Cr(VI) binding. The RO⁻ represented the reactive portion of SOM adsorbed on soil minerals and can affect Cr(VI) binding to soil through different ways. Firstly, the adsorbed SOM can make the surface charges more negative under most pH conditions in this study. The increased negative charges will reduce the adsorption of anions. Secondly, adsorbed SOM molecules reduced the available binding sites for Cr(VI) ions as proposed in the surface complexation models (Tables S2 and S3†). In addition, adsorbed SOM molecules could affect Cr(VI) adsorption through steric hindrance. All these factors, collectively, contributed to the reduced Cr(VI) adsorption on soils due to RO⁻ competitive binding.

The modeling results showed that RO⁻ was an important parameter of predicting the adsorption of Cr(VI) on soils. The main factors influencing the concentrations of RO⁻ in all soils are presented in Fig. 3. It was observed that the concentrations of RO⁻ were positively correlated well with the concentrations of ferrihydrite in soil (Fig. 3a). It appeared that the ROC content also had an impact on RO⁻ concentrations (Fig. 3b), but no obvious relationship was observed between the RO⁻ concentrations and the goethite content (Fig. 3c). The strong correlations between the ferrihydrite content and RO⁻ concentrations were likely related to the large specific surface area, abundant binding sites, and surface charges of ferrihydrite, which played the most important roles in both Cr(VI) and RO⁻ binding. Furthermore, we found that there was a positive correlation between ROC and ferrihydrite concentrations (Fig. S2†), which suggested that soils containing high ferrihydrite concentrations could come from fresh environments with more reactive organic matter. It is also easy to understand the positive correlation between the RO⁻ concentration and the ROC content since RO⁻ represents the reactive part of SOM bound to minerals, which reduces the anion adsorption in soil.⁴⁴ It was a little surprising that RO⁻ had no correlation with the goethite content, possibly due to the small specific surface area for Cr(VI) and RO⁻ binding.

Fig. 3 The relationships between the optimized RO⁻ concentrations and the concentrations of (a) ferrihydrite, (b) ROC (reactive soil organic carbon), and (c) goethite in the 14 soils. Solid lines are the linear regressions.

3.4. The distributions of Cr(VI) in individual soil adsorbents

The model calculated Cr(VI) distributions on ferrihydrite and goethite are shown in Fig. 4, including both the adsorption edge and adsorption isotherm data. Note that the contribution of the Al (hydr)oxides was included in ferrihydrite in the model calculations. Within the range of pH studied (3–7), ferrihydrite played a predominant role in adsorbing Cr(VI) due to the higher specific surface area and binding site density than goethite, which provided a higher capacity for adsorbing Cr(VI). The portion of Cr(VI) adsorbed on goethite was less than 20%. Generally, compared with cation binding to soil components that showed strong pH dependency,^8,10 reaction pH had a smaller impact on the portions of Cr(VI) adsorption on soil components. For example, variations of pH from 3 to 7 only resulted in less than 50% decrease of Cr(VI) adsorption under most conditions (Fig. 1). The distribution of Cr(VI) on goethite slightly decreased with increasing pH. Therefore, the amorphous iron oxides dominated Cr(VI) binding in soil environments, which was affected by the competing ligands such as organic matter.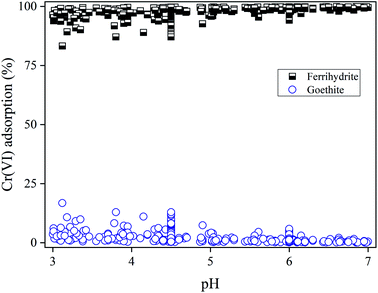

Fig. 4 Relative contributions of ferrihydrite and goethite to Cr(VI) adsorption at pH = 3.0–7.0 for all experimental conditions shown in Fig. 1 and 2. All the symbols were calculated using the model.

3.5. Model assessment

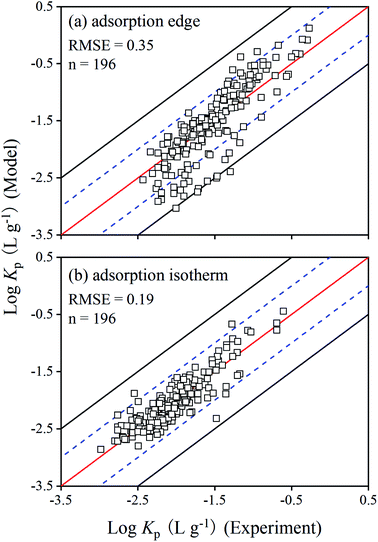
The overall model performance can be assessed by comparing the experimental and predicted Cr(VI) partition coefficients (K_p), in which K_p equals to the adsorbed Cr(VI) (C_p, mg kg⁻¹) divided by the dissolved Cr(VI) (C_w, mg L⁻¹) (K_p = C_p/C_w). The results presented in Fig. 5a showed a good model performance on the adsorption edge data, with a root mean square error (RMSE) of 0.35 for log K_p. For the adsorption isotherms, the comparison of log K_p between model calculations and experimental results in Fig. 5b indicated that the modeling method based on the Visual MINTEQ 3.1 could be applied to other conditions, with an RMSE of 0.19 for log K_p. The optimized RO⁻ concentrations from the adsorption edge data sets were reasonable to predict the Cr(VI) adsorption in soil. Overall, the model described well both the adsorption edge and isotherm data for varying soils and at different initial Cr(VI) concentrations, and the optimization of RO⁻ appeared to be a reasonable approach to account for the competition effects of organic matter on Cr(VI) adsorption.

Fig. 5 Comparison of equilibrium partition coefficients (K_p) between model calculations and experimental results for (a) the adsorption edge data and (b) adsorption isotherm data. The solid red line is the 1 : 1 line, black lines indicate ± 1 order of magnitude deviations, and the dashed lines indicate ± 0.5 orders of magnitude deviations.

In this study, Cr(VI) adsorption to soils was mainly considered with three mineral phases, amorphous Fe (hydr)oxides, amorphous Al (hydr)oxides, and crystalline Fe (hydr)oxides, using different surface complexation models, each of which may have uncertainties in terms of the model parameters. The competition from organic matter was considered using the reactive component RO⁻ but the competition from other anions such as phosphate³⁵ was not considered due to the lack of data. In the current study, the impact of anions was in fact reflected by the RO⁻ values, although the stoichiometry of surface complex formation is not the same for RO⁻ and phosphate ions. Addition of the competition anions may affect the values of RO⁻ obtained, but our study has generally shown the applicability of Visual MINTEQ to predict Cr(VI) adsorption in various soils. Previously, predicting cation binding to soils has been relatively successful while predicting anion binding to soils has been less satisfactory.⁴⁵ Our modeling approach has shown success for predicting Cr(VI) partition equilibrium in soils by accounting for the competition from organic matter. The concentrations of organic matter adsorbed on minerals varied significantly among different soils, indicating varying extents of competition of organic matter for Cr(VI) binding to soils. Based on our modeling results, the competition of organic matter is a key factor governing Cr(VI) adsorption equilibrium in soil environments, which should be specifically considered in predicting Cr(VI) behavior. Future study on quantifying the amount of organic matter adsorption on soil minerals will help to improve the accuracy of current chemical speciation models for predicting ion binding to soils. In addition, Cr redox reactions were not considered, which may be significant in natural soil environments.

4. Conclusions

In this study, the adsorption equilibrium of Cr(VI) on various soils with varying composition and properties was investigated at different pH and Cr(VI) concentrations. The modeling method developed in this study incorporated several surface complexation models implemented in Visual MINTEQ. Using the adsorption edge data, the only fitted parameter, RO⁻, was quantified for each soil. The model with the optimized RO⁻ described well the adsorption edge and isotherm data. Our modeling results have highlighted the importance of considering the competition from organic matter for Cr(VI) when predicting the Cr(VI) partition in soils. It was found that among all soil properties, amorphous Fe and Al (hydr)oxides and ROC were the main factors influencing the concentrations of RO⁻. Among various soil adsorbents, ferrihydrite dominated the binding of Cr(VI) at the investigated range of pHs. This study helps us to understand the partition equilibrium of Cr(VI) in soils and also provides a useful tool to evaluate the equilibrium behavior, bioavailability, and environmental risk of Cr(VI) in Cr contaminated soils.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge the Fundamental Research Funds for the Central Universities (No. 2018PY10) and the Guangdong Innovative and Entrepreneurial Research Team Program (No. 2016ZT06N569) for financial support of this research.

References

1. S. E. Fendorf, Surface reactions of chromium in soils and waters, Geoderma, 1995, 67, 55–71.
2. S. Fendorf, M. J. Eick, P. Grossl and D. L. Sparks, Arsenate and chromate retention mechanisms on goethite. 1. Surface structure, Environ. Sci. Technol., 1997, 31, 315–320.
3. P. C. M. Francisco, T. Sato, T. Otake and T. Kasama, Kinetics of Fe³⁺ mineral crystallization from ferrihydrite in the presence of Si at alkaline conditions and implications for nuclear waste disposal, Am. Mineral., 2016, 101, 2057–2069.
4. L. Peng, P. Liu, X. Feng, Z. Wang, T. Cheng, Y. Liang, Z. Lin and Z. Shi, Kinetics of heavy metal adsorption and desorption in soil: developing a unified model based on chemical speciation, Geochim. Cosmochim. Acta, 2018, 224, 282–300.
5. M. F. Benedetti, C. J. Milne, D. G. Kinniburgh, W. H. Van Riemsdijk and L. K. Koopal, Metal ion binding to humic substances: application of the non-ideal competitive adsorption model, Environ. Sci. Technol., 1995, 29, 446–457.
6. J. P. Gustafsson, P. Pechova and D. Berggren, Modeling metal binding to soils: The role of natural organic matter, Environ. Sci. Technol., 2003, 37, 2767–2774.
7. Z. Shi, H. E. Allen, D. M. Di Toro, S.-Z. Lee, D. M. Flores Meza and S. Lofts, Predicting cadmium adsorption on soils using WHAM VI, Chemosphere, 2007, 69, 605–612.
8. Z. Shi, H. E. Allen, D. M. Di Toro, S.-Z. Lee and J. B. Harsh, Predicting Pb-II adsorption on soils: the roles of soil organic matter, cation competition and iron (hydr)oxides, Environ. Chem., 2013, 10, 465–474.
9. E. Tipping, WHAMC—A chemical equilibrium model and computer code for waters, sediments, and soils incorporating a discrete site/electrostatic model of ion-binding by humic substances, Comput. Geosci., 1994, 20, 973–1023.
10. S. Peng, P. Wang, L. Peng, T. Cheng, W. Sun and Z. Shi, Predicting heavy metal partition equilibrium in soils: roles of soil components and binding sites, Soil Sci. Soc. Am. J., 2018, 82, 839–849.
11. T. Hiemstra and W. H. Van Riemsdijk, A surface structural approach to ion adsorption: The charge distribution (CD) model, J. Colloid Interface Sci., 1996, 179, 488–508.
12. D. A. Dzombak and F. Morel, Surface complexation modeling: hydrous ferric oxide, John Wiley & Sons, New York, 1990.
13. J. P. Gustafsson, Modeling the acid–base properties and metal complexation of humic substances with the stockholm humic model, J. Colloid Interface Sci., 2001, 244, 102–112.
14. E. Tipping, Humic ion-binding model VI: an improved description of the interactions of protons and metal ions with humic substances, Aquat. Geochem., 1998, 4, 3–48.
15. E. Tipping, S. Lofts and J. E. Sonke, Humic Ion-Binding Model VII: a revised parameterisation of cation-binding by humic substances, Environ. Chem., 2011, 8, 225–235.
16. D. G. Kinniburgh, W. H. van Riemsdijk, L. K. Koopal, M. Borkovec, M. F. Benedetti and M. J. Avena, Ion binding to natural organic matter: competition, heterogeneity, stoichiometry and thermodynamic consistency, Colloids Surf., A, 1999, 151, 147–166.
17. S. Lofts and E. Tipping, An assemblage model for cation binding by natural particulate matter, Geochim. Cosmochim. Acta, 1998, 62, 2609–2625.
18. V. Veselská, R. Fajgar, S. Číhalová, R. M. Bolanz, J. Göttlicher, R. Steininger, J. A. Siddique and M. Komárek, Chromate adsorption on selected soil minerals: surface complexation modeling coupled with spectroscopic investigation, J. Hazard. Mater., 2016, 318, 433–442.
19. C. P. Johnston and M. Chrysochoou, Mechanisms of chromate, selenate, and sulfate adsorption on al-substituted ferrihydrite: implications for ferrihydrite surface structure and reactivity, Environ. Sci. Technol., 2016, 50, 3589–3596.
20. C. P. Johnston and M. Chrysochoou, Investigation of chromate coordination on ferrihydrite by in situ ATR-FTIR spectroscopy and theoretical frequency calculations, Environ. Sci. Technol., 2012, 46, 5851–5858.
21. V. Veselská, H. Šillerová, J. Göttlicher, Z. Michálková, J. A. Siddique, S. Číhalová, V. Chrastný, R. Steininger, S. Mangold and M. Komárek, The role of soil components in synthetic mixtures during the adsorption and speciation changes of Cr(VI): Conjunction of the modeling approach with spectroscopic and isotopic investigations, Environ. Int., 2019, 127, 848–857.
22. N. M. Bompoti, M. Chrysochoou and M. L. Machesky, A unified surface complexation modeling approach for chromate adsorption on iron oxides, Environ. Sci. Technol., 2019, 53, 6352–6361.
23. J. D. Kubicki, N. Kabengi, M. Chrysochoou and N. Bompoti, Density functional theory modeling of chromate adsorption onto ferrihydrite nanoparticles, Geochem. Trans., 2018, 19, 8.
24. J. Zhu, Q. Huang, M. Pigna and A. Violante, Competitive sorption of Cu and Cr on goethite and goethite–bacteria complex, Chem. Eng. J., 2012, 179, 26–32.
25. J. Xie, X. Gu, F. Tong, Y. Zhao and Y. Tan, Surface complexation modeling of Cr(VI) adsorption at the goethite–water interface, J. Colloid Interface Sci., 2015, 455, 55–62.
26. R. Weerasooriya and H. Tobschall, Mechanistic modeling of chromate adsorption onto goethite, Colloids Surf., A, 2000, 162, 167–175.
27. M. Villalobos, M. A. Trotz and J. O. Leckie, Surface complexation modeling of carbonate effects on the adsorption of Cr(VI), Pb(II), and U(VI) on goethite, Environ. Sci. Technol., 2001, 35, 3849–3856.
28. M. J. Musorrafiti, C. T. Konek, P. L. Hayes and F. M. Geiger, Interaction of chromium(VI) with the α-aluminum oxide− water interface, J. Phys. Chem. B, 2008, 112, 2032–2039.
29. J. Zachara, C. Cowan, R. Schmidt and C. Ainsworth, Chromate adsorption by kaolinite, Clays Clay Miner., 1988, 36, 317–326.
30. K. G. Bhattacharyya and S. Sen Gupta, Adsorption of chromium(VI) from water by clays, Ind. Eng. Chem. Res., 2006, 45, 7232–7240.
31. K. Csobán and P. Joó, Sorption of Cr(III) on silica and aluminium oxide: experiments and modelling, Colloids Surf., A, 1999, 151, 97–112.
32. E. Alvarez-Ayuso, A. Garcia-Sanchez and X. Querol, Adsorption of Cr(VI) from synthetic solutions and electroplating wastewaters on amorphous aluminium oxide, J. Hazard. Mater., 2007, 142, 191–198.
33. J. Lehmann and M. Kleber, The contentious nature of soil organic matter, Nature, 2015, 528, 60–68.
34. J. P. Gustafsson, Arsenate adsorption to soils: Modelling the competition from humic substances, Geoderma, 2006, 136, 320–330.
35. L. P. Weng, W. H. Van Riemsdijk and T. Hiemstra, Humic nanoparticles at the oxide-water interface: interactions with phosphate ion adsorption, Environ. Sci. Technol., 2008, 42, 8747–8752.
36. Y. Cui and L. Weng, Arsenate and Phosphate Adsorption in Relation to Oxides Composition in Soils: LCD Modeling, Environ. Sci. Technol., 2013, 47, 7269–7276.
37. T. Hiemstra, S. Mia, P.-B. Duhaut and B. Molleman, Natural and Pyrogenic Humic Acids at Goethite and Natural Oxide Surfaces Interacting with Phosphate, Environ. Sci. Technol., 2013, 47, 9182–9189.
38. Y. Deng, L. Weng, Y. Li, J. Ma and Y. Chen, Understanding major NOM properties controlling its interactions with phosphorus and arsenic at goethite-water interface, Water Res., 2019, 157, 372–380.
39. J. P. Gustafsson, Visual MINTEQ ver. 3.1, Verified 8 Jan. 2018, 2015.
40. C. Tiberg, J. Kumpiene, J. P. Gustafsson, A. Marsz, I. Persson, M. Mench and D. B. Kleja, Immobilization of Cu and As in two contaminated soils with zero-valent iron - Long-term performance and mechanisms, Appl. Geochem., 2016, 67, 144–152.
41. J. Lin, S. Hu, T. Liu, F. Li, L. Peng, Z. Lin, Z. Dang, C. Liu and Z. Shi, Coupled Kinetics Model for Microbially Mediated Arsenic Reduction and Adsorption/Desorption on Iron Oxides: Role of Arsenic Desorption Induced by Microbes, Environ. Sci. Technol., 2019, 53, 8892–8902.
42. T. Liu, D. C. W. Tsang and I. M. C. Lo, Chromium(VI) Reduction Kinetics by Zero-Valent Iron in Moderately Hard Water with Humic Acid: Iron Dissolution and Humic Acid Adsorption, Environ. Sci. Technol., 2008, 42, 2092–2098.
43. E. Smith, R. Naidu and A. Alston, Chemistry of inorganic arsenic in soils: II. Effect of phosphorus, sodium, and calcium on arsenic sorption, J. Environ. Qual., 2002, 31, 557–563.
44. M. Verbeeck, T. Hiemstra, Y. Thiry and E. Smolders, Soil organic matter reduces the sorption of arsenate and phosphate: a soil profile study and geochemical modelling, Eur. J. Soil Sci., 2017, 68, 678–688.
45. J. E. Groenenberg and S. Lofts, The use of assemblage models to describe trace element partitioning, speciation, and fate: a review, Environ. Toxicol. Chem., 2014, 33, 2181–2196.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9em00477g

---