Catalytic dioxygen reduction mediated by a tetranuclear cobalt complex supported on a stannoxane core

Abstract

The synthesis, spectroscopic characterization (infrared, electron paramagnetic resonance and X-ray absorption spectroscopies) and density functional theoretical calculations of a tetranuclear cobalt complex Co₄L1 involving a nonheme ligand system, L1, supported on a stannoxane core are reported. Co₄L1, similar to the previously reported hexanuclear cobalt complex Co₆L2, shows a unique ability to catalyze dioxygen (O₂) reduction, where product selectivity can be changed from a preferential 4e⁻/4H⁺ dioxygen-reduction (to water) to a 2e⁻/2H⁺ process (to hydrogen peroxide) only by increasing the temperature from −50 to 30 °C. Detailed mechanistic insights were obtained on the basis of kinetic studies on the overall catalytic reaction as well as by low-temperature spectroscopic (UV-Vis, resonance Raman and X-ray absorption spectroscopies) trapping of the end-on μ-1,2-peroxodicobalt(III) intermediate 1. The Co₄L1- and Co₆L2-mediated O₂-reduction reactions exhibit different reaction kinetics, and yield different ratios of the 2e⁻/2H⁺ and 4e⁻/4H⁺ products at −50 °C, which can be attributed to the different stabilities of the μ-1,2-peroxodicobalt(III) intermediates formed upon dioxygen activation in the two cases. The deep mechanistic insights into the transition-metal mediated dioxygen reduction process that are obtained from the present study should serve as useful and broadly applicable principles for future design of more efficient catalysts in fuel cells.

---

Introduction

Significant, attention has been focused in recent years on the synthesis of transition metal based dendrimer structures owing to their diverse applications in various fields.¹ In particular, these dendrimers, in many cases, allow synergistic interactions between the individual transition metal centers in carrying out a variety of important transformations. The organooxotin clusters are in particular attractive because of the diversity of arrangements that they adopt, such as ladder, O-capped, cube, butterfly, drum, one, two and three-dimensional structures, (1D, 2D, and 3D).^2–6 Furthermore, incorporation of redox-active transition-metal centers into the stannoxane clusters has previously led to the demonstration of important reactivity patterns.^7,8 For example, an extensive cooperative effect between the Cu centers was observed during the cleavage of supercoiled DNA catalyzed by a hexanuclear Cu–porphyrin complex, supported on a stannoxane core.^7a In our group we have previously demonstrated the ability of a non-heme stannoxane based hexanuclear ligand system to undergo O–O bond formation^7b and O–O bond cleavage reactions,⁸ when bound to iron(II) and cobalt(II) centers, respectively. In the present manuscript we report the synthesis, characterization and X-ray structure of a tetranuclear stannoxane based non-heme ligand system (L1), and a detailed kinetic study of the catalytic dioxygen reduction reaction mediated by the corresponding cobalt complex Co₄L1. Notably, catalytic reductions of O₂ to water or H₂O₂ have tremendous technological significance.^9–12 However, in contrast to biology, where cheap and readily available transition-metal complexes of Fe, and Cu are employed for O₂ reduction,¹³ high loadings of a precious metal like platinum is warranted for achieving appreciable reactivity during abiological O₂-reduction reactions.^12d Thus the present study is relevant to the ongoing research activities that are being dedicated towards the development of O₂ reduction catalysts based on nonprecious metals.¹⁴ Furthermore, it provides deep mechanistic insights into the factors that control two- vs. four-electron reductions of O₂, thereby providing useful and broadly applicable principles for the future design of more efficient O₂ reduction catalysts.

Results and disscussion

Synthesis and characterisation of L1

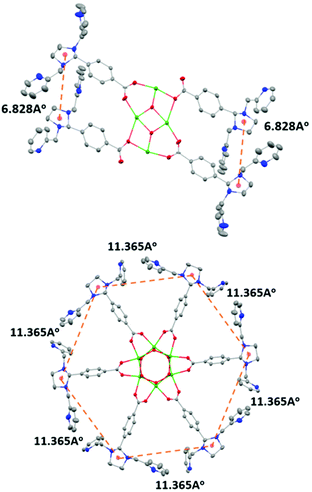
The condensation reaction (Schemes S1 and S2†) of equimolar amounts of di-n-butyltin oxide and 4-(1,3-bis(2-pyridylmethyl)-2-imidazolidinyl)benzoic acid in toluene afforded L1 as a pale yellow solid. The molecular structure of L1 shows that a planar Sn₄O₂ core supports the four metal-binding sites (Fig. 1: top). This is in contrast to the situation reported earlier for the hexanuclear non-heme ligand system L2, where six metal-binding sites were located in a wheel-like arrangement around a central Sn₆O₆ prismane core (Fig. 1: bottom). The stannoxane core in Ligand L1 adopts a ladder framework with two central and two terminal tin atoms. The tetranuclear structure of L1 is maintained in solution. ¹¹⁹Sn NMR spectrum of L1 exhibits two sharp singlets of equal intensity at −210.82 ppm and −213.81 ppm (Fig. S1†), which is the characteristic signature for a planar Sn₄O₂ core.^2–6 The infrared spectrum shows four vibrations at 1622 cm⁻¹, 1591 cm⁻¹, 1569 cm⁻¹, and 1545 cm⁻¹ for the carboxyl absorptions (ν_COO), and one strong band at 682 cm⁻¹ assigned to ν_Sn−O for the Sn₄O₂ core (Fig. S2†).

Fig. 1 Comparison of the distances between the metal binding sites in L1 (top) and L2 (bottom). X-ray crystal structure of L1 and L2 with 30% ellipsoid probability of the atoms. Hydrogen atoms and the n-butyl (ⁿBu-) groups on the tin atoms have been omitted for clarity. Color code: nitrogen-blue; carbon-grey; oxygen-red; tin-green.

Synthesis and characterization of Co₄L1

The reaction of L1 with 4 equiv. of Co(CF₃SO₃)₂ in acetone yields Co₄L1 as a dark yellow powder in 70% yield (Scheme 1). The C, H, and N content of Co₄L1, determined by elemental analysis, established the presence of four cobalt atoms per tetrameric ligand, with two triflates associated with each cobalt (see ESI†).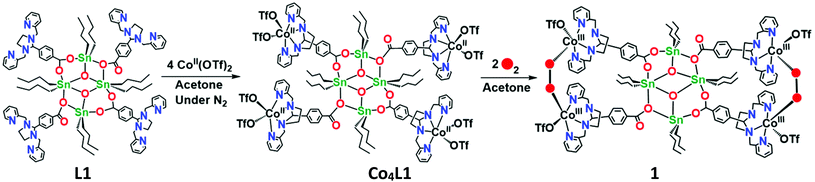

Scheme 1 Synthesis of the tetra-nuclear cobalt(II) complex (Co₄L1) from the tetra-nuclear stannoxane ligand (L1) and the formation of the cobalt(III)–peroxo complex (1).

The infrared spectrum of Co₄L1 depicts the characteristic vibrations of the Sn₄O₂ core at 1625 cm⁻¹, 1593 cm⁻¹, 1572 cm⁻¹, 1549 cm⁻¹, and 682 cm⁻¹ (Fig. S2†). These vibrations are only slightly shifted relative to that of L1, which reveals that the tetranuclear arrangement is also maintained in Co₄L1.

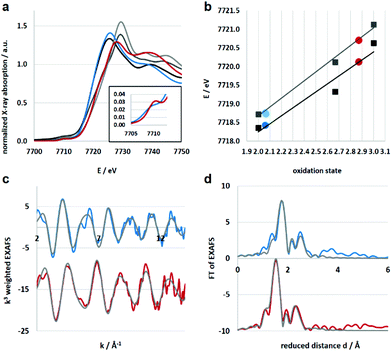
Electronic and structural information of Co₄L1 were obtained from X-ray absorption spectroscopy (XAS) in conjunction with density functional theory (DFT) calculations. The near edge structure (XANES) was used for determination of the oxidation states, whereas the extended fine structure (EXAFS) unraveled the local site geometries around the Co atoms. The spectra are displayed in Fig. 2, the corresponding fit values are collected in Table 1. The XANES spectrum of Co₄L1 (blue trace) is displayed together with spectra from Co reference compounds of known oxidation states (Co²⁺, Co^2.66+, Co³⁺), see Fig. 2a; it is consistent with a Co²⁺ oxidation state in Co₄L1 (Fig. 2b). The EXAFS of Co₄L1 could be well fitted by four shells, with one shorter N-shell with coordination number (N) of 5, a longer N/O-shell with N = 1, and two C-shells with N = 3 and 2 (Fig. 2c and d). Attempts to fit Co₄L1 with a sum of N = 5 in the first two shells (instead of 6) significantly worsen the fit parameters. In principle, there are up to nine C-atoms within a radius of 3.5 Å around the Co-atom, however, due to the pronounced inhomogeneity of the Co–C distances, these shells may partially cancel each other out. The average Co–O/N distance is found to be 2.17 Å.

Fig. 2 (a) Co K-edge XANES spectra of reference compounds (black: Co(OH₂)₆(NO₃)₂, dark grey: Co₃O₄ spinel, grey: CoOOH) and samples (blue: Co4L1, red: 1). The horizontal line at 0.5 is used for determination of the oxidation states. (b) Oxidation states of samples Co₄L1 and 1 derived from linear fit lines extracted from the 0.5 edge-rise positions of reference compounds (black line and squares) and derived from the integral method (grey line and squares). Both methods result in equal oxidation state assignments. (c) k-Space EXAFS spectra (k³ weighted, colored) and respective fits (grey). (d) Fourier transform of the EXAFS spectra (colored) and fits (grey).

Table 1 EXAFS fit parameters for Co₄L1 and 1

Model	Shell	N	R (Å)	Err	σ (Å)	Err
a Value kept constant in the final refinement. Amplitude reduction factor S02 = 0.95. N represents the EXAFS coordination number, R the absorber-backscatter distance and σ the Debye Waller parameter.
Co4L1	Co–N	5	2.14	0.01	0.056	0.007
R f = 18.4	Co–N	1	2.34	0.05	0.056
E 0 = 0.74	Co–C	3	2.94	0.03	0.056
d av = 2.17 Å	Co–C	2	3.06	0.05	0.056
1	Co–N	4	1.91	0.01	0.036	0.009
R f = 15.0	Co–O	1	2.02	0.03	0.036
E 0 = 2.82	Co–C	3	2.78	0.03	0.036
d av = 1.93 Å	Co–C	2	2.92	0.05	0.036

---

Since there are no X-ray diffraction (XRD) structures available for Co₄L1 and the Co atoms are mainly surrounded by O, N and C atoms with similar scattering properties, the EXAFS fits may suffer from non-uniqueness and misinterpretations. In order to reduce this problem as well as to obtain suitable phase functions for the fits, DFT calculations were conducted in the experimentally observed (from EPR; Fig. S3†) S = 3/2 spin state for a series of potential structural variants of the monomeric subsection of the organic ligands, starting from the modified XRD structure of the tetrameric stannoxane ligand (see Fig. 3 and S4†). This approach is justified as there are no intra-molecular electronic interactions detectable between adjacent Co(II) sites, as evident from the X-band EPR spectrum of Co₄L1, which exhibits a major axial signal with effective g′^⊥ = 4.01 and g′^∥ ≈ 2.0 corresponding to the S = 3/2 ground state (Fig. S3†). Structural variants include the coordination of triflate (OTf) and/or solvent acetone molecules in cis- or trans-orientations, and with or without inherent molecular symmetry, (see legend of Fig. S4†). Four of the six DFT models show hexa-coordinated Co(II) (no. 1, 2, 5, and 6), and the other two show penta-coordination (no. 3 and 4; see Table S1†). Since unrestrained EXAFS fits of Co₄L1 clearly indicate hexa-coordination, the corresponding DFT models are considered to be closer to the actual structure of Co₄L1. The average Co–X (X = N, O) bond distances, however, vary in the narrow range of 2.09 to 2.19 Å in all six models, which can hardly be discriminated by EXAFS, but all of them are close to the 2.17 Å obtained from the experiments.

Fig. 3 (a) The DFT calculated coordination environment of the individual Co-centers in Co₄L1, which matches best with the experimental data. The straight green lines reveal the N-capped O₂N₃H–octahedron environment of the central Co(II) center, by taking into account the agostic C–H⋯Co interaction. (b) DFT model of 1 with fixed carboxylate C⋯C atom distance of 6.43123 Å according to the XRD structure of the free ligand. In 1, L1 acts as a tetradentate ligand with one of the nitrogen atoms staying away from the coordination environment of Co.

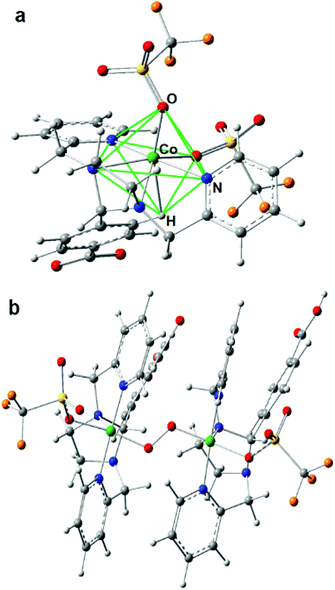
The lowest molecular energy is obtained for the hexa-coordinated model 5, followed by penta-coordinated model 3, which is only 5 kJ mol⁻¹ higher in energy. Fine structural details are visible in the EXAFS wave, which promises more insight into the real structure than geometric and energetic considerations alone. Accordingly, EXAFS was calculated for all six small DFT models and compared to the experimental spectra of Co₄L1, see Fig. S5 in the ESI.† Here again, model 5 apparently gives the best match to the spectrum of Co₄L1, followed by the other hexa-coordinate models 2, 6 and 1, whereas the two penta-coordinate models 3 and 4 give the worst match. Taking all results into account – geometry, energy and EXAFS – DFT model 5 seems to be the closest representative for the structure underlying in the experimental data of Co₄L1 we have so far. In this model, the six O- and N-atoms bound to the central Co-atom are aligned in a low symmetrical fashion, which might be described as quadratic-pyramidal (O₂N₃) with one (extra) N-atom below but close to the quadratic plane, (see Fig. 3). However, these results seemingly are in contradiction with the XANES spectrum of Co₄L1, which looks like typical octahedral or trigonal–bipyramidal (i.e. high local coordination symmetry) compounds, e.g. the hexa–aqua Co(II) compound used for reference (black line in Fig. 2a).

The answer to this riddle might be the potentially underrated electronic and steric effect of the agostic proton in DFT model 5, which is part of the carboxylated phenyl group, see Fig. 3. Since the organic ligand system has only limited flexibility, an unoccupied coordination site can be filled by a C–H⋯Co contact, which changes the picture. Taking the H-atom into account, the coordination geometry is rather an N-capped O₂N₃H–octahedron, see green lines in Fig. 3, than a square pyramid. In order to understand this in more detail, the electronic situation of model 5 was thoroughly analyzed by means of Real-Space Bonding Indicators (RSBIs) extracted from the computed electron density (ED, Fig. S6†). Fig. S6b† shows the spin-density, the majority of which is localized at the Co-atom, as expected, and with minor contributions at all six non-H-atoms. Bond topological analysis of the ED according to the Atoms-In-Molecules (AIM)¹⁵ theory, however, finds bond critical points (bcp) and thus bond paths to all seven O-, N- and H-atoms, see Fig. S6c.† AIM theory also provides atomic basins. Mapping the ED distribution on them discovers bonding regions and strength of chemical interactions. The AIM atomic Co basin has the basic shape of a cube (typical for octahedral ligand sphere) with one edge cropped by the capping N-atom, see Fig. S6d.† The more interesting point, however, is that the shape of the basin is also flat along the Co⋯H axis, although the agnostic interaction is quite weak (only little ED accumulation on the respective cube face). This “regular shape” of the Co-atom is also visible applying the Non-Covalent interactions Index (NCI),¹⁶ which uncovers non-covalent bonding aspects of strong medium and even very weak atom–atom contacts, see Fig. S6e.† Ring-shaped blue-colored NCI basins indicate dominating covalent bonding aspects (one O, one N), whereas disc-shaped blue-colored NCI basins indicate dominating non-covalent bonding aspects (one O, three N). The agostic Co⋯H contact is represented by a flat and extended greenish-blue colored NCI basin, being typical for weak non-covalent interactions, such as H⋯H or metallophilic contacts. AIM and NCI are complemented by the Electron Localizability Indicator (ELI-D),¹⁷ which dissects real-space into regions/basins of (non-) bonding electron pairs, resembling in a way the Lewis-picture of chemical bonding. An iso-surface representation is shown in Fig. S6f.† Highlighted (solid, green) are the six non-bonding d-electron ELI-D basins of the Co-atom, which altogether form a regular polyhedron in order to minimize electron–electron repulsion to the electron pairs from the electron donating ligand atoms, according to the well-known “key-lock” arrangement in transition metal chemistry.

Co₄L1 catalyzed dioxygen reduction reaction

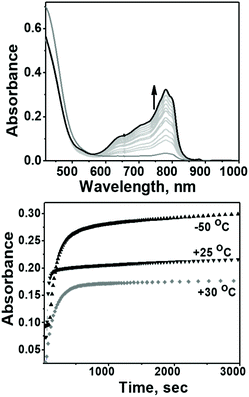
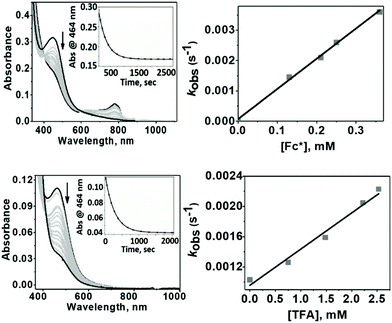
The evaluation of the catalytic activity of Co₄L1 towards oxygen reduction was carried out using the Fukuzumi and Guilard's method;¹⁸ decamethyl–ferrocene was employed as a one electron donor, triflic (TfOH) or fluoroboric (HBF₄) acids were used as proton source, and, in their presence, O₂ was set to react with a catalytic amount of Co₄L1 in acetone. The occurrence of the oxygen reduction reaction was proved by the formation of decamethylferrocenium ion (Fc*⁺) with a characteristic absorption band at 780 nm (Fig. 4; ε_{780 nm} = 520 M⁻¹ cm⁻¹).^19,20 Notably, the rate and yield of formation of Fc*⁺ is not significantly affected by the nature of the proton source (TfOH or HBF₄ Fig. S7d†), thereby suggesting that the conjugate bases (OTf⁻ or BF₄⁻) play no major role in controlling the efficiency of the O₂-reduction reactions. However, the concentration of Fc*⁺ formed in the complex Co₄L1-catalyzed reduction of O₂ by Fc* is dependent on the temperature at which the reactions were performed (Fig. 4 bottom, S7a–c†). At 30 °C 0.35 mM of Fc*⁺ ion is generated in the reaction, which corresponds approximately twice that of the O₂ concentration (0.18 mM). Thus, only two-electron reduction of O₂ occurs at 30 °C. With decreasing temperature, the amount of Fc*⁺ generated from O₂ reduction increases, presumably because of the increasing contribution of the four-electron reduction of O₂. At 25 °C the amount of Fc*⁺ formed is 0.44 mM, which is 2.5 times that of the O₂ concentration. The mechanism shifts predominantly to a four-electron reduction process at −50 °C; the amount of Fc*⁺ generated is 0.62 mM, which represents 3.45 equiv. relative to the initial concentration of O₂ (0.18 mM).

Fig. 4 Top: Spectral changes associated with the catalytic reduction of dioxygen by Co₄L1 (0.04 mM) in the presence of Fc* and TFA. Bottom: Time profiles of the formation of Fc*⁺ monitored at 780 nm during the reduction of O₂ (0.18 mM) by Fc* (3 mM) and Co₄L1 (0.04 mM) in the presence of TFA (10 mM) in acetone at 30 °C, 25 °C as well as at −50 °C.

¹H-NMR spectrum (Fig. 5a) of the reaction mixture of Co₄L1 (0.04 mM), Fc* (3 mM), TFA (10 mM) and O₂ (0.18 mM) at 25 °C in d₆-acetone further confirms the change in mechanism from a predominantly 2e⁻ reduction of O₂ (to H₂O₂) at 30 °C to a 4e⁻ reduction to H₂O at −50 °C. The solution after the Co₄L1 catalysed O₂ reduction at 30 °C shows a signal at 3.88 ppm, whose position is upshifted relative to the signal at 3.93 ppm obtained for an authentic H₂O₂/H₂O mixture (70 weight % H₂O₂ basis) in d₆-acetone at 25 °C. Note that the signal corresponding to a H₂O₂/H₂O mixture undergoes a downshift with increasing amounts of water in the mixture; pure water shows a signal at 4.61 ppm. Thus for a catalytic reaction at 30 °C, a >70% H₂O₂ concentration can be inferred. When the catalysis is performed at 25 °C the signal gets downshifted to 3.99 ppm, thereby confirming the presence of the higher amount of water as the 4e⁻ reduction product. The resultant solution after the catalytic O₂-reduction reaction at −50 °C shows a signal at 4.20 ppm, which lies between the signals at 4.44 ppm and 4.05 ppm obtained for authentic 15% and 30% H₂O₂/H₂O mixtures, respectively. A turnover number (TON) of 28.7 during a lapse of 2000 s was determined in acetone at −50 °C. The TON decreased linearly with increasing temperature to a value of 9 at 25 °C (Fig. S8†).

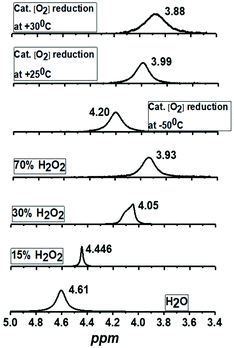Fig. 5 ¹H-NMR spectra of the products formed during the complex Co₄L1 catalyzed dioxygen reduction reactions at 25 °C, 30 °C and −50 °C [Co₄L1 (0.01 mM), Fc* (3 mM), TFA (10 mM) and O₂ (0.18 mM)] in acetone-d₆ and comparison with authentic samples containing 70%, 30%, 15% and 0% (weight percent H₂O₂ basis) H₂O₂/H₂O mixtures. All the ¹H-measurements were performed at 25 °C. The results obtained for Co₄L1 are then compared with that for Co₆L2 in Table 2.

Table 2 Temperature dependence of the catalytic O₂ reductions mediated by Co₄L1 and Co₆L2

Temp.	Catalyst used	mM	Equiv. of O2 reduced	% of H2O2 formed (from NMR)
−50 ^0C	Co4L1	0.01	3.46	20%
+25 ^0C		0.01	2.5	64%
+30 ^0C		0.01	1.92	74%
−50 ^0C	Co6L2	0.01	3.80	0
+25 ^0C		0.01	1.88	70%

---

Reaction of Co₄L1 with dioxygen to form 1

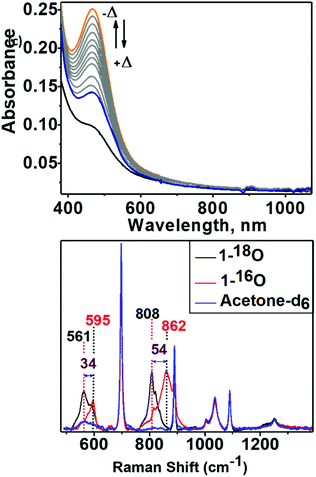
An acetone solution of Co₄L1, when treated with O₂ saturated acetone at −50 °C, results in the formation of an orange species 1 with an intense absorption maximum λ_max (ε_max, M⁻¹ cm⁻¹) centered at 464 nm (12 200 M⁻¹ cm⁻¹). As the temperature is increased, the absorption band at 464 nm due to 1 is decreased (Fig. 6: top one). This process is reversible in the temperature range −50 to 30 °C. The resonance Raman (rR) spectrum (Fig. 6: bottom one) of 1 in acetone-d₆ displays two isotopically sensitive vibrational bands at 862 (O–O stretching mode of a peroxo ligand) and 595 cm⁻¹ (Co–O stretching mode), which are downshifted to 808 and 561 cm⁻¹, respectively, in ¹⁸O₂ prepared samples.

Fig. 6 Top: Absorption spectra showing the reversibility of dioxygen binding to Co₄L1. Bubbling O₂ into an acetone solution of Co₄L1 (0.02 mM) produces 1 (in high yield) at −50 °C (orange, solid line). Increasing the temperature up to 25 °C produces the blue solid spectrum. After recooling to −50 °C the orange solid spectrum can be regenerated. Bottom: Resonance Raman spectra of 1-¹⁶O (red trace), 1-¹⁸O (black trace) with 514 nm laser excitation in acetone-d₆ at −40 °C. Solvent bands are marked by “blue color”.

XAS studies were also performed to probe the oxidation state and the coordination environment of Co in 1. The XANES spectra of 1 when compared with that of Co₄L1 and other reference compounds reveals an almost complete oxidation from Co²⁺ to Co³⁺ during the transformation of Co₄L1 to 1. Additionally, the edge shape of 1 shows minor alterations in comparison with Co₄L1 (rise of the pre-edge – see inset of Fig. 2a, lower steepness of the edge rise, formation of a shoulder in the edge) indicating a slightly lower coordination symmetry and coordination number in 1 (Fig. 2, Table 1). The EXAFS of 1 reveals a 5 coordinate geometry at Co with 4 short Co–N/O distances at 1.91 Å, and one long Co–N/O distance at 2.02 Å. The average Co–O/N distances of 2.17 Å for Co₄L1 and 1.93 Å for 1, is a consequence of the different oxidation states and the lower steric requirements of five versus six ligands attached to the Co-atom. Notably, the 470 nm absorption band, ν(O–O) of 862 cm⁻¹ and ν(Co–O) of 595 cm⁻¹ and the Co–O₂ distance of 1.91 Å of 1 matches the spectroscopic properties of the previously reported end-on μ-1,2-peroxo-dicobalt(III) complexes.²¹ DFT calculations also support an S = 0 end-on μ-1,2-peroxo-dicobalt(III) assignment of 1; the calculated metrical parameters very well match with the experiments.

Reactivity of 1 with protons and electrons

1 exhibited different reactivities with proton and electron donors depending on the reaction temperature. At −50 °C no reaction of 1 with Fc* was observed in the absence of TfOH. Similarly, no reaction of 1 with TfOH was observed in the absence of Fc*. However, in the presence of both TFA and Fc* 1 underwent fast decay, presumably by a proton coupled electron transfer (PCET) mechanism to form water as the major product (Fig. 7 top). At 25 °C in the absence of TFA, no reduction of 1 by Fc* was observed, very similar to our findings at −50 °C. However, in presence of TFA, even in the absence of Fc*, fast decay of 1 was observed (Fig. 7 bottom), with the release of H₂O₂ by a proton transfer (PT) mechanism.

Fig. 7 Top: Changes in the absorption band associated with the reaction of 1 (0.015 mM) with TFA (3 mM) and Fc* (0.15 mM) at −50 °C; Inset: The pseudo-first order decay of the absorption band at 464 nm as a function of time (left) and the linear dependence (right) of the pseudo-first order rate constants (k_obs) on Fc* concentrations (0.13–0.38 mM) that led us to determine the second order rate constant value, k′₂. Bottom: Changes in the absorption band associated with the reaction of 1 (0.015 mM) with TFA (0.75 mM) at +25 °C; inset: the pseudo-first order decay of the absorption band at 464 nm as a function of time (left) and the linear dependence (right) of the pseudo-first order rate constants (k_obs) on TFA concentrations (0.75–2.7 mM) led us to determine the second order rate constant value, k′₂.

The temperature dependence of the PT and PCET processes will be the controlling factor in determining the temperature dependence of the 4e⁻/4H⁺vs. 2e⁻/2H⁺ reductions of dioxygen mediated by 1. We therefore compared the temperature-dependence of the PCET and PT processes of 1 at various temperatures (Fig. 7, 8 and S9†). PCET rates were determined at −50 °C, −40 °C, −30 °C and −20 °C under the condition [1] ≪ [Fc*] ≪ [TFA] to ensure pseudo first-order kinetics (Fig. 7 top; at these temperatures PT rates are negligible). Similarly, PT rates were determined at 20 °C, 22 °C, 25 °C, 30 °C and 32 °C under the condition [1] ≪ [TFA] (Fig. 7 bottom). PT is found to vary with temperature at a much more drastic rate relative to that of PCET, and it becomes the predominant mechanism for the reduction of 1 at temperatures >11 °C (Fig. 8a).

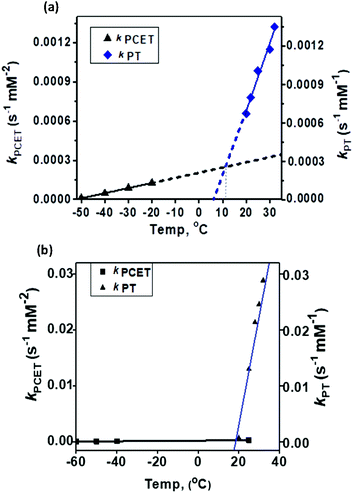Fig. 8 Comparison of the temperature-dependence of the PCET vs. PT rate constants for (a) 1 and (b) 2.

Conclusions

In our previous study⁸ we reported the synthesis and characterization of a hexanuclear cobalt complex Co₆L2 involving a nonheme ligand system, L2, supported on a Sn₆O₆ stannoxane core (Fig. 1: bottom), whose cobalt complex acts as a unique catalyst for dioxygen reduction, whose selectivity can be changed from a preferential 4e⁻/4H⁺ dioxygen-reduction (to water) to a 2e⁻/2H⁺ process (to hydrogen peroxide) only by increasing the temperature from −50 to 25 °C. Herein, we report the synthesis and characterization of a tetranuclear Co₄L1 complex, supported on the stannoxane core, and compare its dioxygen reduction ability with that of Co₆L2 (Fig. 8). The temperature dependence of the product selectivity of the catalytic dioxygen reduction is still observed in Co₄L1; however, some subtle differences are noted relative to Co₆L2, which can be attributed to the different nuclearity and Co–Co distances in the two cases (Fig. 1).

In L2 all the six plausible metal binding sites are equidistant from each other at 11.365 Å. This is in contrast to L1, where only two of the four metal binding sites are in close proximity to each other. The more symmetric nature of L2 ensures an efficient cooperative dioxygen binding in Co₆L2 relative to Co₄L1, which results in the lower stability of 1 compared to that of the corresponding {[L2(Co^III(O₂)Co^III)₃]}¹²⁺ complex 2 that is formed upon dioxygen activation of Co₆L2. The faster self-decay rate (1 × 10⁻⁴ s⁻¹ for 2vs. 2 × 10⁻³ for 1 at 25 °C), as well as the 16 cm⁻¹ downshift in the Co–O vibration energy (ν(Co–O) for 1 is 595 cm⁻¹ and 611 cm⁻¹ for 2)⁸ in 1 relative to 2, is consistent with the lower stability of 1. Accordingly, as previously observed, the high enthalpic stability of 2 makes its formation at −50 °C highly favored that leads to the complete oxygenation of Co₆L2. Complex 2 then undergoes O–O bond cleavage via a PCET mechanism to yield water as the sole product under catalytic turnover conditions. The rate constant of the reaction was found to be independent of the O₂ concentration; the kinetic equation at −50 °C for Co₆L2 is

d[Fc*]/dt = k_obs[Co₆L2]

k_obs = k_cat[Fc*][TFA]

where “k_cat” is the third-order rate constant for the catalytic 4e⁻-reduction of O₂ by Fc* at −50 °C and k_obs is the pseudo first-order rate constant. In contrast, an equilibrium binding of O₂ occurs for Co₄L1, even at −50 °C, so that the rate of the catalytic reaction shows a linear dependence on the O₂ concentration (Fig. S10†). The rate equation for Co₄L1 is

d[Fc*]/dt = k_obs[Co₄L1]

k_obs = k_cat[Fc*][TFA][O₂]

where “k_cat” is the fourth-order rate constant for the catalytic 4e⁻-reduction of O₂ by Fc* at −50 °C and k_obs is the pseudo first-order rate constant. Furthermore, Co₄L1 catalysed O₂ reduction yields 15–30% H₂O₂ at −50 °C, in contrast to Co₆L2 for which no H₂O₂ production could be detected at this temperature. However the rate constant of the two-electron O₂ reduction at +25 °C is a fourth-order process for both Co₆L2 and Co₄L1 (Fig. S11†).

The constraints imposed by the stannoxane core ensure entropic instability of both 1 and 2. This is mainly because of the large reduction in the Co–Co distances that is associated with their formation. Although experimental determination of the Co–Co distances in Co₄L1, Co₆L2, 1 and 2 was not possible, approximate shortening of ∼2.4 Å (from a distance of 6.82 Å in L1 to the DFT calculated distance of 4.48 Å in 1) and ∼7 Å (from a distance of 11.36 Å in L2 to the DFT calculated distance of 4.48 Å in 2) can be predicted for dioxygen binding at Co₄L1 and Co₆L2 complexes, respectively. This would impose a large strain on the μ-1,2-peroxo-dicobalt(III) cores in 1 and 2, which would attribute to their instability at higher temperatures upon protonation leading to the formation of H₂O₂ as the major product. Thus for both Co₄L1 and Co₆L2, an equilibrium binding of O₂ will take place at 25–30 °C, such that only a small portion of Co₄L1 and Co₆L2 will be converted to 1 and 2, respectively. This would also explain the experimentally observed direct correlation of the reaction rates to oxygen concentration at 25–30 °C in both cases.

In summary, the Co₄L1 complex like the previously reported Co₆L2 complex is a unique catalyst for dioxygen-reduction reaction, whereby the product selectivity can be changed from a predominant 4e/4H⁺ reduction process (to water) at −50 °C to a 2e⁻/2H⁺ process at 25–30 °C. μ-1,2-peroxo-dicobalt(III) complexes 1 and 2 are proposed as plausible reactive intermediates, which are reduced to H₂O by a PCET mechanism at −50 °C, or to H₂O₂ by a proton transfer mechanism at 25–30 °C. For both 1 and 2, the PT rates are found to vary drastically with temperature relative to the PCET rates, and PT becomes the predominant mechanism at 11 °C for 1 and at 19.5 °C for 2. The ∼10 °C reduction in the transition temperature for 1 can be attributed to its reduced stability relative to 2, as also evident from the faster self-decay rate and lower ν(Co–O) vibration energy in 1 relative to 2. This study, therefore, underlines the importance of subtle electronic and steric changes in the reactivity of the biologically relevant metal–dioxygen intermediates, and how they can control the 2e⁻/2H⁺vs. 4e⁻/4H⁺ product selectivity in catalytic dioxygen reductions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC 2008 – 390540038 – UniSysCat to K. R., P. H. and H. D. and the Heisenberg-Professorship to K. R.

References

1. (a) J. W. J. Knapen, A. W. Made, J. C. Wilde, P. W. N. M. van Leeuwen, P. Wljkens, D. M. Grove and G. Koten, Nature, 1994, 372, 659; (b) H. P. Dijkstra, P. Steenwinkel, D. M. Grove, M. Lutz, A. L. Spek and G. Koten, Angew. Chem., Int. Ed., 1999, 38, 2185; (c) V. Balzani, A. Juris and M. Venturi, Chem. Rev., 1996, 96, 759; (d) G. Denti, S. Campagna, S. Serroni, A. Juris, M. Ciano and V. Balzani, in Perspectives in Coordination Chemistry, ed. A. F. Williams, C. Floriani and A. E. Merbach, Wiley-VCH, Weinheim, 1992, p. 153.
2. (a) J. Janssen, J. Magull and H. W. Roesky, Angew. Chem., Int. Ed., 2002, 41, 1365; (b) K. Wraage, T. Pape, R. Herbst-Irmer, M. Noltemeyer, H.-G. Schmidt and H. W. Roesky, Eur. J. Inorg. Chem., 1999, 869.
3. (a) D. Dakternieks, K. Jurkschat, D. Schollmeyer and H. Wu, Organometallics, 1994, 13, 4121; (b) M. Mehring, I. Paulus, B. Zobel, M. Schürmann, K. Jurkschat, A. Duthie and D. Dakternieks, Eur. J. Inorg. Chem., 2001, 153; (c) M. Mehring, M. Schürmann, H. Reuter, D. Dakternieks and K. Jurkschat, Angew. Chem., Int. Ed. Engl., 1997, 36, 1112; (d) M. Schulte, M. Schürmann, D. Dakternieks and K. Jurkschat, Chem. Commun., 1999, 1291.
4. (a) V. Chandrasekhar, S. Nagendran and V. Baskar, Coord. Chem. Rev., 2002, 235, 1; (b) R. R. Holmes, Acc. Chem. Res., 1989, 22, 190; (c) F. Ribot, C. E. Baron and C. Sanchez, Phosphorus, Sulfur Silicon Relat. Elem., 1999, 150–151, 41 and references therein.
5. (a) R. R. Holmes, C. G. Schmid, V. Chandrasekhar, R. O. Day and J. M. Holmes, J. Am. Chem. Soc., 1987, 109, 1408; (b) V. Chandrasekhar, R. O. Day and R. R. Holmes, Inorg. Chem., 1985, 24, 1970; (c) V. Chandrasekhar, S. Nagendran, S. Bansal, M. A. Kozee and D. R. Powell, Angew. Chem., Int. Ed., 2000, 39, 1833; (d) R. O. Day, V. Chandrasekhar, K. C. Kumara Swamy, J. M. Holmes, S. D. Burton and R. R. Holmes, Inorg. Chem., 1988, 27, 2887; (e) K. C. Kumara Swamy, R. O. Day and R. R. Holmes, J. Am. Chem. Soc., 1987, 109, 5546; (f) R. O. Day, J. M. Holmes, V. Chandrasekhar and R. R. Holmes, J. Am. Chem. Soc., 1987, 109, 940; (g) R. R. Holmes, K. C. Kumara Swamy, C. G. Schmid and R. O. Day, J. Am. Chem. Soc., 1988, 110, 7060.
6. (a) C. E. Baron, F. Ribot, N. Steunou, C. Sanchez, F. Fayon, M. Biesemans, J. C. Martins and R. Willem, Organometallics, 2000, 19, 1940; (b) F. Ribot, P. Toledano, J. Maquet and C. Sanchez, Inorg. Chem., 1995, 34, 6371; (c) F. Ribot, C. Sanchez, R. Willem, J. C. Martins and M. Biesemans, Inorg. Chem., 1998, 37, 911; (d) C. E. Baron, F. Ribot and C. J. Sanchez, Organomet. Chem., 1998, 567, 137; (e) D. Dakternieks, H. Zhu, E. R. T. Tiekink and R. J. Colton, Organomet. Chem., 1994, 476, 33.
7. (a) V. Chandrasekhar, S. Nagendran, R. Azhakar, M. R. Kumar, A. Srinivasan, K. Ray, T. K. Chandrashekar, C. Madhavaiah, S. Verma, U. D. Priyakumar and G. N. Sastry, J. Am. Chem. Soc., 2005, 127, 2410; (b) S. Kundu, E. Matito, S. Walleck, F. F. Pfaff, F. Heims, B. Rabaý, M. J. Luis, A. Company, B. Braun, T. Glaser and K. Ray, Chem. – Eur. J., 2012, 18, 2787.
8. I. M. Pérez, S. Kundu, A. Chandra, K. E. Craigo, P. Chernev, U. Kuhlmann, H. Dau, P. Hildebrandt, C. Greco, C. Van Stappen, N. Lehnert and K. Ray, J. Am. Chem. Soc., 2017, 139, 15033–15042.
9. (a) A. B. Stambouli and E. Traversa, Renewable Sustainable Energy Rev., 2002, 6, 295; (b) N. M. Marković, T. J. Schmidt, V. Stamenković and P. N. Ross, Fuel Cells, 2001, 1, 105; (c) B. C. H. Steele and A. Heinzel, Nature, 2001, 414, 345.
10. (a) S. Abrantes, E. Amaral, A. P. Costa, A. A. Shatalov and A. P. Duarte, Ind. Crops Prod., 2007, 25, 288–293; (b) S. H. Zeronian and M. K. Inglesby, Cellulose, 1995, 2, 265–272; (c) L. Li, S. Lee, H. L. Lee and H. J. Youn, BioResources, 2011, 6, 721–736.
11. (a) I. Yamanaka and T. Murayama, Angew. Chem., Int. Ed., 2008, 47, 1900; (b) R. S. Disselkamp, Int. J. Hydrogen Energy, 2010, 35, 1049; (c) R. S. Disselkamp, Energy Fuels, 2008, 22, 2771; (d) A. E. Sanli and A. Aytac, Int. J. Hydrogen Energy, 2011, 36, 869.
12. (a) S. Fukuzumi, Y. Yamada and K. D. Karlin, Electrochim. Acta, 2012, 82, 493–511; (b) R. S. Disselkamp, Energy Fuels, 2008, 22, 2771–2774; (c) R. S. Disselkamp, Int. J. Hydrogen Energy, 2010, 35, 1049–1053; (d) B. C. H. Steele and A. Heinzel, Nature, 2001, 414, 345.
13. (a) S. Ferguson-Miller and G. T. Babcock, Chem. Rev., 1996, 96, 2889; (b) G. T. Babcock and M. Wikström, Nature, 1992, 356, 301; (c) E. I. Solomon, P. Chen, M. Metz, S.-K. Lee and A. E. Palmer, Angew. Chem., Int. Ed., 2001, 40, 4570–4590.
14. (a) D. Das, Y.-M. Lee, K. Ohkubo, W. Nam, K. D. Karlin and S. Fukuzumi, J. Am. Chem. Soc., 2013, 135, 2825; (b) M. A. Thorseth, C. E. Tornow, E. C. M. Tse and A. A. Gewirth, Coord. Chem. Rev., 2013, 257, 130; (c) Z. Halime, H. Kotani, Y. Li, S. Fukuzumi and K. D. Karlin, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13990; (d) C. Costentin, H. Dridi and J.-M. Saveant, J. Am. Chem. Soc., 2015, 137, 13535; (e) K. Mase, K. Ohkubo and S. Fukuzumi, J. Am. Chem. Soc., 2013, 135, 2800–2808; (f) R. McGuire Jr., D. K. Dogutan, T. S. Teets, J. Suntivich, Y. Shao-Horn and D. G. Nocera, Chem. Sci., 2010, 1, 411–414; (g) J. Rosenthal and D. G. Nocera, Acc. Chem. Res., 2007, 40, 543–553; (h) E. Kim, E. E. Chufan, K. Kamaraj and K. D. Karlin, Chem. Rev., 2004, 104, 1077–1133; (i) S. Liu, K. Mase, C. Bougher, S. D. Hicks, M. M. Abu-Omar and S. Fukuzumi, Inorg. Chem., 2014, 53, 7780–7788.
15. R. W. F. Bader, Atoms in Molecules. A Quantum Theory, Cambridge University Press, Oxford U.K., 1991.
16. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
17. (a) M. Kohout, Int. J. Quantum Chem., 2004, 97, 651–658; (b) M. Kohout, F. R. Wagner and Y. Grin, Theor. Chem. Acc., 2008, 119, 413–420.
18. S. Fukuzumi, K. Okamoto, C. P. Gros and R. Guilard, J. Am. Chem. Soc., 2004, 126, 10441.
19. Z. Halime, H. Kotani, Y. Li, S. Fukuzumi and K. D. Karlin, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1399.
20. D. Das, Y.-M. Lee, K. Ohkubo, W. Nam, K. D. Karlin and S. Fukuzumi, J. Am. Chem. Soc., 2013, 135, 2825.
21. (a) G. Givaja, M. Volpe, M. A. Edwards, A. J. Blake, C. Wilson, M. Schröder and J. B. Love, Angew. Chem., Int. Ed., 2007, 46, 584; (b) T. Tanase, T. Onaka, M. Nakagoshi, I. Kinoshita, K. Shibata, M. Doe, J. Fujii and S. Yano, Chem. Commun., 1997, 2115; (c) E. Askarizadeh, S. B. Yaghoob, D. M. Boghaei, A. M. Z. Slawin and J. B. Love, Chem. Commun., 2010, 46, 710.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 818335. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0dt00475h

---