Open Access Article
Open Access ArticleSERS and plasmonic heating efficiency from anisotropic core/satellite superstructures†
Christian
Kuttner‡
 *ab,
Roland P. M.
Höller‡
c,
Marta
Quintanilla
*ab,
Roland P. M.
Höller‡
c,
Marta
Quintanilla
 a,
Max J.
Schnepf
c,
Martin
Dulle
a,
Max J.
Schnepf
c,
Martin
Dulle
 d,
Andreas
Fery
d,
Andreas
Fery
 bce and
Luis M.
Liz-Marzán
bce and
Luis M.
Liz-Marzán
 af
af
aCIC biomaGUNE, BioNanoPlasmonics Laboratory, Paseo de Miramón 182, 20014 Donostia-San Sebastián, Spain. E-mail: ckuttner@cicbiomagune.es
bCluster of Excellence Center for Advancing Electronics Dresden (CFAED), Technische Universität Dresden, Helmholtzstraße 18, 01069 Dresden, Germany
cLeibniz-Institut für Polymerforschung Dresden e.V. (IPF), Institute for Physical Chemistry and Polymer Physics, Hohe Straße 6, 01069 Dresden, Germany
dJülich Centre for Neutron Science (JCNS-1), Institute for Complex Systems (ICS-1), Forschungszentrum Jülich GmbH, Wilhelm-Johnen-Straße, 52428 Jülich, Germany
ePhysical Chemistry of Polymeric Materials, Technische Universität Dresden, Bergstraße 66, 01069 Dresden, Germany
fIkerbasque, Basque Foundation for Science, 48013 Bilbao, Spain
First published on 18th September 2019
Abstract
The optical properties of nanoparticle assemblies can be tailored via hybridization of plasmon modes. Isotropic core/satellite superstructures made of spherical nanoparticles are known to exhibit coupled modes with a strongly scattering (radiative) character, and provide hot spots yielding high activity in surface-enhanced Raman scattering (SERS). However, to complement this functionality with plasmonic heating, additional absorbing (non-radiative) modes are required. We introduce herein anisotropic superstructures formed by decorating a central nanorod with spherical satellite nanoparticles, which feature two coupled modes that allow application for both SERS and heating. On the basis of diffuse reflectance spectroscopy, small-angle X-ray scattering (SAXS), and electromagnetic simulations, the origin of the coupled modes is disclosed and thus serves as a basis toward alternative designs of functional superstructures. This work represents a proof-of-principle for the combination of high SERS efficiency with efficient plasmonic heating by near-infrared irradiation.
Introduction
Noble metal nanoparticles (NPs) are versatile building blocks for self-assembled colloidal superstructures with tailored optical functionality.1,2 Hierarchical multi-particle architectures in particular are recognized as “colloidal plasmonic molecules” because their ensemble properties largely differ from those of the individual components.3,4 Their self-assembly can be guided, both in 2D and 3D, by bio-recognition5,6 and other attractive forces.7 Colloidal plasmonic molecules can localize light at the nanoscale, yielding highly confined electric fields which are often exploited for surface-enhanced Raman spectroscopy, e.g. as SERS-encoded tags,8,9 cellular imaging,10 or biomarker detection.11 Strategies for high SERS brightness include spiky12 and undulated particle surfaces,13,14 as well as cluster-encasing15 and multilayer adsorption16 of smaller particles on a central core NP. Assemblies consisting of a larger core NP surrounded by a monolayer of smaller NPs are commonly referred to as core/satellite superstructures.17,18 Such superstructures have been reported as nanosensors for various sensing modalities19 including sensitivity toward enzymatic activity,20 induced disassembly,21 or changes in chiroptical activity.22Today′s applications, however, require multifunctional nanosensors that not only detect analytes, but can also exert a chemical and/or physical stimulus. Controlled nano-heating in particular has become a research focus for applications such as targeted drug delivery,23 photo-thermal therapy,24 and photo-chemotherapy.15 Therefore, efficient nano-heaters are required, which should be designed to absorb and convert incident light into heat.25 Efficient heat transfer can already be observed for small gold nanospheres26 and their aggregates.27 Notwithstanding, the field of thermo-plasmonics and optical heating is currently extending toward more complex plasmonic nanostructures.28–30 A particularly interesting challenge is designing superstructures that allow for both analyte detection at high sensitivity and efficient nano-heating upon excitation at the biologically relevant near-infrared (NIR) regime.31 For this purpose, control over the radiative (scattering) and non-radiative (absorbing) contributions of superstructures plays a key role.32 However, the coupled modes of isotropic core/satellite structures, composed of spherical NPs, are limited to the visible range and become increasingly more radiative with increasing size.18,33 This issue could be circumvented by breaking the symmetry. An anisotropic particle, like a gold nanorod, should allow red-shifting the coupling mode into the NIR range. However, the plasmonic interactions3,34 become more complex in anisotropic structures, as has been shown for single-satellite nanorod pairs35 and substrate-supported clusters.36,37 In addition, we hypothesize that the choice of a suitable anisotropic core can achieve control over the balance between absorbing and scattering contributions. It should be noted that quantification of these contributions is not straightforward because standard UV/vis/NIR transmission spectroscopy only provides information on the total extinction (the sum of both radiative and non-radiative losses). For substrate-supported nanostructures, Link et al. reported the demanding combination of dark-field and photo-thermal imaging to differentiate spectral losses.32 For nanostructures dispersed in liquid, the ensemble-average spectral losses can be measured by diffuse reflectance spectroscopy using an integrating sphere, as recently reported.18
Here we present anisotropic supra-colloidal structures consisting of a nanorod core decorated with spherical satellite NPs. These superstructures exhibit dominantly absorbing coupled modes, which were quantified by diffuse reflectance spectroscopy. Small-angle X-ray scattering was employed to analyse the superstructures’ structural properties. We discuss the origin of the coupled modes to provide insight into the plasmonic coupling phenomena. Finally, we show as a proof-of-principle that high SERS brightness can be combined with efficient plasmonic heating by near-infrared illumination.
Results and discussion
Synthesis of anisotropic assemblies
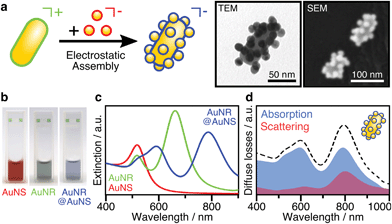
The assembly of anisotropic core/satellite superstructures was directed by electrostatic interactions between oppositely charged building blocks (Fig. 1a). For this purpose, 16 ± 2 nm sized nanospheres (AuNSs) were synthesized following Turkevich et al.38 and subsequently coated by a negatively charged polyelectrolyte P(SS-co-MA), which is a copolymer of 4-styrenesulfonate (SS) and maleic acid (MA). The carboxyl groups of the MA units could enable post-functionalisation by esterification/amidation39 or covalent cross-linking in order to increase the long-term stability of the coating, as well as the core/satellite structure after assembly and thus extend their applicability in biological media.40 Gold nanorods (AuNRs) were prepared by the seeded growth method,41 yielding average length of 74 ± 7 nm and width of 33 ± 2 nm (AR = 2.2 ± 0.3), as determined by TEM image analysis (Fig. S1†). Subsequently, the NRs were functionalized by a two-step ligand exchange of cetyltrimethylammonium bromide (CTAB) against first cetyltrimethylammonium chloride (CTAC) and second 11-mercaptoundecyl trimethylammonium bromide (MUTAB). The transition from a mobile CTA+ bilayer to a more robustly attached monolayer of MUTA+ molecules is driven by the high binding affinity of thiols to gold. After coating, both building blocks were washed multiple times with pure water to remove excess unbound ligands because those might interfere during the assembly step. The UV/vis/NIR extinction spectra of the satellite and core NPs before and after coating/functionalization remained essentially unchanged, indicating colloidal stability and absence of aggregation (Fig. S2, Table S1†). The negatively charged AuNSs (satellites) were found to adsorb onto the positively charged AuNRs (cores) upon mixing, forming core/satellite superstructures (Fig. 1a). An excess of satellites minimizes bridging between non-saturated cores. The electrostatic assembly resulted in AuNR@AuNS superstructures with a high satellite coverage (Fig. S3 and S4†), close to the jamming limit, which will be discussed below.18 After the assembly step, the superstructures were added to a dilute P(SS-co-MA) solution to saturate the free core surface between adsorbed satellites with the copolymer. An excellent long-term stability was evidenced by their unaltered plasmonic signature, which remained almost unchanged, even 6 months after the synthesis (Fig. S5†). The dispersions of the satellites, the cores, and their superstructures display wine-red, greenish, and blueish colours, respectively (Fig. 1b). The spectral features are significantly altered upon assembly (Fig. 1c). The localized surface plasmon resonance of AuNS@P(SS-co-MA) is centred at 521 nm (red line in Fig. 1c); AuNR@MUTAB cores show transversal and longitudinal plasmon modes at 516 nm and 656 nm (green line), respectively. Interestingly, the final purified AuNR@AuNS superstructures show three plasmon bands at 510–545 nm, 598 nm, and 795 nm (blue line). Because the individual spectral losses cannot be discriminated by conventional UV/vis/NIR spectroscopy, we performed diffuse reflectance spectroscopy using an integrating sphere (see ESI.2†). Fig. 1d presents the contributions of absorption (blue line) and scattering (red line) to the total extinction (dashed black line). All coupled modes are found to be dominated by absorption and thus, predominantly non-radiative. Quantification of radiative and non-radiative losses by non-assembled building blocks is shown in Fig. S6.† In the following, we provide detailed characterization of the structural features of the assemblies, to allow a reliable correlation between their optical and structural properties.Structural characterization
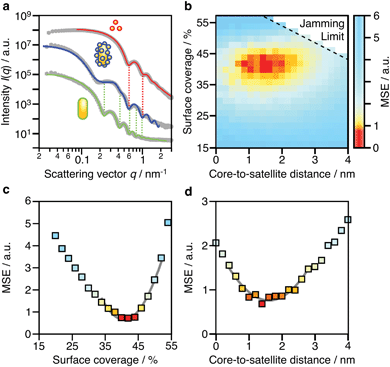
Due to the complex three-dimensional structure, scanning (SEM) and transmission (TEM) electron microscopy techniques can only give a first impression of the structure from a small number of self-assembled nanostructures. The parameters that are particularly critical for plasmonics, such as interparticle distances and average surface coverage, are hardly accessible by EM imaging. Also, the size polydispersity of the NP building blocks (the cores particularly) and the resulting polydispersity in surface coverage should be taken into account in a complete analysis. For these reasons, we decided to use SAXS, which grants access to ensemble-averaged structural information at the nanoscale. The scattering spectra reflect the distribution of sizes and distances for each sample with sub-nanometre resolution. Because repeated distances and sizes appear more prominently, SAXS is the method of choice to evaluate the structural properties of supra-colloidal assemblies.Fig. 2a shows the scattering curves of the NP building blocks (red, green) and their assemblies (blue). The individual NPs display the expected repeating fringes, which can be described analytically considering satellites as spheres and rods as cylinders with hemi-spherical end-caps (see ESI.3†). Polydispersity in size and shape was accounted for in the fits by averaging over a Gaussian distribution of core sizes (length and width, Table S2†). The assemblies show additional scattering contributions, specifically in the range from 0.1 to 0.5 nm−1, which can be attributed to the presence of the satellites. To quantify the ensemble-averaged number of satellites and their distance to the core, numerical modelling in necessary. Although analytical models for similar structures (e.g. raspberry) exist,42,43 they have been shown not to correctly reproduce the high correlation of satellite NPs.18 Therefore, we applied 3D atomistic modelling (ESI.3†),18,41,44 which involves calculating the scattering curves of 3D structures comprising randomly distributed scattering centres using Debye′s scattering equation (eqn (1)).45
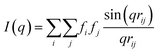 | (1) |
Here, I(q) is the intensity of the scattered wave, q = 4π sin(θ)/λ is the scattering vector, rij = |ri − rj| is the distance between atoms i and j, and fi is the atomic scattering factor of the i-th atom. To validate our numerical approach, the data for nanorods were also evaluated by 3D atomistic modelling (Fig. S7†). Since the resulting parameters (length: 74 ± 8 nm; width: 34 ± 7 nm; see Table S2†) were fully consistent with the analytical SAXS fitting and TEM results (Fig. S1†), we could confidently move on toward modelling of the anisotropic superstructures.
Shown in Fig. 2b is a 2D map for the two main parameters averaged over the whole ensemble: core-to-satellite distance and satellite coverage, i.e. the ratio between the area occupied by all satellites (excluding the NP coating) and the surface area of the core NR (eqn (S1)†). Each point gives the mean square error (MSE) as a measure of the quality of the fit to the experimental data. The uncertainty of these ensemble parameters can be estimated from cross-sections through the global minimum (domain of lowest MSEs) within the parameter space (Fig. 2c and d). It can be assumed with high confidence that the average core-to-satellite distance ranges between 1 and 2 nm (Fig. 2d), whereas the overall surface coverage is 36–45% (in agreement with 39%, as estimated by TEM image analysis; Fig. S4†), which corresponds to 18 ± 2 satellite particles per nanorod (Table S2†). This value is very close to the jamming limit of ca. 50%, i.e. the maximum saturation for randomly sequentially adsorbed (RSA) particles on curved surfaces. We conclude herefrom that the satellites are not closely packed, as could be guessed from TEM images (Fig. S3†). Because of their negative surface charge, the satellites can be considered repulsive with a larger “soft” diameter. Considering the excluded space by electrostatic repulsion, it can be assumed that the core particles are almost completely saturated with randomly distributed satellites. With this configuration, one might initially expect additional plasmonic contributions due to inter-satellite coupling of closely arranged particles, but this is not the case. The nearest-neighbour spacing of satellites is determined by the steric hindrance of their swollen polyelectrolyte coating and repulsive (negative) surface charges. As a consequence, the spacing between two satellites would be at least twice as large as the core-to-satellite spacing (Fig. S8†). Therefore, the satellites’ short-range coupling to the comparatively larger core can be expected to out-range the inter-satellite coupling. To test this assumption, we have taken a closer look into the plasmonic interactions and near-field coupling for such anisotropic superstructures. A detailed description of the coupled modes will also provide information on their optical properties, and thus on the possibilities for multifunctionality.
Correlation of structural and optical properties
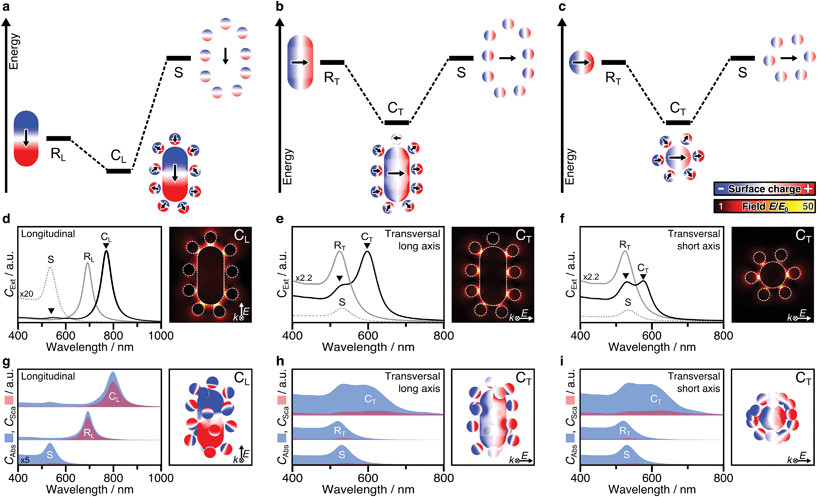
Plasmonic hybridization is an electromagnetic analogue to molecular orbital (MO) theory, which allows to intuitively analyse coupling scenarios.3 With the aim of describing the plasmonic response (shifting and splitting of modes), a complex nanostructure is first conceptually broken down into its elementary building blocks. Then, based on the energetic levels of the elemental plasmons, interactions between the constituents can be predicted or reconstructed. The resulting hybrid modes differentiate between bonding and antibonding modes, in resemblance with MO theory. Hybridization theory has already been applied to dimers of nanospheres3,34,46–48 as well as rod–sphere heterodimers,35 which basically represent single-satellite superstructures (Fig. S12†). The main question here is whether the concept of hybridization can be applied to multi-satellite superstructures. To answer this question, both mode splitting and collective dipole–dipole interactions must be analysed. First, we consider a simplified 2D system that contains only particles in the excitation plane (Fig. S10†), to facilitate the differentiation of the various contributions before proceeding to 3D assemblies.For anisotropic superstructures, plasmonic coupling can take place in all three principal axes (Fig. 3a–c), one representing a longitudinal excitation and two associated with transversal excitations. Either case, on the left of the diagram the mode of the core rod is shown, with a different energy depending on its orientation (RL for the longitudinal one at 690 nm and RT for the transversal one at 520 nm). The orbit of satellites is shown on the right, modelled as a degenerate ensemble of individual dipoles (S, 525 nm). The polarization in each of the components can be deduced from their corresponding surface charge density distributions (the gradient of the local electric field). Hybridization theory predicts that, by combination, mode splitting takes place.
Probably the most intuitive situation is an external field aligned along the longitudinal axis of the nanorod. The 2D superstructure shows a pronounced red-shifted mode (CL, 780–800 nm), representing the energetically favourable state, in which the dominant core charges lead to reorientation of the satellites. Meanwhile, the locations of high surface charge density also correspond to strong confinements of the electric field E/E0. These hot spots are particularly pronounced in the satellite-core gaps near the tips (Fig. 3d). The present dipole–dipole interactions (Fig. S3a†) agree well with the expectations derived from hybridization models of rod–sphere heterodimers as single-satellite assemblies (Fig. S12a†). The second coupled mode is much weaker and located close to the primitive mode of the satellites (S). Initially, one might expect this to indicate the presence of unbound satellites in the solution. However, EM studies have shown that this is not the case. The question arises whether this mode could be assigned to be of antibonding type. Hybridization theory postulates the bonding mode to be redshifted (with respect to the primitive plasmon of the rod core) and the antibonding mode to be blue shifted with respect to the primitive plasmon of the spheres. In practice however, both experimental and theoretical findings have been reported showing slightly red-shifted antibonding modes, at first glance, in disagreement with hybridization theory.3,46,47 This abnormality was attributed to either additional interactions with interband electrons (in the case of heterometallic Au/Ag assemblies46) or to screening/quenching of repulsive interactions (for homometallic Au assemblies47). For the multi-satellite structures, the obtained surface charges reveal dipole–dipole interactions, in line with expectations, but the overall charge pattern is weak (Fig. S13a†). This might be indicative for destructive interactions with other longitudinal modes (possibly of higher-order).
The mode splitting of the transversal rod mode (RT, 520 nm) proceeds analogously, so it can be viewed from two different perspectives (Fig. 3b and c). Although the resulting modes are basically the same, it makes sense to consider both perspectives, as the seamless transition from an anisotropic to an isotropic-core superstructure can be shown very nicely. We first take the perspective in which both the wave vector k and the polarization of the electric field E are perpendicular to the long axis of the nanorod (Fig. 3b). Because the energetic mismatch between core and satellites is low, all components can be excited simultaneously by the external field. The dominant mode at 600 nm shows a uniform charge distribution on the core and a consequent reorientation of the dipolar charges of the satellite particles (close to the tips). The dipole–dipole interactions correspond to a bonding-type mode (Fig. S13b†). Contrary to CL (Fig. 3d), the strongest hot spots of CT are not located near the rod ends but at its sides (Fig. 3e). The weaker second mode at 520–540 nm corresponds to energetically unfavourable dipolar interactions (Fig. S13b†). Second, from the perspective along the nanorod (parallel to k, Fig. 3c), the assembly looks like a superstructure with an isotropic core.18 Comparing the mode splitting in Fig. 3e and f, it appears that the intensity and redshift magnitude of the low-energy mode depend on the number of satellites involved. The corresponding surface charges reveal favourable interactions at lower energy and unfavourable interactions at higher energies (Fig. S13c†). For details, see ESI.5.† In summary, the plasmonic interactions present in 2D multi-satellite rod@sphere assemblies follow the principles of hybridization theory.
So far, we have only considered 2D assemblies (Fig. 3a–f), whereas 3D assemblies are much more affected by satellite disorder and structural diversity, with a multitude of possible configurations. To assess the influence of disorder, 40 randomly generated 3D configurations (based on the best-match parameters of structural analysis, Table S2, Fig. S10†) were averaged. Fig. 3g–i presents the non-radiative (CAbs) and radiative (CSca) contributions of NP building blocks and assemblies. Although the coupled modes (CL, CT) are broadened by ensemble-averaging and inter-satellite coupling (Fig. S11†), they remain dominantly absorbing. The distinct scattering contribution in CL originates from the longitudinal rod mode RL. Still, in all cases, the absorption cross-section is further increased upon assembly. The exemplary surface charge distributions of 3D assemblies in Fig. 3g–i agree well with the coupling behaviour described above (for 2D assemblies).
From this analysis, clear rules for the design of superstructures can be derived: (1) If the elementary modes are mainly absorbing, the coupled modes will also be strongly absorbing. (2) If one of the elementary modes has a significant scattering contribution, this radiative component will be transferred to the coupled mode.
SERS efficiency
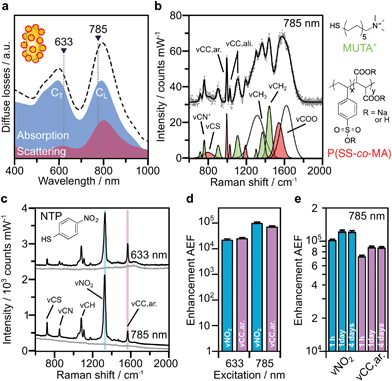
Based on the above theoretical discussion, the suitability of these superstructures as colloidal SERS nanosensors were investigated. Within superstructures with a broken symmetry, the different hot-spot positions (gaps near rod tips versus sides) can be selectively excited by the choice of the respective laser wavelength (Fig. 4a). Here, the question arises which of the coupled plasmon modes displays a higher SERS performance. We first measured the Raman scattering from dispersions of the superstructures without additional analytes (Fig. 4b). A gold concentration of 0.25 mM Au0 (determined spectroscopically by the extinction at 400 nm) was found to be sufficient to detect the local surface chemistry within the hot spots. Although the SERS intensity of 10–40 counts per mW is relatively weak, the SERS signature can be assigned to the characteristic signals of the coating on the nanorod cores, MUTA+, and on the spherical satellites P(SS-co-MA). Guided by reference measurements (Fig. S14, Table S5†), some signals could be assigned to the trimethylammonium head group (vCN+ 760 cm−1, vCH3 1295–1457 cm−1) and the skeletal vibrations of the C11H22 alkyl chain (vCC,ali. 1029–1191 cm−1, vCH2 1215–1461 cm−1) of MUTA+. Likewise, other signals indicate spectral contributions from styrenesulfonate (SS: vCS 793 cm−1, vCC,ar. 995 cm−1) and maleic acid (MA: vCH2 1449 cm−1, vCOO 1578 cm−1) in the P(SS-co-MA) coating.The true quality of SERS amplification is demonstrated by the addition of 4-nitrothiophenol (NTP, Fig. S14†) as an aromatic model analyte. Fig. 4c compares the SERS gains at two different excitation lines, 633 nm and 785 nm, for samples with 0.25 mM Au0 without NTP (grey lines) and at 1 h after addition of NTP (1 μM, black lines). The characteristic signals of NTP occur with significantly higher intensities of up to 1500–1800 counts per mW (Table S3†), keeping all experimental conditions the same. For the quantification of the analytical enhancement factors (AEFs),49 we used the prominent signals of the symmetrical stretching vibration of the nitro group vNO2 at 1330 cm−1 and the stretching of the aromatic phenyl ring vCC,ar. at 1570 cm−1. For this purpose, we first determined experimentally the non-enhanced molar Raman cross-sections (IRS/cRS) of NTP for 633 nm and 785 nm excitation, using a series of reference concentrations below the solubility limit (Fig. S15†). Then, the AEF values were calculated by means of eqn (2), based on the intensity ISERS and NTP concentration (cSERS = 1 μM) in the SERS experiments (Fig. 4d).
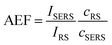 | (2) |
The AEF values quantify the performance of SERS-active liquids (colloidal dispersions) for analytical chemistry applications, provided that all experimental procedures are clearly stated and a sub-monolayer coverage of the analyte is ensured (Table S4†).49 The obtained AEFs (after 1 h) range between (2.3 − 2.6) × 104 at 633 nm excitation and (0.73 − 1.0) × 105 at 785 nm excitation (Fig. 4d, Table S3†). While at 633 nm, the enhancement ratio of the investigated Raman modes is balanced, the signal yield of vNO2 predominates at 785 nm. In a direct comparison, the signal yield at 785 nm is about 3–4 times higher than at 633 nm. This implies that the longitudinal coupled mode CL (in the NIR range) is better suited for SERS than the transverse coupled mode CT. These results suggest that the analyte finds its way into the hot spots, i.e. the gaps between the core and the satellites. It is however unclear whether the analyte adsorbs uniformly throughout the superstructure or at preferred sites. The preferential adsorption of NTP onto the MUTA+-functionalized core could be expected because of coulombic attraction to the NO2− group. However, the positive charge of the NR core should be reversed by the adsorption of P(SS-co-MA)-encapsulated satellite NPs and free P(SS-co-MA) from solution, which was added to saturate the unoccupied sites of the core surface. The thiol group of NTP might in principle bind to all accessible areas of the gold surface. At the same time, part of the core surface might be inaccessible because of MUTA+ ligands. In any case, it is ensured that even for an exclusive adsorption on cores or satellites, the basic precondition of a sub-monolayer of NTP would be met (Table S4†). In addition, incomplete analyte adsorption is a source of error that can affect the significance of SERS results. To evaluate whether all NTP molecules have been removed from the solution after incubation for 1 h, further measurements were carried out after 1 day and after 4 days (Fig. 4e, Table S3†). It turned out that, after 1 day the AEF values increased by about 18–21%, to (0.9 − 1.2) × 105. After 4 days, no further increase could be recorded and the values remained constant, indicating complete adsorption of analyte.
For a Raman marker at non-resonant conditions, the SERS results show a remarkably high signal yield per mole Au (AEF/cAu of 4.88 × 105 mM−1). To the best of our knowledge, this is one of the highest AEF/cAu efficiency values presented in the literature for SERS-active colloidal dispersions.44,50 The normalization of AEF values by cAu is recommended because AEF values by themselves suffer from poor comparability. Especially for colloidal (average) SERS experiments, the analyte to nanostructure surface ratio is a critical parameter. Since the effective surface area and the number of absorbed analyte molecules are hard to evaluate precisely, we utilize the volume content of NPs by cAu51 to relate signal output to material input.
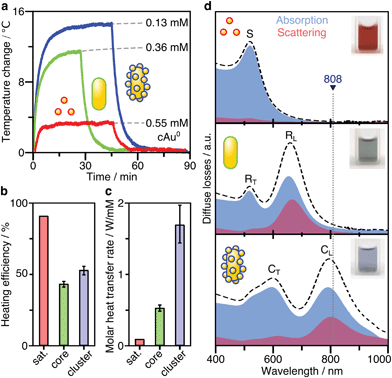
Plasmonic heating efficiency
After SERS activity has been demonstrated, we present the suitability of our superstructures for plasmonic heating. The conversion of absorbed light into heat is based on photo-thermal relaxation processes during the plasmonic excitation.27 Accordingly, non-radiative contributions (absorption cross-section) and matching of the excitation wavelength are crucial factors toward effective heat generation.52 We therefore performed heating experiments to compare the superstructures to the separate building blocks. For this purpose, 1 mL aliquots for each morphology were illuminated with a laser at 808 nm (710 mW), and the temperature reached at the surface was monitored with a thermal camera. In this way, heating and cooling curves (Fig. 5a) were recorded. Once thermal equilibrium with the environment was reached, the spherical NPs used as satellites were found to cause only a slight temperature increase of 2–3 °C, even at a high Au0 concentration of 0.55 mM. The nanorod core NPs yield a temperature increase of about 12 °C, at a lower concentration of 0.36 mM Au0. Finally, the superstructures result in the highest temperature gain (15 °C), with even lower material requirements (0.13 mM Au0).The heating efficiency η is a measure for the quality of the light-to-heat conversion (Fig. 5b). Following the method described by Roper et al.,26 this corresponds to the quotient of the delivered thermal energy ΔQ(Qsample − Qmedium) and the energy provided by the incident laser power P, considering the optical density (extinction, Ext808) of the sample (see ESI.8†).
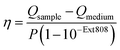 | (3) |
The transient temperatures shown in Fig. 5a display an exponential behaviour. Qsample and Qmedium are obtained by fitting the characteristic decay times of the experimental data (Fig. S16†). The heating efficiency is a property defined for a single particle, and it is independent of concentration. Besides, it does not consider how many photons a particle is interacting with; only how many of such photons are transformed into heat. However, for the comparison that we are doing here, it may be more purposeful to directly compare the generated heat output (ΔQ) to the required material input, in terms of sample concentration (cAu). In this way, we avoid misinterpretations given by very different extinction cross-sections of each particle type. Accordingly, we define the molar rate of heat transfer (Fig. 5c) as
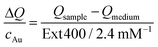 | (4) |
Still, it is not fully understood how nanoscale control over optical heating in complex plasmonic systems can be achieved.54 The superstructures presented herein exemplify an increase of heating efficiency by hierarchical structuring. The interparticle thermalization in this case, appears to be aided by plasmon coupling.28 Because the nanospheres are very strongly absorbing but cannot be excited directly (by the external field of the laser), the core particle is essential for heat generation.55 The nanorod core acts as an optical nanoantenna and is the key element in the conversion of light to heat. As the primary excitable component, it excites the surrounding spherical satellites by its own induced electric field. As a result, the generated heat combines contributions from both the core and coupled satellites. Optically, this can be witnessed by the increased absorption power of the assembly (Fig. 3g and 5d), thereby increasing the efficiency of optical heating.
Conclusions
The decoration of gold nanorods with spherical NPs results in anisotropic superstructures with satellite coverages (36–45%) close to saturation, limited by surface jamming (ca. 50%). The short core-to-satellite gaps of 1.5 ± 0.5 nm, as determined by SAXS analysis, result in strongly coupled building blocks. The characteristic spectral losses of anisotropic colloidal assemblies were investigated, both theoretically and experimentally. Our findings demonstrate that symmetry breaking in the superstructures grants control over the balance between absorption and scattering properties. This was exemplified for nanorod cores which gave access to intense coupling modes with a dominating non-radiative character in the NIR.These superstructures may serve as colloidal SERS nanosensors in dispersed state with enhancements on the order of 104 (transversal) and 105 (longitudinal), by selective excitation at 633 nm or 785 nm, respectively. Their high SERS brightness even allowed to detect the low-intensity spectral background of the coating layers on the building block NPs. The longitudinally coupled mode in the NIR range is particularly well-suited for SERS detection with a remarkably high signal yield per mol Au (AEF/cAu of 4.9 × 105 mM−1) for a Raman marker (NTP) at non-resonant conditions.
The superstructures’ suitability for plasmonic heating was evaluated by laser irradiation at 808 nm, which falls in a region of low attenuation in biological tissues. We demonstrated that the effectiveness of heat generation relies on both the non-radiative character of the specific plasmon mode and matching to the excitation wavelength. The superstructures showed increased heating efficiency (53%) and molar rates of heat transfer (1.7 ± 0.3 W mM−1) compared to their building blocks. Our results evidence that the heating efficiency can be increased by hierarchical structuring. Because the small non-aggregated nanospheres cannot be excited in the NIR, the nanorod core is required as an optical nanoantenna. Aided by the strong plasmon coupling, the excitation is conveyed to the surrounding nanospheres. Consequently, both the core and the coupled satellites may contribute to heating and the light-to-heat conversion efficiency is augmented.
Thus, balancing of non-radiative and radiative contributions is a key step toward the design of multifunctional nanosensors that combine high SERS and heating efficiencies. In the context of increased structural control, guided assembly56 at the core surface might even grant access to chiroptical anisotropic superstructures.57
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The research leading to these results has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 799393 (NANOBIOME). The authors also acknowledge support from the Deutsche Forschungsgemeinschaft (DFG) within the Cluster of Excellence Centre for Advancing Electronics Dresden (CFAED) and the Spanish Ministerio de Economía, Industria y Competitividad (grant MAT2017-86659-R to L. M. L.-M.). This work was performed under the María de Maeztu Units of Excellence Program from the Spanish State Research Agency – Grant No. MDM-2017-0720.References
- A. Klinkova, R. M. Choueiri and E. Kumacheva, Chem. Soc. Rev., 2014, 43, 3976–3991 RSC.
- J. A. Fan, C. Wu, K. Bao, J. Bao, R. Bardhan, N. J. Halas, V. N. Manoharan, P. Nordlander, G. Shvets and F. Capasso, Science, 2010, 328, 1135–1138 CrossRef CAS PubMed.
- E. Prodan, C. Radloff, N. J. Halas and P. Nordlander, Science, 2003, 302, 419–422 CrossRef CAS PubMed.
- C. S. Plüisch and A. Wittemann, in Advances in Colloid Science, InTech, 2016, pp. 237–264 Search PubMed.
- F. Westerlund and T. Bjørnholm, Curr. Opin. Colloid Interface Sci., 2009, 14, 126–134 CrossRef CAS.
- V. Raeesi, L. Y. T. Chou and W. C. W. Chan, Adv. Mater., 2016, 28, 8511–8518 CrossRef CAS PubMed.
- C. Kuttner, M. Chanana, M. Karg and A. Fery, in Macromolecular Self-Assembly, ed. L. Billon and O. V. Borisov, John Wiley & Sons, Inc., Hoboken, New Jersey, 2016, pp. 159–192 Search PubMed.
- L. Fabris, J. Opt., 2015, 17, 114002 CrossRef.
- N. Pazos-Perez, J. M. Fitzgerald, V. Giannini, L. Guerrini and R. A. Alvarez-Puebla, Nanoscale Adv., 2019, 6, 29014 Search PubMed.
- T. Köker, N. Tang, C. Tian, W. Zhang, X. Wang, R. Martel and F. Pinaud, Nat. Commun., 2018, 9, 1578 CrossRef PubMed.
- J. Feng, X. Wu, W. Ma, H. Kuang, L. Xu and C. Xu, Chem. Commun., 2015, 51, 14761–14763 RSC.
- Y. Shang, J. Shi, H. Liu, X. Liu, Z.-G. Wang and B. Ding, Nanoscale, 2018, 10, 9455–9459 RSC.
- V. Tran, C. Thiel, J. T. Svejda, M. Jalali, B. Walkenfort, D. Erni and S. Schlücker, Nanoscale, 2018, 10, 21721–21731 RSC.
- F. Liebig, R. M. Sarhan, C. Prietzel, A. F. Thünemann, M. Bargheer and J. Koetz, Langmuir, 2018, 34, 4584–4594 CrossRef CAS.
- P. T. Sujai, M. M. Joseph, V. Karunakaran, G. Saranya, R. N. Adukkadan, S. Shamjith, R. Thomas, J. B. Nair, R. S. Swathi and K. K. Maiti, ACS Appl. Bio Mater., 2018, 2, 588–600 CrossRef.
- W. Xiong, D. Sikdar, L. W. Yap, M. Premaratne, X. Li and W. Cheng, Nanoscale, 2015, 7, 3445–3452 RSC.
- M. Schütz and S. Schlücker, Phys. Chem. Chem. Phys., 2015, 17, 24356–24360 RSC.
- R. P. M. Höller, M. Dulle, S. Thomä, M. Mayer, A. M. Steiner, S. Förster, A. Fery, C. Kuttner and M. Chanana, ACS Nano, 2016, 10, 5740–5750 CrossRef.
- C. Kuttner, in Plasmonics, ed. T. Gric, IntechOpen, 2018, pp. 151–180 Search PubMed.
- P. D. Howes, R. Chandrawati and M. M. Stevens, Science, 2014, 346, 1247390 CrossRef.
- J. R. Waldeisen, T. Wang, B. M. Ross and L. P. Lee, ACS Nano, 2011, 5, 5383–5389 CrossRef CAS.
- W. Ma, L. Xu, L. Wang, C. Xu and H. Kuang, Adv. Funct. Mater., 2018, 29, 1805512 CrossRef.
- L. Y. T. Chou, K. Zagorovsky and W. C. W. Chan, Nat. Nanotechnol., 2014, 9, 148–155 CrossRef CAS.
- M. R. K. Ali, Y. Wu, Y. Tang, H. Xiao, K. Chen, T. Han, N. Fang, R. Wu and M. A. El-Sayed, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E5655–E5663 CrossRef CAS PubMed.
- N. J. Hogan, A. S. Urban, C. Ayala-Orozco, A. Pimpinelli, P. Nordlander and N. J. Halas, Nano Lett., 2014, 14, 4640–4645 CrossRef CAS.
- D. K. Roper, W. Ahn and M. Hoepfner, J. Phys. Chem. C, 2007, 111, 3636–3641 CrossRef CAS.
- J. Stehr, C. Hrelescu, R. A. Sperling, G. Raschke, M. Wunderlich, A. Nichtl, D. Heindl, K. Kürzinger, W. J. Parak, T. A. Klar and J. Feldmann, Nano Lett., 2008, 8, 619–623 CrossRef CAS.
- G. Baffou, R. Quidant and F. J. Garcia de Abajo, ACS Nano, 2010, 4, 709–716 CrossRef CAS.
- G. Baffou and R. Quidant, Laser Photonics Rev., 2012, 7, 171–187 CrossRef.
- L. M. Maestro, P. Haro-González, A. Sánchez-Iglesias, L. M. Liz-Marzán, J. García Solé and D. Jaque, Langmuir, 2014, 30, 1650–1658 CrossRef CAS.
- A. M. Smith, M. C. Mancini and S. Nie, Nat. Nanotechnol., 2009, 4, 710–711 CrossRef CAS PubMed.
- W.-S. Chang, B. Willingham, L. S. Slaughter, S. Dominguez-Medina, P. Swanglap and S. Link, Acc. Chem. Res., 2012, 45, 1936–1945 CrossRef CAS PubMed.
- B. M. Ross, J. R. Waldeisen, T. Wang and L. P. Lee, Appl. Phys. Lett., 2009, 95, 193112 CrossRef PubMed.
- L. V. Brown, H. Sobhani, J. B. Lassiter, P. Nordlander and N. J. Halas, ACS Nano, 2010, 4, 819–832 CrossRef CAS PubMed.
- L. Shao, C. Fang, H. Chen, Y. C. Man, J. Wang and H.-Q. Lin, Nano Lett., 2012, 12, 1424–1430 CrossRef CAS PubMed.
- M. Hentschel, M. Saliba, R. Vogelgesang, H. Giessen, A. P. Alivisatos and N. Liu, Nano Lett., 2010, 10, 2721–2726 CrossRef CAS PubMed.
- A. Shiohara, S. M. Novikov, D. M. Solís, J. M. Taboada, F. Obelleiro and L. M. Liz-Marzán, J. Phys. Chem. C, 2015, 119, 10836–10843 CrossRef CAS.
- J. Turkevich, P. C. Stevenson and J. Hillier, Discuss. Faraday Soc., 1951, 11, 55–75 RSC.
- A. B. Ruiz-Muelle, C. Kuttner, C. Alarcón-Fernández, J. M. López-Romero, P. Uhlmann, R. Contreras-Cáceres and I. Fernández, Appl. Surf. Sci., 2019, 496, 143598 CrossRef CAS.
- M. Tebbe, C. Kuttner, M. Männel, A. Fery and M. Chanana, ACS Appl. Mater. Interfaces, 2015, 7, 5984–5991 CrossRef CAS PubMed.
- M. J. Schnepf, M. Mayer, C. Kuttner, M. Tebbe, D. Wolf, M. Dulle, T. Altantzis, P. Formanek, S. Förster, S. Bals, T. A. F. König and A. Fery, Nanoscale, 2017, 9, 9376–9385 RSC.
- K. Larson-Smith, A. Jackson and D. C. Pozzo, J. Colloid Interface Sci., 2010, 343, 36–41 CrossRef CAS PubMed.
- G. Despert and J. Oberdisse, Langmuir, 2003, 19, 7604–7610 CrossRef CAS.
- C. Kuttner, M. Mayer, M. Dulle, A. Moscoso, J. M. López-Romero, S. Förster, A. Fery, J. Pérez-Juste and R. Contreras-Cáceres, ACS Appl. Mater. Interfaces, 2018, 10, 11152–11163 CrossRef CAS PubMed.
- P. Debye, Ann. Phys., 1915, 351, 809–823 CrossRef.
- S. Sheikholeslami, Y.-W. Jun, P. K. Jain and A. P. Alivisatos, Nano Lett., 2010, 10, 2655–2660 CrossRef CAS PubMed.
- B. Willingham and S. Link, Appl. Phys. B, 2013, 113, 519–525 CrossRef CAS.
- P. Nordlander, C. Oubre, E. Prodan, K. Li and M. I. Stockman, Nano Lett., 2004, 4, 899–903 CrossRef CAS.
- E. C. Le Ru, E. Blackie, M. Meyer and P. G. Etchegoin, J. Phys. Chem. C, 2007, 111, 13794–13803 CrossRef CAS.
- L. Scarabelli, M. Coronado-Puchau, J. J. Giner-Casares, J. Langer and L. M. Liz-Marzán, ACS Nano, 2014, 8, 5833–5842 CrossRef CAS.
- T. Hendel, M. Wuithschick, F. Kettemann, A. Birnbaum, K. Rademann and J. Polte, Anal. Chem., 2015, 87, 5846–5847 CrossRef CAS.
- M. Quintanilla, C. Kuttner, J. D. Smith, A. Seifert, S. E. Skrabalak and L. M. Liz-Marzán, Nanoscale, 2019 10.1039/c9nr05679c.
- B. Fazio, C. D'Andrea, A. Foti, E. Messina, A. Irrera, M. G. Donato, V. Villari, N. Micali, O. M. Maragò and P. G. Gucciardi, Sci. Rep., 2016, 6, 709 Search PubMed.
- G. Baffou, P. Berto, E. Bermúdez Ureña, R. Quidant, S. Monneret, J. Polleux and H. Rigneault, ACS Nano, 2013, 7, 6478–6488 CrossRef CAS.
- N. Zeng and A. B. Murphy, Nanotechnology, 2009, 20, 375702 CrossRef.
- E. Galati, H. Tao, M. Tebbe, R. Ansari, M. Rubinstein, E. B. Zhulina and E. Kumacheva, Angew. Chem., 2019, 58, 3123–3127 CrossRef CAS PubMed.
- S. Ouhajji, B. G. P. van Ravensteijn, C. Fernández-Rico, K. S. Lacina, A. P. Philipse and A. V. Petukhov, ACS Nano, 2018, 12, 12089–12095 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Details on synthesis, experimental methods, and simulations. See DOI: 10.1039/c9nr06102a |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |