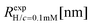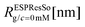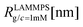Structure and stimuli-responsiveness of all-DNA dendrimers: theory and experiment
Clemens
Jochum†
 a,
Nataša
Adžić†
a,
Nataša
Adžić†
 *b,
Emmanuel
Stiakakis
c,
Thomas L.
Derrien
*b,
Emmanuel
Stiakakis
c,
Thomas L.
Derrien
 d,
Dan
Luo
d,
Gerhard
Kahl
e and
Christos N.
Likos
d,
Dan
Luo
d,
Gerhard
Kahl
e and
Christos N.
Likos
 b
b
aInstitute for Theoretical Physics, TU Wien, Wiedner Hauptstraße 8-10, A-1040 Vienna, Austria. E-mail: clemens.jochum@tuwien.ac.at
bFaculty of Physics, University of Vienna, Boltzmanngasse 5, A-1090 Vienna, Austria. E-mail: natasa.adzic@univie.ac.at
cInstitute of Complex Systems 3, Forschungszentrum Jülich, Leo-Brandt-Straße, D-52425 Jülich, Germany
dDepartment of Biological and Environmental Engineering, Cornell University, Ithaca, New York 14853-5701, USA
eInstitute for Theoretical Physics and Center for Computational Materials Science, TU Wien, Wiedner Hauptstraße 8-10, A-1040 Vienna, Austria
First published on 8th October 2018
Abstract
We present a comprehensive theoretical and experimental study of the solution phase properties of a DNA-based family of nanoparticles - dendrimer-like DNA molecules (DL-DNA). These charged DNA dendrimers are novel macromolecular aggregates, which hold high promise in targeted self-assembly of soft matter systems in the bulk and at interfaces. To describe the behaviour of this family of dendrimers (with generations ranging from G1 to G7), we use a theoretical model in which base-pairs of a single DL-DNA molecule are modeled by charged monomers, whose interactions are chosen to mimic the equilibrium properties of DNA correctly. Experimental results on the sizes and conformations of DL-DNA are based on static and dynamic light scattering; and molecular dynamics simulations are employed to model the equilibrium properties of DL-DNA, which compare favorably to the findings from experiments while at the same time providing a host of additional information and insight into the molecular structure of the nanostructures. We also examine the salt-responsiveness of these macromolecules, finding that despite the strong screening of electrostatic interactions brought about by the added salt, the macromolecules shrink only slightly, their size robustness stemming from the high bending rigidity of the DNA-segments. The study of these charged dendrimer systems is an important field of research in the area of soft matter due to their potential role for various interdisciplinary applications, ranging from molecular cages and carriers for drug delivery in a living organism to the development of dendrimer- and dendron-based ultra-thin films in the area of nanotechnology. These findings are essential to determine if DL-DNA is a viable candidate for the experimental realization of cluster crystals in the bulk, a novel form of solid with multiple site occupancy.
Introduction
All-DNA constructs are complex self-assemblies made solely by DNA. The creation of such nanostructures was initiated in the early 1980s when Seeman proposed the use of DNA as a programmable nanoscale building material,1 laying the foundation for structural DNA nanotechnology.2,3 This interdisciplinary research field has had a striking impact on nanoscience and nanotechnology, demonstrating the construction of a remarkably rich assortment of multidimensional all-DNA nanoarchitectures4–10 with promising applications in areas such as molecular and cellular biophysics,11–15 macromolecular crystallography,16 inorganic nanoparticle templated self-assembly for nanoelectronics,17–19 protein assembly,11,20–23 drug delivery24 and biotechnology.25Very recently, the area of DNA-based self-assembly has been embraced by the research field of soft-matter physics for fabricating all-DNA particles with engineered shape and interaction potentials that could serve as model systems for exploring unconventional bulk phase behaviour of diverse states of matter such as gels26–28 and liquid crystals.29,30 In 2004, Luo and co-workers,31 demonstrated the fabrication of a novel dendrimer-like DNA (DL-DNA) construct. The DL-DNA particles were synthesized in a controlled step-wise fashion from the enzymatic ligation of Y-shaped DNA (Y-DNA) building blocks with rigid arms and specifically designed hybridization regions known as “sticky-ends”, leading to the formation of a highly charged and void-containing macromolecular assembly with tree-like architecture (see Methods for more details). Here, we perform a joint experimental/theoretical analysis of the shapes, sizes, and forms of these constructs, demonstrating their unique properties. We show that they are different from both sterically and charge-dominated dendrimers, they possess a regular spherical shape with voids, and are robust to the influence of added salt.
DL-DNA molecules are a clear example of novel functional nanostructures that can be assembled with remarkable control and subnanometer precision through programmable sticky-end cohesions. Unlike other chemical dendrimers, their built-in modularity allows tailored reshaping of the dendritic scaffold in terms of surface functionalization32 and internal structure modification33 by employing standard tools from biofunctional chemistry. Thus, these DNA-based dendritic architectures have been envisioned to play a promising role in developing nano-barcodes,34,35 DNA-based vaccine36 technologies, and functioning as a structural scaffold as well as a structural probe involving multiplexed molecular sensing processes.37,38 Furthermore, from the fundamental research perspective, their polyelectrolyte character and inherently open architecture near their center of mass endow the DL-DNA particles with an ultrasoft repulsive potential39 and penetrability; features which make the DL-DNA molecules optimal candidates for the experimental realization of the recently proposed cluster-crystal structure.40–42
The investigation of the structural properties of DL-DNAs at a single particle level, including their responsiveness to charge screening, is imperative for the development of emerging applications and for the understanding of intriguing collective phenomena related to this type of novel soft material. Broadly speaking, access on global molecular characteristics such as particle diameter and spatial structure at a very coarse-grained level is feasible with numerous scattering techniques. However, probing in detail the internal and surface morphology of a complex nanostructure is a challenging task. To this end, we adopted an approach of tackling the above issues by combining experiments and simulations to profound insights from the latter into quantities and properties not accessible to experimental techniques. As a prerequisite for establishing the reliability of the latter, we first validate the model by comparing results from the simulation approach with accessible experimental findings.
System description
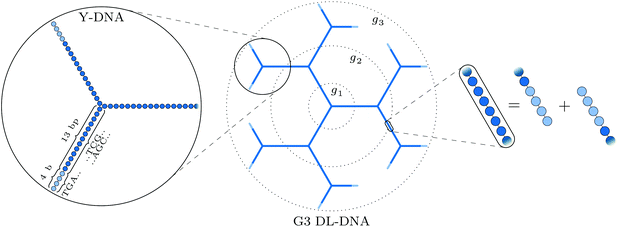
The building block of the dendrimer of interest is the Y-DNA unit, a three-armed structure consisting of double-stranded DNA (dsDNA), formed via hybridization of three single-stranded DNA chains (ssDNA), each of which has partially complementary sequences to the other two. Each arm is made up of 13 base-pairs and a single-stranded sticky end with four nucleobases, see Fig. 1. While a single Y-DNA corresponds to the first dendrimer generation, G1, attaching further Y-DNA elements yields DL-DNA of higher generations, as shown in Fig. 2. This attachment is achieved by enzymatic ligation, where the single-stranded ends of two different arms form a regular double-strand through base-pairing. In this paper we study experimentally and computationally DL-DNA macromolecules from the first generation, G1, up to the sixth generation, G6. We extend the theoretical model also to G7 dendrimer for selective quantities that spread light on the dendrimers’ internal structure. Subgenerations of a GN dendrimer will be indicated by gi, i = 1, 2, …, N.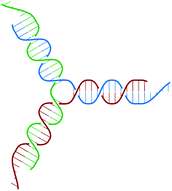 | ||
| Fig. 1 Sketch of the Y-DNA structure: three ssDNA chains (colored red, green, and blue) assemble to form a star-like configuration with sticky ends. | ||
In order to build a model of the DL-DNA nanostructures, we start with a simple and widely used approach by assuming a bead-spring DNA model, where the interactions and the corresponding parameters are carefully chosen to mimic the structural properties of a single dsDNA chain.43,44 This particle-based model for a dsDNA, which is presented in the following, has already been introduced in recent theoretical studies of polyelectrolyte brushes43–45 and its validity has been tested in comparison with experiments in the context of salt-dependent forces between DNA-grafted colloids.46–49 Accordingly, each Y-DNA arm is modeled as a chain of charged monomers consisting of a single dsDNA junction monomer followed by twelve dsDNA chain monomers and a single-stranded end group of four monomers. While the first thirteen monomers correspond to base pairs, the last four represent single nucleobases. The connection between two Y-configurations is established by replacing four + four ssDNA monomers with four dsDNA monomers, see Fig. 2. The numbers of constituents of each generation are given in Table 1.
| Generation | N Y | N bp | N mon |
|---|---|---|---|
| G1 | 1 | 39 | 51 |
| G2 | 4 | 168 | 192 |
| G3 | 10 | 426 | 474 |
| G4 | 22 | 942 | 1038 |
| G5 | 46 | 1974 | 2166 |
| G6 | 94 | 3666 | 4422 |
The beads of the DNA-strands carry electric charges; mobile counterions are introduced in order to preserve the electroneutrality of the system. Additionally, we also introduce different concentrations of monovalent salt ions, Na+ and Cl−, with the purpose of studying the influence of salt on the conformational characteristics of DL-DNA. The properties of each particle type can be seen in Table 2. The steric interaction is described via a truncated and vertically shifted Lennard-Jones potential, which is equivalent to the Weeks–Chandler–Andersen (WCA) potential, here with a possible horizontal shifting by rαβ as follows:
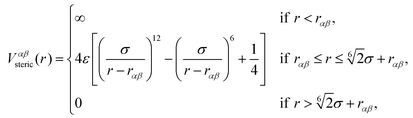 | (1) |
| Particle type | Mass m[u] | Charge q[e] | Radius rα [Å] |
|---|---|---|---|
| Regular monomer (M−) | 660 | −1 | 9 |
| Y-junction monomer (M−) | 660 | −1 | 9 |
| Sticky end-linker (M−) | 330 | −1 | 9 |
| Counterions (C+) | 20 | +1 | 2 |
| Salt particles (S±) | 20 | ±1 | 2 |
This way, the excluded volume interaction between counterion particles reduces to the usual WCA interaction, diverging at zero separation, while the potential between monomers and ions diverges at a center-to-center distance of 7 Å and the interaction between monomers diverges at the distance of 14 Å, accounting for the larger size of the monomers. Thus, the steric interaction acts in the range of r ≤ 18.5 Å, corresponding to the value of the effective DNA helix diameter, which is approximately equal 20 Å.
Consecutive monomers along dsDNA- or ssDNA-strands are connected with bonds described by a harmonic bonding potential:
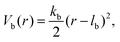 | (2) |
The stiffness of dsDNA is modeled via a harmonic bending-angle potential Vbend(ϕ), which acts on the angle ϕ between the bonds connecting any monomer (index j) to the two neighbouring monomers (indices j + 1 and j − 1):
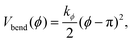 | (3) |
 | (4) |
The bending energy constant value kϕ = 750 kJ mol−1 is chosen to reproduce the typical persistence length L = 500–1000 Å of dsDNA at low ionic strength.52 While the bonds between the three central junction monomers are the same as between all other monomers, the Y-arms are fully flexible, i.e., the bending energy constant is chosen to be zero. Since the persistence length of unpaired ssDNAs is lower than for dsDNAs,53,54 the degree of flexibility of the ssDNA end group monomer is set to kϕ = 150 kJ mol−1.
Since each monomer bears an elementary charge qM− = −e < 0, a corresponding number of counterions with charge e > 0 is added to ensure overall electroneutrality of the system. Any two charged species α and β interact additionally via the Coulomb interaction
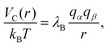 | (5) |
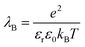 is set to λB = 7 Å. Water is treated as uniformly dielectric with dielectric constant εr = 80.
is set to λB = 7 Å. Water is treated as uniformly dielectric with dielectric constant εr = 80.
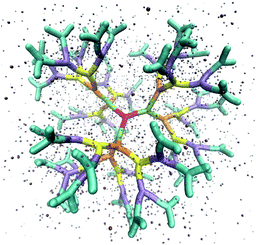
The above described model is used in Molecular Dynamics (MD) simulations, details of the latter are given in Methods. A representative simulation snapshot for a G6 dendrimer is shown in Fig. 3, where monomers pertaining to different subgenerations are presented by different colors.
It can be seen that the connections between successive branching points are rather rigid segments with a strong overlap between neighboring monomers, while the sticky ends (i.e., the segments pertaining to ssDNA belonging to the outermost subgeneration) show a less stiff behaviour. Counterions are found to be absorbed into the interior of the dendrimer to a high degree.
Methods
Here, we briefly specify some of the experimental as well as simulation techniques employed in this work.Experimental
DNA sequences and synthesis of DL-DNA
The DL-DNA nanostructures were fabricated following the synthetic procedure described in the reference,35 which is based on two assembly procedures: (a) self-assembly and (b) enzyme-assisted assembly. Briefly, DL-DNA was prepared from a core three-arm DNA junction (Y-DNA), having each arm terminated with a non-palindromic four-base-long sticky-end. We designate this Y-DNA as a first dendrimer generation (G1). To build up the next generation (G2), the above all-DNA tri-functional core was hybridized with three other Y-DNAs with sticky-ends complementary to the core Y-DNA. The cohesions points were enzymatically sealed using T4 DNA ligase (Promega). Additional generations (G3, G4, G5, etc.) were created by repeatedly ligating Y-DNAs to the sticky-ends of the previous generation. The Y-DNA building block is synthesized by annealing of three partially complementary single-stranded DNAs (ssDNAs) at equal molar ratio, employing a one-pot approach. Purification of excess DNA was performed using a combination amicon ultra spin columns as well as dialysis.The sequences of DNA strands used to create the DL-DNA constructs are slightly modified compared to those reported in reference35 in order to minimize the total number of different strands necessary for synthesizing all-DNA dendrimers up to the 6th generation. The sequences of DNA strands were designed using the program SEQUIN.55 All DNA strands used in this study were purchased from Integrated DNA Technologies, Inc. (http://www.idtdna.com), phosphorylated at their 5′-end, and purified by denaturing polyacrylamide gel electrophoresis. The DNA strand concentrations were determined by measuring the absorbance at 260 nm with a micro-volume spectrometer (NanoDrop 2000).
DNA sequences and construction scheme for synthesizing the all-DNA dendrimers used in this study are listed below. The bold letters correspond to sticky-end sequence and p indicates the position of the phosphate modification.
DNA strand sequences:
□ Y1a: 5′-p-TGAC TGGATCCGCATGACATTCGCCGTAAG-3′
* Y2a: 5′-p-GTCA TGGATCCGCATGACATTCGCCGTAAG-3′
◊ Y3a: 5′-p-ATCG TGGATCCGCATGACATTCGCCGTAAG-3′
Δ Y4a: 5′-p-GCAA TGGATCCGCATGACATTCGCCGTAAG-3′
□ Y1b: 5′-p-TGAC CTTACGGCGAATGACCGAATCAGCCT-3′
* Y2b: 5′-p-CGAT CTTACGGCGAATGACCGAATCAGCCT-3′
◊ Y3b: 5′-p-TTGC CTTACGGCGAATGACCGAATCAGCCT-3′
Δ Y4b: 5′-p-GTCA CTTACGGCGAATGACCGAATCAGCCT-3′
□ Y1c: 5′-p-TGAC AGGCTGATTCGGTTCATGCGGATCCA-3′
* Y2c: 5′-p-CGAT AGGCTGATTCGGTTCATGCGGATCCA-3′
◊ Y3c: 5′-p-TTGC AGGCTGATTCGGTTCATGCGGATCCA-3′
Δ Y4c: 5′-p-GTCA AGGCTGATTCGGTTCATGCGGATCCA-3′
DL-DNA construction scheme:
1st generation DL-DNA: G1 = Y1 = Y1a + Y1b + Y1c
2nd generation DL-DNA: G2 = G1 + 3 × Y2,
where Y2 = Y2a + Y2b + Y2c
3rd generation DL-DNA: G3 = G2 + 6 × Y3,
where Y3 = Y3a + Y3b + Y3c
4th generation DL-DNA: G4 = G3 + 12 × Y4,
where Y4 = Y4a + Y4b + Y4c
5th generation DL-DNA: G5 = G4 + 24 × Y5,
where Y5 = Y1a + Y2b + Y2c
6th generation DL-DNA: G6 = G5 + 48 × Y6,
where Y6 = Y3 = Y3a + Y3b + Y3c
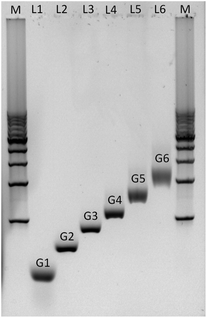
Agarose gel electrophoresis was employed to confirm the successful assembly of all-DNA dendrimers. As shown in Fig. 4, the desired DL-DNA constructs migrate as single bands, showing decreasing mobility with increasing generation. The disparity in the sharpness of the bands is likely to be a result of the increased flexibility of the larger dendrimers, which can explore a variety of confirmations, leading to a diffuse band. The G1 band is likely more diffuse due to having moved further through the gel.
Light scattering experiments
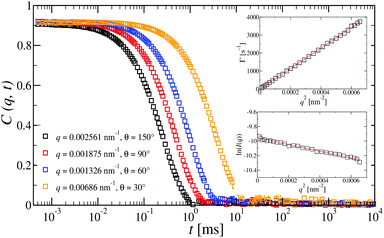
Dynamic light scattering (DLS) and static light scattering (SLS) experiments were performed by employing an ALV goniometer setup equipped with an helium–neon laser operating at λ = 632.8 nm. The effective hydrodynamic radii of the DL-DNA constructs in dilute aqueous solutions at different conditions of salinity (NaCl) were measured with DLS. The Brownian motion of the DL-DNA molecules was recorded in terms of the time auto-correlation function of the polarized light scattering intensity, G(q,t), using an ALV-5000 multi-tau digital correlator. The measurement consisted of obtaining the intermediate scattering (field) function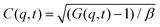 at several scattering wave vectors q = (4πn/λ)(sin(θ)/2), where β is an instrumental factor related to the spatial coherence constant and depends only on the detection optics, n the refractive index of the solvent, and θ the scattering angle. C(q, t) was analyzed via an Inverse Laplace Transform (ILT) using the CONTIN algorithm56 and the average relaxation time was determined from the peak of the distribution of relaxation times. The translational diffusion coefficient, D = Γ/q2, was found to be q-independent (Γ is the measured relaxation rate). The hydrodynamic radius was extracted from the measured diffusion coefficient D assuming validity of the Stokes–Einstein relation, RH = kT/6πηD (k is the Boltzmann constant, T the absolute temperature, and η the solvent viscosity) for spherical objects, (see Fig. 5).
at several scattering wave vectors q = (4πn/λ)(sin(θ)/2), where β is an instrumental factor related to the spatial coherence constant and depends only on the detection optics, n the refractive index of the solvent, and θ the scattering angle. C(q, t) was analyzed via an Inverse Laplace Transform (ILT) using the CONTIN algorithm56 and the average relaxation time was determined from the peak of the distribution of relaxation times. The translational diffusion coefficient, D = Γ/q2, was found to be q-independent (Γ is the measured relaxation rate). The hydrodynamic radius was extracted from the measured diffusion coefficient D assuming validity of the Stokes–Einstein relation, RH = kT/6πηD (k is the Boltzmann constant, T the absolute temperature, and η the solvent viscosity) for spherical objects, (see Fig. 5).
The radius of gyration Rg of the higher DL-DNA generations was extracted from SLS experiments in very dilute aqueous solutions. The scattered intensity of the solution Isol, the solvent Isolv, and the pure toluene Itol were recorded over an angular range from 15° to 150° corresponding to scattering vector q in a range of 3.46 × 103 < q < 2.55 × 102 nm−1. The pure toluene was used as a scattering-angle-independent standard to account the dependence of the scattering volume on the scattering angle. Thus, the scattered intensity I of the DLDNA particles was determined as follows: I(q) = (Isol(q) − Isolv(q))/Itol(q). The Rg was obtained from SLS experiments by performing a Guinier plot: ln(I(q)) = ln(I(0)) − (q2Rg2)/3. All experiments reported here were performed at room temperature.
Simulation
To simulate the behaviour of the above described macromolecular system with given interactions we employ molecular dynamic (MD) simulations. Simulations are performed using two independent platforms, namely ESPResSo57,58 and LAMMPS.59 The time step used is Δt = 10−3τ, where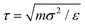 , so that the total running time of the simulations extends over 100 ns (i.e., over 109 simulation steps). The box size is chosen to keep the total particle density, ρp, independent of dendrimer generation. This number density is set to the value of ρp = 5 × 10−7 Å−3 in order to avoid self-interaction via periodic boundaries while keeping the box size small at the same time.
, so that the total running time of the simulations extends over 100 ns (i.e., over 109 simulation steps). The box size is chosen to keep the total particle density, ρp, independent of dendrimer generation. This number density is set to the value of ρp = 5 × 10−7 Å−3 in order to avoid self-interaction via periodic boundaries while keeping the box size small at the same time.
Canonical ensemble is applied and periodic boundary condition are applied. The evaluation of electrostatic interactions is performed using the Ewald summation method60 and the multilevel summation method61,62 (MSM) for ESPResSo and LAMMPS, respectively, with a relative force accuracy of 10−5. Langevin thermostat is chosen and set to preserve the temperature of T = 298 K. We use 1000 snapshots of a simulation run over 0.1 μs (after equilibration) of a single DL-DNA molecule to obtain results that follow.
Results and discussion
Comparison between experiment and simulation
The overall size of the dendrimer can be characterized by its radius of gyration Rg or its hydrodynamic radius RH. In principle, these quantities can be determined in simulations; they are also experimentally accessible by means of different scattering techniques, e.g., SANS, SAXS, or dynamic light scattering. However, in this contribution, we only calculate the radius of gyration, Rg, from simulated systems via the following expression: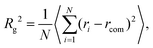 | (6) |
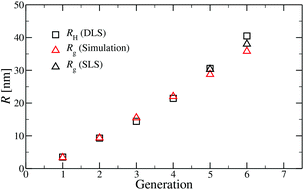
A comparison of the results originating from experiment, RH, and simulation, Rg, is presented in Fig. 6. For G1 to G5 the results of Rg and RH show excellent agreement, indicating the appropriateness of the underlying model. The two sets of data show small discrepancies for DL-DNAs of higher generations, i.e., for G6 DL-DNAs; therefore, we show here also experimental values of Rg for G5 and G6 DL-DNAs. As experiments show, for G5 DL-DNAs the radius of gyration coincides with the hydrodynamic radius Rg = RH, which on the other hand, fits nicely with the obtained simulation value. This matching between results of static and dynamic light scattering for G5 justifies our choice of comparing two different quantities that characterize the size of a dendrimers of lower generation numbers. We observe that both the experimental and simulation data exhibit a concave shape as function of generation index, reflecting the non-linear growth of the dendrimer with increasing generation number. This feature can be explained by the observed increase of the molecules’ sphericity with the growing monomer density at the periphery of the DL-DNA. As the sphericity of the dendrimer increases, as it is the case for G6 DL-DNAs, the ratio between the experimentally measured radius of gyration and the hydrodynamic radius deviates from 1 and goes toward smaller values, i.e., Rg/RH = 0.94. For the sake of comparison, the theoretical value of this ratio is 0.778 for a homogeneous hard sphere64 and 1.0 for hollow spheres with an infinitely thin shell.65 Therefore, the significant discrepancy observed between the experimental RH and Rg obtained from simulation for G6 DL-DNAs and probably also for higher generations becomes reasonable and one has to employ static light scattering in order to obtain better agreement with the results of the performed simulations.
Conformational analysis
A more detailed analysis of the form factor Fmm(q) of the dendrimer provides a deeper insight into the structural properties of the dendrimer. The form factor is defined as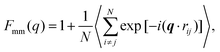 | (7) |
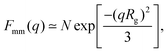 | (8) |
An overview of the results for Fmm(q) from simulation is given in Fig. 7, where this function is shown on different scales. As eqn (8) implies, the form factor becomes equal to the total number of monomers of the molecule in the limit of small wave vectors, i.e., for q → 0. Further, we observe oscillations in Fmm(q) for qσ ∼ 10−1; the first local minimum becomes more pronounced with increasing generation index, signifying that these larger molecules possess a more spherical shape and that the sharpness of the molecules’ boundary at the outermost shell increases. The rigidity of the dsDNA strands within the molecule reflects in the large wave-vector behaviour of Fmm(q), namely, the form factor satisfies the law Fmm(q) ∼ q−1 in the limit of large wave vectors.63 This is the typical scaling law for scattering from rigid rods, which is in contrast to flexible dendrimers, which usually scale with ∼q−4 in the same range of q, according to Porod's law.67 This outcome can be better understood in the context of scattering from fractal aggregates: it can be shown68 that for arbitrary systems of scatterers the scattering intensity Fmm(q) scales with the wave vector as
| Fmm(q) ∼ (qR)−2Dm+Ds for R−1 < q < a−1, | (9) |
| Fmm(q) ∼ (qRg)−D for qRg > 1, | (10) |
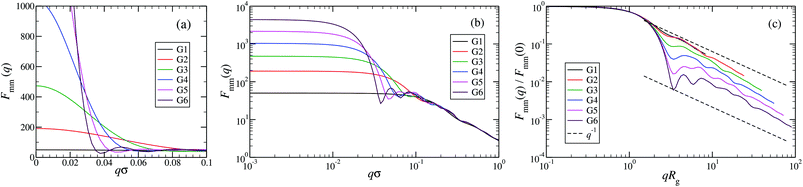 | ||
| Fig. 7 The form factor Fmm(q) of the DL-DNAs of generation G1 to G6 (as labeled) obtained from simulations, given as a function of the dimensionless wave-vector. Data are shown: (a) on a linear scale; (b) on a double-logarithmic scale; and (c) on a double-logarithmic scale with limq→0Fmm(q) rescaled to 1. The dashed lines in panel (c), i.e., Fmm(q) ∼ q−1, correspond to the typical scaling law for the scattering from rigid rods63 for large q-values. | ||
Additional insight into the conformational features of DL-DNAs can be acquired by analyzing the monomer–monomer pair correlation function. In Fig. 8 the radial distribution function gmm(r) for DL-DNAs of generations G1 and G5 is plotted as a function of the distance r, given in units of the equilibrium bond length lb. The well-defined maxima which occur at equidistant positions indicate that the bonds between the monomers are rather stiff. The first and largest peak represents the nearest neighbour separation along the Y-DNA arms. The height of the maxima scales with r−2, which is the rate at which the volume of the spherical shells increases. The two curves of gmm(r) are identical for G1 and G5 in this regime.
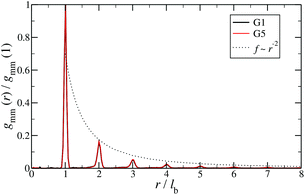 | ||
| Fig. 8 Monomer–monomer radial distribution function gmm(r) for DL-DNAs of generations G1 and G5 plotted as functions of distance r, given in units of the equilibrium bond length lb. | ||
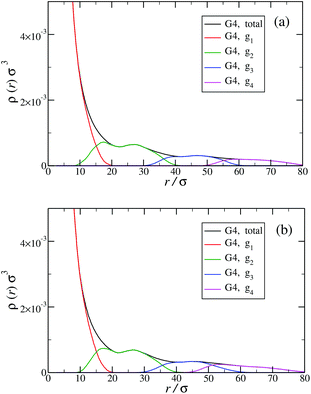
Another quantity that provides detailed information about the complex internal structure of DL-DNAs is the density profile of the constituents of the macromolecule with respect to the center of mass of the dendrimer:
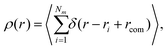 | (11) |
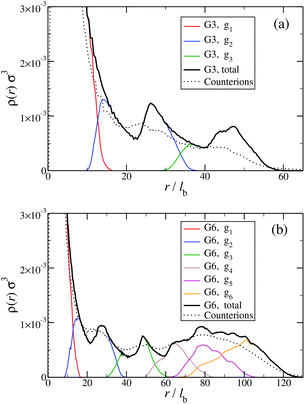
The counterion density distribution closely follows the monomer density due to the system's propensity towards local charge neutrality and the spatial structure of the counterions is less pronounced due to an entropic ‘smearing out’ of the profiles. Overall, we obtain, especially for higher generations, almost flat-density molecules, whose monomer- and counterion-profiles are tunable by varying the generation index, GN. Contrary to the usual, dense-core, flexible dendrimers,67,72 the monomer profile of the DL-DNA does not monotonically drop as one moves from the center of the molecule towards its periphery, but it remains rather flat and constant (with modulations close to the junction points). Moreover, these nanostructures feature very low local monomer packing in their interior, ρ(r)σ3 ∼ 10−3 (see Fig. 9), as opposed to typical values ρ(r)σ3 ∼ 1 for flexible dendrimers.67 Accordingly, they offer a great deal of empty space (voids) in their interior, capable of accommodating smaller molecules, such as a G1-dendrimer, as demonstrated in Fig. 10. Due to their ‘uniform-density’ interior, DL-DNA constructs are also suitable for an analytical description using the Poisson–Boltzmann theory,73,74 since the constant ion density inside the molecule simplifies analytical calculations.
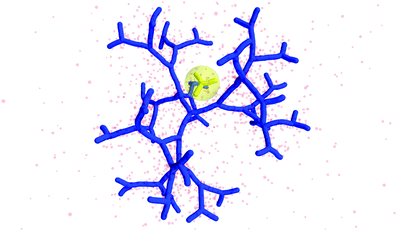 | ||
| Fig. 10 Simulation snapshot of G5 DL-DNA. The encircled G1 DL-DNA is inserted to the figure to guide the eye to better visualization of the void size. | ||
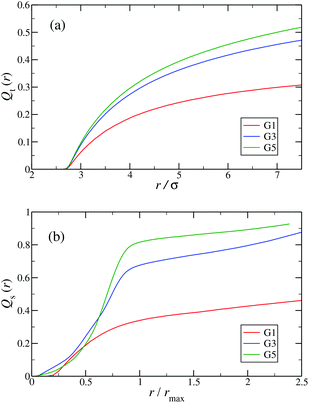
In the following, a more detailed analysis of the counterion condensation is presented. In our investigation we have encircled each arm of the individual Y-DNA elements by a tube of radius r; we have then counted the percentage of ions Qt(r) captured in those cylinders. The dependence of Qt(r) on the tube radius r is depicted in Fig. 11(a). Even though the considered system is electro-neutral, a difference in the value of Qt(r) of approximately 20% between G1 and G5 dendrimers can be observed for tube radii larger than 3rM−C+. This observation is a direct consequence of an increase in the available volume provided by the larger dendrimers. The same effect can be seen in Fig. 11(b), where the total amount of counterions absorbed by the dendrimers is shown, expressed via function Qs(r). When the radius of the sphere r that encircles the dendrimer exceeds the size of the dendrimer rmax only 40% of counterions are absorbed by a G1 DL-DNA, whereas this percentage grows with increasing dendrimer generation number and approaches 90% in the case of a G5 DL-DNA. It is also worth noticing that the transition of the counterion profile from the interior to the exterior becomes increasingly sharp as the dendrimer generation index grows: accordingly, high-G DL-DNA's act as osmotic dendrimers, in full analogy with the osmotic polyelectrolyte stars,75–77 which capture the counterions in their interior. However, in contrast to these, DL-DNA's are very robust against salinity, maintaining their size essentially unaffected by addition of large quantities of monovalent salt, as it will be shown in what follows.
In Fig. 12 the probability of the nearest junction-to-junction separation of successive subgenerations gi and gi+1 within a G6 DL-DNA is shown as a function of distance given in units of bond length. Since each branch extending from junction to junction point consists of 30 monomers, the peak of this function is located slightly above 29lb for the innermost branches and its position decreases monotonically as one moves away toward the exterior of the molecule, (i.e., towards the outer subgroups) while the variance increases at the same time. The shrinkage of bond lengths belonging to the outer branches is a consequence of osmotic swelling which tends, on one hand, to stretch central (inner) branches, while on the other hand, it allows a slightly higher flexibility of the branches belonging to higher subgenerations. To understand the physics behind this, we need to consider the osmotic pressure from the counterions trapped in the interior of the molecule, which tries to swell the dendrimer by exercising an outward force at a fictitious spherical surface of radius rmax that surrounds the molecule, touching the free tips of the outermost Y-junctions (composed of 4-bases long ssDNA). This force is transmitted to the interior of the dendrimer, but the number of Y-junction tips among which it is partitioned is halved each time the subgeneration index decreases by one. Accordingly, the innermost generations are pulled more strongly than the outermost ones; thus they are more rigid, more straight-line looking. This effect is also observable in the simulation snapshot (see Fig. 3), where it can be seen that the innermost branches are more rigid, having the shape of a straight line, while the branches belonging to the outermost subgenerations expose a more wiggly behaviour. This interpretation is corroborated by the analysis of angular fluctuations in what follows.
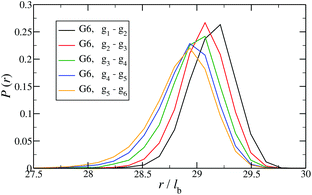 | ||
| Fig. 12 Probability for the nearest junction-to-junction separation of successive subgenerations gi and gi+1 within a G6 DL-DNA given in units of the equillibrium bond length lb. | ||
In order to analyze the internal freedom of the typical conformations of the dendrimers, we measure in the simulations two kinds of bond angles, namely ϕ and θ, for the individual subgenerations. Here, ϕ is defined, according to eqn (3), as the angle between two consecutive bonds within a Y-arm; it is consequently a reliable measure of the rigidity of the Y-DNA arms. The angles θi (i = 1, 2, 3), on the other hand, are defined as the angles between the vectors pointing along the three arms of the Y-DNA, whereby an arm vector is defined as the vector connecting the first and last monomer of a specific Y-DNA arm, i.e., the arm is assumed to be fully rigid. Each Y-DNA element is characterized by three of these angles: θ1, θ2, and θ3. For fully rigid connections between successive Y-junctions in the dendrimer, one would find ϕ = π and θi = 2π/3 for all i.
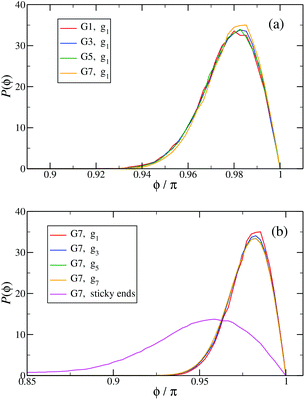
In Fig. 13(a) the probability distribution P(ϕ) of the angle ϕ for the innermost generations, g1, is shown for DL-DNAs of different generation index. The distributions all exhibit a pronounced maximum close to the value of a fully rigid dendrimer, i.e., ϕ ≅ π. This feature again demonstrates that the interactions of our model tend to keep the monomer chains straight. A slight but visible enhancement of the peak (i.e., a reduction of the fluctuations) can be seen for the G7 dendrimer. This indicates, that its inner generation is more stretched and thus more straight as the number of generation grows. This feature is one manifestation of the increased osmotic stretching force from the counterions. If we focus on a G7 molecule and look at the stretching of the various generations gi within the G7 DL-DNA, Fig. 13(b), a similar trend can be observed: the distribution is rather sharply peaked close to the angle ϕ = π, pointing to stretched connections between the junction points. Again, one can notice that the probability distribution P(ϕ) for higher subgenerations displays a ‘leakage’ to smaller ϕ-values, indicating that the branches belonging to the outermost subgenerations are more flexible compared to the innermost branches, which is consistent with the finding on the inter-bonding separation (see Fig. 12) and our interpretation of its physical origin. In addition, we also show in Fig. 13(b) the probability distribution of angle ϕ corresponding to those parts of the chains that are characterized as a sticky-end. As it is expected, the function spreads over a wider range of possible conformational angles, reflecting the fact that sticky ends exhibit a significantly more flexible behaviour.
Fig. 14 shows the corresponding probability distributions P(θi) for the angles θi (i = 1, 2, 3), for DL-DNAs of different generation index. In particular, in Fig. 14(a) we focus on the innermost generation, g1, of various GN-dendrimers and we do not distinguish between the three angles θi, i = 1, 2, 3, since their distributions coincide by symmetry. The distinction is being made in Fig. 14(b), for which we collected statistics of outer angle θ3 and inner angles θ1,2 to determine the three individual distributions Pi(θ) for the three angles denoted in the insets. Here, we can see that the most probable angle of the innermost subgeneration, g1, of dendrimers of different generations is centered around θi = 2π/3, confirming the rigidity of the Y-branches. However, the width of these distributions increases with decreasing generation number GN, as the amplitude of the fluctuations in θi correlates negatively with the size of the dendrimer branch attached to the corresponding arm. With growing generation number, the number of branches grows more rapidly, so that the fluctuations in the angle θ become less probable due to the reduced available volume and the restrictions due to the mutual electrostatic repulsions between the different arms. When examining the distributions of different subgenerations within a G7 DL-DNA, Fig. 14(b), the emergence of differently centered peaks of P(θ3) and P(θ1,2) for the corresponding intermediate subgenerations can be observed.
This phenomenon can be explained by the deformation of Y-DNAs from a conformation with θi = 2π/3, i = 1, 2, 3, into a configuration with θi > 2π/3, with i = 1, 2, and θ3 < 2π/3. This change is caused by the monomers pertaining to the outer (inner) generations that pull (push), respectively, monomers of the intermediate subgenerations outwards via steric and electrostatic interactions. This phenomenon does not occur for Y-DNAs of the last subgeneration, i.e., g7 in the examined case, as these Y-DNAs are not constrained by subgenerations of higher index.
Finally, in Fig. 15 the distribution P(θΣ) is shown for a G7 DL-DNA, where 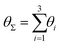 . The data provide evidence that the Y-DNA of the innnermost subgeneration, whose arms are subject to outward forces caused by the subsequent generations, is almost completely planar, i.e., θΣ ≈ 2π. With increasing generation index, however, the Y-DNAs’ deviation from the planar configuration becomes more pronounced, i.e., θΣ < 2π. Underlying to this behaviour are two opposite effects: Coulomb repulsion and the aforementioned outward forces drive the Y-DNAs towards a planar configuration, but at the same time this planarity reduces the number of configurations available to the Y-DNAs and therefore their entropy. As we proceed to the outermost generations, the branches of the Y-junctions have more freedom to fluctuate and entropic contributions become enhanced, enabling fluctuations of the Y-junctions that deviate from planarity.
. The data provide evidence that the Y-DNA of the innnermost subgeneration, whose arms are subject to outward forces caused by the subsequent generations, is almost completely planar, i.e., θΣ ≈ 2π. With increasing generation index, however, the Y-DNAs’ deviation from the planar configuration becomes more pronounced, i.e., θΣ < 2π. Underlying to this behaviour are two opposite effects: Coulomb repulsion and the aforementioned outward forces drive the Y-DNAs towards a planar configuration, but at the same time this planarity reduces the number of configurations available to the Y-DNAs and therefore their entropy. As we proceed to the outermost generations, the branches of the Y-junctions have more freedom to fluctuate and entropic contributions become enhanced, enabling fluctuations of the Y-junctions that deviate from planarity.
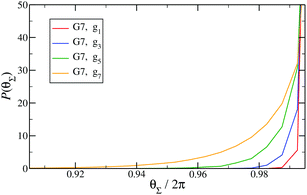 | ||
Fig. 15
P(θΣ), i.e., the probability distribution of the sum of the three junction angles θΣ of the individual subgenerations within a G7 DL-DNA (as labeled). P(θΣ) is normalized as 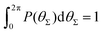 . . | ||
Influence of salt on conformational properties of DL-DNA
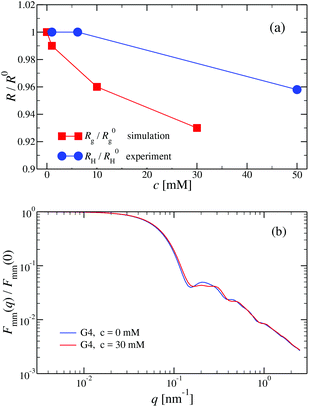
We have also analyzed the effect of a finite salt concentration (NaCl) on the overall size of the dendrimer. The experiments are performed for different values of salt concentrations, extending from a low salt regime (c = 0.1 mM) up to very high salt concentrations (c ≈ 5 M). Due to numerical limitations, only salt concentration up to c ≈ 30 mM could be considered in simulations. Results for the hydrodynamic radius, as obtained from the experiment, are summarized in Fig. 16. By adding salt essentially no change in the size of the dendrimer is observable up to a concentration of c = 10 mM.This observation is confirmed in the simulations (see Table 3). The absence of any significant shrinking at low salt concentrations is the consequence of the rigidity of the molecule, i.e., the high persistence length. In order to overcome the stiffness of the molecule, one has to proceed to higher salt concentrations, i.e., above c = 10 mM; under such conditions the screening of the charge of the molecule starts to affect the Coulomb interaction between the monomers, inducing thereby the shrinking of the molecule. This reduction in size is more pronounced for higher dendrimer generations and it can range from approximately 10% to 15% for extremely high salt concentrations (i.e., c ∼ 1 M). Throughout, the decrease of RH is generation-dependent and the critical salt concentration at which the molecule starts to shrink differs from generation to generation.The inset of Fig. 16 shows the comparison of the experimental results for the radius of gyration and for the hydrodynamic radius of G6 DL-DNA under the change of salt concentration. Both quantities show the same trend but with slightly more expressed shrinkage of RH over Rg.
We have performed simulations of G4 DL-DNA for various values of salt concentration, and the resulting radius of gyration as a function of salt concentration is given in Fig. 17(a). The comparison with the hydrodynamic radius obtained from experiments is also shown. From simulation, we observe the shrinking of the molecule by approximately 7% when varying the salt concentration from c = 1 mM to c = 30 mM, while the experiments show the shrinkage by approximately 5% when varying the salt concentration from c = 1 mM to c = 50 mM. In Fig. 17(b) we present the form factors, comparing two sets of simulation data corresponding to different salt regimes. The curves unambiguously demonstrate that the added salt does not have any impact on the rigidity of the dendrimer, i.e., in the regime of large wave vectors the form factor satisfies the above mentioned q−1 scaling law irrespective of the salt concentration. From these data one can conclude that the Coulomb interactions do stretch the bonds between the monomers, but the related effect is subdominant when compared to the role that rigidity has in suppressing significant changes in bond lengths.
The shrinking of flexible, charged polymers upon addition of salt can be physically traced back to the screening of the electrostatic interaction or to the enhanced osmotic pressure from the co- and counterions at the exterior of the macromolecule.76 For the case at hand, it is not clear that the same physical mechanism is at work, since the shrinkage is minimal and the molecular architecture is different. To shed light into the mechanism behind the size reduction of the nanoparticle, we look at the density profiles with and without salt. In Fig. 18(a) and (b), the monomer density profile for a G4 DL-DNA is shown for the salt-free case and for a NaCl salt solution of concentration c = 30 mM, respectively. One can notice that the only difference between corresponding monomer profiles under different salt conditions appears for the outermost subgeneration g4. In the salt solution enhanced backfolding of the outermost branches arises, resulting in the small shrinkage of the dendrimer's radius of gyration, observed at Fig. 17(a). The interior of the dendrimer remains unaffected by the added salt, an additional manifestation of the combined effect of rigidity and branched architecture of the novel DL-DNA constructs. These are remarkably resistant macromolecules, which nevertheless feature a very low internal monomer concentration, allowing them to absorb counterions or smaller molecules in their interior. In addition, whereas salinity is expected to affect the effective interactions between such dendrimers, practically it does not affect their sizes and shapes, rendering them thus as prime candidates for molecules with tunable, ultrasoft effective repulsions.
Conclusions
We have investigated the structural properties of DL-DNA at a single particle level with sizes ranging from G1 to G7. Additionally, we probed the salt-responsiveness of the complex nanostructure of said molecules with regards to backfolding of dendritic arms, providing a thorough investigation of the structural properties of these all-DNA nanostructures. Through a combination of experiments and molecular modeling we provide an advancement of our understanding of such dendritic DNA constructs, which is essential for developing applications and investigating novel phenomena related to this type of soft material.In colloidal polymer network terms, the high-G DL-DNA and ionic microgels share some common characteristics. Both, highly permeable to solvent molecules, can act as efficient absorbers of their own counterions under salt-free conditions, and at a very coarse-grained level their internal structure has a core–shell morphology. However, our results revealed that the DL-DNA's scaffold architecture and its inherent rigidity grant these all-DNA nanostructures with low internal monomer concentration, regular voids in their interior and, at the same time, a resilience against the addition of salt; intriguing and promising features which are absent in ionic microgels and which are expected to have significant impact on the dendrimers’ collective behaviour. More specific, experimental as well as computational results show that varying the salt concentration only minimally affects the conformation and does not cause any backfolding of dendritic arms. This low salt-responsiveness allows for adjusting the effective interaction between different DL-DNA molecules without the dendrimers collapsing or their structure deforming significantly. In addition, the monomer density profiles revealed that high-G DL-DNA are dendrimers with almost flat density and internal cavities with generation-independent size. The cavity space, located at the dendrimer's center of mass, was found to be comparable to the size of G1, implying that the void interior can be engineered at subnanometer precision (at the level of a single level) by simply adjusting the arm length of the Y-DNA building block belonging to the first generation; thus allowing full control over the degree of dendrimer interpenetrability. We believe that the above properties make these highly charged tailored empty-core/shell nanostructures ideal candidates for exploring novel forms of self-assembly such as cluster crystallization in the bulk. The current work sets the pivotal point for the investigation on the many-body properties of concentrated DL-DNA systems, which will be the subject of the future work.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work has been supported by the Austrian Science Fund (FWF) under grant number I 2866-N36 and by the Deutsche Forschungsgemeinschaft (DFG) under grant number STI 664/3-1. Computation time at the Vienna Scientific Cluster (VSC) is gratefully acknowledged.References
- N. C. Seeman, J. Theor. Biol., 1982, 99, 237–247 CrossRef CAS.
- A. V. Pinheiro, D. Han, W. M. Shih and H. Yan, Nat. Nanotechnol., 2011, 6, 763–772 CrossRef CAS.
- N. C. Seeman and H. F. Sleiman, Nat. Rev. Mater., 2017, 3, 17068 CrossRef.
- N. R. Kallenbach, R. Ma and N. C. Seeman, Nature, 1983, 305, 829–831 CrossRef CAS.
- T. J. Fu and N. C. Seeman, Biochemistry, 1993, 32, 3211–3220 CrossRef CAS.
- E. Winfree, F. Liu, L. A. Wenzler and N. C. Seeman, Nature, 1998, 394, 539–544 CrossRef CAS.
- Y. He, T. Ye, M. Su, C. Zhang, A. E. Ribbe, W. Jiang and C. Mao, Nature, 2008, 452, 198–201 CrossRef CAS.
- P. W. Rothemund, Nature, 2006, 440, 297–302 CrossRef CAS.
- S. M. Douglas, H. Dietz, T. L. B. Högberg, F. Graf and W. M. Shih, Nature, 2009, 459, 414–418 CrossRef CAS.
- Y. Ke, L. L. Ong, W. M. Shih and P. Yin, Science, 2012, 338, 1177–1183 CrossRef CAS.
- S. M. Douglas, J. J. Chou and W. M. Shih, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6644–6648 CrossRef CAS.
- Y. Sannohe, M. Endo, Y. Katsuda, K. Hidaka and H. Sugiyama, J. Am. Chem. Soc., 2010, 132, 16311–16313 CrossRef CAS.
- C. Steinhauer, R. Jungmann, T. L. Sobey, F. C. Simmel and P. Tinnefeld, Angew. Chem., Int. Ed., 2009, 48, 8870–8873 CrossRef CAS.
- R. Jungmann, M. S. Avendaño, J. B. Woehrstein, M. Dai, W. M. Shih and P. Yin, Nat. Methods, 2014, 11, 313–318 CrossRef CAS.
- Y. Suzuki, M. Endo, Y. Katsuda, K. Ou, K. Hidaka and H. Sugiyama, Nat. Commun., 2015, 6, 8052 CrossRef CAS.
- J. Zheng, J. J. Birktoft, Y. Chen, T. Wang, R. Sha, P. E. Constantinou, S. L. Ginell, C. Mao and N. C. Seeman, Nature, 2009, 461, 74–77 CrossRef CAS.
- A. Kuzyk, R. Schreiber, Z. Fan, G. Pardatscher, E. M. Roller, A. Högele, F. C. Simmel, A. O. Govorov and T. Liedl, Nature, 2012, 483, 311–314 CrossRef CAS PubMed.
- G. P. Acuna, F. M. Möller, P. Holzmeister, S. Beater, B. Lalkens and P. Tinnefeld, Science, 2012, 338, 506–510 CrossRef CAS.
- W. Ma, L. Xu, A. F. de Moura, X. Wu, H. Kuang, C. Xu and N. A. Kotov, Chem. Rev., 2017, 117, 8041–8093 CrossRef CAS.
- A. Udomprasert, M. N. Bongiovanni, R. Sha, W. B. Sherman, T. Wang, P. S. Arora, J. W. Canary, S. L. Gras and N. C. Seeman, Nat. Nanotechnol., 2014, 9, 537–541 CrossRef CAS PubMed.
- D. N. Selmi, R. J. Adamson, H. Attrill, A. D. Goddard, R. J. C. Gilbert, A. Watts and A. J. Turberfield, Nano Lett., 2011, 11, 657–660 CrossRef CAS PubMed.
- N. D. Derr, B. S. Goodman, R. Jungmann, A. E. Leschziner, W. M. Shih and S. L. Reck-Peterson, Science, 2012, 338, 662–665 CrossRef CAS PubMed.
- F. Praetorius and H. Dietz, Science, 2017, 335, 5488 CrossRef PubMed.
- E. S. Andersen, M. Dong, M. M. Nielsen, K. Jahn, R. Subramani, W. Mamdouh, M. M. Golas, B. Sander, H. Stark, C. L. P. Oliveira, S. Pedersen, V. Birkedal, F. Besenbacher, K. V. Gothelf and J. Kjems, Nature, 2009, 459, 73–76 CrossRef CAS.
- F. Praetorius, B. Kick, K. L. Behler, M. N. Honemann and H. Dietz, Nature, 2017, 552, 84–87 CrossRef CAS.
- F. Romano and F. Sciortino, Phys. Rev. Lett., 2015, 114, 078104 CrossRef PubMed.
- S. Biffi, R. Cerbino, F. Bomboi, E. M. Paraboschi, R. Asselta and F. S. T. Bellini, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15633–15637 CrossRef CAS.
- F. Bomboi, F. Romano, M. Leo, J. Fernandez-Castanon, R. Cerbino, T. Bellini, F. Bordi, P. Filetici and F. Sciortino, Nat. Commun., 2016, 7, 13191 CrossRef CAS.
- M. Salamonczyk, J. Zhang, G. Portale, C. Zhu, E. Kentzinger, J. T. Gleeson, A. Jakli, C. D. Michele, J. K. G. Dhont, S. Sprunt and E. Stiakakis, Nat. Commun., 2016, 7, 13358 CrossRef CAS.
- M. Siavashpouri, C. H. Wachauf, M. J. Zakhary, F. Praetorius, H. Dietz and Z. Dogic, Nat. Mater., 2017, 16, 849–856 CrossRef CAS.
- Y. G. Li, Y. D. Tseng, S. Y. Kwon, L. D'Espaux, J. S. Bunch, P. L. McEuen and D. Luo, Nat. Mater., 2004, 3, 38–42 CrossRef CAS PubMed.
- D. Yang, M. R. Hartman, T. Derrien, S. Hamada, D. An, K. G. Yancey, R. Cheng, M. Ma and D. Luo, Acc. Chem. Res., 2014, 47, 1902–1911 CrossRef CAS.
- T. Zhou, P. Chen, L. Niu, J. Jin, D. Liang, Z. Li, Z. Yang and D. Liu, Angew. Chem., Int. Ed., 2012, 51, 11271–11274 CrossRef CAS.
- Y. G. Li, Y. T. H. Cu and D. Luo, Nat. Biotechnol., 2005, 23, 885–889 CrossRef CAS PubMed.
- S. H. Um, J. B. Lee, S. Y. Kwon, Y. Li and D. Luo, Nat. Protoc., 2006, 1, 995–1000 CrossRef CAS.
- Y. H. Roh, K. Lee, J. J. Ye and D. Luo, Methods Mol. Biol., 2014, 1143, 159–179 CrossRef CAS PubMed.
- S. H. Um, J. B. Lee, N. Park, S. Y. Kwon, C. C. Umbach and D. Luo, Nat. Mater., 2006, 5, 797–801 CrossRef CAS PubMed.
- H. M. Meng, X. Zhang, Y. Lv, Z. Zhao, N. N. Wang, T. Fu, H. Fan, H. Liang, L. Qiu, G. Zhu and W. Tan, ACS Nano, 2014, 8, 6171–6181 CrossRef CAS PubMed.
- C. N. Likos, Soft Matter, 2006, 2, 478–498 RSC.
- C. N. Likos, R. Blaak and A. Wynveen, J. Phys.: Condens. Matter, 2008, 20, 494221 CrossRef.
- D. A. Lenz, B. M. Mladek, C. N. Likos, G. Kahl and R. Blaak, J. Phys. Chem. B, 2011, 115, 7218–7226 CrossRef CAS PubMed.
- D. A. Lenz, B. M. Mladek, C. N. Likos, G. Kahl and R. Blaak, J. Chem. Phys., 2016, 144, 204901 CrossRef PubMed.
- A. Wynveen and C. N. Likos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 80, 010801 CrossRef PubMed.
- A. Wynveen and C. N. Likos, Soft Matter, 2009, 6, 163–171 RSC.
- P. S. Crozier and M. J. Stevens, J. Chem. Phys., 2003, 118, 3855 CrossRef CAS.
- K. Kegler, M. Salomo and F. Kremer, Phys. Rev. Lett., 2007, 98, 058304 CrossRef CAS PubMed.
- K. Kegler, M. Konieczny, G. Dominguez-Espinosa, C. Gutsche, M. Salomo, F. Kremer and C. N. Likos, Phys. Rev. Lett., 2008, 100, 118302 CrossRef PubMed.
- C. G. Baumann, S. B. Smith, V. A. Bloomfield and C. Bustamante, Proc. Natl. Acad. Sci. U. S. A., 1997, 94, 6185–6190 CrossRef CAS.
- J. R. Wenner, M. C. Williams, I. Rouzina and V. A. Bloomfield, Biophys. J., 2002, 82, 3160–3169 CrossRef CAS PubMed.
- H. M. Berman, W. K. Olson, D. L. Beveridge, J. Westbrook, A. Gelbin, T. Demeny, S. H. Hsien, A. R. Srinivasan and B. Schneider, Biophys. J., 1992, 63, 751–759 CrossRef CAS PubMed.
- A. Wynveen, D. J. Lee, A. A. Kornyshev and S. Leikin, Nucleic Acids Res., 2008, 36, 5540–5551 CrossRef CAS PubMed.
- J. F. Marko and E. D. Siggia, Macromolecules, 1995, 28, 8759–8770 CrossRef CAS.
- B. Tinland, A. Pluen, J. Sturm and G. Weill, Macromolecules, 1997, 30, 5763–5765 CrossRef CAS.
- H. Chen, S. P. Meisburger, S. A. Pabit, J. L. Sutton, W. W. Webb and L. Pollack, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 799–804 CrossRef CAS PubMed.
- N. C. Seeman, J. Biomol. Struct. Dyn., 1990, 8, 573–581 CrossRef CAS PubMed.
- S. W. Provencher, Comput. Phys. Commun., 1982, 27, 213–227 CrossRef.
- A. Arnold, K. Breitsprecher, F. Fahrenberger, S. Kesselheim, O. Lenz and C. Holm, Entropy, 2013, 15, 4569–4588 CrossRef.
- H. J. Limbach, A. Arnold, B. A. Mann and C. Holm, Comput. Phys. Commun., 2006, 174, 704–727 CrossRef CAS.
- S. Plimpton, J. Comp. Physiol., 1995, 117, 1–19 CrossRef CAS.
- P. P. Ewald, Ann. Phys., 1921, 369, 253–287 CrossRef.
- D. J. Hardy, M. A. Wolff, J. Xia, K. Schulten and R. D. Skeel, J. Chem. Phys., 2016, 144, 114112 CrossRef PubMed.
- D. J. Hardy, Z. Wu, J. C. Phillips, J. E. Stone, R. D. Skeel and K. Schulten, J. Chem. Theory Comput., 2015, 11, 766–779 CrossRef CAS PubMed.
- N. J. Wagner, L. M. Walker and B. Hammouda, Macromolecules, 1995, 28, 5075–5081 CrossRef CAS.
- G. S. Grest, L. J. Fetters, J. S. Huang and D. Richter, Advances in Chemical Physics, 1996, vol. 94, pp. 67–163 Search PubMed.
- S. U. Egelhaaf and P. Schurtenberger, J. Phys. Chem., 1994, 98, 8560–8573 CrossRef CAS.
- A. Guinier and G. Fournet, Small angle scattering of X-rays, J. Wiley & Sons, New York, 1955 Search PubMed.
- I. O. Götze and C. N. Likos, Macromolecules, 2003, 36, 8189–8197 CrossRef.
- C. M. Sorensen, Aerosol Sci. Technol., 2001, 35, 648–687 CrossRef CAS.
- R. Blaak, S. Lehmann and C. N. Likos, Macromolecules, 2008, 41, 4452–4458 CrossRef CAS.
- S. Huißmann, A. Wynveen, C. N. Likos and R. Blaak, J. Phys.: Condens. Matter, 2010, 22, 232101 CrossRef PubMed.
- H. M. Harreis, C. N. Likos and M. Ballauff, J. Chem. Phys., 2003, 118, 1979 CrossRef CAS.
- M. Ballauff and C. N. Likos, Angew. Chem., Int. Ed., 2004, 43, 2998–3020 CrossRef CAS PubMed.
- J. S. Kłos, Phys. Chem. Chem. Phys., 2018, 20, 2693–2703 RSC.
- T. Colla, C. N. Likos and Y. Levin, J. Chem. Phys., 2014, 141, 234902 CrossRef PubMed.
- A. Jusufi, C. N. Likos and H. Löwen, Phys. Rev. Lett., 2002, 88, 018301 CrossRef CAS PubMed.
- A. Jusufi, C. N. Likos and H. Löwen, J. Chem. Phys., 2002, 116, 11011 CrossRef CAS.
- J. Zhang, M. P. Lettinga, J. K. G. Dhont and E. Stiakakis, Phys. Rev. Lett., 2014, 113, 268303 CrossRef PubMed.
Footnote |
| † These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |