Open Access Article
Open Access ArticleResolving complex hierarchies in chemical mixtures: how chemometrics may serve in understanding the immune system
Gerjen Herman
Tinnevelt
 * and
Jeroen Jasper
Jansen
* and
Jeroen Jasper
Jansen

Radboud University, Institute for Molecules and Materials, (Anaytical Chemistry), Heyendaalsweg 135, Nijmegen, Netherlands. E-mail: chemometrics@science.ru.nl
First published on 6th February 2019
Abstract
In immunology, the resolution of complex chemical mixtures familiar from omics, comes with an added layer of hierarchy: bioactive immunological surface markers are embedded on the cell membranes of e.g. white blood cells. Therefore, each blood sample actually consists of a comprehensive mixture of cells. The cells need to be resolved based on their surface marker chemistry, to investigate their involvement in an immune response. This mixture may be measured on a single-cell level with Multicolour Flow Cytometry (MFC). Finding such cellular and molecular markers is of the utmost academic and diagnostic importance. Several advanced data analysis methods therefore aim to meet the considerable data challenge of resolving such cell mixtures. These multivariate methods are more resource-efficient than the manual analysis of MFC data, called sequential gating, but also likely provide additional biomedical insight compared to the conventional bivariate approach. To compare such methods more comprehensively than has been done until now, we have developed a list of criteria on how each method recovers the information on both the cell and the underlying molecular levels on an MFC sample of an asthma patient. We compare these methods for the chemometric data analysis commonly used in metabolomics. This shows that all compared methods have their own advantage in recovering the sequential gating results, giving insight into the limitations of sequential gating, providing insight into the chemical relationships between cells within the mixture and resolving information related to chemical heterogeneities between cells. We furthermore show how comparative analyses of different samples may lead to further insight into the subdivision of cells into different types based on their immunological involvement in asthma development, and how sparsity—a currently popular method to enhance the discriminative ability of multivariate models—may reduce the insight into the underlying hierarchical variability in cell chemistry. Although developed for cytometry, the presented chemometrics will be highly valuable to many more chemical systems where hierarchical arrangement of the molecules plays a crucial role.
Introduction
Advances in analytical technology have led to considerably broader and deeper insight into biomedical systems. Omics technologies have greatly increased the breadth of molecular species,1 simultaneously interrogated for disease involvement. Immunology, however, has focused on the analysis of mixtures of protein molecules expressed on the surface of specific cells,2 to assess their role within the immune system. The true value of such analytical technologies only comes forward in the translation of the relatively abstract data they provide, e.g. spectra or chemical profiles, into evidence-based biomedical decision support. Such translation affects the interpretation of the result, which is essential for the end-user to understand how a specific model may support research or treatment decisions.Capture of the considerable diversity in surface protein expression on a mixture of single cells requires separate analysis of the quantitative surface protein expression on each individual cell in e.g. a blood sample. Multicolor Flow Cytometry (MFC) may perform this in high-throughput3,4 by measuring fluorescently conjugated antibodies specifically attached to the surface proteins on the membranes of white blood cells. A laser then excites every cell, which was previously brought into a laminar flow of thousands to millions of cells. The measured fluorescence is then a quantitative readout of the targeted surface protein expression on each cell.
MFC may be used to detect the pedigrees of white blood cell types that exist within the immune system. Identification takes place by a relatively small number of around 250 surface proteins,2 where, currently, standard MFC technology allows the simultaneous measurement of eight—although this number is consistently being increased through technological innovations.5–7 The variability in the quantity and quality of the surface proteins on a cell, however, gives rise to a considerable diversity in both known and unknown cell types, making flow cytometry a potential member of the omics family as a profiling or fingerprinting technology.8
Multicolor flow cytometry, therefore, generates data with a hierarchy of information: the measured molecular mixture on each cell determines its identity, ‘type’, while the number of cells of that type—in combination with all other cell types—determines the activity of the immune system. Understanding the system requires an understanding of how many cells of each type it contains and how much of every surface protein they express, also compared to other samples.
Data from an MFC sample is conventionally analyzed by so-called ‘gating’: arranging cells into pre-specified types by sequentially setting thresholds on each surface protein expression, either alone or in selected bivariate combinations.9 This provides fractions of each cell type within each sample that may be tested e.g. between the control and clinical phenotype samples. Manual gating is therefore resource-intensive, potentially subjective, and expertise-dependent. It precludes analyses of more than two proteins simultaneously and thereby limits the discovery of novel, as yet unknown, cellular activity, as is the objective in omics. The discovery of hitherto unknown systematic continua in protein expression in cells that until then were believed to belong to a group of cells with homogeneous protein expression requires more efficient and automated methods that are less-reliant on prior information.
This need has led to a number of high-impact publications on quantitative methodologies for MFC data10–12 that show the strength of machine learning to cluster the single-cell MFC data into aggregates that align with different cell types. They make extensive use of the recent developments in data science and bioinformatics. However, the connection to the considerable data analysis expertise in metabolomics is sparse. Some authors13 even explicitly dismiss the contributions of chemometric methods, such as principal component analysis, to the systemic analysis of omics data. The chemometrics expertise in the quantitative processing of mass spectrometry and nuclear magnetic resonance spectroscopy data may, however, be both insightful and powerful in resolving chemical variability. Chemometrics is very strong in validation, visualization and data preprocessing. We have recently introduced the hierarchical perspective essential for MFC in the Discriminant Analysis of MultiAspect Cytometry (DAMACY)14 method, with which the abundance of cell types can be systematically compared between samples.
In this paper, we explore the ways in which manual sequential gating, machine learning and chemometrics compare, and show complementary strength in the analyses of the hierarchies of MFC data, to resolve molecular and cell mixtures into insightful contributions to the immune system. We compare SPADE, FlowSOM, t-SNE and PCA biplots, by evaluating how they reproduce sequential gating. Comprehensive assessment and comparison of unsupervised models is challenging. It may be facilitated by an error free ‘golden standard’. Such a comparison was done in FlowCAP.15 However, FlowCAP only quantitatively compares these models based on heuristic measures but not on how well the models are interpreted and how they extract information from the data. We base our analysis on comparisons with sequential manual gating, in terms of resolution, cluster size, recovery of rarer cell types and systematic heterogeneity in surface protein expressions. We use a representative asthma sample from an MFC analysis for the immune response associated to asthma.
Moreover, we evaluate how these methods provide complementary information on the cell composition, in terms of finding a mismatch in the sequential gating where only univariate or bivariate combinations are used instead of the whole multivariate space and in terms of finding new cell subtypes or cellular heterogeneity. Finally, we compare how these methods provide chemical insight in terms of the relationship between proteins or cell clusters, and whether the methods have a heuristic measure of the quality of the model.
In the second part, we compare all samples from the asthma study by calculating the percentage of each cell type found with sequential gating of each individual and subsequently performing multiple two sample t-tests or PCA and compare this with the multivariate method DAMACY and Citrus16 in terms of finding all the relevant discriminating cell (sub)types and describing the complete cellular heterogeneity.
Material and methods
Resolving cell mixtures in an MFC study involves two separate operations: first, the different cells need to be differentiated based on their chemical surface protein profiles. Then, the role of these mixture constituents in a biomedical study needs to be further studied in a comparison between MFC samples. Several approaches are available for both operations.Resolving the cells within an MFC sample
Chemometrics: principal component analysis and partial least squares
Chemometrics is the research field that develops quantitative data analyses for chemical analytical technologies.22 It has proven essential for systematic insight into chromatographic, spectroscopic and otherwise multivariate chemical data and is considered a cornerstone of metabolomics.23Principal Component Analysis (PCA)24 for exploratory analysis and Partial Least Squares (PLS)25 for multivariate regression and discrimination are essential tools for metabolomics. A PCA model results in scores of every sample on the most prominent multivariate correlations between the chemical features measured on the samples in principal components. The loadings express these correlations and indicate correlations between the features. Combinations between the scores and loadings may indicate how these correlations associate to specific samples. The principal components are orthogonal and fit as much variation in the original data as possible. Partial Least Squares Discriminant Analysis (PLS-DA), together with various helpful methodological extensions, employs a similar approach of dimension reduction to predict a class membership (e.g. control or clinical phenotype) for every sample.26
Like cluster-based methods, PCA and PLS are multivariate. This enables prediction of sample properties from relatively large numbers of correlated predictor features, which provides an alternative to the lasso regularized regression used in Citrus:16 for PLS the number of samples in the data restricts the maximum number of features that may be simultaneously identified as biomarkers—although the simplicity of the lasso-imposed sparsity may exceed this simplicity further. However, another concomitant advantage that is also highly important to explore the data with PCA, is the increase in resolution between samples that the linear correlations between predictors may bring, compared to t-tests of the separate features, the ‘multivariate advantage’.27 This has received relatively little attention in the literature.
Linear methods like PCA (and PLS) do, however, come with significant benefits in interpretation and model validation, also for MFC data. The correlation structure between surface protein expressions in the loadings may be simultaneously represented with the PCA scores of every cell. A model of e.g. two PCs may closely resemble the t-SNE map in ordinating each single cell (see Fig. 6) but PCA provides direct feedback to the expression of each protein, and the relationships between proteins, through the loadings that serve as calibrated axes through the biplot map. The loadings may thereby serve as a compass-like guide to show which antibody expressions are most variable and which are highly correlated—indicating co-expressions. They also show on which cells and cell clusters within the MFC sample this co-expression is most prominent. The linearity of PCA also allows the calculation of which percentage of the variation in the original data is represented in the schematic representation, which is at least not-yet available for t-SNE, SPADE and FlowSOM.
Comparing MFC samples
The results from a sequential Boolean gating for a case–control study may be compared by a two sample t-test. This then indicates which cell type fractions are significantly different between the two groups, see Table 2. Alternatively, the resulting fractions from the gating may be analyzed with PCA, see Fig. 7.9 This however relies on sequential Boolean gating with its inherent drawbacks. Therefore, we compared two methods that use the more informative methods to analyze cell mixtures to find hierarchies through which surface proteins drive cellular disease biomarkers.The method first builds a PCA model on the cells from all samples, weighting each MFC sample with the number of cells it contains and applying appropriate centering, to avoid dominance of samples with more cells in the model. As far as we know, DAMACY was the first method to apply such a correction. Instead, some methods use down sampling with the risk of losing important rare cell (sub)types.
The single-cell scores per sample are then transformed into 2D smoothed histograms, of which the bins may be compared between samples. This comparison is then performed with OPLS-DA,26 of which the predictions serve as estimators for class membership and the weights of each bin extracted from the 2D PCA plot may be evaluated for a higher or lower abundance of the corresponding cells for either the control or clinical phenotype individuals, see Fig. 9.14 The loadings from the cell-level PCA biplot may then serve as guides to interpret the surface marker co-expressions on these differentiating bins. We validated the model with the same double cross validation as used in Citrus.
The asthma MFC data set
The data set contains 15 asthma patients (aged 22–78,![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 57) and 10 healthy controls (aged 25–57,
= 57) and 10 healthy controls (aged 25–57, ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) = 40), who were recruited at the respiratory outpatient clinics of the Churchill Oxford University Hospital, UK.37 The study received ethical approval, and written informed consent was obtained. After inclusion, patients filled out symptom questionnaires, sputum induction was performed, blood was taken, and patients underwent FeNO measurements and lung functional testing. All patients were receiving appropriate asthma treatment at the time of blood withdrawal. The blood cells were stained with a panel of 8 antibodies including CD3, CD4, CD8, CD14, CD16, CRTH2 (CD294), CD123 and CD193. After staining, the red blood cells were lysed using a FACS Lysing solution (Becton Dickinson). The cells were measured on a LSR Fortessa flow cytometer (Becton Dickinson). Only single cells were included by using the correlation between the forward scatter (FSC) maximum height and the FSC area under the curve. Debris was removed by setting a minimum threshold based on FSC. The data was compensated to correct for the fluorophore overlap, using a manually optimized compensation matrix following the principles described by Roederer et al.38 The data was preprocessed by applying an arcsinh transformation with cofactor 150 and subsequently autoscaling either using the mean and standard deviation of the one specific asthma patient or of all individuals together corrected for the number of cells measured in each individual.
= 40), who were recruited at the respiratory outpatient clinics of the Churchill Oxford University Hospital, UK.37 The study received ethical approval, and written informed consent was obtained. After inclusion, patients filled out symptom questionnaires, sputum induction was performed, blood was taken, and patients underwent FeNO measurements and lung functional testing. All patients were receiving appropriate asthma treatment at the time of blood withdrawal. The blood cells were stained with a panel of 8 antibodies including CD3, CD4, CD8, CD14, CD16, CRTH2 (CD294), CD123 and CD193. After staining, the red blood cells were lysed using a FACS Lysing solution (Becton Dickinson). The cells were measured on a LSR Fortessa flow cytometer (Becton Dickinson). Only single cells were included by using the correlation between the forward scatter (FSC) maximum height and the FSC area under the curve. Debris was removed by setting a minimum threshold based on FSC. The data was compensated to correct for the fluorophore overlap, using a manually optimized compensation matrix following the principles described by Roederer et al.38 The data was preprocessed by applying an arcsinh transformation with cofactor 150 and subsequently autoscaling either using the mean and standard deviation of the one specific asthma patient or of all individuals together corrected for the number of cells measured in each individual.
Results and discussion
White blood cells from asthma patients (and controls) are analyzed for the quantitative expression of eight surface proteins. Although this data is collected with the current standard in multicolor flow cytometry, the findings may be expected to project directly to e.g. mass cytometry39 and to emerging technologies like single-cell metabolomics.40 None of the advanced data analysis techniques are intrinsically limited to a specific number of features. The study focuses on the identification of different cell types, differentiated by the immunological activity of the selected surface proteins.The chemical resolving power of multivariate analysis
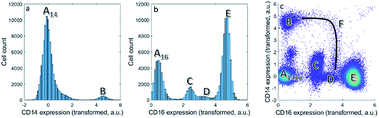
We first focus on one set of cell types within the asthma blood samples: the monocytes. These expressions for a specific MFC sample may be represented as histograms (Fig. 1a and b). Expression of CD14 shows division into two cell populations, we call them here A14 and B. Expression of CD16 shows a division of the cells into four cell populations by similar, visual distinction of expression levels. These four populations we indicate as A16, C, D and E. Populations A14 and A16 are the negative populations that do not, or very slightly, express the surface protein. Naturally, the CD14 histogram does not show whether cells in population B also belong to populations A16, C, D or E: it ignores that expression if both surface proteins occur on the same cells.The bivariate density scatter plot (Fig. 1c) shows the combined expression of both surface proteins on each cell within the sample: the combined expression of both surface proteins resolves the cells A16 into a fraction of cells from A14 and the classical monocytes B that highly and very reproducibly express CD14. In combination with the expression of CD16, A14 may be subdivided into the cells that express very little of CD14 (population A1416 in Fig. 1c). A14 also has contributions from eosinophils (C), non-classical monocytes/natural killer cells (D) and neutrophils (E) with consistent, yet increasing, CD16 expression. Although somewhat trivial, this shows that the combination between two markers reveals more about the surface protein co-expression in these populations.
Combining CD14 and CD16 also reveals the intermediate monocytes F, a relatively small cell fraction (0.8%) that could not be observed in the expression of either separate surface protein, but resolves itself in the bivariate combination of CD14 and CD16. Contrary to the distinct populations A–E, cells F form a heterogeneous non-linear continuum in CD14 and CD16 expression that ranges between the classical and non-classical monocytes (B and D). The existence of this continuum is known,41 but its presentation in different models may show their potential to discovery similar, as-yet unknown, continua.7
Although cell populations C–E may already be identified as somewhat resolved peaks in CD16, they still overlap to a certain degree—specifically populations C and D. This shows that combining surface protein may also increase the resolution in unmixing cells into different populations. In fact, cell population D contains two distinct populations that may only be resolved by adding information on additional surface proteins in subsequent steps of the sequential gating.
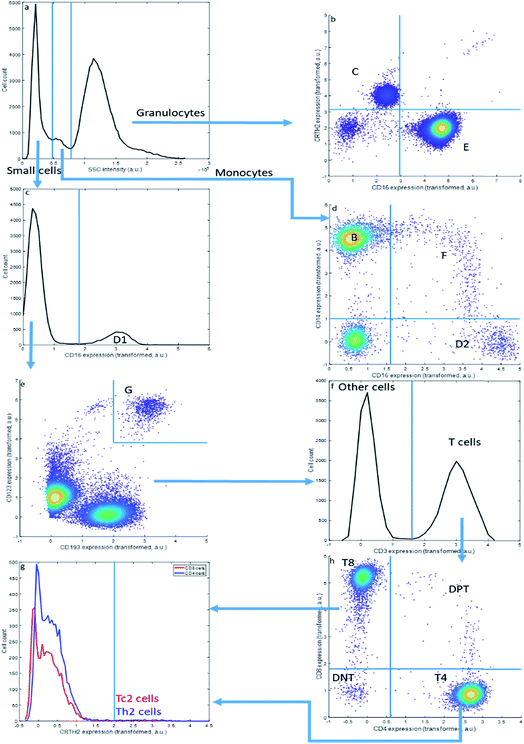
Sequential Boolean gating of the asthma data (Fig. 2) resolves fourteen cell types. The cell types (C–E) may be first distinguished into small cells, monocytes and granulocytes, based on the Sideward SCatter (SSC) of each cell, a parameter representative of cell granularity (Fig. 2a). Subsequently, they can be divided in eosinophils (C), neutrophils (E), NK cells (D1), non-classical monocytes (D2), intermediate monocytes (F) and classical monocytes (B) based on CD16 and CD14 expression. The SSC alone may not perfectly resolve these populations.
This gating strategy results in a subdivision of all cells into the fourteen cell types that could be observed in the asthma data by this approach (Table 3) into fractions for the specific representative sample in Fig. 1 and 2. The sample contains a very high fraction of neutrophils, high fractions of monocytes, eosinophils, CD8 and CD4 T cells, and considerably smaller fractions of basophils, Th2 cells, Tc2 cells, double negative T cells and double positive T cells; all of these cells are, however, important to characterize asthma. The same gating may be performed for all other samples from the same asthma data set, thresholds may even be slightly altered to accommodate a slight shift in thresholds. Of specific relevance here is the sideward scatter, having a much poorer reproducibility between samples than the surface protein expressions. We therefore omitted this feature, as well as the front scatter of each cell, from the quantitative comparisons between MFC analyses presented further.
Although widely used, sequential bivariate gating has serious drawbacks: gating thresholds need to be set manually, using prior biological knowledge or experience, which both introduces arbitrariness and is highly resource-intensive. Gating the asthma data is also limited to interpreting four out of the 28 potential bivariate combinations, which makes it greatly hypothesis driven; even more so when more than eight surface proteins would have been interrogated. Thirdly, the approach does not scale beyond co-expressions of two surface proteins, which limits the resolution of cells defined on the simultaneous expression of more than two surface proteins. Semi-automated methods to define gating thresholds42 do not necessarily improve resolution between different cell populations, due to this bivariate limitation.
Multivariate resolving of the cell mixture within an MFC sample
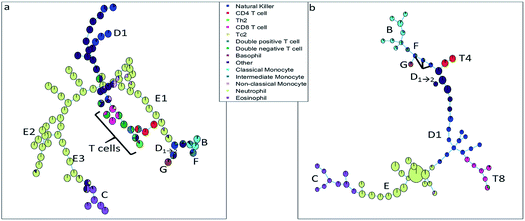
The SOM (Fig. 3a) clearly resolves several sequentially gated populations into distinct nodes (eosinophils, natural killer cells, other cells, neutrophils) and the number of nodes associated with each population corresponds to the fraction of those populations in the blood sample. However, as the model aims to describe all cells well, it will focus on describing the most abundant populations. Many nodes contain exclusively neutrophils and are therefore similar, but do show a systematic heterogeneity, namely increasing sideward scatter in E1, E2 and E3 upon further inspection. Several smaller populations (e.g. monocytes, T cells), especially those with surface protein expressions that do not differ much from other populations, are not resolved into separate nodes. Moreover, the tree does not show how the intermediate monocytes (F) form the continuum between both other monocyte types (located at B and D1→2, respectively), as observed in Fig. 1c. This may be likely solved by increasing the number of nodes to e.g. better resolve the monocyte and T cell branch. However, adding more nodes also makes the tree less-well interpretable and there is no heuristic for the model quality other than compliance to sequential gating.Although the tree may for large parts be well-interpreted, several inconsistencies appear. A group of natural killer cells (D1→2) is located near the intermediate monocytes (F) and classical monocytes (B) at the right-most end of the tree. Further inspection shows that the current sequential gating strategy may introduce an error caused by the limiting resolving power of the sideward scatter, see Fig. 2a. Several cells identified as natural killer cells (D1) are, in fact, non-classical monocytes (D2). For the same reason, the ‘non-classical monocytes’ near the neutrophils (E1) may be small neutrophils. The SOM is thus able to discover mismatches in the sequential gating as it is able to use the ‘multivariate advantage’.
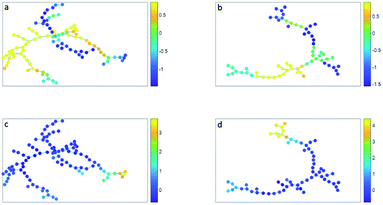
The minimum spanning tree representation in Fig. 3a focuses on how the method reconstructs the sequential gating and does not give any view on the surface protein expression, but the same tree may be colored for average expressions of specific surface proteins (Fig. 4a and c). The tree may have maxima for specific surface proteins (e.g. CD14 for the classical monocytes), but there may be multiple non-connected nodes for which expression is high, like for CD16. Investigating co-expression between proteins is thus limited, because you have to compare the nodes in Fig. 4a with Fig. 4c to find the relationship between CD14 and CD16.
The SOM model needs to describe all surface protein variability simultaneously, which is reflected here in how both branches orient towards each other: basophils (G) and eosinophils (C) are highly similar as they both belong to the granulocyte class, but the minimum spanning tree puts the basophils (G) on the same branch as the monocytes (B and D1→2). In other words, the proximal nodes may be related but the distance between the neighboring nodes may be very large, thus investigating the similarity between nodes is limited.
The SPADE tree of the same representative asthma sample (Fig. 3b) shows that preprocessing with density-dependent down sampling leads to a tree with different characteristics to that from the SOM. The high-abundant neutrophils (E) and eosinophils (C) occupy a much more similar number of nodes as lower-abundant cells (CD8 T cells (T8), NK cells (D1) and monocytes (B and F)) compared with SOM. In SPADE, the number of cells for each cell type is related to the number of nodes and the cluster node area. SPADE resolves cell types well into cell type-specific nodes, even those that are lower-abundant. The continuum of the intermediate monocytes between the classical and non-classical monocytes is reflected in SPADE, although F overlaps with D1→2 and the classical monocytes (B). However, the down sampling removes rarer cell populations such as Tc2 and Th2 cells. Not removing these rare cells is also not wanted as that would result in a model which is very sensitive to outliers.
The tree, however, also gives reflection onto the sequential gating performance. Again, one of these NK cell (D1→2) groups may be wrongly gated as non-classical monocytes (D2).
The representation of the SPADE cluster nodes with the minimum spanning tree suffers from the same limitations as the tree based on the SOM cluster nodes. Namely, the surface protein co-expressions may also only be observed by separate surface protein-based tree representations, see Fig. 4b and d. Also SPADE deems the similarity of the basophils (G) to the monocytes more important than their high similarity to the eosinophils. Moreover, it splits CD4 (T4) and CD8/CD3DN (T8) into separate branches. Thus, the similarity between cluster nodes is limited.
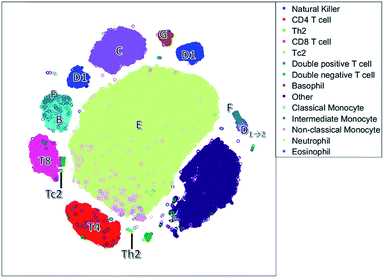
Unlike the cluster nodes of FlowSOM and SPADE, the t-SNE map (Fig. 5) represents each single cell, although the model then aggregates similar cells into distinct clusters. The large neutrophil cluster (E) is surrounded by clusters of other cell populations. Rare cell types, such as Th2 cells and basophils (G), have their own compact cluster. Tc2 cells are next to CD8 cells (T8). The cluster area in t-SNE may be determined by the number of connected cells and their heterogeneity caused by biological or measurement variation in surface protein expression, and therefore may not be attributed to both the number of and heterogeneity between cells.
The continuum of the intermediate monocytes (F) between classical monocytes (B) and wrongfully gated NK cells (D1→2) is represented in two dispersed clusters, corresponding to both continuum endpoints (Fig. 1c). Furthermore, both endpoints are placed at opposite ends of the non-linear map, which does not reflect their similarity in the surface protein expression. Also, in the t-SNE map, surface protein co-expression is not explicitly modelled and may only be revealed by coloring each cell with the expression level of a specific surface protein.
The NK cells split into three clusters, again one cluster (D1→2) may be wrongly gated as non-classical monocytes, but a cluster on the left with a medium CD8 expression is also observed. This distinction between NK cells with very low CD8 expression and with a medium CD8 expression is not very common, but has been found earlier in humans after a bout of exercise.43 Thus, t-SNE may reveal additional information compared to the hypothesis driven approach of sequential bivariate gating. In hindsight, the SOM also describes these NK cells, however these cells are mixed with other cells and thus harder to interpret than in t-SNE.
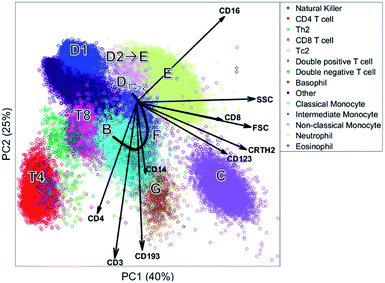
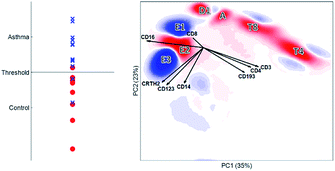
The biplot shows the first two principal components of the PCA model for this MFC sample (Fig. 6). These two PCs describe 65% of the total variation in surface marker expressions. PCA quantifies how well the model reproduces the original data, unlike the other compared methods. These two principal components show how all sequentially gated populations have distinct locations on the map, and some are well-resolved like CD4 (T4), basophils (G) and eosinophils (C). However, many populations—including the high-abundant neutrophils—overlap with cells from other populations. The size of the clusters observed in PCA is determined by the heterogeneity in surface protein expression, but not by the abundance of the cell population: the area covered by the neutrophils is only slightly larger than that of the eosinophils, although their abundance is much higher. This makes the discovery of rare cell populations like Th2 and Tc2 challenging without further visual aids. The continuum between the classical (B) and non-classical (D2) monocytes by the intermediate monocytes (F) is visible in the model, albeit requiring visual aids to highlight the relevant cells due to overlap. The shape of the continuum is somewhat distorted compared to Fig. 1c, but this may be explained by the non-orthogonal orientation of both PCA loadings: as PCA describes all cells, and co-expressions of CD14 and CD16 with all other markers, the continuum is partially recovered and may be chemically interpreted.
Although most cell populations overlap in the map, their proximity and location with respect to each other indicates linearly increasing surface protein expressions, a multivariate extension of sequential gating (Fig. 2). The model loadings (indicated as arrows in Fig. 6) serve as direction indicators to quantify surface marker co-expressions for each cell. For example, basophils (G) and eosinophils (C), positioned next to each other in the PCA biplot, have similar surface protein expressions on CD123, CRTH2 and CD193 as their loadings direct towards these cells. Eosinophils are higher in sideward scatter (SSC), forward scatter (FSC) and CD16 expression, as these loadings direct from G to C. Basophils (G) have above-average expressions of CD3, CD4 and CD14, although the contribution of CD14 is less, indicated by its considerably shorter loading arrow. Here, the heuristic of the percentage of variance explained (65%) also comes into play. For example, the scores of basophils and CD4 T cells for PC2 are similar, which would suggest that both cell types have above-average expression of e.g. CD4, CD3 and CD193. However, CD4 T cells are only high on CD3/CD4 and low/medium on CD193 and basophils vv: principal components 3 and higher will describe such contrasts as they still explain 35% of all variation in surface marker expression.
Table 1 shows an overview of the performance of the methods and Table 2 shows an overview of how each method recovers the sequential gating. The number of nodes in the SOM directly represents the number of cells per cell type. In SPADE, it is a combination between the node area and the number of nodes. In t-SNE, the cluster size is determined by the number of connected nodes and the cellular variability, and in PCA only by the cellular variability. In terms of distinguishing the cell types, t-SNE outperforms other methods as it is optimizing the local structure. SPADE is second best for the larger cell types, but, due to the down sampling, completely detrimental for rare cell types. In SOM and PCA, most cell (sub)types overlap, however this overlap does show the continuous intermediate monocytes F with PCA. The resolving power in t-SNE proved malign for these intermediate monocytes as these cells were counterintuitively split.
| Criteria | SOM | SPADE | t-SNE | PCA |
|---|---|---|---|---|
| Recovery of the sequential gating | ||||
| Size of cell type fractions | Very good | Reasonable | Poor | Poor |
| Resolution of cell types | Reasonable | Good | Very good | Reasonable |
| Rare cell types recovery | Reasonable | Poor | Very good | Poor |
| Continuous intermediate monocytes F | Poor | Reasonable | Poor | Good |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Complementary to sequential gating | ||||
| Sequential gating mismatch discovery | Very good | Very good | Very good | Very good |
| Complementary information on cell types | Heterogeneity in neutrophils | Not found | NK subtype that express CD8 | Surface protein co-expression |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Chemical insight | ||||
| (Co)-expression between proteins | Limited | Limited | Limited | Very good |
| Similarity between proximal clusters | Limited | Limited | No relationship | High relationship |
| Quality of the model | Not present | Not present | Not present | Variance explained per PC |
| Cell (sub)type | SOM | SPADE | t-SNE | PCA | |
|---|---|---|---|---|---|
| D1 | Natural killer | Good | Good | Good+ | Partly A |
| T4 | CD4 T cells | Partly DPT | Good | Good | Partly DPT |
| Th2 | Th2 cells | Partly mix | Missing | Good | Partly DPT/T4 |
| T8 | CD8 T cells | Partly DNT | Completely DNT | Partly DNT/Tc2 | Partly DNT/B/A |
| Tc2 | Tc2 cells | Completely mix | Missing | Partly T8 | Missing |
| DPT | Double positive T cells | Completely T4/DNT | Missing | Partly T4 | Completely T8/Th2 |
| DNT | Double negative T cells | Partly T8 | Completely T8 | Partly T8 | Partly T8 |
| G | Basophils | Partly A | Partly A | Good | Partly B/F |
| A | Other cells | Partly mix | Good | Good | Partly, D1/T8/D2 |
| B | Classical monocytes | Completely F/D2 | Completely F | Completely F | Partly, T8/F/D2/G |
| F | Intermediate monocytes | Completely B/D2 | Completely B/D2 | Partly B/D2 | Partly, B/D2/G |
| D2 | Non-classical monocytes | Completely mix | Completely F | Completely E/F | Completely F/B/E |
| E | Neutrophils | Good+ | Good | Partly D2 | Partly D2 |
| C | Eosinophils | Partly A | Good | Good | Good |
All methods were able to find the mismatched NK cells that were in fact non-classical monocytes. SOM was able to find a heterogeneity in eosinophils, t-SNE found two natural killer subsets and PCA finds surface protein co-expression. Thus, multivariate methods are able to find complementary information.
The principal component biplot ordinates the cells by linearly retaining the quantitative surface protein expressions, i.e. the cell chemistry, into a map constructed on the largest variation in these expressions. Mutual cell distances in the PCA biplot can be associated to quantitative differences in the surface protein expression throughout the map, via the surface protein loadings. This chemical insight is not directly extracted from the figures made by SOM, SPADE and t-SNE, but indirectly extracted when, for each surface marker, a new figure is plotted with the intensity of that surface marker, e.g. see Fig. 4.
PCA furthermore stands out in that it provides a heuristic approach to quantify the recovery of the data by the model, i.e. the variance explained per PC, which is very useful as a warning for over-interpreting the data.
These observations have been performed on only a single data set, but it is the first comparison of such detail among all these methods that we have come across. Additional criteria may be most relevant, where we have omitted that of calculation speed on purpose. Unmixing the cells into different types is, however, a task with a specific objective: this makes each method appropriate for a specific task.
Comparing MFC samples
The methods that were presented to resolve MFC samples into cell populations based on their multivariate surface protein expressions provide insightful views on the distribution of the cells across different types. However, in most applications of MFC technology, the comparison between samples, in e.g. a case–control study, is of primary interest to determine which populations vary between MFC samples and differ between sample groups.Although variability in cell abundances among both control and asthma samples may be considerable (Table 3), the study shows that neutrophils and eosinophils are significantly higher-abundant in asthma patients. Double negative T cells, CD4 and CD8 T cells, natural killer cells and ‘other cells’ are relatively lower-abundant in asthma patients. Note that the cell fractions are closed here to 100%: the chemometric expertise in the analysis of such data is available,44 but beyond the scope of this study.
| Cell (sub)type | Specific sample | Asthma | Control | p-Value | |
|---|---|---|---|---|---|
| DNT | Double negative T cells | 0.45% | 0.90 ± 0.48% | 2.41 ± 0.94% | 2.00 × 10−5* |
| E | Neutrophils | 57.29% | 63.96 ± 7.65% | 51.58 ± 7.80% | 6.60 × 10−4* |
| T4 | CD4 T cells | 6.03% | 8.29 ± 3.62% | 14.68 ± 4.62% | 7.70 × 10−4* |
| T8 | CD8 T cells | 4.14% | 4.56 ± 3.16% | 8.04 ± 2.14% | 5.90 × 10−3* |
| C | Eosinophils | 7.10% | 6.07 ± 4.40% | 2.32 ± 1.43% | 0.016* |
| D1 | Natural killer | 3.97% | 3.91 ± 1.65% | 6.11 ± 2.68% | 0.018* |
| A | Other cells | 14.96% | 5.29 ± 3.38% | 8.52 ± 2.85% | 0.021* |
| DPT | Double positive T cells | 0.14% | 0.54 ± 0.41% | 0.96 ± 0.59% | 0.044 |
| F | Intermediate monocytes | 0.81% | 0.80 ± 1.32% | 1.38 ± 0.93% | 0.049 |
| G | Basophils | 0.88% | 0.76 ± 0.38% | 0.51 ± 0.17% | 0.058 |
| D2 | Non-classical monocytes | 0.53% | 1.32 ± 1.98% | 0.46 ± 0.25% | 0.19 |
| Tc2 | Tc2 cells | 0.03% | 0.17 ± 0.31% | 0.05 ± 0.06% | 0.26 |
| Th2 | Th2 cells | 0.06% | 0.19 ± 0.09% | 0.21 ± 0.08% | 0.64 |
| B | Classical monocytes | 3.96% | 3.37 ± 0.80% | 3.44 ± 1.44% | 0.9 |
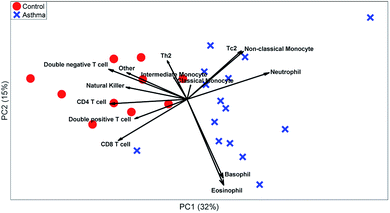
These t-tests give a relevant indication of which cell types are relevant. However, it ignores heterogeneity between individuals or multivariate relationships between the abundances of different cell types. A PCA biplot on the cell-type fractions within all MFC samples (see Fig. 7) already provides much deeper insight into the study. Systematic variation between asthma patients and control samples is the largest source of multivariate variability. The loadings show that most cell types are more abundant for the control than for the asthma samples, but that neutrophils are more abundant for all asthmatic patients, as its loading is directed towards the average of all asthma samples, which agrees with its t-test.
The PCA scores also show how the asthma patients are far more heterogeneous than the control individuals. One group of patients scores low on PC2 and therefore has a far above-average abundance of basophils and eosinophils (low on PC2), while another group scores high on PC2 due to a high abundance of Tc2 cells and classical monocytes (which include some erroneously gated small neutrophils). As the sample-level PCA model in Fig. 8 describes 46% of the variance in the data, PCs 3 and higher may contain even more such subgrouping. This heterogeneity among asthma patients may be the reason that basophils, non-classical monocytes and Tc2 cells do not show significant elevation for asthma patients (Table 3). However, treating each MFC sample as a fully resolved mixture of cells—analogous to an omics approach—reveals such individualized aspects of the disease.
Although the PCA model in Fig. 7 is very insightful, it still requires the expertise and resources of sequentially gating each MFC sample. A comparison using one of the automatically generated models from the previous section may be much more helpful.
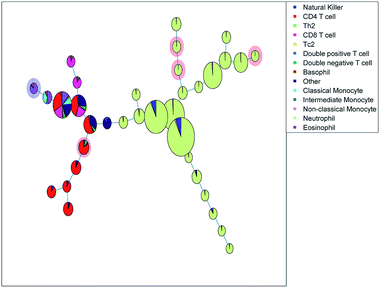
Citrus provided a diagnostic accuracy of 79.4%, using double cross validation. Five out of the 31 cluster nodes were included and highlighted in Fig. 8. One node with basophils and eosinophils was increased in the asthma patients, and a CD4 T cell subset and three neutrophil subsets are decreased in the asthma patients.
Using the same double cross validation as Citrus, we achieved an accuracy of 85.6% for the discriminant analysis using DAMACY (Fig. 9). DAMACY reveals which single cells within the PCA map are more or less abundant in the asthmatic patients. Two cell clusters (indicated as E1 and E3) are higher-abundant and five other cell clusters (E2, D1, A, T8 and T4) are less-occupied. The DAMACY map would suggest that cell cluster E3 could be eosinophils as the loadings CD16, CRTH2 and CD123 are pointing towards this cluster. However, cell clusters E1, E2 and E3 are neutrophils with increasing size by comparing these clusters to the manual gates and their original scatter intensity. Therefore, our hierarchical analysis of the immune system with DAMACY shows additional cell subtyping that could not be resolved by gating separate samples, either sequentially or with the automated methods compared before.
The classification accuracies of 79–86% for both methods are considerable. Although the population-level PCA model (Fig. 7) would allow a seemingly better linear separation between asthma and control samples, both classification accuracies are reported for unseen data and the PCA model validity is limited to the samples in the current data set.
DAMACY shows a direct relationship between surface proteins, cells, cell types and patients: for example, above-average co-expression of CD16 together with CRTH2, CD123 and CD14 is associated with cells that cluster into a ‘big neutrophil’ cell type (E3). This type is higher-abundant together with the small neutrophils (E1), which together are part of the multicellular biomarker for asthma: this increase is more severe for asthma patients with higher disease predictions (Fig. 9, left panel).
DAMACY showed that asthma patients have more ‘small’ (E1) and ‘big’ neutrophils (E3) and less normal-sized neutrophils (E2). Citrus only finds three neutrophil nodes that contain less cells in the asthma patients than in the controls. Table 2 shows that the overall neutrophil population is significantly increased for asthma, but the descent to the single-cell level finds intricacies and heterogeneities within cell populations that aid discrimination between MFC samples and is therefore potentially invaluable to understand asthma.
Apart from the eosinophils (C), DAMACY retrieves all cell types that sequential-based t-tests also found. Citrus came to a similar classification accuracy, needing only the populations that decrease in abundance (together with a single basophil node that DAMACY did not find as higher-abundant). This sparsity is directly aligned with Occam’s razor and therefore statistically favorable. For the analysis of (any type of) omics data, imposing sparsity should be treated with caution. Especially in binary classifications, highly generic or less-informative features may be sufficiently discriminative to reach a certain classification accuracy. This statistically sound limitation is, however, counterproductive for the objective of omics studies, which is the retrieval of all biomolecules associated with a specific biochemical process.
General discussion
Although the data used throughout this study has been carefully collected, measured and preprocessed, all observations are specific for this data set. The study thereby focuses on immunophenotyping, i.e. resolving mixtures of different cell types. Other applications of MFC focus more on the activation of specific cell types, or comparing samples of an individual for different time-points, which might show different results for a similar critical comparison. Secondly, we limited our analyses to the implementation of the methods as they are available in the literature. In principle, quality characteristics could be devised to evaluate how SPADE, FlowSOM and t-SNE recover the original data but this requires further research. Another interesting extension would be the hybridization of different methods, e.g. using t-SNE for DAMACY or the SPADE down sampling in the other methods.In principle, the methods described here are able to analyze every piece of microparticle data. MFC is a high throughput and well established quantitative analytical instrument and is routinely used in hospitals.45 For the representative asthma sample, 0.03% Tc2 cells in a total of 102 thousand cells were measured. This leads to 35 cells measured and already most methods have trouble detecting this group of cells. Most other single cell omics instruments yield only a fraction of the number of cells measured and are thus unable to detect these rarer cell subtypes.40 Moreover, these single cell omics data suffer from more technical variability than MFC, which is enhanced by the number of variables measured and thus it will be harder to distinguish the biological relevant variability from the technical variability.
Conclusions
Multicolor flow cytometry is invaluable to chemically characterize cells in a biomedical sample. Manual sequential gating is extremely labor and resource-intensive, such that automated methods to resolve such a sample into different cell types based on their surface protein expression have considerable intrinsic value. This is supported by the diverse methodologies that have been presented in the literature. Developing quality criteria to describe resolving such cell mixtures are context-specific, but we have qualitatively evaluated the methods based on the analysis of an MFC sample obtained from an asthma patient. Each of the four compared methods provided an insightful overview of the mixture, but each method had pre-defined aspects in which it excelled. Although principal component analysis did not resolve all cell types in the mixture well, using it as a basis for hierarchically comparing MFC samples for disease biomarker cells with specific surface marker expressions revealed even more populations than the analysis of a single sample. We also showed how detrimental the implementation of sparsity might be in comprehensively resolving mixtures in high-dimensional biochemistry. Such hierarchies in mixtures become much more prevalent in analytical chemistry, for example in characterizing the complexome of different proteins within a biofluid. Also, in industrial recycling where objects in heterogeneous waste streams need to be individually chemically characterized and separated, the compared technologies may be directly applied.Conflicts of interest
There are no conflicts to declare.References
- O. Beckonert, H. C. Keun, T. M. Ebbels, J. Bundy, E. Holmes, J. C. Lindon and J. K. Nicholson, Nat. Protoc., 2007, 2, 2692 CrossRef CAS PubMed.
- H. Zola, B. Swart, I. Nicholson, B. Aasted, A. Bensussan, L. Boumsell, C. Buckley, G. Clark, K. Drbal and P. Engel, Blood, 2005, 106, 3123–3126 CrossRef CAS PubMed.
- A. L. Givan, in Flow Cytometry Protocols, Springer, 2011, pp. 1–29 Search PubMed.
- J. Picot, C. L. Guerin, C. Le Van Kim and C. M. Boulanger, Cytotechnology, 2012, 64, 109–130 CrossRef PubMed.
- J. Brummelman, K. Pilipow and E. Lugli, Int. Rev. Cell Mol. Biol., 2018, 63–124 Search PubMed.
- D. R. Bandura, V. I. Baranov, O. I. Ornatsky, A. Antonov, R. Kinach, X. Lou, S. Pavlov, S. Vorobiev, J. E. Dick and S. D. Tanner, Anal. Chem., 2009, 81, 6813–6822 CrossRef CAS PubMed.
- S. C. Bendall, E. F. Simonds, P. Qiu, E.-a. D. Amir, P. O. Krutzik, R. Finck, R. V. Bruggner, R. Melamed, A. Trejo, O. I. Ornatsky, R. S. Balderas, S. K. Plevritis, K. Sachs, D. Pe’er, S. D. Tanner and G. P. Nolan, Science, 2011, 332, 687–696 CrossRef CAS PubMed.
- R. Goodacre, S. Vaidyanathan, W. B. Dunn, G. G. Harrigan and D. B. Kell, Trends Biotechnol., 2004, 22, 245–252 CrossRef CAS PubMed.
- E. Lugli, M. Roederer and A. Cossarizza, Cytometry, Part A, 2010, 77, 705–713 CrossRef PubMed.
- P. Qiu, E. F. Simonds, S. C. Bendall, K. D. Gibbs Jr, R. V. Bruggner, M. D. Linderman, K. Sachs, G. P. Nolan and S. K. Plevritis, Nat. Biotechnol., 2011, 29, 886–891 CrossRef CAS PubMed.
- E.-a. D. Amir, K. L. Davis, M. D. Tadmor, E. F. Simonds, J. H. Levine, S. C. Bendall, D. K. Shenfeld, S. Krishnaswamy, G. P. Nolan and D. Pe’er, Nat. Biotechnol., 2013, 31, 545–552 CrossRef CAS PubMed.
- S. Van Gassen, B. Callebaut, M. J. Van Helden, B. N. Lambrecht, P. Demeester, T. Dhaene and Y. Saeys, Cytometry, Part A, 2015, 87, 636–645 CrossRef PubMed.
- S. C. Bendall, G. P. Nolan, M. Roederer and P. K. Chattopadhyay, Trends Immunol., 2012, 33, 323–332 CrossRef CAS PubMed.
- G. H. Tinnevelt, M. Kokla, B. Hilvering, S. Staveren, R. Folcarelli, L. Xue, A. C. Bloem, L. Koenderman, L. M. Buydens and J. J. Jansen, Sci. Rep., 2017, 7, 5471 CrossRef PubMed.
- N. Aghaeepour, G. Finak, H. Hoos, T. R. Mosmann, R. Brinkman, R. Gottardo and R. H. Scheuermann, Nat. Methods, 2013, 10, 228–238 CrossRef CAS PubMed.
- R. V. Bruggner, B. Bodenmiller, D. L. Dill, R. J. Tibshirani and G. P. Nolan, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E2770–E2777 CrossRef CAS PubMed.
- C. E. Pedreira, E. S. Costa, Q. Lecrevisse, J. J. van Dongen, A. Orfao and E. Consortium, Trends Biotechnol., 2013, 31, 415–425 CrossRef CAS PubMed.
- T. Kamada and S. Kawai, Inf. Process. Lett., 1989, 31, 7–15 CrossRef.
- J. Friedman, T. Hastie and R. Tibshirani, The elements of statistical learning, Springer series in statistics, New York, 2001 Search PubMed.
- R. Wehrens and L. M. Buydens, J. Stat. Software, 2007, 21, 1–19 Search PubMed.
- L. v. d. Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- D. L. Massart, B. G. Vandeginste, L. Buydens, P. Lewi and J. Smeyers-Verbeke, Handbook of chemometrics and qualimetrics: Part A, Elsevier Science Inc., 1997 Search PubMed.
- R. Madsen, T. Lundstedt and J. Trygg, Anal. Chim. Acta, 2010, 659, 23–33 CrossRef CAS PubMed.
- R. Bro and A. K. Smilde, Anal. Methods, 2014, 6, 2812–2831 RSC.
- P. Geladi and B. R. Kowalski, Anal. Chim. Acta, 1986, 185, 1–17 CrossRef CAS.
- M. Bylesjö, M. Rantalainen, O. Cloarec, J. K. Nicholson, E. Holmes and J. Trygg, J. Chemom., 2006, 20, 341–351 CrossRef.
- J. M. Fonville, S. E. Richards, R. H. Barton, C. L. Boulange, T. M. D. Ebbels, J. K. Nicholson, E. Holmes and M.-E. Dumas, J. Chemom., 2008, 24, 636–649 Search PubMed.
- Y. Kosugi, R. Sato, S. Genka, N. Shitara and K. Takakura, Cytometry, 1988, 9, 405–408 CrossRef CAS PubMed.
- J. Van Dongen, L. Lhermitte, S. Böttcher, J. Almeida, V. Van der Velden, J. Flores-Montero, A. Rawstron, V. Asnafi, Q. Lecrevisse and P. Lucio, Leukemia, 2012, 26, 1908 CrossRef CAS PubMed.
- Y. Saeys, S. Van Gassen and B. N. Lambrecht, Nat. Rev. Immunol., 2016, 16, 449 CrossRef CAS PubMed.
- E. Szymańska, E. Saccenti, A. Smilde and J. Westerhuis, Metabolomics, 2012, 8, 3–16 Search PubMed.
- J. J. Jansen, H. C. Hoefsloot, J. van der Greef, M. E. Timmerman, J. A. Westerhuis and A. K. Smilde, J. Chemom., 2005, 19, 469–481 CrossRef CAS.
- A. K. Smilde, J. J. Jansen, H. C. Hoefsloot, R.-J. A. Lamers, J. Van Der Greef and M. E. Timmerman, Bioinformatics, 2005, 21, 3043–3048 CrossRef CAS PubMed.
- R. Tauler, Chemom. Intell. Lab. Syst., 1995, 30, 133–146 CrossRef CAS.
- J. Jaumot, R. Gargallo, A. de Juan and R. Tauler, Chemom. Intell. Lab. Syst., 2005, 76, 101–110 CrossRef CAS.
- R. Bro, Chemom. Intell. Lab. Syst., 1997, 38, 149–171 CrossRef CAS.
- B. Hilvering, S. Vijverberg, J. Jansen, L. Houben, R. Schweizer, S. Go, L. Xue, I. Pavord, J. W. Lammers and L. Koenderman, Allergy, 2017, 72, 1202–1211 CrossRef CAS.
- M. Roederer, Curr. Protoc. Cytom., 2002, 22, 1.14.1–1.14.20 Search PubMed.
- M. H. Spitzer and G. P. Nolan, Cell, 2016, 165, 780–791 CrossRef CAS PubMed.
- R. Zenobi, Science, 2013, 342, 1243259 CrossRef CAS PubMed.
- L. Ziegler-Heitbrock and T. P. Hofer, Front. Immunol., 2013, 4, 23 Search PubMed.
- M. Malek, M. J. Taghiyar, L. Chong, G. Finak, R. Gottardo and R. R. Brinkman, Bioinformatics, 2015, 31, 606–607 CrossRef CAS PubMed.
- J. P. Campbell, K. Guy, C. Cosgrove, G. D. Florida-James and R. J. Simpson, Brain, Behav., Immun., 2008, 22, 375–380 CrossRef CAS PubMed.
- Y. Gagnebin, D. Tonoli, P. Lescuyer, B. Ponte, S. de Seigneux, P.-Y. Martin, J. Schappler, J. Boccard and S. Rudaz, Anal. Chim. Acta, 2017, 955, 27–35 CrossRef CAS PubMed.
- J. P. Robinson and M. Roederer, Science, 2015, 350, 739–740 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2019 |