DOI:
10.1039/C8SC00171E
(Edge Article)
Chem. Sci., 2018,
9, 6659-6669
Theory for polariton-assisted remote energy transfer†
Received
11th January 2018
, Accepted 12th June 2018
First published on 16th June 2018
Abstract
Strong-coupling between light and matter produces hybridized states (polaritons) whose delocalization and electromagnetic character allow for novel modifications in spectroscopy and chemical reactivity of molecular systems. Recent experiments have demonstrated remarkable distance-independent long-range energy transfer between molecules strongly coupled to optical microcavity modes. To shed light on the mechanism of this phenomenon, we present the first comprehensive theory of polariton-assisted remote energy transfer (PARET) based on strong-coupling of donor and/or acceptor chromophores to surface plasmons. Application of our theory demonstrates that PARET up to a micron is indeed possible. In particular, we report two regimes for PARET: in one case, strong-coupling to a single type of chromophore leads to transfer mediated largely by surface plasmons while in the other case, strong-coupling to both types of chromophores creates energy transfer pathways mediated by vibrational relaxation. Importantly, we highlight conditions under which coherence enhances or deteriorates these processes. For instance, while exclusive strong-coupling to donors can enhance transfer to acceptors, the reverse turns out not to be true. However, strong-coupling to acceptors can shift energy levels in a way that transfer from acceptors to donors can occur, thus yielding a chromophore role-reversal or “carnival effect”. This theoretical study demonstrates the potential for confined electromagnetic fields to control and mediate PARET, thus opening doors to the design of remote mesoscale interactions between molecular systems.
1 Introduction
Enhancement of excitation energy transfer (EET) remains an exciting subfield of the chemical sciences. Although Förster resonance energy transfer1 (FRET) is one of the most extensively studied and well known forms of EET, its efficiency range is only at 1–10 nm.2 As such, exploration of EET schemes beyond that of a traditional pair of donor and acceptor molecules has been a highly active area of research. For instance, the theory of multichromophoric FRET3 has been applied to demonstrate the role of coherent exciton delocalization in photosynthetic light harvesting.4–8 This coherence, which is due to excitonic coupling between molecular emitters, has also been argued to increase EET in mesoscopic multichromophoric assemblies,9 with recent studies even reporting micron-sized transfer ranges in H-aggregates.10,11 Along similar lines, a well-studied process is plasmon-coupled resonance energy transfer,12 where molecules which are separated several tens to hundreds of nanometers apart can efficiently transfer energy between themselves due to the enhanced electromagnetic fields provided by the neighboring nanoparticles.13,14 Transfer between molecules across even longer distances can be mediated by the in-plane propagation of surface plasmons (SPs), with micron ranges reported in the literature15,16 (see ref. 17 for an example of micron-range EET via other types of electromagnetic modes). Notably, the plasmonic effects in these last examples occur in the so-called weak-coupling regime, where the frequency of energy exchange between excitons and plasmons is much slower than their respective decays.
An intriguing advancement in PARET has recently been reported by the Ebbesen group for cyanine dye J-aggregates strongly coupled to a microcavity mode.18 For spatially separated slabs of donor and acceptor dyes placed between two mirrors, it was found that increasing the interslab spacing from 10 to 75 nm led to no change in the relaxation rate between the hybrid light–matter states or polaritons, thus revealing a remarkable distance independence of the process. Importantly, such PARET phenomenon was already noted in an earlier work by the Lidzey group19 with a different cyanine-dye system, although the interslab spacing was not systematically varied there; similar work was also previously reported for hybridization of Frenkel and Wannier–Mott excitons in an optical microcavity.20 Motivated by these experiments, we hereby present a quantum-mechanical theory for polariton-assisted energy transfer which aims to characterize the various types of PARET afforded by these hybrid light–matter systems. To be concrete, we do so within a model where the “photonic modes” are SPs in a metal film and consider spatially separated slabs of donors and acceptor dyes which electrostatically couple to one another as well as to the SPs. We present a comprehensive formalism which encompasses the cases where either one or both types of chromophores are strongly coupled to the SPs. We apply our theory to a model system similar to those reported by the Ebbesen and Lidzey groups. Our work complements recent studies proposing schemes to enhance one-dimensional exciton conductance.21,22 In those studies, the delocalization afforded by strong-coupling (SC) is exploited to overcome static disorder within the molecular aggregate. Here, the emphasis is not on disorder (surmountable also by polaritonic topological protection23), but rather on PARET between two different types of chromophores, where energy harvested by one chromophore can be collected in another. This focus on long-range capabilities, as well as in-depth analyses of the rate contributions for the SC-induced states, provide fresh perspectives on PARET. In particular, we offer fascinating predictions for the experimentally unexplored scenario of “photonic modes” strongly coupled to one of donors or acceptors (the latter case was first theoretically investigated for the chromophores in a microcavity24).
As a preview, we highlight the structure and the main conclusions of this work (the latter are summarized in Table 1). We begin by introducing the general Hamiltonian for spatially separated slabs of donors and acceptor chromophores in Section 2. EET rates for a single or both types of chromophores strongly coupled to SPs are presented in Sections 2.1 and 2.2, respectively. In the former case, the rates are “FRET-like”1 and shown to be dependent on spectral overlap (of absorption and emission lineshapes).25,26 For SC to donors, EET can be tuned for enhancement or suppression. This result is in stark contrast with that of acceptors-SPs SC where, surprisingly, EET to acceptor polariton states vanishes for large-enough samples. For the case when both chromophores strongly interact with SPs, transfer is instead mediated by vibrational relaxation in analogy with the theories of Davydov27,28 and Redfield.25,26,29 Nevertheless, PARET is still achieved. In Section 3, we apply the formalism to study a model system resembling cyanine dye J-aggregates. Our numerical simulations demonstrate that applying SC exclusively to donors enables PARET up to 1 micron. We also show that sufficiently intense SC to acceptors induces a “carnival effect” that reverses the role of the donor and acceptor. Lastly, when both chromophores are strongly coupled to SPs, we obtain sizable PARET rates at chromophoric separations over hundreds of nanometers which are in good agreement with experiments.
Table 1 Comparison of different cases of PARET arising from SC to donors and/or acceptors
| SC to |
Features |
| Donors only |
• PARET from donor polariton states; dominated by PRET contribution |
| • Rate of EET from donor dark states ≈ bare (i.e., no SPs) FRET rate |
| • “Förster regime” of PARET |
| |
|
| Acceptors only |
• Low EET to acceptor polariton states due to their low density of states (compared to dark states) and delocalized character |
| • Rate of EET to acceptor dark states ≈ bare FRET rate |
| • “Carnival effect”: acceptor and donor reverse roles |
| • “Förster regime” of PARET |
| |
|
| Donors and acceptors |
• Polariton states are delocalized across donors and acceptors |
| • Rate of PARET from polariton to dark states ≫ rate of PARET from dark/polariton to polariton states due to relative density of final states; dark-state manifolds are dense and act as traps |
| • PARET mediated by vibrational relaxation |
| • “Davydov/Redfield regime” of PARET |
2 Theory
We begin by describing the polaritonic (plexcitonic) setup that we theoretically investigate. Let the chromophore slabs lie above (z > 0) and parallel to the metal film (z < 0) that sustains SP modes (example schematic diagrams are given in Fig. 1a, 2a, 3a, and 4a). We assume the metal film and the slabs are extended along the xy (longitudinal) plane. The slabs of C = D, A (donor, acceptor) chromophores consist of Nxy,C, Nz,C, and NC = Nxy,CNz,C molecules in the xy-plane, z-direction, and total, respectively. An effective Hamiltonian for this setup can be constructed as,| | |
H = HD + HA + HP + HDA + HDP + HAP.
| (1) |
The term HC = H(sys)C + H(B)C + H(sys–B)C is the Hamiltonian for the slab with the C chromophores, where (denoting ℏ as the reduced Planck constant)| |
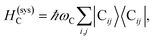 | (2a) |
| |
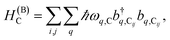 | (2b) |
| |
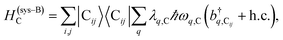 | (2c) |
represent the system (excitonic), bath (phononic), and system–bath-coupling contributions, respectively. The label Cij refers to a C exciton located at the (i,j)-th molecule of the corresponding slab [(i,j) indexes an (xy,z) coordinate]. We take every Cij exciton to have energy ℏωC and neglect inter-site coupling since the latter provides an insignificant contribution to polariton dispersion when compared to the SP dispersion. Specifically, within the wavevector range of interest, inter-site coupling only induces a constant energy shift (which we assume to be included in ωC) to the exciton subsystem. Thus, the exciton dispersion is only relevant at much shorter wavelengths. 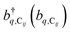 labels the creation (annihilation) of a phonon of energy ℏωq,C at the q-th vibrational mode of the (i,j)-th molecule in the C slab. Given the molecular character of the problem, vibronic coupling is assumed to be local30 (in contrast to that for relatively ordered materials such as crystals31): exciton Cij couples linearly to
labels the creation (annihilation) of a phonon of energy ℏωq,C at the q-th vibrational mode of the (i,j)-th molecule in the C slab. Given the molecular character of the problem, vibronic coupling is assumed to be local30 (in contrast to that for relatively ordered materials such as crystals31): exciton Cij couples linearly to 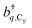 and bq,Cij but not to modes in other molecules;32 these couplings are characterized by Huang–Rhys factors λq,C2.33 The SP Hamiltonian HP = H(sys)P + H(B)P + H(sys–B)P has similar form:34,35
and bq,Cij but not to modes in other molecules;32 these couplings are characterized by Huang–Rhys factors λq,C2.33 The SP Hamiltonian HP = H(sys)P + H(B)P + H(sys–B)P has similar form:34,35| |
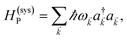 | (3a) |
| |
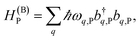 | (3b) |
| |
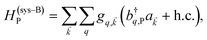 | (3c) |
where 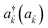 labels the creation (annihilation) of an SP of energy ℏω
labels the creation (annihilation) of an SP of energy ℏω![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) and in-plane wavevector
and in-plane wavevector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) . Bath modes indexed by q,P with corresponding operator
. Bath modes indexed by q,P with corresponding operator 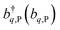 and energy ℏωq,P are coupled to each SP mode
and energy ℏωq,P are coupled to each SP mode ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) with strength gq,
with strength gq,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) . Specifically, these SP interactions occur with either electromagnetic or phonon modes and represent radiative and ohmic losses, respectively.35 The remaining rightmost terms in eqn (1) represent the dipole–dipole interactions amongst donors, acceptors, and SP modes. The HDA term is given by the electrostatic (near-field) dipole–dipole interactions between donors and acceptors,
. Specifically, these SP interactions occur with either electromagnetic or phonon modes and represent radiative and ohmic losses, respectively.35 The remaining rightmost terms in eqn (1) represent the dipole–dipole interactions amongst donors, acceptors, and SP modes. The HDA term is given by the electrostatic (near-field) dipole–dipole interactions between donors and acceptors,| |
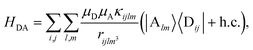 | (4) |
where μC = |![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) Cij| for transition dipole moment (TDM)
Cij| for transition dipole moment (TDM) ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) Cij corresponding to Cij, rijlm is the distance between Dji and Alm, and κijlm =
Cij corresponding to Cij, rijlm is the distance between Dji and Alm, and κijlm = ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Dij·
Dij·![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Alm − 3(
Alm − 3(![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Dij·
Dij·![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ijlm)(
ijlm)(![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Alm·
Alm·![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ijlm) is the orientational dependence of the interaction (we denote
ijlm) is the orientational dependence of the interaction (we denote ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) as the unit vector corresponding to
as the unit vector corresponding to ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) ). We have ignored the corrections to κijlm due to reflected waves from the metal—despite their prominent effects in phenomena such as photoluminescence36—since they are numerically involved and do not significantly change the order of magnitude of the bare dipole–dipole interaction;37 furthermore their expected effects in HDA will be overwhelmed by HCP, as we shall explain in Sections 2.1 and 3. For simplicity, we take the permittivity on top of the metal to be a real-valued positive dielectric constant εd. The light–matter interaction for species C in the rotating-wave approximation38 is also dipolar in nature and is described by39
). We have ignored the corrections to κijlm due to reflected waves from the metal—despite their prominent effects in phenomena such as photoluminescence36—since they are numerically involved and do not significantly change the order of magnitude of the bare dipole–dipole interaction;37 furthermore their expected effects in HDA will be overwhelmed by HCP, as we shall explain in Sections 2.1 and 3. For simplicity, we take the permittivity on top of the metal to be a real-valued positive dielectric constant εd. The light–matter interaction for species C in the rotating-wave approximation38 is also dipolar in nature and is described by39| |
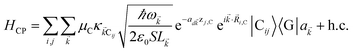 | (5) |
where (![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) i,C,zj,C) are the position coordinates of Cij and |G〉 is the electronic ground state (i.e., with no excitons). Just like in HDA, the interaction between an SP mode and a chromophore (indexed by
i,C,zj,C) are the position coordinates of Cij and |G〉 is the electronic ground state (i.e., with no excitons). Just like in HDA, the interaction between an SP mode and a chromophore (indexed by ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) and Cij, respectively) has an orientation-dependent parameter
and Cij, respectively) has an orientation-dependent parameter 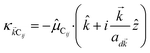 , where
, where 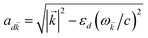 is the real-valued evanescent SP decay constant for the region above the metal. The light–matter coupling also includes the quantization length L
is the real-valued evanescent SP decay constant for the region above the metal. The light–matter coupling also includes the quantization length L![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) (ref. 40) and area S of the SP. We refer the reader to ESI Section S1† for further details of these terms.
(ref. 40) and area S of the SP. We refer the reader to ESI Section S1† for further details of these terms.
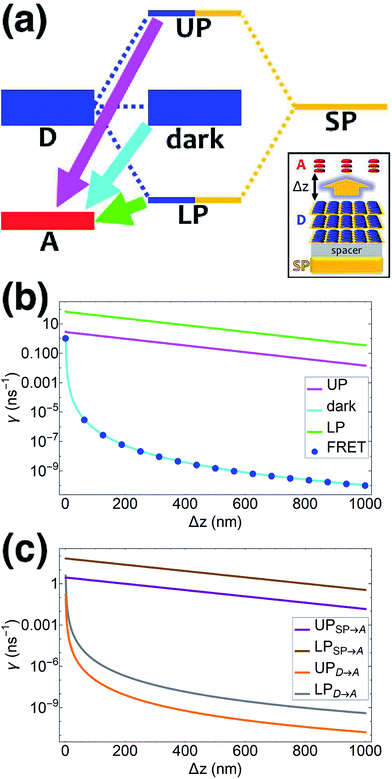 |
| | Fig. 1 (a) Schematic energy-level diagram showing the EET transitions from donors strongly coupled to SPs to bare acceptors. The thickness of the horizontal lines denotes the density of states while the thickness of arrows corresponds to rate of transition (thicknesses not drawn to scale). Inset: representation of the EET process from a thick and dense slab of donors (featuring SC to SPs) to a dilute monolayer of acceptors. (b) Rates as a function of donor–acceptor separation Δz for EET from donor polariton and dark states to acceptors (lines). The rate from dark states and for the bare-donor FRET (dots), are calculated in the same manner. (c) Contributions of rates for transfer from donor UP and LP to acceptor states due to donor–acceptor (FRET) and SP–acceptor (PRET) interactions (see eqn (12a) and immediately preceding discussion). | |
The general Hamiltonian in eqn (1) describes a complex many-body problem consisting of excitons, SPs, and vibrations, all coupled with each other. To obtain physical insight on the opportunities afforded by this physical setup, we consider in the next sections two limit cases where either one or both types of chromophores are strongly coupled to the SP. The study of these two situations already provides considerable perspective on the wealth of novel EET phenomena hosted by this polaritonic system.
2.1 Case (i): SC to only one chromophore C
We consider the case where one of the chromophores C (D or A) is strongly coupled to an SP but the other, C′, is not. This can happen when the concentration or thickness of the C slab is sufficiently high and that of the C′ slab low. Under these circumstances, we write eqn (1) as H = H(i)0 + V(i), where we define the zeroth-order Hamiltonian as H(i)0 = H(i)sys + HB + Hsys–B. The system, bath, and their coupling are respectively characterized by H(i)sys = H(sys)D + H(sys)A + H(sys)P + HCP, HB = H(B)D + H(B)A + H(B)P, and Hsys–B = H(sys–B)D + H(sys–B)A + H(sys–B)P. The perturbation describing the weak interaction between chromophore C′ and the SC species is V(i) = HDA + HC′P, i.e., the electrostatic interaction as in Förster1 theory.25,26 To diagonalize H(i)sys, we introduce a collective exciton basis comprised of bright C states with in-plane momenta matching those of the SP modes and ignore the very off-resonant SP–exciton couplings beyond the first Brillouin zone (FBZ) of the molecular system:39,41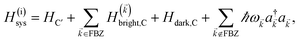 where
where| |
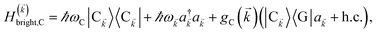 | (6a) |
| |
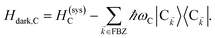 | (6b) |
For each ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -mode in the FBZ, there is only one “bright” collective exciton state
-mode in the FBZ, there is only one “bright” collective exciton state 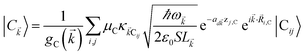 that couples to the
that couples to the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -th SP mode
-th SP mode 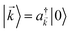 , where
, where 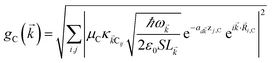 . In addition to the weakly coupled C′ states, H(i)sys has two polariton eigenstates
. In addition to the weakly coupled C′ states, H(i)sys has two polariton eigenstates 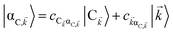 for α = UP, LP (upper polariton and lower polariton, respectively), which are also eigenstates of H(
for α = UP, LP (upper polariton and lower polariton, respectively), which are also eigenstates of H(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) )bright,C for each
)bright,C for each ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ∈ FBZ; throughout this work, cmn = 〈m|n〉. Furthermore, there is a large reservoir of NC − Nxy,C = Nxy,C(Nz,C − 1) “dark” (purely excitonic) eigenstates |dC,
∈ FBZ; throughout this work, cmn = 〈m|n〉. Furthermore, there is a large reservoir of NC − Nxy,C = Nxy,C(Nz,C − 1) “dark” (purely excitonic) eigenstates |dC,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 (d = 0, 1,…, Nz,C − 2) which are also eigenstates of Hdark,C with bare chromophore energy ℏωC.
〉 (d = 0, 1,…, Nz,C − 2) which are also eigenstates of Hdark,C with bare chromophore energy ℏωC.
EET rates between C and uncoupled C′ states can be derived by applying Fermi's golden rule; the corresponding perturbation V(i) connects vibronic-polariton eigenstates of H(i)0 as in FRET and MC-FRET theories.3,42–44 For simplicity, we also invoke weak system-bath coupling Hsys–B, from which the following expression can be obtained,45,46
| |
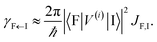 | (7) |
This is the rate of transfer between
H(i)sys eigenstates |I〉 and |F〉, where
JF,I is the spectral overlap between absorption and emission spectra, which depend on
HB and
Hsys–B (see Section S2.1
† for derivation of
γF←I and expression for
JF,I). Since our focus is to understand the general timescales expected for the PARET problem, in Section 3 we treat the broadening of electronic/polaritonic levels due to
Hsys–B as Lorentzian, although more sophisticated lineshape theories can be utilized if needed.
33 Furthermore, we can in principle also refine
eqn (7) to consider the complexities of vibronic mixing between the various eigenstates of
H(i)sys, as done in recent works by Jang and Cao.
3,42–44
It follows from eqn (7) that the rates from donor states—either polaritons with given wavevector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) or a uniform mixture of dark states with occupation
or a uniform mixture of dark states with occupation 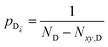 for all d,
for all d,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) —to the incoherent set of all bare acceptor states are,
—to the incoherent set of all bare acceptor states are,
| |
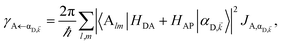 | (8a) |
| |
 | (8b) |
Here, we notice that
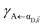
in
eqn (8a) can be enhanced or suppressed relative to bare (in the absence of metal) FRET due to additional SP-resonance energy transfer
47 (PRET) channel given by
HAP, as well as the spectral overlap
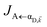
that can be modified by tuning the energy of |α
D,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
〉. Similar findings were obtained for electron transfer with only donors strongly coupled to a cavity mode.
48 Given that |α
D,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
〉 corresponds to a delocalized state, one would expect a superradiant enhancement of the rate;
5,6 in practice, this effect is minor due to the distance dependence of
HDA (see Section S2.3
†). On the other hand,
eqn (8b) presents an average rate
γA←darkD from the dark states and hence does not feature a PRET term. In fact, it converges (see Section S2.5
†) to the bare FRET rate (
eqn (12b) below) in the limit of large
ND≫
Nxy,D (when there are many layers of chromophores along
z) and isotropically averaged and orientationally uncorrelated TDMs
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) Cij
Cij for both C = D, A.
In contrast, strongly coupling the acceptor states to SPs yields the following rates:
| |
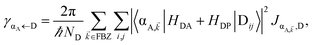 | (9a) |
| |
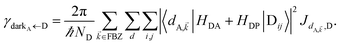 | (9b) |
Here, we have calculated average rates over the
ND possible initial states at the D slab and summed over all final states for each polariton/dark band. Given the asymmetry of Fermi's golden rule with respect to initial and final states (rates scale with the
probabilities of occupation of
initial states and with the
density of
final states),
5 the physical consequences of
eqn (9) are quite different to those of its counterpart in
eqn (8) when
NA ≫
Nxy,A and all TDMs are isotropically averaged and feature no orientational correlations amongst them. Seemingly counterintuitive in light of the various recently reported phenomena which are enhanced upon exciton delocalization,
57 the rate of EET to polariton states is reduced substantially compared to the bare FRET rate (at short donor–acceptor separations; see Section S2.7 for a formal derivation of this statement).
49 Nevertheless, this statement is easily understood from a final-density-of-states argument (see
eqn (9a)): only
Nxy,A bright acceptor collective modes contribute to
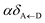
, whereas
NA localized acceptor states contribute to the bare FRET rate. On the other hand,
γdarkA←D behaves similarly to
eqn (8b) in that it converges (see
eqn (13b) and (S30b)
†) to the bare FRET rate. Thus, at donor–acceptor separations where the square of the FRET coupling exceeds on average that for PRET, the inequality
γαA←D≪
γdarkA←D is expected to hold.
Our analyses of eqn (8) and (9) reveal one of the main conclusions of this letter: while strongly coupling to D but not to A might yield a significant D → A EET rate change with respect to the bare case, strongly coupling to A but not to D will change that process in a negligible manner. Interestingly, these trends have also been observed for transfer between layers of donor and acceptor quantum dots selectively coupled to metal nanoparticles in the weak-interaction regime.50 However, polariton formation with A is not useless, for one may consider the intriguing prospect of converting A states into new donors. As we shall show in the next paragraphs, this role reversal or “carnival effect” can be achieved when the UP is higher in energy than the bare donor states. These findings are quite general and should apply to other molecular processes as long as the interactions between reactants and products (taking the roles of donors and acceptors) also decay at large distances, a scenario that is chemically ubiquitous.51
2.2 Case (ii): SC to both donor and acceptor chromophores
We next consider the SC of SPs to both donors and acceptors. We rewrite eqn (1) as H = H(ii)0 + V(ii), where H(ii)0 = H(ii)sys + HB and the perturbation is V(ii) = Hsys–B for interslab distance large enough to neglect interaction HDA in V(ii). Here, H(ii)sys = H(sys)D + H(sys)A + HDP + HAP + HDA + HP is the polariton Hamiltonian. As in the Davydov model,27,28 the EET pathways of interest become those where Hsys–B induces vibrationally mediated relaxation (faster than dipole–dipole coupling in typical organic chromophores separated by 1–10 nm (ref. 2)) among the delocalized states resulting from SC.25,26 The transfer rates describing these processes can be deduced by Fermi's golden rule too, the resulting expressions coinciding with those derived with Redfield29 theory.25,26,52 Although not necessary, we take Nxy,D = Nxy,A = Nxy to avoid mathematical technicalities about working with two ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) grids of different sizes, a complication that does not give more insight into the physics of interest. As done in Section 2.1, we rewrite H(ii)sys in
grids of different sizes, a complication that does not give more insight into the physics of interest. As done in Section 2.1, we rewrite H(ii)sys in ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -space:
-space: 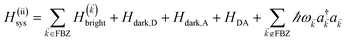 , where
, where| |
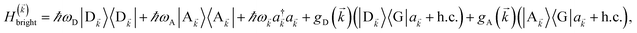 | (10) |
and the terms labeled dark are defined analogously to those in eqn (6b). For each ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ∈ FBZ, there are three polariton eigenstates of H(
∈ FBZ, there are three polariton eigenstates of H(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) )bright that are linear combinations of |D
)bright that are linear combinations of |D![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉, |A
〉, |A![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉, and |
〉, and |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉, and we call them UP, middle polariton (MP), and LP, according to their energy ordering. In addition, the presence of Hdark,C yields NC − Nxy,C dark C eigenstates.
〉, and we call them UP, middle polariton (MP), and LP, according to their energy ordering. In addition, the presence of Hdark,C yields NC − Nxy,C dark C eigenstates.
The resulting expressions for the rates of transfer from a single polariton state or average dark state to an entire polariton or dark state bands are
| |
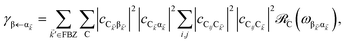 | (11a) |
| |
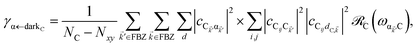 | (11b) |
| |
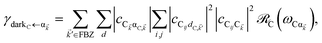 | (11c) |
for α, β = UP, MP, LP and C = D, A (see Section S3.1
† for derivation of
eqn (11)). To intuitively understand
eqn (11a), note that
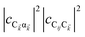
and
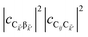
are the fractions of exciton |C
ij〉 in the polariton states |α
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
〉 and
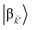
, respectively, while
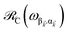
is the single-molecule rate of vibrational relaxation at the energy difference
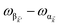
. More specifically,
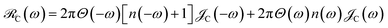
, where
Θ(
ω) is the Heaviside step function,
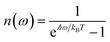
is the Bose–Einstein distribution function (
kB is the Boltzmann constant and
T is temperature) for zero chemical potential
μ = 0, and
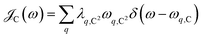
is the spectral density for chromophore C.
52 Hence, one can interpret β ← α
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
as a sum of incoherent processes (over C and
i,
j) where the (local) vibrational modes in C
ij absorb or emit phonons concomitantly inducing population transfer between the various eigenstates of
H(ii)sys.
Eqn (11b) and
(11c) can be interpreted in a similar light. As an aside, we note that these transitions are analogous to the so-called intraband relaxation among collective exciton states in J-aggregates.
53 We now comment on some important qualitative trends in these rates while for simplicity assuming that
Nz,D =
Nz,A =
Nz. First, EET from polariton or dark states to a polariton band (
eqn (11a) and
(11b)) scale as
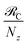
. To see this, note that both
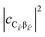
and
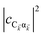
are
O(1), while
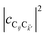
and
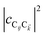
are
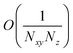
, but the summations
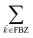
and
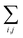
are respectively carried over
Nxy and
NxyNz terms. On the other hand,
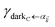
takes values that are on the order of the single-molecule decay
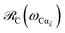
. For sufficiently large
Nz, these scalings are consistent with previous studies on relaxation dynamics of polaritons
54–56 and can be summarized as follows: the dominant channels of relaxation are from the polariton states to a reservoir of dark states that share the same exciton character; their timescales are comparable to those of the corresponding single-chromophore vibrational relaxation; given the large density of states in this reservoir compared to the polariton bands, the dark states act as a population sink or trap from which population can only leak out very slowly.
56,57
3 Application of the theory
The theory above is now applied to study EET kinetics associated with slabs of chromophores with ℏωD = 2.1 eV, ℏωA = 1.88 eV; these transition energies are chosen to match those of the J-aggregated cyanine dyes (TDBC and BRK5714, respectively) used in previous polariton experiments.18,58 For simplicity, this section assumes T = 0 and thus only considers downhill transfers to/from polariton and dark states. We describe the metal with Drude permittivity of silver (ωP = 9.0 eV, ε∞ = 1;59 see Section S1†) and all media at z > 0 (including molecular slabs) with εd = 1. We model spectral overlaps (eqn (8) and (9)) with Lorentzian functions 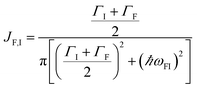 whose parameters are estimated as in Section S2.2;† we set ΓA ≈ ΓD = 47 meV to represent observed values for absorption of TDBC60 and
whose parameters are estimated as in Section S2.2;† we set ΓA ≈ ΓD = 47 meV to represent observed values for absorption of TDBC60 and 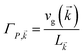 ,39 where vg(
,39 where vg(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) is the SP group velocity. Rigorous treatments of lineshape functions have been previously reported in MC-FRET literature and could be applied to this problem as well,43,44,61,62 although this effort is beyond the scope of our work. We also neglect differences in TDMs and assign μD = μA = 10 D, a typical number for cyanine dyes.63
) is the SP group velocity. Rigorous treatments of lineshape functions have been previously reported in MC-FRET literature and could be applied to this problem as well,43,44,61,62 although this effort is beyond the scope of our work. We also neglect differences in TDMs and assign μD = μA = 10 D, a typical number for cyanine dyes.63
We now proceed to simulations for Case (i), where only one of the molecular species forms polaritons. For simplicity, we assume isotropically oriented and spatially uncorrelated dipoles, upon which we find the interesting observation that the transfer rates in eqn (8) can be approximately decomposed into incoherent sums of FRET and PRET rates (see Sections S2.4 and S2.5† for more explicit expressions, derivations, and justification of validity),
| |
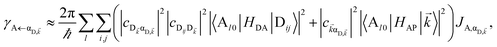 | (12a) |
| |
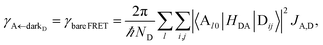 | (12b) |
where, as explained above, only
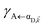
differs from
γbare FRET. More concretely, we consider a 35 nm-thick slab of donors with 1 × 10
9 molecules per μm
3 on top of a 1 nm spacer placed on a plasmonic metal film. We set the monolayer slab of acceptors with 1 × 10
4 molecules per μm
2 at varying distances from the donors (
Fig. 1a). Then the collective couplings of the donor-resonant SP mode (|
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
| = 1.1 × 10
7 m
−1) to donors and acceptors is
gD(
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
) = 155 meV and
gA(
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
) ≤ 2.5 meV, respectively. When there is no separation between donor and acceptor slabs, rates >1 ns
−1 (
Fig. 1b) are obtained for transfer to acceptors from the UP (∼10 ns
−1), LP (∼100 ns
−1), or the set of dark states (∼10 ns
−1). As separation increases however, the rate from dark states decays much faster than those from either UP or LP. This difference stems from the slowly decaying PRET contribution of the polaritons, as well as the totally excitonic character of the dark states, which can only undergo FRET but not PRET (
Fig. 1a and b). In fact, for large distances, the FRET contribution becomes significantly overwhelmed by PRET (
Fig. 1c), in consistency with previous studies in the weak SP-coupling regime.
64 As the distance between slabs approaches 1 μm, it is fascinating that while transfer from dark states (and thus bare FRET) practically vanishes, the rate from either LP (∼1 ns
−1) or UP (∼0.01 ns
−1) is still at or above typical fluorescence decay rates (0.01–10 ns
−1).
65 Roughly speaking (in FRET language), this PARET has a Förster distance in the μm range, or 1000-fold greater than the typical nm-range.
66 Interestingly, the LP rate exceeds the UP one by 1–2 orders of magnitude at all separations due to greater spectral overlap with the acceptor (
Fig. 1a and S1
†).
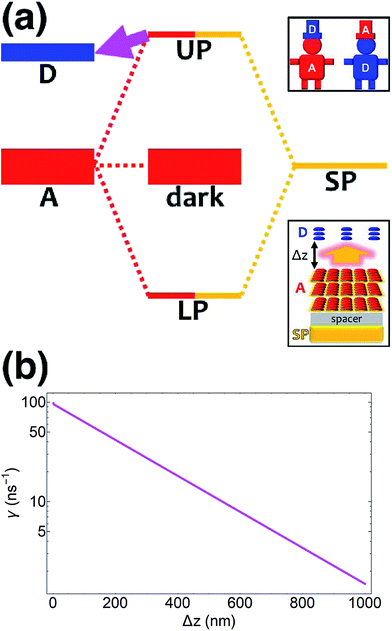
In contrast, strongly coupling the acceptors to a resonant SP mode does not lead to the aforementioned PARET from donors to acceptors (Fig. 2). Making the same assumptions as above, i.e., taking isotropically oriented and spatially uncorrelated dipoles, we obtain (Section S2.7†),
| |
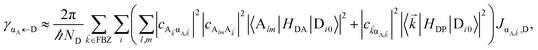 | (13a) |
| |
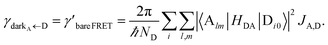 | (13b) |
We consider (
Fig. 2a) a 50 nm-thick acceptor slab with a concentration of 1 × 10
9 molecules per μm
3 on top of the 1 nm spacer placed on the metal, and a monolayer of donors with concentration 1 × 10
4 molecules per μm
2 at varying distances from the acceptors. Notice that
γdarkA←D becomes another bare FRET rate like in
eqn (12b). For
γαA←D, we see that PRET still dominates over FRET for long distances (Fig. S2
†). However, due to the suppression of
γαA←D relative to
γdarkA←D explained in Section 2.1, the limited spatial range of interactions of
HDA and
HDP, and the fact that the donor energy is lower than that of |UP
A,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
〉 for most
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
∈ FBZ (Fig. S3
†), the rates to the acceptor UP band fall below fluorescence timescales
65 and therefore offer no meaningful enhancements with respect to the bare FRET case (
Fig. 2b). While the first two reasons also explain the similarly low rates to the LP band, the major factor is that most states |LP
A,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
〉 essentially overlap only with acceptors that are closer to the metal—and thus farther from the donors—due to the evanescent nature of the SP–exciton coupling (
eqn (5)).
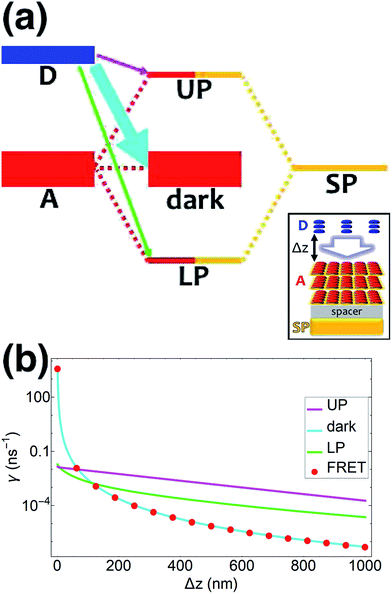 |
| | Fig. 2 (a) Schematic energy-level diagram showing the EET transitions from bare donors to acceptors strongly coupled to SPs. The thickness of the horizontal lines denotes the density of states while the thickness of arrows corresponds to rate of transition (thicknesses not drawn to scale). Inset: representation of the EET process from a dilute monolayer of donors to a thick and dense slab of acceptors (featuring SC to SPs). (b) Rates as a function of donor–acceptor separation Δz for energy transfer from donors to acceptor polaritons and dark states (lines). The rate to dark states and for bare-acceptor FRET (dots), are calculated in the same manner. | |
Coupling SPs to acceptors need not, however, be a disappointment. Increasing the acceptor slab thickness to 140 nm affords for the acceptor-resonant SP mode (|![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) | = 9.8 × 106 m−1) the collective coupling gA(
| = 9.8 × 106 m−1) the collective coupling gA(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) = 237 meV while keeping gD(
) = 237 meV while keeping gD(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) = 1.7 meV. Consequently, the acceptor UP energy
) = 1.7 meV. Consequently, the acceptor UP energy 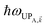 is lifted higher than ℏωD (Fig. 3a and S4†), thus allowing for the carnival effect where the donors and acceptors reverse roles. Due to sufficient spectral overlap between the acceptor UP and donor states (Fig. 3a and S4†), transfer from UP occurs at ∼100 ns−1 for donor–acceptor separation of 1 nm and drops only to ∼1 ns−1 when this separation approaches 1 μm (Fig. 3b). On the other hand, neither the acceptor dark nor LP states contribute to this reversed PARET given their lack of spectral overlap with the donors and detailed balance (especially at T = 0). This result provides the second main conclusion of our work: polaritons offer great versatility to control spectral overlaps without actual chemical modifications to the molecules and can therefore endow them with new physical properties. Before proceeding to simulations for Case (ii), it should first be noted that while our model neglects intermediate- and far-field donor–acceptor dipole–dipole interactions that become relevant at ∼μm distances, these couplings are expected to be small compared to PRET couplings and therefore should not qualitatively change our results for Case (i). The relative insignificance of the far-field, or radiative, contributions is consistent with their correspondence to emission followed by absorption (of a real photon).67 Regardless, these additional interactions can be modeled using a quantum electrodynamics treatment68 of energy transfer in bulk media according to previous literature.69 Second, we highlight that the PARET from polariton states for the donors-only and reversed cases of SC may not be efficient in experiments due to its competition with vibrational relaxation from UP to dark states (∼10–100 fs for exciton-microcavity systems54,70–73) and/or radiative decay (dominated by fast cavity leakage ∼10–100 fs for both microcavities72–74 and SPs75,76). However, conditions may be optimized to suppress these deleterious pathways by detuning the SP energy relative to that of the strongly coupled chromophore such that the polariton state is mostly excitonic and has an enhanced lifetime.77
is lifted higher than ℏωD (Fig. 3a and S4†), thus allowing for the carnival effect where the donors and acceptors reverse roles. Due to sufficient spectral overlap between the acceptor UP and donor states (Fig. 3a and S4†), transfer from UP occurs at ∼100 ns−1 for donor–acceptor separation of 1 nm and drops only to ∼1 ns−1 when this separation approaches 1 μm (Fig. 3b). On the other hand, neither the acceptor dark nor LP states contribute to this reversed PARET given their lack of spectral overlap with the donors and detailed balance (especially at T = 0). This result provides the second main conclusion of our work: polaritons offer great versatility to control spectral overlaps without actual chemical modifications to the molecules and can therefore endow them with new physical properties. Before proceeding to simulations for Case (ii), it should first be noted that while our model neglects intermediate- and far-field donor–acceptor dipole–dipole interactions that become relevant at ∼μm distances, these couplings are expected to be small compared to PRET couplings and therefore should not qualitatively change our results for Case (i). The relative insignificance of the far-field, or radiative, contributions is consistent with their correspondence to emission followed by absorption (of a real photon).67 Regardless, these additional interactions can be modeled using a quantum electrodynamics treatment68 of energy transfer in bulk media according to previous literature.69 Second, we highlight that the PARET from polariton states for the donors-only and reversed cases of SC may not be efficient in experiments due to its competition with vibrational relaxation from UP to dark states (∼10–100 fs for exciton-microcavity systems54,70–73) and/or radiative decay (dominated by fast cavity leakage ∼10–100 fs for both microcavities72–74 and SPs75,76). However, conditions may be optimized to suppress these deleterious pathways by detuning the SP energy relative to that of the strongly coupled chromophore such that the polariton state is mostly excitonic and has an enhanced lifetime.77
 |
| | Fig. 3 (a) Schematic energy-level diagram showing the “carnival-effect”-EET role-reversal process from acceptor UP state to bare donors. Insets: (top) cartoon illustrating the “carnival effect” between donors and acceptors and (bottom) representation of the reversed-role EET process from a thick and dense slab of acceptors (featuring SC to SPs) to a dilute monolayer of donors. (b) Rate as a function of donor–acceptor separation Δz for energy transfer from acceptor UP to bare donors. | |
Finally, when both chromophores are strongly coupled to SPs, we limit ourselves to donor–acceptor separations >10 nm to ignore HDA terms (an approximation discussed in Section 2.2 and validated by the calculations above demonstrating that FRET coupling is significantly diminished at such distances). The thickness (35 nm) and density (1 × 109 molecules per μm3) of each slab is large enough to allow for SC of the donor-resonant SP mode (|![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) |=1.1 × 107 m−1, gD (
|=1.1 × 107 m−1, gD (![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) = 155 meV, and gA(
) = 155 meV, and gA(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) = 142 meV) to both chromophores separated up to ∼400 nm (Fig. S6b†). To evaluate the rates derived (Section S3.2†) from eqn (11) under the condition NC ≫ Nxy,C for C = D, A, we introduce a spectral density representing intramolecular exciton–phonon coupling of TDBC:
) = 142 meV) to both chromophores separated up to ∼400 nm (Fig. S6b†). To evaluate the rates derived (Section S3.2†) from eqn (11) under the condition NC ≫ Nxy,C for C = D, A, we introduce a spectral density representing intramolecular exciton–phonon coupling of TDBC: 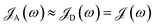 , where
, where
| |
 | (14) |
Γ = 47 meV is equal to the chromophore decay energy, and
BTDBC is the discrete set (Section S3.2
†) of localized vibrational modes which significantly couple to each TDBC exciton. Such coupling has been experimentally
70–73,78 and theoretically
54,55,79–81 supported as the mechanism of vibrational relaxation for the dye; our spectral density has been reconstructed from the works of Agranovich and coworkers.
54,55 By placing the donor slab on top of the spacer on the metal and varying the acceptor position above the donors (
Fig. 4a), we find that for all donor–acceptor separations, the rates of PARET from UP to dark donors (∼10
5 ns
−1) and MP to dark acceptors (∼10
4–10
5 ns
−1) are substantially higher compared to those from dark donors to MP (∼10
3 ns
−1) and dark acceptors to LP (∼10
3 ns
−1) (
Fig. 4b). These observations are in agreement with our discussion above, where the dark state manifolds act as population sinks due to their high density of states. Indeed, we also notice that the rates for UP → dark
D and MP → dark
A are enhanced (
Fig. 4b) compared to those of UP → MP and MP → LP, respectively, by approximately
Nz = 35, the analytically estimated ratio solely based on the associated density of final states. Another interesting detail seen from
Fig. 4b is that the UP → MP (MP → LP) rate with respect to the interslab distance Δ
z is essentially parallel to that of UP → dark
D (MP → dark
A). This is a consequence of the MP (LP) essentially having donor (acceptor) energy and character for most points in the FBZ (see dispersion curve, Fig. S6
†). The UP → dark
A and UP → LP processes behave similarly (Fig. S5
†).
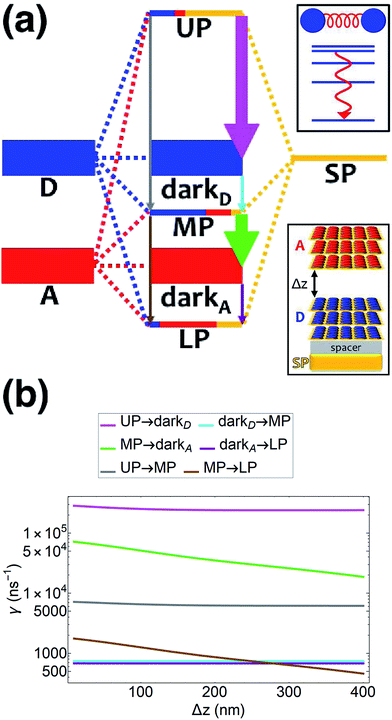 |
| | Fig. 4 (a) Schematic energy-level diagram showing the EET transitions among polariton and dark states for both donors and acceptors strongly coupled to SPs. The SP mode is resonant with the donor transition (for polariton as initial state); the donor slab lies 1 nm above the metal and has fixed position (z > 0) while the acceptor slab is moved in the +z-direction to vary the donor–acceptor separation Δz. The thickness of the horizontal lines denotes the density of states while the thickness of arrows corresponds to rate of transition (thicknesses not drawn to scale). Insets: (top) cartoon illustrating vibrational relaxation, the EET mechanism for this case of SC, and (bottom) representation of the setup of thick and dense slabs for both types of chromophores (featuring SC to SPs) for both types of chromophores. (b) Rates for selected downhill transitions as a function of Δz. | |
These calculated rates establish consistency with a number of recent notable experiments. First, our results corroborate the experimental observation of efficient PARET for separated donor and acceptor slabs of cyanine dyes strongly coupled to a microcavity.18,19 While our SP model for the SC of both excitons cannot account for the exact distance-independent PARET18 between donor and acceptor slabs in a microcavity, the rates are essentially constant over hundreds of nanometers due to the slowly decaying SP fields. Additional validation of our theory is obtained by defining rate parameters 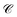 (functions of the γ rates above, see Sections S3.3 and S3.4†) that can be directly compared to those experimentally reported (Table 2).19 Since experimental
(functions of the γ rates above, see Sections S3.3 and S3.4†) that can be directly compared to those experimentally reported (Table 2).19 Since experimental 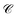 have not been determined for the setup of our work, we instead use those describing a blend of two cyanine dyes where physical separation of the dyes did not significantly change the observed photoluminescence.19 In our work, we obtained rates that assume zero temperature and sum across the whole polariton band in the FBZ; in practice, experiments occur at room temperature and probe polariton photoluminescence around a narrow window of wavevectors close to the anticrossings (∼107 m−1 in (ref. 82)). If we take these experimental details into account when calculating
have not been determined for the setup of our work, we instead use those describing a blend of two cyanine dyes where physical separation of the dyes did not significantly change the observed photoluminescence.19 In our work, we obtained rates that assume zero temperature and sum across the whole polariton band in the FBZ; in practice, experiments occur at room temperature and probe polariton photoluminescence around a narrow window of wavevectors close to the anticrossings (∼107 m−1 in (ref. 82)). If we take these experimental details into account when calculating  , we notice good agreements with our theory (see Table 2). As an aside, we reiterate that there are other experimental subtleties, notably competing processes such as radiative decay, that we have not considered but may compromise the longevity of the polariton states and thereby influence the observation of the EET phenomena predicted throughout this work for the two cases of SC.
, we notice good agreements with our theory (see Table 2). As an aside, we reiterate that there are other experimental subtleties, notably competing processes such as radiative decay, that we have not considered but may compromise the longevity of the polariton states and thereby influence the observation of the EET phenomena predicted throughout this work for the two cases of SC.
Table 2 Comparison between PARET rate parameters  for donor and acceptor cyanine dye J-aggregates strongly coupled to SP (theory) and microcavity (experiment) modesa
for donor and acceptor cyanine dye J-aggregates strongly coupled to SP (theory) and microcavity (experiment) modesa
Given the significant differences between the microcavity-83,84 and SP-based85 systems, let alone experimental uncertainty, the accordance between our theory and the aforementioned experiments highlights the remarkable robustness of cavity SC of donor and acceptor excitons as a method for PARET. Moreover, we have arrived at the third main conclusion of this paper: when donor and acceptors are both strongly coupled to a photonic mode, efficient energy exchange over hundreds of nm can occur via vibrational relaxation; more generally, local vibrational couplings can induce nonlocal transitions given sufficient delocalization of the polariton species—irrespective of spatial separation. Seemingly “spooky”, this action at a (far) distance is a manifestation of donor–acceptor entanglement resulting from strong light–matter coupling.86 While this relaxation mechanism and entanglement is present in typical molecular aggregates,87,88 the novelty in the polariton setup is the remarkable mesoscopic range of interactions that is effectively produced.
4 Conclusions
In summary, we have theoretically calculated experimentally consistent rates of PARET for various cases of SC. We employed a polariton (plexciton) setup consisting of a metal whose SP modes couple to donor and/or acceptor chromophores. For the case where a single type of chromophore is strongly coupled to SPs, we have demonstrated that energy transfer starting from delocalized states can be enhanced due to increased spectral overlap compared to the bare FRET case. Astonishingly, this transfer can remain fast up to 1 μm due to slowly decaying PRET coupling with respect to metal–chromophore separation when compared to the faster decaying interchromophoric dipole–dipole coupling. Also, we have shown that delocalizing the acceptors is a poor strategy to enhance EET starting from the donors, but can lead to an intriguing and efficient role-reversed (”carnival-effect”) EET starting from the acceptors. These observations shed new light on the timely debate of how to harness coherence to enhance molecular processes.49 Given their generality, they can also be applied to guide the design of polaritonic systems to control other chemical processes that have similar donor–acceptor flavor (e.g., charge transfer,89 electron transfer,48 singlet fission77) or reactant-product nature (e.g., cis–trans isomerization,41,90 dissociation89). Finally, our calculated rates support vibrational relaxation as the mechanism of PARET when both donors and acceptors are strongly coupled to a cavity mode. The results obtained in this work affirm light–matter SC as a promising and novel means to engineer novel interactions between molecular systems across mesoscopic length scales, thus opening doors to remote-controlled chemistry.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
M. D., R. F. R., and J. Y.-Z. acknowledge funding from the NSF CAREER Award CHE-164732. L. A. M.-M. was supported by the UC-Mexus CONACyT scholarship for doctoral studies. M. D., R. F. R., J. Y.-Z., and L. A. M.-M. are also grateful for generous UCSD startup funds. V. M. M. acknowledges funding from DOE BES through grant no. DE-SC0017760. M. D. thanks Jorge Campos-González-Angulo and Rahul Deshmukh for useful discussions.
References
- T. Förster, Ann. Phys., 1948, 2, 55–75 CrossRef
 .
. - A. Govorov, P. L. H. Martínez and H. V. Demir, Understanding and Modeling Förster-type Resonance Energy Transfer (FRET): Introduction to FRET, Springer, Singapore, 2016 Search PubMed
 .
. - S. Jang, M. D. Newton and R. J. Silbey, Phys. Rev. Lett., 2004, 92, 218301 CrossRef PubMed
 .
. - S. Jang, M. D. Newton and R. J. Silbey, J. Phys. Chem. B, 2007, 111, 6807–6814 CrossRef PubMed
 .
. - I. Kassal, J. Yuen-Zhou and S. Rahimi-Keshari, J. Phys. Chem. Lett., 2013, 4, 362–367 CrossRef PubMed
 .
. - S. Lloyd and M. Mohseni, New J. Phys., 2010, 12, 075020 CrossRef
 .
. - G. S. Engel, T. R. Calhoun, E. L. Read, T.-K. Ahn, T. Mančal, Y.-C. Cheng, R. E. Blankenship and G. R. Fleming, Nature, 2007, 446, 782 CrossRef PubMed
 .
. - S. Duque, P. Brumer and L. A. Pachón, Phys. Rev. Lett., 2015, 115, 110402 CrossRef PubMed
 .
. - G. D. Scholes, Annu. Rev. Phys. Chem., 2003, 54, 57–87 CrossRef PubMed
 .
. - A. T. Haedler, K. Kreger, A. Issac, B. Wittmann, M. Kivala, N. Hammer, J. Kohler, H.-W. Schmidt and R. Hildner, Nature, 2015, 523, 196–199 CrossRef PubMed
 .
. - S. K. Saikin, M. A. Shakirov, C. Kreisbeck, U. Peskin, Y. N. Proshin and A. Aspuru-Guzik, J. Phys. Chem. C, 2017, 121, 24994–25002 CrossRef
 .
. - L.-Y. Hsu, W. Ding and G. C. Schatz, J. Phys. Chem. Lett., 2017, 8, 2357–2367 CrossRef PubMed
 .
. - X. Zhang, C. A. Marocico, M. Lunz, V. A. Gerard, Y. K. Gunâko, V. Lesnyak, N. Gaponik, A. S. Susha, A. L. Rogach and A. L. Bradley, ACS Nano, 2014, 8, 1273–1283 CrossRef PubMed
 .
. - W. Ding, L.-Y. Hsu and G. C. Schatz, J. Chem. Phys., 2017, 146, 064109 CrossRef PubMed
 .
. - D. Bouchet, D. Cao, R. Carminati, Y. De Wilde and V. Krachmalnicoff, Phys. Rev. Lett., 2016, 116, 037401 CrossRef PubMed
 .
. - J. de Torres, P. Ferrand, G. Colas des Francs and J. Wenger, ACS Nano, 2016, 10, 3968–3976 CrossRef PubMed
 .
. - S. Götzinger, L. d. S. Menezes, A. Mazzei, S. Kühn, V. Sandoghdar and O. Benson, Nano Lett., 2006, 6, 1151–1154 CrossRef PubMed
 .
. - X. Zhong, T. Chervy, L. Zhang, A. Thomas, J. George, C. Genet, J. A. Hutchison and T. W. Ebbesen, Angew. Chem., Int. Ed., 2017, 56, 9034–9038 CrossRef PubMed
 .
. - D. M. Coles, N. Somaschi, P. Michetti, C. Clark, P. G. Lagoudakis, P. G. Savvidis and D. G. Lidzey, Nat. Mater., 2014, 13, 712–719 CrossRef PubMed
 .
. - M. Slootsky, X. Liu, V. M. Menon and S. R. Forrest, Phys. Rev. Lett., 2014, 112, 076401 CrossRef PubMed
 .
. - J. Feist and F. J. García-Vidal, Phys. Rev. Lett., 2015, 114, 196402 CrossRef PubMed
 .
. - J. Schachenmayer, C. Genes, E. Tignone and G. Pupillo, Phys. Rev. Lett., 2015, 114, 196403 CrossRef PubMed
 .
. - J. Yuen-Zhou, S. K. Saikin, T. Zhu, M. C. Onbasli, C. A. Ross, V. Bulovic and M. A. Baldo, Nat. Commun., 2016, 7, 11783 CrossRef PubMed
 .
. - D. M. Basko, F. Bassani, G. C. La Rocca and V. M. Agranovich, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 15962–15977 CrossRef
 .
. - M. Yang and G. R. Fleming, Chem. Phys., 2002, 282, 163–180 CrossRef
 .
. - E. N. Zimanyi and R. J. Silbey, Philos. Trans. R. Soc., A, 2012, 370, 3620–3637 CrossRef PubMed
 .
. - A. S. Davydov, J. Exp. Theor. Phys., 1948, 18, 210–218 Search PubMed
 .
. - A. Davydov, Theory of molecular excitons, McGraw-Hill, New York, 1962 Search PubMed
 .
. - A. Redfield, in The theory of relaxation processes, Elsevier, 1965, vol. 1, pp. 1–32 Search PubMed
 .
. - M. R. Philpott, J. Chem. Phys., 1970, 52, 5842–5850 CrossRef
 .
. - T. F. Soules and C. B. Duke, Phys. Rev. B: Solid State, 1971, 3, 262–274 CrossRef
 .
. - T. Holstein, Ann. Phys., 1959, 8, 325–342 Search PubMed
 .
. - S. Mukamel, Principles of nonlinear optical spectroscopy, Oxford University Press, 1995 Search PubMed
 .
. - D. Walls and G. Milburn, Quantum Optics, Springer-Verlag, 1994 Search PubMed
 .
. - E. Waks and D. Sridharan, Phys. Rev. A: At., Mol., Opt. Phys., 2010, 82, 043845 CrossRef
 .
. - J. Yuen-Zhou, S. K. Saikin and V. Menon, ArXiv e-prints, arXiv: 1711.11213.
- F. Zhou, Y. Liu and Z.-Y. Li, Opt. Lett., 2011, 36, 1969–1971 CrossRef PubMed
 .
. - M. Scully and M. Zubairy, Quantum Optics, Cambridge University Press, New York, New York, 1997 Search PubMed
 .
. - A. González-Tudela, P. A. Huidobro, L. Martín-Moreno, C. Tejedor and F. J. García-Vidal, Phys. Rev. Lett., 2013, 110, 126801 CrossRef PubMed
 .
. - A. Archambault, F. Marquier, J.-J. Greffet and C. Arnold, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 035411 CrossRef
 .
. - L. A. Martínez-Martínez, R. F. Ribeiro, J. A. Campos Gonzalez Angulo and J. Yuen-Zhou, ACS Photonics, 2017 Search PubMed
 .
. - S. Jang, Y. Jung and R. J. Silbey, Chem. Phys., 2002, 275, 319–332 CrossRef
 .
. - S. Jang and R. J. Silbey, J. Chem. Phys., 2003, 118, 9312–9323 CrossRef
 .
. - J. Ma and J. Cao, J. Chem. Phys., 2015, 142, 094106 CrossRef PubMed
 .
. - S. Baghbanzadeh and I. Kassal, Phys. Chem. Chem. Phys., 2016, 18, 7459–7467 RSC
 .
. - S. Baghbanzadeh and I. Kassal, J. Phys. Chem. Lett., 2016, 7, 3804–3811 CrossRef PubMed
 .
. - G. L. Liu, Y.-T. Long, Y. Choi, T. Kang and L. P. Lee, Nat. Methods, 2007, 4, 1015 CrossRef PubMed
 .
. - F. Herrera and F. C. Spano, Phys. Rev. Lett., 2016, 116, 238301 CrossRef PubMed
 .
. - G. D. Scholes, G. R. Fleming, L. X. Chen, A. Aspuru-Guzik, A. Buchleitner, D. F. Coker, G. S. Engel, R. van Grondelle, A. Ishizaki, D. M. Jonas, J. S. Lundeen, J. K. McCusker, S. Mukamel, J. P. Ogilvie, A. Olaya-Castro, M. A. Ratner, F. C. Spano, K. B. Whaley and X. Zhu, Nature, 2017, 543, 647 CrossRef PubMed
 .
. - T. Ozel, P. L. Hernandez-Martinez, E. Mutlugun, O. Akin, S. Nizamoglu, I. O. Ozel, Q. Zhang, Q. Xiong and H. V. Demir, Nano Lett., 2013, 13, 3065–3072 CrossRef PubMed
 .
. - J. A. Hutchison, T. Schwartz, C. Genet, E. Devaux and T. W. Ebbesen, Angew. Chem., Int. Ed., 2012, 51, 1592–1596 CrossRef PubMed
 .
. - V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley, 2011 Search PubMed
 .
. - M. Bednarz, V. A. Malyshev and J. Knoester, J. Chem. Phys., 2002, 117, 6200–6213 CrossRef
 .
. - V. M. Agranovich, M. Litinskaia and D. G. Lidzey, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 085311 CrossRef
 .
. - M. Litinskaya, P. Reineker and V. M. Agranovich, J. Lumin., 2004, 110, 364–372 CrossRef
 .
. - J. del Pino, J. Feist and F. J. Garcia-Vidal, New J. Phys., 2015, 17, 053040 CrossRef
 .
. - A. Canaguier-Durand, C. Genet, A. Lambrecht, T. W. Ebbesen and S. Reynaud, Eur. Phys. J. D, 2015, 69, 24 CrossRef
 .
. - X. Zhong, T. Chervy, S. Wang, J. George, A. Thomas, J. A. Hutchison, E. Devaux, C. Genet and T. W. Ebbesen, Angew. Chem., Int. Ed., 2016, 55, 6202–6206 CrossRef PubMed
 .
. - E. Palik, Handbook of Optical Constants of Solids II, Academic Press, 1985 Search PubMed
 .
. - J. Bellessa, C. Bonnand, J. C. Plenet and J. Mugnier, Phys. Rev. Lett., 2004, 93, 036404 CrossRef PubMed
 .
. - J. Ma, J. Moix and J. Cao, J. Chem. Phys., 2015, 142, 094107 CrossRef PubMed
 .
. - J. M. Moix, J. Ma and J. Cao, J. Chem. Phys., 2015, 142, 094108 CrossRef PubMed
 .
. - S. Valleau, S. K. Saikin, M.-H. Yung and A. A. Guzik, J. Chem. Phys., 2012, 137, 034109 CrossRef PubMed
 .
. - A. O. Govorov, J. Lee and N. A. Kotov, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 125308 CrossRef
 .
. - B. Valeur and M. Berberan-Santos, Molecular Fluorescence: Principles and Applications, Wiley, 2nd edn, 2012 Search PubMed
 .
. - I. Medintz and N. Hildebrandt, FRET – Förster Resonance Energy Transfer: From Theory to Applications, Wiley, 2013 Search PubMed
 .
. - D. L. Andrews, Chem. Phys., 1989, 135, 195–201 CrossRef
 .
. - G. Juzeliūnas and D. L. Andrews, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 8751–8763 CrossRef
 .
. - H. T. Dung, L. Knöll and D.-G. Welsch, Phys. Rev. A: At., Mol., Opt. Phys., 2002, 66, 063810 CrossRef
 .
. - D. M. Coles, P. Michetti, C. Clark, W. C. Tsoi, A. M. Adawi, J.-S. Kim and D. G. Lidzey, Adv. Funct. Mater., 2011, 21, 3691–3696 CrossRef
 .
. - T. Virgili, D. Coles, A. M. Adawi, C. Clark, P. Michetti, S. K. Rajendran, D. Brida, D. Polli, G. Cerullo and D. G. Lidzey, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245309 CrossRef
 .
. - D. M. Coles, P. Michetti, C. Clark, A. M. Adawi and D. G. Lidzey, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 205214 CrossRef
 .
. - N. Somaschi, L. Mouchliadis, D. Coles, I. E. Perakis, D. G. Lidzey, P. G. Lagoudakis and P. G. Savvidis, Appl. Phys. Lett., 2011, 99, 143303 CrossRef
 .
. - D. G. Lidzey, A. M. Fox, M. D. Rahn, M. S. Skolnick, V. M. Agranovich and S. Walker, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 195312 CrossRef
 .
. - M. van Exter and A. Lagendijk, Phys. Rev. Lett., 1988, 60, 49–52 CrossRef PubMed
 .
. - C. Sönnichsen, T. Franzl, T. Wilk, G. von Plessen, J. Feldmann, O. Wilson and P. Mulvaney, Phys. Rev. Lett., 2002, 88, 077402 CrossRef PubMed
 .
. - L. A. Martínez-Martínez, M. Du, R. F. Ribeiro, S. Kéna-Cohen and J. Yuen-Zhou, J. Phys. Chem. Lett., 2018, 9, 1951–1957 CrossRef PubMed
 .
. - D. M. Coles, R. T. Grant, D. G. Lidzey, C. Clark and P. G. Lagoudakis, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 121303 CrossRef
 .
. - J. Chovan, I. E. Perakis, S. Ceccarelli and D. G. Lidzey, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 045320 CrossRef
 .
. - P. Michetti and G. C. La Rocca, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 195301 CrossRef
 .
. - P. Michetti and G. C. La Rocca, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 035325 CrossRef
 .
. - T. K. Hakala, J. J. Toppari, A. Kuzyk, M. Pettersson, H. Tikkanen, H. Kunttu and P. Törmä, Phys. Rev. Lett., 2009, 103, 053602 CrossRef PubMed
 .
. - M. S. Skolnick, T. A. Fisher and D. M. Whittaker, Semicond. Sci. Technol., 1998, 13, 645 CrossRef
 .
. - R. J. Holmes and S. R. Forrest, Org. Electron., 2007, 8, 77–93 CrossRef
 .
. - P. Törmä and W. L. Barnes, Rep. Prog. Phys., 2015, 78, 013901 CrossRef PubMed
 .
. - F. J. Garcia-Vidal and J. Feist, Science, 2017, 357, 1357–1358 CrossRef PubMed
 .
. - V. Kenkre and P. Reineker, Exciton Dynamics in Molecular Crystals and Aggregates, Springer-Verlag, 1982 Search PubMed
 .
. - M. Sarovar, A. Ishizaki, G. R. Fleming and K. B. Whaley, Nat. Phys., 2010, 6, 462–467 Search PubMed
 .
. - J. Flick, M. Ruggenthaler, H. Appel and A. Rubio, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3026–3034 CrossRef PubMed
 .
. - J. Galego, F. J. Garcia-Vidal and J. Feist, Nat. Commun., 2016, 7, 13841 CrossRef PubMed
 .
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc00171e |
|
| This journal is © The Royal Society of Chemistry 2018 |
 Open Access Article
Open Access Article a,
Luis A. Martínez-Martínez
a,
Luis A. Martínez-Martínez a,
Raphael F. Ribeiro
a,
Raphael F. Ribeiro a,
Zixuan Hu
a,
Zixuan Hu bc,
Vinod M. Menon
bc,
Vinod M. Menon de and
Joel Yuen-Zhou
de and
Joel Yuen-Zhou *a
*a
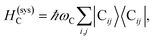
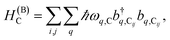
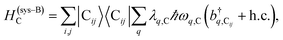
 labels the creation (annihilation) of a phonon of energy ℏωq,C at the q-th vibrational mode of the (i,j)-th molecule in the C slab. Given the molecular character of the problem, vibronic coupling is assumed to be local30 (in contrast to that for relatively ordered materials such as crystals31): exciton Cij couples linearly to
labels the creation (annihilation) of a phonon of energy ℏωq,C at the q-th vibrational mode of the (i,j)-th molecule in the C slab. Given the molecular character of the problem, vibronic coupling is assumed to be local30 (in contrast to that for relatively ordered materials such as crystals31): exciton Cij couples linearly to  and bq,Cij but not to modes in other molecules;32 these couplings are characterized by Huang–Rhys factors λq,C2.33 The SP Hamiltonian HP = H(sys)P + H(B)P + H(sys–B)P has similar form:34,35
and bq,Cij but not to modes in other molecules;32 these couplings are characterized by Huang–Rhys factors λq,C2.33 The SP Hamiltonian HP = H(sys)P + H(B)P + H(sys–B)P has similar form:34,35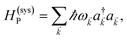
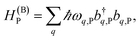
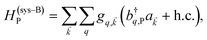
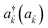 labels the creation (annihilation) of an SP of energy ℏω
labels the creation (annihilation) of an SP of energy ℏω![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) and in-plane wavevector
and in-plane wavevector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) . Bath modes indexed by q,P with corresponding operator
. Bath modes indexed by q,P with corresponding operator 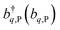 and energy ℏωq,P are coupled to each SP mode
and energy ℏωq,P are coupled to each SP mode ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) with strength gq,
with strength gq,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) . Specifically, these SP interactions occur with either electromagnetic or phonon modes and represent radiative and ohmic losses, respectively.35 The remaining rightmost terms in eqn (1) represent the dipole–dipole interactions amongst donors, acceptors, and SP modes. The HDA term is given by the electrostatic (near-field) dipole–dipole interactions between donors and acceptors,
. Specifically, these SP interactions occur with either electromagnetic or phonon modes and represent radiative and ohmic losses, respectively.35 The remaining rightmost terms in eqn (1) represent the dipole–dipole interactions amongst donors, acceptors, and SP modes. The HDA term is given by the electrostatic (near-field) dipole–dipole interactions between donors and acceptors,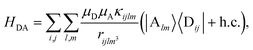
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) Cij| for transition dipole moment (TDM)
Cij| for transition dipole moment (TDM) ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) Cij corresponding to Cij, rijlm is the distance between Dji and Alm, and κijlm =
Cij corresponding to Cij, rijlm is the distance between Dji and Alm, and κijlm = ![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Dij·
Dij·![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Alm − 3(
Alm − 3(![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Dij·
Dij·![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ijlm)(
ijlm)(![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) Alm·
Alm·![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) ijlm) is the orientational dependence of the interaction (we denote
ijlm) is the orientational dependence of the interaction (we denote ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) as the unit vector corresponding to
as the unit vector corresponding to ![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) ). We have ignored the corrections to κijlm due to reflected waves from the metal—despite their prominent effects in phenomena such as photoluminescence36—since they are numerically involved and do not significantly change the order of magnitude of the bare dipole–dipole interaction;37 furthermore their expected effects in HDA will be overwhelmed by HCP, as we shall explain in Sections 2.1 and 3. For simplicity, we take the permittivity on top of the metal to be a real-valued positive dielectric constant εd. The light–matter interaction for species C in the rotating-wave approximation38 is also dipolar in nature and is described by39
). We have ignored the corrections to κijlm due to reflected waves from the metal—despite their prominent effects in phenomena such as photoluminescence36—since they are numerically involved and do not significantly change the order of magnitude of the bare dipole–dipole interaction;37 furthermore their expected effects in HDA will be overwhelmed by HCP, as we shall explain in Sections 2.1 and 3. For simplicity, we take the permittivity on top of the metal to be a real-valued positive dielectric constant εd. The light–matter interaction for species C in the rotating-wave approximation38 is also dipolar in nature and is described by39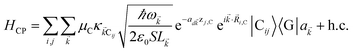
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) i,C,zj,C) are the position coordinates of Cij and |G〉 is the electronic ground state (i.e., with no excitons). Just like in HDA, the interaction between an SP mode and a chromophore (indexed by
i,C,zj,C) are the position coordinates of Cij and |G〉 is the electronic ground state (i.e., with no excitons). Just like in HDA, the interaction between an SP mode and a chromophore (indexed by ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) and Cij, respectively) has an orientation-dependent parameter
and Cij, respectively) has an orientation-dependent parameter 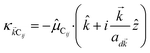 , where
, where 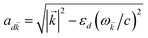 is the real-valued evanescent SP decay constant for the region above the metal. The light–matter coupling also includes the quantization length L
is the real-valued evanescent SP decay constant for the region above the metal. The light–matter coupling also includes the quantization length L![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) (ref. 40) and area S of the SP. We refer the reader to ESI Section S1† for further details of these terms.
(ref. 40) and area S of the SP. We refer the reader to ESI Section S1† for further details of these terms.

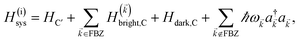 where
where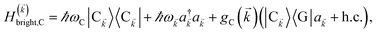
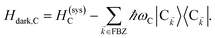
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -mode in the FBZ, there is only one “bright” collective exciton state
-mode in the FBZ, there is only one “bright” collective exciton state 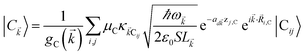 that couples to the
that couples to the ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -th SP mode
-th SP mode 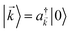 , where
, where 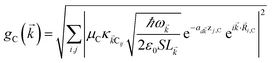 . In addition to the weakly coupled C′ states, H(i)sys has two polariton eigenstates
. In addition to the weakly coupled C′ states, H(i)sys has two polariton eigenstates 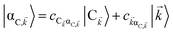 for α = UP, LP (upper polariton and lower polariton, respectively), which are also eigenstates of H(
for α = UP, LP (upper polariton and lower polariton, respectively), which are also eigenstates of H(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) )bright,C for each
)bright,C for each ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ∈ FBZ; throughout this work, cmn = 〈m|n〉. Furthermore, there is a large reservoir of NC − Nxy,C = Nxy,C(Nz,C − 1) “dark” (purely excitonic) eigenstates |dC,
∈ FBZ; throughout this work, cmn = 〈m|n〉. Furthermore, there is a large reservoir of NC − Nxy,C = Nxy,C(Nz,C − 1) “dark” (purely excitonic) eigenstates |dC,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 (d = 0, 1,…, Nz,C − 2) which are also eigenstates of Hdark,C with bare chromophore energy ℏωC.
〉 (d = 0, 1,…, Nz,C − 2) which are also eigenstates of Hdark,C with bare chromophore energy ℏωC.
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) or a uniform mixture of dark states with occupation
or a uniform mixture of dark states with occupation 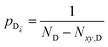 for all d,
for all d,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) —to the incoherent set of all bare acceptor states are,
—to the incoherent set of all bare acceptor states are,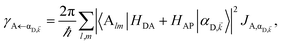

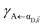 in eqn (8a) can be enhanced or suppressed relative to bare (in the absence of metal) FRET due to additional SP-resonance energy transfer47 (PRET) channel given by HAP, as well as the spectral overlap
in eqn (8a) can be enhanced or suppressed relative to bare (in the absence of metal) FRET due to additional SP-resonance energy transfer47 (PRET) channel given by HAP, as well as the spectral overlap 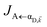 that can be modified by tuning the energy of |αD,
that can be modified by tuning the energy of |αD,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉. Similar findings were obtained for electron transfer with only donors strongly coupled to a cavity mode.48 Given that |αD,
〉. Similar findings were obtained for electron transfer with only donors strongly coupled to a cavity mode.48 Given that |αD,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 corresponds to a delocalized state, one would expect a superradiant enhancement of the rate;5,6 in practice, this effect is minor due to the distance dependence of HDA (see Section S2.3†). On the other hand, eqn (8b) presents an average rate γA←darkD from the dark states and hence does not feature a PRET term. In fact, it converges (see Section S2.5†) to the bare FRET rate (eqn (12b) below) in the limit of large ND≫Nxy,D (when there are many layers of chromophores along z) and isotropically averaged and orientationally uncorrelated TDMs
〉 corresponds to a delocalized state, one would expect a superradiant enhancement of the rate;5,6 in practice, this effect is minor due to the distance dependence of HDA (see Section S2.3†). On the other hand, eqn (8b) presents an average rate γA←darkD from the dark states and hence does not feature a PRET term. In fact, it converges (see Section S2.5†) to the bare FRET rate (eqn (12b) below) in the limit of large ND≫Nxy,D (when there are many layers of chromophores along z) and isotropically averaged and orientationally uncorrelated TDMs ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) Cij for both C = D, A.
Cij for both C = D, A.
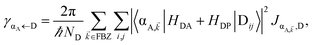
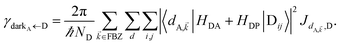
 , whereas NA localized acceptor states contribute to the bare FRET rate. On the other hand, γdarkA←D behaves similarly to eqn (8b) in that it converges (see eqn (13b) and (S30b)†) to the bare FRET rate. Thus, at donor–acceptor separations where the square of the FRET coupling exceeds on average that for PRET, the inequality γαA←D≪γdarkA←D is expected to hold.
, whereas NA localized acceptor states contribute to the bare FRET rate. On the other hand, γdarkA←D behaves similarly to eqn (8b) in that it converges (see eqn (13b) and (S30b)†) to the bare FRET rate. Thus, at donor–acceptor separations where the square of the FRET coupling exceeds on average that for PRET, the inequality γαA←D≪γdarkA←D is expected to hold.
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) grids of different sizes, a complication that does not give more insight into the physics of interest. As done in Section 2.1, we rewrite H(ii)sys in
grids of different sizes, a complication that does not give more insight into the physics of interest. As done in Section 2.1, we rewrite H(ii)sys in ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) -space:
-space: 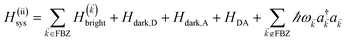 , where
, where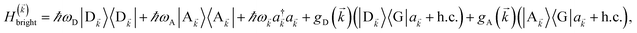
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ∈ FBZ, there are three polariton eigenstates of H(
∈ FBZ, there are three polariton eigenstates of H(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) )bright that are linear combinations of |D
)bright that are linear combinations of |D![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉, |A
〉, |A![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉, and |
〉, and |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉, and we call them UP, middle polariton (MP), and LP, according to their energy ordering. In addition, the presence of Hdark,C yields NC − Nxy,C dark C eigenstates.
〉, and we call them UP, middle polariton (MP), and LP, according to their energy ordering. In addition, the presence of Hdark,C yields NC − Nxy,C dark C eigenstates.
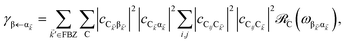
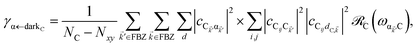
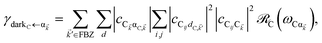
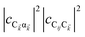 and
and 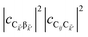 are the fractions of exciton |Cij〉 in the polariton states |α
are the fractions of exciton |Cij〉 in the polariton states |α![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 and
〉 and 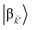 , respectively, while
, respectively, while 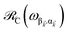 is the single-molecule rate of vibrational relaxation at the energy difference
is the single-molecule rate of vibrational relaxation at the energy difference 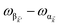 . More specifically,
. More specifically, 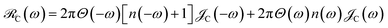 , where Θ(ω) is the Heaviside step function,
, where Θ(ω) is the Heaviside step function, 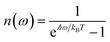 is the Bose–Einstein distribution function (kB is the Boltzmann constant and T is temperature) for zero chemical potential μ = 0, and
is the Bose–Einstein distribution function (kB is the Boltzmann constant and T is temperature) for zero chemical potential μ = 0, and 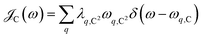 is the spectral density for chromophore C.52 Hence, one can interpret β ← α
is the spectral density for chromophore C.52 Hence, one can interpret β ← α![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) as a sum of incoherent processes (over C and i,j) where the (local) vibrational modes in Cij absorb or emit phonons concomitantly inducing population transfer between the various eigenstates of H(ii)sys. Eqn (11b) and (11c) can be interpreted in a similar light. As an aside, we note that these transitions are analogous to the so-called intraband relaxation among collective exciton states in J-aggregates.53 We now comment on some important qualitative trends in these rates while for simplicity assuming that Nz,D = Nz,A = Nz. First, EET from polariton or dark states to a polariton band (eqn (11a) and (11b)) scale as
as a sum of incoherent processes (over C and i,j) where the (local) vibrational modes in Cij absorb or emit phonons concomitantly inducing population transfer between the various eigenstates of H(ii)sys. Eqn (11b) and (11c) can be interpreted in a similar light. As an aside, we note that these transitions are analogous to the so-called intraband relaxation among collective exciton states in J-aggregates.53 We now comment on some important qualitative trends in these rates while for simplicity assuming that Nz,D = Nz,A = Nz. First, EET from polariton or dark states to a polariton band (eqn (11a) and (11b)) scale as 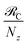 . To see this, note that both
. To see this, note that both 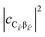 and
and 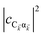 are O(1), while
are O(1), while 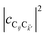 and
and 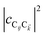 are
are 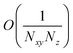 , but the summations
, but the summations 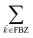 and
and 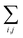 are respectively carried over Nxy and NxyNz terms. On the other hand,
are respectively carried over Nxy and NxyNz terms. On the other hand, 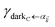 takes values that are on the order of the single-molecule decay
takes values that are on the order of the single-molecule decay 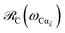 . For sufficiently large Nz, these scalings are consistent with previous studies on relaxation dynamics of polaritons54–56 and can be summarized as follows: the dominant channels of relaxation are from the polariton states to a reservoir of dark states that share the same exciton character; their timescales are comparable to those of the corresponding single-chromophore vibrational relaxation; given the large density of states in this reservoir compared to the polariton bands, the dark states act as a population sink or trap from which population can only leak out very slowly.56,57
. For sufficiently large Nz, these scalings are consistent with previous studies on relaxation dynamics of polaritons54–56 and can be summarized as follows: the dominant channels of relaxation are from the polariton states to a reservoir of dark states that share the same exciton character; their timescales are comparable to those of the corresponding single-chromophore vibrational relaxation; given the large density of states in this reservoir compared to the polariton bands, the dark states act as a population sink or trap from which population can only leak out very slowly.56,57
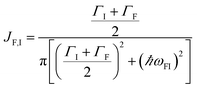 whose parameters are estimated as in Section S2.2;† we set ΓA ≈ ΓD = 47 meV to represent observed values for absorption of TDBC60 and
whose parameters are estimated as in Section S2.2;† we set ΓA ≈ ΓD = 47 meV to represent observed values for absorption of TDBC60 and 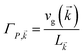 ,39 where vg(
,39 where vg(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) is the SP group velocity. Rigorous treatments of lineshape functions have been previously reported in MC-FRET literature and could be applied to this problem as well,43,44,61,62 although this effort is beyond the scope of our work. We also neglect differences in TDMs and assign μD = μA = 10 D, a typical number for cyanine dyes.63
) is the SP group velocity. Rigorous treatments of lineshape functions have been previously reported in MC-FRET literature and could be applied to this problem as well,43,44,61,62 although this effort is beyond the scope of our work. We also neglect differences in TDMs and assign μD = μA = 10 D, a typical number for cyanine dyes.63
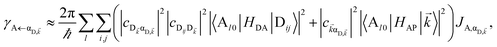
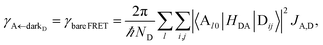
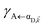 differs from γbare FRET. More concretely, we consider a 35 nm-thick slab of donors with 1 × 109 molecules per μm3 on top of a 1 nm spacer placed on a plasmonic metal film. We set the monolayer slab of acceptors with 1 × 104 molecules per μm2 at varying distances from the donors (Fig. 1a). Then the collective couplings of the donor-resonant SP mode (|
differs from γbare FRET. More concretely, we consider a 35 nm-thick slab of donors with 1 × 109 molecules per μm3 on top of a 1 nm spacer placed on a plasmonic metal film. We set the monolayer slab of acceptors with 1 × 104 molecules per μm2 at varying distances from the donors (Fig. 1a). Then the collective couplings of the donor-resonant SP mode (|![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) | = 1.1 × 107 m−1) to donors and acceptors is gD(
| = 1.1 × 107 m−1) to donors and acceptors is gD(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) = 155 meV and gA(
) = 155 meV and gA(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) ≤ 2.5 meV, respectively. When there is no separation between donor and acceptor slabs, rates >1 ns−1 (Fig. 1b) are obtained for transfer to acceptors from the UP (∼10 ns−1), LP (∼100 ns−1), or the set of dark states (∼10 ns−1). As separation increases however, the rate from dark states decays much faster than those from either UP or LP. This difference stems from the slowly decaying PRET contribution of the polaritons, as well as the totally excitonic character of the dark states, which can only undergo FRET but not PRET (Fig. 1a and b). In fact, for large distances, the FRET contribution becomes significantly overwhelmed by PRET (Fig. 1c), in consistency with previous studies in the weak SP-coupling regime.64 As the distance between slabs approaches 1 μm, it is fascinating that while transfer from dark states (and thus bare FRET) practically vanishes, the rate from either LP (∼1 ns−1) or UP (∼0.01 ns−1) is still at or above typical fluorescence decay rates (0.01–10 ns−1).65 Roughly speaking (in FRET language), this PARET has a Förster distance in the μm range, or 1000-fold greater than the typical nm-range.66 Interestingly, the LP rate exceeds the UP one by 1–2 orders of magnitude at all separations due to greater spectral overlap with the acceptor (Fig. 1a and S1†).
) ≤ 2.5 meV, respectively. When there is no separation between donor and acceptor slabs, rates >1 ns−1 (Fig. 1b) are obtained for transfer to acceptors from the UP (∼10 ns−1), LP (∼100 ns−1), or the set of dark states (∼10 ns−1). As separation increases however, the rate from dark states decays much faster than those from either UP or LP. This difference stems from the slowly decaying PRET contribution of the polaritons, as well as the totally excitonic character of the dark states, which can only undergo FRET but not PRET (Fig. 1a and b). In fact, for large distances, the FRET contribution becomes significantly overwhelmed by PRET (Fig. 1c), in consistency with previous studies in the weak SP-coupling regime.64 As the distance between slabs approaches 1 μm, it is fascinating that while transfer from dark states (and thus bare FRET) practically vanishes, the rate from either LP (∼1 ns−1) or UP (∼0.01 ns−1) is still at or above typical fluorescence decay rates (0.01–10 ns−1).65 Roughly speaking (in FRET language), this PARET has a Förster distance in the μm range, or 1000-fold greater than the typical nm-range.66 Interestingly, the LP rate exceeds the UP one by 1–2 orders of magnitude at all separations due to greater spectral overlap with the acceptor (Fig. 1a and S1†).
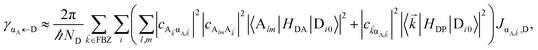
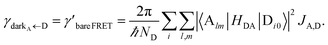
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 for most
〉 for most ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ∈ FBZ (Fig. S3†), the rates to the acceptor UP band fall below fluorescence timescales65 and therefore offer no meaningful enhancements with respect to the bare FRET case (Fig. 2b). While the first two reasons also explain the similarly low rates to the LP band, the major factor is that most states |LPA,
∈ FBZ (Fig. S3†), the rates to the acceptor UP band fall below fluorescence timescales65 and therefore offer no meaningful enhancements with respect to the bare FRET case (Fig. 2b). While the first two reasons also explain the similarly low rates to the LP band, the major factor is that most states |LPA,![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) 〉 essentially overlap only with acceptors that are closer to the metal—and thus farther from the donors—due to the evanescent nature of the SP–exciton coupling (eqn (5)).
〉 essentially overlap only with acceptors that are closer to the metal—and thus farther from the donors—due to the evanescent nature of the SP–exciton coupling (eqn (5)).
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) | = 9.8 × 106 m−1) the collective coupling gA(
| = 9.8 × 106 m−1) the collective coupling gA(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) = 237 meV while keeping gD(
) = 237 meV while keeping gD(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) = 1.7 meV. Consequently, the acceptor UP energy
) = 1.7 meV. Consequently, the acceptor UP energy 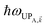 is lifted higher than ℏωD (Fig. 3a and S4†), thus allowing for the carnival effect where the donors and acceptors reverse roles. Due to sufficient spectral overlap between the acceptor UP and donor states (Fig. 3a and S4†), transfer from UP occurs at ∼100 ns−1 for donor–acceptor separation of 1 nm and drops only to ∼1 ns−1 when this separation approaches 1 μm (Fig. 3b). On the other hand, neither the acceptor dark nor LP states contribute to this reversed PARET given their lack of spectral overlap with the donors and detailed balance (especially at T = 0). This result provides the second main conclusion of our work: polaritons offer great versatility to control spectral overlaps without actual chemical modifications to the molecules and can therefore endow them with new physical properties. Before proceeding to simulations for Case (ii), it should first be noted that while our model neglects intermediate- and far-field donor–acceptor dipole–dipole interactions that become relevant at ∼μm distances, these couplings are expected to be small compared to PRET couplings and therefore should not qualitatively change our results for Case (i). The relative insignificance of the far-field, or radiative, contributions is consistent with their correspondence to emission followed by absorption (of a real photon).67 Regardless, these additional interactions can be modeled using a quantum electrodynamics treatment68 of energy transfer in bulk media according to previous literature.69 Second, we highlight that the PARET from polariton states for the donors-only and reversed cases of SC may not be efficient in experiments due to its competition with vibrational relaxation from UP to dark states (∼10–100 fs for exciton-microcavity systems54,70–73) and/or radiative decay (dominated by fast cavity leakage ∼10–100 fs for both microcavities72–74 and SPs75,76). However, conditions may be optimized to suppress these deleterious pathways by detuning the SP energy relative to that of the strongly coupled chromophore such that the polariton state is mostly excitonic and has an enhanced lifetime.77
is lifted higher than ℏωD (Fig. 3a and S4†), thus allowing for the carnival effect where the donors and acceptors reverse roles. Due to sufficient spectral overlap between the acceptor UP and donor states (Fig. 3a and S4†), transfer from UP occurs at ∼100 ns−1 for donor–acceptor separation of 1 nm and drops only to ∼1 ns−1 when this separation approaches 1 μm (Fig. 3b). On the other hand, neither the acceptor dark nor LP states contribute to this reversed PARET given their lack of spectral overlap with the donors and detailed balance (especially at T = 0). This result provides the second main conclusion of our work: polaritons offer great versatility to control spectral overlaps without actual chemical modifications to the molecules and can therefore endow them with new physical properties. Before proceeding to simulations for Case (ii), it should first be noted that while our model neglects intermediate- and far-field donor–acceptor dipole–dipole interactions that become relevant at ∼μm distances, these couplings are expected to be small compared to PRET couplings and therefore should not qualitatively change our results for Case (i). The relative insignificance of the far-field, or radiative, contributions is consistent with their correspondence to emission followed by absorption (of a real photon).67 Regardless, these additional interactions can be modeled using a quantum electrodynamics treatment68 of energy transfer in bulk media according to previous literature.69 Second, we highlight that the PARET from polariton states for the donors-only and reversed cases of SC may not be efficient in experiments due to its competition with vibrational relaxation from UP to dark states (∼10–100 fs for exciton-microcavity systems54,70–73) and/or radiative decay (dominated by fast cavity leakage ∼10–100 fs for both microcavities72–74 and SPs75,76). However, conditions may be optimized to suppress these deleterious pathways by detuning the SP energy relative to that of the strongly coupled chromophore such that the polariton state is mostly excitonic and has an enhanced lifetime.77![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) |=1.1 × 107 m−1, gD (
|=1.1 × 107 m−1, gD (![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) = 155 meV, and gA(
) = 155 meV, and gA(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) = 142 meV) to both chromophores separated up to ∼400 nm (Fig. S6b†). To evaluate the rates derived (Section S3.2†) from eqn (11) under the condition NC ≫ Nxy,C for C = D, A, we introduce a spectral density representing intramolecular exciton–phonon coupling of TDBC:
) = 142 meV) to both chromophores separated up to ∼400 nm (Fig. S6b†). To evaluate the rates derived (Section S3.2†) from eqn (11) under the condition NC ≫ Nxy,C for C = D, A, we introduce a spectral density representing intramolecular exciton–phonon coupling of TDBC: 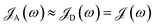 , where
, where
 (functions of the γ rates above, see Sections S3.3 and S3.4†) that can be directly compared to those experimentally reported (Table 2).19 Since experimental
(functions of the γ rates above, see Sections S3.3 and S3.4†) that can be directly compared to those experimentally reported (Table 2).19 Since experimental  have not been determined for the setup of our work, we instead use those describing a blend of two cyanine dyes where physical separation of the dyes did not significantly change the observed photoluminescence.19 In our work, we obtained rates that assume zero temperature and sum across the whole polariton band in the FBZ; in practice, experiments occur at room temperature and probe polariton photoluminescence around a narrow window of wavevectors close to the anticrossings (∼107 m−1 in (ref. 82)). If we take these experimental details into account when calculating
have not been determined for the setup of our work, we instead use those describing a blend of two cyanine dyes where physical separation of the dyes did not significantly change the observed photoluminescence.19 In our work, we obtained rates that assume zero temperature and sum across the whole polariton band in the FBZ; in practice, experiments occur at room temperature and probe polariton photoluminescence around a narrow window of wavevectors close to the anticrossings (∼107 m−1 in (ref. 82)). If we take these experimental details into account when calculating  , we notice good agreements with our theory (see Table 2). As an aside, we reiterate that there are other experimental subtleties, notably competing processes such as radiative decay, that we have not considered but may compromise the longevity of the polariton states and thereby influence the observation of the EET phenomena predicted throughout this work for the two cases of SC.
, we notice good agreements with our theory (see Table 2). As an aside, we reiterate that there are other experimental subtleties, notably competing processes such as radiative decay, that we have not considered but may compromise the longevity of the polariton states and thereby influence the observation of the EET phenomena predicted throughout this work for the two cases of SC. for donor and acceptor cyanine dye J-aggregates strongly coupled to SP (theory) and microcavity (experiment) modesa
for donor and acceptor cyanine dye J-aggregates strongly coupled to SP (theory) and microcavity (experiment) modesa
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.