Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
U–Th–Pb geochronology and simultaneous analysis of multiple isotope systems in geological samples by LA-MC-ICP-MS
Lie-Wen
Xie
 *ab,
Noreen J.
Evans
*ab,
Noreen J.
Evans
 c,
Yue-Heng
Yang
c,
Yue-Heng
Yang
 ab,
Chao
Huang
ab and
Jin-Hui
Yang
ab
ab,
Chao
Huang
ab and
Jin-Hui
Yang
ab
aState Key Laboratory of Lithospheric Evolution, Institute of Geology and Geophysics, Chinese Academy of Sciences, P. O. Box 9825, Beijing 100029, P. R. China. E-mail: xieliewen@mail.iggcas.ac.cn; Fax: +86-010-62010846; Tel: +86-010-82998599
bInstitutions of Earth Science, Chinese Academy of Sciences, P. O. Box 9825, Beijing 100029, P. R. China
cSchool of Earth and Planetary Science, John de Laeter Centre, Curtin University, WA, Australia
First published on 17th August 2018
Abstract
Laser ablation single/multiple collector inductively coupled plasma mass spectrometry (LA-SC/MC-ICP-MS) has become one of the most widely used in situ micro-analytical tools for the determination of isotopic ratios and trace element signatures in solid geological materials. The advantages include high spatial resolution, high sample throughput, good precision and accuracy, and limited sample preparation. For the application of these techniques in U–Th–Pb geochronology, the main challenges involve ion counter drift, matrix differences between reference materials and samples, laser-induced downhole elemental fractionation and common lead corrections. Given the requirement to achieve the maximum amount of geochemical information within the limited analytical domain of complexly zoned or small samples, simultaneous analysis of multiple isotopic systems and/or trace elements using laser ablation split stream (LASS) techniques is now widely applied. This article summarizes recent advances in LA-SC/MC-ICP-MS U–Th–Pb geochronology and LASS techniques. We review recent efforts to improve spatial resolution, calibrate ion counter drift, and correct for common lead contamination, elemental fractionation and matrix mismatching. A summary of the range of minerals utilized for LA-MC-ICP-MS geochronology and LASS is provided, along with a discussion of potential directions for future research.
1. Introduction
Accurate U–Th–Pb geochronology of accessory minerals (e.g., zircon, baddeleyite, monazite, apatite, rutile, titanite, allanite, xenotime, uraninite, perovskite, loparite, bastnaesite, eudialyite, columbite–tantalite, andradite, schorlomite and others) is critical for deciphering geological processes. The most commonly used techniques are isotope dilution thermal ionization mass spectrometry (ID-TIMS), secondary ion mass spectrometry (SIMS) and laser ablation single/multiple collector inductively coupled plasma mass spectrometry (LA-SC/MC-ICP-MS). Walder et al. (1993)1 successfully introduced a method for measuring the Pb isotope ratios of solid samples, showing its potential to yield very high-precision isotopic ratio measurements for natural materials with high spatial resolution. Laser probe methods provide several advantages over high precision ID-TIMS including the ability to directly and rapidly measure small volumes of material with limited sample preparation, and to provide ages at a high spatial resolution, with accuracy to within 1% of those obtained using ID-TIMS (e.g., ref. 2), although it is also important to consider error propagation when inter-method comparisons are made.3 In addition, compared with the relatively time-consuming SIMS approach, laser methods offer higher ionization efficiency and analytical throughput (particularly if data acquisition on the MS is triggered from an automated laser sequence, accommodating hundreds of ablations in a single day), with lower polyatomic interference (particularly in the case of the newly introduced tandem MS/collision cell MS systems; e.g. Agilent 8900-QQQ, Thermo Fisher TQ series; Nu Plasma Sapphire) and matrix effects.Measurement of isotopic compositions by LA-MC-ICP-MS (multi-collector) offers significant advantages over LA-SC-ICP-MS (single collector) methods. Multi-collectors simultaneously measure all isotopic signals over flat-topped peaks so that (1) the detection efficiency is significantly improved and relatively high spatial resolution is obtained,4,5 and (2) the effects of spectral skew and flicker noise from the plasma source or ablated particles are removed or significantly reduced, resulting in improved counting statistics and lower internal and external uncertainties in isotopic ratios.2,6,7 As a consequence, LA-MC-ICP-MS techniques have rapidly developed and are now widely used for geochronology and isotopic geochemistry (e.g., measuring Sr, Nd, Hf and U–Th–Pb isotopic ratios), with high precision and accuracy and at high spatial resolution (e.g., ref. 1 and 8–11).
For studies on complexly zoned minerals, small grains (<10 microns) and detrital/inherited minerals, researchers must obtain the maximum amount of geochemical information (geochronology, isotope composition and trace element concentration) on a single ablated volume. The coupling of laser systems and more than one MS system where the carrier gas flow (and, therefore, the ablated product) is split between the mass spectrometers has been termed laser ablation split stream (LASS) analysis.12,13 Simultaneous measurement of isotopic signatures (e.g. U–Th–Pb and Lu–Hf, U–Th–Pb and Sm–Nd, and Sm–Nd and Lu–Hf) on a MC-ICP-MS and trace elements (or U–Th–Pb) on a SC-ICP-MS (or another MC-ICP-MS/high resolution ICP-MS) means that several datasets can be obtained on a single ablation volume, preserving provenance information and the spatial relationship between key chronological and geochemical tracer records (e.g., ref. 4 and 12–17).
In this article we provide an overview of LA-MC-ICP-MS dating techniques with ion counter (IC) calibrations, and corrections for common lead, mass fractionation and matrix matching issues. Recent improvements in ultra-high spatial resolution U–Th–Pb dating is reviewed, as is the current state of LASS analysis in various mineral phases. Finally, we present our perspective on future developments that might further resolve the challenges associated with these techniques.
2. Background
The significant increase in the availability of inductively coupled plasma mass spectrometers with multiple Faraday collectors (MFCs) and/or multiple ion counters (MICs) has greatly improved research on stable and radiogenic isotopic systems in the past two decades. Coupled with laser ablation (LA) systems (including nanosecond or femtosecond lasers), in situ high spatial resolution isotope analysis of solid geological samples has become relatively routine. The MFC systems can provide a wider dynamic linear range of over five to six orders of magnitude and a more stable performance, compared with the MIC systems, which utilize the standard–sample bracketing technique (SSB).18 Laser ablation or solution sampling MFC-ICP-MS systems yield Sr, Nd and Hf isotope compositions with high precision, using an internal isotope pair to correct for mass fractionation.9,19,20 However, a Faraday cup is about 100 times less sensitive than a secondary electron multiplier (SEM).21 The signal to noise ratio of Faraday collectors with the default 1011 ohm amplifier is too low to obtain high precision data when the signal intensities are low,22,23 and the application of LA-MFC-ICP-MS techniques to U–Th–Pb dating is limited to either very old minerals or minerals with a high U content and high radiogenic Pb complement (e.g., ref. 2, 22, 24 and 25).To improve the precision of measurements obtained using small ion beams on MFC systems, amplifiers equipped with 1012 and 1013 ohm resistors in the feedback loop were developed, increasing the gain by a factor of 10 and 100 times and improving the theoretical signal to noise ratio by a factor of 3 and 10, respectively, compared to the default 1011 ohm resistors.23 For example, Kimura et al. (2015)26 used a 193 nm excimer laser and 200/266 nm femtosecond laser coupled with an enhanced sensitivity MFC-ICP-MS (Neptune) using 1012 ohm amplifiers to determine the U–Pb ages of reference zircon and monazite crystals with an internal precision of 1–2% from a crater of dimensions 50 μm × 10 μm (diameter × depth) at a repetition rate of 2 Hz for 30 s.
In contrast, the MIC system provides a powerful ability to measure small ion signals, which are the norm for high spatial resolution U–Th–Pb dating.23 The precision of the measured 206Pb/207Pb ratio on two ion counters is remarkably superior to that produced by an ion counter in conjunction with a Faraday cup (with the 1011 ohm amplifier) when the measured signals are less than 12.5 mV (Fig. 1).5 Many MC-ICP-MS instruments can be equipped with a series of MFC and MIC detectors with the primary analytical application dictating the ideal detector configuration. In U–Th–Pb dating, one detector configuration places the Hg isotopes and most/all of the Pb isotopes on ion counters and the other isotopes (including 232Th, 235U and 238U) on Faraday cups, such as in the U–Th–Pb dating of zircon, monazite, and titanite by Simonetti et al. (2006).27 An alternate approach places all measured isotopes on ion counters, such as U–Pb dating of zircon by Hattori et al. (2017)7 and Xie et al. (2017).5 The precision of zircon U–Pb dating with MIC systems is about 1% (2 s), which is comparable to that achieved by SIMS at high ion intensities.28,29 The stability of ion counters, however, is worse than that of Faraday cups. Some aspects of MIC systems, such as non-linear behavior, drift in counting efficiency depending on the count rate, and the difficulty in determining the IC dead time, can limit their precision.7,30
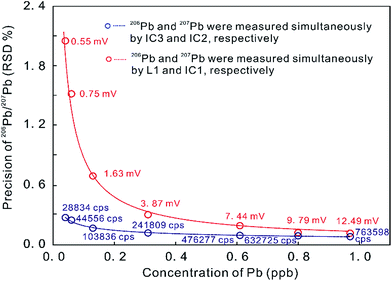 | ||
| Fig. 1 Precision of Pb ratio determination at a range of Pb concentrations as measured on ion counters and on a combination of ion counters and Faraday cups (with a 1011 ohm amplifier) on a Neptune Plus MC-ICP-MS. Red data indicate 206Pb signal intensities on L1 in millivolt [mV] and blue data indicate 206Pb signal intensities on IC3 in counts per second [cps]. Better internal 206Pb/207Pb precision was obtained in MIC mode, compared to using a combination of ion counters and Faraday cups (from ref. 5). | ||
3. U–Th–Pb geochronology
3.1 Ion counter corrections
The secondary electron multiplier (SEM) is used extensively as an ion detector in mass spectrometers. A typical discrete dynode electron multiplier has 12 to 24 dynodes, and can amplify a small ion current by a factor of 104–108.31 This ability makes it valuable for in situ laser ablation analysis of geological samples where a highly sensitive detection method is required. Applications using SEMs in ion counting mode, however, suffer from variability in detection efficiency, which is associated with time and ion beam size.7,30,32 In order to obtain high accuracy and precision chronological data using LA-MC-ICP-MS systems with ion counters, it is necessary to characterize each detector in detail so that corrections can be applied (e.g. cross-calibration of the relative yield between ion counters and/or Faraday cups, dead time and non-linearity).When the operating voltage of a SEM is at its plateau, almost all incident ions are detected. A beam with an ion count rate of 6.25 × 107 cps (counts per second) measured on a SEM should theoretically produce a signal intensity of 1 V on a Faraday cup with a 1011 ohm resistor. In fact, the count rate responses between Faraday cups and SEMs are different, and these two detection systems have to be experimentally cross-calibrated to obtain the FC-SEM yield.33 Previous studies have described different methods for determining FC-SEM yield.28,33,34
Detector dead time is the time during which the ion counting system is unable to count incoming ions after the impact of a previous ion. This parameter is a feature of both the detector itself and the ion counting electronics, which depend on the pulse amplifiers.30 Dead time is corrected by applying the equation It = I0/(1 − I0τ), where It is the count rate corrected for dead time losses, I0 is the count rate obtained with no dead time correction applied (i.e., dead time ∼0 ns) and τ is the apparent dead time of the detection system.31 Several methods have been developed to determine the dead time (e.g., ref. 35–38). Nelms et al. (2001)32 evaluated four methods of dead time calculation on two quadrupole SC-ICP-MS instruments and found that the most suitable method was the one based on studies of the 204Pb/208Pb isotope ratio measured for a series of Pb solutions with different Pb concentrations. The raw isotope ratios were recalculated using different dead time settings and the optimum dead time was obtained by plotting linear regression lines through the data with a gradient of zero (i.e. the dead time was independent of concentration). The dead time for each ion counter on an MC-ICP-MS was recently ascertained by measuring isotopic ratios in U series solutions (IRMM-072) and Ba, Lu and W solutions in static mode, which makes the procedure independent of plasma instability and therefore is an ideal method for MC-ICP-MS instruments.7,30
The reason for the non-linear response of ion counters is still not well understood. A non-linear response results in relatively more pulses counted at higher beam intensities,31,33 perhaps due to a memory effect. At higher beam intensity, sustained elevated SEM yield over 15–20 s suggests that each new pulse might experience interference from a decaying predecessor pulse. In contrast, Zhang et al. (2015)34 observed the opposite phenomenon, low SEM responses at count rates higher than a threshold of ∼320![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cps. Furthermore, Hoffmann et al. (2005)33 observed that the nonlinearity starts at count rates as low as 10 cps, much lower than that of the 104 to 105 cps threshold reported by Richter et al. (2001).31 Richter et al. (2009, 2016)30,39 reported insignificant non-linearity in the responses of SEMs on the same ion counters (MasCom) used by Zhang et al. (2015).34 These studies highlight the importance of detailed characterization of each ion counter on a new system. In order to avoid the influence of typical ion beam intensity fluctuation, combined SEM–Faraday cup measurements in static mode, where the SEM is used to detect a low-abundance isotope of a certified isotopic reference material and Faraday cups detect the major isotopes, may be more suitable for determining nonlinearity effects than the peak jump method.30,33,39
000 cps. Furthermore, Hoffmann et al. (2005)33 observed that the nonlinearity starts at count rates as low as 10 cps, much lower than that of the 104 to 105 cps threshold reported by Richter et al. (2001).31 Richter et al. (2009, 2016)30,39 reported insignificant non-linearity in the responses of SEMs on the same ion counters (MasCom) used by Zhang et al. (2015).34 These studies highlight the importance of detailed characterization of each ion counter on a new system. In order to avoid the influence of typical ion beam intensity fluctuation, combined SEM–Faraday cup measurements in static mode, where the SEM is used to detect a low-abundance isotope of a certified isotopic reference material and Faraday cups detect the major isotopes, may be more suitable for determining nonlinearity effects than the peak jump method.30,33,39
3.2 Challenges in U–Th–Pb geochronology
Common Pb from the accessory mineral itself can be corrected for by using Tera and Wasserburg (1972)44 concordia or isochron plots of a suite of co-genetic grains with a large spread in common Pb/radiogenic Pb ratio, which do not require an estimate of the initial Pb isotopic composition, or by applying an appropriate initial Pb isotopic composition to individual analyses.45–47 The first approach can be employed in U–Th–Pb dating with highly variable proportions of common Pb, such as the U–Th–Pb dating studies by LA-MC-ICP-MS for titanite (e.g., ref. 28, 41, 46 and 48), apatite (e.g., ref. 41 and 49), rutile (e.g., ref. 46 and 50) and zircon (e.g.ref. 29 and 46), projecting a regression line through a data point without preliminary common-Pb correction data on a Tera–Wasserburg (1972)44 concordia diagram, to deduce the precise common Pb component on the 207Pb/206Pb axis. The 238U/206Pb age can then be calculated as the regression lower intercept 206Pb/238U age on the concordia (Ludwig et al., 1998).51
The alternative approach usually includes three different methods (i.e., 204Pb-, 207Pb- and 208Pb-correction) detailed by Williams (1998)52, involving estimates of initial Pb composition, which can be obtained by analyzing a low-U co-genetic phase (e.g., K-feldspar or plagioclase) with negligible radiogenic Pb, or from Pb evolution models (e.g., ref. 53). The latter is the only option for U–Th–Pb dating of detrital accessory minerals containing common Pb.46
The simultaneous collection of flat-topped peaks during LA-MC-ICP-MS analysis makes it possible to accurately measure 204Pb abundance and correct for the isobaric interference from 204Hg on the basis of the natural 202Hg (or 201Hg)/204Hg ratio. Any additional 204Pb measured during the ablation is assumed to have been derived from the sample (i.e., common-Pb) and is used to correct the 206Pb, 207Pb and 208Pb peaks according to Stacey and Kramers' (1975)53 common lead model values for 206Pb/204Pb, 207Pb/204Pb and 208Pb/204Pb, given an appropriate estimate of the mineral age without the assumption of concordance. For most zircons, variation in background corrected 204Pb counts is high and the mean abundance is so low that the common Pb correction becomes insignificant (e.g., ref. 5 and 54). 204Pb-correction is theoretically the most precise and accurate way to perform common Pb correction (e.g., ref. 2, 43, 55 and 56); however, the initial 206Pb/238U age estimated from the raw data considerably overestimates the true age when the common Pb/radiogenic Pb ratio is high. To address this, Thomson et al. (2012)56 applied a five-step iterative process using Stacey and Kramers' (1975)53 common Pb model to accurately reproduce the age of apatite and achieve ages with a precision of <2% (2 s).
Both the 207Pb- and 208Pb-correction methods of U–Th–Pb analyses make assumptions of ideal concordance of 206Pb/238U and 207Pb/235U or 208Pb/232Th without the measurement of 204Pb (e.g., ref. 57). The 207Pb-correction method requires the measurement of 238U/206Pb and 207Pb/206Pb ratios and an appropriate estimate for common Pb composition, which is widely used in U–Pb dating by SIMS (e.g., ref. 58). The 208Pb-correction method is less commonly applied, requiring measurement of 208Pb/206Pb and 232Th/238U ratios and an appropriate estimate of common Pb composition. However, for extremely low Th/U ratios (<0.003) in rutile, where almost all of the 208Pb measured is from common Pb, the 208Pb-correction method can be routinely applied as an initial common lead correction.59
Methods to correct downhole fractionation have been developed and can be subdivided according to whether or not standard–sample bracketing (SSB) is employed in modeling downhole fractionation patterns.65 For a given laser spot diameter and energy density, time-dependent elemental fractionation can be corrected by (1) using a linear model between elemental ratios and hole depth;60 (2) using a least squares linear fit of the elemental ratio data for each spot analysis, which does not require all analyses to have the same fractionation pattern;67 or (3) using exponential curves and smoothed cubic splines to more efficiently correct complex fractionation trends.65
However, the popular SSB method takes the average ratio of the time interval in the reference material(s) to correct unknowns, and the reference material is used to correct for instrumental mass fractionation and laser-induced elemental fractionation simultaneously, without any requirement to observe or model the fractionation behavior (e.g., ref. 64 and 71). This approach assumes that the features of downhole fractionation in the reference material can be used to model its effects in the unknowns. A similar method was specifically developed for small volume sampling with high spatial resolution, where all ions measured during an ablation are treated together as “total counts”.72,73
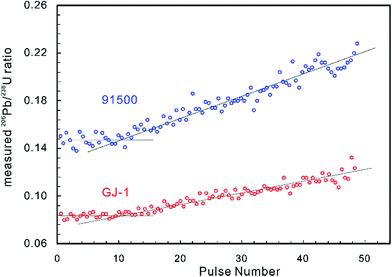
Laser-induced elemental fractionation of Pb from U is observed to be a linear function of the number of laser pulses (crater depth), and is inversely exponentially correlated with spot size.60 Therefore, longer (deeper) ablations can require even more severe corrections. Experimental results have demonstrated that the LA-MIC-ICP-MS measured 206Pb/238U ratios for the standard reference zircons 91500 (ref. 74) and GJ-1 (ref. 64) are stable in the first 1.3 μm of the ablation (approx. 10 pulses and 130 nm per pulse) and then increase with increasing ablation depth (Fig. 2) (using a G2 laser ablation system at a laser fluence of 4 J cm−1, repetition rate of 4 Hz and beam size of 5 μm).5 This shows that shallow ablations can reduce the degree of laser-induced downhole fractionation.5,7
If the pulse width of the laser is greater than the electron–photon relaxation time of the target, heat is transferred to the sample and elemental fractionation can occur.77 The short pulse width of femtosecond lasers addresses this issue, theoretically reducing fractionation, especially between volatile and refractory elements of particular interest such as Pb and U.78–81 Femtosecond laser ablation (fs-LA) offers additional advantages over ns-LA with the production of more uniform and favorably sized particles (about ∼0.1–0.2 μm), enhancing transport and ionization efficiency, and enhancing precision, accuracy and detection limits.76,79,80 This reduction in matrix effects and potential elimination of laser-induced fractionation has obvious implications for LA geochronology.82 Horn and Blanckenburg (2007)83 illustrated that elemental fractionation between Pb and U was absent during fs-LA and that no matrix match between the standard and the sample was needed. Kimura et al. (2011)84 indicated that there was no downhole fractionation of 206Pb/238U using 200 nm ultra-violet fs-LA.
However, the elemental fractionation effect is not totally eliminated under some fs-LA experimental conditions. Laser-induced downhole fractionation of 206Pb and 238U was detected during zircon dating using a 260 nm NWR fs-LA and attributed to thermal effects by Hattori et al. (2017)7, although the observed fractionation was smaller than that induced during ns-LA. In addition, comparable elemental fractionation effects have been noted using 193 nm nanosecond-LA (ns-LA), 265 nm fs-LA and 795 nm fs-LA,85,86 and elemental fractionation was observed on 66Zn/65Cu and 208Pb/238U ratios in the aerosol produced by fs-LA of silicate glass (SRM NIST 610) by Koch et al. (2006).87 Heat diffusion processes can penetrate a zone encompassing several hundreds of nm even using short pulse length fs-LA,88 and the chemical composition of aerosols produced during the fs-LA of natural and synthetic solids is dependent on particle size and morphology as pronounced element partitioning into different particle size fractions has been observed.89 Furthermore, these particles vaporize at different positions within the ICP, so non-matrix matched quantification capabilities will be limited.90 Kimura et al. (2011)84 demonstrated that 200 nm fs-LA yielded absolute 206Pb/238U ratios that deviated from the natural ratios in zircon by 1.4% when synthetic glass was utilized as a standard, indicating that performing fs-LA solid analyses using non-matrix matched calibration may restrict accuracy.91 These studies indicate that fs-LA may offer improvements over ns-LA, but that matrix matching of standards and unknowns is still recommended at this stage.
The SSB method assumes that reference materials and unknowns behave identically during ablation. It is essential to age determination accuracy that the mineral unknown analyses are bracketed by a reference material of the same phase (e.g., using a zircon reference material to normalize zircon unknowns). Using non-matrix matched reference materials can result in a 10–20% age offset from the TIMS age.56,92 To complicate matters, even in single mineral phases, features such as accumulated radiation damage, trace element composition, crystal colour and crystallographic orientation could affect ablation efficiency and consequently limit accuracy and precision. Therefore, any reduction in matrix differences between unknowns and reference materials will improve age accuracy and precision.93
Most matrix effect studies focus on zircon dating (e.g., ref. 93–98) and reveal that the laser ablation rate in zircon is dependent on the optical and mechanical character of the zircon matrices.99 The optical and physical properties of zircons change with their crystalline state, which is governed by lattice defects caused by both radiation damage and the substitution of certain trace elements within the zircon crystal structure.100,101 For example, the laser penetration rate correlates positively with increased structural strain and distortion due to ion substitution into the Zr crystallographic site by REEs and Hf, and/or into the Si site by P although this dependence is not very significant.94,102 Changes in ablation rate could also reflect the degree of structural damage produced by alpha-decay,93,97–99,102 optical and mechanical properties of different crystallographic planes,103 crystal orientation and change in crystal color.99,102 In addition, a slight increase in laser fluence produces a subtle increase in penetration depth (1–2 μm for 200 pulses) and a significant increase in the 206Pb/238U ratio (1–2%) measured by LA-ICP-MS. A systematic age bias (relative to ID-TIMS) is strongly correlated with the offset in ablation rates between the ‘standard’ and the ‘unknown’ (Fig. 3).99 However, structural damage produced by alpha-decay plays the most important role in defining the ablation behavior of zircon102 and the ablation behavior in turn affects the amount of laser-induced U–Th–Pb fractionation, the magnitude and accuracy of the correction required and the subsequent accuracy and precision of ages calculated.104
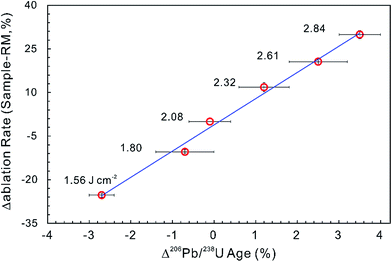 | ||
| Fig. 3 The influence of ablation rate on corrected LA-ICP-MS 206Pb/238U ages. Different energy densities (given in J cm−2) were used to achieve slightly different ablation rates. The ablation rate offset was calculated relative to the ablation rate of the ‘standard’ zircon at a laser fluence of 2.08 J cm−2. The age offset was calculated for the measured LA-ICP-MS 206Pb/238U age relative to the accepted ID-TIMS age. Error bars represent 2SE uncertainty (data from ref. 99). | ||
In order to improve matrix effect corrections, several studies have attempted to establish a firm relationship between the degree of radiation damage and parameters that can be used as proxies for the ablation rate and/or penetration depth. For example, the systematic offset in LA-ICP-MS ages relative to the ID-TIMS age is positively correlated with the alpha dose per gram calculated from U and Th concentrations and U–Pb age, and with FWHM values (FWHM = full width at half maximum of the ν3 (SiO4) band measured by Raman spectroscopy, which is directly proportional to the amount of radiation damage accumulated in the zircon structure).97–99,102,104,105 Based on these studies, it is reasonable to assume that the alpha dose per gram or the FWHM values can be used to predict the laser ablation rate and penetration depth in zircon. However, the calculated alpha dose per gram provides a sensible estimate of the radiation damage only if the zircon structure has experienced no significant annealing of radiation damage since crystallization,106,107 and obtaining FWHM values for individual crystals is only feasible for a limited number of grains representative of magmatic populations99,102 and is not practical for detrital studies, for example, where >120 grains per sample are often analyzed to derive statistically significant population distributions (e.g., ref. 105–109).
Potential approaches to reducing the difference in radiation damage between zircon reference materials and unknowns (and thereby reduce differences in laser penetration) include applying thermal annealing to repair crystal-lattice damage97,102,104 and/or chemical abrasion to remove domains in which Pb loss has occurred.110,111 Allen and Campbell (2012)97 demonstrated that the percentage offset between ID-TIMS and LA-ICP-MS 206Pb/238U ages showed an obvious correlation with the alpha dose per gram, suggesting that any difference in the alpha dose between ‘standards’ and ‘unknowns’ could result in inaccurate and imprecise 206Pb/238U ages (Fig. 4a). The correlation between the alpha dose and the age offset was eliminated after thermal annealing, showing that annealing can efficiently repair the crystal-lattice of zircon (Fig. 4b), yielding more accurate, but not necessarily more internally precise, LA-ICP-MS 206Pb/238U ages. Solari et al. (2015)112 demonstrated that thermal annealing prior to zircon LA-ICP-MS analyses not only produced more accurate U–Pb ages, but also significantly reduced the scatter of the U–Pb age, trace element content and Hf isotope data. A comparison between thermal annealing of samples at 850 °C for 48 h and 1000 °C for 36 h by Marillo-Sialer et al. (2016)102 indicated that incomplete reconstitution of the crystal structure occurs for partially to highly metamict zircon matrices treated at 850 °C. It follows that pre-analysis annealing of reference and unknown zircons could improve the accuracy of LA-ICP-MS zircon U–Pb dating.
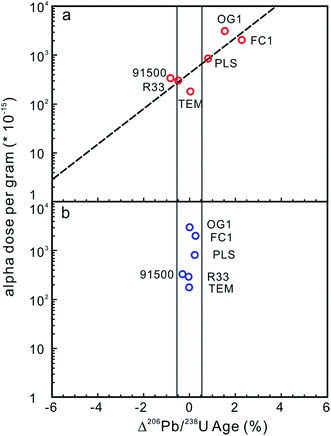 | ||
| Fig. 4 (a) The effect of alpha dose on the corrected 206Pb/238U age for the zircon analyses. The x-axis is the percentage offset in the 206Pb/238U age measured by LA-ICP-MS and ID-TIMS. The y-axis is the corresponding alpha dose calculated from the average U and Th contents and the ID-TIMS age. The field shown is the 2 standard error internal precision for Temora 3 (primary reference standard treated as an unknown), which is 0.51%. The percentage offset in the 206Pb/238U age showed obvious correlation with the alpha dose, indicating that differences in the alpha dose between ‘standards’ and ‘unknowns’ could result in inaccurate and imprecise 206Pb/238U ages. (b) The percentage offsets in the 206Pb/238U age for zircon analyses after annealing. The y-axis is the same as in Fig. 3a. The x-axis is the percentage offset in the 206Pb/238U age measured by LA-ICP-MS after annealing relative to that obtained using ID-TIMS. The correlation between the alpha dose and the age offset has been eliminated, indicating that annealing improves accuracy but not internal precision (modified from ref. 97). | ||
3.3 Ultra-high spatial resolution U–Th–Pb dating
U–Th–Pb geochronology of accessory minerals (e.g., zircon, monazite, apatite, rutile and titanite) has become one of the most powerful techniques for dating a variety of high temperature igneous and metamorphic events, and to constrain provenance.113,114 The complex zonation in natural crystals with inherited cores and younger rims has tremendous potential for unraveling complicated geological histories. However, analysis of these complex accessory minerals, together with the analysis of tiny mineral grains (e.g., zircon from ultramafic rocks) or sub-domains in larger crystals (e.g., in monazite), requires in situ dating techniques with high spatial resolution.5 Modified collector configurations coupling Faraday collectors with ion counters are ideally suited to this type of analysis (e.g., ref. 2, 22, 24, 28, 29, 43, 50, 55, 56 and 115–118), enabling signals of <1 mV to be measured with confidence (e.g., ref. 4, 27, 54, 72 and 73).With Pb and Hg isotopic signals collected on ion counters and U and Th measured on Faraday cups, a spatial resolution of 5–40 μm can be achieved for zircon, monazite, titanite and rutile,27,50 even in standard petrographic thin sections where textural information is also retained. Simonetti et al. (2006)27 utilized well-characterized external mineral reference materials to correct for mass fractionation and the 206Pb/238U and 207Pb/235U values (obtained from a Nu Plasma MC-ICP-MS equipped with ETP ion counters) were reported at an external reproducibility (2σ) of less than 3%. Furthermore, the aspiration of a Tl solution was used to simultaneously correct for instrumental mass bias in the measured 207Pb/206Pb value, to improve precision (2σ values were between ∼0.3 and 1%). Low Pb yields obtained from zircon with intricate isotopic zoning at spatial scales as small as 12–14 μm (diameter) by 4–5 μm (depth, measured with a MicroXAM-100 3D surface profiler) can be determined with a GV Isoprobe MC-ICP-MS equipped with Channeltron detectors and using a total count integration method to calculate U and Pb isotope ratios and ages precisely and accurately within 2%.72 The technique was successfully applied to provenance studies of detrital zircon in fine-grained mudstones and shales, and to create zircon U–Pb age maps to investigate the detrital and metamorphic history of granulite-facies paragneiss. If water is aspirated during laser ablation analysis, it can double sensitivity and reduce 204Pb signal intensities when the ablated material is carried into the plasma. This method has been applied to age and U/Th ratio mapping of zoned zircon. The results measured with a GV Isoprobe MC-ICP-MS demonstrate that core and rim ages are resolvable (92.6 ± 1.3 Ma and 58.3 ± 1.1 Ma, respectively)43 and the method, with a smallest pit size of 10 μm diameter and ∼3 μm depth measured with an NT9800 optical interferometer, has also been applied to baddeleyite, which is often the smallest datable mineral in samples.118
However, after the laser is fired, a signal delay can be observed before the 238U Faraday cup reaches its peak signal intensity relative to the 206Pb ion counter (Fig. 5),5,73 and this time offset phenomenon can adversely affect data quality. Using a low volume ablation cell, isotope ratios from an individual laser pulse can be calculated by integrating the baseline-subtracted total counts for the entire pulse. This ‘total signal integration’ method can eliminate the effect of different detector response times and data obtained for reference zircons using a Nu Plasma HR MC-ICP-MS, which indicates that it is possible to consistently measure 206Pb/238U and 207Pb/206Pb ratios with external reproducibilities of 2% and 2.8% (2SD), respectively.73 Isotopic depth profiles for two grains of zoned zircon from an augen gneiss sample from the Greater Himalayan Series of north-central Bhutan were generated by analyzing consecutive laser pulses from the same ablation site using a 50 μm spot size and a depth resolution of ∼0.1 μm per pulse based on the scanning electron microscope secondary electron images of ablation craters (Fig. 6).73 Another approach to eliminating the effect of the time offset is to collect all isotopes on ion counters (LA-MIC-ICP-MS).5,7 For collecting a small signal, the ion counter has an obvious advantage over the Faraday cup (Fig. 1), so this approach can provide higher spatial resolution. LA-MIC-ICP-MS techniques make it possible to date zircon with a 238U signal of less than 0.5 mV at a beam diameter of 5.8–7.4 μm and sampling depth of 1–3 μm (measured by atomic force microscopy) using a laser fluence of 4 J cm−2, with accuracy and precision of less than 1% (2 s) for the weight mean 206Pb/238U age (using a Neptune Plus MC-ICP-MS).5 A 1 s ablation at a fluence of about 1.6 J cm−2 (8 laser shots) produced a 25 μm pit with a depth of <1 μm (estimated using a Leica DVM5000 HD digital microscope with 2000× magnification) in zircon standard Plĕsovice and yielded a U–Pb concordia age of 339.5 ± 6.7 Ma (ref. 7) (Nu Plasma HR MC-ICP-MS), which is within the uncertainty of the recommended value (337.13 ± 0.37 Ma (ref. 119)). These techniques offer the opportunity to accurately date complex accessory minerals with ultra-high spatial resolution, comparable to that of SIMS techniques.
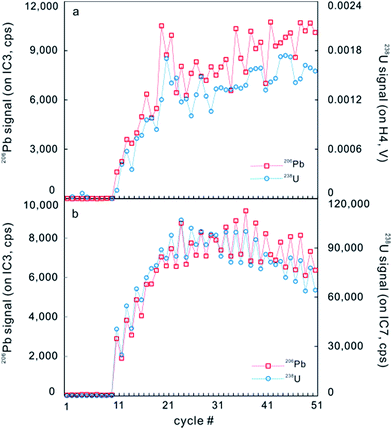 | ||
| Fig. 5 A typical time-resolved profile on GJ-1 zircon for continuous laser ablation analysis measured on a Neptune Plus. (a) Signals of 206Pb (red) and 238U (blue) were counted on IC3 and Faraday cup H4, respectively. (b) Signals of 206Pb (red) and 238U (blue) were counted on IC3 and IC7, respectively (from ref. 5). | ||
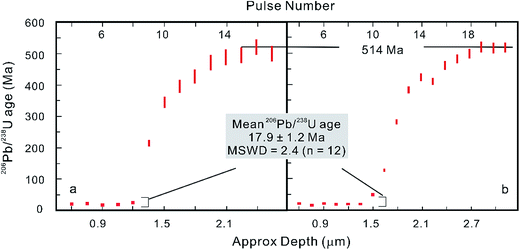 | ||
| Fig. 6 Consecutive laser pulse analyses of two zoned zircon grains are shown in (a) and (b), indicating that LA-MC-ICP-MS with a MIC system can be applied to isotopic depth profile analysis with a high depth resolution of ∼0.1 μm per pulse (modified from ref. 73). | ||
4. Simultaneous analysis of multiple isotope systems
4.1 Overview
Measurement of U–Th–Pb ages, Sr/Nd/Hf isotopic compositions and trace element contents in minerals using SIMS or LA-SC-ICP-MS, and LA-MC-ICP-MS has historically been conducted sequentially, on different volumetric domains (e.g., ref. 9, 10, 20, 56, 120 and 121). Typical analytical protocols involve (1) age determination via SIMS followed by Sr/Nd/Hf isotopic analysis via LA-MC-ICP-MS over the shallow SIMS crater (e.g., ref. 122 for Hf isotopes in zircon), (2) measurement of the age and trace elements by LA-SC-ICP-MS using a relatively small pit, followed by LA-MC-ICP-MS Sr/Nd/Hf isotopic analysis using a large crater placed over the top of the earlier age pit, or (3) placing the LA-MC-ICP-MS ablation for Sr/Nd/Hf isotopic analysis near the age pit, but presumably in the same zone as indicated by cathodoluminescence imagery or similar means (e.g., ref. 123–125 for Hf isotopes in zircon; ref. 20 and 126 for Sr and Nd isotopes). For relatively simple samples, these procedures can produce robust results. However, for complexly zoned or detrital/inherited minerals, modeling different geochemical systems using data generated from different analytical volumes could result in erroneous interpretation, particularly as zonation continues at depth and may not be represented by the cathodoluminescence image of the grain surface. In the three analytical approaches outlined above, two very different sample volumes for the U–Th–Pb age and Sr/Nd/Hf isotope composition are measured, which can lead to de-coupling of the age–isotope system and result in inaccurate initial isotope compositions.15 For example, Harrison et al. (2005)127 dated and determined the Lu–Hf isotopic composition of the >4 billion year old zircons from the Jack Hills metasedimentary belt in Western Australia, a rare and valuable opportunity to elucidate early Earth conditions. Ages were determined using SIMS, on a pit <1 μm deep, while the Hf isotopic composition was determined using LA-MC-ICP-MS with larger spot sizes of 60–80 μm and 1000 times more material analyzed. Extreme heterogeneity in initial εHf (both positive and negative values) was interpreted as reflecting processes of plate tectonics and continental growth on the early Earth. However, later studies by Harrison et al. (2008)128 and Kemp et al. (2009)122 using quasi-simultaneous techniques (see below) revealed a much simpler Lu–Hf evolution for the source materials of the Jack Hills zircons. This emphasizes the importance of simultaneous measurement of multiple isotope systems, an approach which also significantly enhances the analytical throughput and permits analysis of smaller grains that cannot accommodate two analytical spots.1294.2 Quasi-simultaneous analysis
A quasi-simultaneous approach to measure the zircon 207Pb/206Pb age and Hf isotope composition was first reported by Woodhead et al. (2004),130 followed by Harrison et al. (2008)128 and Kemp et al. (2009).122 This method involved alternating cycles during a single ablation (e.g., one cycle for Hf analysis and the next cycle for measurement of Pb isotopes) and employed a 193 nm ArF excimer laser-ablation system coupled to a Nu Instruments MC-ICP-MS. Unfortunately, determination of the U–Pb age was not successful, and because 207Pb/206Pb dating is generally not suitable for Phanerozoic zircons, the applicability of the method was limited to Precambrian grains. For this reason, an improved method was reported by Xia et al. (2011)131 in which quasi-simultaneous determination Hf isotope composition and U–Pb ages of zircon with a Nu Plasma HR MC-ICP-MS was conducted, allowing the concordance of the measured ages to be assessed, Pb loss to be identified, and physical mixing of cores and rims during analysis to be noted. Nevertheless, this alternative approach does not provide authentic simultaneous measurement of both isotopic systems and the precision of both U–Pb age and Hf isotope ratio also appears to be compromised by the relatively short counting times given the requirement for alternating measurement. Additionally, precious analytical time is lost to magnet settling, depending on the collector configuration (e.g., about 25% and 33% in Kemp et al. (2009)122 and Xia et al. (2011)131, respectively).4.3 Laser ablation split stream (LASS) methods
Simultaneous in situ determination of U–Th–Pb age, trace elements, and Sr/Nd/Hf isotopes from a single laser spot can be accomplished by connecting two independent ICP-MS instruments to a single laser (e.g., ref. 12–15, 17, 132 and 133). The ablated aerosol from the sample cell is split downstream into two separate paths using a ‘‘Y’’ shaped three-way connection pipe. In the most common configuration, one path leads to a MC-ICP-MS for measuring Sr/Nd/Hf isotopes or ages, and the other passes to a SC-ICP-MS for U–Th–Pb dating and/or trace element analysis. Appropriately, this method is called laser ablation split stream (LASS). Due to the different concentrations of Sr, Nd, Hf, U, Th and Pb in the analyzed minerals, the proportions of ablated aerosol carried into the two sets of ICP-MSs may need to be adjusted in order to obtain both isotopic compositions and U–Pb ages with high precision. Experimental results have shown that there is no significant element or mass fractionation resulting from splitting the ablated product, or from adjusting the proportions of ablated material between MSs.13,16Many mass spectrometry instrument models (e.g., MC-ICP-MSs including Nu Plasma HR, Nu Plasma II, Thermo Neptune and Neptune Plus; and SC-ICP-MSs including Elan 6100DRC, Agilent 7500a and 7700s, Nu AttoM and Element XR) have been applied in LASS analysis and the most common instrument models and applications are summarized in Table 1.
| Isotope system and the mineral | Instrument model/type | Reference | ||
|---|---|---|---|---|
| MC-ICP-MS | SC/MC-ICP-MS | Laser ablation system | ||
| Lu–Hf (MC) and U–Th–Pb–trace elements (SC) for zircon | Nu Plasma HR | Elan 6100DRC | GeoLas Plus | 12 |
| Lu–Hf (MC) and U–Th–Pb–trace elements (SC) for zircon | Nu Plasma II | Agilent 7700s | RESOlution LR S155 | 17 |
| Lu–Hf (MC) and U–Th–Pb–trace elements (SC) for zircon and baddeleyite | Neptune | Agilent 7500a | GeoLas Plus | 13 |
| Lu–Hf (MC) and U–Th–Pb (SC) for zircon | Neptune Plus | Element XR | Photon Machines Analyte | 14 |
| (1) U–Th–Pb (MC) and trace elements (SC) for zircon and monazite. (2) Lu–Hf (MC) and U–Th–Pb–REE (SC) for zircon | Nu Plasma HR | Nu AttoM | Photon Machines Analyte | 132 |
| Lu–Hf (MC) and U–Th–Pb (SC) for zircon | Neptune | Element 2 | NewWave 213 nm Nd:YAG | 15 |
| Sm–Nd (MC) and U–Th–Pb (SC) for monazite | Neptune | Element XR | GeoLas Pro | 133 |
| U–Th–Pb (MC) and trace elements (SC) for monazite | Nu Plasma HR | Nu AttoM/Agilent 7700s | Photon Machines Analyte | 135 |
| U–Th–Pb (MC) and trace elements (SC) for titanite and zircon | Nu Plasma HR | Agilent 7700x | Photon Machines Analyte | 138 |
| (1) Rb–Sr and Sm–Nd for apatite, perovskite, loparite and eudialyte. (2) Sm–Nd and Lu–Hf for eudialyte and zirconolite | Neptune | Neptune Plus | Photon Machines Analyte | 16 |
| U–Th–Pb (MC) and trace elements (SC) for titanite | Nu Plasma HR | Nu AttoM | Photon Machines Analyte | 139 |
| Sr isotopes (MC) and elemental ratios (SC) for otoliths | Nu Plasma HR | NexION 350D | NWR193 | 190 |
| Sm–Nd (MC) and U–Th–Pb–REE (SC) for monazite | Neptune | Element 2 | NewWave 213 nm Nd:YAG | 149 |
| S and Pb isotopes for pyrite, chalcopyrite, galena and sphalerite | Nu Plasma II | Nu Plasma 1700 | RESOlution M50A | 140 |
Due to its rapid scanning capability, a single collector quadrupole ICP-MS is a better LASS option than a single collector sector field ICP-MS (e.g., Thermo Fisher Element XR) when a large range of masses are required during a single ablation (e.g., U–Th–Pb + trace elements). However, compared with a single quadrupole ICP-MS, a sector field ICP-MS (Element XR) has about 10× higher sensitivity.134 The internal and external reproducibility of isotope composition, element concentration and ratio depend primarily on instrument drift, matrix difference between reference materials and samples, signal stability and signal intensity. Typical uncertainties (2 s) are about 1%, 1–2% and 1–3% for 206Pb/238U ages measured with a MC-ICP-MS, sector field ICP-MS and single quadrupole ICP-MS, respectively,12,13,17,132,135 0.007–0.01% for 176Hf/177Hf,12–14,17 0.01% for 143Nd/144Nd16,133 and 0.015% for 86Sr/87Sr.16 However, the main limitation of simultaneous measurement of multiple isotope systems is that the signal intensity on the individual ICP-MS instruments decreases, compared to that obtained from separate measurements of Sr, Nd, Hf, and U–Pb isotopes and trace elements. Signal intensity can be improved if the He carrier gas is mixed with a small amount of N2 (less than 5 mL min−1) before it enters the ICP.136 When measuring Lu–Hf isotopes on a Neptune instrument, the sensitivity can be improved by a factor of about 1.4 if the MS is equipped with a standard nickel sample cone and a nickel ‘‘X’’ skimmer cone.137 Careful optimization of the make-up gas flow, the carrier gas flow and composition and the proportions of the split between the two MSs is required to obtain optimum precision in all analyses. In addition, laser ablation parameters (including spot size, fluence and frequency) should be optimized because signal intensity also depends on the volume of the ablated material. In fact, not all minerals are suited to the LASS approach due to the limitations of low concentration and potential interference with the isotopes of interest.16 However, single shot-LASS can be used for high resolution depth profiling (about 100–150 nm per pulse) with some sacrifice of precision (e.g., determining the U–Pb age and trace element concentrations in zircon and titanite by Viete et al. (2015)138 and Stearns et al. (2016)139, respectively).
Sulphide deposit formation usually involves multiple mineralization stages, which produce complicated mineral assemblages (e.g., zoned minerals and simple mineral grains originating at different stages of deposit formation). Deconvolving this multi-stage genesis is critical to the generation of effective exploration models and for prospectivity assessment and LASS can play an important role. Recently, Yuan et al. (2018)140 reported that a laser coupled to two MC-ICPMSs was used to conduct simultaneous analysis of S and Pb isotopes of sulfide minerals from a single ablation of pyrite, chalcopyrite, galena, and sphalerite, expanding the scope of LASS application to studies of mineral deposits.
The raw data produced from two sets of ICP-MSs can be reduced separately but recently Fisher et al. (2017)141 introduced a multiple-DRS functionality into the Iolite software (Paton et al., 2011)142 for reduction of datasets collected simultaneously via the LASS technique. This approach allows the researcher to synchronize, visualize, and simultaneously reduce concurrently acquired multi-stream analyses and will vastly improve our ability to efficiently process large quantities of data.
5. Minerals utilized for U–Th–Pb dating and LASS
In situ U–Pb dating, trace element analysis and isotopic analysis are used in geoscience to resolve a wide range of research questions, often in combination. The choice of analytical approach depends on the scientific aims, the mineralogy of samples and the availability of appropriate instrumentation, standards and methodologies. The size of the targets, concentration of parent and daughter isotopes, approximate age and desired precision should also be considered when analytical strategies are being assessed.The common accessory phases zircon and monazite commonly contain high U concentrations and low common lead content. Both have a relatively high U–Pb closure temperature (more than 800 °C for zircon;143 about 750 °C for monazite144) and strong physical and chemical resistance during post-crystallization processes, designating them as priority targets for placing age constraints on high-temperature geological events. Zircon U–Th–Pb–Hf–O isotopic systems and trace element signatures are utilized extensively as zircon is ubiquitous in most rock types.145,146 Accessible to either ion or laser probe techniques, zircon is an ideal mineral for LASS research where age, trace element composition, and Lu–Hf isotopic signatures can be obtained from a single laser spot (25–60 μm), owing to its low concentration of Lu.12–15,17,132,147 Monazite has a high Th content (up to 20% (ref. 148)) and can be utilized for Th–Pb dating. Elemental signatures (i.e., REEs) in complex monazite grains are linked to formation age and can inform the crystallization sequence and metamorphic processes (e.g., ref. 25 and 148). Monazite is suited to LASS for Sm–Nd–U–Th–Pb isotope and trace element analysis and the spot size can be reduced if the concentration of the elements of interest is high enough (the beam diameter is usually 10–60 μm depending on the application) (e.g., ref. 132, 133 and 135). Recently, the Sm–Nd and U–Th–Pb isotope systems and trace element signatures in detrital monazite have been applied to a crustal evolution study, comparing the age and tracer isotope signatures in sediments from two large rivers draining the South China block.149
Other high U minerals suited to U–Th–Pb dating are apatite, titanite (sphene) and rutile, common accessory minerals in natural samples but with relatively high common lead content. The U–Pb closure temperatures are 450–550 °C for apatite,150 650–700 °C for titanite151 and 640–510 °C for rutile,152 and thus their U–Pb ages can constrain mid- to high-temperature geological events, such as metamorphism and hydrothermal alteration (e.g., ref. 153–156). In terms of trace elements, apatite is usually characterized by high Sr and Nd contents (up to several thousand ppm) and extremely low Rb/Sr ratios (normally 87Rb/86Sr < 0.0001).10,157 Therefore, apatite is suited to Sr and Nd isotopic analysis (e.g., ref. 10, 158 and 159) and U–Pb geochronology by LA-MC-ICP-MS (e.g., ref. 45, 46, 56, 157 and 160) and will no doubt be utilized for LASS Nd–Sr–U–Th–Pb isotope and trace element analysis in future. The crystal structure of titanite can accommodate high levels of trace elements including REEs, F, Nb, Ta, Zr, Hf, U, Th, Sr, Sn and Pb,161 making it useful for geochemical and isotopic fingerprinting of geological processes.47,162In situ Sm–Nd isotope analyses of titanite have been conducted using LA-MC-ICP-MS methods (e.g., ref. 163–165). For zoned titanite, high resolution depth profiling with simultaneous measurement of U–Pb isotopes and trace element concentrations using single shot LASS can distinguish between cooling and (re)crystallization ages, and determine the potential for preservation of thermally mediated diffusive loss profiles.138,139 The incorporation of Zr into rutile during formation is strongly temperature-dependent, so rutile can be potentially used for both geochronology and/or Zr-in-Rutile (ZiR) thermometry.166 However, the typically low U content in rutile may limit its applicability to LASS, particularly for small grains.
A serious issue in laser ablation U–Th–Pb dating of apatite, titanite and rutile is the lack of well-characterized matrix-matched reference materials with low common lead. For apatite, several LA-ICP-MS geochronology reference materials with a range of ages are widely available including Durango,167 McClure Mountain,168 Kovdor, Otter Lake and Slyudyanka,45 MAD,56 SDG,49 AP1 and AP2 (ref. 169), and NW-1 (ref. 157). Among these materials, NW-1 apatite, extracted from a carbonatite collected from the Prairie Lake alkaline–carbonatite complex in Ontario, Canada, is probably the best characterized over a range of isotopic systems, and has the lowest common lead content (0.75 ppm, with a 204Pb-based f206 of 0.5–4.4% (ref. 160)). NW-1 has a 206Pb–238U age of 1168.3 ± 4.5 Ma (ref. 157), 143Nd/144Nd ratio of 0.512104 ± 11 and 87Sr/86Sr ratio of 0.702504 ± 19.10 Several titanite age reference materials are widely available including Khan,170 BLR171 and OLT.172 However, the recently characterized MKED1 titanite,162 sampled from the skarn rocks of the Elaine Dorothy Cu–Au–REE prospect at Mount Isa Inlier, Queensland, Australia, contains the lowest levels of common Pb (<0.5 ppm, 206Pb/204Pb > 6000) and is also characterized for 143Nd/144Nd (0.510365 ± 3) and age (206Pb–207Pb age of 1521.02 ± 0.55 Ma). Commonly utilized natural rutile reference materials for LA-ICP-MS geochronology include R10, R19 and Diss,173 R13 and JIMP-1B,174 Sugluk-4 and PCA-S207 (ref. 50), and R632.1 Among these materials, Axelsson et al. (2018)166 reported that R632 has a relatively low common Pb content (<1%; f206% < 1%), a relatively high U content (>300 ppm) and a moderate U–Pb age of 496 ± 3 Ma. Furthermore, the homogeneous and high Zr content of R632 (4294 ± 196 ppm) makes it a suitable reference material for Zr-in-rutile thermometry. These characteristics may facilitate standardization for rutile LASS U–Pb and trace element analysis.
In addition to the minerals outlined above, baddeleyite, allanite, perovskite, eudialyte, xenotime, zirconolite, loparite, columbite–tantalite, bastnaesite, calzirtite, schorlomite, andradite-rich garnet and cassiterite have either been utilized in U–Pb geochronology and/or LASS isotopic analysis, or are potential candidate minerals, although in many cases, matrix matched standards are scarce or not yet available. Example reference materials include Phalaborwa and SK10-2 for baddeleyite,9,175 EM-1 and LE40010 for allanite,176,177 AFK for perovskite,178 LV01 for eudialyte,179 MG-1 and BS-1 for xenotime,180 ZrKA for zirconolite (calzirtite),181 LOP01 for loparite,182 coltan 139 for columbite,183 and K-9 for bastnaesite.10,184,185
Zr-bearing minerals like eudialyte, zirconolite and calziritite are ideally suited for U–Th–Pb dating and Nd–Hf–(Sr) isotopic analysis by LA-(MC)-ICP-MS. Eudialyte, one of a group of complex Na–Ca zirconosilicate minerals that generally occur in peralkaline agpaitic syenites, is the only mineral investigated to date for which it is possible to simultaneously determine U–Pb ages and Sr, Nd and Hf isotopic compositions.179 Huang et al. (2015)16 simultaneously measured Nd–Hf isotopes for eudialyte and zirconolite using two MC-ICP-MS instruments (Neptune and Neptune Plus). The calcium- and titanium-bearing zirconosilicates, zirconolite and calzirtite, also have potential for U–Pb age determination together with Hf–Nd, and possibly Sr, isotopic analysis.181
Yang et al. (2009)186 reported precise in situ U–Pb age, trace element content, and Sr–Nd isotopic analysis of perovskite by LA-(MC)-ICP-MS (Neptune), in order to obtain the age and initial Sr–Nd isotopic compositions of the Menyin kimberlites. The results are significantly different to data obtained on whole rock samples, indicating that the initial Sr–Nd isotopic ratios of whole rocks are likely to record mixed isotopic signatures, due to crustal contamination and/or subsequent alteration. These authors also described in situ analysis of loparite, a perovskite group mineral with extremely low Rb/Sr ratios and high rare earth content, by LA-(MC)-ICP-MS for the determination of U–Pb ages and Sr and Nd isotopic composition.182 Simultaneous measurement of Sr–Nd isotopes for perovskite and loparite can also be performed by LASS.16
Additional ore minerals (bastnaesite, xenotime, columbite–tantalite (coltan) and cassiterite) have been studied for U–Th–Pb dating and determination of Sr or Nd or Hf isotopic composition using LA-(MC)-ICP-MS.10,187 Analysis of an in-house bastnaesite reference material (K-9) first demonstrated that precise and accurate U–Th–Pb ages can be obtained after common Pb correction with a laser or ion probe.10,184,185 The moderate Sr and extremely high Nd contents in bastnaesites, but generally low Rb–Sr ratios, also potentially allow for the precise determination of in situ Sr–Nd isotopic analyses by LA-MC-ICP-MS or LASS. These results will have significant implications for understanding the genesis of endogenous ore deposits and the formation processes related to metallogenic geochronology. Columbite–tantalite (coltan) is characterized by high U and low common Pb contents, making it an ideal mineral for U–Pb isotopic dating of Nb–Ta mineralization. Che et al. (2015)183 used a coltan U–Pb dating method to date the Nanping pegmatite (NP155), an important Nb–Ta deposit in China.
More recently, U–Pb dating of andraditic or Ti-bearing garnet has become attractive, and, combined with trace element data, will potentially provide a significant tracer tool for carbonates, and alkaline or skarn deposits.188–190 Seman et al. (2017)189 first presented U–Pb geochronology data for grossular–andradite garnet using LA-SC-ICP-MS and developed three potential reference materials for LA-ICP-MS. However, the sample investigated had a low U content (<10 ppm), in addition to significant amounts of common Pb. Deng et al. (2017)188 demonstrated U–Pb age determination by LA-SC-ICP-MS for andradite-rich garnet in alkaline igneous rocks and skarn deposits. The consistency between the garnet and zircon U–Pb ages confirmed the reliability and accuracy of garnet U–Pb geochronology. Yang et al. (2018)190 reported the first U–Pb geochronological investigation of schorlomite garnet from carbonatite and alkaline complexes and demonstrated its applicability for U–Pb age determination using LA-ICP-MS due to its relatively high U and Th abundances and negligible common Pb content. Garnet U–Pb geochronology is considered to be a promising new technique for understanding the genesis of carbonatites, alkaline rocks, and related rare-metal deposits.
Spatially resolved elemental and isotopic signatures of biological materials have been used to trace the seasonal growth of organisms. For example, Sr isotopes and elemental ratios were simultaneously measured in otoliths of lenok salmon in order to assess habitat use and migration in a river system.191
6. Summary and future focus
LA-MC-ICP-MS techniques can now provide unprecedented levels of precision and spatial resolution in U–Th–Pb accessory mineral geochronology. The flexibility of the approach and the universality of its application are compounded by a high analytical throughput, compared to other methods (e.g., SIMS). For small minerals or those with fine scale growth domains, consecutive single-pulse-analyses (∼0.1 μm per pulse) and a short ablation time at a low fluence are the choice for ultra-high resolution isotopic mapping and depth profiling. Accuracy and precision of less than 1% for the 206Pb/238U age can be achieved.4,5,7,73The recently developed technique for simultaneous measurement of multiple geochemical systems (LASS) provides geoscientists an opportunity to maintain the integrity of coupled isotopic and geochronological systems while maximizing the amount of data that can be obtained from a single analysis. This approach has proven useful in studies of detrital or metamorphic minerals in areas with complex geological systems that require coupled geochronology, isotopic composition and trace element characterization at high spatial resolution and analytical throughput.
However, some challenges remain in the application of these analytical techniques and future efforts should focus on the following aspects: (1) the procedures for ion counter corrections remain relatively complicated and potentially hinder the broader application of the technique. (2) Matrix effects that limit the accuracy of U–Th–Pb ages can be reduced using fs-LA but can be eliminated if perfectly matrix-matched reference materials are utilized. However, characterization of such reference materials is a challenging and time-consuming process and a simple, broadly applicable correction method would be ideal. Most studies of matrix effects have focused on zircon and perhaps more studies on other minerals are needed. (3) Common lead contamination and interference (Hg) from the plasma gas and carrier gas make it difficult to accurately measure 204Pb and correct for common lead, although this can be partially solved by installing a gold or carbon trap on the gas line or using collision cell gases to remove interference. (4) Normalizing to an accessory mineral reference material without common lead is a popular practice for the correction of mass fractionation. However, apart from the common zircon and monazite reference materials, a reliable reference material without common lead is difficult to find for other accessory minerals. (5) In the application of the LASS technique, the signal intensities measured decrease as the ablated aerosol is divided into two streams for analysis with the instruments. The signal intensities required for reliable measurement of different isotopic systems vary, particularly considering the desired uncertainties in different isotopic ratios (e.g., usually <3% for the 206Pb/238U ratio and about 0.01% for the 176Hf/177Hf ratio). Therefore, those minerals containing lower concentration of target elements (e.g., Lu–Hf, Rb–Sr and Sm–Nd) are currently not candidates for LASS. Enhancing the sensitivity of MC-ICP-MS, for example, by using a modified cone system and a small volume sample cell, adding N2 before the aerosol enters the ICP and enhancing the Faraday detection system with amplifiers equipped with 1012 or 1013 ohm resistors, will improve the flexibility of simultaneous measurement techniques.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the invitation from the editorial board of JAAS to write this review. Two referees are thanked for their constructive comments, which helped to improve the manuscript significantly. This work was supported by the National Natural Science Foundation of China (No. 41473012 and 41525012).References
- J. Walder, I. Platzne and P. A. Freedman, J. Anal. At. Spectrom., 1993, 8, 19–23 RSC.
- M. S. A. Horstwood, G. L. Foster, R. R. Parrish, S. R. Noble and G. M. Nowell, J. Anal. At. Spectrom., 2003, 18, 837–846 RSC.
- M. S. A. Horstwood, J. Košler, G. Gehrels, S. E. Jackson, N. M. McLean, C. Paton, N. J. Pearson, K. Sircombe, P. Sylvesterk, P. Vermeesch, J. F. Bowring, D. J. Condon and B. Schoene, Geostand. Geoanal. Res., 2016, 40, 311–332 CrossRef.
- J. M. Cottle, A. R. C. Kylander-Clark and J. C. Vrijmoe, Chem. Geol., 2012, 332–333, 136–147 CrossRef.
- L. W. Xie, J. H. Yang, Q.-Z. Yin, Y. H. Yang, J. B. Liu and C. Huang, J. Anal. At. Spectrom., 2017, 32, 975–986 RSC.
- R. N. Taylor, T. Warneke, J. A. Milton, I. W. Croudace, P. E. Warwick and R. W. Nesbitt, J. Anal. At. Spectrom., 2003, 18, 480–484 RSC.
- K. Hattori, S. Sakata, M. Tanaka, Y. Orihashic and T. Hirata, J. Anal. At. Spectrom., 2017, 32, 88–95 RSC.
- G. L. Foster and D. Vance, J. Anal. At. Spectrom., 2006, 21, 288–296 RSC.
- F. Y. Wu, Y. H. Yang, L. W. Xie, J. H. Yang and P. Xu, Chem. Geol., 2006, 234, 105–126 CrossRef.
- Y. H. Yang, F. Y. Wu, J. H. Yang, D. M. Chew, L. W. Xie, Z. Y. Chu, Y. B. Zhang and C. Huang, Chem. Geol., 2014, 385, 35–55 CrossRef.
- T. E. Johnson, C. L. Kirkland, D. R. Viete, S. Fischer, S. M. Reddy, G. S. Lister, N. J. Evans and B. J. McDonald, Geosci. Front., 2017, 8, 1469–1478 CrossRef.
- H. L. Yuan, S. Gao, M. N. Dai, C. L. Zong, D. Günther, G. H. Fontaine, X. M. Liu and C. Diwu, Chem. Geol., 2008, 247, 100–118 CrossRef.
- L. W. Xie, Y. B. Zhang, H. H. Zhang, J. F. Sun and F. Y. Wu, Chin. Sci. Bull., 2008, 53, 1565–1573 Search PubMed.
- D. L. Tollstrup, L. W. Xie, J. B. Wimpenny, E. Chin, C. T. Lee and Q. Z. Yin, Geochem., Geophys., Geosyst., 2012, 13, Q03017 CrossRef.
- M. Fisher, J. D. Vervoort and S. A. DuFrane, Geochem., Geophys., Geosyst., 2014, 15, 121–139 CrossRef.
- C. Huang, Y. H. Yang, J. H. Yang and L. W. Xie, J. Anal. At. Spectrom., 2015, 30, 994–1000 RSC.
- C. J. Spencer, A. J. Cavosie, T. D. Raub, H. Roloinson, H. Jeon, M. P. Searle, J. A. Miller, B. J. McDonald and N. J. Evans, Geology, 2017, 45, 975–978 CrossRef.
- J.-I. Kimura, Q. Chang and H. Kawabata, J. Anal. At. Spectrom., 2013, 28, 1522–1529 RSC.
- J.-I. Kimura, T. Takahashi and Q. Chang, J. Anal. At. Spectrom., 2013, 28, 945–957 RSC.
- Y. H. Yang, F. Y. Wu, L. W. Xie, J. H. Yang and Y. B. Zhang, Acta Pet. Sin., 2009, 25, 3431–3441 Search PubMed.
- A. Cocherie and M. Robert, Chem. Geol., 2007, 243, 90–104 CrossRef.
- C. Bouman and J. Schwieters, Scientific, Application Note 30021 of Thermo Fischer Scientific, 2004, 1–6.
- J. M. Koornneef, C. Bouman, J. B. Schwieters and G. R. Davies, Anal. Chim. Acta, 2014, 819, 49–55 CrossRef PubMed.
- B. J. A. Willigers, J. A. Baker, E. J. Krogstad and D. W. Peate, Geochim. Cosmochim. Acta, 2002, 66, 1051–1066 CrossRef.
- G. Foster, H. D. Gibson, R. Parrish, M. Horstwood, J. Fraser and A. Tindle, Chem. Geol., 2002, 191, 183–207 CrossRef.
- J. I. Kimura, Q. Chang, K. Itano, T. Iizuka, B. S. Vaglarova and K. Tanic, J. Anal. At. Spectrom., 2015, 30, 494–505 RSC.
- A. Simonetti, L. M. Heamana, T. Chacko and N. R. Banerjee, Int. J. Mass Spectrom., 2006, 253, 87–97 CrossRef.
- A. Simonetti, L. M. Heaman, R. P. Hartlaub and R. A. Creaser, J. Anal. At. Spectrom., 2005, 20, 677–686 RSC.
- A. Cocherie, C. M. Fanning, P. Jezequel and M. Robert, Geochim. Cosmochim. Acta, 2009, 73, 1095–1108 CrossRef.
- S. Richter, S. Konegger-Kappel, S. F. Boulyga, G. Stadelmann, A. Koepf and H. Siegmund, J. Anal. At. Spectrom., 2016, 31, 1647–1657 RSC.
- S. Richter, S. A. Goldberg, P. B. Mason, A. J. Traina and J. B. Schwieters, Int. J. Mass Spectrom., 2001, 206, 105–127 CrossRef.
- S. M. Nelms, C. R. Quétel, T. Prohaska, J. Vogl and P. D. P. Taylor, J. Anal. At. Spectrom., 2001, 16, 333–338 RSC.
- D. L. Hoffmann, D. A. Richards, T. R. Elliott, P. L. Smart, C. D. Coath and C. J. Hawkesworth, Int. J. Mass Spectrom., 2005, 244, 97–108 CrossRef.
- W. Zhang, Z. C. Hu, L. Yang, Y. S. Liu, K. Q. Zong, H. J. Xu, H. H. Chen, S. Gao and L. Xu, Geostand. Geoanal. Res., 2015, 39, 467–487 CrossRef.
- A. A. Van Heuzen, T. Hoekstra and B. van Wingerden, J. Anal. At. Spectrom., 1989, 4, 483–489 RSC.
- G. P. Russ III in Applications of Inductively Coupled Plasma Mass Spectrometry, ed. A. R. Date and A. L. Gray, Blackie, Glasgow, 1989, ch. 4 Search PubMed.
- A. Held and P. Taylor, J. Anal. At. Spectrom., 1999, 14, 1075–1079 RSC.
- J. P. Valles Mota, J. R. Encinar, M. R. Fernández de la Campa, J. I. Garcia Alonso and A. Sanz-Medel, J. Anal. At. Spectrom., 1999, 14, 1467–1473 RSC.
- S. Richter, A. Alonso, Y. Aregbe, R. Eykens, F. Kehoe, H. Kühn, N. Kivel, A. Verbruggen, R. Wellum and P. D. P. Taylor, Int. J. Mass Spectrom., 2009, 281, 115–125 CrossRef.
- T. Hirata, T. Iizuka and Y. Orihashi, J. Anal. At. Spectrom., 2005, 20, 696–701 RSC.
- C. D. Storey, T. E. Jeffries and M. Smith, Chem. Geol., 2006, 227, 37–52 CrossRef.
- A. K. Souders and P. J. Sylvester, J. Anal. At. Spectrom., 2008, 23, 535–543 RSC.
- G. E. Gehrels, V. A. Valencia and J. Ruiz, Geochem., Geophys., Geosyst., 2008, 9, 1–13 CrossRef.
- F. Tera and G. J. Wasserburg, Earth Planet. Sci. Lett., 1972, 14, 281–304 CrossRef.
- D. M. Chew, P. J. Sylvester and M. N. Tubrett, Chem. Geol., 2011, 280, 200–216 CrossRef.
- D. M. Chew, J. A. Petrus and B. S. Kamber, Chem. Geol., 2014, 363, 185–199 CrossRef.
- C. L. Kirkland, J. Hollis, M. Danišík, J. Peterson, N. J. Evans and B. McDonald, Precambrian Res., 2017, 300, 107–120 CrossRef.
- N. R. Banerjee, A. Simonetti, H. Furnes, K. Muehlenbachs, H. Staudigel, L. Heaman and M. J. Van Kranendonk, Geology, 2007, 35, 487–490 CrossRef.
- H. Y. Zhou, J. Z. Geng, Y. R. Cui, H. K. Li and H. M. Li, Acta Geosci. Sin., 2012, 33, 857–864 Search PubMed.
- L. Bracciali, R. R. Parrish, M. S. A. Horstwood, D. J. Condon and Y. Najman, Chem. Geol., 2013, 347, 82–101 CrossRef.
- K. R. Ludwig, Geochim. Cosmochim. Acta, 1998, 62, 665–676 CrossRef.
- I. S. Williams, U–Th–Pb geochronology by ion microprobe, in Applications of microanalytical techniques to understanding mineralizing process, Reviews in Economic Geology, ed. M. A. McKibben, W. C. Shanks III and W. I. Ridley, 1998, vol. 7, pp. 1–35. Search PubMed.
- J. S. Stacey and J. D. Kramers, Earth Planet. Sci. Lett., 1975, 26, 207–221 CrossRef.
- C. Lana, F. Farina, A. Gerdes, A. Alkmim, G. Gonçalves and A. C. Jardim, J. Anal. At. Spectrom., 2017, 32, 2011–2023 RSC.
- A. Cocherie and M. Robert, Gondwana Res., 2008, 14, 597–608 CrossRef.
- S. N. Thomson, G. E. Gehrels and J. Ruiz, Geochem., Geophys., Geosyst., 2012, 13, Q0AA21, DOI:10.1029/2011GC003928.
- K. Ludwig, Isoplot/Ex, rev. 2.49, A Geochronological Toolkit for Microsoft Excel, Berkeley Geochronology Center, Berkeley, CA, USA, 2001, Special Publication No. 1a Search PubMed.
- Q. L. Li, X. H. Li, Z. W. Lan, C. L. Guo, Y. N. Yang, Y. Liu and G. Q. Tang, Contrib. Mineral. Petrol., 2013, 166, 65–80 CrossRef.
- T. Zack, D. Stockli, G. Luvizotto, M. Barth, E. Belousova, M. Wolfe and R. Hinton, Contrib. Mineral. Petrol., 2011, 162, 515–530 CrossRef.
- I. Horn, R. L. Rudnick and W. F. McDonough, Chem. Geol., 2000, 164, 281–301 CrossRef.
- H. P. Longerich, D. Günther and S. E. Jackson, Fresenius' J. Anal. Chem., 1996, 355, 538–542 Search PubMed.
- J. Košler and P. J. Sylvester, Rev. Mineral. Geochem., 2003, 53, 243–275 CrossRef.
- M. Tiepolo, Chem. Geol., 2003, 199, 159–177 CrossRef.
- S. E. Jackson, N. J. Pearson, W. L. Griffin and E. A. Belousova, Chem. Geol., 2004, 211, 47–69 CrossRef.
- C. Paton, J. D. Woodhead, J. C. Hellstrom, J. M. Hergt, A. Greig and R. Maas, Geochem., Geophys., Geosyst., 2010, 11, Q0AA06, DOI:10.1029/2009GC002618.
- S. M. Eggins, L. P. J. Kinsley and J. M. G. Shelley, Appl. Surf. Sci., 1998, 127–129, 278–286 CrossRef.
- J. Košler, H. Fonneland, P. Sylvester, M. Tubrett and R. B. Pedersen, Chem. Geol., 2002, 182, 605–618 CrossRef.
- J. Košler, M. Wiedenbeck, R. Wirth, J. Hovorka, P. Sylvester and J. Míková, J. Anal. At. Spectrom., 2005, 20, 402–409 RSC.
- R. Hergenröder, J. Anal. At. Spectrom., 2006, 21, 505–516 RSC.
- I. Kroslakova and D. Günther, J. Anal. At. Spectrom., 2007, 22, 51–62 RSC.
- H. L. Yuan, S. Gao, X. M. Liu, H. M. Li, D. Günther and F. Y. Wu, Geostand. Geoanal. Res., 2004, 28, 353–370 CrossRef.
- S. Johnston, G. Gehrels, V. Valencia and J. Ruiz, Chem. Geol., 2009, 259, 218–229 CrossRef.
- J. M. Cottle, M. S. A. Horstwood and R. R. Parrish, J. Anal. At. Spectrom., 2009, 24, 1355–1363 RSC.
- M. Wiedenbeck, P. Alle, F. Corfu, W. L. Griffin, M. Meier, F. Oberli, A. Von Quadt, J. C. Roddick and W. Spiegel, Geostand. Newsl., 1995, 19, 1–23 CrossRef.
- S. Zhang, M. He, Z. Yin, E. Zhu, W. Hang and B. Huang, J. Anal. At. Spectrom., 2016, 31, 358–382 RSC.
- J. Pisonero and D. Günther, Mass Spectrom. Rev., 2008, 27, 609–623 CrossRef PubMed.
- C. Schäfer, H. M. Urbassek and L. V. Zhigilei, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 2–70 CrossRef.
- M. E. Shaheen, J. E. Gagnon and B. J. Fryer, Spectrochim. Acta, Part B, 2015, 107, 97–109 CrossRef.
- F. Poitrasson, X. Mao, S. S. Mao, R. Freydier and R. E. Russo, Anal. Chem., 2003, 75, 6184–6190 CrossRef PubMed.
- F. Poitrasson and F. X. d'Abzac, J. Anal. At. Spectrom., 2017, 32, 1075–1091 RSC.
- K. P. Jochum, B. Stoll, U. Weis, D. E. Jacob, R. Mertz-Kraus and M. O. Andreae, Geostand. Geoanal. Res., 2014, 38, 265–292 CrossRef.
- Z. Li, Z. C. Hu, Y. S. Liu, S. Gao, M. Li, K. Q. Zong, H. H. Chen and S. H. Hu, Chem. Geol., 2015, 400, 11–23 CrossRef.
- I. Horn and F. von Blanckenburg, Spectrochim. Acta, Part B, 2007, 62, 410–422 CrossRef.
- J. I. Kimura, Q. Chang and K. Tani, Geochem. J., 2011, 45, 283–296 CrossRef.
- M. Ohata, D. Tabersky, R. Glaus, J. Koch, B. Hattendorf and D. Günther, J. Anal. At. Spectrom., 2014, 29, 1345–1353 RSC.
- M. Ohata, N. Nonose, L. Dorta and D. Günther, Anal. Sci., 2015, 31, 1309–1315 CrossRef PubMed.
- J. Koch, M. Walle, J. Pisonero and D. Günther, J. Anal. At. Spectrom., 2006, 21, 932–940 RSC.
- R. Le Harzic, N. Huot, E. Audouard, C. Jonin, P. Laporte, S. Valette, A. Fraczkiewicz and R. Fortunier, Appl. Phys. Lett., 2002, 80, 3886–3888 CrossRef.
- F. X. d'Abzac, A. M. Seydoux-Guillaume, J. Chmeleff, L. Datas and F. Poitrasson, J. Anal. At. Spectrom., 2012, 27, 108–119 RSC.
- R. Glaus, R. Kaegi, F. Krumeich and D. Günther, Spectrochim. Acta, Part B, 2010, 65, 812–822 CrossRef.
- D. Günther and B. Hattendorf, Trends Anal. Chem., 2005, 24, 255–265 CrossRef.
- J. F. Sun, J. H. Yang, F. Y. Wu, L. W. Xie, Y. H. Yang, Z. C. Liu and X. H. Li, Chin. Sci. Bull., 2012, 57, 2506–2516 CrossRef.
- U. Klötzli, E. Klötzli, Z. Günes and J. Košler, Geostand. Geoanal. Res., 2009, 33, 5–15 CrossRef.
- L. Black, S. Kamo, C. Allen, D. Davis, J. Aleinikoff, J. Valley, R. Mundil, I. Campbell, R. Korsch, I. Williams and C. Foudoulis, Chem. Geol., 2004, 205, 115–140 CrossRef.
- J. Mikova, J. Košler, H. Longerich, M. Wiedenbeck and J. Hanchar, J. Anal. At. Spectrom., 2009, 24, 1244–1252 RSC.
- E. Kooijman, J. Berndt and K. Mezger, Eur. J. Mineral., 2012, 24, 5–21 CrossRef.
- C. Allen and I. Campbell, Chem. Geol., 2012, 332–333, 157–165 CrossRef.
- A. Steely, J. Hourigan and E. Juel, Chem. Geol., 2014, 372, 92–108 CrossRef.
- E. Marillo-Sialer, J. Woodhead, J. Hergt, A. Greig, M. Guillong, A. Gleadow, N. Evans and C. Paton, J. Anal. At. Spectrom., 2014, 29, 981–989 RSC.
- R. Ewing, Rev. Mineral. Geochem., 2003, 53, 387–425 CrossRef.
- M. Klinger, U. Kempe, A. Pöpl, R. Böttcher and M. Trinkler, Eur. J. Mineral., 2012, 24, 1005–1016 CrossRef.
- E. Marillo-Sialer, J. Woodhead, J. M. Hanchar, S. M. Reddy, A. Greig, J. Hergt and B. Kohna, Chem. Geol., 2016, 438, 11–24 CrossRef.
- R. Finch and J. Hanchar, in Structure and chemistry of zircon and zircon-group minerals, ed. J. M. Hanchar and P. Hoskin, Zircon. Mineralogical Society of America, Washington, DC, 2003, pp. 1–21 Search PubMed.
- J. Thompson, S. Meffre and L. Danyushevsky, J. Anal. At. Spectrom., 2018, 33, 221–230 RSC.
- L. Nasdala, G. Irmer and D. Wolf, Eur. J. Mineral., 1995, 7, 471–478 CrossRef.
- L. Nasdala, P. W. Reiners, J. I. Garver, A. K. Kennedy, R. A. Stern, E. Balan and R. Wirth, Am. Mineral., 2004, 89, 219–231 CrossRef.
- P. Vermeesch, Earth Planet. Sci. Lett., 2004, 224, 441–451 CrossRef.
- M. Barham, S. Reynolds, C. L. Kirkland, M. J. O'Leary, N. J. Evans, H. Allen, P. W. Haines, R. M. Hocking and B. J. McDonald, Gondwana Res., 2018, 58, 122–140 CrossRef.
- V. Markwitz, C. L. Kirkland, K. H. Wyrwoll, L. Hancock, N. J. Evans and Y. Lu, Tectonics, 2017, 36, 2477–2496 CrossRef.
- A. von Quadt, D. Gallhofer, M. Guillong, I. Peytcheva, M. Waelle and S. Sakata, J. Anal. At. Spectrom., 2014, 29, 1618–1629 RSC.
- Q. Crowley, R. Key and S. Noble, Gondwana Res., 2015, 27, 1381–1391 CrossRef.
- L. A. Solari, C. Ortega-Obregón and J. P. Bernal, Chem. Geol., 2015, 414, 109–123 CrossRef.
- A. K. Schmitt, K. R. Chamberlain, S. M. Swapp and T. M. Harrison, Chem. Geol., 2010, 269, 386–395 CrossRef.
- V. A. Valencia, J. Ruiz, F. Barra, G. Geherls, M. Ducea, S. R. Titley and L. Ochoa-Landin, Miner. Deposita, 2005, 40, 175–191 CrossRef.
- J. K. Vry and J. A. Baker, Geochim. Cosmochim. Acta, 2006, 70, 1807–1820 CrossRef.
- B. Bühn, M. M. Pimentel, M. Matteini and E. Dantas, An. Acad. Bras. Cienc., 2009, 81, 99–114 CrossRef.
- L. M. Florisbal, V. A. Janasi, M. F. Bitencourt and L. M. Heaman, Precambrian Res., 2012, 216–219, 132–151 CrossRef.
- M. Ibanez-Mejia, G. E. Gehrels, J. Ruiz, J. D. Vervoort, M. P. Eddy and C. Li, Chem. Geol., 2014, 384, 149–167 CrossRef.
- J. Sláma, J. Košler, D. Condon, J. Crowley, A. Gerdes, J. Hanchar, M. Horstwood, G. Morris, L. Nasdala, N. Norberg, U. Schaltegger, B. Schoene, M. Tubrett and M. J. Whitehouse, Chem. Geol., 2008, 249, 1–35 CrossRef.
- X. H. Li, X. Liang, M. Sun, Y. Liu and X. Tu, Eur. J. Mineral., 2000, 12, 1015–1024 CrossRef.
- W. C. McClelland, J. A. Gilotti, F. K. Mazdab and J. L. Wooden, Eur. J. Mineral., 2009, 21, 1135–1148 CrossRef.
- A. I. S. Kemp, G. L. Foster, A. Scherstén, M. J. Whitehouse, J. Darling and C. Storey, Chem. Geol., 2009, 261, 244–260 CrossRef.
- Y. B. Wu, Y. F. Zheng, Z. F. Zhao, B. Gong, X. Liu and F. Y. Wu, Geochim. Cosmochim. Acta, 2006, 70, 3743–3761 CrossRef.
- W. L. Griffin, N. J. Pearson, E. Belousova, S. E. Jackson, E. van Achterbergh, S. Y. O'Reilly and S. R. Shee, Geochim. Cosmochim. Acta, 2000, 64, 133–147 CrossRef.
- T. Iizuka, T. Komiya, S. P. Johnson, Y. Kon, S. Maruyama and T. Hirata, Chem. Geol., 2009, 259, 230–239 CrossRef.
- T. Iizuka, O. Nebel and M. T. Mcculloch, Earth Planet. Sci. Lett., 2011, 308, 350–358 CrossRef.
- T. M. Harrison, J. Blichert-Toft, W. Muller, F. Albarède, P. Holden and S. J. Mojzsis, Science, 2005, 310, 1947 CrossRef PubMed.
- T. M. Harrison, A. K. Schmitt, M. T. McCulloch and O. M. Lovera, Earth Planet. Sci. Lett., 2008, 268, 476–486 CrossRef.
- W. Q. Ji, F. Y. Wu, S. L. Chung, J. X. Li and C. Z. Liu, Chem. Geol., 2009, 262, 229–245 CrossRef.
- J. D. Woodhead, J. M. Hergt, M. Shelley, S. Eggins and R. Kemp, Chem. Geol., 2004, 209, 121–135 CrossRef.
- X. P. Xia, M. Sun, H. Y. Geng, Y. L. Sun, Y. J. Wang and G. C. Zhao, J. Anal. At. Spectrom., 2011, 26, 1868–1871 RSC.
- A. R. C. Kylander-Clark, B. R. Hacker and J. M. Cottle, Chem. Geol., 2013, 345, 99–112 CrossRef.
- D. J. Goudie, C. M. Fisher, J. M. Hanchar, J. L. Crowley and J. C. Ayers, Geochem., Geophys., Geosyst., 2014, 15, 2575–2600 CrossRef.
- M. Wälle and C. A. Heinrich, J. Anal. At. Spectrom., 2014, 29, 1052–1057 RSC.
- B. R. Hacker, A. R. C. Kylander-Clark, R. Holder, T. B. Andersen, E. M. Peterman, E. O. Walsh and J. K. Munnikhuis, Chem. Geol., 2015, 409, 28–41 CrossRef.
- M. Shaheen and B. J. Fryer, J. Anal. At. Spectrom., 2010, 25, 1006–1013 RSC.
- Z. Hu, Y. Liu, S. Gao, S. Xiao, L. Zhao, D. Günther, M. Li, W. Zhang and K. Zong, Spectrochim. Acta, Part B, 2012, 78, 50–57 CrossRef.
- D. R. Viete, A. R. C. Kylander-Clark and B. R. Hacker, Chem. Geol., 2015, 415, 70–86 CrossRef.
- M. A. Stearns, J. M. Cottle, B. R. Hacker and A. R. C. Kylander-Clark, Chem. Geol., 2016, 422, 13–24 CrossRef.
- H. L. Yuan, X. Liu, L. Chen, Z. Bao, K. Y. Chen, C. L. Zong, X. C. Li and J. W. Qiu, J. Asian Earth Sci., 2018, 154, 386–396 CrossRef.
- C. M. Fisher, C. Paton, D. G. Pearson, C. Sarkar, Y. Luo, D. B. Tersmette and T. Chacko, Geochem., Geophys., Geosyst., 2017, 18, 4604–4622 CrossRef.
- C. Paton, J. Hellstrom, B. Paul, J. Woodhead and J. Hergt, J. Anal. At. Spectrom., 2011, 26, 2508–2518 RSC.
- D. J. Cherniak and E. B. Watson, Chem. Geol., 2001, 172, 5–24 CrossRef.
- H. A. Smith and B. J. Giletti, Geochim. Cosmochim. Acta, 1997, 61, 1047–1055 CrossRef.
- Y. F. Zheng, Z. F. Zhao, Y. B. Wu, S. B. Zhang, X. M. Liu and F. Y. Wu, Chem. Geol., 2006, 231, 135–158 CrossRef.
- J. H. Yang, F. Y. Wu, J. A. Shao, S. A. Wilde, L. W. Xie and X. M. Liu, Earth Planet. Sci. Lett., 2006, 246, 336–352 CrossRef.
- R. X. Chen, Y. F. Zheng and L. W. Xie, Lithos, 2010, 114, 132–154 CrossRef.
- M. J. Kohn and M. A. Malloy, Geochim. Cosmochim. Acta, 2004, 68, 101–113 CrossRef.
- X. C. Liu, Y. B. Wu, C. M. Fisher, J. M. Hanchar, L. Beranek, S. Gao and H. Wang, Geology, 2017, 45, 103–106 CrossRef.
- D. J. Cherniak, W. A. Lanford and F. J. Ryerson, Geochim. Cosmochim. Acta, 1991, 55, 1663–1673 CrossRef.
- D. J. Scott and M. R. St-Onge, Geology, 1995, 23, 1123–1126 CrossRef.
- E. Kooijman, K. Mezger and J. Berndt, Earth Planet. Sci. Lett., 2010, 293, 321–330 CrossRef.
- B. R. Frost, K. R. Chamberlain and J. C. Schumacher, Chem. Geol., 2000, 172, 131–148 CrossRef.
- H. Timmermann, V. Štědrá, A. Gerdes, S. R. Noble, R. R. Parrish and W. Dörr, J. Petrol., 2004, 45, 1311–1338 CrossRef.
- B. Schoene and S. A. Bowring, Geochim. Cosmochim. Acta, 2007, 71, 165–185 CrossRef.
- T. A. Ewing, J. Hermann and D. Rubatto, Contrib. Mineral. Petrol., 2013, 165, 757–779 CrossRef.
- F. Y. Wu, R. H. Mitchell, Q. L. Li, C. Zhang and Y. H. Yang, Geol. Mag., 2017, 154, 217–236 CrossRef.
- M. S. A. Horstwood, J. A. Evans and J. Montgomery, Geochim. Cosmochim. Acta, 2008, 72, 5659–5674 CrossRef.
- A. L. Henderson, G. L. Foster and Y. Najman, Earth Planet. Sci. Lett., 2010, 297, 42–49 CrossRef.
- Q. L. Li, X. H. Li, F. Y. Wu, Q. Z. Yin, H. M. Ye, Y. Liu, G. Q. Tang and C. L. Zhang, Gondwana Res., 2012, 21, 745–756 CrossRef.
- M. Tiepolo, R. Oberti and R. Vannucci, Chem. Geol., 2002, 191, 105–119 CrossRef.
- C. Spandler, J. Hammerli, P. Sha, H. Hilbert-Wolf, Y. Hu, E. Roberts and M. Schmitz, Chem. Geol., 2016, 425, 110–126 CrossRef.
- Y. H. Yang, J. F. Sun, L. W. Xie, H. R. Fan and F. Y. Wu, Chin. Sci. Bull., 2008, 53, 1062–1070 Search PubMed.
- C. M. Fisher, C. R. M. McFarlane, J. M. Hanchar, M. D. Schmitz, P. J. Sylvester, R. Lam and H. P. Longerich, Chem. Geol., 2011, 284, 1–20 CrossRef.
- J. Hammerli, A. I. S. Kemp and C. Spandler, Earth Planet. Sci. Lett., 2014, 392, 133–142 CrossRef.
- E. Axelsson, J. Pape, J. Berndt, F. Corfu, K. Mezger and M. M. Raith, Geostand. Geoanal. Res., 2018, 42, 319–338 CrossRef.
- F. W. McDowell, W. C. McIntosh and K. A. Farley, Chem. Geol., 2005, 214, 249–263 CrossRef.
- B. Schoene and S. A. Bowring, Contrib. Mineral. Petrol., 2006, 151, 615–630 CrossRef.
- Q. Zhou, In situ U-Pb isotopic dating of accessory minerals in meteorites, Ph. D. Dissertation, University of Chinese Academy of Sciences and Institute of geology and geophysics, Chinese Academy of Sciences(Supervisor of Prof. Fu-Yuan Wu. Chapter 2: 19-22 (in Chinese with English abstract)), 2013.
- P. D. Kinny, N. J. McNaughton, C. M. Fanning and R. Maas, ICOG8, US Geol. Surv. Circ., Berkeley, 1994, vol. 1107, p. 171 Search PubMed.
- J. N. Aleinikoff, R. P. Wintsch, R. P. Tollo, D. M. Unruh, C. M. Fanning and M. D. Schmitz, Am. J. Sci., 2007, 307, 63–118 CrossRef.
- A. K. Kennedy, S. L. Kamo, L. Nasdala and N. E. Timms, Can. Mineral., 2010, 48, 1423–1443 CrossRef.
- G. L. Luvizotto, T. Zack, H. P. Meyer, T. Ludwig, S. Triebold, A. Kronz, C. Münker, D. F. Stockli, S. Prowatke, S. Klemme, D. E. Jacob and H. von Eynatten, Chem. Geol., 2009, 261, 346–369 CrossRef.
- A. K. Schmitt and T. Zack, Chem. Geol., 2012, 332–333, 65–73 CrossRef.
- I. Horn, W. F. McDonough and R. L. Rudnick, Abstract of Ninth Goldschimdt conference, 1999, p. 7646 Search PubMed.
- D. Rubatto, D. Regis, J. Hermann, K. Boston, M. Engi, M. Beltrando and S. R. McAlpine, Nat. Geosci., 2011, 4, 338–342 CrossRef.
- A. J. Smye, N. M. Roberts, D. J. Condon, M. S. Horstwood and R. R. Parrish, Geochim. Cosmochim. Acta, 2014, 135, 1–28 CrossRef.
- F. Y. Wu, A. A. Arzamastsev, R. H. Mitchell, Q. L. Li, J. Sun, Y. H. Yang and R. C. Wang, Chem. Geol., 2013, 353, 210–229 CrossRef.
- F. Y. Wu, Y. H. Yang, M. A. W. Marks, Z. C. Liu, Q. Zhou, W. C. Ge, J. S. Yang, Z. F. Zhao, R. H. Mitchell and G. Markl, Chem. Geol., 2010, 273, 8–34 CrossRef.
- I. R. Fletcher, N. J. McNaughton, J. A. Aleinikoff, B. Rasmussen and S. L. Kamo, Chem. Geol., 2004, 209, 295–314 CrossRef.
- F. Y. Wu, Y. H. Yang, R. H. Mitchell, F. Bellatreccia, Q. L. Li and Z. F. Zhao, Chem. Geol., 2010, 277, 178–195 CrossRef.
- R. H. Mitchell, F. Y. Wu and Y. H. Yang, Chem. Geol., 2011, 280, 191–199 CrossRef.
- X. D. Che, F. Y. Wu, R. C. Wang, A. Gerdesc, W. Q. Ji, Z. H. Zhao, J. H. Yang and Z. Y. Zhu, Ore Geol. Rev., 2015, 65, 979–989 CrossRef.
- E. B. Sal'nikova, S. Z. Yakovleva, A. V. Nikiforov, A. B. Kotov, V. V. Yarmolyuk, I. V. Anisimova, A. M. Sugorakova and Y. V. Plotkina, Dokl. Earth Sci., 2010, 430, 134–136 CrossRef.
- X. X. Ling, Q. L. Li, Y. Liu, Y. H. Yang, Y. Liu, G. Q. Tang and X. H. Li, J. Anal. At. Spectrom., 2016, 31, 1680–1687 RSC.
- Y. H. Yang, F. Y. Wu, S. A. Wilde, X. M. Liu, Y. B. Zhang, L. W. Xie and J. H. Yang, Chem. Geol., 2009, 264, 24–42 CrossRef.
- Z. C. Liu, F. Y. Wu, C. L. Guo, Z. F. Zhao, J. H. Yang and J. F. Sun, Chin. Sci. Bull., 2011, 56, 2948–2956 CrossRef.
- X. D. Deng, J. W. Li, T. Luo and H. Q. Wang, Contrib. Mineral. Petrol., 2017, 172, 71–81 CrossRef.
- S. Seman, D. F. Stockli and N. M. McLean, Chem. Geol., 2017, 460, 106–116 CrossRef.
- Y. H. Yang, F. Y. Wu, J. H. Yang, R. H. Mitchell, Z. F. Zhao, L. W. Xie, C. Huang, Q. Ma, M. Yang and H. Zhao, J. Anal. At. Spectrom., 2018, 33, 231–239 RSC.
- T. Prohaska, J. Irrgeher and A. Zitek, J. Anal. At. Spectrom., 2016, 31, 1612–1621 RSC.
| This journal is © The Royal Society of Chemistry 2018 |